Dielectric properties of water under extreme conditions and transport of carbonates in the deep Earth

Abstract

Water is a major component of fluids in the Earth’s mantle, where its properties are substantially different from those at ambient conditions. At the pressures and temperatures of the mantle, experiments on aqueous fluids are challenging, and several fundamental properties of water are poorly known; e.g., its dielectric constant has not been measured. This lack of knowledge of water dielectric properties greatly limits our ability to model water–rock interactions and, in general, our understanding of aqueous fluids below the Earth’s crust. Using ab initio molecular dynamics, we computed the dielectric constant of water under the conditions of the Earth’s upper mantle, and we predicted the solubility products of carbonate minerals. We found that MgCO₃ (magnesite)—insoluble in water under ambient conditions—becomes at least slightly soluble at the bottom of the upper mantle, suggesting that water may transport significant quantities of oxidized carbon. Our results suggest that aqueous carbonates could leave the subducting lithosphere during dehydration reactions and could be injected into the overlying lithosphere. The Earth’s deep carbon could possibly be recycled through aqueous transport on a large scale through subduction zones.

Water, a major component of fluids in the Earth’s mantle (1, 2), is expected to play a substantial role in hydrothermal reactions occurring in the deep Earth at supercritical conditions (3, 4). Pressure (P) and temperature (T) increase with increasing depth (5) and at ∼400 km, where seismic discontinuities define the bottom boundary of the upper mantle, the pressure can reach ∼13 GPa and the temperature can be as high as 1,700 K (6–8). In this regime the properties of water and thus of aqueous fluids are remarkably different from those at ambient conditions. For example, water has an unusually large static dielectric constant ε₀ ∼ 78 at ambient conditions; however, at the vapor–liquid critical point at 647 K, ε₀ deceases to less than 10 (9), implying that ion–water interactions in solution are greatly modified. In turn these changes affect the solubility of minerals and hence chemical reactions occurring in aqueous solutions under pressure (10, 11).

Measurements of the dielectric constant of water date back to the 1890s (12), but they are still limited to P < 0.5 GPa and T < 900 K, corresponding to crustal metamorphic conditions. Indeed, it is challenging to measure ε₀ at high P and T because water becomes highly corrosive (11). Several models correlating experimental data suggested extrapolations of ε₀ to ∼1 GPa and ∼1,300 K (e.g., refs. 13–15), which corresponds to only very shallow mantle conditions under the oceans; however, deeper mantle conditions relevant to plate tectonic processes could not be reached and different extrapolations showed poor agreement with each other (1). The current lack of knowledge of the dielectric constant of water under the P and T of the mantle hampers our ability to model water–rock interactions, to study the solubility of minerals, and hence our understanding of geochemical processes involving aqueous fluids below the Earth’s crust.

We computed the dielectric constant of hot, compressed water using ab initio calculations (16, 17) with semilocal density functionals (18) and used our results to predict the solubility of carbonates in the Earth’s upper mantle, well into subduction zones. We predict that MgCO₃—an important mineral stable in the mantle up to 82 GPa (19) and insoluble in water at ambient conditions—becomes slightly soluble, at least millimolal levels at ∼10 GPa and 1,000 K. This result suggests that aqueous fluids may be carbon hosts and transport carbonate in the deep Earth, with important implications for the dynamics of the global carbon cycle (20, 21). We validated our results at lower pressure, by comparing them with solubility data for calcite, finding good agreement with experiment. Our ab initio simulations open the way to studying the solubility of minerals at conditions beyond the reach of current experiments in the Earth’s mantle. They also give insight into the basic physical properties of water under extreme conditions. In particular, we carried out an analysis of the variation of the water dielectric properties under pressure, showing remarkable variations of the molecular dipole moment but modest changes in the Kirkwood factor (22), which accounts for hydrogen-bonding correlations.

Results

Equation of State of Water Under Pressure.

As a first step of our investigation, we validated the description of the equation of state of water under pressure provided by density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional (18). We previously used the same level of theory to investigate dissociation of water under pressure (17, 23, 24) and the ice-melting line (25). Details of our calculations are given in Methods. In Table 1, we compare the calculated pressures for several densities at 1,000 and 2,000 K, with those obtained by widely used models in the geochemistry community, e.g., in refs. 2 and 26. Zhang and Duan (26) showed that the simple point charge extended (SPC/E) water model (27) reproduces experimental equation of state (EOS) data with an accuracy of less than 1%, for P up to 5.0 GPa. Not surprisingly, the results of our SPC/E molecular dynamics (MD) simulations are in good agreement with the EOS data of ref. 26. However, ab initio calculations predict larger pressures than SPC/E, in better agreement with the EOS obtained by Zhang and Duan (2) in 2009, which was designed to reproduce the properties of C-O-H fluids in the Earth mantle. Note that EOS experimental data are limited to P < 5 GPa; refs. 2 and 26 are in good agreement with ab initio result at ∼1 GPa and 1,000 K. However, the difference between DFT-PBE and SPC/E results, including the data in ref. 26, is substantial for P > 5 GPa at 1,000 K, whereas the agreement is good at 2,000 K. As for ref. 2, above 5 GPa, at 1,000 K it yields almost identical pressure to our ab initio calculation at ∼11.4 GPa, whereas at 2,000 K it overestimates the pressure by about 1 GPa. Hence results above 5 GPa reported in refs. 2 and 26 should be treated with caution. Overall, the comparison between our ab initio results and those of available EOS is satisfactory and we conclude the PBE functional (18) may be used to predict the dielectric constant of water under pressure.

Table 1.

Equation of state data of water under pressure as obtained from models and simulations

T, K	, g/cm3	P*, GPa	P†, GPa	P‡, GPa	P§, GPa
1,000	0.88	0.91	0.93	0.91 (0.04)	1.1 (0.2)
	1.32	4.48	5.00	4.44 (0.08)	5.8 (0.6)
	1.57	9.49	11.5	9.78 (0.11)	11.4 (0.4)
2,000	1.13	4.80	5.00	4.71 (0.15)	5.2 (0.5)
	1.36	8.93	10.0	8.80 (0.25)	8.9 (1.0)

Within parentheses we report the SDs of the data obtained in our simulations (P, pressure; , density; T, temperature).

^*Ref. 26.

^†Ref. 2.

^‡This work, MD simulations with the SPC/E potential.

^§This work, ab initio MD simulations with the PBE functional.

Dielectric Constants.

We calculated the static dielectric constant at the conditions reported in Table 1. Using periodic boundary conditions, for an isotropic and homogeneous fluid, ε₀ may be obtained from the fluctuations of the total dipole moment M, using the equation (28, 29)

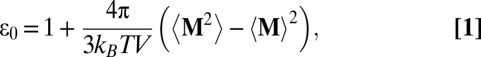where k_B is the Boltzmann constant, and T and V are the temperature and volume of the MD simulation. The angled brackets represent ensemble averages.

In our ab initio simulations, we computed M as the sum of dipole moments of each water molecule 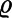, where R_O, R_H1, and R_H2 are the coordinates of the oxygen and hydrogen atoms of molecule i, and R_Wj are the centers of the four doubly occupied maximally localized Wannier Functions associated to molecule i. The electronic part of the dielectric constant ε_∞ was computed separately and added to the average value of the dipole fluctuations in Eq. 1. Values of ε_∞ were obtained using density-functional perturbation theory (DFPT) (30), as implemented in the Qbox code (see Methods). We find that at 1,000 K, ε_∞ increases from 1.76 to 2.41 with increasing pressure from ∼1 GPa to ∼10 GPa. In the same pressure regime but close to 0 K, water can freeze to a high-pressure solid phase, ice VIII. Ab initio calculations (31) of ice VIII using DFT-PBE gave a similar value, ε_∞ ∼ 2.3, in good agreement with the experimental result ∼2.1 (obtained for ice VII and extrapolated to P = 0) (32). When increasing T from 1,000 to 2,000 K along an isobar, ε_∞ decreases slightly by 0.1–0.2, but overall in the P-T range studied here, it does not substantially change. This result is not surprising, as the fluid and the solid are both molecular in this regime (24, 25, 33).

One of the challenges in obtaining ε₀ from MD simulations is the requirement for fairly long trajectories, to properly calculate the fluctuations of the square of the total dipole moment, M² in Eq. 1. For example, at ambient conditions, Gereben and Pusztai (34) showed that trajectories of several nanoseconds are required to obtain converged values of ε₀, which are unaffordable using ab initio MD. However, within the T range of the Earth’s mantle, water molecules diffuse and rotate much faster than at ambient conditions: The diffusion coefficient of water at 0.88 g/cm and 1,000 K is about one order of magnitude larger than that at ambient conditions, and this makes it possible to compute ε₀ over picosecond-long trajectories. (We found that for the SPC/E water model at 0.88 g/cm³ and 1,000 K, the diffusion coefficient is ∼4.2 × 10⁻⁴, whereas at 100 kPa and 298 K, it is ∼2.6 × 10⁻⁵). With increasing pressure along an isotherm, the diffusion coefficient decreases and ab initio calculations are expected to become again very challenging. For water at the conditions of Table 1, using MD simulations with empirical potentials, we compared the results obtained for the dielectric constant with 1-ns trajectories and 1,728 water molecules with those obtained with 20-ps trajectories and 128 molecules; we found values differing by less than 5% (Fig. S1). We therefore chose to carry out ab initio MD simulations with supercells containing 128 molecules, over 20 ps.

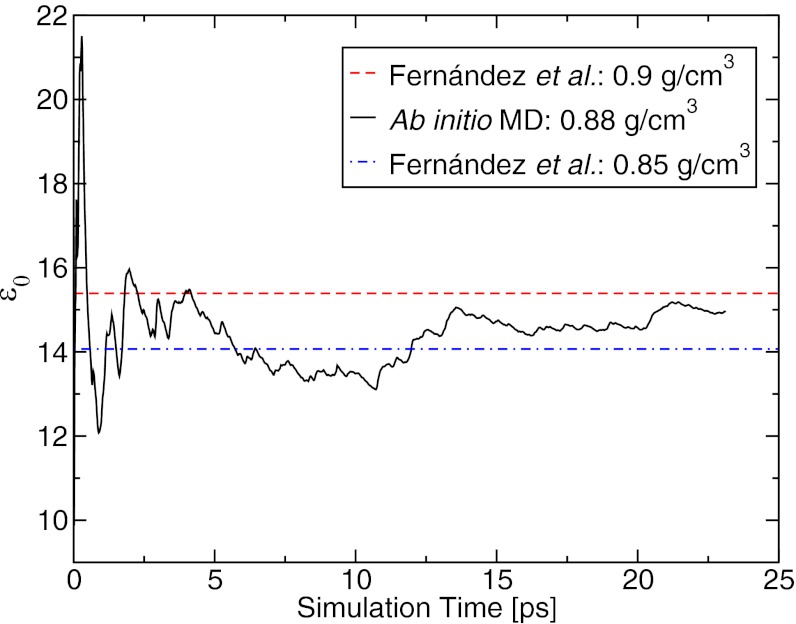
Fig. 1 shows the dielectric constant of water obtained by ab initio MD as a function of the simulation time at ∼1 GPa and 1,000 K. We compared our results with those of the database compiled by Fernández et al. (9), which covers the published experimental data until 1995 at P and T up to 1.2 GPa and 873 K, and extrapolated data up to 1 GPa and 1,200 K (13). Our ab initio MD simulations predict a static dielectric constant of ∼15 at 0.88 g/cm³, a value that is between those reported by Fernández et al. at 0.85 and 0.90 g/cm³ (Fig. 1). Therefore, although we cannot compare directly with experiments, due to the lack of data, the agreement shown in Fig. 1 gives us confidence that our simulations are accurate.

Fig. 1.

Static dielectric constant of water, ε₀, as a function of simulation time, as obtained with ab initio molecular dynamics (MD) simulations at the density (ρ) of 0.88 g/cm³, P ∼ 1 GPa, and T = 1,000 K (solid line). Values of ε₀ from Fernández et al.’s formulation (13) are shown by a dashed (ρ = 0.9 g/cm³) and a dotted-dashed line (ρ = 0.85 g/cm³).

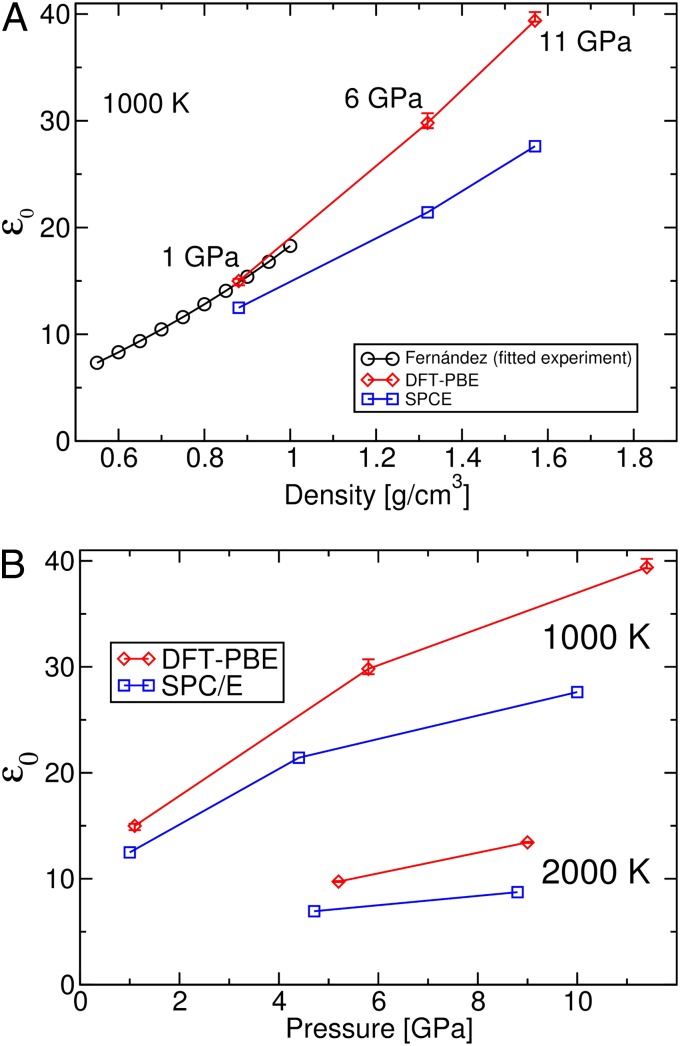
Fig. 2 shows how ε₀ varies with the density and pressure at 1,000 K. For both ab initio and empirical (SPC/E) simulations, ε₀ monotonically depends on the density at fixed temperature. When the temperature rises from 1,000 K to 2,000 K, ε₀ decreases by about 70% along an isobar, whereas with P increasing from ∼1 GPa to ∼11 GPa, ε₀ increases by only about 2.5 times at 1,000 K. The same trend is also found in Fernández et al.’s experimental database (9), showing that the static dielectric constant of water is more sensitive to temperature along an isobar than to pressure along an isotherm. In Eq. 1, ε₀ depends on T and V explicitly, and it is straightforward to understand how T affects ε₀; the effect of pressure is indirect, through the volume dependence, and V changes slowly under the conditions examined here (e.g., at 1,000 K when increasing pressure by a factor of ∼11, the volume V decreases only ∼1.8 times; the density varies from 0.88 to 1.57 g/cm³). As a result, the dielectric constant of water decreases considerably with increasing temperature, whereas it shows only a moderate variation with increasing pressure.

Fig. 2.

The static dielectric constant of water, ε₀, under high P-T conditions. (A) ε₀ as a function of density reported by Fernández et al. (13) and obtained in classical (SPC/E) and ab initio (DFT-PBE) simulations (this work) at 1,000 K. (B) ε₀ as a function of pressure as obtained with ab initio and SPC/E simulations at 1,000 and 2,000 K.

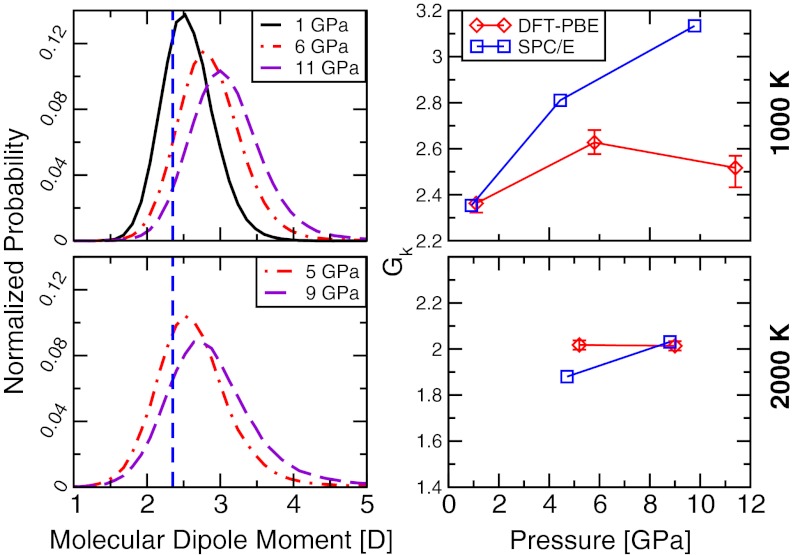
The observed changes in the dielectric constant are accompanied by notable changes in the molecular dipole moment. Under pressure, water molecules exhibit a broad range of dipole moments (Fig. 3), whose average value increases as P and T increase. At both 1,000 and 2,000 K, the increasing pressure enhances the average molecular dipole moment, μ, whereas increasing temperature along an isobar has the opposite effect. From ∼1 to ∼11 GPa, μ varies from 2.5 to 3.0 D at 1,000 K, and at 2,000 K it increases from 2.6 to 2.8 D between ∼5 and ∼9 GPa. We note that in the rigid SPC/E model, water has a fixed molecular dipole moment of 2.35 D, which is close to that found with ab initio simulations at ∼1 GPa, 1,000 K and at ∼5 GPa, 2,000 K; it is therefore not surprising that under these conditions, ε₀ obtained using the SPC/E model and DFT-PBE are similar (Fig. 2). With increasing pressure, however, the SPC/E potential cannot reproduce the change in the distribution of dipole moments reported in Fig. 3, and ab initio and empirical results are substantially different.

Fig. 3.

Molecular dipole moments and the finite-system Kirkwood factor (G_k) of water under pressure. Shown are the distribution of the molecular dipole moment of water obtained in ab initio MD simulations (Left) and the variation of G_k with pressure (Right). (Left) Vertical lines indicate the fixed value of the dipole moment of water in the SPC/E model. Temperatures are 1,000 K (Upper) and 2,000 K (Lower), respectively. (Right) Results obtained with both ab initio simulations (DFT-PBE) and the empirical potential SPC/E are shown.

Not only does the individual molecular dipole moment of water affect the value of ε₀, but also the whole structure of the hydrogen bond network influences the value of ε₀; such the network made of N water molecules can be characterized by the finite-system Kirkwood factor (22) 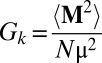, accounting for the dipolar orientational order. For a fully random system, e.g., an ideal gas, G_k is 1, and for an ice Ih crystal (hexagonal ice stable at ambient pressure) with perfect tetrahedral order, G_k is ∼3 (35). In our ab initio simulations, G_k appears to be less sensitive to P than the value of the molecular dipole moments. Fig. 3 shows that G_k at the DFT-PBE level of theory is ∼2.5 at 1,000 K, and it does not substantially vary with increasing pressure along an isotherm. On the contrary, at the same P-T conditions, G_k obtained with the SPC/E potential increases from ∼2.4 to more than 3.1, implying that at ∼10 GPa the dipolar orientational orders given by ab initio and empirical simulations are substantially different.

Solubility of Carbonates Under Pressure.

We now turn to evaluating the solubility product constants of several carbonate minerals at the conditions of the Earth’s upper mantle, using the ab initio computed values of ε₀ (Fig. 2 and Table S1). To this end we revised the Helgeson–Kirkham–Flowers (HKF) model (36, 37) for aqueous species, using ab initio computed values of ε₀, to cover the conditions of the whole upper mantle region, where carbon may be mainly stored in the form of carbonate minerals. One of the most important terms in the HKF model for the Gibbs free energy of formation of an aqueous species is based on the Born function for the average Gibbs energy of solvation, 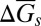(38),

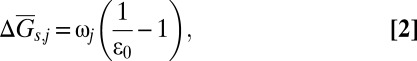where 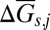accounts for the solvation part of the free energy change when moving the ion j from vacuum into water with the dielectric constant of ε₀, and ω_j is the electrostatic Born parameter for the ion j, which is available for hundreds of aqueous species, e.g., in the geochemical database, SUPCRT92 (39).

Raman spectroscopy data show that 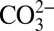becomes increasingly dominant instead of CO₂ and 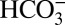in the aqueous solution at equilibrium with an aragonite crystal when P > 4 GPa at 573–673 K;* hence, depending on the temperature, it may be reasonable to assume that the carbonate ion is a significant aqueous carbon species in equilibrium with carbonate minerals as pressure approaches 10 GPa in the upper mantle. In any case, the minimum solubility of a carbonate mineral in water at these conditions is given by the reaction

where M is Ca, Mg, Ca_0.5Mg_0.5, or Fe, and s refers to the solid state. The solubility product constant 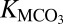for this reaction is

where a is the activity of the corresponding ion. Values of 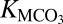were calculated from the revised HKF model for the standard partial molal Gibbs free energies of the aqueous ions (37, †). The standard Gibbs free energies of the minerals were calculated according to ref. 40 in which the volumes of the minerals were assumed constant with pressure and temperature, as the effects of pressure and temperature tend to cancel. For magnesite, the mineral of greatest relevance to the mantle, the difference in log K (for Eq. 4) associated with this assumption is only about 0.1 unit between 1.0 and 10.0 GPa at 1,000 K, in comparing calculations based on ref. 40 with calculations based on ref. 41. Similar small discrepancies would be obtained using other representations of the volumes of carbonate minerals as functions of pressure and temperature (42, 43); however, these discrepancies represent an uncertainty that is small compared to those in the enthalpies of formation of some of the carbonate minerals at ambient conditions. Those discrepancies are also small compared to the uncertainty of whether or not the free energies are consistent with those of silicate minerals in high pressure/temperature phase equilibria and solubility experiments.

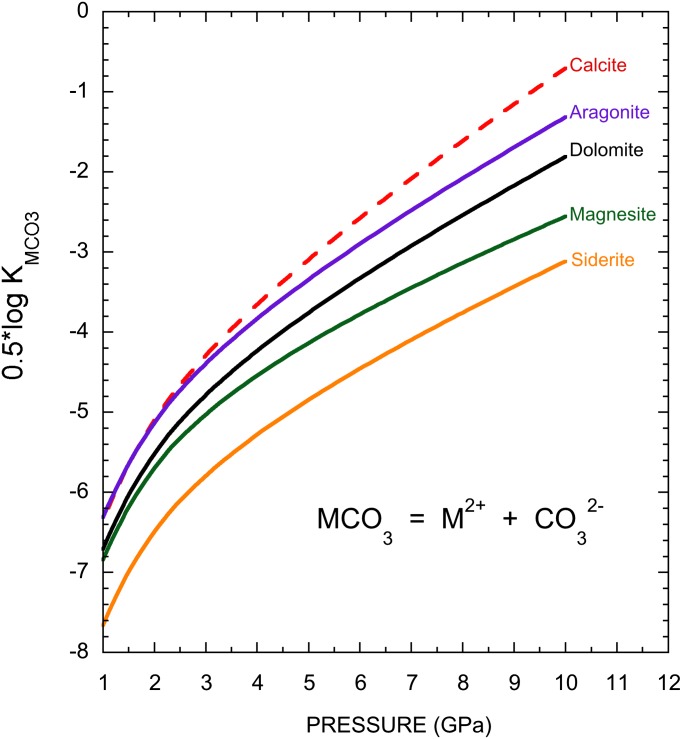
On the basis of Eq. 4, the logarithms of the activities of dissolved metals or the carbonate ion are given by 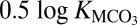and are shown in Fig. 4. Assuming that the aqueous activities can be approximated by molalities, it can be seen in Fig. 4 that at 1,000 K, the minimum solubilities of carbonate minerals increase substantially with increasing pressure as ε₀ increases. For example, when magnesite, expected to be an important carbonate mineral in the mantle stable up to 82 GPa (19), comes into contact with water, we predict that the aqueous fluid may contain at least millimolal levels of Mg²⁺ and 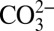at ∼10 GPa and 1,000 K. As a result, magnesite is slightly soluble at the bottom of the upper mantle. Therefore, we predict that in the Earth’s upper mantle aqueous fluids may be important hosts of oxidized carbon in addition to the solid phases and may transport a significant amount of dissolved carbon as carbonate ions.

Fig. 4.

Pressure dependence of the solubility products of carbonate minerals. The solubility products of calcite, aragonite, dolomite, magnesite, and siderite are predicted at pressures of the Earth's upper mantle at 1,000 K.

Conclusions

In conclusion, by using ab initio MD simulations, we computed the dielectric constant of water under P-T conditions of the Earth’s upper mantle, predicting values beyond the reach of current experiments. At depths greater than 300 km and at 1,000 K, the dielectric constant reaches ∼38, roughly half of the value at ambient conditions. The dielectric constant monotonically depends on pressure and decreases dramatically with increasing temperature. We found important variations of the dipole moment of water molecules under pressure, but modest changes of the angular correlation of water dipole moments.

We used our DFT results to extend the revised HKF model of the free energy of aqueous species to upper mantle conditions in the Earth. We predicted the solubility products of carbonate minerals. Compared with experimental measurements of calcite solubility up to 1.6 GPa at 973 K (44), our predictions show very good agreement^†. Furthermore, we found that magnesite is slightly soluble in water at ∼10 GPa and 1,000 K, indicating that in the upper mantle aqueous fluids may carry a significant amount of dissolved oxidized carbon, with possible implications for the dynamics of the global carbon cycle. Carbonates in fluids could leave the subducting lithosphere during dehydration reactions and could be injected into the overlying lithosphere. If aqueous environments are indeed important hosts for carbon in the Earth’s upper mantle, one may speculate that the Earth’s deep carbon could possibly be recycled through aqueous transport on a large scale through subduction zones. The increase in magnesite solubility with pressure demonstrates that there is a strong potential for magnesite precipitation during decompression of aqueous fluids sourced in the upper mantle. Finally we emphasize that the availability of ab initio data for the dielectric constant of water opens the way to solubility studies of a variety of minerals present in the deep Earth, thus greatly contributing to the modeling of geochemical fluids during water–rock interactions.

Methods

Molecular Dynamics (MD) with Classical Force Fields.

We carried out MD with empirical potentials, using the Gromacs package, v.4.0.7 (45). A time step of 1 fs was used, and a Nosé-Hoover thermostat (46, 47) was used, with a relaxation time of 1 ps. The Lennard–Jones (LJ) potential and the real part of the Ewald sum for the Coulomb potential were truncated at 10 Å, except for the small supercell containing 128 water molecules, where we used a cutoff radius of 6 Å. Long-range corrections to the energy and pressure were added to the LJ potential. The data for the SPC/E water were obtained with 1,728 water molecule supercells and runs of at least 1 ns.

Ab Initio Molecular Dynamics.

Ab initio MD simulations were performed in the Born–Oppenheimer approximation with the Qbox code, v.1.54.2 (48) http://eslab.ucdavis.edu/software/qbox/, with a time step of 0.24 fs. We used the PBE (18) exchange-correlation functional and norm-conserving pseudopotentials (49, 50) (pseudopotential table, http://fpmd.ucdavis.edu/potentials/), with a kinetic energy cutoff of 85 Ry, which was increased to 220 Ry for the calculation of pressure. Our cubic supercell with periodic boundary conditions contained 128 heavy water molecules (D₂O). We considered heavy instead of light water for computational efficiency (use of a larger time step in MD simulations). According to empirical MD studies (34, 51) and our DFT-MD tests at ∼1 GPa and 1,000 K H₂O, the isotopic effect is negligible on dielectric constant calculations. The density of water mentioned in the main text is for H₂O. The temperature was controlled by a thermostat, using stochastic velocity rescaling (τ = 24.2 fs) (52), to generate a canonical (i.e., NVT) ensemble. By using the empirical potential with 1,728 water molecules, we compared the results by NVT and NPT with variable cell sizes under constant pressure. The differences are less than 5%, within the statistical error bar. Molecular dipole moments were calculated using maximally localized Wannier function centers (53, 54). Our ab initio simulations were started from configurations generated by empirical MD runs and were carried out for at least 21 ps.