Five-vertex Archimedean surface tessellation by lanthanide-directed molecular self-assembly

Abstract

The tessellation of the Euclidean plane by regular polygons has been contemplated since ancient times and presents intriguing aspects embracing mathematics, art, and crystallography. Significant efforts were devoted to engineer specific 2D interfacial tessellations at the molecular level, but periodic patterns with distinct five-vertex motifs remained elusive. Here, we report a direct scanning tunneling microscopy investigation on the cerium-directed assembly of linear polyphenyl molecular linkers with terminal carbonitrile groups on a smooth Ag(111) noble-metal surface. We demonstrate the spontaneous formation of fivefold Ce–ligand coordination motifs, which are planar and flexible, such that vertices connecting simultaneously trigonal and square polygons can be expressed. By tuning the concentration and the stoichiometric ratio of rare-earth metal centers to ligands, a hierarchic assembly with dodecameric units and a surface-confined metal–organic coordination network yielding the semiregular Archimedean snub square tiling could be fabricated.

The tiling of surfaces is relevant for pure art (1), mathematics (2, 3), material physics (4), and molecular science (5). Johannes Kepler’s pertaining, rigorous analysis revealed four centuries ago that in the Euclidean plane 11 tessellations based on symmetric polygonal units exist (6): three consist of a specific polygon (so-called regular tilings with squares, triangles, or hexagons, respectively), whereas eight require the combination of two or more different polygons (named semiregular or Archimedean tilings from triangles, squares, hexagons, octagons, and dodecagons).

Manifestations of regular tessellations at the atomic and molecular level are ubiquitous, including crystalline planes and surfaces of elemental or molecular crystals, and honeycomb structures encountered, e.g., for graphene sheets, strain relief and supramolecular lattices. In addition, the family of semiregular Archimedean tilings features intriguing characteristics. They may represent geometrically frustrated magnets (7) or provide novel routes for constructing photonic crystals (8). However, with the exception of the frequently realized trihexagonal tiling (also known as the Kagomé lattice) (9–15), the other semiregular Archimedean tiling patterns remain largely unexplored.

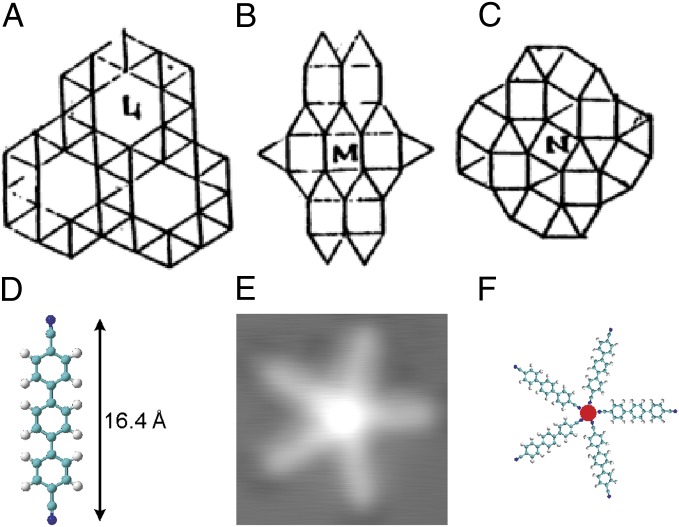
Three of the semiregular Archimedean tilings correspond to five-vertex configurations (Fig. 1 A–C): the snub hexagonal tiling (four triangles and one hexagon at each vertex, labeled 3.3.3.3.6), the elongated triangular tiling (three triangles and two squares join at each vertex in a 3.3.3.4.4 sequence), and the snub square tiling (three triangles and two squares at each vertex; labeled 3.3.4.3.4). They have been identified in bulk materials, such as layered crystalline structures of complex metallic alloys (4, 16–18), supramolecular dendritic liquids (19), liquid crystals (20), special star-branched polymers (21, 22), and binary nanoparticle superlattices (23). Moreover, recent experiments with colloids at a quasicrystalline substrate potential induced by five interfering laser beams, conceived to specifically address the surface tiling problem, yielded a distorted, 2D Archimedean-like architecture (24).

Fig. 1.

Five-vertex motifs. (A–C) Five-vertex Archimedean tilings of the plane as sketched by Johannes Kepler in Harmonices Mundi. (A) Snub hexagonal tiling, (B) elongated triangular tiling, and (C) snub square tiling. (D–F) Fivefold coordination node of cerium and carbonitrile linkers on Ag(111). (D) Paraterphenyl-dicarbonitrile; C (H, N) atoms in green (white, blue). (E and F) High-resolution STM image (size, 44 Å × 44 Ų, V_bias = 0.8 V, I = 0.1 nA measured at 6 K) and model of isolated pentameric Ce–carbonitrile coordination unit.

In the last decade, the tools of supramolecular chemistry on surfaces have provided new ways to engineer a diversity of surface-confined molecular architectures, mainly exploiting molecular recognition of functional organic species or the metal-directed assembly of molecular linkers (5). Self-assembly protocols have been developed to achieve regular surface tessellations, including the semiregular Kagomé lattice (11–13), and even more complex tiling patterns or surface decorations (25–30). Despite the striking advances, five-vertex structures remain a challenging issue, reflecting the lack of adequate complementary polygonal molecular modules and planar fivefold coordination nodes, respectively.

Here, we introduce an approach toward complex surface tessellations by the combination of rare earth metal centers with ditopic linear molecular linkers on a smooth Ag(111) substrate. Our molecular-level scanning tunneling microscopy (STM) observations reveal the expression of distinct fivefold coordination nodes, which are flexible and thus useful for intricate periodic surface tessellations, including the five-vertex semiregular Archimedean snub square tiling. A further important aspect of the demonstrated 2D lanthanide metal–organic coordination networks is the integration of f-block elements, with their unique optical, magnetic, and chemical properties (31), in specific metal–ligand configurations, which bears promise for a new generation of surface nanoarchitectures.

Results and Discussion

The used dicarbonitrile-polyphenyl species, NC-(Ph)_n-CN (n = 3, 4; Fig. 1D) have been previously employed for the engineering of 2D metal–organic networks on surfaces with transition metal centers, where threefold and fourfold coordination nodes prevail (30, 32). Carbonitrile endgroups have also been successfully used for synthesis of 3D lanthanide–organic compounds, mainly targeting molecular magnetic materials (33–35). Here, as with other systems, the lanthanide ions typically present high coordination numbers, ranging from 6 to 12 (31). Accordingly, rare-earth metals are promising candidates to explore high coordination number metal–ligand chemistry on surfaces.

Indeed, we find upon the combination of NC–Ph₃–CN molecular linkers with Ce atoms on Ag(111) that at small surface concentrations individual pentameric units are formed, corresponding to a 5:1 (linker/Ce) stoichiometric ratio (Fig. 1 E and F). This spontaneous expression of a fivefold planar coordination node is unprecedented and directly contrasts the bonding motifs identified for the linkers on the same surface (12, 36) where threefold lateral coordination to cobalt centers prevails and only by space limitations higher coordination numbers occurred. It is suggested that the fivefold lateral coordination of the cerium center by the carbonitrile units results from the balance of the linkers’ surface confinement, the size of the lanthanide and its propensity toward high coordination numbers, and possibly steric limitations at the coordination sphere, where the phenyl rings come rather close. The isolated supramolecules could be laterally manipulated as a whole with the STM tip by applying voltage pulses, highlighting the robustness of the supramolecular structure. The pentamers present, moreover, a geometry with opening angles ranging from 65° ± 5° to 81° ± 5° between two adjacent molecular linkers, i.e., deviations from the ideal 72° pentagonal angle are allowed.

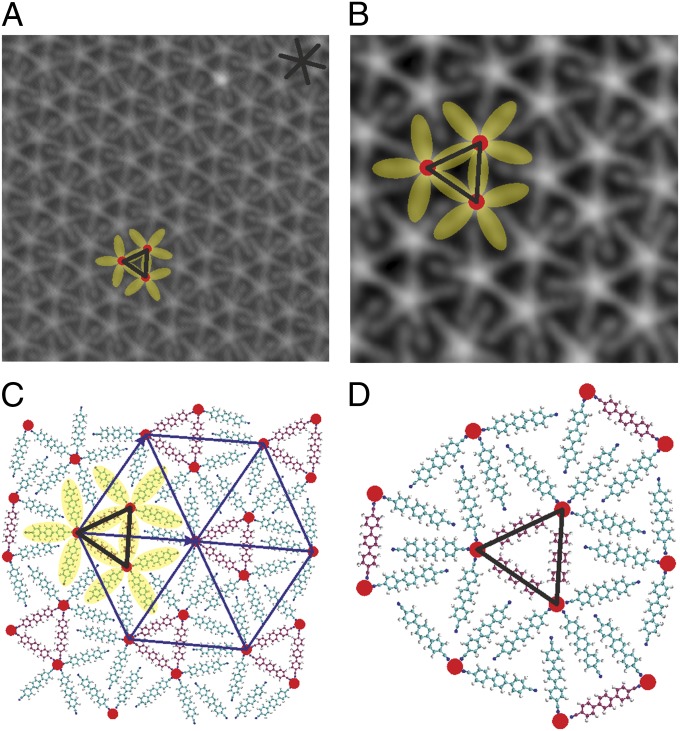
For increased surface concentrations and a stoichiometry (linker/Ce) ∼ (4:1), a regular network phase evolves forming extended domains. An overview image and high-resolution data, along with structure models, are depicted in Fig. 2. We observe again the appearance of distinct coordination nodes, systematically interconnected by the linkers spanning a complex crystalline lattice. Each individual Ce center, imaged as bright protrusion, is strictly surrounded by five molecules, imaged as rods, i.e., the planar fivefold coordination predominates again.

Fig. 2.

Hierarchic metallosupramolecular network from Ce-directed assembly of NC–Ph₃–CN linkers on Ag(111), for a 4:1 (linker/Ce) stoichiometric ratio. (A and B) STM images revealing a dodecameric building unit of a hierarchic hexagonal supramolecular network based on a simultaneous expression of CN–Ce fivefold coordination and lateral CN···phenyl interactions. The black star marks high-symmetry substrate directions. Data were obtained at 6 K. Image size: (A) 232 Å × 232 Ų; (B) 116 × 116 Ų. Scanning parameters: V_bias = −0.1 V, I = 0.1 nA. (C and D) Atomistic model of the network: linkers involved in a single coordination are depicted in green, and those connecting two Ce centers are in pink. The yellow transparent lobes highlight the dodecamer repeat unit with the three Ce centers involved spanning a black triangle. The red circles are Ce centers. The hierarchic superlattice is depicted in violet.

The network follows a design rule in which two of five molecular modules are establishing contacts between two Ce atoms, whereas the remaining three linkers are singly coordinated to a Ce node. Moreover, three Ce centers are always arranged in the form of equilateral triangles (emphasized in Fig. 2), i.e., the three connected Ce atoms and their 12 associated linkers constitute a dodecamer (shadowed in yellow in Fig. 2). A careful analysis of the data reveals that this supramolecular motif constitutes a hexagonal network, defined by the Ce centers, with unit cell vectors 42 Å long forming an angle of 10° with respect to the close-packed <1–10> directions of the Ag(111) surface, as depicted in Fig. 2C. Herein, the projected Ce–Ce distance is 20.8 ± 0.5 Å, implying a length of the Ce–NC bond of 2.2 ± 0.5 Å (assuming an unaffected linker extension upon adsorption) (37). Within the network, we identify for each dodecamer three linkers engaged in Ce coordination at both ends, and nine molecular modules where the proximity of carbonitrile groups and aromatic moieties from adjacent dodecamers reflects CN···phenyl attractive interactions (38). The projected CN···H distances typically range from 2.7 ± 0.5 to 3.2 ± 0.5 Å. Importantly, the Ce–ligand coordination node is adaptive and the opening angles of the linkers present values of 60° ± 5° (defining the triangle), 74° ± 5°, 74° ± 5° (78° ± 5°), 78° ± 5° (74° ± 5°) and 74° ± 5°, respectively. The atomistic model depicted in Fig. 2D shows how the complex surface assembly implies a simultaneous expression of CN–Ce coordination and lateral noncovalent molecule–molecule interactions, i.e., it is a hierarchic organization.

Complementary density functional theory (DFT) calculations of this periodic structure confirm the stability of the fivefold planar coordination nodes with distances between the nitrogen atoms and neighboring Ce centers in the range of 2.45–2.51 Å, whereby the latter reside 2.56 Å above the average height of the first layer of Ag and slightly below the average height of the molecular linkers. The electronic structure of the Ce atoms is furthermore affected by the presence of the surface atomic lattice, whereas the molecular linkers are practically unaffected.

Upon increasing the proportion of cerium, domains of a fully reticulated 2D metal–organic network are detected (Fig. 3). In particular, for a stoichiometry (linker/Ce) = 5:2, the condition for a surface tessellation with all linkers connected at both sides to Ce centers is met. As illustrated in Fig. 3, we now observe a new phase corresponding to a periodic architecture. The assembly of this phase is more delicate than that of the hierarchic structure described above. We achieved the best results by in situ preparation at T ∼300 K, whereby regular domains of a maximum size of 300 Å × 300 Å evolve. Following the previous data interpretation, we assign the vertex protrusions to cerium atoms that are connected by the rod-like molecular linkers. The minority of Ce centers imaged with different height obeys the lattice order and their appearance can be changed by the STM tip, whence they are associated with metal centers axially ligated by contaminants from the residual gas in the vacuum chamber.

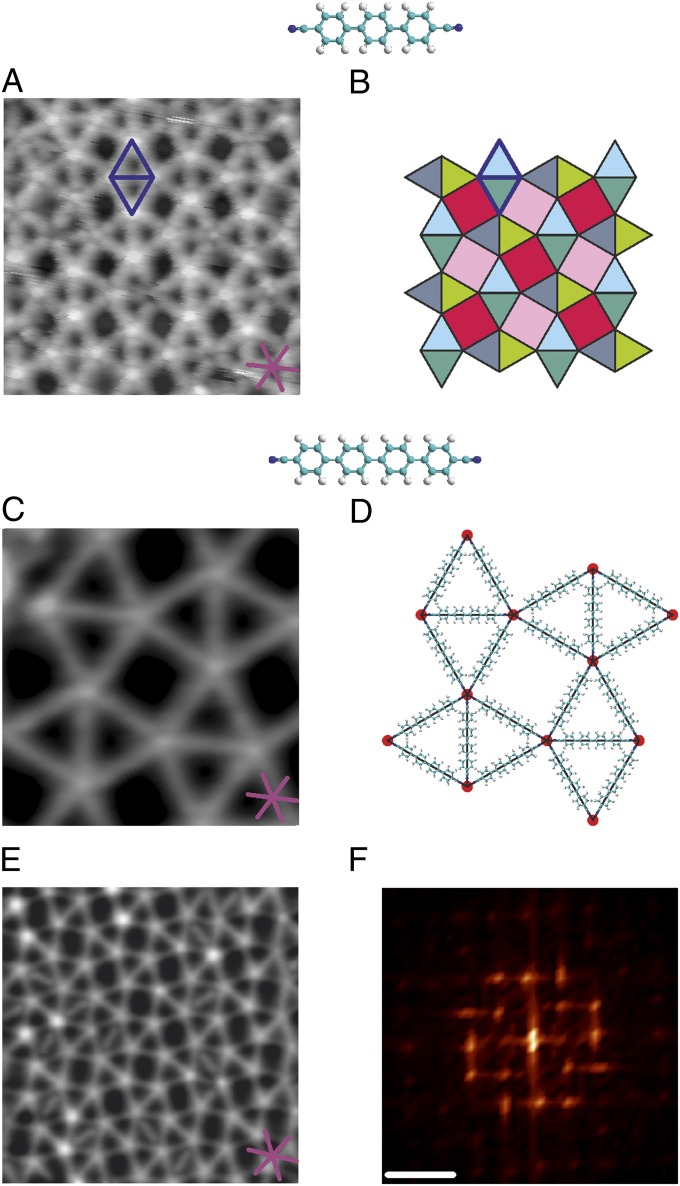
Fig. 3.

Supramolecular Archimedean snub square tilings. (A) STM image of the lanthanide-directed assembly of a supramolecular snub square tessellation on Ag(111) for appreciable surface concentrations and a NC–Ph₃–CN to Ce stoichiometry of 5:2. The high-symmetry directions of Ag(111) are depicted in purple. (Data were obtained at 150 K. Image size: 146 Å × 146 Ų; scanning parameters: V_bias = 1.7 V, I = 0.1 nA.) (B) Tessellation scheme of A with 3.3.4.3.4 sequence of triangular and square tiles. Tiles presenting the same orientation are filled in with the same color. (C) High-resolution image of a snub square tiling motif constituted of NC–Ph₄–CN linkers and Ce centers. (Data were measured at 6 K. Image size: 85 Å × 85 Ų; scanning parameters: V_bias = 0.2 V, I = 0.05 nA.) (D) Structure model of C showing the fivefold coordination of the Ce centers (depicted as solid red circles). The interconnection of the Ce centers by the linkers gives rise to triangle and square units, yielding the motif of the semiregular snub square tiling. (E) STM image of a snub square tiling domain involving NC–Ph₄–CN linkers and Ce centers. (Data were measured at 6 K. Image size: 231 Å × 231 Ų; scanning parameters: V_bias = 0.2 V, I = 0.08 nA.) (F) Fast Fourier transform of E revealing the spatial periodicity of the tiling pattern. (The white scale bar represents 0.04 Å⁻¹.)

The Ce centers represent fivefold vertices, and together with the regular linker interconnection a semiregular tiling of two squares and three equilateral triangles is defined, as depicted by the model reproduced in Fig. 3B. This surface tessellation corresponds to the snub square tiling, in a 3.3.4.3.4 vertex configuration, as described in the introduction (Fig. 1C). To our knowledge, this is a genuine molecular-level realization of a 2D superstructure exhibiting this kind of surface tessellation. A detailed data analysis reveals a projected Ce–Ce distance of 21 ± 0.5 Å, i.e., a Ce–N bond length of 2.4 ± 0.5 Å, in agreement with the DFT results for the hierarchic network described above. A high-resolution image of the snub square tiling motif obtained with the more extended NC–Ph₄–CN linker species is shown in Fig. 3C, Fig. S1, and Fig. S2 (Ce–N distance 2.7 ± 0.5 Å), i.e., the assembly protocol does not fundamentally vary with a different linker length (32).

Within the realized Archimedean tessellation, the molecular modules exhibit six different orientations with respect to the substrate, giving rise to three organizational periodic domains related by a 60° rotation. The corresponding structural model in Fig. 3D illustrates that these orientations are the result of the adaptive fivefold Ce–NC coordination sphere, which presents opening angles between two neighboring Ce–ligands of 60° and 90°, respectively, appreciably deviating from the value of 72° of an ideal pentameric coordination node.

The local regularity of the tiling pattern is revealed by the corresponding Fourier transform for a larger area reproduced in Fig. 3 E and F, which nicely matches earlier observations of related structures (20) (for further details, see Fig. S2; note that in several square units linkers are trapped). In addition to the regular domains, we also found tiling schemes with a different arrangement of triangular and square units, reminiscent of dodecagonal quasicrystalline tiling schemes as identified for nanoparticle and polymeric assemblies (22, 23). The mesoscale quality of the 2D semiregular Kepler tiling remains generally markedly inferior to those of honeycomb lattices achieved with similar linkers and Co centers (32, 39), i.e., the self-correction in the metallosupramolecular assembly is less efficient. It is suggested that the poorer symmetry match and registry to the surface atomic lattice, as well as the tendency of Ce-clustering, hinder the expression of domains over entire substrate terraces for the present system. Taking into account the errors originating from the large unit cell and distance calibration, it remains unclear whether the Kepler is a commensurate superlattice on the Ag substrate, albeit no regular long-range corrugation modulations could be found hinting to a moiré structure. In view of the commonalities regarding chemical properties of rare-earth species, we furthermore expect similar unusual coordination motifs and network formations with lanthanide centers other than cerium.

Concluding Remarks

Based on the versatility of surface-confined coordination chemistry concepts (40, 41), we expect that our approach is of general relevance for other molecular linkers and f-block metal centers, thus opening avenues for a distinct class of intricate low-dimensional architectures and networks. By developing assembly protocols on surfaces that make use of the propensity of high coordination numbers and specific functionalities provided with the family of the lanthanides, complex metal–organic nanoarchitectures and networks with unique metal–organic bonding motifs and surface tessellations can be engineered.

Materials and Methods

The experiments were performed using two custom-designed ultrahigh vacuum systems that hosted a variable-temperature Aarhus 150 STM and a SPS-Createc low-temperature STM, respectively. The base pressure was below 2 × 10⁻¹⁰ mbar in the low-temperature STM system and below 1 × 10⁻⁹ mbar in the variable-temperature STM system. V_bias in tunneling conditions is applied to the sample.

The Ag(111) substrate was prepared using standard cycles of Ar⁺ sputtering (800 eV) and subsequent annealing to 723 K for 10 min. All STM images were taken in constant-current mode with electrochemically etched tungsten tips.

The supramolecular networks based on Ce–ligand coordination motifs described in the manuscript were fabricated in a two-step process as follows (see SI Text): (i) The molecular linkers NC–Ph₃–NC (NC–Ph₄–NC) (ref. 12) were deposited by organic molecular beam epitaxy from a quartz crucible held at T = 478 K (503 K) onto a clean Ag(111) crystal held at ∼300 K. (ii) Subsequently, Ce atoms were evaporated from a homemade water-cooled cell by resistively heating a W filament enclosing a Ce ball of high purity (99.9999%; MaTecK) onto the sample held at ∼300 K.

The DFT calculations were performed using the CP2K package (www.cp2k.org/) using four layers of substrate in the slab geometry, using a generalized gradient approximation and an added empirical van der Waals correction to account for the weak interactions.