Abstract
We consider decision makers who know that payoff-relevant observations are generated by a process that belongs to a given class M, as postulated in Wald [Wald A (1950) Statistical Decision Functions (Wiley, New York)]. We incorporate this Waldean piece of objective information within an otherwise subjective setting à la Savage [Savage LJ (1954) The Foundations of Statistics (Wiley, New York)] and show that this leads to a two-stage subjective expected utility model that accounts for both state and model uncertainty.
Consider a decision maker who is evaluating acts whose outcomes depend on some verifiable states, that is, on observations (workers’ outputs, urns’ drawings, rates of inflation, and the like). If the decision maker (DM) believes that observations are generated by some probability model, two sources of uncertainty affect his evaluation: model uncertainty and state uncertainty. The former is about the probability model that generates observations, and the latter is about the state that obtains (and that determines acts’ outcomes).
State uncertainty is payoff relevant and, as such, it is directly relevant for the DM’s decisions. Model uncertainty, in contrast, is not payoff relevant and its role is instrumental relative to state uncertainty. Moreover, models cannot always be observed: Whereas in some cases they have a simple physical description (e.g., urns’ compositions), often they do not have it (e.g., fair coins). For these reasons, the purely subjective choice frameworks à la Savage (1) focus on the verifiable and payoff-relevant state uncertainty. They posit an observation space S over which subjective probabilities are derived via betting behavior.
In contrast, classical statistical decision theory à la Wald (2) assumes that the DM knows that observations are generated by a probability model that belongs to a given subset M, whose elements are regarded as alternative random devices that nature may select to generate observations. [As Wald (ref. 2, p. 1) writes, “A characteristic feature of any statistical decision problem is the assumption that the unknown distribution 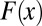 is merely known to be an element of a given class Ω of distributions functions. The class Ω is to be regarded as a datum of the decision problem.”] In other words, Wald’s approach posits a model space M in addition to the observation space S. In so doing, Wald adopted a key tenet of classical statistics, that is, to posit a set of possible data-generating processes (e.g., normal distributions with some possible means and variances), whose relative performance is assessed via available evidence [often collected with independent identically distributed (i.i.d.) trials] through maximum-likelihood methods, hypothesis testing, and the like. Although models cannot be observed, in Wald’s approach their study is key to better understanding state uncertainty.
is merely known to be an element of a given class Ω of distributions functions. The class Ω is to be regarded as a datum of the decision problem.”] In other words, Wald’s approach posits a model space M in addition to the observation space S. In so doing, Wald adopted a key tenet of classical statistics, that is, to posit a set of possible data-generating processes (e.g., normal distributions with some possible means and variances), whose relative performance is assessed via available evidence [often collected with independent identically distributed (i.i.d.) trials] through maximum-likelihood methods, hypothesis testing, and the like. Although models cannot be observed, in Wald’s approach their study is key to better understanding state uncertainty.
Is it possible to incorporate this Waldean key piece of objective information within Savage’s framework? Our work addresses this question and tries to embed this classical datum within an otherwise subjective setting. In addition to its theoretical interest, this question is relevant because in some important economic applications it is natural to assume, at least as a working hypothesis, that DMs have this kind of information [e.g., Sargent (3)].
Our approach takes the objective information M as a primitive and enriches the standard Savage framework with this datum: DMs know that the true model m that generates data belongs to M. Behaviorally, this translates into the requirement that their betting behavior (and so their beliefs) be consistent with M,
where xFy and xEy are bets on events F and E, with x ≻ y. We do not, instead, consider bets on models and, as a result, we do not elicit prior probabilities on them through hypothetical (because models are not in general observable) betting behavior. Nevertheless, our basic representation result, Proposition 1, shows that, under Savage’s axioms P.1–P.6 and the above consistency condition, acts are ranked according to the criterion
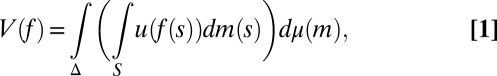 |
where μ is a subjective prior probability on models, whose support is included in M. We call this representation classical subjective expected utility because of the classical Waldean tenet on which it relies.
The prior μ is a subjective probability that may also reflect some personal information on models that the DM may have, in addition to the objective information M. Uniqueness of μ corresponds to the linear independence of the set M. For example, M is linearly independent when its members are pairwise orthogonal. Remarkably, some important time series models widely used in economic and financial applications satisfy this condition, as discussed later in the paper. For this reason, our Wald–Savage setup provides a proper statistical decision theory framework for empirical works that rely on such time series.
Each prior μ induces a predictive probability 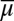 on the sample space S through model averaging:
on the sample space S through model averaging:
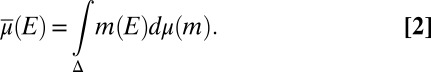 |
In particular, setting 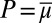 ,
,
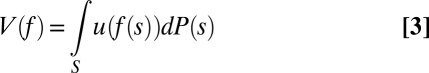 |
is the reduced form of V, its subjective expected utility (SEU) representation à la Savage. On the other hand, when M is a singleton {m}, we have 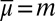 for all priors μ and we thus get the von Neumann–Morgenstern expected utility representation
for all priors μ and we thus get the von Neumann–Morgenstern expected utility representation
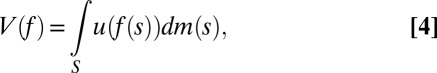 |
where subjective probabilities do not play any role. [Lucas (ref. 4, p. 15) writes that “Muth (5) … [identifies] … agents’ subjective probabilities … with ‘true’ probabilities, calling the assumed coincidence of subjective and ‘true’ probabilities rational expectations” [Italics in the original]. In our setting, this coincidence is modeled by singleton M and results in the expected utility criterion (4).] Classical SEU thus encompasses both the Savage and the von Neumann–Morgenstern representations.
In particular, the Savage criterion [3] is what an outside observer, unaware of datum M, would be able to elicit from the DM’s behavior. It is a much weaker representation than the “structural” one ([1]), which is the criterion that, instead, an outside observer aware of M would be able to elicit. For, this informed observer would be able to focus on the map 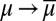 from priors with support included in datum M to predictive probabilities. Under the linear independence of datum M, by inverting this map the observer would be able to recover prior μ from the predictive probability
from priors with support included in datum M to predictive probabilities. Under the linear independence of datum M, by inverting this map the observer would be able to recover prior μ from the predictive probability 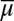 , which can be elicited through standard methods. The richer Waldean representation [1] is thus summarized by a triple (u, M, μ), with suppμ ⊆ M, whereas for the usual Savagean representation [3] is enough a pair (u, P).
, which can be elicited through standard methods. The richer Waldean representation [1] is thus summarized by a triple (u, M, μ), with suppμ ⊆ M, whereas for the usual Savagean representation [3] is enough a pair (u, P).
Summing up, although the work of Savage (1) was inspired by the seminal decision theoretic approach of Wald (2), his purely subjective setup and the ensuing large literature did not consider the classical datum central in Wald’s approach. [See Fishburn (6), Kreps (7), and Gilboa (8). See Jaffray (9) for a different “objective” approach.] In this paper we show how to embed this datum in a Savage setting and how to derive the richer Waldean representation [1] by considering only choice behavior based on observables. Battigalli et al. (10) use the Wald–Savage setup of the present paper to study self-confirming equilibria, whereas we are currently using it to provide a behavioral foundation of the robustness approach in macroeconomics pioneered by Hansen and Sargent (11).
Preliminaries
Subjective Expected Utility.
We consider a standard Savage setting, where (S, Σ) is a measurable state space and X is an outcome space. An act is a map f: S → X that delivers outcome f (s) in state S. Let ℱ be the set of all simple and measurable acts. [Maps 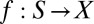 such that
such that 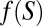 is finite and
is finite and 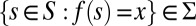 for all
for all 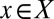 .]
.]
The DM’s preferences are represented by a binary relation ≿ over ℱ. We assume that ≿ satisfies the classic Savage axioms P.1–P.6. By his famous representation theorem, these axioms are equivalent to the existence of a utility function u: X → ℝ and a (strongly) nonatomic finitely additive probability P on S such that the SEU evaluation 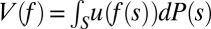 represents ≿. [Strong nonatomicity of P means that for each
represents ≿. [Strong nonatomicity of P means that for each 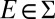 and
and 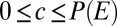 there exists
there exists 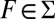 such that
such that  and
and 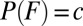 . See ref. 12, p. 141–143 for the various definitions and properties of nonatomicity of finitely additive probabilities.] In this case, u is cardinally unique and P is unique.
. See ref. 12, p. 141–143 for the various definitions and properties of nonatomicity of finitely additive probabilities.] In this case, u is cardinally unique and P is unique.
Given any f, g ∈ ℱ and E ∈ Σ, f Eg is the act equal to f on E and to g otherwise. The conditional preference ≿E is the binary relation on ℱ defined by f ≿E g if and only if f Eh ≿ gEh for all h ∈ ℱ. By P.2, the sure thing principle, ≿E is complete. An event E ∈ Σ is said to be null if ≿E is trivial (ref. 1, p. 24); in the representation, this amounts to P(E) = 0 (E is null if and only if it is P-null).
For each nonnull event E, the conditional preference ≿E satisfies P.1–P.6 because the primitive preference does [e.g., Kreps (ref. 7, Chap. 10)]. Hence, Savage’s theorem can be stated in conditional form by saying that ≿ satisfies P.1–P.6 if and only if there is a utility function u: X → ℝ and a nonatomic finitely additive probability P on S such that, for each nonnull event E,
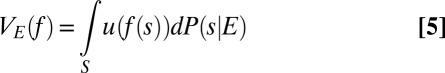 |
represents ≿E, where P(⋅|E) is the conditional of P given E.
Models, Priors, and Posteriors.
As usual, we denote by Δ = Δ(S, Σ) the collection of all (countably additive) probability measures on S. Unless otherwise stated, in the rest of this paper all probability measures are countably additive.
In the sequel, we consider subsets M of Δ. Each subset M of Δ is endowed with the smallest σ-algebra ℳ that makes the real valued and bounded functions on M of the form m ↦ m(E) measurable for all E ∈ Σ and that contains all singletons. In the important special case M = Δ, we write 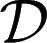 instead of ℳ.
instead of ℳ.
Probability measures μ on Δ are interpreted as prior probabilities. The observation of a (non-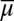 -null) event E allows us to update prior μ through the Bayes rule
-null) event E allows us to update prior μ through the Bayes rule
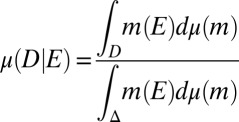 |
for all D ∈ 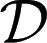 , thus obtaining the posterior of μ given E.
, thus obtaining the posterior of μ given E.
A finite subset M = {m1, … , mn} of Δ is linearly independent if, given any collection of scalars {α1, … , αn} ⊆ ℝ,
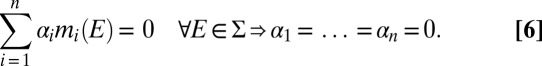 |
Two probability measures m and m′ in Δ are orthogonal (or singular), written m ⊥ m′, if there exists E ∈ Σ such that m(E) = 0 = m′(Ec). A collection of models M ⊆ Δ is orthogonal if its elements are pairwise orthogonal.
If E ∈ Σ and m(E) = 0 imply m′(E) = 0, m′ is absolutely continuous with respect to m and we write m′ ≪ m.
Finally, we denote by Δna the collection of all nonatomic probability measures. By the classical Lyapunov theorem, the range {(m1(E), … , mn(E)): E ∈ Σ} of a finite collection 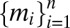 of nonatomic probability measures is a convex subset of ℝn.
of nonatomic probability measures is a convex subset of ℝn.
Representation
Basic Result.
The first issue to consider in our normative approach is how DMs’ behavior should reflect the fact that they regard M as a datum of the decision problem. To this end, given a subset M of Δ, say that an event E is unanimous if m(E) = m′(E) for all m, m′∈ M. In other words, all models in M assign the same probability to event E.
Definition 1.
A preference ≿ is consistent with a subset M of Δ if, given E, F ∈ Σ, with E unanimous,
for all outcomes x ≻ y.
Consistency requires that the DM is indifferent among bets on events that all probability models in M classify as equally likely. The next stronger consistency property requires that DMs prefer to bet on events that are more likely according to all models.
Definition 2.
A preference ≿ is order consistent with a subset M of Δ if, given E, F ∈ Σ, with E unanimous,
for all outcomes x ≻ y.
Both these notions are minimal consistency requirements among information and preference that behaviorally reveal (to an outside observer) that the DM considers M as a datum of the decision problem. Note that order consistency implies consistency because the premise of [7] implies that also F must be unanimous (this observation also emphasizes how weak an assumption is consistency).
We can now state our basic representation result, which considers finite sets M of nonatomic models.
Proposition 1.
Let M be a finite subset of Δna. The following statements are equivalent:
i) ≿ is a binary relation on ℱ that satisfies P.1–P.6 and is order consistent with M;
ii) there exist a nonconstant utility function u: X → ℝ and a prior μ on Δ with suppμ ⊆ M, such that
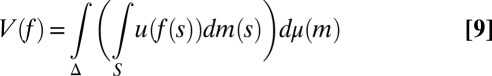 |
represents ≿.
Moreover, u is cardinally unique for each ≿ satisfying statement i, whereas μ is unique for each such ≿ if and only if M is linearly independent.
Although uniqueness of the utility function u is well known and well discussed in the literature, uniqueness of the prior μ is an important feature of this result. In fact, it pins down μ even though its domain is made of unobservable probability models. Because of the structure of Δ, it is the linear independence of M—not just its affine independence—that turns out to be equivalent to this uniqueness property. This simple, but useful, fact is well known [e.g., Teicher (13)].
Each prior μ: 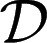 → [0, 1] induces a predictive probability
→ [0, 1] induces a predictive probability 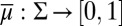 on the sample space through the reduction [2]. The reduction map
on the sample space through the reduction [2]. The reduction map 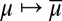 relates subjective probabilities on the space M of models to subjective probabilities on the sample space S, that is, prior and predictive probabilities. [Note that probability measures on S can play two conceptually altogether different roles: (subjective) predictive probabilities and (objective) probability models.] Clearly, [9] implies that
relates subjective probabilities on the space M of models to subjective probabilities on the sample space S, that is, prior and predictive probabilities. [Note that probability measures on S can play two conceptually altogether different roles: (subjective) predictive probabilities and (objective) probability models.] Clearly, [9] implies that
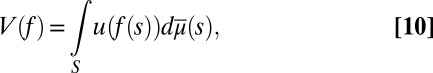 |
which is the reduced form of V, its Savage’s SEU form. As observed in the introductory section, this is the criterion that an outside observer, unaware of datum M, would be able to elicit from the DM’s behavior. It is a much weaker representation than the structural one ([9]), which can be equivalently written as
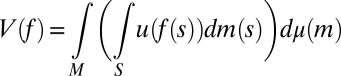 |
because suppμ ⊆ M (recall that finite subsets of 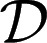 are measurable). This is the criterion that, instead, an outside observer aware of M would be able to elicit. In fact, denote by Δ(M) the collection of all priors μ:
are measurable). This is the criterion that, instead, an outside observer aware of M would be able to elicit. In fact, denote by Δ(M) the collection of all priors μ: 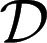 → [0, 1] such that suppμ ⊆ M. The informed observer would be able to focus on the restriction of the reduction map
→ [0, 1] such that suppμ ⊆ M. The informed observer would be able to focus on the restriction of the reduction map 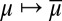 to Δ(M). If M is linearly independent, such correspondence is one-to-one and thus allows prior identification from the behaviorally elicited Savagean probability
to Δ(M). If M is linearly independent, such correspondence is one-to-one and thus allows prior identification from the behaviorally elicited Savagean probability 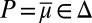 through inversion.
through inversion.
The structural representation [9] is a version of Savage’s representation that may be called classical SEU because it takes into account Waldean information, with its classical flavor. [Diaconis and Freedman (14) call “classical Bayesianism” the Bayesian approach that considers as a datum of the statistical problem the collection of all possible data-generating mechanisms.] In place of the usual SEU pair (u, P) the representation is now characterized by a triple (u, M, μ), with suppμ ⊆ M. According to the Bayesian paradigm, the prior μ quantifies probabilistically the DM’s uncertainty about which model in M is the true one. This kind of uncertainty is sometimes called (probabilistic) model uncertainty or parametric uncertainty.
In the introductory section, we observed that when datum M is a singleton, the classical SEU criterion [9] reduces to the von Neumann–Morgenstern expected utility criterion [4], which is thus the special case of classical SEU that corresponds to singleton data. In contrast, when M is nonsingleton but the support of a prior μ is a singleton, say suppμ = {m′} ⊆ M, then it is the DM’s personal information that prior μ reflects, which leads him to a predictive that coincides with 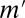 . In this case,
. In this case,
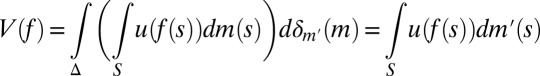 |
is a Savage’s SEU criterion.
Support.
In Proposition 1 the support of the prior is included in M; i.e., suppμ ⊆ M. In fact, because of consistency, models are assigned positive probability only if they belong to datum M. However, the DM may well decide to disregard some models in M because of some personal information. This additional information is reflected by his subjective belief μ, with strict inclusion and μ(m) = 0 for some m ∈ M. (In fact, the interpretation of μ is purely subjective, not at all logical/objective à la Carnap and Keynes.)
Next we behaviorally characterize suppμ as the smallest subset of M relative to which ≿ is consistent. These are the models that the DM believes to carry significant probabilistic information for his decision problem. In this perspective it is important to remember that M is a datum of the problem whereas suppμ is a subjective feature of the preferences.
We consider a linearly independent M in view of the identification result of Proposition 1.
Proposition 2.
Let M be a finite and linearly independent subset of Δna and ≿ be a preference represented as in point ii of Proposition 1. A model m ∈ M belongs to suppμ if and only if ≿ is not consistent with M\m.
Therefore, consistency arguments not only reveal the acceptance of a datum M, but also allow us to discover what elements of M are subjectively maintained or discarded.
Variations.
We close by establishing the conditional and orthogonal versions of Proposition 1. We begin with the conditional version, i.e., with the counterpart of representation [5] under Waldean information.
Proposition 3.
Let M be a finite subset of Δna. The following statements are equivalent:
i) ≿ is a binary relation on ℱ that satisfies P.1–P.6 and is order consistent with M;
ii) there exist a nonconstant utility function u: X → ℝ and a prior μ on Δ with suppμ ⊆ M, such that
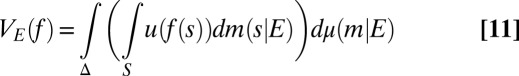 |
represents
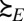 for all non-
for all non-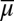 -null events
-null events
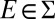 .
.
Moreover, u is cardinally unique for each
 satisfying statement i, whereas μ is unique for each such
satisfying statement i, whereas μ is unique for each such
 if and only if M is linearly independent.
if and only if M is linearly independent.
The representation of the conditional preferences 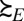 thus depends on the conditional models
thus depends on the conditional models 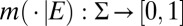 and on the posterior probability
and on the posterior probability 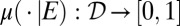 that, respectively, update models and prior in the light of E. Criterion [11] shows how the DM currently plans to use the information he may gather through observations to update his inference on the actual data-generating process. [As Marschak (ref. 15, p. 109) remarked “to be an ‘economic man’ implies being a ‘statistical man’.” Some works of Jacob Marschak (notably refs. 15 and 16 and his classic book, ref. 17, with Roy Radner) have been a source of inspiration of our exercise, as we discuss in ref. 18. Our work addresses, inter alia, the issue that he raised in ref. 16, in which he asked how to pin down subjective beliefs on models from observables. In so doing, our analysis also shows that to study general data M, possibly linearly dependent, it is necessary to go beyond betting behavior on observables.]
that, respectively, update models and prior in the light of E. Criterion [11] shows how the DM currently plans to use the information he may gather through observations to update his inference on the actual data-generating process. [As Marschak (ref. 15, p. 109) remarked “to be an ‘economic man’ implies being a ‘statistical man’.” Some works of Jacob Marschak (notably refs. 15 and 16 and his classic book, ref. 17, with Roy Radner) have been a source of inspiration of our exercise, as we discuss in ref. 18. Our work addresses, inter alia, the issue that he raised in ref. 16, in which he asked how to pin down subjective beliefs on models from observables. In so doing, our analysis also shows that to study general data M, possibly linearly dependent, it is necessary to go beyond betting behavior on observables.]
The conditional predictive probability is
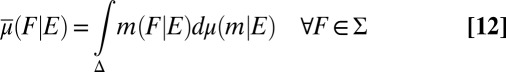 |
and therefore the reduced form of [11] is
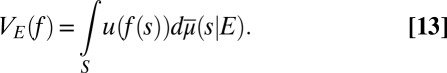 |
The conditional representations [11] and [13] are, respectively, induced by the primitive representations [9] and [10] via conditioning.
Orthogonality is a simple, but important, sufficient condition for linear independence that, as the next section shows, some fundamental classes of time series models satisfy. Because of its importance, the following result shows what form the classical SEU representation of Proposition 1 takes in this case.
Proposition 4.
Let M be a finite and orthogonal subset of
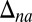 . The following statements are equivalent:
. The following statements are equivalent:
i)
 is a binary relation on ℱ that satisfies P.1–P.6 and is consistent with M;
is a binary relation on ℱ that satisfies P.1–P.6 and is consistent with M;ii) there exist a nonconstant utility function
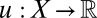 and a prior μ on Δ with
and a prior μ on Δ with
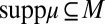 , such that
, such that
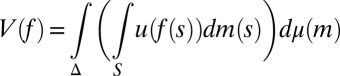 |
represents
 .
.
Moreover, for each
 satisfying i, u is cardinally unique and μ is unique.
satisfying i, u is cardinally unique and μ is unique.
Note that here consistency suffices and that the prior μ is automatically unique because of the orthogonality of M. In ref. 18 we also show that a representation with an infinite M can be derived in the orthogonal case.
The reduction map 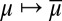 between prior and predictive probabilities is easily seen to be affine. More interestingly, in the orthogonal case it also preserves orthogonality and absolute continuity.
between prior and predictive probabilities is easily seen to be affine. More interestingly, in the orthogonal case it also preserves orthogonality and absolute continuity.
Proposition 5.
Under the assumptions of Proposition 4, two priors μ and ν on Δ with support in M are orthogonal (resp., absolutely continuous) if and only if their predictive probabilities
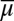 and
and
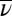 on S are orthogonal (resp., absolutely continuous).
on S are orthogonal (resp., absolutely continuous).
Intertemporal Analysis
Setup.
Consider a standard intertemporal decision problem where information builds up through observations generated by a sequence 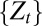 of random variables taking values on observation spaces
of random variables taking values on observation spaces 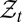 . For ease of exposition, we assume that the observation spaces are finite and identical, each denoted by
. For ease of exposition, we assume that the observation spaces are finite and identical, each denoted by 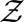 and endowed with the σ-algebra
and endowed with the σ-algebra 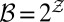 .
.
The relevant state space S for the decision problem is the sample space 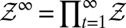 . Its points are the possible observation paths generated by the process
. Its points are the possible observation paths generated by the process 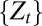 . Without loss of generality, we identify
. Without loss of generality, we identify 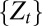 with the coordinate process such that
with the coordinate process such that 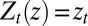 for each
for each 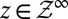 .
.
Endow 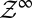 with the product σ-algebra
with the product σ-algebra 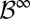 generated by the elementary cylinder sets
generated by the elementary cylinder sets 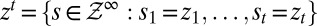 . These sets are the observables in this intertemporal setting. In particular, the filtration
. These sets are the observables in this intertemporal setting. In particular, the filtration 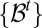 , where
, where 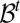 is the algebra generated by the cylinders
is the algebra generated by the cylinders 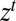 , records the building up of observations. Clearly,
, records the building up of observations. Clearly, 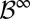 is the σ-algebra generated by the filtration
is the σ-algebra generated by the filtration 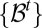 .
.
In this intertemporal setting the pair 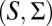 is thus given by
is thus given by 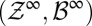 . The space of data-generating models Δ consists of all probability measures m on
. The space of data-generating models Δ consists of all probability measures m on 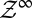 . The outcome space X has also a product structure
. The outcome space X has also a product structure 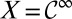 , where
, where 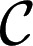 is a common instant outcome space. Acts
is a common instant outcome space. Acts 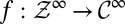 can thus be identified with the processes
can thus be identified with the processes 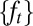 of their components. When such processes are adapted, the corresponding acts are called plans [here
of their components. When such processes are adapted, the corresponding acts are called plans [here 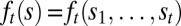 is the outcome at time t if state s obtains]. By Proposition 3, the conditional version of the classical SEU representation at
is the outcome at time t if state s obtains]. By Proposition 3, the conditional version of the classical SEU representation at 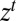 is
is
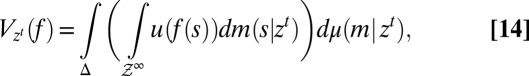 |
where 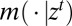 and
and 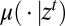 are, respectively, the conditional model and the posterior probability given the observation history
are, respectively, the conditional model and the posterior probability given the observation history 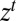 . Under standard conditions, the intertemporal utility function
. Under standard conditions, the intertemporal utility function 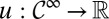 in [14] has a classic discounted form
in [14] has a classic discounted form 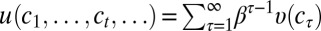 , with subjective discount factor
, with subjective discount factor 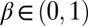 and bounded instantaneous utility function
and bounded instantaneous utility function 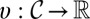 .
.
Stationary Case.
The next known result (e.g., ref. 19, p. 39) shows that models are orthogonal in the fundamental stationary and ergodic case, which includes the standard i.i.d. setup as a special case.
Proposition 6.
A finite collection M of models that make the process
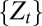 stationary and ergodic is orthogonal.
stationary and ergodic is orthogonal.
By Proposition 4, if  satisfies P.1–P.6 and is consistent with a finite collection M of nonatomic, stationary and ergodic models, then there are a cardinally unique utility function u and a unique prior μ, with
satisfies P.1–P.6 and is consistent with a finite collection M of nonatomic, stationary and ergodic models, then there are a cardinally unique utility function u and a unique prior μ, with 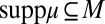 , such that [14] holds. Its reduced form
, such that [14] holds. Its reduced form 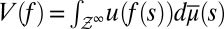 features a predictive probability
features a predictive probability 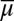 that is stationary (exchangeable in the special i.i.d. case).
that is stationary (exchangeable in the special i.i.d. case).
Because a version of Proposition 6 holds also for collections of homogenous Markov chains, we can conclude that time series models widely used in applications satisfy the orthogonality conditions that ensure the uniqueness of prior μ. The Wald–Savage setup of this paper provides a statistical decision theory framework for empirical works that rely on such time series (as is often the case in the finance and macroeconomics literatures).
Under these orthogonality conditions, there is full learning. Formally, denoting by
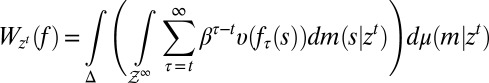 |
the continuation value at 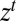 of any act f and by
of any act f and by 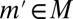 the true model, it can be shown that
the true model, it can be shown that
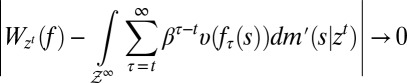 |
for 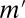 almost every z in
almost every z in 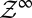 . As observations build up, DMs learn and eventually behave as SEU DMs who know the true model that generates observations. The above convergence result shows how the Classical SEU framework of this paper allows to formalize, in terms of learning, the common justification of rational expectations according to which “with a long enough historical data record, statistical learning will equate objective and subjective probability distributions” [Sargent and Williams (ref. 20, p. 361)]. Further intertemporal results are studied in ref. 18 (the working paper version of this paper), which we refer the interested reader to.
. As observations build up, DMs learn and eventually behave as SEU DMs who know the true model that generates observations. The above convergence result shows how the Classical SEU framework of this paper allows to formalize, in terms of learning, the common justification of rational expectations according to which “with a long enough historical data record, statistical learning will equate objective and subjective probability distributions” [Sargent and Williams (ref. 20, p. 361)]. Further intertemporal results are studied in ref. 18 (the working paper version of this paper), which we refer the interested reader to.
Appendix: Proofs and Related Analysis
Letting M be a subset of 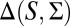 , a probability measure
, a probability measure 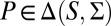 is said to be a predictive of a prior on M (or to be M-representable) if there exists
is said to be a predictive of a prior on M (or to be M-representable) if there exists 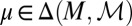 such that
such that 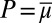 . If in addition such μ is unique, then P is said to be M-identifiable (13).
. If in addition such μ is unique, then P is said to be M-identifiable (13).
We state the next result for any M because the proof for the finite case is only slightly simpler. We say that a subset M of 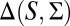 is measure independent if, given any signed measure
is measure independent if, given any signed measure 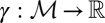 ,
,
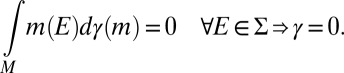 |
If M is finite, measure independence reduces to the usual notion ([6]) of linear independence.
Lemma 1.
Let
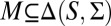 . The following statements are equivalent:
. The following statements are equivalent:
i) every predictive of a prior on M is M-identifiable;
ii) the map
 from
from
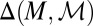 to
to
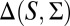 is injective;
is injective;iii) M is measure independent.
Proof:
The equivalence of statements i and ii is trivial.
Statement iii implies ii. If 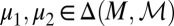 are such that
are such that 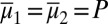 , then
, then 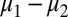 is a signed measure on M and
is a signed measure on M and
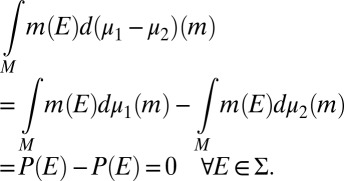 |
Because M is measure independent, it follows that 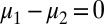 ; i.e.,
; i.e., 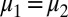 .
.
Statement ii implies iii. Assume, per contra, that M is not measure independent. Then, there is a signed measure γ on M such that
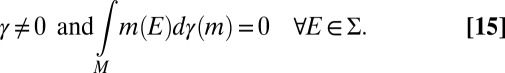 |
By the Hahn–Jordan decomposition theorem, 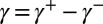 , where
, where 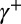 and
and 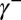 are, respectively, the positive and negative parts of γ. By [15],
are, respectively, the positive and negative parts of γ. By [15],
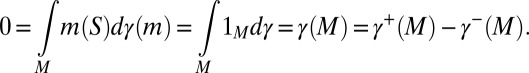 |
Because 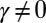 , this implies that
, this implies that 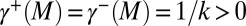 . Then
. Then 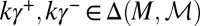 ,
, 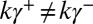 (else
(else 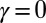 ), and, by [15], for each
), and, by [15], for each 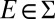
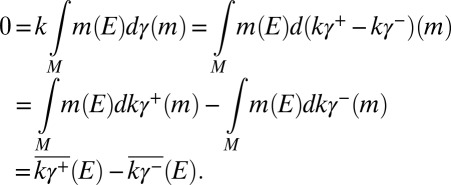 |
Therefore, 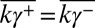 , negating injectivity. ▪
, negating injectivity. ▪
Lemma 2.
If
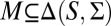 is finite, then
is finite, then
Moreover, the map
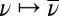 from
from
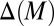 to
to
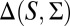 is injective if and only if M is linearly independent.
is injective if and only if M is linearly independent.
Proof:
The equality 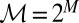 follows from the fact that ℳ contains all singletons. Next we show that
follows from the fact that ℳ contains all singletons. Next we show that 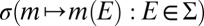 contains all singletons. Note that if
contains all singletons. Note that if 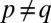 in M, there exists
in M, there exists 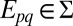 such that
such that 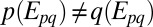 . Then for each
. Then for each 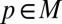 ,
,
is a finite intersection of 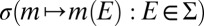 -measurable sets and so it is measurable too.
-measurable sets and so it is measurable too.
Recall that 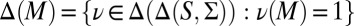 whereas
whereas 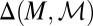 is the set of all probability measures
is the set of all probability measures 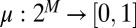 .
.
Let  . Setting
. Setting 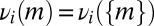 for all
for all 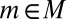 , it follows that
, it follows that 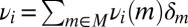 and
and 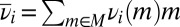 . Denote by
. Denote by 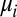 the restriction of
the restriction of 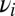 to
to 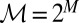 and note that
and note that 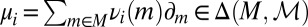 , where
, where 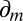 is the restriction of
is the restriction of 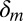 (defined on
(defined on 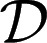 ) to ℳ, and that
) to ℳ, and that 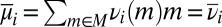 . If M is linearly independent, then
. If M is linearly independent, then 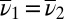 implies
implies 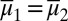 . By Lemma 1,
. By Lemma 1, 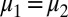 . Thus,
. Thus, 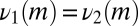 for all
for all 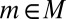 and
and 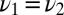 . This proves injectivity.
. This proves injectivity.
Conversely, if M is not linearly independent, by Lemma 1 there exist 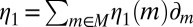 and
and 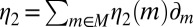 in
in 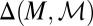 such that
such that 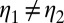 but
but 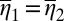 . Now, setting
. Now, setting 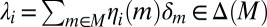 for
for 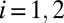 , it follows that
, it follows that 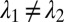 but
but 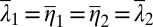 . This negates injectivity. ▪
. This negates injectivity. ▪
Proof of Proposition 1:
Statement i implies ii. By the Savage representation theorem, there are a nonconstant function 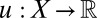 and a unique (strongly) nonatomic and finitely additive probability P on S such that setting
and a unique (strongly) nonatomic and finitely additive probability P on S such that setting 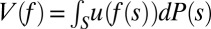 ,
,
By assumption, each m is nonatomic. By the Lyapunov theorem, there is a unanimous event 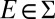 , say with
, say with 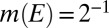 for all
for all 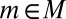 . By order consistency, for each
. By order consistency, for each 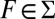
and
By ref. 21, Theorem 20, P belongs to the convex cone generated by M, because 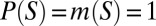 for all
for all 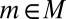 , and then
, and then 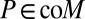 and representation [9] holds.
and representation [9] holds.
Statement ii implies i. Define 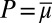 . Because each
. Because each 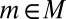 is a nonatomic probability measure, so is P. By the Savage representation theorem, it follows that
is a nonatomic probability measure, so is P. By the Savage representation theorem, it follows that  satisfies P.1–P.6. Finally, we show that
satisfies P.1–P.6. Finally, we show that  is order consistent with M. Let
is order consistent with M. Let 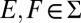 and assume
and assume 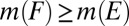 for each
for each 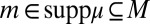 . Then for all outcomes
. Then for all outcomes 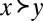 , normalizing u so that
, normalizing u so that 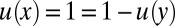 ,
, 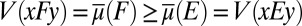 , and so
, and so 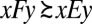 . A fortiori order consistency is satisfied (with respect to both
. A fortiori order consistency is satisfied (with respect to both 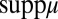 and M).
and M).
Moreover, for each  satisfying statement i, the cardinal uniqueness of u and the uniqueness of
satisfying statement i, the cardinal uniqueness of u and the uniqueness of 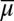 follow from the Savage representation theorem. If M is linearly independent, for each
follow from the Savage representation theorem. If M is linearly independent, for each  satisfying i,
satisfying i, 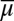 is unique and Lemma 2 delivers the uniqueness of μ. Conversely, if M is not linearly independent, by Lemma 2 there exist two different
is unique and Lemma 2 delivers the uniqueness of μ. Conversely, if M is not linearly independent, by Lemma 2 there exist two different 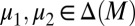 such that
such that 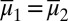 ; arbitrarily choose a nonconstant
; arbitrarily choose a nonconstant 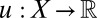 to obtain a binary relation
to obtain a binary relation  satisfying i that is represented both by
satisfying i that is represented both by 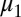 and by
and by 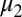 (together with u) in the sense of ii. ▪
(together with u) in the sense of ii. ▪
Proof of Proposition 2:
Let 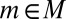 . Replicating the last part of the previous proof, if m does not belong to
. Replicating the last part of the previous proof, if m does not belong to 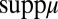 , then
, then  is consistent with
is consistent with 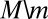 . Now assume that
. Now assume that  is consistent with
is consistent with 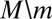 . Take
. Take 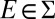 such that
such that 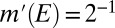 for all
for all 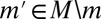 ; by consistency, if
; by consistency, if 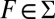 , then
, then
If m belongs to 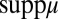 , then
, then
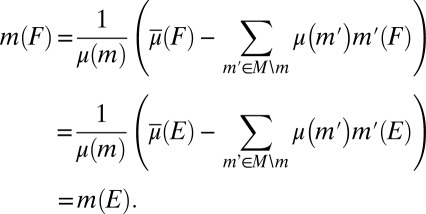 |
Because each element of M is nonatomic, by ref. 21, Theorem 20, 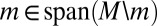 , which contradicts the linear independence of M. ▪
, which contradicts the linear independence of M. ▪
Proof of Proposition 3:
Clearly statement ii of this proposition implies point ii of Proposition 1, which in turn implies i.
Conversely, statement i of this proposition implies point ii of Proposition 1, which together with [5] implies that 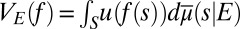 represents
represents 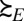 for all nonnull
for all nonnull 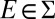 . However,
. However, 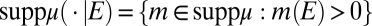 and hence
and hence
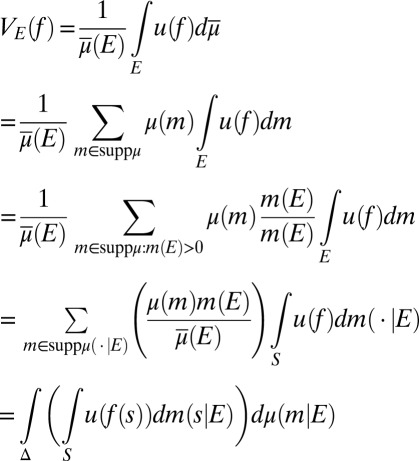 |
so that ii holds.
The rest follows immediately from Proposition 3. ▪
Proof of Proposition 4:
The proof of statement i implies ii of Proposition 3 has to be modified because consistency yields only [16]. Then ref. 21, Theorem 20, yields only that P belongs to the vector subspace generated by M. In any case, there exists a collection 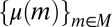 of scalars such that
of scalars such that 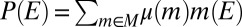 for all
for all 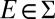 . From
. From 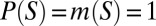 for all
for all 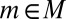 , it follows that
, it follows that 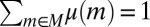 . Moreover, by orthogonality, there exists a partition
. Moreover, by orthogonality, there exists a partition 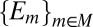 of S in Σ such that
of S in Σ such that 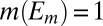 and
and 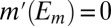 for all distinct
for all distinct 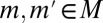 (see the beginning of the next proof). Hence, for each m it holds that
(see the beginning of the next proof). Hence, for each m it holds that 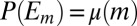 , and so
, and so 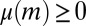 . We conclude that
. We conclude that 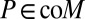 again. The rest of the proof is very similar to that of Proposition 3. ▪
again. The rest of the proof is very similar to that of Proposition 3. ▪
Proof of Proposition 5:
We consider orthogonality and leave absolute continuity to the reader. Suppose 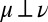 , i.e., there is
, i.e., there is 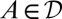 such that
such that 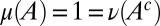 . Next we show that there exists a partition
. Next we show that there exists a partition 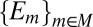 of S in Σ such that
of S in Σ such that 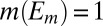 and
and 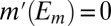 for all distinct
for all distinct 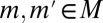 . [Note that
. [Note that 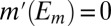 for all
for all 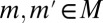 such that
such that 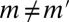 actually follows from the fact that
actually follows from the fact that 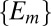 is a partition and
is a partition and 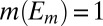 for all
for all 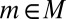 .] Let
.] Let 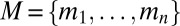 . For
. For 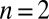 , the result is true by definition of orthogonality. Assume
, the result is true by definition of orthogonality. Assume 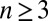 and the result holds for
and the result holds for 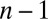 . Then there exists a partition
. Then there exists a partition 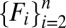 of S in Σ such that
of S in Σ such that 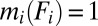 for all
for all 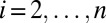 . However,
. However, 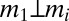 for each
for each 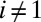 , and hence there is
, and hence there is 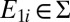 such that
such that 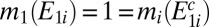 . By setting
. By setting 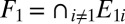 and
and 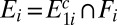 we then have
we then have 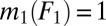 and
and 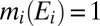 for each
for each 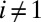 . The desired partition is obtained by setting
. The desired partition is obtained by setting 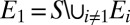 .
.
Set 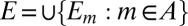 . Clearly,
. Clearly, 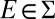 . Moreover,
. Moreover, 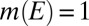 for all
for all 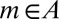 and
and 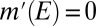 for all
for all 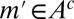 . Then,
. Then,
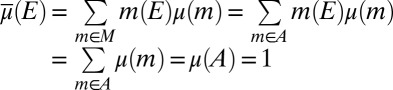 |
and
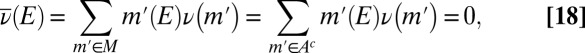 |
which implies 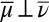 . As to the converse, suppose
. As to the converse, suppose 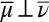 . There is
. There is 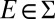 such that
such that 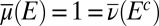 . Set
. Set 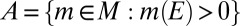 . We have
. We have 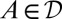 because A is finite. It holds that
because A is finite. It holds that
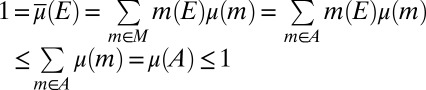 |
and so 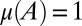 . Moreover,
. Moreover,
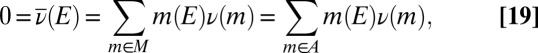 |
whence 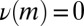 for all
for all 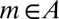 because
because 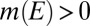 . We conclude that
. We conclude that 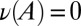 and
and 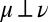 . ▪
. ▪
Acknowledgments
The financial support of ERC (advanced Grant BRSCDP-TEA) is gratefully acknowledged.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Savage LJ. The Foundations of Statistics. New York: Wiley; 1954. [Google Scholar]
- 2.Wald A. Statistical Decision Functions. New York: Wiley; 1950. [Google Scholar]
- 3.Sargent TJ. Evolution and intelligent design. Am Econ Rev. 2008;98:3–37. [Google Scholar]
- 4.Lucas RE., Jr . Understanding business cycles. In: Brunner K, Meltzer AH, editors. Stabilization of the Domestic and International Economy. Amsterdam: North-Holland; 1977. pp. 7–29. [Google Scholar]
- 5.Muth JF. Rational expectations and the theory of price movements. Econometrica. 1961;29:315–335. [Google Scholar]
- 6.Fishburn PC. Utility Theory for Decision Making. New York: Wiley; 1970. [Google Scholar]
- 7.Kreps DM. Notes on the Theory of Choice. Boulder, CO: Westview Press; 1988. [Google Scholar]
- 8.Gilboa I. Theory of Decision under Uncertainty. Cambridge, UK: Cambridge Univ Press; 2009. [Google Scholar]
- 9.Jaffray J-Y. Linear utility theory for belief functions. Oper Res Lett. 1989;8:107–112. [Google Scholar]
- 10. Battigalli P, Cerreia-Vioglio S, Maccheroni F, Marinacci M (2011) Selfconfirming equilibrium and model uncertainty. Working paper 428 (Innocenzo Gasparini Institute for Economic Research, Milan)
- 11.Hansen LP, Sargent TJ. Robustness. Princeton: Princeton Univ Press; 2007. [Google Scholar]
- 12.Bhaskara Rao KPS, Bhaskara Rao M. Theory of Charges. New York: Academic; 1983. [Google Scholar]
- 13.Teicher H. Identifiability of finite mixtures. Ann Math Stat. 1963;34:244–248. [Google Scholar]
- 14.Diaconis P, Freedman D. On the consistency of Bayes estimates. Ann Stat. 1986;14:1–26. [Google Scholar]
- 15.Marschak J. Neumann’s and Morgenstern’s new approach to static economics. J Polit Econ. 1946;54:97–115. [Google Scholar]
- 16.Marschak J. Personal probabilities of probabilities. Theory Decis. 1975;6:121–153. [Google Scholar]
- 17.Marschak J, Radner R. Economic Theory of Teams. New Haven: Yale Univ Press; 1972. [Google Scholar]
- 18. Cerreia-Vioglio S, Maccheroni F, Marinacci M, Montrucchio L (2011) Classical subjective expected utility. Working paper 400 (Innocenzo Gasparini Institute for Economic Research, Milan)
- 19.Billingsley P. Ergodic Theory and Information. New York: Wiley; 1965. [Google Scholar]
- 20.Sargent TJ, Williams N. Impacts of priors on convergence and escapes from Nash inflation. Rev Econ Dyn. 2005;8:360–391. [Google Scholar]
- 21.Marinacci M, Montrucchio L. Subcalculus for set functions and cores of TU games. J Math Econ. 2003;39:1–25. [Google Scholar]


