Characterization of biaxial mechanical behavior of porcine aorta under gradual elastin degradation

Abstract

Arteries are composed of multiple constituents that endow the wall with proper structure and function. Many vascular diseases are associated with prominent mechanical and biological alterations in the wall constituents. In this study, planar biaxial tensile test data of elastase-treated porcine aortic tissue (Chow et al. 2012) is re-examined to characterize the altered mechanical behavior at multiple stages of digestion through constitutive modeling. Exponential-based as well as recruitment-based strain energy functions are employed and the associated constitutive parameters for individual digestion stages are identified using nonlinear parameter estimation. It is shown that when the major portion of elastin is degraded from a cut-open artery in the load-free state, the embedded collagen fibers are recruited at lower stretch levels under biaxial loads, leading to a rapid stiffening behavior of the tissue. Multiphoton microscopy illustrates that the collagen waviness decreases significantly with the degradation time, resulting in a rapid recruitment when the tissue is loaded. It is concluded that even when residual stresses are released, there exists an intrinsic mechanical interaction between arterial elastin and collagen that determines the mechanics of arteries and carries important implications to vascular mechanobiology.

Introduction

The arterial wall is a complex combination of multiple structurally significant components such as elastin, collagen fibers, and smooth muscle cells. Together, these constituents determine the mechanical response of the arterial wall. The passive mechanical behavior of arteries is believed to be mainly dominated by elastin in the toe region of the stress-strain response where collagen fibers are undulated. Collagen fibers are progressively recruited and dominate the wall mechanical response at higher stretch levels (Fung et al. 1979; Holzapfel et al. 2000; Humphrey 2002). Changes in the mechanical behavior of the wall in vascular diseases are associated with alterations in its structure. For instance, decrease in elastin content, disruption of elastin network, as well as elevated collagen content (He and Roach 1994; Menashi et al. 1987; Campa et al. 1987; Carmo et al. 2002) are common features of Abdominal Aortic Aneurysms (AAAs). These structural changes are associated with a remarkable increase in stiffness of the AAA wall (Vorp 2007; Vande Geest et al. 2006; Humphrey and Taylor 2008). Elastin degradation is thought to contribute to the growth of aneurysms early on, whereas rupture of the lesion is attributed to the loss of collagen integrity (Dobrin et al. 1984). Changes in the mechanical response and ultimately failure of the AAA wall are suggested to be the result of defects in the collagen network, rather than defects at the molecular level (Lindeman et al. 2010).

Prior to focusing on the critical role of mechanobiology in the development and the progression of AAAs, we need to improve our knowledge of the aortic wall mechanics as it not only drives the arterial AAAs growth and remodeling (Humphrey and Holzapfel 2012) but also determines the failure of the tissue through wall stress or strain (Vorp and Vande Geest 2005). Therefore, the sequences of structural alterations and the resulting mechanical responses due to elastin degradation are particularly important. The roles of elastin and collagen in arterial mechanics are suggested to be highly coupled and interactive (Fonck et al. 2007; Collins et al. 2012; Ferruzzi et al. 2011b; Chow et al. 2012). Chow et al. (2012) recently conducted in vitro degradation of elastin in order to study the resulting progressive changes in the arterial structure and mechanical behavior. Elastin and collagen assays were performed to quantify biochemical changes in the extracellular matrix while histological assessments revealed gradual changes in the microstructure and planar biaxial tensile tests showed progressive changes in the mechanical response due to elastin degradation.

Continuum mechanics theory has been widely used to describe arterial mechanics with a variety of strain energy functions (see reviews by Holzapfel and Ogden 2010; Holzapfel et al. 2000; Humphrey 2003). In this study, we use multiple constitutive relations to describe the mechanical responses of digested aortic tissues in planar biaxial tensile tests (Chow et al. 2012) and to relate the gradual changes in the mechanical response with the structural alterations. In doing so, we choose representative exponential-based as well as recruitment-based strain energy functions to model the observed changes in the mechanical response. Multiphoton microscopy is used to observe the underlying microstructural changes as a result of elastin digestion.

Materials and Methods

Sample preparation, chemical degradation and mechanical testing

The experimental procedure of elastin degradation and the mechanical testing have been described in detail by Chow et al. (2012). Briefly, a total of 60 porcine thoracic aortas from 12–24 month old pigs are cut into square samples (~1.5×1.5cm) and divided into five groups undergoing various digestion times (6, 12, 24, 48, and 96 hours of digestion; 12 samples for each group). A 5 U/mL ultra-pure elastase solution (MP Biomedicals, Solon, OH) is used to degrade tissues at 37°C with gentle stirring. A custom designed biaxial tensile testing device is used to characterize the planar biaxial mechanical behavior of the fresh and digested samples. Samples are preconditioned through 8 loading cycles up to 30N/m. Following the preconditioning cycles, a preload of 2±0.050N/m is applied in order to keep sutures straightened. The preloaded configuration is chosen as the reference configuration for stress and stretch calculations. Eight cycles of equi-biaxial tension are applied to capture the stress-stretch responses. The maximum stress in the samples generally exceeds 100kPa and is chosen to obtain as much data from the physiologically relevant pressure range without irreversibly damaging the tissue. The mechanical test data of the 12 samples in each group are then averaged and used as the representative behavior of that time group for the constitutive modeling.

Constitutive modeling

To describe the biaxial mechanical behavior of samples using constitutive models, the corresponding strain energy functions are decomposed into two additive parts, i.e., W = W_e + W_c (Holzapfel and Ogden 2010). The elastin-dominated ground substance is represented by a neo-Hookean form of the strain energy functions, W_e = c_e/2(I₁ − 3), where c_e is a parameter associated with elastin and I₁ = tr(C); the first invariant of the right Cauchy-Green deformation tensor C (Holzapfel and Weizsacker 1998; Humphrey 1999; Watton et al. 2009). Based on previous literature, an exponential-based as well as two recruitment-based strain energy functions representing collagen fibers are chosen as:

Model A: Motivated by Fung (1967), Holzapfel et al. (2000) proposed a multi-layer fiber-reinforced composite model for the arterial wall that considers the histological structure of arteries along with an exponential form that represents the prominent stiffening characteristics of the arterial collagen. Assuming one-layer and multiple families of collagen fibers, we use (Baek et al. 2007; Ferruzzi et al. 2011a; Wicker et al. 2008; Zeinali-Davarani et al. 2009):

$$W_c={\displaystyle \sum _{k=1}^N}\frac{c_1^{(k)}}{{\mathit{\text{Nc}}}_2^{(k)}}\left[\text{exp }\right\{c_2^{(k)}{({\lambda }_k^2-1)}^2\}-1]\text{ where }{\lambda }_k=\sqrt{{({\lambda }_{\theta }\text{ sin }{\alpha }_k)}^2+{({\lambda }_z\text{ cos }{\alpha }_k)}^2}$$ (1)

In Eq. (1) λ_k, $c_1^{(k)},\text{ and }{c}_2^{(k)}$ are the stretch and constitutive parameters associated with the fiber family k oriented with an angle of α_k with respect to the longitudinal direction. N is the total number of fiber families chosen to be two (two diagonal fiber families with equal mechanical properties, i.e., $c_1^{(1)}=c_1^{(2)}\text{ and }{c}_2^{(1)}=c_2^{(2)}$, and symmetric orientations with respect to the longitudinal direction, i.e., α₁ = −α₂ = α) or four (four-fiber-family model considering two additional fiber families in longitudinal and circumferential directions, i.e., α₃ = 0° and α₄ = 90°).

Model B: Collagen fibers embedded in tissues naturally have an undulated structure. Each fiber becomes straight and engages in load bearing at a different level of stretch (i.e., recruitment stretch) depending on its degree of waviness. Zulliger et al. (2004) proposed a two-fiber-family model that considers a log-logisitic statistical distribution for the recruitment of fibers. The total strain energy stored in two families of fibers can be expressed by:

$$W_c={\displaystyle \sum _{k=1}^2}\frac{1}{2}{\psi }_f*{\rho }_f={\displaystyle \sum _{k=1}^2}\frac{1}{2}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}{\psi }_f(E_k-x){\rho }_f(x)\mathit{\text{dx}}$$ (2)

where $E_k=1/2({\lambda }_k^2-1)$ is the strain in the direction of fiber families. Individual collagen fibers are assumed to behave linearly, i.e., ${\psi }_f(E_k)=1/2c_c{E}_k^2$ (Rezakhaniha et al. 2011) and engage with a log-logistic probability distribution as

$${\rho }_f(E_k)=\{\begin{array}{cc}\frac{a_k}{b_k}\frac{{\left(\frac{E_k}{b_k}\right)}^{a_k-1}}{{[1+{\left(\frac{E_k}{b_k}\right)}^{a_k}]}^2}\hfill & E_k>0\hfill \\ 0\hfill & E_k\le 0\hfill \end{array}$$ (3)

where c_c = 200 MPa, an elastic constant stemming from intrinsic properties of collagen fibers (Zulliger et al. 2004; Rezakhaniha et al. 2011; Fonck et al. 2007). a_k > 0 and b_k > 0 are parameters that determine the shape of the engagement distribution of fiber family k. Smaller b_k induces engagement at lower stretch levels while smaller a_k results in a more spread out (slower) engagement of fibers. Two symmetric diagonal fiber families are considered to have equal properties of engagement (a₁ = a₂ and b₁ = b₂).

Model C: Lanir (1979) presented a structural model for the biaxial stress-strain response of collagenous tissues considering non-uniform angular as well as waviness distributions of fibers. A normal statistical distribution was suggested for the recruitment stretch as:

$${\rho }_f(E_k)=\frac{1}{d_k\sqrt{2\pi }}\text{exp }(-\frac{{(E_k-m_k)}^2}{2d_k^2})$$ (4)

where m_k > 0 and d_k > 0 represent the mean and standard deviation of the normal distribution, defining the shape of the engagement distribution. The normal distribution is incorporated into the Eq. (2) considering two families of diagonal fibers with equal properties of engagement (m₁ = m₂ and d₁ = d₂).

Given the strain energy functions, the Cauchy stress can be calculated as (Holzapfel 2000; Humphrey 2002):

$$\mathbf{T}=-p\mathbf{I}+\mathbf{F}\frac{\partial W}{\partial \mathbf{C}}{\mathbf{F}}^T$$ (5)

where F is the deformation gradient and p is a Lagrange multiplier obtained using the incompressibility and plane stress assumptions.

Parameter estimation

Parameters associated with each constitutive relation are estimated separately by minimizing the difference between the calculated stress from the constitutive relations, T^c, and the stress obtained from the biaxial tests (Chow et al. 2012), T^e, in the form of an objective function as

$$S={\displaystyle \sum _{i=1}^n}\{w_1{{(T_{11}^c-T_{11}^e)}_i}^2+w_2{{(T_{22}^c-T_{22}^e)}_i}^2\}$$ (6)

where n is the sample size and subscripts 1 and 2 correspond to the longitudinal and circumferential directions. w₁ and w₂ are constant weight parameters. A direct search method, built in Matlab Optimization Toolbox, is employed to minimize the objective function with appropriate constraints on the constitutive parameters. As a measure of the goodness-of-fit, a root-mean-square (RMS) measure of error is calculated as (Wagner and Humphrey 2011)

$$\mathit{\text{RMS}}=\sqrt{\frac{{\mathrm{\Sigma }}_1^n{(T_{11}^c-T_{11}^e)}^2}{n}}+\sqrt{\frac{{\mathrm{\Sigma }}_1^n{(T_{22}^c-T_{22}^e)}^2}{n}}$$ (7)

Multiphoton microscopy

A mode-locked Ti:sapphire laser (Maitai-HP, wavelength 800 nm, 100 fs pulse width, 80 MHz repetition rate, Spectra-Physics) is used to generate second-harmonic generation (SHG) from collagen at 400 nm (417/80 nm) and two-photon excitation autofluorescence from elastin at 525 nm (525/45 nm). An average power of 25 mW is delivered to the sample. Image acquisition is performed on a multiphoton video-rate microscope (Veilleux et al. 2008) over a 1 cm² area by systematic random sampling (3.24% of the surface area - Mouton 2002) on both the adventitia and the intima side. At each location, a 3D volume is recorded over a depth of 60 µm and with a field of view of 360 µm. A quarter-wave plate is placed just before the objective (60X, NA1.0W, LUMPlanN, Olympus) to generate a quasi-circular polarization (1.8 dB) in order to alleviate the excitation polarization dependence of the SHG. For the assessment of collagen fiber reorganization upon chemical degradation, the imaging experiment is repeated with multiple fresh and digested (6hr, 12hr, 24hr and 48hr) planar samples that were not fixed or loaded.

Quantification of waviness for collagen fibers

The waviness property of collagen fibers is quantified for a subset of adventitial images at different stages of digestion using NeuronJ (a plug-in of ImageJ). NeuronJ, originally developed for neuron tracing (Meijering et al. 2004; Meijering 2010), has been successfully used for analysis of the adventitial collagen by Rezakhaniha et al. (2012). Given the Euclidean distance between the end points of a fiber bundle (L) as well as the fiber length (l) by the software, the straightness parameter (P_s = L/l) is calculated to measure the degree of waviness. The larger the P_s, the more straight the fiber. P_s = 1 indicates a completely straight fiber.

Statistical analysis

The straightness parameters and elastin contents at various digestion time points are compared using a factorial analysis of variance. A two-tailed p < 0.05 is considered statistically significant with post-hoc testing using the Tukey’s method to adjust for multiple comparisons. Statistical analysis is performed using the JMP statistical package (version 9.0.2, 2010 SAS Institute Inc.).

Results

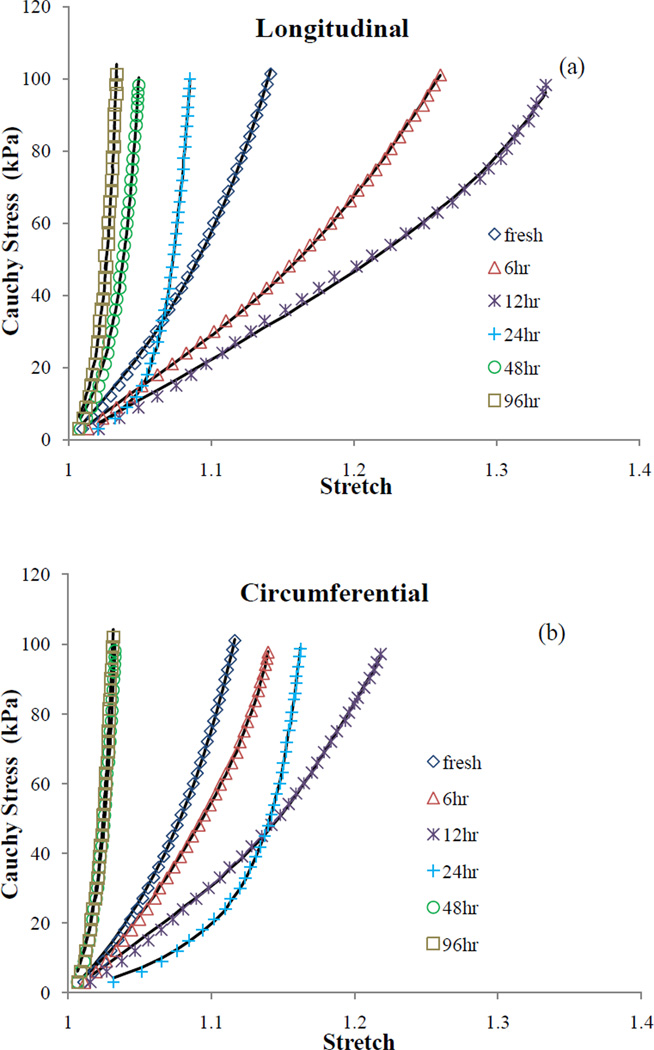
Analyses of histology as well as elastin and collagen biological assays at different stages of digestion have been elaborated by Chow et al. (2012). Figure 1 shows the stress-stretch data in longitudinal and circumferential directions averaged between all samples in each time group (i.e., 12 samples). Due to the gradual elastin digestion the stress-strain response exhibits an initial softening followed by an S-shaped elastomer-like response which eventually turns into a stiff collagen scaffold response (see Chow et al. 2012 for more details). The fitted curves using Model A assuming two diagonal fiber families are also overlaid in Figure 1. The estimated parameters associated with each time groups are shown in Table 1. The estimated parameter for collagen, $c_2^{\mathrm{i}}$, is much larger at 24, 48, and 96hr digestion time steps compared to the initial stages of digestion. Lower values for the ratio of $c_1^i/c_2^i$ in these stages of degradation also imply more contribution of collagen fibers to the stored energy (Collins et al. 2012; Ferruzzi et al. 2011a). An initial increase, followed by a decreasing trend in c_e can be noticed, contrary to the notion that the contribution of elastin is consistently reducing due to degradation. In Table 2 parameters associated with Model A considering four families of collagen fibers are presented. Fitted curves are not shown as there is no considerable difference in the quality of fit between 2-fiber-family and 4-fiber-family models in this study which can be noticed from the fairly close values of RMS error in Tables 1 and 2. A similar trend in the material parameters can be observed in the diagonal directions (i = 3,4) with digestion, implying a stiffer response for a highly digested arterial tissue.

Figure 1.

Cauchy stress vs. stretch plots of the biaxial test data (symbols) as well as the fitted curves (lines) using the estimated parameters of Model A in (a) longitudinal and (b) circumferential directions for multiple digestion time steps.

Table 1.

Estimated parameters using Model A assuming two symmetric collagen fiber families.

	fresh	6hr	12hr	24hr	48hr	96hr
$c_1^1=c_1^2(\mathit{\text{kPa}})$	211.0	81.9	35.6	29.8	382.0	424.0
$c_2^1=c_2^2$	4.27	2.07	1.35	33.9	151.0	283.0
ce (kPa)	7.12×10−14	28.9	31.3	15.4	6.03×10−12	4.56×10−12
α (°)	45.5	48.9	49.9	42.5	45.4	45.1
RMS	1.86×103	1.36×103	2.21×103	1.30×103	3.55×103	4.28×103

Table 2.

Estimated parameters using Model A assuming four collagen fiber families.

	fresh	6hr	12hr	24hr	48hr	96hr
$c_1^1(\mathit{\text{kPa}})$	72.1	29.4	2.06×10−24	2.77×10−12	5.53×10−26	1.92×10−14
$c_1^2(\mathit{\text{kPa}})$	1.22×10−9	1.01×10−12	1.89×10−13	7.89×10−14	1.14×10−11	6.95×10−12
$c_1^3=c_1^4(\mathit{\text{kPa}})$	175.0	82.6	35.6	29.8	382.0	424.0
$c_2^1$	1.64	4.60×10−13	3.45×10−11	0.158	1.36×10−12	1.23×10−3
$c_2^2$	4.82×10−11	2.00×10−18	1.75×10−21	1.13×10−18	5.30×10−14	0.0152
$c_2^3=c_2^4$	4.96	2.24	1.35	33.9	151.0	283.0
ce (kPa)	5.35×10−13	21.5	31.3	15.4	1.97×10−19	2.51×10−13
α (°)	51.3	54.9	49.9	42.5	45.4	45.1
RMS	1.75×103	1.11×103	2.21×103	1.30×103	3.55×103	4.28×103

Estimated parameters associated with Model B are given in Table 3. Elastin parameter, c_e, consistently decreases with the digestion time suggesting a diminishing contribution of elastin to the strain energy in the biaxial deformation. Smaller values of b_k and larger values for a_k estimated in the advanced stages of degradation (24, 48, 96 hours) indicate earlier engagement of collagen fibers with a narrower distribution. Table 4 presents the parameters estimated for Model C. Both the mean value, m, and the standard deviation, d, of the recruitment distribution show an overall decreasing trend with the digestion time while the contribution of elastin to the strain energy (i.e., reduction in the parameter c_e) continuously drops.

Table 3.

Estimated parameters using Model B assuming two collagen fiber families.

	fresh	6hr	12hr	24hr	48hr	96hr
a1 = a2	1.01	0.948	1.11	4.70	1.39	1.65
b1 = b2	31.8	138.0	126.0	0.308	0.558	0.234
ce (kPa)	55.4	47.4	39.8	32.6	1.50×10−11	3.35×10−17
α (°)	46.3	51.2	51.7	41.6	45.4	45.0
RMS	7.28×102	1.47×103	2.52×103	2.48×103	2.37×103	4.16×103

Table 4.

Estimated parameters using Model C assuming two collagen fiber families.

	fresh	6hr	12hr	24hr	48hr	96hr
d1 = d2	2.99	2.42	1.17	0.0636	0.0710	0.0380
m1 = m2	5.21	5.80	3.60	0.264	0.169	0.0970
ce (kPa)	56.1	49.6	40.8	28.5	3.17×10−11	6.30×10−17
α (°)	46.3	51.6	51.9	41.8	45.4	45.1
RMS	7.22×102	1.46×103	2.45×103	2.02×103	1.68×103	3.48×103

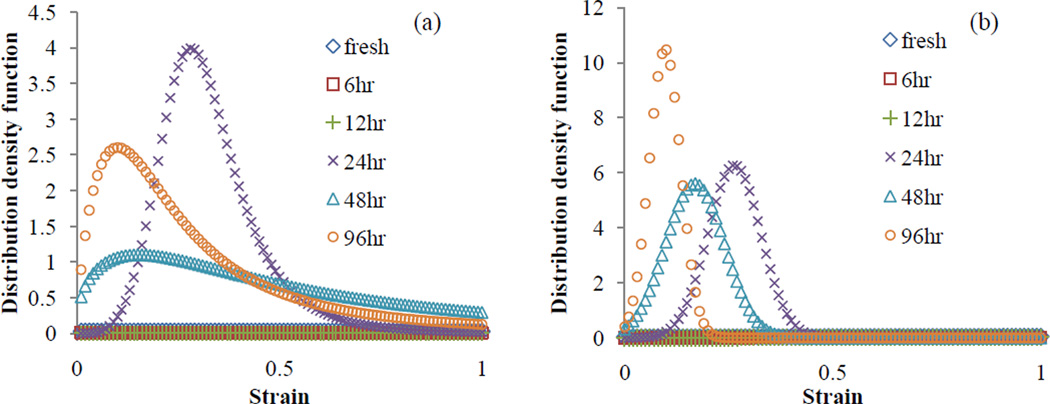
Figure 2 illustrates the resulting recruitment distribution density functions using the estimated parameters for Models B and C. Recruitments of fibers peaks earlier at 24, 48 and 96hr stages compared to the recruitments at the initial stages (fresh, 6, and 12hr) which appear to be relatively negligible within the same range of strain. Although the peak values (sharpness) of distributions at the advanced stages are apparently higher than the initial stages, they do not show consistent trend within themselves. It should be noted that the time to peak (determined by parameters b_k, m_k) together with the peak value of distribution (determined by parameters a_k, d_k) both relate to the structure of fibers (waviness) and are not inherently independent parameters.

Figure 2.

Distribution density functions vs. strain in the direction of fibers using the engagement distribution parameters of (a) Model B, and (b) Model C estimated for each digestion time step.

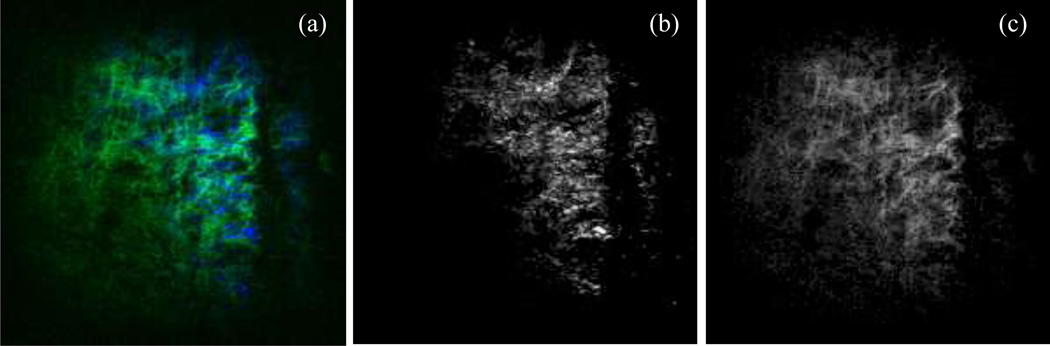
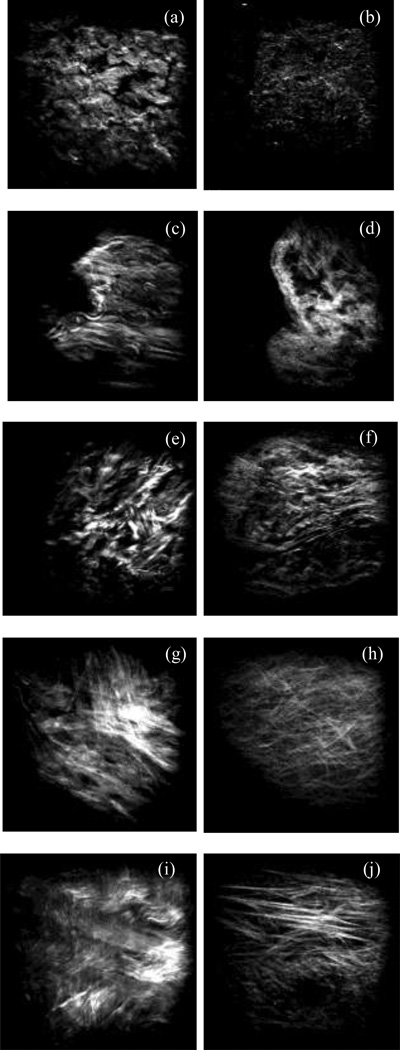
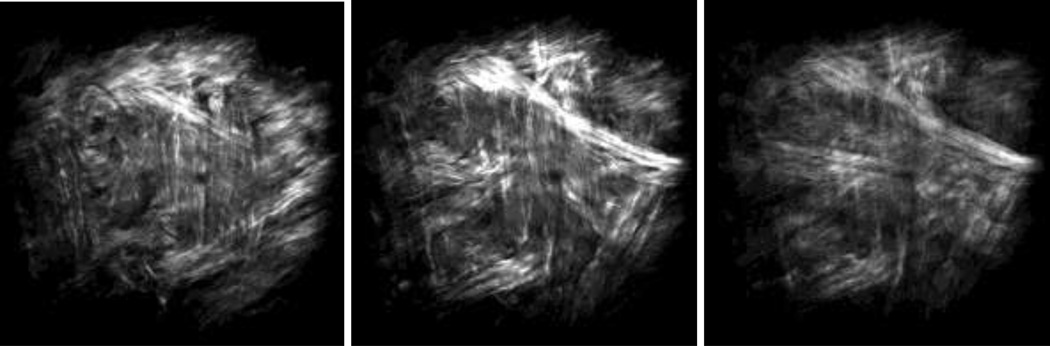
Figure 3a shows a representative image of collagen (blue) and elastin (green) recorded simultaneously from the intima side of a fresh sample using multiphoton microscopy. The image is then split into separate images of collagen (Figure 3b) and elastin (Figure 3c). After 6 hours of digestion no elastin network appears in our microscopic images from either the adventitia or the intima side due to scanning depth limitations of the multiphoton microscope. Representative images of collagen fibers captured from both adventitia and intima sides of fresh and digested samples are depicted in Figure 4. Undulated bundles of collagen can be seen in the fresh sample as well as 6hr and 12hr digestion stages from both sides. As the degradation proceeds (after 24 hours), collagen fibers straighten out and turn into straight bundles of fibers. Figure 5 further illustrates multiple families of straight collagen fibers in the adventitia of a sample after 48 hours of digestion at various scanning depths (6 µm spacing).

Figure 3.

A representative microscopic image of collagen (blue) and elastin (green) captured simultaneously from the intima side of a fresh sample (a) and split into separate images of collagen (b) and elastin (c). Horizontal direction represents the circumferential direction (Images are 360×360 µm).

Figure 4.

Representative microscopic images of collagen from the adventitia and intima sides at fresh (a, b), 6hr (c, d), 12hr (e, f), 24hr (g, h), and 48hr (i, j) stages. Horizontal direction represents the circumferential direction (Images are 360×360 µm).

Figure 5.

Microscopic images of collagen from the adventitia side of a sample under 48 hours of elastin digestion. Images correspond to a single longitudinal and circumferential location but different scanning depth (with 6 µm spacing). Multiple families of fibers with preferred orientations can be distinguished (Images are 360×360 µm).

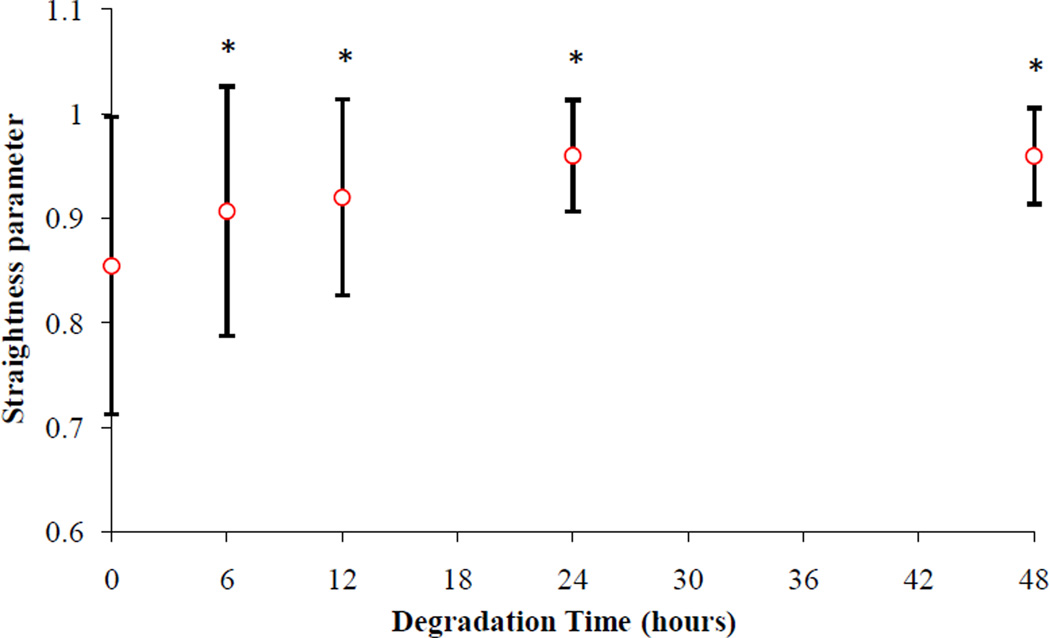
Figure 6 presents the measured waviness of the adventitial collagen obtained from SHG images at different stages of elastin degradation. The increasing trend in the straightness parameter indicates reduced waviness of collagen as a result of elastin digestion. Analysis of variance reveals that collagen fibers are significantly more undulated at the fresh stage compared to the other stages and fibers become straighter with longer digestion time. While there is no significant difference in the waviness between 6hr and 12hr (p=0.7423) as well as between 24hr and 48hr (p=1), the 6hr and 12hr stages are significantly more undulated compared to the 24hr and 48hr stages.

Figure 6.

Straightness parameter (P_s) vs. degradation time. All time points are significantly greater than the fresh time point. 24hr and 48hr stages are significantly greater than 6hr and 12hr stages. (^*p<0.05)

Discussion

Elastin fibers form a resilient network that contributes to the elasticity of the arterial wall. The integrity of elastin fibers, known to have a very low turnover rate, can be compromised due to the fatigue-related damages and aging (Avolio et al. 1998; Tsamis et al. 2011; Marque et al. 2001). In addition to biological impacts (Arribas et al. 2006; Brooke et al. 2003; Wachi 2011), loss of elastin can have direct biomechanical consequences on arteries and demands further investigations.

In this work we employed the constitutive modeling approach along with multiphoton microscopy to further elucidate the role of elastin on the arterial mechanics during a progressive in vitro degradation. We re-examined planar biaxial tensile test data of digested aortic tissues to estimate parameters of multiple strain energy functions previously proposed in the literature. We showed that as elastin is digested, collagen fibers straighten out and engage earlier, describing the higher rate of stiffening and reduced extensibility. Rapid recruitment of collagen fibers seems to occur only when a large portion of elastin is degraded from the arterial tissue.

Independent studies of Ferruzzi et al. (2011b) and Fonck et al. (2007) showed that elastin degradation dramatically increases the stiffness of mouse and rabbit carotid arteries through biaxial mechanical tests. Those studies focused on the effects of near complete loss of elastin, whereas in the current study progressive changes of the aortic tissue structure and mechanics with the gradual digestion of elastin were investigated. It is more realistic to assume that the pathologic degeneration process of elastin in diseases such as AAA occurs gradually. Consistent with the previous studies, we observed a highly coupled mechanical role for elastin and collagen using either exponential-based (Model A) or recruitment-based (Models B and C) strain energy functions. Even when the arterial wall is cut-open, the elastin network is pre-stretched, applying compressive forces on collagen fibers and contributing to their undulation (Figure 4; fresh, 6, 12, and 24hr stages). Removal of elastin reduces the undulation of fibers, resulting in an increase in the unloaded planar tissue dimensions (Chow et al. 2012) or the diameter of arterial segments (Ferruzzi et al. 2011b; Collins et al. 2012; Dobrin and Canfield 1984). While being less undulated in the digested tissue, collagen fibers are ready to be recruited if the tissue is loaded. It is plausible to assume that collagen fibers resist against the recoil of the stretched elastin network. In fact, Collins et al. (2012) illustrated that treatment with collagenase resulted in reduced dimensions of arteries. This is consistent with Dobrin and Canfield (1984) who found a significant reduction in the tissue volume as a result of collagenase treatment.

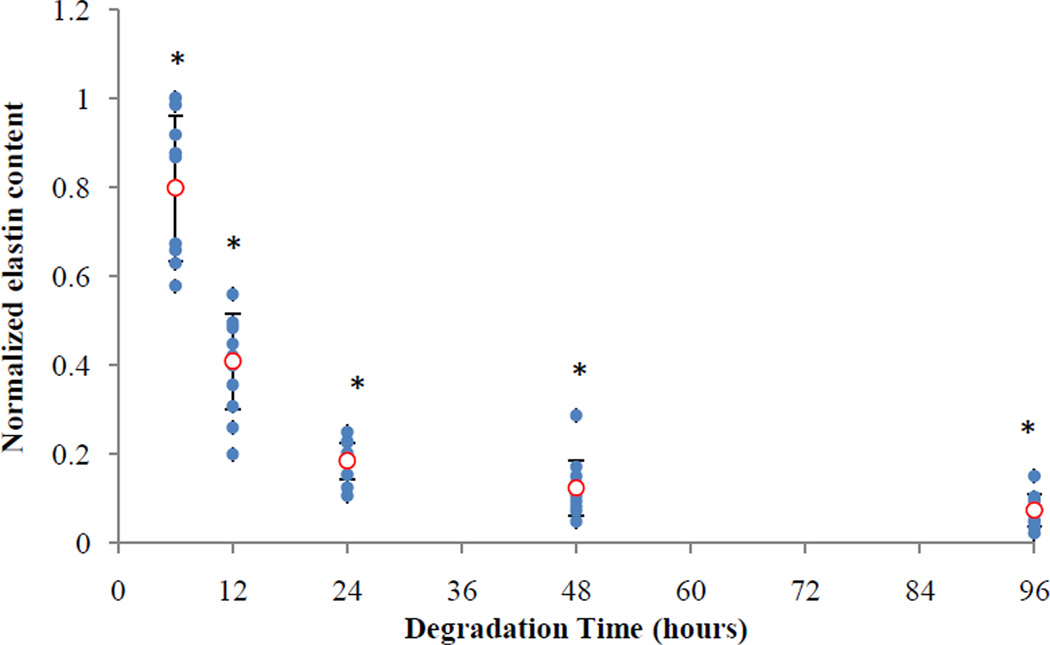
We performed multiphoton microscopy on both the adventitia and intima sides to observe the underlying microstructural changes as a result of elastin digestion. In addition to collagen, our imaging technique allowed us to simultaneously image elastin (Figure 3). However, elastin was no longer visible with our imaging setup after 6 hours of digestion from either the adventitia or the intima side. It is therefore reasonable to suggest that what we observed from both the adventitia and intima sides (e.g. Figure 4) is a representation of what occurs in the collagen microstructure as a result of digestion. Images of collagen in our study started to show the most noticeable change in the undulation of fibers after 24 hours of degradation. Measurements of waviness for adventitial collagen also revealed that the straightness parameter reaches its maximum at 24 hours (no significant change after the 24hr stage). At this stage only about 20% of original elastin content remains (Figure 7). It appears that the presence of elastin even in small proportions contributes to the tissue elasticity and tends to keep the collagen fibers undulated. The extended toe region before the sharp stiffening behavior in the stress-stretch response at the 24hr stage further confirms this hypothesis (Figure 1). Estimated parameters of Models A and B did not show an increasing trend in the recruitment of collagen fibers between fresh to 24hr stage despite a sharp decrease in the elastin content (Tables 1, 2 and 3). After removal of the major portion of elastin, however, the engagement of collagen in load bearing was remarkably enhanced. At 6 hours of digestion, there was a moderate reduction in the slope of stress-strain curves (Chow et al. 2012). Accordingly, a temporary reduction in collagen parameters $c_1^i,c_2^i$ for diagonal fibers (i = 1,2 in 2-fiber-family and i = 3,4 in 4-fiber-family models) was anticipated by Model A. Model B also predicted a temporary delay in the engagement of fibers (i.e., increase in b_k) at the 6hr stage, contrary to the measurements results for waviness that indicate fibers are straighter at the 6hr stage compared to the non-digested condition. Originally, the circumferential direction was found to be prominently stiffer than the longitudinal direction whereas at the 24hr stage the longitudinal direction became stiffer than the circumferential direction (Chow et al. 2012). Interestingly, at the 24hr stage, assuming mechanically identical diagonal fibers, our models also predicted α < 45°, suggesting a change in the alignment of fibers toward the longitudinal direction. However, complete digestion (after 48 or 96 hours) resulted in a fairly similar mechanical response in the circumferential and longitudinal directions (i.e., α ≃ 45° predicted by our models).

Figure 7.

Elastin contents normalized with respect to the values at the fresh stage (0hr) vs. degradation time (Chow et al. 2012). All time points are significantly less than the fresh time point. (^*p<0.05)

Model A presents the gradual engagement of collagen fibers with an exponential function while Models B and C consider the mechanism of engagement of collagen fibers assuming either log-logistic or normal distributions. All those models provided reasonable fits to the biaxial test data with comparable goodness of fits and were able to describe the overall behavior of arterial tissue under degradation (Fitting curves for Models B and C are not shown). Meanwhile, the engagement-based models predicted a declining trend in the parameter associated with elastin that is in accordance with the reducing mass fraction (Vande Geest et al. 2004, 2006; Ferruzzi et al. 2011a). In contrast, using the exponential-based model, this parameter was estimated to be almost zero in the fresh as well as the fully digested stages with no consistent trend.

Recently, Hill et al. (2012) quantified the gradual recruitment of collagen fibers using multiphoton microscopy while the tissues were being loaded in a uniaxial extension device. They considered a Gamma function for the distribution of recruitment stretch, similar to Sacks and Sun (2003). In a separate attempt to quantify the adventitial collagen structure, Rezakhaniha et al. (2012) suggested a Beta distribution for the waviness of fibers in a zero-stress state. The measurements of waviness in our study could be used to determine the shapes of the engagement distribution density functions (as in Models B and C) at every digestion time steps. The focus of the current study, however, was not to suggest the use of a specific model that best suits vascular mechanics. Rather, it was to reflect the need for microstructural based models that are able to capture the evolving structure and mechanical properties of the arterial wall.

The multiphoton imaging in our study also revealed collagen fibers with preferred orientations, particularly, when the majority of elastin is digested and fibers become straightened (Figures 4 and 5). Four major orientations for collagen fibers have been identified by Rezakhaniha et al. (2012) while multi-fiber-family representation of collagen fibers has been suggested as a reasonable approximation when predicting the resulting mechanical response of arteries (Baek et al. 2007; Zeinali-Davarani et al. 2009; Wicker et al. 2008; Ferruzzi et al. 2011a). The single fiber resolution offered by the multiphoton microscopy opens the way for the quantitative characterization of fiber dispersion and allows for a better determination of the optimal model representing the arterial wall mechanics (Gasser et al. 2006). There have been many efforts to either quantify collagen fiber dispersion or include a dispersion parameter in the constitutive models to represent the distributed architecture of collagen in soft tissues (Lanir 1979, 1983; Holzapfel et al. 2005; Gasser et al. 2006; Sacks and Sun 2003; Haskett et al. 2010; Hill et al. 2012; Schriefl et al. 2012; Rezakhaniha et al. 2012; Agianniotis et al. 2011; Lokshin and Lanir 2009).

Limitations

Non-uniqueness of best-fit parameters is an issue that arises in the nonlinear least squares estimation problems (Ogden et al. 2004), particularly when the number of parameters in the model increases (Zeinali-Davarani et al. 2009). To address this concern, we have repeated the optimization process with multiple random starting points to approach global minima. The precision of the estimated parameters can be evaluated using statistical analysis such as bootstrap technique (Ferruzzi et al. 2011a) to provide a confidence interval for the parameters. In this work, however, we focused on the average response of multiple samples subjected to the same digestion time step, rather than estimating parameters for individual samples. The main reason for this approach is the large variability in the mechanical behavior between samples of the same group, partly due to samples having different thicknesses (1.32±0.21 mm) and therefore being at a different stage of degradation considering the fixed digestion time. Ideally, we would like to perform multiple stages of digestion as well as mechanical tests on the same tissue sample to reduce the inter sample variability. However, in practice, it is difficult to perform multiple stages of chemical digestion and tensile tests on a single sample.

In addition, we considered the arterial wall as a single layer that undergoes homogenous degradation. Constitutive models considering multiple layers (Kroon and Holzapfel 2008; Holzapfel et al. 2005) might be more appropriate as the digestion process starts from the outer layers and proceed toward the middle layer of samples (Chow et al. 2012). Multiphoton microscopy cannot image throughout the entire thickness of aorta which is a relatively thick artery. Imaging both sides (with 60µm depth from the surfaces) of the artery was the best available approach to assess the artery structure with our experimental set up.

The role of mass fractions was considered to be inherent in the constitutive parameters. However, mass fractions could have been considered explicitly in the constitutive formulations as prescribed parameters obtained from microstructural studies (Rezakhaniha et al. 2011; Zulliger et al. 2004). In addition, the assumption of isotropic response for elastin can also be regarded as a limitation of the current work since a number of studies have indicated that anisotropy of arterial elastin needs to be considered in modeling (Agianniotis et al. 2011, Rezakhaniha et al. 2011). In fact, recent work by Zou and Zhang (2009) has demonstrated anisotropic response of arterial elastin. Equibiaxial mechanical testing was performed in this work since the focus of this study was mainly on the role of elastin degradation on the evolution of tissue microstructure and mechanical properties. Non-equibiaxial tests, however, are preferred to fully characterize the highly nonlinear and anisotropic behavior of soft tissues (Billiar and Sacks 2000; Sacks 2000; Vande Geest et al. 2006; Zou and Zhang 2009). Finally, it is also noteworthy that the role of biological remodeling was overlooked in our in vitro tests. Aneurysms are accompanied by a remarkable cell mediated remodeling of collagen which tends to compensate the loss of elastin. Therefore, interactions between multiple constituents either through direct mechanical coupling or adaptive processes are responsible for alterations of mechanical properties in diseased arterial wall.

Conclusions

In this study we investigated progressive changes in the mechanical behavior of porcine aortic tissue under gradual elastin degradation through constitutive modeling and multiphoton imaging of the arterial wall. As a result of elastin digestion from the load-free planar samples, arterial tissues elongated in both longitudinal and circumferential directions and the collagen fibers uncoiled. An earlier and sharper recruitment as well as preferred orientations of collagen fibers was noticed in response to biaxial loads. These findings indicate an important mechanical coupling between arterial elastin and collagen and may have considerable implications in vascular mechanics and mechanobiology.