Scalar social dynamics in female vervet monkey cohorts

Abstract

Primate social life and behaviour is contingent on a number of levels: phylogenetic, functional and proximate. Although this contingency is recognized by socioecological theory, variability in behaviour is still commonly viewed as ‘noise’ around a central tendency, rather than as a source of information. An alternative view is that selection has acted on social reaction norms that encompass demographic variation both between and within populations and demes. Here, using data from vervet monkeys (Chlorocebus aethiops pygerythrus), we illustrate how this alternative approach can provide a more nuanced account of social structure and its relation to contingent events at the ecological and demographic levels. Female vervets in our South African study population live in large groups, where they experience demographic stress and increased levels of feeding competition relative to an East African population in Amboseli, Kenya. Females in the South African population did not respond to this stress by intensifying competition for high-value grooming partners to help alleviate the effects of this stress, did not show the expected rank-related patterns of grooming, nor did they show any spatial association with their preferred grooming partners. Increased group size therefore resulted in a reorganization of female social engagement that was both qualitatively and quantitatively different to that seen elsewhere, and suggests that female vervets possess the flexibility to shift to alternative patterns of social engagement in response to contingent ecological and demographic conditions.

1. Introduction

In an important comparative analysis, Johnson [1] showed that, as human social groups grow in size, they are able to counter the disruptive effects of an unavoidable, nonlinear increase in information load and the attendant difficulties of coordination by incorporating some form of hierarchical control or linguistic mediation. He also demonstrated that reorganization in the face of such ‘scalar stress’ was consistent across different levels of organization and that 6 (±2) interacting units was the point at which the ‘unit of renormalization’ [2] (i.e. an additional layer of hierarchical control) emerged. In this way, egalitarian, non-hierarchical human groups acquire leaders once membership exceeds five, and these internally structured groups themselves come under regulatory control once the actions of six or more groups must be coordinated.

Intriguingly, there is evidence that non-human primate groups may face similar problems of social coordination. In cercopithecines, adult females are only able to groom across the entire female cohort (i.e. the total number of females in the group) when this is below some threshold size [3–5]. Beyond this, the size of a female's grooming clique (the number of other females she grooms) tends to remain relatively constant as cohort size increases, even in captive groups [5]. This raises the question of whether these asymptotic grooming clique sizes are, as in humans, associated with some form of internal reorganization [3] as an adaptive response to the difficulties of coordination [2] (so demonstrating that linguistic mediation is not necessary), or whether females simply strive to preserve valuable associations in the absence of any internal reorganization?

There is strong support for the latter in the long-held view that patterns of female association are geared to the maintenance of valuable relationships in the face of intragroup competition. Seyfarth [6] provided the initial argument, backed by empirical support, from baboons (Papio hamadryas ursinus) [7] and vervet monkeys (Chlorocebus aethiops pygerythrus) [8]. Observed patterns of allogrooming, as a measure of association, were argued to reflect competition for access to valuable coalition partners, as measured by rank [6]. His vervet data, in particular, presented a clear, consistent pattern of association across similarly sized cohorts at a single site. High rates of grooming were associated with high rates of coalition formation, high ranking females received more grooming than they gave, females competed for access to grooming partners, and this competition therefore resulted in most grooming being exchanged between closely ranked females who also maintained spatial proximity [8].

In extending this framework, the argument has been that, within any local population, larger groups experience both greater competition for resources and reduced social time. Under these conditions, with grooming being increasingly necessary for the maintenance of valuable coalitionary relationships, the capping or restriction, of grooming clique size reflects the need to allocate a limited amount of grooming time in the most optimal fashion. When this cannot be sustained (i.e. when there is too little time available to service relationships adequately), groups will undergo fission (subject to local predation pressure), in order to restore grooming time to appropriate levels [9–11].

Comparative analyses, based on the premise of time-budget constraints, have identified, for different populations of various species, the ‘maximum ecologically tolerable group size’ (METGS), which is the size beyond which group fission is predicted to occur [9–12]. The null expectation here is that the internal organization of large female cohorts in which grooming cliques are capped will be similar to that of cliques in smaller cohorts, but simply reflects increasing competition for partners. We therefore test whether this is the case. To do so, we adapt Potts' [13] idea concerning ‘generalist’ and ‘specialist’ strategies. Potts [13] proposed, in the context of human evolution, that environmental variability would select for behavioural versatility, as reflected in ‘generalist strategies’: response sets that, while not optimal in any single context, work better than specialist strategies in the aggregate. By contrast, specialist strategies excel in a single context. Applying this terminology to vervets, we can ask whether vervet monkeys deploy a ‘specialist’ strategy in the face of changing conditions or whether they show a response that could be viewed as indicative of greater behavioural flexibility, and hence are ‘generalists’. Asking the question in this way treats behavioural variability as a source of information, rather than as ‘noise’ around a central tendency, i.e. it moves us away from the categorical approach of earlier socioecological theory towards an alternative view in which selection is argued to act on social reaction norms that encompass demographic variation both between- and within-populations and demes. Adopting the latter approach also moves us away from the increasingly insecure view that a species can be adequately characterized by consideration of a single representative group from a single population.

Vervet monkeys, although widely distributed, have a constrained range of group sizes, generally being found in groups of 20 or smaller, even in more productive tropical habitats [14–16]. This makes it difficult to identify a sufficiently broad range of female cohort sizes within a single population or habitat type. We therefore take advantage of (i) the very detailed and comprehensive analysis of grooming interactions at Amboseli [8] and (ii) the large female cohorts of the same subspecies in our study population at Samara, South Africa [17]. Our general objective is to delineate the relationship between dominance rank, spatial association and grooming allocation and to identify whether these properties of association are susceptible to scalar effects [1,2]. Our use of cross-population comparisons makes it necessary to confirm that our large study groups manifest the expected ‘demographic stress’ associated with large group size. To do so, we use a recent model published for vervet monkeys [10] to determine where the five troops sit in relation to the predicted METGS for their populations. As the results indicate that both study groups at Samara are larger than the model's estimate, whereas those at Amboseli are smaller, and as values of foraging and social time are in the predicted direction, we assume that comparison of the two populations will reveal trends that are at least qualitatively correct. We confirm that vervet monkey grooming clique sizes are capped once female cohorts reach a certain size. We also use comparative data from baboons and Japanese macaques (Macaca fuscata) to establish that this ceiling on clique size is not merely a vervet idiosyncrasy but conforms to a more general cercopithecine pattern. We then test the following predictions:

(a). Between populations

• (1) Rates of female–female (FF) aggression will be higher at Samara and will reflect an increase in both food-related agonism and, consequently, competition for access to grooming partners.

• (2) Following prediction (1), dominance hierarchies will be steeper at Samara.

• (3) The frequency of coalition formation among females will be greater at Samara than at Amboseli.

• (4) The relationship between rank and grooming will be more pronounced at Samara. While there is no statistically significant relationship between rank and the ratio of grooming received to grooming given in Seyfarth's vervet data [18], which is the formal requirement of his grooming allocation model, all three Amboseli groups showed strong correlations between ordinal rank (OR) and the absolute amount of grooming received (higher ranking females received more grooming than lower ranking ones). If this relationship is driven by the value of, and competition for, high ranking partners, then we expect (i) to find the same for the Samara females and that the relationship between grooming received by the higher ranking female and the rank distance separating two members of a dyad will be stronger than at Amboseli; and (ii) the negative relationship between rank distance and amount of shared grooming found for Amboseli will be more pronounced in the two Samara troops (RBM, RST).

(b). At Samara

By extension, we should see the same group-size effects in our two groups at Samara. Along with these, following expectations derived from the increased competition and more pronounced time-budget constraints associated with larger groups [9–11] as well as empirical findings [3–5], we predict that

• (1) Mean grooming clique size will be smaller in the larger cohort (RST).

• (2) If grooming facilitates coalition formation and is itself facilitated by spatial association, as the positive correlations at Amboseli suggest (table VII in Seyfarth [8]), then, following prediction (a (2)), we expect strong associations between these three aspects of female engagement at Samara, with the larger female cohort exhibiting stronger correlations.

2. Methods

The new data presented here were collected from two habituated troops of vervet monkeys (RBM, RST) in the Samara Game Reserve, Eastern Cape, South Africa (N_RBM = 48, N_RST = 72). Although the study population has some unique features [17], it shares with Amboseli its location in a semi-arid acacia habitat [17,19,20] and its vulnerability to three different predator classes [17,21]. Indeed, of all surveyed populations, the historical Amboseli population resembles Samara most closely, with one valuable exception. Although population densities are very similar [17], the three Amboseli troops (AmbA, AmbB, AmbC) studied by Seyfarth [8] were very much smaller (N_AmbA = 29, N_AmbB = 17, N_AmbC = 29). Kinship was not known at either site.

All adults were recognizable from natural markings and were followed on foot at a distance of 3–10 m from dawn (05.00–07.30 h) to dusk (17.00–20.00 h) on each observation day. We extracted aggressive interactions, grooming times and partner identities (IDs) from focal data samples of all adult females (N_{RBM females} = 15, N_{RST females} = 23) collected over a 12-month cycle (January–December 2009). Data were collected by N.F. and R.B., following a standardized protocol, and were acquired using electronic data loggers loaded with Pendragon Forms software. Focal samples were set at a duration of 15 min but were extended, when necessary, to allow any ongoing allogrooming to finish. We used instantaneous scan samples, taken at 30-min intervals, during which we recorded the activity of all observable animals, as well as the identity and distance of their nearest neighbours (NNs), to estimate the time allocated to grooming and foraging, as well as the identity of and distance to female NN. The frequency data collected during scans were expressed as proportions, either of each female's, or the total time budget, as appropriate. Additional data on vervet grooming clique and cohort size, as well as for time available for grooming, were provided for two troops (Picnic, Donga) occupying mixed woodland at Loskop Dam Nature Reserve [22] by Dr A.S. Barrett (2010, personal communication). There were four and six adult females in his two study troops. The Loskop vervet data, as well as published data on baboons and macaques, were used in the comparative analysis of clique size (figure 1).

Figure 1.

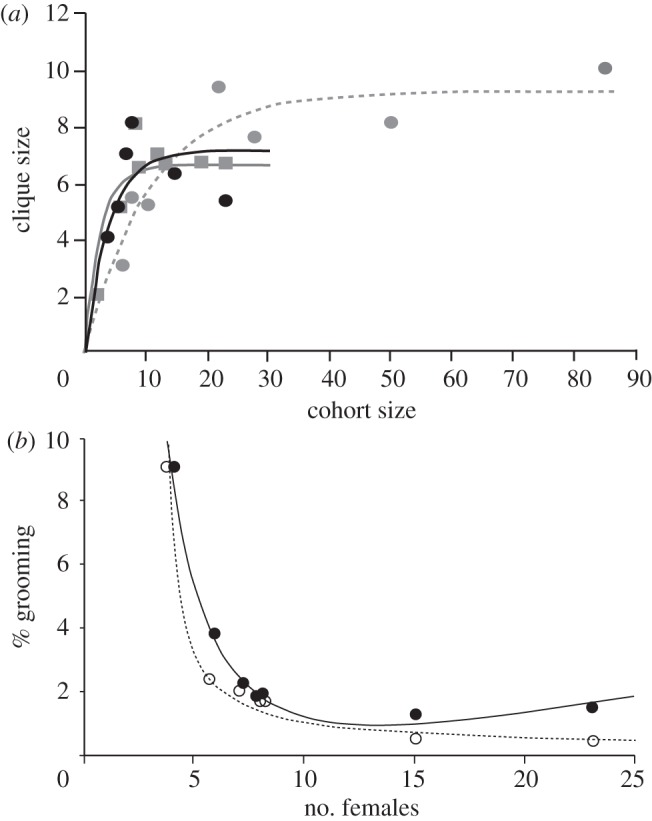
(a) The relationship between clique and cohort size, together with exponential growth curves, in vervets (black circles, black solid line. Clique size for the Loskop troops were: Picnic = 4, Donga = 5), baboons (grey squares, grey solid line) and macaques (grey circles, grey dashed line). Macaque data are from Nakamichi & Shizawa [5] and represent a mixture of wild, provisioned and captive troops. Baboon data are from wild troops in Drakensberg National Park, South Africa [4], De Hoop Nature Reserve, South Africa (S. P. Henzi and L. Barrett 2007, unpublished data), Moremi Game Reserve, Botswana [23], Mountain Zebra National Park, South Africa [7] and Tana River Forest Reserve, Kenya (V. Bentley-Condit 1992, unpublished data). (b) The relationship between cohort size and the mean percentage of social time in vervet monkeys available to each female were she to allocate time only to other clique members (solid line, solid circles) or to all other adult females (dashed line, open circles) equally. Data come from Samara, Loskop and Amboseli (time-budget values for Amboseli taken from Isbell & Young [24]). The best-fit curve for the restriction of grooming allocation to other clique members is described by the equation: y = 1.72 + 1.365 × x + 1.64/x² (r² = 0.99), while that available if time is allocated to all other cohort members is: y = 1/(9.22 + 7.44 × ln(x)) (r² = 0.99), where y is proportion grooming time and x is number of females groomed.

We used data from focal samples and ad libitum observations to construct dominance hierarchies for each troop based on the outcome of all observed decided agonistic events (N_RBM aggression = 345, N_RST aggression = 1332). Each female's dominance status at Samara was expressed as a normalized David's score (NDS) [25], whereas the data provided in table I of Seyfarth [8] were used to do the same for the three Amboseli female cohorts (AmbA: N_females = 8; AmbB: N_females = 7; AmbC: N_females = 8). Higher rank is signified by a higher NDS. The steepness of each hierarchy is then the absolute slope of the linear regression of NDS onto each female's OR.

To compare the relationship between rank and grooming allocation across the two sites, we followed Trusina et al. [26] and defined an allocation of grooming index (G_i) to qualify the hierarchical nature of the grooming networks. The allocation of grooming index was estimated as the ratio of average amount of time spent grooming individuals with a higher NDS index to the average amount of time spent grooming anyone:

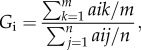where NDSk > NDSi, aik ≠ 0 and aij ≠ 0.

For a given female i, m is the number of females with NDS greater then i and n is the total number of individuals −1; aik is the time female i spends grooming individual k and aij is the time individual i spends grooming individual j.

If females did not prefer to allocate grooming towards higher ranking partners, then G_i = 1 while, if they did prefer to do so, G_i > 1. G is approximately normally distributed, centred on 1. To compare groups of different size, we standardized all NDS (StdRank):

where the highest ranking female has StdRank = 1.

All statistical models were fitted using lme4 v. 0.999375-39 in R v. 2.12.0, using the Akaike information criterion (AIC) and ΔAIC for model selection. All other analyses used JMP v. 7.1 [27], with alpha set at 0.05. Curves were fitted with CurveExpert Professional v. 1.6 [28].

3. Results

(a). Maximum ecologically tolerable group size

Combined female scan data for the two Samara troops indicate that 40.6 per cent of their time (3728/9174 scans) was spent feeding (RBM = 37%; RST = 43%). Amboseli vervets spent 35.4 per cent of their time feeding [10]. Entering these values into the time-budget estimate of METGS,

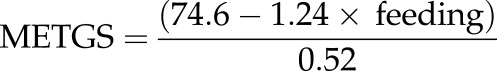produces METGS_Samara = 46.55 and METGS_Amboseli = 59.04. Although the two Samara troops were both larger than the predicted METGS, the three Amboseli troops were smaller.

(b). Grooming clique size

The mean number of grooming partners in the two troops (RBM = 6.26, range: 2–10; RST = 5.32, range: 1–12) did not differ significantly (Wilcoxon test: z =−1.28; N_RBM = 15, N_RST = 23, p = 0.2). There was no correlation between NDS and the number of grooming partners (RBM: r = 0.18, N = 15, p = 0.51; RST: r =−0.002, N = 23, p = 0.99). All females groomed one another in the three Amboseli troops (Clique sizes: AmbA = 8; AmbB = 7; AmbC = 8).

We modelled the relationship between clique and cohort size in vervets, together with comparative data from baboons and Japanese macaques, with a two-phase exponential growth model:

confirming the visual impression of capped clique sizes in all three taxa (figure 1a; vervets: a = 7.29; b = 0.29, r = 0.71, 6 d.f., p < 0.05; baboons: a = 7.13, b = 0.26, r = 0.89, 7 d.f., p < 0.01; macaques: a = 10.2, b = 0.1, r = 0.92, 6 d.f., p < 0.01).

As this relationship may be complicated by the constraints of site-specific time budgets [4,9], we also compared the average grooming time that was available for allocation, either to other clique members only, or to all other cohort members for each vervet population (figure 1b). This shows that as the size of the female cohort increases, the amount of time allocated per female drops, then rises again for clique members, but not for the total cohort, suggesting that clique size, and so grooming allocation, is adjusted in larger groups. Note that these values are of comparative relevance only, because grooming time also reflects time spent interacting with non-adult female group members.

(c). Aggression and dominance hierarchies

We assessed the rate and contexts of aggression, using 225 instances of FF agonism collected over 224.4 h of focal data from RBM (1.00 instances h⁻¹ or 0.067 instances per female h⁻¹) and 383 instances over 375.6 h from RST (1.02 instances h⁻¹ or 0.044 instances per female h⁻¹). The rate at Amboseli varied from 2.6 to 3.5 instances h⁻¹ [8].

Most aggression was associated with food competition (N_RBM = 117, 52.0%; N_RST = 207, 54.04%), occurring at a rate of approximately 0.53 instances h⁻¹ (Amboseli: 0.13–0.26 instances h⁻¹ [8]), suggesting that coalitions might be advantageous to females. However, FF coalitions against female targets accounted for only 1.33 per cent of all aggression in RBM (N = 3) and 0.78 per cent in RST (N = 3). The Samara mean of 1.05 per cent was very similar to the Amboseli value of 0.9 per cent (extrapolated from Wittig et al. [29] and Seyfarth [8, p. 809]). There were correspondingly few instances of aggression over access to grooming partners (N_RBM = 3, 1.33%; N_RST = 3, 0.78%. Amboseli: approximately 10.5 per cent; table V of Seyfarth [8]).

We fitted three general linear models to test the prediction that hierarchies were steeper at Samara (for model structure and performance, as well as for the illustration of rank slopes, see the electronic supplementary material). Dominance hierarchies were linear in both populations but, against prediction, shallower at Samara (table 1).

Table 1.

Coefficients for the model that included an interaction term between troop and ordinal rank as effect on the variation in standardized rank. The model explained most of the variability in this rank measure (F_9,47 = 281, p < 0.00001, r² = 0.978). The base level for the troop categorical variable was AmbA (Amboseli troop A). Asterisks mark terms with coefficients significantly different from zero.

term	coefficient	s.e.	t	p
intercept	1.19	0.032	37.1	<0.00001***
ordinal rank	−0.15	0.0064	−22.9	<0.00001***
troop: AmbB	−0.040	0.047	−0.8	0.41
troop: AmbC	−0.055	0.045	−1.2	0.24
troop: RBM	−0.22	0.040	−5.6	<0.00001***
troop: RST	−0.14	0.037	−3.9	0.0003***
rank: AmbB	−0.015	0.010	−1.5	0.13
rank: AmbC	0.0044	0.009	0.49	0.63
rank: RBM	0.097	0.0071	13.8	<0.00001***
rank: RST	0.10	0.0065	16.1	<0.00001***

(d). Grooming allocation

(i). Rank effects

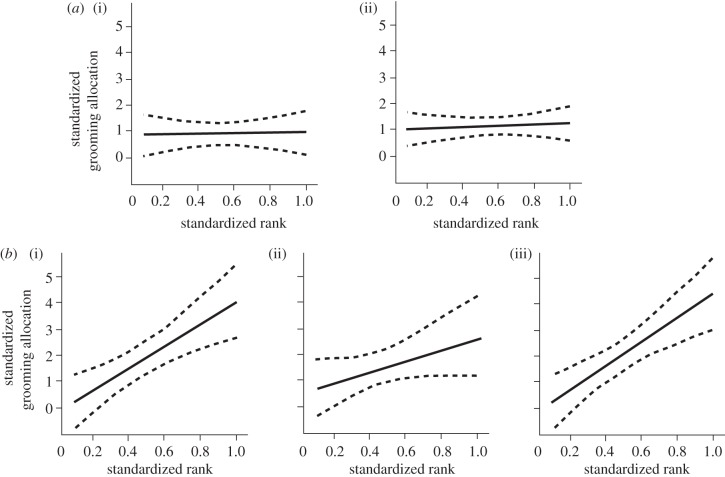
We assessed the preference for grooming up the hierarchy by comparing four linear models (for model structure and performance, see the electronic supplementary material). The best model included an interaction term between rank and site, with little support for the other variables. Figure 2 indicates preferential grooming allocation to higher ranking females at Amboseli, but not at Samara.

Figure 2.

Predicted grooming allocation (±95% CI) at (a) Samara ((i) RBM, (ii) RST) and (b) Amboseli ((i) AmbA, (ii) AmbB, (iii) AmbC), given the effects of standardized rank and site from model 4 (see the electronic supplementary material).

(ii). Rank distance effects

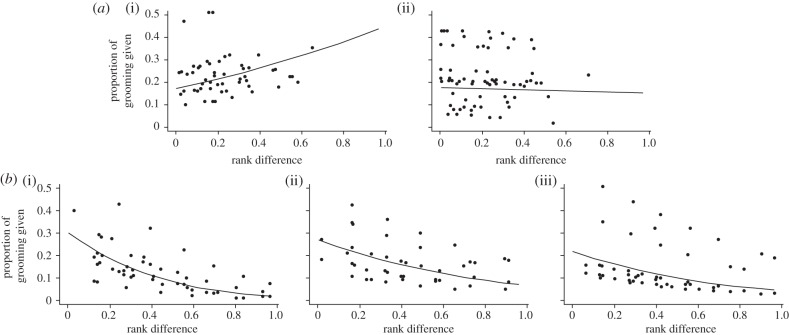
We estimated the proportion (P) of grooming female i gave to j (Gij≠Gji) given the total amount of grooming i gave. We then assessed the effect of troop identity and standardized rank difference between pairs on this measure of grooming allocation given the heterogeneity in the amount of grooming received between individuals (with recipient identity as a random effect). We fitted generalized linear mixed effects models, with varying fixed effects and a binomial error distribution. Fixed effects were selected by maximizing the likelihood and final estimates of variance were obtained, using restricted maximum-likelihood estimation. We used AIC and likelihood ratio tests for model selection because models were nested. Residuals plotted against fitted and quantile–quantile plots showed that all models met assumptions. The best-fitting model (model 4; table 2) included a variation of the effect of rank difference between troops and indicated that, whereas there was a decline in grooming as rank distance increased at Amboseli, this was not so at Samara, where RBM showed an increase with increasing rank distance, whereas there was no relationship in RST (figure 3).

Table 2.

The structure and performance of the models used to assess the relationships between grooming allocation (P_G), standardized rank distance (StdRank diff) and troop identity (troop). χ² is used to test whether terms have coefficients that differ from zero and asterisks marks terms with coefficients significantly different from zero.

model	d.f.	log likelihood		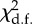AIC	ΔAIC
1. PG ∼ 1	2	−10 719		21 441	932
2. PG ∼ StdRank_diff	3	−10 629		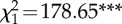21 265	756
3. PG ∼ troop	6	−10 717		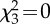21 445	935
4. PG ∼ StdRank_diff + troop	7	−10 628		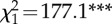21 270	761
5. PG ∼ StdRank_diff × troop	11	−10 244		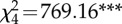20 509	0

Figure 3.

Fitted (lines) and observed (points) proportion of grooming given depending on the standardized rank difference between the receiver and the giver i at (a) Samara ((i) RBM, (ii) RST) and (b) Amboseli ((i) AmbA, (ii) AmbB, (iii) AmbC). Fitted values are modelled using the best-fitting generalized mixed effect model in table 2.

(iii). Partner preferences

To determine whether females groomed all their partners relatively equally, we compared the proportionate allocation of grooming with the ordinal allocation of grooming (the order of ‘preference’). We calculated this relationship (using log-transformed proportions) for each female and then fitted a linear model to assess whether the mean slope differed between troops. The results indicate that the slopes are steeper at Samara, indicating greater grooming investment in more preferred clique members (F_4,4.44 = 4.18; p < 0.005; figure 4).

Figure 4.

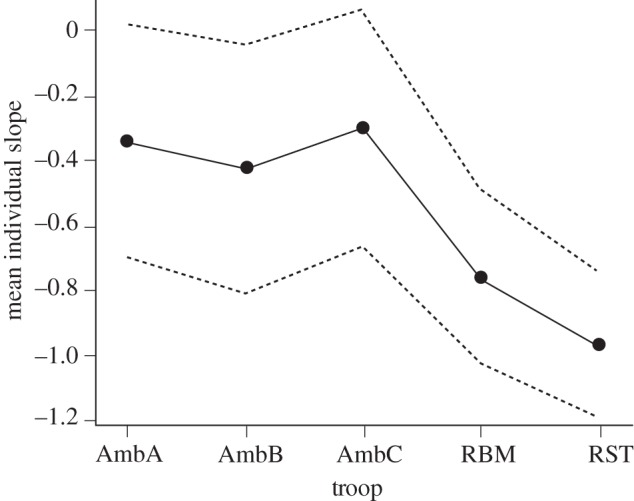
The modelled inter-troop comparisons of the mean slope (±95% confidence limits) of the relative allocation of grooming time by females to each of their partners, in descending order of preference, at Samara (RBM, RST) and Amboseli (AmbA, AmbB, AmbC).

(e). Spatial association

Figure 1b indicates that, whereas available time for cohort members continues to decline with increasing cohort size, time available to other clique members stabilizes. This raises the question of whether asymptotic clique size is a strategic response or whether it is a by-product of group-size-related changes in spatial association that impede social coordination [4]. We used scan data from Samara to identify each female's nearest female neighbour when she was foraging in order to assess the null model that grooming cliques mirrored general spatial associations, i.e. when females were free to groom, they engaged with those females in their vicinity.

(i). The number of grooming partners

In contrast to the restricted number of grooming partners, females in both Samara troops encountered many more females as NN (mean_RBM = 11.46 ± 2.74 s.d.; mean_RST = 18.26 ± 3.75 s.d.). Neither distribution differed from a Poisson model (Kolmogorov test: D_RBM = 0.19, N = 15, p = 0.43; D_RST = 0.19, N = 23, p = 0.18).

(ii). Rank effects

To determine whether there was a relationship between rank and number of NN, we entered number of neighbours as a proportion of the female cohort as the dependent variable and StdRank and troop identity as main effects in a full factorial model (F_3,34 = 0.42, p = 0.73, adj. r² =−0.05). Neither troop identity (F₁ = 0.28, p = 0.59), StdRank (F₁ = 0.025, p = 0.87) nor their interaction (F₁ = 0.9, p = 0.34) were significant. Similarly, there was no relationship between female dominance rank and the ordinal spatial rank of her most frequent NN (r_RBM = 0.145, N = 15, p = 0.6; r_RST = 0.13, N = 21, p = 0.59).

(iii). Rank distance effects

We compared the proportion of scans in which a pair of females were NN with the rank distance between the two females by fitting generalized linear mixed models, using restricted maximum-likelihood estimation, with ID (within troop) as a random effect. The best model (for random effect, see the electronic supplementary material) included an interaction term (standardized rank difference + troop + troop × standardized rank difference + random effect). Comparison of the fixed effects (table 3), using each troop in turn as the reference in the troop variable, indicated that the proportion of time an individual spent as NN was not related to rank difference at RBM but that this was the case in RST, where increasing rank distance makes it more likely that females will be NN.

Table 3.

Structure and performance of models to assess the relationships between proportion time spent as nearest neighbour, rank distance and troop identity.

model	AIC	ΔAIC
1. proportion NN ∼ troop	1985.1	3.8
2. proportion NN ∼ troop + rank difference	1985.5	4.2
3. proportion NN ∼ troop × rank difference	1981.3	0

(f). The relationship between relative grooming allocation and spatial association

We fitted five linear mixed effect models to determine the relationship between grooming and ordinal spatial ranks, with ID (troop) as a random effect (for model performance, see the electronic supplementary material). We derived ordinal spatial rank simply by allocating rank 1 to the female who, of all her grooming partners, was most frequently the target female's NN. So, although the four grooming partners of a target female might have the actual spatial ranks of 6, 12, 14 and 18, their ordinal spatial ranks would be 1, 2, 3 and 4. The results indicate that model 5 (intercept only) performed the best (0.181 ± 0.015 s.e.), with no variance attributable to the random effect (approx. 0). To indicate the lack of correspondence between grooming and spatial ranks in another way, we calculated the mean spatial association rank of each female's top-ranked grooming partner. For RBM this was 6.0 (±2.45 s.d.), whereas for RST it was 9.8 (±6.9 s.d.). Note that two females in RST had top-ranked grooming partners that were never recorded as their NNs when they were foraging.

4. Discussion

(a). Social responses to increased group size

Our results show that Samara vervet troops exceed the predicted METGS for the habitat, and that Samara troops are larger than would be expected if there were no constraints on fission. This is corroborated by a recent examination of environmental constraints on fission probability in this population [17] and, according to the conventional view, indicates that these are animals experiencing demographic stress. In line with this, Samara females experienced higher rates of feeding competition than those at Amboseli. Against this view, however, they did not experience higher levels of aggression overall, nor did they form coalitions at a higher rate or compete for grooming partners. In addition, dominance hierarchies were shallower at Samara, and rank and grooming effects were conspicuously absent, or the reverse of those expected: although Amboseli females preferred to groom higher ranking females, and showed a decline in grooming with rank distance, Samara females showed no preference to groom up the hierarchy, and there was either no relationship with rank distance or females were more likely to groom those that were distantly, rather than closely, ranked.

Notably, these patterns were produced in the context of a capping of clique size in the Samara troops (at around five to six females, in what appears to be a general cercopithecine pattern, possibly tied to the social constraints imposed by matriline size), and females invested more grooming effort in their preferred clique partners. They did not, however, associate spatially with these females, nor did females simply groom those females with whom they were spatially associated (i.e. they did not simply groom whichever female happened to be nearby). Rank had no influence on spatial association, and the effects of rank distance were seen in only one of the study troop, where increasing rank distance between females increased the likelihood that females would be NNs. Overall, then, Samara females' response to greater demographic stress did not give rise to the expected social outcome; that is, there was no evidence that females were attempting to maintain valuable coalitions and grooming relationships with those females best placed to help alleviate the negative effects of increased competition. While it is clear that our vervet females do not direct their efforts at high ranking individuals, we cannot confirm that they do not preferentially associate with matrilineal kin. Our results are intriguing because the consensus, both generally and for vervets specifically [30,31], is that, in female-bonded groups, adult kin are adjacently ranked to one another. Our findings therefore indicate either that females in larger groups no longer sustain matrilineal kin associations or that the mechanism of adult rank acquisition has changed [31]. Much the same conclusion was reached by Bentley-Condit & Smith [32], whose data on a large female baboon cohort, by indicating both the dissolution of rank-based associations generally and the link between grooming and spatial association specifically, also support the idea of a phase shift in social dynamics in the wake of the capping of clique size.

(b). Scalar effects on vervet social structure

Two interesting observations emerge from our finding that grooming clique size is capped in large cercopithecine groups. The first is that the range of the points of renormalization in the three non-human species (approx. 7–10; figure 1a) is very similar to that identified for humans. This may, therefore, reflect a more general primate trend that speaks to intrinsic problems of coordination in social groups and which might profitably be investigated further. Second, the vervet data suggest that, as with humans, this point is linked to a recalibration or realignment of individual interactions: the capping of clique size is not, it appears, a strategy that allows Samara females simply to reduce their effective group size and so operate on the same organizing principles as they do in the smaller Amboseli groups. Instead, the capping of clique size appears integral to the process by which females renegotiate the nature of social engagement. In other words, the patterns suggest the kinds of scalar effects seen in human groups, where some form of ‘renormalization’ is required once groups exceed five to six individuals.

Of course, another simpler explanation for these differences is that the Samara troops were not really demographically stressed. Because rates of FF aggression at Amboseli were much higher than at Samara, there would be less need to pursue rank-based associations, explaining the absence of competition for access to grooming partners. Although this is testable (i.e. one would predict no rank-related effects in small cohorts experiencing little aggression), a closer look at the extent and contexts of aggression, in conjunction with spatial association patterns, indicates something different. As already noted, food-related aggression occurred much more frequently at Samara and, when the values are adjusted to reflect the rate experienced by the average female, the two populations are very similar (Samara: 0.027 instances h⁻¹; Amboseli: 0.024 instances h⁻¹), suggesting both populations would experience a similar need for access to high ranking, valuable females. This holds true even though we can discount the strategic value of coalitions, which were rare at both sites. On the whole, then, the data argue against the likelihood that female vervet monkeys deploy a specialist social strategy centred on rank. At the same time, the evidence does not support the possibility that we have witnessed a descent into chaos. The capping of clique size, together with the fact that females do not simply groom others in proportion to the probability that they are neighbours, indicates that they are acting to preserve sufficient social time to allocate to particular partners [4].

One possibility is that differences in social patterns may follow simply and directly from the ease with which females can sustain proximity to one another. Females in smaller cohorts clearly can do so, as indicated by the positive correlation between proximity and grooming at Amboseli and in captivity [8,30]. As such, they are also therefore more likely to find themselves able to defend access to preferred grooming partners, explaining why the proportion of aggression associated with grooming was so much higher at Amboseli. While coalitionary aggression is rare, spatial coherence may mean that higher ranking Amboseli females effectively constitute ‘passive’ spatial coalitions [18]. That is, the simple avoidance of clusters of higher ranking females by lower ranking ones can explain the much lower proportion of resource-related competition at Amboseli. A similar argument has been made about small cohorts of capuchin monkey, Cebus capucinus [33].

However, although closely ranked (and therefore, following general findings, presumably closely related matrilineally [30]) females may find it increasingly difficult to remain together, one might expect that they would seize the opportunity to groom at times when they were close, especially if such grooming underpinned the maintenance of important rank-related social bonds [9,12,34]. Taken in conjunction with the capping of grooming cliques, the fact that Samara females do not do so suggests that there may be increasing stochasticity, not only in spatial coordination, but also in activity scheduling [35]. That is, two females, who might be inclined to interact, may find themselves near each other at times when they are unable to coordinate their schedules. The growing ease with which accurate spatial information can be incorporated into daily data collection [36,37] now offers a realistic prospect of addressing such questions of coordination in space and time.

(c). Individual flexibility in social behaviour and social specialization

This line of argument raises a further interesting consideration. Despite its theoretical centrality and enormous explanatory value [34,38], nepotistic intervention among adults, or the exercise of rank-based matrilineal power, in female-bonded primate groups may not represent a strategy in the sense of an evolved ‘genetically based decision rule’ [39, p. 132], so much as possibility for action that simply emerges from local conditions. In other words, the ‘standard’ patterns may arise from a developmentally acquired social preference for kin [40], expressed under particular conditions—smaller groups, high visibility habitats, provisioning [41]—that facilitate spatial coherence, and this produces the effects that we have come to see as basal social form.

Despite some documented intraspecific variation [42], primate social organization is not particularly labile [43]. This is noteworthy, given the variability recorded in other taxa, such as rodents and social invertebrates [42], and is likely to derive from a long-standing need to sustain relatively large groups in the face of predation [44]. The consequence is that primate flexibility cannot be organizational in the way we usually understand it but is, instead, directed at responding rapidly and adaptively to changing conditions within social units. That is, to use Schradin's [43] terminology, vervets show flexibility in social behaviour at the individual level, but not social flexibility at the population level, whereby social organization (i.e. the composition of groups) shifts in response to ecological conditions. As Schradin [43] notes, individual flexibility in social behaviour alleviates any need for group-level adjustment and makes possible the conservation of species-specific social organization, which is likely to explain why group-level flexibility is rare among the primates. This allows us a partial response to the question of what a flexible ‘generalist’ social strategy might look like. At the very least, an adaptive fine-tuning to contingency [18] requires, not only the ability to register shifts in the world, but also, to put it in human terms, an ‘easy come, easy go’ attitude to others. The flexible monkey plays the cards that she is dealt.