A novel computational sheep atria model for the study of atrial fibrillation

Abstract

Sheep are often used as animal models for experimental studies into the underlying mechanisms of cardiac arrhythmias. Previous studies have shown that biophysically detailed computer models of the heart provide a powerful alternative to experimental animal models for underpinning such mechanisms. In this study, we have developed a family of mathematical models for the electrical action potentials of various sheep atrial cell types. The developed cell models were then incorporated into a three-dimensional anatomical model of the sheep atria, which was recently reconstructed and segmented based on anatomical features within different regions. This created a novel biophysically detailed computational model of the three-dimensional sheep atria. Using the model, we then investigated the mechanisms by which paroxysmal rapid focal activity in the pulmonary veins can transit to sustained atrial fibrillation. It was found that the anisotropic property of the atria arising from the fibre structure plays an important role in facilitating the development of fibrillatory atrial excitation waves, and the electrical heterogeneity plays an important role in its initiation.

1. Introduction

Atrial fibrillation (AF) is the most common sustained arrhythmia in the developed world, affecting approximately 1.5 per cent of its population [1]. The prevalence of AF increases with age; therefore, in an ageing population AF is set to become a leading factor in morbidity and quality of life of the general population [2,3]. Although AF is a common arrhythmia, its genesis is not well understood, and, therefore, further studies to provide insights into its mechanisms are paramount. Computational models have been shown to be a powerful tool in elucidating the mechanisms underlying cardiac arrhythmias [4–7], as they allow a level of control over the system that is not possible in an experimental setting. This is because of limiting factors such as lack of specific ion channel blockers and/or difficulties in extrapolating data taken from single-cell experiments to their effect on the whole organ. But these limitations can be easily overcome when using biophysically validated computational techniques. Sheep are often used as experimental animal models to study cardiac diseases such as AF [8–12]. However, there are currently no species-specific mathematical models for sheep atria that can help interpret these data using integrative system biology approaches.

In this study, we have developed a new family of mathematical models for the electrical action potentials (APs) of different cell types of the sheep atria such as  the pectinate muscles (PMs), crista terminalis (CT), right atrial appendage (RAA), Bachmann's bundle (BB), the left atrium (LA) and the pulmonary veins (PVs). These single-cell models take into account the experimentally observed electrical heterogeneity of sheep atrial cells in the kinetics and current densities of their ion channels. The models were based on, and validated against, extant experimental data from sheep atrial cells from Lenaerts et al. [13] and Deroubaix et al. [14]. In the cases where no experimental data were available, cross-species modelling techniques were adopted using data from Burashnikov et al. [15], Li et al. [16], Ehrlich et al. [17] and Ramirez et al. [18] for canine atrial cells.

Recently, we have reconstructed a three-dimensional anatomical model of the sheep atria using extended volume imaging [19]. This reconstruction includes details of the complex fibre structure of the tissue, and the segmentation of the atria into known distinctive atrial regions. The developed single-cell models were then incorporated into this anatomically detailed reconstruction, providing a computational platform that could be used to investigate the genesis of AF and the importance of electrical heterogeneity and fibre structure on its development and sustainability.

Previous simulation studies have shown important roles for tissue electrical heterogeneity and anisotropy in the initiation of atrial re-entry in response to fast tissue pacing in rabbit [20] and human [21] atria. In sheep atria, an experimental study [22] has also revealed the important role of abrupt changes in tissue anisotropy because of the mismatch of fibre orientations between the posterior LA and the PVs in producing wavebreak leading to re-entry. However, the individual contribution of a tissue's electrical heterogeneity and anisotropy in generating AF in sheep atria, especially in the PV region, has not been studied in detail, though the PV region is a potentially arrhythmogenic area [23] and is the most common ablation site when AF is treated surgically [24]. In this study, the relative contribution to arrhythmogenesis from electrical heterogeneity and structural anisotropy in the PV region was investigated by rapid pacing, which has been demonstrated to be able to initiate re-entry in a three-dimensional model of isolated canine PVs [25]. To determine the role that heterogeneity and anisotropy play in AF initiation a series of simulations were run, both including and ignoring these factors, to identify their relevant roles in the process.

2. Methods

2.1. Developing single-cell models

Although sheep are often used in an experimental setting, they are not used for single-cell studies because of the difficulties associated with both disassociating cells and their suitability for patch clamp experiments. Therefore, there is a large amount of tissue preparation data available, but very few data on the kinetics and properties of individual ion channels, which are the type of data commonly used to develop species-specific mathematical models [4,18,26,27]. There are, however, AP recordings available from Lenaerts et al. [13], as well as AP morphology data from Deroubaix et al. [14]. To use the available data effectively to generate a model for the sheep atria the Ramirez et al. [18] mathematical models of the canine atrium were used as a base. The parameters of this model could then be adapted to represent sheep APs.

The Ramirez et al. [18] model set includes detailed descriptions of cell electrical APs in the right atrium (RA)—especially the CT, PM, RAA and atrio-ventricular ring bundle—but do not include models for the fast conduction pathway of BB, the LA or the PVs. However, these models have previously been developed for canine atria by Aslanidi et al. [28] using detailed experimental data from Li et al. [16], Ehrlich et al. [17] and Burashnikov et al. [15].

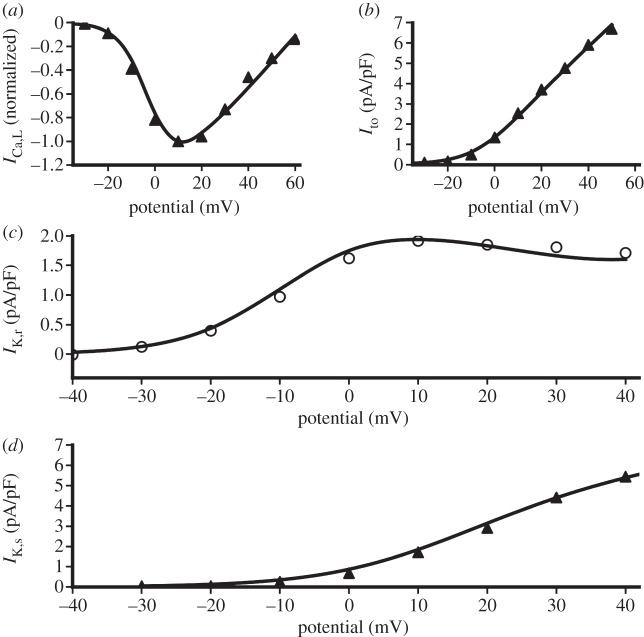
Both the Ramirez et al. [18] and Aslanidi et al. [21] model sets used voltage clamp simulations to match the mathematical current formulation to the experimental recordings. This was achieved by optimally fitting ion channel current parameters (such as steady-state activation, inactivation and current density) to experimental data. Simulated current–voltage relationships for the canine LA model are shown with the respective experimental data in figure 1. As can be seen from this figure, a good fit has been achieved for all of the currents. A similar method was used to develop all of the cell models, ensuring an electrophysiologically accurate mathematical model set.

Figure 1.

Simulated current–voltage relationships with experimental data for canine LA cells. Filled triangles adapted from Ehrlich et al. [17], open circles adapted from Li et al. [16]. The lines show results from a simulated voltage clamp using the canine LA model. I_Ca,L, L-type Ca²⁺ channel current; I_to, transient outward K⁺ channel current; I_K,r, rapidly delayed rectifier K⁺ channel current; I_K,s, slowly delayed rectifier K⁺ channel current.

From this complete set of canine atrial APs, it was possible to derive models specific to the sheep. To create these models, parameters of the RAA canine cell model were adjusted so that the simulated AP morphology matched experimentally recorded sheep APs from Lenaerts et al. [13]. Table 1 shows experimental data on the difference in AP characteristics between the canine and sheep RAA APs. As can be seen from this table, the resting potential of the sheep AP is at a more depolarized voltage. To model this, the reversal potential of the inward rectifying K⁺ current, I_K1, was shifted by −5 mV and the time constant of activation was reduced by 10 per cent. To reduce the overshoot of the AP the fast Na⁺ current, I_Na, was reduced by 50 per cent, and the transient outward K⁺ current, I_to, was reduced by 70 per cent to bring the notch to a more depolarized potential. The ultra-rapid delayed K⁺ current, I_K,ur, and the L-type Ca²⁺ current, I_Ca,L, were reduced by 70 and 20 per cent, respectively, to ensure that the action potential duration (APD) matched the recorded value of Deroubaix et al. [14]. This resulted in a maximum I_Ca,L current density of −3 pA/pF, which matches the reported values of both Lenaerts et al. [13] and Deroubaix et al. [14]. These changes resulted in a species-specific sheep RAA AP that matches well with reported AP properties [13,14]. It was then assumed that the same ionic changes used to differentiate between different cell types of the canine atria would apply to the sheep atria. This produced a full set of mathematical models for the sheep atria, shown in §3.1.

Table 1.

Experimental data on AP properties for canine and sheep RAA from Ramirez et al. [18] and Lenaerts et al. [13], respectively. APD₉₀, action potential duration at 90% repolarization.

	canine	sheep
overshoot (mV)	31	22
resting potential (mV)	−84	−75
notch potential (mV)	−8	7
APD90 (ms)	205	202
amplitude (mV)	114	97

All equations for the single-cell sheep models are available in the electronic supplementary material.

2.2. Developing the three-dimensional atria model

The computational three-dimensional atria model was developed by incorporating the formulated single-cell models into an anatomically detailed three-dimensional geometry of sheep atria. The three-dimensional sheep atria were previously reconstructed using extended volume imaging [19]. In brief, the tissue was set in resin, then imaged at 50 μm intervals using a high-resolution camera with an in-plane resolution of 8 μm [29]. The complex fibre structure of the tissue was extracted using three-dimensional eigenanalysis of the structure tensor constructed from the image volume [29]. In addition to reconstructing the fibre orientation data, the tissue was also segmented into different atrial regions. The left and right atria were segmented along the atrial groove, and the posterior LA (including the four PVs) was segmented from the rest of the atria (figure 2). The CT, BB and PMs were segmented based on their distinguishing anatomical structure and aligned fibre orientation, the results of which are shown in figure 2.

Figure 2.

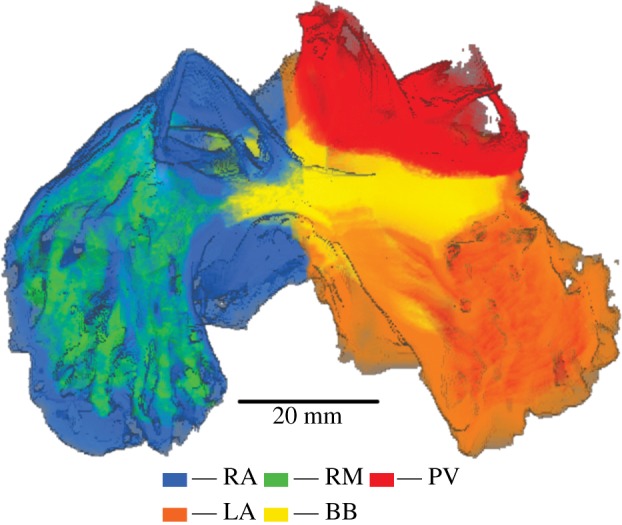
Reconstruction of the three-dimensional sheep atria segmented into different atrial regions. The regions of the right atrium (RA), left atrium (LA), pectinate muscles (PM), Bachmann's bundle (BB) and pulmonary veins (PV) were identified and colour coded.

The AP propagation throughout the tissue was simulated using the monodomain reaction–diffusion equation [20],

2.1

where V is the membrane potential, t is the time, D is the diffusion tensor describing the AP spread in relation to the orientation of the myofibres, I_ion is the total ionic membrane current and C_m is the capacitance of the cell membrane. Equation (2.1) was solved in the three-dimensional spatial domain provided by the tissue geometry. Single-cell models were mapped onto the respective segmented regions of the atria as regional variations of I_ion. The ratio of the diffusion coefficients that make up the diffusion tensor, D, was chosen so that the produced activation time and conduction velocities of the atria match those measured experimentally [22,30,31]. It was found that a diffusion ratio of 6 : 1 (parallel : perpendicular to fibre direction) gave good agreement with these data. The fibre orientation vectors were averaged to provide local directions of fibres in 0.9 mm³ voxels. The simulations used a finite difference numerical scheme using a forward Euler integration method with time and space steps of 0.005 ms and 0.3 mm, respectively.

2.3. Investigating the mechanisms of atrial fibrillation

The arrhythmogenic properties of the PV region were investigated; in particular, the genesis of AF through rapid spontaneous excitation from the PV sleeves. A series of short-coupled stimuli (three stimuli with a cycle length of 100 ms) were given to a small section of the sleeve of the right anterior PV. After this point no more excitations were given to the tissue. This was carried out for three cases. The first considered both the electrical heterogeneity and the complex fibre structure of the atria. Each cell type in the tissue was simulated using the appropriate AP model, and preferential conduction was modelled along the direction of the myofibres. The second case considered only the electrical heterogeneity, ignoring the myofibre architecture. In this simulation, the conduction was isotropic. The third case included anisotropic conduction, but the whole tissue was simulated using the AP model of the RAA, ignoring the electrical heterogeneity of the atria.

3. Results

3.1. Three-dimensional sheep atria

Figure 3 shows the simulated APs of variant canine atrial cells based on detailed electrophysiological data (as shown in figure 1). The characteristics of the simulated APs (shown in figure 3) fit well to experimental recordings. The resting potential of the simulated LA and BB APs (−83 mV) is the same as that of the Ramirez et al. [18] RA models. This is in accordance with findings of Li et al. [16], who reported no difference between LA and RA resting potentials, and Burashnikov et al. [15], who measured the BB AP experimentally. The overshoot and amplitude of the LA AP are also in agreement with experimental data from Ehrlich et al. [17] and Li et al. [16], with values of 30 and 113 mV, respectively. The simulated APD₉₀ of the LA cell is 164 ms, which lies near the mean of the measured values of Li et al. [16] and Ehrlich et al. [17] of 140 and 180 ms, respectively. The amplitude of the model BB cell is 115 mV, with an APD₉₀ of 279 ms, both of which match well with recordings from Burashnikov et al. [15]. The resting potential of the PV cell model is −65.7 mV, the amplitude is 75.7 mV and the APD₉₀ is 162 ms, all of which match experimental data from Ehrlich et al. [17].

Figure 3.

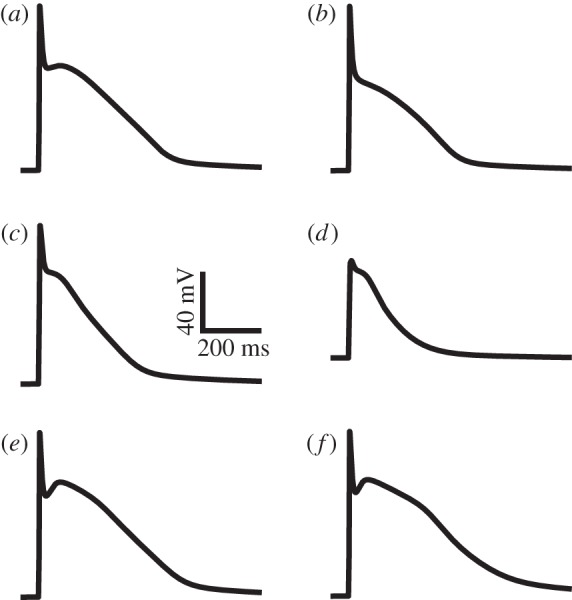
Simulated action potentials from the developed canine models for the (a) right atrial appendage, (b) pectinate muscles, (c) left atrium, (d) pulmonary veins, (e) crista terminalis and (f) Bachmann's bundle.

The developed set of canine atrial AP models was then modified to simulate APs for sheep atrial cells. Results are shown in figure 4. As can be seen in figure 4a, the AP simulation from the RAA matches well with the experimental recording from Lenaerts et al. [13]. The APD₉₀ of the RAA AP is 202 ms, the resting potential is −75 mV, the overshoot is at 22 mV and the amplitude of this AP is 97 mV. These parameters match well with data from Deroubaix et al. [14], as well as with those from Lenaerts et al. The APs from the other cell types in the atria show the same relative morphological differences (such as APD₉₀, resting potential and amplitude) as those found in other mammalian atrial models such as the canine and rabbit [15,18,20]. The resting potentials of the PM, CT, BB and LA are also −75 mV, whereas the PV model has a higher resting potential of −67 mV, which matches qualitatively with the results of the canine APs. The same is true of the AP amplitude, which is 97 mV for all cell types except PV, which has a smaller amplitude of 70 mV. The APD distribution throughout the atria matches the same pattern seen experimentally in other species [15,18,20], with the longest duration in the BB cell, then the CT, RAA, PM, LA and the shortest duration in the PV. The AP properties of the canine cell models are shown in figure 5a. The AP properties for the new sheep cell models are shown in figure 5b, which illustrates how the AP heterogeneities across the atria match well with those seen in the canine model set.

Figure 4.

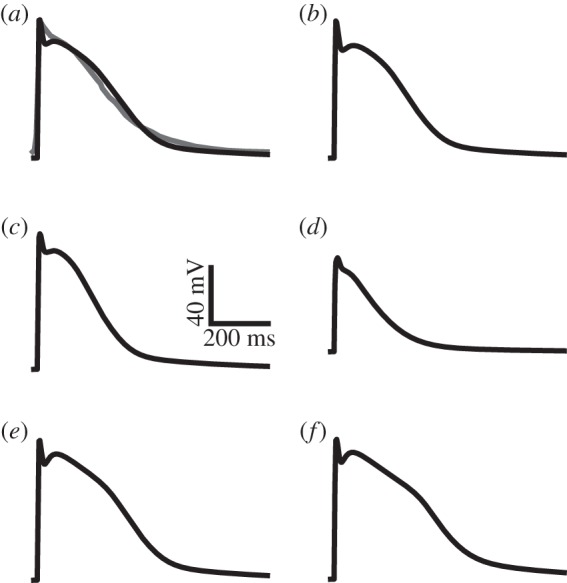
Simulated action potentials from the developed sheep models for the (a) right atrial appendage, (b) pectinate muscles, (c) left atrium, (d) pulmonary veins, (e) crista terminalis and (f) Bachmann's bundle. The grey line in (a) shows the experimentally recorded sheep action potential from Lenaerts et al. [13].

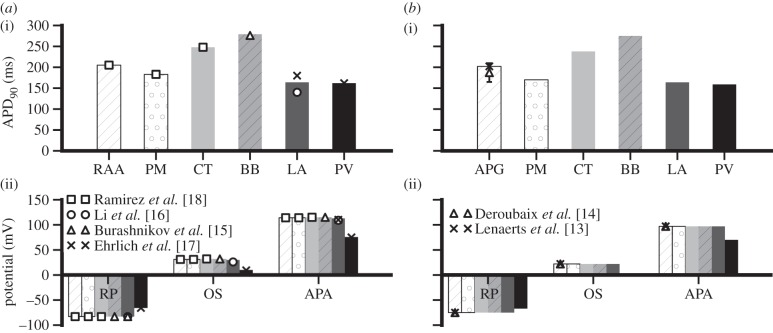
Figure 5.

Simulated AP properties with available experimental data for (a) canine and (b) sheep models. APD₉₀ values for each atrial cell type are shown in (i). In (ii) the resting potential (RP), overshoot (OS) and AP amplitude (APA) are shown for the same cell types. The source of the experimental data is labelled for each species in (ii) [13–18].

The sheep atrial AP models were then incorporated into the three-dimensional atrial geometry using the finite difference method. Experimental studies using sheep often concentrate on a section of either the RA or LA [22,32,33]; therefore, data for the atrial activation time in the entire atria are not available. However, it is possible to validate the three-dimensional model based on experimental conduction velocity measurements. Simulated conduction velocities in the atria are between 0.8 and 1.5 m s⁻¹, with the fastest conduction being seen along BB. These results are consistent with experimental conduction velocity measurements from sheep atria [22,30,31]. In addition to BB, preferential conduction is also seen along other organized fibre structures such as the CT and PMs, as would be expected.

3.2. Role of electrical heterogeneity and anisotropy in atrial fibrillation

A series of three short-coupled stimuli (with a time interval of 100 ms) applied to a small section of the sleeve of the right anterior PV was able to initiate a re-entrant excitation wave that degenerated into multiple re-entrant wavelets (AF). Results are shown in figure 6. In simulations, it was found that a re-entrant excitation wave could be initiated when the electrical heterogeneity of the atria was considered. Such an initiation of a re-entrant excitation wave by rapid pacing in the PV region was independent of the consideration of structural anisotropy, as it was initiated both with and without the fibre orientation data. However, the development of AF (i.e. degeneration of a re-entrant excitation wave into multiple re-entrant wavelets) was found to be different between these two cases.

Figure 6.

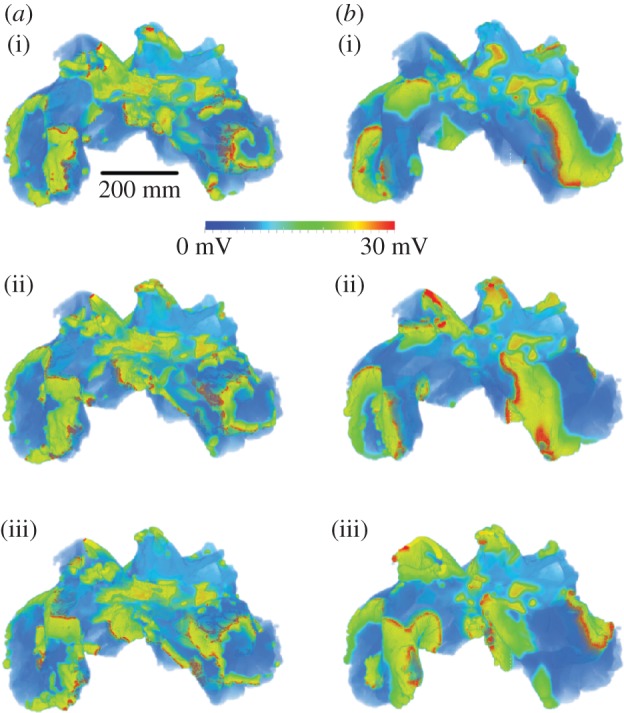
Snapshots of simulated atrial fibrillation in the three-dimensional sheep atria at 5 ms intervals (superior–anterior view), (a) with and (b) without consideration of the complex fibre orientation. Snapshots taken from 7000 ms simulation time (i) to 7010 ms (iii).

3.2.1. Simulation with heterogeneity and anisotropy

When a re-entrant excitation wave began in the tissue, it first occurred around the sleeves of the PVs. When the fibre structure was modelled, the re-entry was conducted anisotropically, leading to breakdown of the wavefront of excitation waves, forming a fibrillatory pattern with a driving rotor seen in the LA (figure 6a). This resulted in an irregular and fibrillatory atrial excitation pattern throughout most of the tissue. Spectrum analysis of recorded time series of APs from RA and LA shows a broader range of frequencies in the RA than in the LA, but with the dominant frequency in the LA higher than in the RA, suggesting that the re-entrant wave in the LA is the driving rotor. The driving rotor in the LA maintains regular excitation in this part of the tissue, whereas the breakdown of wavelets in the RA leads to a higher level of disorganization. This is in agreement with electroanatomic and optical mapping of the whole atria [34–36], where dominant driving frequencies were seen in the LA with more disorganized activation in the RA. The fibrillation persists for the duration of the simulation (more than 10 s).

3.2.2. Simulation with heterogeneity but no anisotropy

When the fibre orientation was ignored the re-entrant waves also move from the PV region to the LA, but, as can be seen in figure 6b, they co-exist and rotate around the whole area of the LA and RA. This leads to wavelets of a longer wavelength that produce a more homogeneous fibrillatory pattern, and a more even distribution of frequencies throughout the atria. Again, the fibrillation persists for the duration of the simulation (more than 10 s).

3.2.3. Simulation with anisotropy but no heterogeneity

When the electrical heterogeneity was not modelled AF could not be induced using this pacing protocol, and planar wave excitation was seen consistently. These results are consistent with previous studies of AF initiation in the human RA [21].

4. Discussion

A biophysically detailed computational model of the three-dimensional sheep atria has been developed, which includes heterogeneous cellular models for the electrical APs of the sheep atrial myocytes. The characteristics of simulated atrial APs from these models are consistent with experimental measurements of electrophysiological details such as APD₉₀, resting potential and amplitude [13,14], and the conduction velocities within the three-dimensional model are consistent with experimental recordings [22,30,31]. To facilitate the development of these models, it was necessary to use cross-species modelling techniques using electrophysiologically detailed models of canine atria [18,28]. These canine models also match well with experimental data for both individual ion channels and AP properties [16–18].

The developed computational platform has been used to investigate the initiation of AF through rapid stimuli in the PV region, in an attempt to elucidate the individual contribution of electrical heterogeneity and anisotropy to the initiation and development of fibrillation within the atria. It is clear that AF can be initiated through spontaneous activity in the PV region, with simulations showing clear AF both with and without the complex fibre structure of the atria. This shows that electrical heterogeneity plays a key role in AF initiation, and may also explain why the PV region is a common source of arrhythmogenesis, as the largest electrical differences are seen in this region, between the PVs and the LA. However, it is also clear that the fibre structure plays an important role in the development of AF. When the fibre structure was ignored regular re-entrant patterns were seen, with macroscopic re-entrant wavelets (figure 6b). When the fibre structure was considered the fibrillatory waves broke down further, with multiple small wavelets throughout the tissue (figure 6a). This difference in wavelengths can, at least in part, be attributed to a change in conduction velocity between the two cases. The diffusion coefficients were chosen such that the average conduction velocity in the LA between the two cases was constant. However, owing to the absence of a preferential conduction direction when the fibre orientation is ignored, there is a reduction in conduction velocity in other regions of the tissue such as the RA (specifically along the PMs and CT) and BB in this case. This could lead to the difference in fibrillatory patterns observed. In the case considering anisotropy and heterogeneity a mother rotor is seen in the LA which appears to drive the fibrillation, with a more disorganized activation pattern in the RA. When the conduction is isotropic the waves break down only when they encounter a structure such as the PVs or superior vena cava, or when re-entrant wavelets collide. The difference in wavelengths between the two cases would contribute to this behaviour, as would the differences in anisotropy. The fibre structure in the LA is much more homogeneous than the complex structures of the PV region and the RA, which contains the CT and PMs. When fibre orientation is considered the highly anisotropic conduction caused by these structures could cause the rapid breakdown of re-entrant waves. This shows the importance of including fibre orientation data when simulating arrhythmogenesis, especially in the atria. As the fibre structure does not follow an organized pattern such as that seen in the ventricles, it has often been ignored by the modelling community. This study highlights the crucial role that fibre structure can play in arrhythmogenesis, and the importance of its consideration when devising treatment strategies.

5. Limitations

Similar to all other models for the electrical AP of cardiac myocytes, the presented models for sheep atrial myocytes do have intrinsic limitations. Though possible sheep-specific data have been used, data from other species (canine) have to be taken  because of the lack of available data on ionic channel kinetics and properties of sheep atrial myocytes. In addition, it was assumed that the same currents are present in sheep atria as in canine atria, which might not necessarily be the case as it is possible that some other currents are present in sheep atria, but not in canine atria. However, so far there are no data to suggest that the types of ion channels vary between canine and sheep, and the currents modelled are those present in the atria of several other species [20,21,37], which indicates that this is a valid assumption.

Experimentally, it has been reported that to sustain AF it is necessary to induce electrical or structural changes through protocols such as prolonged tachypacing, or the application of acetylecholine to reduce the APD [31,38,39]. In our simulations, persistent AF was generated without involving such electrical or structural changes. This may be owing to the limitations of the model, which warrants further studies. However, such discrepancy between the simulation results and previous experimental studies [31,36,37] on sustained AF does not alter our conclusions regarding the role of electrical heterogeneity and anisotropy in AF initiation and development.

6. Relevance of the study

This study is the first to dissect the relevant contribution of anisotropy and heterogeneity in the onset and development of AF through PV stimulation using computational methods. It adds support to the conclusions of the studies of Aslanidi et al. [20,21] in showing the important role of electrical heterogeneity and anisotropy in AF genesis. But the current study is distinct from those previous computational studies [20,21] as the present study focuses on the role of electrical heterogeneity and anisotropy in the initiation of AF in the PV region, rather than in the junction of the PM and CT [20]. In the study of Aslanidi et al. [21], simulations were carried out in a model of human atria that implemented rule-based fibre orientation, not anatomically accurate structure determined from experimental reconstruction. The present study is, therefore, the first computational study that investigates the development of AF using an anatomically detailed model that includes heterogeneous electrophysiologically detailed cell models. This study extends our previous work describing the development of the anatomical three-dimensional sheep geometry [29], which used simplified Fenton–Karma AP models to simulate activation in the tissue.

Klos et al. [22] conducted an experimental AF study using Langendorff perfused sheep hearts and investigated the role of anisotropy in the initiation of fibrillation. Their study revealed that abrupt changes in tissue anisotropy between the LA and the PVs play an important role in AF genesis. Our simulation results are consistent with their findings, and this agreement validates our three-dimensional model. Our study is distinct from that of Klos et al. [22] as, being a mathematical investigation, we were able to eliminate anisotropy from the tissue completely to dissect its role in AF initiation. We also studied the effects of electrical heterogeneity and how AF progresses through the atria, whereas Klos et al. [22] focused on AF initiation in a section of the LA and PVs only. Calvo et al. [40] recently conducted a study investigating the differences between spontaneous and induced AF. They concluded that induced AF closely matched spontaneous AF, which validates the clinical relevance of this study.

7. Conclusions

In conclusion, we have developed a novel biophysically detailed model for three-dimensional sheep atria that considers electrical heterogeneity and anatomical anisotropy. We have used this model to show that electrical heterogeneity is key to the initiation of AF, and that anisotropy because of the fibre structure of the tissue plays an important role in its development. The developed model provides a basis for further development of the sheep-specific three-dimensional atria model, and provides a powerful tool for investigating the mechanisms underlying cardiac arrhythmias, and its detailed electrophysiological basis makes it suitable for studying the effects of surgical and pharmacological actions on the progression of atrial fibrillation.