Heterogeneous and anisotropic integrative model of pulmonary veins: computational study of arrhythmogenic substrate for atrial fibrillation

Abstract

Mechanisms underlying the genesis of re-entrant substrate for the most common cardiac arrhythmia, atrial fibrillation (AF), are not well understood. In this study, we develop a multi-scale three-dimensional computational model that integrates cellular electrophysiology of the left atrium (LA) and pulmonary veins (PVs) with the respective tissue geometry and fibre orientation. The latter is reconstructed in unique detail from high-resolution (approx. 70 μm) contrast micro-computed tomography data. The model is used to explore the mechanisms of re-entry initiation and sustenance in the PV region, regarded as the primary source of high-frequency electrical activity in AF. Simulations of the three-dimensional model demonstrate that an initial break-down of normal electrical excitation wave-fronts can be caused by the electrical heterogeneity between the PVs and LA. High tissue anisotropy is then responsible for the slow conduction and generation of a re-entrant circuit near the PVs. Evidence of such circuits has been seen clinically in AF patients. Our computational study suggests that primarily the combination of electrical heterogeneity and conduction anisotropy between the PVs and LA tissues leads to the generation of a high-frequency (approx. 10 Hz) re-entrant source near the PV sleeves, thus providing new insights into the arrhythmogenic mechanisms of excitation waves underlying AF.

1. Introduction

Atrial fibrillation (AF), associated with irregular electrical activations and contractions of the atria, is the most common sustained cardiac arrhythmia [1]. AF is a major cause of morbidity and decreased quality of life: the rate of hospitalization for AF and costs of its treatment are increasing in epidemic proportions [2]. The myocardial sleeves of the pulmonary veins (PVs) extending into the left atrium (LA) have been recognized as the primary sources of high-frequency electrical activity during AF, and PV ablation is routinely used to terminate AF clinically [1,3]. However, the mechanisms by which the PVs can generate arrhythmic substrate are unclear, and its clinical treatments have significant intrinsic limitations [1].

Electro-anatomical animal studies of the PV sleeves [4,5] have revealed significant repolarization heterogeneities and a complex arrangement of fibres resulting in conduction discontinuities and unstable re-entrant waves. Similar activation patterns have been observed at the PV–LA junctions during catheter mapping in AF patients [6], which led to suggestions that high-frequency activity in the PVs can be sustained by re-entry. However, the role of predisposing conditions—such as electrical heterogeneity and conduction anisotropy in the PVs—in the generation of arrhythmic substrate have not been dissected.

Computational modelling provides a framework for integrating multi-scale and multi-modal data and understanding arrhythmogenesis in the heart [7], including the atria [8]. However, owing to the lack of complete experimental datasets from human or a large animal species, existing models of the atria often use a simplistic description of electrical properties or caricature tissue micro-architecture and anisotropy [9]. Thus, even the most recent three-dimensional models of the entire atria [8,9] have not included descriptions of PV electrophysiology and PV anisotropy, and hence have not considered important factors that may predispose to AF.

The aim of this work is primarily to develop and study an integrative biophysically detailed model of canine PVs and surrounding LA tissue, the missing link in three-dimensional atrial modelling. The details of tissue geometry and fibre orientation are based on a recent contrast micro-computed tomography (micro-CT) reconstruction of canine atria [10]. The anatomical models are integrated with previously developed detailed biophysical models for the canine LA and PV cell [11]. The latter are based on multi-scale (ionic channel to cellular action potential (AP)) electrophysiological data from the dog [12,13]. The resultant integrative three-dimensional model is used to dissect the role of electrical heterogeneity and anisotropy in the genesis of re-entrant waves underlying AF.

2. Methods

2.1. Tissue geometry

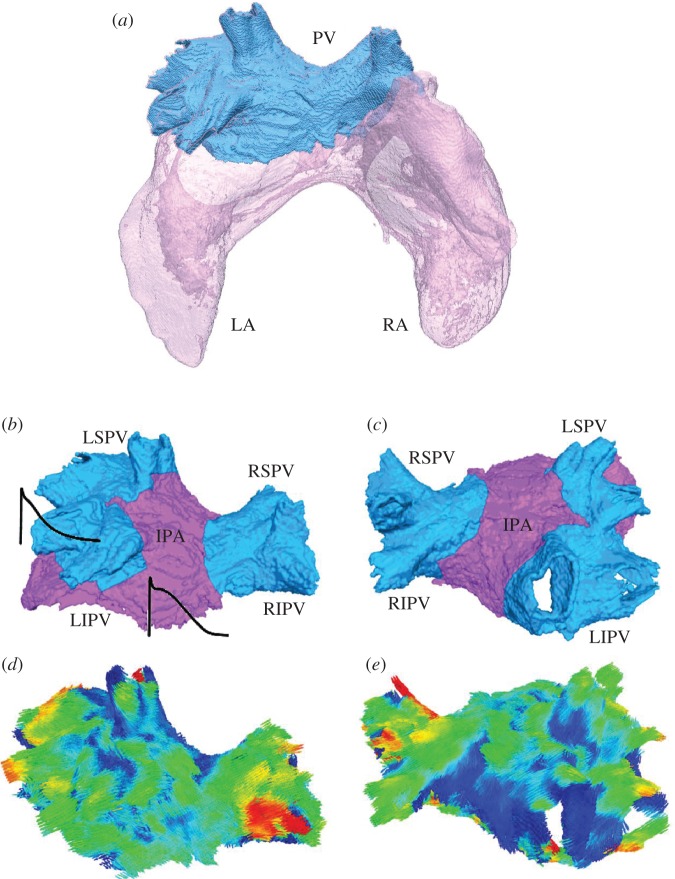
Micro-CT uses differential X-ray absorption by biological tissues to reconstruct their three-dimensional geometries at micrometre resolution. Recent ex vivo studies have shown that contrast between cardiac myofibres and connective tissue in micro-CT images can be enhanced by iodine staining [10,14]. This technique was applied to reconstruct a canine heart—primarily, the atria [10]—with an effective resolution of approximately 70 μm [10]. Figure 1a illustrates the three-dimensional atrial geometry reconstructed from micro-CT images, with the segmented region of the LA adjacent to the insertion of the PVs. The latter PV region (seen in figure 1a) was further segmented into four PV sleeves and the inter-pulmonary area (IPA) (figure 1b,c).

Figure 1.

Geometry of the PV region. (a) Anterior view of the entire atria (translucent pink), with the segmented PV region (blue). The PV region has been segmented previously [10] based on its distinctive structural features (such as the fibre arrangement and wall thickness) compared with the LA. (b,c) Anterior and posterior views, respectively, of the PV region. The PV sleeves and joint inter-pulmonary area (IPA) are shown in blue and purple, respectively. LSPV, left superior PV; RSPV, right superior PV; LIPV, left inferior PV; RIPV, right inferior PV. (d,e) Fibre orientation in the PV region shown in the same anatomical orientation as anterior view and posterior view, respectively. Arrows are coloured according to the main local fibre orientation component along the anterior–posterior direction, so that blue/red arrows represent fibres mostly pointing towards the posterior/anterior direction, and green arrows represent fibres mostly transverse to the anterior–posterior direction.

Segmentation of the PV region into the PV sleeves and IPA used a computational approach guided by detailed histological data [15]. First, activation of the PV region was simulated using a histology-based three-dimensional sheep atria model [15]. For each of the PV sleeves—segmented from the histological data [15]—a distal site was chosen 5 mm away from the PV ostium. An electrical stimulus was applied to each distal PV site, resulting in the conduction from the chosen PV sleeve towards the IPA with a velocity of approximately 1.5 m s⁻¹. Time, T_act, required for the activation of the entire PV sleeve was measured. Second, an expansion algorithm was used to segment the PV sleeves in the canine model. As in the sheep model, an anatomically matched distal site was chosen in each of the PV sleeves 5 mm away from the PV ostium, and the respective activation with a velocity of approximately 1.5 m s⁻¹ was simulated. For each PV sleeve in the canine model, tissue activated during time T_act—known from the respective simulations of the histological model—was segmented. As a result, all four PV sleeves were segmented (blue areas in figure 1b,c), with rest of the tissue assigned as the IPA (purple area in figure 1b,c).

2.2. Fibre orientation

Structure tensor analysis [15,16] was applied to the segmented micro-CT images in order to determine the main orientation of the myofibres on a voxel-by-voxel basis. The obtained fibre orientation field is shown in figure 1d,e, and in more detail in figure 2d,e. Open-source software for scientific visualization, Paraview v. 3.10.1 (Kitware, Clifton Park, NY), was used to visualize three-dimensional streamline trajectories propagating from a set of starting seed points in several regions of interest. Such regions of interest were chosen through the left superior PV (LSPV), right superior PV (RSPV), left inferior PV (LIPV), right inferior PV (RIPV) and IPA. Separate bundles corresponding to different regions/sets of seed points were visualized with contrasting colours to produce a clear image of fibre tracks in the entire PV region (figure 2a).

Figure 2.

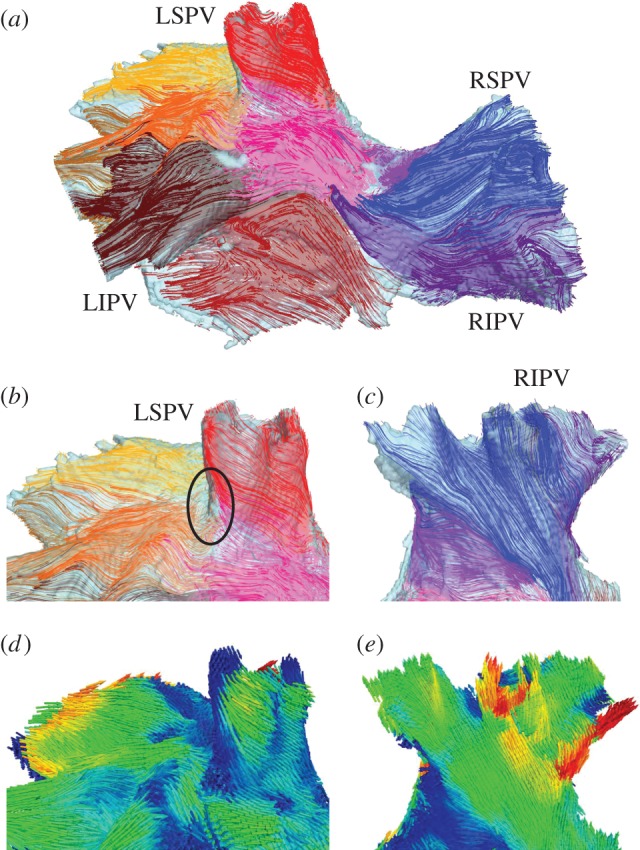
Fibre orientation in the PV region. (a) Anterior view of the PV region, showing the main fibre bundles in several areas (an arbitrary colour is chosen to distinguish each bundle). (b) Details of the main fibre tracts near the sleeve of the LSPV. Most of the fibres wrap around the vein's ostium in an oblique direction. An area of sharp changes in the fibre directions between the LSPV and IPA is shown with a black circle. (c) Detail of the main fibre tracts along the sleeve of the RIPV. It can be seen that most of the fibres are oriented longitudinally or obliquely in relation to the vein. Fibre orientation patterns in (b) and (c) are in good agreement with anatomical observations [17]. (d) and (e) Main fibre directions shown in the same view as (b) and (c), respectively. Colours are the same as in figure 1d,e.

Details of the main fibre tracts along the sleeves of the LSPV and RIPV are shown in figure 2b,c, respectively, whereas figure 2d,e visualizes local fibre orientation using arrows aligned with the fibre orientation vectors. The majority of the fibres run down the PV sleeves in ‘spiralling’ oblique directions, eventually merging with longitudinal fibres in the IPA. This is in good agreement with anatomical observations [17]. However, such a change of direction cannot be smooth everywhere around the veins, which leaves areas with abrupt fibre angle changes between the PVs and IPA (figure 2b). Such abrupt changes have been observed in other studies [4,17] and linked with arrhythmogenic conduction changes [4].

2.3. Conduction anisotropy

Conduction of electrical signals in the heart depends strongly on the arrangement of cardio-myofibres. This is because gap junctions, membrane-spanning protein structures that permit intercellular electrical excitation conduction, are more abundant in the terminal ends of myofibres than in their lateral walls [18]. As a consequence, conduction in cardiac tissue is anisotropic: it is faster along each fibre than transverse to it. This can be modelled using two different characteristics for electrical coupling in cardiac tissue: the longitudinal, D_||, and transverse, D_⊥, diffusion coefficients. These characteristics are tissue-type dependent. Values of the diffusion coefficients in our model were set as follows: D_⊥ = 0.15 mm² s⁻¹ throughout the atria, with the anisotropy ratio, D_||: D_⊥, of 10 : 1 in the IPA and 16 : 1 in the PV sleeves. The choice of values enabled us to simulate conduction velocities of approximately 1.5 and 0.25 m s⁻¹ along and transverse to the PV bundles, and 0.9 m s⁻¹ along the IPA bundles in the three-dimensional model. These velocity values are in agreement with respective experimental data from the dog: approximately 1.3–1.5 m s⁻¹ along and 0.2–0.3 m s⁻¹ transverse to the PV bundles [4], and approximately 0.8–1.0 m s⁻¹ in the high LA [19].

In order to obtain sustained re-entry, the normal values of both diffusion coefficients, D_|| and D_⊥, were reduced by 30%, which mimics experimentally observed decreases in gap junction coupling associated with the early stages of AF-induced structural remodelling [18,20]. After such a reduction in coupling, the conduction velocities simulated with the model were reduced from approximately 1.5 to 1.25 m s⁻¹ along the PV sleeves, from approximately 0.25 to 0.20 m s⁻¹ transverse to the PV sleeves, and from approximately 0.9 to 0.75 m s⁻¹ in the IPA. This is in good agreement with experimental measurements [21] that showed that the conduction velocities in the remodelled canine atria are decreased by approximately 15% during the first week of AF-induced remodelling.

2.4. Cell electrophysiology

The rhythmic beating of the heart is driven by periodic waves of electrical excitation—APs—that spread through the cardiac chambers triggering their contractions. The AP generation is underlain by the dynamics of ionic currents across the cell membrane [11–13,22]. Cardiac cell models describing such ionic currents and the resultant AP are normally based on the tissue-specific electrophysiological data. Thus, experimentally validated models have been developed for canine atrial cells [22], including the specific LA and PV regions [11]. Note that the IPA is electrophysiologically similar to the LA wall, rather than PVs [13]. Therefore, the previously developed AP model for the LA cell [11] is used for the IPA, and the previously developed AP model for the PV cell [11] was used in all four PV sleeves.

Figure 1b illustrates varying AP morphologies in the PV and IPA/LA cells. The observed difference in the AP duration (APD₉₀, commonly measured at 90% repolarization) is linked with the refractory period—the time period following an AP, during which a new AP cannot be initiated and conduction fails. The simulated APD₉₀ in the IPA/LA cell was 169 ms, which is within the experimentally reported range of 153 [12] to 193 ms [13]. The simulated APD₉₀ in the PV cell was 157 ms. Shorter APDs in the PV than in the LA also agree with the experimental data [13]. Detailed comparisons between the AP characteristics simulated using the PV and LA models and measured experimentally can be found elsewhere [11,23].

2.5. Three-dimensional simulations

The AP propagation through the PV region was simulated by solving the monodomain equation on a three-dimensional geometry grid, as described previously [8]. Briefly, each voxel in the 100 × 200 × 200 grid that belonged to the tissue was labelled as the PV or IPA, and assigned the respective AP model [11], a local fibre orientation vector and diffusion coefficients. All simulations were run using a time step of 0.001 ms and 0.14 mm spatial resolution (which is half the resolution of the original micro-CT dataset [10]). Simulations were performed under these baseline conditions and also under isotropic and homogeneous conditions. The role of heterogeneity was studied by using the PV cell model only throughout the entire tissue. The role of anisotropy was studied by setting an average value D_|| = D_⊥ = (1.50 + 0.15)/2.0 = 0.825 mm² s⁻¹ throughout the tissue, such that the anisotropy ratio was 1 : 1.

The same electrical pacing protocol was applied in all simulations: three successive baseline S1 stimuli were applied in the LSPV (figure 3) at a cycle length of 120 ms, followed by an ectopic S2 stimulus short-coupled at less than 100 ms after the last S1 stimulus. The latter mimics an ectopic excitation independent of the regular S1 pacing—such ectopics could be caused by spontaneous AP firing in the PVs [3,5]. Short coupling of ectopic beats is crucial for the initiation of re-entry [24]. Thus, re-entry in the current study can be initiated in a range of S2 coupling intervals between 88 and 95 ms (see §3). Note also that the initial conditions were chosen based on a standard procedure: the respective single PV and LA cells were paced 10 times at the baseline cycle length of 120 ms, and values of all the state variables at the end of such single-cell simulations were used as initial conditions for the respective three-dimensional tissue simulations. Hence, the model state was adjusted to the cycle length.

Figure 3.

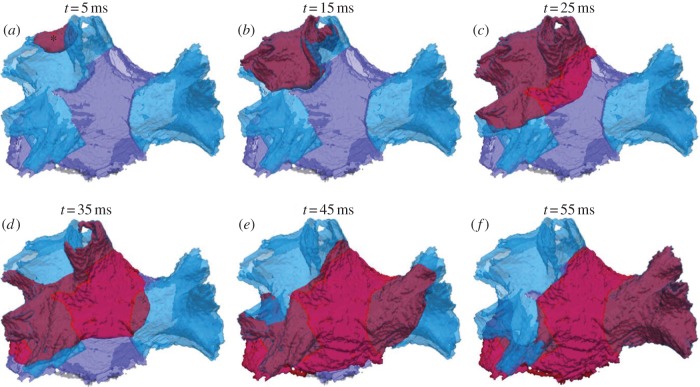
Normal wave propagation in the PV region. (a–f) Snapshots of wave-front propagation following the S1 stimulus applied to a site in the LSPV (shown with an asterisk). The wave propagates through the LSPV and LIPV, then spreads into the IPA and terminates in the RSPV and RIPV. Here and below in figure 4, time t = 0 ms is given as the moment of the stimulus application. Waves are always shown as red iso-surface of the membrane potential V =−30 mV. The PV sleeve and IPA tissue regions are shown in transparent blue and purple colours, respectively. The anatomical orientation is the same as in figure 1b.

3. Results

Pacing in the LSPV resulted in various patterns of wave propagation through the PV region.

3.1. Normal propagation

Figure 3 shows the normal AP conduction following the last of three S1 stimuli. The AP starts in the LSPV sleeve and propagates as a regular wave-front into the LIPV and IPA, and then after spreading through the IPA terminates in the RSPV and RIPV sleeves. The total activation time for the entire PV region is approximately 55 ms. Average conduction velocity in the PV sleeves is larger than in the IPA: approximately 1.25 m s⁻¹ in the PVs compared with approximately 0.75 m s⁻¹ in the IPA (see §2). However, because of the high level of fibre disorganization at the border between the LSPV and IPA (seen in figure 2b), the average conduction velocities in this area is decreased to approximately 0.6 m s⁻¹.

3.2. Re-entry generation

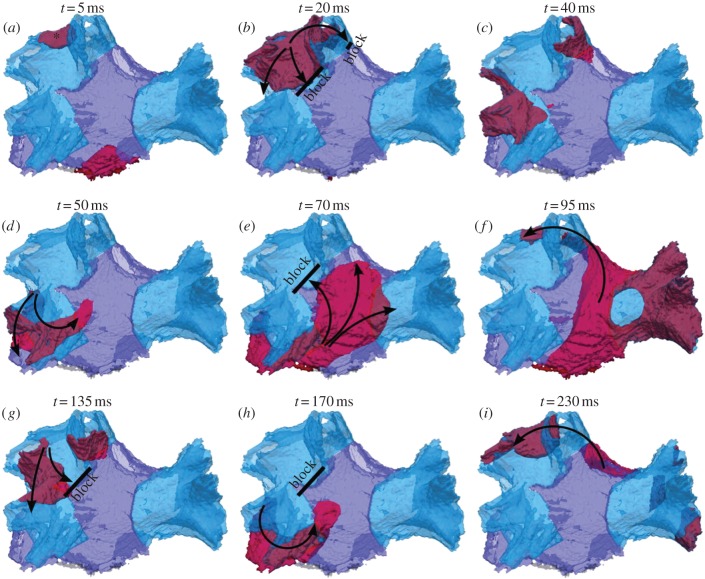
Figure 4 shows the propagation of excitation wave-fronts initiated by applying an S2 stimulus at 90 ms after three baseline S1 stimuli (see §2). Application of such a short-coupled ectopic S2 stimulus in the LSPV resulted in a break-down of the regular excitation wave-front, leading to the generation of a re-entrant circuit. Primarily, whereas the normal S1 wave propagated from the LSPV into the IPA in approximately 15 ms (figure 3b), the ectopic S2 wave failed to pass through the same area (figure 4b). Conduction at the junction between the LSPV and IPA was slowed owing to the combination of electrical heterogeneity (figure 1b) and complex anisotropic fibre arrangement (figure 2b). The S2 wave can propagate through the LSPV, which has already recovered from the S1 wave (as the APD here is relatively short; see figure 1b). However, the S2 wave fails to propagate into the IPA, as the area has not repolarized after the S1 wave propagation (because the APD and the refractory period here are relatively long; see also figure 1b). Therefore, a conduction block is observed between the LSPV and IPA (figure 4b).

Figure 4.

Genesis of re-entry in the PV region. (a–i) snapshots of wave-front propagation following a short-coupled ectopic S2 applied to a site in the LSPV (shown with an asterisk). Arrows indicate the directions of wave-front propagation. Thick solid black lines indicate conduction block areas. The wave from the LSPV is blocked towards the IPA owing to a combination of large heterogeneity and anisotropy in the border area (see circle in figure 2b). The wave therefore propagates down into the LIPV and from there into the IPA and the rest of the PV region, eventually re-entering the now-recovered LSPV after approximately 95 ms.

The S2 wave propagates in the inferior direction to the LIPV (figure 4c). After approximately 50 ms, it reaches the IPA, which by this time has fully repolarized, and hence the wave propagates into the IPA inferiorly (figure 4d). Excitation then spreads throughout the IPA in multiple directions (figure 4e), towards the right PVs and back towards the LSPV. The wave reaches the initial stimulation site in the now-recovered LSPV after approximately 95 ms, thus completing the re-entrant circuit (figure 4f). Similar patterns of re-entry rotation are sustained with a period of approximately 100 ms (figure 4g–i). Thus, a stable re-entry is generated and circulates around the left PVs. Note that a 30% reduction in the intercellular coupling in these simulations resulted in decreases in the conduction velocities throughout the PV region (see §2), which contributed to the generation of conduction blocks (figure 4b,e) and re-entry (figure 4f,i). Note also that re-entry was initiated in a narrow range of S2 coupling intervals (vulnerability window) between 88 and 95 ms. For S2 coupling intervals greater than 95 ms, normal conduction (similar to that shown in figure 3) was observed. For S2 coupling intervals less than 88 ms, AP conduction failed because of the refractory properties of the tissue, as it did not have time to recover after the S1 wave.

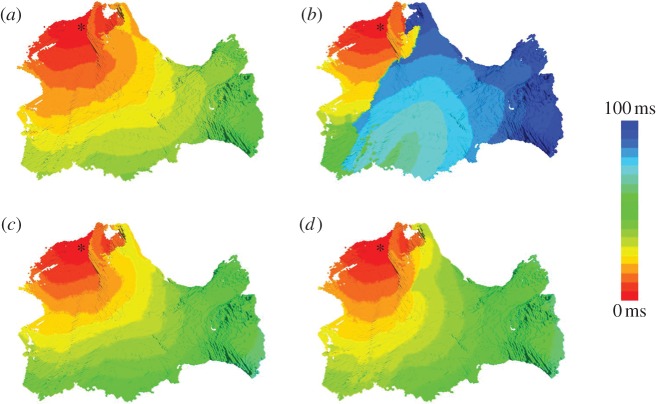
Figure 5 illustrates the differential activation patterns during the normal conduction following the last of three baseline S1 stimuli applied at 120 ms (figure 5a) and re-entry following an ectopic S2 stimulus applied at 90 ms after the last of three S1 stimuli (figure 5b).

Figure 5.

Activation patterns in the canine PV region. Simulated activation times in the three-dimensional model are shown using a standard rainbow palette. The activation time at each voxel is measured as the interval between the stimulus application and the AP initiation in that voxel. The stimulation site is shown with an asterisk. The anatomical tissue orientation is the same as in figures 3 and 4. (a) Normal activation after the last of three baseline S1 stimuli—details of the propagation pattern are shown in figure 3. (b) Re-entry generation after an ectopic S2 stimulus (short-coupled at 90 ms)—details of the propagation pattern are shown in figure 4. (c,d) Quasi-normal activations after an ectopic S2 stimulus (short-coupled at 90 ms) in the homogeneous and isotropic models, respectively. Ectopic S2 stimuli in (c) and (d) result in activation patterns similar to those seen during baseline S1 stimulation in (a). Such quasi-normal activations are observed in our simulations of the homogeneous and isotropic models with any S2 coupling interval leading to AP conduction.

3.3. Effects of heterogeneity

Figure 5c illustrates the effect of the removal of AP heterogeneity between the PVs and IPA. As the APD gradient between the two areas is now absent, the ectopic S2 wave is no longer blocked towards the IPA (cf. figure 5b). Instead, a regular excitation wave-front propagates throughout the entire PV region, similarly to the normal conduction after the S1 stimuli (figure 5a). Note that the short-coupled S2 wave is slowed down compared with the S1 wave, primarily as the tissue has not fully recovered after the preceding S1 wave. As a result, the activation time of the entire PV region by the S2 wave is approximately 10 ms longer than that by the S1 wave (compare figure 5c with figure 5a). The next section shows that the AP heterogeneity alone may not account for the genesis of re-entry and that fibre arrangement is also important.

3.4. Effects of anisotropy

Figure 5d illustrates the effect of the removal of conduction anisotropy from the entire PV region. The absence of the abrupt change in fibre direction between the LSPV sleeve and IPA in this case means that the ectopic S2 wave is no longer blocked towards the IPA (cf. figure 5b). The S2 wave is slowed down at the junction between the LSPV and IPA owing to the presence of the APD gradient between these two areas (compare figure 5d with figure 5a). However, as the APD gradient is no longer enhanced by the anisotropic coupling, temporary wave-breaks (seen in figure 5d) due to the AP heterogeneity between the PV sleeves and IPA quickly recover, and the wave propagates through the IPA before decaying in the RSPV and RIPV. Recovery of the wave-fronts can be explained by the absence of anisotropic conduction pathways. When such pathways are present (figure 5b), the wave-breaks can be easily pulled apart by following such pathways in diverging longitudinal fibre directions, while also being slowed down and blocked in the transverse directions. In the isotropic case, no clear pathways or lines of the conduction block are observed and no re-entry is generated (figure 5d). These results are in agreement with other computational [8,24] and experimental [4,25] studies.

4. Discussion

We developed a biophysically detailed three-dimensional computational model (figure 1) that integrated the PV and LA cell electrophysiology [11] with the respective three-dimensional atrial tissue geometry and fibre orientation reconstructed from micro-CT data [10]. The model simulations demonstrated that a combination of the electrical AP heterogeneity and conduction anisotropy near the PV sleeves entering into the LA can cause a break-down of the regular electrical excitation wave-fronts, leading to the generation of a high-frequency (approx. 10 Hz) re-entrant source near the PVs (figure 4). Evidence of such re-entrant sources has been seen clinically in AF patients [1,3,6].

Contributions of the electrical heterogeneity and anisotropy to the re-entry initiation mechanisms have recently been quantified by measuring APD in atrial tissues [24]: the APD gradients were the highest in areas combining high heterogeneity and anisotropy, such that intrinsic APD differences were not diminished by electrotonic interactions. Such areas have been shown to generate conduction blocks and lead to re-entry in the right atrium [8,24]. The present work expands these results into the LA and PVs, demonstrating that a combination of AP heterogeneity and anisotropy between the PVs and IPA/LA provides the substrate for re-entry initiation and sustenance. This is also consistent with electro-anatomical studies [4,6].

4.1. Comparison with experimental data

The reconstruction of fibre orientation (figure 2) was crucial for dissecting the mechanisms of re-entry generation in the PV region. The reconstructed fibre directions agree with available (however, limited) anatomical knowledge of this region [17]: the majority of the fibres run down the PV sleeves in ‘spiralling’ oblique directions, eventually merging with longitudinal fibres in the IPA. Areas with abrupt fibre angle changes between the PVs and IPA (seen in figure 2b) have also been reported in histological [15] and electro-anatomical [4] studies.

A detailed electro-anatomical study by Hocini et al. [4] has correlated the arrangement of fibres in the canine PV region with electical conduction patterns. Areas of conduction delay/block were observed near the PVs and linked with abrupt changes in fibre direction. Such changes were suggested to facilitate re-entry associated with ectopic activity [4]. This study demonstrates that such abrupt changes in fibre orientation, in combination with electrophysiologically validated AP differences between the PV sleeves and IPA/LA [13], can result in re-entry generation due to a properly timed and located ectopic stimulus (figure 4). Short coupling of the ectopic S2 beat (which must be timed within the vulnerability window of approximately 88–95 ms in our simulations) is crucial in re-entry initiation. Note that Hocini et al. [4] also used S2 stimulation short-coupled at 135 ms to produce conduction delays at the PVs.

Computational results of the present study also agree with the clinical assessment of electrophysiological properties of the PVs in AF patients. A study by Kumagai et al. [6] used multi-electrode basket catheter mapping to record substantial conduction delay/block at the PV–LA junction in AF patients. During initiation of AF, a short-coupled ectopic stimulus originating from the PV formed an unstable re-entrant circuit near the PV–LA junction [6]. This study also suggested that the complex arrangement of myocardial fibres at the junction may be a possible reason for the observed conduction delay and block, and may be crucial in the generation of re-entry. Hence, our computational results help to dissect the mechanisms of re-entry initiation predicted in earlier experimental and clinical studies [4,6].

Note also that high-frequency sources of electrical activity are often observed in paroxysmal AF patients near the PV sleeves [3,25], with clinically recorded cycle lengths of approximately 170 ms (frequency of approx. 6 Hz). This is in qualitative agreement with our simulation results. Quantitative differences from our simulation results—cycle length of approximately 100 ms (frequency of approx. 10 Hz)—can be explained by the shorter APD in the dog when compared with humans [8,22].

4.2. Comparison with other models

Biophysically detailed three-dimensional computational models have been developed for major parts of the heart [7,9], with several models accounting for various details of atrial electrophysiology and anatomy [8,9,26–29]. Comprehensive review of such models can be found elsewhere [9]. However, even the most detailed three-dimensional models have not included accurate descriptions of fibre architecture in the atria. Fibre orientation has been included in atrial models manually based on anatomical observations [8,26,27] or semi-automatically based on known atrial activation patterns [28,29]. Besides, even the most recent atrial models [8,28,29] have not accounted for electrophysiological heterogeneity and anisotropy of the PV region, which are crucial in the genesis of AF [1–5]. Our three-dimensional model of the canine PV region overcomes such limitations and provides a missing link in the large-scale modelling of the entire three-dimensional atria and heart.

Primarily, contrast micro-CT data used in this study enabled a detailed fibre orientation in the PV sleeves to be reconstructed (figure 2). The high resolution of this dataset (approx. 70 µm) is a significant improvement over the resolution of 330 µm provided by the widely used Visible Female dataset [8,26,28]. From the structural perspective, the resolution of 70 × 70 × 70 μm³ is much closer to the dimensions of an atrial myocyte (approx. 120 × 10 × 10 μm³ [30]) than 330 × 330 × 330 μm³. Hence, the resolution of 70 µm enables the reconstruction of very thin (approx. several cell diameters) fibre bundles and cardiovascular walls, which is not possible with the fivefold lower resolution of 330 µm. The spatial scale of 70 μm is also sufficient to resolve a direction change between two collateral approximately 120 μm long atrial cells. Such subtle fibre direction changes cannot be resolved on the spatial scale of 330 μm. Figure 2 shows the level of fibre orientation detail (including angle changes) provided by high-resolution micro-CT data.

From a computational perspective, the spatial resolution of cardiac tissue models can be an important factor influencing both stability and accuracy of numerical simulations [31]. Spatial resolutions (translated into spatial steps of numerical integration) of greater than 0.2 mm can result in substantial inaccuracies of simulation results, for example in diverging conduction velocities and APD [31]. Besides, coarse spatial resolution can lead to artificial break-downs of re-entrant waves in anisotropic tissues with sharp fibre angle changes [32]. Hence, spatial resolution/integration steps of 70 μm can provide better stability and accuracy of numerical simulations than 330 μm, which is primarily important in computational studies of re-entry mechanisms and AF arrhythmogenesis in highly anisotropic three-dimensional atrial tissue models.

4.3. Limitations

Knowledge of the atrial micro-architecture is limited [17], and hence validation of the micro-CT reconstruction of fibre orientation is not straightforward. In addition, quantitative comparisons between various experimental studies are extremely difficult considering the varying atrial shape, size, wall thickness and complex fibre pattern. Hence, qualitative similarities between the micro-CT reconstruction of the PV fibres (figure 2) and the respective histological [15], anatomical [17] and electro-anatomical data [4] may be the only validation currently available for this region. Note also that the PV sleeves were segmented based on a histology-guided computational approach under the assumption that conduction pathways in the PVs are similar across species. Under this assumption, waves propagating with similar velocities in our canine model and the respective histology-based model of sheep atria [15,23] will cover a similar area over a similar time T_act (see §2). The resultant PV segmentation in the canine model (figure 1b,c) agrees with histological [15] and anatomical [17] data, but needs further validation.

The current three-dimensional model does not consider the role of a re-entrant circuit in the PV region (figure 4) in the development of AF at the entire atria level. Wave-fronts emanating from such a high-frequency (approx. 10 Hz) source have the potential to overtake the normal cardiac rhythms and generate complex electrical activations underlying AF [3,8]. In order to expand the results of the current study to the entire atria, the reconstructed three-dimensional atrial geometry (figure 1a) needs to be segmented into areas with tissue-specific electrophysiological properties [11] and integrated with the respective fibre orientation [10]. Understanding the complex mechanisms of AF arrhythmogenesis will also require modelling of multiple pathophysiological factors associated with AF, such as electrophysiological [21,33] and structural [29,34] remodelling. Such an integrative three-dimensional model of the entire atria is currently being developed in our group.