Systems pharmacology of the nerve growth factor pathway: use of a systems biology model for the identification of key drug targets using sensitivity analysis and the integration of physiology and pharmacology

Abstract

The nerve growth factor (NGF) pathway is of great interest as a potential source of drug targets, for example in the management of certain types of pain. However, selecting targets from this pathway either by intuition or by non-contextual measures is likely to be challenging. An alternative approach is to construct a mathematical model of the system and via sensitivity analysis rank order the targets in the known pathway, with respect to an endpoint such as the diphosphorylated extracellular signal-regulated kinase concentration in the nucleus. Using the published literature, a model was created and, via sensitivity analysis, it was concluded that, after NGF itself, tropomyosin receptor kinase A (TrkA) was one of the most sensitive druggable targets. This initial model was subsequently used to develop a further model incorporating physiological and pharmacological parameters. This allowed the exploration of the characteristics required for a successful hypothetical TrkA inhibitor. Using these systems models, we were able to identify candidates for the optimal drug targets in the known pathway. These conclusions were consistent with clinical and human genetic data. We also found that incorporating appropriate physiological context was essential to drawing accurate conclusions about important parameters such as the drug dose required to give pathway inhibition. Furthermore, the importance of the concentration of key reactants such as TrkA kinase means that appropriate contextual data are required before clear conclusions can be drawn. Such models could be of great utility in selecting optimal targets and in the clinical evaluation of novel drugs.

1. Background

Antibodies developed to bind to nerve growth factor (NGF) exhibit potent analgesic effects in some pain states [1]. It is therefore possible that other interesting targets exist within the NGF response pathway that could lead to the development of further novel agents for the treatment of pain. For example, an intervention amenable to an orally bio-available small molecule will have benefits relative to an injection-only medication such as a monoclonal antibody (mAb). However, identifying this target with confidence prior to engaging in a costly drug discovery programme is likely to be challenging. This reality is reflected in an evaluation of pharmaceutical company productivity, which concluded that only a small proportion of the targets investigated lead to a marketed drug, with the percentage of first in human trial registered drugs that are subsequently approved currently being about 10 per cent [2]. The majority of these failures were because of a lack of efficacy or safety during phase II clinical trials. It could be argued that this is because of the limited understanding of the behaviour of the complex human biology. Furthermore, surrogate systems such as animal models and ex vivo tissue assays do not fully address this, as extrapolation from animal model results carries a risk of generating false positives and negatives [3] and in vitro assay compounds can exhibit ‘pluridimensional efficacy’ [4] whereby estimates of potency appear to be context dependent. A further barrier may be the risk of robustness in pain response [5]. In general, this hypothesis holds that biological responses that are essential to the viability of an organism exhibit robustness and, in turn, this may mean meaningful pharmacological intervention requires polypharmacology [6]. In this case, selecting the right multiple targets from a large number of species in a given pathway is a significant combinatorial problem, with, for example, the number of pairs of targets selectable at random from 99 being 4851. With three targets, this increases dramatically to 156 849.

An alternative approach to target selection is to use mathematical models to develop an improved understanding of the system (e.g. the disease state) before engaging significant resource. This has been most notably applied in academic research where systems biology has become a mainstream feature of research and funding priorities [7]. This is also being explored within the pharmaceutical industry [8–10]. The purpose of the work described in this study was to explore the utility of systems modelling approaches in the context of the NGF pathway, to extract relevant conclusions and to suggest optimal ways to test these experimentally.

The biology of the NGF response lends itself well to such an approach as it has been studied over a number of years and there is a good database of information. At a summary level, it is known that NGF acts via binding to the NGF receptor (NGFR; frequently known as tropomyosin receptor kinase A; TrkA) at the extracellular cell surface, triggering auto-phosphorylation of the TrkA domain of the receptor. This engagement of Trk receptors leads to activation of Ras, phosphatidylinositol 3-kinase, phospholipase C-γ1 and signalling pathways controlled through these proteins, including the mitogen-activated protein kinases [11]. In sensory neurons, once NGF engages TrkA and following the auto-phosphorylation, the NGF : TrkA complex is internalized and trafficked to the neuronal cell bodies. Here, it is then thought to cause an accumulation of diphosphorylated extracellular signal-regulated kinase (dppERK) in the nucleus and subsequently the expression of numerous genes related to neuronal survival and pain sensation [12]. Arguably, the dppERK concentration could therefore be regarded as a biomarker of pain response. The precise molecular events leading to the dppERK migration to the nucleus are complex, but have been studied extensively and summarized in the form of a systems model containing 99 species [13]. It was concluded from this work that sustained ERK activation depends on the final concentration of NGF but not on the temporal rate of increase. ERK dynamics depend on Ras and Rap1 dynamics, the inactivation processes of which are growth factor dependent and independent, respectively. The Ras and Rap1 systems capture the temporal rate and concentration of growth factors, and encode these distinct physical properties into transient and sustained ERK activation, respectively. In addition, the nuclear–cytoplasmic shuttling of ERK and mitogen-activated protein kinase (MEK) has been investigated [14]. Specifically, using fluorescent probes, the levels of signalling molecules, the activation and nuclear translocation of ERK, the dissociation constants of molecular interactions and the nucleo-cytoplasmic shuttling of ERK and MEK were measured. These parameters were used to construct a model of the reactions that were found to be consistent with experimental data. Hence, together, the Fujioka and Sasagawa models provide the most comprehensive detailed description of the NGF pathway available in the literature. Nevertheless, caveats apply: the models were constructed using data from in vitro preparations (e.g. PC12 cells) rather than native tissues in situ. Furthermore, the models assume a single compartment. In reality, the relevant NGF pathway is expressed within neuronal cell lines, and these are located in specific physiological compartments of the body, connected to the interstitial fluid compartment.

From a drug discovery perspective, the most interesting components of a pathway are those that are most influential on the outcome of interest and amenable to intervention using a small molecule. Such targets have been referred to as ‘druggable’ [15]. One method for the identification of such influential points is time-dependent sensitivity analysis. This involves the calculation of the time-dependent sensitivities of species states with respect to species initial conditions and parameter values in the model. Sensitivity can be calculated at given time points to give a time-dependent picture and, by integrating the absolute values over the desired time domain, a summary measure of the relative importance of a given parameter on a species can be obtained [16].

Using the models developed by Sasagawa and Fujioka as a starting point, we have identified the species and parameters most sensitive to intervention. Next, we have incorporated appropriate physiology and drug pharmacology. The resulting tool was then used for exploring potential scenarios in drug discovery, allowing prioritization of critical experiments. The implications of this for target selection and clinical dose setting will be discussed.

2. Methods

2.1. Mathematical models

All models were developed and analysed using DBSolve Optimum v. 7 (ISBSPb, Moscow, Russia) and Matlab/SimBiology version 2010b or 2011b (Matlab, Natick, MA, USA). Model 1 was constructed as a series of differential equations using the data described by Sasagawa et al. [13] and Fujioka et al. [14], and comprised 59 molecular species and 233 parameters. The parameter set comprised 143 rates constants, 82 Michaelis–Menten parameters and the remainder are constant species or volume values. NGF synthesis and degradation was set to give steady-state NGF levels of approximately 30 pM (NGFext). Model 2 was developed from model 1 by incorporating an extracellular body water compartment and a connected neuronal compartment. The details of the signal transduction pathway from model 1 were incorporated in the neuronal compartment (scheme 1). Cross-membrane molecular interactions were modelled, using the approach of Benson et al. [17]. Model 3 was generated by terminating the signalling pathway from model 2 at the phosphorylation of TrkA, and the concentration of the phosphorylated-NGF–TrkA complex was monitored as a target molecule. Physiological parameters were incorporated into this model using the volumes of 15 l for the extracellular body water compartment and 1×10^–3 l for the neuron [18,19].

Scheme 1.

Diagram of model 2. (1) refers to compartment 1, the extra cellular body water compartment of 15 l. (2) is the neuronal intracellular compartment (0.001 l). Detailed descriptions of parameters and values used are given in the electronic supplementary material. I refers to a Mg.ATP non-competitive inhibitor of TrkA kinase and is assumed to be in rapid equilibrium between the compartments. The grey box labelled model 1 indicates that the components of model 1 are included in compartment 2.

A virtual NGF-binding antibody drug was included using published population average pharmacokinetic parameters (http://www.page-meeting.org/pdf_assets/7203-PageAthensCleton.pdf). The antibody was introduced into the model via a bolus into the plasma compartment, at a typical antibody drug dose of 0.14 or 1 mg kg⁻¹, and the change in target molecule concentration monitored compared against no drug. We assumed that the NGF-binding mAb bound NGF according to a simple one-step binding model with k_on 2.7 × 10⁵ M⁻¹ s⁻¹, k_off 3 × 10⁻⁶ s⁻¹, K_i = 0.011 nM. Hypothetical TrkA kinase inhibitors were also introduced via a bolus into the extracellular body water compartment. In all cases, we assumed that the inhibitor bound to both the NGFR and NGFR_NGF species according to a simple binding model with k_on 1×10⁷ M⁻¹ s⁻¹, k_off 1×10⁻³ s⁻¹, K_i = 0.1 nM. All concentrations refer to free drug. We assumed rapid equilibration of the TrkA kinase inhibitor across biological membranes, whereas antibody exhibited zero permeability.

Sensitivity analysis was carried out as follows, using a non-normalized method. Assuming a model has a species of interest, x, and two parameters, y and z, the time-dependent sensitivities of x with respect to each parameter value are the time-dependent derivatives

2.1

where the numerator is the sensitivity output and the denominators are the sensitivity inputs. This principle can be applied to n parameters. The absolute time integral was calculated as in the manufacturers' software.

3. Results

To describe as much of the known quantitative understanding of NGF signalling as possible, we have constructed an integrated ODE model of NGF signalling and the nuclear: cytoplasmic cycling of ERK (see the electronic supplementary material). On challenge with constant NGF, the concentration of diphosphorylated nuclear ERK dimer (dppERKnuc) increased rapidly from zero peaking at approximately 0.26 μM after 7 min and then decreased biphasically to an approximate steady-state value of approximately 0.14 μM (figure 1). The simulations were consistent with published data [13]. We analysed the behaviour of model 1 via time-dependent sensitivity analysis (equation (2.1)). The molecular species concentrations and parameters were analysed separately. Figure 2a shows the sensitivity as a function of time. By defining the absolute area under the curve (AUC) up to 100 min post stimulus as a summary measure of impact, with greater AUC implying higher sensitivity, the influence of each of the species can be ranked (figure 2b and table 1). This analysis showed clearly that the most influential species is the concentration of NGF (NGFext). The concentration of complexes Grb2_SOS_pShc_pTrkA, pShc_pTrkA and Shc_pTrkA is the next most influential, with the fifth most influential being the phosphorylated TrkA concentration. It was notable that a large variability in the integral of sensitivity was observed, of the order of 10⁴.

Figure 1.

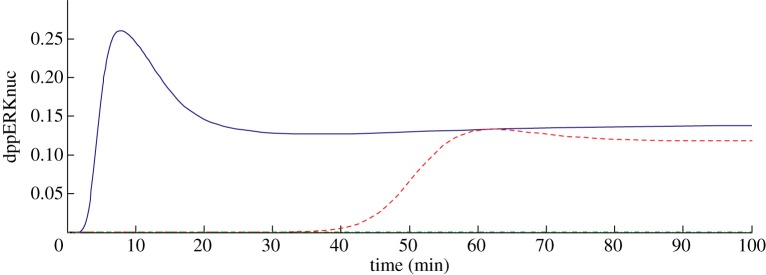
Model 1 simulated time course of dppERKnuc response to 30 pM NGF (solid line). The dashed line shows the response in the presence of a TrkA binding inhibitor given at t = 0, K_i = 0.1 nM (at 1000×K_d of the inhibitor) and the dashed-dotted line at 1×10 000×K_i. (Online version in colour.)

Figure 2.

Sensitivity analysis of model 1 using the initial concentrations of species or reactants. (a) Examples of the time-dependent sensitivities for NGFext (dashed line), pTrkA (solid line) and Grb2_SOS_pShC_pTrkA (dashed-dotted line). See table 1 for relative influence. (b) Time integral matrix subplot showing the influence of the concentration of each species in the model over the first 100 min of the response. (Online version in colour.)

Table 1.

Summary of the results of the sensitivity analysis of model 1 with respect to the species.

rank (dppERKnuc)	species	initial value	description
1	NGFext	30 pM	NGF concentration in extracellular matrix
2	Grb2_SOS_pShc_pTrkA	0 µM	downstream multi-protein complex
3	pShc_pTrkA	0 µM	downstream multi-protein complex
4	Shc_pTrkA	0 µM	downstream multi-protein complex
5	pTrkA	0 µM	phosphorylated TrkA concentration
6	L_NGFR	0 µM	NGF–NGFR complex
7	FRS2_pTrkA	0 µM	downstream multi-protein complex
8	pFRS2_pTrkA	0 µM	downstream multi-protein complex
9	Crk_C3G_pFRS2_pTrkA	0 µM	downstream multi-protein complex
10	Grb2_SOS_pShc_pTrkA_endo	0 µM	downstream multi-protein complex

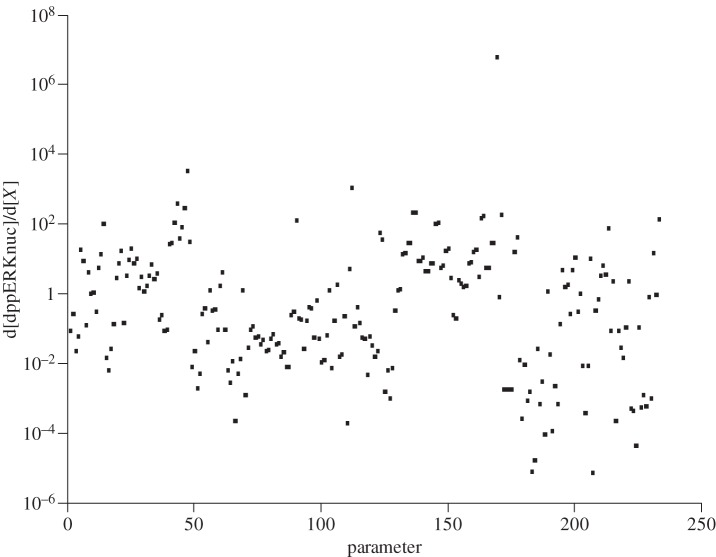
Table 2 summarizes the results of a similar sensitivity analysis with respect to the parameters of the model. It was found that the most sensitive parameter was clearly the synthesis rate for NGFext, with a large range of integrals observed from approximately 10⁻⁶ to 10⁶. The next most influential parameters were kb_56 (the reverse rate for the pDok de-phosphorylation reaction), MKP3nuc (the concentration of the MKP3nuc species) and Rap1GAP (the concentration of the Rap1GAP (GTPase activating protein) species). Figure 3 shows the time-dependent sensitivity integral plot.

Table 2.

Summary of the results of the sensitivity analysis of model 1 with respect to the parameters.

rank (dppERKnuc)	species	value	description
1	kf147	4.25×10−8 µM min−1	synthesis rate of NGFext
2	kb_56	6.00×10−4 min−1	reverse rate for pDok de-phosphorylation reaction
3	MKP3nuc	0.006 µM	concentration of MKP3nuc species
4	Rap1GAP	0.012 µM	concentration of Rap1GAP (GTPase activating protein) species
5	kf117	2.1 min−1	degradation of ppMEKnuc_ERKnuc
6	kf116	2.1 min−1	formation of ppMEKcyt_ERKcyt
7	kf141	0.42 min−1	degradation of dppERKnuc
8	kf150	0.001283 min−1	degradation of NGFext
9	pro-TrkA	0.020631 µM	concentration of TrkA generative species
10	kf140	0.42 min−1	rate of degradation of dppERKnuc

Figure 3.

Sensitivity analysis of model 1 using the parameter values. Time integral matrix subplot showing the influence of each parameter in the model over the first 100 min of the response on a logarithmic scale.

By introducing a hypothetical inhibitor of TrkA kinase activity with K_i 0.1 nM at 10 000×K_i, we were able to show that this can essentially block the appearance of dppERKnuc (figure 1).

To introduce a more realistic compartment structure to the model, we created model 2, the ‘systems pharmacology’ model. This version included the estimates of typical physiological system parameters as described in §2 and comprised two compartments: a neuronal compartment, and an extracellular body water compartment. The reactions from model 1 were included within the neuronal compartment, whereas NGF production and degradation and NGFR binding occurred within the extracellular body water compartment (scheme 1). We introduced a hypothetical TrkA kinase inhibitor into the extracellular body water compartment to mimic a dose of a small molecule drug administered intravenously (figure 4). We found that the inhibitor could essentially block the dppERKnuc signal at 1000 × K_i. Using the typical binding data for an anti-NGF antibody as described in §2, we found that the antibody could block the dppERKnuc signal at 1000 × K_i to a very similar extent to the TrkA inhibitor (not shown). In order to further understand the nature of the inhibition of the pathway, we also developed model 3. This was identical to model 2, except that the model was simplified by including only the events up to and including the formation of TrkA-phosphate in the neuron. Using this model, we evaluated the inhibition of the rate of formation of TrkA-phosphate and found that the reaction was almost completely blocked at 100×K_i (figure 5).

Figure 4.

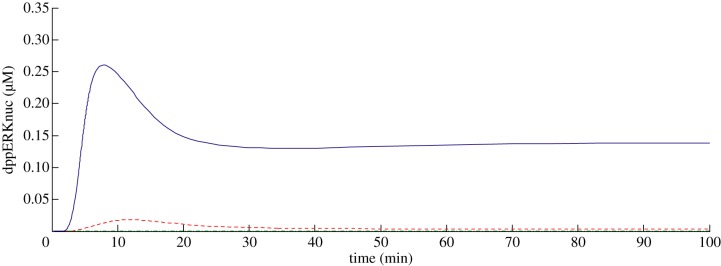
Model 2 simulated time course of dppERKnuc response to NGF (solid line). The dashed line shows the response in the presence of a TrkA binding inhibitor K_i = 0.1 nM (at 100 × K_i of the inhibitor) and the dashed-dotted line at 1000 × K_i, both given at t = 0. (Online version in colour.)

Figure 5.

Model 3 simulations with and without hypothetical inhibitor of TrkA kinase, given at t = 0, K_i = 0.1 nM. Graph shows the accumulation of phosphorylated-NGF–TrkA complex concentration in the neuronal compartment over time with and without TrkA inhibitor. No inhibitor (solid line) 10×K_i (dashed line) 100×K_i (dashed-dotted line). (Online version in colour.)

4. Discussion

By integrating two published models we have, to the best of our knowledge, produced the most comprehensive description of the known behaviour of NGF signalling to date (model 1). However, the caveat applies that this model lacks physiological context and was developed using data derived largely from non-human, non-native cell lines such as PC12 cells. Clearly, further data generated in more relevant cell types and, indeed, an in vivo context are required to build confidence in this model, before application to questions about human in vivo responses can be made. In addition, although the model contains 59 species it remains, in all likelihood, a simplification of the actual biology. Nevertheless, the model reproduces the known measured data and thus arguably represents the best current understanding of this pathway.

The observation from our sensitivity analysis that NGF is most influential in controlling dppERKnuc is consistent with the known behaviour of NGF-binding drugs such as mAbs in vitro [20], in animal models [21,22] and in man [23]. Interestingly, the model also indicated that a number of other intracellular species or parameters in the pathway may be potential drug targets. Some of these are of intrinsically more interest than others, from a drug discovery perspective, and these selection criteria can be used to prioritize the candidate targets. For example, targeting the reactions leading to the formation of important complexes via inhibition of their binding may be possible (e.g. via siRNA or other technology), but, in general, protein–protein interactions are regarded as not tractable to conventional small molecule approaches, and the preferred option in drug discovery medicinal chemistry would be to target receptors and enzymes with known well-defined substrate and ligand binding sites [24]. One such ‘druggable’ target class is the kinases and hence of the top potential targets from this sensitivity analysis, targeting the kinase domain of TrkA would appear to be the most attractive. Such an inhibitor of TrkA would be required to inhibit the catalytic function of the enzyme, preventing the intra-molecular phosphorylation. Several mechanistic possibilities exist, e.g. non-competitive with Mg.ATP, Mg.ATP competitive and/or binding to the pro-TrkA. For the purpose of the current simulations, we assumed that the inhibitor was Mg.ATP non-competitive and bound to the NGFR and the NGF bound NGFR. In model 1, we found that an inhibitor with K_i = 0.1 nM, at 10 000 × K_i, could essentially block the pathway, as shown by formation of dppERKnuc, with a steady-state maximum effect on this endpoint comparable to that of a saturating concentration of an NGF binder. In the context of drug discovery, it is not only an understanding of the systems biology that is important, but also how a drug will perturb this system. This has been called ‘systems pharmacology’ to reflect the requirement for the integration of systems biology and pharmacokinetics and pharmacodynamics [25]. Hence, model 2 was constructed to capture a more realistic multi-compartment situation, as would be the case when a drug is used in patients. The volumes of the plasma and interstitial compartments are generally agreed, having been extensively researched over many years [26], although some inter-individual variability is observed and hence the numbers used must be regarded as typical. The estimate of the volume of the neuronal compartment is more difficult to accurately define and should be regarded as having lower confidence, although there are efforts to resolve this question [27]. Using model 2, we found that the same hypothetical TrkA kinase inhibitor used in model 1 could essentially block the pathway, at 1000 × K_i, 10 times less than in model 1. This apparent discrepancy no doubt reflects the large difference in mass given between delivering drug into the extracellular body water versus into the single compartment model 1. In the model 1 scenario, the significantly lower amount of drug delivered means that it is consumed by the reaction more rapidly and over the time course observed the inhibition appears to be less. Figure 6 illustrates the difference between the apparent consumption of TrkA inhibitor in models 1 and 2. The model 2 scenario is more likely to be realistic, and this observation highlights the need for the introduction of appropriate physiological model details when exploring the impact of physiology and pharmacology in systems models.

Figure 6.

(a) Model 1 predicted change in TrkA inhibitor concentration in the neuron at 1000×K_i (K_i = 0.1 nM) at t = 0. (b) Same plot and conditions but simulated using model 2. (Online version in colour.)

Interestingly, at inhibitor concentrations of 100 × K_i, a significant response was observed, with for example the inhibited dppERKnuc concentration at peak equal to about 10 per cent of the control (figure 4). Assuming simple saturation of inhibition, approximately 99 per cent inhibition would be expected at this multiple of K_i and so it appears that the inhibition is less than would be expected given the assumptions of simple binding.

Although including physiological components, model 3 lacked the reactions following the auto-phosphorylation of TrkA. We investigated the impact of our hypothetical inhibitor in this model and found that the rate of TrkA phosphorylation was essentially completely blocked with 100×K_i of inhibitor (figure 5), in contrast to model 2 where up to 1000×K_i (figure 4) was required. One explanation for this may be the presence of a possible negative feedback loop in the pathway; activated TrkA phosphorylates FRS2 and shc leading to the response, but it also phosphorylates Dok. pDok then binds to RasGap and this complex accelerates the turnover of RasGTP to GDP, in turn attenuating the dppERKnuc response. Hence, inhibiting TrkA kinase would block the signal in one way, but may relax any feedback inhibition. It has been observed previously that kinases in such negative feedback loops can exhibit attenuated inhibition relative to expectation [28]. Interestingly, we also found that in model 2, to asymptote towards total inhibition of the dppERKnuc response, the plasma concentration of an NGF-binding mAb needed to be ≫ K_d (approx. 1000×). Whether this reflects the strong coupling of the NGF to the response and the fairly rapid synthesis rate of the NGF, or the aforementioned negative feedback, or a combination of these factors requires further investigation. In more general terms, it is clear that these models are sensitive to assumptions about the most relevant endpoint in a pathway. Because the relationship between pERK or TrkA-phosphate and pain outcomes is not well elucidated, a degree of uncertainty will be associated with how any intermediate biomarker will translate to clinical outcome and these relationships need to be investigated further.

Other interesting targets highlighted were involved in the processes controlling the concentration of pDok and Rap1GAP. In our model, Rap1GAP binds to Rap1 and accelerates the turnover of GTP to GDP. In addition, pDok binds RasGAP, and this complex binds to Ras accelerating the turnover of GTP to GDP. As it is the GTP form of the Ras GTPases that are responsible for signal transduction, then the inference from this is that inhibiting the formation of Ras_GTP and/or Rap1_GTP may be an attractive alternative target to TrkA kinase. Consistent with this notion is the observation that loss of function mutations in neurofibromin (a GAP for p21Ras) are associated with chronic pain phenotypes [29,30].

Notably, the steady-state concentration of TrkA had a strong influence on phospho-TrkA concentrations in both model 1 and model 2. The initial levels of TrkA according to Sasagawa et al. [13] were approximately 60 nM, with a steady-state level after initiation of reaction with NGF approximately 10 nM. However, this model was developed using an over-expressing PC12 cell line. Given the apparent critical importance of the TrkA kinase concentration in determining the response, then data in relevant human cell types would be very useful to test whether this in vitro observation reflects the reality in human tissue in situ. In addition, an improved understanding of how dppERKnuc signal amplitude relates to pain gene expression would be valuable.

It was also interesting to note that the p75 levels in the PC12 and DRG cells are high and the next iteration of this model should include these data, together with the developing understanding of p75/TrkA interactions [31]. In addition, in this enquiry we have introduced drugs assuming simple steady-state concentrations. However, in vivo drugs exhibit complex time-dependent pharmacokinetics. Using model 2, it will be possible to introduce drug pharmacokinetics parameters and rationally explore the optimal drug properties such as dose, regimen and compartment of action.

Although certain species, such as NGF, are clearly most influential, there appears to be a distribution of control across the species and parameters thereafter. This study describes one method for prioritizing these, but the question of where, and indeed if, a line can be drawn remains. From a drug discovery perspective, this may mean that valid targets are present, but do not feature uppermost in the ranking by integral. Furthermore, the potential exists for multiple targets that yield additive or even synergistic effects and it would be of interest to explore this. An additional key caveat is that the approach described in this study assumes an absence of uncertainty in model structure or parameters. This is very unlikely to be the case, and others have investigated the use of stochastic methods to explore the impact of parameter variability on the conclusions drawn [32]. Ultimately, though, further data will be required to test the model assumptions, predictions and to refine models. Finally, developments in computational methods and technology may allow for a detailed time-dependent sensitivity analysis in the future, which is currently impractical for large models such as the one described in this study in a drug discovery setting.

5. Conclusion

We have shown that sensitivity analysis is a powerful tool for ranking the relative influence of control points in our ODE NGF pathway model. From a drug discovery perspective, these targets can be further prioritized according to empirical principles, indicating the probability of developing a successful drug against that target class. Interestingly, supporting evidence for the actual viability of at least some of the targets identified by our models exists. We have also shown that integration of the pathway model into a more realistic physiological context can facilitate the exploration of the potential for given drug interventions. This exercise suggested that inhibitors of TrkA kinase may be an interesting approach for novel pain medications, but highlights that achieving saturating inhibition may require higher unbound plasma drug concentrations than might be expected according to simple pharmacological theory. Data-validated systems pharmacology models such as described in this study (and in other areas such as central nervous system diseases [33], oncology [34], osteoporosis [35], endometriosis [9] and safety [36]) could be of great utility in drug discovery.