Nonsteady State Oxygen Transport in Engineered Tissue: Implications for Design

Abstract

Engineered tissue constructs are limited in size, and thus clinical relevance, when diffusion is the primary mode of oxygen transport. Understanding the extent of oxygen diffusion and cellular consumption is necessary for the design of engineered tissues, particularly those intended for implantation into hypoxic wound sites. This study presents a combined experimental and computation model to predict design constraints for cellularized fibrin tissues subjected to a step change in the oxygen concentration to simulate transplantation. Nonsteady state analysis of oxygen diffusion and consumption was used to estimate the diffusion coefficient of oxygen (mean±SD, 1.7×10⁻⁹±8.4×10⁻¹¹ m²/s) in fibrin hydrogels as well as the Michaelis-Menten parameters, V_max (1.3×10⁻¹⁷±9.2×10⁻¹⁹ mol·cell⁻¹·s⁻¹), and K_m (8.0×10⁻³±3.5×0⁻³ mol/m³), of normal human lung fibroblasts. Nondimensionalization of the governing diffusion-reaction equation enabled the creation of a single dimensionless parameter, the Thiele modulus (φ), which encompasses the combined effects of oxygen diffusion, consumption, and tissue dimensions. Tissue thickness is the design parameter with the most pronounced influence on the distribution of oxygen within the system. Additionally, tissues designed such that φ<1 achieve a near spatially uniform and adequate oxygen concentration following the step change. Understanding and optimizing the Thiele modulus will improve the design of engineered tissue implants.

Introduction

Engineered implantable tissues have the potential to revolutionize the therapy of tissue damaged by disease or trauma by providing an alternative to supply limited organ transplants.¹ However, the viability of thick (>1 cm) engineered tissue is limited by the supply of oxygen and other nutrients, as well as the removal of toxic waste products, both of which occur via diffusion in most in vitro systems.² The diffusion limit of cell-dense tissues, such as skeletal muscle, in vivo is generally considered to be <200 μm.³ For thicker tissues, transport of nutrients and waste products is enhanced by convection in the vascular system.^4,5

Preservation of cellular viability and function upon implantation relies on the rapid ingrowth of new blood vessels to overcome mass transport limitations. Prevascularizing the implantable tissue can shorten the time it takes for the implant to fully integrate with the host^6–8; however, normal perfusion remains difficult and requires additional time after implantation to allow for vessel remodeling. Depending on the tissue design, this may take on the order of days to weeks.^9,10 Additionally, tissue implants are forced to transition from the artificially abundant supply of oxygen generally present in vitro (∼20% O₂), to either a physiological oxygenation state (∼5% O₂), or a hypoxic wound bed where the oxygen concentration can be <1%.^11–15 Such steep oxygen gradients can be particularly damaging for oxygen-sensitive cells such as cardiomyocytes and stem cells.^12,13,16,17 We have previously reported that when prevascularized fibrin tissues cultured at 20% O₂ for 7 days were subjected to a simulated implantation in which the oxygen concentration was decreased to 1%, the sustained hypoxia degraded the capillary network within 4 days.¹⁸ An improved understanding of oxygen diffusion and consumption in engineered tissues upon implantation will facilitate improved viability and function.

There are many published mathematical models that describe oxygen transport through engineered tissue, correlating spatial gradients of oxygen concentration to cell density,^19,20 viability,^21–23 metabolism,²⁴ organization,^25–27 and growth factor expression.^28,29 However, most models utilize steady state approximations. An engineered tissue may be implanted fully oxygenated (i.e., 20% O₂ from an incubator), but the temporal change in oxygen upon implantation can impact tissue survival and function. For example, the duration and severity of hypoxia following equilibration to in vivo conditions and preceding re-oxygenation via host integration can impact gene expression, phenotype, and even apoptosis in susceptible cells.³⁰ Toward this end, we propose a combined experimental and computational approach toward examining the effects of a step change in oxygen tension (simulated implantation) on the temporal and spatial distribution of oxygen within a thick cellularized tissue construct.

The objectives of this study are to (1) build a nonsteady state model of oxygen transport through thick metabolically active tissue; (2) introduce an experimental platform that, when combined with the nonsteady state mathematical model, characterizes the diffusion and reaction of oxygen within the tissue construct; and (3) use computational simulations to predict design constraints for implantable tissues. Using a nondimensionalized form of the diffusion-reaction equation, we show that a single dimensionless parameter, the Thiele modulus, captures the combined effects of oxygen diffusion, chemical consumption, and tissue dimensions, and thus can assist in the design of engineered tissues.

Materials and Methods

Oxygen-sensing system

A polymethyl methacrylate (PMMA) mold was fabricated to contain a single 10-mm-diameter well, which served as the optically transparent experimental tissue culture container. Optical oxygen sensors (PreSens, Germany) were used for continuous monitoring of the oxygen concentration. The sensors utilize dynamic fluorescence quenching, and allow for noninvasive measurements through transparent material without consuming oxygen (measurement range: 0%–100% O₂, accuracy:±0.4% O₂, 90% response time: <6 s). A 10-mm-diameter spot sensor was placed inside the fabricated tissue culture mold to facilitate measurement of oxygen tension at the base of the well. A fiber-optic cable was fixed opposite the spot sensor, and connected to a transmitter that reported real-time oxygen measurements.

Cell culture

Normal human lung fibroblasts (NHLFs, Lonza) were cultured in the fibroblast growth medium (FGM-2, Lonza). Cells were maintained at 37°C in humidified air containing 5% CO₂, and the medium was changed every 48 h. Cells were passaged at 80% confluence with 0.025% trypsin, and used at passage 6–7.

Fibrin tissue assembly

The tissue constructs were prepared using sterile filtered 2.5 mg/mL or 10 mg/mL fibrinogen solutions in Dulbecco's phosphate-buffered saline (DPBS). For the cellularized tissues, NHLFs were suspended in the fibrinogen solution for a total concentration of 3×0⁶ cells/mL. The fibrinogen solution was then mixed with thrombin (for a final concentration of 2 units/mL), and placed in the PMMA oxygen-sensing well to achieve a desired thickness (range 1–5 mm). The tissue construct (cellularized gel) was left undisturbed for 5 min at room temperature, and then transferred to a 37°C incubator, maintained at 5% CO₂ and balance air for 20 min, to allow the fibrinogen to completely polymerize. To achieve a near constant initial value of an ambient oxygen concentration (20%) throughout the entire thickness, the tissues were used for experimentation immediately after polymerization.

Cell viability

Cell viability within the tissue constructs was quantified using the LIVE/DEAD Cell Viability Assay (Invitrogen, Carlsbad, CA) and Hoechst nucleic acid staining. The tissues were first washed with PBS, and then incubated at room temperature with 8 mM ethidium homodimer (EthD) and 5 μg/mL of the Hoechst solution for 30 min. After another PBS wash, the tissues were imaged using a fluorescence microscope (Nikon Eclipse TE300).

Hypoxic chamber and experimentation

Assembled fibrin tissues were transferred from the 20% O₂ incubator to a hypoxic chamber for experimentation. The hypoxic chamber contained 1% O₂, 5% CO₂, and balance N₂. The entire oxygen-sensing unit was housed inside the chamber. Acellular and cellular 2.5 mg/mL fibrin gels were constructed at five thicknesses (1, 2, 3, 4, and 5 mm), with three replicates per condition, for a total of 30 gels.

Mathematical Model

Geometry

The proposed mathematical model describes the cellularized fibrin hydrogel construct as detailed in the Materials and Methods section. A fibrin gel of thickness h and a radius of 10 mm has an oxygen concentration of C(z,t) (Fig. 1). The bulk environment directly above the fibrin gel (at z=0) is assumed to maintain a uniform oxygen concentration (C_b).

FIG. 1.

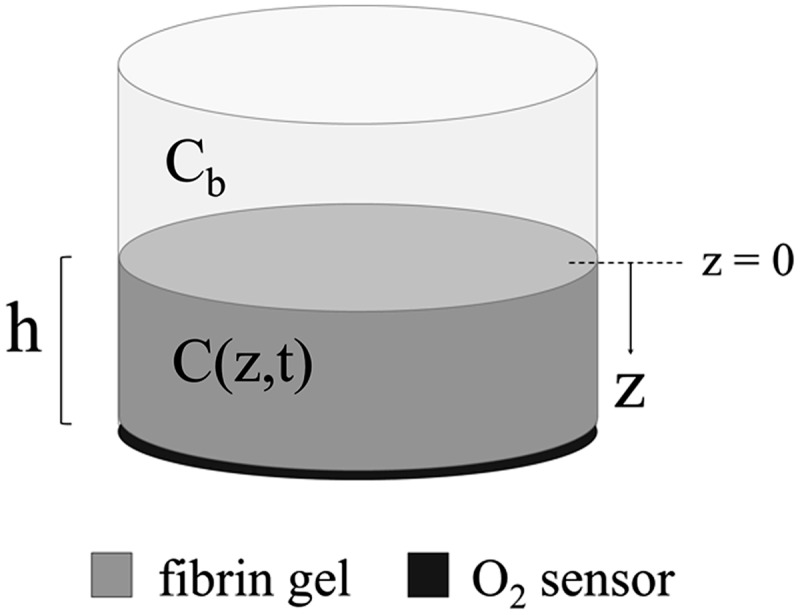
Schematic representation of the fibrin gel and oxygen sensor system. In this setup, the fibrin gel is constructed on top of the sensor, which transmits oxygen measurements at z=h to an exterior probe. C(z,t) is the concentration of oxygen within the fibrin gel, and C_b represents the concentration of oxygen at the z=0 boundary.

Oxygen diffusion

Under static incubation conditions, mass transfer through the model system occurs by net diffusion in the z-direction only. The concentration of oxygen is assumed to be independent of the radial and circumferential dimensions. Fick's second law with a reaction term describes the mass balance of oxygen in the gel:

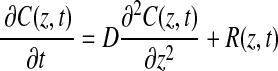(1)

where C (mol O₂/m³) is the concentration of oxygen as a function of space and time, D (m²/s) is the molecular diffusion coefficient of oxygen in the fibrin gel (assumed constant in space and time), and R (mol O₂·m³·s⁻¹) is the cellular oxygen consumption rate per unit volume of tissue. Cellular proliferation and death during the time scale of the cellular experiments (<4 h) are assumed negligible.

Cellular oxygen consumption

Cellular oxygen consumption was modeled using Michaelis-Menten kinetics,^31–33 where R(z,t) depends on the available oxygen concentration C(z,t):

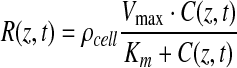(2)

V_max (mol·cell⁻¹·s⁻¹) is the maximum rate of oxygen consumption per cell, K_m (mol/m³) is the concentration of oxygen at which the oxygen consumption rate is half that of V_max, and ρ_cell (cells/m³) is the volumetric cell density of the uniformly distributed cellularized gel. At high oxygen concentrations, the system is saturated and R(z,t) equates to the maximum rate of reaction ρ_cellV_max (mol·m³·s⁻¹).

Initial and boundary conditions

The dissolved oxygen concentration in the fibrin gel equates to the product of the head gas partial pressure (% O₂ or Torr) and the solubility coefficient of oxygen, S_O2 (mol·m³·Torr⁻¹).³⁴ Atmospheric air is 20.9% oxygen, which is reduced to 19.9% in tissue culture incubators by the presence of 5% CO₂. This correction does not apply for the gas mixture in the hypoxic chamber, which was preformulated to contain 1% O₂. Therefore, the dissolved oxygen concentration for 19.9% and 1% O₂ head gas partial pressures are 2.0×10⁻¹ and 9.9×10⁻³ mol/m³, respectively. Model simulations examined an additional 5% O₂ fixed boundary, which equates to 4.9×10⁻² mol/m³. For simplicity, all presented data will be referred to by their oxygen volume fractions (i.e., 20%, 5%, 1% O₂).

No flux boundary conditions were used for all boundaries except the top surface of the gel (z=0), which was held constant at C_b. Because all experimental gels were formulated under ambient conditions and maintained in a 20% O₂ incubator before experimentation, the initial concentration of oxygen in the gel, C₀, is assumed to be 20% O₂. Therefore, the applied initial and boundary conditions were

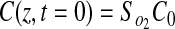(3)

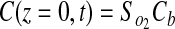(4)

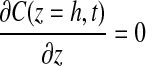(5)

Because the base of the tissue (the boundary at z=h, also where the oxygen sensor is located) represents the furthest distance from the oxygen source, it provides the minimum oxygen concentration within the system.

Nondimensionalization of the diffusion equation

The governing equation may be made dimensionless by introducing the following dimensionless groups:

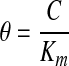(6)

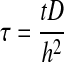(7)

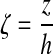(8)

where θ, τ, and ζ represent dimensionless concentration, time, and length, respectively. Equation 1 can then be reduced to the following dimensionless form:

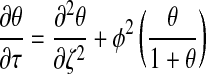(9)

subject to the initial and boundary conditions:

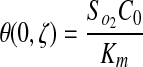(10)

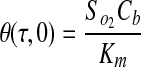(11)

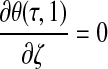(12)

where . Thus, after nondimensionalization, the effects of five dimensional parameters D, V_max, K_m, ρ_cell, and h are captured in a single dimensionless parameter, φ, which has been classically defined as the Thiele modulus.^35,36 A summary of all parameters used in both the dimensional and nondimensional models is presented in Table 1.

Table 1.

Summary of Model Parameters

Parameter	Definition	Reported value or units	Source
C	Dissolved oxygen concentration in gel	% or mol/m3	-
Cb	Oxygen concentration at air-gel boundary	% or mol/m3	-
Co	Initial oxygen concentration in gel	% or mol/m3	-
z	Distance from air-gel boundary	m	-
h	Gel thickness	m	-
t	Time in culture	s	-
D	Oxygen diffusion coefficient in fibrin	1.7×10−9 m2/s	measured
Vmax	Maximum oxygen consumption rate	1.3×10−17 mol cell−1 s−1	measured
Km	Half-maximum rate oxygen concentration	8.0×10−3 mol/m3	measured
ρcell	Volumetric cell density	2.85×106 cells/mL	measured
So2	Solubility coefficient of oxygen in culture medium at 37°C	1.3×10−3 mol m−3 Torr−1	32
θ	Dimensionless concentration	-	-
τ	Dimensionless time	-	-
ζ	Dimensionless length	-	-
φ	Thiele modulus	-	-
Ceq	Oxygen concentration at equilibrium	% or mol/m3	-
Cmin,eq	Minimum oxygen concentration at equilibrium	% or mol/m3	-
Cmin	Minimum oxygen concentration	% or mol/m3	-
t90	Time to 90% equilibrium	s	-

Model range

While the absolute values of D, V_max, and K_m will impact the oxygen tension within the tissue, their values will not change significantly between the engineered tissues used in our study (same matrix and cell type). Thus, the model was used to examine a range of cell densities and tissue thicknesses relevant for tissue-engineering applications. Connective tissue constructs, such as skin grafts, require densities of 2–10×10³ cells/mL,^37–40 while cell-dense tissues, such as skeletal muscle or liver, can require 0.6–10×10⁸ cells/mL.^8,41 The cell densities examined here thus ranged from 10³–10⁸ cells/mL. Tissue thickness was evaluated up to twice that of clinically relevant thickness for engineered tissue (approximately 5 mm),⁴² or up to 10 mm.

Model simulations

Two different step changes in oxygen tension were examined: (1) the transition from ambient conditions (20% O₂) to a physiological oxygenation state (5% O₂), or “Simulation 1” and (2) the transition from ambient conditions to a hypoxic wound bed (1% O₂), or “Simulation 2.” The two simulations and their corresponding initial and boundary conditions are summarized in Table 2. The oxygen concentration at equilibrium (C_eq) and the minimum oxygen concentration at equilibrium (C_min,eq) were used as indices for the steady state component of the solution. Likewise, the time-dependent minimum concentration of oxygen (C_min) and the time to 90% equilibrium (t₉₀) were used as indices of the nonsteady state component of the solution.

Table 2.

Scenarios Simulated in Computational Model

	Simulation 1	Simulation 2
C0	20% O2	20% O2
Cb	5% O2	1% O2
Physical significance	Implantation into physiological oxygenation state	Implantation into hypoxic wound bed

Solution

Equations 1 and 9 were solved with finite element methods using the commercial software COMSOL Multiphysics. The built-in module for diffusion-reaction equations was used, as well as a time-dependent solver for nonsteady state analysis and a predefined extra fine mesh size.

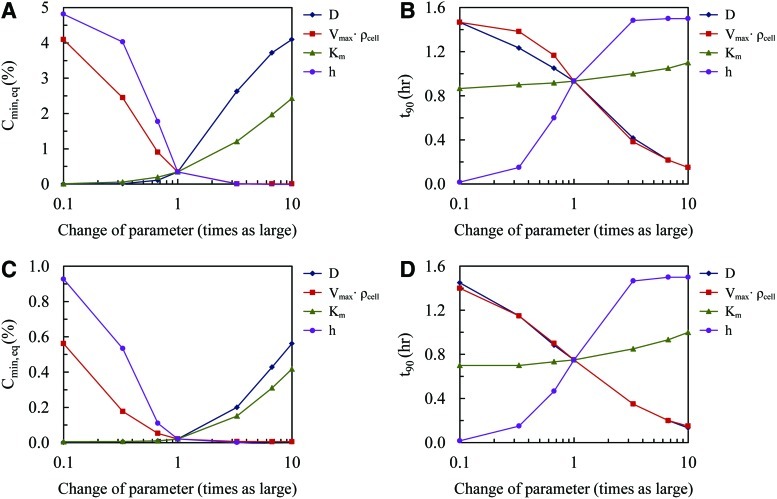
Sensitivity analysis

Sensitivity analysis was performed on the model parameters D, V_max, K_m, ρ_cell, and h. The parameter values were changed to 0.1 and 10 times their baseline value, while holding the remaining parameters constant. Changes in C_min,eq and t₉₀ were evaluated for all cases.

Parameter estimation

We estimated values for the unknown model parameters D, V_max, and K_m by comparing the model solution to experimental data. D was determined first using an additional set of five acellular 3 mm gels for each of 2.5 mg/mL and 10 mg/mL fibrin concentrations. In this case, R was set equal to zero in Equation 1. Next, to determine V_max and K_m, five cellularized 3 mm gels (for each of 2.5 mg/mL and 10 mg/mL fibrin concentrations) were examined, using an initial cell seeding density of 3×10⁶ NHLFs/mL. For all parameter estimation analysis, C₀=20% O₂ and C_b=1% O₂. The minimum oxygen concentration was monitored over time until steady state was reached. The mean of the experimental results were fit with model numerical solutions using parametric sweeps, and the values of D, V_max, and K_m were determined by minimizing the Residual Sum of Squares. The values reported are the mean and standard error of the best fit for each gel (n=5 for parameter estimation gels only).

Statistics

Statistical comparisons between experimental conditions were performed using one-way analysis of variance (ANOVA). Results are considered statistically significant for p<0.001.

Results

Cell viability

Fluorescence microscopy demonstrated that the average viable cell density for ten fibrin gels seeded with 3×0⁶ NHLFs/mL fibrinogen was 2.85×10⁶±0.04×10⁶ cells/mL (95% viability) within 1 h of tissue formation. This value was used for the volumetric cell density parameter, ρ_cell, in the model. No significant changes in cell density were found after the tissues were subjected to experimental conditions for 4 h. Additionally, Hoechst nuclei staining confirmed uniform cell distribution throughout the fibrin gel.

Gel thickness and cellular content affect oxygen concentration profiles

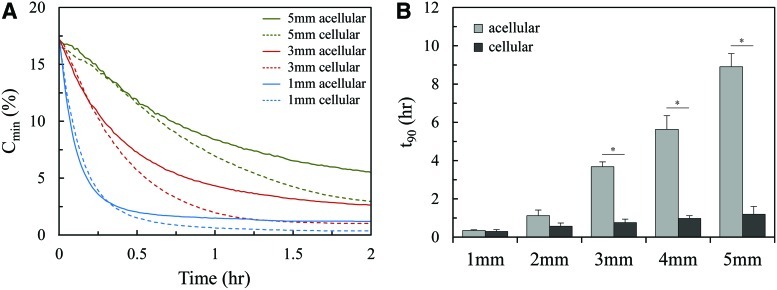
The oxygen concentration at the base of acellular and cellular 2.5 mg/mL fibrin gels constructed with thicknesses of 1, 2, 3, 4, and 5 mm was monitored experimentally as the gels were subjected to a step change (20% to 1%) in the O₂ concentration. Figure 2A shows C_min as a function of time for tissues of sample thicknesses 1, 3, and 5 mm. The cellularized gel demonstrated a lower oxygen concentration over time for each case compared to the acellular gel. Figure 2B shows the average t₉₀ for each condition. For both the acellular and cellular sets of gels, equilibrium was reached more quickly as the gel thickness decreased. Additionally, for any given gel thickness, the cellular condition exhibited steeper gradients of oxygen loss over time, and reached equilibrium significantly faster than the acellular condition.

FIG. 2.

(A) A minimum oxygen concentration of experimental acellular and cellular fibrin gels subjected to a 20% to 1% O₂ step change at t=0. (B) Average time to 90% equilibrium for acellular and cellular fibrin gels of varying thicknesses (*p<0.001). Color images available online at www.liebertpub.com/tea

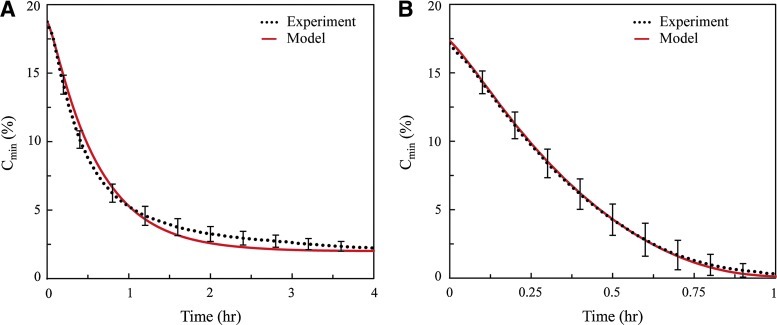
Estimation of system parameters

D, V_max, and K_m were calculated by fitting experimental data to model data (Fig. 3A, B). There was no statistical difference for any of the model parameters between the 2.5 mg/mL and 10 mg/mL fibrin gel systems. The mean (±SE) D was 1.7×0⁻⁹ (±8.4×10⁻¹¹ or 4.9%) m²/s, which is approximately 57% of aqueous diffusivity, or 3.0×10⁻⁹ m²/s.^19,27 Similarly, the values of V_max and K_m for NHLFs embedded in a fibrin gel were 1.3×0⁻¹⁷ (±9.2×10⁻¹⁹, or 7.3%) mol·cell⁻¹·s⁻¹ and 8.0×10⁻³ (±3.5×10⁻³, or 44%) mol/m³, respectively, which is consistent with previously published values for human fibroblasts.⁴³ Good correlations were found between experimental and computational results for both acellular (r²=0.99) and cellular (r²=0.93) sets of data.

FIG. 3.

Estimation of system parameters was achieved by fitting experimental results with model solutions using the Residual Sum of Squares method. The mean of the experimental data and its corresponding best-fit curve is represented here. (A) Acellular gels were used to characterize the diffusion coefficient D (r²=0.99) and (B) cellular gels were used to characterize the Michaelis-Menten parameters V_max and K_m (r²=0.93). Color images available online at www.liebertpub.com/tea

Thiele modulus dependence on gel thickness and cell density

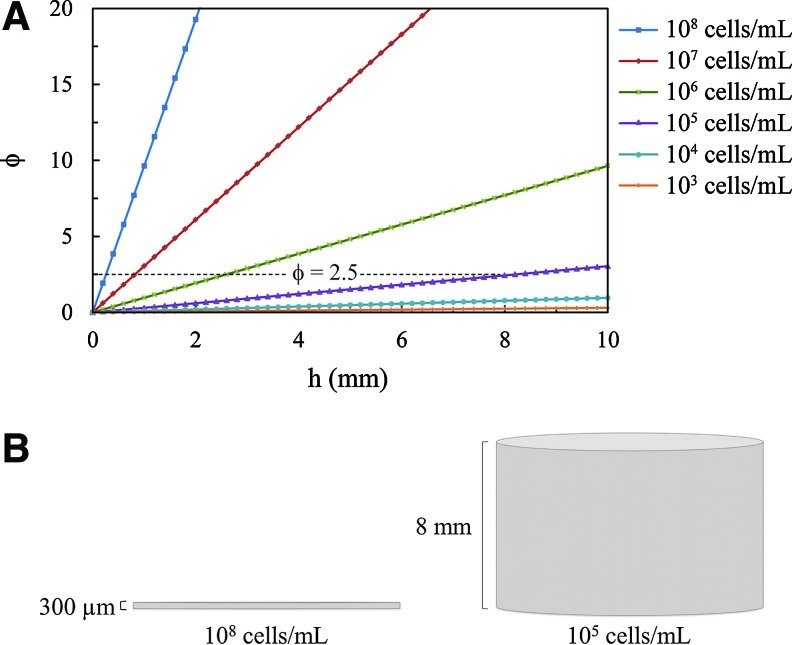
Figure 4A presents the calculated Thiele moduli for 0<h<10 mm, and for 10³<ρ_cell<10⁸. The Thiele modulus is proportional to h, but only to the square root of ρ_cell; thus, φ is more sensitive to h as ρ_cell increases. The dotted line in Figure 4A demonstrates how different combinations of gel thickness and cell density can yield φ=2.5; and Figure 4B illustrates two examples of gels with φ=2.5.

FIG. 4.

(A) The Thiele modulus as a function of gel thickness for varying cell densities. (B) A gel of 300-μm thickness and with 10⁸ cells/mL (left) has the same Thiele modulus (φ=2.5) as a gel of 8-mm thickness and with 10⁵ cells/mL (right). Color images available online at www.liebertpub.com/tea

Model predictions of oxygen step change

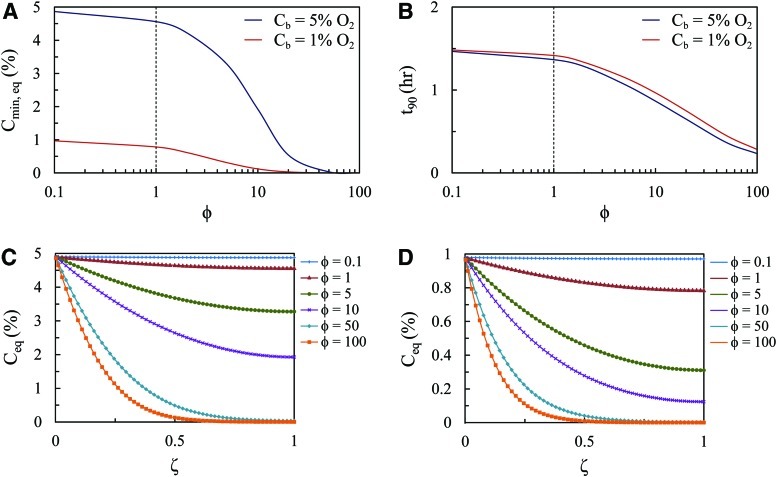
Equation 9 was solved using a range of φ from 0.1 to 100, which represents the approximate Thiele moduli calculated for h=10 mm and ρ_cell ranging 10³–10⁸. Simulation 1 (C_b=5% O₂) covers a wider range of C_min,eq compared to Simulation 2 (C_b=1% O₂), with both cases approaching a 0% O₂ limit with increasing φ (Fig. 5A). Both cases were comparable when assessed for t₉₀ (Fig. 5B).

FIG. 5.

Model predictions of fibrin tissue subjected to oxygen step change. (A) The minimum oxygen concentration at equilibrium and (B) the time to 90% equilibrium as a function of the Thiele modulus for Simulation 1 (C_b=5% O₂) and Simulation 2 (C_b=1% O₂). An equilibrium oxygen concentration throughout the tissue thickness for (C) Simulation 1 and (D) Simulation 2 for a range of Thiele moduli. Color images available online at www.liebertpub.com/tea

For both simulations, the model predicted a threshold Thiele modulus at which C_min,eq and t₉₀ become much more dependent on φ (dotted line in Fig. 5A, B). For φ<1, C_min,eq as well as t₉₀ remains relatively constant. Conversely, for φ>1, both C_min and t₉₀ decrease more sharply with the increasing Thiele modulus.

Finally, the model was used to predict the steady state oxygen concentration profile throughout the entire thickness of the tissue (Fig. 5C, D). Again, for φ<1, the equilibrium concentration of oxygen remains moderately steady throughout the entire tissue. As the Thiele modulus increases above 1, the tissue exhibits a larger spatial distribution of oxygen.

Sensitivity analysis reveals dependence on model parameters

Sensitivity analysis was conducted on the main input parameters D, V_max, K_m, ρ_cell, and h to determine their relative influence on the model Simulation 1 (Fig. 6A, B) and Simulation 2 (Fig. 6C, D). The effects of V_max and ρ_cell are treated as a single parameter because of their presence as a product in the governing equation. A decrease in V_max or h, as well as an increase in D led to an increase in C_min,eq. Increasing K_m resulted in an increase in C_min,eq, but did not have a significant impact on t₉₀. Both V_max and D strongly impacted t₉₀ in an inverse relationship, whereas h strongly impacted t₉₀ in a positive relationship.

FIG. 6.

Sensitivity analysis shows influence of model parameters on minimum oxygen concentrations at equilibrium and time to 90% equilibrium for (A, B) Simulation 1 and (C, D) Simulation 2, respectively. Color images available online at www.liebertpub.com/tea

Discussion

The advancement of tissue engineering relies on the development of thicker and more cell-dense constructs that more closely represent physiological tissue. Analyzing the diffusion and consumption of oxygen and other nutrients within cell-seeded scaffolds is crucial toward achieving an understanding of the design limitations for engineered tissues. It has been previously shown that spatial oxygen gradients are prevalent in 3D tissues cultured under ambient conditions,^27,44,45 but we have shown here that hypoxic implantation conditions further exacerbate these gradients. The severity and longevity of restricted oxygen supply during the time period between implantation and host integration (that establishes blood flow) may compromise cellular viability and function. We have modeled the dynamics of oxygen transport postimplantation that steady state models cannot capture. Computational simulations were used to assess the influence and design constraints of model parameters D, V_max, K_m, ρ_cell, and h. In doing so, we are able to demonstrate measurable constraints, in the form of the dimensionless Thiele modulus, that create spatially uniform and adequate oxygenation of thick implantable tissues. These results may be used to quantitatively inform a design strategy for tissue engineers who wish to optimize their own systems to sustain a threshold oxygen concentration upon implantation.

The Thiele modulus

The model governing equation was nondimensionalized to highlight how a single dimensionless parameter φ can quantify the relative importance of diffusion and reaction phenomena in the system. Mathematically, φ² is a ratio of the characteristic rate of reaction, 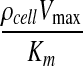, to the characteristic rate of diffusion, 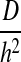, both with units of inverse time. If the rate of diffusion is fast compared to the rate of reaction, then the Thiele modulus is small. For example, thin tissues with low cell densities (e.g., skin and cartilage) would have relatively small Thiele moduli. This correlates to a moderately uniform oxygen concentration profile throughout the gel because diffusion is fast enough to maintain a sufficient supply of oxygen. Conversely, for cell-dense, thick tissues (e.g., the cardiac muscle and liver), the Thiele modulus would be large and the system diffusion limited. Physically, this implies a greater degree of spatial heterogeneity in the oxygen concentration throughout the tissue (Fig. 5C, D) because oxygen cannot diffuse far, relative to the thickness of the tissue, before it is consumed. Our model simulations suggest that the separation between tissues that behave as “thin, less cell-dense” and those that are “thick, cell-dense” is φ<1 and φ>1, respectively (Fig. 5).

Design considerations for tissue-engineered constructs

Our model of oxygen transport offers predictive capabilities that can be used to optimize values for system parameters when culturing 3D tissues. Although the Thiele modulus contains five major model parameters (D, V_max, K_m, ρ_cell, and h), in effect, h is the only parameter over which tissue engineers have complete control. Researchers are typically restricted to a certain cell type for a given application; thus, V_max and K_m, which characterize cellular oxygen consumption, are generally prescripted. Similarly, while researchers may choose from natural (e.g., fibrin) or synthetic (e.g., PLGA) matrices, the diffusive property for oxygen (i.e., D) is not likely to vary,^{19,26,46–48} and should not be considered a design parameter. Even accounting for matrices that may have varied parameters, such as the polymer volume fraction,⁴⁸ diffusivities are still generally within an order of magnitude of aqueous diffusivity.²⁷ Furthermore, replicating in vivo tissue-specific function (e.g., cardiac muscle) constrains cell density. Hence, tissue thickness emerges as the key design parameter over which researchers maintain considerable flexibility.

Figure 4B highlights the significance of the Thiele modulus being able to encompass the effects of the major model parameters into a single parameter. Two gels are presented, composed of the same matrix material and embedded with the same cells. However, one gel contains a significantly higher cell density, while the other is constructed with a significantly larger thickness. Physically, they look quite different, but because they have the same calculated Thiele modulus (φ=2.5), both gels will exhibit the exact same solution to the governing equation for an oxygen concentration, and will thus behave the same way subject to any given set of initial and boundary conditions.

For the experimental gels used here to estimate the system parameters, the Thiele modulus is approximately 5. It is clear from this calculation as well as from Figure 2B that this model system is reaction dominated. We have shown that the transport behavior of the system shifts significantly for φ>1; specifically, C_min,eq and t₉₀ decrease sharply with the increasing Thiele modulus (Fig. 5A, B). Variation in the spatial distribution of oxygen also becomes more pronounced for φ>1 (Fig. 5C, D). If a spatially uniform oxygen concentration is desired, then the tissue construct should be designed to maintain φ<1. A doubling in the gel thickness, for example, would have to be balanced out by a fourfold (square dependence) decrease in cell density.

It should be noted that the literature is rich with experimental tissue-engineered models that support both diffusive and convective modes of transport for oxygen and other nutrients.^49–52 Limitations in diffusion, as described here, will certainly be alleviated by the presence of efficient convective transport. For these advanced systems, one or more additional dimensionless groups would be required to capture the effect of convection the mathematical model.

Model parameter estimation and sensitivity

Two fibrin concentrations relevant to tissue-engineering applications were investigated: 2.5 mg/mL and 10 mg/mL. 2.5 mg/mL is the approximate concentration of fibrin found in a physiological clot, and serves as the protein concentration of matrices in common tissue culture models of angiogenesis.⁵³ 10 mg/mL fibrin matrices have greater mechanical integrity, and support the growth of mature microvessel networks capable of anastomosis with the host upon implantation.⁶ It has been shown previously that increasing the protein concentration from 2.5 mg/mL to 10 mg/mL in fibrin hydrogels significantly restricted diffusive transport of molecules greater than 10 kDa.⁵⁴ In contrast, we found that the oxygen diffusivity was the same for 10 mg/mL and 2.5 mg/mL fibrin gels. This result suggests that oxygen molecules (32 Da) are small enough to not be restricted by any change in physical properties (e.g., porosity, viscosity) between 2.5 and 10 mg/mL. Likewise, the values for V_max and K_m were the same for both 10 mg/mL and 2.5 mg/mL fibrin gels. Because V_max and K_m are intrinsic cellular properties, it is perhaps not surprising that they do not depend on the range of fibrin concentration employed in our study.

Sensitivity analysis on D, V_max, K_m, ρ_cell, and h demonstrates that parameter estimation depends on whether the model solution is at a steady state or an unsteady state. For example, t₉₀ is nearly independent of K_m (Fig. 6B, D), but depends strongly on D, V_max, ρ_cell, and h. In contrast, C_min,eq depends strongly on D and K_m for larger values (1–10 times the baseline value), and depends strongly on V_max, ρ_cell, and h for smaller values (0.1–1 times the baseline value) (Fig. 6A, C). Thus, while D and V_max can be estimated by the unsteady and steady state features of the problem, K_m is best determined once the steady state is achieved, and for values larger than that present in our system. Our estimates of V_max, K_m, and D were accomplished using the unsteady parts of the oxygen concentration in the tissue construct (Fig. 3); hence, the estimate of K_m exhibited a higher standard error (44%) compared with either D (4.9%) or V_max (7.3%).

Conclusion

Understanding the mass transfer limitations of key nutrients such as oxygen is integral for the design of successful engineered tissues, particularly for those intended for implantation. In this study, oxygen diffusion and consumption within thick metabolically active fibrin tissues was modeled experimentally and computationally. Hypoxic implantation conditions were simulated to highlight the unsteady state behavior of the oxygen concentration, which has traditionally been neglected in similar studies. We have shown that both spatial and temporal oxygen gradients and the absolute oxygen concentration are particularly sensitive (squared dependence compared to D, V_max, K_m, and ρ_cell) to the sole design parameter—tissue thickness. Fortunately, a single dimensionless parameter, the Thiele modulus (φ), captures the combined effect of D, V_max, K_m, ρ_cell, and h, and designing a tissue such that φ<1 minimizes undesirable gradients or particularly low values in the oxygen concentration.

Acknowledgments

We would like to thank Nicole Mendoza for her assistance with the cell viability characterization experiments. This work was supported by National Institute of Health grants RC1 ES018361 and UH2 TR000481.

Disclosure Statement

No competing financial interests exist.