On the measurement of ¹⁵N-{¹H} nuclear Overhauser effects. 2. Effects of the saturation scheme and water signal suppression

Abstract

Measurement of steady-state ¹⁵N-{¹H} nuclear Overhauser effects forms a cornerstone of most methods to determine protein backbone dynamics from spin-relaxation data, since it is the most reliable probe of very fast motions on the ps-ns timescale. We have, in two previous publications (J. Magn. Reson. 192 (2008), 302-313; J. Am. Chem. Soc. 131 (2009), 6048-6049) reevaluated spin-dynamics during steady-state (or “saturated”) and reference experiments, both of which are required to determine the NOE ratio. Here we assess the performance of several windowed and windowless sequences to achieve effective saturation of protons in steady-state experiments. We also evaluate the influence of the residual water signal due to radiation damping on the NOE ratio. We suggest a recipe that allows one to determine steady-state ¹⁵N-{¹H} NOE's without artifacts and with the highest possible accuracy.

Introduction

Significant efforts have been invested in the quantitative measurement and detailed interpretation of spin relaxation rates in solution-state NMR [1; 2; 3]. Spin-relaxation rates provide detailed insight into protein dynamics, and allow one to assess the effects of interactions with small molecules, other proteins and nucleic acids on these internal dynamics. Changes in dynamics provide estimates of variations in conformational entropy upon complex formation [4; 5], a quantity that is inaccessible by other means. While methods to interpret spin-relaxation measurements more accurately in terms of dynamic [6; 7] or thermodynamic parameters [8] continue to be developed, the most common NMR experiments used for measuring spin-relaxation rates have remained essentially unchanged for many years. Measurements of the spin-lattice (R₁) and spin-spin (R₂) relaxation rates of backbone amide ¹⁵N nuclei together with steady-state ¹⁵N-{¹H} nuclear Overhauser effects (NOE's) are nowadays performed routinely by specialists and non-specialist alike [9]. Minor modifications to schemes for measuring relaxation rates involving ¹⁵N nuclei have been proposed [10] by incorporating TROSY [11] enhancements. This has allowed studies of larger proteins without modifying the overall framework of the experimental schemes. However, certain effects, while small for medium static field strengths (500-600 MHz) commonly used a decade ago, lead to curious phenomena at the ultra-high fields (800 MHz and higher) that are accessible today [12]. Thus, a reassessment of the underlying spin-dynamics for these spin-relaxation experiments appears timely, to improve the accuracy by reducing deleterious effects and allowing for a proper interpretation of the measured relaxation rates in terms of protein dynamics. This is especially true for NOE's, which provide access to very high-frequency motional modes centered around the ¹H resonance frequency [13].

We have recently shown that the interference between the chemical shift anisotropy (CSA) of the ¹⁵N nucleus and the ¹⁵N-¹H^N dipolar coupling, in combination with evolution under offsets and one-bond ¹⁵N-¹H^N scalar couplings (J_NH) leads to a modified steady state. This results in erroneous NOE values when using a commonly employed saturation scheme that consists of a train of 120° pulses applied to the ¹H nuclei [14]. These errors can be cancelled by two minor modifications to the experimental scheme: (1) applying 180° pulses to the ¹H nuclei to achieve effective saturation and (2) using delays between these 180° pulses that are matched to k/J_NH, where k is an integer [14]. In addition, we have also demonstrated, using Average Liouvillian Theory (ALT) [15; 16] that a symmetric saturation scheme obviates the need for a complete saturation of the ¹H magnetization [13]. This is especially advantageous for surface-exposed amide groups where ¹H^N nuclei exchange with solvent ¹H nuclei.

In this paper, we further investigate the role of the scheme used to irradiate protons. We compare the effects of 180° pulses, broadband inversion pulses (BIP) [17] and common composite pulse decoupling schemes such as WALTZ-16 [18] and GARP [19]. We also investigate the effects of incomplete water suppression originating from radiation damping during the chemical shift evolution period for ¹⁵N nuclei. Finally, we combine these novel steps with those of our previous work and prescribe a recipe for the measurement of ¹⁵N-{¹H} nuclear Overhauser effects with minimal errors.

Theory

In this section, we provide the theoretical basis for numerical calculations used to assess the performance of various pulse sequences to obtain steady-state ¹⁵N-{¹H} NOE's.

Let us start with a remark about our nomenclature. Although both experiments recorded to measure NOE ratios are initiated after the spin systems have reached a steady state, we prefer to use this term to describe the experiment where the polarization of nitrogen-15 nuclei is measured after the proton irradiation. We believe that the term “steady-state” is less confusing and more accurate than the term “saturated” since we have shown that a proper saturation of the protons is not necessary: only an effective saturation where the proton polarization vanishes on average is required [13]. Therefore, we will distinguish the two experiments as (1) the reference experiment (without proton irradiation) and (2) the steady-state experiment.

We consider an isolated heteronuclear two-spin 1/2 system (an amide ¹H^N and ¹⁵N spin-pair, for example). The evolution of the density operator σ(t) is described by the Homogeneous Master Equation (HME) [20; 21; 22]:

$$\frac{\text{d}\sigma \left(t\right)}{\text{d}t}=-\widehat{L}(t)\sigma (t)$$ (1)

The Liouvillian superoperator L̂(t) is the sum of three terms and is given by

$$\begin{array}{c}\widehat{L}(t)=i\widehat{H}(t)+\widehat{\Gamma }(t)+\widehat{\Theta }(t)\\ =i\widehat{H}(t)+{\widehat{\Gamma }}_f(t)\end{array}$$ (2)

Ĥ(t) is the Hamiltonian superoperator, related to the Hamiltonian operator H(t) by:

$$\widehat{H}(t)=H(t)\otimes E-E\otimes H(t)$$ (3)

The full relaxation superoperator Γ̂_f(t) includes relaxation (Γ̂(t)) and thermal correction (Θ̂(t)) [15; 23] components. E is the identity matrix in a Hilbert space of appropriate dimensions, in the present case of a two-spin system it may be represented by a 4 × 4 matrix.

To analyze the effects of radiofrequency (RF) irradiation of the protons on the longitudinal polarization of nitrogen-15, we reduce the full density operator to a subspace of the Liouville space spanned by the basis operators {E/2,H_x,H_y,H_z,N_z,2H_xN_z,2H_yN_z,2H_zN_z}. In this basis, the rotating-frame Hamiltonian superoperator is:

$$i\widehat{H}=i{\widehat{H}}_{\mathit{\text{cs}}}+i{\widehat{H}}_{\mathit{\text{rf}}}(\phi )+i{\widehat{H}}_J=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& \Omega & -{\omega }_{1y}& 0& 0& \pi J_{\mathit{\text{NH}}}& 0\\ 0& -\Omega & 0& {\omega }_{1x}& 0& -\pi J_{\mathit{\text{NH}}}& 0& 0\\ 0& {\omega }_{1y}& -{\omega }_{1x}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& \pi J_{\mathit{\text{NH}}}& 0& 0& 0& \Omega & -{\omega }_{1y}\\ 0& -\pi J_{\mathit{\text{NH}}}& 0& 0& 0& -\Omega & 0& {\omega }_{1x}\\ 0& 0& 0& 0& 0& {\omega }_{1y}& -{\omega }_{1x}& 0\end{array}\right)$$ (4)

where Ĥ_cs, Ĥ_rf(φ), and Ĥ_J are the Hamiltonian superoperators for chemical shifts, radiofrequency fields and scalar-coupling interactions, respectively; Ω is the proton offset, J_NH the scalar coupling constant, while ω_1x and ω_1y are the amplitudes of the projection of the RF-field applied to the proton channel along the x and y axes of the rotating frame, respectively, with:

$$\begin{array}{c}{\omega }_{1x}={\omega }_{1}cos(\phi )\\ {\omega }_{1y}={\omega }_{1}sin(\phi )\end{array}$$ (5)

where ω₁ and φ are the amplitude and phase of the RF pulse, respectively. The full relaxation superoperator in this case is given by:

$${\widehat{\Gamma }}_f=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& {\rho }_H^{\mathit{\text{in}}}& 0& 0& 0& {\delta }_H^t& 0& 0\\ 0& 0& {\rho }_H^{\mathit{\text{in}}}& 0& 0& 0& {\delta }_H^t& 0\\ {\theta }_H& 0& 0& {\rho }_H^l& {\sigma }_{\mathit{\text{NH}}}& 0& 0& {\delta }_H^l\\ {\theta }_N& 0& 0& {\sigma }_{\mathit{\text{NH}}}& {\rho }_N^l& 0& 0& {\delta }_N^l\\ 0& {\delta }_H^t& 0& 0& 0& {\rho }_H^{\mathit{\text{anti}}}& 0& 0\\ 0& 0& {\delta }_H^t& 0& 0& 0& {\rho }_H^{\mathit{\text{anti}}}& 0\\ {\theta }_{\mathit{\text{NH}}}& 0& 0& {\delta }_H^l& {\delta }_N^l& 0& 0& {\rho }_{\mathit{\text{NH}}}^l\end{array}\right)$$ (6)

where the auto-relaxation rates are: ${\rho }_H^{\mathit{\text{in}}}$ for in-phase coherences (the transverse relaxation rate of the proton); ${\rho }_H^{\mathit{\text{anti}}}$ for anti-phase coherences; ${\rho }_H^l$ for longitudinal polarization (the longitudinal relaxation rate of the proton); ${\rho }_N^l$ for nitrogen-15 longitudinal polarization; and ${\rho }_{\mathit{\text{NH}}}^l$ for proton-nitrogen-15 two-spin order. The proton transverse cross-relaxation rate ${\delta }_H^t$ is due to the cross-correlation between the proton chemical shift anisotropy (CSA) and the dipole-dipole coupling (DD) with the nitrogen-15; the corresponding longitudinal cross-correlated cross-relaxation rate is ${\delta }_H^l$; and the nitrogen-15 longitudinal cross-relaxation rate due to the cross-correlation of the nitrogen-15 CSA and the proton-nitrogen-15 DD interactions is ${\delta }_N^l$. The thermal correction terms are chosen so that the nitrogen-15 longitudinal polarization is normalized to 1 [13; 16; 21; 23]:

$$\begin{array}{c}{\theta }_H={\sigma }_{\mathit{\text{NH}}}+\frac{{\gamma }_H}{{\gamma }_N}{\rho }_H^l\\ {\theta }_N={\rho }_N^l+\frac{{\gamma }_H}{{\gamma }_N}{\sigma }_{\mathit{\text{NH}}}\\ {\theta }_{\mathit{\text{NH}}}={\delta }_N^l+\frac{{\gamma }_H}{{\gamma }_N}{\delta }_H^l\end{array}$$ (7)

where γ_n and γ_h are the gyromagnetic ratios of the nitrogen-15 nucleus and proton, respectively. This normalization makes comparisons of simulations and experiments straightforward, since the expectation value of the longitudinal nitrogen-15 polarization at the steady state is equal to the NOE ratio (I_ss/I_ref), where I_ss is the signal intensity in the steady-state, and I_ref the signal intensity in the reference experiment.

For windowed sequences, during RF pulses, it is assumed that the evolution of the spin system is determined solely by chemical shifts (Ĥ_cs) and RF terms (Ĥ_rf(φ)), i. e., Ĥ_J and Γ̂_f are set to 0. During the delays (or ‘windows') between pulses, the Hamiltonian superoperator comprises the sum of chemical shift and scalar-coupling (Ĥ_j) terms, while the full relaxation superoperator (Γ̂_f of Eq. (6) is active. The solution to Eq. (1) for a sequence (τ/2 - β - τ/2) that is repeated n times, using a pulse of flip-angle β and a delay τ is:

$$\sigma (n\tau )={\widehat{U}}^n\sigma (0)$$ (8)

where the propagator Û is given by:

$$\widehat{U}=exp[-(i{\widehat{H}}_{\mathit{\text{cs}}}+i{\widehat{H}}_J+{\widehat{\Gamma }}_f)\tau /2]exp[-(i{\widehat{H}}_{\mathit{\text{cs}}}+i{\widehat{H}}_{\mathit{\text{rf}}}(\phi ))\beta /{\omega }_1]exp[-(i{\widehat{H}}_{\mathit{\text{cs}}}+i{\widehat{H}}_J+{\widehat{\Gamma }}_f)\tau /2]$$ (9)

Consider now a windowless sequence such as a composite-pulse decoupling (CPD) scheme which consists of a series of m contiguous pulses with nutation angles β_k and phases φ_k, with a total duration:

$${\tau }_{\mathit{\text{CPD}}}=\sum _{k=1}^m{\beta }_k/{\omega }_1$$ (10)

In this case, the solution to Eq. (1) is

$$\sigma (n{\tau }_{\mathit{\text{CPD}}})={({\widehat{U}}_{\mathit{\text{CPD}}})}^m\sigma (0)$$ (11)

with the propagator

$$\begin{array}{l}{\widehat{U}}_{\mathit{\text{CPD}}}({\tau }_{\mathit{\text{CPD}}})=\underset{k=1}{\overset{m}{\Pi }}exp[-(i{\widehat{H}}_{\mathit{\text{cs}}}+i{\widehat{H}}_J+i{\widehat{H}}_{\mathit{\text{rf}}}({\phi }_k)+{\widehat{\Gamma }}_f){\beta }_k/{\omega }_1]\end{array}$$ (12)

Using Eqs. (8) - (9) for windowed sequences comprising periods of free-precession interrupted by RF pulses; and Eqs. (10) - (12) for windowless sequences, we can predict the NOE ratio (I_ss/I_ref) for a variety of proton irradiation schemes.

Material and methods

Some experiments were performed on a Bruker Avance 500 MHz NMR spectrometer using a TXI cryoprobe with z-axis gradients on a sample of perdeuterated, uniformly ¹⁵N-labeled ubiquitin (0.5 mM, in buffer containing 50 mM ammonium acetate, 300 mM NaCl at pH 4.8). Other experiments were performed on a Bruker Avance III 600 MHz NMR spectrometer with a TXI room-temperature probe equipped with triple-axis gradients on a sample of perdeuterated, uniformly ¹³C and ¹⁵N-labeled ubiquitin (1.5 mM, in a buffer containing 50 mM ammonium acetate at pH 4.5). A sample of uniformly ¹⁵N labeled ubiquitin (1.5 mM, in a buffer containing 50 mM ammonium acetate at pH 4.5) was also studied with the latter equipment.

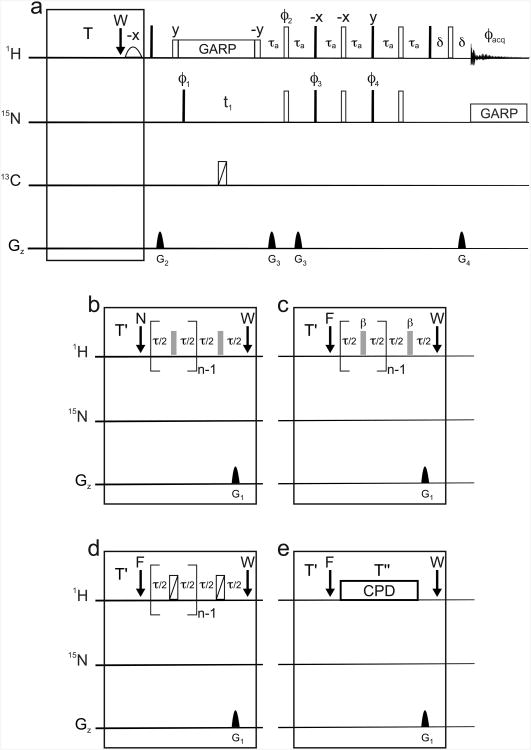
The pulse sequences used are presented in Fig. 1. Three different schemes were used to irradiate the protons. Figs. 1b and 1c show repetitions of the basic sequence [delay τ/2 - pulse β - delay τ/2]. The interpulse delay τ was either 5 ms or 22 ms, while the flip angle of the pulse β was usually 180° on resonance, with the exception of one experiment run with β = 10°. Inversion pulses that are less prone to offset effects, such as BIP pulses [17], were employed in a similar motif [delay τ/2 - BIP pulse - delay τ/2], as shown in Figure 1d. Finally, composite pulse decoupling schemes that have been previously employed in steady-state experiments were evaluated (Fig. 1e).

Figure 1.

Pulse sequences used to record steady-state ¹⁵N-{¹H} nuclear Overhauser effects. For each measurement, reference and steady-state experiments were recorded in an interleaved manner. The reference experiment is shown in (a). At the end of the recovery delay T = 10 s, the proton carrier is placed on resonance with the water signal and a very selective water-flip-back pulse is applied (3 ms sinc shaped). To record steady-state experiments, the boxed sequence in (a) was substituted by the schemes shown in (b-e) for the effective saturation of amide proton resonances. The recommended effective saturation scheme is shown in (b): after an optional delay T′ = 2 s for stable detection of the lock signal, the proton carrier is placed at the center of the amide region (at 8.2 ppm) as shown by the arrow labeled N. The motif [delay τ/2 – 180° pulse - delay τ/2] is repeated n times. The interpulse delay τ is typically 22 ms (11 ms may also be used, see text). The RF amplitude for the pulses was 7.5 kHz at 500 MHz Larmor frequency and 9 kHz at 600 MHz. A gradient G₁ is applied at the end of the last τ/2 delay to suppress all transverse components of the proton polarization. The carrier was then moved on-resonance with the water signal as indicated by the W arrow. To evaluate the influence of several effects the scheme (c) was used. The carrier was set to frequency F during proton irradiation, a delay τ of 5 ms or 22 ms was used and pulses with variable tilt angles β were employed. (d) Same irradiation scheme as in (c) was used, except that the square RF pulses were replaced by Broadband inversion pulses (BIP) [17] with durations of 72 μs and RF amplitudes of 18 kHz. (e) Composite pulse decoupling (CPD) with GARP [19] and WALTZ-16 scheme was used for proton effective saturation with a duration T″ = 4 s and RF amplitudes of 1 or 1.2 kHz (see text). Similarly, when schemes b-d were used, the number of cycles n was always set so that the total duration for effective saturation was 4 s. All narrow (filled) and (wide) open rectangles represent 90° and 180° pulses respectively. Pulse phases are along the x-axis of the rotating frame unless otherwise mentioned. Proton composite pulse decoupling during the delay t₁ was performed with a GARP scheme and an RF amplitude of 1 kHz. Composite-pulse decoupling during acquisition was performed on the ¹⁵N channel with a GARP scheme and an RF amplitude of 1090 Hz. The delay τ_a was set to 2.56 ms. The phases were: φ₁ = {y, -y}; φ₂ = {x, x, -x, -x}; φ₃ = {x, x, -x, -x}; φ₄ = {-y, -y, y, y}; φ_acq = {x, -x, -x, x}. The amplitude profile of pulsed-field gradient was a sine bell shape. At 600 MHz, their durations and peak amplitudes over the x, y and z directions were, respectively: G₁; 600 ms, 15 G.cm^-1, 15 G.cm^-1, 0; G₂; 1 ms, 0, 0, 25 G.cm^-1; G₃; 1 ms, 0, 0, 40 G.cm^-1; G₄; 1 ms, 0, 0, 8.1 G.cm^-1 . At 500 MHz, their durations and peak amplitudes along the z direction were, respectively: G₁; 500 ms, 18 G.cm^-1; G₂; 1 ms, 25 G.cm^-1; G₃; 1 ms, 40 G.cm^-1; G₄; 1 ms, 8.1 G.cm^-1 . The carrier was set at 117 ppm on the ¹⁵N channel. The duration of acquisition was 90 ms at 600 MHz and 100 ms at 500 MHz. In the indirect dimension, 64 complex points were recorded with a spectral width of 24 ppm. Coherence selection was achieved by inverting the amplitude of the gradient G₃ and phase φ₄.

Two proton decoupling schemes during the interval t₁ where the nitrogen-15 chemical shifts evolve (see Fig. 1a) were compared. Composite pulse decoupling (Fig. 1a) was compared with a more classical scheme (not shown) where a single 180° pulse is applied on the proton channel at the midpoint of the t₁ delay. The rest of the sequence is typical of sensitivity- and gradient-enhanced HSQC type experiments [24].

Result and discussion

Windowed Sequences

The accuracy of ¹⁵N-{¹H} NOEs strongly depends on the scheme employed to saturate the proton resonances [13; 14]. In particular, common schemes [delay τ/2 - pulse β - delay τ/2] with β ≠180° couple coherences and populations and may lead to undesirable effective cross-relaxation pathways such as:

$$H_z\stackrel{\beta }{\to }{H}_y\stackrel{H_J+H_{\mathit{\text{cs}}}}{\to }2N_z{H}_y\stackrel{\beta }{\to }2N_z{H}_z\stackrel{{\delta }_N^l}{\to }{N}_z$$

The first β pulse creates an in-phase proton coherence, which may be converted into an anti-phase coherence with the same phase during the following interpulse delay under the concomitant effect of the scalar coupling and chemical shift. The next pulse can thus generate two-spin order, which can cross-relax (due to CSA/dipole cross-correlation effects) to nitrogen-15 longitudinal polarization during the next interpulse delay. This effect can be virtually suppressed by the use of a flip angle β = 180°, and errors due to the deviations of the actual flip angle from the optimal value can be minimized by the use of an interpulse delay τ = k/J_nh where k is an integer [14].

To achieve the best accuracy of ¹⁵N-{¹H} NOE's, we have recorded experiments with various proton saturation schemes that are designed to suppress the undesired cross-relaxation pathway presented above. The first windowed sequence under study comprises a repetition of the motif [delay τ/2 - pulse β - delay τ/2] with τ = k/J_NH where k is an integer and β = 180°. To minimize heating of the sample, the 180° pulses are applied with an RF amplitude ω₁ that is attenuated with respect to high-power pulses used in the remainder of the sequence.

Fig. 2a shows the difference in NOE's for rigid ¹⁵N- ¹H pairs in ubiquitin when the proton carrier is moved from the center of the amide region at 8.2 ppm to 0 ppm, with ω₁/(2π) = 9 kHz on a 600 MHz spectrometer and τ = 22 ms. Significant deviations from the ideal behavior can be observed for several ¹⁵N-¹H pairs. The average deviation is -0.008, with a standard deviation of 0.009, and the average of the experimental errors is 0.004. The amplitude of the deviations predicted by numerical simulations, using the methodology described in the Theory section, is very similar (Fig. 2b). When lower RF amplitudes ω₁ are employed, the deviations increase as expected. For instance, with ω₁/(2π) = 4 kHz, the standard deviation jumps to 0.05, with an average deviation of -0.03 and identical experimental errors (data not shown). The deviations observed with ω₁/(2π) = 9 kHz are much smaller than those previously reported [14] using the standard sequence with β = 120° and τ = 5 ms, which leads to a standard deviation of 0.03. The deviations observed with off-resonance 180° pulses arise from effects similar to those previously discussed [14]. First the coupling between populations and coherences arises from tilted effective fields (i.e., nutation around a tilted axis does not result in a proper inversion). Second, transverse cross-relaxation due to the cross correlation of the proton CSA and the dipolar coupling with the nitrogen-15 nucleus can give rise to a conversion between in-phase and antiphase proton coherences during the τ intervals. Nevertheless, these effects are far smaller than for the sequence commonly used with β = 120° and τ = 5 ms. Numerical calculations (data not shown) show that deviations from accurate NOE's are always smaller than 1 % over the entire amide region when the RF amplitude is: ω₁/ω_H =1.5 10⁻⁵, e.g., ω₁/(2π) = 9 kHz if the Larmor frequency of the protons is ω_H/(2π) = 600 MHz, provided that the carrier is placed in the center of the amide region (see Fig. 1b).

Figure 2.

Deviations of NOE ratios at 600 MHz when the proton carrier is placed at 0 ppm during the effective saturation of protons. (a) Difference between the NOE ratios measured for all rigid ¹⁵N-¹H pairs of human ubiquitin with the proton carrier placed at 0 ppm or 8.2 ppm. Each point corresponds to the amide ¹⁵N-¹H pair for a specific residue. The RF amplitude during effective proton saturation was 9 kHz, the interpulse delay 22 ms, and the duration of saturation 4 s. (b) Numerical calculations of the NOE deviation with the carrier placed at 0 ppm. Parameters used in the simulations are the same as in experiments with the following parameters for local dynamics: S² = 0.7 and τ_e = 60 ps, and a correlation time for the overall motion τ_c = 4.5 ns.

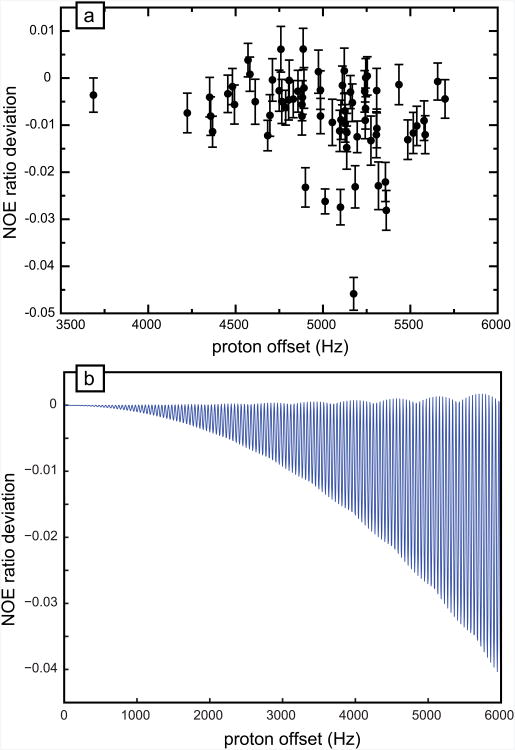
When the 180° pulses are applied far off-resonance, the above-mentioned deviations become significantly larger. We have carried experiments to exacerbate offset effects, deliberately using a small RF amplitude ω₁/(2π) = 4 kHz; a nominal flip angle β = 180° (on resonance) and an interpulse delay τ = 5 ms, which is close to 1/(2J_NH). The carrier was moved progressively from the center of the amide region down to -100 ppm. Results are presented in Fig. 3a. As expected, the deviations are very small at the edges of the amide region when the carrier is placed at 8.2 ppm, the standard deviation of the difference with the reference experiment is 0.003 compared to an average error is 0.004. When the carrier is placed near the water resonance during saturation, significant errors arise, with a standard deviation of 0.004. These deviations grow significantly when the offset Ω increases beyond the RF amplitude ω₁, becoming very large when Ω > 2ω₁. The deviations remain large when the offset is much larger than the RF field amplitude. Similarly, calculations of Fig. 3b show that the deviations can be larger than one, particularly for large offsets.

Figure 3.

Deviations of NOE ratios at 600 MHz over a wide range of proton offsets. (a) The difference with the NOE ratios measured in a reference experiment are displayed for all ¹⁵N-¹H pairs in human ubiquitin with the proton carrier placed at 8.2 ppm (black); 4.7 ppm (blue); 0 ppm (green); -4 ppm (red); -8 ppm (magenta); and -100 ppm (orange). In this series of experiments, the interpulse delay was τ = 5 ms; the RF amplitude ω₁/(2π) = 4 kHz. In the reference experiment, the RF amplitude during effective proton saturation was ω₁/2π = 9 kHz, the interpulse delay,τ = 22 ms. In all experiments, the nominal flip angle was β = 180°, and the duration of saturation 4 s. (b) Simulations of the deviation from the correct NOE value. As in the experiments, the interpulse delay was τ = 5 ms and the RF amplitude ω₁/2π = 4 kHz. The microdynamic parameters were S² = 0.7 and τ_e = 60 ps.

Results obtained for offsets Ω > ω₁ are unexpected. Under such conditions, each pulse results in an effective rotation of the proton magnetization through less than 90° with respect to the longitudinal axis, thus attenuating the magnitude of the transverse magnetization. One should remember that the τ/2−β−τ/2 sequence is repeated many times with short τ delays between pulses. Therefore, the largest transverse proton magnetization created by each pulse is achieved for effective flip angles smaller than 90°. This effect is conceptually related to the Ernst angle [25]. Simulations show the optimal Ernst angle to be close to β = 10° in our case.

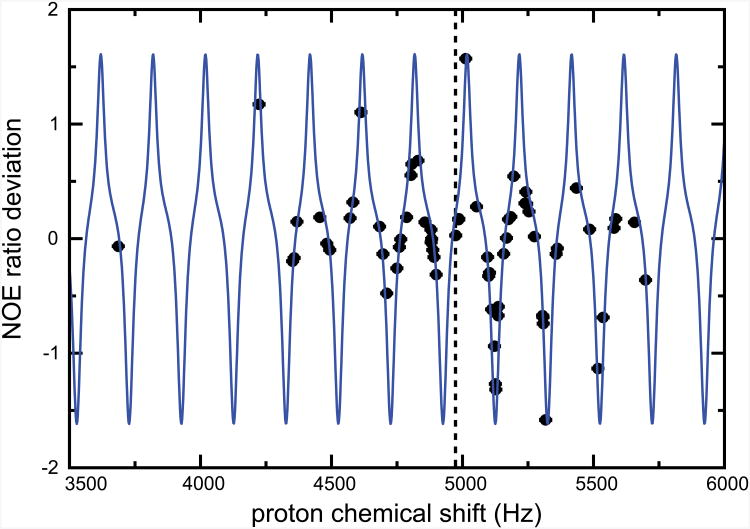
Experiments were carried out with β = 10° to illustrate this property. Results are shown in Fig. 4. Deviations from accurate NOE's are very large. The agreement with simulations is remarkable, indicating that the relative dependence of deviations on dynamic parameters (e.g., S², τ_e) is less pronounced than with other sequences. These results, combined with data obtained at large offsets, show that the longitudinal nitrogen-15 polarization may be altered dramatically by a small but repeated perturbation of the proton polarization.

Figure 4.

Deviations of NOE ratios from the accurate value with a flip angle β = 10° and an interpulse delay τ = 5 ms. The differences between NOE ratios measured with β = 10° and β = 180° are shown as black dots. Numerical calculations (solid blue line) of the difference between the NOE ratios obtained with β = 10° and β = 180° for a ¹⁵N-¹H pair with S² = 0.7 and τ_e = 60 ps. In both experiments and simulations, the RF amplitude was ω₁/(2π) = 9 kHz, the carrier was placed at 8.2 ppm, and the Larmor frequency of the protons was 600 MHz.

This has to be considered when far off-resonance irradiation is employed for temperature compensation. For instance, one may apply, during the reference experiment, the same proton irradiation scheme as in the steady-state experiment far off-resonance. As shown here, this may be extremely dangerous with windowed irradiation schemes. Simulations show that even a continuous wave proton irradiation with an RF amplitude ω₁/2π = 1 kHz at an offset of 200 kHz leads to significant deviations with respect to the nitrogen-15 equilibrium polarization. It is therefore advisable to favor proton irradiation schemes with the least power (such as in Fig. 1b) to alleviate the need for any temperature-compensation scheme in the reference experiment.

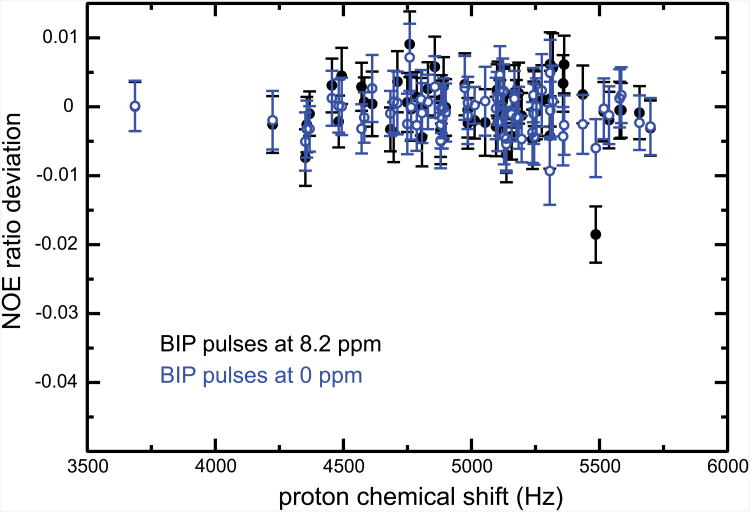
In order to improve the tolerance to large offsets, similar as those explored in Fig. 2, we have evaluated the performance of windowed schemes that use broadband inversion pulses (BIP) [17] as in Fig. 1d. Results are shown in Fig. 5. NOE's measured with this scheme are virtually identical to those obtained with 180° pulses applied at the center of the amide region. Interestingly, the response is the same when the carrier is placed at 0 ppm, i.e., with Ω/(2π) reaching up to 5.5 kHz. BIP pulses significantly improve the robustness to large (i.e., Ω/2π ≥ 5 kHz) offsets. BIP pulses are much less sensitive to RF inhomogeneities or miscalibration of proton pulses. Their use would therefore be safer when the sample is not restricted (as it would be with Shigemi tubes) to the region of the probe where the RF field is most homogeneous or in routine experiments with minimal set up (though proton pulses must always be precisely calibrated). Additional experiments should be run to evaluate the contribution of regions of low proton RF field homogeneity to the signal in order to assess the need for such a scheme. Besides, motions from these regions to the active volume of the probe for biomolecules through translational diffusion or convection are negligible. The dominant displacement due to convection is expected to be less than one millimeter at 37° C during the whole duration of the proton irradiation and much lower at 25° C [26]. On the other hand, the disadvantage of BIP pulses is that they lead to more heating than simple 180° pulses. Although no sample heating was noted in any of our experiments, one should always strive to minimize RF power to ensure that reference and steady-state experiments are recorded with identical temperatures in the light of the fact that, as discussed above, commonly employed temperature compensation schemes lead to deleterious effects.

Figure 5.

Deviations of NOE ratios when a BIP pulse is used in the effective saturation scheme, as presented in Fig. 1d. Experimental details are given in Fig. 1, the proton Larmor frequency was 600 MHz. Solid black circles correspond to data obtained with BIP pulses applied at 8.2 ppm. Open blue circles are deviations obtained with the carrier positioned at 0 ppm during saturation. Each point corresponds to the amide ¹⁵N-¹H pair for a specific residue in human ubiquitin. As in other figures, deviations were derived using as the “accurate” value of NOE ratios those obtained with the scheme of Fig. 1b, ω₁/(2π) = 9 kHz; τ = 22 ms; β = 180°; and the duration of saturation 4 s.

Windowless Sequences - composite Pulse Decoupling

Composite pulse decoupling (CPD) or other windowless schemes offer alternative approaches that can be used to achieve effective proton saturation in steady-state experiments. Windowless sequences were quite popular in the early days of relaxation measurements of nitrogen-15 backbone nuclei [27; 28]. Most CPD sequences suppress the evolution under heteronuclear scalar couplings and proton chemical shifts while averaging the longitudinal polarization of protons to zero. These properties make such schemes well suited for application to the measurement of accurate {¹H}-¹⁵N NOE's. A series of experiments was recorded with variable CPD schemes, carrier frequency, and RF amplitude using deuterated and protonated samples.

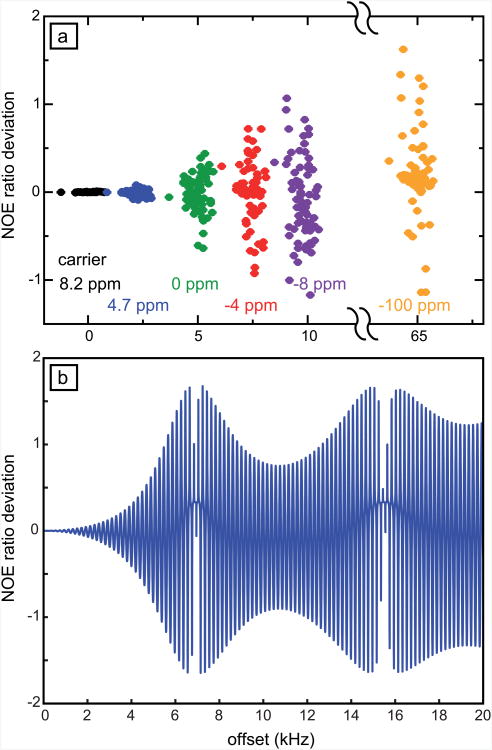
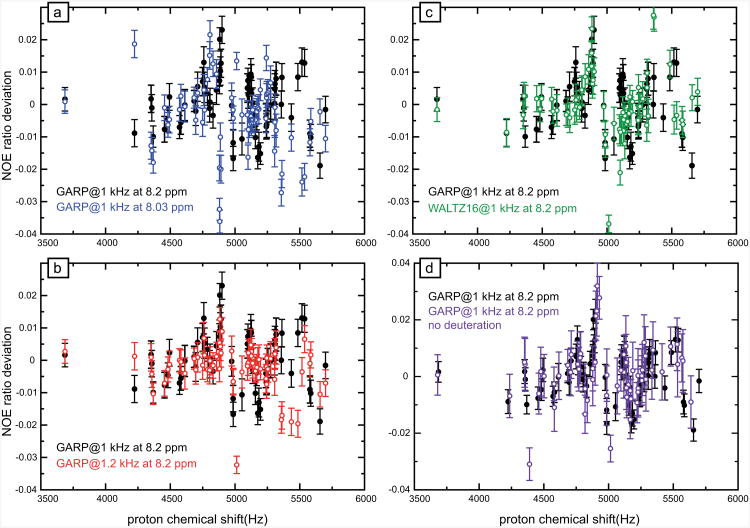
Deviations of NOE's obtained with GARP decoupling with an RF amplitude ω₁/(2π) = 1 kHz and a proton carrier at 8.2 ppm (black circles in Fig. 6a) are small but larger than experimental errors for many residues: the standard deviation is 0.014 with an average deviation of 0.001 and an average error of 0.004. A second experiment was recorded with the proton carrier shifted by -100 Hz (to 8.03 ppm) during saturation (blue symbols in Fig. 6a). While the statistics of deviations are very similar, the actual |deviations are different from those measured with a carrier positioned at 8.2 ppm for most ¹⁵N-¹H pairs. If the NOE's determined with GARP were indeed accurate, their values should have remained unchanged when the carrier is shifted slightly within the amide region. We can therefore conclude that NOE's obtained with GARP decoupling with ω₁/(2π) = 1 kHz are not of the highest accuracy and show a small deviation with respect to the most accurate values obtained to date. With ω₁/(2π) = 1.2 kHz, deviations are reduced, with a standard deviation of 0.007, about twice the average error. Such systematic errors are, on average, smaller than the experimental errors of most steady-state NOE's. If higher RF amplitudes can be employed, satisfactory measurements can be obtained. However, sample heating may become non-negligible with larger amplitude CPD applied during 4 s every 6 s. As a comparison, the scheme presented in Fig. 1b at 600 MHz is equivalent to a windowless sequence applied with only ω₁/(2π) = 450 Hz.

Figure 6.

Deviations of NOE ratios at 600 MHz with several CPD schemes for effective saturation of protons. (a-d) Deviations of NOE's measured with a GARP decoupling scheme applied with the carrier at 8.2 ppm and an RF amplitude ω₁/(2π) = 1 kHz are shown as black solid circles for comparison. (a) NOE ratio deviations (blue open circles) when the carrier is placed at 8.03 ppm (-100 Hz shift) with an identical GARP effective saturation scheme. (b) NOE ratio deviations when WALTZ-16 CPD is used with the same carrier and RF amplitude (green open circles). (c) NOE ratio deviations when the RF amplitude is increased to 1.2 kHz with the same GARP CPD with identical carriers (red open circles). (d) NOE ratio deviations measured on a fully protonated sample of human ubiquitin (open magenta circles). The datasets on both samples were recorded with identical experimental parameters on the same spectrometer. The reference value for NOE ratio was recorded with the same experimental parameters as for Figs. 2-5. Each point corresponds to a ¹⁵N-¹H pair for a rigid residue in human ubiquitin.

Searching for robust alternatives, WALTZ-16 was applied under the same conditions as GARP (Fig. 6c). Statistics of the deviations are very similar. Experiments with GARP with the carrier at 0 ppm (at 600 MHz proton Larmor frequency, data not shown) show small deviations (average 0.003; standard deviation 0.011). Interestingly, all numerical calculations (not shown) of CPD sequences predict a good accuracy of NOE's over a wide range of offsets, no deviation being larger than 0.02 for offsets below 4 kHz. Deviations identified in experiments are larger than experimental errors but they cannot be rationalized in the framework our current theoretical model.

In order to investigate the influence of ³J(¹H^N,¹H^α) scalar couplings and proton-proton dipolar relaxation (including auto- and cross-correlated cross-relaxation), we compared, on the same spectrometer, the deviations of NOE's obtained with GARP with the NOE's obtained with the scheme of Fig. 1b on samples of protonated and perdeuterated ubiquitin, as shown in Fig. 6d. The profiles displayed in Fig. 6d are remarkably similar. Although this result does not rule out that proton-proton scalar couplings and dipolar relaxation may play a role, it is likely that the deviations of NOE's come from other factors, such as imperfections of CPD pulses. Numerical simulations were carried out in a few cases, but neither small pulse miscalibrations nor undesired delays between nominally windowless pulse sequences (tested for delays up to 200 μs) significantly affect the steady state. In particular, none of the hypotheses that we have tested led to significant deviations close to resonance.

Minimizing the effects of Radiation Damping

An important source of inaccuracy originates from non-linear macroscopic effects know as radiation damping while manipulating fully polarized water nuclear spins [29]. This is especially true for high-Q cryogenic probes, where the water magnetization aligned along the -z position evolves to the +z position within an interval 1 < t < 100 ms [30]. Let us first consider the reference experiment. In this experiment, (see Figure 1a) the spin system has to be as close to equilibrium as possible when the first 90° pulse is applied on the ¹⁵N channel. This implies that the water protons should be close to equilibrium. Water flip-back schemes can significantly reduce deviations from equilibrium [31].

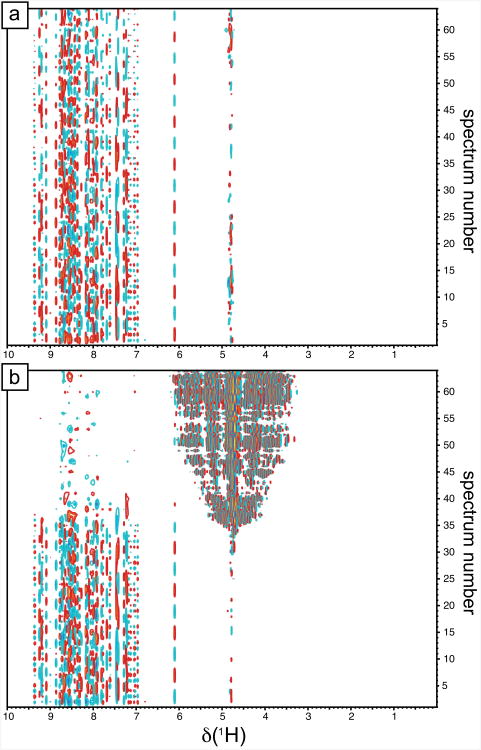
When proton decoupling is performed with a single proton pulse 180° at the midpoint of the t₁ delay, the water proton polarization spends the second half t₁/2 of the evolution interval along the -z position. Fig. 7b shows that this may be too long, particularly when high-Q cryogenic probes are used. In this case, after about 15 ms, the water polarization leaves the -z position, subsequent water suppression is no longer efficient and the water resonance becomes partially saturated. This has two effects: First, if a short recovery delay T is used, the polarization of water and of many ¹⁵N-¹H spin systems in the protein will not have enough time to reach equilibrium between scans, leading one to underestimate the ¹⁵N longitudinal polarization at equilibrium. Second, the decreased efficiency of the water suppression may lead to a water signal that is so large that it can saturate the receiver, thereby altering the signal from the protein. This second effect is dominant in the case presented in Fig. 7b. A careful user should identify such an error by proceeding first to the Fourier transformation in the direct dimension only (see Fig. 7). Such effects are more difficult to observe if both dimensions are Fourier transformed at once. Unfortunately, only the most modern NMR spectrometers issue an error message upon saturation of the receiver. Nevertheless, we need to offer an NOE experiment that can be used whether high-resolution is needed in the indirect dimension or not.

Figure 7.

Two-dimensional datasets for the reference experiment. Fourier transform was performed in the direct dimension only. Data were acquired on a spectrometer equipped with a cryoprobe with z-axis gradient and a proton Larmor frequency of 500 MHz. (a) Reference experiment recorded with the sequence presented in Fig. 1a. (b) Reference experiment recorded with the sequence presented in Fig. 1a modified so that the proton decoupling during the delay t₁ is performed with a single 180° pulse at the midpoint of the delay t₁, further phases are corrected to preserve the water flip-back scheme [31]. Only odd-numbered spectra are displayed (numbered 1-64 out of 1-128). The maximum value of t₁ was t_1max = 52.6 ms in both experiments.

Simple solutions can be to flank the proton 180° pulse with selective water flip-back pulses [31] or to apply more than a single pulse, for instance two pulses at time points t₁/4 and 3t₁/4 (note that one should make sure the water polarization is along the +z direction in the interval between these two pulses). Another practical solution consists of applying composite pulse decoupling during the entire t1 duration (see Fig. 7a). When 90° pulses flank the CPD sequence, the water polarization is locked during decoupling, so that losses of the water polarization are solely due to transverse relaxation. In addition, by preventing the buildup of nitrogen-15 antiphase coherences, effective relaxation of nitrogen-15 coherences during t₁ is minimized, particularly in non-deuterated proteins, which leads to increased sensitivity. In large deuterated proteins, TROSY selection is be favored and no proton decoupling takes place during t₁[13].

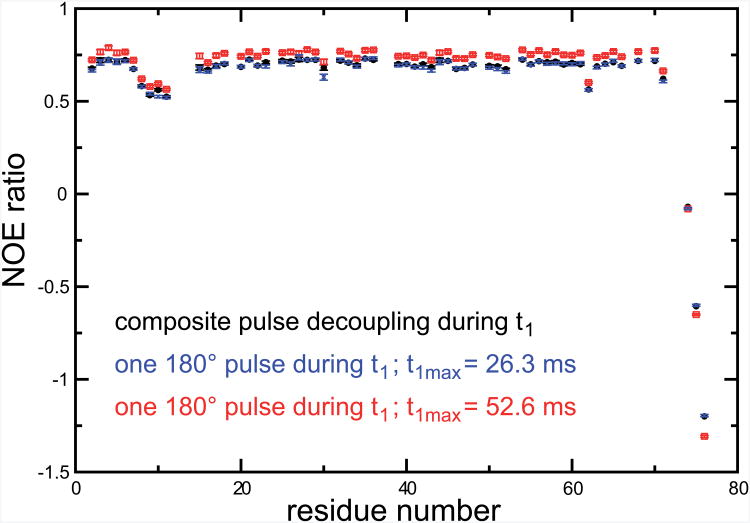
It is worth mentioning that radiation damping not only decreases the sensitivity, but alters the accuracy of NOE's in the following way: During the steady-state experiment, the water polarization is partially saturated, leading to a considerable reduction of non-linear effects. Proper suppression of the water signal is achieved even for long t₁ delays, and the intensities of signals in the steady-state spectrum are not affected. However, lack of irradiation during the reference experiment results in radiation damping effects to be active during the t₁ period. This leads to a reduction in the intensity of amide signals in the reference experiment due to the effect of the radiation damped water signal on the receiver as discussed above. As a consequence, the absolute values of NOE's measured under these conditions will be overestimated, as shown is Fig. 8. On average the absolute values of NOE's are overestimated by 7 %, leading to systematic errors that are larger than most errors discussed above (see Figs. 2, 5 and 6). To demonstrate the error is due to the saturation of the receiver for long t₁ delays, the data obtained in Fig. 7b were re-processed with t₁^max = 26.3 ms. This restores the proper NOE's, as can be seen in Fig. 8.

Figure 8.

NOE ratios measured at 500 MHz on a sample of perdeuterated human ubiquitin. In all experiments, the saturation scheme of Fig. 1b was employed. NOE ratios measured with the sequence presented in Figure 1a are shown as black circles, the maximum value of t₁ was t_1max = 52.6 ms. Open red squares represent NOE ratios measured under the same conditions with a modified sequence with no CPD during t₁, as introduced in Fig. 7b. Blue crosses show the NOE ratios obtained from the same dataset but keeping only time points in the indirect dimensions with t₁ ≤ 26.3 ms.

Finally, the question arises whether radiation damping can influence the effective saturation of protons during the steady-state experiment. Indeed, if the water polarization is not effectively saturated, the polarization of amide protons which exchange or cross-relax with water protons may not be properly saturated either. As discussed above, after an initial phase of the irradiation, the water polarization is sufficiently saturated to avoid significant radiation damping effects. Although we found that the water polarization does not remain along the -z direction for more than 15 ms when it is not saturated if we use a high-Q cryogenic probe, partial water saturation resulting from proton irradiation should ensure that an interpulse delay τ = 22 ms has no significant effect on the accuracy of the experiment. In extreme cases, the evolution towards the correct steady state may be slightly delayed, an issue worth investigating in the future. For amide protons in exchange with water protons, a shorter interpulse delay τ = 11 ms is recommended.

We have shown in a preceding study [13] how errors in the NOE ratio propagate in a typical dynamics analysis using the Lipari-Szabo approach as implemented in modern software e. g. [32]. In most cases an error of the order of 10 % in the NOE ratio leads to an error of the order of 1 % in the order parameter S² . Such a small error does not impact the qualitative interpretation of order parameters but may significantly bias quantitative analysis [4; 33; 34]. In contrast, the timescales of fast motions are highly sensitive to errors in the NOE ratio. These timescales are generally not interpreted and considered as a by-product in model-free analyses. We believe that the availability of robust and reliable NOE experiments will now permit the interpretation of timescales for fast motions.

Conclusions

We have evaluated the influence of proton irradiation schemes on the measurement of {¹H}-¹⁵N steady-state NOE's. Based on this analysis we find that repetition of the symmetric scheme [τ/2 - β - τ/2] using hard β = 180° pulses provides the most reliable effective saturation of proton magnetization in the steady-state experiment. The optimal delay is τ = 2/J_NH = 22 ms. We have shown earlier that a symmetric windowed scheme is to be preferred over asymmetric schemes where the spin system is not observed at the optimal time for effective saturation, leading to systematic errors in the NOE's [13]. The optimal scheme is depicted in Figs. 1a and 1b. Even with this scheme, significant errors in NOE's can be observed for unusually large offsets. Broadband inversion pulses such as the BIP pulses [17] that are less sensitive to offset effects and pulse calibration errors may be used instead of hard 180° pulses. However, BIP pulses require higher RF amplitudes and may lead to sample heating. Care should be taken when using short proton pulses far off-resonance in the reference experiment to compensate for sample heating effects. Indeed, we have found that proton pulses applied far off-resonance can result in very large deviations of steady states, especially for small flip angles. Composite pulse decoupling schemes can also lead to errors unless large RF amplitudes are used. Especially when using cryogenic probes, particular care has to be taken to suppress the water signal in the reference experiment to avoid radiation-damping effects, which may lead to overestimate the absolute value of NOE's. Composite pulse proton decoupling should be used throughout the evolution interval t₁ instead of a single proton 180° pulse at the center of this interval. The water signal does not have a major influence on the steady-state experiment though in cases where radiation damping is pronounced, a delay τ = 1/J_NH = 11 ms may be used instead of τ = 22 ms. Incorporation of these minor changes into well-known experimental schemes allows one to measure extremely accurate NOE's and opens the way to the proper characterization of the timescales of fast local motions in biomolecules.

Research highlights.

• The effect of the proton offset in ¹⁵N-{¹H} NOE experiments is investigated.

• Various proton irradiation schemes are compared under normal and extreme conditions.

• Radiation damping may ead to inaccurate intensities in the reference experiment.

• A recipe to record ¹⁵N-{¹H} NOE's is presented.

Appendix

The expressions of relaxation rates used in numerical simulations, following typical expressions [9] are given here:

$$\begin{array}{l}{\rho }_N^l=\frac{1}{10}{d}_{\mathit{\text{NH}}}^2(3J({\omega }_N)+J({\omega }_N-{\omega }_H)+6J({\omega }_N+{\omega }_H))+\frac{2}{15}{d}_N^{2}J({\omega }_N)\\ {\rho }_H^l=\frac{1}{10}{d}_{\mathit{\text{NH}}}^2(J({\omega }_N-{\omega }_H)+3J({\omega }_H)+6J({\omega }_N+{\omega }_H))+\frac{2}{15}{(d_{\mathit{\text{Hx}}}+d_{\mathit{\text{Hy}}})}^{2}J({\omega }_H)+\frac{2}{10}{d}_{\mathit{\text{HH}}}^2(J(0)+3J({\omega }_H)+6J(2{\omega }_H))+\lambda \\ {\rho }_H^{\mathit{\text{in}}}=\frac{1}{20}{d}_{\mathit{\text{NH}}}^2(4J(0)+J({\omega }_N-{\omega }_H)+3J({\omega }_H)+6J({\omega }_N)+6J({\omega }_N+{\omega }_H))+\frac{1}{45}{(d_{\mathit{\text{Hx}}}+d_{\mathit{\text{Hy}}})}^2(4J(0)+3J({\omega }_H))+\frac{1}{10}{d}_{\mathit{\text{HH}}}^2(5J(0)+9J({\omega }_H)+6J(2{\omega }_H))\\ {\rho }_H^{\mathit{\text{anti}}}=\frac{1}{20}{d}_{\mathit{\text{NH}}}^2(4J(0)+J({\omega }_N-{\omega }_H)+3J({\omega }_H)+6J({\omega }_N)+6J({\omega }_N+{\omega }_H))+\frac{1}{45}{(d_{\mathit{\text{Hx}}}+d_{\mathit{\text{Hy}}})}^2(4J(0)+3J({\omega }_H))+\frac{1}{10}{d}_{\mathit{\text{HH}}}^2(5J(0)+9J({\omega }_H)+6J(2{\omega }_H))\\ {\rho }_{\mathit{\text{NH}}}^l=\frac{3}{10}{d}_{\mathit{\text{NH}}}^2(J({\omega }_N)+J({\omega }_H))+\frac{2}{15}{d}_N^{2}J({\omega }_N)+\frac{2}{15}{(d_{\mathit{\text{Hx}}}+d_{\mathit{\text{Hy}}})}^{2}J({\omega }_H)+\frac{2}{10}{d}_{\mathit{\text{HH}}}^2(J(0)+3J({\omega }_H)+6J(2{\omega }_H))+\lambda \\ {\sigma }_{\mathit{\text{NH}}}=\frac{1}{10}{d}_{\mathit{\text{NH}}}^2(6J({\omega }_H+{\omega }_N)-J({\omega }_H-{\omega }_N))\\ {\delta }_N^l=\frac{2}{5}{d}_{\mathit{\text{NH}}}{d}_N{J}_N({\omega }_N)\\ {\delta }_H^l=\frac{2}{5}{d}_{\mathit{\text{NH}}}(d_{\mathit{\text{Hx}}}{J}_{\mathit{\text{Hx}}}({\omega }_H)+d_{\mathit{\text{Hy}}}{J}_{\mathit{\text{Hy}}}({\omega }_H))\\ {\delta }_H^l=\frac{1}{30}{d}_{\mathit{\text{NH}}}[d_{\mathit{\text{Hx}}}(4J_{\mathit{\text{Hx}}}(0)+3J_{\mathit{\text{Hx}}}({\omega }_H))+d_{\mathit{\text{Hx}}}(4J_{\mathit{\text{Hy}}}(0)+3J_{\mathit{\text{Hy}}}({\omega }_H))]\end{array}$$ (A1)

with: $d_{\mathit{\text{NH}}}=({\mu }_0/4\pi )\hslash {\gamma }_N{\gamma }_H{\gamma }_{\mathit{\text{NH}}}^{-3}$; $d_{\mathit{\text{HH}}}=({\mu }_0/4\pi )\hslash {\gamma }_H^2{\gamma }_{\mathit{\text{HH}}}^{-3}$; $d_N={\omega }_N\Delta {\sigma }_N$; $d_{\mathit{\text{Hx}}}={\omega }_H({\sigma }_{\mathit{\text{Hxx}}}-{\sigma }_{\mathit{\text{Hzz}}})$; $d_{\mathit{\text{Hy}}}={\omega }_H({\sigma }_{\mathit{\text{Hyy}}}-{\sigma }_{\mathit{\text{Hzz}}})$; ${\omega }_N=-{\gamma }_N{B}_0$; ${\omega }_H=-{\gamma }_H{B}_0$. μ₀ is the permittivity of free space; r_NH is the distance between the ¹⁵N nucleus and its neighboring ¹H nucleus; r_HH is the distance between two ¹H nuclei; Δσ_N is the chemical shift anisotropy of the ¹⁵N nucleus (considered to be axially symmetric); σ_Hxx, σ_Hyy and σ_Hzz are the three principal components of the ¹H chemical shift tensor; B₀ is the static magnetic field. In addition to the intra ¹⁵N-¹H system interactions, CSA's and dipolar coupling, relaxation of proton operators takes into account dipolar interactions with two additional protons at a distance r_HH . Under these conditions, calculated proton longitudinal relaxation rates would still be smaller than expected so that a constant λ = 0.2 s^-1 was added to obtain more realistic rates [14].

The spectral density function used for auto-correlated relaxation is of the typical model free form [35]:

$$J(\omega )=S^{\text{2}}\frac{{\tau }_c}{1+{\omega }^2{\tau }_c^2}+(1-S^2)\frac{{\tau }_e}{1+{\omega }^2{\tau }_e^2}$$ (A2)

where S² is the generalized order parameter, τ_c the correlation time for the overall tumbling time and τ_e is defined from the correlation time for local motions τ_loc by: ${\tau }_e^{-1}={\tau }_c^{-1}+{\tau }_{\mathit{\text{loc}}}^{-1}.$ Under isotropic global and local motions, the spectral density functions for cross-correlated relaxation can be derived from auto-correlated spectral density functions by the relationships:

$$\begin{array}{l}{J}_N(\omega )=\frac{3{cos}^2({\theta }_N)-1}{2}J(\omega )\\ J_{\mathit{\text{Hx}}}(\omega )=\frac{3{cos}^2({\theta }_{\mathit{\text{Hx}}})-1}{2}J(\omega )\\ J_{\mathit{\text{Hy}}}(\omega )=\frac{3{cos}^2({\theta }_{\mathit{\text{Hy}}})-1}{2}J(\omega )\end{array}$$ (A3)

where the angle θ_n describes the relative orientation of the NH vector and the principal axis of the axially symmetric ¹⁵N chemical shift anisotropy tensor; θ_Hx and θ_Hx describe the relative orientation of the NH vector and the x and y principal axes of the ¹H CSA tensor respectively.

The values employed for the above-mentioned parameters are: r_NH = 101 pm; r_HH = 290 pm; Δσ_N = 164 ppm; θ_N = 19°; σ_Hxx = 14.6 ppm; σ_Hyy = 8.2 ppm; σ_Hzz = 2.1 ppm; θ_Hx = 90°; θ_Hy = 99°.