Application of System Identification Methods for Decoding Imagined Single-Joint Movements in an Individual with High Tetraplegia

Abstract

This study investigated the decoding of imagined arm movements from M1 in an individual with high level tetraplegia. The participant was instructed to imagine herself performing a series of single-joint arm movements, aided by the visual cue of an animate character performing these movements. System identification was used offline to predict the trajectories of the imagined movements and compare these predictions to the trajectories of the actual movements. We report rates of 25 – 50% for predicting completely imagined arm movements in the absence of a priori movements to aid in decoder building.

I. Introduction

The goal of the current study was to investigate the decoding of neural activity related to intended arm movements by individuals with high level tetraplegia, using system identification techniques. Humans with paralysis due to spinal cord injury have the ability to generate neural commands related to movement, though these commands can no longer activate the peripheral musculature. By using implantable functional electrical stimulation (FES) systems to reanimate the peripheral muscles, these individuals can perform functional movements such as grasping and multi-joint arm reaches [1-3]. Typically, the user controls these FES systems by the position of a joint or the electromyographic (EMG) activity of a muscle under voluntary control [4]. Such a control scheme works well for individuals with low level injuries, but is limited for individuals with high level spinal cord injury due to the limited number of remaining movements under voluntary control. Cortical control of FES systems is attractive because neural activity directly related to movement can be recorded from appropriate cortical areas and potentially used as control commands for electrical stimulation. Furthermore, the possible number of controlled dimensions is much greater than that of current methods.

It is well established that from the neural activities recorded from the primary motor cortex (M1) of non-human primates, a plethora of kinematic and dynamic movement parameters can be decoded. Specifically, computer cursor as well as hand positions and velocities, hand grasping force, and muscle activation patterns have been decoded offline, as well as online for real-time control [5-7]. In humans, brain-computer-interface (BCI) systems have allowed individuals to control switches and two-dimensional computer cursors [8-10]. Finally, paralyzed humans have also been able to control two-dimensional cursors using the neural firing rates recorded from chronically-implanted microelectrodes [11, 12]. For successful control of an FES system for a multi-joint arm, it must be possible to be able to control more than just two independent degrees-of-freedom (DOF). System Identification (SID) has been used as a white-box technique to discern linear relationships of many biological systems, and is likely useful as a method for cortical decoding. Thus, the aim of this work was to determine if, in the absence of a priori arm movements, SID could decode specific information on the intended movement of individual joints from the neural activity of an individual with high level tetraplegia.

II. Materials and Methods

A. Participant Information

The BrainGate2 pilot clinical investigation is conducted under an Investigation Device Exemption (IDE)^† from the US Food and Drug Administration. The study participant is a female fifty-five years of age who sustained a brainstem stroke nine years prior to enrollment. After completion of informed consent and medical and surgical screening procedures, the 4 × 4-mm microelectrode array (Blackrock Microsystems, Salt Lake City, Utah, USA) was implanted into the hand/knob area of the primary motor cortex using a pneumatic insertion technique [13]. Details of the human surgical procedure as well as the BrainGate system hardware have been previously reported [11].

B. Experimental Protocol

The research participant was placed approximately 40 cm away from a computer monitor which showed a virtual three-dimensional world that was developed in house using the Gamestudio Development Environment (Conitech Datensysteme GmbH, La Mesa, CA). In the world sat a virtual character that performed each of eight distinct single-joint arm movements. The movements performed were shoulder elevation in the 0° plane (i.e. abduction / adduction), shoulder elevation in the 90° plane (i.e. flexion / extension), shoulder rotation, elbow flexion / extension, forearm pronation / supination, wrist flexion / extension, wrist ulnar / radial deviation, and hand opening / closing. The animate character performed each movement for forty-five seconds, tracing a sinusoidal trajectory with a 0.4 Hz frequency. Each block consisted of two trials of each movement, and the order of movements was randomized within each block. The participant was given instructions to “watch the movements of the animate character and imagine yourself performing the same movements at the speed observed, to the best of your ability”.

While the participant observed the movements of the virtual character, neural activity was recorded from the hand/knob area of M1 with a 96-channel chronically implanted microelectrode array (BlackRock Microsystems, Salt Lake City, Utah). Single-unit action potentials (SUA) and multi-unit spike trains (MSP) were sorted online by a human operator based upon standard time-amplitude windowing. The timestamps of the train of action potentials of each single unit were recorded and analyzed offline. Full broadband data was also collected and used to derive local field potentials (LFP).

C. Data Analysis

A 50ms smoothing window was applied to the timestamps of the individual SUAs, as well as the multi-spike trains (MSPs), resulting in firing rates with a 20 Hz update rate. The root-mean-square of the low-passed LFP signal (LFPrms) was derived as an input feature. The average power of the LFP signal was calculated using a short-time-Fourier-transform (LFPstft), in four distinct frequency bands (0-6 Hz, 6-12 Hz, 12-63 Hz, and >63 Hz). Neural and kinematic data was separated into training (50%) and validation sets (50%). System identification techniques [14-16] were used to build impulse response filters (IRF) relating the SUA and MSP firing rates and the LFPrms amplitudes and LFPstft power in each band to the kinematic trajectories of the observed movements in the training data set. Given the system input matrix X (neural data) and output matrix Y (movement kinematics), the IRF function H is calculated such that Y = X*H, where ‘*’ is the convolution operator. H satisfies the least squares criterion such that

$$\mathbf{H}={\left({\mathbf{X}}^{\mathbf{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{Y}.$$ (1)

The calculated IRFs were applied to the neural data in the validation set and used to predict the trajectories of the movements that were imagined by the participant. These predicted trajectories were then compared to the trajectories of the movements observed by the participant. The predictive strength of the neural filters was quantified by the Variance Accounted For (VAF%) measure, given by

$$\mathit{VAF}\%=100\%\times \left(1-\frac{E\left[{\left(y\right(t)=\widehat{y}(t\left)\right)}^2\right]}{E\left[y{\left(t\right)}^2\right]}\right).$$ (2)

We calculated the VAF% of each individual neural feature, as well as that of the optimal neural populations using a forward recursive selection addition algorithm.

III. Results

Figure 1 shows a color map of the microelectrode array representing the results of the SUA analysis of imagined wrist flexion / extension from a single recording session. Each set of four squares represents a single electrode, and the four squares in each set represent four potential SUAs on a given electrode. The square color represents the VAF% of each single unit. White squares represent no unit. The majority of units exhibited individual VAF% of 0-8% with respect to the prediction of the wrist position during flexion / extension, though two units showed VAF% of 14% and 30%.

Figure 1.

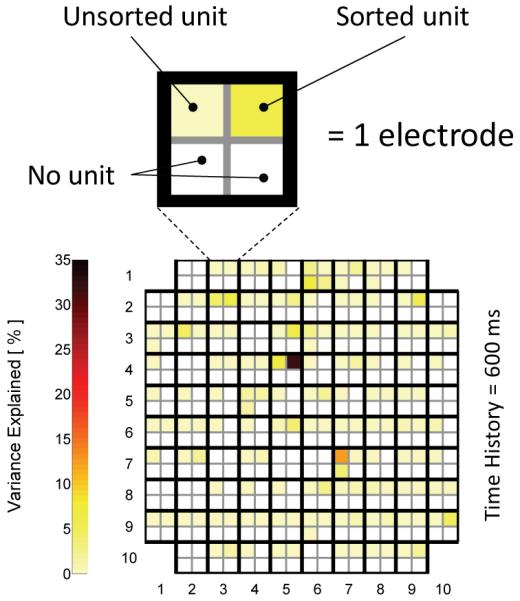
Color plot of electrode array where a group of four squares is an electrode (top left unit is unsorted) and individual squares are potentially sorted units with variance explained of wrist flexion position shown by cell color. Results are from one trial 966 days post-implant.

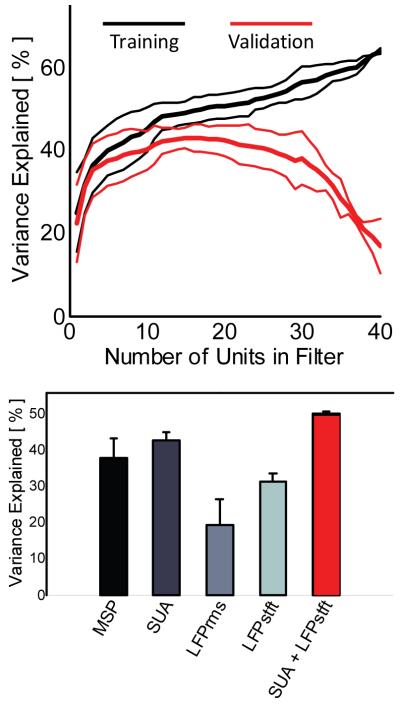
We then determined the optimal combination of SUA features by using a recursive feature selection algorithm in which the units were added to the filter sequentially based upon how much of an increase in the VAF% resulted from that unit. Figure 2A shows the results of the recursive feature selection algorithm for prediction of wrist flexion / extension. In cross-validation, seventeen SUAs produced the maximum VAF% of approximately 42%. Including additional units in the filter past this mark actually decreased the overall predictive strength of the filter in cross-validation.

Figure 2.

(Top) Recursive feature selection curves (mean ± SD) show the VAF% of the predicted position of the wrist during flexion / extension. 17 SUAs produced the maximal VAF% of 42%. (Bottom) Recursive feature selection was performed on each neural signal type, as well as on the combination of SUA and LFPstft signal type. Combining SUA and LFPstft in the same filter statistically significantly increased the predictive strength of the neural decoder (p < 0.05). Results are from one trial 966 days post-implant.

Forward recursive feature selection was also used to build filters using the MSP, LFPrms, and LFPstft neural signals, and the predictive strengths of these filters with respect to wrist flexion / extension are shown in Figure 2B. Of interest is that when filters were built using a combination of the SUA and LFPstft feature types, the predictive strength statistically significantly (p < 0.05) improved over any signal type by itself (50% VAF%, red bar). Similar results are shown in Figure 3 for all eight individual joint movements observed by the participant.

Figure 3.

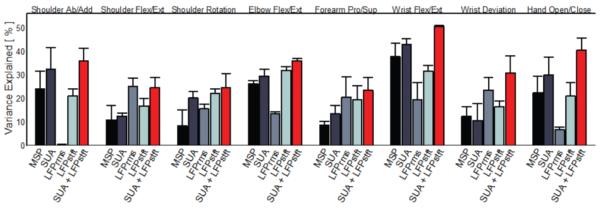
Results of recursive feature selection for all eight observed degrees of freedom. Combining SUA and LFPstft signal types produced neural filters with greater predictive strength than each signal individually. In cases where another individual signal type was the most informative (e.g. LFPrms in shoulder flexion / extension), the combined signal decoders performed as well or better than the other signal type. Results are from one trial 966 days post-implant.

IV. Discussion

While many studies have reported the ability to predict movement parameters from neural activity in M1, these studies rely on the ability to record a priori kinematics to build the neural decoders. The advantage of recording a priori arm movements is not realizable in individuals who are paralyzed. The preliminary results of this study demonstrate that it is possible, in the absence of prior arm movements, to predict the kinematic positions of single-joint movements as imagined by the participant using SID theory. Prediction strengths seem to be enhanced by including multiple signal types in the decoders, though it should be noted that this data is from a single recording session. Validation of this finding from future recording sessions would be of note because most studies focus on using exclusively a single signal type rather than multiple signal types in movement predictions. Finally, it should be stated that the current findings are interpreted in light of the knowledge that it is impossible to know the actual trajectories imagined by the participant. In effect, the comparison is between what should have been imagined (trajectories made by the virtual character) to what was predicted. Given this lack of knowledge of what was actually imagined, it is of greater encouragement that prediction strengths were well beyond that of chance. Future work includes extending the current work to include the prediction of multi-joint whole arm reaches.