Analyzing Repeated Measures Data on Individuals Nested within Groups: Accounting for Dynamic Group Effects

Abstract

Researchers commonly collect repeated measures on individuals nested within groups such as students within schools, patients within treatment groups, or siblings within families. Often, it is most appropriate to conceptualize such groups as dynamic entities, potentially undergoing stochastic structural and/or functional changes over time. For instance, as a student progresses through school more senior students matriculate and more junior students enroll, administrators and teachers may turn over, and curricular changes may be introduced. What it means to be a student within that school may thus differ from one year to the next. This paper demonstrates how to use multilevel linear models to recover time-varying group effects when analyzing repeated measures data on individuals nested within groups that evolve over time. Two examples are provided. The first example examines school effects on the science achievement trajectories of students, allowing for changes in school effects over time. The second example concerns dynamic family effects on individual trajectories of externalizing behavior and depression.

In psychology and allied disciplines, researchers commonly collect repeated measures on individuals who are nested (or clustered) within groups. In but a few examples, a study might track siblings within families, adolescents within peer groups, patients within group treatment programs, or students within schools. Often it is expected that individuals within the same group will be more similar to one another than individuals from different groups. For instance, both selection and socialization effects tend to increase within-group similarity and between-group differences in friendship groups. Likewise, siblings within a family share both a common environment and common genes. Put in statistical terms, the observations obtained for individuals within groups tend to be dependent, or correlated. Unfortunately, many statistical models (such as ANOVA and linear regression) assume independent observations (or, more technically, independent residuals). Such models are thus poorly suited to the analysis of repeated measures data on individuals clustered within groups.

One statistical model that does not assume independence of observations is the Multilevel Model (MLM; a.k.a. mixed effects model, or hierarchical linear model; see Goldstein, 2011; Hox, 2010; Raudenbush and Bryk, 2002; Snijders and Bosker, 2012). The MLM is an extension of the general (or generalized) linear model that was expressly developed to capture sources of dependence in nested data. More specifically, dependence is modeled in MLMs through random effects that represent distinct sources of variability in the data (see Singer and Willett, 2003, and Hedeker and Gibbons, 2006, for overviews of longitudinal MLMs). For repeated measures data on individuals clustered within groups, a typical MLM would include sources of random variation at the group level, the person level, and the observation level. First, a random effect for the group (or a random intercept at the group level) is included in the model to account for between-group differences on the dependent variable. Sometimes, an additional random effect (or random slope) is also included at the group level to allow for group-level variation in time trends. Second, random effects for the individual are included to account for person-to-person differences in the repeated measures and how they change over time. Finally, a residual term is included at the observation level.

This modeling strategy is perfectly reasonable in many instances, but it may not always conform optimally to our theoretical model of change over time. In particular, the modeling strategy described above assumes that the group is a stable entity that either exerts a constant effect on the individual over time (in the case that only a random intercept is included at the group level) or an effect that changes systematically with time (in the case that a random time slope is also included at the group level). In many cases, however, groups may undergo structural and/or functional changes over time that are more stochastic in nature, producing time-varying group-effects that are not captured well by conventional model specifications.

For instance, suppose we wish to model growth in achievement for students nested within schools. Though the brick and mortar of the school may be constant, a significant proportion of the people within the school turn over from year to year (especially students, but also teachers, staff, and administrators), and changes may also occur in the school curricula. Though much of the school culture may be carried over from one year to the next, we might also expect some drift to occur over time. A similar argument can be made when examining the development of siblings within a family. We might expect structural changes to the family, such as the entrance or exit of family members (due to birth, death, divorce, etc.), to alter the effect of the family on siblings. We might also expect events, such as the onset of a disability, or the entry or exit of a parent from the work force, to “shock” the family system and potentially alter family functioning. The natural evolution of the group, or its members, may also alter group effects. A nascent peer group, for instance, may establish and consolidate behavioral norms over time, progressively increasing within-group homogeneity (a kind of “snowball effect” of group membership).

It is useful to distinguish the type of group dynamics described above from another case that has received greater attention in recent literature: where individuals move between groups over time, such as when repeated measures are collected on students who transition between teachers or schools. The approach most commonly used to accommodate this kind of group mobility is the cross-classified random effects model (Luo & Kwok, 2012; Palardy, 2010; Raudenbush, 1993; Raudenbush & Bryk, 2002; Rowan, Correnti & Miller, 2002). As typically specified, these models assume that groups exert independent effects that are encountered by individuals at different points in time as they transition between groups. Here, however, we are concerned with how to model group effects when each individual is at all times a member of a single group (i.e., there is no group mobility) and groups evolve over time while nevertheless maintaining their fundamental integrity. For example, although changes may occur in family structure and circumstances over time, the Smith family remains distinct from the Jones family. As with Theseus’ Paradox, the question could be raised at what point a group can or should be considered distinct and new from what it was before. Indeed, this very question was raised by Goldstein et al (2000) in considering how to model data from individuals residing within dynamic household structures.¹ From a pragmatic point of view, however, it matters not whether we consider the group “new” at each point in time or “the same,” so long as we allow for the possibility that the group effect will neither be constant (as assumed in a hierarchical model with only a random intercept at the group level) nor independent (as assumed in a typical cross-classified random effects model).

In this paper, we review and demonstrate several variations of the MLM which allow for stochastic group-effects that are time varying but correlated. We refer to these models as “dynamic group models” to reflect the fact that not only are individuals changing with time, but so are groups and therefore group effects.² Dynamic group models are three-level models for repeated measures data and, as such, can be specified and fitted within many standard software packages. They differ from more conventional MLM specifications, however, by allowing group effects to vary and covary over time according to specific structures (e.g., autoregressive). Applications using similar specifications for group-level effects are rare in the literature, but important exceptions include Leckie and Goldstein (2009, 2011), who evaluated across-cohort correlations in school effects,³ and Paddock et al. (2011), who recommended allowing for autoregressive group effects in open enrollment, rolling treatment group data. We regard these model specifications as more widely applicable and our hope is that the review provided here will enable more researchers to recognize the potential utility of dynamic group models.

In what follows, we detail the specification of dynamic group models and how they can be applied in practice. By way of introduction, we first describe more conventional MLM specifications for three-level over-time data. We then show how an alternative specification of the three-level MLM accommodates dynamic group effects. Finally, we provide two empirical demonstrations. In the first demonstration, we examine over-time science achievement data on students nested within schools. In the second demonstration, we examine trajectories of externalizing behavior and depression for siblings nested within families.

Stable Group Models

As a starting point, let us consider a relatively simple multilevel model for repeated measures data on individuals who are clustered within groups (e.g., students tracked across grade levels, where students are nested within schools). Supposing that the outcome changes linearly with time, we can write this model as follows:

$$y_{tij}={\beta }_0+{\beta }_1{\mathit{\text{time}}}_{tij}+u_j+r_{0ij}+r_{1ij}{\mathit{\text{time}}}_{tij}+e_{tij}$$ (1)

where j indexes group, i indexes individual, and t indexes the observation. The first two terms in Equation (1) are the fixed effects, which trace out the average trajectory of change over time, i.e., E(y_tij | time_tij) = β₀ + β₁time_tij. The term β₀ can thus be interpreted as the expected value of y when time is zero (often coded to indicate the earliest time point). Likewise, β₁, represents the average rate at which y changes with time in the population. The remaining terms in Equation (1) are the random effects (or residuals). Appearing first is u_j, representing the group effect and intended to account for stable mean-level differences in y across groups. The next two terms of the model are the random effects for the person. The random intercept, r_0ij, captures individual differences in the level of y at time zero (around β₀ + u_j) whereas the random effect of time, r_1ij, captures individual differences in the rate of change of y (around β₁). Last, we have the residual, e_tij, which captures time-specific variation in y around individuals’ growth trajectories (i.e., scatter around the individual trajectories due to noise, measurement error, or omitted time-varying covariates). Typically these time-specific residuals are assumed to be homoscedastic and independent over time (net of the underlying growth trajectory for the individual), although these assumptions can be relaxed when necessary (see Kwok, West, & Green, 2007, for further discussion). It is also conventional to assume that the distributions of the random effects are independent and normally distributed, or

$$u_j~N(0,{\sigma }_u^2)\left(\begin{array}{c}\hfill r_{0ij}\hfill \\ \hfill r_{1ij}\hfill \end{array}\right)~N\left[\right(\begin{array}{l}\hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{cc}\hfill {\sigma }_{r_0}^2\hfill & \hfill \hfill \\ \hfill {\sigma }_{r_0,r_1}\hfill & \hfill {\sigma }_{r_1}^2\hfill \end{array}\left)\right]e_{tij}~N(0,{\sigma }_e^2)$$

The model in Equation (1) can be extended in a variety of ways. For instance, it could be modified to allow for nonlinear growth. Additionally, predictors (other than time) could be entered at any of the three levels of the model, for instance time-varying covariates, person-level predictors, or group-level predictors. Of particular concern here is the specification of the group effects. In Equation (1) the group effect is constant over time, implicit in the absence of a t subscript for the effect. We thus refer to this model as a “stable group” model. The assumption that group effects are constant may, however, be implausible for longitudinal data. As noted previously, groups are often both structurally and functionally dynamic. In turn, the effect of the group on the individual may also vary over time.

A more complex version of the stable group model is somewhat less restrictive in this regard. In this version of the model we add a random slope for time at the group level. This addition might be motivated by the idea that, like individuals, groups follow trajectories (e.g., some peer groups increase in their average level of deviance over time whereas others decrease). The model in Equation (1) would assume these group-level trajectories to differ only in their intercepts, whereas the addition of a random slope would permit group-level variation in the time trends as well (see Raudenbush & Bryk, 2002). In the simple case of straight-line growth, the augmented model would be

$$y_{tij}={\beta }_0+{\beta }_1{\mathit{\text{time}}}_{tij}+u_{0j}+u_{1j}{\mathit{\text{time}}}_{tij}+r_{0ij}+r_{1ij}{\mathit{\text{time}}}_{tij}+e_{tij}$$ (2)

The group effect for a given observation is now a linear function of time, or u_0j + u_1jtime_t. It is possible, although not common, for the time variables governing the trajectories of individuals and groups to differ. For instance, in examining growth trajectories of achievement for students nested within schools, the relevant time variable for the individual may be grade, whereas the relevant time variable for the school may be calendar year (where students from different cohorts enter the school at different years). The measure of time associated with u_1j would then differ from the measure associated with r_1j.

Despite the time-contingent nature of the group effect in Equation (2), this model is still not fully satisfying for evaluating individual change within dynamic groups. In particular, the groups are still conceived of as stable entities (e.g., Rockbridge High School is Rockbridge High School, even if ¾ of the student body turns over between freshman and senior years, administrators and teachers come and go, and curricula standards evolve). Time-varying group effects are only an implication of the fact that groups follow their own trajectories (e.g., Rockbridge High School is on an upward achievement trajectory), and not due to changes in the structure or function of the group itself. Such changes may occur stochastically, rather than systematically, in which case a random time slope at the group level will not adequately capture the process. For these reasons we continue to refer to the model in Equation (2) as a stable groups model. In the next section, we suggest the use of dynamic group models as a more attractive alternative.

Dynamic Group Models

In dynamic group models, we reformulate the MLM to explicitly recognize the time-varying nature of group effects, and we allow for various temporal structures for these effects. Continuing with the simple example of straight-line growth, a dynamic group model can be specified as follows

$$y_{tij}={\beta }_0+{\beta }_1{\mathit{\text{time}}}_{tij}+u_{tj}+r_{0ij}+r_{1ij}{\mathit{\text{time}}}_{tij}+e_{tij}$$ (3)

Note that this model is strikingly similar to the stable group model in Equation (1), but with the important exception that the group effect, u_tj, is now subscripted by t to indicate that it is time varying. Simply put, given T time points, we have T values for the effect of being in group j. These values are assumed to be normally distributed and related to one another across time, i.e.,

$${\mathbf{u}}_j=N(\mathbf{0},{\mathbf{\Sigma }}_u)$$

where u_j is the vector of time-specific group effects, u_j = (u_1j, u_2j, …, u_Tj)′. At the group level, this specification parallels the model introduced by Leckie and Goldstein (2009, 2011) for assessing school effects across independent cohorts of students.

With this specification, the covariances among the observed repeated measures implied by the dynamic groups model include contributions from both group- and individual-level change processes. In particular, Equation (3) implies the following form for the lagged covariances among the observed repeated measures for an individual:

$$\mathit{\text{COV}}(y_{tij},y_{t\prime ij})={\sigma }_{u_{tt\prime }}+[{\sigma }_{r_0}^2+({\mathit{\text{time}}}_t+{\mathit{\text{time}}}_{t\prime }){\sigma }_{r_0{r}_1}+{\mathit{\text{time}}}_t+{\mathit{\text{time}}}_{t\prime }{\sigma }_{r_1}^2]$$ (4)

where t ≠ t′ and σ_utt′ designates the element of Σ_u corresponding to times t and t′. This equation shows that the covariance at any given lag is dependent on both the group effect covariance σ_utt′ and a set of terms (in brackets) based on the underlying growth process for the individual.⁴ In Equation (4) these terms are implied by the linear growth model specified in Equation (3), whereas other functional forms of growth (e.g., quadratic) would imply a different set of terms (see Bollen & Curran, 2006). When considering two separate individuals from the same group, the model-implied lagged covariance simplifies to

$$\mathit{\text{COV}}(y_{tij},y_{t\prime ij})={\sigma }_{u_{tt\prime }}$$ (5)

Thus, the covariance between the repeated measures of the group members depends on when they were assessed (e.g., the proximity in time with which they were members of the same group). This time-dependence is an attractive property of dynamic group models, given that the groups are expected to evolve over time.

In fitting a dynamic group model, a key objective is to determine the associations among the group effects over time, contained within the covariance matrix Σ_u. For generally stable groups, we might expect relatively little change in the group effect over time, and hence a high correlation from one time point to the next. For more dynamic groups, however, we might expect the group effect to change more rapidly, such that the over-time correlation decays rapidly with increasing time lags. Thinking about group effects in this way clarifies the restrictiveness of the static group model in Equation (1). Equation (3) reduces to Equation (1) if we assume u_tj = u_j. Put another way, we can say that the two models are equivalent if the group effect is constant and therefore perfectly correlated over time. For instance, with four time points, the structure of Σ_u implied by Equation (1) can be factored into the group-effect variance, ${\sigma }_u^2$, and the correlation matrix of the group effects as follows:

$${\mathbf{\Sigma }}_u={\sigma }_u^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]$$ (5)

For many applications, such a correlation structure (correlations of unity over time) would strain credulity. The model in Equation (2) is again more realistic in this regard, as it permits group effects to vary linearly with time (i.e., u_tj = u_0j +u_jtime_t), implying a more complex pattern of correlation. But often it may be most reasonable to assume that group effects vary stochastically with time, and it may then be preferable to determine the specific correlation structure for the group effects that is most consistent with theory and most optimal for the data at hand.

One option is to specify a completely unrestricted covariance matrix for the group effects. That is, we could attempt to estimate each unique element within the Σ_u matrix without the imposition of any constraints. This specification was used by Leckie and Goldstein (2011) in their model for assessing school effectiveness. Although this option is appealingly free of assumptions about the temporal structure of Σ_u, it is also unlikely to be viable in applications with many repeated measures because the number of unique elements in Σ_u expands rapidly with the number of time points T. In particular, the number of unique elements in Σ_u is T (T +1)/2. Even with just four time points, there are 10 unique variance-covariance parameters at the group-level to estimate (not to mention the other variance-covariance parameters still to be estimated at lower levels of the model). The data demands to reliably estimate so many parameters may be considerable. At a minimum, the number of groups in the sample would need to exceed the number of elements estimated in Σ_u, but a far greater number may be required to obtain reliable estimates. In our experience, the model may fail to converge, or may converge to a degenerate solution (in which some parameters are linearly dependent and the estimated matrix is non-positive definite).

Additionally, an unrestricted specification of Σ_u, by definition, provides little insight into the structure of the group effects and how they change over time. For instance, Leckie and Goldstein (2011) identified a pattern of group effect correlations consistent with an autoregressive decay process, but they did not actually fit this structure to estimate the autoregressive parameter. We argue that fitting a restricted covariance structure is more parsimonious, feasible, and informative. A variety of possible structures is illustrated in Table 1, but this list is not intended to be comprehensive. Different software programs offer different options for covariance structures at the group level, and not all of the specifications shown in Table 1 may be available within all programs.

Table 1.

Alternative Covariance Structures for Group Effects in Dynamic Group Models, Shown for Four Time Points

Name	Structure for Σu	Description
Fully Banded (Toeplitz)A1,B1	${\sigma }_u^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill a\hfill & \hfill b\hfill & \hfill c\hfill \\ \hfill a\hfill & \hfill 1\hfill & \hfill a\hfill & \hfill b\hfill \\ \hfill b\hfill & \hfill a\hfill & \hfill 1\hfill & \hfill a\hfill \\ \hfill c\hfill & \hfill b\hfill & \hfill a\hfill & \hfill 1\hfill \end{array}\right]$	One parameter is estimated for each time lag; the correlation of the group effects one time point apart is a, two time points apart is b, three time points apart is c, etc.
Stabilizing Banded (SB)B2	${\sigma }_u^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill a\hfill & \hfill b\hfill & \hfill b\hfill \\ \hfill a\hfill & \hfill 1\hfill & \hfill a\hfill & \hfill b\hfill \\ \hfill b\hfill & \hfill a\hfill & \hfill 1\hfill & \hfill a\hfill \\ \hfill b\hfill & \hfill b\hfill & \hfill a\hfill & \hfill 1\hfill \end{array}\right]$	Assumes the over-time correlation for the group effects stabilizes at a set value at a particular distance in time, here shown to stabilize at lag 2 to the value b.
Compound Symmetric (CS)B3	${\sigma }_u^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill a\hfill & \hfill a\hfill & \hfill a\hfill \\ \hfill a\hfill & \hfill 1\hfill & \hfill a\hfill & \hfill a\hfill \\ \hfill a\hfill & \hfill a\hfill & \hfill 1\hfill & \hfill a\hfill \\ \hfill a\hfill & \hfill a\hfill & \hfill a\hfill & \hfill 1\hfill \end{array}\right]$	Assumes that the over-time correlation for the group effects, a, is the same at every time lag.
First-Order Autoregressive (AR)A3	${\sigma }_u^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill \rho \hfill & \hfill {\rho }^2\hfill & \hfill {\rho }^3\hfill \\ \hfill \rho \hfill & \hfill 1\hfill & \hfill \rho \hfill & \hfill {\rho }^2\hfill \\ \hfill {\rho }^2\hfill & \hfill \rho \hfill & \hfill 1\hfill & \hfill \rho \hfill \\ \hfill {\rho }^3\hfill & \hfill {\rho }^2\hfill & \hfill \rho \hfill & \hfill 1\hfill \end{array}\right]$	Assumes that the over-time correlation for the group effects decays exponentially toward zero with the time lag, i.e., the autocorrelation is ρd where d is the distance in time between assessments.
First-Order Autoregressive Moving Average (ARMA)A2	${\sigma }_u^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill \gamma \hfill & \hfill \gamma \rho \hfill & \hfill \gamma {\rho }^2\hfill \\ \hfill \gamma \hfill & \hfill 1\hfill & \hfill \gamma \hfill & \hfill \gamma \rho \hfill \\ \hfill \gamma \rho \hfill & \hfill \gamma \hfill & \hfill 1\hfill & \hfill \gamma \hfill \\ \hfill \gamma {\rho }^2\hfill & \hfill \gamma \rho \hfill & \hfill \gamma \hfill & \hfill 1\hfill \end{array}\right]$	As above, assumes that the over-time correlation for the group effects decays rapidly toward zero in accordance with the autoregressive and moving average parameters ρ and γ.

Note. Structures that share the same superscript letter (A or B) are nested in their covariance parameters. More restricted structures have higher numbers (e.g., the AR structure, A3, is nested within the ARMA structure, A2, as well as the Toeplitz structure, A1).

Each of the structures shown in Table 1 assumes the variance of the group effect is the same at each point in time and that the repeated measures for the group are taken at equal intervals. Relaxing the first assumption, some software programs permit the application of heterogeneous variance versions of these same covariance structures (e.g., a heteroscedastic Toeplitz or heteroscedastic autoregressive structure), and these may be particularly useful in instances when group differences are thought to become dampened or, alternatively, amplified over time. Regarding the assumption of equal intervals of measurement, it is important to recognize that this assumption operates at the group rather than individual level. When the relevant time metrics differ between the individual and group levels, data may be at unequal intervals at the individual level but still equal in spacing at the group level. Additionally, even at the group level, not all groups must be measured at the same occasions, so that unequal spans which can be viewed as a consequence of missing data are permissible (e.g., where any one group is observed at only a subset of possible occasions). Our empirical examples illustrate both of these points. Finally, some alternative covariance structures could allow for group-specific and variable time intervals (e.g., a continuous-time autoregressive structure). Nevertheless, the structures shown in Table 1 are available in current software and likely to be useful in a variety of applications.

The choice of a covariance structure should be motivated by both theoretical expectations and empirical fit. Some covariance structures, such as the first-order autoregressive (AR) and autoregressive moving average (ARMA), assume that the correlations among the group effects decay rapidly toward zero as the time lag increases. A first-order AR pattern arises when the current state of the group effect is dependent on the immediately prior state. For instance, if the siblings within a family display higher than average psychopathology at one point in time, this may portend higher than average psychopathology at the next time point as well. When it is expected that external “shocks”, such as family disruptions, produce some of these carry-over effects, then the ARMA model may be preferable.

In other cases, it may be expected that there will always be some ambient non-zero correlation, making AR or ARMA processes less plausible. Continuing with the example of family effects on psychopathology, one might speculate that such a non-zero correlation could reflect the presence of a constant genetic liability shared by the siblings. The Toeplitz, or stabilizing banded (SB) structures would be more consistent with this theoretical expectation, as they neither impose an assumption of rapid decay nor a lower asymptote of zero for the correlation among family effects over time. The compound symmetric (CS) structure is an extreme form of this pattern where the correlation stabilizes at its ambient value at the first time lag. Constant correlations over time are rarely observed at the individual level, however, and we speculate that this structure may often be unrealistic at the group level as well (Fitzmaurice, Laird & Ware, 2004, p. 168).

Aside from theoretical plausibility, another important criterion for deciding on a covariance structure is empirical fit. All of the covariance structures listed in Table 1 are nested in their parameters relative to an unrestricted structure, permitting the use of likelihood ratio tests to evaluate how well they fit the data. In our experience, however, we have found that the unrestricted model will not always be estimable, rendering such tests impossible. Many of the restricted covariance structures are, however, also nested relative to one another, permitting tests of relative fit. Specifically, the Toeplitz, SB, and CS structures are nested in their parameters (via restrictions setting certain bands of the covariance matrix to be equal), as are the Toeplitz, ARMA, and AR structures (ARMA reduces to AR when γ = ρ, and both AR and ARMA structures impose nonlinear restrictions on the Toeplitz). When comparing between non-nested structures (e.g., SB versus AR), information criteria, such as Bayes Information Criterion (BIC) and Akaike’s Information Criterion (AIC), can be used to inform model selection.

Choosing an appropriate temporal structure for Σ_u is important for two reasons. First, by estimating the parameters within Σ_u we gain insights into the nature of group effects and how they change over time. Second, even if group effects are of little theoretical interest, misspecifying the structure of Σ_u could result in problems elsewhere in the model. Several studies have shown that misspecification of the random effects leads to biased estimates of the variance components, biased standard error estimates for fixed effects, and confidence intervals with inaccurate coverage rates (Berkhof and Kampen, 2004; Ferron, Dailey, and Yi, 2002; Kwok, West, and Green, 2007; Lange and Laird, 1989; Moerbeek, 2004). Thus, by choosing an appropriate structure for Σ_u we not only gain insight into the nature of group-level influences, we also improve our estimates and inferences for other model parameters.

When modeling individual repeated measures, it is common to begin by fitting a relatively simple base model (or unconditional growth model) and proceed to a more complex full model incorporating predictors of individual change (or conditional growth model). A natural question is at which stage of the modeling sequence to determine the covariance structure for the group effects. Some authors suggest that all fixed effects of potential interest should be included in the model used to select a covariance structure (e.g., Fitzmaurice, Laird & Ware, 2004). In this case, it may be preferable to select the fixed effects for the model based on use of the full information maximum likelihood estimator (FIML; which allows for likelihood ratio tests among models nested in their fixed effects), and then switch to the restricted maximum likelihood estimator (REML) to test between nested covariance structures (reducing small sample bias in the covariance parameter estimates; Goldstein, 2011, p. 42). Another potentially useful strategy, which we illustrate below, is to evaluate and compare estimates of group effects and their covariances in both the base and full models to observe the influence of the predictors on group effects over time. Because the group effects represent deviations from the model-implied means at each time point, we recommend that the base model include such terms as are necessary to capture the primary time trends in the data. We now turn to two empirical examples showing how dynamic group models can be applied in practice.

Example 1: Schools as Dynamic Groups

For our first example, we evaluate individual trajectories of change in science achievement during high school (10^th to 12^th grades). One objective of the analysis is to see whether science achievement can be predicted by fundamentalist attitudes toward religion and science. Another objective is to understand how schools influence student achievement and how stable these effects are over time. We use data drawn from the Longitudinal Study on American Youth (LSAY; Miller, Hoffer, Suchner, Brown, and Nelson, 1992), which began in 1987, and includes two longitudinal cohorts of students. When the study began, the first cohort of students was in 10^th grade, whereas the second cohort began 10^th grade three years later, in 1990. For the most part, students from the second cohort ultimately attended the same high schools as students in the first cohort. For our demonstration, we include only data from schools attended by members of both cohorts, providing us with a six-year span of data for any given high school.⁵ By fitting dynamic groups models we can evaluate the stability of school effects on science achievement over this six year period. It should be noted that our longitudinal design differs from other school effectiveness research in which school effects are compared across cohorts assessed at a single age (e.g., Leckie & Goldstein, 2009, 2011).

In addition to cohort and grade level, the three other variables used in our analysis are science achievement, socioeconomic status (SES), and fundamentalist attitudes. Science achievement was assessed annually for each student and quantified as a scale score (with scores calibrated using item response theory to allow comparisons across cohorts; M=63.79, SD=11.09). The average of the two parents’ Duncan Socioeconomic Index scores was used as the measure of SES (Stevens and Featherman, 1981; M=40.83, SD=16.32). Finally, a summary measure of fundamentalist attitudes toward religion and science was created as the mean of four items administered to the students’ parents in 1988, namely “We need less science, more faith,” “The theory of evolution is true” (reversed), “Science undermines morality,” and “The bible is God’s word” (M=2.54, SD=.50). The analysis sample included all observations with valid values for these predictors as well as a valid school code. In total, our analysis sample consisted of 51 schools with an average of 69 students (ranging from 19 to 149), for a total of 3498 students (2091 from the first cohort and 1407 from the second cohort) and 7756 observations.

Two sets of models were fitted to the data. Within each set of models, the general form of the model was the same but the covariance structure for the school effects was varied. The first set of models aimed to evaluate the basic pattern of growth in science achievement over high school and included fixed effects of grade, cohort, and cohort × grade. More specifically, these models were of the form

$${\mathit{\text{science}}}_{tij}={\beta }_0+{\beta }_1{\mathit{\text{grade}}}_{tij}+{\beta }_2{\mathit{\text{cohort}}}_{ij}+{\beta }_3{\mathit{\text{cohort}}}_{ij}\times {\mathit{\text{grade}}}_{tij}+u_{tj}+r_{0ij}+r_{1ij}{\mathit{\text{grade}}}_{tij}+e_{tij}$$ (6)

To facilitate interpretation, the variable grade was centered at 10^th grade and cohort was coded as 0=first, 1=second. We will refer to this set of models collectively as Model 1.

The second set of models included our predictor of interest, fundamentalist attitudes, as well as the control variable SES. Within-school effects were assessed by performing school-mean centering, and between-school effects were assessed by including the school means (grand-mean centered) as additional predictors (Enders and Tofighi, 2007; Kreft, de Leeuw, and Aiken, 1995). These models were of the form

$${\mathit{\text{science}}}_{tij}={\beta }_0+{\beta }_1{\mathit{\text{grade}}}_{tij}+{\beta }_2{\mathit{\text{cohort}}}_{ij}+{\beta }_3{\mathit{\text{cohort}}}_{ij}\times {\mathit{\text{grade}}}_{tij}+{\beta }_4{\mathit{\text{studentSES}}}_{ij}+{\beta }_5{\mathit{\text{studentatt}}}_{ij}+{\beta }_6{\mathit{\text{schoolSES}}}_j+{\beta }_7{\mathit{\text{schoolatt}}}_j+u_{tj}+r_{0ij}+r_{1ij}{\mathit{\text{grade}}}_{tij}+e_{tij}$$ (7)

where β₄ and β₅ capture within-school effects of SES and attitudes, and β₆ and β₇ capture between-school effects of SES and attitudes, respectively. The set of models with this form are referred to collectively as Model 2.⁶

For both Model 1 and Model 2 we compared a variety of possible covariance structures for the school effects to determine the optimal structure for the data. In particular, we fit each of the dynamic group structures shown in Table 1. For comparison purposes, we also fit the two stable group structures described earlier: a model with random intercepts across schools and a model with both random intercepts and slopes across schools. The former model assumes that the school effect is perfectly correlated over time whereas the latter model assumes that the school effect changes linearly in accordance with a school-level trajectory. All models were fit using the MIXED procedure in SAS 9.2 with restricted maximum likelihood estimation (REML).

Table 2 presents comparative fit statistics for both the static and dynamic groups models. Results were consistent across Models 1 and 2 – the dynamic group models displayed universally superior fit to the two stable group models, as indexed by both AIC and BIC. The best fit to the data was obtained with the stabilizing banded structure, with the correlation between school effects stabilizing at lag 4 [i.e., SB(4)]. Further supporting adoption of the SB(4) structure, likelihood ratio tests conducted for CS, SB(2), SB(3), SB(4) and Toeplitz structures indicated significant improvements in fit between each successive pair of models except SB(4) and Toeplitz. The SB(4) structure is thus retained as optimal for the data.

Table 2.

Comparative Fit of Models with Different Covariance Structures for School Effects over Time.

	Stable		Dynamic
	Intercept	Intercept + Slope	UN*	Toeplitz	SB(4)	SB(3)	SB(2)	CS	AR	ARMA
Parameters	5	7	25	10	9	8	7	6	6	7
Model 1: Includes Cohort, Grade and Cohort × Grade Effects
−2LL	52267.9	52190.2	52090.1	52109.2	52110.2	52131.3	52131.3	52142.2	52122.8	52122.7
AIC	52277.9	52204.2	52140.1	52129.2	52128.2	52147.3	52145.3	52154.2	52134.8	52136.7
BIC	52287.5	52217.7	52188.4	52148.5	52145.5	52162.8	52158.9	52165.8	52146.4	52150.2
Model 2: Includes Cohort, Grade, Cohort × Grade, Socioeconomic Status and Attitude Effects
−2LL	52045.0	51967.6	51866.2	51883.1	51883.8	51904.9	51905.0	51917.2	51897.1	51897.1
AIC	52055.0	51981.6	51916.2	51903.1	51901.8	51920.9	51919.0	51929.2	51909.1	51911.1
BIC	52064.6	51995.1	51964.5	51922.5	51919.2	51936.4	51932.5	51940.7	51920.7	51924.6

^*Estimated group-effects covariance matrix was non-positive definite.

Note: Parameters refers to the number of unique variance/covariance parameters estimated in the model, −2LL is the log-likelihood of the model multiplied by a factor of −2 (i.e., the model deviance), AIC is Akaike’s Information Criterion, BIC is Bayes’ Information Criterion. Bolded entries indicate best fit. Covariance structures were specified as defined in Table 1: UN = unrestricted, Toeplitz = fully banded Toeplitz, SB(t) = Stabilizing banded – stabilizing at lag t, CS = compound symmetric, AR = first-order autoregressive, and ARMA = first order autoregressive moving average.

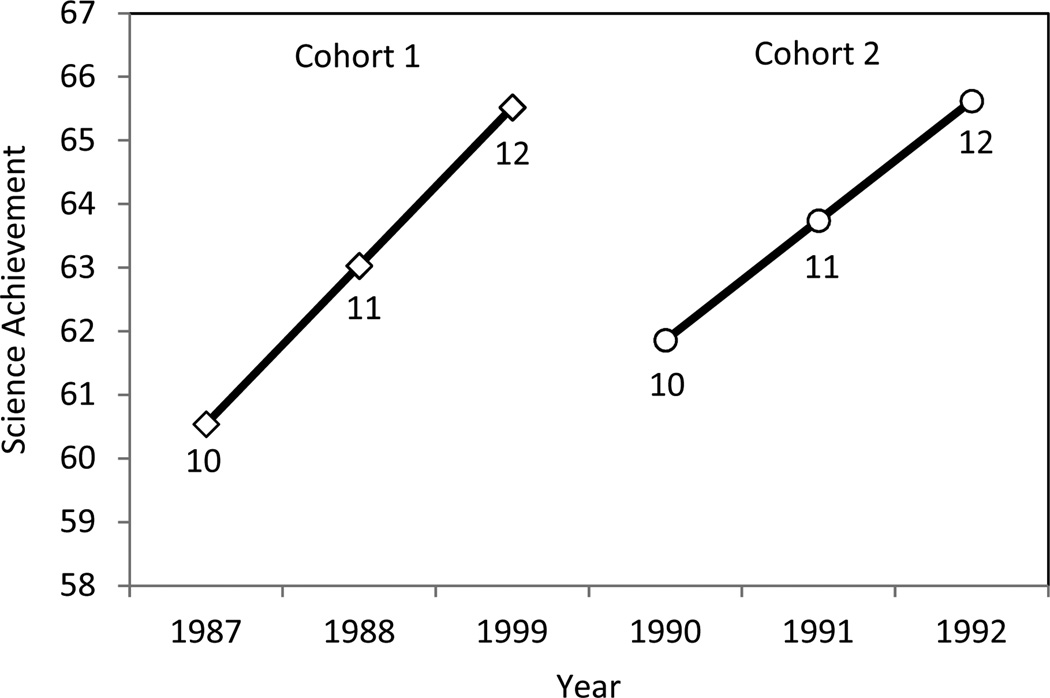
The estimates obtained from the SB(4) models are presented in Table 3, and Figure 1 displays the estimated mean trajectory of each cohort. Model 1 provides information on the basic growth pattern in the two cohorts (without the inclusion of substantive predictors). The results indicate that the second cohort has higher average science achievement scores in 10^th grade. The scores of the second cohort increase more slowly over time, however, so that the two cohorts display comparable average levels of science achievement at grade 12. The single largest variance component is for the student-level intercept, indicating that individual differences between students make up the largest source of variability in baseline science achievement scores. The school effect variance is, however, also of significant magnitude, indicating that science achievement scores vary between schools.

Table 3.

Parameter Estimates and 95% Confidence Intervals (CIs) Obtained by Fitting Stabilizing Banded School Effects Structure (Stabilizing at Lag 4) to the LSAY Data, Predicting Science Achievement

	Model 1		Model 2
Parameter	Estimate	95% CI	Estimate	95% CI
Fixed Effects
Intercept	60.48*	(59.32, 61.65)	60.54*	(59.55, 61.54)
Grade	2.49*	(2.18, 2.80)	2.49*	(2.17, 2.80)
Cohort	1.48*	(.54, 2.42)	1.32*	(0.39, 2.25)
Grade × Cohort	−0.62*	(−1.09,−.15)	−0.61*	(−1.09, −0.13)
Student Socioeconomic Status			0.13*	(0.10, 0.15)
Student Fundamentalist Attitudes			−2.68*	(−3.37, −1.98)
School Socioeconomic Status			0.12	(−0.09, 0.33)
School Fundamentalist Attitudes			−8.38*	(−16.42, −0.34)
Variance/Covariance Parameters
Within-Time Residual	10.12*	(9.48, 10.82)	10.12*	(9.48, 10.82)
Student Intercept (I)	93.71*	(88.93, 98.90)	87.97*	(83.45, 92.88)
Student Grade Slope (S)	4.71*	(4.02,5.59)	4.70*	(4.02, 5.58)
Student I,S Covariance	−1.27	(−2.75, 0.21)	−1.42	(−2.86, 0.02)
School Variance	14.57*	(10.07, 22.95)	9.99*	(6.81, 16.08)
School Covariance, Lag 1	13.56*	(9.16, 22.13)	8.99*	(5.92,15.28)
School Covariance, Lag 2	12.83*	(8.51, 21.55)	8.20*	(5.23, 14.68)
School Covariance, Lag 3	12.28*	(8.01, 21.19)	7.63*	(4.73, 14.38)
School Covariance, Lag 4+	10.79*	(6.67, 20.40)	6.18*	(3.46, 14.06)

^*p < .05

Figure 1.

Estimated mean trajectories of students from the two cohorts (based on Model 2, lag-4 stabilizing banded covariance structure); markers annotated to indicate the grade-levels of the students.

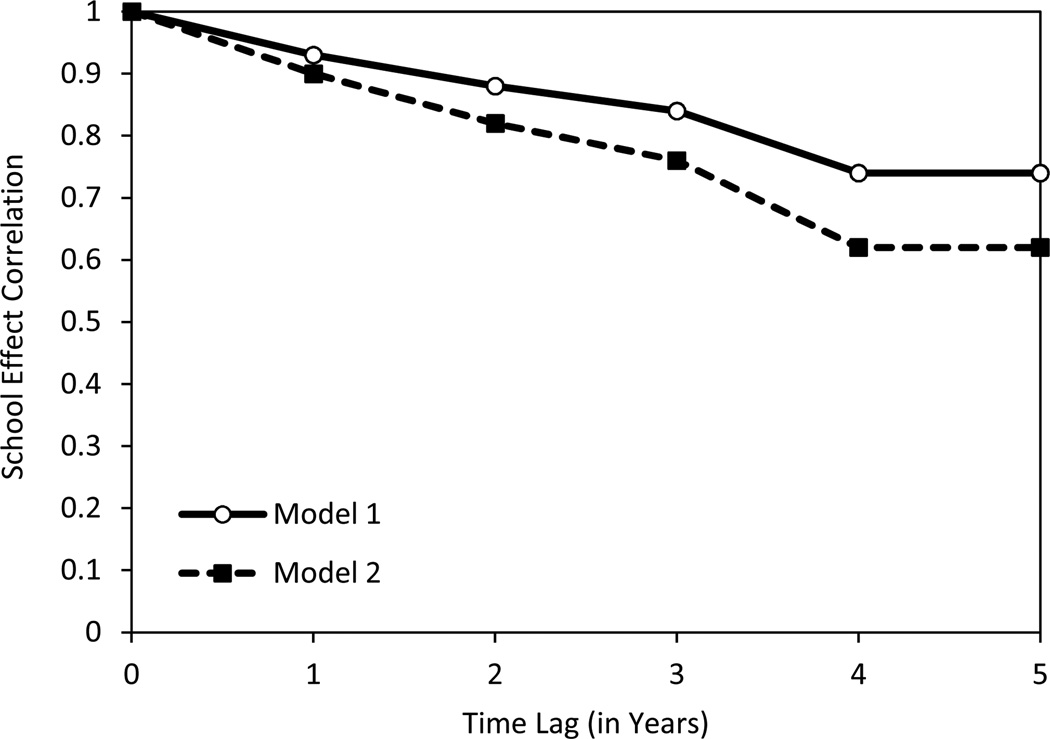
The estimated correlations among the school effects (obtained by rescaling the covariance estimates in Table 3) are shown in Figure 2. Note the high correlation of .93 between adjacent years and the eventual stabilization of the correlation across years at .74 at the fourth lag. This pattern implies that high-performing schools tend to stay high performing from one year to the next (and low-performing schools tend to stay low-performing) but that over longer periods of time there is some drift in how a given school influences student performance.

Figure 2.

Over-time autocorrelation of school effects on students’ science achievement. Model 1 includes grade and cohort as predictors; Model 2 also includes within- and between-school effects of socioeconomic status and attitudes towards religion and science.

Turning to Model 2, we see that there is a significant student-level effect of fundamentalist attitudes towards religion and science, controlling for socioeconomic status. Thus, within a given school, students whose parents hold more fundamentalist attitudes score more poorly on science achievement tests than other students. The between-school effect of attitudes is similarly negative but more difficult to pinpoint, as indicated by its large confidence interval. Part of the reason why the confidence interval is so large is that attitudes and SES are highly correlated at the school level (r = −.81), reflecting that poorer communities tend to hold more fundamentalist religious beliefs and making it difficult to partial the effect of one predictor from the other. The within-school correlation of fundamentalist attitudes and SES is, by contrast, much smaller (r = −.18), permitting reasonably precise estimates at the student level. Additionally, of course, the larger standard errors at the school level reflect the fact that there are far fewer schools (N=51) than students (N=3498).

Comparing the variance estimates of Models 1 and 2 in Table 3, we can see that the variance components at the student level remain quite large even after accounting for attitudes and SES, but the variance component at the school level is much reduced. Indeed, these two variables explain approximately 31% of the across-schools variance in students’ science achievement. The inclusion of these predictors also diminishes the correlations among the school effects, as shown in Figure 2. The year-to-year correlation is now .90, decaying to a value of .62 by the fourth lag. These lower correlations indicate that part of the stability of the school effects observed in Model 1 was due to the influence of presumably stable school differences in SES and fundamentalist attitudes. From a substantive perspective, is also interesting to note that our results are quite consistent with those of Leckie and Goldstein (2009), who found that (value added) school effects were correlated .64 across cohorts separated by five years, despite differences in sampling, fitted models, and covariate sets.

To summarize, the advantages of the dynamic groups model for this data, relative to a more conventional model specification, are threefold. First, the dynamic groups model with SB(4) covariance structure provided a better fit to the data. Thus, empirically, it better captures the nature of group effects and how they change over time. Second, the dynamic groups model likely provides more accurate inferences about the fixed effects. As previously noted, standard error estimates can be biased when implementing a non-optimal covariance structure. For this example, the standard error estimates obtained for Model 2 from the SB(4) structure are 25% larger, on average, than the standard error estimates obtained from the random intercept structure (results not shown). Likewise, the standard errors are 13% larger than those obtained from the random intercept and slope structure. To the extent that the standard error estimates obtained from these more conventional specifications are negatively biased, the resultant confidence intervals would be too narrow and the risk of Type I errors would be elevated. Finally, the third and perhaps most important advantage of the dynamic groups model is that it focuses attention and provides additional information on the nature of group effects and their stability over time. For this example, we obtained quite high lag 1 correlations but more moderate lag 4 and 5 correlations, and these findings may have important substantive implications (see Leckie & Goldstein, 2009). We shall now turn to a second example which illustrates these same advantages in a much different data analytic context: the development of psychopathology for siblings nested within families.

Example 2: Families as Dynamic Groups

In this example, we investigate how families influence child trajectories of externalizing behavior and depression across adolescence. Previous research indicates that children of alcoholics are at increased risk for a variety of social, emotional, and behavioral problems (Chassin, Rogosch, and Barrera, 1991; Connell and Goodman, 2002; Hussong et al., 2010; Puttler, Zucker, Fritzgerald & Bingham, 1998; Sher, 1997; West and Prinz, 1987). Beyond the observable influence of parent alcoholism, however, families influence psychological functioning through myriad additional pathways only some of which will be measured in a given data set. When repeated measures are collected on multiple siblings, dynamic group models offer the opportunity to estimate the magnitude of these effects and their stability (or instability) over time.

In the current demonstration, we examine trajectories of self-reported externalizing behavior and depression for children of alcoholics and matched controls in the Michigan Longitudinal Study (MLS; see Zucker, Fitzgerald, Refior, Puttler, Pallas and Ellis, 2000). Continuous scale scores were obtained for externalizing (M=.30, SD=.79) and depression (M=-1.27, SD=1.06) by applying item response theory models to subsets of the Child Behavior Checklist/Youth Report Form items (Hussong et al., 2011; see also Bauer and Hussong, 2009). We included annual assessment data from children who were between 11 and 17 years of age. We also required complete data on the predictor set which included age (see Table 4), gender (71.1% male children) and three measures of lifetime history of parental impairment (either parent): alcoholism (77.5% of families), diagnosis of major depression or dysthymia (24.6% of families), and diagnosis of antisocial personality (ASP; 16.4% of families). In interpreting the effects of these predictors it is important to note that ASP almost exclusively co-occurred with parental alcoholism (Zucker, Ellis, Bingham, Fitzgerald and Sanford, 1996). In total, our analysis sample was comprised of 2468 repeated measures from 588 children in 280 families.

Table 4.

Observation Frequency by Child Age

Child Age	Frequency
11	168
12	289
13	350
14	408
15	418
16	420
17	415
Total	2468

The number of families with one, two, three, four and five children in the analysis sample was 68, 134, 61, 16 and 1, respectively. Siblings were not always assessed within the same visit, but visits often took place within the same calendar year, and this is the time metric we use for evaluating family effects. Assessments included in this analysis took place over a period of 12 calendar years, from 1997 to 2008. The modal number of years of data for a given family was 5 years, with a range from 1 to 11 years. Table 5 displays the number of families providing outcome data for at least two siblings across each pair of years. These frequencies suggest that it should be possible to differentiate temporal patterns in family effects from child-level trajectories or time-specific noise.

Table 5.

Number of Families Contributing Information from Two or More Siblings by Interview Occasion Pairing

Year	1	2	3	4	5	6	7	8	9	10	11	12
1	74
2	64	161
3	55	125	167
4	62	140	144	187
5	65	137	140	160	184
6	48	113	124	141	137	156
7	38	100	115	131	133	119	143
8	32	70	77	90	95	87	86	104
9	24	54	59	75	77	69	73	58	84
10	19	49	55	69	64	62	61	51	48	71
11	9	29	39	48	48	43	44	36	37	42	50
12	2	13	10	13	11	12	12	6	9	12	9	14

Trajectory models were estimated separately for externalizing behavior and depression. Following the same strategy as the last example, we fitted two sets of models. The first set of models, referred to collectively as Model 1, included no predictors other than age. Based on a visual examination of the time plots and model comparisons, individual trajectories for both outcomes were modeled as quadratic functions of age. Thus, for externalizing behavior (ext), Model 1 was an unconditional growth model of the form

$${\mathit{\text{ext}}}_{tij}={\beta }_0+{\beta }_1{\mathit{\text{age}}}_{tij}+{\beta }_2{\mathit{\text{age}}}_{tij}^2+u_{tj}+r_{0ij}+r_{1ij}{\mathit{\text{age}}}_{tij}+r_{2ij}{\mathit{\text{age}}}_{tij}^2+e_{tij}$$ (8)

and, likewise, for depression (dep) it was

$${\mathit{\text{dep}}}_{tij}={\beta }_0+{\beta }_1{\mathit{\text{age}}}_{tij}+{\beta }_2{\mathit{\text{age}}}_{tij}^2+u_{tj}+r_{0ij}+r_{1ij}{\mathit{\text{age}}}_{tij}+r_{2ij}{\mathit{\text{age}}}_{tij}^2+e_{tij}$$ (9)

where t, i and j index the repeated measure, child, and family, respectively. To facilitate interpretation, the variable age was centered at 14 years, the midpoint of the age range. The intercept is then interpretable as the expected value at age 14, and the linear trend is the expected rate of change at age 14. The quadratic trend indicates whether the rate of change is accelerating or decelerating over time.

Holding the fixed effects of the model constant, we evaluated a variety of covariance structures for the random family effect. Two stable group model structures were considered. The first of these models included only a random intercept for family, implicitly assuming a constant family effect over years, whereas the second model added a random effect of interview year, to allow for the possibility that the strength and direction of family-mediated effects could worsen over time for some families while improving for others. Several dynamic group model structures were also considered, including Toeplitz, SB, CS, AR and ARMA.⁷

Model 2 was a conditional growth model and included the child- and family-level predictors of interest. Main effects were included for each predictor and interactions between the predictors and age were tested and retained if significant. The final form of Model 2 for externalizing behavior was

$${\mathit{\text{ext}}}_{tij}={\beta }_0+{\beta }_1{\mathit{\text{age}}}_{tij}+{\beta }_2{\mathit{\text{age}}}_{tij}^2+{\beta }_3{\mathit{\text{male}}}_{ij}+{\beta }_4{\mathit{\text{age}}}_{tij}\times {\mathit{\text{male}}}_{ij}+{\beta }_5{\mathit{\text{age}}}_{tij}^2\times {\mathit{\text{male}}}_{ij}+{\beta }_6{\mathit{\text{pAlc}}}_j+{\beta }_7{\mathit{\text{pDep}}}_j+{\beta }_8{\mathit{\text{pASP}}}_j+u_{tj}+r_{0ij}+r_{1ij}{\mathit{\text{age}}}_{tij}+r_{2ij}{\mathit{\text{age}}}_{tij}^2+e_{tij}$$ (10)

whereas for depression Model 2 was

$${\mathit{\text{dep}}}_{tij}={\beta }_0+{\beta }_1{\mathit{\text{age}}}_{tij}+{\beta }_2{\mathit{\text{age}}}_{tij}^2+{\beta }_3{\mathit{\text{male}}}_{ij}+{\beta }_4{\mathit{\text{age}}}_{tij}\times {\mathit{\text{male}}}_{ij}+{\beta }_5{\mathit{\text{pAlc}}}_j+{\beta }_6{\mathit{\text{pDep}}}_j+{\beta }_7{\mathit{\text{pASP}}}_j+u_{tj}+r_{0ij}+r_{1ij}{\mathit{\text{age}}}_{tij}+r_{2ij}{\mathit{\text{age}}}_{tij}^2+e_{tij}$$ (11)

where pAlc, pDep, and pASP are indicator variables scored one if the family includes a parent with a lifetime history of alcoholism, depression/dysthymia, or ASP, respectively, and scored zero otherwise. Equations (10) and (11) are equivalent in form with the caveat that the quadratic fixed effect on externalizing is moderated by gender whereas no such effect was detected for depression. We again evaluated the optimal covariance structure for the family effects over years on each outcome.

Fit statistics for Models 1 and 2 are reported in Table 6 for externalizing behavior and Table 7 for depression. In fitting alternative covariance structures for the family effects, we found that the Toeplitz, SB(>1) and ARMA covariance structures consistently resulted in non-positive definite solutions, suggesting that the complexity introduced by these structures could not be empirically supported by the data. Since these structures did not result in proper solutions they are not reported in Tables 6 and 7. Of the simpler covariance structures (random intercept only, random intercept and slope, AR, and CS) the AR structure fit best for both outcomes.

Table 6.

Comparative Fit of Models with Different Covariance Structures for Family Effects over Time on Child Externalizing Behavior

	Stable		Dynamic
	Intercept	Intercept + Slope	CS	AR
Parameters	8	10	9	9
Model 1: Includes Age Trends Only
−2LL	4850.2	4845.0	4847.6	4825.9
AIC	4866.2	4865.0	4865.6	4843.9
BIC	4895.3	4901.3	4898.3	4876.6
Model 2: Includes Age and Child- and Family-Level Predictors
−2LL	4753.5	4748.9	4752.0	4736.5
AIC	4769.5	4768.9	4770.0	4754.5
BIC	4798.6	4805.2	4802.7	4787.2

Note: Parameters refers to the number of unique variance/covariance parameters estimated in the model, −2LL is the log-likelihood of the model multiplied by a factor of −2 (i.e., the model deviance), AIC is Akaike’s Information Criterion, BIC is Bayes’ Information Criterion. Bolded entries indicate best fit. Covariance structures were specified as defined in Table 1: CS = compound symmetric, AR = first-order autoregressive.

Table 7.

Comparative Fit of Models with Different Covariance Structures for Family Effects over Time on Child Depression

	Stable		Dynamic
	Intercept	Intercept + Slope	CS	AR
Parameters	8	10	9	9
Model 1: Includes Age Trends Only
−2LL	6259.0	6253.8	6257.3	6251.5
AIC	6275.0	6273.8	6257.4	6269.5
BIC	6304.0	6310.2	6308.0	6302.2
Model 2: Includes Age and Child- and Family-Level Predictors
−2LL	6235.9	6232.7	6234.2	6227.9
AIC	6251.9	6252.7	6252.3	6245.9
BIC	6280.9	6289.0	6284.9	6278.6

Note: Parameters refers to the number of unique variance/covariance parameters estimated in the model, −2LL is the log-likelihood of the model multiplied by a factor of −2 (i.e., the model deviance), AIC is Akaike’s Information Criterion, BIC is Bayes’ Information Criterion. Bolded entries indicate best fit. Covariance structures were specified as defined in Table 1: CS = compound symmetric, AR = first-order autoregressive.

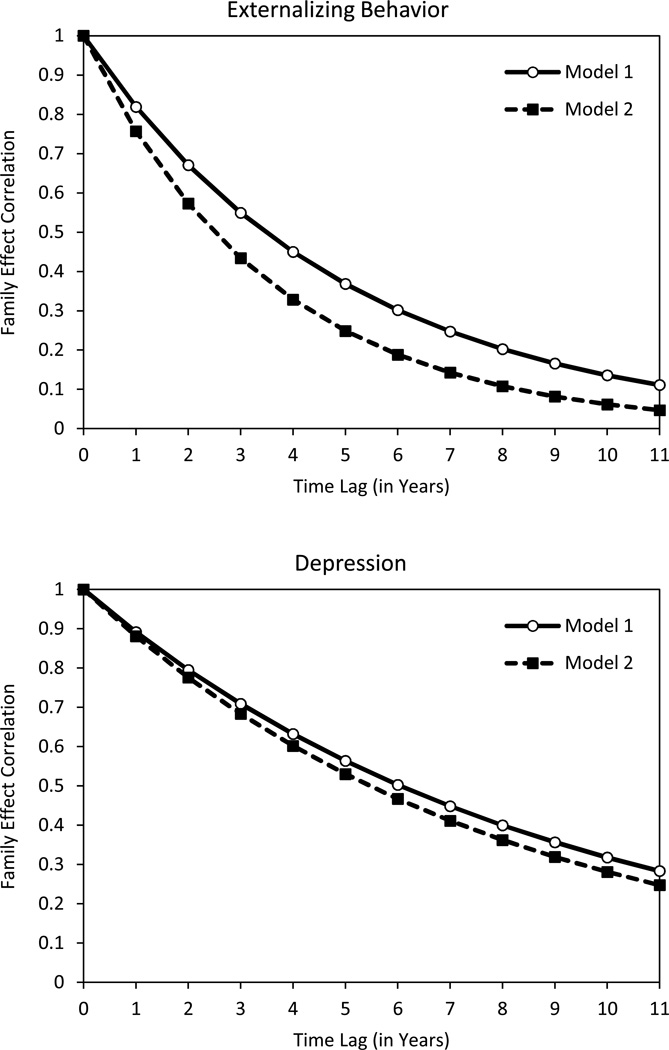
The parameter estimates obtained from fitting Models 1 and 2 to externalizing behavior, using the AR covariance structure for the family effects, are displayed in Table 8. Model 1 provides baseline estimates of the average growth function and the variance/covariance parameters for the random effects. Of particular concern are the variance for the family effect and the autocorrelation parameter, both of which are sizeable and statistically significant. The autocorrelation parameter indicates a year to year correlation of .82 in family effects on externalizing behavior. The AR structure further implies that the over-time correlation in family effects decays exponentially with the time elapsed, as shown in Figure 3. The decay is rapid: after five years, the correlation in family effects is .37, and after 10 years the correlation is only .14.

Table 8.

Parameter Estimates and 95% Confidence Intervals (CIs) Obtained by Fitting First-Order Autoregressive Family Effects Structure to the MLS Data, Predicting Externalizing Behavior

	Model 1		Model 2
Parameter	Estimate	95% CI	Estimate	95% CI
Fixed Effects
Intercept	.390*	(.324,.456)	−.133	(−.272,.006)
Age	.009	(−.008,.025)	.055*	(.027,.084)
Age2	−.015*	(−.022,−.008)	−.034*	(−.047,−.021)
Male			.217*	(.096,.338)
Age × Male			−.070*	(−.104,−.036)
Age2 × Male			.028*	(.012,.043)
Parental Alcoholism			.415*	(.291,.540)
Parental Depression/Dysthymia			.098	(−.027,.223)
Parental ASP			.207*	(.049,.364)
Variance/Covariance Parameters
Within-Time Residual	.210*	(.191,.232)	.212*	(.193,.235)
Child Intercept (I)	.281*	(.224,.363)	.265*	(.213,.338)
Child Linear Age Trend (L)	.008*	(.005,.015)	.008*	(.005,.014)
Child Quadratic Age Trend (Q)	.001*	(.000,.004)	.001	(.000,.004)
Child I,L Covariance	.013*	(.001,.024)	.016*	(.006,.027)
Child I,Q Covariance	−.006*	(−.012,−.000)	−.007*	(−.013,−.002)
Child L,Q Covariance	−.002*	(−.003,−.000)	−.001	(−.002,.000)
Family Variance	.136*	(.096,.208)	.086*	(.056,.151)
Family Autocorrelation	.819*	(.723,.915)	.757*	(.613,.901)

^*p < .05;

ASP = Antisocial Personality Disorder

Figure 3.

Over-time autocorrelation of family effects on children’s externalizing behavior (top panel) and depression (bottom panel). Model 1 includes age as a predictor; Model 2 also includes the effects of gender and parental history of alcoholism, depression/dysthymia, and antisocial personality disorder.

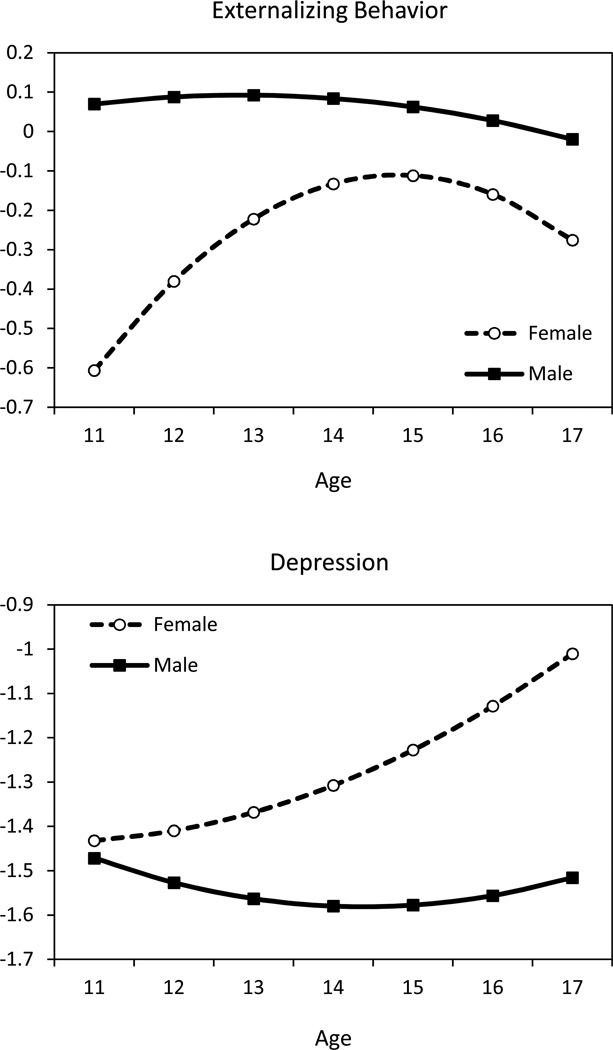
Examining the fixed effect estimates for Model 2, we see a complex pattern of gender differences. These effects are clarified by plotting the simple trajectories for male and female adolescents without impaired parents, shown in Figure 4 (Bauer and Curran, 2005). Here we can see that the trajectory for boys is higher and flatter than the trajectory for girls. Girls’ externalizing behavior increases over early adolescence, approaching the level observed for boys, but then decreases. In addition to these gender differences, children of alcoholics tend to be higher in externalizing behavior problems and parental history of ASP augments this effect. Comparing the variance component estimates for the family effects between Models 1 and 2, we can see that the predictors account for 37% of the between-family variance. As these predictors are time-stable, it is not surprising that the autocorrelation parameter is also reduced in magnitude in Model 2. Some of the family-effect stability captured by the autocorrelation parameter in Model 1 has been explained in Model 2 by the effects of the predictors, principally parental impairment. In other words, parental impairment accounts for some of the stability of inter-family differences in externalizing behavior.

Figure 4.

Expected trajectories of externalizing behavior (top panel) and depression (bottom panel) for boys and girls without impaired parents.

Corresponding results for depression are displayed in Table 9. For this outcome, too, Model 1 indicates that there is a sizeable family effect. The autocorrelation parameter, .89, implies a somewhat stronger sequence of correlations for the family effects over years, as shown in Figure 3. Turning to Model 2, the fixed effects indicate that boys and girls start off with similarly low levels of depression at age 11, but girls’ depression increases over adolescence whereas boys’ depression does not (see Figure 4). Like externalizing, we find that being the child of an alcoholic predicts a higher level of depression. Having an alcoholic parent who also has a lifetime history of antisocial personality disorder more than doubles this effect (consistent with Puttler et al, 1998). These effects are, however, weaker for depression than they were for externalizing. Comparing the variance component estimates from Models 1 and 2 in Table 9, we can see that the predictors have accounted for very little of the family-level variance (6%) in depression and that the autocorrelation parameter is largely unchanged.

Table 9.

Parameter Estimates and 95% Confidence Intervals (CIs) Obtained by Fitting First-Order Autoregressive Family Effects Structure to the MLS Data, Predicting Depression

	Model 1		Model 2
Parameter	Estimate	95% CI	Estimate	95% CI
Fixed Effects
Intercept	−1.267*	(−1.357,−1.178)	−1.307*	(−1.495,−1.120)
Age	.016	(−.006,.039)	.070*	(.031,.110)
Age2	.009	(−.001,.019)	.010	(−.000,.020)
Male			−.273*	(−.410,−.135)
Age × Male			−.078*	(−.124,−.031)
Parental Alcoholism			.207*	(.024,.390)
Parental Depression/Dysthymia			.179	(−.004,.363)
Parental ASP			.257*	(.028,.486)
Variance/Covariance Parameters
Within-Time Residual	.362*	(.328,.401)	.361*	(.327,.400)
Child Intercept (I)	.506*	(.411,.637)	.483*	(.391,.611)
Child Linear Age Trend (L)	.022*	(.015,.034)	.021*	(.014,.033)
Child Quadratic Age Trend (Q)	.003*	(.002,.006)	.003*	(.002,.006)
Child I,L Covariance	.030*	(.009,.050)	.024*	(.003,.044)
Child I,Q Covariance	−.022*	(−.032,−.011)	−.021*	(−.032,−.011)
Child L,Q Covariance	−.000	(−.002,.002)	.000	(−.002,.002)
Family Variance	.230*	(.162,.351)	.215*	(.151,.332)
Family Autocorrelation	.892*	(.809,.975)	.881*	(.792,.970)

^*p < .05;

ASP = Antisocial Personality Disorder

In sum, the results obtained across the two outcomes suggest that family-level differences in externalizing behavior and depression are equally strong and show similar patterns of stability. In both cases, a high level of stability is observed in the short term, from one year to the next, but over longer spans of time the correlation in the family effects decays rapidly. By implication, a family that is troubled in one year is likely to continue to function poorly in the next year or two, but may right itself over the longer term. Conversely, a family functioning well at one point in time is not immune from later difficulties. For externalizing behavior, but not depression, some of the stability of family effects over time can be accounted for by parental history of impairment, particularly alcoholism and ASP. These findings would not have emerged from the application of a more conventional MLM to the data.⁸

Conclusions

Psychologists and other social and health science researchers routinely collect longitudinal data on individuals clustered within groups. These groups can be expected to evolve in both structure and function over time, yet the models most often used to analyze repeated measures data assume that groups are entirely stable entities. In this paper we proposed a variation on the multilevel model that allows for dynamic group effects. These models allow for the effect of the group on the individual to change from one time point to the next, and they allow researchers to evaluate whether and why group effects are stable over time.

We provided two empirical examples of the use of dynamic group models with repeated measures data. Though the contexts of the two examples were radically different, in both cases dynamic group models fit the data significantly better than traditional stable group models. Further, the dynamic group models shed new light on the impacts of groups on individuals over time. Interestingly, school effects on student achievement were more stable than family effects on children’s externalizing behavior. At a time lag of five years, school effects on science achievement were still correlated .74 (Figure 2, Model 1), whereas family effects were correlated .56 for depression and only .37 for externalizing behavior (Figure 3, Model 1). This difference in stability is perhaps not surprising. Schools are large institutions with a great deal of inertia, whereas families are small groups that are potentially more vulnerable to stochastic events (such as changes in economic circumstances, changes in family structure, maturational events, etc.).

It is important to emphasize that the model specifications presented in this paper assume no mobility of individuals between Level 2 units. For any given student, all observations are made while the student is a member of a single school. Likewise, each sibling is assumed to reside within the same household across all assessments. In the event that there is mobility or cross-over between groups, it may be necessary to combine elements of the dynamic groups model with a multiple membership model (as in Goldstein et al., 2000) or a cross-classified random effects model (Luo & Kwok, 2012; Palardy, 2010; Raudenbush, 1993; Raudenbush & Bryk, 2002; Rowan, Correnti & Miller, 2002). Such extensions would offer the exciting opportunity to model dynamic group effects when the group membership of the sampled individuals is also unstable over time.

Additional research is also needed to determine the sample sizes and other data characteristics under which dynamic group models will perform optimally. Based on our experience, we anticipate that sample size requirements will increase with the complexity of the group-effects covariance structure and that at modest sample sizes it may not always be possible to uniquely estimate all of the parameters of more complex structures (e.g., one may often obtain a non-positive definite solution). Such difficulties can also arise with more conventional growth models and, in practice, are often taken to imply that a simpler covariance structure should be specified (e.g., Huttenlocher et al, 1991; Peugh, 2010). Simulation studies are needed to evaluate this practice with dynamic group models. For the time being, however, it is important to recognize that the general multilevel model, of which dynamic group models represent a specific case, is both well-studied and widely accessible in commonly used statistical software. Further, specific code for fitting the dynamic groups models from our example analyses are provided at <web site to be determined; supplemental file>. We therefore believe that the models proposed and illustrated here can be put to immediate use. Groups are fluid and dynamic entities, and the models we use to analyze grouped data over time should reflect that reality.