A direct D-bar reconstruction algorithm for recovering a complex conductivity in 2-D

Abstract

A direct reconstruction algorithm for complex conductivities in W^2,∞ (Ω), where Ω is a bounded, simply connected Lipschitz domain in ℝ², is presented. The framework is based on the uniqueness proof by Francini [Inverse Problems 20 2000], but equations relating the Dirichlet-to-Neumann to the scattering transform and the exponentially growing solutions are not present in that work, and are derived here. The algorithm constitutes the first D-bar method for the reconstruction of conductivities and permittivities in two dimensions. Reconstructions of numerically simulated chest phantoms with discontinuities at the organ boundaries are included.

1 Introduction

The reconstruction of admittivies γ from electrical boundary measurements is known as the inverse admittivity problem. The unknown admittivity appears as a complex coefficient γ(z) = σ(z) + iωε(z) in the generalized Laplace equation

$$\nabla ·(\gamma (z)\nabla u(z))=0,z\in \mathrm{\Omega },u{\mid }_{\partial \mathrm{\Omega }}=f,$$ (1)

where u is the electric potential, σ is the conductivity of the medium, ε is the permittivity, and ω is the temporal angular frequency of the applied electromagnetic wave. The data is the Dirichlet-to-Neumann, or voltage-to-current density map defined by

$${\mathrm{\Lambda }}_{\gamma }u={\gamma \frac{\partial u}{\partial \nu }|}_{\partial \mathrm{\Omega }},$$ (2)

where u ∈ H¹(Ω) is the solution to (1). By the trace theorem Λ_γ: H^1/2(∂Ω) → H^−1/2(∂Ω).

In this work we present a direct reconstruction algorithm for the admittivity γ. The majority of the theory is based on the 2000 paper by Francini [21] in which it is established that if σ, ε ∈ W^2,∞(Ω), where Ω is a bounded domain in ℝ² with Lipschitz boundary, then the real-valued functions σ and ε are uniquely determined by the Dirichlet-to-Neumann map, provided that the imaginary part of the admittivity is sufficiently small. The proof in [21] is based on the D-bar method and is nearly constructive, but equations linking the scattering transform and the exponentially growing solutions to the Dirichlet-to-Neumann data are not used in the proof, and so it does not contain a complete set of equations for reconstructing the admittivity. In this work, we derive the necessary equations for a direct, nonlinear reconstruction algorithm for the admittivity γ. Furthermore, we establish the existence of exponentially growing solutions to (1), which prove to be useful in relating the Dirichlet-to-Neumann data to the scattering transform. The reconstruction formula in [21] is for the potential Q_γ, whose relationship to γ is described below. We provide a direct formula for γ from the D-bar equations in [21], which is computationally advantageous as well.

The inverse admittivity problem has an important application known as electrical impedance tomography (EIT). The fact that the electrical conductivity and permittivity vary in the different tissues and organs in the body allows one to form an image from the reconstructed admittivity distribution. In the 2-D geometry, EIT is clinically useful for chest imaging. Conductivity images have been used for monitoring pulmonary perfusion [9, 23, 48], determining regional ventilation in the lungs [24, 22, 52], and the detection of pneumothorax [16], for example. In three dimensions, conductivity images have been used, for instance, in head imaging [51, 50] and knowledge of the admittivity has been applied to breast cancer detection [8, 31, 32].

Reconstruction algorithms based on a least-squares approach that reconstruct permittivity include [19, 8, 30]. The aforementioned algorithms are iterative, whereas the work presented here is a direct method that makes use of exponentially growing solutions, or complex geometrical optics (CGO) solutions, to the admittivity equation. The steps of the algorithm are to compute these CGO solutions from knowledge of the Dirichlet-to-Neumann map, to compute a scattering transform matrix, to solve two systems of ∂̄ (D-bar) equations in the complex frequency variable k for the CGO solutions to a related elliptic system, and finally to reconstruct the admittivity from the values of these solutions at k = 0. In this work, we provide a complete implementation of this algorithm and present reconstructions of several numerical phantoms relevant to medical EIT imaging. The phantoms we consider here are discontinuous at the organ boundaries, which is actually outside the theory of the algorithm. The work [26] contains computations of smooth admittivities and validates our formulas and computations by comparing the results of the intermediate functions (CGO solutions and scattering transforms) with those computed from knowledge of the admittivity.

We briefly review the history of results using CGO solutions on the inverse conductivity problem in dimension 2. The inverse conductivity problem was first introduced by A.P. Calderón [12] in 1980, where he proved that, in a linearized version of the problem, the Dirichlet-to-Neumann map uniquely determines the conductivity, and he proposed a direct reconstruction method for this case. An implementation in dimension two for experimental data is found in [6]. In 1996, Nachman [44] presented a constructive proof of global uniqueness for twice differentiable conductivities using D-bar methods. The D-bar algorithm following from [44, 46] has been applied to simulated data in [39, 41, 27, 38] and to experimental data on tanks and in vivo human data in [28, 29, 42, 18]. While the initial scattering transform was regularized using a Born approximation, a more recent paper [40] contains a full nonlinear regularization analysis, including estimates on speed of convergence in Banach spaces, for twice differentiable conductivities. The regularity conditions on the conductivity were relaxed to once-differentiable in [10]. The proof uses D-bar techniques and formulates the problem as a first-order elliptic system. A reconstruction method based on [10] can be found in [33, 34, 35]. Francini [21] provided a proof of unique identifiability for the inverse admittivity problem for σ, ε ∈ W^2,∞ (Ω), with ω small. Her work provides a nearly constructive proof based on D-bar methods on a first-order elliptic system similar to that in [10]. A non-constructive proof that applies to complex admittivities with no smallness assumption is found in [11]. Astala and Päivärinta provide a CGO-based constructive proof for real conductivities σ ∈ L^∞(Ω), and numerical results related to this work can be found in [3, 4].

The paper is organized as follows. In Section 2 we describe the direct reconstruction algorithm, which is comprised of boundary integral equations for the exponentially growing solutions to (1) involving the Dirichlet-to-Neumann data, boundary integral equations relating those CGO solutions and the CGO solutions Ψ of the first order system, equations for the scattering transform involving only the traces of Ψ, the ∂̄_k equations established in [21], and the direct reconstruction formula for Q_γ and thus γ. Derivations of the novel equations are found in this section. Section 3 describes the numerical implementation of the algorithm. Results on noisy and non-noisy simulated data of a cross-sectional chest with discontinuous organ boundaries are found in Section 4.

2 The Direct Reconstruction Algorithm

In this section we will provide the equations for the direct reconstruction algorithm, completing the steps for the proof in [21] to be completely constructive. In particular, boundary integral equations relating the CGO solutions to the Dirichlet-to-Neumann (DN) map are derived.

Let Ω ⊂ ℝ² be a bounded open domain with a Lipschitz boundary. Throughout we assume that there exist positive constants σ₀ and β such that

$$\sigma (z)>{\sigma }_0,z\in \mathrm{\Omega }\subset {\mathbb{R}}^2$$ (3)

and

$${\left|\right|\sigma \left|\right|}_{W^{1,\infty }(\mathrm{\Omega })},{\left|\right|\epsilon \left|\right|}_{W^{1,\infty }(\mathrm{\Omega })}\le \beta .$$ (4)

We extend σ and ε from Ω to all of ℝ² such that σ ≡ 1 and ε ≡ 0 outside a ball with fixed radius that contains Ω, and (3) and (4) hold for all of ℝ². In fact, all that is required is that γ is constant outside that ball of fixed radius; for convenience we look at the case where γ ≡ 1.

The proof in [21] closely follows that of [10] for conductivities σ ∈ W^1,p(Ω), p > 2. The matrix potential Q_γ is, however, defined slightly differently, and since the potential in [21] is not Hermitian, the approach in [21] is to consider the complex case as a perturbation from the real case provided the imaginary part of γ is small. Define Q_γ(z) and a matrix operator D by

$$Q_{\gamma }(z)=\left(\begin{array}{cc}0& -\frac{1}{2}{\partial }_{z}log\gamma (z)\\ -\frac{1}{2}{\overline{\partial }}_{z}log\gamma (z)& 0\end{array}\right),D=\left(\begin{array}{cc}{\overline{\partial }}_z& 0\\ 0& {\partial }_z\end{array}\right).$$ (5)

Thus we define

$$Q_{12}(z)=-\frac{1}{2}{\partial }_{z}log\gamma (z)\text{and}{Q}_{21}(z)=-\frac{1}{2}{\overline{\partial }}_{z}log\gamma (z),$$ (6)

and equivalently we can write

$$Q_{12}(z)=-\frac{{\partial }_z{\gamma }^{1/2}(z)}{{\gamma }^{1/2}(z)}\text{and}{Q}_{21}(z)=-\frac{{\overline{\partial }}_z{\gamma }^{1/2}(z)}{{\gamma }^{1/2}(z)},$$ (7)

or

$$Q_{12}(z)=-\frac{1}{2}{\gamma }^{-1}(z)\partial \gamma (z)\text{and}{Q}_{21}(z)=-\frac{1}{2}{\gamma }^{-1}(z)\overline{\partial }\gamma (z).$$ (8)

Defining a vector

$$\left(\begin{array}{c}v\\ w\end{array}\right)={\gamma }^{1/2}\left(\begin{array}{c}\partial u\\ \overline{\partial }u\end{array}\right),$$ (9)

in terms of the solution u to (1), one sees that

$$D\left(\begin{array}{c}v\\ w\end{array}\right)-Q_{\gamma }\left(\begin{array}{c}v\\ w\end{array}\right)=0.$$

The uniqueness result in [21] is

Theorem 2.1. (Theorem 1.1 [21])

Let Ω be an open bounded domain in ℝ² with Lipschitz boundary. Let σ_j and ε_j, for j = 1, 2 satisfy assumptions (3) and ||σ||_{W^{2, ∞} (Ω)}, ||ε||_{W^{2, ∞}(Ω)} ≤ β. There exists a constant ω₀ = ω₀(β, σ₀, Ω) such that if γ_j = σ_j + iωε_j for j = 1, 2 and ω < ω₀ and if

$${\mathrm{\Lambda }}_{{\gamma }_1}={\mathrm{\Lambda }}_{{\gamma }_2},$$

then

$${\sigma }_1={\sigma }_2\mathit{and}{\epsilon }_1={\epsilon }_2.$$

2.1 CGO solutions

Francini shows in [21] that for ω sufficiently small and γ satisfying (3) and (4) there exists a unique 2 × 2 matrix M(z, k) for k ∈ ℂ satisfying

$$M(·,k)-I\in L^p({\mathbb{R}}^2),\text{for}\text{some}p>2,$$ (10)

that is a solution to

$$(D_k-Q_{\gamma }(z))M(z,k)=0,$$ (11)

where D_k is the matrix operator defined by

$$D_{k}M=DM-ik\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)M^{\text{off}},$$

and “off” denotes the matrix consisting of only the off-diagonal entries of M. The system (11) is equivalent to the following set of equations, included for the reader’s convenience

$$\begin{array}{rr}\hfill {\overline{\partial }}_z{M}_{11}-Q_{12}{M}_{21}=0& \hfill ({\overline{\partial }}_z-ik)M_{12}-Q_{12}{M}_{22}=0\\ \hfill ({\partial }_z+ik)M_{21}-Q_{21}{M}_{11}=0& \hfill {\partial }_z{M}_{22}-Q_{21}{M}_{12}=0.\end{array}$$ (12)

Thus, there exists a unique matrix Ψ(z, k) defined by

$$\mathrm{\Psi }(z,k)=M(z,k)\left(\begin{array}{cc}{e}^{\mathit{izk}}& 0\\ 0& e^{-i\overline{z}k}\end{array}\right)=\left(\begin{array}{cc}{e}^{\mathit{izk}}{M}_{11}(z,k)& e^{-i\overline{z}k}{M}_{12}(z,k)\\ e^{\mathit{izk}}{M}_{21}(z,k)& e^{-i\overline{z}k}{M}_{22}(z,k)\end{array}\right),$$ (13)

that is a solution to

$$(D-Q_{\gamma })\mathrm{\Psi }=0,$$ (14)

or equivalently

$$\begin{array}{cc}{\overline{\partial }}_z{\mathrm{\Psi }}_{11}-Q_{12}{\mathrm{\Psi }}_{21}=0& {\partial }_z{\mathrm{\Psi }}_{21}-Q_{21}{\mathrm{\Psi }}_{11}=0\\ {\overline{\partial }}_z{\mathrm{\Psi }}_{12}-Q_{12}{\mathrm{\Psi }}_{22}=0& {\partial }_z{\mathrm{\Psi }}_{22}-Q_{21}{\mathrm{\Psi }}_{12}=0.\end{array}$$ (15)

These CGO solutions Ψ(z, k) are key functions in the reconstructions, but the proof in [21] does not provide a link from these functions to the DN data. A useful link can be established through exponentially growing solutions to the admittivity equation (1). For γ − 1 with compact support, equation (1) can be studied on all of ℝ², and introducing the complex parameter k, two distinct exponentially growing solutions, which differ in their asymptotics, exist. We will denote these solutions by u₁ and u₂ where $u_1~\frac{e^{\mathit{ikz}}}{ik}$ and $u_2~\frac{e^{-ik\overline{z}}}{-ik}$ in a sense that is made precise in Theorems 2.2 and 2.3, where the existence of such solutions is established. The proof will make use of the following lemma proved in the real case by Nachman [44]; the complex version shown here also holds and was used in [21]. The lemma is also true if ∂̄_z is interchanged with ∂_z.

Lemma 2.1

Let 1 < s < 2 and $\frac{1}{r}=\frac{1}{s}-\frac{1}{2}$.

1. If the complex function v ∈ L^s(ℝ²), then there exists a unique complex function u ∈ L^r(ℝ²) such that (∂_z + ik)u = v.

2. If the complex function v ∈ L^r(ℝ²) and ∂̄_zv ∈ L^s(ℝ²), k ∈ ℂ\{0}, then there exists a unique complex function u ∈ W^1,r(ℝ²) such that (∂_z+ik)u = v.

3. If the complex function v ∈ L^r(ℝ²) and ∂̄_zv ∈ L^s(ℝ²), k ∈ ℂ\{0}, then there exists a unique complex function u ∈ W^1,r(ℝ²) such that (∂̄_z − ik)u = v.

The following lemma will also be used in the proofs of Theorems 2.2 and 2.3.

Lemma 2.2

For ω sufficiently small and γ satisfying (3) and (4), the following identities hold:

$${\overline{\partial }}_{\text{z}}(\gamma {(z)}^{-1/2}{M}_{11}(z,k)-1)=({\partial }_{\text{z}}+ik)(\gamma {(z)}^{-1/2}{M}_{21}(z,k))$$ (16)

$${\partial }_z(\gamma {(z)}^{-1/2}{M}_{22}(z,k)-1)=({\overline{\partial }}_z-ik)(\gamma {(z)}^{-1/2}{M}_{12}(z,k)).$$ (17)

Proof

By the product rule,

$$\begin{array}{l}{\overline{\partial }}_{\text{z}}\left(\gamma {(z)}^{-1/2}{M}_{11}(z,k)-1\right)={\overline{\partial }}_{\text{z}}\left(\gamma {(z)}^{-1/2}\right)M_{11}(z,k)+\gamma {(z)}^{-1/2}{\overline{\partial }}_{\text{z}}(M_{11}(z,k))\\ =\gamma {(z)}^{-1/2}{Q}_{21}(z)M_{11}(z,k)+\gamma {(z)}^{-1/2}{Q}_{12}(z)M_{21}(z,k)\\ =\gamma {(z)}^{-1/2}({\partial }_{\text{z}}+ik)M_{21}(z,k)+\gamma {(z)}^{-1/2}{Q}_{12}(z)M_{21}(z,k).\end{array}$$

The second and third equalities utilized (6) and (12), respectively.

We also have

$$\begin{array}{l}({\partial }_{\text{z}}+ik)\left(\gamma {(z)}^{-1/2}{M}_{21}(z,k)\right)={\partial }_{\text{z}}\left(\gamma {(z)}^{-1/2}{M}_{21}(z,k)\right)+ik\gamma {(z)}^{-1/2}{M}_{21}(z,k)\\ ={\partial }_{\text{z}}\left(\gamma {(z)}^{-1/2}\right)M_{21}(z,k)+\gamma {(z)}^{-1/2}{\partial }_{\text{z}}(M_{21}(z,k))+ik\gamma {(z)}^{-1/2}{M}_{21}(z,k)\\ =\gamma {(z)}^{-1/2}{Q}_{12}(z)M_{21}(z,k)+\gamma {(z)}^{-1/2}({\partial }_{\text{z}}+ik)M_{21}(z,k).\end{array}$$

This establishes (16).

Similarly, using (6) and (12),

$$\begin{array}{l}{\partial }_{\text{z}}\left(\gamma {(z)}^{-1/2}{M}_{22}(z,k)-1\right)={\partial }_{\text{z}}\left(\gamma {(z)}^{-1/2}\right)M_{22}(z,k)+\gamma {(z)}^{-1/2}{\partial }_{\text{z}}(M_{22}(z,k))\\ =\gamma {(z)}^{-1/2}{Q}_{12}(z)M_{22}(z,k)+\gamma {(z)}^{-1/2}{Q}_{21}(z)M_{12}(z,k)\\ =\gamma {(z)}^{-1/2}({\overline{\partial }}_{\text{z}}-ik)M_{12}(z,k)+\gamma {(z)}^{-1/2}{Q}_{21}(z)M_{12}(z,k).\end{array}$$

We also have

$$\begin{array}{l}({\overline{\partial }}_{\text{z}}-ik)\left(\gamma {(z)}^{-1/2}{M}_{12}(z,k)\right)={\overline{\partial }}_{\text{z}}\left(\gamma {(z)}^{-1/2}{M}_{12}(z,k)\right)-ik\gamma {(z)}^{-1/2}{M}_{12}(z,k)\\ ={\overline{\partial }}_{\text{z}}\left(\gamma {(z)}^{-1/2}\right)M_{12}(z,k)+\gamma {(z)}^{-1/2}{\overline{\partial }}_{\text{z}}(M_{12}(z,k))-ik\gamma {(z)}^{-1/2}{M}_{12}(z,k)\\ =\gamma {(z)}^{-1/2}{Q}_{21}(z)M_{12}(z,k)+\gamma {(z)}^{-1/2}({\overline{\partial }}_{\text{z}}-ik)M_{12}(z,k).\end{array}$$

This establishes (17).

Knudsen establishes the existence of exponentially growing solutions to the conductivity equation in the context of the inverse conductivity problem in [33]. The proofs of their existence for the admittivity equation and the associated boundary integral equations are in the same spirit as [33].

Theorem 2.2

Let γ(z) ∈ W^1,p(Ω), with p > 2 such that σ and ε satisfy (3) and (4), and let γ(z) − 1 have compact support in W^1,p(Ω). Then for all k ∈ ℂ\{0} there exists a unique solution

$$u_1(z,k)=e^{\mathit{ikz}}\left[\frac{1}{ik}+w_1(z,k)\right],$$ (18)

to the admittivity equation in ℝ² such that w₁(·, k) ∈ W^1,r(ℝ²), 2 < r < ∞. Moreover, the following equalities hold:

$$({\partial }_{\text{z}}+ik)\left[e^{-\mathit{ikz}}{u}_1(z,k)-\frac{1}{ik}\right]={\gamma }^{-1/2}(z)M_{11}(z,k)-1$$ (19)

$${\overline{\partial }}_{\text{z}}\left[e^{-\mathit{ikz}}{u}_1(x,k)-\frac{1}{ik}\right]={\gamma }^{-1/2}(z)M_{21}(z,k),$$ (20)

and

$${\Vert e^{-\mathit{ikz}}{u}_1(x,k)-\frac{1}{ik}\Vert }_{W^{1,r}({\mathbb{R}}^2)}\le C\left(1+\frac{1}{\mid k\mid }\right),$$ (21)

for some constant C.

Theorem 2.3

Let γ(z) satisfy the hypotheses of Theorem 2.2. Then for all k ∈ ℂ\{0} there exists a unique solution

$$u_2(z,k)=e^{-ik\overline{z}}\left[\frac{1}{-ik}+w_2(z,k)\right],$$ (22)

to the admittivity equation in ℝ² with w₂(·, k) ∈ W^1,r(ℝ²), 2 < r < ∞. Moreover, the following equalities hold:

$$({\overline{\partial }}_{\text{z}}-ik)\left[e^{ik\overline{z}}{u}_2(z,k)+\frac{1}{ik}\right]={\gamma }^{-1/2}(z)M_{22}(z,k)-1$$ (23)

$${\partial }_{\text{z}}\left[e^{ik\overline{z}}{u}_2(z,k)+\frac{1}{ik}\right]={\gamma }^{-1/2}(z)M_{12}(z,k),$$ (24)

and

$${\Vert e^{ik\overline{z}}{u}_2(z,k)+\frac{1}{ik}\Vert }_{W^{1,r}({\mathbb{R}}^2)}\le C\left(1+\frac{1}{\mid k\mid }\right),$$ (25)

for some constant C.

We will prove Theorem 2.2; the proof of Theorem 2.3 is analogous.

Proof

Assume u is a solution of the admittivity equation of the form (18), and let (v, w)^T = γ^1/2(∂_z u, ∂̄_z u)^T be the corresponding solution to (D − Q_γ) Ψ = 0. Define the complex function v via v(z, k) = γ(z)^−1/2M₁₁(z, k) − 1. We will first show there exists a unique complex function w₁ ∈ W^1,r(ℝ²), where r > 2 such that (∂_z+ik)w = v, for k ∈ ℂ\{0}. Let us rewrite v as follows:

$$v(z,k)=\gamma {(z)}^{-1/2}\left[M_{11}(z,k)-1\right]+\left[\gamma {(z)}^{-1/2}-1\right].$$

Let r > 2 and 1 < s < 2 with $\frac{1}{r}=\frac{1}{s}-\frac{1}{2}$. We know by Theorem 4.1 of [21] that there exists a constant C > 0 depending on β, σ₀ and p such that sup ||M₁₁ (z, k) − 1||_L^r(ℝ²) ≤ C for every r > 2, and that γ(z)^−1/2 − 1 has compact support in W^1,r(ℝ²). It follows that v ∈ L^r(ℝ²), and by Minkowski’s Inequality

$${\left|\right|v(z,k)\left|\right|}_{L^r}={\Vert \gamma {(z)}^{-1/2}\left[M_{11}(z,k)-1\right]+\left[\gamma {(z)}^{-1/2}-1\right]\Vert }_{L^r}\le C_{r,\gamma },$$

where C_r,γ depends on r and the bounds on σ and ε.

From (8),

$$\begin{array}{l}{\overline{\partial }}_{\text{z}}v(z,k)={\overline{\partial }}_{\text{z}}(\gamma {(z)}^{-1/2}{M}_{11}(z,k)-1)\\ =({\overline{\partial }}_{\text{z}}\gamma {(z)}^{-1/2})M_{11}(z,k)+\gamma {(z)}^{-1/2}({\overline{\partial }}_{\text{z}}{M}_{11}(z,k))\\ =\gamma {(z)}^{-1/2}{Q}_{21}(z)M_{11}(z,k)+\gamma {(z)}^{-1/2}{Q}_{12}(z)M_{21}(z,k)\\ =\gamma {(z)}^{-1/2}{Q}_{21}(z)[M_{11}(z,k)-1]+\gamma {(z)}^{-1/2}{Q}_{21}(z)+\gamma {(z)}^{-1/2}{Q}_{12}(z)M_{21}(z,k)\end{array}$$

We know that γ(z)^−1/2Q₂₁(z) ∈ L^α(ℝ²) with 1 ≤ α ≤ p since Q₁₂(z) has compact support. It follows that γ(z)^−1/2Q₂₁(z) ∈ L^s(ℝ²) ∩ L²(ℝ²). By the generalized Hölder’s inequality and the fact that ||M₁₁(z, k) − 1||_L^s is bounded with $\frac{1}{s}=\frac{1}{r}+\frac{1}{2}$, we have ∂̄_z v ∈ L^s(ℝ²) and ||∂̄_z v||_L^s(ℝ²) ≤ K_{r, γ}, where K_{r, γ} depends only on r and the bounds on σ and ε. Thus, by Lemma 2.1 (2), there exists a unique solution w₁(z, k) ∈ W^1,r(ℝ²) such that

$$({\partial }_{\text{z}}+ik)w_1(z,k)=\gamma {(z)}^{-1/2}{M}_{11}(z,k)-1.$$ (26)

We have by (16),

$$\overline{\partial }(\gamma {(z)}^{-1/2}{M}_{11}(z,k)-1)=({\partial }_{\text{z}}+ik)\left(\gamma {(z)}^{-1/2}{M}_{21}(z,k)\right).$$ (27)

Taking ∂̄_z of both sides of (26) and using (27),

$$\begin{array}{l}{\overline{\partial }}_{\text{z}}({\partial }_{\text{z}}+ik)w_1(z,k)={\overline{\partial }}_{\text{z}}\left(\gamma {(z)}^{-1/2}{M}_{11}(z,k)-1\right)\\ =({\partial }_{\text{z}}+ik)\left(\gamma {(z)}^{-1/2}{M}_{21}(z,k)\right).\end{array}$$ (28)

Using the fact ∂̄(∂ + ik) = (∂ + ik)∂̄, it follows that

$$({\partial }_{\text{z}}+ik)\left({\overline{\partial }}_{\text{z}}{w}_1(z,k)-{(z)}^{-1/2}{M}_{21}(z,k)\right)=0.$$ (29)

Since ∂̄_z w₁(z, k) − γ(z)^−1/2M₂₁(z, k) ∈ L^r(ℝ²), by Lemma 2.1 (1), we must have

$${\overline{\partial }}_{\text{z}}{w}_1(z,k)=\gamma {(z)}^{-1/2}{M}_{21}(z,k).$$ (30)

We now define

$$u_1(z,k)=e^{\mathit{ikz}}\left[w_1(z,k)+\frac{1}{ik}\right],$$ (31)

then by (26)

$$({\partial }_{\text{z}}+ik)\left(e^{-\mathit{ikz}}{u}_1(z,k)-\frac{1}{ik}\right)=({\partial }_{\text{z}}+ik)w_1(z,k)={\gamma }^{-1/2}(z)M_{11}(z,k)-1,$$

which proves (19), and by (30)

$${\overline{\partial }}_{\text{z}}\left(e^{-\mathit{ikz}}{u}_1(z,k)-\frac{1}{ik}\right)={\overline{\partial }}_{\text{z}}{w}_1(z,k)={\gamma }^{-1/2}(z)M_{21}(z,k),$$

which proves (20).

The norm estimate given by (21) follows by Minkowski’s Inequality, the constant C depends on r, the bound on γ − 1, and the bounds on σ and ε.

Remark

Note that from (19)

$$\begin{array}{l}{\gamma }^{-1/2}{M}_{11}(z,k)-1=({\partial }_{\text{z}}+ik)\left(e^{-\mathit{ikz}}{u}_1(z,k)-\frac{1}{ik}\right)\\ ={\partial }_{\text{z}}(e^{-\mathit{ikz}}{u}_1)+{\mathit{ike}}^{-\mathit{ikz}}{u}_1(z,k)-1\\ =e^{-\mathit{ikz}}{\partial }_{\text{z}}{u}_1(z,k)-1,\end{array}$$ (32)

and from (20)

$$\begin{array}{l}{\gamma }^{-1/2}{M}_{21}(z,k)={\overline{\partial }}_{\text{z}}\left(e^{-\mathit{ikz}}{u}_1(z,k)-\frac{1}{ik}\right)\\ =u_1(z,k){\overline{\partial }}_{\text{z}}(e^{-\mathit{ikz}})+e^{-\mathit{ikz}}{\overline{\partial }}_{\text{z}}{u}_1(z,k)\\ =e^{-\mathit{ikz}}{\overline{\partial }}_{\text{z}}{u}_1(z,k).\end{array}$$ (33)

Thus, we can equivalently rewrite (19) and (20), respectively, as

$${\gamma }^{1/2}(z){\partial }_{\text{z}}{u}_1(z,k)=e^{\mathit{ikz}}{M}_{11}(z,k)={\mathrm{\Psi }}_{11}(z,k)$$ (34)

$${\gamma }^{1/2}(z){\overline{\partial }}_{\text{z}}{u}_1(z,k)=e^{\mathit{ikz}}{M}_{21}(z,k)={\mathrm{\Psi }}_{21}(z,k).$$ (35)

In a similar manner, we can rewrite (23) and (24), respectively, as

$${\gamma }^{1/2}(z){\overline{\partial }}_{\text{z}}{u}_2(z,k)=e^{-ik\overline{z}}{M}_{22}(z,k)={\mathrm{\Psi }}_{22}(z,k)$$ (36)

$${\gamma }^{1/2}(z){\partial }_{\text{z}}{u}_2(z,k)=e^{-ik\overline{z}}{M}_{12}(z,k)={\mathrm{\Psi }}_{12}(z,k).$$ (37)

Useful boundary integral equations for the traces of u₁ and u₂ can be derived under the additional assumption that γ ∈ W^2,p and u₁, u₂ ∈ W^2,p, p > 1. The following proposition shows a relationship between the exponentially growing solutions ψ_S(z, k) (when they exist) to the Schrödinger equation

$$(-\mathrm{\Delta }+q_S(z)){\psi }_S(z,k)=0,$$ (38)

and the CGO solutions u₁ and u₂ to (1). The solution ψ_S to (38), where q_S is complex, is asymptotic to e^ikz in the sense that

$$w_S\equiv e^{-\mathit{ikz}}{\psi }_S(·,k)-1\in L^{\overline{p}}\cap L^{\infty },$$

where $\frac{1}{\stackrel{\sim }{p}}=\frac{1}{p}-\frac{1}{2}$ and 1 < p < 2. The question of the existence of a unique solution to (38) is addressed for real γ in [44], where it is shown to exist if and (roughly) only if $q_S=\frac{\mathrm{\Delta }{\gamma }^{1/2}}{{\gamma }^{1/2}}$. The solutions ψ_S will be used to derive the boundary integral equations for u₁ and u₂, but not in the direct reconstruction algorithm.

Lemma 2.3

Let γ(z) = σ(z) + iωε(z) ∈ W^2,p(Ω), with p > 2 such that σ and ε satisfy (3) and (4), and let γ(z) − 1 have compact support in W^1,p(Ω). Let u₁ be the exponentially growing solution to the admittivity equation as given in Theorem 2.2, and let ψ_S be the exponentially growing solution to the Schrödinger equation (38), when it exists. Then

$${\mathit{iku}}_1(z,k)={\gamma }^{-1/2}(z){\psi }_S(z,k).$$ (39)

Proof

From (18),

$$\begin{array}{l}{\mathit{iku}}_1(z,k)=e^{\mathit{ikz}}(1+{\mathit{ikw}}_1(z,k))\\ =e^{\mathit{ikz}}{\gamma }^{-1/2}(z)\left[{\gamma }^{1/2}(z)+{\gamma }^{1/2}(z){\mathit{ikw}}_1(z,k)\right]\\ =e^{\mathit{ikz}}{\gamma }^{-1/2}(z)\left(1+\left[{\gamma }^{1/2}(z)-1\right]+{\gamma }^{1/2}(z){\mathit{ikw}}_1(z,k)\right)\end{array}$$

satisfies the admittivity equation with [γ^1/2(z)−1]+γ^1/2(z)ikw₁(z, k) ∈ W^1,r(Ω) for r > 2. We also know that when it exists,

$${\gamma }^{-1/2}(z){\psi }_S(z,k)=e^{\mathit{ikz}}{\gamma }^{-1/2}(z)(1+w_S(z,k))$$ (40)

is also a solution to the admittivity equation with w_S(z, k) ∈ W^1,p̄ (ℝ²). Hence, these exponentially growing solutions must be equal.

Lemma 2.4

Let γ(z) = σ(z) + iωε(z) ∈ W^2,p(Ω), with p > 2 such that σ and ε satisfy (3) and (4), and let γ(z) − 1 have compact support in W^1,p(Ω). Let u₂ be the exponentially growing solution to the admittivity equation as given in Theorem 2.3, and let ψ_S be the exponentially growing solution to the Schrödinger equation (38), when it exists. Then

$$-{\mathit{iku}}_2(z,k)={\gamma }^{-1/2}(-\overline{z}){\psi }_S(-\overline{z},k).$$ (41)

Proof

From (22),

$$\begin{array}{l}-{\mathit{iku}}_2(z,k)=e^{-ik\overline{z}}(1-{\mathit{ikw}}_2(z,k))\\ =e^{-ik\overline{z}}{\gamma }^{-1/2}(-\overline{z})\left(1+\left[{\gamma }^{1/2}(-\overline{z})-1\right]-{\gamma }^{1/2}(-\overline{z}){\mathit{ikw}}_2(z,k)\right)\end{array}$$

satisfies the admittivity equation with [γ^1/2(−z̄) − 1] − γ^1/2(−z̄)ikw₂(z, k) ∈ W^1,r(Ω) for r > 2. From (40),

$${\gamma }^{1/2}(-\overline{z}){\psi }_S(-\overline{z},k)=e^{-ik\overline{z}}{\gamma }^{1/2}(-\overline{z})(1+w_S(-\overline{z},k))$$

satisfies the admittivity equation with w_S(−z̄, k) ∈ W^1,p̄(ℝ²). Thus, these exponentially growing solutions must be equal, and so

$$-{\mathit{iku}}_2(z,k)={\gamma }^{-1/2}(-\overline{z}){\psi }_S(-\overline{z},k).$$

Let us recall some terminology arising from [44] before establishing boundary integral equations involving the exponentially growing solutions. Let Λ_σ be the Dirichlet-to-Neumann map when Ω contains the conductivity distribution σ, and Λ₁ is the Dirichlet-to-Neumann map for a homogeneous conductivity equal to 1. The Faddeev Green’s function G_k(z) is defined by

$$G_k(z):=e^{ik·z}{g}_k(z),-\mathrm{\Delta }{G}_k=\delta ,$$ (42)

where

$$g_k(z):=\frac{1}{{(2\pi )}^2}{\int }_{{\mathbb{R}}^2}\frac{e^{iz·\xi }}{\xi (\overline{\xi }+2k)}d\xi ,(-\mathrm{\Delta }-4ik\overline{\partial })g_k=\delta ,$$ (43)

for k ∈ ℂ\{0}. In the real-valued case γ = σ, the trace of the function ψ_S(·, k) on ∂Ω satisfies the integral equation [44]

$${\psi }_S(z,k)=e^{\mathit{ikz}}-{\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{\sigma }-{\mathrm{\Lambda }}_1){\psi }_S(\zeta ,k)dS(\zeta ),z\in \partial \mathrm{\Omega },$$ (44)

where k ∈ ℂ\{0}. The equation (44) is a Fredholm equation of the second kind and uniquely solvable in H^1/2(∂Ω) for any k ∈ ℂ\{0}.

The boundary integral equations for u₁ and u₂ are similar to (44).

Theorem 2.4

Let γ ∈ W^2,p(Ω) for p > 1 and suppose γ = 1 in a neighborhood of ∂Ω. Suppose σ and ε satisfy (3) and (4), and let γ(z) − 1 have compact support in W^2,p(Ω). Then for any nonexceptional k ∈ ℂ\{0}, the trace of the exponentially growing solution u₁(·, k) on ∂Ω is the unique solution to

$$u_1(z,k)=\frac{e^{\mathit{ikz}}}{ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u_1(\zeta ,k)dS(\zeta ),z\in \partial \mathrm{\Omega }.$$ (45)

Proof

Let $\frac{1}{p}=\frac{1}{r}-\frac{1}{2}$, where 1 < r < 2 and p > 2. Let {γ_n}_n∈N ⊂ W^{2, r}(Ω) be a sequence converging to γ ∈ W^1,p(Ω). Then by the Sobolev Embedding Theorem, {γ_n}_n∈ℕ ⊂ W^1,r (Ω). Let ψ_n be the exponentially growing solutions to the Schrödinger equation with potential ${\gamma }_n^{-1/2}\mathrm{\Delta }{\gamma }_n^{1/2}$, and uⁿ be the CGO solutions defined by Theorem 2.2 to the admittivity equation with admittivity γ_n. Then for each n ∈ ℕ, the complex γ version of (44) holds for nonexceptional k ∈ ℂ\{0}

$${\psi }_n(z,k){\mid }_{\partial \mathrm{\Omega }}=e^{\mathit{ikz}}{\mid }_{\partial \mathrm{\Omega }}-{\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{{\gamma }_n}-{\mathrm{\Lambda }}_1){\psi }_n(\zeta ,k)dS(\zeta ),$$ (46)

where γ_n = 1 in the neighborhood of ∂Ω.

It follows by (39) that for each complex number k ≠ 0, and for each n ∈ ℕ

$$\frac{{{\gamma }_n}^{-1/2}(z)}{ik}{\psi }_n(z,k)=u^n(z,k)\to u_1(z,k)\text{in}{H}^{1/2}(\partial \mathrm{\Omega }).$$ (47)

We claim that for each n, uⁿ satisfies (45). To see this, by (39), for z ∈ ∂Ω,

$$\begin{array}{l}\frac{e^{\mathit{ikz}}}{ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u^n(\zeta ,k)dS(\zeta )\\ =\frac{e^{\mathit{ikz}}}{ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)\frac{{\gamma }_n^{-1/2}(\zeta )}{ik}{\psi }_n(\zeta ,k)dS(\zeta )\\ =\frac{{\gamma }_n^{-1/2}(z)}{ik}{\psi }_n(z,k)\\ =u^n(z,k),\end{array}$$ (48)

where we used the fact that γ_n = 1 in a neighborhood of ∂Ω. Thus, uⁿ satisfies (45) for each n ∈ ℕ.

We know by Theorem 3.1 of [21] that M(z, k) depends continuously on γ. From (47), we can conclude that

$${\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{{\gamma }_n}-{\mathrm{\Lambda }}_1)u^n(\zeta ,k)dS(\zeta )\mapsto {\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u_1(\zeta ,k)dS(\zeta ).$$ (49)

Thus, by (47), (48), and (49), we have that u₁(·, k)|_∂Ω satisfies (45). The uniqueness of u₁(·, k)|_∂Ω follows by Theorem 2.2.

An analogous theorem holds for u₂.

Theorem 2.5

Let γ ∈ W^2,p(Ω) for p > 1 and suppose γ = 1 in a neighborhood of ∂Ω. Suppose σ and ε satisfy (3) and (4), and let γ(z) − 1 have compact support in W^2,p(Ω). Then for any nonexceptional k ∈ ℂ\{0}, the trace of the exponentially growing solution u₂(·, k) on ∂Ω is the unique solution to

$$u_2(z,k)=\frac{e^{-ik\overline{z}}}{-ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}+\overline{\zeta })({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u_2(\zeta ,k)dS(\zeta ),z\in \partial \mathrm{\Omega }.$$ (50)

Proof

Let p, r, {γ_n}_n∈N ⊂ W^2,r(Ω), and ψ_n be as in the proof of Theorem 2.4. Let uⁿ be the CGO solutions defined in Theorem 2.3 to the admittivity equation with admittivity γ_n. Then for each n ∈ ℕ, for nonexceptional k ∈ ℂ\{0}, evaluating (46) at −z̄,

$${\psi }_n(-\overline{z},k){\mid }_{\partial \mathrm{\Omega }}=e^{-ik\overline{z}}{\mid }_{\partial \mathrm{\Omega }}-{\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}-\zeta )({\mathrm{\Lambda }}_{{\gamma }_n}-{\mathrm{\Lambda }}_1){\psi }_n(\zeta ,k)dS(\zeta ),$$ (51)

where γ_n = 1 in a neighborhood of ∂Ω.

It follows by (41) that for each complex number k ≠ 0, and for each n ∈ ℕ

$$\frac{{{\gamma }_n}^{-1/2}(-\overline{z})}{-ik}{\psi }_n(-\overline{z},k)=u^n(z,k)\to u_2(z,k)\text{in}{H}^{1/2}(\partial \mathrm{\Omega }).$$ (52)

We claim that for each n, uⁿ satisfies (50). To see this, by (41), for z ∈ ∂Ω,

$$\begin{array}{l}\frac{e^{-ik\overline{z}}}{-ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}+\overline{\zeta })({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u^n(\zeta ,k)dS(\zeta )\\ =\frac{e^{-ik\overline{z}}}{-ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}+\overline{\zeta })({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)\frac{{\gamma }_n^{-1/2}(-\overline{\zeta })}{-ik}{\psi }_n(-\overline{\zeta },k)dS(\zeta )\\ =\frac{e^{-ik\overline{z}}}{-ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}-\overline{\zeta })({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)\frac{{\gamma }_n^{-1/2}(\stackrel{\sim }{\zeta })}{-ik}{\psi }_n(\stackrel{\sim }{\zeta },k)dS(\stackrel{\sim }{\zeta })\\ =\frac{{\gamma }_n^{-1/2}(-\overline{z})}{-ik}{\psi }_n(-\overline{z},k)\\ =u^n(z,k),\end{array}$$ (53)

using the change of variables −ζ̄ ↦ ζ̄ and the fact that γ_n = 1 in a neighborhood of ∂Ω. Thus, uⁿ satisfies (50) for each n ∈ ℕ.

We know by Theorem 3.1 of [21] that M(z, k) depends continuously on γ. From (52), we can conclude that

$${\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}+\overline{\zeta })({\mathrm{\Lambda }}_{{\gamma }_n}-{\mathrm{\Lambda }}_1)u^n(\zeta ,k)dS(\zeta )\mapsto {\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}+\overline{\zeta })({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u_2(\zeta ,k)dS(\zeta ).$$ (54)

Thus, by (52), (53), and (54), we have that u₂(·, k)|_∂Ω satisfies (50). The uniqueness of u₂(·, k)|_∂Ω follows by Theorem 2.3.

2.2 The Scattering Transform Matrix

The scattering transform S_γ(k) of the matrix potential Q_γ is defined in [21] by

$$S_{\gamma }(k)=\frac{i}{\pi }{\int }_{{\mathbb{R}}^2}\left(\begin{array}{cc}0& Q_{12}(z)e(z,-\overline{k})M_{22}(z,k)\\ -Q_{21}(z)e(z,k)M_{11}(z,k)& 0\end{array}\right)d\mu (z),$$ (55)

where e(z, k) = exp{i(zk + z̄k̄)}. Thus we are only concerned with computing the off-diagonal entries of S_γ, which we will denote by S₁₂(k) and S₂₁(k).

Boundary integral formulas for the off-diagonal entries of S_γ(k) in (55) can be computed by integration by parts as follows

$$\begin{array}{l}{S}_{12}(k)=\frac{i}{\pi }{\int }_{\mathrm{\Omega }}{Q}_{12}(z)e^{-i\overline{k}z}{\mathrm{\Psi }}_{22}(z,k)d\mu (z)\\ =\frac{i}{\pi }{\int }_{\mathrm{\Omega }}{e}^{-i\overline{k}z}{\overline{\partial }}_{\text{z}}{\mathrm{\Psi }}_{12}(z,k)d\mu (z)\\ =\frac{i}{2\pi }{\int }_{\partial \mathrm{\Omega }}{e}^{-i\overline{k}z}{\mathrm{\Psi }}_{12}(z,k)({\nu }_1+i{\nu }_2)dS(z)-\frac{i}{\pi }{\int }_{\mathrm{\Omega }}{\overline{\partial }}_{\text{z}}{e}^{-i\overline{k}z}{\mathrm{\Psi }}_{12}(z,k)d\mu (z)\\ =\frac{i}{2\pi }{\int }_{\partial \mathrm{\Omega }}{e}^{i\overline{k}z}{\mathrm{\Psi }}_{12}(z,k)({\nu }_1+i{\nu }_2)dS(z)\end{array}$$ (56)

and similarly,

$$S_{21}(k)=-\frac{i}{2\pi }{\int }_{\partial \mathrm{\Omega }}{e}^{i\overline{k}\overline{z}}{\mathrm{\Psi }}_{21}(z,k)({\nu }_1-i{\nu }_1)dS(z),$$ (57)

where ν = ν₁ + iν₂ denotes the outward unit normal to the boundary ∂Ω.

Theorem 2.6

The trace of the exponentially growing solutions Ψ₁₂(z, k) and Ψ₂₁(z, k) for k ∈ ℂ\{0} can be determined by

$${\mathrm{\Psi }}_{12}(z,k)={\int }_{\partial \mathrm{\Omega }}\frac{e^{i\overline{k}(z-\zeta )}}{4\pi (z-\zeta )}[{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_2(\zeta ,k)dS(\zeta )$$ (58)

$${\mathrm{\Psi }}_{21}(z,k)={\int }_{\partial \mathrm{\Omega }}\overline{\left[\frac{e^{ik(z-\zeta )}}{4\pi (z-\zeta )}\right]}[{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_1(\zeta ,k)dS(\zeta ),$$ (59)

where u₁ and u₂ are calculated via equations (45) and (50) respectively.

Proof

We use the relations in (35) and (37) to obtain boundary integral equations for Ψ₂₁ and Ψ₁₂ for z ∈ ∂Ω from Equations (45) and (50), respectively. Let us begin with Ψ₁₂:

$$\begin{array}{l}{\mathrm{\Psi }}_{12}(z,k)={\gamma }^{1/2}(z){\partial }_{\text{z}}{u}_2(z,k)\\ ={\gamma }^{1/2}(z){\partial }_{\text{z}}\left[\frac{e^{-ik\overline{z}}}{-ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}+\overline{\zeta })[{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_2(\zeta ,k)dS(\zeta )\right]\\ =-{\gamma }^{1/2}(z){\int }_{\partial \mathrm{\Omega }}{\partial }_{\text{z}}[G_k(-\overline{z}+\overline{\zeta })][{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_2(\zeta ,k)dS(\zeta ).\end{array}$$ (60)

Similarly,

$$\begin{array}{l}{\mathrm{\Psi }}_{21}(z,k)={\gamma }^{1/2}(z){\overline{\partial }}_{\text{z}}{u}_1(z,k)\\ ={\gamma }^{1/2}(z){\overline{\partial }}_{\text{z}}\left[\frac{e^{\mathit{ikz}}}{ik}-{\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )[{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_1(\zeta ,k)dS(\zeta )\right]\\ =-{\gamma }^{1/2}(z){\int }_{\partial \mathrm{\Omega }}{\overline{\partial }}_{\text{z}}[G_k(z-\zeta )][{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_1(\zeta ,k)dS(\zeta ).\end{array}$$ (61)

A thorough study of the properties of the Faddeev Green’s function G_k and its derivatives is given in [47]. The calculations for the specific derivatives needed here are shown below. By the definition of G_k (42)

$${\partial }_{\text{z}}{G}_k(-\overline{z}+\overline{\zeta })={\partial }_{\text{z}}\left[e^{ik(-\overline{z}+\overline{\zeta })}{g}_k(-\overline{z}+\overline{\zeta })\right]=e^{ik(-z+\overline{\zeta })}{\partial }_{\text{z}}{g}_k(-\overline{z}+\overline{\zeta }).$$ (62)

Using the definition of g_k (43),

$$\begin{array}{l}{\partial }_{\text{z}}{g}_k(-\overline{z}+\overline{\zeta })={\partial }_{\text{z}}\frac{1}{{(2\pi )}^2}{\int }_{{\mathbb{R}}^2}\frac{e^{i(-\overline{z}+\overline{\zeta })·\xi }}{\xi (\overline{\xi }+2k)}d\xi \\ =\frac{1}{{(2\pi )}^2}{\int }_{{\mathbb{R}}^2}\frac{{\partial }_{\text{z}}\left[e^{-(i/2)(\overline{z}\overline{\xi }+z\xi )}\right]e^{i\overline{\zeta }·\xi }}{\xi (\overline{\xi }+2k)}d\xi \\ =\frac{1}{{(2\pi )}^2}{\int }_{{\mathbb{R}}^2}\frac{(i\xi /2)e^{i(-\overline{z}+\overline{\zeta })·\xi }}{\xi (\overline{\xi }+2k)}d\xi \\ =\frac{e^{i(-\overline{z}+\overline{\zeta })·(-2\overline{k})}}{4}\frac{1}{{(2\pi )}^2}{\int }_{{\mathbb{R}}^2}\frac{2e^{i(-\overline{z}+\overline{\zeta })·(\xi +2\overline{k})}}{i\left(\overline{\xi +2\overline{k}}\right)}d\xi \\ =\frac{e^{i(-\overline{z}+\overline{\zeta })·(-z\overline{k})}}{4\pi \left(\overline{-\overline{z}+\overline{\zeta }}\right)}\\ =-\frac{e^{-ik(-\overline{z}+\overline{\zeta })}{e}^{-i\overline{k}(-z+\zeta )}}{4\pi (z-\zeta )}\end{array}$$ (63)

by the definition of the inverse Fourier transform and the well known result

$${\mathcal{F}}^{-1}{\left\{\frac{2}{i\overline{\xi }}\right\}}^{\wedge }(z)-\frac{1}{\pi \overline{z}}.$$

Therefore, by (62) and (63)

$${\partial }_{\text{z}}{G}_k(-\overline{z}+\overline{\zeta })=-\frac{e^{i\overline{k}(z-\zeta )}}{4\pi (z-\zeta )}.$$ (64)

The ∂̄_z derivative for Ψ₂₁ is calculated in a similar manner,

$${\overline{\partial }}_{\text{z}}{G}_k(z-\zeta )=-\overline{\left[\frac{e^{ik(z-\zeta )}}{4\pi (z-\zeta )}\right]}.$$ (65)

Substituting the representations for ∂_z G_k(−z̄ + ζ̄) and ∂̄_z G_k(z − ζ), given in (64) and (65), back into the equations for Ψ₁₂ and Ψ₂₁, given in (60) and (61) respectively, proves the theorem.

2.3 From S(k) to M

The dependence of M on the complex parameter k is related to the scattering transform through the following ∂̄_k system.

Theorem 2.7 (Theorem 4.1 [21])

Let σ and ε satisfy (3) and (4) and let M be the unique solution to (11) satisfying (10). The map k → M(·, k) is differentiable as a map into $L_{-\beta }^r$, and satisfies the equation

$${\overline{\partial }}_{k}M(z,k)=M(z,\overline{k})\left(\begin{array}{cc}e(z,\overline{k})& 0\\ 0& e(z,-k)\end{array}\right)S_{\gamma }(k),$$ (66)

where

$$S_{\gamma }(k)=\frac{i}{\pi }{\int }_{{\mathbb{R}}^2}\left(\begin{array}{cc}e(z,-\overline{k})& 0\\ 0& -e(z,k)\end{array}\right){(Q_{\gamma }M)}^{\mathit{off}}(z,k)d\mu (z).$$ (67)

Moreover, for every p > 2,

$$\underset{k}{sup}{\left|\right|M(z,·)-I\left|\right|}_{L^p({\mathbb{R}}^2)}\le K_2,$$

where K₂ depends on β, σ₀, Ω, and p.

Notice that Equation (66) can be written as the following two systems of equations:

$$\{\begin{array}{cc}{\overline{\partial }}_k{M}_{11}(z,k)=& M_{12}(z,\overline{k})e(z,-k)S_{21}(k)\\ {\overline{\partial }}_k{M}_{12}(z,k)=& M_{11}(z,\overline{k})e(z,\overline{k})S_{12}(k)\end{array},$$ (68)

and

$$\{\begin{array}{cc}{\overline{\partial }}_k{M}_{21}(z,k)=& M_{22}(z,\overline{k})e(z,-k)S_{21}(k)\\ {\overline{\partial }}_k{M}_{22}(z,k)=& M_{21}(z,\overline{k})e(z,\overline{k})S_{12}(k)\end{array},$$ (69)

included for the reader’s convenience.

2.4 From M to γ

Theorem 2.8 (Theorem 6.2 [21])

For any ρ > 0,

$$Q_{\gamma }(z)=\underset{k_0\to \infty }{lim}\mu {(B_{\rho }(0))}^{-1}{\int }_{\{k:\mid k-k_0\mid <\rho \}}{D}_{k}M(z,k)d\mu (k).$$ (70)

This provides a reconstruction formula for the entries of Q_γ, and one can recover γ from $Q_{12}=-\frac{1}{2}{\partial }_{\text{z}}log(\gamma )$ or $Q_{21}=-\frac{1}{2}{\overline{\partial }}_{\text{z}}log(\gamma )$. However, this formula is computationally impractical as it requires a large k limit of integrals involving ∂̄_z and ∂_z derivatives of M(z, k).

We have derived computationally advantageous formulas for recovering the entries of Q_γ that only require knowledge of the CGO solutions at k = 0. Theorem 2.9 provides this direct relation between the CGO solutions M(z, 0) (from the ∂̄_k equation (66)) and the matrix potential Q_γ(z), eliminating the large k limit required in equation (70) above.

Theorem 2.9

The entries of the potential matrix Q_γ(z) defined in (5) can be calculated using only knowledge of the CGO solutions M(z, 0) via

$$Q_{12}(z)=\frac{{\overline{\partial }}_{\text{z}}{M}_{+}(Q_{\gamma },z,0)}{M_{-}(Q_{\gamma },z,0)}$$ (71)

$$Q_{21}(z)=\frac{{\partial }_{\text{z}}{M}_{-}(Q_{\gamma },z,0)}{M_{+}(Q_{\gamma },z,0)}.$$ (72)

where,

$$M_{+}(Q_{\gamma },z,k)=M_{11}(Q_{\gamma },z,k)+e(z,-k)M_{12}(Q_{\gamma },z,k)$$ (73)

$$M_{-}(Q_{\gamma },z,k)=M_{22}(Q_{\gamma },z,k)+e(z,k)M_{21}(Q_{\gamma },z,k).$$ (74)

Proof

We follow an idea similar to that in [5] and define

$$M_{+}(Q_{\gamma },z,k)=M_{11}(Q_{\gamma },z,k)+e(z,-k)M_{12}(Q_{\gamma },z,k)$$ (75)

$$M_{-}(Q_{\gamma },z,k)=M_{22}(Q_{\gamma },z,k)+e(z,k)M_{21}(Q_{\gamma },z,k).$$ (76)

Note that M₊ and M₋ are only dependent on the Q_γ matrix, not $-Q_{\gamma }^T$ as is required in [5]. Therefore,

$$\begin{array}{l}{\overline{\partial }}_{\text{z}}{M}_{+}(Q_{\gamma },z,k)=Q_{12}(z)e(z,-k)[M_{-}(Q_{\gamma },z,k)=+i(k-\overline{k})M_{12}(Q_{\gamma },z,k)]\\ {\partial }_{\text{z}}{M}_{-}(Q_{\gamma },z,k)=Q_{21}(z)e(z,k)M_{+}(Q_{\gamma },z,k),\end{array}$$

so that

$$\begin{array}{l}{\overline{\partial }}_{\text{z}}{M}_{+}(Q_{\gamma },z,0)=Q_{12}(z)M_{-}(Q_{\gamma },z,0)\\ {\partial }_{\text{z}}{M}_{-}(Q_{\gamma },z,0)=Q_{21}(z)M_{+}(Q_{\gamma },z,0).\end{array}$$

One can then reconstruct the log of the admittivity γ from either Q₁₂ or Q₂₁ by inverting the ∂_z or ∂̄_z operator respectively, and exponentiate to recover explicitly

$$log(\gamma (z))=-\frac{2}{\pi }{\int }_{\mathbb{C}}\frac{Q_{12}(\zeta )}{\overline{z}-\zeta }d\mu (\zeta )=-\frac{2}{\pi }{\int }_{\mathbb{C}}\frac{Q_{21}(\zeta )}{z-\zeta }d\mu (\zeta ).$$ (77)

2.5 The steps of the algorithm

We now have all the necessary steps for a direct reconstruction algorithm:

1. Compute the exponentially growing solutions u₁(z, k) and u₂(z, k) to the admittivity equation from the boundary integral formulas (45) and (50)

   $$\begin{array}{l}{u}_1(z,k){\mid }_{\partial \mathrm{\Omega }}={\frac{e^{\mathit{ikz}}}{ik}|}_{\partial \mathrm{\Omega }}-{\int }_{\partial \mathrm{\Omega }}{G}_k(z-\zeta )({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u_1(\zeta ,k)dS(\zeta )\\ u_2(z,k){\mid }_{\partial \mathrm{\Omega }}={\frac{e^{ik\overline{z}}}{-ik}|}_{\partial \mathrm{\Omega }}-{\int }_{\partial \mathrm{\Omega }}{G}_k(-\overline{z}+\overline{\zeta })({\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1)u_2(\zeta ,k)dS(\zeta ).\end{array}$$
2. Compute the off diagonal entries of the CGO solution Ψ(z, k) for z ∈ ∂Ω from the boundary integral formulas (58) and (59)

   $$\begin{array}{l}{\mathrm{\Psi }}_{12}(z,k)={\int }_{\partial \mathrm{\Omega }}\frac{e^{i\overline{k}(z-\zeta )}}{4\pi (z-\zeta )}[{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_2(\zeta ,k)dS(\zeta )\\ {\mathrm{\Psi }}_{21}(z,k)={\int }_{\partial \mathrm{\Omega }}\overline{\left[\frac{e^{ik(z-\zeta )}}{4\pi (z-\zeta )}\right]}[{\mathrm{\Lambda }}_{\gamma }-{\mathrm{\Lambda }}_1]u_1(\zeta ,k)dS(\zeta ).\end{array}$$
3. Compute the off-diagonal entries of the scattering matrix S_γ(k) from (56) and (57)

   $$\begin{array}{l}{S}_{12}(k)=\frac{i}{2\pi }{\int }_{\partial \mathrm{\Omega }}{e}^{-i\overline{k}z}{\mathrm{\Psi }}_{12}(z,k)({\nu }_1+i{\nu }_2)dS(z)\\ S_{21}(k)=-\frac{i}{2\pi }{\int }_{\partial \mathrm{\Omega }}{e}^{i\overline{k}\overline{z}}{\mathrm{\Psi }}_{21}(z,k)({\nu }_1-i{\nu }_2)dS(z).\end{array}$$
4. Solve the ∂̄_k equation (66) for the matrix M(z, k)

   $${\overline{\partial }}_{k}M(z,k)=M(z,\overline{k})\left(\begin{array}{cc}e(z,\overline{k})& 0\\ 0& e(z,-k)\end{array}\right)S_{\gamma }(k).$$

5. Reconstruct Q_γ from Theorem 2.9 and use (77) to compute γ.

3 Numerical Implementation

In this section, we describe the implementation of the algorithm. Greater detail of the numerical methods and validations of the computations for admittivity distributions with twice differentiable real and imaginary parts can be found in [26], where the solution to the forward problem (11) is computed and used to validate formulas (58) an (59), as well as computations of the scattering transform. In this work, we consider examples with discontinuities at the organ boundaries.

3.1 Computation of the DN map

An approximation to the DN map was computed by simulating voltage data by the finite element method (FEM), and then computing a matrix approximation to the map by computing the inner product of the applied currents with the voltages. This approximation to the DN map has been discussed, for example, in [28, 18, 40]. It can be formed analogously in the complex case.

Gaussian white noise was added independently to the real and imaginary parts of the simulated voltages for each current pattern by adding a random vector of amplitude η > 0 multiplied by the maximum voltage value for that current pattern and real or imaginary component to the computed voltages. We consider noise levels η = 0 and η = 0.0001, which corresponds to 0.01% noise, the published level of the ACT 3 system [19], which applies the trigonometric current patterns used in the simulations here.

3.2 Computation of the CGO solutions and S_γ(k)

The CGO solutions on the boundary of Ω were computed for each k in a grid [−K, K]² in the complex plane. The choice of K, which serves as a cut-off frequency, was determined by the behavior of the scattering transforms S₁₂ and S₂₁. As in [40] for the D-bar algorithm for conductivity reconstructions, the cutoff frequency K has a regularizing effect, and was chosen here empirically to balance smoothing and numerical error. We do not address the selection of K by more sophisticated means in this work.

3.2.1 Computation of u₁ and u₂

A boundary integral equation of the form (45) was solved in [18] and [40]. In this work, as in [18], we employ an approximation to the Faddeev’s Green’s function G_k that allows for very rapid computation of u₁ and u₂ from (45) and (50) respectively. Namely, G_k is approximated by the fundamental solution for the Laplacian

$$G_0(z)=\frac{1}{2\pi }log\mid z\mid .$$

Denoting the solutions to (45), (50) by $u_1^0$ and $u_2^0$, respectively, the convolution integrals

$$\begin{array}{l}{u}_1^0(z,k){\mid }_{\partial \mathrm{\Omega }}={\frac{e^{\mathit{ikz}}}{ik}|}_{\partial \mathrm{\Omega }}-{\int }_{\partial \mathrm{\Omega }}{G}_0(z-\zeta )({\mathrm{\Lambda }}_{\gamma }-{\gamma }_1)u_1^2(\zeta ,k)dS(\zeta )\\ u_2^0(z,k){\mid }_{\partial \mathrm{\Omega }}={\frac{e^{-ik\overline{z}}}{-ik}|}_{\partial \mathrm{\Omega }}-{\int }_{\partial \mathrm{\Omega }}{G}_0(-\overline{z}+\overline{\zeta })({\mathrm{\Lambda }}_{\gamma }-{\gamma }_1)u_2^0(\zeta ,k)dS(\zeta )\end{array}$$

were computed for z = z_ℓ, the center of the ℓth electrode, via Simpson’s rule, and G₀ was set to 0 when ζ = z_ℓ. Note that by the definition of G₀, G₀(z − ζ) = G₀(−z̄ + ζ̄).

3.2.2 Computation of Ψ₁₂ and Ψ₂₁

The boundary integral formulas (58) and (59) for Ψ₁₂ and Ψ₂₁, respectively, require knowledge of [Λ_γ − Λ₁] u_j(ζ, k) for j = 1, 2, with ζ ∈ ∂Ω, and k ∈ ℂ\{0}. These values are already computed during the evaluation of u₁ and u₂ via (45) and (50). Therefore, we merely recall those values and approximate the boundary integral using a finite sum. One should note that G₀(z − ζ), ∂̄_z G_k(z − ζ), and ∂_z G_k(−z̄ + ζ̄) are all undefined for z = ζ. We removed these points in the computation by setting their values to zero.

3.2.3 Computation of the scattering transform

The off-diagonal entries of the scattering transform matrix, namely S₁₂(k) and S₂₁(k), were computed inside the square [−K, K]² (with k = 0 not included since the formulas for the CGO solutions do not hold for k = 0). We compute S₁₂(k) and S₂₁(k) using a finite sum approximation to (56) and (57):

$$\begin{array}{l}{S}_{12}(k)\approx \frac{i}{L}\sum _{\ell =1}^L{e}^{-i\overline{k}{z}_{\ell }}{\mathrm{\Psi }}_{12}(z_{\ell },k)z_{\ell }\\ S_{21}(k)\approx -\frac{i}{L}\sum _{\ell =1}^L{e}^{-i\overline{k}\overline{z_{\ell }}}{\mathrm{\Psi }}_{21}(z_{\ell },k)\overline{z_{\ell }},\end{array}$$

where z_l denotes the coordinate of the ℓ^th equally spaced electrode around ∂Ω (in this case the unit circle).

3.3 Solution of the system of D-bar equations

The two systems of ∂̄_k equations (68) and (69) can be written as the convolutions

$$\{\begin{array}{cc}1=& M_{11}(z,k)-\frac{1}{\pi k}\ast (M_{12}(z,\overline{k})e(z,-k)S_{21}(k))\\ 0=& M_{12}(z,k)-\frac{1}{\pi k}\ast (M_{11}(z,\overline{k})e(z,\overline{k})S_{12}(k))\end{array},$$ (78)

and

$$\{\begin{array}{cc}1=& M_{22}(z,k)-\frac{1}{\pi k}\ast (M_{21}(z,\overline{k})e(z,\overline{k})S_{21}(k))\\ 0=& M_{12}(z,k)-\frac{1}{\pi k}\ast (M_{22}(z,\overline{k})e(z,-k)S_{21}(k))\end{array}.$$ (79)

A numerical solver for equations of the form

$${\overline{\partial }}_{k}v(k)=T(k)\overline{v(k)}.$$

was developed in [36] for the inverse conductivity problem. The solver is based on the fast method by Vainikko [37] that uses FFT’s for solving integral equations with weakly singular kernels.

In this work, we must solve the systems of equations (78) and (79) rather than a single equation. Furthermore, the unknowns M(z, k) are not conjugated, but instead the argument k is conjugated. To address this, we interpolated the scattering data S_γ, computed above in Section 3.2.3, to a new k-grid that includes the origin k = 0 at the center and has an odd number of grid points in both the horizonal and vertical directions. We solve the systems (78) and (79) on this new k-grid using appropriate flip operations to ensure that we access the correct entries in the matrix corresponding to M(z, k̄).

To perform the convolution we used Fourier transforms as follows:

$$\begin{array}{l}\frac{1}{\pi k}\ast (M_{12}(z,\overline{k})e(z,-k)S_{21}(k))\\ =h_{\kappa }^2\text{IFFT}\left(\text{FFT}\left(\frac{1}{\pi k}\right)·\text{FFT}(M_{12}(z,\overline{k})e(z,-k)S_{21}(k))\right),\end{array}$$

and similarly

$$\begin{array}{l}\frac{1}{\pi k}\ast (M_{11}(z,\overline{k})e(z,\overline{k})S_{12}(k))\\ =h_{\kappa }^2\text{IFFT}\left(\text{FFT}\left(\frac{1}{\pi k}\right)·\text{FFT}(M_{11}(z,\overline{k})e(z,\overline{k})S_{12}(k))\right),\end{array}$$

where h_k is the step size of the uniform k-grid of size 129 × 129, and · denotes componentwise multiplication. We used GMRES to solve the resulting linear systems for each value of z in a grid of 128 equally spaced points between [−1.1,1.1] in both the x and y directions and computed M(z, k) for all |z| ≤ 1.1. The step size in z was h_z ≈ 0.0173.

3.4 Computation of the admittivity

The admittivity is computed by solving first for Q₂₁ from (72) (note that equivalently one could use Q₁₂ from (71)), and then solving (77) for log(γ) in the Fourier domain using FFT’s. The functions M₊ and M₋ in equations (73) and (74) were evaluated using the entries of M(z, 0) recovered when solving the ∂̄_k equation (see Section 3.3 above). We used centered finite differences (with a step size of h_z ≈ 0.0173) to evaluate the ∂̄_z and ∂_z derivatives of M₊ and M₋ respectively. We then performed componentwise division to compute Q₁₂ and Q₂₁ for |z| ≤ 1.1. Finally, the computed log(γ) was exponentiated to recover γ inside the unit disk.

4 Numerical Results

We consider several test problems simulating a simplified cross-section of a human torso. In each example, the admittivity is given by γ = σ + iε. That is, the imaginary component includes the temporal angular frequency ω. Since this is a known value, there is no loss of generality in representing γ this way in the simulations. The complete electrode model (CEM), originally described in [14], was implemented in the FEM in order to solve the forward problem. The CEM takes into account both the shunting effect of the electrodes and the contact impedances between the electrodes and tissue. In our computations, Ω was chosen to be a disk of radius 0.15m, and the FEM computations were performed on a mesh with 4538 triangular elements and 32 equispaced electrodes 0.029m × 0.024m placed on the boundary. The effective contact impedance was chosen to be z = 0.0057Ωm² on all electrodes in our simulations. The current amplitude was chosen to be C = 2mA, and the applied current patterns are the trigonometric patterns

$$I_{\ell }^j=\{\begin{array}{lll}Ccos(j{\theta }_{\ell }),\hfill & 1\le \ell \le L,\hfill & 1\le j\le \frac{L}{2}\hfill \\ Csin((\frac{L}{2}-j){\theta }_{\ell }),\hfill & 1\le \ell \le L,\hfill & \frac{L}{2}+1\le j\le L-1,\hfill \end{array}$$ (80)

where ${\theta }_{\ell }=\frac{2\pi \ell }{L}$, |e_ℓ| is the area of the ℓ^th electrode, I_ℓ is the current on the ℓ^th electrode, and L denotes the total number of electrodes. As in [28, 18], the currents were normalized to have ℓ²-norm of 1, and the voltages were normalized accordingly. Also, the DN map was scaled to represent data collected on the unit disk using the relation Λ_γ,1 = rΛ_γ,r, where the second subscript represents the radius of the disk.

Where indicated, we added 0.01% Gaussian relative noise to the simulated voltages as follows. Denote the (complex-valued) vector of computed voltage for the j-th current pattern by V^j, let η = 0.0001 denote the noise level, and N a Gaussian random vector (generated by the randn commmand in MATLAB) that is unique for each use of the notation N. Denoting the noisy data by Ṽ^j we then have Ṽ^j = Re(Ṽ^j) + i Im(Ṽ^j) where

$$\begin{array}{l}Re({\stackrel{\sim }{V}}^j)=Re(V^j)+\eta max\mid Re(V^j)\mid N\\ Im({\stackrel{\sim }{V}}^j)=Im(V^j)+\eta max\mid Im(V^j)\mid N.\end{array}$$

We solve the boundary integral equations (45) and (50) for the traces of the CGO solutions u₁ and u₂ for k ∈ [−K, K]², with K varying for each test problem in this work. The solution M(z, k), to the ∂̄_k equation (66), is computed in parallel by the method described in Section 3.3. The low-pass filtering by taking k ∈ [−K, K]² results in smooth functions M_jp, j, p = 1, 2, which are differentiated by centered finite differences to recover Q₂₁, as described in Section 3.4. The admittivity γ was then computed by (77).

Define the dynamic range of the conductivity, and likewise the permittivity, by

$$\frac{max{\sigma }^{(K)}-min{\sigma }^{(K)}}{max\sigma -min\sigma }·100\%,$$ (81)

where the maximum and minimum values are taken on the computational grid for the reconstruction and σ^(K) denotes the reconstructed conductivity σ that was computed using a scattering transform computed on the truncated k grid.

4.1 Example 1

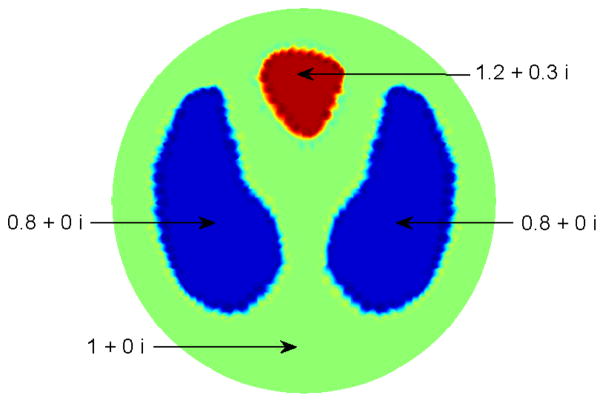
The first test problem is an idealized cross-section of a chest with a background admittivity of 1+0i. We do not include units or frequency in these examples, since our purpose is to demonstrate that the equations in this paper lead to a feasible reconstruction algorithm for complex admittivities. Reconstructions from more realistic admittivity distributions or experimental data are the topic of future work. Figure 1 shows the values of the admittivity in the simulated heart and lungs. Noise-free reconstructions with the scattering transform computed on a 128×128 grid for k ∈ [−5.5, 5.5]² are found in Figure 2. The reconstruction has a maximum conductivity and permittivity value of 1.1452 + 0.1802i, occurring in the heart region and a minimum of 0.8286 − 0.0247i, occurring in the lung region, resulting in a dynamic range of 79% for the conductivity and 60% for the permittivity when the negative permittivity value is set to 0. Although this decreases the dynamic range, we set the permittivity to 0 when it takes on a negative value in any pixel, since physically the permittivity cannot be less than 0. The reconstruction has the attributes of good spatial resolution and good uniformity in the reconstruction of the background and its value.

Figure 1.

The test problem in Example 1.

Figure 2.

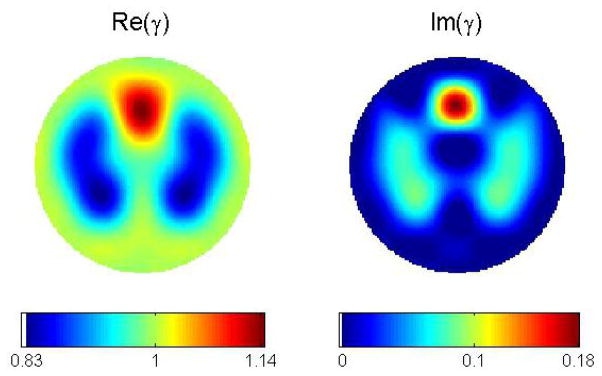
Reconstruction from noise-free data for Example 1 with the real part of γ (conductivity) on the left, and the imaginary part (permittivity) on the right. The cut-off frequency was K = 5.5. The dynamic range is 79% for the conductivity, and 60% for the permittivity.

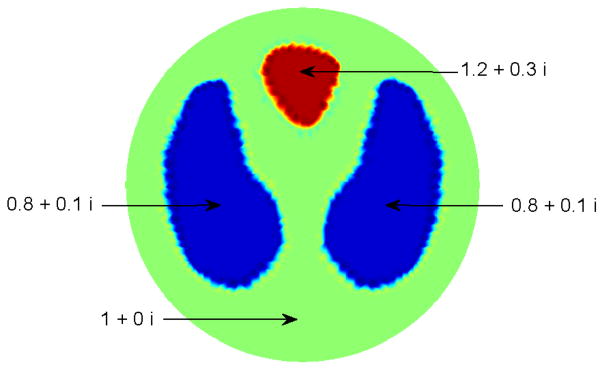
4.2 Example 2

This second example was chosen with conductivity values the same as in Example 1, but with permittivity values in which the “lungs” match the permittivity of the background. This is motivated by the fact that at some frequencies, physiological features may match that of the surrounding tissue in the conductivity or permittivity component. This example, purely for illustration, mimics that phenomenon. The admittivity values can be found in Figure 3. Noise-free reconstructions with the scattering transform computed on a 128 × 128 grid for k ∈ [−5.5, 5.5]² are found in Figure 4. The maximum value of the conductivity and permittivity occur in the heart region, 1.1429 + 0.1828i, and the minimum value of the conductivity and permittivity is 0.8271 − 0.0204i. In this example, the dynamic range is 79% for the conductivity and 61% for the permittivity when the negative permittivity value is set to 0. Again the spatial resolution is quite good, and the background is quite homogeneous, although some small artifacts are present in both the real and imaginary parts.

Figure 3.

The test problem in Example 2. Notice that in this case, the permittivity of the lungs matches the permittivity of the background, and so only the heart should be visible in the imaginary component of the reconstruction.

Figure 4.

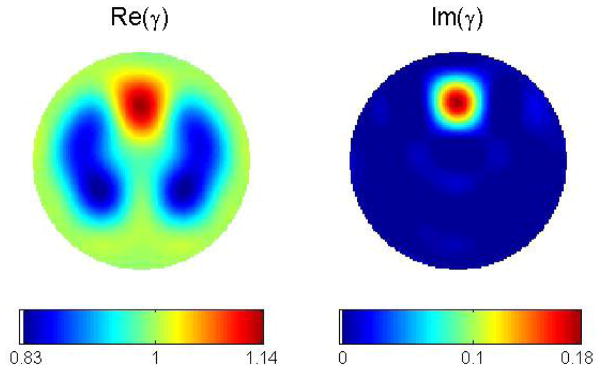
Reconstruction from noise-free data for Example 2 with the real part of γ (conductivity) on the left, and the imaginary part (permittivity) on the right. The cut-off frequency was K = 5.5. The dynamic range is 79% for the conductivity, and 61% for the permittivity.

4.3 Example 3

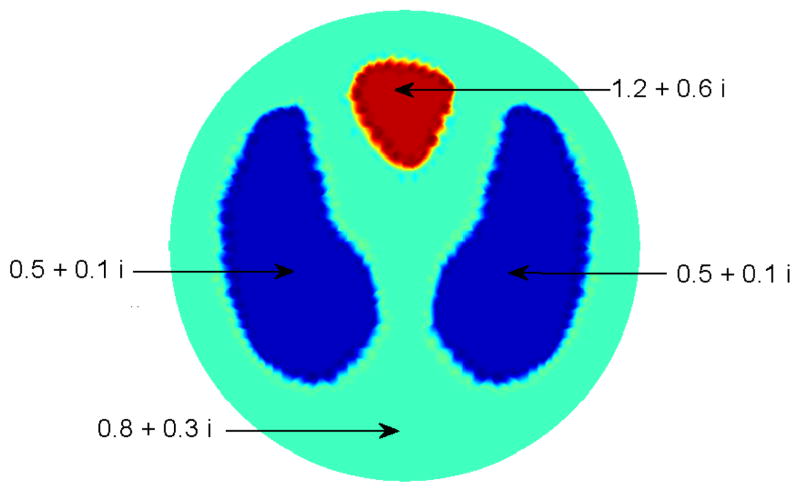
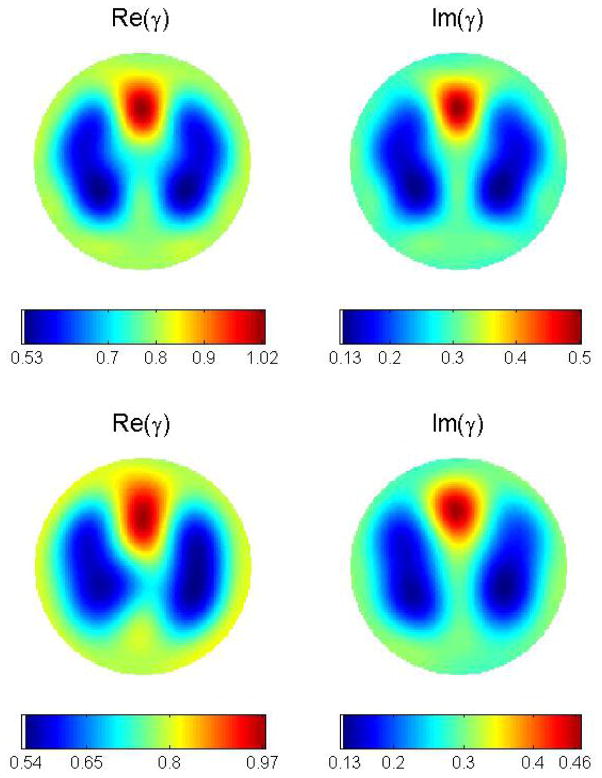
Example 3 is an admittivity distribution of slightly higher contrast, and a non-unitary background admittivity of γ₀ = 0.8 + 0.3i. See Figure 5 for a plot of the phantom with admittivity values for the regions. Due to the non-unitary background, the problem was scaled, as was done, for example, in [18, 28], by defining a scaled admittivity γ̃ = γ/γ₀ to have a unitary value in the neighborhood of the boundary and scaling the DN map by defining Λ_γ̃ = γ₀Λ_γ, solving the scaled problem, and rescaling the reconstructed admittivity. The scattering data for the noise-free reconstruction was computed on a 128 × 128 grid for k ∈ [−5.2, 5.2]. Noisy data was computed as described above in the beginning of this section, and the scattering data was also computed on a 128 × 128 grid for |k| ≤ 5.5. The reconstructions are found in Figure 6. The maximum and minimum values are given in Table 1. In this example, for the noise-free reconstruction, the dynamic range is 71% for the conductivity and 75% for the permittivity. Again the spatial resolution is quite good. There is some degradation in the image and the reconstructed values in the presence of noise. We chose this noise level to be comparable to that of the 32 electrode ACT3 system at RPI [15]. A thorough study of the effects of noise and stability of the algorithm with respect to perturbations in the data is beyond the scope of this paper. The scattering transform began to blow up for noisy data, requiring a truncation of the admissible scattering data to a circle of radius 5.5, resulting in a dynamic range of 62% for the conductivity and 68% for the permittivity. A thorough study of the effects of the choice of K and its method of selection is not included in this paper.

Figure 5.

The test problem in Example 3. In this case, the background admittivity is 0.8 + 0.3i, rather than 1 + 0i as in Examples 1 and 2.

Figure 6.

Top row: Reconstruction from noise-free data for Example 3. The cut-off frequency was K = 5.2. The dynamic range is 71% for the conductivity, and 75% for the permittivity. Bottom row: Reconstruction from data with 0.01% added noise. The cut-off frequency was |k| ≤ 5.5. The dynamic range is 62% for the conductivity, and 68% for the permittivity.

Table 1.

Maximum and minimum values in Example 3 with the non-unitary background were found in the appropriate organ region. The table indicates these values of the admittivity in the appropriate region.

	Admitivity of test problem	Reconstruction from noise-free data	Reconstruction from noisy data
heart	1.2 + 0.6 i	1.0246 + 0.5014 i (max)	0.9740 + 0.4679 i (max)
lungs	0.5 + 0.1i	0.5262 + 0.1258 i (min)	0.5390 + 0.1281 i (min)

5 Conclusions

A new direct method is presented for the reconstruction of a complex conductivity. This method has the attributes of being fully nonlinear, parallelizable, and the direct reconstruction does not require a high frequency limit. It was demonstrated on numerically simulated data representing a cross-section of a human chest with discontinuous organ boundaries that the method yields reconstructions with good spatial resolution and dynamic range on noise-free and noisy data. This was the first implementation of such a method, and although efforts were made to realistically simulate experimental data by including discontinuous organ boundaries, data on a finite number of electrodes, and simulated contact impedance, actual experimental data will surely prove more challenging. While this study with simulated data gives very promising results, more advanced studies of stability and robustness may be necessary to deal with the more difficult problem of reconstructions from experimental data.