Origin of B₀ orientation dependent R₂^* (=1/T₂^*) in white matter

Abstract

Recent MRI studies have demonstrated that the relative orientation of white matter fibers to the B₀ field significantly affects ${\text{R}}_2^{\ast }$ measurement. In this work, the origin of this effect was investigated by measuring R₂ and ${\text{R}}_2^{\ast }$ in multiple orientations and fitting the results to magnetic susceptibility-based models and magic angle-based models. To further explore the source of magnetic susceptibility effect, the contribution of tissue iron to the orientation dependent ${\text{R}}_2^{\ast }$ contrast was investigated. Additionally, the effects of temperature on ${\text{R}}_2^{\ast }$ and orientation dependent ${\text{R}}_2^{\ast }$ contrasts were studied to understand the differences reported between a fixed specimen at room temperature and in vivo at body temperature. The results suggest that the B₀ dependent ${\text{R}}_2^{\ast }$ variation is better explained by the magnetic susceptibility-based model with susceptibility anisotropy. However, extracting tissue iron did not reduce the orientation dependent ${\text{R}}_2^{\ast }$ contrast, suggesting iron is not the origin of the contrast. This leaves susceptibility effects from myelin as the most probable origin of the contrast. Temperature showed large contribution on both ${\text{R}}_2^{\ast }$ and orientation dependent ${\text{R}}_2^{\ast }$ contrasts, explaining a portion of the contrast difference between the in-vivo and in-vitro conditions.

Introduction

Assessing the integrity of myelin in brain white matter is important for diagnosis and prognosis of brain disorders and injuries (e.g. multiple sclerosis). Several MRI methods such as MRI relaxometry (Bock et al., 2011; Cohen-Adad et al., 2012; Deoni et al., 2003; Glasser and Van Essen, 2011), diffusion imaging (Basser et al., 1994; Werring et al., 1999), magnetization transfer imaging (Balaban and Ceckler, 1992; McGowan et al., 1998), and myelin water imaging (Du et al., 2007; Laule et al., 2004; Mackay et al., 1994) have been proposed as potential biomarkers for myelin, each with different advantages and disadvantages (Laule et al., 2007). In high field MRI, magnetic susceptibility weighted images, both ${\text{T}}_2^{\ast }$ and phase contrasts, have been suggested to be sensitive to myelin (Langkammer et al., 2011; Lee et al., 2012; Li et al., 2009; Liu et al., 2011; Lodygensky et al., 2012). The exact mechanism of these contrasts, however, are more complex with other contributors including deoxy-hemoglobin, ferritin, calcium, structural shape and orientation, and chemical exchange, playing important roles (Bender and Klose, 2010; Chu et al., 1990; Denk et al., 2011; Duyn et al., 2007; Fukunaga et al., 2010; Haacke et al., 2005; Haacke et al., 2004; He and Yablonskiy, 2009; Lee et al., 2010a; Lee et al., 2010b; Lee et al., 2011; Li et al., 2012a; Liu, 2010; Luo et al., 2010; Marques et al., 2009; Reichenbach et al., 1997; Schafer et al., 2009; Schweser et al., 2010; Sedlacik et al., 2008; Shmueli et al., 2011; Wiggins et al., 2008; Wu et al., 2009; Zhong et al., 2008). In particular, tissue iron, which has large concentration variations within and between tissue types including white matter (Hallgren and Sourander, 1958), has been shown to significantly affect these contrasts (Duyn et al., 2007; Fukunaga et al., 2010; Haacke et al., 2005). Hence, ${\text{T}}_2^{\ast }$ or phase contrast alone has limited specificity in detecting myelin.

Recently, several studies have demonstrated that the relative orientation of white matter fibers to the B₀ field significantly affects ${\text{R}}_2^{\ast }(=1/{\text{T}}_2^{\ast })$ measurement (Bender and Klose, 2010; Cherubini et al., 2009; Denk et al., 2011; Lee et al., 2011; van Gelderen et al., 2012; Wiggins et al., 2008). This dependence has been exploited to generate a new ${\text{T}}_2^{\ast }$-based fiber orientation map as well as a $\mathrm{\Delta }{\text{R}}_2^{\ast }$ map, a measure of voxel-wise ${\text{R}}_2^{\ast }$ change defined as the ${\text{R}}_2^{\ast }$ measurement when fibers of a voxel are perpendicular to ${\text{B}}_0({\text{R}}_{2\perp }^{\ast })$ minus that of the parallel measurement ( ${\text{R}}_{2\left|\right|}^{\ast }$) (Lee et al., 2011). This $\mathrm{\Delta }{\text{R}}_2^{\ast }$ can reach up to 14.7 Hz (= 43.5 Hz – 28.8 Hz) in vivo at 7 T (Sati et al., 2011; Wiggins et al., 2011), demonstrating a substantial effect size. Hence, it has potentials to be used as a diagnostic contrast. The origin of this B₀ orientation dependent ${\text{R}}_2^{\ast }$ contrast has been attributed to the magnetic susceptibility of myelin and its structure (Lee et al., 2011). The contrast may be altered by changes in myelin structure and/or susceptibility from injury or disease and, therefore, may be used as a potential biomarker for myelin integrity.

However, other sources of magnetic susceptibility, most notably iron, may have additional contributions to the orientation dependent ${\text{R}}_2^{\ast }$ contrast. In white matter, iron-positive cells (ferritin) are often found to be aligned along fibers (Connor et al., 1990). Therefore, it is plausible that the presence of iron may influence the contrast. Additionally, the magic angle effect, a well-known B₀ orientation dependent contrast mechanism observed in tendons, cartilages and peripheral nerves (Chappell et al., 2004; Fullerton et al., 1985; Henkelman et al., 1994), can be another origin of the contrast in addition to the magnetic susceptibility effect.

In this study, we have performed a series of experiments on fixed human brain specimens to estimate the contribution of the magic angle effect and tissue iron to the B₀ orientation dependent ${\text{R}}_2^{\ast }$ contrast. We also investigated the effects of temperature on the ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ contrasts to gain an insight into the contrast difference between fixed specimens at room temperature (21°C) and at body temperature (38°C).

Theory

Transverse Relaxations

In MRI, transverse relaxation is caused by the loss of coherence in transverse magnetization. It is often modeled by an exponential decay function with a time constant of T₂ or its reciprocal, a transverse relaxation rate, R₂ (i.e. R₂ = 1/ T₂). Experimentally, this transverse relaxation rate can be estimated using a spin echo (SE) sequence with multiple echoes. The resulting R₂ estimation frequently deviates from intrinsic R₂ due to diffusion and chemical exchange of spins and is affected by acquisition parameters (Carr and Purcell, 1954; Luz and Meiboom, 1963; Meiboom and Gill, 1958). For this reason, the measured R₂ is often referred to as apparent R₂ (R_2,apparent). In the presence of diffusion and exchange of spins, it can be defined as follows (Haacke and Reichenbach, 2011):

$${\text{R}}_{2,\text{apparent}}={\text{R}}_{2,\text{intrisic}}+{\text{R}}_{2,\text{diffusion}}+{\text{R}}_{2,\text{exchange}}$$ (Eq. 1)

where R_2,intrinsic is the intrinsic transverse relaxation rate, and R_2,diffusion and R_2,exchange are additional relaxation terms from diffusion and exchange respectively.

In gradient echo (GRE) measurement, the transverse relaxation rate is further increased by the field inhomogeneity originating from magnetic susceptibility and other sources. In a static dephasing regime where spin motion is ignored, this relaxation rate can be written as:

$${\text{R}}_2^{\ast }={\text{R}}_{2,\text{intrinsci}}+{\text{R}}_2^{\prime }$$ (Eq. 2)

where ${\text{R}}_2^{\ast }$ is the accelerated relaxation rate, R₂ is the intrinsic transverse relaxation rate, and ${\text{R}}_2^{\prime }$ is the field inhomogeneity-induced relaxation rate.

B₀ Orientation Dependent Transverse Relaxations

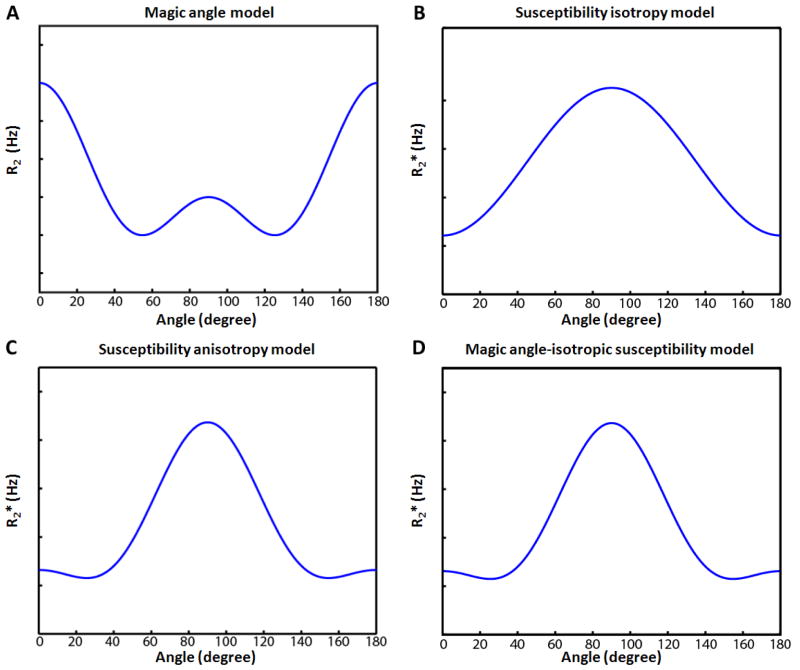
In a certain tissue with anisotropic microstructure, these relaxation rates (R₂ and ${\text{R}}_2^{\ast }$) are modulated by the orientation of the anisotropic microstructure relative to the main magnetic field. One of these phenomena is referred to as a magic angle effect and is observed at tendons, ligaments, and menisci. The effect exhibits a decrease in R₂ when the anisotropic microstructure is orientated at specific angles (magic angles; 54.7° and 124.7°) relative to B₀. This decrease in R₂ increases MR signal in SE or GRE. As a result, the tissues, that are not visible in other angles, become visible at the magic angles. The origin of this effect has been ascribed to dipole-dipole interaction in highly ordered collagen-rich fibers (Chappell et al., 2004; Fullerton et al., 1985; Henkelman et al., 1994). The dipole interaction changes as a function of 3 cos²θ − 1 where θ is the angle between the orientation of the structure and B₀ (Chappell et al., 2004). As a result, the dipolar interaction effect is minimized at the magic angles resulting in a decrease in R₂. The orientation dependence R₂ can be written as follows:

$${\text{R}}_2(\theta )={\text{R}}_{2,\text{orientation}\text{independent}}+c_m·{(3{cos}^2\theta -1)}^2$$ (Eq. 3)

where R₂ is the transverse relaxation rate, R_{2,orientation independent} is the R₂ component that is independent of the orientation, c_m is a constant (≥ 0) for the orientation dependent component of the magic angle effect, and θ is the angle between the orientation of the anisotropic structure and B₀ (Fig. 1A). To observe the magic angle effect, a SE sequence is commonly used because the dipole-dipole interaction affects R₂. This effect has been observed in peripheral nerve fibers (Chappell et al., 2004), hinting that it can be a possible mechanism for the orientation dependent contrast observed in white matter of the brain. But a previous study at low field (1.5 T) did not detect such an effect (Henkelman et al., 1994), which might have been due to a limited SNR at the low field.

Figure 1.

Orientation dependence of the magic angle (A), isotropic susceptibility (B), susceptibility anisotropy model (C), and magic angle-isotropic susceptibility model (D). Both susceptibility anisotropy model and magic angle-isotropic susceptibility model can reveal the same orientation dependency with a high order angular term (cos4θ) deviating from the isotropic susceptibility model.

Another mechanism for the B₀ orientation dependent relaxation is the magnetic susceptibility, which affects ${\text{R}}_2^{\prime }$. It has been shown that highly anisotropic structure with magnetic susceptibility deviating from the surrounding medium exhibit a ${\text{R}}_2^{\ast }$, more specifically ${\text{R}}_2^{\prime }$, change as a function of the angle between the structure and B₀ (Yablonskiy et al., 1997; Yablonskiy and Haacke, 1994). In a set of parallel cylinders, ${\text{R}}_2^{\prime }$ shows a sin²θ or −cos2θ dependency where θ is a relative orientation of the long axis of the cylinders and B₀. In white matter of the brain, axons and myelin sheaths form cylindrical structures and magnetic susceptibility difference exists between the lipid-rich myelin and surrounding water in axon/extracellular space. When axons in a voxel are predominantly aligned, ${\text{R}}_2^{\ast }$ measurements have shown an angular dependence similar to −cos2θ (Fig. 1B) (Bender and Klose, 2010; Cherubini et al., 2009; Denk et al., 2011; Lee et al., 2011). Recently, more detailed studies at high field have revealed that this angular dependency has an additional angular component (Denk et al., 2011; Lee et al., 2011), which was modeled by a cos4 θ function (Lee et al., 2011). This additional term was explained by susceptibility anisotropy or tensor (Lee et al., 2011), which was suggested to originate from myelin (Li et al., 2012a). The susceptibility anisotropy implies that magnetic susceptibility of white matter is not a constant but is dependent on the relative orientation between axons and B₀ (Lee et al., 2010b; Liu, 2010). Hence, the full model of the angular dependent ${\text{R}}_2^{\ast }$ in white matter can be reformulated as follows (Lee et al., 2011):

$${\text{M}}_{\mathit{suscep}-\mathit{aniso}}(\theta )=c_{\text{orientation}\text{independent}}-c_{\mathit{iso}}·cos2\theta +c_{\mathit{ansio}}·cos4\theta$$ (Eq. 4)

where c_{orientation independent} is the orientation independent ${\text{R}}_2^{\ast }$ or R₂ component, c_iso and c_aniso are constants (≥ 0) for isotropic and anisotropic components respectively, and θ is the relative orientation between the fiber orientation and B₀ (Fig. 1C). This model will be referred to as a susceptibility anisotropy model (suscep-aniso model).

In highly myelinated nerve fibers, the magnetic susceptibility effect may co-exist with the magic angle effect in ${\text{R}}_2^{\ast }$ measurement. When the magic angle effect is assumed to exist in conjunction with isotropic susceptibility, ${\text{R}}_2^{\ast }$ can be written as follows (Fig. 1D):

$${\text{M}}_{\mathit{magic}-\mathit{iso}}(\theta )=c_{\text{orientation}\text{independent}}+c_m·{(3{cos}^2\theta -1)}^2-c_{\mathit{iso}}·cos2\theta .$$ (Eq. 5)

This model will be referred to as a magic angle-isotropic susceptibility model (magic-iso model). The expansion of the magic angle term becomes 1.375 + 1.5· cos2θ + 1.125· cos4 θ, showing cos2θ and cos4θ orientation dependence. Therefore, both the suscep-aniso model and the magic-iso model can result in the same ${\text{R}}_2^{\ast }$ orientation dependency (Figs.1C and 1D) with the higher order orientation dependent term (cos4 θ) originating either from the susceptibility anisotropy or from the magic angle effect. Hence, in GRE-based ${\text{R}}_2^{\ast }$ measurement, it is difficult to confirm whether the magic angle effect or the susceptibility anisotropy effect is the primary contributor to the higher order term that makes ${\text{R}}_2^{\ast }(\theta )$ deviating from cos2θ.

In SE, the contribution of the magnetic susceptibility effect is expected to be minimized by a refocusing RF pulse. Only residual effects from the spin diffusion (R_2,diffusion term in Eq. 1) and finite data acquisition duration (Duyn, 2004) may persist. On the other hand, the magic angle effect will have the same magnitude both in SE and GRE because ${\text{R}}_2^{\ast }$ has contribution from R₂ (Eq. 2). Hence, if the magic angle effect is the only source for the orientation dependency, R₂ estimation from SE will show the change as a function of Eq. 3. If the residual magnetic susceptibility effect coexists with the dominating magic angle effect, R₂ estimation will follow Eq. 5 with the coefficient of the higher order term (cos4 θ) the same in GRE and SE. On the contrary, if the magnetic susceptibility effect is the dominant origin, little or no R₂ change over the orientations is expected except the residual magnetic susceptibility effect that has not been nullified by the refocusing pulses. The angular dependency of the residual susceptibility will be the same as ${\text{R}}_2^{\ast }$ (Eq. 4; suscep-aniso model) but the effect size will be substantially reduced. Hence, measuring GRE and SE in multiple angles will allows us to separate the magnetic susceptibility effect from the magic angle effect.

Materials and Methods

To investigate the primary sources and mechanisms for the B₀ orientation dependent ${\text{R}}_2^{\ast }$ contrast in white matter, we performed three experiments using human brain specimens. Firstly, ${\text{R}}_2^{\ast }$ and R₂ were measured in multiple orientations to explore the contribution of the magic angle effect and the magnetic susceptibility effect. Secondly, the contribution of tissue iron was tested by comparing the $\mathrm{\Delta }{\text{R}}_2^{\ast }$ contrast before and after iron extraction from the specimens. Lastly, the effect of temperature on ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ contrasts was studied.

Specimen Preparation and MRI Scan Setup

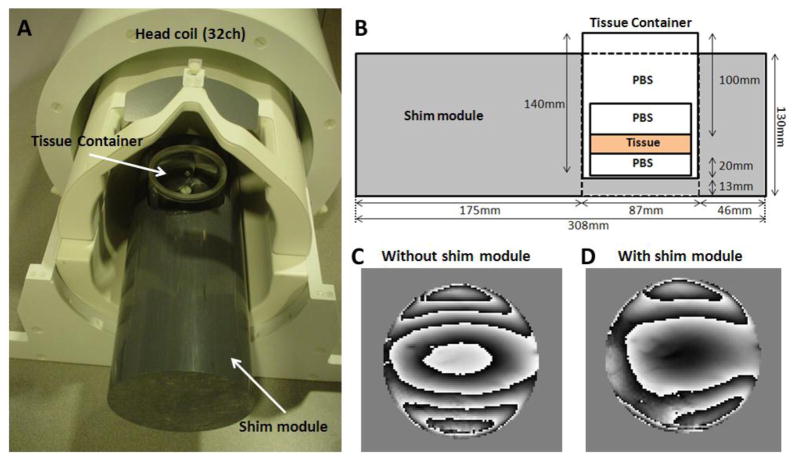
Three coronal slabs of formalin fixed human brains from two adult subjects with no known neurologic deficit or abnormality were used for the experiments. The thickness of the slabs was approximately 10 mm. The slabs were cut into cylindrical shape (approximately 60 mm diameter), which included corpus callosum. One of the slabs was used for the orientation dependent R₂ and ${\text{R}}_2^{\ast }$ measurements in corpus callosum, and another for the iron extraction and temperature experiments in corpus callosum and basal ganglia. The third specimen was used to test the orientation dependent ${\text{R}}_2^{\ast }$ contrast in basal ganglia, and also used for an additional iron extraction experiment. At least two days before the MRI scan, the specimen was stored in a container (cylindrical shape, diameter = 62 mm, and length = 65 mm) filled with phosphate buffered saline (PBS) to restore the relaxation parameters (Shepherd et al., 2009). This container was placed in a larger size container (cylindrical shape, diameter = 87mm, and length = 140 mm) either filled with a heat shield for the temperature experiment or with PBS for the other experiments. The larger container was designed to fit tightly in a custom designed shim module (Figs. 2A and 2B). The shim module (cylindrical shape, diameter = 130 mm and length = 308 mm) was made out of PVC that has a similar susceptibility to water. The long axis of the module was aligned to the main magnetic field of an MRI. The specimen was positioned proximal to the phased-array coils to increase SNR. The shim module substantially improved field homogeneity (Figs. 2C and 2D)

Figure 2.

(A) Shim module and specimen container with a 32ch head coil. (B) Cross-sectional diagram of the shim module and specimen container. Acquired tissue phase images without (C) and with (D) the shim module.

All the MRI scans were performed with a 7 T whole body MRI (Siemens Medical System GmbH, Erlangen, Germany) using a head-only CP transmit and 32-channel phased-array receive coil (Nova Medical, Wilmington, MA).

B₀ Orientation Dependent R₂ and ${\text{R}}_2^{\ast }$ Measurements

To measure the orientation dependence in corpus callosum, a specimen was scanned at 12 different orientations, each one being incremented by approximately 15° in the x-z magnet plane (x is left-right and z is the B₀ field direction). The specimen was positioned such that the rotation can change the angle of the major fibers at the corpus callosum from 0° to 180° relative to B₀. R₂ was measured first and ${\text{R}}_2^{\ast }$ was acquired on a separate day.

For R₂ estimation, a 2D multi-slice SE sequence with a single echo was used to avoid complications from multiple refocusing pulses. A short readout duration of 1.26 ms was used to reduce ${\text{T}}_2^{\ast }$ weighting during the acquisition. Other scan parameters were: in-plane resolution = 0.75 × 0.75 mm², slice thickness = 1 mm, FOV = 96 × 96 mm², matrix size = 128 × 128, number of slices = 20, TR = 2500 ms, flip angle = 90°, and pixel bandwidth = 795 Hz/pixel. The data acquisition scan time was 5.3 min. The single echo acquisition was repeated 7 times with a different TEs from 9 to 39 ms every 5 ms. Once all 7 echoes were acquired, the specimen container was rotated manually by 15° to acquire the next orientation. The total acquisition time was approximately 8 hours (5.3 min. × 7 echoes × 12 orientations).

For ${\text{R}}_2^{\ast }$ estimation, a 3D multi-echo GRE sequence was used. The same in-plane resolution (= 0.75 × 0.75 mm²), slice thickness (= 1 mm), FOV (= 96 × 96 mm²), matrix size (= 128 × 128), and number of slices (= 20) were used as in the SE sequence. Other parameters were: TR = 100 ms, flip angle = 15°, bandwidth = 379 Hz/pixel, and TE = 4 to 39 ms in every 5 ms (8 echoes). The data acquisition took 4.2 min for each orientation and the total acquisition time was less than 1 hour (4.2 min. × 12 orientations).

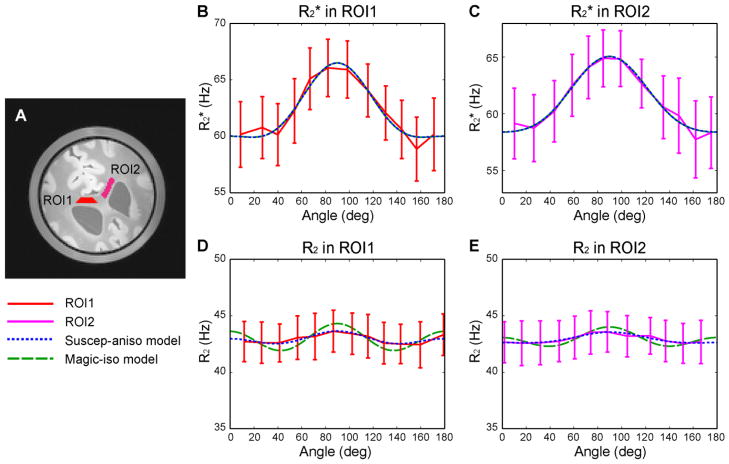
After data acquisition, all the reconstructed images, both SE and GRE, were aligned to the first orientation image of the SE data. The images were aligned manually in 6 degrees of freedom (x-, y-, z-translations and roll-, pitch-, yaw-rotations) based on the first echo images. The relative rotational angle was estimated by the alignment result. The angle of corpus callosum fibers in the first acquired SE data image was estimated by the left side borderline of the corpus callosum and the ventricle. The subsequent angles in the rotated data were determined by this angle and the alignment information. The voxel-wise R₂ and ${\text{R}}_2^{\ast }$ values were estimated by a nonlinear fitting of an exponential decay function. To estimate the orientation dependence, two regions of interest (ROIs) were manually drawn in the corpus callosum in multiple slices. The ROIs covered areas where the axonal orientation was expected to be relatively uniform (Fig. 3A).

Figure 3.

ROIs in the specimen (A) and ${\text{R}}_2^{\ast }$ measurements and model-fitted curves in ROI1 (B) and ROI2 (C). R₂ measurements and model-fitted curves in ROI1 (D) and ROI2 (E). The solid red lines are used for the measured data in ROI1; solid magenta lines for the measured data in ROI2; dotted blue lines for the suscep-aniso model; dashed green lines for the magic-iso model. The magic angle model alone (Eq. 3) did not fit the data (plot not shown), resulting in R² = 0 in all measurements.

For each angle, the averaged R₂ and ${\text{R}}_2^{\ast }$ values and its standard deviation within the ROI were calculated to generate orientation dependent R₂ and ${\text{R}}_2^{\ast }$ curves. These curves were then fitted to the suscep-aniso model (Eq. 4) and the magic-iso model (Eq. 5) using a linear least-squares fitting with nonnegative constraints to calculate the goodness of fit (adjusted R²) of each model except for the magic-iso model for the R₂ curves. A phase offset was added in each model and changed from 0° to 180° in a 0.1° increment to find an angle that resulted in maximum R².

A slightly modified approach was used to fit the magic-iso model for the R₂ curve. Since the magic-iso model assumes that the higher order orientation term (cos4 θ) originates from the magic angle effect, and the effect exists in the same magnitude in both R₂ and ${\text{R}}_2^{\ast }$ measurements, the regression result of the cos4 θ term from the ${\text{R}}_2^{\ast }$ measurements will stay the same in the R₂ measurements. Based on this assumption, we first fitted the magic-iso model to the ${\text{R}}_2^{\ast }$ measurements, and then the regression result of the cos4 θ regressor (i.e. the regression coefficient multiplied by the regressor) was subtracted from the R₂ curve. After that, the isotropic susceptibility term and a constant were fitted to the residual R₂ curve to calculate an adjusted R² value. Note that all the regressors were orthogonal to each other. The goodness of fit was estimated by adjusted R², which was adjusted by the number of regressors.

Another specimen was tested for the orientation dependent ${\text{R}}_2^{\ast }$ contrast in basal ganglia, using the same protocol described above. For the analysis, the suscep-aniso model, which has the same orientation dependency as the magic-iso model in ${\text{R}}_2^{\ast }$, was fitted to the measurements to calculate R². Since there was no clear orientation direction in basal ganglia, a phase offset was added to the model and changed from 0° to 180° in a 0.1° increment. Then the phase offset that resulted in a maximum R² was reported. The result showed a relatively poor fit to the model (maximum R² = 0.51 when the specimen was 101° rotated relative to a neighboring corpus callosum area) with small $\mathrm{\Delta }{\text{R}}_2^{\ast }(=-1.0\text{Hz})$ (Supplementary Figure 1). The coefficient for the cos4 θ term was zero. These results suggested limited, if any, orientation dependency in basal ganglia. The same specimen was used as a additional specimen for the iron extraction experiment.

Iron Extraction

To estimate the contribution of tissue iron to the B₀ orientation dependent ${\text{R}}_2^{\ast }$ contrast, we compared $\mathrm{\Delta }{\text{R}}_2^{\ast }$ (= ${\text{R}}_2^{\ast }$ measurement when the fibers in a voxel are perpendicular to B₀ minus ${\text{R}}_2^{\ast }$ when the fibers are parallel to B₀; ${\text{R}}_{2\perp }^{\ast }-{\text{R}}_{2\left|\right|}^{\ast }$). Iron was removed from the specimens by using iron chelating solution (1 mM desferrioxamine and 2 mM sodium dithionite). This approach has been used to remove iron from fixed brain specimens in previous studies (Fukunaga et al., 2010; Schenck et al., 2006). Two specimens were used for the experiment. Before the iron extraction, control ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ values were measured (see below for the scan protocol). For the first specimen, it was stored in the iron extraction solution for 14 days. The iron extraction solution was replaced every 1 to 3 days. The ${\text{R}}_2^{\ast }$ values were measured on day 2, 4, 6, 8, 10, 12 and 14 to check the iron extraction induced ${\text{R}}_2^{\ast }$ changes. On day 14, $\mathrm{\Delta }{\text{R}}_2^{\ast }$ was acquired to compare the results with the control. For the second specimen, which was used to measure the orientation effect in basal ganglia, $\mathrm{\Delta }{\text{R}}_2^{\ast }$ was measured every other day for 16 days.

For ${\text{R}}_2^{\ast }$ estimation, a 3D multi-echo GRE sequence was used with in-plane resolution = 1 × 1 mm², slice thickness = 1 mm, FOV = 128 × 128 mm², matrix size = 128 × 128, number of slices = 16, TR = 75 ms, flip angle = 19°, pixel bandwidth = 210 Hz/pixel, and TE = 4 ms to 36 ms in every 4 ms (9 echoes). The scan time was only 2.3 min. The left side of corpus callosum where an ROI was drawn (Fig. 4A and Supplementary Fig. 2A) was aligned parallel to B₀. For $\mathrm{\Delta }{\text{R}}_2^{\ast }$ measurement, the GRE images of the same parameters were acquired at two different orientations such that the corpus callosum was aligned either parallel or perpendicular to the B₀ direction. For the basal ganglia ROI in the second specimen, the estimated orientation was approximately perpendicular (deviated by 11°) to that of the corpus callosum ROI. As a result, measuring $\mathrm{\Delta }{\text{R}}_2^{\ast }$ in the corpus callosum allowed us to measure $\mathrm{\Delta }{\text{R}}_2^{\ast }$ in the basal ganglia simultaneously. The maximum $\mathrm{\Delta }{\text{R}}_2^{\ast }$ estimation error from the 11° deviation was less than 8%. The orientation was viewed from a localizer scan and carefully refined to reduce errors from misalignment. After data acquisition, the orientation difference was estimated by manually aligning the two data sets using a linear transformation. In all measurements, angular offsets from the parallel or perpendicular to the B₀ direction were less than 6°. The ${\text{R}}_2^{\ast }$ values were estimated by the nonlinear exponential fitting mentioned before. The ROIs were drawn in two different areas, one at the corpus callosum and the other at the basal ganglia, to estimate ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ before and after iron extraction.

Figure 4.

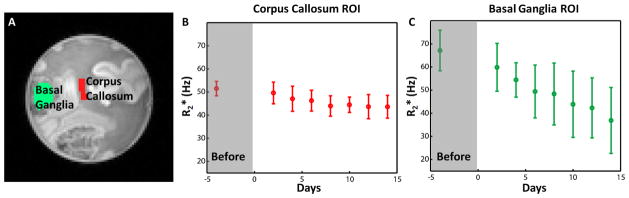
ROIs in the specimen (A) and ${\text{R}}_2^{\ast }$ changes over 14 days in the iron extracting solution for corpus callosum (B) and basal ganglia (C).

Temperature

To measure the temperature effects on ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$, a specimen was scanned at room temperature (21°C) and at approximate body temperature (38°C). This experiment was performed before the iron extraction using the first specimen in the iron extraction experiment. Scanning was performed at two orientations: one at which the corpus callosum fibers was parallel to B₀ and the other perpendicular to B₀ to measure $\mathrm{\Delta }{\text{R}}_2^{\ast }$ as well as ${\text{R}}_2^{\ast }$. The same 3D multi-echo GRE sequence as in the iron extraction experiment was used with the same method for the ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ estimations.

In the experiment, the two different orientation ${\text{R}}_2^{\ast }$ data were first collected at room temperature. The temperature of the specimen was measured using a mercury thermometer with the tip gently placed on the surface of the specimen. After the measurements, the specimen container was placed in a water bath and the bath was heated up to 38°C using a double boiler. The temperature was monitored using the thermometer in contact with the specimen. To ensure homogeneous temperature distribution within the specimen, the container was kept in the water bath for 10 min after reaching 38°C. During this period, the temperature was carefully controlled to avoid overheating of the specimen. After 10 min, the container was removed from the water bath and stored in a custom-designed heat-shielded container. The MRI scan was performed immediately afterward. The total scan time including the localization, shimming and GRE data acquisition was less than 4 min. After the data acquisition, the temperature was measured again and showed less than 2°C drop. This procedure was repeated for the other orientation to complete $\mathrm{\Delta }{\text{R}}_2^{\ast }$ measurement. After data acquisition, the images were aligned and ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ were calculated. The same two ROIs, drawn for the iron extraction experiment, were used for the comparison.

Results

The orientation dependent ${\text{R}}_2^{\ast }$ and R₂ results in corpus callosum are summarized in Fig. 3. The same range of y-axis (15 Hz) was used for all plots to demonstrate the effect size difference between the ${\text{R}}_2^{\ast }$ and R₂ measurements. The two ROIs commonly used for the ${\text{R}}_2^{\ast }$ and R₂ analysis are colored in red and magenta (Fig. 3A). The total number of voxels was 196 in ROI1 and 257 in ROI2. The mean ${\text{R}}_2^{\ast }$ measured by GRE in each angle are shown in Figures 3B and 3C for ROI1 and ROI2 respectively, and those of R₂ by SE are shown in Figures 3D (ROI1) and 3E (ROI2). In each plot, the red (ROI1) or magenta (ROI2) lines (solid) represent the measurement curve with the standard deviation in each angle as an error bar. The blue (dotted) and green (dashed) lines represent the model fitted results from the suscep-aniso model (Eq. 4) and the magic-iso model (Eq. 5) respectively. Note that the magic angle model alone (Eq. 3) did not fit to the SE data (R² = 0 for ROI1 and ROI2). The fitting resulted in a flat line with no dip in R₂ at the magic angles.

The ${\text{R}}_2^{\ast }$ curves in Figs. 3B and 3C clearly demonstrate B₀ orientation dependence in the corpus callosum. They show much larger signal variations than the R₂ curves in Figs. 3D and 3E. The peak to peak orientation dependence was 6.0 (in ROI1) and 7.0 (in ROI2) times larger in ${\text{R}}_2^{\ast }$ than in R₂. The maximum ${\text{R}}_2^{\ast }$ measurements were observed when the fibers were roughly perpendicular to the B₀ field (66.1 ± 2.5 Hz at 82° in ROI1 and 64.9 ± 2.5 Hz at 85° in ROI2) whereas substantially lower ${\text{R}}_2^{\ast }$ values were observed when the fiber orientations were parallel to B₀ (58.9 ± 2.8 Hz at 157° in ROI1 and 57.7 ± 3.4 Hz at 162° in ROI2). When the two models, the suscep-aniso model and the magic-iso model, were fitted to the curves, the adjusted R² resulted in the same values (adjusted R² = 0.95 in ROI1 and 0.97 in ROI2) (Table 1). This confirms that the ${\text{R}}_2^{\ast }$ measurements alone cannot distinguish the two models.

Table 1.

Adjusted R² values for the susceptibility anisotropy model and magic angle-isotropic susceptibility model.

		Adjusted R2 suscep-aniso model	Adjusted R2 magic-iso model
ROI 1	${\text{R}}_2^{\ast }$	0.95	0.95
	R2	0.77	< 0
ROI 2	${\text{R}}_2^{\ast }$	0.97	0.97
	R2	0.89	< 0

The R₂ measurements, more specifically R_2,apparent measurements, from SE reveal much reduced orientation dependence compared to the ${\text{R}}_2^{\ast }$ measurements. The overall shapes of the R₂ curves are similar to those of ${\text{R}}_2^{\ast }$ with the maximum R₂ values measured when the fibers are perpendicular to B₀ (43.6 ± 1.8 Hz at 87° in ROI1 and 43.6 ± 1.8 Hz at 88° in ROI2) and the minimum R₂ values measured when the fibers are parallel (42.4 ± 2.0 Hz at 160° in ROI1 and 42.6 ± 1.8 Hz at 152° in the ROI2). When the suscep-aniso model was fitted to the R₂ curves, it resulted in the adjusted R² values of 0.77 in ROI1 and 0.89 in ROI2. On the other hand, when the magic-iso model was fitted to the R₂ curves with the assumption of having the same cos4θ coefficient as in ${\text{R}}_2^{\ast }$, it resulted in negative adjusted R² values (−0.75 and −2.49 for ROI1 and ROI2 respectively), suggesting the model did not explain the measurements. The fitted results (Figs. 3D and 3E) show large deviations of the magic-iso model, originating from the subtraction of the cos4 θ term estimated in ${\text{R}}_2^{\ast }$. Hence, the suscep-aniso model better explains the orientation dependent ${\text{R}}_2^{\ast }$ and R₂ than the magic-iso model. The large R² of the suscep-aniso model in the SE measurements indicates that, even though the effect is substantially reduced, magnetic susceptibility effect contributes to the SE measurements. This may have originated from the finite data acquisition duration and water diffusion effects in SE.

Figure 4 shows the results from the iron extraction experiment. Two ROIs, one in corpus callosum and the other in basal ganglia were used for the analysis (Fig. 4A). In both ROIs, ${\text{R}}_2^{\ast }$ values were dropped substantially over the two weeks of iron extraction period. The ${\text{R}}_2^{\ast }$ reductions were much larger in basal ganglia yielding 30.2 Hz reduction ( ${\text{R}}_2^{\ast }=67.1\pm 8.8\text{Hz}$ before the iron extraction and 36.9 ± 14.2 Hz on day 14, p < 0.001; paired t-test) compared to 7.7 Hz in corpus callosum ( ${\text{R}}_2^{\ast }=51.3\pm 3.1\text{Hz}$ before the iron extraction and 43.6 ± 4.9 Hz on day 14, p < 0.001; paired t-test) (Table 2). This can be explained by larger concentration of iron in basal ganglia than corpus callosum (Hallgren and Sourander, 1958).

Table 2.

Effects of iron on ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$

Iron		Before	After (day 14)	p-value
Corpus Callosum	${\text{R}}_{2\left|\right|}^{\ast }$	51.3 ± 3.1 Hz	43.6 ± 4.9 Hz	< 0.001
	${\text{R}}_{2\perp }^{\ast }$	47.5 ± 2.7 Hz	39.2 ± 3.5 Hz	< 0.001
	$\mathrm{\Delta }{\text{R}}_2^{\ast }$	4.0 ± 3.0 Hz	4.5 ± 4.9 Hz	0.131
Basal Ganglia	${\text{R}}_{2\left|\right|}^{\ast }$	67.1 ± 8.8 Hz	36.9 ± 14.2 Hz	< 0.001
	${\text{R}}_{2\perp }^{\ast }$	66.6 ± 8.3 Hz	36.4 ± 14.2 Hz	< 0.001
	$\mathrm{\Delta }{\text{R}}_2^{\ast }$	0.5 ± 10.2 Hz	0.5 ± 15.6 Hz	0.993

Despite the large changes in R₂*, $\mathrm{\Delta }{\text{R}}_2^{\ast }(={\text{R}}_{2\perp }^{\ast }-{\text{R}}_{2\left|\right|}^{\ast })$, measured before the iron extraction and 14 days later, showed limited change. In the corpus callosum, $\mathrm{\Delta }{\text{R}}_2^{\ast }$ changed from 4.0 ± 3.0 Hz to 4.5 ± 4.9 Hz (p = 0.131; paired t-test) and, in basal ganglia, it changed from 0.5 ± 10.2 Hz to 0.5 ± 15.6 Hz (p = 0.993; paired t-test). If iron is an important source for the R₂* orientation contrast, one would expect to observe decreased $\mathrm{\Delta }{\text{R}}_2^{\ast }$ after the iron extraction. Therefore, the results suggest that despite the alignment of iron-positive cells along the fibers in white matter (Connor et al., 1990), iron may not be the origin of the orientation dependency. This result is further consolidated by an additional iron extraction experiment that measured $\mathrm{\Delta }{\text{R}}_2^{\ast }$ every other day (Supplementary Figure 2). When all 8 measurements from day 2 to 16 were compared to the control measurement (before the iron extraction; day 0), $\mathrm{\Delta }{\text{R}}_2^{\ast }$ showed no decrease in corpus callosum, demonstrating the robustness of the measurements. The results rather showed a slight increase in $\mathrm{\Delta }{\text{R}}_2^{\ast }$ (see Discussion).

The results from the temperature change experiment are summarized in Table 3. Temperature increase from 21°C to 38°C showed decreases in ${\text{R}}_2^{\ast }$ at the ROIs shown in Fig. 4A. This decrease is consistent with lower ${\text{R}}_2^{\ast }$ values observed in vivo at body temperature (Li et al., 2006) than fixed brains at room temperature (Lee et al., 2012), suggesting that a certain portion of decrease in ${\text{R}}_2^{\ast }$ in fixed specimens originates from the temperature difference. The $\mathrm{\Delta }{\text{R}}_2^{\ast }$ value in corpus callosum was increased from 4.0 ± 3.0 Hz at room temperature to 5.9 ± 3.0 Hz at body temperature (p < 0.001; paired t-test), which is also consistent with larger $\mathrm{\Delta }{\text{R}}_2^{\ast }$ observed in vivo (Sati et al., 2011; Wiggins et al., 2011). The $\mathrm{\Delta }{\text{R}}_2^{\ast }$ values in basal ganglia show little contrast change at both temperatures (0.5 ± 10.2 Hz at room temperature to −0.3 ± 12.4 Hz at body temperature; p = 0.134; paired t-test). These temperature-dependent changes in ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ may have originated from changes in magnetic susceptibility and molecular motion (see Discussion).

Table 3.

Effects of temperature on ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$

Temperature		21°C	38°C	p-value
Corpus Callosum	${\text{R}}_{2\left|\right|}^{\ast }$	51.5 ± 3.1 Hz	47.5 ± 3.0 Hz	< 0.001
	${\text{R}}_{2\perp }^{\ast }$	47.5 ± 2.7 Hz	41.5 ± 2.1 Hz	< 0.001
	$\mathrm{\Delta }{\text{R}}_2^{\ast }$	4.0 ± 3.0 Hz	5.9 ± 3.0 Hz	< 0.001
Basal Ganglia	${\text{R}}_{2\left|\right|}^{\ast }$	67.1 ± 8.8 Hz	58.4 ± 8.9 Hz	< 0.001
	${\text{R}}_{2\perp }^{\ast }$	66.6 ± 8.3 Hz	58.7 ± 7.6 Hz	< 0.001
	$\mathrm{\Delta }{\text{R}}_2^{\ast }$	0.5 ± 10.2 Hz	−0.3 ± 12.4 Hz	0.134

Discussions and Conclusions

In this study, we investigated the origins of the fiber orientation dependent ${\text{R}}_2^{\ast }$ contrast in white matter. The relative orientation between white matter fibers and the B₀ field predominately affects ${\text{R}}_2^{\ast }$ as compared to R₂, suggesting that the primary origin of the contrast is magnetic susceptibility. This is further confirmed by the overall angular dependent patterns observed in the ${\text{R}}_2^{\ast }$ and R₂ measurements, which matched better with the susceptibility anisotropy model than with the magic angle-isotropic susceptibility model. In the tissue iron extraction experiment, significant changes in ${\text{R}}_2^{\ast }$ were observed before and after the iron extraction but $\mathrm{\Delta }{\text{R}}_2^{\ast }$ was not decreased, indicating that iron is not the primary source for the orientation dependent ${\text{R}}_2^{\ast }$ contrast. The temperature increase from room temperature to body temperature showed a decrease in ${\text{R}}_2^{\ast }$ and an increase in $\mathrm{\Delta }{\text{R}}_2^{\ast }$ in white matter, which is consistent with the observation that a fixed tissue has a higher ${\text{R}}_2^{\ast }$ and a reduced $\mathrm{\Delta }{\text{R}}_2^{\ast }$ compared to in vivo.

In the GRE and SE experiments, the results indicate that the magic angle effect may not be a primary source for the ${\text{R}}_2^{\ast }$ orientation contrast. However, this result does not fully exclude the existence the magic angle effect in white matter. The transverse signal decay in white matter has been shown to have multiple components with the shortest T₂ (or ${\text{T}}_2^{\ast }$) component attributed to myelin water (Du et al., 2007; Mackay et al., 1994). If the magic angle effect exists in white matter, the myelin water is most likely to be affected because of the proximity of water molecules to myelin. Since T₂ of myelin water in a fixed tissue at high field is very short, the effect may not have been observed in our experiment due to the long TEs (minimum 9 ms). Measuring the magic angle effects in myelin water will be challenging because of the small fraction and short T₂.

The ${\text{R}}_2^{\ast }$ equation in Eq. 4 can be reformulated as follows:

$${\text{R}}_2^{\ast }={\text{R}}_{2,\text{orientation}\text{dependent}}^{\ast }+{\text{R}}_{2,\text{orientation}\text{independent}}^{\ast }$$ (Eq. 6)

In our experiment, iron showed large effects on ${\text{R}}_2^{\ast }$ but limited effects on $\mathrm{\Delta }{\text{R}}_2^{\ast }$. This suggests that iron (e.g. ferritin) is primarily affecting the B₀ orientation independent ${\text{R}}_2^{\ast }$ term as compared to the B₀ orientation dependent ${\text{R}}_2^{\ast }$ term. Hence when modeling ${\text{R}}_2^{\ast }$, one needs to take into account this orientation independent component and R₂ cannot be estimated from ${\text{R}}_2^{\ast }$ by removing the orientation dependent component.

In our experiment, small errors in orienting fibers may have affected $\mathrm{\Delta }{\text{R}}_2^{\ast }$ or ${\text{R}}_2^{\ast }$ measurements. As mentioned before, during the data acquisition, the alignment errors between the fibers parallel or perpendicular to B₀ and the reference (the left side border line between corpus callosum and ventricle) were less than 6° (mean ± standard deviation = 2.25 ± 2.05°). Based on the orientation dependent ${\text{R}}_2^{\ast }$ curve reported previously (Lee et al., 2011), the ${\text{R}}_2^{\ast }$ variation from this maximum error will be less than 2.64 % of the peak to peak variation. Therefore, the misalignment had little effect on the overall results.

In the iron extraction experiment, slight increases in $\mathrm{\Delta }{\text{R}}_2^{\ast }$ after iron extraction were observed in both tissues (Table 2, and Supplementary Figure 2). This is the opposite directional change if the orientation dependent $\mathrm{\Delta }{\text{R}}_2^{\ast }$ is assumed to originate from iron and, therefore, supports that iron is not the primary source for the orientation contrast. The observation may be explained as follows: when iron exists, spins near the iron experience a dipole-patterned field perturbation. This field perturbation changes the phase of the spins and results in the loss of signal from phase cancellation. Once the iron is removed, more spins contribute to the orientation dependent ${\text{R}}_2^{\ast }$ contrast. Hence, the increase in the number of protons contributing to the contrast may increase $\mathrm{\Delta }{\text{R}}_2^{\ast }$, and explain our experimental measurements.

In the iron extraction and temperature experiments, the ROIs in the basal ganglia may contain internal capsule fibers. These fiber are oriented in the through plane direction (see figure 6 in (Lee et al., 2011)) and, therefore, may not contribute to the ${\text{R}}_2^{\ast }$ change.

Temperature is an important factor that may explain the contrast difference between in vivo and fixed tissue. Our experimental results show that at 38 °C, ${\text{R}}_2^{\ast }$ was lower and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ was larger than those at 20 °C. This trend agrees with the measurements in the literatures where much larger $\mathrm{\Delta }{\text{R}}_2^{\ast }$ was observed in vivo (Sati et al., 2011) than in fixed tissues (Lee et al., 2011) and ${\text{R}}_2^{\ast }$ was lower in vivo (Li et al., 2006) than in fixed tissue (Lee et al., 2011). The temperature dependent ${\text{R}}_2^{\ast }$ and $\mathrm{\Delta }{\text{R}}_2^{\ast }$ can be explained by the changes in magnetic susceptibility and molecular motion including spin exchange and diffusion. Increased temperature enhances motion, resulting in reduced R₂ and ${\text{R}}_2^{\ast }$ by increased spin interaction and motional averaging of spin phase. In addition, the volume magnetic susceptibility also increases with temperature, and the rate of change depends on the tissue type (Stollberger et al., 1998). Thus as temperature increases, ${\text{R}}_2^{\ast }$ may be increased by the magnetic susceptibility change but this effect is opposed by the molecular motion. In our experiment, decreased ${\text{R}}_2^{\ast }$ was observed at a higher temperature, suggesting that the molecular motion dominates the magnetic susceptibility effects. On the other hand, we observed increased $\mathrm{\Delta }{\text{R}}_2^{\ast }$ in white matter at a higher temperature, indicating that increased magnetic susceptibility effect may have influenced the $\mathrm{\Delta }{\text{R}}_2^{\ast }$ contrast assuming the motional effect is additive in ${\text{R}}_2^{\ast }$. Note that the temperature does not fully explain the contrast difference observed between in vivo and fixed tissue and other factors including microstructural change during fixation may have influenced the contrasts.

In our experiment, approximately 2°C temperature drop (from 38°C to 36°C) was observed before and after the MRI scan. Compared to the overall temperature change (17°C, from 21°C to 38°C), this has limited effects on $\mathrm{\Delta }{\text{R}}_2^{\ast }$.

Our study suggests that iron is not a primary source for the orientation contrast. This leaves myelin as a primary candidate of the $\mathrm{\Delta }{\text{R}}_2^{\ast }$ contrast. The $\mathrm{\Delta }{\text{R}}_2^{\ast }$ measurement showed a substantial level of contrast at 7 T in vivo (Sati et al., 2011; Wiggins et al., 2011). Hence, $\mathrm{\Delta }{\text{R}}_2^{\ast }$ may be used as a new biomarker for myelin. One of the challenges in acquiring this contrast is positioning a head in multiple orientations. Recently, methods have been suggested to reduce the number of orientations (2 to 4) required for the orientation dependent magnetic susceptibility contrasts (Li et al., 2012b; Oh et al., 2012). With a few orientations in small angles, the contrast may be used to generate a myelin content map to assess myelination changes in neurological disorders.