A review of calibrated blood oxygenation level-dependent (BOLD) methods for the measurement of task-induced changes in brain oxygen metabolism

Abstract

The dynamics of the blood oxygenation level-dependent (BOLD) response are dependent on changes in cerebral blood flow, cerebral blood volume and the cerebral metabolic rate of oxygen consumption. Furthermore, the amplitude of the response is dependent on the baseline physiological state, defined by the haematocrit, oxygen extraction fraction and cerebral blood volume. As a result of this complex dependence, the accurate interpretation of BOLD data and robust intersubject comparisons when the baseline physiology is varied are difficult. The calibrated BOLD technique was developed to address these issues. However, the methodology is complex and its full promise has not yet been realised. In this review, the theoretical underpinnings of calibrated BOLD, and issues regarding this theory that are still to be resolved, are discussed. Important aspects of practical implementation are reviewed and reported applications of this methodology are presented.

INTRODUCTION

The introduction of blood oxygenation level-dependent (BOLD) contrast in the early 1990s heralded a revolution in functional neuroimaging (1–4) that led to the widespread application of functional MRI (fMRI) to map patterns of activation in the human brain. However, the BOLD response to task-related activation is a complex function of underlying changes in cerebral blood flow (CBF) and cerebral metabolic rate of oxygen consumption (CMRO₂). This is characterised by a disproportionate increase in CBF relative to the accompanying increase in CMRO₂ generated by increased neuronal activity (5). It is important to note, however, that the relative changes in CBF and CMRO₂ alone do not determine the amplitude of the BOLD response. The scaling of the BOLD response is also determined by the baseline physiological state of the individual under examination. This baseline is determined by the total amount of deoxyhaemoglobin present in the voxel, which is a function of the subject’s haematocrit (Hct), baseline oxygen extraction fraction (OEF) and baseline cerebral blood volume (CBV). As these physiological variables are typically unknown in an fMRI experiment, it is not possible to interpret the BOLD signal in a quantitative manner.

Combining a BOLD response measurement with an additional measurement of CBF, acquired with an arterial spin labelling (ASL) experiment, provides a more quantitative insight into the underlying physiological changes. However, this still does not provide sufficient information to estimate CMRO₂, because of the unknown baseline state variables. The calibrated BOLD approach seeks to measure this baseline condition through a calibration experiment (6). When combined with measurements of CBF and BOLD acquired during a stimulation experiment, the percentage change in CMRO₂ during the stimulation can be measured. The development and evolution of calibrated BOLD methods have been reviewed recently by Pike (7).

Although BOLD fMRI alone is essentially a qualitative index of brain activity, the calibrated BOLD method offers the potential to make fMRI into a quantitative probe of brain physiology with the promise of an expanded clinical role. The methodology is complex, however, and this promise has not yet been realised. In this review, we discuss the theoretical underpinnings of calibrated BOLD, and issues regarding this theory that still need to be resolved. We also review aspects of practical implementation and reported applications of this methodology.

THEORETICAL UNDERPINNINGS

Physiology of the BOLD response

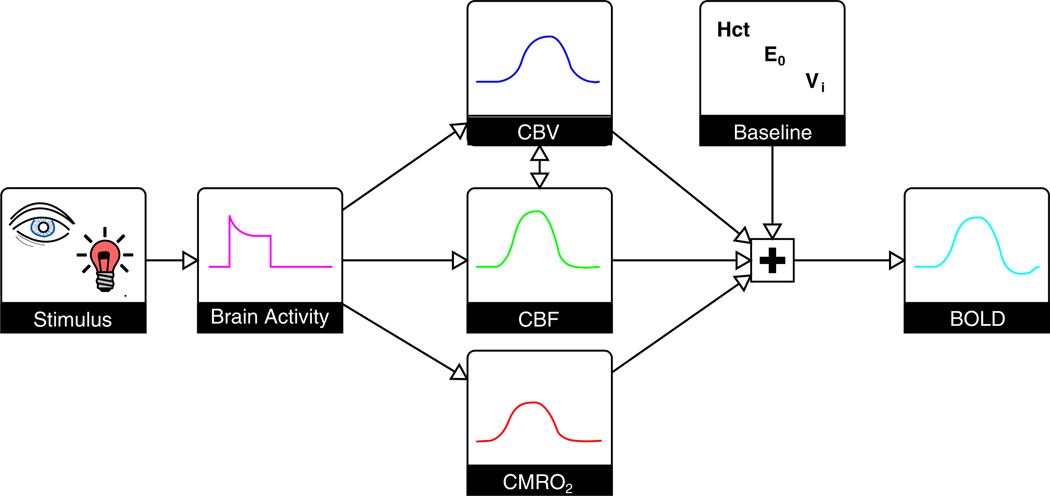
The interpretation of the relative changes in the BOLD signal in terms of metabolic activity is much more difficult than merely mapping its location, because the BOLD signal depends on CBF, CBV and CMRO₂ in a complex manner (Fig. 1). Together, these parameters determine the amount of deoxyhaemoglobin present in the imaging voxel. This is important as haemoglobin exists in two forms: paramagnetic deoxyhaemoglobin and diamagnetic oxyhaemoglobin (8). The deoxyhaemoglobin concentration within the blood is therefore the major determinant of its magnetic susceptibility, in turn altering the MR signal both within the vessel and around it (1). At rest, arterial blood is nearly fully oxygenated with approximately 40% of the oxygen extracted during its transit across the capillary bed (9,10). This creates a significant amount of deoxyhaemoglobin in the venous and capillary vessels. If, during neural activation, OEF remained constant, the deoxyhaemoglobin concentration would be unchanged, and only small changes in the MR signal would occur as a result of volume exchange effects (11). Fortunately for the neuroimaging community, neural activation is accompanied by a much larger increase in CBF than in CMRO₂ (5), resulting in a disproportionate increase in blood oxygenation. As the deoxyhaemoglobin concentration of the blood is decreased, the MR signal is increased, giving rise to the classic positive BOLD response (12). Changes in CBV add to this complexity by altering the total amount of deoxyhaemoglobin in the voxel and also through volume exchange effects, whereby the intravascular blood volume replaces extravascular tissue volume. The establishment of a firm understanding of the relationship between the BOLD signal and the underlying neurophysiology, including CBF, CBV and CMRO₂, remains a challenging yet vital task for the accurate interpretation of fMRI studies.

Figure 1.

The blood oxygenation level-dependent (BOLD) response is a complex signal. Basic sensory stimuli elicit an increase in neural activity, resulting in an increase in the cerebral blood flow (CBF) and cerebral metabolic rate of oxygen consumption (CMRO₂). CBF increases to a larger degree than CMRO₂, and also leads to a local increase in the cerebral blood volume (CBV). The amplitude of the resulting BOLD response is not only dependent on these changes, but also on the baseline physiological state. This baseline is determined by the blood haematocrit (Hct), resting oxygen extraction fraction (OEF) and CBV. An increase in CBF causes an increase in the BOLD signal, whereas increases in venous CBV (CBV_v) and CMRO₂ cause a decrease. Typically, the CBF effect is dominant, creating a positive BOLD response. The maximum BOLD signal change is determined by the baseline physiological state and increases with increasing Hct, OEF and CBV.

Modelling the BOLD response

A key component of the calibrated BOLD method is an accurate mathematical model describing how the BOLD signal depends on the underlying physiological changes. We first describe the standard model that typically has been used for the calibrated BOLD method, together with the calibration methods that have been proposed, and then consider some of the potential issues.

The Davis model was originally derived as a basic biophysical model of the dependence of the BOLD signal on changes in deoxyhaemoglobin content (6). The paramagnetic nature of deoxyhaemoglobin results in a large susceptibility difference between deoxygenated blood vessels and the diamagnetic tissue surrounding them. This difference in susceptibility results in microscopic magnetic field gradients outside of the vessels, which enhance the rate of decay of tissue protons that experience them. Theoretical and Monte Carlo numerical analyses of the extravascular change in $R_2^{*}$ resulting from this effect $(\mathrm{\delta }{R}_2^{*})$ have shown that it is a function of venous CBV (CBV_v, V₀) and the blood concentration of deoxyhaemoglobin ([dHb]₀) (13–15). This latter parameter is proportional to the product of Hct and the resting OEF (E₀). The effect of $\mathrm{\delta }{R}_2^{*}$ can be intuitively described as the signal difference between the normal resting deoxyhaemoglobin content and the case in which all of the deoxyhaemoglobin has been removed:

$$\delta R_2^{*}=\kappa V_0{[\text{dHb}]}_0^{\beta },\text{ where }{[\text{dHb}]}_0\propto E_0\text{Hct}$$ [1]

The constant κ incorporates several properties of brain tissue, including vessel geometry, magnetic field strength and the susceptibility difference between blood and tissue. The value of β is described as being dependent on the diameter of the blood vessels involved as a result of diffusion effects around the smallest vessels, with β = 1 for larger vessels (venules and larger draining veins) and β = 2 for capillaries (13). Davis et al. (6) performed Monte Carlo simulations to determine an average value of β given the distribution of vessel sizes in the brain, and suggested a value of 1.5 for experiments at 1.5 T.

The BOLD signal change can be expressed in terms of the change in $R_2^{*}$ between activated and rest states $(\mathrm{\Delta }{R}_2^{*})$, where V and [dHb] are CBV_v and the deoxyhaemoglobin concentration in the activated state, respectively:

$$\mathrm{\Delta }{R}_2^{*}=\kappa V{[\text{dHb}]}^{\beta }-\kappa V_0{[\text{dHb}]}_0^{\beta }$$ [2]

For small changes in $\mathrm{\Delta }{R}_2^{*}$, this can be linearised (16):

$$\frac{\mathrm{\Delta }S}{S_0}={\mathrm{e}}^{-\text{TE}\mathrm{\Delta }{R}_2^{*}}-1\approx -\text{TE}\mathrm{\Delta }{R}_2^{*}$$ [3]

Substituting for $\mathrm{\Delta }{R}_2^{*}$ in Equation [3] leads to:

$$\frac{\mathrm{\Delta }S}{S_0}=\text{TE}\kappa V_0{[\text{dHb}]}_0^{\beta }[1-\frac{V}{V_0}{\left(\frac{[\text{dHb}]}{{[\text{dHb}]}_0}\right)}^{\beta }]$$ [4]

This equation describes the basic extravascular physiological changes underlying the BOLD response, including the effect of baseline deoxyhaemoglobin content. This baseline effect is incorporated in a constant $M=\text{TE}\kappa V_0{[\text{dHb}]}_0^{\beta }$, representing the maximum signal change, sometimes known as the ceiling effect (17).

Traditionally, the measurement of CBV has proved difficult; therefore, in calibrated BOLD, this is generally inferred from measurements of CBF. This assumes a power law relationship CBV = k·CBF^α, where α = 0.38 is the classic value assumed from the early work of Grubb et al. (18). Following Fick’s principle (CMRO₂ = C_α·CBF·E), Equation [4] can be rewritten in terms of CBF and CMRO₂:

$$\frac{\mathrm{\Delta }S}{S_0}=M[1-{\left(\frac{\text{CBF}}{{\text{CBF}}_0}\right)}^{\alpha -\beta }{\left(\frac{{\text{CMRO}}_2}{{\text{CMRO}}_{2,0}}\right)}^{\beta }]$$ [5]

This is more commonly written in terms of CBF and CMRO₂ normalised to baseline values: f and r, respectively. Here, the fractional change in the BOLD signal (ΔS/S₀) is given the symbol δs:

$$\delta s=M[1-f^{\alpha -\beta }{r}^{\beta }]$$ [6]

This classic Davis model demonstrates the basic dependence of the BOLD response on CBF, the physiological maximum BOLD signal change M and changes in CMRO₂.

Although the parameter α in the Davis model has a relatively straightforward interpretation in terms of venous volume change, the parameter β is more complicated and has led to some confusion. In the original derivation, the physical motivation for β > 1 was the physics of how localised magnetic susceptibility differences create $R_2^{*}$ depending on whether diffusion is important (β = 2, capillaries) or unimportant (β = 1, veins) (13). However, the Davis model only takes into account extravascular signal changes and, as such, ignores contributions from the intravascular signal change. This contribution could be significant as $R_2^{*}$ of blood increases quadratically with increasing deoxygenation of haemoglobin (19–21). At magnetic field strengths below 3.0 T, the intravascular signal from the veins represents an important fraction of the BOLD signal and is estimated to be approximately 57% at 1.5 T and approximately 36% at 3.0 T (11). At 7.0 T, the venous signal is negligible in extravascular BOLD-weighted images. However, the effect of deoxygenated capillary blood becomes increasingly important at this field strength and contributes to the increased specificity of spin echo fMRI (22). Fortunately, the Davis model can be adapted to correct for the intravascular signal. Taking β > 1 provides a mathematical form that captures the basic effect produced by intravascular signal changes because it means that the BOLD response does not depend only on total deoxyhaemoglobin (i.e. V[dHb]). As a simple example of the expected effect of intravascular signal changes, let us suppose that activation induces an increase in blood oxygenation (decreased [dHb]) with an increase in CBV_v (V) which perfectly balances to create no change in total deoxyhaemoglobin: will there be a BOLD signal change? We might expect the extravascular BOLD effect to be minimal because total deoxyhaemoglobin does not change, but we would expect an intravascular BOLD effect because the intrinsic blood concentration of deoxyhaemoglobin is reduced. Because β > 1, the Davis model predicts a BOLD response for this scenario. Simulations with a much more detailed model of the BOLD response, including mixed effects of both small and large vessels, have found that the Davis model is reasonably accurate despite the limitations of the original derivation. It has also been shown that, if the parameters α and β are treated simply as fitting parameters, the predictions of the detailed model can be approximated more closely with reduced values of α and β. Nevertheless, the original values are reasonably accurate (23). It is important to note, however, that the parameter β captures multiple effects, and should not be interpreted in the way in which it was originally introduced. Other models have sought to directly incorporate intravascular signal changes (24) and measurements of CBV (25), but these methods still rely on the basic Davis model. The quantitative BOLD method developed by Yablonskiy and colleagues (26,27) uses a similar contrast mechanism to calibrated BOLD, but does not rely on the Davis model. In the quantitative BOLD model, the extravascular BOLD signal is effectively modelled by β = 1. However, β > 1 is not required to model the intravascular signal as this is an explicit part of the quantitative BOLD model.

The calibrated BOLD method is motivated by the mathematical form of Equation [6], which illustrates the fundamental complexity of the BOLD signal. Even if the values of α and β are assumed to be constant across subjects, there still remains uncertainty in the value of M. Because this parameter captures a number of aspects of the baseline physiological state, which are variable and unknown in most studies, it must be determined individually for a quantitative determination of the CMRO₂ change. It should be noted that, if M is known, a combined measurement of BOLD and CBF signals in response to a stimulus makes it possible to measure the fractional CMRO₂ change from Equation [6]. The goal of the calibration part of the experiment is to measure M.

Hypercapnia calibration

The administration of a hypercapnic gas mixture to the subject is used to elicit a CBF response and concomitant BOLD signal change with the assumption that only CBF is changed, with CMRO₂ unaffected (6). This gas mixture typically consists of 5% carbon dioxide, 21% oxygen and 74% nitrogen (6). Simultaneous measurements of CBF and BOLD during such a challenge are then combined with the Davis model Equation [6] to estimate the calibration parameter M:

$$M_{\text{hc}}=\frac{\delta s}{1-f^{\alpha -\beta }{r}^{\beta }}$$ [7]

Subscript ‘hc’ is used to differentiate this formulation from that of the other calibrations described below. Constants α and β represent flow/volume coupling (18) and the relationship between blood oxygenation and the BOLD signal (13), respectively. Modern practice sets the value of α as 0.2 based on measurements of CBV_v change, the vascular compartment that underlies the BOLD response (28). Similarly, β is chosen to be 1.3 for experiments at 3.0 T (29). The usual assumption that CMRO₂ is not altered by hypercapnia corresponds to r = 1.

As an alternative to gas administration, hypercapnia calibration has also been performed by means of a breath-hold. Similar changes in the arterial partial pressure of CO₂ (PCO₂) have been reported, but also result in a reduced arterial PO₂ (30). Whether such a stimulus has an effect on resting CMRO₂ is an unknown and complex issue. For a realistic breath-hold duration, only mild hypoxia is experienced, which may be at least partially compensated by increases in PCO₂ (31). Reasonable values for M_hc have been measured (30,32), with breath-holds of greater than 15 s duration also having been shown to be very reproducible (33). However, an altered arterial PO₂ may confound these estimates by producing an additional arterial signal weighting not present in artificially induced hypercapnia.

Hyperoxia calibration

With the hypercapnia approach to calibration, the idea is to measure the BOLD signal when CBF is varied by a known amount, but CMRO₂ is constant. In the hyperoxia approach, the goal is to measure the BOLD signal when venous oxygenation is changed by a known amount, but both CBF and CMRO₂ remain constant. In hyperoxia calibration, air with an enhanced oxygen level is administered to the subject (34). Hyperoxic gas mixtures containing between 25% (29) and 100% (34) oxygen have been reported in the literature. Because arterial haemoglobin is nearly fully saturated in normoxia, the extra inhaled O₂ is carried as dissolved gas in plasma. Because of this extra O₂ delivered to tissue, the venous haemoglobin oxygen saturation will increase slightly, producing a BOLD signal change. In the ideal experiment, CBF does not change during the inhalation of the hyperoxic gas mixture, meaning that measurements of CBF are not required to calculate M. Here, we use subscript ‘ho’ to differentiate the hyperoxic calibration parameter. For constant V, Equation [4] leads to Equation [8]:

$$M_{\text{ho}}=\frac{\delta s}{1-{(1+\frac{\mathrm{\Delta }[\text{dHb}]}{{[\text{dHb}]}_0})}^{\beta }}$$ [8]

The value of β takes the same definition as for hypercapnia calibration, leaving only the fractional change in deoxyhaemoglobin concentration (Δ[dHb]/[dHb]₀) to be determined. This is achieved using a model of the oxygen-carrying capacity of the blood and measurements of the end-tidal oxygen partial pressure (P_ETO₂). These measurements are used to infer the arterial partial pressure of oxygen (P_aO₂) after taking into account the alveolar–arterial oxygen gradient and assuming that arterial blood is well equilibrated with gas in the alveoli (34). [For details on how to perform such calculations, see Xu et al. (35).] This latter assumption relies on healthy lung function for its validity. At normoxia, oxygen is mostly carried bound to haemoglobin, with only a small amount dissolved in plasma. The amount of oxygen carried by arterial blood is determined by P_aO₂, which is linearly related for plasma (εP_aO₂) and nonlinearly related by the oxygen dissociation curve for haemoglobin saturation (S_aO₂). This latter component can be approximated by the following relation (36):

$$S_{\mathrm{a}}{\mathrm{O}}_2=\frac{1}{\frac{23400}{{(P_{\mathrm{a}}{\mathrm{O}}_2)}^3+150P_{\mathrm{a}}{\mathrm{O}}_2}+1}$$ [9]

As a result of the sigmoidal form of Equation [9], an increase in P_aO₂ caused by hyperoxia causes only a slight increase in S_aO₂. However, an increase in P_aO₂ results in a much larger increase in the amount of oxygen carried by the plasma, such that, during hyperoxia, the plasma contributes to a greater degree to the total delivery of oxygen than during normoxia. As blood passes through the capillary bed, the extraction of the excess oxygen in plasma offsets the extraction of oxygen bound to haemoglobin, so that, overall, the venous haemoglobin saturation increases. Regardless of the increase in oxygen carried by arterial plasma, the amount of oxygen carried by venous plasma remains small, as the venous partial pressure (P_vO₂) is low. Therefore, the assumption that P_vO₂ is negligible should not result in a large error, allowing Δ[dHb]/[dHb]₀ to be estimated as:

$$\frac{\mathrm{\Delta }[\text{dHb}]}{{[\text{dHb}]}_0}=\frac{\varphi [\text{Hb}]\mathrm{\Delta }{S}_{\mathrm{a}}{\mathrm{O}}_2+\epsilon \mathrm{\Delta }{P}_{\mathrm{a}}{\mathrm{O}}_2}{\varphi [\text{Hb}](1-S_{\mathrm{a}}{\mathrm{O}}_2(1-E_0))-\epsilon P_{\mathrm{a}}{\mathrm{O}}_2(1-E_0)}$$ [10]

where ϕ is the oxygen-carrying capacity of haemoglobin (1.34 mL O₂/g Hb), ε is the solubility coefficient of oxygen in plasma (0.0031 mL O₂/dL/mmHg) and ΔS_aO₂ and ΔP_aO₂ are the changes in these parameters as a result of hyperoxia relative to normoxia. For the calculation of M_ho, the haemoglobin concentration ([Hb]) is assumed to be 15 g Hb/dL (29,34) and the resting OEF (E₀) is assumed to be 0.3 (29). Essentially, these assumed values amount to a strong assumption that the venous deoxyhaemoglobin concentration in the baseline state is the same for all brain regions and all subjects. However, as [Hb] is related to Hct (Hct ≈ 0.03 × [Hb]), which is known to vary amongst subjects, this may be a source of error. In addition, this value of OEF is lower than the value of 0.4 generally reported (10), and OEF may well vary across the brain, particularly in disease. Unfortunately, CBF has been observed to decrease during hyperoxia (37). In this case, an additional measurement of CBF can be used to perform a correction for this effect (34):

$$M_{\text{ho}}=\frac{\delta s}{1-f^{\alpha }{(\frac{\mathrm{\Delta }[\text{dHb}]}{{[\text{dHb}]}_0}+\frac{r}{f})}^{\beta }}$$ [11]

Here, Δ[dHb]/[dHb]₀ reflects changes in the venous deoxyhaemoglobin concentration resulting from an increase in P_aO₂, and r/f accounts for changes that result from an alteration of CMRO₂ or CBF. It is assumed that CMRO₂ does not change during hyperoxia (r = 1). Although there is still debate about the validity of this assumption, the change in CMRO₂ is generally thought to be small (34,38).

R₂′ calibration

Although calibration can be performed without the administration of gases by asking the subject to hold his or her breath, it is also possible to calibrate the BOLD response without performing any respiratory manipulation at all, thereby avoiding physiological confounders, such as changes in CBF and CMRO₂. One way to achieve this is by estimating the baseline deoxyhaemoglobin content through a measurement of the relaxation properties of brain tissue (39,40). More specifically, the sensitivity of different aspects of transverse relaxation to deoxygenated blood vessels within brain tissue is exploited to make this possible. Transverse relaxation can be separated into processes that may be refocused by a spin echo and those that cannot, where R₂ is the irreversible relaxation and $R_2^{*}$ is the sum of the reversible and irreversible decay. The difference between these quantities is R₂′ (reversible relaxation alone). This parameter is sensitive to magnetic field inhomogeneity from several sources that act at different length scales. The macroscopic scale represents distances that are greater than the voxel dimension and result from differences in susceptibility at boundaries, e.g. the air–tissue interface. At the opposing extreme, the microscopic scale represents processes that occur at the atomic and molecular level. The space between these scales is defined as the mesoscopic scale. Importantly, at this scale, deoxygenated blood vessels cause local magnetic field inhomogeneities in the tissue. The magnitude of these fields, and hence their effect on the MR signal, is proportional to the deoxyhaemoglobin content of the voxel.

As a motivation for the use of R₂′ to estimate M, we note that if all of the effects underlying the BOLD response were reversible with a spin echo, then $\mathrm{\delta }{R}_2^{*}$ in Equation [1] (the change in $R_2^{*}$ caused by the presence of deoxyhaemoglobin) would be R₂′. From this, it follows that M is simply TE multiplied by R₂′ in the baseline state:

$$M_{{R\prime }_2}=\text{TE}\kappa V_0{[\text{dHb}]}_0^{\beta }=\text{TE}{R\prime }_2$$ [12]

Again, the subscript ‘R₂′’ is used to differentiate this definition of M from the two previous definitions. It is interesting to note that, in this definition, a value of β is not required as it is inherent in the measurement of R₂′. As an additional benefit, this method does not alter resting CMRO₂ or CBF, as may be the case with hypercapnia or hyperoxia. The central problem with this general argument, however, is that the effects leading to $\mathrm{\Delta }{R}_2^{*}$ are not all reversible. The diffusion-dependent simulations of Ogawa (13) suggest that both reversible and irreversible components exist, and perhaps, more importantly, intravascular signal changes at long refocusing intervals are expected to be largely irreversible. Nevertheless, simulations with a detailed model of the BOLD response suggest that these other effects approximately scale with R₂′ in the baseline state (40). However, R₂′ is also sensitive to the macroscopic field inhomogeneity caused by air–tissue susceptibility gradients in the head. To be a viable calibration method, the effects of this large-scale field inhomogeneity must be removed from the measurement of R₂′ in order to accurately estimate the baseline physiological state.

PRACTICAL IMPLEMENTATION

Multimodal imaging: combining measurements of BOLD and CBF

Calibrated BOLD relies on an inherently multimodal approach to imaging. Although the complexity of the BOLD response creates difficulties for the interpretation of the experimental results, when combined with measurements of CBF (and/or CBV) this complexity becomes an advantage. This combination allows changes in CMRO₂ to be investigated given a suitable mathematical framework (6,17,25). Measurements of CBF can be made using a range of ASL techniques. The specific details of the ASL method will not be covered here, as they are covered elsewhere in this special issue, but issues relevant to calibrated BOLD are discussed.

Although, initially, ASL and BOLD data were acquired in separate experiments (6), it is now far more common to acquire both within the same experiment. This is achieved in one of two ways: interleaved or single shot. In the interleaved method, the ASL and BOLD data are acquired from separate excitations, e.g. ASL tag image, BOLD image, ASL control image, BOLD image (16,30,34). The benefit of this approach is that images can be acquired at the optimal TE for each of the modalities. For ASL, the shortest attainable TE should be used (41), whereas it has been shown that the BOLD response is maximised when TE = T₂* (42). However, as this is a combination of two experiments, the ultimate temporal resolution is reduced, with a minimum around 4.5 s (30). The single shot method enables a higher temporal resolution by acquiring both ASL and BOLD from the same excitation (29,43–47). ASL and BOLD signals are disentangled by performing a surround subtraction or addition, respectively (48–50). In the simplest implementation of this method, a single echo is used with a TE selected as a trade-off between the optimal ASL or BOLD TE (29,45,47). However, a dual echo approach is recommended, giving more accurate CBF and BOLD measurements, as well as a greater degree of independence between datasets (43,44,51).

The term ‘arterial spin labelling’ applies to a collection of techniques developed to isolate and quantify the component of the MR signal that is derived from inflowing arterial blood delivered to capillary beds within the image voxel. The modelling of this signal can be performed to quantify local perfusion, more commonly referred to as ‘CBF’ (41). Many different perfusion-sensitive techniques have been created since the development of the first ASL method in 1992 (52), and each possesses a unique set of features designed to address one or more challenges associated with the measurement of CBF. These techniques can be broken down into two categories: pulsed ASL (PASL) (53) and continuous ASL (CASL) (52). Currently, the PASL technique is most commonly used in calibrated BOLD experiments, although CASL methods are seeing a resurgence with pseudo-continuous ASL (PCASL) methods (54). In the context of calibrated BOLD, it is important to consider several systematic errors that must be accounted for if accurate measurements of CBF are to be made. Of particular importance are the tagging efficiency, alterations to the T₁ of blood and accounting for transit delays. These sources of error have different implications for PASL and CASL techniques. In the latter case, we only consider PCASL, as CASL is rarely used in practice.

The tagging efficiency describes the effectiveness of a tagging pulse (or pulse train) at producing a bolus of blood with fully inverted magnetisation. This is an assumed value within the model used to quantify perfusion, required for the accurate measurement of CBF in physiological units (41). However, for calibrated BOLD, a measurement of absolute CBF is not necessary, as fractional changes are the only requirement of the Davis model Equation [6]. Therefore, as long as the tagging efficiency is constant throughout the experiment, its precise value is no longer important. A decreased tagging efficiency will, however, result in reduced signal-to-noise ratio in the acquired data. This assumption is valid for PASL techniques, but may be problematic for PCASL, which relies on a flow-driven inversion and is therefore dependent on the velocity of blood in the arterial blood vessels at the tagging location (55). Undermost experimental conditions, this velocity will remain fairly constant; however, under hypercapnia, a large increase in blood velocity within the internal carotid and vertebral arteries has been observed (55). It has been suggested that this will result in a reduced tagging efficiency, which will lead to a reduced fractional change in CBF.

The T₁ of arterial blood is similarly important in the quantification of CBF, and is assumed to be constant (41). Again, in general, this is a fair assumption, except under hyperoxia, where T₁ is known to be shortened by the presence of paramagnetic oxygen within the plasma (56,57). If this reduction in T₁ is not accounted for in the analysis, the expected flow reduction will be overestimated (37). This problem will affect both PASL- and PCASL-based techniques.

Finally, a key requirement of any ASL sequence is to produce a bolus of tagged blood with a well-defined temporal width and to ensure that the timing of the sequence allows for all of the tagged blood to be delivered to the tissue by the time images are acquired (48). An important problem in meeting this latter requirement is the variability of the transit delay time of arterial blood: the time required for blood to move from the tagging plane to the capillaries of the imaging voxel. The goal in an ASL experiment is to create a well-defined bolus of tagged blood and to wait a sufficiently long time for that bolus to clear from the large arteries and be delivered to the microvasculature within the image voxel. If the time between tagging and imaging is too short (i.e. an insufficiently long inversion time), regional CBF will be inaccurately measured. This will lead to an overestimation of CBF if tagged blood remains in the arterial macrovasculature. However, if the large vessel blood signal is suppressed, most commonly by the application of diffusion weighting, CBF will be underestimated, as not all of the tagged bolus has been delivered to the tissue at the time of imaging. In addition, the transit delay is not uniform across the brain, requiring that this variability must be accounted for in multislice imaging (58,59). This effect has the potential to affect both PASL and PCASL techniques.

Multimodal imaging: incorporating measurements of CBV

The incorporation of a measurement of CBV removes the assumptions about CBF/CBV coupling, but is complicated by the need to measure the volume change within the vascular compartment that underlies the BOLD response, primarily CBV_v. Techniques to measure CBV (60) predate both BOLD (1) and ASL (52) techniques. However, typically, they are sensitive to the total blood volume, i.e. the sum of arterial, capillary and venous volumes. In humans, these methods include gadolinium-based contrast agent techniques (61,62), as well as endogenous contrasts, such as vascular space occupancy (VASO) (63). Unfortunately, it has been shown that, during the active condition, arterial volume changes are proportionately larger than venous changes (64–66), and hence these techniques have the potential to overestimate the contribution of CBV_v to the BOLD response.

Formerly, it was assumed that the majority of blood volume change occurs in venous vessels (12,67). This motivated some researchers to incorporate a measurement of CBV into their calibrated protocol using the VASO technique (25,68). This provides a very elegant protocol, as it is possible to measure CBF, CBV and BOLD in a single experiment using a combined pulse sequence (69). However, the data of Lin et al. (25) suggest that α = 0.62, given a 68% increase in CBF and a 38% increase in CBV. This is consistent with positron emission tomography (PET) measurements of CBF/CBV coupling, where α = 0.64 was measured for total CBV in cortical grey matter (70). A larger value of α is consistent with a larger increase in CBV relative to CBF, which we would expect to be the case if arterial blood volume changes dominate.

To address this issue, new methods have been developed to specifically measure CBV_v. The venous refocusing for volume estimation (VERVE) method has been used to measure CBF/CBV_v coupling during neuronal activation (28) and in response to a hypercapnia challenge (71). However, this method is not easily incorporated into an ASL–BOLD pulse sequence and hence cannot be acquired simultaneously. CBV_v has also been measured using hyperoxia as a contrast agent (72,73), and has recently been incorporated into a calibrated BOLD measurement (74). Similar to VERVE, this method cannot be simultaneously acquired alongside ASL and BOLD data, as it requires BOLD-weighted data acquired at normoxia and hyperoxia. Finally, a new technique based on the principles of the VASO method has been developed to selectively image arterial CBV, known as inflow-based VASO (75). In combination with conventional VASO, this technique allows CBV_v to be estimated, but is critically dependent on accurate quantification in both methods.

Respiratory challenges

Hypercapnia and hyperoxia calibrations require the administration of gases to the subject, breath-holding excepted. There are many ways in which respiratory challenges can be performed, but they can largely be placed into two categories: those that present a gas with a fixed composition and those that target a specific end-tidal partial pressure of carbon dioxide (P_ETCO₂) or oxygen (P_ETO₂). The former methods benefit from experimental simplicity, whereas the latter provide greater repeatability across sessions and between subjects. A brief summary of both approaches is now presented.

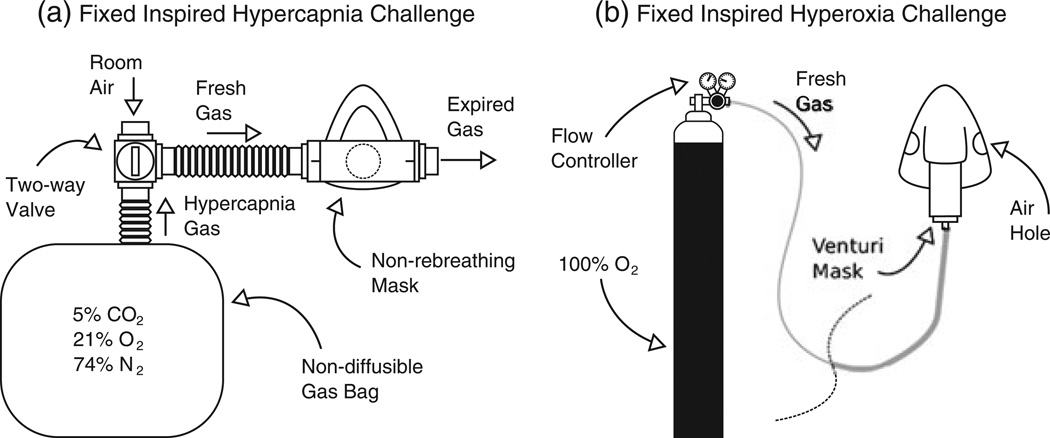
The fixed inspired hypercapnia challenge is typified by the use of a non-rebreathing mask connected to a large gas reservoir (Fig. 2a). A non-rebreathing mask ensures that the subject breathes in the prescribed CO₂ concentration. However, such a system does not control for the large difference in ventilatory response observed across the population (76). This can lead to large differences in P_ETCO₂ across subjects. Periods of normocapnia are interleaved with periods of hypercapnia in a block design by switching between room air and a premixed gas mixture. As noted above, hypercapnia calibration typically utilises a 5% CO₂–21% O₂–74% N₂ mixture (6), but other variations have also been employed. A lower 4% CO₂–21% O₂–75% N₂ mixture is used by some to mitigate the effects of any accompanying CMRO₂ reduction (30), whereas much higher 10% CO₂–90% O₂ carbogen mixtures have also been used to provide a more direct measurement of M by attempting to increase CBF to such a degree that deoxyhaemoglobin is completely washed out in order to produce the maximum possible BOLD signal (51).

Figure 2.

Schematic diagrams of the apparatus typically used to generate a fixed inspired hypercapnia challenge (a) and a fixed inspired hyperoxia challenge (b). In (a), a manually actuated valve enables the inspired gas to be switched between room air and a 5% CO₂–air mixture, whereas, in (b), during baseline subjects breathe room air through holes in the mask and hyperoxia is induced by allowing 100% O₂ to flow into the mask. Mixing with entrained room air reduces the inspired fraction of oxygen to approximately 50%.

With a fixed inspired hyperoxia challenge, a non-rebreathing mask is normally replaced with a standard venturi mask, or a nasal cannula (Fig. 2b). In both cases, 100% O₂ from a pressurised source is delivered to the mask/cannula, where it mixes with air entrained from the room, resulting in an O₂ concentration of approximately 50%. Interleaved blocks of normoxia and hyperoxia are achieved by switching off the oxygen source during normoxia, causing the subject to breathe room air through holes in the mask, and re-establishing flowing oxygen during hyperoxic periods. In a similar manner to the fixed inspired hypercapnia challenge, the final P_ETO₂ is dependent on each individual’s ventilatory response to the hyperoxic gas mixture.

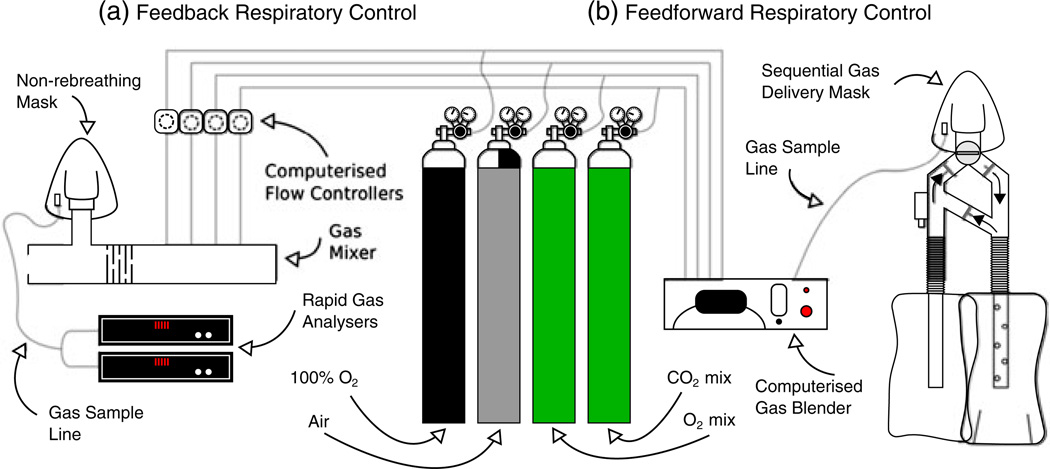
There are two end-tidal targeting methods currently in use with MRI that rely on either feedback (77,78) or feedforward (79) algorithms coupled to a computer-controlled gas mixer. Basically, the feedback method works by analysing the gas composition of the preceding breath of a subject and adjusting the composition of the inflowing fresh gas to force the end-tidal value towards the targeted value in the following breath. Hence, this method is often referred to as ‘dynamic end-tidal forcing’. This method requires fast gas analysers, and gas mixing must be performed close to the subject in order for rapid changes in composition to be made (Fig. 3a). The feedforward method relies on a model of alveolar gas exchange and the principles of sequential gas delivery. The inspired gas composition required to reach the targeted end-tidal value is determined prior to the start of the experiment. Gases are mixed outside of the magnet room and conveyed over gas lines to a sequential gas delivery mask worn by the subject (Hi-Ox⁸⁰, VIASYS Healthcare, Yorba Linda, CA, USA) (Fig. 3b). However, this method requires values for each subject’s metabolic rates of CO₂ production and O₂ consumption. These can be estimated from a look up chart, and are often refined by performing several test runs. For hypercapnia, calibration changes in P_ETCO₂ between 3 and 9 mmHg have been performed, whereas, for hyperoxia, changes in P_ETO₂ between 140 and 340 mmHg have been used (29). The advantage of using an end-tidal targeting method is that this targeted P_ETCO₂/O₂ level is independent of each subject’s ventilatory response, unlike fixed inspired challenges, giving rise to reduced intersession and intersubject variability (80,81).

Figure 3.

Schematic diagrams of the automated respiratory challenge apparatus currently in use with feedback (a) and feedforward (b) algorithms. The feedback algorithm works by analysing the gas composition of the preceding breath and adjusting the composition of the inflowing fresh gas to force the subject’s end-tidal values towards the targeted values in the following breath. The feedforward algorithm works by calculating the required gas composition to reach the given target end-tidal values using a model of alveolar gas exchange prior to the start of the experiment.

Relaxometry

There are two main ways to measure R₂′. Both methods exploit an asymmetric spin echo (ASE), but differ in how the images are acquired. We refer to these methods as single shot ASE (82) and gradient echo sampling of spin echo (GESSE) (26). The ASE experiment is a modification of the spin echo experiment, in which a 180° refocusing pulse is applied at TE/2 and the signal is acquired at TE. In the ASE experiment, the signal is still acquired at TE, but the 180° pulse is shifted in time by τ/2. This results in a spin echo being formed at TE − τ, and hence the signal is acquired with additional R₂′ weighting. However, it will also include additional signal decay as a result of the macroscopic magnetic field inhomogeneity, leading to the attenuation factor F, which is similarly a function of τ:

$$S_{\text{ASE}}=S_0{\mathrm{e}}^{-\text{TE}{R}_2}{\mathrm{e}}^{-\tau {R\prime }_2}F(\tau )$$ [13]

For a linear through-plane gradient under the assumption of a square slice profile, this attenuation factor can be described by a sinc function (26):

$$F(\tau )=\frac{\text{sin }(\tau \mathrm{\Delta }\omega /2)}{\tau \mathrm{\Delta }\omega /2}$$ [14]

where Δω is the frequency difference across the voxel. This is a function of the gradient (G_z) and the slice thickness (Δz), where γ is the gyromagnetic ratio for hydrogen.

$$\mathrm{\Delta }\omega =\gamma G_z\mathrm{\Delta }z$$ [15]

Therefore, care must be taken to account for the macroscopic field inhomogeneity. This is typically achieved by acquiring a high-resolution field map, calculating the derivative in the slice direction and correcting the intensity data using Equations [13]–[15] (26,27,83).

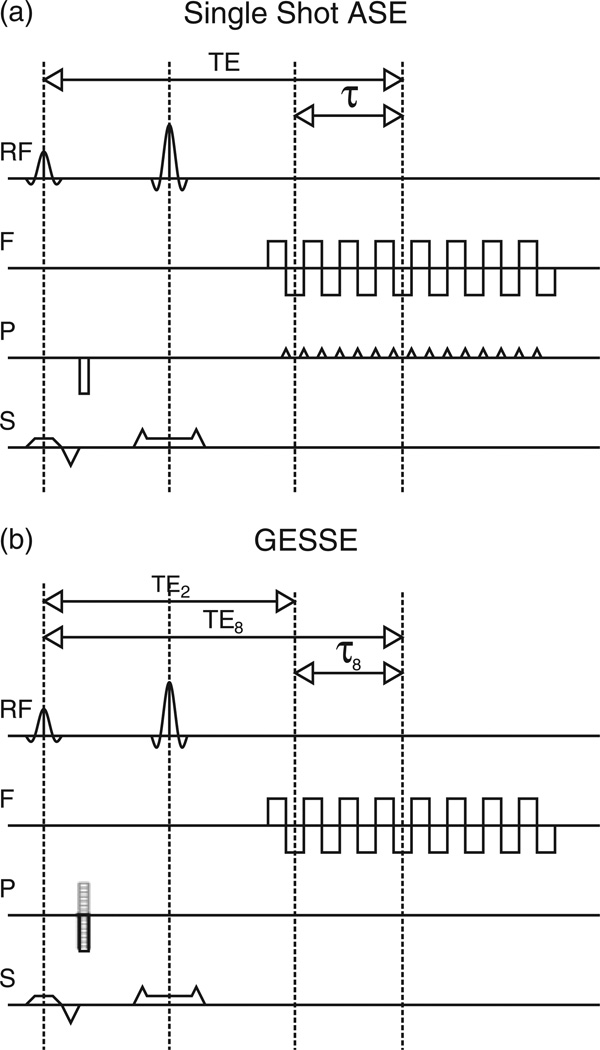
For single shot ASE, images are acquired using echo planar (82) or spiral (84) imaging techniques (Fig. 4a). Multiple experiments are performed with different values of τ, whilst keeping TE constant. As a constant TE leads to constant R₂ weighting Equation [13], R₂′ is easily measured by plotting S_ASE versus τ. However, correction for the magnetic field inhomogeneity can only be performed by acquiring a field map in a separate imaging experiment.

Figure 4.

Pulse sequence diagrams for the most common asymmetric spin echo (ASE) methods: (a) single shot ASE; (b) gradient echo sampling of spin echo (GESSE). The methods look very similar, but differ in the way in which phase encoding is applied. For the single shot approach, phase encoding is incremented between k-space traversals in the frequency encode direction using a phase encoding blip. The GESSE method takes a multi-shot approach in which phase encoding is applied prior to the switched frequency encoding gradient. Each lobe of this gradient produces multiple echoes with the same phase encoding. This phase encoding is then incremented across repetitions to fully sample k space.

At first glance, the image acquisition for the GESSE technique may seem to be remarkably similar. The switched gradient of the echo planar imaging sequence is retained, but rather than playing a blipped phase encode prior to each k-space line traversal, phase encoding is applied before the switched gradient and is incremented with each repetition of the whole sequence. Multiple shots are therefore required to cover the whole of k space. In this way, it is akin to a multi-echo spin warp sequence with the addition of spin echo refocusing (85). Lines of k space with the same effective TE are grouped together and reconstructed to form many images with a short interecho spacing. Unlike single shot ASE, both TE and τ are varied simultaneously, requiring that both R₂ and R₂′ be fitted. There are two ways of achieving this: simultaneous fitting of R₂ and R₂′ using Equation [13] (26) or fitting for R₂ first, then R₂′ (86). In the latter method, pairs of echoes either side of the spin echo are divided to remove R₂′ weighting and plotted versus 2τ to measure R₂. On removing the R₂ effect from the original data, R₂′ can be measured. Despite a more complicated fitting procedure, the data generated by the GESSE experiment can also be used to produce a field map without increasing the acquisition time (83,87). This can then be used to correct for the magnetic field inhomogeneity.

Finally, the temporal characteristics of the signal decay must also be considered when measuring R₂′. It has been shown that, for small values of τ, i.e. at points close to the spin echo, the signal decay is quadratically exponential, whereas, at longer τ, it reverts to the more usual monoexponential decay (14). This behaviour is a result of the susceptibility difference between deoxygenated blood within blood vessels and the surrounding tissue. This results in magnetic field gradients in tissue causing additional signal decay of tissue protons, and is the origin of the extravascular BOLD signal. This regime can be avoided by choosing values of τ ≥ 1.5 t_c, where t_c is dependent on the geometry of the vessels (4/3), the gyromagnetic ratio of hydrogen (γ), the magnetic field strength (B₀), the susceptibility difference between purely deoxygenated blood and tissue (Δω) and the venous blood oxygen saturation (Y):

$$t_{\mathrm{c}}=\frac{1}{\frac{4}{3}\pi \gamma B_0\mathrm{\Delta }\chi (1-Y)}$$ [16]

Typical values predict t_c to be of the order of 20 ms at 1.5 T and 10 ms at 3.0 T (14). Hence, at 3.0 T, only data with τ > 15 ms should be used for the calculation of R₂′.

POTENTIAL SOURCES OF ERROR

Hypercapnia calibration

Hypercapnia calibration relies on the assumption that hypercapnia is an isometabolic stimulus, i.e. it does not alter CMRO₂. Hence, in Equation [7], r is assumed to be unity. However, recently, it was observed that the inhalation of a 5% CO₂ mixture causes an appreciable reduction in resting metabolism (88). Using a combination of the T₂ relaxation under spin tagging (TRUST) method and phase contrast flow measurements, a 13.4% drop in CMRO₂ was measured. This is consistent with intracortical recordings that show a reduction in spontaneous neuronal activity during hypercapnia (89). In this case, inhalation of a 6% CO₂ mixture resulted in an approximately 15% reduction in multiunit activity. It must be noted, however, that the blood CO₂ levels reached in these artificially ventilated animal experiments will be higher than those expected in free-breathing humans, as humans are able to increase their ventilation rate and lower their PCO₂. Conversely, measurements using a susceptometry-based oximetry method did not observe any change in CMRO₂ in response to a 5% CO₂ challenge (90). A recent study with magnetoencephalography (MEG) found a fractional decrease in MEG power in the gamma band of 11% with the inhalation of 5% CO₂ in humans (91). Assuming that this translates to an equal fractional reduction in CMRO₂, the authors estimated the degree to which the assumption of isometabolism with CO₂ inhalation affects the estimates of CMRO₂ change.

The question of the degree of CMRO₂ reduction with mild hypercapnia requires further study, but this is an important concern for the accuracy of the hypercapnia calibration. Reduced resting CMRO₂ would lead to an overestimated M_hc value and, in turn, an overestimated stimulus-evoked CMRO₂ change. To estimate the magnitude of this error, we can substitute standard literature values into Equation [7], assuming r = 1 (no CMRO₂ change) or r = 0.87 (13% reduction in CMRO₂). With a true M_hc of 6.4%, a flow change caused by hypercapnia of 44% [cf. ref. (29)] and α/β = 0.2/1.3, the value of M_hc is predicted to be 35% overestimated. Given a 1.2% stimulus-evoked BOLD response and accompanying 48% flow change, this results in an approximately 5% overestimation of the stimulus-evoked CMRO₂ change. As a result of the nonlinear form of the Davis model, this error could vary considerably for different conditions, i.e. different BOLD/CBF changes, values of α and β, etc.

Hyperoxia calibration

It has also been observed that hyperoxia may alter resting CMRO₂ (38). In this work, a 10% reduction in CMRO₂ was observed in response to a 50% O₂ mixture. However, stimulus-evoked CMRO₂ changes have been shown to be unaltered by the inhalation of 100% O₂ (92), and PET data acquired in patients with traumatic brain injury showed no change in resting CMRO₂ (93).

Assuming, for the sake of argument, that CMRO₂ is reduced during hyperoxia, then M_ho will be overestimated in the calibration experiment. In turn, this will cause the stimulus-evoked CMRO₂ change to be overestimated. The same approach as for hypercapnia calibration can be used to estimate this error with a hyperoxic r = 0.9. Following the data analysis approach of Mark et al. (29) and using their measured M_ho value of 5.2% as truth, we found that M_ho was overestimated by 53%. This results in an 8% overestimate of the change in CMRO₂. These estimates include the same caveats as mentioned for hypercapnia.

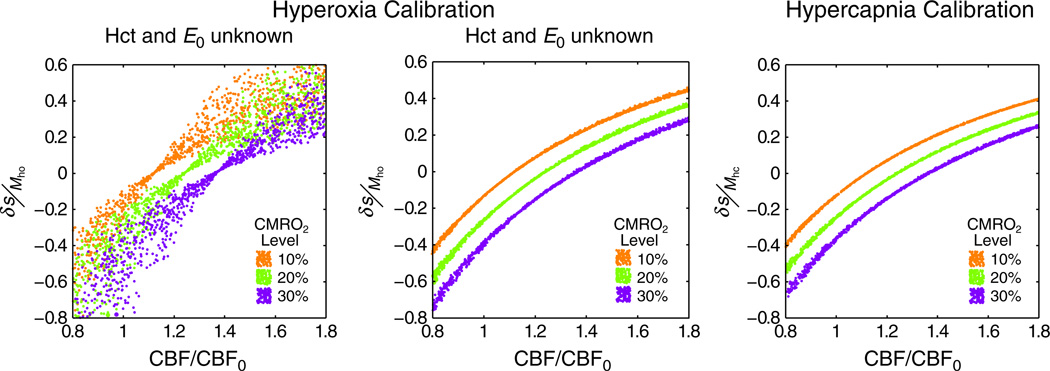
In addition to the assumption of isometabolism, hyperoxia-calibrated BOLD requires strong assumptions about the baseline physiology of the subject. In order to calculate the change in deoxyhaemoglobin concentration (Δ[dHb]/[dHb]₀) using Equation [10], values for the total haemoglobin concentration ([Hb], approximately equivalent to Hct/0.03) and OEF (E₀) are required. The former is standardly assumed to be 15 g Hb/dL (Hct ≈ 0.45) (29,34), whereas the latter is assumed to be 0.3 (29). This value of OEF is lower than generally reported values of 0.4 in the PET literature (10). Recent simulations have shown that these assumed values do not enable hyperoxia calibration to account for differences in physiological baseline across the population (40). Figure 5 propagates these errors through to the measurement of the stimulus-evoked CMRO₂ change for three different levels: 10%, 20% or 30% increase in CMRO₂. Random combinations of the variables Hct, E₀ and V_i (total CBV) were selected from the following ranges: Hct = 0.37–0.50, E₀ = 0.3–0.55 and V_i = 0.01–0.10. Each point in Fig. 5 represents one of these combinations, with corresponding BOLD responses and M values calculated for each combination [see ref. (40) for further details]. The effect of this variability on the standard hyperoxia calibration approach can be seen in Fig. 5a. It is not possible to distinguish different lines of CMRO₂ change, apart from very low CBF changes. In contrast, when the values of Hct and OEF are known, and can be substituted into Equation [10], this variability is drastically reduced (Fig. 5b). For comparison, Fig. 5c displays the simulation for hypercapnia calibration in which assumptions about baseline physiology are not required. Unfortunately, information about local OEF is not easy to obtain, even though the systemic Hct is easily measured from a sample of the subject’s blood. Whole brain measurements of OEF can be made using the TRUST technique by measuring the oxygen saturation of blood in the sagittal sinus (94). Local information regarding vessel geometry and CBV_v can then be retained by substituting this information into Equation [10], although spatial information will inevitably be lost because of the use of a global value of OEF.

Figure 5.

Simulation of the effect of baseline physiological variability on two calibration methods. (a) Using the standard approach to hyperoxia calibration results in a high degree of uncertainty in the resultant measurement of the cerebral metabolic rate of oxygen consumption (CMRO₂) because of the use of an assumed haematocrit (Hct) and resting oxygen extraction fraction (OEF). The blood oxygenation level-dependent (BOLD) signal change normalised by the BOLD scaling parameter (δ S/M) is plotted against the change in cerebral blood flow (CBF) normalised to baseline (CBF₀). (b) If these values are known on an individual subject basis, this uncertainty is markedly reduced. (c) For comparison, the standard approach to hypercapnia does not suffer from the same uncertainty as it does not require assumptions about baseline physiology.

Finally, as noted above, the presence of paramagnetic oxygen in plasma causes a reduction in blood T₁ that confounds the estimation of CBF using ASL. This effect has additional implications for BOLD measurements using rapid gradient echo imaging. However, typically, the repetition time of ASL/BOLD acquisitions is greater than 2.4 s, where such T₁ effects will be insignificant.

R₂′ calibration

Although R₂′ calibration does not require assumptions of isometabolism or physiological baseline, it is sensitive to macroscopic field inhomogeneity. This residual field distortion is caused by susceptibility differences within the head, i.e. at the nasal sinuses, where tissue and air have very different susceptibilities. The resulting ASE signal Equation [13] therefore suffers an additional attenuation (F) which is dependent on the magnitude of the magnetic field gradient across the slice and the value of τ. This is evidently a potential source of error in R₂′ calibration and could lead to an overestimation of M_R′2 and the stimulus-evoked CMRO₂ change. Assuming M_R′2 = 6.4% [i.e. equivalent to M_hc in ref. (29)] would require an R₂′ value of 2.14 s⁻¹ given the standard BOLD-weighted TE of 30ms Equation [12]. Taking a typical frequency difference across a voxel of 20 s⁻¹ (40), this would increase R₂′ to 2.64 s⁻¹. Consequently, M_R′2 is overestimated by 24% and the stimulus-evoked CMRO₂ change by 3%. This estimation is based on the same BOLD and CBF changes as used for the other calibrations, and is subject to the same provisos.

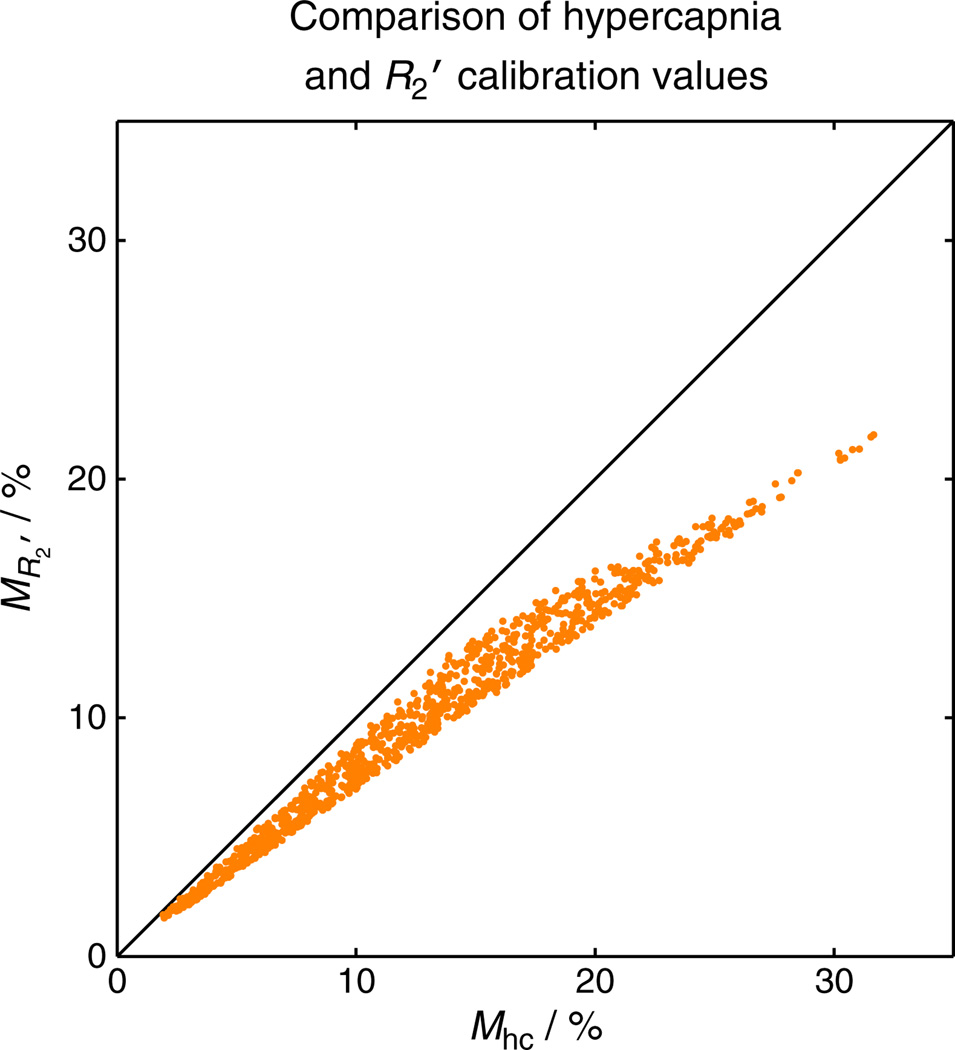
As a consequence of acquiring M_R′2 in the resting condition, it is likely that it will be underestimated with respect to M_hc. This is a result of the use of a 180° radiofrequency pulse and its efficiency at refocusing the dephasing of protons surrounding vessels of different scales. This effect is characterised by two regimes: static dephasing and motional narrowing. In the former regime, protons are considered to be static with respect to deoxygenated blood vessels. Under this condition, the amount of phase accrued before and after the refocusing pulse is equal but opposite in sign, enabling the signal to be refocused. In practice, to satisfy this condition, the proton must only diffuse a small distance relative to the diameter of the blood vessel to retain its spin history. However, in the motional narrowing regime, the diffusion length of the proton is large compared with the vessel diameter and, as such, will sample a large number of different field gradients. In this case, the spin history of the proton is lost and the signal cannot be recovered. Equation [1] models this effect through the parameter β, with β = 1 for static dephasing and β = 2 for motional narrowing. The transition between these regimes occurs around a diameter of approximately 7 µm, with capillaries below this threshold and venules and larger draining veins above it. In addition, the motional narrowing regime is at play within the vessels in which proton diffusion lengths are greater than the diameter of the deoxyhaemoglobin-containing red blood cells. Therefore, we expect to be missing extravascular signal contributions from capillaries and intravascular signals from blood. Following the simulation methodology of Blockley et al. (40), we can calculate this underestimate for a reasonable range of physiological variability: Hct = 0.37–0.50, E₀ = 0.3–0.55 and V_i = 0.01–0.10. Figure 6 plots the results of the generation of M values for each random combination of physiological parameters. Although M_R′2 tracks linearly with M_hc, it is not directly proportional. Fitting to this data reveals that the value of M_R′2 is only approximately 75% of M_hc. However, simulations to assess the variability of this scaling with variations in physiology have shown this value to be relatively stable (40).

Figure 6.

Simulation of blood oxygenation level-dependent (BOLD) scaling parameter M for the hypercapnia and R₂′ calibration methods. As a result of the effect of diffusion around capillaries, the spin echo refocusing pulse is unable to recover signal lost to dephasing around these vessels. Therefore, R₂′ calibration will give a value of M that is lower than that measured using hypercapnia. Further simulations suggest that the required scaling between these methods is relatively stable across different physiological baseline conditions.

Finally, R₂′ calibration assumes that deoxyhaemoglobin is the dominant source of paramagnetism in the brain (95). However, the presence of another source of paramagnetism is not sufficient to confound the use of R₂′ as a calibration. The geometry of the inclusion determines its effect on R₂′, with maximal effect when the length scale of the deposit is in the static dephasing regime. This dimension is approximately equivalent to a cylinder with a radius of 7 µm, but falls away rapidly with reduced radius (15). There are two main conditions in which an elevated R₂′ has been measured as a result of paramagnetic deposits: Parkinson’s disease and brain haemorrhage. Parkinson’s disease is known to result in increased deposition of iron in the substantia nigra, consisting of neuromelanin granules and iron-filled Lewi bodies (96). This has been shown to result in elevated R₂′ measurements (97). Brain haemorrhage causes bleeding into the extravascular space and the production of haemosiderin, leading to an increase in R₂′ (98). Care must be taken when performing R₂′ calibration in individuals with these conditions. Other brain iron sources, such as ferritin and transferrin, have sufficiently small dimensions such that they do not exhibit an R₂′ effect as a result of motional narrowing. For example, changes in R₂ are measured in Alzheimer’s disease, but changes in R₂′ have not been reported, suggesting that iron inclusions in this disease are in the motional narrowing regime. Further work is required to examine other diseases in which iron is thought to be deposited for their effect on R₂′, such as multiple sclerosis, Huntington’s disease, neuroferritinopathy and Friedrich’s ataxia.

CBF/CBV coupling

In general, changes in CBV are inferred from measurements of CBF in the calibrated BOLD experiment (6). This is achieved by assuming a power law relationship between CBF and CBV based on the animal work performed by Grubb et al. (18); hence, the exponent is often referred to as the Grubb constant α:

$$\mathrm{\upsilon }=f^{\alpha }$$ [17]

Here v and f are the normalised changes in CBV and CBF. Grubb et al. measured α to be 0.38. Recently, work based on measurements of CBV_v, the vascular compartment that underlies the BOLD response, have caused this value to be revised to between 0.18 and 0.23 (28,71). However, these values only represent the mean coupling ratio and, in practice, there could be substantial variation across subjects. A recent simulation study examined the sensitivity of the Davis model to the value of α, alongside other physiological parameters (23). Although α was not the largest driver of variation in M, it was shown to cause the largest error in the estimate of the change in CMRO₂. Further simulations showed that this error was not as large for hypercapnia calibration as for hyperoxia and R₂′ calibrations (40). This is presumably a result of the inclusion of α in both the calibration Equation [7] and CMRO₂ estimation Equation [6] steps of hypercapnia calibration, leading to some compensation for inaccuracies in the value of α.

APPLICATIONS

Coupling of CBF and CMRO₂

A number of studies have investigated the variability in the coupling of CBF and CMRO₂. This is often characterised by the parameter n, the ratio of the fractional changes in CBF and CMRO₂:

$$n=\frac{f-1}{r-1}$$ [18]

One study investigating the reproducibility of calibrated BOLD studies found that the value of n was more reproducible than the values of the CBF and BOLD responses themselves, consistent with the idea that a subject’s response to the same stimulus could vary day to day, but the CBF/CMRO₂ coupling ratio is more stable (99). In comparing different reported values of n, it is important to keep in mind the potential biases in these measurements related to the estimate of M (43,100): for given CBF and BOLD responses to a stimulus, if M is overestimated, n will be underestimated.

Studies measuring n in motor and visual areas have found values in the range 2–4, with perhaps a trend for higher values in motor areas (6,16,43,99,101–103). Two studies in subcortical regions both found n < 2 (104,105). These studies also emphasise that the BOLD response is sensitive to the value of n when n ~ 2. For example, n was found to be reduced in basal ganglia structures when compared with visual cortex (105). Although the basal ganglia BOLD response to a complex finger-tapping task was about seven times weaker than the visual cortex BOLD response to a visual task, the ratio of the CMRO₂ response was only around two-fold weaker. This effect was not caused by differences in M, but rather to a modest change in n, from approximately 1.7 in the basal ganglia to approximately 2.3 in the visual cortex. This illustrates that the relative magnitudes of the BOLD responses are a poor quantitative guide to the magnitudes of the underlying physiological changes. To date, there have been a few studies of CBF/CMRO₂ coupling in deactivations (102,106,107), but this remains an area that requires further exploration.

More recently, the effect of stimulus strength was investigated by varying the contrast of a simple visual stimulus; it was found that, within the same region of visual cortex, n increased with increasing stimulus contrast (108). Similarly, a change in n with the frequency of the visual stimulus has been reported based on PET measurements (109) and, more recently, using calibrated BOLD (110). In another recent study looking at the effects of attention, it was found that n was substantially larger when a stimulus was attended compared with when it was unattended (111). Finally, a few promising studies have begun to look at CBF/CMRO₂ coupling during resting state spontaneous activity (112,113), and this is another area of future growth.

In short, the interesting idea suggested by calibrated BOLD studies is that the coupling ratio n is not fixed, and can vary depending on the neural activity evoked. This basic uncoupling is consistent with current ideas about the drivers of CBF and CMRO₂ changes in response to neural activity. Although the CMRO₂ response may simply reflect the energy cost of the evoked neural activity, the fast CBF response associated with fMRI signals is thought to be driven directly by neural signalling itself (114), with the astrocytes as intermediaries (115,116), and not by the energy metabolism change. This may be a feedforward response, increasing CBF in anticipation of a need for increased CMRO₂ in order to prevent a decrease in tissue oxygen (17,117). The important bottom line, however, is that the variation of n, even in the healthy brain, has a substantial effect on the BOLD response, justifying more routine application of the calibrated BOLD methodology.

Prior to the introduction of calibrated BOLD methods, PET methods were used to measure the CBF/CMRO₂ coupling ratio under different stimulus conditions. However, the early results measured by both techniques revealed a discrepancy. For example, the seminal PET study of Fox and Raichle (5) with somatosensory stimulation found n ~ 5, whereas the pioneering calibrated BOLD studies of Davis et al. (6) and Hoge et al. (16) found n ~ 2–3 in visual cortex. However, subsequent PET studies have found a broader range of n [including n ~ 2 in visual cortex (118)]. At this point, it is unclear whether there is a systematic difference between the methodologies (17,25) and, in part, the variability may reflect the true variability across the brain and with different stimuli, as discussed below.

Pharmacological confounders of the BOLD response

The potential effect of drugs on the BOLD response is one of the most important confounding effects that must be addressed when performing fMRI studies in disease populations. Any drug that alters baseline CBF, CMRO₂ or, plausibly, even Hct could alter M. In an early study of the effect of acetazolamide, a carbonic anhydrase inhibitor, a modest increase in baseline CBF (~20%) was observed and an associated larger decrease in the BOLD response (~35%) to a simple finger-tapping task (119). This strong effect on the BOLD response is consistent with the expected reduction in M caused by a 20% increase in baseline CBF with no change in baseline CMRO₂. Similarly, the effect of indomethacin on CBF and CMRO₂ has been investigated using calibrated BOLD (120). Indomethacin is a nonsteroidal antiinflammatory drug commonly used to reduce fever, pain and stiffness. Baseline CBF was observed to decrease following indomethacin administration, and the CBF and BOLD responses to a finger-tapping task were reduced (46% and 22%, respectively) when compared with the pre-drug responses. The CMRO₂ response, as calculated using the Davis model (6), did not change between the pre- and post-drug states, which was interpreted as evidence that indomethacin has a purely vasoactive effect on the brain. However, in this analysis, changes in CBF and BOLD were calculated with respect to the resting condition of the respective pre- or post-drug trials. It was shown later that, when these changes were calculated with respect to the resting condition of pre-drug trials, baseline CMRO₂ and the CMRO₂ response to stimulus were also reduced by indomethacin (121). This led to the alternative interpretation that indomethacin could have a primary effect on CMRO₂, with an associated coupled change in CBF.

Caffeine provides a useful pharmacological test of the calibrated BOLD methodology (44,45,122). It is a vasoconstrictor within the brain (123) and acts as an antagonist of adenosine receptors (124). Adenosine is an inhibitor of excitatory neural activity; therefore, the blocking of adenosine receptors by substances such as caffeine should result in the disinhibition of affected neurons. Experiments examining the effect of caffeine on the BOLD response have yielded conflicting results (123,125,126), with a number of studies reporting a reduction in baseline CBF (127–129). Calibrated BOLD, therefore, offers a way to disentangle the multiple effects that give rise to these results. Initial experiments confirmed a reduced baseline CBF (44,45) and an increased M value following caffeine administration (45). This latter finding is consistent with increased oxygen extraction at rest as a result of a decrease in CBF. However, both of these studies measured BOLD and CBF relative to their prestimulus baselines. This approach does not take into account the baseline shifts in absolute CMRO₂ and CBF, and led to the belief that CBF was more strongly affected than CMRO₂ by caffeine (44). More recently, the data of Perthen et al. (44) were revisited with a view to accounting for changes in baseline (122). This was achieved by quantifying the ASL data in physiological units and calculating $R_2^{*}$ from dual-echo BOLD-weighted data. Both measures are relatively robust absolute values, enabling pre- and post-caffeine data to be referred to the pre-caffeine baseline. This analysis showed a reduced CBF baseline, as before, and a smaller CBF response to stimulus. In addition, a trend towards increased baseline CMRO₂ was observed and a significant increase in the absolute CMRO₂ response to stimulus was found. These results offer a possible explanation for previous inconsistencies in the literature. The observed changes in CBF and CMRO₂ have opposing effects on the BOLD response, and it is easy to imagine the balance between them shifting to produce variable changes in the BOLD response.

Effects of ageing on the BOLD response

The use of calibrated BOLD in studies of ageing can help to disentangle the multiple effects at play. In one study, the effect of ageing on the stimulus-evoked response in the visual cortex was investigated (130). Hypercapnia calibration combined with a visual stimulus experiment was performed in two groups: younger (age, 21–35 years) and older (age, 45–60 years). Older subjects were observed to have lower baseline CBF in the visual cortex, but decreased values of M. This is somewhat paradoxical, as we would expect that reduced baseline CBF should increase oxygen extraction, leading to a larger value of M. However, a reduced M value could occur if CMRO₂ were also to decrease with CBF. During neural activation, the BOLD response was observed to decrease with age, but CBF and CMRO₂ were unaffected. This corresponds to a constant CBF/CMRO₂ coupling with age.

A further study of ageing used hyperoxia calibration with the aim of improving subject comfort and tolerance (47). In contrast with the previous study, this work examined the effect of ageing using a cognitive task rather than a basic visual stimulus. Unlike the study using a visual stimulus, the BOLD response was observed to increase with age in cognitive areas, but the CBF response did not. As the task was cognitive, performance accuracy data enabled the older subject group to be split into low- and high-performing groups. This further subdivision of the group revealed that the difference in BOLD, CBF and CMRO₂ responses to stimulus were not significant between young and old high-performing groups. However, the BOLD and CMRO₂ responses of young versus old low-performing groups were significantly different. These results suggest that the CBF/CMRO₂ coupling ratio (n) of the older high-performing group is not that different from that of the young group, but that the older low-performing subjects have an increased value of n. Further work is evidently required in the field of ageing to account for baseline changes in CMRO₂, and to confirm the reduction hypothesised by Ances et al. (130).

Measurement of resting CMRO₂ using calibrated BOLD

The next step in the development of calibrated BOLD has led researchers to consider its use for the measurement of the absolute resting CMRO₂ (131,132). It has always been clear that M contains information about baseline CMRO₂ because of its dependence on the resting OEF, but a means to disentangle its contribution to M has not existed until recently. Two methods have been proposed and both hinge on the idea of estimating M by two independent methods: hypercapnia and hyperoxia. Both also rely on the sensitivity of the hyperoxia method to Hct and baseline oxygen extraction (see section on Potential sources of error). However, they differ in the way in which OEF is estimated from the data. When this measurement of oxygen extraction is combined with CBF data, baseline CMRO₂ can be estimated via Fick’s law.

The method of Bulte et al. (132) uses Equation [7] to calculate M_hc, substitutes this value into Equation [8] and then rearranges for Δ[dHb]/[dHb]₀. For the ideal hyperoxia experiment, this gives:

$$\frac{\mathrm{\Delta }[\text{dHb}]}{{[\text{dhb}]}_0}={[1-\frac{\delta s}{M_{\text{hc}}}]}^{\frac{1}{\beta }}-1$$ [19]

where δs is the signal change caused by hyperoxia challenge. Given a measurement of Hct, Equation [10] can be rearranged to provide a measurement of OEF. The method proposed by Gauthier et al. (131) takes a subtly different approach. They previously proposed a generalised calibration model (GCM) suitable for calibration experiments with any combination of hypercapnia and/or hyperoxia (51). A single equation, based on Equation [4], can then be used to estimate M for a respiratory challenge with any combination of CO₂ and/or O₂:

$$\delta s=M[1-f^{\alpha }{\left(\frac{[\text{dHb}]}{{[\text{dHb}]}_0}\right)}^{\beta }]$$ [20]

The GCM enables [dHb]/[dHb]₀ to be calculated:

$$\frac{[\text{dHb}]}{{[\text{dHb}]}_0}=\underset{A}{\underbrace{\left(\frac{\frac{C_{\mathrm{a}}{O}_2{|}_0{E}_0}{\varphi [\text{Hb}]}}{1-\frac{C_{\mathrm{a}}{O}_2{|}_0}{\varphi [\text{Hb}]}(1-E_0)}\right)}}\frac{1}{f}+\underset{B}{\underbrace{\left(\frac{1-\frac{C_{\mathrm{a}}{O}_2}{\varphi [\text{Hb}]}}{1-\frac{C_{\mathrm{a}}{O}_2{|}_0}{\varphi [\text{Hb}]}(1-E_0)}\right)}}$$ [21]

where C_aO₂ is the amount of oxygen carried by arterial blood during the respiratory challenge and at baseline (subscript 0). All other parameters are as defined in the section on Theoretical underpinnings. Part A of Equation [21] deals with changes in oxygenation caused by a change in flow, whereas part B models changes caused by a change in P_aO₂. This equation enables M to be determined as a function of OEF (E₀). Gauthier et al. (131) plot the hypercapnic and hyperoxic M values for the full range of OEF. The intercept of these lines then defines the local OEF of the subject under examination. It is interesting to note that hypercapnia calibration only requires part A of Equation [21] and, for plausible values of OEF, can be reduced to 1/f. In this case, the methods of Gauthier et al. (131) and Bulte et al. (132) are mathematically equivalent. However, the use of GCM enables alternative calibration gases to be used, such as carbogen (5% CO₂, 95% O₂) (131).

There is one caveat related to this novel application of combined hypercapnia and hyperoxia calibrations that deserves comment. In deriving the modelling equations, we followed the historical development of the Davis model, which led to an expression for M as the particular lumped set of parameters in Equation [4]. However, we know that this form was derived by considering only extravascular signal changes, and more recent modelling indicates that intravascular signal changes and volume exchange effects play a significant role. For this reason, Equation [4] does not capture all of the effects that contribute to M. Nevertheless, this is not a problem in applying the Davis model for standard calibrated BOLD with hypercapnia calibration, as long as these other effects basically track with the extravascular effects, and more detailed modelling supports this (23). Put another way, the exact form of M in terms of the underlying physiological variables is never used in the hypercapnia-calibrated method; the scaling parameter M is simply measured. However, the combined hyperoxia and hypercapnia methods appear to require that Equation [4] is accurate, which is problematic given current modelling studies. This is an issue that requires further investigation.

SUMMARY AND FUTURE DIRECTIONS

The calibrated BOLD approach is beginning to mature as it has been adopted by a growing number of investigators. The technique has enormous potential to make fMRI quantitative, and to significantly improve the study of disease populations and the measurement of drug effects. In comparing responses in these applications, BOLD fMRI alone cannot distinguish between variations in the CBF response, CBF/CMRO₂ coupling (n) or the baseline state (M) (133). Calibrated BOLD offers the promise to resolve these ambiguities and to provide quantitative measurements of basic physiological variables. Nevertheless, there are still questions that need to be resolved and which deserve further investigation.

How large and how reproducible are the CMRO₂ changes with moderate hypercapnia?

The literature is variable on this question, and more experiments are needed to quantify this effect, particularly with regard to regional variation in the brain. If a given level of CMRO₂ reduction can be assumed, the hypercapnia calibration can be improved with an assumed value of r in Equation [7].

Is hyperoxia reliable for calibration?

The theoretical analysis suggests that the calibration is very sensitive to the assumed value of OEF. Although OEF at rest is relatively uniform in the healthy brain (134), this assumption could be problematic in studies of disease or drug effects.

Can the R₂′ method yield robust measurements?

This depends in part on the technical issue of correcting for the effects of large-scale field gradients on R₂′. In addition, R₂′ does not capture all of the effects associated with the BOLD signal change, as described above. For this reason, the derived estimate of M needs to be scaled up. Theoretical calculations suggest that this scaling is relatively stable in the face of variable physiology (40), but direct experimental comparisons between the calibration methods are needed.

How much does CBV_v change with activation?

This remains one of the most important confounding effects in the calibrated BOLD method. An advantage of the hypercapnia method is that it is less sensitive to the assumed change, because it is involved in the calibration experiment as well [although it is still important to consider whether the CBV change is different for hypercapnia and neural activation (135)]. The other two methods, however, do not involve CBV changes in the calibration, and it is thus critical to determine whether the assumed CBV change during neural stimulation is accurate. Further experimental work to determine the CBV_v change is needed.

Can we apply steady-state models to dynamic changes?

One of the most exciting possibilities of the calibrated BOLD method is to provide a way to measure, for the first time, the dynamics of CMRO₂ (136). A central question for future investigations is how our models need to be modified to make them accurate for dynamic changes.

Abbreviations used

ASE

asymmetric spin echo

ASL

arterial spin labelling

BOLD

blood oxygenation level dependent

CASL

continuous ASL

CBF

cerebral blood flow

CBV

cerebral blood volume

CBV_v

venous CBV

CMRO₂

cerebral metabolic rate of oxygen consumption

[dHb]

deoxyhaemoglobin concentration

fMRI

functional MRI

GCM

generalised calibration model

GESSE

gradient echo sampling of spin echo

[Hb]

haemoglobin concentration

Hct

haematocrit

M

BOLD scaling parameter

MEG

magnetoencephelography

n

CBF/CMRO₂ coupling ratio

OEF

oxygen extraction fraction

P_aO₂

arterial partial pressure of oxygen

PASL

pulsed ASL

PCASL

pseudo-continuous ASL

PET

positron emission tomography

P_ETO₂/CO₂

end-tidal partial pressure of oxygen/carbon dioxide

P_vO₂

venous partial pressure of oxygen

S_aO₂

arterial haemoglobin saturation

TRUST

T₂ relaxation under spin tagging

VASO

vascular space occupancy

VERVE

venous refocusing for volume estimation