Investigating differences in treatment effect estimates between propensity score matching and weighting: A demonstration using STAR*D trial data

Abstract

Purpose

The choice of propensity score (PS) implementation influences treatment effect estimates not only because different methods estimate different quantities, but also because different estimators respond in different ways to phenomena such as treatment effect heterogeneity and limited availability of potential matches. Using effectiveness data, we describe lessons learned from sensitivity analyses with matched and weighted estimates.

Methods

With subsample data (N=1,292) from Sequenced Treatment Alternatives to Relieve Depression, a 2001–2004 effectiveness trial of depression treatments, we implemented PS matching and weighting to estimate the treatment effect in the treated and conducted multiple sensitivity analyses.

Results

Matching and weighting both balanced covariates but yielded different samples and treatment effect estimates (matched RR 1.00, 95% CI:0.75–1.34; weighted RR 1.28, 95% CI:0.97–1.69). In sensitivity analyses, as increasing numbers of observations at both ends of the PS distribution were excluded from the weighted analysis, weighted estimates approached the matched estimate (weighted RR 1.04, 95% CI 0.77–1.39 after excluding all observations below the 5th percentile of the treated and above the 95th percentile of the untreated). Treatment appeared to have benefits only in the highest and lowest PS strata.

Conclusions

Matched and weighted estimates differed due to incomplete matching, sensitivity of weighted estimates to extreme observations, and possibly treatment effect heterogeneity. PS analysis requires identifying the population and treatment effect of interest, selecting an appropriate implementation method, and conducting and reporting sensitivity analyses. Weighted estimation especially should include sensitivity analyses relating to influential observations, such as those treated contrary to prediction.

INTRODUCTION

Observational comparative effectiveness studies are vulnerable to selection bias and confounding.¹ Increasingly, researchers use propensity scores to address these threats.² The propensity score is a person’s probability of assignment to a particular treatment, given his or her pre-treatment characteristics. A well-estimated propensity score can be used to balance treatment and comparison groups on measured covariates,³ making estimates of the average treatment effect unbiased under the assumption of no unmeasured confounding.^4–6

Propensity scores can be implemented in a number of ways, including stratification, matching, weighting, and covariance adjustment.^{3, 7–11} The choice of propensity score implementation influences treatment effect estimates not only because different methods estimate different quantities,¹² but also because different estimators respond in different ways to phenomena such as treatment effect heterogeneity⁸ and limited availability of potential matches.¹³

In the current study, we used data from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) Study to examine the effect of medication augmentation versus medication switching on remission from depression among patients whose initial citalopram treatment had failed. This question interested us because only 30% of patients recover through initial antidepressant treatment;¹⁴ medication monotherapy and medication combinations are among the second-line treatment options,¹⁵ but the available evidence about these strategies has limited generalizability.¹⁶ Further, it seemed reasonable to make such a comparison because the original STAR*D study made randomized comparisons among augmentation agents and among switch agents and found no difference within either category.^{17, 18}

Specifically, we intended to measure the effect of medication augmentation in the population receiving augmentation. Given that some participants realistically were candidates for only one of the two strategies (i.e., augmentation or switching), we had greater interest in this treatment effect than in an estimate of the population average treatment effect. To estimate the average treatment effect in the treated (ATT), we used both matching without replacement and weighting by the odds (ATT or Standardized Mortality/Morbidity Ratio [SMR] weights, described in detail below). Both estimators can be used to measure the treatment effect in the treated, but unless a match is available for every treated observation, they may not yield similar estimates.¹³ Our final substantive findings appear in a separate paper, which resulted from additional analyses and provides a thorough treatment of the substantive aspects of the study.¹⁹ In the current paper we focus on the lessons learned from sensitivity analyses with matched and weighted estimates.

METHODS

Sample and data

STAR*D compared prospectively several treatments for outpatients with non-psychotic major depressive disorder who had an unsatisfactory response to one or more treatments.²⁰ To simulate real-world care, treatment assignment followed an equipoise randomization scheme in which patient choice could influence treatment selection.²¹ In STAR*D, patients had clear preferences for treatment strategies, and patients who received augmentation differed from those who switched antidepressants.^{22, 23} As a result, the original STAR*D analyses used randomization to compare outcomes within the augment and switch arms, but randomized comparisons between the two arms were not possible.

The initial sample included 4,041 participants representative of patients receiving depression treatment in U.S. primary care and specialty clinics. Of those, 1,439 discontinued an aggressive initial trial of citalopram due to side effects, lack of recovery after at least 9 weeks, or individual choice. We used a public-release dataset from the National Institute of Mental Health to examine outcomes for the 1,292 participants who continued to the second stage of the trial and either augmented their current antidepressant therapy (with bupropion SR or buspirone; n=565) or switched antidepressants (to bupropion SR, sertraline, or venlafaxine XR; n=727).

The Biomedical Institutional Review Board of the University of North Carolina at Chapel Hill determined that the current study did not require its approval.

Statistical analysis

In this study of second-line depression treatment, the primary outcome was depression remission, measured using the Quick Inventory of Depression Symptomatology-Self Report (QIDS-SR₁₆). Using the switch group as a comparator, we wished to compare the outcomes experienced by the augment group to the outcomes they would have experienced if they had switched medications instead. Because a crude comparison would likely be affected by selection bias, we applied propensity score methods to balance the groups on pre-treatment covariates. After addressing missingness, we used logistic regression to estimate propensity scores, implemented propensity score matching^{3, 8, 24} and ATT weighting^{11, 25} to estimate the treatment effect in the treated, and conducted several sensitivity analyses.

Most observations (82%) had a missing value on at least one variable in the analysis model, making a complete-case analysis impractical and likely biased. However, the missing values constituted only 5% of the values needed for analysis, which made it possible to build an imputation model that provided good information about the missing data. We used the expectation-maximization method in SAS PROC MI (SAS Institute, Cary, NC) to impute missing values based on observed variable distributions.^26–29 Although multiple imputation would be the method of choice for a substantive analysis, we used a single imputed dataset to compare methods and conduct sensitivity analyses.

The original STAR*D trial included rigorous measurement of about 100 variables potentially associated with depression outcomes. Our propensity score model incorporated 47 demographic and clinical covariates selected based on theory and published evidence, plus 30 interaction terms iteratively selected to improve between-group covariate balance. To seek a match for each augment observation, we employed a 5-to-1-digit greedy matching algorithm,³⁰ which made five passes through the treatment group in random order. On each pass the algorithm performed caliper matching without replacement, examining potential matches in random order. At the end of each pass, the caliper width was increased by a factor of 10, so that it ranged from ±.000005 to ±.05. To allow weighted estimates, each augment patient received a weight of 1 and each switch patient received a weight of ps/(1-ps), where ps is the propensity score. This approach up-weights switch patients with a high propensity for receiving augmentation and down-weights switch patients with a low propensity for receiving augmentation, so that the weighted covariate distribution in the switch group (the “untreated”) resembles the covariate distribution in the augment group (the “treated”).^{11, 25, 31} The approach has been called “ATT” weighting for “Average Treatment effect in the Treated;”³² “SMR” weighting because, like a standardized mortality/morbidity ratio, it allows a counterfactual estimate of the treatment effect in the treated;²⁵ and “weighting by the odds” because each observation from the comparison group is weighted by its odds of receiving treatment, conditional on covariates.³³ We measured balance in the matched and weighted cohorts using the average standardized absolute mean (ASAM) difference across the 47 covariates.¹¹ We used additional balance measures developed by Rubin³⁴ to confirm that balance was acceptable after both matching and weighting.

Sensitivity of treatment effect estimates to propensity score implementation

In both the matched cohort and the weighted cohort, we estimated the effect of augmentation on depression remission using the FREQ and SURVEYFREQ procedures in SAS. We also assessed the sensitivity of the weighted results to extreme observations in two ways. First we truncated extreme weights, which reduces variability in the treatment effect estimate and provides a way to explore the tradeoff between bias and variance.³⁵ We used several pairs of cutoff values, corresponding to percentiles of the distribution of weights in the switch group (the only group with varying weights): 0 and 100, 1 and 99, 5 and 95, 10 and 90, 25 and 75, 50 and 50. When a weight was more extreme than the nearest cutoff value, we made the weight equal to the cutoff value. For example, when the cutoffs were percentiles 1 and 99, weights below the first percentile were increased to equal the first percentile, and weights above the 99^th percentile were decreased to equal the 99^th percentile. The first pair of cutoffs implied no restriction on the weights; the last pair implied constant weighting (i.e., the crude treatment effect estimate).

Next, instead of truncating extreme weights we excluded observations in the tails of the joint propensity score distribution, based on cutoff values derived from observations treated contrary to prediction.³⁶ This exclusion, or trimming, removes observations treated contrary to prediction as well as their counterparts in the other treatment group, thus yielding unbiased estimates for a more restricted population. Again we used several pairs of cutoff values: percentiles 0 and 100, 1 and 99, 2.5 and 97.5, 5 and 95. We applied the minimum cutoff to the propensity score distribution in the augment group and the maximum cutoff to the distribution in the switch group, excluding observations in both groups whose scores were beyond the cutoffs. For example, when the cutoffs were 0 and 100, we excluded observations whose propensity scores were lower than the augment group’s minimum or higher than the switch group’s maximum. Thus, the first pair of cutoffs implies restriction to the common support region, and subsequent pairs exclude additional observations at both ends of the common (overlapping) propensity score distribution.

RESULTS

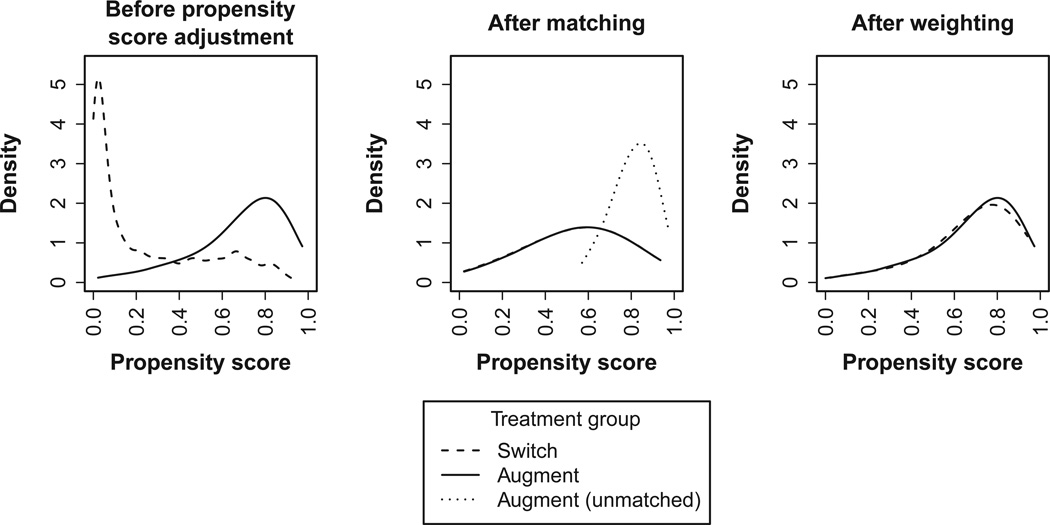
Figure 1 shows the propensity score distributions in the original, matched, and weighted cohorts. Before propensity score adjustment the augment and switch groups were dissimilar with regard to the pre-treatment characteristics measured by the propensity score, and the two distributions were skewed in opposite directions. Twenty-three percent of switch participants had propensity scores below the augment group’s minimum propensity score, and 2% of augment participants had propensity scores above the switch group’s maximum propensity score.

Figure 1. Propensity Score Distribution in the Augment and Switch Groups Before Propensity Score Application, After Matching, and After Weighting.

The figure, based on kernel density estimation, shows distributions of propensity scores estimated using logistic regression. Horizontal axes indicate ranges of propensity score values. Weights are for the treatment effect in the medication augmentation group.

The matching procedure selected a sample (n=538) from the middle of the propensity score distribution. Many augment participants with high propensity scores were unmatched (dotted line in center panel of Figure 1); these patients tended to have greater tolerance for initial treatment and lower depressive severity after initial treatment.¹⁹ Unlike matching, weighting forced the propensity score distribution of the switch group to resemble that of the augment group. This was achieved mainly by up-weighting the few switchers with high propensity scores. The effect of the weighting can be observed by comparing the left and right panels of Figure 1. Both matching and weighting resulted in good covariate balance (ASAM difference 0.20 before adjustment, 0.03 after matching, 0.02 after weighting).

The crude risk ratio for remission favored augmentation (RR: 1.41, 95% confidence interval [CI]: 1.19 to 1.67). The propensity-score-matched risk ratio for remission indicated no benefit for augmentation (RR: 1.00, 95% CI: 0.75 to 1.34), but after weighting, remission appeared to be more likely for patients receiving treatment augmentation rather than switching (RR: 1.28, 95% CI: 0.97 to 1.69).

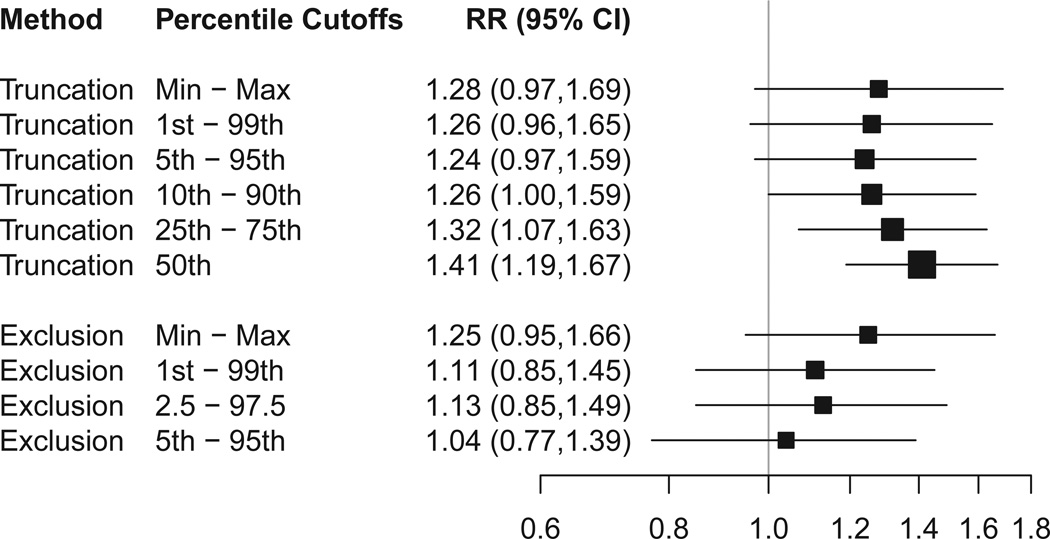
Because extreme weights may give a large amount of influence to a few patients, we assessed the sensitivity of the weighted estimates to truncation of extreme weights (Figure 2). Regardless of the cutoffs used, the weighted estimates remained in the 1.2 to 1.4 range.

Figure 2. Sensitivity of Weighted Estimates to Truncation of Weights and to Exclusion of Observations with Extreme Propensity Scores.

CI=confidence interval; RR=risk ratio. The figure shows RRs for remission based on estimated propensity scores that were applied using standardized mortality ratio weights. Percentile cutoffs are relative to the propensity score distribution in the medication switch group. Truncation means that weights below the lower cutoff were increased to equal the lower cutoff, and weights above the higher cutoff were decreased to equal the higher cutoff. Exclusion means that observations outside the indicated range were omitted from the analysis. Box size indicates relative precision. Lines indicate 95% confidence intervals.

We also assessed the sensitivity of the weighted estimates to the exclusion of patients in the tails of the overlapping propensity score range. These tails include patients treated contrary to prediction (i.e., switch observations with extremely large propensity scores and augment observations with extremely small propensity scores) (Figure 2). We found that as increasing numbers of these observations were excluded, along with their counterparts in the other treatment group, the weighted estimates approached a risk ratio of 1.0 (close to the matched estimate).

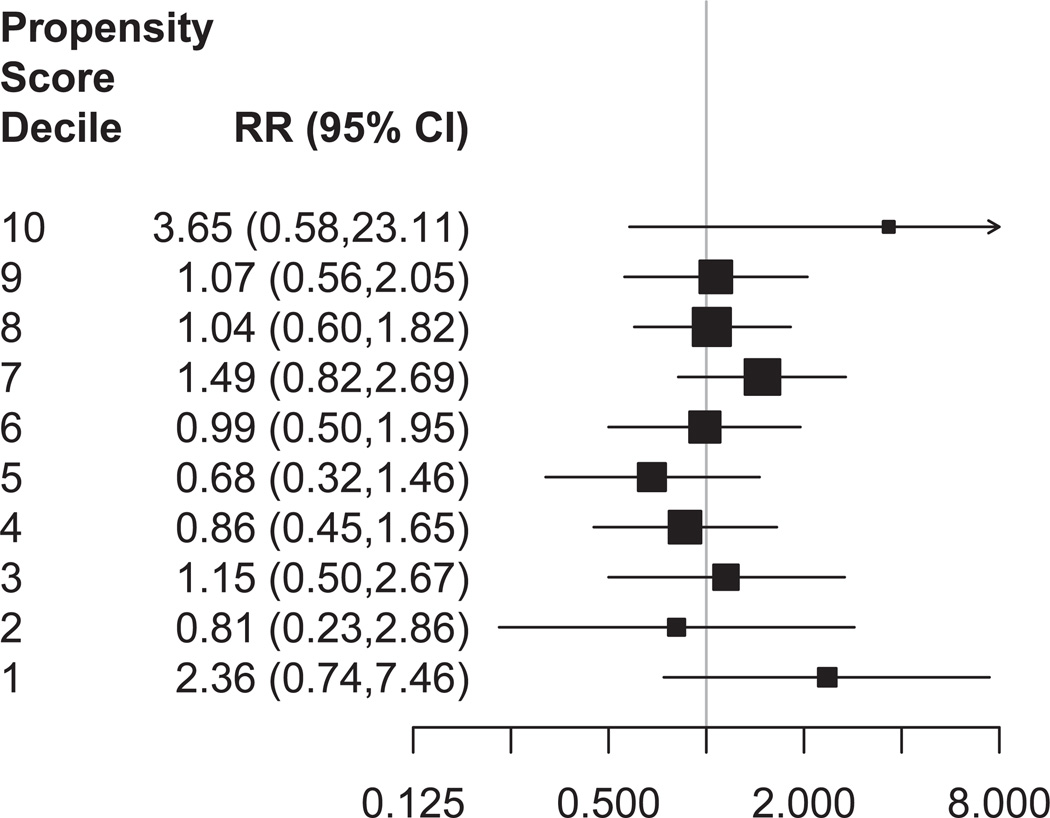
Finally, to increase our understanding of the sensitivity of the weighted estimates to extreme observations and the difference between the matched and weighted estimates, we stratified by propensity score decile and examined the heterogeneity of the treatment effect across propensity score strata (Figure 3). Initially there were no augment observations in the lowest decile, so we restricted to the common support region for this analysis. Relative to switching, augmentation had little effect on remission except in the lowest stratum (RR: 2.36, 95% CI: 0.74 to 7.46, augment n = 5, switch n = 106) and in the highest stratum (RR: 3.65, 95% CI: 0.58 to 23.11, augment n = 103, switch n = 8).

Figure 3. Heterogeneity of Treatment Effect.

CI=confidence interval; RR=risk ratio. The figure shows RRs for remission after restricting to the common support region and stratifying by the estimated propensity score. Box size indicates relative precision. Lines indicate 95% confidence intervals.

DISCUSSION

We examined and compared propensity-score-matched and ATT-weighted treatment effect estimates in a comparative effectiveness study. Although both the matching procedure and the weighting procedure resulted in covariate balance, they yielded different estimates of the treatment effect. Both 95% confidence intervals were consistent with the null hypothesis of no treatment effect, but an estimated 28% increase in the probability of remission differs meaningfully from an estimate indicating no treatment effect. Three factors likely contributed to these results: (1) due to incomplete matching, the matched and weighted samples had different propensity score distributions and therefore represented different populations; (2) the weighted estimates were sensitive to extreme observations; and (3) augmentation appeared to benefit patients only in the highest and lowest propensity score deciles.

When propensity score matching is incomplete, the matched sample represents a different population than the ATT-weighted sample. The matched-sample estimate can then be labeled as the “treatment effect in treated patients for whom matches could be found” or, in the current study, the “treatment effect in augmentation patients who were candidates for both augmentation and switching.” Although this population may be difficult to describe, it includes only people who were candidates for both treatments, so the corresponding treatment effect estimate may be more clinically relevant than the treatment effect among all augmentation patients (some of whom might not realistically be candidates for switching) or the treatment effect in the entire population (including patients in both groups who realistically might be candidates for only one of the two treatments).

ATT weighting, in contrast to matching, forces the propensity score distribution in the untreated to be the same as the propensity score distribution in the treated. This method clearly leads to an estimate of the average treatment effect in the treated, but the estimate will be sensitive to extreme observations. If two dissimilar groups are being compared, then ATT weighting constitutes extrapolation. In this case it is important to consider the meaning of the effect being estimated and the degree to which the data support such an estimate. In the current study, the ATT-weighted estimate represented the treatment effect in the augment group, but this estimate required the up-weighting of the few switch participants with high propensity scores, and the estimate was sensitive to the exclusion of these observations.^{35, 37–40}

If the treatment effect were completely uniform, then the choice of estimator would be inconsequential. In the current example, treatment effect heterogeneity appeared to contribute to the difference between the matched and weighted estimates. An alternative explanation would be unmeasured confounding among patients in the tails of the propensity score distribution. Our propensity score model included a large group of covariates that were carefully selected and measured, providing protection from unmeasured confounding. However, the apparently strong benefit of augmentation among patients unlikely to receive augmentation defies explanation. Therefore, unmeasured confounding cannot be ruled out. Alternatively, the apparent treatment effect heterogeneity may have been due to chance. Very few patients in the highest propensity score decile switched medications, and very few in the lowest decile received augmentation, leading to wide confidence intervals for these estimates. In any case, caution must be exercised when interpreting treatment effect estimates for areas of limited overlap on the propensity score, because these estimates are sensitive to misspecification in the propensity score and outcome models.⁴¹

Because our findings arise from a single empirical example, we do not know the true treatment effect for any population, and we are uncertain whether treatment effect hetereogeneity existed. Further, we caution that the substantive findings reported here serve only as an example and do not represent our final substantive results. Nonetheless, this study highlights the importance of deciding clearly which population and treatment effect estimate are of interest. For example, if the research question involves the effect of a treatment on those currently receiving it, then the “treatment effect in the treated” (ATT) is of interest. If there is not a match for every treated observation, then researchers face a trade-off between incomplete matching on the one hand, which restricts the sample and therefore the study population, and extrapolation through weighting on the other. If all assumptions are met, including no unmeasured confounding, then weighting results in the better estimate of the treatment effect in the treated. If some assumptions are violated, the matched estimate may be more robust because (1) the matched sample inherently excludes extreme observations and (2) the matched estimate depends only on similarities between propensity score values,³ whereas the weighted estimate depends on exact propensity score values.⁴² In some cases, multiple estimates may be relevant, especially if propensity score distributions differ greatly between treatment groups before adjustment, matching is incomplete, the treatment effect is heterogeneous, or there is interest in more than one population.

One way of presenting multiple treatment effect estimates is to stratify by the propensity score, complementing the more general information provided by estimates of the marginal treatment effect in specific populations. Stratification allowed us to describe a specific, U-shaped pattern of apparent treatment effect heterogeneity. In substantive studies, clinical interpretation can be aided by using variables other than the propensity score to describe subgroups with different clinical outcomes. For example, in the current study, the augmentation recipients in the highest propensity score decile were characterized by their tolerance for longer initial treatment and by milder depressive severity after initial treatment.¹⁹

Conclusion

Using data from the STAR*D study, we implemented propensity score matching and weighting methods, both intended to measure the treatment effect in patients who received augmentation with a second antidepressant. We found that the two methods yielded different samples and treatment effect estimates due to incomplete matching, sensitivity of the weighted estimates to extreme observations, and apparent treatment effect heterogeneity. In propensity score analysis, crucial steps include identifying the population and treatment effect estimate of interest, selecting an appropriate propensity score implementation method, and conducting and presenting results from sensitivity analyses. Weighted estimation in particular should always include sensitivity analyses relating to influential observations, such as those treated contrary to prediction.

Key points.

• Propensity-score-matched and -weighted treatment effect estimates differed in this setting.

• The primary causes were incomplete matching, sensitivity of weighted estimates to extreme observations, and possibly treatment effect heterogeneity.

• In propensity score analysis, crucial steps include identifying the population and treatment effect of interest, selecting an appropriate implementation method, and conducting and reporting sensitivity analyses.

• Weighted estimation should always include sensitivity analyses relating to influential observations.