Atomic-level simulation of current–voltage relationships in single-file ion channels

Abstract

The difficulty in characterizing ion conduction through membrane channels at the level of individual permeation events has made it challenging to elucidate the mechanistic principles underpinning this fundamental physiological process. Using long, all-atom simulations enabled by special-purpose hardware, we studied K⁺ permeation across the K_V1.2/2.1 voltage-gated potassium channel. At experimentally accessible voltages, which include the physiological range, the simulated permeation rate was substantially lower than the experimentally observed rate. The current–voltage relationship was also nonlinear but became linear at much higher voltages. We observed permeation consistent with a “knock-on” mechanism at all voltages. At high voltages, the permeation rate was in accordance with our previously reported K_V1.2 pore-only simulations, after the simulated voltages from the previous study were recalculated using the correct method, new insight into which is provided here. Including the voltage-sensing domains in the simulated channel brought the linear current–voltage regime closer to the experimentally accessible voltages. The simulated permeation rate, however, still underestimated the experimental rate, because formation of the knock-on intermediate occurred too infrequently. Reducing the interaction strength between the ion and the selectivity filter did not increase conductance. In complementary simulations of gramicidin A, similar changes in interaction strength did increase the observed permeation rate. Permeation nevertheless remained substantially below the experimental value, largely because of infrequent ion recruitment into the pore lumen. Despite the need to apply large voltages to simulate the permeation process, the apparent voltage insensitivity of the permeation mechanism suggests that the direct simulation of permeation at the single-ion level can provide fundamental physiological insight into ion channel function. Notably, our simulations suggest that the knock-on permeation mechanisms in K_V1.2 and KcsA may be different.

INTRODUCTION

Ion permeation facilitated by selective membrane channels controls nerve conduction, and understanding the mechanistic principles underlying such conduction is of profound physiological importance (Hodgkin and Keynes, 1955; Hille, 2001). The ion permeation process has been viewed conceptually as an electrodiffusive barrier–crossing phenomenon, as was originally inferred from current–voltage characterizations of ion movements across bilayer-spanning channels (Attwell and Jack, 1978; Levitt, 1986; Andersen, 1989). At the atomic level, potassium channel crystal structures have more recently been instrumental in addressing key questions regarding ion permeation and selectivity (Doyle et al., 1998; Zhou et al., 2001; Long et al., 2005, 2007), and experimental data have been complemented by computational studies, often molecular dynamics (MD) simulations based on these x-ray structures (Åqvist and Luzhkov, 2000; Bernèche and Roux, 2001, 2003; Jensen et al., 2010). Because computational limitations have until recently precluded the direct simulation of ion permeation at the atomic level, analysis of thermodynamics, which underlies the conduction processes of interest, has dominated computational studies that address questions regarding permeation mechanisms and rates (Åqvist and Luzhkov, 2000; Bernèche and Roux, 2001, 2003; Allen et al., 2006a,b; Furini and Domene, 2009; Kim and Allen, 2011).

Special-purpose hardware has now enabled millisecond-timescale MD simulations (Shaw et al., 2009), allowing a much wider range of biological processes to be studied at an atomic level of detail (Dror et al., 2010; Shaw et al., 2010; Lindorff-Larsen et al., 2011; Jensen et al., 2012). A typical ion permeation process occurs on the submicrosecond scale and thus can be directly assessed computationally at the single-ion level (Jensen et al., 2010). From MD simulations, we can directly observe up to thousands of individual permeation events for a single channel, which, in principle, provide a basis for characterizing the conduction process at a structural and temporal level of detail otherwise inaccessible to experimental measurements, in part because of the limited time resolution of single-channel patch-clamp experiments (Hille, 2001; Dror et al., 2010).

Recent results suggest that MD simulations may complement experiments and provide novel insight into the conduction process (Jensen et al., 2010), but the sensitivity of the results to differences among, and limitations of, the force fields used is uncertain. Certain thermodynamics-based force field corrections, for example, have been proposed for narrow, single-file channels like K⁺ channels and gramicidin A (gA) (Roux and Bernèche, 2002; Allen et al., 2006b). These modifications were found to be critical for elucidating permeation mechanisms (Bernèche and Roux, 2001; Allen et al., 2006b) and rates (Bernèche and Roux, 2003) with MD simulations.

Here, we begin by reviewing how a membrane potential is applied in MD simulations. We then show that simulation of K⁺ permeation across a voltage-gated K⁺ channel, the K_V1.2/2.1 “paddle chimera” (Long et al., 2007), substantially underestimates the permeation rate at experimental voltages but otherwise produces permeation characteristics that agree reasonably well with corresponding experimental data. Although our simulations fail to provide the correct permeation rate at experimentally accessible voltages, which include the physiological range, the “knock-on” permeation mechanism—originally hypothesized based on experimental data (Hodgkin and Keynes, 1955) and later observed in MD simulations (Bernèche and Roux, 2001, 2003; Jensen et al., 2010)—was observed at all simulated voltages. We also show that our earlier K_V1.2 pore-only simulations—after recalculating the previously underestimated voltages in these simulations using the correct method (Roux, 2008)—give a similar permeation rate to our current simulations, which include the voltage sensors. The main effect of including the voltage sensors is to move the linearly conducting regime in the simulations closer to experimentally accessible voltages. Force field modifications suggested on the basis of thermodynamic calculations to increase permeation rates in the related KcsA channel (Bernèche and Roux, 2001; Roux and Bernèche, 2002; Allen et al., 2006b) caused the dominant K_V1.2/2.1 permeation mechanism to change from knock-on to a mechanism that bypasses the formation of a knock-on intermediate, whereas for KcsA these modifications reproduced a knock-on mechanism consistent with the original results of Bernèche and Roux (2001, 2003).

We also obtained permeation data from MD simulations of gA. The permeation rates observed in our simulations were again substantially below the corresponding experimental values; infrequent ion recruitment into the pore lumen appeared to play a substantial role in the low overall rate. Although these rates were somewhat improved by altering the interactions between the ions and the pore’s vestibules and lumen, polarizable force fields and improved membrane models would probably be required to simulate ion permeation through single-file channels with high accuracy at physiological and experimentally accessible voltages.

MATERIALS AND METHODS

Electric field

We imposed a membrane potential (i.e., an applied voltage), V, by applying a force, F_i = q_iE, in the z direction (the direction perpendicular to the membrane) to every particle, i, proportional to its charge, q_i. The constant of proportionality, E, is the applied electric field and is thus an adjustable parameter that determines V:

$$V=E·l_z,$$ (1)

where l_z is the length of the simulation box in the z direction. We also define the local electrostatic potential Φ(z) to within an additive constant by

$$\Phi \left(z_2\right)-\Phi \left(z_1\right)=-{\displaystyle {\int }_{z_1}^{z_2}(E+E_{\text{GSE}}(z’\left)\right)\text{d}z’=-E(z_2-z_1)+{\Phi }_{\text{GSE}}\left(z_2\right)-{\Phi }_{\text{GSE}}\left(z_1\right),}$$ (2)

where Φ_GSE contains all other contributions to the potential apart from the applied field, in particular those arising from particle charges and those arising from the choice of boundary conditions. Because our simulations were performed with periodic boundary conditions, we calculated Φ_GSE using the Gaussian split Ewald (GSE) method with the standard tinfoil boundary conditions, under which there is no constant contribution to E_GSE (Shan et al., 2005).

To see the validity of Eq. 1 (Roux, 2008), note that all contributions to E_GSE and hence Φ(z) have a period equal to an integer multiple of l_z. As a result, Φ_GSE(z + l_z) = Φ_GSE(z), so the membrane potential, which is simply the potential difference across the simulation box, V = Φ(z) − Φ(z + l_z), reduces to E · l_z. (The membrane potential, which is the change in potential going from the exterior to the interior of the cell, has this overall sign because we define the positive z direction as being from the interior to the exterior of the cell.)

In our previous study we used a different method to compute the simulation voltage (Jensen et al., 2010), leading to a 5.8-fold underestimated voltage; data from our earlier work discussed in this paper has had the voltage recomputed using Eq. 1. In the Appendix we present an alternative derivation of Eq. 1 that exposes the problem with the previous method.

Hardware

All simulations were performed on a special-purpose machine, Anton, designed for MD simulations (Shaw et al., 2009).

K_V1.2/2.1 simulations

The pore and voltage-sensing domains (VSDs; residues 148–421) of the K_V1.2/2.1 paddle chimera (Protein Data Bank [PDB] accession no. 2R9R; Long et al., 2007) were embedded in a neutral palmitoyl oleoyl phosphatidylcholine (POPC) bilayer solvated in 0.6 M KCl; the functionally nonessential (Kobertz and Miller, 1999) tetramerization domain (T1) and the regulatory β subunit were omitted. The system counted ∼107,000 atoms and measured 110 × 110 × 87 ų. Residue protonation states corresponded to pH 7. We applied constant electric fields of 0.0125 ≤ E ≤ 0.2 kcal · mol⁻¹ · Å⁻¹ · e⁻¹, corresponding to the voltage range 47 ≤ V ≤ 753 mV (see Eq. 1 and Table S1). Two additional simulations with different system sizes—one with ∼158,000 atoms (110 × 110 × 131 ų) and one with ∼186,000 atoms (110 × 110 × 152 ų) with E = 0.1 kcal · mol⁻¹ · Å⁻¹ · e⁻¹ corresponding to V = 568 mV and V = 661 mV, respectively—and one simulation (E = 0.1 kcal · mol⁻¹ · Å⁻¹ · e⁻¹; V = 381 mV) at 0.3 M KCl were performed to examine possible finite-size and concentration effects. We also performed a control simulation, in a POPC bilayer and solvated in 0.6 M KCl, with the T1 retained at V = 377 mV (∼230,000 atoms; see Jensen et al., 2012). The aggregate simulation time was ∼500 µs, and most individual simulation times were >10 µs (Table S1).

KcsA simulations

KcsA was modeled using a low-resolution structure of the open, inactivated pore (PDB accession no. 3F7V; Cuello et al., 2010) with the active selectivity filter (SF) conformation substituted in (PDB accession no. 1K4C; Zhou et al., 2001). Missing residues were added at the N and C termini. The Glu71Ala mutation was introduced to ensure a conducting SF; the SF was further stabilized by adding Gly77 and Gly79 torsional backbone corrections similar to those used for K_V1.2/2.1. The protein was solvated and membrane embedded as for K_V1.2/2.1. An electric field of 0.1 kcal · mol⁻¹ · Å⁻¹ · e⁻¹, corresponding to a voltage of ∼430 mV (Eq. 1 and Table S5), was applied.

gA simulations

The gA dimer (PDB accession no. 1MAG; Ketchem et al., 1996, 1997) was similarly embedded in a POPC bilayer solvated in 1.0 M KCl. N and C termini were formyl- and ethanolamine-capped. Tryptophan force field parameters with an improved side-chain dipole moment were used (Macias and MacKerell, 2005). The system measured 72 × 72 × 72 ų. Electric fields of 0.06 ≤ E ≤ 0.27 kcal · mol⁻¹ · Å⁻¹ · e⁻¹, corresponding to the voltage range 184 ≤ V ≤ 829 mV (Eq. 1 and Table S2), were applied.

Force fields

We used the CHARMM27 force field for the protein, ions, and water (MacKerell et al., 1998, 2004) and the CHARMM36 force field for lipids (Klauda et al., 2010). For K_V1.2/2.1, torsional backbone corrections were added to SF residues Gly376 and Gly378 to prevent SF deterioration (Jensen et al., 2012).

Four additional K_V1.2/2.1 simulations with weaker interactions between the six SF backbone carbonyl oxygen atoms per subunit (24 atoms in total) and all K⁺ ions were performed by increasing the Lennard-Jones (LJ) parameter σ, which specifies the effective van der Waals radius for the K⁺–O interaction, from 3.0859 Å (MacKerell et al., 1998) to 3.2874 Å (Bernèche and Roux, 2001; Roux and Bernèche, 2002; Allen et al., 2006b; the original K⁺ LJ parameter set otherwise used in this study is: σ = 3.0859 Å; ε = 0.10218 kcal · mol⁻¹). This increase corresponds to increasing the position of the minimum in the LJ potential R_min = 2^1/6 · σ (the parameter of choice in CHARMM27; MacKerell et al., 1998) from 3.46375 to 3.69000 Å. Increasing σ (R_min) weakens the K⁺–O interaction because the electrostatic attraction becomes weaker at the LJ minimum. E was 0.0125, 0.025, 0.0500, and 0.15 kcal · mol⁻¹ − Å⁻¹ · e⁻¹, equal to 47, 95, 189, and 566 mV (Table S1). For KcsA, we performed a single control simulation using similar weakened K⁺–O interactions with E = 0.1 kcal · mol⁻¹ · Å⁻¹ · e⁻¹, corresponding to 427 mV (Table S5).

Six additional gA simulations, with similarly altered LJ interactions between the backbone carbonyl oxygen atoms (32 atoms in total including the formyl oxygen atoms) and all K⁺, were performed by setting σ to 2.9399, 3.0000, 3.1000, 3.1500, 3.2000, and 3.2874 Å, as opposed to the native CHARMM27 value (σ = 3.0859 Å; MacKerell et al., 1998). E was 0.2 kcal · mol⁻¹ · Å⁻¹ · e⁻¹, corresponding to 646 mV (Table S2).

Energy profiles

To compute a free energy profile, W(z), we performed four sets of simulations in the absence of an applied field. The first set consisted of two 3-µs simulations sampling ion entry into, and exit from, the outer channel regions (sites 1–2 and 9–10; see Fig. 4 D). No restraining potential was used in this first set of simulations. In the other sets of simulations, we used flat-bottom potentials that were equal to zero for ion positions within a prescribed range, and which rose harmonically beyond that range. The central region of the channel was sampled using two different flat-bottom potentials, with the first confining the ion within sites 3–8 (−6.5 < z < 6.5 Å), and the second, used to improve sampling near the top of the barrier, confining the ion within sites 4–7 (−5.0 < z < 5.0 Å). A set of 12 0.3-µs simulations was performed for each potential (12 different initial configurations with varying ion positions, taken from simulation 5 [Table S2], were used in each set). A flat-bottom potential encompassing these sites and centered at z = 0 Å was applied, and the first 10% of each run was discarded. To ensure sampling overlap in the region where the vestibule and lumen join, a final set of two ∼1-µs simulations with flat-bottom potentials centered at sites 3 and 8, respectively, were performed to sample transitions between sites 2 and 4 and sites 7 and 9. From these four simulation sets we constructed separate histograms of the ion positions, ρ(z); in the simulations with a flat-bottom potential, the ion densities within 0.5 Å of the repulsive walls were discarded. Energy profiles encompassing these individual channel regions were obtained from the ion density profiles as −RTln(ρ(z)) and were joined to yield a single potential of mean force (PMF) for the entire channel.

Figure 4.

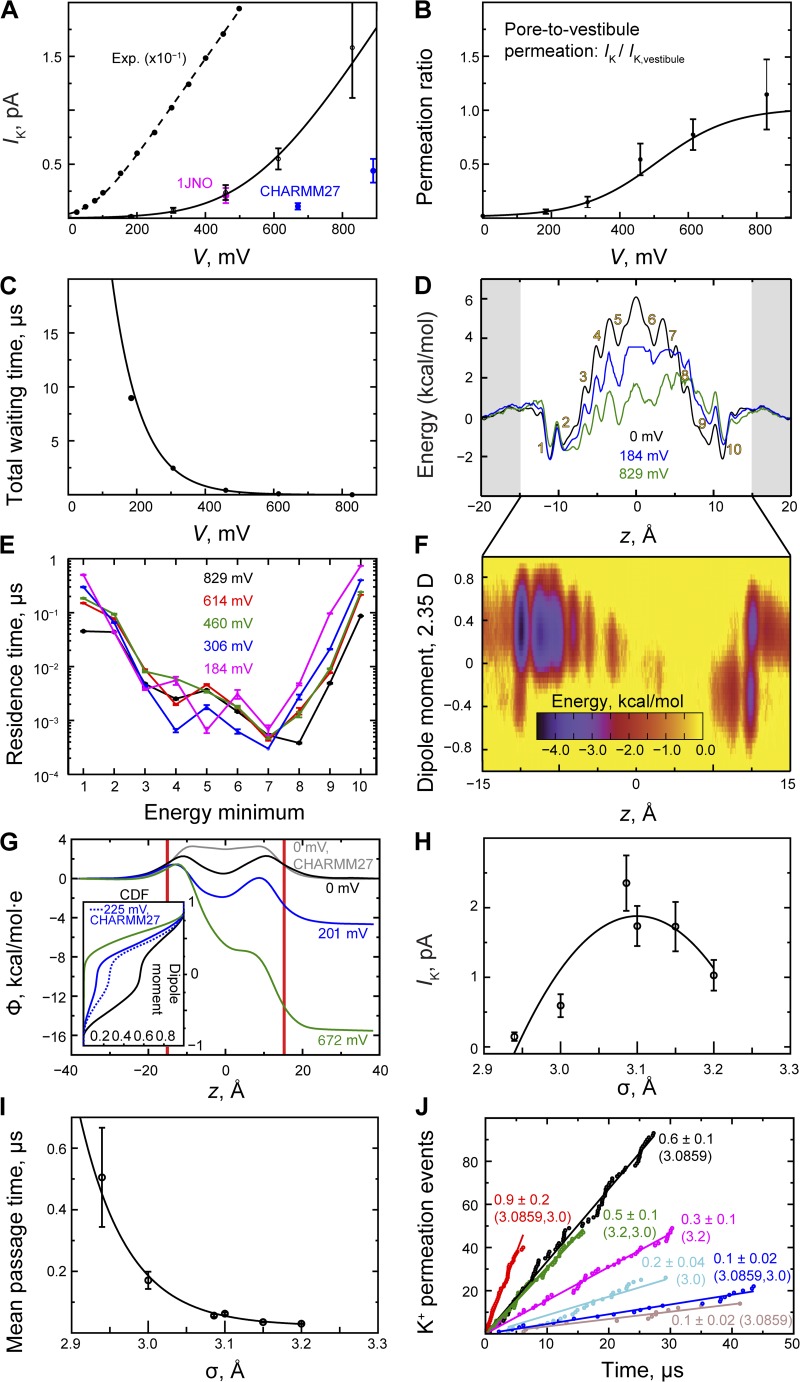
Permeation in gA. (A) gA current–voltage relationship. K⁺ current; fits (black lines) of the I-V curves were performed as described in Materials and methods (see also the Fig. 2 A legend). The temperature-adjusted (to 310 K) experimental data are from Andersen (1983). A slope conductance of 66 pS was derived from these currents measured up to 500 mV. (B) Ratio of pore permeation to vestibule permeation (I_K/I_K,vestibule). (C) Total waiting time between two permeation events. (D) PMF, W(z), of K⁺ permeation as a function of ion position, and two biased energy profiles obtained at low and high voltage (see Materials and methods). K⁺-binding sites are labeled 1–10; sites 1, 2 and 9, 10 comprise the pore vestibules. (E) K⁺ residence binding-site times (see D). (F) Two-dimensional (biased) energy profile (kcal · mol⁻¹). The average contribution per pore water molecule to the z component of the dipole moment as a function of ion position within the pore. The dipole moment is given in units of the TIP3P water dipole moment (2.35 D; Jorgensen et al., 1983), so it may take values between +1 and −1. The concerted water reorientation step, which changes the dipole moment from −0.4 to +0.4, occurs toward the end of the ion transfer at z ≈ 12 Å. (G) Electrostatic potential (Φ(z)) computed from ∼5-µs trajectories at zero, low, and high voltage with zero ion concentration; Φ(z; V = 0) obtained with CHARMM27 lipid parameters is shown for comparison. Inset is a cumulative distribution function (CDF) of the total water dipole moment. (H) K⁺ current shown as a function of σ. (I) K⁺ pore mean passage time versus the LJ parameter, σ. (J) K⁺ permeation obtained with different σ values. By assigning vestibule and lumen different K⁺–carbonyl oxygen interaction strengths (i.e., different σ parameters), a twofold increase in current (red) relative to the native interaction strength (black) could be observed at high voltage (∼646 mV), whereas a smaller increase occurred at lower voltage (∼300 mV); currents (in pA) are shown next to each permeation curve; the (dual) σ value(s) is shown here in parentheses (see Table S2).

The K⁺ velocity autocorrelation function (VACF) was used to estimate D as an average over 28 individual diffusion constants from a set of 28 200-ns simulations performed at zero voltage and in the absence of any confining potential. Each diffusion constant was obtained within 2-Å regions along z by time integration of the VACF up to 1.5 ps.

By binning the z position of all permeating ions, we also obtained ion density profiles, from which we computed, at each voltage, a biased energy profile as −RTln(ρ(z)).

Estimation of conductance

At each voltage, the K⁺ current was determined from the average waiting time between two successive permeation events, and the standard error was estimated by block analysis of the waiting times (Flyvbjerg and Petersen, 1989). Given that the simulated current (“I”) versus voltage (“V”) I-V curves were nonlinear except at high voltages, we estimated high-voltage (V ≥ V′), single-channel conductance (g) by fitting the K⁺ currents to I_K = g(V − V′)/{1 − exp[−b(V − V′)]}, as discussed in Jensen et al. (2010). This equation has an exponential form at low voltages and the linear form, g(V − V′), at high voltages. The crossover between the two forms occurs around V = V′, over a voltage interval of ∼b⁻¹. We refer to V > V′ and V < V′ as the high-voltage and low-voltage regions, respectively. The high-voltage (slope) conductance estimated in this way is larger than the I/V-estimated (chord) conductance that is standard in electrophysiology measurements, but it allows us to deduce a single value for the high-voltage conductance. (In this way, we also derived a gA high-voltage experimental conductance from data measured up to 500 mV in 1.0 M KCl [Andersen, 1983].) It is difficult to determine an accurate low-voltage conductance because of the nonlinear behavior of the I-V curve and the smaller number of permeation events observed in this regime. We here determined a low-voltage value from fitting a straight line through the origin to the current data obtained at the three (K_V1.2/2.1) and two (gA) lowest voltages.

The low-voltage experimental conductances were temperature corrected (using g(T_sim) = g(T_exp)Q₁₀^{(Tsim−Texp)/10}) to 73 pS for Shaker (0.6 M KCl; Heginbotham and MacKinnon, 1993) using Q₁₀ = 1.5 (Rodríguez et al., 1998) and to 30 pS for gA (1.0 M KCl; Q₁₀ = 1.4; Busath et al., 1998; Ingólfsson et al., 2011) to take into account the temperature difference between simulation (T_sim = 310 K) and experiment. Similarly, we temperature corrected the experimental high-voltage gA conductance to 66 pS for comparison with our simulated high-voltage conductance in this channel.

Online supplemental material

Tables S1, S2, and S5 summarize the simulations and key permeation data. Tables S3 and S4 summarize additional gA kinetic data. Figs. S1 and S2 show for K_V1.2 and gA the K⁺ distribution in SF and pore vestibule and lumen, respectively. Figs. S3 and S4 show deuterium quadrupole splittings (DQS) and rotameric states for tryptophan residues in gA. Fig. S5 shows differences in the electrostatic-potential profile of KcsA with different residues at the SF. Figs. S6–S8 show water dipole orientation, DQS, and rotameric states for tryptophan residues at different applied voltages in gA. The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210820/DC1.

RESULTS

Applied potential

For each E, we computed the applied potential, V, by multiplying the (average) simulation box length by E (Eq. 1). In addition, using Eq. 2 we calculated the total potential profile, Φ(z), along the pore axis, relative to a reference value (in bulk-like solution) at the edge of the simulation box. In Fig. 1, the net potential difference (i.e., V) is visible as the difference in potential between the left and right edges of the simulation box. Fig. 1 also shows that the potential drop Φ(−z) − Φ(z) measured across the membrane reaches an almost constant value equal to the membrane potential over ∼10 Å before z reaches ±l_z/2, suggesting that the simulation box is sufficiently large that distant from the membrane we have bulk-like solution.

Figure 1.

The applied potential. The time-averaged electrostatic potential profile Φ(z) is shown along the K_V1.2/2.1 pore axis, with the SF centered at z = 0. Ions are present in the simulation, including in the SF; the potential shown does not have the potential obtained at zero applied field subtracted. The calculation of Φ used a three-dimensional grid at 0.8-Å resolution; points falling within a 1.6-Å xy radius from the pore axis were included. The total electrostatic potential, Φ, is approximately constant in the bulk regions but increases substantially across the K⁺-occupied SF. The z-integrated total electric field, E_T = E_GSE + E ≈ E_GSE, yields the total electrostatic potential, Φ, to within an additive constant. Although E is much smaller in magnitude than E_GSE, the latter equals zero when integrated over the box; the applied voltage here thus becomes V = Φ(−l_z/2) − Φ(l_z/2) = E <l_z> = 189 mV (Table S1, simulation 9).

K_V1.2/2.1

From the individual currents (Table S1) we estimated a low-voltage (V < 300 mV) conductance of ∼2 pS, which is significantly below the (temperature-corrected to 310 K) experimental conductance of 73 pS (Heginbotham and MacKinnon, 1993). We also estimated a high-voltage, single-channel conductance of 58 ± 18 pS (Fig. 2 A; in the linear regime, V > 300 mV), but experimental measurements are not possible in this range.

Figure 2.

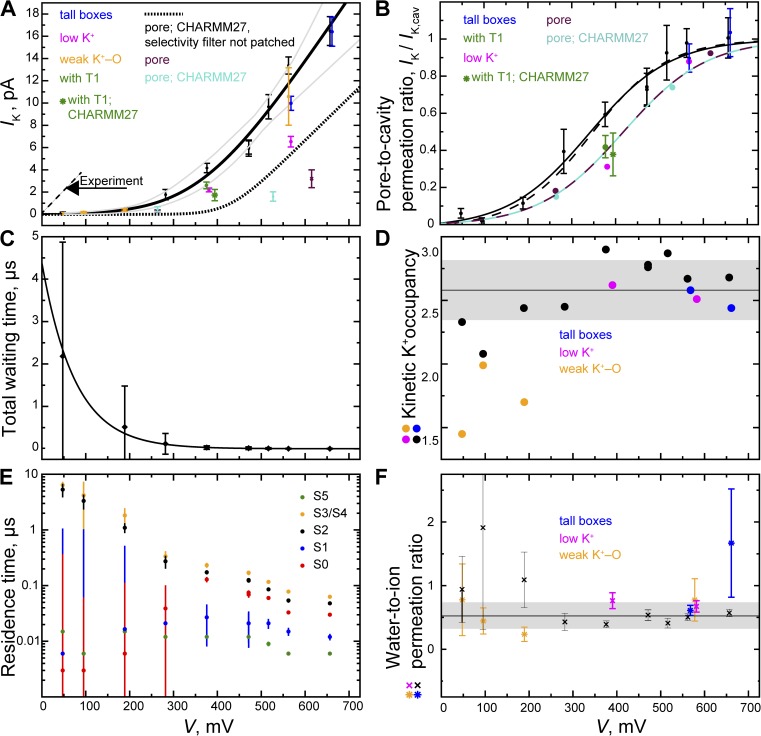
Permeation in K_V1.2/2.1. (A) K_V1.2/2.1 current–voltage relationship. K⁺ current is shown as black points (simulations 1–11; see Table S1). Colored points denote simulations with increased box sizes (larger l_z; referred to as “tall boxes” in the figure key and in Results; simulations 12 and 13), with the T1 retained (simulations 14 and 15), with reduced K⁺ concentration (simulations 16 and 17), and with reduced LJ interaction between K⁺ and SF carbonyl oxygen atoms (simulations 18–21). The experimental data are from Heginbotham and MacKinnon (1993). The I-V curve (black line) was fit as described in Materials and methods; gray curves delineate a 67% confidence interval. The temperature-adjusted (to 310 K) experimental value, measured at much lower voltages (V ≤ 90 mV), is 73 pS for Shaker (the experiment was performed at 22°C and 0.6 M KCl; Heginbotham and MacKinnon, 1993). A fit to our (voltage-corrected) pore-only permeation data (Jensen et al., 2010) is shown as a dotted line. (B) Ratio of pore to cavity-only permeation (I_K/I_K,cav; full channel only). Ions entering 2 Å below Pro407, part of the intracellular gate (Jensen et al., 2012), and permeating up to 2 Å below SF site S5 were counted as cavity permeation events; the mean waiting time between two such consecutive events was used to determine the cavity current. (C) Total waiting time between two permeation events. (D) SF kinetic K⁺ occupancy (average 2.6 ± 0.2; black line). (E) K⁺ residence times in SF sites S0–S5 as a function of voltage. (F) Water-to-K⁺ permeation ratio (average 0.5 ± 0.2; black line).

We found no finite-size effect on permeation nor significant influence from the T1 on permeation; two additional simulations performed with taller boxes (larger l_z) and E lowered in proportion (Table S1) both provided currents falling on the I-V curve, as did the single simulation in which the T1 was retained. Changing the bulk K⁺ concentration from 0.6 to 0.3 M reduced the permeation twofold, from 4.2 ± 0.4 to 2.2 ± 0.2 pA (Fig. 2 A and Table S1).

In contrast with our earlier microsecond-scale simulations (Jensen et al., 2010), in the much longer simulations reported here we observed K⁺ permeation below 300 mV. The current was much lower than that observed experimentally, however, and our I-V curve was not linear in V across all voltages (Fig. 2 A). At lower voltages, ∼40% or less of the ions recruited into the pore cavity subsequently permeated the SF, whereas at higher voltages, all recruited ions also permeated the pore (Fig. 2 B). The waiting time between two consecutive permeation events—the time to enter and then completely permeate the pore—decreased exponentially as the voltage was increased (Fig. 2 C); single-ion analysis indicated that the K⁺ residence time in the SF was much shorter in sites S4/S3 and S2 as the voltage was increased (Fig. 2 E).

The T1 and VSDs appeared to have opposite effects on the initial part of the permeation process. Relative to the pore-only construct, a larger fraction of the cavity-recruited ions also permeated the SF with the VSDs present, whereas with the additional presence of the T1, the fraction of fully permeating to cavity-recruited ions was similar to that observed for the pore-only construct (Fig. 2 B). Lowering the SF-K⁺–carbonyl oxygen interaction strength by increasing σ did not increase the current (see Materials and methods and Fig. 2 A).

The SF kinetic occupancy by K⁺ was 2.6 ± 0.2 (Table S1 and Fig. 2 D; kinetic occupancy is the average occupancy by ions in the process of permeating, so ions associating from the extracellular side are omitted from the average). This is consistent with the Hodgkin–Keynes knock-on mechanism (Hodgkin and Keynes, 1955; Bernèche and Roux, 2001, 2003; Jensen et al., 2010), which further analysis (Fig. 3) confirmed as the principal mechanism of conduction. At reduced interaction strength, the kinetic occupancy became <2, indicating that a different permeation mechanism predominated (Fig. 3). The water-to-K⁺ co-permeation ratio was 0.5 ± 0.2 (Fig. 2 F).

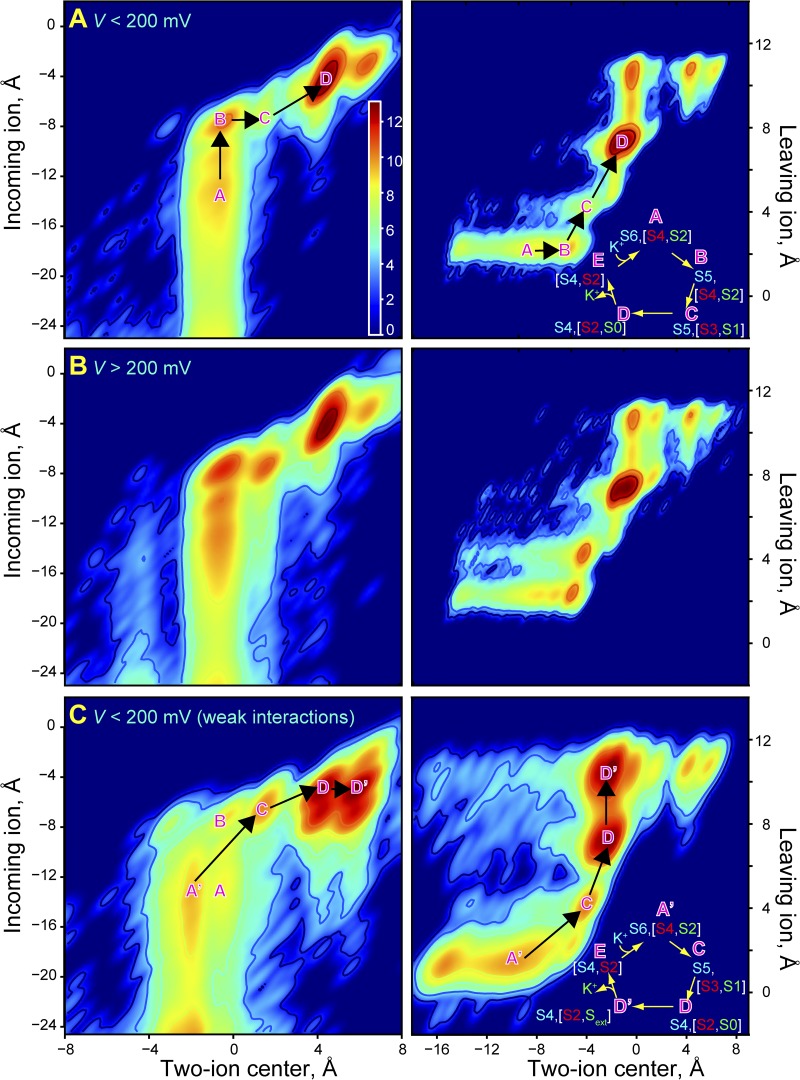
Figure 3.

K_V1.2/2.1 permeation mechanism. (A and B) Position of the incoming ion versus the centroid of the two SF-bound ions above it (left panels) and position of the leaving ion versus the centroid of the two SF-bound ions below it (right panels) at low (A) and high (B) voltages. The color bar is in units of log(ρ[x,y]); ρ[x,y] is the two-dimensional histogram of ion positions averaged over either low- or high-voltage simulations. The minima represent the four predominant three-ion configurations in the knock-on permeation mechanism; the mechanism is indicated in A (right), with S0–S6 denoting SF ion-binding sites (see Fig. S1). The knock-on intermediate is S5[S4,S2]; its formation is the rate-limiting step in the indicated mechanism (Jensen et al., 2010). (C) Low-voltage data similar to those in A, but obtained with weakened K⁺–carbonyl oxygen interactions (Roux and Bernèche, 2002; Allen et al., 2006b). The predominant permeation mechanism, in which the knock-on intermediate is not formed, is shown in the right panel.

gA

We observed no ion permeation below 150 mV, and at voltages below 400 mV, the conductance of ∼0.1 pS was much lower than that found experimentally (Fig. 4 A and Table S2). At voltages above 400 mV, the current was approximately linear in V, with a high-voltage conductance of 5 ± 2 pS (Fig. 4 A). A control simulation using the alternate gA structure (PDB accession no. 1JNO; Townsley et al., 2001) yielded a statistically identical permeation rate (Fig. 4 A; see also Table S2). The identical permeation rates reflect the fact that the two gA structures (1MAG and 1JNO) relaxed into the same conformation. In both relaxed structures, tryptophan (Trp) residues 9 and 11 have similar NMR DQS, which agree with corresponding experimental data (Koeppe et al., 1994); in fact, all of the Trp rotameric states appear highly similar between the two relaxed structures (Figs. S3 and S4). Two control simulations with the older CHARMM27 lipid model (and the 1MAG structure) resulted, in contrast, in four- to eightfold lower permeation rates (Fig. 4 A).

At lower voltages, ∼25% or less of ions recruited into—and permeating—the gA vestibule (−15 < z < −8 Å; residues 10–15) also permeated the pore, whereas at higher voltages, all recruited ions permeated the pore (Fig. 4 B). The total waiting time between two consecutive permeation events—the time to enter the vestibule and then permeate the pore—decreased exponentially as the voltage was increased (Fig. 4 C). The mean passage time for permeating the pore, decomposed into residence times within each of the local pore binding sites, denoted 1–10, was longer at the pore vestibules than in the internal binding sites, where the residence time also was less voltage dependent (Fig. 4, D and E).

Biased energy profiles, calculated from the non-equilibrium ion density observed in simulations at individual voltages, suggested an ∼4–5 kcal · mol⁻¹ conduction barrier (Fig. 4 D), a reduction caused by the applied voltage of ∼3–4 kcal · mol⁻¹ below the actual free energy barrier we obtained at V = 0, W(z) (symmetrized and then fit to a series of sine functions; Fig. 4 D).

For a one-ion conduction process and at saturating K⁺ concentrations, W(z) is related to the conductance as: g = e² · (k_BTL²)⁻¹ · <D(z)⁻¹ · exp(W(z)/k_BT)>⁻¹ <exp(−W(z)/k_BT)>⁻¹; L = 28 Å is the pore length, and averaging is over all positions within the pore (Roux and Karplus, 1991). From the position-dependent diffusion constant, D(z), we obtained an average diffusion constant of D = 0.027 ± 0.003 Ų · ps⁻¹ (see Materials and methods); this is similar to the ∼0.037-Ų · ps⁻¹ estimate of Mamonov et al. (2006), but we note that larger values have also been obtained (Allen et al., 2006a,b). Using D(z), we also obtained g = 0.03 ± 0.004 pS from the PMF (g = 0.07 ± 0.01 pS using the average diffusion constant, <D(z)>), which is in line with the conductance we obtained from a linear fit to the low-voltage (∼184 < V < 306 mV) currents, which gave g ≈ 0.1 pS.

A K⁺-binding constant of 0.17 M was obtained (within −14 < z < 14 Å), consistent with the 0.30-M value obtained by Allen et al. (2006a) and with experimental values that range from 0.02 to 0.73 M (Hinton et al., 1986).

At varying ion–carbonyl interaction strength, the K⁺ mean passage time across the pore was longest at stronger interactions and decreased exponentially as the interaction strength was weakened. The current was maximal at native σ (Fig. 4, H and J, and Table S2). Because gA’s vestibule (sites 1, 2 and 9, 10; Fig. 4 D) is solvent exposed whereas its lumen is within the bilayer core, we also assigned these two regions separate σ values (Table S2). At stronger interactions in the vestibule (residues 10–15; σ_vestibule < σ_lumen) no permeation occurred, whereas with reversed interactions (σ_vestibule > σ_lumen) permeation increased about twofold over that observed with the native σ parameter (Fig. 4 J).

DISCUSSION

K_V1.2/2.1

As opposed to our earlier pore-only simulations, we here observed permeation at experimentally accessible voltages (Table S1 and Fig. 2 A) because the present simulations were at least 10 times longer than those in Jensen et al. (2010). At these lower voltages (<300 mV), however, the conductance of only ∼2 pS was ∼40-fold below the experimental value. The high-voltage conductance was 58 ± 18 pS (Fig. 2 A), but the conductance only approached this value at voltages much larger than those used to obtain the experimental value of 73 pS for Shaker (temperature corrected; see Materials and methods; Heginbotham and MacKinnon, 1993).

The left-shift of the I-V curve observed when the VSDs are retained suggests that the VSDs increase the dielectric constant adjacent to the pore cavity and SF; this brings the linear I-V regime somewhat closer to experimentally accessible voltages, because the electrostatic barrier to permeation is decreased by the presence of the VSDs. Our high-voltage conductance estimate is in broad agreement with the corrected (see Materials and methods) value obtained from our earlier K_V1.2 pore-only simulations (Jensen et al., 2010).

The waiting time between two permeation events decreased exponentially as the voltage was increased, which reflects the overall nonlinear I-V curve. The single-ion residence times in sites S4 and S2, in particular, decreased with increasing voltage; these are the sites in which SF-bound ions await their knock-on (Figs. 2 E, 3 A, and S1). The underestimated low-voltage conductance was thus caused by too infrequent formation of the rate-limiting knock-on intermediate: three K⁺ SF-bound in the configuration S5[S4,S2] (Jensen et al., 2010).

Although no shortage of ions entering and permeating the cavity up to 2 Å below site S5 was evident below 300 mV, less than 10% of the recruited ions also permeated the pore (Fig. 2 B and Table S1). The knock-on step was potentially negatively influenced by shortcomings of the force field such as its lack of polarizability and the high membrane dipolar potential, which is two- to threefold overestimated relative to the experimental value (Klauda et al., 2010); however, we would expect the membrane potential to play less of a role in a K_V channel than in a thinner channel like gramicidin, for which we approximately quantify its effect below.

A force field correction ensuring an intact SF (Jensen et al., 2012) appeared to have a modest and nonsystematic effect on permeation: the current in pore-only simulations with this correction was fairly close to our original pore-only data (Jensen et al., 2010, noting that lipid type and certain lipid force field parameters differ between these sets of simulations; Table S1).

The SF kinetic K⁺ occupancy of 2.6 ± 0.2 (Fig. 2 D and Table S1) was identical to what we found in our pore-only simulations and thus remains in accordance with the Hodgkin and Keynes value of 2.5, leading to the hypothesis that permeation in (voltage-gated) K⁺ channels may occur via a knock-on mechanism (Hodgkin and Keynes, 1955). The predominant permeation mechanism—apparent from all our simulations, regardless of voltage—was indeed the knock-on mechanism that we extensively characterized in Jensen et al. (2010), now also confirmed in Fig. 3 (A and B) for the K_V1.2/2.1 channel with the VSDs retained.

The water-to-K⁺ permeation ratio was ∼0.5 ± 0.2 (Fig. 2 F and Table S1); however, we expect it to be quite sensitive to force field parameters and the exact details of the SF. The most accurate experimental value, obtained for the human ether-à-go-go–related gene product, which is a slightly different voltage-gated K⁺ channel yet has the same overall conserved SF architecture as K_V1.2, varies with K⁺ concentration and is above one (Ando et al., 2005). In this light, the overall agreement between experiment and simulation seems satisfactory.

Weakening the ion–carbonyl interaction by increasing the LJ σ parameter to 3.2874 Å relative to CHARMM27, a parameter change suggested by Bernèche and Roux (2001) based on thermodynamic principles, lowered the SF kinetic K⁺ occupancy from 2.6 ± 0.2 to 1.7 ± 0.3 (Fig. 2 D and Table S1). For K_V1.2/2.1, this implies that the weakened interactions do not lead to a knock-on mechanism (Fig. 3 C). For KcsA, weakening this interaction was suggested to be potentially critical if a permeation rate close to the experimental value and a plausible conduction mechanism were to be obtained (Bernèche and Roux, 2001, 2003). For K_V1.2/2.1, however, we also found no increase in permeation as the ion–carbonyl interaction was reduced (Fig. 2 A and Table S1).

At weakened interactions, the ions bound at either end of the channel (in sites S5 and S0) dissociated more readily from the SF, which lowered the SF kinetic occupancy and altered the SF K⁺ distribution (Fig. S1). The weakened interaction strength did not negatively affect the rate of collisions between incoming ions in site S5 and the SF-bound ion pair awaiting knock-on in state [S4,S2], but these interactions were usually followed by dissociation of the incoming ion. As reflected in the lack of coalescence of K⁺-binding sites S4 and S3 (Fig. S1; site S4/S3 separated into two separate sites, S4 and S3, as the interactions were weakened), successful formation of the knock-on intermediate S5[S4,S2] was thus much reduced at the weakened interaction strength, which explains the lack of a rate increase despite the reduced SF–K⁺ friction. The alternate (three-ion) mechanism that predominated at weakened interaction strength appeared to be a mechanism in which the knock-on intermediate was bypassed (Fig. 3 C).

Preliminary simulations of a constitutively open KcsA mutant using the same weakened SF–K⁺ interaction parameters indicated a knock-on mechanism in agreement with the original result of Bernèche and Roux (2001). The average ion occupancy was 2.2, and a dual two/three-ion resting state, [S4,S2,(S0)], and water co-permeation were observed (i.e., a mechanism similar to the one we found for K_V1.2/2.1 with unmodified LJ parameters). In KcsA, the unmodified parameters led, in marked contrast, to a different knock-on mechanism with an occupancy of ∼3.3, a predominant three-ion resting state [S4,S2,S1], and no water co-permeation. However, the absolute permeation rates observed in our KcsA simulations remain uncertain (Table S5).

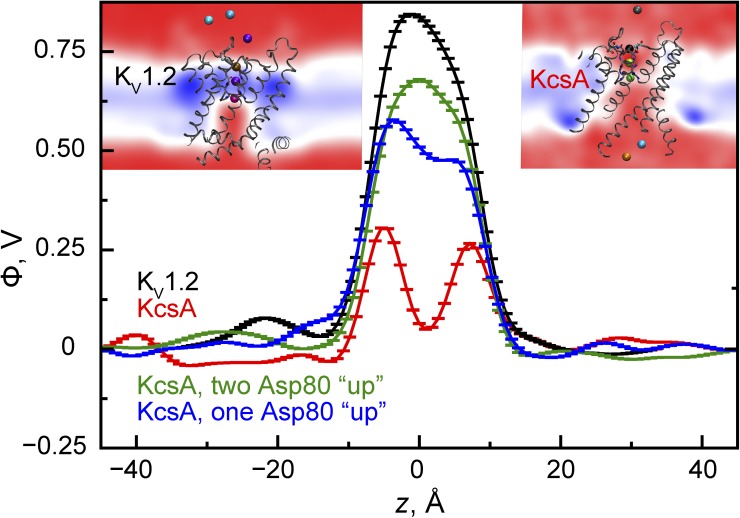
These results suggest, nonetheless, that SF structural features influence the exact permeation mechanism. In KcsA, Asp80 is oriented with its carboxylate group toward the SF center, and its movement is restricted by nearby Tyr82, whereas Asp379, the equivalent residue in K_V1.2/2.1, is extracellular facing, which renders the internal SF electrostatic potential in KcsA relatively more negative (Fig. 5). This possibly explains why the unmodified SF–K⁺ interactions led to fully dehydrated K⁺ populating S1 and S2 simultaneously and thus to the overall higher SF ion occupancy (Table S5). Forcing Asp80 in KcsA to be extracellular facing (OSM) led to a knock-on mechanism, with an occupancy of ∼2.8, similar to that of K_V1.2/2.1, but a three-ion resting state [S4/S3,S2,S0] predominated. It thus appears that slightly different knock-on mechanisms could operate in different K⁺ channels. It has also been suggested that multiple mechanisms can coexist in a single channel (Furini and Domene, 2009).

Figure 5.

K_V1.2 (pore-only) and KcsA (Glu71Ala noninactivating mutant) pore electrostatic potential profiles and three-dimensional maps (colored insets; color scale [in volts]: 0 (red) to 1.1 [blue]) obtained without an applied electric field and with the same number (three) of SF-bound K⁺. The potential in KcsA is overall less positive than in K_V1.2. The potential minima at the SF center (z = 0 Å) became increasingly pronounced with fewer Asp80 residues pointing “up”; “up” was the predominant orientation of the equivalent residue, Asp379, in K_V1.2 (see also Fig. S5).

gA

Permeation in gA was absent below 150 mV, whereas the conductance for ∼150 < V < 300 mV was ∼0.1 pS. The corresponding (temperature-corrected) experimental value is ∼30 pS (Busath et al., 1998; Ingólfsson et al., 2011). In the linear, high-voltage regime (V > 500 mV), we obtained a slope conductance of 5 ± 2 pS, but even this value is much lower than the (temperature-corrected) experimental slope conductance of 66 pS derived from currents measured up to 500 mV; at 500 mV the current in the simulations is about two orders of magnitude lower than in experiments at the same voltage (Andersen, 1983).

In the case of a linear, idealized I-V curve, the ratio of forward transitions between two adjacent sites should be similar at each voltage, whereas the net number of such transitions should increase linearly with V. In our simulations of gA this is not the case. The number of ions that entered site 3 from site 2 relative to the number of ions that entered site 2 from site 1, the 2→3/1→2 ratio, was approximately four times larger at the highest voltage than at the lowest (simulations 1 and 5; Table S4). The 3→4/2→3 and 4→5/3→4 ratios were, in contrast, only ∼2.5 and 2 times higher at the highest voltage than at the lowest, respectively, suggesting that the underestimated low-voltage permeation rate may in part be attributed to the difficulty of recruiting ions into site 3 and, to a lesser extent, onwards into site 4.

The voltage dependency of the lumen residence times (sites 3–8) was small and these residence times were short relative to the total waiting time between two permeation events of ∼3–9 µs (Fig. 4, C and E). This is consistent with the above conclusion that the underestimated low-voltage permeation rate is caused by insufficient ion recruitment into the pore lumen (i.e., recruitment into site 3). The intrinsic electrostatic potential in the lumen was significantly higher at lower voltage (Fig. 4 G), which hampered ion recruitment into the lumen, consistent with the PMF in this region, where there is a relatively large energy difference between sites 1 and 3 (vestibule and lumen, respectively; Fig. 4 D). We also observed that the residence times were longest, ∼0.5 µs, at pore entrance sites 1 and 2 and exit sites 9 and 10, which suggests that slow dissociation of the ions after lumen permeation may also have contributed to the underestimated low-voltage permeation rates. The electrostatic potential appears to hamper this dissociation process as well (Fig. 4 G); we note that this potential is higher when CHARMM27 is used for the lipids instead of CHARMM36.

We also investigated the contribution from the pore water molecules to the electrostatic potential: at ∼200 mV, the water molecules were aligned such that their total normalized dipole moment was less than zero for ∼25% of the time. With this orientation they could not bind an ion coming into the vestibule, whereas at ∼700 mV they aligned such that their dipole moment was greater than zero; they were thus always able to bind the ion (Figs. 4 G and S6). However, the orientation of the pore water molecules appears to have only a modest effect on the low-voltage permeation rate.

Modifications of the K⁺–carbonyl oxygen LJ interactions did not increase permeation (Fig. 4, H and I, and Table S2). As the interaction strength was increased, the K⁺ mean passage time through the pore increased, whereas the current decreased. 1→2 transitions, and thus also subsequent forward transitions, were relatively fewer because entering and exiting ions remained in sites 1 and 10, which increased the kinetic occupancy (Tables S2 and S4, and Fig. S2).

As the interaction was weakened, the mean passage time decreased exponentially, but the frequency of ion recruitment from water also decreased, because the ion–vestibule interaction became too weak. The optimal current, where ion recruitment from the water and friction between pore and ion were best balanced, occurred at the native interaction strength (Fig. 4 H).

Allen et al. (2006a) analyzed permeation in gA using different force fields and obtained maximal conductance with the native CHARMM27 (MacKerell et al., 1998) and AMBER94 (Cornell et al., 1995) parameters. The PMF barrier estimated using these force fields was ∼9–12 kcal · mol⁻¹; our PMF barrier of ∼8 kcal · mol⁻¹ (Fig. 4 D) is thus broadly consistent with the lower bound of their barrier height estimates. We did not correct our PMF, whereas Allen et al. rescaled their PMF to compensate for the overestimated membrane dipolar potential: there is a 300-mV difference between the CHARMM27 membrane dipolar potential applied by Allen et al. and the CHARMM36 membrane dipolar potential (Klauda et al., 2010) applied in the present study. After correcting their barrier to ∼9 kcal · mol⁻¹, a conductance of 4–5 pS was obtained (Allen et al., 2006a; Ingólfsson et al., 2011; both use a larger estimate for the diffusion constant than that used here). Another independent Drude oscillator–based dielectric correction brought the conductance to 9.3 pS (Allen et al., 2006a) and thus closer to the experimental value of 21 pS (Busath et al., 1998).

Taking into account the use of the different membrane models, our and Allen et al.’s PMF results appear to be in good agreement: both sets of results consistently suggest that the underestimated permeation rate is caused by force field shortcomings, including deficiencies in the lipid model and the force fields’ lack of polarizability. In this regard it is worth noting that a twofold difference in conductance between glycerol monooleate and phosphatidylcholine bilayers was observed experimentally (Busath et al., 1998); the difference in dipolar potentials between these two lipids is ∼120 mV (Hladky, 1974). A smaller conductance difference of 30–40% was seen between dioleylphosphatidylcholine ether lipids (DoPC, a dialkyl phospholipid) and dioleoylphosphatidylcholine lipids (DOPC, a diacyl phospholipid), presumably because the dipolar potential in ester lipids (e.g., DOPC) is ∼100 mV higher than in ether lipids (e.g., DoPC; Gawrisch et al., 1992; Providence, et al., 1995). Given the fact that current force fields overestimate the experimental dipolar potential by ∼300–400 mV (Klauda et al., 2010), there could be roughly fivefold difference in conductance between simulations and experiments attributable to this factor. Because the overall discrepancy between simulation and experimental permeation rates is approximately two orders of magnitude, other force field shortcomings (such as lack of polarizability) presumably have a greater influence on permeation rates.

Two control simulations, performed with the older CHARMM27 (POPC) lipid model, confirmed the prediction that the magnitude of the dipolar potential has an influence on permeation rates in line with the above estimate. (The CHARMM27 dipolar potential is 300 mV larger than in the CHARMM36 parameter set [Klauda et al., 2010].) The permeation rate in these two control simulations was reduced four- to eightfold (Fig. 4 A), whereas in a corresponding control simulation of K_V1.2/2.1 (Fig. 2 A), the permeation rate was only reduced by ∼35%, because the permeation pathway in this channel is relatively more protected from the low-dielectric membrane environment. Additional CHARMM27 control simulations with zero ion concentration indicated that the diffusive water permeability of gA (at V = 0) was 2.9 ± 0.7 × 10⁻¹⁵ cm³ · s⁻¹, whereas with the CHARMM36 parameter set, the permeability was twofold higher, 5.7 ± 0.7 × 10⁻¹⁵ cm³ · s⁻¹, which is close to the experimental value of 6.6 × 10⁻¹⁵ cm³ · s⁻¹ (Dani and Levitt, 1981). The orientation of the pore water was also different between these two parameter sets (Fig. 4 G, inset). Intriguingly, in aquaporin water channels, where the water permeation pathway is better screened from the low membrane dielectric than in gA, the water permeation rate was observed to decrease with increased membrane cholesterol concentration (Tong et al., 2012), which raises the magnitude of membrane dipolar potential (Haldar et al., 2012).

Our PMF-based conductance estimate is very close to the observed low-voltage conductance of ∼0.1 pS, suggesting that the one-dimensional PMF captures the essence of the ion permeation process in gA. Other factors would need to be accounted for in a more detailed analysis, but the agreement between our two independent low-voltage conductance estimates suggests that these are relatively small effects. The two-dimensional biased energy profile in Fig. 4 F indicates, for example, that reorientation of pore water molecules during permeation may contribute only ∼1 kcal · mol⁻¹ to the overall barrier, and the water orientation data in Figs. 4 G and S6 suggest that binding of an incoming ion is only modestly hampered by unfavorable water orientation at low voltage.

Other methodological shortcomings also exist. Current force fields fail, for instance, to address the fact that gA’s vestibule and lumen are exposed to aqueous and hydrophobic environments, respectively, and that these two pore regions thus should have different σ values. We explored the effect on permeation of introducing such dual parameters (Table S2). At relatively lower K⁺ affinity in the lumen (σ_vestibule < σ_lumen), 3→4 and 4→5 forward transitions were rare (Table S4), and no permeation occurred. With increased relative affinity in the lumen (σ_vestibule > σ_lumen), 3→4 transitions and transitions between subsequent binding sites were, in contrast, more frequent; with σ_vestibule = 3.09 Å, permeation increased twofold as ions were more readily recruited than with σ_vestibule = 3.2 Å, where the native parameter–like currents prevailed (Fig. 4 J).

Summary, limitations, and outlook

The current–voltage characterization of ion movement across bilayer-spanning channels (Attwell and Jack, 1978; Levitt, 1986; Andersen, 1989) led to the understanding that ion permeation is an electrodiffusive barrier–crossing process. Recent technological advances have now made it feasible to conduct all-atom MD simulations of single-file ion permeation across selective ion channels in the presence of a constant electric field. In principle, this allows the barrier-crossing process to be observed at the single-ion level, and it allows correlation effects in multi-ion processes to be addressed. The extent to which long MD simulations prove capable of contributing to the further elucidation of ion channel behavior will, however, be determined in part by various technical issues, some of which we have discussed in this paper.

For both K_V1.2/2.1 and gA, our simulated single-channel permeation rates were found to significantly underestimate the corresponding experimental rates. Their respective permeation mechanisms, however, were voltage independent, suggesting that direct MD simulation of ion permeation can provide key insights into the permeation mechanisms at a single-ion level of detail. A knock-on conduction mechanism was observed in K_V1.2/2.1, with ion occupancy and a water–ion cotransport ratio consistent with experimental data, and the underestimated conduction rates at lower voltages were found to be caused by slow formation of the knock-on intermediate (the rate-limiting step). At experimentally accessible voltages, the underestimated permeation rates in gA appear to be largely attributable to insufficient ion recruitment into the pore lumen, but force field modifications reflecting the different environments of the terminal and internal pore lumen regions improved these rates.

Certain force field modifications have been introduced to improve the thermodynamics of ion binding to the channel (Bernèche and Roux, 2001; Roux and Bernèche, 2002; Allen et al., 2006b). We found, however, that these modifications did not increase permeation rates. For K_V1.2/2.1, they caused a change in the dominant permeation mechanism from knock-on to a mechanism that bypassed the formation of the knock-on intermediate. Although different conduction mechanisms may coexist (Bernèche and Roux, 2001; Furini and Domene, 2009), experimental data (Hodgkin and Keynes, 1955) suggest that the main flux in K_V channels may likely be associated with a knock-on mechanism; thus, the original unmodified simulation parameters, which our results show produce the knock-on mechanism, appear satisfactory for K_V1.2/2.1. Our preliminary simulation data for KcsA further suggest that the details of the knock-on mechanism in this channel (Bernèche and Roux, 2001, 2003; Morais-Cabral et al., 2001; Zhou and MacKinnon, 2003; Roux, 2005) may be different from that in K_V1.2/2.1 because of differences in the electrostatic potential in the ion-selective region between these two channels.

Reducing the influence of the low membrane dielectric constant on the permeation process by including the voltage sensors in the K_V1.2/2.1 simulations, or using dual LJ parameters in the gA simulations, improved the permeation rates. However, the intrinsic membrane electrostatic dipolar potential is too high, hindering accurate permeation rates from being obtained at lower voltages, particularly for thin pores such as gA, in which the permeation pathway is nearer the low-dielectric environment of the membrane. Nevertheless, the effect of the dipolar potential can only explain a minority of the rate discrepancy, even for gA. Collectively, these observations suggest that polarizable force fields and membrane models with improved dipolar potential and dielectric constants could together lead to more accurate simulated permeation rates at experimentally accessible voltages.

APPENDIX

We here present a different derivation of the relation V = l_z · E between the applied field and the potential drop that is intended to make more intuitively clear why this relation holds and the relation V ≈ l_M · E (l_M is the membrane thickness) that we used earlier (Jensen et al., 2010) is incorrect. The latter relation is suggested by the following specious argument: The potential drop across the simulation box is $V={\displaystyle {\int }_{-l_z/2}^{+l_z/2}E/\epsilon dz}$; if the system consists of an ionic solution (dielectric constant ε = ∞), and a membrane in the xy plane of thickness l_M and dielectric constant ε = ε_M, then V ≈ −l_M · E/ε_M, or simply V ≈ l_M · E, if we additionally take ε_M = 1.

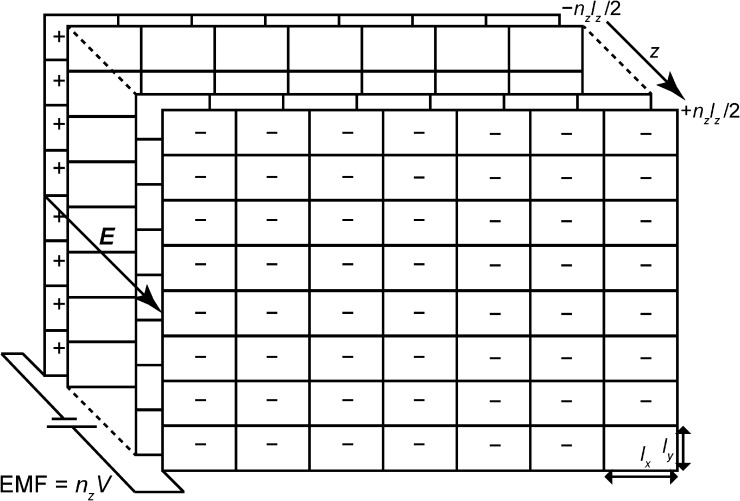
To clarify why the above argument fails, we choose boundary conditions for which it is clear that the potential drop across a simulation box is V, and then show that simulations with these boundary conditions are equivalent to those under the standard tinfoil boundary conditions with an additional applied field, E = V/l_z. For simplicity, we restrict ourselves to a system in thermodynamic equilibrium (no current flow) and for which the dimensions of the simulation box (l_x × l_y × l_z) are held fixed during the simulation. We use periodic boundary conditions, but instead of the usual tinfoil boundary conditions, we choose the boundary conditions illustrated in Fig. A1. In these boundary conditions, the replicated system resembles a pancake with the number of replicas in the x and y dimensions approaching infinity more rapidly than the number of replicas n_z in the z direction, and there are conducting plates at ±n_zl_z/2 maintained by an external electromotive force at a potential difference of n_zV. This ensures that the constant contribution to the electric field lies in the z direction, and that the potential drop across an individual simulation cell is V.

Figure A1.

Sketch of the boundary conditions. The simulation box, which has dimensions of l_x × l_y × l_z, is periodically replicated in all dimensions, but the number of copies in the x and y directions approaches infinity more rapidly than the number of copies in the z direction, so that the shape of the resulting replicated system resembles a pancake. Each face of the pancake is in contact with one of two conducting plates (shown at the front and back of figure) maintained at a voltage difference (back minus front) of n_zV by an external electromotive force. With the conventions used here, the situation illustrated corresponds to a positive membrane potential V and applied field E; the quantities Q and Q_µ (see text) are negative and positive, respectively.

The total free energy per simulation box is:

$$\beta F=-\text{log}{\displaystyle \int e^{-\beta (U+QV)}d\mathit{r}dQ,}$$ (A1)

where β is inverse temperature, r denotes the particle positions within one simulation box, Q is the amount of charge (per box area, A = l_x · l_y) transferred between the conducting plates at ±n_z · l_z/2, and U is the energy (per simulation box) of all interactions, including those between the particles themselves, between the particles and the charged plates, and between the charges on the plates themselves:

$$U(\mathit{r},Q)=U_{\text{particles}}\left(\mathit{r}\right)+U_{\text{particles}-\text{plate}}(\mathit{r},Q)+U_{\text{plate}}\left(Q\right).$$ (A2)

It is straightforward to calculate the Q-dependent terms and then carry out the integration over Q in the partition function (Eq. A1). First, because the electric field generated by the plate charges alone is Q/(Aε₀), we have:

$$U_{\text{plate}}\hspace{0.17em}=\frac{1}{2}{\epsilon }_0{\left(\frac{Q}{A{\epsilon }_0}\right)}^{2}A{l}_z\hspace{0.17em}=\frac{l_z}{2{\epsilon }_{0}A}{Q}^2.$$ (A3)

Similarly, defining Q_µ(r) = µ_z(r)/l_z, where µ_z(r) is the simulation box dipole moment in the z direction, we have:

$$U_{\text{particle}-\text{plate}}\hspace{0.17em}=\frac{l_z}{2{\epsilon }_{0}A}\left({\left(Q+Q_{\mu }\right)}^2-Q^2-Q_{\mu }^2\right)=\frac{l_z}{{\epsilon }_{0}A}{Q}_{\mu }Q.$$ (A4)

Finally, integration over Q in the partition function leads to:

$$\beta F=-\text{log}{\displaystyle \int }{e}^{-\beta U_{\text{eff}}}d\mathit{r}\hspace{0.17em}+\hspace{0.17em}\text{constant},$$ (A5)

where the effective energy is:

$$U_{\text{eff}}\hspace{0.17em}=\hspace{0.17em}{U}_{\text{particles}}-\frac{l_z}{2{\epsilon }_{0}A}{Q}_{\mu }^2-V{Q}_{\mu }.$$ (A6)

The second and third terms reflect the interactions of the particles with the reaction field, Q_µ/(Aε₀), and applied field, respectively. The static component of the electric field generated by the particles leads to a contribution to the particle–particle energy not included in U_GSE (the usual energy calculated in MD simulations with tinfoil boundary conditions and no applied field); this contribution is of equal magnitude and opposite sign to the reaction field contribution, U_particles = U_GSE + l_z Q_µ²/(2ε₀A). Thus,

$$U_{\text{eff}}=U_{\text{GSE}}-V{Q}_{\mu }=U_{\text{GSE}}-E{\displaystyle \sum {}_i}{z}_i{q}_i,$$ (A7)

where we have identified E = V/l_z. Simulations with the boundary conditions described here (in which the membrane voltage is set to V) are thus equivalent to simulations with tinfoil boundary conditions and an added electric field E = V/l_z, which is Eq. 1 of the main text. The derivation also makes clear that E is not the total field coming from external sources (i.e., the charged conducting plates) because it does not include the reaction field, Q_µ/(Aε₀); it is thus not true that $V={\displaystyle {\int }_{-l_z/2}^{+l_z/2}E/\epsilon dz}$. This explains why the argument given at the beginning of this Appendix fails. For this reason, we avoid referring to E as “external.”