Quantitative properties and receptor reserve of the DAG and PKC branch of G_q-coupled receptor signaling

Abstract

G_q protein–coupled receptors (G_qPCRs) of the plasma membrane activate the phospholipase C (PLC) signaling cascade. PLC cleaves the membrane lipid phosphatidylinositol 4,5-bisphosphate (PIP₂) into the second messengers diacylgycerol (DAG) and inositol 1,4,5-trisphosphate (IP₃), leading to calcium release, protein kinase C (PKC) activation, and in some cases, PIP₂ depletion. We determine the kinetics of each of these downstream endpoints and also ask which is responsible for the inhibition of KCNQ2/3 (K_V7.2/7.3) potassium channels in single living tsA-201 cells. We measure DAG production and PKC activity by Förster resonance energy transfer–based sensors, and PIP₂ by KCNQ2/3 channels. Fully activating endogenous purinergic receptors by uridine 5′triphosphate (UTP) leads to calcium release, DAG production, and PKC activation, but no net PIP₂ depletion. Fully activating high-density transfected muscarinic receptors (M₁Rs) by oxotremorine-M (Oxo-M) leads to similar calcium, DAG, and PKC signals, but PIP₂ is depleted. KCNQ2/3 channels are inhibited by the Oxo-M treatment (85%) and not by UTP (<1%), indicating that depletion of PIP₂ is required to inhibit KCNQ2/3 in response to receptor activation. Overexpression of A kinase–anchoring protein (AKAP)79 or calmodulin (CaM) does not increase KCNQ2/3 inhibition by UTP. From these results and measurements of IP₃ and calcium presented in our companion paper (Dickson et al. 2013. J. Gen. Physiol. http://dx.doi.org/10.1085/jgp.201210886), we extend our kinetic model for signaling from M₁Rs to DAG/PKC and IP₃/calcium signaling. We conclude that calcium/CaM and PKC-mediated phosphorylation do not underlie dynamic KCNQ2/3 channel inhibition during G_qPCR activation in tsA-201 cells. Finally, our experimental data provide indirect evidence for cleavage of PI(4)P by PLC in living cells, and our modeling revisits/explains the concept of receptor reserve with measurements from all steps of G_qPCR signaling.

INTRODUCTION

This paper continues our analysis (see Dickson et al. in this issue) of the quantitative properties of signaling from membrane receptors coupling to G_q (G_q protein–coupled receptors [G_qPCRs]). It was motivated by our study of receptor modulation of KCNQ2/3 potassium ion channels. Upon activation of G_qPCR, G_q binds to and activates PLC. PLC in turn hydrolyzes the minor plasma membrane lipid phosphatidylinositol 4,5-bisphosphate (PIP₂) into the two prominent signaling second messengers, inositol 1,4,5-trisphosphate (IP₃) and diacylglycerol (DAG). Cytosolic IP₃ triggers release of calcium from intracellular stores through IP₃ receptors (IP₃Rs), whereas membrane DAG binds with and activates PKC.

Here, we study the kinetic properties of DAG production and PKC activation. We have previously analyzed the kinetics of the G_q-coupled muscarinic receptor (M₁R) (Suh et al., 2004; Horowitz et al., 2005; Jensen et al., 2009; Falkenburger et al., 2010a) and of PIP₂ depletion and synthesis (Falkenburger et al., 2010b). In our companion paper, we have analyzed the IP₃/calcium branch of G_qPCR signaling (Dickson et al., 2013). In addition, we ask whether any of these second messengers have a strong modulatory effect on KCNQ channels, the substrate of neuronal M current. Finally, we describe the details of our augmented kinetic model that supports all our experimental data.

Several mechanisms have been discussed for KCNQ2/3 channel inhibition. We have shown that simple depletion of PIP₂ is sufficient (Suh and Hille, 2002; Suh et al., 2006; Falkenburger et al., 2010b), without the involvement of other second messengers. However, phosphorylation by PKC and elevation of calcium are also reported regulators (Hoshi et al., 2003, 2010; Gamper et al., 2004; Bal et al., 2008a, 2010). Regulation of KCNQ by PKC is said to involve the scaffolding protein A kinase–anchoring protein (AKAP)79 (homologous to mouse AKAP150). AKAP79 binds to the C terminus of the KCNQ2 subunit (Hoshi et al., 2003, 2010) and coordinates the localization of cAMP-dependent protein kinase and PKC.

We performed kinetic measurements of DAG production and PKC activation using fluorescent reporters in individual living cells. We then used these measurements together with those of our companion paper (Dickson et al., 2013) to extend our kinetic model of G_qPCR signaling to IP₃/calcium and DAG/PKC signaling. We show that elevations in cytosolic calcium and activation of PKC are not sufficient for the inhibition of KCNQ2/3 channels after M₁R activation in tsA cells. In addition, we provide the first in-cell evidence for possible direct cleavage of PI(4)P by PLC by studying the effects of a PIP₂ 5-phosphatase on the production of DAG and IP₃ by G_qPCR activation.

MATERIALS AND METHODS

Experiments with cells

The general methods follow those of our companion paper (Dickson et al., 2013). In brief, tsA-201 cells were cultured and transiently transfected with KCNQ2/3 channels, M₁Rs, or various genetically expressible optical probes labeled with fluorescent proteins, CFP and/or YFP, for FRET and translocation experiments. Calcium concentrations and Förster resonance energy transfer (FRET) were measured photometrically on an epifluorescence microscope at room temperature. Whole-cell electrophysiology was performed to measure KCNQ2/3 current as described in our companion paper (Dickson et al., 2013). Additional fluorescent probes used here and not in our companion paper are: C kinase activity reporter (CKAR), AKAP79, and AKAP-CKAR (provided by J. Scott, University of Washington, Seattle, WA), calmodulin (CaM)-YFP (provided by M. Shapiro, University of Texas, San Antonio, TX), CFP-CAAX (from K-Ras; provided by K. Jalink, The Netherlands Cancer Institute, Amsterdam, Netherlands), and C1(PKCγ)-citrine (C1-YFP). For C1-YFP, the C1 domain of PKCγ was amplified from C1A(PKCγ)-EGFP (provided by T. Meyer, Stanford University, Stanford, CA) by PCR and inserted into pcDNA3-TRPV2-citrine (provided by S. Gordon, University of Washington, Seattle, WA) replacing TRPV2, using SacII and NheI.

Modeling

A kinetic model of G_qPCR signaling was formulated as ordinary differential equations and solved as a “compartmental” model in the Virtual Cell simulation framework (University of Connecticut Health Center). “Compartmental” means that species reside in well-stirred compartments (e.g., cytosol or plasma membrane) wherein diffusion is not rate limiting and thus not considered. The modeling continues the evolution of the kinetic descriptions we have published previously (Suh et al., 2004; Horowitz et al., 2005; Falkenburger et al., 2010a,b). The formulation, parameters, and outputs are described in the Results section. The entire Virtual Cell Model, “FalkenburgerDicksonHille2013,” is publicly available and new simulations can be run at http://www.vcell.org under Public BioModels/bfalken:FalkenburgerDicksonHille2013. All model parameters were selected manually to best reproduce the experimental results, and all simulations used the same set of parameters except where noted.

Statistics

Summarized data include one data point per cell. Statistics in the text and bars on graphs represent mean ± SEM. Statistical tests were performed using GraphPad Prism 5.0 (GraphPad Software).

Online supplemental material

Fig. S1 shows expression patterns of FRET probes. Fig. S2 shows model predictions for oxotremorine-M (Oxo-M) as compared with uridine 5′-triphosphate (UTP). Fig. S3 illustrates the dependence of the LIBRAvIII response on parameters k_IP₃ase and K_D_LIBRAvIII. Fig. S4 shows model predictions for a concentration series of Oxo-M, and Fig. S5. is a computational study of voltage-sensitive 5-phosphatase (VSP) activation during Oxo-M. Fig. S6. shows a model without PIP hydrolysis by PLC. Figs. S1–S6 are available at http://www.jgp.org/cgi/content/full/jgp.201210887/DC1.

RESULTS

The DAG–PKC pathway is readily activated

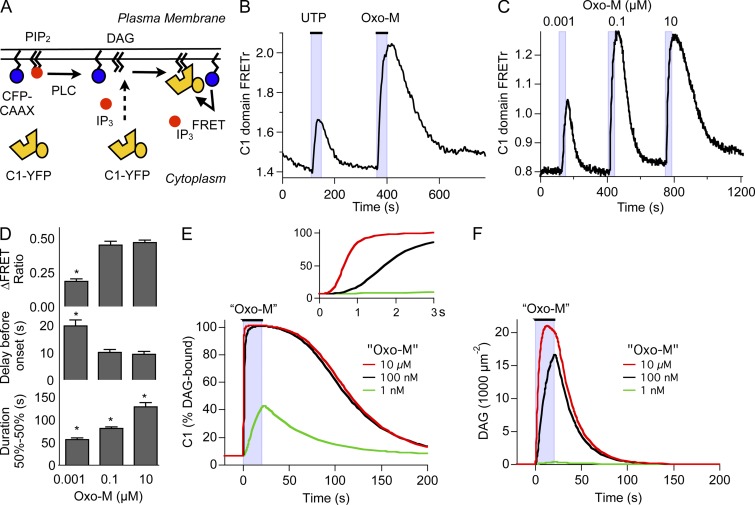
We continue our study of signaling from G_qPCR in tsA-201 cells starting now with the production of DAG. Migration to membranes of the DAG-binding C1 domain of PKCγ can be used to follow DAG production in many membranes (Oancea et al., 1998; Horowitz et al., 2005; Gallegos et al., 2006). To analyze DAG production specifically at the plasma membrane we used FRET between a YFP-tagged C1 domain (C1-YFP) and a CFP anchored to the plasma membrane by farnesylation (CFP-CAAX; Fig. 1 A). Confocal images from control cells show that C1-YFP assumes a cytosolic distribution at rest, whereas CFP-CAAX is tightly localized to the plasma membrane 24 h after transfection, provided expression levels were kept low (Fig. S1). C1 domain translocation was measured by ratiometric FRET using single-cell photometry (not imaging). FRET ratio (FRETr) was calculated from the total fluorescence with 440-nm excitation in the YFP (YFP_C) and CFP (CFP_C) emission channels (Falkenburger et al., 2010b). In the first experiments, we compared activation of M₁R transfected at high density with activation of endogenous purinergic receptors (eP2Y₂Rs). These were identified as P2Y₂Rs in our companion paper. The application of 100 µM UTP increased YFP_C and decreased CFP_C, corresponding on average to a 21% increase in FRETr above baseline (Fig. 1 B). This index of DAG production rose with a time constant of 43 ± 10 s (n = 6 cells). The response to 10 µM Oxo-M was roughly twice as large, corresponding on average to a 47% increase in FRETr and four times as fast (time to half-maximum for Oxo-M, 11 ± 1 s; n = 15). The Oxo-M response also lasted twice as long (duration for Oxo-M, 130 ± 9 s; for UTP, 58 ± 13 s). Thus, DAG production is evoked by both receptors, but activation by eP2Y₂R is clearly weaker than by high-density M₁R.

Figure 1.

Measurement of DAG production. (A) Schematic of DAG measurement by FRET photometry. YFP-tagged C1 domain is recruited to the plasma membrane by DAG production, leading to FRET with a membrane-anchored CFP (CFP-CAAX). (B) Representative recording of DAG production by FRET between C1-YFP and CFP-CAAX in response to 100 µM UTP, acting on eP2Y₂Rs, and 10 µM Oxo-M, acting on overexpressed M₁Rs. (C) Representative recording of FRET between C1-YFP and CFP-CAAX in response to a concentration series of Oxo-M (1 nM, 0.1 µM, and 10 µM). (D) Summary of experiments as in C (n = 5–6). Groups were compared by ANOVA. *, significance (P < 0.05) in posthoc test from neighboring bar. (E) Output of the computational model for the time course of DAG-bound C1 domain in response to a concentration series of Oxo-M. Quotation marks remind us that this is a computer simulation. Concentration of C1 domain was 0.5 µM. (F) Output of the computational model for the density of DAG molecules in response to a concentration series of Oxo-M. Concentration of C1 domain was set at 0 µM.

Our companion paper (Dickson et al., 2013) reports that PLC responses measured by IP₃ production, calcium release, and KCNQ2/3 current inhibition are weaker with full activation of eP2Y₂R than with full activation of M₁R. The weaker PLC responses to activation of eP2Y₂R could be mimicked by activating only a small fraction of M₁R with a reduced concentration of muscarinic agonist. Similarly here, the C1 domain FRET response elicited by 1 nM Oxo-M acting on high-density M₁Rs mimicked those with saturating UTP stimulation acting on eP2Y₂R (Fig. 1 C). With 1 nM Oxo-M, they were smaller, shorter, and rose more slowly than with 10 µM (Fig. 1 D). The responses with 100 nM Oxo-M were about as large and as fast as with 10 µM Oxo-M, but they were shorter. Our kinetic model nicely reproduced this concentration dependence of C1-domain responses (Fig. 1 E) and allowed us to predict the underlying changes of DAG (Fig. 1 F). Comparison of Fig. 1 E with Fig. 1 F demonstrates that the C1-domain probe is a very sensitive indicator of DAG, successfully reporting the small amount of DAG produced with 1 nM Oxo-M. Thus, as an assay for reporting G_qPCR activation, C1/CAAX FRET combines the high sensitivity of Fura-4F calcium measurements (e.g., Fig. 4 A in Dickson et al., 2013) with a broader dynamic range, showing differences in response duration even between 0.1 and 10 µM Oxo-M, where the calcium response amplitude is already saturated.

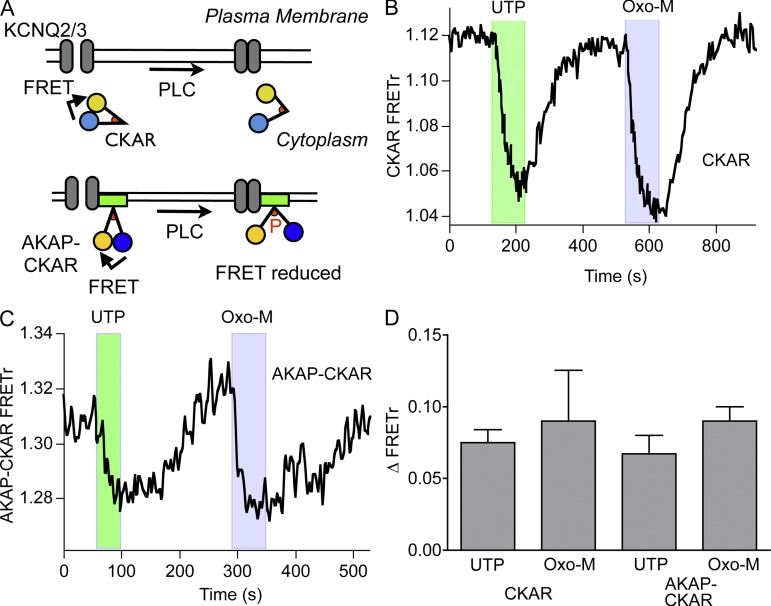
DAG is the physiological stimulus for recruiting and activating PKC at the plasma membrane. Accordingly, we monitored signaling from PKC using two CKARs: the cytosolic CKAR (Violin et al., 2003) and AKAP-CKAR, which localizes near the plasma membrane by a fusion to the scaffolding protein AKAP79 (Fig. S1; Hoshi et al., 2010). CKARs are FRET-based reporters comprising CFP and YFP linked by a PKC substrate peptide and an FHA2 phosphopeptide-binding domain. There is FRET between CFP and YFP at rest, and upon phosphorylation of the substrate sequence, the FHA2 domain binds the phosphopeptide and the FRET decreases (Fig. 2 A). CKAR is continually being dephosphorylated by endogenous phosphatases and therefore can provide a dynamic readout of PKC activity, or more precisely, a gauge of the phosphorylation state of PKC substrates. CKAR and AKAP-CKAR reported similar, modest changes in FRETr upon stimulation of either eP2Y₂R with 100 µM UTP or high-density M₁R with 10 µM Oxo-M (Fig. 2, B and C). Neither the delay nor the onset time constant was significantly different between UTP and Oxo-M (Fig. 2 D). Thus, even though far more DAG is produced with saturating Oxo-M than with UTP (Fig. 1 B), phosphorylation of the PKC target CKAR appears similar for both stimuli, suggesting that the PKC-CKAR reporter system is saturated by small amounts of DAG. This means that PKC, similar to the calcium response (Dickson et al., 2013), is sufficiently activated to phosphorylate substrates even when the number of stimulated receptors is small. We might have anticipated this result because PKC is the source of the highly DAG-sensitive C1 domains used in Fig. 1. The signal-to-noise ratio of the two CKAR probes is insufficient to resolve small quantitative differences. Our measurements show that for M₁Rs at high density, there is a very large receptor reserve (spare receptors) for stimulation of the PKC pathway through DAG.

Figure 2.

Weak stimulation of PLC suffices to activate phosphorylation by PKC strongly. (A) Schematic of real-time phosphorylation measurement by the CKAR and AKAP-CKAR probes. FRET at rest is reduced by the conformational change resulting from CKAR phosphorylation. CKAR is cytosolic, whereas AKAP-CKAR is located at the plasma membrane (see Fig. S1). (B) Cell expressing CKAR and M₁R. Representative recording of changes in FRETr in response to 100 µM UTP and 10 µM Oxo-M. (C) Cell expressing AKAP-CKAR and M₁R. Representative recording of the FRETr response to 100 µM UTP and 10 µM Oxo-M. (D) Summary of experiments as in B and C. There are no significant differences between responses to UTP and Oxo-M of CKAR (UTP, n = 8; Oxo-M, n = 5) and AKAP-CKAR (UTP, n = 7; Oxo-M, n = 6).

Does KCNQ2/3 current respond to second messengers?

We digress from our metabolic focus to revisit the possible contributions of second messengers to direct modulation of KCNQ2/3 potassium currents in tsA-201 cells, our original intention in starting this study. Others have implicated calcium-CaM signaling and AKAP/PKC signaling in KCNQ2/3 inhibition (Bofill-Cardona et al., 2000; Gamper and Shapiro, 2003; Hoshi et al., 2003, 2010; Gamper et al., 2005; Bal et al., 2008b, 2010; Kosenko et al., 2012). It is puzzling then that we have seen little evidence for either signal as a significant modulator of current in tsA cells. For example, in Fig. 1 A of our companion paper (Dickson et al., 2013), stimulation with 100 µM UTP does not inhibit KCNQ2/3 currents detectably, yet it evokes an appreciable global Ca²⁺ elevation, and in Fig. 2 (B–D) of this paper, it stimulates PKC activity strongly. The same stimulation of Ca²⁺ elevation without KCNQ2/3 current inhibition occurs with 1 nM Oxo-M (compare Fig. 4, A and B, in Dickson et al., 2013, with Fig. 6, D and E, in Jensen et al., 2009). Consistent with our model that attributes KCNQ2/3 reduction to PIP₂ depletion, neither 100 µM UTP nor 1 nM Oxo-M measurably depletes PIP₂ (Fig. 3 D in Dickson et al., 2013, and Fig. 5 F in Jensen et al., 2009).

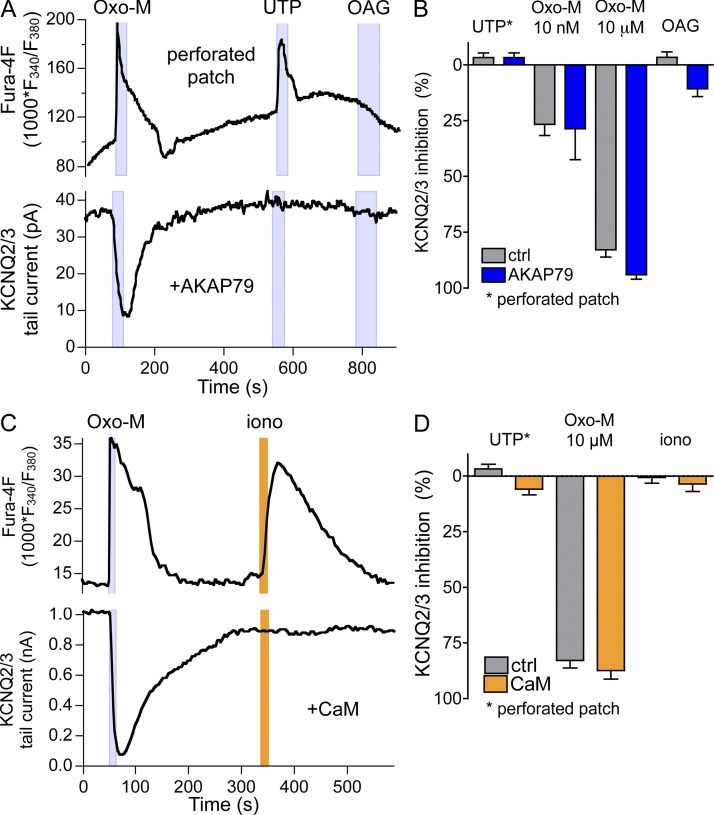
To test whether endogenous levels of AKAP79 might be insufficient for a PKC-dependent channel inhibition in tsA-201 cells, we overexpressed AKAP79 together with KCNQ2/3. However, even in these cells, UTP did not inhibit KCNQ2/3 current (Fig. 3, A and B). The presence of a Ca²⁺ transient showed that receptors had been activated. Maximal PKC activation with the application of the DAG analogue oleoyl-acetyl glycerol (OAG) inhibited KCNQ2/3 current by a mere 10% (Fig. 3, A and B). When AKAP79 was not overexpressed, OAG did not inhibit KCNQ2/3, consistent with our earlier findings (Suh and Hille, 2006) and with a recent report by the Hoshi group (Kosenko et al., 2012). The “physiological” level of PKC activation resulting from UTP application does not suffice to inhibit KCNQ2/3 current, and if phosphorylation of KCNQ2 by PKC changes PIP₂ affinity, this does not suffice to inhibit KCNQ2/3 current unless PIP₂ is decreased as well (Kosenko et al., 2012). We did not detect an effect of overexpressing AKAP79 on the extent of KCNQ2/3 inhibition by 10 nM or 10 µM Oxo-M (Fig. 3 B).

Figure 3.

Overexpression of AKAP or CaM does not augment KCNQ2/3 current modulation. (A) Simultaneous recording of calcium responses (Fura-4F; top) and KCNQ2/3 tail currents (bottom) in a cell expressing M₁R, KCNQ2/3, and AKAP79. Responses were elicited by 10 µM Oxo-M, by 100 µM UTP (acting on endogenous P2Y₂Rs), and by 10 µM of the DAG analogue OAG. (B) Summary of experiments as in A from cells without and with AKAP79 transfection. Responses to 100 µM UTP were recorded in the perforated-patch configuration (without and with AKAP79, n = 11 and 6). Responses to Oxo-M (n = 9 and 5 for 10 nM; n = 23 and 15 for 10 µM) and 10 µM OAG (n = 6 and 27) were not significantly different for whole-cell and perforated-patch configuration and therefore were pooled. Two-way ANOVA showed no significant effect of AKAP79 expression. (C) Simultaneous recording of calcium responses (Fura-4F; top) and KCNQ2/3 tail currents (bottom) from a cell expressing M₁R, KCNQ2/3, and CaM-YFP. Responses were elicited by 10 µM Oxo-M and 100 µM UTP, or by 5 µM ionomycin (extracellular calcium, 2 mM). (D) Summary of experiments as in C from cells without and with CaM-YFP expression. Responses to UTP were recorded in the perforated-patch configuration (n = 11 and 5). Responses to Oxo-M (n = 23 and 13) and ionomycin (n = 7 and 10) were not significantly different for whole-cell and perforated-patch configuration and therefore were pooled. Two-way ANOVA showed no significant effect of CaM expression.

Using similar logic, perhaps the endogenous levels of CaM are insufficient for a Ca²⁺-CaM–dependent channel inhibition in tsA-201 cells. We therefore overexpressed YFP-tagged CaM together with KCNQ2/3 channels. In these cells, there may be a small (<10% and not statistically significant) inhibition of KCNQ2/3 current by UTP and by treatment with the Ca²⁺ ionophore ionomycin that was absent without CaM overexpression (Fig. 3, C and D). Responses to Oxo-M were similar with and without CaM-YFP, regardless of Oxo-M concentration.

Thus, in our tsA-201 expression system, global Ca²⁺ elevations and general stimulation of PKC do not mimic the large inhibition of KCNQ2/3 currents seen, for example, with 10 µM or even 10 nM Oxo-M (Fig. 3). We conclude that the major KCNQ2/3 inhibition in response to Oxo-M in our experiments is caused by the extensive net depletion of PIP₂.

DAG may be produced directly from PI(4)P

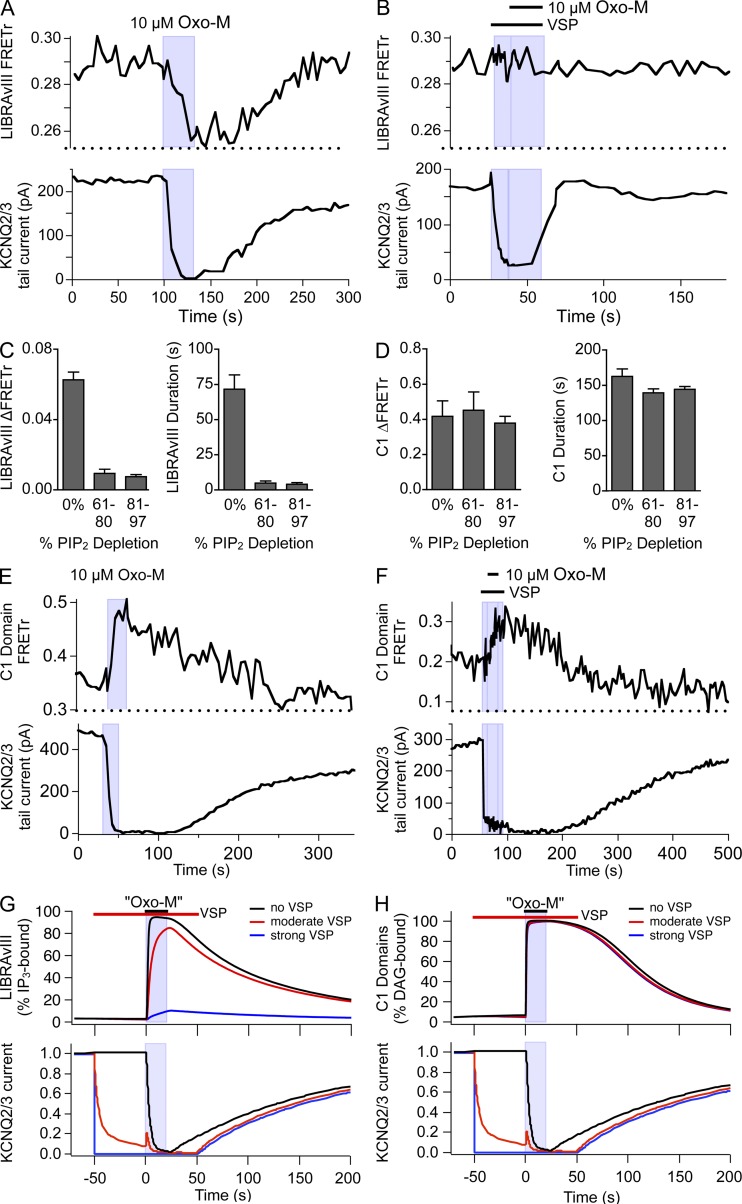
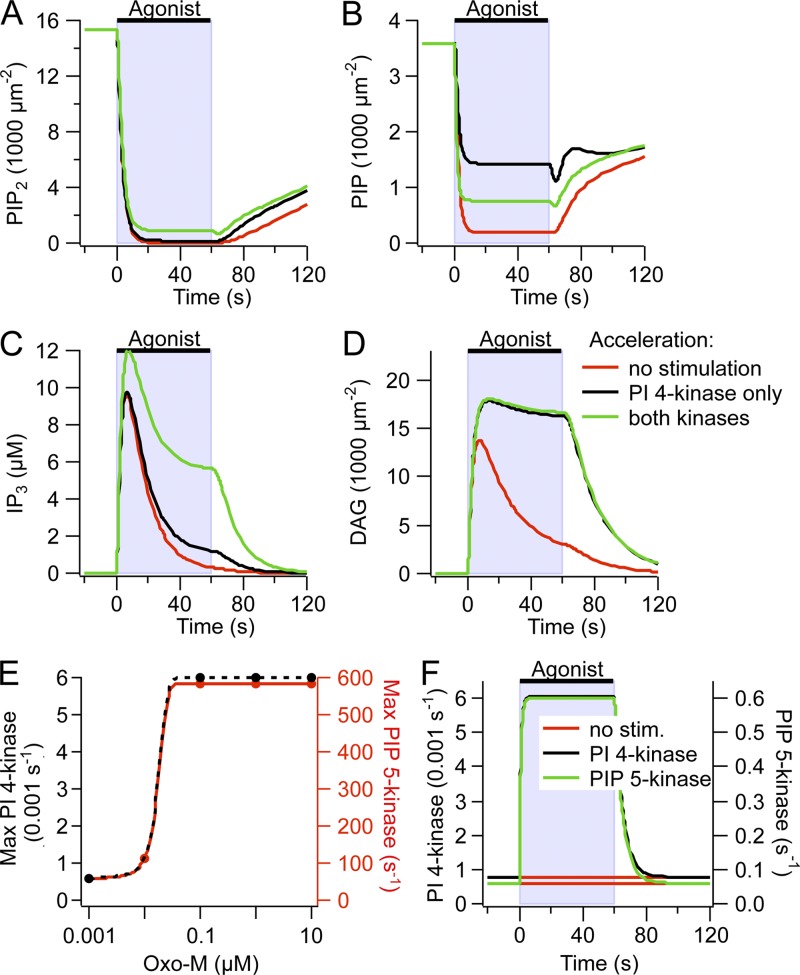
General consensus holds that PIP₂ is the major substrate of PLC, but it is possible that PLC can also cleave PI(4)P, yielding DAG and IP₂. A slow cleavage of PI(4)P was advanced by Wilson et al. (1984) on biochemical evidence and adopted by us in our previous kinetic modeling to explain considerable depletion of PI(4)P during activation of PLC (Horowitz et al., 2005; Falkenburger et al., 2010b). To address this possibility experimentally in intact living cells, we used the voltage-dependent PIP₂ 5-phosphatase, VSP. VSP is activated by depolarization to +120 mV and converts PIP₂ into PI(4)P (Murata and Okamura, 2007; Falkenburger et al., 2010b). Repeated activation of VSP for short periods of time (200 ms) serves to deplete the plasma membrane pool of PIP₂ reversibly and keep it low over tens of seconds. This protocol probably augments the pool of PI(4)P at the same time (see Figs. 7 and S6 in Dickson et al., 2013). PIP₂ levels were continuously monitored in such experiments by recording PIP₂-dependent KCNQ2/3 currents. In the series of experiments shown in Fig. 4, we activated PLC by M₁R either in control conditions (Fig. 4, A and E) or during continual PIP₂ dephosphorylation (Fig. 4, B and F) and observed the formation of the products DAG and IP₃. IP₃ was measured by LIBRAvIII as in our companion paper; DAG was measured by C1/CAAX FRET. We found that even submaximal PIP₂ dephosphorylation by VSP strongly reduced the amount of IP₃ produced (compare Fig. 4, A and B, quantified in C). In striking contrast, the amount of DAG reported by C1/CAAX FRET was unchanged, even when >80% of PIP₂ had been converted to PI(4)P (Fig. 4, E and F, quantified in D). Although indirect and dependent on relative affinities of the two probes, this result would be consistent with the hypotheses that PLC, or some PLC-dependent reaction, is capable of hydrolyzing PI(4)P into DAG (and IP₂). Fitting our kinetic model to this experiment (Figs. 4, G and H, S5, and S6) also supports that conclusion. As a corollary to this experiment, we can conclude that, as would be anticipated from classical binding experiments (Rivera et al., 1990), the LIBRAvIII reporter (a) is not responsive to IP₂ and further (b) does not report small amounts of IP₃ (see Dickson et al., 2013).

Figure 4.

DAG, but not IP₃, can be synthesized directly from PI(4)P. (A and B) Simultaneous recording of FRETr from the LIBRAvIII IP₃ probe (top) and KCNQ2/3 currents (bottom) in a cell also expressing M₁R and VSP. Unless noted otherwise, KCNQ2/3 currents were activated by depolarization from −60 to +40 mV for 200 ms every 600 ms and quantified by tail currents. Note that the zebrafish VSP is not activated significantly at +40 mV. (A) Decrease in LIBRAvIII FRETr, reflecting IP₃ production, and KCNQ2/3 current, reflecting PIP₂ depletion, upon the application of Oxo-M. (B) KCNQ2/3 currents and VSP were activated by depolarization to +120 mV for 200 ms every 600 ms during the time indicated (bar). Note that KCNQ2/3 activation is close to saturated at +40 mV, and VSP activation leads to a decrease in KCNQ2/3 current. Subsequent Oxo-M application did not elicit a LIBRAvIII FRETr response. (C) Summary of LIBRAvIII responses (amplitude and duration) in experiments as in A and B (n = 6). Cells were grouped by the extent of PIP₂ depletion during VSP as estimated from KCNQ2/3 current inhibition. 0% corresponds to no VSP activation. (D) Summary of experiments as in E and F (n = 10). (E) Simultaneous recording of KCNQ2/3 currents (bottom) and FRETr from C1-YFP/CFP-CAAX (top, reflecting DAG production) in cells also expressing M₁R and VSP. M₁R activation with 10 µM Oxo-M leads to an inhibition of KCNQ2/3 tail currents and an increase in FRETr, indicating PIP₂ depletion and DAG production. (F) Activation of VSP by depolarization to +120 mV for 200 ms every 600 ms (bar) reduces KCNQ2/3 tail currents without increase in FRETr. Subsequent Oxo-M application did elicit a C1-YFP/CFP-CAAX FRETr increase. (G and H) Simulations from the kinetic model reproducing the observed 70% reduction in the LIBRAvIII response (G) by prior VSP activation but no change in C1-domain response (H). VSP_max was 0 for “no VSP,” 0.3 s⁻¹ during “moderate” VSP activation, and 20 s⁻¹ during “strong” VSP activation. Note that moderate VSP reproduces the time course of KCNQ2/3 current inhibition by VSP that was observed experimentally. [LIBRAvIII] = 6 µM; [C1] = 0.5 µM.

Formulation of the kinetic model

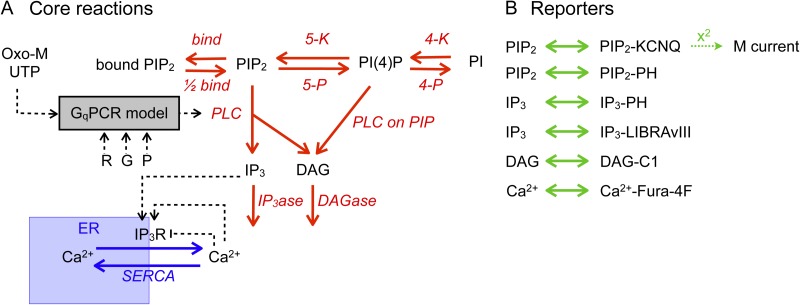
To further test hypotheses about the functioning of G_qPCR signaling from our observations, we constructed a quantitative model that reproduces almost all experimental observations. This model is summarized in Fig. 5. Fig. 5 A gives an overview of the biological part of the model, and Fig. 5 B summarizes the reactions of reporters, indicators, and the ion channel with the signaling molecules. Model species and initial conditions are listed in Table 1. Model equations (“reactions”) follow mass-action kinetics and are listed in Table 2. All units follow the conventions of Virtual Cell: seconds, micromolar, and micrometers.

Figure 5.

Schematic representation of computational model of G_qPCR signaling. (A and B) Activation of PLC by agonists of G_q-coupled receptors is as described in Falkenburger et al. (2010a) and represented as a box (G_qPCR model; R, receptor; G, G protein; P, PLC), with all reactions and constants taking their previous values with the exception of agonist concentration and receptor density (R). Reactions of phosphoinositides are depicted in red, calcium permeation is in blue, and reactions used to report changes in signaling molecules are depicted in green. Model species and their initial conditions are listed in Table 1. Model equations (reactions) are reversible and follow mass-action kinetics. They are listed in Table 2

Table 1.

Model initial conditions and parameters

Species/Constant	Value	Rationale
R for M1	500 µm−2	From fluorescencea
R for eP2Y2	1 µm−2	Fig. S7; Fig. 2 A in Dickson et al., 2013
G (G proteins)	40 µm−2	To fit concentration–response curve of currenta
P (PLC)	10 µm−2	To fit concentration–response curve of currenta
(free) PIP2	5,000 µm−2	From distribution of PH domainsb
Bound PIP2	10,000 µm−2	See Fig. 6 B; generally (fold_PIP2-1) * 5,000 µm−2
PI(4)P	4,000 µm−2	To allow doubling of PIP2 by PIP 5-kinase
PI	140,000 µm−2	As previouslyb
IP3 (cytosol)	0.01 µM	Steady state of basal PLC and IP3ase
DAG	23 µm−2	Steady state of basal PLC and DAGase
Ca2+ (cytosol)	0.13 µM	Steady state of basal IP3R Ca2+ flux and SERCA (bistable equilibrium, also stable at 0.02 µM)
Ca2+ (ER)	400 µM	Jafri and Keizer, 1995; Duman et al., 2008
h	0.8	h3 is the fraction of noninactivated IP3Rs
LIBRAvIII	6 µM	As estimated from fluorescencea
IP3 (pipette)	1–100 µM	Used only to simulate calibration experiment
Fura-4F	1 µM	Excessive buffering in the model above 1 µM
C1 domain	0.5 µM	From fluorescence assuming low expressiona; reproduces 1 nM Oxo-M response in relation to 10 µM Oxo-M response
size_pipette	10,000 µm3	Reproduce steady-state values of Fig. 6 D in Dickson et al., 2013
Surface (membrane)	1,500 µm2	From cell capacitance
size_cytosol	2,500 µm3	From surface–volume ratio
size_ER	462 µm3	18% cytosol, from Jafri and Keizer, 1995, and Duman et al., 2008.
fold_PIP2	3	See Fig. 6 B
k_4K (rest)	0.00078 s−1	KCNQ2/3 current recovery after Oxo-Mb; generally fold_PIP2 * 0.00023 s−1
k_5K (rest)	0.06 s−1	KCNQ2/3 current recovery after VSPb; generally fold_PIP2 * 0.02 s−1
k_4K (agonist) & k_5K (agonist)	see Fig. 7 (E and F)c	Concentration dependence informed by Oxo-M dose–response curveb; transition smoothed by an exponential to avoid transients
k_4K (recovery) & k_5K (recovery)	see Fig. 7 (E and F)c	KCNQ2/3 current recoveryb; transition smoothed by an exponential to avoid transients
k_PLC	0.6 µm2s−1	From KCNQ2/3 inhibitionb; fold_PIP2 * 0.2 µm2s−1
k_IP3ase	0.08 s−1	Reproduce duration of LIBRAvIII and Fura-4F responses (Figs. 6 and 4 in Dickson et al., 2013); as in Xu et al., 2003
k_DAGase	0.05 s−1	To fit C1 decay
KIP3 (IP3R)	0.1 µM	To have maximum activity with 1 nM Oxo-M
KCa (IP3R)	0.2 µM	Bezprozvanny et al., 1991
kCa (IP3R)	0.2 µM	Bezprozvanny et al., 1991
kP (SERCA)	1.3 µM	Duman et al., 2008
vP (SERCA)	0.3	Height of plateau in Fura-4F response to Oxo-M; see Fig. S8 B in Dickson et al., 2013
k_pipette	0.03 s−1	Giving approximately a time constant of 50 s as observed for diffusion of dyes and the onset of Fig. 6 B in Dickson et al., 2013
KD_LIBRAvIII	0.5 µM	Tanimura et al., 2009
KD_C1	0.3 µM	Oxo-M concentration–response of C1/CAAX FRET
KD_Fura-4F	0.77 µM	Invitrogen

^aFalkenburger et al., 2010a.

^bFalkenburger et al., 2010b.

^cThe steady-state Oxo-M concentration dependence of PIP₂ synthesis was inferred from the concentration dependence of KCNQ2/3 inhibition (Fig. 9 C in Falkenburger et al., 2010b). Specifically, k_4K values that reproduced the Oxo-M concentration dependence of KCNQ2/3 inhibition (markers in Fig. 7 E) were fitted by a sigmoid and the concentration dependence of k_5K computed with the same midpoint and slope. The extent of PI 4-kinase and PIP 5-kinase acceleration was fine-tuned to reproduce the >90% depletion of PIP₂ and 80% depletion of PIP measured biochemically for 10 µM Oxo-M (i.e., 7.5-fold acceleration of the PI 4-kinase 10-fold acceleration of the PIP 5-kinase). In addition, the onset of the acceleration of PIP₂ synthesis was smoothed by an exponential to avoid positive PIP₂ transients resulting from too fast acceleration (<1-s time constant); the recovery of PIP₂ synthesis to resting values was smoothed by an exponential (5-s time constant) to avoid negative PIP₂ transients upon Oxo-M wash (Fig. 7 F; see Fig. S9 in Dickson et al., 2013). Thus, k_4K (agonist) = k_4K_rest + stim_4K * (1 − e^{−t/τ_onset}) with stim_4K = 0.0078/(1 + e^{4.86-278*agonist}) and k_5K (agonist) = k_5K_rest + stim_5K * (1 − e^{−t/τ_onset}) with stim_5K = 0.2 /(1 + e^{4.86-278*agonist}); τ_onset = 1 s. k_4K_recovery = k_4K_rest + stim_4K * e^{(end−t)/τ_recovery}, and k_5K_recovery = k_5K_rest + stim_5K * e^{(end−t)/τ_recovery} with τ_recovery = 5 s.

Table 2.

Model differential equations

Reaction	Rate equation
4-K	k_4K * PI
4-P	0.03 s−1 * PI(4)P
5-Ka	k_5K * PI(4)P
5-Pa	0.042 s−1 * PIP2
PIP2 to bound PIP2	(fold_PIP2−1) * 1 s−1 * PIP2−1 s−1 * bound_PIP2
PLCb	k_PLC * GαGTP-PLC * PIP2
PLC on PIP	k_PLC * GαGTP-PLC * PI(4)P
IP3ase	k_IP3ase * IP3
DAGase	k_DAGase * DAG
h reaction	((kCa − ((Ca2+cyt + kCa) * h)) * 2.7 µm2 µM−1 s−1)
IP3R	200 * (1 − Ca2+cyt/Ca2+ER) * [(h*IP3*Ca2+cyt)/(IP3 + KIP3)(Ca2+cyt + KCa)]3
SERCA	vP * (Ca2+cyt)2/[kP2 + (Ca2+cyt)2]
VSPac	VSP_max * f(VM) * fold_PIP2 * PIP2
IP3_dialysis	k_pipette * (IP3_pipette – IP3_cytosol)
PIP2 to KCNQ	0.05 µm2s−1 * PIP2 * KCNQ − 100 s−1 * PIP2-KCNQ; [Kd = 2,000 µm−2]
KCNQ2/3 current	(KCNQ_PIP2)2
PH to PIP2	1 µM−1 s−1 * PIP2 * PH − 2 s−1 * PIP2-PH; [Kd = 2 µM]
PH to IP3	10 µM−1s −1 * IP3 * PH − 1 s−1 * IP3-PH; [Kd = 0.1 µM]
LIBRAvIII to IP3	1 µM−1s −1 * IP3 * LIBRAvIII − KD_LIBRAvIII* IP3-LIBRAvIII
C1 to DAG	10 µM−1s −1 * PIP2 * PH − KD_C1 * 10 µM−1s−1 * PIP2-PH
Ca2+ to Fura-4F	10 µM−1s −1 * Ca2+ * Fura-4F − KD_Fura-4F * 10 µM−1 s−1 * Ca2+-Fura-4F

^aRate constants from Falkenburger et al., 2010b.

^bG_αGTP-PLC from model described in Falkenburger et al., 2010a.

^cAs in Falkenburger et al., 2010b; f(V_M) = 1/(1 + exp(−1.5*q_e*(V_M − V_half)/k_BT)) with k_BT/q_e = 25 mV, Vhalf = 100 mV; V_M was 120 mV during the bars “VSP” and −60 mV otherwise [f(120 mV) = 1; f(−60 mV) = 0.00006].

Receptors and G proteins

For signaling from ligand binding to PLC activation, we used our earlier “G_qPCR model” (Falkenburger et al., 2010a) that reproduces kinetic and dose–response characteristics of the conformational change in the receptor resulting from ligand binding, the interaction of the receptor with G proteins, and the rearrangement within the G protein heterotrimer, down to the interaction of Gα_q with PLC. The equations describing signaling at receptors, G proteins, and PLC are taken unchanged from this study (Falkenburger et al., 2010a), and for simplicity, they are represented as the box “G_qPCR” in Fig. 5 A with inputs of agonist, receptor (R), G protein (G), and PLC (P). Parameters for phosphoinositide metabolism (Fig. 5 A, top arrows) have been altered in a few respects from our previous description (Falkenburger et al., 2010b) to account for new experimental evidence: A pool of reversibly bound PIP₂ has been added. Consequently, the rate constants for PIP₂ synthesis and hydrolysis were adjusted to account for the increased amount of total PIP₂ (bound and free).

Our Western blot analysis indicated that overexpression of P2Y₂Rs increases their levels by 100-fold (Fig. 2 A in Dickson et al., 2013). We assume a density of overexpressed M₁Rs of 500 µm⁻² (Falkenburger et al., 2010a). The kinetics, concentration dependence of ligand binding, and G protein interaction have not been as fully developed for P2Y₂Rs as for M₁Rs; therefore, we model endogenous P2Y₂Rs as “low-density M₁Rs.” To do this, we maintain all the same parameters for M₁Rs but restrict P2Y₂ density to 1–5 per µm². (We have previously assumed a density of endogenous receptors of 1 per µm² based on reported ratios of receptors to G proteins.) This assumption is sufficient to reproduce our experimental results fully (Fig. S2), including Fura-4F responses of equal size to 100 µM of agonist acting on eP2YRs as to 10 µM of agonist acting on high-density M₁Rs (see Figs. 1, 4, and 5 in Dickson et al., 2013).

Fluorescent reporters

Quantitative reporting of PIP₂ by KCNQ2/3 current and pleckstrin homology (PH) domains of PLCδ1 has been described previously by us and others (Xu et al., 2003; Falkenburger et al., 2010b), and reporting of calcium by Fura-4F is used widely. We now consider reporting of IP₃ by LIBRAvIII. LIBRAvIII reports changes in IP₃ a few seconds before Fura-4F reports changes in calcium (Fig. 6 G in Dickson et al., 2013). Thus, LIBRAvIII binds and reports IP₃ quickly. In published calibration experiments using permeabilized cells (Tanimura et al., 2009), half-maximal FRET response was achieved with 0.5 µM of cytosolic IP₃, and maximal response at 10 µM IP₃. We therefore chose a K_d of 0.5 µM IP₃ for LIBRAvIII. When we patched LIBRAvIII-expressing cells with IP₃ in the patch pipette, we saw a half-maximal FRETr change with 2–5 µM in the pipette and saturation with ≥10 µM (Fig. 6 B in Dickson et al., 2013). The maximal FRETr amplitude for LIBRAvIII was reached faster with 100 µM IP₃ than with 10 µM IP₃ in the pipette. This calibration experiment was reproduced in our model (Fig. 6 B in Dickson et al., 2013) using the rate constants for IP₃ metabolism (k_IP₃ase), diffusion of IP₃ from the patch pipette into the cell (k_pipette), LIBRAvIII concentration in the cytosol, and functional volume of the patch pipette listed in Table 1. In these calibration experiments, cytosolic IP₃ is in a dynamic steady state of influx and degradation. Because diffusion from a patch pipette is slower than through a permeabilized membrane, more IP₃ is needed for half-maximal LIBRAvIII response in our experiments than in those of Tanimura et al. (2009).

PIP₂, DAG, and IP₃

The amplitude of the LIBRAvIII response to 10 µM Oxo-M application was close to the saturating response with 10 or 100 µM IP₃ in the patch pipette (Fig. 6 B in Dickson et al., 2013). This suggests that a near saturating concentration of IP₃ in the cytosol is reached in response to 10 µM Oxo-M. Based on the observed distribution of PH domains between plasma membrane (bound to PIP₂) and cytosol (free or bound to IP₃), and using published dissociation constants, we and others estimated the density of free PIP₂ molecules at the plasma membrane as 5,000 µm⁻². With the surface-to-volume ratio we assumed, a complete hydrolysis of these PIP₂ molecules would yield only 5 µM IP₃ in the cytosol. However, IP₃ is degraded by IP₃ 5-phosphatases and buffered by any LIBRAvIII as it is made (Fig. S5 in Dickson et al., 2013). Therefore, hydrolysis of 5,000 µm⁻² PIP₂ is insufficient to explain the saturation of LIBRAvIII in response to 10 µM Oxo-M. To achieve a saturating IP₃ peak, we make two assumptions in our model: (1) PIP₂ synthesis is accelerated during G_qPCR activation, and (2) there is a reserve pool of PIP₂ bound to proteins and in rapid equilibrium with the free pool.

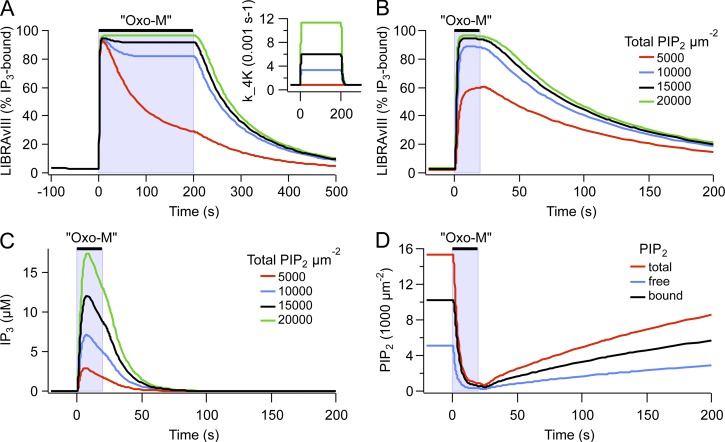
We first discuss stimulated PIP₂ synthesis because we have provided evidence in our companion paper that PIP₂ synthesis needs to be accelerated during Oxo-M application (Dickson et al., 2013). Using the IP₃ probe LIBRAvIII, we had found that significant IP₃ production continues during long Oxo-M applications. In our model, the resting rates of PI 4-kinase and PIP 5-kinase take their values from the recovery time courses after M₁R and VSP activation, and the rate of stimulated PLC activity is informed by the time courses of the decrease of KCNQ2/3 current and PH domain FRET during Oxo-M application. The resting kinase rates are insufficient to sustain IP₃ production during Oxo-M (Fig. 6 A, red trace). Accelerating the rate of the PI 4-kinase by a factor of 7.5 during Oxo-M reproduced the time course of the LIBRAvIII signal during a 200-s exposure to Oxo-M (Fig. 6 A, black trace). A similar increase in PI 4-kinase activity was previously sufficient to explain a difference in concentration–response curves between PLC activation and KCNQ2/3 inhibition (Falkenburger et al., 2010b). Acceleration of the PI 4-kinase alone would lead to the accumulation of PI(4)P during Oxo-M application and would prevent the depletion of PI(4)P that is observed biochemically (Willars et al., 1998; Horowitz et al., 2005, Balla et al., 2008). Therefore, the PIP 5-kinase needs to be accelerated along with the PI 4-kinase. Acceleration of the PIP 5-kinase by 10-fold was sufficient to account for all these findings (Fig. 7, A and B). Similarly, in their model, Xu et al. (2003) used a 3.5-fold acceleration of the PI 4-kinase and a 20-fold acceleration of the PIP 5-kinase to model their experimental findings during bradykinin action.

Figure 6.

Modeling results suggesting a pool of reversibly bound PIP₂. (A) Model predictions of the response of LIBRAvIII (percentage of IP₃ bound) after a 200-s application of 10 µM Oxo-M with or without 4-kinase acceleration. Inset shows the different rates of 4-kinase activity during Oxo-M. (B) Model simulation showing the response of LIBRAvIII (percentage of IP₃ bound) after a 20-s application of 10 µM Oxo-M computed for different values of the parameter fold_PIP₂ (1, 2, 3, 4) and therefore different amounts of bound PIP₂ (0, 5,000, 10,000, and 15,000 µm⁻²). Free PIP₂ was kept at 5,000 µm⁻². (C) Model prediction of the concentration of IP₃ produced after a 20-s application of Oxo-M computed for different values of the parameter fold_PIP₂ as in C. (D) Model prediction of the response of free, bound, and total (free plus bound) PIP₂ after a 20-s exposure to 10 µM Oxo-M with fold_PIP₂ = 3. [LIBRAvIII] was 6 µM for A and B and 0 µM for C and D. To maintain the kinetic properties of the model, the rate constants for all reactions of PI metabolism (4-K, 4-P, 5-K, 5-P, and PLC) were scaled by fold_PIP₂ (see Tables 1 and 2).

Figure 7.

Adjusting the acceleration of lipid kinases in the model. (A–D) Time courses of PIP₂, PIP, IP₃, and DAG computed for different rates of PIP₂ synthesis. For the red trace, the rate constant of PI 4-kinase (k_4K) was informed by recovery of PIP₂ after Oxo-M, and the rate constant of the PIP 5-kinase (k_5K) was informed by recovery of PIP₂ after VSP (k_4K = 7.8 × 10⁻⁴ s⁻¹; k_5K = 0.06 s⁻¹; see Falkenburger et al., 2010b). For the black trace, k_4K, k_5K and k_PLC were increased as necessary to reproduce continual IP₃ synthesis during Oxo-M and a time constant of PIP₂ depletion as observed experimentally (k_4K = 7.8 × 10⁻³ s⁻¹; k_5K = 0.06 s⁻¹; see Dickson et al., 2013). For the green trace, k_5K was adjusted to allow for sufficient depletion of PIP during Oxo-M, as observed biochemically (k_4K = 7.8 × 10⁻³ s⁻¹; k_5K = 0.6 s⁻¹). (E) Concentration dependence of k_4K (left axis) and k_5K (right axis). (F) Time course of k_4K (left axis) and k_5K (right axis) that best eliminates transients in KCNQ2/3 current with Oxo-M application and wash (see Fig. S9 in Dickson et al., 2013).

This accelerated PIP₂ synthesis is still not sufficient to predict the saturating LIBRAvIII response observed with 10 µM Oxo-M (Fig. 6 B, red trace). Therefore, communicating rapidly with the pool of 5,000 free PIP₂ molecules per µm² of plasma membrane, we have introduced a second pool of 10,000 µm⁻² PIP₂ molecules reversibly bound to proteins (“bound PIP₂” in Fig. 5). A pool of 5,000 µm⁻² bound PIP₂ would have been sufficient to explain our observations (Fig. 6 B), but we chose 10,000 µm⁻² because Golebiewska et al. (2008) conclude from fluorescence correlation spectroscopy experiments that two thirds of PIP₂ is reversibly bound to proteins. Hilgemann (2007) reports total amounts of PIP₂ >20,000 µm⁻². The large size of the putative-bound pool implies that a vast number of membrane and cytosolic molecules may be influenced by plasma membrane PIP₂. Note that the speed of IP₃ degradation (k_IP₃ase) and the K_d of LIBRAvIII for IP₃ strongly affect the duration and recovery time constants of the LIBRAvIII response (Fig. S3). Changing these parameters from their literature-informed values (Table 1) was therefore not an alternative to obtain a saturated LIBRAvIII response.

These new assumptions, acceleration of PIP₂ synthesis and a pool of bound PIP₂, suffice to explain a saturating LIBRAvIII response with 10 µM Oxo-M (Fig. 6 B) (Fig. 6, B, E, and F, in Dickson et al., 2013). Under these conditions, IP₃ rises to ∼10 µM (Fig. 6 C). The time course of the different pools of PIP₂ during Oxo-M is illustrated in Fig. 6 D. Consistent with our experimental findings (Fig. 6, C and D, in Dickson et al., 2013), the predicted amplitude of the LIBRAvIII response is indistinguishable between 0.1 and 10 µM Oxo-M, but the time to half-maximal response is about double with 0.1 µM (5 vs. 2 s; Fig. S4 D).

Consider the production of DAG. Assuming a 300-nM equilibrium dissociation constant for DAG from the C1-YFP probe and a cytosolic probe concentration of 0.5 µM, we can reproduce a response to 1 nM Oxo-M that has ∼50% the amplitude of the response to 10 µM Oxo-M and a difference in rise time between 0.1 and 10 µM Oxo-M (Fig. 1, E and F). The assumed dissociation constant is between that of our previous model (2 µM; Horowitz et al., 2005) and biochemical measurements (10 nM; Ananthanarayanan et al., 2003) for C1A(PKCγ). In C1/CAAX FRET experiments, we selected cells with a low expression level to ensure restriction of CAAX-CFP to the plasma membrane. Correspondingly, in the model we chose a cytosolic concentration of C1 domains on the lower end of cells we typically select for FRET measurements (see Falkenburger et al., 2010a). As for LIBRAvIII, the responses of C1/CAAX FRET to UTP and to a concentration series of Oxo-M were reproduced reasonably (Figs. 1, S2, and S4) (Fig. 6 G in Dickson et al., 2013). Still, the difference in duration of the response to 0.1 and 10 µM Oxo-M computed by the model is less pronounced than that observed experimentally (Figs. 1, S2, and S4) (Fig. 6 D in Dickson et al., 2013). This implies that further differences exist between the response to 0.1 and 10 µM Oxo-M, such as, for example, a shorter or less intense acceleration of PIP₂ synthesis by 0.1 µM Oxo-M.

Calcium dynamics

We have to consider release of Ca²⁺ from Ca²⁺ stores initiated by IP₃ and clearance of Ca²⁺ from the cytoplasm by transporters. The kinetic properties of IP₃R opening have been reported extensively at the single-channel level. For our modeling, we would need a mathematical kinetic description of the probability of channel opening in the face of wide and continuous variations of Ca²⁺ and IP₃. The time resolution need be no better than 1 s, but any slow relaxations such as inactivation should be included. The original work of Bezprozvanny et al. (1991) used channels incorporated in planar bilayers. They found that in addition to being IP₃ dependent, calcium release is both activated and inhibited by occupancy of two independent classes of calcium-binding sites. They described the Ca²⁺ dependence of release as being proportional to the third power of [Ca]k_Ca/{([Ca] + K_Ca)([Ca] + k_Ca)}, with K_Ca = 0.2 µM and k_Ca = 0.2 µM, respectively, being dissociation constants for the activating and inhibitory sites for calcium on the IP₃R. This broadly specified, continuous equilibrium formulation was developed into a kinetic model by De Young and Keizer (1992) and simplified by Li and Rinzel (1994). In the subsequent two decades, a large number of elegant studies were made by direct patch clamp of the cell nucleus, whose outer membrane is an extension of the ER. These were done in insect, bird, Xenopus laevis, and mammalian cells sometimes using endogenous IP₃Rs and often overexpressed ones. They also find activation by IP₃ and Ca²⁺ and inhibition by Ca²⁺ interpreted as binding to multiple binding sites in the channel tetramer, sometimes regarded as allosterically interacting. Many empirical steady-state (stationary) equations for open probability (P_open) from this work are summarized in Foskett et al. (2007). There are also detailed time-dependent Markov-like kinetic models for subsecond-level channel fluctuations (Shuai et al., 2006; Mak et al., 2007; Gin et al., 2009; Palk et al., 2010; Siekmann et al., 2012; Ullah et al., 2012), but in most cases, they provide pseudo–first-order kinetic values for just two or three specific concentrations of IP₃ and Ca²⁺ and no extension to other concentrations. Although such models represent significant steps forward in exploring channel gating steps, they lack applicability to the wide range of varying Ca²⁺ and IP₃ values seen in our experiments on living cells. An exception from these more recent authors is the whole-cell model of Shuai et al. (2006), which uses a formalism like that of De Young and Keizer (1992).

For these reasons, we followed a kinetic model based on the Bezprozvanny et al. (1991) and De Young and Keizer (1992) ideas as simplified by Li and Rinzel (1994) and used in many subsequent calcium dynamics models, including Hernjak et al. (2005) from which we adopted it. The simplified kinetic form notes that Ca²⁺ occupancy of the inhibitory (inactivation) site relaxes slowly (∼1 s), whereas the activation by Ca²⁺ and IP₃ is rapid and could be described by an equilibrium formulation. In their Hodgkin–Huxley-like model, the time varying fraction of inhibitory sites not occupied is denoted by h. The open probability of IP₃Rs is then proportional to:

$${\text{h}}^3{\left\{\right[{\text{Ca}}^{2+}]/(\left[{\text{Ca}}^{2+}\right]+{\text{K}}_{\text{Ca}}\left)\right\}}^3{\left\{\right[{\text{IP}}_3]/(\left[{\text{IP}}_3\right]+{\text{K}}_{\text{IP3}}\left)\right\}}^3.$$ (1)

Using the third power of the occupancy of each of the sites makes a very sharp turn-on as Ca²⁺ and IP₃ increase. The power probably reflects cooperative activation of the tetrameric structure of IP₃Rs. We assumed an IP₃ dissociation constant of 0.1 µM for the IP₃R, within the range found by others (e.g., 0.3 µM; Kaftan et al., 1997), while noting that the apparent affinity for IP₃ varies greatly between cell types (Khodakhah and Ogden, 1993). As suggested by Bezprozvanny et al. (1991), we assumed a dissociation constant of 0.2 µM for calcium at the activating and the inhibitory-binding sites of the IP₃R.

The equation and calcium dissociation constant of the SERCA pump were taken from a previous model from our laboratory (Duman et al., 2008). With this model, the duration of the calcium response was strongly dependent on the duration of the IP₃ elevation and K_IP3 (Fig. S8 C in Dickson et al., 2013) and much less so on the activity of the SERCA pump (not depicted). The deactivation kinetics of the IP₃R was unaltered from its original description. Overall, the Fura-4F response to a concentration series of Oxo-M and to activation of purinergic receptors by UTP was reproduced reasonably (Figs. S2 and S4) (Figs. 4 and 5 in Dickson et al., 2013).

VSP activation

We reproduced the responses of Fura, LIBRAvIII, and C1/CAAX to Oxo-M application during activation of the VSP 5-phosphatase (Fig. 4, G and H) (Fig. 7 C in Dickson et al., 2013). The equations for VSP were taken from our previous model (Falkenburger et al., 2010b). In the experiments, we had used intermittent VSP activation to monitor the time course of KCNQ2/3 currents between VSP activations. In the model, we used a continuous submaximal activation of VSP that produced a similar time course and degree of PIP₂ depletion, as had been observed experimentally by measuring KCNQ2/3 current. As in the experiments, the computed amplitude of the Fura-4F response to Oxo-M was unaltered by prior VSP activation (Fig. 7 C in Dickson et al., 2013). We then considered the Oxo-M–induced IP₃ production in response to 10 µM Oxo-M, as reported by LIBRAvIII. We found that in the model, the predicted LIBRAvIII response could be reduced by VSP in a manner that graded with the extent of VSP activation (Fig. 4 G). VSP had to be activated much more strongly to reduce the LIBRAvIII response (Fig. 4 G, “strong VSP”) than had been expected from the time course of current inhibition (“moderate VSP”). Consistent with the experiments, in our standard model (with PLC acting on PIP as well as on PIP₂) the DAG response reported by C1/CAAX was unaltered even by the strongest extent of VSP activation (Fig. 4 H). Here, much of the DAG would derive from PIP. Time courses of model IP₃, DAG, PI(4)P, and PIP₂ during this experiment are depicted in Fig. S5 (A–C).

In the model that we used, PI(4)P and PIP₂ were equally susceptible to PLC, thus creating more DAG than IP₃. We tried to consider whether the very high sensitivity of the C1 domain reporter distorted our idea of how much DAG is generated in response to Oxo-M application. Therefore, we tested an alternative model that did not include PI(4)P hydrolysis by PLC (Fig. S6). The figure legend describes some of the changes that were made. They include adjusting the kinase acceleration and adjusting the strength of VSP activation to try to reproduce several experimental observations. Under these conditions, we were unable to find parameters that reproduced all our experiments. Depending on the extent of VSP activation, the LIBRAvIII and C1/CAAX FRET responses were either both decreased or both unchanged. Thus, our modeling findings remain most compatible with the concept that PLC activation leads to the hydrolysis of PI(4)P in living cells.

DISCUSSION

To provide a more complete description of signaling by two different G_q-coupled receptors, we have performed quantitative kinetic measurements of PIP₂, DAG, IP₃, calcium, PKC activity, and KCNQ2/3 channel current in response to agonist application in this and in our companion paper (Dickson et al., 2013). Our work here shows that (a) PKC is strongly turned on by the small amount of DAG generated at the foot of the activation curve for M₁Rs (as was the case for calcium release [Dickson et al., 2013], there are many spare receptors for PKC activation); (b) a kinetic model augmented from our earlier work (Horowitz et al., 2005; Falkenburger et al., 2010a,b) explains and helps us test these ideas; and (c) with the two receptors we have tested here in tsA-201 cells, we are able to explain KCNQ2/3 channel modulation in terms of PIP₂ depletion and have not had to implicate contributions of calcium, CaM, AKAP79, or PKC signals to the suppression of current. In addition, experimental evidence validated by model calculations continues to suggest that PLC can hydrolyze PI(4)P in addition to PI(4,5)P₂.

KCNQ2/3 channel modulation

Typically, all of the five consequences of PLC activation that we have studied occur together, and it is challenging to determine which pathway underlies a given effect of receptor activation. The inhibition of KCNQ2/3 potassium channels by M₁Rs is an example. Does it require IP₃ production, calcium release, DAG production, PKC activation, or PIP₂ depletion? We and others have shown that KCNQ2/3 channels require PIP₂ for full function: they are inhibited whenever PIP₂ is depleted and recover only when PIP₂ is resynthesized or resupplied (Suh and Hille, 2002; Zhang et al., 2003; Horowitz et al., 2005; Li et al., 2005; Winks et al., 2005; Suh et al., 2006; Falkenburger et al., 2010b). Nevertheless, there are many reports that other factors inhibit channels directly or sensitize muscarinic inhibition. The list includes calcium and/or CaM (Cruzblanca et al., 1998; Wen and Levitan, 2002; Gamper and Shapiro, 2003; Kosenko et al., 2012), PKC augmented by AKAP79/150 proteins (Hoshi et al., 2003, 2010; Zhang et al., 2011), and Src tyrosine kinase (Gamper et al., 2003). We summarize the evidence we have against any emphasis on these factors for the muscarinic response in our expression system. Some of the evidence remains indirect and correlative.

We start with PKC and AKAP. With 100 µM UTP acting on eP2Y₂Rs, we observe a PKC activation comparable to that with 10 µM Oxo-M acting on M₁R; however, UTP did not deplete PIP₂ or inhibit KCNQ2/3 channels, whereas Oxo-M did both. Both CKAR and AKAP79-CKAR report a saturating phosphorylation of PKC substrates by UTP. AKAP79-bound CKAR should be a good proxy for PKC phosphorylation of AKAP79-bound KCNQ2. Thus, a strong PKC activation achieved by receptor activation with UTP does not suffice to inhibit KCNQ2/3 channels. Overexpression of the PKC-tethering protein AKAP79 did not make channels sensitive to UTP. By extension, we infer that the activation of PKC by Oxo-M is similarly insufficient to inhibit channels. In contrast to these observations, it was found by others in primary neurons and other expression systems that transfection of a dominant-negative AKAP79 that does not bind PKC reduces KCNQ2/3 channel sensitivity to inhibition by Oxo-M (Hoshi et al., 2003), and that overexpression of AKAP79 sensitizes KCNQ2/3 channels to inhibition by Oxo-M (Bal et al., 2010). This difference might be resolved by a recent observation that in superior cervical ganglion neurons, AKAP79 recruits KCNQ2/3 channels to a signaling complex that includes M₁ muscarinic and AT₁ angiotensin receptors (Zhang et al., 2011), thus changing the spatial organization of G_qPCR (and possibly the extent of PIP₂ hydrolysis).

We turn to calcium and CaM. Again, UTP acting on eP2Y₂Rs gave a calcium response comparable in amplitude to those with Oxo-M but did not inhibit KCNQ2/3 channels. Overexpression of CaM did not make the channels sensitive to UTP. CaM has clear constitutive effects on the channels, acting almost as an auxiliary subunit. Both WT and dominant-negative CaM bind to the C terminus of KCNQ2 (Wen and Levitan, 2002) and (a) mutations in KCNQ2 that affect CaM binding, (b) expression of dominant-negative CaM, or (c) expression of a “CaM sponge” lead to retention of KCNQ2 homomeric channels in the ER (Wen and Levitan, 2002; Etxeberria et al., 2008; Etzioni et al., 2011). Moreover, binding of WT CaM to KCNQ2 can moderately reduce the constitutive current through KCNQ2 homomeric channels by changing channel structure (Etzioni et al., 2011). In addition to these constitutive effects, some groups report a dynamic CaM-dependent reduction of KCNQ2/3 currents after a rise in cytosolic calcium (Gamper and Shapiro, 2003), whereas others have not (Wen and Levitan, 2002). Possibly, previously reported direct strong channel inhibition by Ca²⁺ in neurons may have involved a local Ca²⁺ increase that achieved a very much higher Ca²⁺ concentration at the channels than happens with global changes (Cruzblanca et al., 1998; Delmas and Brown, 2002; Gamper and Shapiro, 2003; Gamper et al., 2005).

The paradoxical existence of alternative modes of modulation of KCNQ2/3 channels in neurons and other cells remains unexplained. We are certain that PIP₂ depletion by itself will suffice because we have numerous ways to accomplish that without using a G_qPCR. It may be, as other have suggested, that in other cell types the plasma membrane spatial organization and signaling microdomains differ, and certainly other cells express other signaling molecules that may contribute to the effects reported. Our kinetic model was able to reproduce the qualitative differences between UTP and Oxo-M from a mere difference in receptor density; it did not incorporate any alternatives to channel inhibition besides PIP₂ depletion in a homogeneous plasma membrane compartment.

Validity of the model

Several questions arise about the range of applicability of our results. We start with transfection. Transient transfection of DNAs in cell lines affords much experimental versatility and in our case the possibility of expressing as many as six different foreign proteins simultaneously. However, we showed in the experiments and modeling work of Falkenburger et al. (2010a,b) that to meet typical demands of conventional live FRET photometry or live confocal imaging, expressed optical probes need high densities of at least several hundred per square micrometer on the plasma membrane or almost 1 µM in the cytosol, which might distort cell responses. Nevertheless, we also showed that the density parameters of a model fitted to the experimental results can be scaled back to predict behavior that compares favorably with physiological measurements. In particular, the model contains all the buffering effects of the translocation- and FRET-indicator molecules we used. For most simulations of DAG, IP₃, and calcium responses shown here, the concentration of these indicators was scaled back to zero. Surprisingly, the overall responses of KCNQ channels in untransfected sympathetic neurons and in high-density M₁R-transfected tsA cells are virtually identical. They show the same onset and recovery times for muscarinic inhibition, and they show PIP₂ depletion (PH domain migration) and KCNQ current inhibition with identical concentration–response curves and midpoints at 1 µM Oxo-M (e.g., compare our Fig. 8 with Winks et al., 2005). The density of M₁Rs on neurons is not known, but they act like high-density M₁R-transfected cells. Perhaps in neurons, the receptors and channels have an effective high density in local domains where PIP₂ is present (Cui et al., 2010; Wang and Richards, 2012).

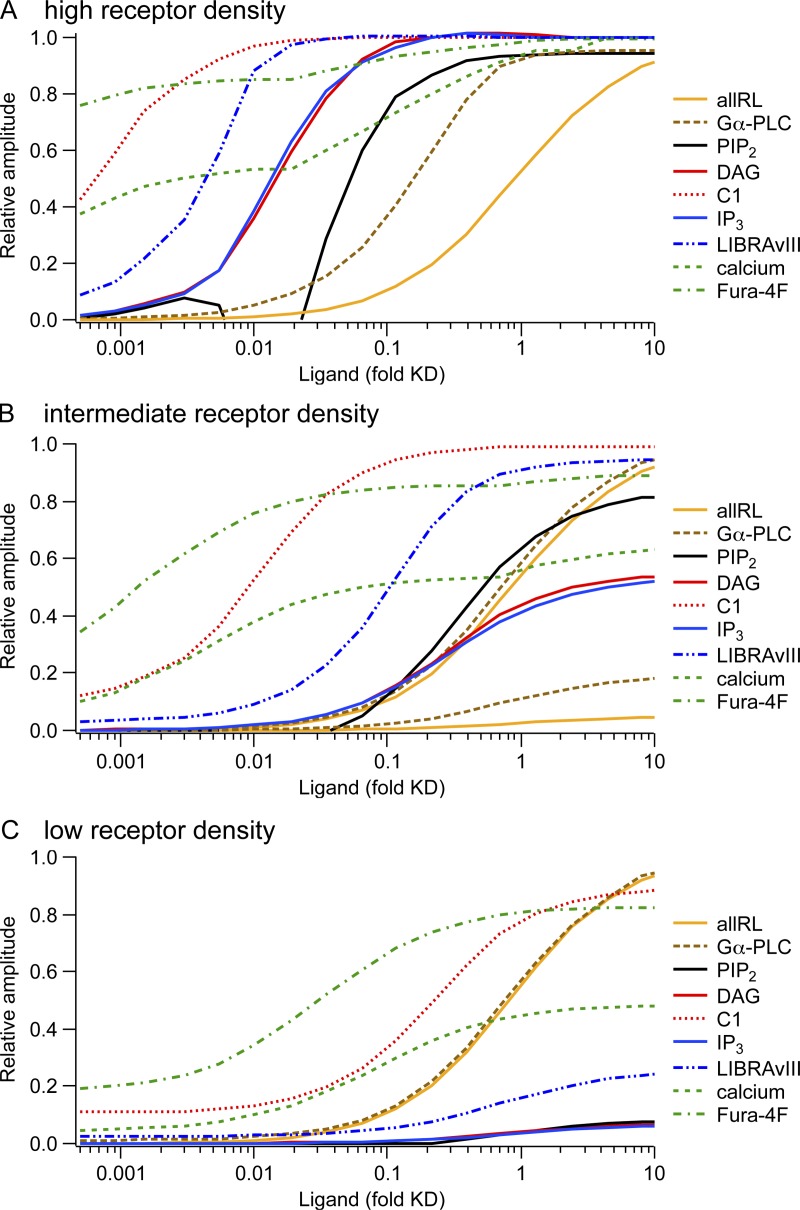
Figure 8.

Concentration–response curves from the model illustrating the concept of receptor reserve. Panels show predicted responses from the computational model for three different receptor densities (R was 500 µm⁻² for A, “high density”; 25 µm⁻² for B, “intermediate density;” and 1.25 for C, “low density”). The x axis represents agonist concentration in reduced units of concentration divided by K_d, the dissociation constant for receptors in the absence of G proteins. For reference, 1.0 on this axis corresponds to 2 µM Oxo-M or possibly 5 µM UTP. Curves show the responses of many signaling intermediates normalized to their extreme values (maxima or minima), with increasing species normalized to the maximum and decreasing species normalized so that 0 corresponds to the resting value and 1 corresponds to the minimum with receptor saturation. For A, PI 4-kinase and PIP₂ 5-kinase were accelerated during agonist as described in Fig. 7. For B, acceleration of PI 4-kinase and PIP 5-kinase was 20-fold less. For C, PI 4-kinase and PIP 5-kinase were not accelerated. The y-scaling was kept constant between A, B, and C with the following exceptions: B contains two traces “allRL” and two traces “Gα-PLC,” one of each on the same scale as in panel A to illustrate the difference in maximum amplitude and a second one of each that was rescaled to its maximum to better compare midpoints between A and B. In C, “allRL” and “Gα-PLC” are shown only rescaled to maximum. The dip in the PIP₂ depletion curve between 0.005 and 0.02 agonist/K_d of A is probably an artifact of our model. It occurs because, for this concentration range, accelerated PIP₂ synthesis outweighs PLC activation, leading to a net increase in PIP₂. We have no direct evidence for this occurring in real cells, suggesting that the model (Fig. 7 E) introduces too much acceleration of PIP₂ synthesis in this intermediate agonist concentration range.

Our model differs from previous models of the G_qPCR signaling cascade (e.g., Lemon et al., 2003) because the kinetics and concentration dependence of each step is informed by measurements in single living cells. These measurements require the versatility of transfection and thus entail the problems noted above. Even though all experimental data and subsequent modeling have been performed on tsA-201 cells, we believe that the parameters describing affinities and rate constants of binding constrained by measurements do apply to other cells that express these proteins because they should not depend on the cellular environment. The overall behavior can nonetheless be affected by perturbations in subcellular distribution of signaling molecules and by differences in the expressed subtype, for example, of protein kinases C or IP₃Rs.

At present, our combined model omits many known aspects of calcium dynamics. It neglects the strong calcium buffering of cytosolic and store compartments; it does not develop significant depletion of stores during calcium release; it has no store-operated calcium entry or ryanodine receptor channels and no plasma membrane calcium pumps or leaks. These issues, which we have dealt with in previous work on other cell types (Chen et al., 2003; Duman et al., 2006, 2008; Dickson et al., 2012), remain for future consideration in tsA cells when more data to inform these aspects have been obtained. The largest change would be cytosolic buffering because the cytosolic calcium-binding ratio κ is expected to be on the order of 100. However, this problem is temporarily averted simply by reducing all calcium transport fluxes by the same factor.

Ligand concentration–response curves and spare receptors

Ligand binding.

It is instructive to compare the ligand concentration–response relationships between branches of G_qPCR signaling with three different densities of receptor expression: low, medium, and high (Fig. 8, A–C). The curves come from the model, which is informed by the experiments. Note that the concentration axis is in reduced, dimensionless units of concentration divided by receptor K_d. Although we explored M₁Rs the most, our experiments suggest that the curves would apply equally well for P2Y₂Rs and perhaps for others, and we make that assumption here. We start with the concentration–response relationship for ligand binding. The maximum binding scales with the density of expressed receptors in the three panels, but the midpoint is not changed. We assume that in 1 µm² of membrane, there are 500 receptors with high-density expression (Fig. 8 A), 40 endogenous G_q proteins, and only 10 endogenous PLCs. A saturating concentration of ligand activates almost all of the 500 receptors, and 25 of the 40 G proteins. Already at 0.7-fold K_d (equivalent to ∼1.4 µM Oxo-M), 9 of the 10 PLC molecules are activated by the G proteins. Thus, the concentration dependence of PLC activation is much left-shifted when compared with the midpoint of receptor–ligand binding (Fig. 8 A). This early saturation of PLC and the excess of available G proteins explain why it is possible to accelerate receptor-stimulated PIP₂ hydrolysis further by overexpressing PLC in cells with high-density M₁Rs (Jensen et al., 2009). With intermediate and low-density receptors (Fig. 8, B and C), a maximum of only 2 and 0.1 of 10 PLC molecules per µm² become activated, hence no left-shift of the PLC activation curve relative to receptor activation.

PIP₂ cleavage.

With high-density receptors, the midpoints of depletion of plasma membrane PI(4,5)P₂ and inhibition of KCNQ2/3 current are more sensitive to agonist than PLC is. This left-shift results from a “floor effect.” Even submaximal PLC activity overtakes PIP₂ synthesis. The left-shift is not present at lower receptor densities where maximal agonist does not completely deplete PIP₂ (Fig. 8, B and C). Without acceleration of PIP₂ synthesis during agonist, the predicted concentration–response curves for PIP₂ depletion, IP₃ synthesis, and DAG synthesis would be exactly superimposed. This is the case for low-density receptors (Fig. 8 C), where we do not have evidence for stimulated PIP₂ synthesis. With stimulated synthesis (Fig. 8 A), the curves for PIP₂, IP₃, and DAG do start together, but the assumed acceleration of PIP₂ synthesis becomes relevant above 0.05-fold K_d (∼0.01 µM Oxo-M), allowing boosted production of IP₃ and DAG while reducing net PIP₂ depletion. The dip in the PIP₂ depletion curve between 0.05- and 0.02-fold K_d (∼0.01 and 0.04 µM Oxo-M) is an artifact of our model (see legend to Fig. 8).

Downstream signals.

Farthest left are the curves for calcium and the recruitment of C1 domain–containing proteins to the plasma membrane, that is, the effectors downstream of IP₃ and DAG. As we have already discussed, they show this high sensitivity because only a minute activation of PLC will suffice to make the small amounts of IP₃ and DAG that will saturate these pathways. With a high-density of receptors, the peak amplitude of the calcium response changes by only 50% between 0.0005- and 50-fold K_d (∼1 nM and 100 µM Oxo-M), and the amplitude of the Fura-4F response changes even less, as explained in Dickson et al. (2013). A theoretical account as to why responses become more switch-like along a signaling pathway was contributed by Ferrell (1997). We note that in the model, the calcium response has two phases. Below 0.01-fold K_d (0.02 µM), there is only a slow peak (e.g., Fig. S3 E and Fig. 4 C in Dickson et al., 2013), which increases in a saturation curve with increasing agonist. A fast, initial peak surpasses the slow peak at around 0.03 µM Oxo-M (0.015 K_d) and leads to a second component in the concentration–response curve. Interestingly, the amplitude of the fast calcium peak increases even above 0.15-fold K_d (0.3 µM Oxo-M), where the IP₃ amplitude is already saturated. This is a consequence of the faster rise of IP₃: Activation of PLC still increases above 0.3 µM Oxo-M, and IP₃ rises more quickly, as does the LIBRAvIII response (Fig. 6 D in Dickson et al., 2013). The amplitude of the IP₃ response is limited because the supply of new PIP₂ cannot quite keep up with the PLC activity, as indicated by a “sag” in the LIBRAvIII response to 200 s of 10 µM Oxo-M (Fig. 8 in Dickson et al., 2013). In our model, the IP₃R channel is activated by IP₃ and calcium and inhibited with a delay (modeled by the “h” reaction) by calcium. Thus, if IP₃ rises more quickly, more calcium can be released before IP₃Rs become inactivated by calcium. With mid- and low-density receptors, the concentration dependence of the calcium response moves to the right. The maximum is unaltered, but the fast initial peak is not observed with low-density receptors (Fig. S2 E) (Fig. 5 B in Dickson et al., 2013). We conclude that with high-density receptors, the agonist concentration affects primarily kinetic parameters (time to peak, existence of a fast initial component), whereas with low-density receptors, the agonist concentration changes the amplitude of the response.

The CKAR and AKAP-CKAR probes reported apparently saturating levels of phosphorylation by PKC already with UTP acting on eP2Y₂R This concentration of UTP would generate only as much DAG and cytosolic calcium elevation as 1 nM Oxo-M. Thus, the PKC phosphorylation concentration–response should be far to the left for high receptor density in Fig. 8 A. Conventional PKC isoforms bind DAG, PIP₂, and calcium. We know the dissociation constant of the C1 domain of PKCγ from our experiments but do not know the rules for regulation by calcium and PIP₂. To illustrate the potentially antagonistic effects of DAG production and PIP₂ depletion on PKC activation, we have plotted the behavior of a hypothetical enzyme that binds DAG as does our C1 domain and PIP₂ as does our PH domain in Figs. S2 I and S4 I. As this conceptual construct is entirely fictitious, we have not included PKC activation in the modeled agonist concentration–response curves in Fig. 8.

Summary of concentration–response.

Fig. 8 illustrates several consequences of receptor density. (a) With high receptor density, the ligand is a full agonist, and some responses show midpoints well to the left of the midpoint of agonist binding, the classical signature of spare receptors. (b) Each response has its own midpoint, and the more downstream the response, the further left the midpoint is likely to be. (c) As receptor density is lowered, all these left-shifted curves move to the right closer to the binding midpoint. (d) In addition, the ligand may remain a full agonist for the most left-shifted curves, but as receptor density falls, it gradually becomes only a partial agonist for those that approach the midpoint of ligand binding. (e) Similarly, there can be spare receptors for some responses (the ones with midpoints to the left) even when there are no spare receptors for many other responses, and the agonist may be only a partial agonist for the latter.

For high-density G_qPCR, such as high-density M₁Rs (Fig. 8 A), our experimental observations suggest two “gears” of signaling. Low agonist concentrations induce “full” calcium release and PKC activation (first gear), whereas only higher concentrations induce significant PIP₂ depletion and KCNQ2/3 current inhibition (second gear). M₁Rs are primarily extrasynaptic in cortex and hippocampus (Yamasaki et al., 2010). Therefore, the acetylcholine concentrations they see in response to physiological stimuli may be low. We do not know the density of M₁R, G proteins, and PLC in these neurons. Yet, it is possible that at low concentrations, acetylcholine activates only the first gear. However, the second gear may become activated during stronger signaling or excess release of neurotransmitters in pathological conditions such as seizures, hypoxia, or the hyperactivity of the subthalamic nucleus in Parkinson’s disease. These events would then evoke a qualitatively new response. Our simulations in Fig. 8 indicate that the receptor density needs to be high (at least in the vicinity of PLC molecules) for a second gear to arise in differentiated cells. In sympathetic ganglia, the second gear appears to be reached with normal preganglionic synaptic input (Marrion 1997; Winks et al., 2005). In principle, such phenomena could occur with any G_qPCR agonist, and all of the G_q-coupled inputs on a neuron would be summed as augmented activation of G_q signaling. It is interesting to speculate about the pharmacological consequences of these two gears: A subsaturating concentration of antagonist would block access to the second gear but not the first, and an antagonist with partial intrinsic activity may even elicit a full-size calcium response while preventing PIP₂ depletion. Such branch-specific effects may explain some benefits of such drugs in clinical practice.

Dissociation of PIP₂ hydrolysis, DAG production, and IP₃ production

We had started our investigation with the idea that PIP₂ hydrolysis, DAG production, and IP₃ production generally occur together. To explain our experimental observations, we now have to assume that several features of G_qPCR signaling dissociate these three basic events from one another. The acceleration of PIP₂ synthesis by G_qPCR activation and the presence of a pool of “bound” PIP₂ favor the production of DAG and IP₃ over PIP₂ depletion. Potential hydrolysis of PI(4)P by PLC, the activation of a PI 5-phosphatase (e.g., VSP; see Fig. 4), and an acceleration of the PI 4-kinase without acceleration of the PIP 5-kinase would boost DAG production over IP₃ production (see Fig. 7, A–D). In addition, PIP 5-kinase acceleration not only may change the relative amounts of IP₃ and DAG produced by G_qPCR but also the relative extent of PIP versus PIP₂ depletion. The PIP/PIP₂ ratio emerged in a recent collaboration with the Inoue group as an important factor in determining the actin phenotype resulting from PIP₂ synthesis (membrane ruffles vs. actin comets; Ueno et al., 2011). PIP 5-kinases and 5-phosphatases thus emerge as important players to select among signaling events related to changes in PIP₂. Accordingly, mutations in many of these enzymes have been associated with human diseases (McCrea and De Camilli, 2009).

It can be difficult to determine experimentally which branch of G_qPCR signaling, IP₃/calcium, DAG/PKC, or PIP₂ is responsible for a given downstream effect. The reduction of IP₃ production but not of DAG production by activation of a PIP₂ 5-phosphatase that we observed in Fig. 4 can in principle be induced also by rapamycin-induced dimerization (Suh et al., 2006; Dickson et al., 2013). This strategy might be helpful in dissecting the contributions of DAG and IP₃/calcium to a given downstream signaling event.

Conclusion

We have performed quantitative and kinetic measurements of signals downstream of the activation of PLC. As is observed with various G_qPCRs, the further down the signaling pathway, the more spare receptors (receptor reserve) there are for a response. There are also apparent qualitative differences between actions of different receptors. We have constructed a mathematical simulation of these signaling pathways and find that it explains the spare receptor findings over four orders of magnitude of agonist concentration, and it shows that the apparent qualitative differences in signaling from two classes of receptors may be understood almost fully as just a difference in their receptor density.