Analysis of Occupational Asbestos Exposure and Lung Cancer Mortality Using the G Formula

Abstract

We employed the parametric G formula to analyze lung cancer mortality in a cohort of textile manufacturing workers who were occupationally exposed to asbestos in South Carolina. A total of 3,002 adults with a median age of 24 years at enrollment (58% male, 81% Caucasian) were followed for 117,471 person-years between 1940 and 2001, and 195 lung cancer deaths were observed. Chrysotile asbestos exposure was measured in fiber-years per milliliter of air, and annual occupational exposures were estimated on the basis of detailed work histories. Sixteen percent of person-years involved exposure to asbestos, with a median exposure of 3.30 fiber-years/mL among those exposed. Lung cancer mortality by age 90 years under the observed asbestos exposure was 9.44%. In comparison with observed asbestos exposure, if the facility had operated under the current Occupational Safety and Health Administration asbestos exposure standard of <0.1 fibers/mL, we estimate that the cohort would have experienced 24% less lung cancer mortality by age 90 years (mortality ratio = 0.76, 95% confidence interval: 0.62, 0.94). A further reduction in asbestos exposure to a standard of <0.05 fibers/mL was estimated to have resulted in a minimal additional reduction in lung cancer mortality by age 90 years (mortality ratio = 0.75, 95% confidence interval: 0.61, 0.92).

Exposure to asbestos fibers has been associated with an increased risk of lung cancer mortality in a number of prospective occupational studies (e.g., the studies by Doll (1) and Hein et al. (2)), and there is consensus that asbestos exposure increases the risks of lung cancer and mesothelioma (3). However, the evidence base derived from occupational studies is susceptible to the healthy worker survivor bias. The healthy worker survivor bias may occur when leaving the workplace while being at risk for the outcome is a time-varying confounder affected by prior exposure (4, 5). A time-varying confounder is a variable that is associated with subsequent levels of the time-varying exposure and is an independent predictor of the outcome (6). Employment status is a time-varying predictor of workplace asbestos exposure; in many settings, cessation of employment is associated with subsequent increases in mortality. If the level of a time-varying confounder, such as employment status, is affected by prior asbestos exposure, standard statistical methods will fail to consistently estimate the net effect (i.e., direct and indirect) of exposure on the outcome (6).

Robins (7) developed the parametric G formula to account for time-varying confounding, such as that which occurs with the healthy worker survivor bias. However, to our knowledge, there have been few published examples of the parametric G formula regarding cases with time-varying exposures (8–10), with a single early paper that applied the parametric G formula to a setting with the healthy worker survivor bias (7). The G formula (11), G estimation of structural nested models (12), and inverse probability weighting of marginal structural models (6, 13) are collectively known as G methods, where G stands for “generalized.” These methods can be used to estimate contrasts of potential outcomes when exposures are time-varying and time-varying confounders are affected by prior exposure. In addition, these methods can be used to adjust for confounders affected by prior exposure without inducing collider-stratification bias (14), and they allow epidemiologists to circumvent issues of noncollapsibility of effect estimates (15). Here we use the parametric G formula to analyze the lung cancer mortality that would have been observed under various asbestos standards in a cohort of persons occupationally exposed to asbestos fibers in the textile manufacturing industry.

MATERIALS AND METHODS

Study population

The cohort included 3,072 men and women employed at a textile production plant for at least 1 month (the run-in period) between January 1, 1940, and December 31, 1965. The plant was located in South Carolina and began production using raw chrysotile asbestos fibers in 1909 (16). For analyses, we began follow-up at 18 years of age; therefore, we excluded 70 of the 3,072 persons who left work before reaching age 18 years.

Date of birth, year of study entry, sex, race (i.e., Caucasian vs. non-Caucasian), prevalent asbestos exposure (prior to completion of the 1-month run-in period), and a time-varying indicator of employment status were ascertained from employment records. Participants were followed until loss to follow-up (i.e., dropout), death, or administrative censoring at age 90 years or December 31, 2001. Data were administratively censored at 90 years of age because estimates made at older ages were imprecise due to the small number of persons at risk. This study was conducted on deidentified existing records and therefore was deemed not to be research on human subjects.

Mortality ascertainment

Vital status through 1978 was determined using information from the Social Security Administration, the Internal Revenue Service, the postal mail correction service, state driver's license files, and vital statistics offices (2, 16, 17). Persons not identified using these sources were further investigated using telephone listings, property records, voter registration lists, and local funeral home records. Between 1979 and 2001, the National Death Index was used to obtain vital status. Persons who were confirmed as alive on January 1, 1979, with valid Social Security numbers and not shown to be deceased by the National Death Index between 1979 and 2001 were considered to be alive as of 2001. Those lost to follow-up before January 1, 1979, were censored at the date on which they were last known to be alive. Prior to 1979, death certificates were obtained from the state vital records offices, and the underlying cause of death was coded by a qualified nosologist. After 1979, the National Death Index provided underlying causes of death for deceased persons. All deaths were coded according to the revision of the International Classification of Diseases that was in effect at the time of death. The outcome of interest was lung cancer mortality (code 162 in the Eighth and Ninth revisions of the International Classification of Diseases and codes C33−C34 in the Tenth Revision).

Exposure assessment

Detailed work histories listing beginning and ending dates in departments and operations were available for each cohort member, as previously described (2). Each day during those years in which the participant was not employed was assigned an asbestos exposure of zero. Each day during years in which the person was employed was assigned a chrysotile exposure concentration, expressed as fibers longer than 5 µm per milliliter of air (fibers/mL). Exposure concentrations were estimated using a department-, operation-, and calendar-time-specific job exposure matrix (18). Annual exposure was defined as the product of the amount of the year worked and the average exposure concentration, and was expressed as fiber-years per milliliter (fiber-years/mL). This job exposure matrix and fiber-years/mL exposure metric have been used in prior analyses of this cohort (2, 16, 19–22).

Statistical methods

The 3,002 participants were indexed by i = 1 to N. Age (in years) was indexed by j = 18 to 90, with S_i denoting age at entry. Time was discretized as years of age. Let uppercase letters represent random variables and lowercase letters represent possible realizations.

For participant i, let 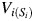be the vector of time-fixed covariates measured at entry, namely calendar year, prevalent asbestos exposure, and indicators of female sex and non-Caucasian race. Let W_ij = 1 indicate that participant i was at work during age j, and 0 otherwise. Note that at study entry, all participants were at work, or 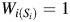for all i. Let X_ij represent asbestos exposure during age j, measured in fiber-years/mL. Note that when a participant was not at work during a given year, there was no opportunity for workplace-based exposure; that is, if W_ij = 0, then X_ij = 0. Let C_ij = 1 indicate censoring due to dropout at age j. Let D_ij = 1 indicate death due to causes other than lung cancer at age j. Finally, let Y_ij = 1 indicate death due to lung cancer at age j. For each age j, we assume the following temporal order: 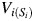, W_ij, X_ij, C_ij, D_ij, Y_ij. The history of a time-varying variable is denoted with an overbar. For example, the observed exposure history for individual i up to age j is denoted 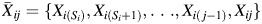. Below, we sometimes suppress the subscript i to simplify notation.

The cumulative lung cancer mortality in the observed data by age j can be written as

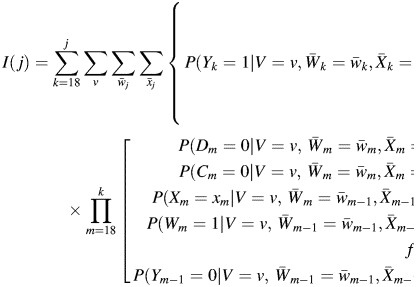(1)

for j = 18 to 90, where, by design, I(17) = D₁₇ = C₁₇ = Y₁₇ = Y₁₆ = 0.

Under the identifying assumptions of exchangeability (conditional on covariates), positivity, and consistency, the G formula can be used to consistently estimate the mean of a potential outcome under a hypothetical treatment intervention (23). Here, we consider interventions of the form, “If at work, set the exposure history to a specified value, 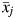, and allow no censoring by dropout, 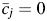.” When our observed data structure is used, the G formula for cumulative lung cancer mortality by age j under an intervention of this form is

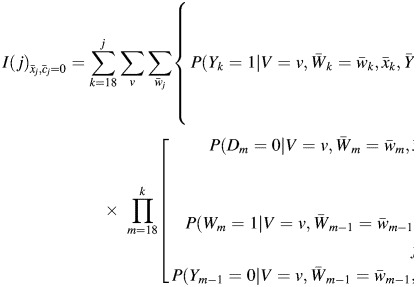(2)

In this analysis, we are specifically interested in evaluating the right side of equation 2 for 5 different exposure scenarios. First, as a check on the parametric models and as our reference setting, we assess lung cancer mortality under the natural course observed in the data. In other words, we compute lung cancer mortality (using equation 2) under the exposure history observed for each individual. Second, we estimate the lung cancer mortality that would have been observed had the 1971 Occupational Safety and Health Administration (OSHA) asbestos exposure standard of <5 fibers/mL been enforced throughout the entire study period. If a participant's asbestos exposure exceeded 5 fibers/mL in any year, it was capped at that level. Third, we assess the lung cancer mortality that would have been observed had the 1976 OSHA asbestos standard of <2 fibers/mL been enforced. Fourth, we assess the lung cancer mortality that would have been observed had the current OSHA asbestos standard of <0.1 fiber/mL been enforced. Fifth, we assess the lung cancer mortality that would have been observed had a possible standard of <0.05 fiber/mL been enforced. We implement these standards by setting those person-years with asbestos exposure greater than the standard to the standard as if the participant had been monitored and removed from the exposed workplace when the standard was exceeded. Therefore, we are estimating the total effect of the following dynamic regime: If at work, receive asbestos exposure no greater than q fibers/mL in any year, and if not at work, receive no asbestos exposure, for q = {5, 2, 0.1, 0.05}, compared with the natural course of exposure. For all scenarios explored, censoring due to dropout is abolished, but left-truncation at the age of study entry, administrative censoring at age 90 years, and deaths due to competing causes remain. These features are accounted for using an extension of the Kaplan-Meier approach that accommodates left-truncation, right-censoring, and competing risks and yields an estimate of the cumulative subdistribution (of lung cancer mortality) function (24).

When there are relatively few, discrete-valued covariates, the data are low-dimensional, and one can calculate the right side of equation 2 nonparametrically. In high-dimensional data, parametric models are required to estimate each component in equation 2, and a Monte Carlo simulation is required to approximate the sum, because directly computing the sum becomes infeasible as all possible covariate histories cannot be enumerated.

The steps needed to estimate lung cancer mortality using a Monte Carlo algorithm for the parametric G formula are as follows. First, the observed data are used, and parametric models are fitted for 1) the probability of remaining at work, 2) the probability of incurring any asbestos exposure, 3) the level of asbestos exposure among the exposed, 4) the probability of being lost to follow-up, 5) the probability of dying from a competing cause, and 6) the probability of dying from lung cancer. Second, a large Monte Carlo sample is drawn randomly with replacement from the observed participants. Third, the fit of the parametric models in the first step is used to recreate the follow-up experience for each person in the Monte Carlo sample. Fourth, the survival curve is estimated by using the Monte Carlo sample to obtain the cumulative lung cancer mortality through 90 years of age. Details of the Monte Carlo algorithm are presented in the Web Appendix, which is available at http://aje.oxfordjournals.org/. For further technical details, refer to the paper by Taubman et al. (8), Young et al. (9), or Westreich et al. (10).

For each exposure scenario, we quantify lung cancer mortality by using the cumulative mortality curve, and we estimate the differences and ratios of lung cancer mortality by 90 years of age as measures of association. As a measure of precision, we present 95% confidence intervals with the standard error estimated as the standard deviation from 200 nonparametric bootstrap resamples with replacement, each of size 3,002. For each exposure scenario, the number of persons required to follow that scenario to reduce the lung cancer mortality by age 90 years by 1 case—that is, the number needed to treat—was calculated as the reciprocal of the estimated risk difference (25). To assess the sensitivity of findings to the prolonged follow-up after 1980 when asbestos exposure had greatly diminished, we also present results administratively censoring follow-up in 1980. SAS software, version 9.2 (SAS Institute, Inc., Cary, North Carolina), was used for analyses.

RESULTS

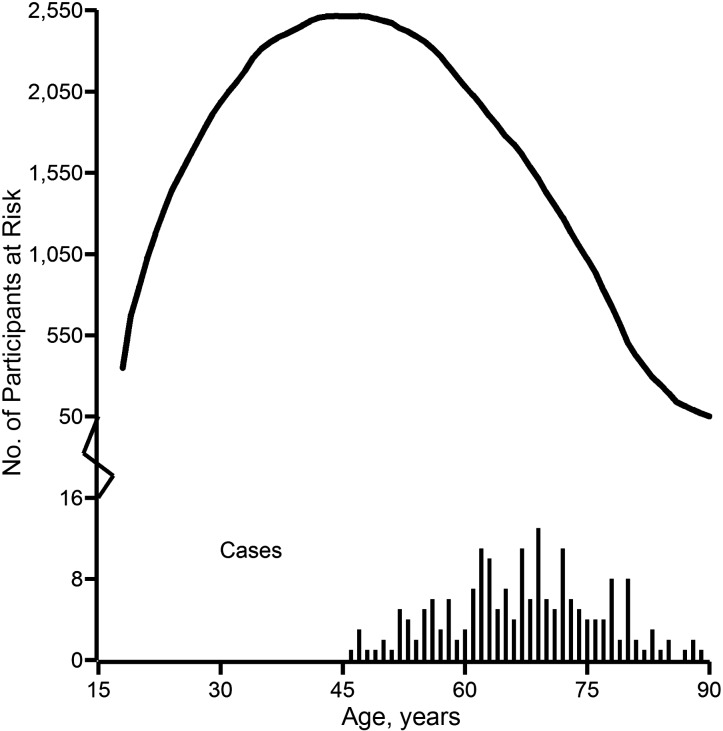
Table 1 provides the characteristics of the cohort and person-time under follow-up. At study entry, the cohort of 3,002 persons had a median age of 24 years; 58% were male and 81% were Caucasian. During 117,471 person-years of follow-up, 195 lung cancer deaths and 1,703 other deaths occurred, and 297 (10%) of 3,002 persons were lost to follow-up. Figure 1 depicts the number of persons at risk for lung cancer mortality and the number of lung cancer deaths by age. These overlaid histograms provide the distribution of person-years and indicate the age at which lung cancer mortality occurred. While 2,653 (88%) of the 3,002 persons entered follow-up after age 18 years, only 103 (3%) entered follow-up at or after the age of 46 years, which was the youngest age at which a lung cancer death occurred.

Table 1.

Characteristics of 3,002 South Carolina Textile Workers at Entry Into a Study of Lung Cancer Mortality by Occupational Asbestos Exposure and During 117,471 Person-Years of Follow-up Between 1940 and 2001

Characteristic	Study Entry (n = 3,002)			Follow-up (n = 117,471)
	Median (IQR)	No.	%	Median (IQR)	No.	%
Age, years	24 (20–31)			48 (36–60)
Calendar year	1943 (1941–1947)			1967 (1955–1981)
Male sex		1,749	58		67,178	57
Caucasian race		2,436	81		97,277	83
Employed		3,002	100		21,867	19
Asbestos exposure
Exposed		2,984	99		19,312	16
Fiber-years/mLa	1.83 (0.89–3.51)			3.30 (1.49–5.00)

Abbreviation: IQR, interquartile range.

^a Among the exposed.

Figure 1.

Number of persons at risk for lung cancer mortality (solid curve) and number of cases of lung cancer death (solid vertical lines) by age among 3,002 South Carolina textile workers exposed to asbestos, during 117,471 person-years of follow-up between 1940 and 2001.

Sixteen percent of person-years involved exposure to any asbestos (n = 19,312) or to more than 0.1 fiber-year/mL (n = 18,994); 12% of annual exposures were greater than 2 fiber-years/mL (n = 13,747), and 4% were greater than 5 fiber-years/mL (n = 4,745).

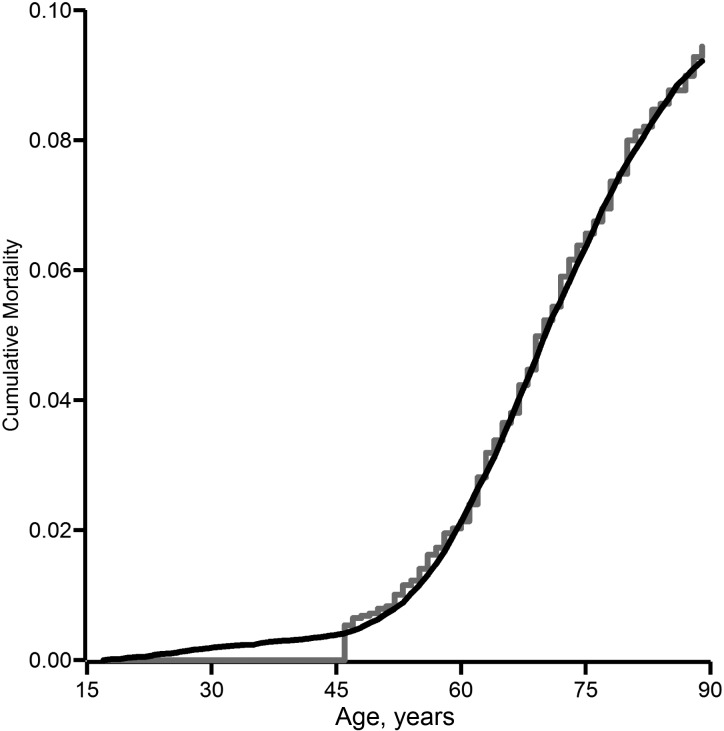
Table 2 shows participants’ characteristics according to person-years of data collection, as well as for each of the 5 simulated exposure scenarios. The natural-course scenario replicates the observed data well. For example, the median age is 1 year different from the observed data, and sex, employment status, and exposure status are each within 4% of the observed data. However, note the exception that the exposure distribution among the exposed is slightly higher for the simulated natural course than for the observed data. Importantly, Figure 2 shows the overlap between cumulative lung cancer mortality in the observed data and the simulated natural course.

Table 2.

Characteristics of 3,002 South Carolina Textile Workers Exposed to Asbestos, in Observed Data and Simulated Scenarios, During 117,471 Person-Years of Follow-up Between 1940 and 2001

Characteristic	Observed Data		Simulated Exposure Scenario, fiber-years/mL
			Natural Coursea		<5b		<2b		<0.1b		<0.05
	Median (IQR)	%	Median (IQR)	%	Median (IQR)	%	Median (IQR)	%	Median (IQR)	%	Median (IQR)	%
Age, years	48 (36–60)		49 (37–63)		50 (37–63)		50 (37–63)		50 (37–63)		50 (37–63)
Calendar year	1967 (1955–1981)		1969 (1956–1984)		1969 (1955–1984)		1969 (1956–1984)		1969 (1956–1984)		1969 (1956–1984)
Male sex		57		55		55		55		55		55
Caucasian race		83		83		83		83		83		83
Employed		19		15		13		9		6		6
Asbestos exposure
Exposed		16		13		11		8		4		4
Fiber-years/mLc	3.30 (1.49–5.00)		4.33 (2.17–6.70)		3.46 (1.64–5.00)		2.00 (0.59–2.00)		0.10 (0.09–0.10)		0.05 (0.05–0.05)

Abbreviation: IQR, interquartile range.

^a Uses the G formula to generate data under the observed exposures without dropout.

^b 1971, 1976, and current Occupational Safety and Health Administration asbestos exposure standards are <5, <2, and <0.1 fibers/mL, respectively.

^c Among the exposed.

Figure 2.

Cumulative lung cancer mortality according to asbestos exposure in the observed data (gray line) and under the simulated natural course of exposure (black line) among 3,002 South Carolina textile workers during 117,471 person-years of follow-up between 1940 and 2001.

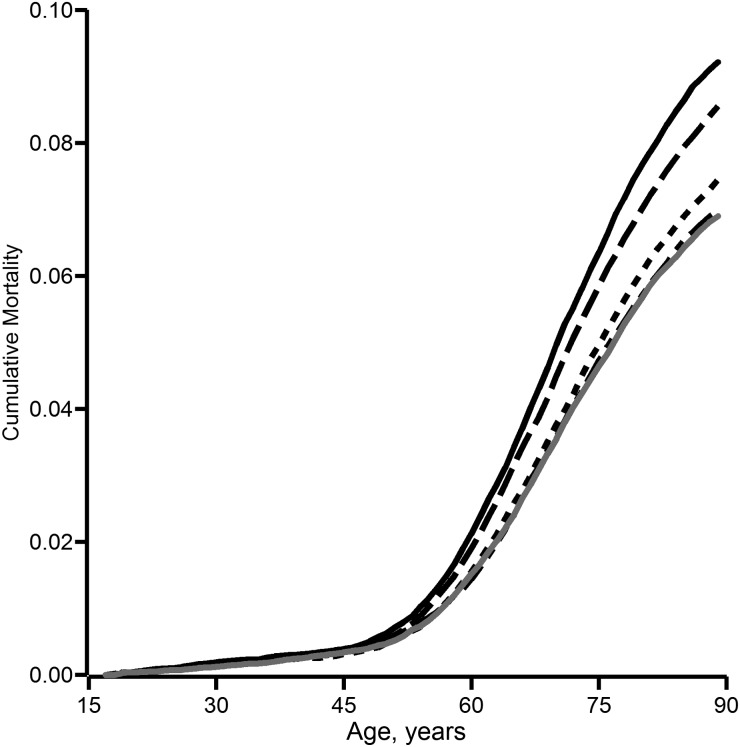
Figure 3 depicts cumulative lung cancer mortality under the explored exposure scenarios. We observe a dose response whereby a reduction in asbestos exposure results in a reduction in cumulative lung cancer mortality. In Table 3, we numerically summarize the results for cumulative lung cancer mortality at 90 years of age. For instance, the absolute difference in lung cancer mortality by age 90 years was −2.23 fiber-years/mL (95% confidence interval (CI): −3.79, −0.66) when the current OSHA standard was compared with the natural course; the mortality risk ratio for this comparison was 0.76 (95% CI: 0.62, 0.94). Compared with the current OSHA standard of <0.1 fiber/mL, the possible reduced standard of <0.05 fiber/mL showed a near-null reduction in cumulative risk of lung cancer mortality by age 90 years (mortality risk ratio = 0.99, 95% CI: 0.95, 1.04).

Figure 3.

Cumulative lung cancer mortality according to asbestos exposure under the simulated natural course of exposure (solid black line) and under simulated exposure to asbestos at a level of <5 fiber-years/mL (long-dashed black line), <2 fiber-years/mL (short-dashed black line), <0.1 fiber-years/mL (short- and long-dashed black line), and <0.05 fiber-years/mL (solid gray line) among 3,002 South Carolina textile workers during 117,471 person-years of follow-up between 1940 and 2001.

Table 3.

Cumulative Lung Cancer Mortality by Age 90 Years Under Various Simulated Asbestos Exposure Scenarios for 3,002 South Carolina Textile Workers During 117,471 Person-Years of Follow-up Between 1940 and 2001

Exposure Scenario, fiber-years/mLa,b	Lung Cancer Mortality, %	Risk Difference, %	Risk Ratio	95% Confidence Intervalc
Natural coursed	9.22	0	1	Reference
<5	8.56	−0.66	0.93	0.88, 0.99
<2	7.45	−1.77	0.81	0.71, 0.93
<0.1	6.99	−2.23	0.76	0.62, 0.94
<0.05	6.90	−2.32	0.75	0.61, 0.92

^a 1971, 1976, and current Occupational Safety and Health Administration asbestos exposure standards are <5, <2, and <0.1 fibers/mL, respectively.

^b Simulation was based on a Monte Carlo sample size of 50,000.

^c Standard error calculated as the standard deviation of 200 bootstrap samples.

^d Lung cancer mortality by age 90 years in observed data was 9.44%.

The numbers needed to treat to protect 1 person were 152, 56, 45, and 43 for exposure scenarios of <5, <2, <0.1, and <0.05 fiber-years/mL, respectively, all compared with the natural course. With the current OSHA standard as the reference level, the number needed to treat to protect 1 person was 1,111 under the exposure scenario of <0.05 fiber-years/mL.

When data were administratively censored in 1980, 64 of the 195 lung cancer deaths had occurred during 87,623 person-years. The mortality differences, compared with the natural course, were −0.94%, −2.05%, −2.37%, and −2.47% for exposure scenarios of <5, <2, <0.1, and <0.05 fiber-years/mL, respectively.

DISCUSSION

We combined data from 3,002 adult textile workers who were occupationally exposed to asbestos fibers and were followed for mortality for up to 60 years with quantitative methods built to accommodate the healthy worker survivor effect. We estimated the total effect of asbestos exposure on lung cancer mortality; some of this total effect may have been mediated by leaving work. We found that when the current OSHA workplace standard of <0.1 asbestos fiber per milliliter was applied throughout the follow-up period, there was a notable reduction in lung cancer mortality compared with the observed exposure.

The lung cancer mortality risk of approximately 7% by age 90 years estimated under asbestos exposure of <0.1 fiber-years/mL may be expected given the likely high proportion of persons who smoked during this calendar period (e.g., 40% of blue-collar workers smoked in 1986 (26)). Lifetime lung cancer mortality among smokers has been estimated to be as high as 17% (27).

In the present work, we assumed counterfactual consistency, or that exposure levels corresponded to well-defined interventions (28). Beyond possible issues surrounding fiber length, this assumption probably holds, because the exposures explored were interventions that cap annual exposure to asbestos fibers. One can imagine personal monitoring devices that would alert the worker and supervisor once a threshold has been reached, as used in workplaces with radiation exposure. We would likely have observed even stronger associations if, rather than capping exposure values larger than the OSHA standard, we had set all actively employed persons to the OSHA standard. We followed the more conservative route here because it more closely mimics hypothetical monitoring of asbestos exposure.

We also assumed conditional exchangeability, which implies that we adequately accounted for confounding and selection bias. First, it is possible that there was uncontrolled confounding—for example, by smoking. While smoking is an established cause of lung cancer mortality, its association with occupational asbestos exposure in this cohort is not well understood. Because the association between smoking and lung cancer is strong, any confounding of the relationship between asbestos exposure and lung cancer mortality by smoking is constrained primarily by the association between smoking and asbestos exposure: If smoking behavior were similar for all participants regardless of asbestos exposure, then confounding would be small. Second, we did not attempt to estimate the total effect of exposures incurred prior to study entry (e.g., prevalent asbestos exposure) because of possible selection bias. Specifically, persons who entered the study had survived any prior exposures (29, 30). Finally, other time-varying confounders (e.g., intermittent time off work, use of protective equipment) may also cause bias, but here we were limited to studying leaving the workplace because of available data.

In addition, we assumed correct specification of the models for employment status, competing risk of death, and lung cancer mortality. We did not need a correct parametric model for the distribution of each of the baseline variables because we drew values from the joint empirical distribution using a nonparametric bootstrap. Specification of the models for exposure and censoring was less important than for the aforementioned models, because we intervened on these variables. The overlap between the cumulative lung cancer mortality in the observed data and the simulated natural course (Figure 2) supports the assertion that we adequately captured the salient features of these data in the parametric models used for the G formula. While persons exposed in the generated data had somewhat higher median asbestos exposure, we are not overly concerned because 1) our parametric models were able to recreate the cumulative lung cancer mortality under the observed exposure in the natural-course scenario (Figure 2), 2) the generated data closely approximated features of the observed data (Table 2), and 3) we used the generated (rather than observed) natural course as the reference group. On a related point, we assume that the G null paradox is not an explanation for our nonnull findings. The G null paradox states that, under the null hypothesis, it may be impossible to correctly specify the parametric models required for the G formula (11). Therefore, in large samples, the parametric G formula may reject the null hypothesis, even when it is true. In our context we are not overly concerned about the G null paradox, because asbestos is an established cause of lung cancer (31).

Positivity, or the condition that there are exposed and unexposed persons at every level of confounders (32), is required generally for inference (23). However, as discussed by Robins (7, p. 145s), the G formula can be used to estimate the effects of dynamic exposure regimes defined in such a way as to circumvent nonpositivity. Recall, we are estimating the total effect of the dynamic regime: If at work, receive asbestos exposure no greater than q fibers/mL in any year, and if not at work receive no asbestos exposure, for various q. This dynamic regime circumvents nonpositivity caused by there being no exposure among persons who have left the workplace. However, we are precluded from decomposing this total effect into the direct effect of asbestos on lung cancer mortality not mediated through leaving the workplace, because there is no asbestos exposure among persons who have left the workplace.

There have been few implementations of the parametric G formula. Robins (7) published a first example on occupational exposure to arsenic and mortality. Taubman et al. (8) published an example on lifestyle behaviors (e.g., smoking, exercise, and diet) and cardiovascular disease. Young et al. (9) and Westreich et al. (10) published examples on treatment for human immunodeficiency virus and progression to acquired immunodeficiency syndrome or death. Our implementation differed from that of Taubman et al. (8) and Young et al. (9) only in that we calculated a distinct outcome for each person-year, rather than the conditional probability of the outcome for each year. While our implementation provides more flexibility in calculating outcome measures, it is computationally more intensive. Future implementations might explore the introduction of prior knowledge into the parametric G formula through Bayesian methods.

The present work had several strengths. First, the data were extensive in terms of the sample of 3,002 persons, the 195 lung cancer deaths, and the 60-year follow-up. Second, the data were of high quality, with asbestos exposure assessed by job exposure matrix and detailed mortality ascertainment. Third, we used an innovative quantitative method that allowed comparisons that are of more direct use to health policy planning than typical associations of asbestos exposure and risk of lung cancer mortality. As a final strength, in occupational cohort studies, often a lengthy amount of time is required between beginning employment and cohort enrollment. In such cases, the resultant cohort is selected for persons who survive long enough to enter, and may induce survivor bias. Moreover, in such settings it is impossible to consistently estimate the effect of exposure prior to study entry (11). Here we had a relatively short 1-month window, which should not have induced notable survivor bias.

In conclusion, when compared with the observed asbestos exposure, the current OSHA asbestos standard of <0.1 fiber/mL yielded 24% less lung cancer mortality by age 90 years. A further reduction to a possible standard of <0.05 fiber/mL yielded no discernible additional reduction in lung cancer mortality.