Review: Groundwater flow and transport modeling of karst aquifers, with particular reference to the North Coast Limestone aquifer system of Puerto Rico

Abstract

Karst systems have a high degree of heterogeneity and anisotropy, which makes them behave very differently from other aquifers. Slow seepage through the rock matrix and fast flow through conduits and fractures result in a high variation in spring response to precipitation events. Contaminant storage occurs in the rock matrix and epikarst, but contaminant transport occurs mostly along preferential pathways that are typically inaccessible locations, which makes modeling of karst systems challenging. Computer models for understanding and predicting hydraulics and contaminant transport in aquifers make assumptions about the distribution and hydraulic properties of geologic features that may not always apply to karst aquifers. This paper reviews the basic concepts, mathematical descriptions, and modeling approaches for karst systems. The North Coast Limestone aquifer system of Puerto Rico (USA) is introduced as a case study to illustrate and discuss the application of groundwater models in karst aquifer systems to evaluate aquifer contamination.

1. INTRODUCTION

Karst aquifers provide drinkable water for hundreds of millions of people, accounting for 25% of the world and 40% of the US groundwater resources (Ford and Williams 2007; Quinlan and Ewers 1989). Karst aquifers have complex characteristics that make them different from other aquifers (Bakalowicz 2005). They form in soluble rocks, such as dolomite and limestone, and the dissolution process creates complex networks of preferential flow pathways that are difficult to locate. Flow within the aquifer ranges from Darcian to turbulent flow depending upon the relative contribution and interplay of matrix, fracture and conduit permeability (Burdon and Papakis 1963; Schuster and White 1971; Atkinson 1977).

The estimation of groundwater flow and solute transport is an essential component of conservation, management and protection of aquifers against contamination. Mathematical models are frequently used to characterize aquifer behavior and make predictions. Numerical groundwater flow models have been applied since 1960s (Sauter et al. 2006). The application of numerical models to karst aquifers is especially challenging. Karst aquifers exhibit complex characteristics generated by the high heterogeneity of hydraulic aquifer properties. Traditional numerical methods have strong limitations in modeling groundwater flow in karst where Darcy's law is not applicable (e.g., Field 1997). In the last two decades, however, mathematical models of groundwater flow have been developed that account for the hydraulic characteristics of karst aquifers (Király 2003). This paper presents an overview of groundwater flow and transport modeling in karst aquifers. Conceptual models of karst aquifers are introduced, and different modeling approaches are described and their applications are discussed. The North Coast Limestone aquifer system of Puerto Rico (USA) is used as an example to illustrate the application of numerical groundwater models in karst terrains.

2. CONCEPTUAL MODELS

Conceptual models are simplified representations of specific characteristics and processes (e.g., recharge, permeability distributions, and geological structures) of the real aquifer system, and can be presented as a picture, diagram, flowchart or in written form. There are numerous conceptual models of karst aquifers illustrated in the literature (e.g., Mangin 1975; White 1977; Quinlan 1978; Stringfield et al. 1979; Blavoux and Mudry 1983; Chen 1988; Lee and Krothe 2001, Palmer et al. 1999, Ford and Williams 2007). In this section, conceptual models for karst systems are introduced, followed by more specific conceptual models that focus on the permeability, recharge, discharge conditions, and contaminant transport in karst groundwater systems.

2.1. Karst Systems

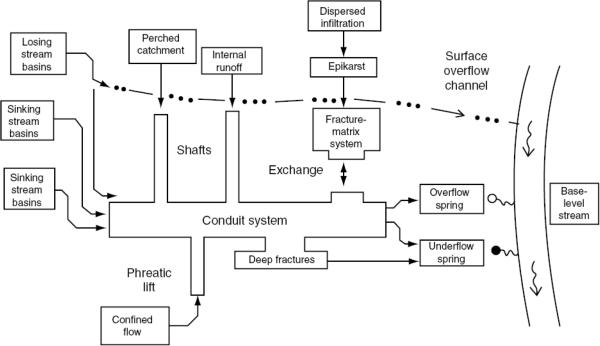
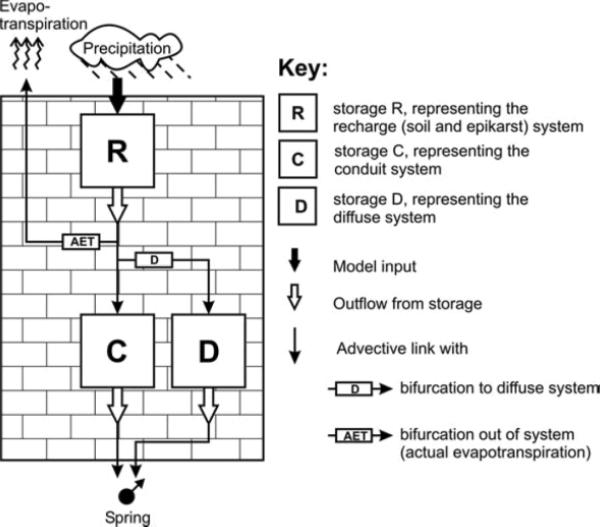
A karst aquifer is typically characterized by sinkholes, caves, springs, conduits and underground drainage systems (Figure 1) formed by dissolution, internal drainage, and collapse processes. Proper quantitative assessment of flow and transport processes in these aquifers requires knowledge on recharge characteristics and location of major conduits systems. The manner in which infiltrating water is transmitted through the system also controls system response to recharge. The karst conduit system occupies only a small portion of the total aquifer porosity but may have a major impact on the hydraulic behavior of the karst system.

Fig 1.

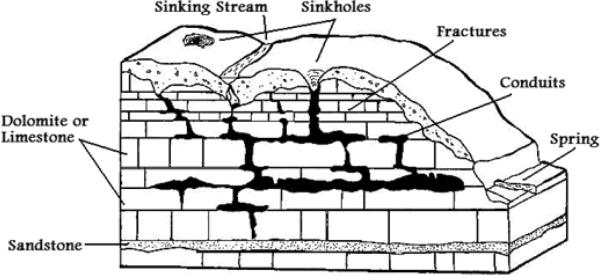
Conceptual model for a karst aquifer

White (2003) presented a comprehensive physical framework including essential components for mathematical models in karst aquifers (Figure 2). This scheme illustrates how the water and substances are added to, stored in, transmitted through, and discharged from the groundwater system. The three fundamental attributes governing the behavior of karst aquifers are recharge, storage, and transmission. Karstic areas often lacks surface water because karst bedrocks are highly permeable and connected to the surface, so sinking streams of karst basins often disappear from the surface. After overland storm runoff is stored in surface depressions, internal runoff occurs through sinkhole drains. In addition, precipitation water can be stored in the epikarst for a few weeks before infiltrating through the rock matrix. Local perched aquifers that may exist above local less permeable beds are elevated above the regional water table and can discharge into the regional karst aquifer through vadose shafts and fracture systems. The conduit system exchanges the collected water with the surrounding fractures and matrix and transfers it towards springs.

Fig 2.

Conceptual scheme for a karst aquifer (White 2003)

2.2. Permeability

Permeability is the capacity of an aquifer for transmitting water and it represents the relative ease with which the aquifer transmits groundwater. In karst aquifers, permeability may be associated with three types of system porosity: matrix, fractures and conduits (Table 1). Conduits are underground pipes formed by dissolution of carbonate rocks that carry water from the recharge area to an outlet spring (Figure 1). Groundwater storage occurs mostly in the matrix with inter particle primary porosity, and the matrix permeability determines the leakage into and out of storage blocks between the elements of secondary porosity such as fractures or conduits (Atkinson 1977). The significance of matrix permeability depends on the nature of the matrix porosity, and tends to diminish when more fractures are present (Matthäi and Belayneh 2004). Fracture permeability depends on fracture apertures, typically ranging from 10 μm up to 10 mm (Table 1), the density and orientation of the fractures, and their interconnectivity. Based on the relative permeability of the fractures and the matrix blocks, fractured porous media can be classified as purely fractured media with impervious blocks, double-porosity media with open fractures, and heterogeneous media where fractures are filled with a porous material (Streltsova 1977).

Table 1.

Flow characteristics of triple porosity components in karst aquifers

Permeability	Dimension	Travel Time	Flow Mechanism	Distribution
Matrix	μm to mm	Long	Darcy law, laminar flow	Continuous
Fracture	10 μm to 10 mm	Intermediate	Cube law, usually laminar flow	Localized
Conduit	> 10 mm	Short	Darcy-Weisbach, open channel and pipe flow, turbulent flow	Localized

Drogue (1974, 1980) simplified conduit system geometry with fracture patterns that have a greater hydraulic conductivity than the matrix blocks that are between the fractures (Figure 3). The lower-permeability blocks also are dissected by low-permeability fractures to represent diffuse flow. Under this concept, fractured aquifers have a double porosity nature consisting of two parts, the low-permeability matrix and the high-permeability fractures. Generally, upper aquifer layers are associated with a greater degree of fracturing due to higher decomposition phenomena close to the ground surface and their greater capacity to store and infiltrate precipitation.

Fig 3.

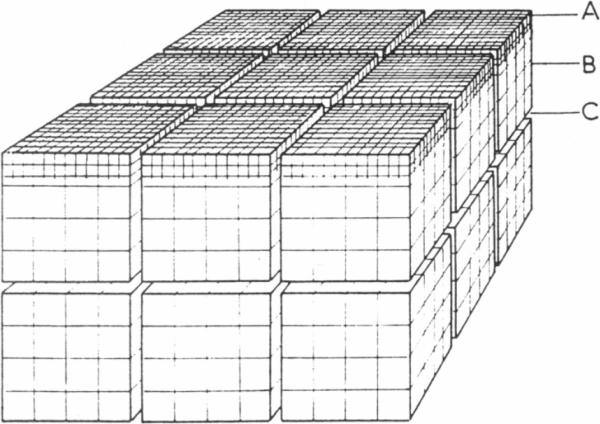
Conceptual model of a karst aquifer with double-fissured porosity system: upper more cracked epikarst (A), matrix blocks (B), and fractures with higher permeability (C) (Drogue 1980)

Considering karst aquifers as being composed of these functionally different components yields a concept referred to as the triple porosity concept for which the characteristics are summarized in Table 1 (White 2007):

2.3. Recharge

Several conceptual models describe the recharge and infiltration processes in karst aquifers. Water enters into the karst systems through concentrated allogenic and autogenic recharge in sinking streams and sinkholes, and diffuse allogenic and autogenic recharge in low permeability regions. Mangin (1975) and Williams (1983) introduced the concept of the epikarst as a shallow, high permeability karstified zone below the soil zone. Infiltration into an aquifer follows the sequence of soil and epikarst, vadose zone (vertical infiltration through a network of fissures and conduits), and phreatic zone. Epikarst may delay recharge and catch the rainfall water by draining, storing, infiltrating and channeling it into the karst system through either vertical fractures or shafts or dispersed infiltration (Figure 1), which may reduce the amount of time available for evaporation. According to White (1977), major recharge sources are surface water injected by sinking streams, drainage from sinkholes and depressions, and infiltration of precipitation through the soil into the epikarst and then through the rock matrix or along fractures to the saturated zone.

2.4. Discharge

Most discharge from karst systems is via a limited number of springs (Ford and Williams 2007). Underflow springs discharge continuously, and overflow springs are those discharging only at high-flow periods like storm or flooding conditions (Worthington 1991). The conduit system can act as source or sink for the matrix based on flow conditions. In a karst aquifer with a well-developed conduit system, regional flow occurs primarily within conduits during base flow conditions. Dispersed infiltration is transferred via laminar Darcian flow in the matrix to a nearby conduit and then overall flow is conveyed (often turbulently) through the conduit network to springs. In contrast, during flood conditions the seepage is from pressurized conduits to the matrix, which is equivalent to bank storage in surface streams (Field 1992–93).

2.5. Contaminant Transport

Contaminants may enter karst groundwater systems through infiltration of surface runoff and waste leachate, industrial and wastewater discharges, and accidental spills. Often surface runoff contains pathogens (bacteria and viruses), nutrients (e.g., phosphorus, nitrogen), hydrocarbons, and other organic contaminants and metals species. The heterogeneity of karst systems, which affects contaminant transport, storage, and reactivity, leads to highly variable spatial input of these contaminants into the aquifer. Particulate matter and sediment and attached organic contaminants, nutrients, or bacteria can be stored and rapidly transported through karst aquifers as a result of rapid flow in the conduit network (Thrailkill 1989, Mahler et al. 2003).

2.5.1. Solute Transport

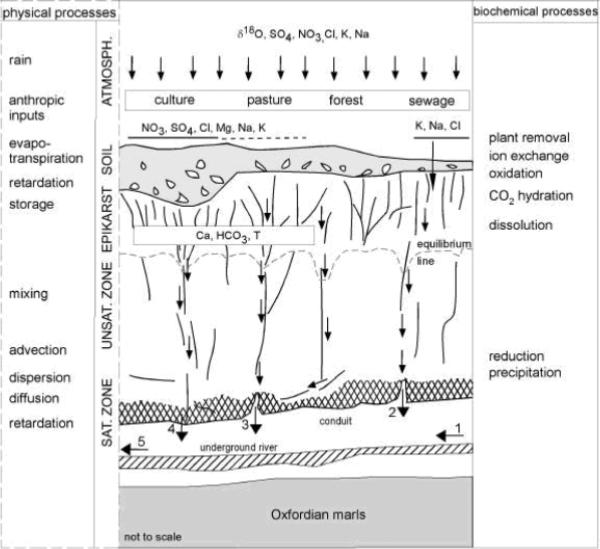
Generally, just as in porous aquifers, solute transport in karst aquifers is controlled by the processes of advection, dispersion and adsorption. However, the high heterogeneity of karst systems and the interaction between the conduit and the matrix system make solute transport in karst aquifers a complex process. Perrin (2003) developed a conceptual model of solute transport for the Milandre test site in the Swiss tabular Jura to show the physical and chemical processes affecting groundwater chemistry (Figure 4). The chemistry of water in a karst conduit is changed by mixing with groundwater recharged from different infiltration zones (e.g., soil, epikarst). The chemical load (major ions such as sulfate, chloride, nitrate and potassium) of infiltrating rainwater is also affected by the land use in the catchment (e.g. pasture, forest). In cultivated or urban areas fertilizers, sewage, and salt for road works release large quantities of ions into the system. Physical, chemical, and biochemical processes such as evapotranspiration, plant consumption, ion exchange, oxidation-reduction, retardation, etc., occur in the soil and epikarst zone. An equilibrium line can be used to indicate a surface below which the groundwater becomes chemically equilibrated under different hydraulic conditions in the aquifer.

Fig 4.

Conceptual model of solute transport at Milandre test site (Perrin 2003)

2.5.2. Behavior of NAPLs

A distinction must be made between solute transport and non-aqueous phase liquid (NAPL) transport. NAPLs do not dissolve readily in water and are of two types: less dense NAPLs (light non-aqueous phase liquids, LNAPLs) and NAPLs denser than water (dense non-aqueous phase liquids, DNAPLs). Typical examples of LNAPLs are petroleum hydrocarbons (gasoline, mineral oil, etc.). DNAPLs include, for example, chlorinated solvents used in the metal fabricating industry as degreasers. In contrast to dissolved contaminants, the transport of NAPLs in aquifers is strongly influenced by buoyancy effects and surface tension properties. This makes the transport behavior of NAPLs less directly related to groundwater flow and more difficult to predict. When LNAPLs are released, they will migrate until reaching a physical barrier or the water table and mostly continue along the direction of the maximum potentiometric gradient (Newell et al. 1995). A large amount of LNAPLs may hydrostatically depress the water table, but generally migrate laterally and undergo spreading, volatilization, and adsorption. Efficient techniques for characterizing LNAPL transport in karstic settings are currently not available (Newell and Ross 1992).

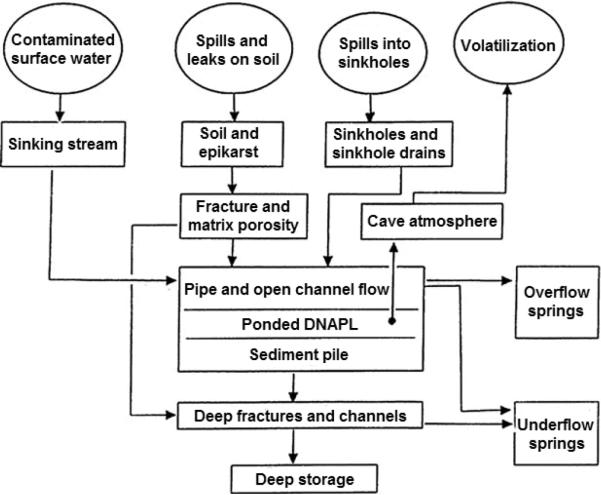
Upon release of DNAPLs into the environment, they migrate downward due to gravity, and partially are retained by capillary forces in the unsaturated zone (Wolfe et al. 1997). DNAPLs will also initially float on and depress the groundwater surface until the organic entry pressure is exceeded. Once the organic entry pressure is exceeded, the groundwater is displaced and the DNAPL will begin to sink in long stringers until either the DNAPL source is exhausted or an impermeable surface is reached. After reaching an impermeable surface, the DNAPL will proceed to migrate down the dip of the surface regardless of the prevailing groundwater flow direction. In karst aquifers, the DNAPL will always tend to concentrate in open conduits. Wolfe et al. (1997) developed conceptual models for DNAPL transport with emphasis on DNAPL accumulation in different subsurface regions, including regolith, top of bedrock, diffuse-flow zones, conduits, and openings isolated from groundwater flow. Determining the presence and migration of DNAPL plumes becomes more difficult with increasing depth, distance from the source, and complexity of the flow system. The complicated processes of DNAPL storage and transport in karst aquifers have been reviewed by Loop and White (2001). Their transport conceptual model is given in Figure 5.

Fig 5.

Conceptual model for DNAPL storage and transport in karst aquifers (Loop and White 2001)

Although DNAPLs are easily injected into karst aquifers through sinkholes and sinking streams, contaminant discharge through springs may be significantly delayed depending on transport mechanisms, storm water recharge, and storage sites within the karst aquifer. DNAPLs can be stored in the epikarst, dead volume regions within the geologic media, pools and depressions within underground streams, incorporated within clastic sediments, adsorbed onto organic materials, manganese oxides, iron oxides, and other substrates, and migrated to deep zones within the fracture system.

3. MATHEMATICAL DESCRIPTIONS OF KARST SYSTEMS

Flow and transport in karst aquifer systems can be conceptualized and then mathematically described. Because flow and transport behavior is different for the matrix, fracture, and conduit system, different mathematical descriptions are necessary for these flow systems. When describing the entire system, it is necessary to couple the matrix, fracture, and conduit flow systems. Their coupling can be mathematically expressed by a linear exchange term and the difference in the hydraulic potential in these systems (e.g., Liedl et al. 2003). Other authors (e.g., Faulkner et al. 2009) used the Beavers-Joseph interface conditions (Beavers and Joseph1967) to simulate exchange between the matrix and the conduit system.

3.1. Flow and Transport in Matrix

Groundwater flow through the porous rock matrix is intrinsically the same as groundwater flow in porous media (White and White 2005), and can be described using the matrix flow formulation of Darcy, which states that the discharge, Q, is proportional to the hydraulic gradient and the cross-sectional area, with the hydraulic conductivity being the proportionality factor:

$$Q=-KiA$$ (1)

where, A is the cross-sectional area [L²], K is the hydraulic conductivity [LT⁻¹] and i is the hydraulic gradient. The general form of the solute transport equation in the rock matrix is:

$$R\frac{\partial c}{\partial t}=D\frac{{\partial }^{2}c}{\partial x^2}-v\frac{\partial c}{\partial x}-\lambda nc\mp r$$ (2)

Where R is the retardation factor in the matrix, c is the matrix solute concentration [ML⁻³], D is the matrix dispersion coefficient [L²T⁻¹] defined as the sum of mechanical dispersion and molecular diffusion, v is the groundwater velocity [LT⁻¹], λ is the decay constant [T⁻¹] (λ=ln2/t₅₀ in which t₅₀ is the solute half-life), n is the matrix porosity, and r is the chemical reaction rate [ML⁻³T⁻¹].

3.2. Flow and Transport in Fractures

The fracture flow formulation simplifies the fractures to have parallel walls and uniform aperture b (Delleur 1999). Assuming impermeability for fracture walls, the steady state flow rate is described by the cubic law derived from Navier-Stokes equation for a viscous and incompressible fluid,

$$Q=\left(\frac{-w\rho g{b}^3}{12\mu }\right)i$$ (3)

Where w is the fracture width [L], b is the aperture of the fracture [L], μ is the water viscosity [ML⁻¹T⁻¹], ρ is the water density [ML⁻³], g the gravitational acceleration [LT⁻²], and i the hydraulic gradient. The cubic law is valid for laminar flow in open or closed fractures (Witherspoon et al. 1980).

The average flow velocity in the fractures expressed by a single parallel plate model is:

$$v^{\prime }=\left(\frac{\rho g{b}^2}{12\mu }\right)i$$ (4)

where v' is the mean channel velocity. Witherspoon et al. (1980) experimentally confirmed the cubic law (Q ~ b³) valid for “ideal” parallel plates for samples of granite, basalt, and marble. They summarized the constant parameters of equation (3) into a single constant C=−wρg/(12μ); and then added an empirical friction factor, f, ranging from 1.04 to 1.65, in order to account for differences between “ideal” parallel plates and parallel plates formed by real rocks:

$$Q=\frac{C}{f}{b}^{3}i$$ (5)

Solute transport in fractures is influenced by advection, dispersion, diffusion into the rock matrix, decay, chemical reactions, and precipitation-dissolution, and/or adsorption-desorption processes (Delleur 1999). Within fractures, transport occurs primarily by advection while dispersion is a minor factor (Lapcevic et al. 1999; Witthüser et al. 2003).

Mutch et al. (1993) studied the solute exchange between matrix and fractures after a source started to release the solute and detected three phases of solute diffusion from fracture to clean matrix, diffusion from matrix to fractures and to matrix center after removing the solute source, and lastly diffusion from matrix center to fractures. Tang et al. (1981) derived the equation (6) to describe solute transport in a single fracture:

$${\phantom{\mid }R\frac{\partial c}{\partial t}=D\frac{{\partial }^{2}c}{\partial x^2}-v\frac{\partial c}{\partial x}+\lambda c\mp r-\frac{2nD}{b}\frac{\partial c^{\prime }}{\partial z}\mid }_{z=\frac{b}{2}}=0$$ (6)

where the x-coordinate and z-coordinate indicate the direction of the fracture and perpendicular direction to fracture axis, respectively. Also R is the retardation factor in the fracture, c is the fracture solute concentration [ML⁻³], c' is the solute concentration in the matrix [ML⁻³], D is hydrodynamic dispersion coefficient in the fracture [L²T⁻¹], v is the average fracture velocity [LT⁻¹], λ is a first order decay constant, and r is the chemical reaction rate in the fracture [ML⁻³T⁻¹].The last term is the diffusive loss term and represents diffusive mass flux crossing the fracture-matrix interface (at z=b/2).

3.3. Flow and Transport in Conduits

The main characteristic that distinguishes karst aquifers from porous and fractured-rock aquifers is the conduit network. Besides matrix blocks and fractures, karst aquifers include conduits with high often rapid flow and low storativity. The conduit network can act as a boundary condition for the matrix and fractured rock. Water may flow in conduits in a free surface open-channel regime derived by gravitational gradients, or as pipe flow under pressure. Both open-channel flow and pipe flow may occur in different reaches of a conduit. Open channel steady flow is described by the Manning equation:

$$v=\frac{1}{n}{R}^{2∕3}{S}^{1∕2}$$ (7)

Where Manning's n is a roughness factor [T/L^1/3], R is the channel hydraulic radius [L], and S is the channel slope [L/L]. Water may flow in open channels in either laminar or turbulent regimes. For turbulent pipe flow the Darcy-Weisbach equation is used to calculate steady flow (Thrailkill 1968):

$$Q=\frac{2\pi g^{0.5}{r}^{2.5}}{f^{0.5}}{\left(i\right)}^{0.5}=K^{\prime }{A}_c\sqrt{i}$$ (8)

Where f is the empirical Darcy-Weisbach friction factor, g [LT⁻²] the gravitational acceleration, r [L] is the radius, i is the hydraulic gradient, A_c is the conduit cross sectional area [L²] and K'=2g^0.5r^0.5/f^0.5is the turbulent flow effective hydraulic conductivity [LT⁻¹], typically ranging between 1 and 10 m/s (Sauter et al. 2006). Under turbulent flow conditions, conduit flow is a function of the square root of the hydraulic gradient (in contrast to laminar matrix and fracture flow, where flow is proportional to the gradient). A Froude number (Fr, the ratio of inertial force to gravitational force) of less than one indicates a subcritical regime (vs. supercritical regime) and a Reynolds number (Re, the ratio of inertial force to viscous force) of less than 2000 indicates laminar flow (vs. turbulent flow) (De Marsily 1986):

$$Fr=\frac{v}{g{y}_h}$$ (9)

$$Re=\frac{vD}{\vartheta }$$ (10)

Where v is the groundwater velocity [LT⁻¹], y_h is the hydraulic depth [L], D is the hydraulic diameter [L], and ϑ is the kinematic viscosity [L²T⁻¹]. A summary and application of case studies is provided by Jeannin and Maréchal (1995) and Jeannin (2001).

Li (2009) described the complicated conduit transport with a conceptual model in which contaminant is released from the matrix into the conduit, mixes with uncontaminated flow entering the conduit, and is transported along the conduit (x-axis). Using a relatively simple one-dimensional equation (based on solute mass conservation), the solute transport equation through a conduit is given by:

$$\frac{\partial c}{\partial t}=D\frac{{\partial }^{2}c}{\partial X^2}-v^{\prime }\frac{\partial c}{\partial x}+\frac{2}{\alpha }j{c}^{\prime }q$$ (11)

Where c is the solute concentration in the conduit [ML⁻³], α is the conduit radius [L], v' is the mean velocity of conduit flow [LT⁻¹], D is the dispersion coefficient in the conduit [L²T⁻¹], q is the Darcian flow [LT⁻¹] from matrix into conduits, c' is the solute concentration in the matrix, and j is the specific flux of solute at the wall.

4. MODELING APPROACHES

The mathematical descriptions presented in the previous section form the basis for models that are used to simulate whole karst systems. Early models were based on analytical solutions to the equations and they necessitated making significant simplifying assumptions. Modern models are generally based on numerical solutions and taking advantage of significant advances in computing technology. Selecting the best approach and computer code to solve the flow or transport equations is primarily based on available data, dominant flow mechanism (matrix, fracture, conduit flow), and modeling objective (regional groundwater budget calculation, drinking water management, groundwater flow or contaminant transport modeling) (Teutsch and Sauter 1998).

Flow models may simulate hydraulic heads, groundwater fluxes and discharge at springs, while transport models simulate the transport and distribution of substances in the aquifer (Scanlon et al. 2003). The performance of typical transport models in karst aquifers, especially at local scales, is poor due to the significant uncertainty in subsurface geometry. For an accurate estimation of transport processes, a detailed description of conduits, caves and fractures is required, which is not easily obtained.

Because of the high heterogeneity and anisotropy of hydraulic parameters in a karst system, determination of their distribution over the system always deals with approximations in conceptual and numerical models. The effect of such approximations must be addressed as uncertainties in the results (e.g., Kovacs and Sauter 2007).There are two general modeling approaches in karst systems, (1) spatially lumped and (2) spatially distributed models.

4.1. Spatially Lumped Models

Spatially lumped models (sometimes also called global models) simulate the global hydraulic, physical or chemical response of the aquifer output at a spring (e.g., spring discharge, concentrations in spring water) to the input into the aquifer system in the spring catchment (e.g., groundwater recharge, infiltrating rainfall and solutes) (Sauter et al. 2006). Spatial variations of flow patterns in the aquifer are not considered. Lumped-parameter models involve a mathematical analysis of temporal variations in spring discharge (hydrograph) or in spring chemical concentration (chemograph) to give an understanding of the overall water balance in the karst system or an interpretation of groundwater quality, and fundamental information on the hydraulic behavior of the entire system. Lumped-parameter models are, however, limited in their ability to provide direct information about karst aquifer hydraulic parameters, flow directions, and velocity. The main advantage of this approach is its relatively low data demand because actual hydraulic parameters (e.g., hydraulic conductivities) and the distribution of the hydraulic head do not have to be experimentally determined.

Lumped-parameter models include only a few adjustable global parameters and ignore heterogeneity, so their calibration is faster than that of more complex distributed models. Lumped-parameter models are used to convert input (recharge) into output (discharge), and since water flow and solute transfer within cells are not considered, the equations are simpler (Scanlon et al. 2003), and only ordinary linear differential equations need to be solved. Many modeling studies (e.g., Wanakule and Anaya 1993; Zhang et al. 1996; Barrett and Charbeneau 1996; Scanlon et al. 2003; Jukić and Denić-Jukić 2009) take advantage of the reduced data needs and simulation costs of lumped-parameter modeling approaches to address important problems in karst areas, such as predicting flow rates and substance concentrations, water levels and spring discharge. In the following, two different lumped-parameter modeling approaches, hydrograph-chemograph analyses and rainfall-discharge models, are introduced.

4.1.1. Hydrograph-Chemograph Analyses

Hydrograph-Chemograph Analyses (or Single Event methods) are based on the analysis of the hydrograph or chemograph to evaluate the lumped hydraulic response of the karst aquifer to rainfall events. Such an approach was first introduced by Mero (1963, 1969) and subsequently used by others (e.g., Guilbot 1975; Bezes 1976). Tallaksen (1995) and Dewandel et al. (2003) developed empirical equations to describe spring hydrograph recessions. In contrast to empirical equations, which are based only on measured data, physical equations are derived from flow equations and have the ability to provide quantitative information of aquifer parameters such as storage and permeability or solute transport parameters (Troch et al. 1993; Szilagyi et al. 1998; Field and Pinsky 2000).

Recession analysis uses methods that fit the recession curve with quadratic or exponential formulas (Dewandel et al. 2003). The first approach attempts to describe the entire recession curve by one mathematical formula (Drogue 1972) to express this curve with a recession coefficient:

$$Q\left(t\right)=\frac{Q_0}{{(1+\alpha t)}^m}$$ (12)

Where Q (t) and Q₀ are the discharge [L³T⁻¹] at time t and the initial discharge at an earlier time, respectively, α is the recession coefficient [T⁻¹] and m is a constant that ranges between 0.5 to 5, used to calibrate the model. Hyperbolic models provide a very good fit of modeled to measured recession curves. Kovacs (2003) found m=1.5 to be the most appropriate value, agreeing with almost 60% of the cases he investigated.

The exponential reservoir model, first proposed by Maillet (1905), approximates the whole karst system with one reservoir and assumes that the spring discharge is an exponential function of water stored in the aquifer, with:

$$Q\left(t\right)=Q_0{e}^{-\alpha t}$$ (13)

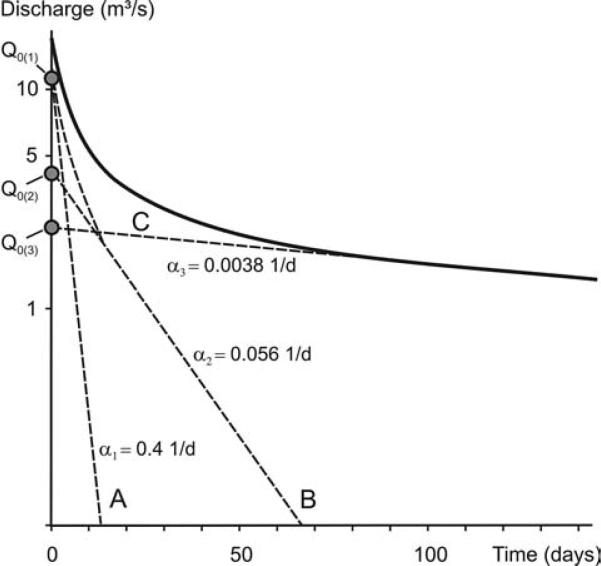
First developed by Forkasiewicz and Paloc (1967), and later also used by others (e.g., Torbarov 1976), multiple exponential reservoir models describe the spring recession curve by fitting a series of exponential sub-curves to different hydrograph segments (Figure 6). The different exponential terms may reflect different parallel aquifer reservoirs with different permeability, such as the conduit network, fractures, and the porous matrix. This interpretation, however, is not generally accepted, and some authors (Király and Morel 1976; Eisenlohr et al. 1997) claim that the different exponential components do not necessarily reflect different aquifer reservoirs with different hydraulic conductivities.

Fig 6.

Three reservoir recession curves: A, B and C (Forkasiewitz and Paloc1967)

The multiple exponential reservoir models are expressed as the sum of exponential terms:

$$Q\left(t\right)=Q_{01}{e}^{-{\alpha }_{1}t}+Q_{02}{e}^{-{\alpha }_{2}t}+\cdots +Q_{0n}{e}^{-{\alpha }_{n}t}$$ (14)

where n is the total number of reservoirs.

Lee and Krothe (2001) established an isotopic mixing model, where the chemograph of dissolved inorganic analyses is interpreted based on mixing of rain, soil, epikarst and phreatic water. There are additional approaches of hydrograph-chemograph analysis, including cascade models (Mero 1963, 1969; Mero and Gilboa 1974; Guilbot 1975; Bezes 1976), and fractal approaches (Hergarten and Birk 2007).

4.1.2. Linear Storage (Box) Models

Linear Storage models (sometimes called box models or Rainfall-Discharge models or Time Series Analyses) state a relationship between the global hydraulic response of a karst system to recharge patterns caused by a succession of rainfall events (input-output relationship) (Sauter et al. 2006). They can be used to simulate the variation in discharge (hydrograph) and substance concentration (chemograph) at a spring over a period of time that includes different hydrological conditions (several rainfall events). Model input requires precipitation and evapotranspiration in the catchment of the spring to simulate flow, and substance input to simulate concentration. Spring discharge and chemical concentrations at the spring can be used to calibrate the models. Different flow systems within the aquifer are represented by linear storages, which are advectively connected. The outflow Q_out [L³ T⁻¹ of a storage is proportional to the storage's volume V_s [L³]:

$$Q_{out}=\beta V_s$$ (15)

where β [T⁻¹] is the outflow coefficient that represents a mean residence time in the storage.

The simplest representation of a karst system includes storages for different compartments such as the recharge system (soil and epikarst), the diffuse flow (matrix) and conduit flow systems. The storages represent these flow systems globally for the entire aquifer. Figure 7 schematically illustrates a possible model setup. Flow and substance concentrations are numerically calculated, based on the principle of mass (or volume) conservation. For flow calculation, the water volume of each storage is calculated by:

$$\frac{d{V}_i}{dt}=Q_{in,i}-Q_{out,i}$$ (16)

Where dV_i/dt is the change in water volume over time in compartment i, Q_in,i is inflow into the storage of compartment i and Q_out,i is the outflow from the storage of compartment i. Q_in,i is either the model input (e.g., precipitation, evapotranspiration) or it is given by the outflow from a connected storage. Q_out,i is given by the linear outflow from the storage as defined in equation (15).

Fig 7.

Rainfall-discharge model of a karst aquifer with linear storages for the recharge (soil and epikarst) system, the diffuse flow (matrix) system and the conduit flow system (from Butscher C, Huggenberger 2008).

Butscher and Huggenberger (2008) used such a rainfall-discharge model to estimate the sensitivity of a karst spring to contamination. Other applications include the work of Fleury et al. (2007) to model the functioning of a karst aquifer in Southern France, and Geyer et al. (2008) to quantify the temporal distribution of recharge in karst systems from spring hydrographs.

The main advantage of rainfall-discharge models over distributed modeling approaches is the relatively low data need. For example, the flow dynamics of a karst spring can be modeled based on data provided by a weather station in the catchment and discharge monitoring at the spring (e.g., Butscher and Huggenberger 2008). The modeling does not require hydraulic head data or the knowledge of the geometry of the karst conduits. Such information is often costly to obtain and may require borehole drillings and geophysical investigations. In contrast to hydrograph-chemograph analysis, the approach allows the assessment of the time-dependent response of the karst system under variable hydrological conditions. However, the lumped modeling approach is very limited in assessing the spatial distribution of hydrological processes (e.g, distribution of contaminants in the aquifer).

4.1.3. Soft Computing Methods

Soft Computing methods such as fuzzy logic, genetic algorithm, and Artificial Neural Networks (ANNs) are widely used in hydrological studies and also to simulate flow discharges from heterogeneous aquifer systems. These methods construct computationally intelligent systems capable of imitating the human reasoning and learning process. Soft computing methods have been used in karst systems to represent the transformation of rainfall into discharge in the aquifer system. In fuzzy systems, relationships are represented explicitly in the form of if-then rules, while in Artificial Neural Networks relationships are implicitly encoded within the networks (Kourtulus and Razack 2010). Fuzzy set theory could be developed to incorporate imprecise data into transient groundwater flow simulation. Fuzzy numbers are used to represent imprecise parameters as a measure of the uncertainty of input data (Dou et al. 1997a, Dou et al. 1997b).

An ANN works as an intelligent nonlinear input-output model, which gains knowledge from experiences to solve new problems. It is defined as a network of connected neurons, where each neuron receives an array of input signals, processes them and transforms it into a single output signal. The neurons are arranged in different layers (an input layer, hidden layers and an output layer). The measurable variables of daily rainfall data and discharge data are used as model inputs. The input data are used for calibration (training and validation) and for a prediction test of the ANN model. A training period is necessary to establish the connections among the neurons during which the ANN learns more and more about the presented data (input-output relationship). The validation phase is considered to stop the training early and to prevent over-training of the network by probable noises in the data. Before using the model for forecasting purposes, estimated outputs by the calibrated ANN must be compared with known outputs (Kurtulus and Razack 2007).

ANN models were used to determine the influential parameters of aquifer outflow, and for simulation and forecasting of spring discharge in karstic and fractured porous media (Lallahem and Mania 2003, Hu et al. 2008, Sepúlveda 2008). Kurtulus and Razack (2007) demonstrated the ability of ANNs to model the behavior of rainfall-discharge relationships of the La Rochefoucauld karstic aquifer in France. They developed a multi-layer feed-forward ANN model with Levenberg Marquart back-propagation training algorithms. The ANN model used raw daily rainfall data (instead of effective rainfall) as input and resulted in predicted daily discharges to observed discharges that were statistically well comparable. Furthermore, the predicted hydrograph adequately followed the shape of the observed hydrograph. ANN models also have deficiencies, e.g. their application struggles with less accurate or ambiguous input data and a fuzzy system might then work better (Moghaddamnia et al. 2009, Tabari et al. 2012). Kurtulus and Razack (2010) compared the capability of fuzzy logic and Artificial Neural Networks for modeling non-linear heterogeneous karst aquifers and developed neuro-fuzzy systems by combining the semantic transparency of rule-based fuzzy systems with the learning capability of neural networks.

4.2. Distributed Models

Distributed models discretize the model domain into a grid of homogeneous sub-units. Each sub-unit is assigned specific hydraulic properties (parameters), and specific conditions are defined at the model boundaries. The model numerically solves the differential flow and transport equations for the model domain. The boundary conditions and hydraulic parameters can be spatially variable. Boundary conditions and certain hydraulic parameters (e.g., recharge) can also be temporally variable. The need to define spatially distributed hydraulic parameters and boundary conditions requires much more extensive investigations compared to lumped models.

The challenge of distributed modeling approaches to represent karst groundwater systems is to cope with the high spatial heterogeneity (matrix, fractures and conduits) of karst aquifers. Approaches focus on the fracture or conduit network or on treating the matrix as impermeable blocks, or they only include aquifer porosity ignoring high permeability features, or they consider both. Table 2 gives an overview of the different approaches and the various names used in the literature.

Table 2.

Differently named distributed modeling approaches in the literature

Modeling Approach	Other Names	Type
Equivalent Porous Medium Approach (EPM)	Single Continuum Porous Equivalent Approach (SCPE) Heterogeneous Continuum Approach Distributed Parameter Approach Smeared Conduit Approach Single Continuum Approach	Distributed
Double Porosity Model (DPM)	Double Continuum Approach (DC) Double Continuum Porous Equivalent Approach (DCPE)	Distributed
Discrete Fracture Network Approach (DFN)	Parallel Plate Model Two types: Discrete Singular Fracture Set Approach (DSFS) Discrete Multiple Fracture Set Approach (DMFS)	Distributed
Discrete Channel Network Approach (DCN)	Discrete Conduit Network Approach (DCN)	Distributed
Hybrid Model (HM)	Combined Discrete-Continuum Approach (CDC) Combined Single Continuum - Discrete Fracture Set Approach (SCPE-DSFS)	Distributed
Hydrograph-Chemograph Analyses	Single Event Methods	Lumped
Linear Storage Models	Rainfall-Discharge Models Time Series Analyses Box Models	Lumped
Soft computing Methods	Computationally Intelligence Methods	Lumped

Sauter et al. (2006) reviewed the different approaches and discussed their advantages and disadvantages in terms of the investigation effort, practical applicability and capacity to simulate heterogeneities; the approaches are discussed in following sections (Figure 8).

Fig 8.

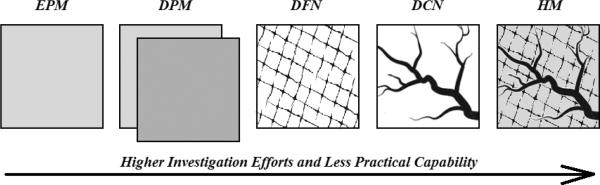
Distributed modeling approaches in karst aquifers

4.2.1. Equivalent Porous Medium (EPM)

The simplest distributed modeling approach is the Equivalent Porous Medium (EPM) approach. It treats the fractured rock with conduits as an equivalent porous medium, using bulk parameters instead of the properties of the matrix and individual fractures and conduits (Lapcevic et al. 1999). In karst systems, the transport of contaminant depends primarily on karst network architecture. Therefore, the EPM approach is very limited in reproducing the complex processes of pollutant propagation in karstic aquifers. EPM models have been successfully used to simulate groundwater flow on a regional scale and nonpoint source contaminant transport in slightly karstified aquifers (e.g., Barrett and Charbeneau 1996). EPM models have also been studied and examined in the field by other authors (e.g., Ryder 1985; Greene 1992; Kuniansky 1993; Teutsch 1993; Angelini and Dragoni 1997; Keeler and Zhang 1997; and Larocque et al. 1999). However, EPM models are limited in many applications by their reduced ability to simulate point source contaminant transport, especially at intermediate or local scales (Huntoon 1995). They do not account for strong heterogeneity of karst aquifers and do not simulate the local direction and rate of groundwater flow, because major conduits are not explicitly represented in the models and turbulent flow in conduits is not accounted for (Thrailkill 1986; Kuniansky and Holligan 1994; Teutsch and Sauter 1998; Kuniansky et al. 2001; Scanlon et al. 2003). EPM models are therefore not suitable for highly karstified aquifers (Teutsch 1993; Keeler and Zhang 1997; Scanlon et al. 2003).

EPMs solve the continuity equations (e.g., Darcy's law) valid for conditions when the velocity of groundwater is slow (laminar flow regime). Such conditions are typically met when pore sizes are small (diameter<10 mm). EPM models are applicable in karst systems when the study area is large enough to be approximated by an equivalent porous medium (Pankow et al. 1986; Neuman 1987; Scanlon et al. 2003). This is the case if the grid size is equal to or smaller than a representative elementary volume (REV). A REV is the minimum volume that is large enough to represent the aquifer by a constant hydraulic parameter (e.g., porosity), independent of the location within the REV (Singhal and Gupta 1999).

The data needs for an EPM model typically includes aquifer thicknesses, horizontal and vertical hydraulic conductivities, effective porosity, dispersivity, initial and boundary conditions, recharge conditions (rainfall infiltration), evapotranspiration, riverbed hydraulic conductivity, groundwater withdrawals (pumping rates and locations), and chemical reaction rates. Table 3 summarizes typical applications of common groundwater models, among which MODFLOW is the most widely used for (equivalent) porous media, based on the evaluation by Kumar (2006). In section 5, a case study from Puerto Rico is presented to illustrate an application of the EPM approach to simulate groundwater flow and transport in karst aquifers in more detail.

Table 3.

Common groundwater models for (equivalent) porous media

Model	Dimensions	Numerical Technique	Modeling Capabilities	Applications
MODFLOW	3-D	Finite-Difference	Groundwater Flow	Confined or unconfined aquifers, flow to wells, areal recharge, evapotranspiration, flow to drains, and flow through riverbeds
FEFLOW	2-D / 3-D	Finite-Element	Groundwater Flow, Soule and Heat Transport	Complex geometric and parametric situation, phreatic aquifers, perched water tables, moving meshes, saturated-unsaturated zones, salinity dependent and temperature dependent transport
HST3D	3-D	Finite-Difference	Groundwater Flow, Solute and Heat Transport	Subsurface-waste injection, landfill leaching, saltwater intrusion, freshwater recharge and recovery, radioactive waste disposal, water geothermal systems, and subsurface energy storage
MT3D	3-D	Finite-Difference	Solute Transport	Advection in flow fields, anisotropic dispersion, first-order decay and production reactions, and linear and nonlinear sorption. It can also handle bioplume-type reactions, monad reactions, and daughter products
SEAWAT	3-D	Finite-Difference	Groundwater Flow, Solute and Heat Transport	Variable-density groundwater flow, saltwater intrusion in coastal aquifers
Chemflo	1-D	Finite-Difference	Groundwater Flow and Solute Transport	Water and chemical movement in unsaturated soils
AQUA3D	3-D	Finite-Element	Groundwater Flow, Solute and Heat Transport	Inhomogeneous and anisotropic flow conditions, transient transport of contaminants and heat with convection, decay, adsorption and velocity-dependent dispersion.
3DFEMFAT	3-D	Finite-Element	Groundwater Flow and Solute Transport	Infiltration, wellhead protection, agricultural pesticides, sanitary landfill, radionuclide disposal sites, hazardous waste disposal sites, density-induced flow and transport, saltwater intrusion

4.2.2. Double Porosity Model (DPM)

To better account for the dual flow characteristic of karst aquifers, Double Porosity Models (DPM) can be employed. DPM uses one continuum with relatively small hydraulic conductivity but high storativity (usually matrix) and another overlapped continuum with high hydraulic conductivity but small storativity. Each continuum has separate flow equations, and coupling of the two continua is performed with adding a source/sink term in both equations. The two continuums are linked via flux exchange at the grid nodes (Teutsch and Sauter 1998; Lapcevic et al. 1999), which depends on a linear exchange term and the difference in hydraulic potential (Sauter et al. 2006). The approach is applicable to moderately-to-highly karstified systems and can also be used to simulate contaminant transport. For example, DPMs have been successfully used for spring discharge and water table fluctuations simulation (Teutsch 1993) and tracer transport simulation. DPM does not require knowledge of the geometry of conduits (Teutsch 1993; Sauter 1993), and are therefore applicable if details of the aquifer geometry are not available (Teutsch and Sauter 1998). While DPM are capable of reproducing the dynamics of karst systems in terms of slow flow in the matrix and fast flow in the conduit network, they cannot be used to locate them in the aquifer. Therefore, DPM may be used to simulate a contaminant breakthrough at a spring or well, but they are limited in simulating the spatial distribution of a contaminant in the aquifer.

4.2.3. Discrete Fracture Network (DFN) and Discrete Conduit Network (DCN)

Discrete Fracture Network (DFN) models are used to simulate flow and transport in aquifers within individual fractures or fracture sets (Berkowitz 2002; Cacas et al. 1990). Fractures were simplified to one-dimensional elements in two dimensional matrix elements (Sudicky and McLaren 1992), or also as two dimensional planes in three dimensional matrix blocks (Therrien and Sudicky 1996; Graf and Therrien 2007a; Graf and Therrien 2007b; Weatherhill et al. 2008). The DFN approach assumes negligible permeability for the rock matrix and attributes flow and transport only to the fractures. The application of this approach depends on availability of detailed information on fracture geometry (Sauter et al. 2006). Both laminar and turbulent flow conditions can be accounted for in fracture flow.

Long et al. (1985) developed a model for steady flow in 3D networks of fractures with disc shape discontinuities that are set randomly in an impermeable matrix with any desired distribution of aperture, radius orientation, and density. A mixed analytical-numerical technique was used to calculate the steady flow in the model grid of nodes (intersections between discs) as a function of the average head at each node, assuming that each node is a source (or sink) of uniform strength. A set of mass balance equations was constructed to calculate flux between adjacent nodes and was solved for the average head at each node. Similarly, Andersson and Dverstorp (1987) investigated flow through a network of discrete fractures using the DFN approach. They estimated the mean fracture radius, fracture orientation parameters, and fracture density with observing real fractures on a wall. They developed a numerical model to generate a fracture network of desired statistical properties. Large fractures and high fracture density implies good network interconnectivity that affect the variance in the flow. Dverstorp et al. (1992) used the DFN approach to simulate solute transport through sparsely fractured rock and calibrated the model with a tracer test as a case study in Sweden.

Similar to the DFN approach, the discrete Conduit Network (DCN) approach approximates flow in a karst aquifer by flow in interconnected conduits situated in an impermeable matrix. The conduits are typically represented by 1D or 2D elements in a 2D or 3D domain, but may be attributed with properties that account for their 3D nature, such as the conduit diameter, assuming a circular shape. Flow in the conduit system is typically turbulent. The approach requires the network geometry to be determined by either direct observations or geometric transformations from stochastic discrete conduit networks. Jeannin (2001) presented a DCN model to simulate the hydraulics of a variably saturated large cave system in Switzerland.

4.2.4. Hybrid Models (HM)

Hybrid models (HM), or coupled continuum pipe flow (CCPF) models, integrate discrete models (DCN, DFN) and equivalent porous media models. HM were first developed by Király and Morel (1976), considering both conduit and matrix permeability in a karst system by using a finite difference method to simulate conduits and fractures as 1-D or 2-D elements located in a low permeability 3-D matrix. Further early applications include the work of Király (1985, 1988) and Király et al. (1995). Embedding discrete high conductivity features within a low permeability matrix continuum improves the pure continuum approach by introducing a spatially distributed high hydraulic conductivity network for the whole model area. Teutsch and Sauter (1998) suggested that the investigation efforts needed to use this modeling approach are between continuum models and discrete models. Examples of HM include the coupled continuum-pipe flow and reactive transport code CAVE (Carbonate Aquifer Void Evolution) (Liedl et al. 2003). Hybrid models similar to CAVE were also developed or used by other authors, e.g. Annable and Sudicky (1998), Kaufmann and Braun (2000), Bauer et al. (2000, 2003), Birk et al. (2003), Király (1998) and Liedl et al. (2003).

Water mass exchange between the continuum (matrix rock) and the discrete conduit system is modeled by a first order exchange rate method. The exchange rate is linearly proportional to the head difference between the matrix rock and conduit system, and modeled flow is highly sensitive to the chosen exchange parameter (Barenblatt and ZheltovIu 1960; Cao et al. 1988; Sauter 1992; Teutsch 1989). The exchange parameter is difficult to determine and is a lumped parameter that entails modeling uncertainties. Hu (2010) claimed that HM usually overestimate flow and head in the matrix and underestimate solute transport in the conduit system. HM are mostly used in synthetic situations to investigate processes related to flow, transport and dissolution dynamics in karst aquifers. There are only a few studies (Hill et al. 2008) so far that show the applicability of HM through field studies.

The conduit flow module implemented in CAVE has recently been further developed and is released as the Conduit Flow Process (CFP) for the well-known US Geological Survey (USGS) flow model MODFLOW-2005 (Shoemaker et al. 2008). CFP can be run in three modes. In mode 1, CFP represents the conduit system with a discrete pipe network in which the Darcy-Weisbach equation for turbulent flow and the Hagen-Poiseuille equation for laminar flow are used to calculate flow within fully or partially water-filled pipes. Major input parameters in mode 1 are the position, diameter, tortuosity, and roughness of the conduits, and a conduit wall exchange parameter. Mode 2 simulates flow within preferential flow layers. Also in this mode, CFP can switch between laminar and turbulent flow. Mode 3 is a combination of the first two modes and allows simultaneous simulation of flow through a discrete pipe network and preferential flow layers. Reimann and Hill (2009) examined the CFP code by performing benchmark tests for laminar and turbulent flow in a single conduit surrounded by a matrix. They compared the performance of CFP mode 1 and a corresponding EPM that considers the bulk properties of the matrix and conduit networks using MODFLOW 2005, and concluded that considering turbulent flow in a discrete conduit network model improves the performance of the model, especially during extreme hydrological condition such as low recharge conditions. Presently, CFP cannot simulate solute transport or chemical reactions.

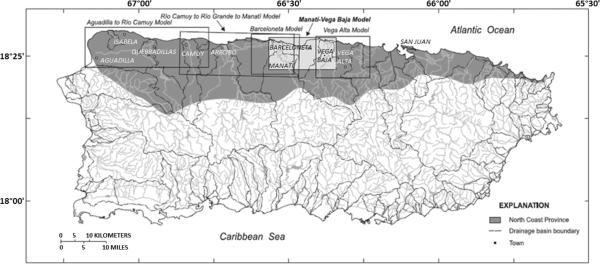
5. CASE STUDY: North Coast Limestone aquifer system of Puerto Rico

This section briefly introduces the hydrogeology of the North Coast Limestone Aquifer in Puerto Rico and various existing models to assess groundwater flow and transport in this area (Figure 9). Focus is placed on the Vega Alta region to illustrate the application, performance, and limitations of an EPM modeling approach to evaluate the release and transport of volatile organic carbons (VOC). Puerto Rico has the highest rate of preterm birth among the states and territories of the US (Mathews and MacDorman 2011) and, at the same time, contains many sites contaminated by chlorinated solvents and phthalates (Hunter and Arbona 1995). These circumstances make this island an ideal test site for exploring the threat posed by contaminant exposure in karst areas.

Fig 9.

Puerto Rico historical modeling areas (modified from Cherry 2001)

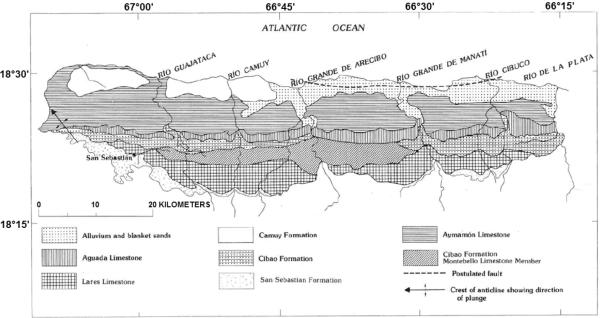
5.1. Geology and Hydrogeology of the North Coast Aquifer

The North Coast Aquifer System of Puerto Rico consists of a series of limestone formations with interbedded siliciclastic units that have been deposited on a shallow platform during Oligocene and Miocene, and emerged from the sea in Pliocene about 4 million years ago. Structurally, the rocks form a gently North dipping wedge, abutting southward against a volcanic mountain chain and thickening northward to about 1,400 m by the seashore (Giusti 1978). Four generalized hydrogeological units are distinguished that include the upper water-table aquifer, the middle confining unit, a lower confined aquifer, and a basal confining unit (Renken et al. 2002). The highly permeable Aymamón and Aguada Limestone (Figure 10) make up the upper aquifer (Renken et al. 2002). These units range from chalky beds on the bottom of the Aguada to pure limestone at the top of the Aymamon Formation (Monroe 1980), and extend from the land surface to depths of up to 330 m below land surface (Rodríguez 1995). They show highly variable porosity and permeability with high permeability contrasts in short distances reflecting the variable distribution of conduit porosity. The middle confining unit consists of clay and marl contained within the upper Cibao Formation. The lower aquifer occurs within various members of the Cibao Formation (Montebello, Quebrada Arenas, and Rio Indio Limestone Members), the Mucarabones Sand, and the Lares Limestone (Figure 10). The lower confining unit consists of the siliciclastic San Sebastian Formation. Groundwater enters the system through surface infiltration and direct injection of runoff into karstic conduits via sinkholes. Groundwater in the upper and lower aquifers generally flows northward toward the Atlantic Ocean. Rodríguez (1998) characterized several springs of the aquifer system as conduit type springs that are interconnected by an integrated conduit network.

Fig 10.

Geologic formations of the north coast limestone, Puerto Rico (modified from Giusti 1978)

Hydrological investigations (Giusti and Bennett 1976; Rodríguez 1995) suggest that water-bearing conduits are present between Rio Camuy and the Aguadilla area (Figure 9), although the importance of conduits for groundwater flow was not evaluated. Rodríguez and Hartley (1994) verified the presence of caverns in test wells drilled in Hatillo and Isabela in the north and northwest of Puerto Rico. Using aerial photographs and geophysical methods, Rodríguez and Richards (2000) investigated the Rio Camuy to Aguadilla area to detect the presence of conduits and probability of conduit controlled groundwater flow. The exact location of highly transmissive features such as cavities, conduits and fractures in this area, however, is uncertain.

5.2. Existing Models of the North Coast Aquifer

In the last two decades, various models were developed to simulate groundwater flow in different regions across Puerto Rico (Figure 9). None of the models relied on any subsurface hydrological tracer data, which represents a serious flaw in the models (in fact no systematic groundwater tracing efforts have ever been undertaken along the north coast of Puerto Rico). All of the models use an EPM modeling approach, neglecting the impact of conduit flow on groundwater hydraulics. Measurements from well tests indicate a high variability of aquifer transmissivity due to preferential flow through fractures and conduits. In view of this, using an EPM approach implies a simplification that assumes “laminar flow everywhere and an effective transmissivity that is uniform throughout each cell of the model” (Kuniansky and Holligan 1994).

Torres-González et al. (1996) developed a MODFLOW (McDonald and Harbaugh 1988) model in north-central Puerto Rico between the Río Grande de Manatí and Río Cibuco and between the Río Cibuco and Río de la Plata (Figure 10). Torres-González (1985) simulated flow in an aquifer near Barceloneta also using the MODFLOW computer code. The goal of this simulation was to study the effect of aquifer stress events such as precipitation, stream-water infiltration, and groundwater withdrawal on the water balance of the limestone aquifer. It was concluded that, if the model could account for localized highly transmissive features (conduit network), more accurate hydraulic heads could be computed. Cherry (2001) developed a MODFLOW model of the Manatí-Vega Baja aquifer. The model was used to simulate historical changes in the potentiometric groundwater surface and to model the water balance in order to estimate the impact of groundwater withdrawals and large-scale dewatering on the water level in the aquifer.

5.3. The EPM Model for the Vega Alta Aquifer

The region of Vega Alta, with an area of about 80km² and a population of 40,000 inhabitants, is located in the east of the North Coast Limestone aquifer system west of the capital San Juan (see Figure 9). In March1983, USGS realized that water samples from public water supply wells in the Vega Alta aquifer had been contaminated with VOCs, among which trichloroethylene (TCE) had the highest concentration (Guzmán and Quiñones 1984). To evaluate the TCE contamination and potential remediation scenarios, various hydrogeologic investigations (e.g., Gómez and Torres-Sierra 1988) were performed in the Vega Alta area in the last two decades. The Vega Alta landfill and an industrial park have been recognized as possible sources for TCE and other VOCs.

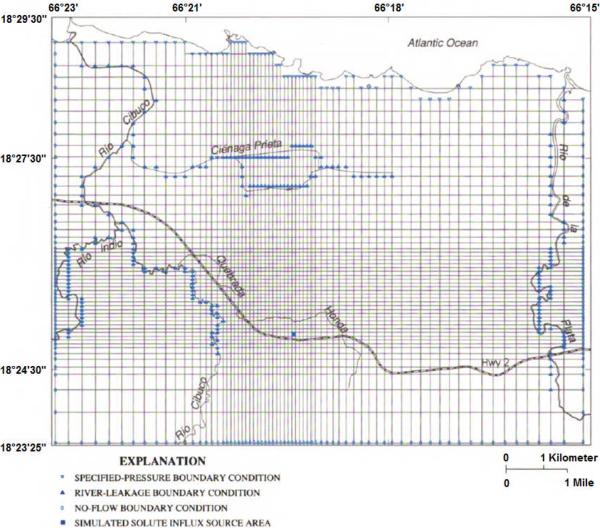
To evaluate the efficiency of remedies to reduce and control the TCE plume, Sepúlveda (1999) developed a three dimensional groundwater flow and solute transport model using the USGS computer code HST3D (Kipp 1987). The rectangular modeling area of about 13716 × 10668 m is bounded by the low permeability Cibao Formation in the South, the Atlantic Ocean coast in the north, the river Rio de la Plata in the west and the river Rio Indio in the east (Figure 11). The thickness of the karst aquifer increases from the south (southern karst uplands) to the central model area (karst upland plateau), and subsequently decreases to the coastal plane in the north. Based on similar hydraulic characteristics and TCE concentrations, the Vega Alta aquifer was divided into six layers with different thicknesses.

Fig 11.

Top element layer of the Vega Alta HST3D model, grid design and boundary conditions (modified from Sepúlveda 1999)

The initial distribution of hydraulic heads and of TCE concentrations were specified using well observation and water sample data. The eastern and western boundaries of the model were set as no-flow boundary conditions (BC) because of the predominantly northward flow in the groundwater system. A no-flow BC was also imposed along the southern boundary, where the strata are bound by the low permeability Cibao Formation, and on the aquifer bottom, which is underlain by the Cibao formation toward the south and by the saltwater interface toward the northern area of the system. A constant head BC was applied to the northern boundary along the coastline. Major streams were included as a transfer (leakage) BC based on river stage measurements at two stream gage stations.

Horizontal hydraulic conductivities of the aquifer were determined by slug and specific-capacity tests, ranging between 0.061 and 292.6 m/d. Generally, conductivities were higher near the water table than in deeper zones of the aquifer. The transmissivity, estimated by multiplying the thickness of different zones by its horizontal hydraulic conductivity, exceeded 1858 m²/s in the karst upland plateau.

Among possible TCE sources, the northeastern area of an industrial park was considered as the only TCE source. Based on water level and TCE concentration data, the Vega Alta model was calibrated for flow (net recharge, hydraulic conductivity, riverbed vertical conductivity, effective porosity) and transport parameters (dispersivity, dimensionless distribution coefficient, TCE influx from the source).

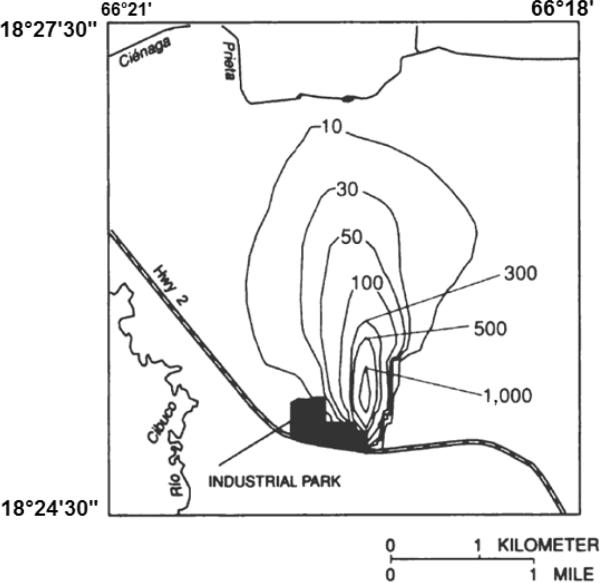
Four remediation scenarios were simulated to assess remedial alternatives designed to reduce TCE contamination in the aquifer and to restore the aquifer for public-water supply. The remedial alternatives consisted of different scenarios for the location and rate of extraction wells. Comparison of their performance was based on the amount of TCE mass removed from the aquifer at the end of a 30-year simulation period. Figure 12 shows the extent of the TCE contaminant plume without remediation activities in March 2022, and simulated heads are shown in Figure 13.

Fig 12.

Simulated TCE concentration contours (in μg/L) without remedial alternatives (no-action scenario) in the Vega Alta aquifer in March 2022, Puerto Rico (modified from Sepúlveda 1999)

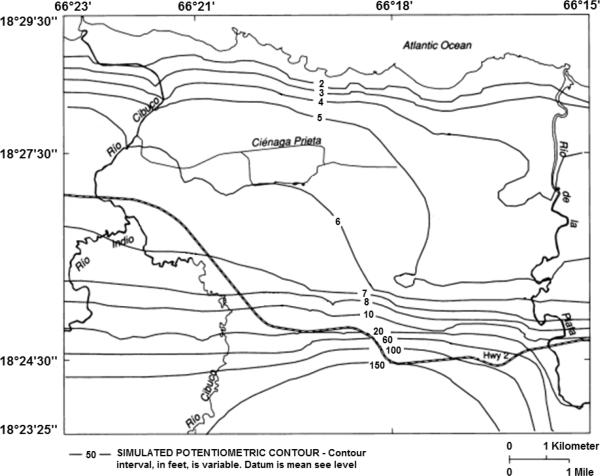
Fig 13.

Simulated and measured heads contours (in feet) at the top layer of the Vega Alta model, Puerto Rico, April 1992 (modified from Sepúlveda 1999). 1 foot = 0.3048 m

5.4. Strengths and Weaknesses of the EPM Approach for Modeling Flow and Transport in the Vega Alta Aquifer

Using an EPM approach, the model by Sepúlveda (1999) assumes that the hydraulic properties (e.g., hydraulic conductivity) are homogeneous within a limited number of aquifer regions, and groundwater flow can be described using Darcy's law (laminar flow). The North Coast Karst Aquifer is known to be highly karstified and having developed a distinctive conduit network (Rodríguez 1998; Giusti and Bennett 1976; Rodríguez 1995; Rodríguez and Hartley 1994; Rodríguez and Richards 2000). In addition, the contamination in the Vega Alta region is a point source type pollution (e.g., Gómez and Torres-Sierra 1988). EPM models, which do not account for preferential flow in the conduit network, have limited abilities to simulate point source contaminant transport in karst areas, especially at local and intermediate scales (e.g., Huntoon 1995; Thrailkill 1986; Kuniansky and Holligan 1994; Teutsch and Sauter 1998; Kuniansky et al. 2001; Scanlon et al. 2003).

The simulations are well suited to address general groundwater flow towards observation wells and contaminant concentrations in these wells under hydraulic conditions present during observation. The existence of preferential flow paths in karst conduits with unknown location and properties, however, leads to highly irregular spatial distribution of the contaminant in the system that cannot be recognized and simulated using the EPM approach. In addition, contaminant transport may be temporally highly variable under different flow conditions (storm flow vs. base flow conditions) resulting in temporally highly variable contaminant concentrations in the wells. Both the modeling approach (EPM) and the temporal resolution of the transient model (5 periods within 2 years and 3 months) limit the applicability of the model to quantify actual contaminant transport. Consequently, estimates of contaminant release and of the amount (mass) of the contaminant present in and extracted from the aquifer by pumping, remain uncertain.

A better assessment of the temporal variability of flow and transport conditions would be supported using a DPM modeling approach, where matrix flow and transport is attributed to one porous medium continuum, and conduit flow to a second porous medium continuum. Such an approach would require aquifer recharge and hydraulic head and contaminant concentration data with high temporal resolution (in karst areas typically on the order of one measurement per day). The simulation of spatially highly heterogeneous groundwater flow and contaminant transport in karst conduits would require a combination of a continuum approach for the rock matrix with a discrete conduit network approach (hybrid approach, coupled continuum pipe flow model; see section 4.2.5). However, the large challenge to determine the location and properties of the conduit network remains a problem that, so far, has not been satisfyingly resolved in karst hydrogeology for an actual field site.

6. CONCLUSIONS

Groundwater flow and contaminant transport models are a widely used tool in water resources management, quality and risk assessment, and remediation. Modeling karst groundwater systems is particularly challenging, because of their original and highly heterogeneous characteristics, which is typically expressed in the presence of a conduit network. This review paper gives an overview of existing concepts, mathematical descriptions and modeling approaches of karst groundwater systems. The often used equivalent porous medium approach is presented in more detail, using an example from the North Coast Aquifer in Puerto Rico. The goal of this review is to help researchers decide which modeling approach is preferable for an actual project, based on available data and the purpose of the study.

Spatially lumped models have the great advantage that the heterogeneous structure of the karst aquifer does not need to be known. Hydraulic data requirements are also low compared to spatially distributed models. Spatially lumped models can be used, for example, to make predictions about spring water quality based on recharge and spring discharge data. They are not capable, however, of assessing the spatial distribution of the water quality.

Spatially distributed models are preferable if groundwater quality parameters must be assessed at (many) different locations within an aquifer. This may include, for example, simulating the development of a contaminant distribution. The various existing approaches account to a different degree for the presence of a conduit network. While continuum approaches are limited in representing the processes occurring in the conduit system, they are nevertheless often employed because of little information about the conduit system. Hybrid models that combine a continuum approach to represent matrix flow with a discrete network approach to represent conduit flow are best suited to simulate the actual physical processes of interacting matrix and conduit flow. However, this approach is most demanding with respect to both data requirements and modeling efforts, as well as computational costs.