Agent-based models in translational systems biology

Abstract

Effective translational methodologies for knowledge representation are needed in order to make strides against the constellation of diseases that affect the world today. These diseases are defined by their mechanistic complexity, redundancy, and nonlinearity. Translational systems biology aims to harness the power of computational simulation to streamline drug/device design, simulate clinical trials, and eventually to predict the effects of drugs on individuals. The ability of agent-based modeling to encompass multiple scales of biological process as well as spatial considerations, coupled with an intuitive modeling paradigm, suggests that this modeling framework is well suited for translational systems biology. This review describes agent-based modeling and gives examples of its translational applications in the context of acute inflammation and wound healing.

THE ‘TRANSLATIONAL’ CHALLENGE OF BIOLOGY’S MULTIPLE SCALES

The sheer volume of biomedical research threatens to overwhelm the capacity of individuals to process this information effectively. In particular, there are significant barriers to the effective integration of discovered knowledge that arise from both the nature of biological systems and the structure of the biomedical research community. What is needed is the development of effective methodologies for breaching these barriers to understanding, or more precisely, there is an acute need to translate knowledge both ‘vertically’ from the bench to the bedside, and be able to link ‘horizontally’ across multiple researchers from various disciplines focused on different diseases. We note that the traditional use of the term ‘translational research’ refers primarily to the ‘vertical’ movement of knowledge from bench to bedside. However, given the nested, multiscale organization of biological systems and the barriers to understanding arising from that structure, the restriction of the term ‘translation’ to a narrow focus belies the scope of the challenge facing the biomedical research community. Therefore, we will use the term ‘translation’ to refer to the transcending of these barriers wherever they may manifest. Furthermore, it should be noted that there are different types of ‘scale’ in biomedical research. These include multiple levels of organization (gene → protein/enzyme → cell → tissue → organ → organism),¹ or of abstraction.² For instance, knowledge is generated from research at multiple levels of organization, and the existence of these multiple levels presents significant challenges to the movement, application, and translation of mechanistic knowledge generated at one organizational level to phenomena observed at a higher level. Furthermore, the organization of the biomedical research community mirrors the multiscale structure of biological systems, where specialized research domains have evolved with focus on the processes at one particular level, but with little, if any, connection to adjacent processes and phenomena.¹ This inherently fragmented structure has led to a disparate and compartmentalized research community and resultant disorganization of biomedical knowledge. The consequences of this disconnect are seen primarily in difficulties in developing effective therapies for diseases resulting from disorders of internal regulatory processes. In these settings, knowledge of internal mechanistic processes has not provided adequate insight into the behavior of the system as a whole. Examples of such diseases are cancer, autoimmune disorders and sepsis, all of which demonstrate complex, nonlinear behavior. Moreover, attempts at developing therapies for these diseases have highlighted the epistemological barriers to inferences of cause and effect that result from such complexity,^3,4 and therefore require the development of translational methodologies to overcome these barriers.

AGENT-BASED MODELING: DYNAMIC KNOWLEDGE REPRESENTATION

What is needed, then, is a means by which the mechanistic information that is generated at one level of basic science research can be integrated with concurrent parallel processes to produce recognizable phenomenological behaviors of the greater system as a whole. This urgent need requires methods of formalizing the synthesis process of science, such that discrete and partitioned knowledge can be represented dynamically to bring hypotheses to ‘life,’ which in the clinical setting means the generation of improved therapies for the complex diseases that vex both modern, industrialized societies as well as developing nations. Mathematical modeling and computer simulation offer a method for achieving this translational goal.^3,4 More specifically, computer modeling can be seen as a means of dynamic knowledge representation that can form a basis for formal means of testing, evaluating and comparing what is currently known within the research community.⁵ In this context, dynamic computational models can be considered a means of ‘conceptual model verification,’ by which mental or conceptual models generated by researchers from their understanding of the literature—and used to guide their research—can be instantiated computationally and executed so that the behavioral consequences of the researcher’s belief structure/hypothesis can be evaluated.^5–7 This rapid cycle of prototyping and testing holds the promise of bringing to biomedicine the precision and efficiency inherent to engineering disciplines.

Agent-based modeling is a rule-based, discrete-event and discrete-time computational modeling methodology that employs computational objects that focuses on the rules and interactions among the individual components (‘agents’) of system.^8–11 The goal of this type of simulation is the generation of populations of those system components and simulation of their interactions in a ‘virtual world’, to create an in silico experimental model. It should be noted that agent-based models (ABMs) are not inductive models, as are most mathematical and computational biomedical models, insofar that they are not based on patterns of data. Inductive models start with a set of data and make inferences with respect to the mechanisms that might lead to that data. ABMs, on the other hand, start with mechanisms or rules for behavior (albeit hypotheses in themselves) and seek to reconstruct through the computational instantiation of those mechanisms the observed patterns of data. This is a critical point, because if the goal of a modeling endeavor is to find patterns in an existing dataset, then agent-based modeling is likely not the appropriate method. However, if the goal is to test the veracity of a set of identified/presumed mechanisms in a system, then agent-based modeling can be extremely useful. There are several characteristics of agent-based modeling that set it apart from other object-oriented, rule-based modeling systems (such as Petri nets or Network models):

1. ABMs easily incorporate space. Agent-based modeling has its origins in two-dimensional cellular automata. As a result, many ABMs are ‘grid-based.’ This legacy readily allows the spatial representation of the structural relationships within a system as the two-dimensional grid has been expanded into three dimensions^5,12 and hexagonical space^13,14 depending upon the needs and goals of the developed model. As a result, nonmathematicians can model fairly complex topologies with relative ease, leading to more intuitive knowledge translation into a simulation that can be manipulated, calibrated to data, and verified. The spatial nature of ABMs also supports modeling agents with ‘bounded knowledge,’ i.e., input constrained by locality rules that determine its immediate environment. The emphasis on behavior driven by local interactions also matches closely with the mechanisms of stimulus and response observed in biology. It should be noted, however, that not all ABM use physical space to define their virtual environments (for instance, ABMs of network interactions define the agent’s neighborhood via the connection network rather than physical proximity).

2. ABMs utilize parallelism. In an ABM, each agent class has multiple manifestations as computational objects forming a population of agents that interact in (a usually emulated) parallel processing environment. Differing local conditions lead to different behavioral trajectories of the individual agents, such that the heterogeneous behavior of an individual agent within a population of agents results in aggregated system dynamics. These population dynamics are the observable output of the ABM that represents higher-level system behavior. A classic example of this phenomenon is the behavior of flocks of birds, in which simulations utilizing relatively simple interaction rules among birds can lead to sophisticated flocking patterns without an overall controller.¹⁵

3. ABMs incorporate stochasticity. Many systems, particularly biological ones, include behaviors that appear to be random.^16,17 ‘Appear to’ is an important distinction, since what may appear to be random at an observational level may be fully deterministic from a mathematical standpoint. However, despite the fact that a particular system may follow deterministic rules, at the observational level it is difficult or impossible to define the rules or initial conditions within the system with only observation. ABMs address this issue via the generation of populations of agents. Probabilities of a particular behavior are determined for the population as a whole, and resulting in the determination of a probability function for the behavior of a single agent, which is in turn incorporated into the agent’s rules. As a population of agents is executed, each agent follows a particular trajectory of behavior as its behavior rules’ probabilities collapse (i.e. are resolved) as the simulation progresses. This process enables the generation of a population of behavioral outputs from a single ABM, producing system behavioral spaces consistent with population-level biological observation.

4. ABMs have a modular structure. The behavior of an ABM is largely defined by the rules of its constituent parts, its agents. New information can be added either through the introduction of new agent-types or by the modification of existing agent rules without having to reengineer the entire simulation. For instance, an ABM that is valid at one level of abstraction, but with a relatively generic cell type, is expanded to include a finer degree of detail with respect to subcategories of the generic cell type. To accomplish this new agent-classes and corresponding rules would be implemented, but the remainder of the ABM would remain essentially intact. Similarly, if there is a desire to include a new mediator into the model, this is done by creating a new cellular-state or environmental variable, along with corresponding rules, without changing core aspects of the original ABM. Finally, multiple ABMs can be aggregated, providing that their points of contact and interaction are consistent across the incorporated ABMs (see the Functional Unit Representation Method (FURM) described by Hunt et al.¹⁴ and An’s multiscale gut–lung model⁵).

5. ABMs reproduce emergent properties. Because of the parallelism, intrinsic stochasticity, and locally-constrained agent rules, a central hallmark of ABM is that they generate systemic dynamics that could not have been reasonably inferred from examination of the rules of the agents alone. This feature is termed emergent behavior. To return to the example of the bird flock, superficial observation would seem to suggest the need for an overall leader to generate flock behavior, ostensibly requiring a means of determining rules for flock-wide command and control communication. This, however, is not nature’s way; birds function on a series of locally-constrained interaction rules, and the flocking behavior emerges from the aggregate of these interactions.¹⁵ The capacity to generate emergent behavior is a vital advantage of using ABM for conceptual model verification, as it is often the paradoxical, nonintuitive nature of emergent behavior that breaks a conceptual model.

6. ABMs can be constructed in the absence of complete knowledge, keeping the rules as simple and verifiable as possible, even at the expense of some detail. Meta-analyses of existing basic research provide structure and function to the ABM.¹⁸ This process of modeling also forces the question of how much is really known. Hypothesis testing via ABM provides qualitative verification of possible outcomes given incomplete knowledge. Since mechanisms in biology are to some degree always incompletely known, ABM maps well to the means by which experimental biomedical knowledge is currently expressed. Spatially influenced combinatorial freedom among agents means that the emergent behavior has a range of stochasticity, similar to real biology. These outcomes can be subjected to statistical analysis to assess qualitative trends based on the available prior knowledge.¹⁰ It should be noted that there is a relationship between the fidelity of mapping between the ABM and its biological counterparts, and the strength of the correlation between the simulation result and the real-world behaviors. In general, a more detailed ABM will lead to a stronger correlation to the real-world and a greater confidence in the ability of the ABM to describe observable phenomena. However, it should also be noted that given the inherent incompleteness of biological knowledge, the relationship between the ABM and the reference system’s behavior will likely never rise to the level of strict prediction.

Finally, a vital aspect of the use of agent-based modeling as an integrative modeling framework that moves toward the goal of communicable dynamic knowledge representation is the ease with which biomedical researchers can translate their conceptual models into executable form.⁵ While the era of multidisciplinarily trained researchers is dawning, it is still most likely that for the foreseeable future the majority of biomedical researchers will not be extremely facile in the use of computational tools and methods. Agent-based modeling, by its object-oriented nature, has the advantage of mapping well to the means by which biomedical knowledge is currently expressed, and is generally more intuitive for nonmathematicians/computer scientists to use than alternative modeling methods such as ordinary differential equations, partial differential equations, and their variants that allow for modeling stochastic processes (see below). As such, ABMs present a low barrier to entry for researchers who can be thus empowered to ‘bring to life’ their conceptual models, with subsequent comparison to traditional in vitro and in vivo experimental results.¹⁹ In addition, since ABM are constitutive models, meaning that they are constructed from the bottom-up to instantiate mechanisms (as opposed to inductive models, in which mechanisms are inferred with the goal of explaining data), the application of agent-based modeling arises from different questions than equation-based inductive models. For instance, ABMs are not appropriate if the starting point is a mass of raw data; rather, one must have already had some idea of potential mechanisms that lead to the generation of the data. Therefore, one can envision an iterative process by which inductive models are applied to large data sets, wet lab experiments are carried out to evaluate and refine the mechanisms inferred from the inductive model, and the experimentally confirmed mechanisms are used as a basis of an ABM which would close the discovery loop by recapitulating the original data set. An excellent example of this process can be found in a recent paper by Bailey et al., in which the authors developed a multicell ABM of human adipose-derived stromal cell trafficking during acute skeletal muscle ischemia.²⁰ In this study, the authors showed that trafficking phenomena within cell populations emerged from well-vetted interactions among adhesion molecules, cytokines/chemokines, adhesion molecules, vascular hemodynamics, and the structure of the microvascular network. Their ABM reproduced key aspects of ischemia and trafficking behavior. Importantly, the authors’ simulations predicted the necessity of an unknown adhesion molecule to some of the observed phenomena, a prediction that was verified in vitro. Given the fact that intravenous delivery of human adipose-derived stromal cells is a promising option for the treatment of ischemic injury, this study may have major translational implications.

TOOLS FOR AGENT-BASED MODELING

Agent-based modeling has its origins in the fields of ecology, social science, and anthropology.^8,10 Also, the necessary components of an agent-based modeling environment require addressing certain software issues not often dealt with in more traditional object-oriented programming tools. These issues include means of emulating parallel processing, issues related to concurrency, and the development of schedulers to account for the multiple iterations that constitute an ABM run. Many ABMs are created using existing, general-purpose ABM development environments. These software packages are aimed at striking a balance between representational capacity, computational efficiency, and user-friendliness. Among the most popular ABM toolkits are Swarm (http://www.swarm.org/index.php/Swarmmain page), Mason (http://cs.gmu.edu/~eclab/projects/mason/), RePast (http://repast.sourceforge.net/), NetLogo (http://ccl.northwestern.edu/netlogo/) and StarLogo (http://education.mit.edu/starlogo/). All these platforms represent some trade-off among the triad of goals mentioned above. For an excellent review and comparison of agent-based modeling toolkits, see Ref. 21. An example of a RePast ABM can be seen in Figure 1, an example of a NetLogo-ABM is presented in Figure 2, and Figure 3 demonstrates an ABM implemented in Mason (see below).

FIGURE 1.

Description of the three zones of activity of the Basic Immune Simulator (BIS). (a) zone 1 is the parenchymal tissue zone. This represents a generic functional tissue (yellow circles represent parenchymal cell agents) that becomes infected with a virus (represented as the red, diffusing signal). If the average diameter of a cell to be approximated to be 0.01 mm, then zone 1 represents an area of approximately 1.0 mm² of tissue. 1b zone 2 is the secondary lymphoid tissue zone. Secondary lymphoid tissue includes the lymph nodes and spleen. This is the site where the lymphoid cells, represented as B cell agents, T cell agents, and cytotoxic T lymphocyte agents, reside. This is also the site where agents representing antigen presenting cells (dendritic cell agents) interact with the lymphoid agents causing them to proliferate. (c) Zone 3 is the blood and lymphatic circulation, and represents a transitional space between the site of initial infection (zone 1) and the lymphoid tissue (zone 2). As the agents in the secondary lymphoid tissue proliferate (zone 2) they migrate into the lymph/blood (zone 3) and then travel back to the initial infection site (zone 1). This ABM was created using RePast software. (Reprinted with permission from Ref 22. Copyright 2007 http://www.biomedcentral.com).

FIGURE 2.

The multi-bilayer topology of the gut–lung ABM. Cubes and spheres are cell-level agents; these agents incorporate molecular-level rule systems (scale-level 1). These rule systems result in cellular behaviors (scale-level 2). Panel (a) is the pulmonary bilayer, with aqua cubes representing pulmonary epithelial cell agents, red cubes representing pulmonary endothelial cell agents, and below are spherical inflammatory cell agents. Panel (b) is the gut bilayer, with a similar configuration, the only difference being that gut epithelial cell agents are pink. Each of these bilayers therefore represents an abstracted organ system (scale-level 3). Circulating inflammatory cell agents move between these two bilayers. Additionally, bilayer level aggregated-variables representing inflammatory mesenteric lymph and blood-borne oxygen also move between the simulated gut and lung. This interconnection models the gut–lung axis, or multiorgan cross talk (scale-level 4). This ABM was created using NetLogo software. ABM, agent-based model. (Reprinted with permission from Ref 5. Copyright 2008 http://www.biomedcentral.com).

FIGURE 3.

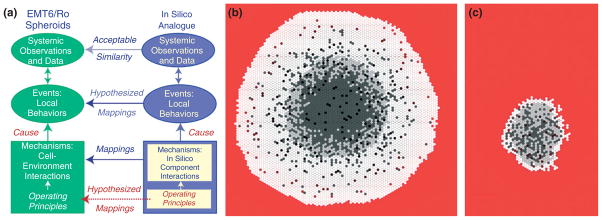
Simulated spheroid tumor growth using axiomatic operating principles (rules). Panel (a) demonstrates the relationship between the simulated multicellular tumor spheroids (SMS) and EMT6 spheroids (in vitro mouse mammary tumor cell cultures). An SMS is comprised of agents simulating quasi-autonomous cell components interacting with surrounding agents and their environment using a set of axiomatic operating principles (rules). There is a clear mapping between the SMS components and the EMT6 counterparts. Following execution, the interacting components cause local and systemic behaviors. Measures of cell and system behaviors provide a set of attributes—the SMS phenotype. These attributes were calibrated to a target set of EMT6 attributes, suggesting a semiquantitative mapping between in silico and in vitro events. Panels (b) and (c) demonstrate the behavior of the SMS, with white circles = proliferating ‘cells’; light gray circles = quiescent ‘cells’; dark gray circles = ‘necrotic cells.’ The background gradient (from red to black) represent ‘nutrient’ levels relative to the maximum level in red. Panel (b) demonstrates growth in a high ‘nutrient’ environment, while panel (c) demonstrates growth in a low ‘nutrient’ environment. This ABM was created using Mason software. (Reprinted with permission from Ref 13. Copyright 2008. ABM, agent-based model.)

Recently, a team at the University of Pittsburgh has developed a native ABM framework, SPARK (Simple Platform for Agent-based Representation of Knowledge), a cross-platform freeware (downloadable at www.pitt.edu/~cirm/spark). SPARK is specifically designed as a biomedical ABM toolkit, and as such focuses its functionality on the ABM rules suggested in Ref 1. A comparison of the above-mentioned ABM software platforms is described in Table 1, and an example of a SPARK-based ABM is described in Figure 4 (see below).

TABLE 1.

List of features of Three ABM Frameworks

	NetLogo	Repast	SPARK
Open source	No	Yes	Yes
Multiple platform	Yes	Yes	Yes
User target	General	Social science	Designed for biomedical modeling

FIGURE 4.

Chronic hepatitis C infection leads to hepatocellular carcinoma. Panel (a) shows a model simulation of viral levels after infection with hepatitis C. As reflected in clinical presentation measured by ALT levels, the typical course of infection shows an acute peak in viral load, followed by a low, chronic presence of the virus over a long period of time. Panel (b) shows the agents involved as inflammation progresses. Green represent healthy hepatocytes, gray are infected hepatocytes. As infected hepatocytes age and die, they become lighter in shade and turn white when dead, releasing virus (small black dots). The damage caused by infection and cell death provokes an inflammatory response mediated by macrophages (cyan circles), which secrete proinflammatory and anti-inflammatory cytokines. This promotes growth of the initial tumor cells (black mass in the center) over the course of years. Panel (c) shows hepatocellular carcinoma after a few decades of chronic inflammation. Tumor-associated macrophages cluster within the tumor, which develops a hypoxic core with both cancer and dead cells, and angiogenesis (red) as the mass becomes malignant. This ABM was created using SPARK software. ALT, alanine transaminase; ABM, agent-based model; SPARK, Simple Platform for Agent-based Representation of Knowledge.

USES AND APPROACHES TO AGENT-BASED MODELING

As noted above, agent-based modeling is only one of an array of methods that have been used for dynamic computational simulations. These other methods include equation-based modeling with ordinary or partial differential equations, stochastic models such as Markov chain Monte Carlo methods, and other discrete-event models such as Petri Nets or Neural Networks. It is important to recognize that each of these modeling techniques has its strengths and weaknesses, and that the modeling method chosen needs to be tailored to the question being asked of the model.²³ The scope of this article does not allow for the comprehensive comparison of all these methods; the focus is on the applicability of agent-based modeling in systems biology. Therefore, the following section will list a series of ABMs that have been used in biomedical research, with particular attention to specific insights obtained through the choice of utilizing agent-based modeling.

Intracellular Modeling

The characterization of intracellular pathways and their behavior is the original focus of systems biology. As such, the systems biology community has a long history of work and achievement in the development of mathematical models of cellular signaling and metabolic control. These models are generally based on differential equations derived from experimentally defined biochemical kinetics, and, more recently, have been executed using stochastic methods based on the Gillespie Algorithm. The use of discrete-event, particle-based modeling exemplified by agent-based modeling has not been as well explored in this arena; however, there are certain insights that have been obtained through the use of ABMs.

As mentioned above, the ability of ABMs to incorporate spatial relationships is a central bene-fit of their use, and this is particularly important in the complex, compartmentalized environment of the intracellular milieu. As opposed to the well-mixed systems found in a chemistry laboratory, enzymatic reactions within the intracellular environment are affected by the relationships not only among the reactants but also with noninvolved molecules interposed between the reactants of interest. Moreover, the presence of some components in subcellular structures, organelles, and compartments imposes further spatial constraints. Using an ABM of intracellular signaling, Ridgway et al.²⁴ demonstrated that the reaction dimension that determines biochemical kinetics within a prokaryotic cytoplasm was reduced from the expected three dimensions to nearly two. This finding has significant consequences for the dynamic modeling of control loops in which subtle changes in feedback determine the direction of a molecular switch. In another ABM of the control pathways affecting the transcription factor nuclear factor kappa B (NF-κB), Pogson et al.²⁵ demonstrated the need to account for nuclear translocation of the constitutive inhibitor of NF-κB, I-kappa-B (IκB) based on the spatial distribution and activity of the reactions, particularly with respect to the binding of IκB to actin. This mechanism has been subsequently identified in their laboratory.²⁶ Finally, it is recognized that cells are not merely bags of molecules dissolved in water, but rather that their cytoskeleton lends them a physical structure that serves as a scaffold for enzymatic components of intra-cellular pathways. This spatial concept was implemented in an agent-based architecture called Spatially Configured Stochastic Reaction Chambers and used to demonstrate that even an abstract representation of enzyme kinetics could, if sufficient component detail was included within a spatial configuration, reproduce canonical behavior at the cellular level, in this case the effect of preconditioning on the behavior of the toll-like receptor 4 (TLR-4) signaling pathway.²⁷

Cell-level Tissue Modeling

Perhaps the most obvious level of biologically-oriented agent-based modeling is that which uses cells as the primary agent level. This type of component representation provides an intuitive link between the laboratory-derived basic mechanistic knowledge and the structure of an ABM. It is therefore not surprising that the earliest examples of biomedically-relevant ABMs are focused at this level.^11,28 More details with respect to the implementation and integration of agent-based modeling with wet lab experimental procedures can be seen in Refs 5,14,29,30.

One of the earliest insights via the use of cell-level ABMs was the recognition that even abstract agent rules could produce very recognizable dynamics, and in so doing provide vital insights into the essential characterization of a disease process. To draw upon the example of modeling sepsis, an early ABM of systemic inflammation viewed the inflammatory process as being mediated and propagated by interactions at the endothelial blood interface.¹¹ This ABM further demonstrated that the differing trajectories of model-system behavior could be generated purely by altering the degree of initial perturbation, and that these four different trajectories matched the four primary clinical scenarios associated with systemic inflammatory response. This ABM also demonstrated that the mechanistic basis of inflammation was the same whether the initiating insult was infectious, as in classical endotoxin sepsis, or tissue damage, as in massive trauma. These concepts have gained general acceptance in recent years, but at the time that this ABM was created these were novel and controversial hypotheses.

As with the intracellular ABMs, cell-level ABMs are well suited to modeling pathophysiological processes that have a significant spatial component. Examples of this utility can be seen in the modeling of granuloma formation,³¹ tumor growth,^12,13,28,32 morphogenesis,^30,33–35 angiogenesis,³⁶ and wound healing.^37–39 A few highlights of this work are described below.

In the first case, the propagation of Mycobac-terium tuberculosis was modeled to demonstrate granuloma formation resulting from the control processes influencing cell-to-cell interactions.³¹ In the case of tumor growth, the ABMs developed from the Deis-boeck laboratory demonstrated the importance of cell-to-cell interactions in generating the differential zones of proliferation and senescence among tumor cells, thus also having implications with respect to the delivery and efficacy of chemotherapeutic agents.^12,28,40,41 A different approach to tumor growth by the Hunt lab focused on using the ability of agent-based modeling to produce complex behaviors from abstract rules to identify key functions associated with tumor growth^13,32 (more on this use of ABMs below). Similarly, the ability of agents to reconstruct complex spatial configurations has been beneficial in the study of morphogenesis. Cell-to-cell interactions alone have been experimentally identified as being sufficient to create morphological structures³³ and ABMs have been able to reproduce these types of behavior in silico.^30,33–35 The work of Peirce et al. on angiogenesis was able to use cellular response rules to reproduce patterns of neovascularization from vascular networks mapped from actual tissue.³⁶ Finally, the simulations of wound healing were able to shed basic insights on the spatial nature of the skin wound healing process,³⁷ to reproduce the impaired processes leading to the development of diabetic wounds and to posit potential mechanistic targets for therapeutics development,³⁸ and offer the potential for modeling individual responses to injury and therapy in vocal chord trauma.³⁹ In the impaired skin healing studies,³⁸ a simulation of normal skin healing was used to determine the phenotypic effects of diabetes-associated derangements in single factors out of a complex cascade (namely underactivation of latent transforming growth factor-β₁ or overproduction of tumor necrosis factor-α). Simulating these single derangements was associated with a host of emergent features characteristic of diabetic ulcers. Moreover, this ABM was used to test in silico the effects of both current therapies for diabetic ulcers (namely wound debridement and treatment with platelet-derived growth factor) as well as novel interventions (e.g., inhibition of tumor necrosis factor-α or provision of transforming growth factor-β₁).³⁸ In the last case, an ABM of vocal fold inflammation and healing was calibrated using data on cytokine levels in laryngeal secretions of individual human volunteers subjected to experimental phonotrauma (loud phonation). Patient-specific computational simulations were created based on baseline levels of cytokines as well as levels at 1 and 4 hours after phonotrauma. These simulations were largely capable of predicting the levels of cytokines at much later time points (24 hours), and were used as the basis for simulated vocal fold therapy.³⁹

Recently, an ABM of hepatitis C-induced inflammation and hepatocellular carcinoma was created recently using SPARK (Dutta-Moscato et al., manuscript in preparation). This model simulates the onset and progression of hepatocellular carcinoma in a patch of liver, arising from only a few cells (hypothetical cancer stem cells; Figure 4), in the presence of a low, chronic inflammatory state [Figure 4(b)]. The tissue environment of pro- and anti-inflammatory responses present in chronic infections, such as hepatitis C virus [Figure 4(a)], causes progressive tissue damage and accelerates tumor formation [Figure 4(b)]. Associated processes are also modeled, including the formation of a hypoxic core in the center of the growing tumor, as well as tumor angiogenesis [Figure 4(c)].

These examples are far from comprehensive, but are intended to give a flavor of the types of inflammation-related ABM that have been focused at the tissue level. Below, we discuss the integration of models at various scales.

Multiscale Approaches

As noted above, biological systems exhibit a multiscale organization, and transcending these scales is a primary goal of dynamic computational modeling. From a translational perspective, the payoff to linking processes at multiple scales lies in bridging studies of therapeutic targets at the molecular/cellular level to the effects of modulation of these targets at the tissue, organ, and whole-organism levels. While a two-scale accounting is intrinsic to most modeling methods, in which scale 1 = mechanism and scale 2 = mechanism consequence/output, agent-based modeling is particularly well suited to multiscale representation, as this type of modeling automatically transcends these two scales and can account for a third scale of behavior, namely population dynamics of parallel mechanism consequences/output. Indeed, there are multiple examples of multiscale modeling approaches using an ABM framework.

One approach to representing multiple scales is to view sequential levels from an anatomic standpoint. The Basic Immune Simulator (BIS) developed by Folcik et al.²² is an example of this approach. The BIS incorporates multiple tiers of tissue spaces where immunological processes occur. These tiers are labeled ‘zones’ in the BIS, and consist of zone 1, which represents generic parenchymal/peripheral tissue that is subjected to an infectious insult, zone 2, which represents regional lymphoid tissue in which the initial specialized immunological response occurs, and zone 3, a circulatory compartment that provides a conduit for immune-activated cells from zone 2 to migrate back to the site of initial insult in zone 1 (Figure 1). This model reproduces the general dynamics of viral infection, including a ‘hyperimmune’ response that is analogous to acute hypersensitivity reaction. The BIS is quite abstract, as it is intended to be a basic platform that can be shared and modified as individual researchers incorporate and test their own hypotheses. Interested readers are encouraged to examine the primary text and download the application.

The structural/anatomic approach to multiscale modeling is taken one step further with the introduction of a modular multiscale ABM architecture focusing on acute inflammation.⁵ This architecture incorporates multiple structural and anatomic spaces (e.g., endothelial and epithelial surfaces, aggregated cell-types into organ-specific tissues and finally organ-to-organ interconnections and cross talk). Furthermore, this architecture also translates knowledge across domain specialties, such as capturing mechanisms and behaviors derived from in vitro studies, leading to ex vivo tissue experiments and observations, leading to patterns of organ-specific physiology, and finally to a clinically relevant, interconnected, multiorgan physiological and pathophysiological axis (Figure 2). Interested readers are encouraged to examine the referenced text for additional details.

As mentioned above, differing biological processes may warrant differing modeling approaches, and this is especially true in terms of the differing characteristics of the multiple levels present in a multiscale model. Utilizing the advances and resources of the traditional systems biology community, Athale et al. have incorporated differential equation models describing the behavior of epidermal growth factor receptor (EGFR) as the rule sets for a cell-level ABM, and used this model to examine the dynamics of tumor growth in various cancers.^41,42 Similarly, the behaviors of certain cell populations can be modeled more efficiently using differential equations, leading to hybrid models. One such model, described by Wake-land et al.⁴³ takes the previously described ABM of systemic inflammation and applies a systems dynamics model (ordinary differential equation) to more efficiently represent the dynamics of the inflammatory life cycle. It is virtually certain that the more comprehensive and detailed models of the future will have some sort of hybrid structure along the lines of the Athale and Wakeland models.

Obtaining Essential Biological Insights

The preceding examples of biomedical ABMs have focused on implementing known mechanistic details obtained from wet lab experiments into in silico analogues of their biological reference systems. This approach represents a dynamic representation of knowledge that allows the examination of the resulting ABM behaviors as a means of evaluating the veracity of the underlying hypotheses/mental model. This type of application of agent-based modeling is generally carried out with an explicit translational goal in mind (be it translation across organizational scales, domains of expertise, or to the bedside). However, there is a slightly different use of agent-based modeling that is directed at obtaining insights into the function and actions of biological systems. The ability of ABMs to generate complex behavior from relatively simple rules allows a different tack to be applied to the perceived need for continually increasing mechanistic detail. By constructing ABMs with rules that represent core and basic functions, they may aid in identifying functional modules that represent yet another scale of organization for cellular behavior.

When this approach is used in the study of intracellular and subcellular processes, these modules may lead to the identification of potential points of biomolecular control. There are strong suggestions that while the functional modules may be internally robust, they have finely regulated control points at their articulations with other modules, essentially creating ‘bottlenecks’ that regulate the outcome of signaling events. This phenomenon has been variably described as the ‘hourglass’ or ‘bowtie’ structure of dynamic biological systems.^44,45 One example of this can be seen in an ABM of bilayer membrane structure and behavior.⁴⁶ This ABM uses a series of rules, similar to that of the canonical bird flocking ABM, to represent the interactions present among the constituent molecules of a semifluid cell membrane. This model is particularly notable for being able to reproduce the self-organization and subsequent properties of a cell membrane while ignoring the issue of polarity of the constituent molecules. Even if the balance between attraction and repulsion within a molecule is represented uniformly, the tendency to self-organize into spheroids and micelles still predominates.

The work of the Hunt laboratory presents this approach more formally and explicitly in their models of tumor spheroid growth.^13,32 Again, by concentrating on representing key functional behaviors as agent rules, Hunt and colleagues were able to identify nine key behaviors (which they term ‘axioms’) that form the necessary and sufficient set of behaviors for the development of tumor topologies (Figure 3). The identification of these ‘essential’ behavioral sets may provide a means of refining the characterization of those mechanisms to be targeted in the design of therapeutic interventions.

Cancer research has also provided examples of this use of agent-based modeling. One recent example is the work of Abbott et al.⁴⁷ I in which the authors implemented an ABM of Hanahan and Weinberg’s six ‘Hallmarks of Cancer,’⁴⁸ and predicted the most likely pathways for tumor formation, as well as other insights that have the potential to lead to new targets for clinical work. Another example is the work of the Maley laboratory that has examined the evolutionary and ecological aspects of tumor growth.⁴⁹ By using an ABM of cellular differentiation, they have identified cellular characteristics and properties that are susceptible to evolutionary forces leading to neoplastic dynamics.⁵⁰ These findings have implications with respect to the robustness of certain cellular properties to modification, and thus suggest mechanisms of tumor cell resistance to chemotherapeutic modalities.

Despite these successes, various challenges remain to the widespread use of ABM in the translational process. We discuss some of these limitations below.

CHALLENGES TO THE USE OF AGENT-BASED MODELING

In the foregoing discussion, we have highlighted the advantages of and advances made with ABM. However, this modeling framework is not without its limitations. A key limitation of ABM is shared with all computational modeling methods: the quality and reliability of the models are directly related to the reliability of the underlying assumptions of the model and the quality of their implementation during construction of the model. Given the shifting nature and intrinsic incompleteness of biomedical knowledge, the primary means of addressing this issue in the agent-based modeling community has been to emphasize transparency with respect to underlying assumptions. Toward this end, the agent-based modeling community has made significant efforts to provide detailed and explicit references to the knowledge base underlying their models, and the relationship between the in silico implementation and their biological referents (the following list is not comprehensive but provide excellent examples of this process^{11,14,27,38,51–53}).

One perceived shortcoming of agent-based modeling is the difficulty in applying formal analysis to the relationship between the agent rules and the behavior of the system. Because of the combined stochastic behavior of agents, the very feature that allows ABM to transcend the epistemological boundaries inherent to multiscale structure, it is extremely difficult to systematically analyze how each part or parameter of an ABM simulation affects the output or behavior of the ABM. This stands in contrast to equation-based modeling, for which analytical tasks such as parameter sensitivity analysis, bifurcation analysis, and behavior-space determination can be carried out using well-established procedures. The difficulty in carrying out similar procedures for ABMs can make researchers with a more traditional mathematical modeling background apprehensive in their ability to evaluate an ABM. This apprehension can be addressed by viewing ABMs as objects more akin to wet lab experimental platforms rather than more traditional, equation-based mathematical models. Using the principles of pattern-oriented analysis, in which corresponding patterns of dynamic behavior are used to relate the computational ABM to its real-world referent, ABM can be measured and analyzed in the same fashion as wet lab systems or organisms.¹⁰ In this context, the stochastic nature of ABMs actually aids in recreating the robustness of dynamic behavior seen in complex systems, perhaps a more realistic property than the ‘brittleness’ often seen in equation-based models. The downside of this characteristic, however, is that modelers using ABM must rely upon brute force computation in order to generate dense data sets amenable to statistical analysis.

On one hand, the in silico nature of ABM provides an advantage over wet lab approaches because of their ability to generate these dense and extensive data sets; electrons are much cheaper and faster than cells, animals, and reagents. On the other hand, there is a high computational cost associated with running ABM as compared to equation-based models. Current freely available ABM platforms run as emulated parallel processing systems based on a single-threaded central processing unit. The execution of an ABM in these settings requires multiple iterated computations as each discrete event is carried out, many more than for equation-based simulations. This iterative process results in significantly greater computational demands, and these increased demands constrain the size of ABM implementations that can be run in the typical academic setting. The natural solution to this bottleneck is to implement ABMs on the newest generation of high performance supercomputers and other distributed computing platforms. However, there are intrinsic properties of ABMs, namely related to spatial continuity and agent-to-agent communication, that challenge the ability to implement ABM in a distributed environment. To address this bottleneck, researchers have started to explore novel computing environments for agent-based modeling, such as using Graphical Processing Units (GPUs).⁵⁴ In addition, work has been initiated on parallelizing aspects of the SPARK code (A. Solovyev, M. Mikheev, Q. Mi, and Y. Vodovotz, unpublished observations). It should be noted that there are nontrivial modeling issues associated with parallel implementation of ABM, aside from the computer science challenges. These primarily derive from the selection of the scale of process to be distributed across the multiple processors and the consequences that decision has with respect to the mapping of the simulation behavior back to the biological referent. For instance, thus far the approaches listed above have not explored the distribution of a single agent’s execution across multiple processors, and have opted for the ‘cleaner’ distribution scale of expanding the interaction space and implementing the agents on the same level.

Other methods are also being implemented in order to increase the feasibility of large ABM-based simulations. Several groups have pursued work related to the development of ‘hybrid’ model systems, in which differential equations are used to model those aspects of a system in which mean-field approximations are valid, while ABMs are utilized where spatial heterogeneity and its effects are significant.^41,43 Additionally, methods are being developed to algorithmically increase the efficiency of the evaluation and analysis of complex, multiscale models.⁵⁵

CONCLUSION

The coming era of translationally useful computational simulations raises the potential for the development of highly predictive, personalized simulations that hold the promise of streamlining the design of therapies, simulating the clinical application of these therapies in population studies (clinical trials), and predicting the effects of drugs on individuals. Agent-based modeling, developed originally for the social sciences, has been central to this rapidly expanding field of translational systems biology. The majority of algorithms and methods utilized for dynamical simulations have been in the realm of equation-based modeling. However, developments in computational methods specific to agent-based modeling are likely to greatly increase the utility of this user-friendly approach to modeling complex biological systems.

The agent-based paradigm, incorporating encapsulation, modularity and parallelism, can provide an overarching architecture for the computational representation of biological systems. By decreasing the threshold for the general researcher to utilize computational modeling, agent-based modeling allows investigators to ‘see’ the consequences of a particular hypothesis-structure/conceptual model, such that the mechanistic consequences of each hypothesis can be observed and evaluated. This type of dynamic knowledge representation enables the instantiation of ‘thought experiments,’ i.e., trying out possible alternative solutions, so long as these hypotheses and assumptions are made explicit. This concept draws upon the experience in the Artificial Life community by creating ‘alternative worlds’ driven by these proposed rules. These models can aid in the scientific process by providing a transparent framework for this type of speculation, which can then be used as jumping off points for the planning and design of further wet laboratory experiments and measurements. It is hoped that the increasing use of this type of knowledge representation and communication will foster the further development of ‘virtual laboratories’ and in silico investigations.