The local Dirichlet process

Abstract

As a generalization of the Dirichlet process (DP) to allow predictor dependence, we propose a local Dirichlet process (lDP). The lDP provides a prior distribution for a collection of random probability measures indexed by predictors. This is accomplished by assigning stick-breaking weights and atoms to random locations in a predictor space. The probability measure at a given predictor value is then formulated using the weights and atoms located in a neighborhood about that predictor value. This construction results in a marginal DP prior for the random measure at any specific predictor value. Dependence is induced through local sharing of random components. Theoretical properties are considered and a blocked Gibbs sampler is proposed for posterior computation in lDP mixture models. The methods are illustrated using simulated examples and an epidemiologic application.

1 Introduction

In recent years, there has been a dramatic increase in applications of non-parametric Bayes methods, motivated largely by the availability of simple and efficient methods for posterior computation in Dirichlet process mixture (DPM) models (Lo 1984; Escobar 1994; Escobar and West 1995). The DPM models incorporate Dirichlet process (DP) priors (Ferguson 1973, 1974) for components in Bayesian hierarchical models, resulting in an extremely flexible class of models. Due to the flexibility and ease in implementation, DPM models are now routinely implemented in a wide variety of applications, ranging from machine learning (Beal et al. 2002; Blei et al. 2004) to genomics (Xing et al. 2004; Kim et al. 2006).

In many settings, it is natural to consider generalizations of the DP and DPM-based models to accommodate dependence. For example, one may be interested in studying changes in a density with predictors. Following Lo (1984), one can use a DPM for Bayes inference on a single density as follows:

$$f\left(y\right)={\int }_{\Omega }k(y,u)G\left(du\right),$$ (1)

where k(y, u) is a non-negative valued kernel defined on ($\mathcal{D}\times \Omega ,\mathcal{F}\times \mathcal{B}$) such that for each $u\in \Omega ,{\int }_{\mathcal{D}}k(y,u)\mathrm{d}y=1$ and for each $y\in \mathcal{D}$, ${\int }_{\Omega }k(y,u)G\left(du\right)<\infty$ with $\mathcal{D}$, Ω Borel subsets of Euclidean spaces and $\mathcal{F}$, $\mathcal{B}$ the corresponding σ-fields, and G is a finite randomprobabilitymeasure on (Ω, $\mathcal{B}$) following a DP. A natural extension for modeling of a conditional density f (y|x) for $\mathbf{x}\in \mathcal{X}$, with $\mathcal{X}$ a Lebesgue measurable subset of ${\mathfrak{R}}^p$, is as follows:

$$f(y\mid \mathbf{x})={\int }_{\Omega }k(y,u)G_{\mathbf{x}}\left(du\right),$$ (2)

where the mixing measure G_x is now indexed by the predictor value. We are then faced with modeling a collection of random mixing measures denoted as ${\mathcal{G}}_{\mathcal{X}}=\{G_{\mathbf{x}}:\mathbf{x}\in \mathcal{X}\}$.

Recent work on defining priors for collections of random probability measures has primarily relied on extending the stick-breaking representation of the DP (Sethuraman 1994). This literature was stimulated by the dependent Dirichlet process (DDP) framework proposed by MacEachern (1999, 2000, 2001), which replaces the atoms in the Sethuraman (1994) representation with stochastic processes. The DDP framework has been adopted to develop ANOVA-type models for random probability measures (De Iorio et al. 2004), for flexible spatial modeling (Gelfand et al. 2004), in time series applications (Caron et al. 2006), and for inferences on stochastic ordering (Dunson and Peddada 2008). The specification of the DDP used in applications incorporates dependence only through the atoms while assuming fixed weights. In other recent work, Griffin and Steel (2006) proposed an order-based DDP (πDDP) which allows varying weights, while Duan et al. (2005) developed a multivariate stick-breaking process for spatial data.

Alternatively, convex combinations of independent DPs can be used for modeling collections of dependent random measures. Müller et al. (2004) proposed this idea to allow dependence across experiments and discrete dynamic settings were considered by Pennell and Dunson (2006) and Dunson (2006). Recently, the idea has been extended to continuous covariate cases by Dunson et al. (2007) and Dunson and Park (2008).

Some desirable properties of a prior for a collection, ${\mathcal{G}}_{\mathcal{X}}=\{G_{\mathbf{x}}:\mathbf{x}\in \mathcal{X}\}$, of predictor-dependent probability measures are: (1) increasing dependence in G_x and G_x′ with decreasing distance between x and x′; (2) simple and interpretable expressions for the expectation and variance of each G_x as well as the correlation between G_x and G_x′; (3) G_x has a marginal DP prior for all $\mathbf{x}\in \mathcal{X}$; (4) posterior computation can proceed efficiently through a straightforward MCMC algorithm in a broad variety of applications. Although the DDP, πDDP and the prior proposed by Duan et al. (2005) achieve (1), πDDP and Duan et al. (2005) approaches are not straightforward to implement in general applications. The fixed stick-breaking weights version of the DDP tends to be easy to implement, but has the disadvantage of not allowing locally adaptive mixture weights. The kernel mixture approaches of Dunson et al. (2007) and Dunson and Park (2008) lack the marginal DP property (3). Property (3) is appealing in that there is rich theoretical literature on DPs, showing posterior consistency (Ghosal et al. 1999; Lijoi et al. 2005) and rates of convergence (Ghosal and Van der Vaart 2007).

This article proposes a simple extension of the DP, which provides an alternative to the fixed weights DDP in order to allow local adaptivity, while also achieving properties (1)–(4). The prior is constructed by first assigning stick-breaking weights and atoms to random locations in a predictor space. Each predictor-dependent random probability measure is formulated using the random weights and atoms located in a neighborhood about that predictor value. Dependence is induced by local sharing of random components. We call this prior the local Dirichlet process (lDP).

Section 2 describes stick-breaking priors (SBP) for collections of predictor-dependent random probability measures. Section 3 introduces the lDP and discusses properties. Computation is described in Sect. 4. Sections 5 and 6 include simulation studies and an epidemiologic application. Section 7 concludes with a discussion. Proofs are included in appendices.

2 Predictor-dependent stick-breaking priors

2.1 Stick-breaking priors

Ishwaran and James (2001) proposed a general class of SBPs for random probability measures. This class provides a useful starting point in considering extensions to allow predictor dependence.

Definition 1 A random probability measure, G, has a SBP if

$$G=\sum _{h=1}^N{p}_h{\delta }_{{\theta }_h},0\le p_h\le 1,\sum _{h=1}^N{p}_h=1a.s.,$$ (3)

where δ_θis a discrete measure concentrated at θ, $p_h=V_h{\prod }_{l<h}(1-V_l)$ are random weights with $V_h\stackrel{\mathrm{ind}}{~}Beta(a_h,b_h)$ independently from ${\theta }_h\stackrel{\mathrm{iid}}{~}{G}_0$ with G₀ a non-atomic base probability measure. For N = ∞, the condition ${\Sigma }_{h=1}^N{p}_h=1$ a.s. is satisfied by Lemma 1 in Ishwaran and James (2001). For finite N, the condition is satisfied by letting V_N = 1.

There are many processes that fall into this class of SBP. The DP corresponds to the special case in which N = ∞, a_h = 1 and b_h = α as established in Sethuraman (1994). The two-parameter Poisson-DP corresponds to the case where N = ∞, a_h = 1 − a, and b_h = b + ha with 0 ≤ a < 1 and b > −a (Pitman 1995, 1996). Additional special cases are listed in Ishwaran and James (2001).

2.2 Predictor-dependent stick-breaking priors

Consider an uncountable collection of predictor-dependent random probability measures, of ${\mathcal{G}}_{\mathcal{X}}=\{G_{\mathbf{x}}:\mathbf{x}\in \mathcal{X}\}$. The predictor space $\mathcal{X}$ is Lebesgue measurable subset Euclidian space and the random measures G_x are defined on (Ω, $\mathcal{B}$) where Ω is a complete and separable metric space and $\mathcal{B}$ is a corresponding Borel σ-algebra. Let $\mathcal{P}$ be a probability measure on ($\mathcal{M}$, $\mathcal{N}$ ) where $\mathcal{M}$ is the space of uncountable collections of random probability measures G_x and $\mathcal{N}$ is the corresponding Borel σ-algebra. Then, ${\mathcal{G}}_{\mathcal{X}}~\mathcal{P}$ denotes that $\mathcal{P}$ is a prior on the random collection ${\mathcal{G}}_{\mathcal{X}}$.

We call $\mathcal{P}$ a predictor-dependent stick-breaking prior (${\mathrm{SBP}}_{\mathcal{X}}$) if $G_{\mathrm{x}}\in {\mathcal{G}}_{\mathcal{X}}~\mathcal{P}$ can represented as:

$$\begin{array}{cc}\hfill G_{\mathbf{x}}& =\sum _{h=1}^{N\left(\mathbf{x}\right)}{p}_h\left(\mathbf{x}\right){\delta }_{{\theta }_h\left(\mathbf{x}\right)}\hfill \\ \hfill & \text{with}0\le p_h\left(\mathbf{x}\right)\le 1\text{and}\sum _{h=1}^{N\left(\mathbf{x}\right)}{p}_h\left(\mathbf{x}\right)=1a.s.,\forall \mathbf{x}\in \mathcal{X},\hfill \end{array}$$ (4)

where the random weights p_h(x) have a stick-breaking form, p_h(x) and θ_h(x) are predictor-dependent, and N(x) is also indexed by the predictor value x. Depending on how we form p_h(x), θ_h(x) and N(x), different dependencies among G_x are induced. Several interesting priors, such as the DDP, πDDP and the prior proposed by Duan et al. (2005) fall into the ${\mathrm{SBP}}_{\mathcal{X}}$ class. In the next section, we propose a new choice of ${\mathrm{SBP}}_{\mathcal{X}}$ deemed the lDP.

3 Local Dirichlet process

3.1 Formulation

Formulating the lDP starts with obtaining the following three sequences of mutually independent global random components:

$$\Gamma =\{{\Gamma }_h,h=1,\dots ,\infty \},\mathbf{V}=\{V_h,h=1,\dots ,\infty \},ϴ=\{{\theta }_h,h=1,\dots ,\infty \},$$ (5)

where ${\Gamma }_h\stackrel{\mathrm{iid}}{~}H$ are locations, $V_h\stackrel{\mathrm{iid}}{~}Beta(1,\alpha )$ are probability weights, and ${\theta }_h\stackrel{\mathrm{iid}}{~}{G}_0$ are atoms. G₀ is a probability measure on (Ω, $\mathcal{B}$) on which G_x will be defined and H is a probability measure on (${\mathcal{X}}^{\prime }$, $\mathcal{A}$) where $\mathcal{A}$ is a Borel σ-algebra of subsets of ${\mathcal{X}}^{\prime }$ and ${\mathcal{X}}^{\prime }$ is a Lebesgue measurable subset of Euclidian space that may or may not correspond to the predictor space $\mathcal{X}$. For a given predictor space $\mathcal{X}$, we introduce the probability space (${\mathcal{X}}^{\prime }$,$\mathcal{A}$, H) such that it satisfies the following regularity condition from which one can deduce $\mathcal{X}\subset {\mathcal{X}}^{\prime }$:

Condition 1 For all $\mathbf{x}\in \mathcal{X}$ and ψ > 0, $H\left({\eta }_{\mathbf{x}}^{\psi }\right)>0$, where ${\eta }_{\mathbf{x}}^{\psi }=\{{\mathbf{x}}^{\prime }:d({x,x}^{\prime })<\psi ,{\mathbf{x}}^{\prime }\in {\mathcal{X}}^{\prime }\}$ is defined as a ψ-neighborhood around a point $\mathbf{x}\in \mathcal{X}$ with $d:\mathcal{X}\times {\mathcal{X}}^{\prime }\to {\mathfrak{R}}^{+}$ being some distance measure.

Next, focusing on a local predictor point $\mathbf{x}\in \mathcal{X}$, we define sets of local random components for x as:

$$\Gamma \left(\mathbf{x}\right)=\{{\Gamma }_h,h\in {\mathcal{L}}_{\mathbf{x}}\},\mathbf{V}\left(\mathbf{x}\right)=\{V_h,h\in {\mathcal{L}}_{\mathbf{x}}\},ϴ\left(\mathbf{x}\right)=\{{\theta }_h,h\in {\mathcal{L}}_{\mathbf{x}}\},$$ (6)

where $\mathcal{L}\mathbf{x}=\{h:d(\mathbf{x},{\Gamma }_h)<\psi ,h=1,\dots ,\infty \}$ is a predictor-dependent set indexing the locations belonging to the ψ-neighborhood of x, ${\eta }_{\mathbf{x}}^{\psi }$, which is defined on ${\mathcal{X}}^{\prime }$ by ψ and d(·, ·). Hence, the sets V(x) and Θ(x) contain the random weights and atoms that are assigned to the locations Γ(x) in ${\eta }_{\mathbf{x}}^{\psi }$. Here, ψ controls the neighborhood size. For simplicity, we treat ψ as fixed throughout the paper, though one can obtain a more flexible class of priors by assuming a hyper prior for ψ.

Using the local random components in (6), we consider the following form for G_x:

$$G_{\mathbf{x}}=\sum _{l=1}^{N\left(\mathbf{x}\right)}{p}_l\left(\mathbf{x}\right){\delta }_{{\theta }_{{\pi }_l\left(\mathbf{x}\right)}}\text{with}{p}_l\left(\mathbf{x}\right)=V_{{\pi }_l\left(\mathbf{x}\right)}\prod _{j<l}(1-V_{{\pi }_j\left(\mathbf{x}\right)}),$$ (7)

where N(x) is the cardinality of ${\mathcal{L}}_{\mathbf{x}}$ and π_l(x) is the lth ordered index in ${\mathcal{L}}_{\mathbf{x}}$. Then, Condition 1 ensures that the following lemma holds (refer to the Proof of Lemma 1 in the Appendix).

Lemma 1 For all $\mathbf{x}\in \mathcal{X}$, N(x) = ∞ and ${\sum }_{l=1}^{N\left(\mathbf{x}\right)}{p}_l\left(\mathbf{x}\right)=1$ almost surely.

By Lemma 1, it is apparent that G_x formed as in (7) is a well-defined stick-breaking random probability measure for x. It is also straightforward that we can define G_x for all $\mathbf{x}\in \mathcal{X}$ by (6) and (7) using the global components in (5). Therefore, given α, G₀, H, ψ) with a choice of d(·, ·), the steps from (5) to (7) defines a new choice of predictor-dependent SBP (${\mathrm{SBP}}_{\mathcal{X}}$ ) for ${\mathcal{G}}_{\mathcal{X}}$ , deemed the lDP. We use the shorthand notation ${\mathcal{G}}_{\mathcal{X}}=\{G_{\mathbf{x}}:\mathbf{x}\in \mathcal{X}\}$ ~ lDP(α, G₀, H, ψ) to denote that ${\mathcal{G}}_{\mathcal{X}}$ is assigned a lDP with hyperparameters α, G₀, H, ψ.

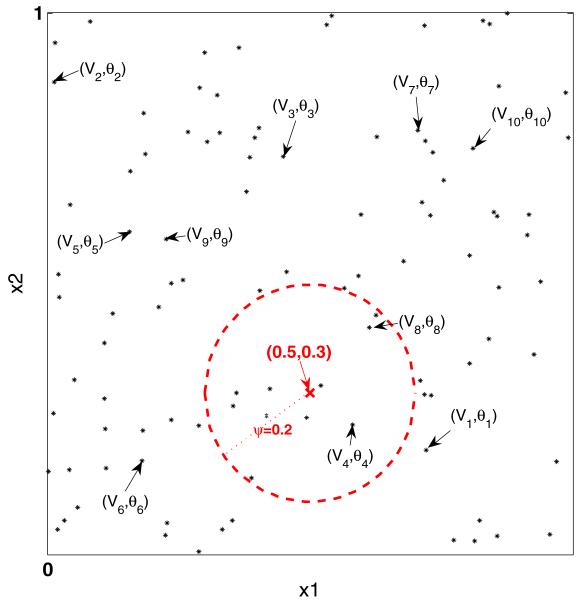
Figure 1 illustrates the lDP formulation graphically for a case where $\mathcal{X}={[0,1]}^2$ and ${\mathcal{G}}_{\mathcal{X}}~\mathrm{IDP}(\alpha ,G_0,H,\psi )$ with H =Uniform([0, 1]²) leading to $\mathcal{X}={\mathcal{X}}^{\prime }$ and ψ = 0.2. For a simple illustration, we consider Euclidian distance for d(·, ·) for bivariate predictors. Random locations in [0, 1]² are generated from a uniform distribution, with the first 100 locations plotted as ‘*’ in Fig. 1. The random pair of weight and atom (V_h, θ_h) is placed at location Γ_h, with the first ten pairs labeled in Fig. 1. For a predictor value x = (0.5, 0.3)′, the red dashed circle indicates the neighborhood of x, ${\eta }_{\mathbf{x}}^{\psi }$. Then, G_x at x = (0.5, 0.3)′ is constructed using the weights and atoms within the dashed circle in the order of the index to formulate the stick-breaking representation. For all other $\mathbf{x}\in \mathcal{X}$, G_x are formed following the same steps.

Fig. 1.

Graphical illustration for lDP formulation. Black asterisks are the first 100 random locations generated on ${\mathcal{X}}^{\prime }={[0,1]}^2$ from H = Uniform ([0,1]²). Red dashed circle indicates the neighborhood of the red crossed predictor point x = (0.5, 0.3)′ determined by Euclidian distance d(·,·) and ψ = 0.2. (V_h, θ_h) for h = 1, … , 10 are the first ten random pairs of weight and atom assigned to the first ten random locations Γ_h for h = 1, … , 10

From Fig. 1, it is apparent that the dependence between G_x and G_x′ increases as the distance between x and x′ decreases. For closer x and x′, their neighborhoods overlap more so that similar components are used for constructing G_x and G_x′, while if x and x′ are far apart, there will be at most a small area of intersection so that few to none of the random components are shared. In the non-overlapping case, G_x and $G_{\mathbf{x}}^{\prime }$ are assigned independent DP priors, as is clear from Theorem 1 and the subsequent development.

Theorem 1 If ${\mathcal{G}}_{\mathcal{X}}~IDP(\alpha ,G_0,H,\psi )$, for any $\mathbf{x}\in \mathcal{X}$, G_x ~ DP(αG₀).

The marginal DP property shown in Theorem 1 is appealing in allowing one to rely directly on the rich literature on properties of the DP to obtain insight into the prior for the random probability measure at any particular predictor value. However, unlike the DP, the lDP allows the probability measure to vary with predictors, while borrowing information across local regions of the predictor space. This is accomplished through incorporating shared random components. Due to the sharing and to the almost sure discreteness property of each G_x, the lDP will induce local clustering of subjects according to their predictor values. Theorem 2 illustrates this local clustering property more clearly.

Theorem 2 Suppose ${\mathcal{G}}_{\mathcal{X}}~IDP(\alpha ,G_0,H,\psi )$ and ${\varphi }_i\mid G_{{\mathbf{x}}_i}\stackrel{\mathrm{ind}}{}{G}_{{\mathrm{x}}_i}$, for i = 1, … , n, with x_i denoting the predictor value for subject i. Then,

$${\kappa }_{{\mathbf{x}}_i,{\mathbf{x}}_j}=Pr({\varphi }_i={\varphi }_j\mid {\mathbf{x}}_i,{\mathbf{x}}_j,\alpha ,\psi )=\frac{2P_{{\mathbf{x}}_i,{\mathbf{x}}_j}}{(1+P_{{\mathbf{x}}_i,{\mathbf{x}}_j})\alpha +2},forany{\mathbf{x}}_i,{\mathbf{x}}_j\in \mathcal{X},$$

where $P_{{\mathrm{x}}_i,{\mathbf{x}}_j}=\frac{H({\eta }_{{\mathbf{x}}_i}^{\psi }\cap {\eta }_{{\mathbf{x}}_j}^{\psi })}{H({\eta }_{{\mathbf{x}}_i}^{\psi }\cup {\eta }_{{\mathbf{x}}_j}^{\psi })}$ is the conditional probability of Γ_h falling within the intersection region ${\eta }_{{\mathbf{x}}_i}^{\psi }\cap {\eta }_{{\mathbf{x}}_j}^{\psi }$ given ${\Gamma }_h\in {\eta }_{{\mathbf{x}}_i}^{\psi }\cup {\eta }_{{\mathbf{x}}_j}^{\psi }$.

The clustering probability κ_{xi ,xj} increases from 0 when ${\eta }_{{\mathbf{x}}_i}^{\psi }\cap {\eta }_{{\mathbf{x}}_j}^{\psi }=\oslash$ to 1/(α + 1) when x_i = x_j which is the case of P_{xi ,xj} = 1. This implies that, for fixed α, the clustering probability under ${\mathcal{G}}_{\mathcal{X}}~\mathrm{IDP}(\alpha ,G_0,H,\psi )$ is bounded above by the clustering probability under the global DP, which takes $G_{\mathbf{x}}\equiv G~\mathrm{DP}\left(\alpha G_0\right)$, leading to Pr(φ_i = φ_j | α) = 1/(α + 1). Also, note that small values of the precision parameter α will induce V_h values that are close to one. This in turn causes a small number of atoms in each neighborhood to dominate, inducing few local clusters. However, when ψ is small and hence neighborhood sizes are small, there will still be many clusters across $\mathcal{X}$.

It is interesting to consider relationships between the lDP and other priors proposed in the literature in limiting special cases. First, note that the lDP converges to the DP as ψ → ∞, so that all the neighborhoods around each of the predictor values encompass the entire predictor space. Also, the lDP(α, G₀, H, ψ) corresponds to a limiting case of the kernel stick-breaking process (KSBP) (Dunson and Park 2008), in which the kernel is defined as K(x, Γ) = 1 (d(x, Γ) < ψ) and the DP placed at each location have precision parameters → 0.

3.2 Moments and correlation

From Theorem 1 and properties of the DP, ${\mathcal{G}}_{\mathcal{X}}~\mathrm{IDP}(\alpha ,G_0,H,\psi )$ implies, for any $\mathbf{x}\in \mathcal{X}$,

$$E\left\{G_{\mathbf{x}}\right(B\left)\right\}=G_0\left(B\right)\text{and}\mathrm{Var}\left\{G_{\mathbf{x}}\right(B\left)\right\}=\frac{G_0\left(B\right)(1-G_0(B\left)\right)}{1+\alpha },\forall B\in \mathcal{B}.$$ (8)

Next, let us consider the correlation between G_x1 and G_x2, for any x₁, ${\mathbf{x}}_2\in \mathcal{X}$. First, we show the correlation conditionally on the locations Γ but marginalizing out the weights V and atoms Θ. As discussed in Sect. 3.1, if Γ is given, the lDP can be regarded as a special case of the πDDP. Hence, following Theorem 1 in Griffin and Steel (2006), for any x₁, ${\mathbf{x}}_2\in \mathcal{X}$,

$$\begin{array}{cc}\hfill {\rho }_{{\mathbf{x}}_1,{\mathbf{x}}_2}\left(\Gamma \right)& =\mathrm{Corr}\left\{G_{{\mathbf{x}}_1}\right(B),G_{{\mathbf{x}}_2}(B)\mid \Gamma \}\hfill \\ \hfill & =\frac{2}{\alpha +2}\sum _{h\in {\mathcal{L}}_{{\mathbf{x}}_1}\cap {\mathcal{L}}_{{\mathbf{x}}_2}}{\left(\frac{\alpha }{\alpha +2}\right)}^{\#{\mathcal{S}}_h}{\left(\frac{\alpha }{\alpha +1}\right)}^{\#{\mathcal{S}}_h^{\prime }},\forall B\in \mathcal{B},\hfill \end{array}$$ (9)

where #S is the cardinality of the set $\mathcal{S}$, ${\mathcal{S}}_h={\mathcal{A}}_{1h}\cap {\mathcal{A}}_{2h}$, ${\mathcal{S}}_h^{\prime }={\mathcal{A}}_{1h}\cup {\mathcal{A}}_{2h}-{\mathcal{S}}_h$, and ${\mathcal{A}}_{kh}=\left\{{\pi }_j\right({\mathbf{x}}_k):j<l,{\pi }_l({\mathbf{x}}_k)=h\}$ for $h\in {\mathcal{L}}_{{\mathbf{x}}_1}\cap {\mathcal{L}}_{{\mathbf{x}}_2}$. In other words, #S_h is the number of indices on the locations Γ that are below h and are shared in the neighborhoods of x₁ and x₂, while $\#{\mathcal{S}}_h^{\prime }$ is the number of indices that are below h and belong to the neighborhoods of either x₁ or x₂ but not both. For a given h, reducing #S_h by one induces adding two elements to ${\mathcal{S}}_h^{\prime }$, thus reducing the correlation, as expected. From expression (9), it is clear that the neighborhoods around x₁ and x₂ are increasingly overlapping and the correlation between G_x1 and G_x2 increases as x₁ → x₂. Expression (9) is particularly useful in being free of dependence on B.

Marginalizing the correlation in (9) over the prior for the random locations Γ is equivalent to marginalizing out the #S_h and $\#{\mathcal{S}}_h^{\prime }$ for $h\in {\mathcal{L}}_{{\mathbf{x}}_1}\cap {\mathcal{L}}_{{\mathbf{x}}_2}$. In considering the correlation between G_x1 and G_x2, we can ignore the Γ_h for $h\in \{1,\dots ,\infty \}\backslash {\mathcal{L}}_{{\mathbf{x}}_1}\cup {\mathcal{L}}_{{\mathbf{x}}_2}$ and focus on the Γ_h only for $h\in {\mathcal{L}}_{{\mathbf{x}}_1}\cup {\mathcal{L}}_{{\mathbf{x}}_2}$. Let γ_j be the jth ordered component of ${\mathcal{L}}_{{\mathbf{x}}_1}\cup {\mathcal{L}}_{{\mathbf{x}}_2}$. For example, if ${\mathcal{L}}_{{\mathbf{x}}_1}\cup {\mathcal{L}}_{{\mathbf{x}}_2}=\{1,3,5,6,7,8,\dots \}$, γ₁ = 1, γ₂ = 3,γ₃ = 5, γ₄ = 6, …. Let $Z_{{\gamma }_j}=1({\gamma }_j\in {\mathcal{L}}_{{\mathbf{x}}_1}\cap {\mathcal{L}}_{{\mathbf{x}}_2})$ be an indicator for whether Γ_γj are shared by the neighborhoods of x₁ and x₂ or not. Then, the formula in (9) can be reexpressed with respect to Z_γj as follows:

$$\begin{array}{cc}\hfill {\rho }_{{\mathbf{x}}_1,{\mathbf{x}}_2}\left(\Gamma \right)& =\mathrm{Corr}\left\{G_{{\mathbf{x}}_1}\right(B),G_{{\mathbf{x}}_2}(B)\mid \Gamma \}\hfill \\ \hfill & =\frac{2}{\alpha +2}\sum _{j=1}^{\infty }{Z}_{{\gamma }_j}{\left(\frac{\alpha }{\alpha +2}\right)}^{{\Sigma }_{k=1}^{j-1}{Z}_{{\gamma }_k}}{\left(\frac{\alpha }{\alpha +1}\right)}^{j-1-{\Sigma }_{k=1}^{j-1}{Z}_{{\gamma }_k}}.\hfill \end{array}$$ (10)

Note that it is straightforward to show that $Z_{{\gamma }_j}\stackrel{\mathrm{iid}}{~}\text{Bernoulli}\left(P_{{\mathbf{x}}_1,{\mathbf{x}}_2}\right)$ Bernoulli(P_x1,x2), for j = 1, … ,∞, with $P_{{\mathbf{x}}_1,{\mathbf{x}}_2}=\frac{H({\eta }_{{\mathbf{x}}_1}^{\psi }\cap {\eta }_{{\mathbf{x}}_2}^{\psi })}{H({\eta }_{{\mathbf{x}}_1}^{\psi }\cup {\eta }_{{\mathbf{x}}_2}^{\psi })}$ the conditional probability of Γ_h falling within the intersection region ${\eta }_{{\mathbf{x}}_1}^{\psi }\cap {\eta }_{{\mathbf{x}}_2}^{\psi }$ given ${\Gamma }_h\in {\eta }_{{\mathbf{x}}_1}^{\psi }\cup {\eta }_{{\mathbf{x}}_2}^{\psi }$. Finally, marginalizing out ${\left\{Z_{{\gamma }_j}\right\}}_{j=1}^{\infty }$ results in the following Theorem.

Theorem 3 If ${\mathcal{G}}_{\mathcal{X}}~IDP(\alpha ,G_0,H,\psi )$, for any ${\mathbf{x}}_1,{\mathbf{x}}_2\in \mathcal{X}$,

$${\rho }_{{\mathbf{x}}_1,{\mathbf{x}}_2}=\mathrm{Corr}\left\{G_{{\mathbf{x}}_1}\right(B),G_{{\mathbf{x}}_2}(B\left)\right\}=\frac{2P_{{\mathbf{x}}_1,{\mathbf{x}}_2}(\alpha +1)}{(1+P_{{\mathbf{x}}_1,{\mathbf{x}}_2})\alpha +2},\forall B\in \mathcal{B}.$$

The correlation is expressed only in terms of P_x1,x2 and α. Regardless of α, the correlation is 1 if x₁ = x₂ which implies the neighborhoods around x₁, x₂ are identical and P_x1,x2=1. Also, the correlation is 0 when the neighborhoods are non-overlapping with P_x1,x2=0. In addition, P_x1,x2 ≤ ρ_x1,x2 ≤ 1 and ρ_x1,x2 increases as α increases for fixed P_x1,x2 . When α → 0, the correlation converges to P_x1,x2. Meanwhile, when α → ∞, the correlation converges to $\frac{2P_{{\mathbf{x}}_1,{\mathbf{x}}_2}}{1+P_{{\mathbf{x}}_1,{\mathbf{x}}_2}}$.

Note that P_x1,x2 depends on H, ψ, and the locations x₁ and x₂ given a choice of d(·, ·). When ${\mathcal{X}}^{\prime }$ for H is chosen to satisfy Condition 2, some appealing properties result.

Condition 2 For all $\mathbf{x}\in \mathcal{X}$ with $\mathcal{X}$ being p-dimensional, $\{{\mathbf{x}}^{\ast };d({\mathbf{x}}^{\ast },\mathbf{x})<\psi ,{\mathbf{x}}^{\ast }\in {\mathfrak{R}}^p\}\subset {\mathcal{X}}^{\prime }$.

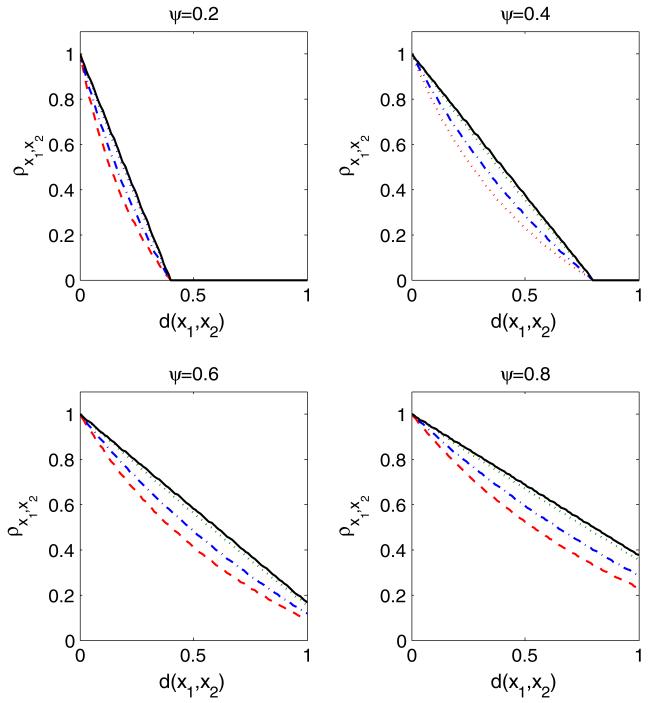
From Condition 2, one can deduce that ${\mathcal{X}}^{\prime }$ contains all the points in ${\mathfrak{R}}^p$ within the distance of ψ from x for any $\mathbf{x}\in \mathcal{X}$. Under Condition 2, with H chosen to be a uniform probability measure on a bounded space ${\mathcal{X}}^{\prime }$, P_x1,x2 depends only on ψ and d(x₁, x₂) which is the distance between x₁ and x₂, but not on the exact locations of x₁ and x₂ in $\mathcal{X}$. Hence, upon examination of Theorem 3, it is apparent that Condition 2 implies an isotropic correlation structure, which is an appealing default in the absence of prior knowledge of changes in the correlation structure according to the locations in $\mathcal{X}$. Figure 2 shows how the correlation ρ_x1,x2 changes as a function of d(x₁, x₂) in the case where $\mathbf{x}\in \mathcal{X}=[0,1]$ and H is Uniform([−ψ, 1 + ψ]) so that ${\mathcal{X}}^{\prime }=[-\psi ,1+\psi ]$ and Condition 2 holds for different ψ with d(·, ·) corresponding to the Euclidian distance. The ρ_x1,x2 decays from 1 to 0 as d(x₁, x₂) increases and the decay is faster for smaller ψ. As ψ → ∞, the decay line gets closer to a horizontal line at ρ_x1,x2 = 1, which is the case of lDP=DP. Also, for a given ψ and d(x₁, x₂), the ρ_x1,x2 is higher as α → ∞. Although the choice of d(·, ·) being Euclidian makes the curves in Fig. 2 close to linear, the curvature can easily be changed by choosing a different distance measure d(·, ·).

Fig. 2.

Change in correlation ρ_x1,x2 over the change in distance d(x₁, x₂) for different α and ψ: α = 0.0001 (red dashed), α = 1 (blue dot-dashed), α = 10 (green dotted), α = 10, 000 (black solid)

3.3 Truncation approximation

Finite approximations to infinite SBPs form the basis for commonly used computational algorithms (Ishwaran and James 2001). In this subsection, we discuss a finite dimensional approximation to the lDP.

Since the lDP has the marginal DP property, let us recall the finite dimensional DP. Ishwaran and James (2001) defines an N-truncation of the DP (DP^N) by discarding the N + 1, N + 2, … , ∞ terms and replacing p_N with $1-{\sum }_{h=1}^{N-1}{p}_h$ in the DP stick-breaking form in (3). They show that the DP^N approximates the DP well in terms of the total variation (tv) norm of the marginal densities of the data obtained from the corresponding DPM models. According to their Theorem 2,

$$\mid \mid {\mu }_N-{\mu }_{\infty }\mid \mid \le 4\left[1-E\left\{{\left(\sum _{h=1}^{N-1}{p}_h\right)}^n\right\}\right]\approx 4n\times \exp \{-(N-1)∕\alpha \},$$ (11)

where || · || is tv norm, μ_N and μ_∞ are the marginal probability measures for the data from the DPM^N and DPM models, and n is the sample size. Note that the sample size has a modest effect on the bound for a reasonably large value of N and the bound decreases exponentially with N increasing, implying that even for a fairly large sample size, the DPM^N approximates the DP well with moderate N.

Following a similar route, let us define an N-truncation of the lDP (lDP^N) as follows:

Definition 2 For a finite N, let Γ^N ={Γ_h, h = 1, … , N}, V^N ={V_h, h =1, … , N}, and Θ^N = {θ_h, h = 1, … , N} be the sets of global random locations, weights, and atoms, respectively. Distributional assumptions for Γ_h, V_h, and θ_h are the same as in (5) and the corresponding local sets are defined as in (6). Then, ${\mathcal{G}}_{\mathcal{X}}~ID{P}^N(\alpha ,G_0,H,\psi )$ if

$$\begin{array}{cc}\hfill G_{\mathbf{x}}& =\sum _{l=1}^{N\left(\mathbf{x}\right)-1}{p}_l\left(\mathbf{x}\right){\delta }_{{\theta }_{{\pi }_l\left(\mathbf{x}\right)}}+\left(1-\sum _{l=1}^{N\left(\mathbf{x}\right)-1}{p}_l\left(\mathbf{x}\right)\right){\delta }_{{\theta }_{{\pi }_{N\left(\mathbf{x}\right)}\left(\mathbf{x}\right)}}\hfill \\ \hfill & \text{with}{p}_l\left(\mathbf{x}\right)=V_{{\pi }_l\left(\mathbf{x}\right)}\prod _{j<1}(1-V_{{\pi }_j\left(\mathbf{x}\right)})\text{for}l=1,\dots ,N\left(\mathbf{x}\right)-1.\hfill \end{array}$$

The G_x in Definition 3 has a similar form to $G={\sum }_{h=1}^N{p}_h{\delta }_{{\theta }_h}$ obtained from the DP^N except that N in G is replaced by N(x) in G_x and N in DP^N is fixed while N(x) in lDP^N is random. Focusing on a particular predictor value x, it is easy to show that N(x) ~ Binomial(N,P_x), where N is the total number of global locations in lDP^N and $P_{\mathbf{x}}=H\left({\eta }_{\mathbf{x}}^{\psi }\right)$ is the probability that a location belongs to the neighborhood around x, ${\eta }_{\mathbf{x}}^{\psi }$. Then, marginalizing out N(x) in the bound on the tv distance between the marginal densities of an observation obtained at a particular predictor value x from the lDPM and lDPM^N models results in Theorem 4.

Theorem 4 Define a model (2) with ${\mathcal{G}}_{\mathcal{X}}~IDP(\alpha ,G_0,H,\psi )$ as local Dirichlet process mixture (lDPM) model). lDPM^N corresponds to (2) with ${\mathcal{G}}_{\mathcal{X}}~ID{P}^N(\alpha ,G_0,H,\psi )$. Suppose an observation is obtained from lDPM^N and lDPM models at x. Then,

$$\mid \mid {\mu }_N\left(\mathbf{x}\right)-{\mu }_{\infty }\left(\mathbf{x}\right)\mid \mid \le 4\left(\frac{\alpha +1}{\alpha }\right){\left\{1-\left(\frac{1}{\alpha +1}\right)P_{\mathbf{x}}\right\}}^N,$$

where μ_N (x) and μ_∞(x) are the marginal probability measures for the observation. Notice that the bound decreases exponentially with N increasing, suggesting that we can obtain a good approximation to the lDP using a moderate N, as long as α is small and the neighborhood size is not too small. In particular, we require a large N for a given level of accuracy as ψ → 0, since P_x decreases as the size of ${\eta }_{\mathbf{x}}^{\psi }$ decreases.

4 Posterior computation

We develop an MCMC algorithm based on the blocked Gibbs sampler (Ishwaran and James 2001) for an lDPM^N model. For simplicity in exposition, we describe a Gibbs sampling algorithm for a particular hierarchical model, though the approach can be easily adapted for computation in a broad variety of other settings. We let

$$\begin{array}{cc}\hfill f(y_i\mid {\mathbf{x}}_i,\tau )& =\int f(y_i\mid {\mathbf{x}}_i,{\beta }_i,\tau )\mathrm{d}{G}_{{\mathbf{x}}_i}\left({\beta }_i\right)\text{for}i=1,\dots ,n\hfill \\ \hfill {\mathcal{G}}_{\mathcal{X}}& ~{\mathrm{IDP}}^N(\alpha ,G_0,H,\psi ),\hfill \end{array}$$ (12)

where f (y_i|x_i, β_i, τ) = N(y_i; ${\mathbf{x}}_i^{\prime }$, β_i, τ⁻¹) β_i = (β_i1, … ,β_ip)′. For simplicity, we consider a univariate predictor case where p = 2 and ${\mathbf{x}}_i^{\prime }=(1,x_i)$ with d(·, ·) Euclidian distance but the generalization to multiple predictors or to using different distance metric is straightforward. G₀ is assumed to be N_p(μ_β, Σ_β), H is assumed to be Uniform(a_Γ, b_Γ) and additional conjugate priors are assigned for τ, α, μ_β and Σ_β.

Let K_i be an indicator variable denoting that K_i = h implies ith subject is assigned to the hth mixture component. Then, the hierarchical structure of the model (12) with respect to the random variables is recast as follows.

$$\begin{array}{cc}\hfill (y_i\mid {\mathbf{x}}_i,{\beta }^{\ast },\tau ,\mathbf{K}& ~N({\mathbf{x}}_i^{\prime }{\beta }_{K_i}^{\ast },{\tau }^{-1}),i=1,\dots ,n\hfill \\ \hfill (K_i\mid \mathbf{V},\Gamma )& ~\sum _{l=1}^{N\left({\mathbf{x}}_i\right)}{p}_l\left({\mathbf{x}}_i\right){\delta }_{{\pi }_l\left({\mathbf{x}}_i\right)}(\cdot ),i=1,\dots ,n\hfill \\ \hfill (V_h\mid \alpha & ~\text{Beta}(1,\alpha ),h=1,\dots ,N\hfill \\ \hfill \left({\Gamma }_h\right)& ~\text{Uniform}(a_{\Gamma },b_{\Gamma })h=1,\dots ,N\hfill \\ \hfill ({\beta }_h^{\ast }\mid {\mu }_{\beta },{\Sigma }_{\beta })& ~N_p({\mu }_{\beta },{\Sigma }_{\beta }),h=1,\dots ,N\hfill \\ \hfill {\mu }_{\beta }& ~N_p({\mu }_0,{\Sigma }_{\mu })\hfill \\ \hfill {\Sigma }_{\beta }^{-1}& ~\text{Wishart}({\left\{{\nu }_0{\Sigma }_0\right\}}^{-1},{\nu }_0)\hfill \\ \hfill \tau & ~\text{Gamma}({\nu }_1,{\nu }_2)\hfill \\ \hfill \alpha & ~\text{Gamma}({\eta }_1,{\eta }_2),\hfill \end{array}$$ (13)

where ${\beta }^{\ast }=\{{\beta }_h^{\ast },h=1,\dots ,N\}$, K = {K_i, i = 1 …, n}, V = {V_h, h = 1, …, N}, and Γ = {Γ_h, h = 1, …, N}. The full conditionals for each of the random components are based on the following joint distribution.

$$(\mathbf{y},\mathbf{K},\mathbf{V},\Gamma ,{\beta }^{\ast },{\mu }_{\beta },{\Sigma }_{\beta },\tau ,\alpha )\propto (\mathbf{y}\mid {\beta }^{\ast },\tau ,\mathbf{K})(\mathbf{K}\mid \mathbf{V},\Gamma )(\mathbf{V}\mid \alpha )\left(\Gamma \right)({\beta }^{\ast }\mid {\mu }_{\beta },{\Sigma }_{\beta })\left({\mu }_{\beta }\right)\left({\Sigma }_{\beta }\right)\left(\tau \right)\left(\alpha \right)$$ (14)

Then, the Gibbs sampler proceeds by sampling from the following conditional posterior distributions:

1. Conditional for K_i, i = 1, … , n

   $$\begin{array}{cc}\hfill (K_i\mid \mathbf{y},\mathbf{V},\Gamma ,{\beta }^{\ast },\tau & ~\sum _{l=1}^{N\left({\mathbf{x}}_i\right)}{p}_l^{\prime }\left({\mathbf{x}}_i\right){\delta }_{{\pi }_l\left({\mathbf{x}}_i\right)}\left(K_i\right)\hfill \\ \hfill p_l^{\prime }\left({\mathbf{x}}_i\right)& =\frac{N(y_i;{\mathbf{x}}_i^{\prime }{\beta }_{{\pi }_l\left({\mathbf{x}}_i\right)}^{\ast },{\tau }^{-1})p_l\left({\mathbf{x}}_i\right)}{\sum _{l=1}^{N\left({\mathbf{x}}_i\right)}N(y_i;{\mathbf{x}}_i^{\prime }{\beta }_{{\pi }_l\left({\mathbf{x}}_i\right)}^{\ast },{\tau }^{-1})p_l\left({\mathbf{x}}_i\right)}\hfill \\ \hfill p_l\left({\mathbf{x}}_i\right)& =V_{{\pi }_l\left({\mathbf{x}}_i\right)}\prod _{j<l}(1-V_{{\pi }_j\left({\mathbf{x}}_i\right)})\text{for}l<N\left({\mathbf{x}}_i\right)\hfill \\ \hfill p_l\left({\mathbf{x}}_i\right)& =\prod _{j<1}(1-V_{{\pi }_j\left({\mathbf{x}}_i\right)})\text{for}l=N\left({\mathbf{x}}_i\right)\hfill \end{array}$$
2. Conditional for V_h, h = 1, … , N

   $$(V_h\mid \mathbf{K},\Gamma ,\alpha )~\text{Beta}\left(1+\sum _{i=1}^{n}1(K_i=h\text{and}{K}_i\ne {\pi }_{N\left(x_i\right)}({\mathbf{x}}_i\left)\right),\alpha +\sum _{i=1}^{n}1(K_i>h)\right)$$
3. Conditional for Γ_h, h = 1, … , N

   $$({\Gamma }_h\mid \mathbf{K},\mathbf{V})~\text{Uniform}\left(\max \left[\underset{i=K_i=h}{\max }(x_i-\psi ),a_{\Gamma }\right],\min \left[\underset{i=K_i=h}{\min }(x_i+\psi ),a_{\Gamma }\right]\right)$$
4. Conditional for ${\beta }_h^{\ast },h=1,\dots ,N$

   $$\begin{array}{cc}\hfill ({\beta }_h^{\ast }\mid \mathbf{y},\mathbf{K},{\mu }_{\beta },{\Sigma }_{\beta },\tau )& ~N_p({\widehat{\mu }}_{\beta h},{\widehat{\Sigma }}_{\beta h})\hfill \\ \hfill {\widehat{\mu }}_{\beta h}& ={\widehat{\Sigma }}_{\beta h}[{\Sigma }_{\beta }^{-1}{\mu }_{\beta }+\tau {\mathbf{X}}_{ih}{\mathbf{y}}_{ih}]\hfill \\ \hfill {\widehat{\Sigma }}_{\beta h}& ={[{{\Sigma }_{\beta }}^{-1}+\tau {\mathbf{X}}_{ih}{\mathbf{X}}_{ih}^{\prime }]}^{-1},\hfill \end{array}$$

   where y_ih is n_h × 1 response vector and ${\mathbf{X}}_{ih}^{\prime }$ is n_h × p design matrix for the subjects with K_i = h and n_h is the number of those subjects.
5. Conditional for μ_β

   $$\begin{array}{c}\hfill ({\mu }_{\beta }\mid {\beta }^{\ast },{\Sigma }_{\beta })~N_p({\widehat{\mu }}_0,{\widehat{\Sigma }}_{\mu })\hfill \\ \hfill {\widehat{\mu }}_0={\widehat{\Sigma }}_{\mu }\left[{\Sigma }_{\mu }^{-1}{\mu }_0+{\Sigma }_{\beta }^{-1}\sum _{h=1}^N{\beta }_h^{\ast }\right]\hfill \\ \hfill {\widehat{\Sigma }}_{\mu }={[{\Sigma }_{\mu }^{-1}+N{\Sigma }_{\beta }^{-1}]}^{-1}\hfill \end{array}$$
6. Conditional for ${\sum }_{\beta }^{-1}$

   $$({\Sigma }_{\beta }^{-1}\mid {\beta }^{\ast },{\mu }_{\beta })~\text{Wishart}\left({\left[\sum _{h=1}^N({\beta }_h^{\ast }-{\mu }_{\beta }){({\beta }_h^{\ast }-{\mu }_{\beta })}^{\prime }+{\nu }_0{\Sigma }_0\right]}^{-1},N+{\nu }_0\right)$$
7. Conditional for τ

   $$(\tau \mid \mathbf{y},{\beta }^{\ast },\mathbf{K})~\text{Gamma}\left({\nu }_1+\frac{n}{2},{\nu }_2+\frac{1}{2}\sum _{i=1}^n{(y_i-{{\mathbf{x}}_i}^{\prime }{\beta }_{K_i}^{\ast })}^2\right)$$
8. Conditional for α

   $$(\alpha \mid \mathbf{V})~\text{Gamma}\left({\eta }_1+N,{\eta }_2-\sum _{h=1}^N\log (1-V_h)\right)$$

   Note that this Gibbs sampling algorithm consists only of simple steps for sampling from standard distributions and is no more complex than blocked Gibbs samplers for DPMs. In addition, we have observed good computational performance, in terms of mixing and convergence rates, in simulated and real data applications.

5 Simulation examples

We obtained data from two simulated examples, where n = 500 and a univariate predictor x_i was simulated from Uniform(0,1). Case 1 was a null case where y_i was generated from a normal regression model N(y_i; −1 + 2x_i, 0.01). Case 2 was a mixture of two normal linear regression models, with the mixture weights depending on the predictor, with the error variance differing, and with a nonlinear mean function for the second component:

$$f(y_i\mid {\mathbf{x}}_i)=e^{-2x_i}N(y_i;x_i,0.01)+(1-e^{-2x_i})N(y_i;x_i^4,0.04).$$ (15)

We applied the lDPM^N model in (12) to the simulated data with N = 50. Based on the results, N = 50 seems to be chosen to be large enough since the higher clusters having higher indices are not used in any of the subjects or are used in only a small proportion of them. Also, repeating the analysis for twice N, we obtained very similar results, suggesting that the results are robust to the choice of N, as long as N is not chosen to be small.

For the hyperparameters, we let ν₁ = ν₂ = 0.01, η₁ = η₂ = 2, ν₀ = p, Σ₀ = I_p, μ₀ = 0, Σ_μ = n(X′X)⁻¹, a_Γ = −0.05, and b_Γ = 1.05. The neighborhood size ψ = 0.05 was chosen such that the average number of subjects belonging to the neighborhoods around each predictor value in the sample is ≈n/10. We analyzed the simulated data using the proposed Gibbs sampling algorithm run for 10,000 iterations with a 5,000 iteration burn-in. The convergence and mixing of the MCMC algorithm were good (trace plots not shown). Also, results tended to be robust to repeating analysis with reasonable alternative hyperparameter values.

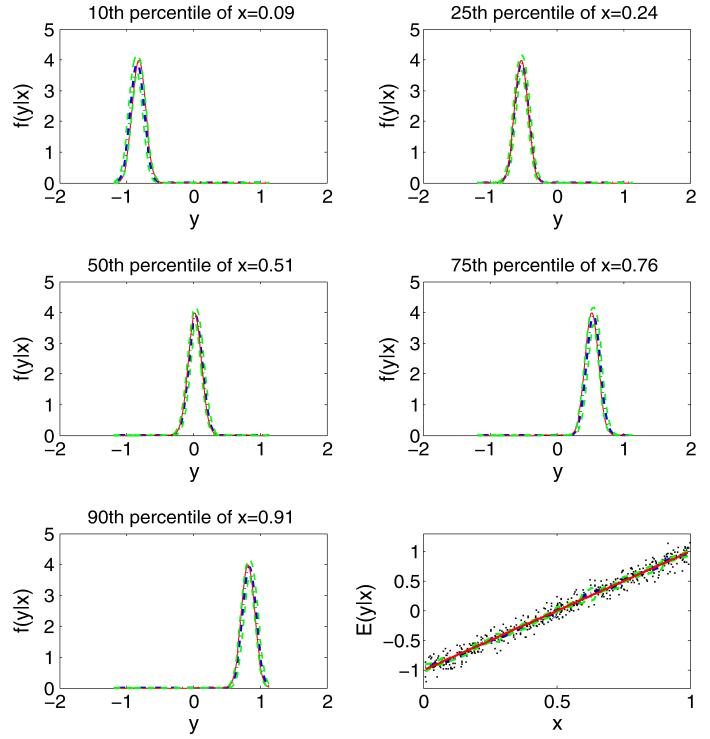
For Case 1, as shown in Fig. 3, the predictive mean regression curve (blue dashed, right bottom panel), the true linear regression function (red solid), and the pointwise 95% credible intervals (green dashed) were almost the same. Figure 3 also shows the predictive densities (blue dashed) at the 10th, 25th, 50th, 75th, and 90th sample percentiles of x_i, with these densities almost indistinguishable from the true densities (red solid).

Fig. 3.

Results for simulation Case 1: true conditional densities of y|x (red solid), predictive conditional densities (blue dot-dashed), and 95% pointwise credible intervals (green dashed). The lower right panel shows the data (black dots), along with true (red solid) and estimated mean (blue dashed) regression curves superimposed with 95% credible line (green dashed)

For Case 2, Fig. 4 shows an x – y plot (right bottom panel) of the data along with the estimated predictive mean curve (blue dashed), which closely follows the true mean curve (red solid). Figure 4 also shows the estimated predictive densities (blue dashed) correspond approximately to the true densities (red solid) in most cases and the 95% credible intervals (green dashed) closely cover the true densities in all cases.

Fig. 4.

Results for simulation Case 2: true conditional densities of y|x (red solid), predictive conditional densities (blue dot-dashed), and 95% pointwise credible intervals (green dashed). The lower right panel shows the data (black dots), along with true (red solid) and estimated mean (blue dashed) regression curves superimposed with 95% credible line (green dashed)

Repeating the analysis for Case 2, but with ${\beta }_i\stackrel{\mathrm{iid}}{~}G$ and G ~ DP(αG₀), we obtained poor results estimates diverged substantially from true densities, posterior mean curve failed to capture true nonlinear function), suggesting that a DPM model is inadequate.

6 Epidemiological application

6.1 Background and motivation

In diabetic studies, interest often focuses on the relationship between 2-h serum insulin levels (indicator for insulin sensitivity/resistence) and 2-h plasma glucose levels (indicator for diabetic risk) that are measured in the oral glucose tolerance test (OGTT). Although most studies examine the mean change of the 2-h insulin versus 2-h glucose, it would be more interesting to assess the whole distributional change of the 2-h insulin level across the range of the 2-h glucose levels.

We obtained data from a study which followed a sample of Pima Indians from a population near Phoenix, Arizona since 1965. This study was conducted by the National Institute of Diabetes and Digestive and Kidney Disease, with the Pima Indians chosen because of their high risk of diabetes. Using these data, our goal is conducting inferences on changes in the 2-h serum insulin distribution with changes in 2-h glucose level without making restrictive assumptions, such as normality or a constant residual variation. Certainly, it is biologically plausible that the insulin distribution is non-normal and should change as the glucose level changes not only in mean but also in other features such as skewness, residual variation, and modality.

6.2 Analysis and results

For woman i (i = 1, … , 393), let y_i correspond to the 2-h serum insulin level measured in μU/ml (micro Units per milliliter) and let x_i denote the 2-h plasma glucose level measured in mg/dl (milligrams per deciliter). We applied the lDPM^N model described in (12), after scaling y and x by dividing by 100. Hyperparameters were set to be the same as in the simulation study except that ψ = 0.08 such that n/10 subjects belong to each neighborhood on average and a_Γ = min(x_i) − ψ, and b_Γ = max(x_i) + ψ) such that the edge effects are avoided in the inference. We analyzed the data using the proposed Gibbs sampling algorithm run for 10,000 iterations with a 5,000 iteration burn-in. The convergence and mixing of the MCMC algorithm were good (Trace plots not shown) and results were robust with reasonable alternative hyperparameter values.

Figure 5 shows the predictive distributions for the insulin level at various empirical percentiles of the glucose level. As the glucose level increases, there is a slightly nonlinear change in the mean insulin level (right bottom panel) and a dramatic increase in the heaviness of the right tail of the insulin distribution. Also, some multi-modality in the insulin distribution appears as the glucose level falls into the pre-diabetes range (140–200mg/dl) and closer to the cut point (200mg/dl) for the diagnosis of diabetes. This shift in the shape of the insulin distribution biologically implies that the women with pre-diabetes are expected to have different insulin sensitivities, which may further induce different diabetic risks even for the same glucose level. This may be due to unadjusted covariates or unmeasured risk factors. Such distributional changes in response induced by predictors (e.g. risk factor, exposure, treatment, and, etc.) is pervasive in epidemiologic studies, but is not at all well characterized by standard regression models that do not allow the whole distribution to flexibly change with predictors.

Fig. 5.

Results for Pima Indian Example: predictive conditional densities (blue dot-dashed), and 95% pointwise credible intervals (green dashed). The lower right panel shows the data (black dots), along with estimated mean (blue dashed) regression curves superimposed with 95% credible line (green dashed)

7 Discussion

This article proposed a new SBP for the collection of predictor-dependent random probability measures. The prior, called the lDP, is a useful alternative to recently developed prior models that induce predictor-dependence among distributions. Its marginal DP structure should be useful in considering theoretical properties, such as posterior consistency and rates of convergence. A related formulation was independently developed by Griffin and Steel (2008) although the lDP is appealing in its simplicity for construction and computation. In particular, the construction is intuitive and leads to simple expressions for the dependence in random measures at different locations, while also leading to straightforward posterior computation relying on truncation with a fair amount of accuracy.

Although we have focused on a conditional density estimation application, there are many interesting applications of the lDP to be considered in future work. First, the DP is widely used to induce a prior on a random partition or clustering structure (Quintana 2006; Kim et al. 2006). In such settings, the DP has the potential disadvantage of requiring an exchangeability assumption, which may be violated when predictors are available that can inform about the clustering. The lDP provides a straightforward mechanism for local, predictor-dependent clustering, which can be used as an alternative to product partition models (Quintana and Iglesias 2003) and model-based clustering approaches (Fraley and Raftery 2002). It is of interest to explore the theoretical properties of the induced prior on the random partition. In this respect, it is likely that the hyperparameter ψ plays a key role. Hence, as a more robust data-driven approach one may consider fully Bayes or empirical Bayes methods for allowing uncertainty in ψ.

Appendix

Proof of Lemma 1 An infinite number of locations Γ = {Γ_h, h = 1, …, ∞} are generated from H on ${\mathcal{X}}^{\prime }$. Any ψ-neighborhood of x defined as ${\eta }_{\mathbf{x}}^{\psi }=\{{\mathbf{x}}^{\prime }:d(\mathbf{x},{\mathbf{x}}^{\prime })<\psi ,{\mathbf{x}}^{\prime }\in {\mathcal{X}}^{\prime }$ with ψ > 0 is a subsect of ${\mathcal{X}}^{\prime }$. The regularity Condition 1 for H ensures that there is a positive probability for a location Γ_h to be generated in any ${\eta }_{\mathbf{x}}^{\psi }$. Therefore, there are also an infinite number of locations in ${\eta }_{\mathbf{x}}^{\psi }$ for all $\mathbf{x}\in \mathcal{X}$ and ψ > 0, which implies N(x) = ∞. Then, ${\sum }_{l=1}^{N\left(\mathbf{x}\right)}{p}_l\left(\mathbf{x}\right)$ almost surely by Lemma 1 in Ishwaran and James (2001).

Proof of Theorem 1 Assume that ${\mathcal{G}}_{\mathcal{X}}~\mathrm{IDP}(\alpha ,G_0,H,\psi )$. Then, from the definition of the lDP in (5)–(7), we can reexpress (7) as $G_{\mathbf{x}}={\sum }_{l=1}^{N\left(\mathbf{x}\right)}{V}_l^{\left(\mathbf{x}\right)}{\prod }_{j<l}(1-V_j^{\left(\mathbf{x}\right)}){\delta }_{{\theta }_l^{\left(\mathbf{x}\right)}}$, where $V_l^{\left(\mathbf{x}\right)}$ is the lth element of V(x) and ${\theta }_l^{\left(\mathbf{x}\right)}$ is the lth element of Θ(x). Note that it follows from the proof of Lemma 1 that N(x) = ∞. Since the random weights and atoms are generated by iid sampling from Beta(1, α) and G₀, respectively, independently from the location, we have $V_l^{\left(\mathbf{x}\right)}\stackrel{\mathrm{iid}}{~}\text{Beta}(1,\alpha )$ independently from ${ϴ}_l^{\left(\mathbf{x}\right)}\stackrel{\mathrm{iid}}{~}{G}_0$, for l = 1, … , ∞. Hence, it follows directly from Sethuraman’s (1994) representation of the DP, that $G_{\mathbf{x}}~\mathrm{DP}\left(\alpha G_0\right),{\forall }_{\mathbf{x}}\in \mathcal{X}$.

Proof of Theorem 2 Given Γ and V,

$$\begin{array}{cc}\hfill Pr({\varphi }_i={\varphi }_j\mid {\mathbf{x}}_i,{\mathbf{x}}_j,\Gamma ,\mathbf{V},\psi )& =\sum _{\left\{\right(k,l):{\pi }_k({\mathbf{x}}_i)={\pi }_l({\mathbf{x}}_j\left)\right\}}{p}_k\left({\mathbf{x}}_i\right)p_l\left({\mathbf{x}}_j\right)\hfill \\ \hfill & =\sum _{h\in {\mathcal{L}}_{{\mathbf{x}}_j}\cap {\mathcal{L}}_{{\mathbf{x}}_j}}{V}_h^2\prod _{m\in {\mathcal{S}}_h}{(1-V_m)}^2\prod _{n\in {\mathcal{S}}_h^{\prime }}(1-V_n).\hfill \end{array}$$

For the definition of ${\mathcal{S}}_h$ and ${\mathcal{S}}_h^{\prime }$, refer to the Eq. (9) in Sect. 3.2. Marginalizing out V over the Beta distribution,

$$Pr({\varphi }_i={\varphi }_j\mid {\mathbf{x}}_i,{\mathbf{x}}_j,\Gamma ,\alpha ,\psi )=\frac{2}{(\alpha +1)(\alpha +2)}\sum _{h\in {\mathcal{L}}_{{\mathbf{x}}_i}\cap \mathcal{L}{\mathbf{x}}_j}{\left(\frac{\alpha }{\alpha +2}\right)}^{\#{\mathcal{S}}_h}{\left(\frac{\alpha }{\alpha +1}\right)}^{\#{\mathcal{S}}_h^{\prime }}.$$

In order to marginalize out ${\mathcal{S}}_h$ and ${\mathcal{S}}_h^{\prime }$, we introduce $Z_{{\gamma }_j}\stackrel{\mathrm{iid}}{~}\text{Bernoulli}\left(P_{{\mathbf{x}}_i,{\mathbf{x}}_j}\right)$ as described in the formulations from (9) to (10) in Sect. 3.2. Then,

$$Pr({\varphi }_i={\varphi }_j\mid {\mathbf{x}}_i,{\mathbf{x}}_j,\Gamma ,\alpha ,\psi )=\frac{2}{(\alpha +1)(\alpha +2)}\sum _{j=1}^{\infty }{\mathrm{Z}}_{{\gamma }_j}{\left(\frac{\alpha }{\alpha +2}\right)}^{\sum _{k=1}^{j-1}{\mathrm{Z}}_{{\gamma }_k}}\times {\left(\frac{\alpha }{\alpha +1}\right)}^{j-1-\sum _{k=1}^{j-1}{\mathrm{Z}}_{{\gamma }_k}}.$$

(After marginalizing out the ${\left\{Z_{{\gamma }_j}\right\}}_{j=1}^{\infty }$ as in the Proof of Theorem 3, we obtain:

$$\begin{array}{cc}\hfill Pr({\varphi }_i={\varphi }_j\mid {\mathbf{x}}_i,{\mathbf{x}}_j,\alpha ,\psi )& =\left[\frac{2}{(\alpha +1)(\alpha +2)}\right]\left[\frac{P_{{\mathbf{x}}_i,{\mathbf{x}}_j}(\alpha +2)(\alpha +1)}{\alpha (1+P_{{\mathbf{x}}_i,{\mathbf{x}}_j})+2}\right]\hfill \\ \hfill & =\frac{2P_{{\mathbf{x}}_i,{\mathbf{x}}_j}}{(1+P_{{\mathbf{x}}_i,{\mathbf{x}}_j})\alpha +2}.\hfill \end{array}$$

Proof of Theorem 3 From (10),

$$\mathrm{Corr}\left\{G_{{\mathbf{x}}_i}\right(B),G_{{\mathbf{x}}_2}(B)\mid \Gamma \}=\frac{2}{\alpha +2}\sum _{j=1}^{\infty }{\mathrm{Z}}_{{\gamma }_j}{\left(\frac{\alpha +1}{\alpha +2}\right)}^{\sum _{k=1}^{j-1}{\mathrm{Z}}_{{\gamma }_k}}{\left(\frac{\alpha }{\alpha +1}\right)}^{j-1},$$

where Z_γj are iid draws from Bernoulli(P_{x1, x2}). Taking expectation of ${\left\{Z_{{\gamma }_j}\right\}}_{j=1}^{\infty }$ with respect to Bernoulli((P_{x1, x2})),

$$E\left[\mathrm{Corr}\right\{G_{{\mathbf{x}}_i}\left(B\right),G_{{\mathbf{x}}_2}\left(B\right)\left\}\right]=\frac{2}{\alpha +2}{P}_{{\mathbf{x}}_1,{\mathbf{x}}_2}\sum _{j=1}^{\infty }{\left(\frac{\alpha }{\alpha +1}\right)}^{j-1}E\left[{\left(\frac{\alpha +1}{\alpha +2}\right)}^{Y_j}\right],$$

where Y_j ~ Binomial(j − 1, P_x1,x2). Using the Binomial Theorem, the expectation on the right is marginalized out with respect to Binomial(j – 1, P_x1,x2), which results in

$$\mathrm{Corr}\left\{{G_{\mathbf{x}}}_1\right(B),{G_{\mathbf{x}}}_2(B\left)\right\}=\frac{2}{\alpha +2}{P}_{{\mathbf{x}}_1,{\mathbf{x}}_2}\sum _{j=1}^{\infty }{\left[\frac{-\alpha P_{{\mathbf{x}}_1,{\mathbf{x}}_2}}{(\alpha +2)(\alpha +1)}+\frac{\alpha }{\alpha +1}\right]}^{j-1}.$$

Since $\mid \frac{-\alpha P_{{\mathbf{x}}_1,{\mathbf{x}}_2}}{(\alpha +2)(\alpha +1)}+\frac{\alpha }{\alpha +1}\mid \le 1$, the infinite sum on the right converges. Then,

$$\mathrm{Corr}\left\{G_{{\mathbf{x}}_1}\right(B),G_{{\mathbf{x}}_2}(B\left)\right\}=\left(\frac{2P_{{\mathbf{x}}_1,{\mathbf{x}}_2}}{\alpha +2}\right)\left(\frac{(\alpha +2)(\alpha +1)}{\alpha (1+P_{{\mathbf{x}}_1,{\mathbf{x}}_2})+2}\right)=\frac{2P_{{\mathbf{x}}_1,{\mathbf{x}}_2}(\alpha +1)}{(1+P_{{\mathbf{x}}_1,{\mathbf{x}}_2})\alpha +2}.$$

Proof of Theorem 4 Due to the marginal DP property and using the inequality on the left in (11) with n = 1, we get $\mid \mid {\mu }_N\left(\mathbf{x}\right)-{\mu }_{\infty }\left(\mathbf{x}\right)\mid \mid \le 4\left(1-E\left[\left({\sum }_{h=1}^{N\left(\mathbf{x}\right)-1}{p}_h\right)\right]\right)$, where μ_N, μ_∞, N in (11) are replaced by μ_N(x), μ_∞(x), N(x), respectively, and n is substituted by 1. Here, N(x) is random differently from N in (11). Conditioned on N(x) but marginalizing out p_h, we get $\mid \mid {\mu }_N\left(\mathbf{x}\right)-{\mu }_{\infty }\left(\mathbf{x}\right)\mid \mid \le 4E\left[{\left(\frac{\alpha }{1+\alpha }\right)}^{N\left(\mathbf{x}\right)-1}\right]$. Note that N(x) ~ Binomial(N, P_x) as discussed in Sect. 3.3. Then, using the Binomial Theorem, we obtain $\mid \mid {\mu }_N\left(\mathbf{x}\right)-{\mu }_{\infty }\left(\mathbf{x}\right)\mid \mid \le 4\left(\frac{\alpha +1}{\alpha }\right){\left[1-\left(\frac{1}{\alpha +1}\right)P_{\mathbf{x}}\right]}^N$.