Abstract
Peripheral T cell populations are maintained by production of naive T cells in the thymus, clonal expansion of activated cells, cellular self-renewal (or homeostatic proliferation), and density dependent cell life spans. A variety of experimental techniques have been employed to quantify the relative contributions of these processes. In modern studies lymphocytes are typically labeled with 5-bromo-2′-deoxyuridine (BrdU), deuterium, or the fluorescent dye carboxy-fluorescein diacetate succinimidyl ester (CFSE), their division history has been studied by monitoring telomere shortening and the dilution of T cell receptor excision circles (TRECs) or the dye CFSE, and clonal expansion has been documented by recording changes in the population densities of antigen specific cells. Proper interpretation of such data in terms of the underlying rates of T cell production, division, and death has proven to be notoriously difficult and involves mathematical modeling.
We review the various models that have been developed for each of these techniques, discuss which models seem most appropriate for what type of data, reveal open problems that require better models, and pinpoint how the assumptions underlying a mathematical model may influence the interpretation of data. Elaborating various successful cases where modeling has delivered new insights in T cell population dynamics, this review provides quantitative estimates of several processes involved in the maintenance of naive and memory, CD4+ and CD8+ T cell pools in mice and men.
2 Introduction
Despite great advances in immunological research during the last decades, relatively little is known about the quantitative characteristics of lymphocyte population kinetics. There are widely divergent estimates of the production rates, division rates, and life-spans of mouse and human lymphocyte populations [28]. As a consequence, fundamental issues like the maintenance of memory, the maintenance of a diverse naive lymphocyte repertoire, and the nature of homeostatic mechanisms remain largely unresolved, and may be different in different species. Thus, while mice are the most frequently studied experimental animal in immunology they may not provide information directly applying to humans [57]. Many current questions in immunology are of a quantitative nature. For example, it is important to reveal how human diseases such as HIV infection and rheumatoid arthritis, and therapeutic interventions such as chemotherapy or hematopoietic stem cell transplantation affect lymphocyte kinetics, but as long as there is controversy about the lymphocyte kinetics in healthy individuals such questions remain difficult to address.
Recently, several experimental techniques have been developed that have enabled the generation of quantitative data on lymphocyte dynamics. Some are based on the quantification of natural properties of lymphocytes that change with their kinetics, such as lymphocyte telomere lengths and T cell receptor excision circles (TRECs). Others have made use of different lymphocyte labeling techniques, using agents such as the fluorescent dye carboxy-fluorescein diacetate succinimidyl ester (CFSE), the base analog 5-bromo-2′-deoxyuridine (BrdU), deuterated glucose (2H2-glucose), or heavy water (2H2O). Although these techniques are used widely, the interpretation of kinetic data obtained using these labeling methods has turned out to be notoriously difficult [6, 8, 41, 45, 46, 51, 56, 79, 81, 103, 162, 163, 186, 188, 189]. Here we review how mathematical models have given insights into the possibilities and limitations of the different experimental techniques, and have thereby helped the quantitative interpretation of immunological data.
Immunology papers using mathematical modeling to better interpret experimental data typically describe the details of the model in an appendix or a methods section. This is natural because the mathematical details tend to be poorly appreciated by the general readership of these journals, but it is also unfortunate because in several studies these technical details on the mathematics do matter as much as the details of the experimental setup. For example, if the same BrdU data is fitted with different mathematical models, estimated turnover rates that result may differ [28, 45, 46]. Similarly, labeling the same T cell populations with the seemingly so similar methods of using deuterated glucose or deuterated water, yields labeling curves that are so radically different [28] that different mathematical models are required for proper interpretation of the methods. For these reasons we provide a technical review that contains mathematical details so as to fairly present the advantages and disadvantages of the various models that researchers currently use to interpret experimental data on T lymphocyte turnover.
In addition to the mathematics details we need to provide a necessary background in immunobiology of T lymphocytes. T cell populations are comprised of millions to billions of clones that carry a unique T cell receptor (TCR) defining the binding affinity of that clone to complexes of short peptides bound to molecules of the major histocompatibility complex (MHC). Clones are said to be specific for a particular combination of a peptide bound to an MHC (pMHC) when the binding affinity of this pMHC ligand to the TCR characterizing the clone is sufficient to activate the T cells of that clone. A pMHC complex is typically called an epitope (or an antigen), and if the peptide is derived from a protein within the body it is called a self epitope, otherwise it is a foreign epitope. T cells typically only respond to foreign epitopes because the clones specific for self pMHC complexes are inactivated during their development in the thymus. T lymphocytes are subdivided into two major populations, CD4+ helper T cells and CD8+ cytotoxic T cells, having different functions and activation requirements. CD8+ T cells are activated upon recognition of peptides bound to class I MHC molecules that are present on almost every cell in the body. Cytotoxic T cells will kill infected cells and tumor cells that present foreign peptides on their MHC molecules, and because they are restricted to MHC class I they can kill infected cells of almost any cell type. CD4+ T cells bind peptides bound to class II MHC molecules that are present on antigen presenting cells like dendritic cells and macrophages. Helper CD4+ T cells produce cytokines that orchestrate the cellular CD8+ T cell responses, and the humoral responses of B cells that produce antibody.
Each T cell clone is further subdivided into naive, activated, effector, and memory cells. Naive T cells are defined as cells that have never been activated by foreign pMHC. They are generated in the thymus where they mature from progenitor cells arriving there from the bone marrow. After a few weeks they leave the thymus to become peripheral naive T cells that circulate through the spleen and lymph nodes via the blood and the lymph. Within these lymphoid tissues, naive T cells have a small chance to become activated (i.e., primed) by foreign epitopes. Such an event will trigger a specific immune response as the primed naive T cells slowly enter a phase of rapid cell division, called clonal expansion. After a few days of proliferation the initial small clone of naive T cells will have expanded into a large clone of effector cells that leave the lymphoid tissue to migrate to inflamed tissues to clear the antigen. After about a week, the immune response strongly contracts, mostly by apoptotic cell death, leaving behind a subpopulation of memory T cells that persist for a long time. Both naive and memory T cell pools are maintained by a process called “renewal”, which amounts to infrequent and probably stochastic cell divisions [36, 93]. To have stable naive and memory pool sizes the renewal process has to depend on the population density, which may mechanistically come about by non-specific competition for cytokines, e.g., IL-7 and IL-15, and specific competition for ligands like self pMHC. The maintenance and normal turnover rate of the pools of naive and memory T cells is one of the main subjects of this review. Since MHC molecules typically bind several peptides from the various proteins of a pathogen, infections trigger a number of different naive T cell clones to undergo clonal expansion and contraction. The largest clone during an immune response is said to be immunodominant.
3 General models for the immune response
The mathematical models used for describing the population kinetics of T lymphocytes are typically written as ordinary differential equations (ODEs) defining the rate at which the populations change over time, in units of say cells per day. The most common class of models to describe an immune response resembles ecological predator-prey models where the immune effectors are the predators clearing a prey-like pathogen that is stimulating the effectors to grow [4, 50, 169]. A general predator-prey type model for the immune response to an exponentially growing pathogen, e.g., B (for bacteria), can be written as
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where, , is a saturation function of the concentration of the pathogen, and h defines the pathogen concentration at which the function is half-maximal; i.e., when . The variables N, A, and M are the naive, activated, and memory T cells of one clone of T cells responding to this antigen. We assume that naive T cells become activated by the pathogen at rate , the activated cells then proliferate at rate , and enter the memory pool at rate [48]. Memory T cells are assumed to self-renew at rate rM and become activated at rate . Naive, activated and memory cells die at rates, dN, dA, and dM, respectively. Note, the activation, a, and proliferation, p, rates were made proportional to whereas the deactivation rate, m, of activated cells into memory cells was made proportional to () [48]. For such a clone of cells the source of naive cells from the thymus, σ, will be small, and should in fact be treated as a stochastic variable. In Fig. 1 where we show numerical solutions of this model, we therefore set the source to zero, and start the immune response with a clone of one hundred naive T cells. The pathogen is killed by the activated cells, which we here assume are immune effector cells, according to a mass-action term kBA, where k is a killing rate [75]. The r and d parameters in this model are renewal rates, and death rates, respectively. This model forms a basis that we will simplify to study a specific acute immune response, and to study the average turnover rates of naive and memory T cells with labeling techniques.
Figure 1.
The immune response of one antigen-specific clone modeled by the ODE model given by Eqs. (1-5). The activation function, (heavy black line), is determined by the antigen concentration of Eq. (1) (which is not shown). At time zero one clone of a 100 naive T cells (N: light black line) becomes activated and starts to proliferate (A or P: red). After about one week proliferation stops because the activation function drops to zero when antigen is rejected. Choosing parameter values that are reasonably realistic for humans, we start with one clone of a hundred naive T cells, i.e., σ = rN = 0, dN = 0.001 day−1, aN = day−1. Effector cells, E, disappear by rapid cell death, dE = 1 day−1, and a small fraction become memory cells, m = 0.05 day−1. Memory cells accumulate and have an expected life span of a hundred days (rM = 0; aM = 1 and dM = 0.01 day−1).
In a more realistic version of this model, the parameters which are here treated as constants, could be replaced by functions of the age of the infected individual and the cell population densities. For instance, thymic output σ declines with age, the renewal rates, r, are expected to decline with cell population density, and the cell death rates, d, are expected to increase with population density, due to competition for resources like space and cytokines [73]. Additionally, the mechanisms by which memory T cells are formed during or after an immune response remain poorly understood, and we here simply write that a fraction of the short-lived activated T cells revert to long-lived memory cells when the antigen concentration is low.
Depending on the antigen concentration, activated cells proliferate at a rate . De Boer & Perelson [50] derive various functional forms for the proliferation rate from a generalized Michaelis-Menten analysis of the process of T cells binding antigen presenting cells, and propose various saturation functions like Eq. (5) allowing for a maximum proliferation rate when antigen concentrations are high. Alternatively, one can assume mass-action kinetics by replacing Eq. (5) with and obtain Lotka-Volterra like predator-prey models for the immune response [169, 170]. An example of the behavior of this model using the saturation function of Eq. (5), and parameter estimates for a human immune response, is shown in Fig. 1. There are too little data on acute immune responses in humans to know whether or not this behavior is realistic for a vigorous infection in humans, but we do know that Fig. 1 realistically describes the vigorous immune response of mice infected with the lymphocytic choriomeningitis virus (LCMV) (see Fig. 2). Note that in Fig. 1 the activation function, , gradually approaches one, and rather abruptly switches off when the antigen is cleared after about one week. During the initial phase is small, allowing the formation of some memory cells, which maybe somewhat unrealistic, although there are some reports of early generation of some memory cells during immune response to epitopes of low avidity [246]. However, in the model most memory cells are formed after the clonal expansion phase (Fig. 1).
Figure 2.
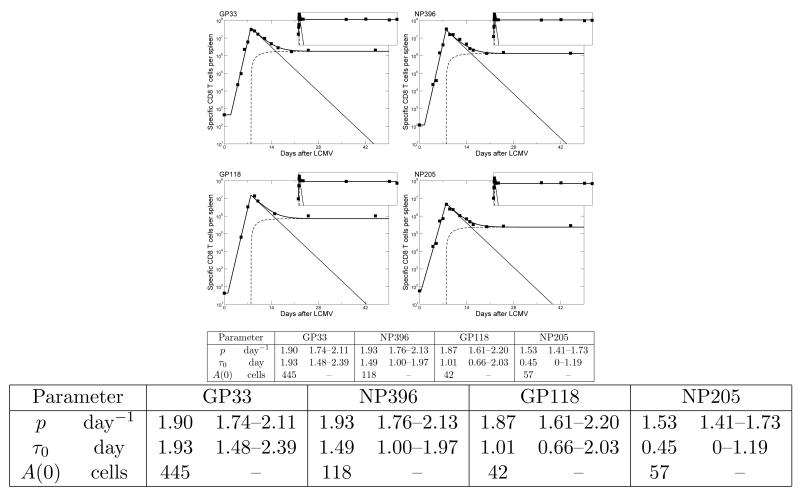
Fitting the model of Eqs. (6-7) to the data of Homann et al. [107] using the precursor frequencies estimated by Kotturi et al. [131], and given in the Table above as the A(0) values. The data is comprised of the CD8+ T cell responses to four epitopes from LCMV (GP33, NP396, GP118 & NP205), for which we have both time course data and estimates for the initial number of precursor cells. The light solid lines depict the total number of activated cells, A, per spleen, the dashed lines show the corresponding number of memory cells, M, and the heavy solid lines give the total, T = A+M, number of cells that was fitted to the data (symbols) using non-linear least-square regression [153]. Each inset shows the same data over a time span of 921 days. Ranges in the table indicate 95% confidence intervals determined by bootstrapping the residuals one thousand times. Common parameters: dM = 0, dA = 0.395 (0.330-0.479) day−1, m = 0.019 (0.015-0.023) day−1, τ = 7.91 (7.71-8.11) days. Allowing dM > 0, or allowing any of these common parameters to vary between the epitopes hardly improved the quality of the fit. These four fits are similar to those of De Boer et al. [44] and only extend them with the precursor frequencies estimated by Kotturi et al. [131].
Because pathogens like Listeria monocytogenes (LM) and LCMV replicate rapidly and evoke vigorous immune responses, cells are hardly limited by antigen availability, implying that most naive T cells are triggered rapidly, and swiftly adopt the maximal proliferation rate [10, 107, 120]. In some work the activation function, , has therefore been simplified by arguing that there is a time point, τ0, at which all naive T cells start to proliferate at the maximal rate [48]. Similarly, in these vigorous infections all immune responses seem to shut down at approximately the same time, τ, which is called the peak of the response, after which contraction starts (Fig. 1). Such a program of cell expansion followed by a contraction phase can conveniently be modeled by an on/off function
| (6) |
Note that here is a function of time, t, rather than of the antigen load, B. To fit the experimental data from acute immune responses to viruses and bacteria we have used Eq. (6) to reformulate Eqs. (2-4) of the general model into a piecewise linear model for the response to one specific epitope:
| (7) |
where A is the number of activated cells, and M is the number of memory cells of a population of T cells that are specific for the epitope of interest, and we use T = A + M to define the total size of the immune response. For a primary immune response, one sets M(0) = 0 and A(0) = A(τ0) as the initial number of cells. Then A(τ) = T (τ) is the total number of cells at the peak of the response, since in this strict on/off model memory cells only start to form after the peak [44, 48]. The number of epitope specific precursor cells, A(0), varies and is 10-1000 cells per mouse depending on the epitope [9, 24, 93, 131, 164]. To illustrate that this model describes the data well, we have combined the time course data of four CD8+ T cell immune responses to LCMV [107] with their estimated initial precursor densities [131], and fitted Eqs. (6-7) to the data (see Fig. 2). The experimental data typically provide the total number of T cells that are specific for one particular epitope from this mouse virus, which in Eq. (7) corresponds to A(t) when t ≤ τ and A(t) + M(t) after the peak. Note that this piecewise linear model has a behavior resembling that of the larger ODE model (Eqs. (2-4)) that also includes naive T cells (compare Figs. 1 with 2).
Another approach for modeling the clonal expansion phase of an immune response is to explicitly write a cascade of equations that follow every division that the cells have completed [119]. Activation of naive or memory T cells recruits the cells into the first stage of the proliferation cascade, P0, where the index denotes the number of completed divisions. For the closure of clonal expansion one assumes that after a certain number of divisions the cells differentiate into effector cells, E, that will leave the lymphoid tissue to clear antigen, and become memory cells
| (8) |
| (9) |
| (10) |
where can be either a function of time, or the concentration of antigen, and nmax is the number of divisions cells complete during clonal expansion. Equation (2) for the naive T cells can stay the same, but the first term in the memory cell equation, Eq. (4), has to become . Because the birth-death ODE model of Eq. (9) is linear it implicitly assumes an exponential distribution of cell cycle times. This allows cells to rapidly proceed through the whole division cascade [51], and effector cells will appear immediately after the P0 compartment is populated by activation. This model therefore does not allow for a strict time window of clonal expansion, and to allow for this one needs models with strict time delays representing the minimal time to complete cell division [51].
The rules determining the proliferation of cells during clonal expansion are not completely understood. During the vigorous immune responses to LM and LCMV lymphocytes continue to proliferate when the pathogen is removed, and all response seem to stop at approximately the same time, even if antigen persists. It has therefore been suggested that predator-prey models, where clonal expansion depends on the antigen concentration (i.e., the prey feeding the predator), are inadequate, and that one should resort to on/off models like that of Eqs. (6-7), allowing for a “programmed” immune response where the “off-time” is not dependent on the concentration of antigen [4, 5]. There are various ways to implement such a program. Even the simple saturation function, , used in Eqs. (2-4) made the immune response relatively independent of the concentration of antigen (Fig. 1), due to the assumed rapid growth of the pathogen which causes to rapidly change from 0 to 1. With the on/off model, Eqs. (6-7), one can easily define a programmed response, allowing cells to proliferate within a certain time window that is determined by an externally defined signal [4]. The nature of the signal is not known but could be inflammation, cytokines or chemokines [5, 129]. Alternatively, with the cascade model of Eq. (9) one could define a program with an intra-cellular signal (or internal signal [4]) allowing each cell to perform a pre-defined number of divisions. In strong immune responses where most naive T cells are triggered at approximately same time, these different programs result in very similar behavior [4].
To correctly model a program where individual cells proliferate for a certain amount of time following activation one can write an age-structured population model [59], or formulate the model as a system of delay differential equations (DDE) [59, 78]. To illustrate the latter approach we again split the activated cells of Eq. (3) into into proliferating activated cells, P, and effector cells, E, that have completed their clonal expansion. One then writes
| (11) |
| (12) |
According to this the model primed naive T cells, N, are involved in clonal expansion for a period of τN days during which time they divide at rate p and die at a rate dP. At the end of this proliferative phase they move into the effector population. The e(p−dPτ) terms are the net dimensionless clonal expansion factors describing the expected clone size per primed cell given the division rate p and the death rate dP. The H(t − τ) terms are Heaviside functions preventing the usage of negative time points, i.e., H(t) = 0 whenever t < 0 and H(t) = 1 otherwise. Memory cells, M, maintain themselves by division (i.e., self-renewal), at rate rM, die at rate dM, and may become primed by antigen at rate, aM, to perform another round of clonal expansion for τM days. Formulating clonal expansion in delay differential equations is mathematically convenient, but need not be the best formulation for studying the model numerically. The exponential growth term, pP, in Eq. (11) has to be compensated exactly with the large delayed expansion terms, and we have observed numerically instabilities solving this model, even using the excellent retard algorithm described in [86].
We have studied the behavior of this model after omitting the pathogen growth and killing of Eq. (1), and after replacing by a simple on/off function if 0 < t < 5, and otherwise). Thanks to the time window of clonal expansion and the subsequent contraction phase, the model does a good job describing acute immune responses to pathogens (compare Fig. 3 that is parameterized for humans with Fig. 2 showing four dominant CD8+ T cell responses in B6 mice to LCMV). The naive T cells are strongly depleted by the activation until day five, and start to proliferate rapidly for one week. Contraction starts around day seven because most naive cells have completed their seven days of clonal expansion (τN = 7), and although antigen is absent () from day five onwards, the formation of memory cells only starts at day seven after Fthe completion of clonal expansion. Note that each naive T cell has ep7 = 1097 expected progeny, i.e., expands about a 1000-fold. Following the peak, the contraction of the effector cells is relatively slow and appears to be dominated by the relatively slow recruitment of the naive T cells because their respective logarithmic down-slopes run parallel until day 12, which corresponds to the end of naive T cell activation plus one week of clonal expansion. Indeed, increasing the activation of naive T cells (aN) 10-fold gives a much sharper peak and a steeper contraction rate that now reflects the rapid death of effector cells (dE = 1 day−1) (see Fig. 3b). Finally, we allow for reactivation of memory cells by considering a chronic infection during which antigen persists by defining if 0 < t < 5, and otherwise (see Fig. 3c). The dynamics of immune responses to persistent pathogens are important, but poorly understood. According to this model a chronic immune response can be maintained by reactivating memory cells and having repeated rounds of clonal expansion (Fig. 3c), and/or by increased renewal rates of memory cells specific for persistent foreign antigens (not shown).
Figure 3.
The immune response of one antigen-specific clone modeled by the DDE model given by Eqs. (2) & (4) and Eqs. (11) & (12). The activation function switches at predefined time points: in Panels (a & b) when t < 5 days and otherwise, whereas in (c) we let antigen persist by defining when t > 5 (which falls off the scale of the vertical axis). At time zero one clone of a 100 naive T cells (N: black) becomes activated and starts to proliferate (A or P: red). After about one week the response starts to contract because for most cells the time window of proliferation, τN = 7 days, has ended. After day seven effector cells (E: green) and/or memory (M: blue) cells are formed. The parameters are the same as those in Fig. 1 and are reasonably realistic for humans. In Panel (a) we mimic Fig. 1 by setting aN = 1 day−1 and in Panels (b & c) we increase the activation of naive T cells 10-fold to aN = 10 day−1. In Panel (c) memory cells are reactivated because from day five onwards. By repeated rounds of reactivation of memory T cells and proliferation a chronic immune response is maintained.
Finally, division cascade models like Eq. (9) have been used many times for modeling immune responses and renewing cells in a homogeneous population [7, 47, 51, 77, 79, 176, 186, 238]. Because self renewal is in theory not bounded by a maximum number of divisions, unless cells run into the Hayflick limit [142, 180], one can write an infinite cascade of random birth death equations that in keep track of the number of divisions cells have completed. Subdividing the cells into subpopulations, Pn, that have completed n divisions one would write
| (13) |
where n is the number of divisions cells have completed. If P (t) is the total number of proliferating cells at time t then . For the initial condition P0(0) = T(0) and Pn(0) = 0 for n = 1, …, ∞, where T (0) is the initial number of undivided cells, the general solution is
| (14) |
where is the total number of divided cells, and the second term of the right hand side of Eq. (14) gives the distribution of the cells over the division numbers. This is a Poisson distribution
| (15) |
with a mean, μ, and variance, σ2, both increasing linearly in time with a slope 2p [47, 51, 79].
Another approach is to normalize Eq. (13) by the number of divisions the cells have completed [81, 91, 168, 227], by defining ρn = Pn/2n. Then
| (16) |
By letting the normalized total, , one then has and ρ(t) = ρ(0)e−dt. From the general solutions in Eq. (14) one writes ρn(t) = ρ(t)gn(t) where ρ(0) = ρ0(0) = P(0) is the initial number of proliferating cells, and where gn now is a Poisson distribution with mean and variance
| (17) |
Both models are very general and have been used extensively to study telomere erosion [47, 238], CFSE [7, 51, 79, 186], and BrdU dilution [77, 176] (see the next sections).
3.1 Quantifying immune responses by fitting these models to data
Vigorous infections with rapidly replicating pathogenic bacteria, like LM, or viruses, like the well-studied mouse virus LCMV, trigger strong innate and adaptive immune responses. Since clonal expansion typically continues after the pathogen has been cleared [135], it has been suggested that after proper antigenic stimulation the acute immune response of T cells is programmed, and no longer determined by the current concentration of antigen [4, 5, 107, 120, 217]. Badovinac et al. [10] treated LM infected mice with antibiotics and showed that clonal expansion continued, although the peak response was somewhat lower than in untreated control animals. They also showed that the contraction after the peak takes place even if the antigen persists [10].
As illustrated in Figs. 2 and 3, a programmed response can be modeled with a piecewise linear model as described by Eqs. (6-7), or the more elaborate DDE model of Eqs. (11-12). Eqs. (6-7) have been used extensively to fit data from the cellular immune responses in mice to LCMV. At the time this model was fitted to the data from various CD8+ immune responses to LCMV [44, 48] there were no measurements from early time points because one could not detect the small individual clones before cells were expanded by proliferation. De Boer et al. [48] used this model to fit data from CD8+ T immune responses to two LCMV epitopes (NP118 & GP283) in BALB/c mice assuming that both responses started with A(τ0) = 60 cells per spleen [24]. When data on several more immune responses in C57BL/6 mice became available [107], it was no longer reasonable to assume that these all started with similar precursor frequencies [44]. Since one cannot estimate both the time of onset, τ0, and the initial condition A(τ0), in the absence of data from such early time points, the model of Eqs. (6-7) was simplified by setting τ0 = 0, and by interpreting the initial condition A(0) as a generalized recruitment parameter, i.e., as the initial number of cells that would be needed to proliferate to the level A(τ0) at time τ0 [2, 44]. The larger A(0), the larger the presumed precursor frequency and/or the earlier and the better the precursor cells were triggered by antigen. Formally we assumed that A(τ0) = A(0)epτ0, and estimated A(0) from the data by ignoring the initial time delay and letting clonal expansion start at time zero [44]. Since the first data point was at day four (which is known to be later than τ0) this does not affect the estimates of the other parameters (p, dA, dM, and m).
Using non-linear least-square regression [153], Eqs. (6-7) with τ0 = 0 was fitted to the data from the CD8+ T cell responses to six epitopes from LCMV (GP33, NP396, GP118, GP276, NP205 & GP92), where the major question was to identify the kinetic differences between these immune responses [44]. Fitting all data simultaneously, allowing only the proliferation rate, p, and the recruitment parameter, A(0), to vary, the model described the data well, i.e., with similar quality to the fits as those shown in Fig. 2, where τ0 was allowed to vary. For the four dominant epitopes we estimated a maximum proliferation rate of p = 1.9 day−1 (i.e., a doubling time of 8 hours), an apoptosis rate of dA = 0.4 day−1, and deactivation rates of m = 0.02 day−1. The two sub-dominant epitopes, i.e., NP205 and GP92, required somewhat slower proliferation rates, i.e., p = 1.5 day−1 and p = 1.1 day−1, respectively. Thus, the model described the four largest immune responses very well while assuming they had identical kinetic parameters, and differed only in their recruitment parameter A(0) [44]. Understanding the mechanisms underlying the immunodominance ranking of the various immune responses is an important general question in immunology.
As shown in Fig. 2, memory cells did not decline over the 2.5 years of the experiment, i.e., dM ≃ 0, which is probably due to a steady state being established between their renewal and death [36] (see below in the section on CFSE labeling). In Eq. (7) self-renewal of memory cells is ignored, so dM = 0 represents this steady state. The six responses all peak around τ = 8 days, but differ in magnitude at that time. The largest response is called immunodominant and was comprised of more than 107 cells per spleen. Using an estimated initial condition of approximately a 100 cells [24, 131], this corresponds to a 105-fold expansion, or approximately 16-17 cell divisions (i.e., 216 < 105 < 217) assuming no death during the clonal expansion phase. As expected, these results remain very similar when we now add the more recently estimated precursor frequencies [131] to a subset of the epitopes (see Fig. 2).
The original analysis suggested that the immunodominance ranking of the largest responses was mainly determined by their initial recruitment, and that the antigenic stimulation of the clones comprising the smallest responses may have been suboptimal [44]. The significant role that the initial precursor frequency plays in determining the immunodominance ranking was confirmed by Kotturi et al. [131], who found a strong positive correlation between the naive precursor frequency and the response hierarchy after LCMV infection (see also Fig. 2). Other factors found to influence the immunodominance ranking were the affinity with which a peptide binds MHC [131], and the functional avidity of the T cells for the pMHC complex [185]. The latter plays a complicated role as the functional avidity increases over time [185, 197].
The model of Eqs. (6-7) was extended with a biphasic apoptosis phase to fit the data on CD4+ T cell responses in these mice. We found that CD4+ T cell responses have a somewhat slower maximum proliferation rate, i.e., p = 1.5 day−1 (i.e., a doubling time of 11 hours), they peak approximately one day later (τ ≃ 9 days), and have a slower and biphasic contraction phase [44]. Because CD4+ T cells proliferate more slowly the magnitude of their immune responses tends to be lower than that of CD8+ cells. Interestingly, the population size of the memory CD4+ T cells was not stable as the density of these cells in the spleen declined with a half-life of 500 days [44]. In these experiments it was not determined whether CD4+ memory cells could have left the spleen and accumulated in the bone marrow [206-208].
Several variants of mouse LCMV exist, and these evoke quite distinct infections. The data discussed above were all derived from infections with LCMV Armstrong which causes a vigorous acute infection that is cleared within a week. Another variant, called “clone 13”, causes at least as vigorous an acute infection, but establishes a chronic infection with high virus loads in several organs. Genetically these two viral variants are very similar, differing in only a few amino acids [155, 156]. Hence they evoke the same set of CD8+ T cell immune responses during phase of the acute infection. Clone 13 is probably more virulent because it also infects interdigitating dendritic cells, which reduces antigen presentation when these cells are cleared by CD8+ effector cells [29]. To investigate the kinetic differences between the CD8+ immune response during acute and chronic infection, Eq. (7) was fit to data from LCMV Armstrong and clone 13 infections from various laboratories [2]. The main differences between the specific immune responses were that (1) the peak of the response occurred about one day earlier, and (2) the apoptosis rates during the contraction phase were faster in responses to clone 13 compared to those to LCMV Armstrong [2]. One possible interpretation is that the immune system shuts off earlier and more prominently when it is unsuccessful, and the infection becomes chronic. Around day seven when the clone 13 response has its peak, the viral load is much higher than that of LCMV Armstrong.
Comparing data from different laboratories, Althaus et al. [2] found that there are large differences in the observed magnitudes of the immune responses to the same antigens across laboratories, which are probably related to the procedures used for estimating total cell numbers. Generally, it is much more difficult to count total cell numbers in, for instance, a spleen, than to estimate relative frequencies of different populations (which is readily achieved by flow cytometry). Allowing for a “fudge” factor to scale the differences in total population sizes reported by the different laboratories, Althaus et al. [2] found that kinetic parameters like the proliferation and death rates, and the time of the peak, were much more similar than total cell numbers. Miller et al. [160] performed thymectomy (i.e., surgical removal of the thymus) before mice were infected to study the importance of continuous recruitment of recently produced naive T cells into an ongoing immune response to LCMV. Fitting Eq. (7) to that data it was found that the effect of thymectomy can simply be explained by the lower numbers of precursor cells, A(0), that one expects to be present in thymectomized mice [2].
Since lymphocyte populations grow exponentially during immune responses and their densities vary over several orders of magnitude it seems reasonable to log-transform the data before they are fitted with Eq. (7); otherwise the highest data points dominate the summed squared residuals. Statistically speaking, the choice between using the raw data or first performing a log-transformation formally depends on the nature of the errors in the data. Measurement noise in these cell counts is most likely to be a relative error, arguing that log-transformation is the appropriate model. Milutinović & De Boer [161] confirmed that log-transformation provides the best explanation of the data, but even then the model is only consistent with the data if there is substantial measurement error. Although, large measurement noise is normal in this type of experimental data, they proceeded to explore the noise that one is expected to see when Eq. (7) is treated as a stochastic process. This variation arising from the stochasticity of the interactions between individual cells is defined as “process noise”. Milutinović & De Boer [161] wrote master equations for the expected cell numbers during the expansion and contraction phases, performed stochastic Gillespie [82] simulations, and found that 50% of the total variance could be attributed to process noise. Although this argues that process noise cannot a priori be neglected, the estimated contribution of 50% of the total variance is an upper bound because the authors started their stochastic process with A(0) cells at time zero, and should have started with A(τon) cells at the time τon when clonal expansion starts. The latter was not possible, however, because there was no data allowing one to estimate τon and A(τon). Using system size expansion [216], the corresponding Langevin equations were derived (arguing that this should be reasonable approximation given the fairly large cell numbers [161]). Assuming a Gaussian distribution for the measurement noise, the Langevin equations were used for maximum-likelihood parameter estimation (now avoiding the τon problem by starting with the first data point at day four). This resulted in fairly similar parameter estimates as found with the deterministic model [44], reduced the standard deviation of the relative error in a single measurement to 30%, and made process noise the dominant source of variation in the data [161]. The large effect of variations in the initial number of precursors was later confirmed by Kotturi et al. [131], who found large variations in the initial precursor frequencies of individual mice so that clones that typically dominate the immune response can be very minor in some mice.
The exact mechanism by which memory cells are generated during and after an immune reaction has been debated widely in immunology [80]. The model given by Eq. (7) describes only one possible mechanism. However, Antia et al. [5], Kohler [128] and Ganusov [74] have developed and evaluated a set of mathematical models on the basis of how well they explain various data sets on T cell memory. For instance, the LCMV data discussed above were also modeled assuming that both memory and effector cells can be formed beginning at the time the cells are triggered into clonal expansion, and that both cell types expand at the same rate p [128]. Two variants of this alternative model were considered, one in which memory cells become effector cells, and another where effectors cells become memory cells (like in Eq. (7)). These models have the same number of parameters as Eq. (7), i.e., p, dA, dM, and m, and an initial cell number P (0) or M(0), and all fit the data equally well [128]. Most of the parameter estimates derived from fitting these various models to data were very similar, suggesting that these are fairly robust biological estimates [42, 158], and the main difference was in the transition rate, m, between memory and effector cells, which has a different interpretation in each of these models [128].
Although the concept of a programmed response seems reasonable for T cell responses during vigorous infections, proliferation does depend on the antigen concentration in conditions when antigen is limiting [4, 5]. Kaech & Ahmed [120] infected mice with various doses of LM and reported that the antigen dose largely determines the fraction of CD8+ T cell precursors that were recruited into proliferation. Once recruited, the number of divisions that were completed by the cells hardly depended on the initial dose of LM, which suggested a strict program. Subsequent mathematical modeling of that data demonstrated that the program was not strict, and that the rate at which cells were proliferating was correlated with the fraction of cells recruited, i.e., with the antigen dose [4, 5]. Recent experiments measuring the recruitment of individual CD8+ T cell precursors into immune responses to various doses of LM conversely suggest that the recruitment is nearly complete at all doses, and that the magnitude of the response is largely determined by the degree of clonal expansion [215], which –for unknown reasons-contradicts the data of Kaech & Ahmed [120].
It has been argued that the acute immune response of CD4+ T cells is not as “programmed” as that of CD8+ T cells, as it depends much more strongly on the antigen concentration [184, 235, 240], but also see Corbin & Harty [38] for the opposite result. Further, recent data tracking the size of a TCR transgenic CD4+ T cell clone during an acute immune response to pigeon cytochrome c by deep sequencing, suggested that the maximal expansion of that clone depends strongly on the initial number of precursor cells [25, 184]. Varying the initial precursor density from 3 to 3 × 104 cells per mouse the population density after one week of proliferation and subsequent contraction was approximately cells, where P0 is number of naive precursors [25]. This difference in clonal expansion came about at a late stage in the response, and was not due to differences in recruitment, because before day three the fold expansion seemed independent of the precursor density. Using a 6 hour pulse of BrdU labeling (see below) it was shown that between day three and five in the response about 60% of the cells had divided (i.e., picked up BrdU) when the response started with 300 cells, whereas only 20% (day 4.5) to 40% (day 3.5) of the cells had divided when starting with 30,000 cells [25, 184]. During this immune response of one week the fraction of dividing cells declined for both precursor densities over time, starting to decline at least around day four for the high density, and around day five for the low density. Indeed the peak of the response occurred earlier when the initial precursor density was higher, and the estimate peak size of the response was well described by [25].
This data was fitted to a mathematical model where cells, after priming by antigen, differentiate from slowly dividing cells, to rapidly proliferating cells, to non-dividing cells, to non-divided mature cells [25]. In the model, the mature cells in the developmental cascade down-regulate the differentiation of slowly dividing cells into rapidly proliferating cells. This allows for a similar initial expansion that is independent of the initial precursor frequency, because the regulatory mature cells only appear later, and for earlier and increased downregulation of the expansion at large population sizes [25].
De Boer & Perelson [52] have re-analyzed the same data to study whether a mechanism where T cells acquire cognate pMHC complexes from the surface of antigen presenting cells (APCs), thereby increasing the loss rate of pMHC, can also be responsible for the tight regulation of T cell expansion over four orders of magnitude of precursor densities. During cognate interactions with APCs, CD4+ T cells tend to acquire a variety of cell surface molecules, including the antigen specific pMHC complexes binding the T cell receptors in the immunological synapse [111, 113, 122, 201, 232, 233]. This leads to a form of antigen specific competition between T cells binding the same pMHC on the same APCs [122, 236], which would be perfectly consistent with the observations of Quiel et al. [184] because T cells of another specificity hardly affected the fold expansion. Their observation that increasing the antigen concentration, or the density of APCs, increased the fold expansion at all precursor densities in a similar manner [184], indeed suggest that pMHCs on APCs become a limiting resource at all precursor densities tested. Developing a simple mathematical model implementing this “T cell grazing” mechanism, we showed that this explains the data equally well [52]. As a consequence, the Quiel et al. [184] data no longer unequivocally support the previous explanation [25], and the increased loss of pMHC complexes on APCs at high T cell densities is an equally valid interpretation of this striking data.
4 DNA labeling techniques
To study the population dynamics of T cells immunologists have used various labeling techniques. During cell division cells duplicate their DNA. Using non-radioactively labeled molecules that are incorporated into de novo synthesized DNA, one can estimate the rate of cell division in any particular population. There are two widely used DNA labeling techniques that use a label that can be provided in the drinking water. One is bromodeoxyuridine (BrdU), which is an analog of thymidine (i.e., one of the four bases making up DNA). BrdU can be detected in a cell with antibodies. The other is deuterium, which can be provided as heavy water or deuterated glucose. Deuterium labeling uses mass-spectrometry to detect the deuterium atoms that have replaced some of the hydrogen atoms in newly synthesized DNA.
Since individual clones in the T cell repertoire are small, BrdU and deuterium labeling is typically measured at the level the whole population of interest, e.g., by just sorting for CD4+ or CD8+ T cells. Thus, rather than modeling one clone of cells responding to an antigen, we have to develop models averaging over the whole repertoire. One problem is that not all clones in the repertoire need to have the same turnover rate. Similarly the population of interest may be comprised of subpopulations like naive, proliferating, effector and memory cells having different rates of turnover. Thus, T cell populations are kinetically heterogeneous, with a slow time scale for turnover of resting naive T cells and memory T cells, and a rapid time scale for clonal expansion and contraction (see Fig. 3). This we define as “kinetic” heterogeneity: each population that is being labeled will be composed of subpopulations with different rates of turnover [8]. Additionally, there is heterogeneity in history, i.e., what has recently happened to the cell [148], which we call “temporal” heterogeneity. A good example is a cell that has recently divided, and hence picked up label, may temporally have a different lifespan than the average quiescent cell [53]. This may be true after each rare and stochastic division [36, 167], and is definitely true for cells that were recently involved in clonal expansion [84] because these become short-lived during the contraction phase (see Fig. 3).
To estimate daily turnover rates immunologists have sorted naive from memory T cells to measure the fraction of labeled cells (BrdU) or DNA strands (deuterium) in each population. For naive T cells the problem of heterogeneity seems relatively minor because after sorting none of the proliferating and activated cells, A, P and E, should be present in the naive subset. In real data this not the case because the CD45RA marker that is used to define human naive T cells is only lost after several divisions of a primed naive T cell [147], and thus one detects CD45RA+ T cells in the proliferating subpopulations (A or P). In mice, where the CD44 marker is used to differentiate between CD44low naive and CD44high memory T cells, it was also shown that naive CD8+ T cells stimulated during an influenza infection become CD44high only after several divisions [242]. One can see from the general model for one clone of naive T cells, Eq. (2), that the simplest average model for the total number of naive T cells has only has three parameters corresponding to a source term, a renewal term, and a loss term combining death and priming:
| (18) |
Assuming that the total population size, T, does not change during labeling, i.e., dT/dt = 0, one eliminates one parameter from the model, i.e., σ = (d−p)T. Further, in labeling studies one measures the fraction of cells that are labeled, and the total population size does not matter. Thus, without loss of generality, one can scale the total population size to one, and obtain a simple two parameter model that can be fitted to labeling data (see below).
Let us also use this model to clearly define what we mean by the average turnover rate and expected cell life span. According to Eq. (18) new cells are produced via the source and by cell division, and die at rate d. The average turnover rate of the population is defined by the average death rate of the cells, d, and the expected life span of the cells is the inverse of their death rate, 1/d. Because we consider populations at steady state the per capita production rate is equal to the turnover rate, i.e., the turnover rate is the cell replacement rate at steady state. The total production rate in Eq. (18) is σ + pT and at steady state σ + pT = dT.
T cell subsets that are sorted for memory markers also include activated subpopulations, and hence one should allow for both kinetic and temporal heterogeneity when analyzing labeling data from this “memory” subset. There is kinetic heterogeneity because memory T cells are maintained by a slow process of renewal [36], and the activated proliferating and effector cells tend to be short-lived. Clonal expansion of recently activated cells brings in temporal heterogeneity because the expansion phase ends with contraction [84]. For a normal healthy individual one could argue that only a very small fraction of the total immune repertoire is recruited into clonal expansion at any time. If this is the case, then most of the label accrual in memory T cells would be due to renewal, i.e., be due to the rMM term of Eq. (4). In that case, i.e., when pA ≪ rMM for most of the clones, the source of activated cells, mA, in Eq. (4) should on average be small, i.e., , and one could simplify the T cell equation into an equation identical to Eq. (18), where the source averages over all small m′A terms resulting from all ongoing clonal expansions, the proliferation term represents renewal, rMM, and the death term should largely be death, dMM, because we assume that on average few cells are recruited in clonal expansion, i.e., . Importantly, for both naive and memory T cells the source in Eq. (18) should then consist of cells that have recently divided, either in the thymus or during clonal expansion. Several labeling experiments have indeed used the very general model of Eq. (18) to study labeling in total T cells, naive T cells and memory T cells [26, 45, 46, 162, 163], but have made different assumptions about the fraction of labeled cells in the source (see below).
If, as might occur during chronic infection, most of the label accrual in the sorted memory T cells were to occur during the proliferation of clonally expanding cells, and the division involved in renewal was small, i.e., if pA ≫ rMM, one could write
| (19) |
| (20) |
where σ is a small source due to naive T cells that are recruited into clonal expansion on a daily basis, and where the primes denote average parameters describing all clones, and implicitly incorporate the and () terms that were used to describe responses of single clones. Except for the source, this model is identical to the two-compartment model proposed by Ribeiro et al. [189], who had the small source in their compartment of “resting” cells that here corresponds to Eq. (20). Alternatively, one could keep track of the number of divisions proliferating cells have completed during the immune response [84], and write a set of equations like Eq. (9), and/or allow for time delays as in Eqs. (11-12). During chronic infections the source from the naive compartment should be negligible, i.e., σ ≃ 0, because antigen specific naive T cells should have been depleted by chronic activation. Unfortunately, even then the model given by Eqs. (19-20) has too many parameters to be estimated by fitting to labeling data, demanding further simplification (see below).
4.1 Deuterium labeling
T cell dynamics have been studied by labeling animals or humans with deuterated glucose (2H2-glucose) or heavy water (2H2O) for one day [103, 148, 150, 151, 225], five days [133] to one week [163, 231], or several months [105, 134, 223, 231], and subsequently following the loss of label during a washout phase. This method has been particularly valuable in HIV research since this type of labeling is safe to use in humans. After deuterium labeling one sorts the T cell population of interest, isolates the DNA from the cells, and uses mass-spectrometry to determine the enrichment of deuterium in the DNA [31, 32, 149, 222]. During the labeling period some fraction of the hydrogen atoms in the body will we replaced by deuterium, and dividing cells will incorporate both deuterium and hydrogen in the DNA molecules that are being synthesized. Since not all hydrogen is replaced by deuterium, the enrichment of deuterium in the DNA will never become 100%. To account for the fraction of deuterium in the body one either multiplies with a known fixed factor [148-151, 163, 225], or one scales to the fraction of labeling achieved in a rapidly turning over population [105, 166, 223], and/or with the fraction of deuterium in the urine [223]. Ultimately, the data correspond to a fraction of labeled DNA, 0 ≤ L < 1, which increases during the labeling phase, and which decreases once deuterium has been withdrawn (see Fig. 4).
Figure 4.

One week of deuterated glucose labeling of a healthy human volunteer showing the deuterium enrichment in CD4+ and CD8+ T cells taken from the blood [163]. The data were fitted with Eq. (26) for n = 2 subpopulations, giving average turnover rates d̄ = 0.006 day−1 and d̄ = 0.0044 day−1, for CD4+ and CD8+ T cells, respectively. We have shifted time by one day to allow for a short delay before labeled cells appear in the blood [163]. Note that fitting the same data with the temporal heterogeneity model of Eq. (29) would have given identical fits and average turnover rates, with a radically different interpretation of the parameters,; d1 and d2, of Eq. (26) [53].
Because deuterium labeling does not affect the dynamics of the cells one typically assumes steady state of the population. Further, because the deuterium enrichment in the DNA is a fraction, the total population size does not matter. Thus, when fitting the “source” model dT/dt = σ+(p−d)T of Eq. (18) to data, one assumes dT/dt = 0, and scales the steady state population size, such that T̄ = 1. As a consequence, one parameter is eliminated because σ = d−p. Because the measurements are done on DNA strands, and not on cells, one writes models in terms the fraction of labeled DNA strands, L, and unlabeled DNA strands U, with (U + L = 1). Recall that DNA replication is semi-conservative, i.e., as DNA replicates it is only copied so the original strand remains and a new strand with label incorporated is generated, i.e., U → U + L and L → 2L, where here U and L refer to individual DNA strands. Further, during the labeling phase unlabeled strands can only be lost by cell death, and assuming that new DNA strands arriving from the source are all labeled, unlabeled strands disappear according to dU/dt = −dU. During the washout or “de-labeling” phase labeled strands should no longer be produced, and can only be lost by cell death, i.e., dL/dt = −dL. Since U + L = 1 this model with the initial condition U(0) = 1 and L(0) = 0, delivers an exponential increase in L with slope d during labeling, and an exponential decrease with the same exponent d during de-labeling
| (21) |
where tend is the time labeling ends, defining the length of the labeling phase. The labeling part of this model is a generalization of the classical precursor-product relationship used to estimate turnover rates, d, from measurements made at a single time point [149].
Let us use this model to clearly define the up- and down-slopes of labeling curves. Deuterium labeling data is typically depicted using a linear scale for the fraction of labeled cells L(t) (see Fig. 4). The initial up-slope of such a graph, L(t)′ = de−dt, approaches the turnover rate d for t ↓ 0, and the absolute value of the initial down-slope, −L(t)′ = dL(tend)e−d(t−tend), approaches dL(tend) for t ↓ tend, which is smaller than d because L(tend) < 1, and depends on the length of the labeling phase. Thus, on a linear scale the initial down-slope, dL(tend), is always smaller than the initial up-slope, d, and only approaches the up-slope when L(tend) → 1. Since, the equation for the de-labeling phase is basically of the form L(t) = L(0)e−dt (which can be obtained by shifting time such that t = 0 corresponds to the start of the de-labeling phase), one can also define an “logarithmic down-slope”, which is the observed down-slope when L(t) is plotted on a logarithmic scale. This logarithmic down-slope reflects the rate at which L(t) declines, which here is the turnover rate d, and does not depend on the length of the labeling phase. Note that there is no “logarithmic up-slope” because the initial slope at L(0) = 0 is not defined on a logarithmic axis. For a given length of the labeling phase, this model has only one free parameter, d, and in several experiments this was insufficient to properly fit the data. Different authors have added different parameters to this “one compartment” model, and we will see below that the initial down-slope will always be smaller than the initial up-slope.
Studying turnover rates of total CD4+ and CD8+ T cells in humans, i.e., naive plus memory T cells, Mohri et al. [163] allowed for a source of unlabeled cells during the labeling phase, i.e., they wrote dU/dt = σU − dU to obtain
| (22) |
with an initial up-slope of d − σU, which is slower than the turnover rate d, an asymptote in the labeling phase corresponding to L(∞) = (1 − σU/d), implying that ultimately not all cells will become labeled, and an initial absolute down-slope dL(tend). In a subset of their data the source of unlabeled cells had to be relatively large to properly fit the data [163], and as a result they found that the estimated rate of cell division, p, was smaller than the death rate d. Note that the interpretation of this source of unlabeled cells is different from the σ in Eq. (18) as derived from the general model, because both for naive T cells (Eq. (2)) and memory T cells (Eq. (4)) the source is expected to be labeled (albeit with a delay for the naive T cells to account for the emigration from the thymus). After a sufficiently long labeling period the vast majority of thymic emigrants, σ, and clonally expanded cells mA, should be labeled. One possible interpretation of σU is an inflow from a large compartment of resting cells [188], or of cells that are turning over slowly [26] (see below).
Asquith et al. [8] have criticized the “source model” because the estimated contribution of the source to the maintenance of the cells was much larger than the contribution of cell division. They suggested that heterogeneity is a superior explanation for the fact that death rates were estimated to be faster than division rates, because the death rate of cells that have recently picked up label is expected to be larger than the average death rate. One reason is the temporal heterogeneity illustrated above with the general model of Eqs. (3-4) and Eqs. (11-12) and below with Eq. (29). Another reason is kinetic heterogeneity of the population of T cells: subpopulations turning over more rapidly than average will tend to be labeled more extensively, and as a consequence the labeled fraction of the whole population is enriched for cells with a more rapid turnover. When label is withdrawn the death rate of labeled cells is therefore higher than average. Asquith et al. [8] only wrote an equation for the fraction of labeled strands during the labeling period, i.e., dL/dt = p(U + L) − dL = p − dL, where p is the average proliferation rate, and d is the death rate of cells carrying labeled strands. For the de-labeling phase they assumed dL/dt = −dL, resulting in the following model
| (23) |
with an initial up-slope of p, where d ≥ p so that the asymptote p/d ≤ 1, an initial absolute down-slope dL(tend), and a logarithmic down-slope d, which is larger than p. Since there is no source, the average proliferation rate, p, in this model defines the average turnover rate of the population [8], and should be equal to the average death rate if the population is at steady state. The death rate of labeled cells, d (which was originally called d*), is expected to be larger than the average turnover rate p because the labeled subpopulation will be enriched in cells with a more rapid turnover. Thus, in this model d does not represent the average death rate of T cells. Only after long labeling periods, i.e., when a large enough fraction of the populations is labeled, Asquith et al. [8] expect that the death rate of labeled cells approaches the average turnover, i.e., d → p. Summarizing, the reason that ultimately not all cells become labeled in Eq. (23) is an artifact of the assumption that for any labeling period the model assumes a fixed death rate, d, although this death rate should actually be declining and ultimately approach the average turnover p. Hence, this model seems most appropriate for experiments with short labeling periods, like one day deuterated glucose experiments [148, 150, 151, 225].
For experiments with such long labeling periods that a considerable fraction of the DNA in the cells is labeled (e.g., [163, 223], it seems more appropriate to allow the death rate d of labeled cells to decline over time. Similarly, this model cannot be used to concurrently describe experiments with different labeling periods, because each labeling period may require its own death rate to account for its unique de-labeling curve, whereas all labeling curves should fall on the same smooth continuous line [231]. Another criticism is that if a population is truly heterogeneous the labeling and de-labeling curves in the data should not be single exponentials, and instead should reflect the ignored change in the turnover rates of unlabeled and labeled cells over time.
Fortuitously, these three models Eqs. (21-23) are mathematically identical to the more general model
| (24) |
having an asymptote, α, in the labeling phase, and a single exponent, d, for both the labeling and de-labeling phase. A direct way of arriving at this general model is to argue that the population of interest is heterogeneous and consists of a population of size α that is turning over at rate d, and a long-lived population of size 1 − α that has a negligible turnover over on the time scale of the experiment [45, 46]. The initial up-slope of this model is αd, which reflects the average turnover rate of the population, and the initial absolute down-slope is dL(tend), which also approaches the average turnover rate αd when L(tend) → α. Thus, in Eqs. (21-24) the initial absolute down-slope is always smaller than the initial up-slope. Nevertheless, these models reasonably describe the data obtained with deuterium labeling [148, 150, 151, 163, 225], and although there is discussion in the literature on what model is most appropriate [8, 28, 84], and hence how these parameters should be interpreted, they fortuitously all deliver the same or similar estimates for the average turnover rate when fitted to the same set of data [76].
Explicit kinetic heterogeneity
While discussing the heterogeneity of T cell subsets sorted for memory markers we derived Eqs. (19-20) from the general model, and argued that this was similar to the two-comparment model proposed by Ribeiro et al. [189]. Variants of this model have been used by various authors [26, 45, 188, 189] to analyze labeling experiments performed on total T cell populations, i.e., naive plus memory T cells, which involves heterogeneity because naive T cells tend to turnover much more slowly than the average cell expressing memory markers.
Fitting this model to labeling data obtained from the total CD4+ or CD8+ T cell pools would be “overfitting” because the model has too many parameters, that are all contributing to the complicated exponentials in its solutions [189]. The model was therefore simplified by assuming that on the time scale of the experiment the slowest compartment involved hardly any death, division, or clonal expansion [188]. Thus, writing a model composed of a fraction of long-lived resting cells, R, and a fraction of activated cells, A, that becomes labeled during proliferation one obtains
| (25) |
From the steady state condition one can see that aR = rA and p = d, simplifying the model to three parameters. Using A + R = 1, the steady state of dR/dt gives that a/(a + r) is the fraction of activated cells. Because activation of resting cells does not involve clonal expansion in this model, the proliferation term, pA, is the only process corresponding to uptake of deuterium. This model fits deuterated glucose data from uninfected volunteers and HIV infected patients well [188], and delivers similar average turnover rates as Eq. (22) gave for this data [28, 163, 188]. Because the data involved total T cells, i.e., naive plus memory cells, the resting cells, R, most likely correspond to naive T cells plus resting memory cells. Activation of naive T cells is expected to involve clonal expansion, see Eq. (11), but this could be rare enough to be ignored in this one week labeling experiment. Activation of resting memory T cells could be interpreted as a renewal process not involving clonal expansion. A more trivial way of deriving Eq. (25) from the general model is to assign a slow time scale to the resting cells, and let R be a constant, which simplifies dA/dt in Eq. (25) to Eq. (18) with σ = aR [49]. Since Mohri et al. [163] were comparing deuterated glucose labeling of healthy human volunteers with that in HIV-1 infected patients, it could however be that Eq. (18) is valid for healthy volunteers, and that allowing for time delays and temporal heterogeneity (see Eqs. (11-12)) would be more realistic for the chronically infected patients.
The generalized precursor product-relationship of Eq. (21) (and similarly Eq. (24)) can be further generalized to explicitly model kinetic heterogeneity by assigning different turnover rates for subpopulations i = 1, …, n, i.e.,
| (26) |
where αi is the fraction of cells with turnover rate di [76]. This model is valid for populations maintaining themselves by a source and/or division because, in the absence of temporal heterogeneity, one can model the labeling phase by considering the loss of unlabeled strands (at rate di) and the de-labeling phase by the loss of labeled strands (at the same rate di) for all subpopulations; see Eq. (21). The initial up-slope reflects the average turnover rate, d̄ = ∞ αidi, and the initial down-slope is ΣidiLi(tend), where Li(tend) = αi(1−e−ditend). Since, Li(tend) ≤ αi we again obtain that the initial down-slope cannot exceed the initial up-slope. The major advantage of this “multi-compartment” model is that for n > 1 the shape of the labeling and de-labeling curves can be described with several exponentials, and no longer needs to be monophasic. Another new property is that the loss rate of L(t), i.e., the logarithmic down-slope, depends on the length of the labeling phase because the contribution of each eigenvalue, di, depends on the degree of labeling in that population, αi(1 − e−ditend) [76]. Thus, this model provides a more mechanistic interpretation for what Eq. (23) aimed to describe, namely that the estimated rate, d*, at which L(t) decreases during the de-labeling phase depends on the length of the labeling phase. For n = 2 this however comes at the cost of one additional parameter. Hence, a straightforward procedure of estimating an average turnover rate from deuterium labeling data would be to fit Eq. (26) to the data for i = 1, 2, …, n compartments, until one finds that increasing the number of compartments no longer increases the quality of the fit, or the estimate of the average turnover rate. The estimates of the individual compartment sizes, αi, and turnover rates, di, will probably be noisy and have large confidence levels, but the mean turnover rate, d̄, tends to be more robust [45, 46, 53, 231].
To illustrate this procedure we fitted the CD4+ and CD8+ T cell data from a healthy volunteer who was labeled with deuterated glucose for one week [163], with the model of Eq. (26) for n = 1 and n = 2 compartments. The quality of the n = 1 fits were poor (not shown), whereas those with n = 2 compartments explain the data reasonably well (Fig. 4). The estimated average turnover rates of the CD4+ and CD8+ T cells, were d̄= 0.006 day−1 and d̄ = 0.0044 day−1, respectively (corresponding to expected life spans, 1/d̄, of 167 and 227 days). Similar expected life spans were found when the two compartment model of Eq. (25), or the temporal heterogeneity model of Eq. (29), was used to fit the same data [28, 53, 188]. Thus, although the values of the underlying parameters α, d1 and d2 can have very different physical interpretations [53], the estimates for the average turnover rate, d̄, seem reasonably robust.
After proposing Eq. (26), Ganusov et al. [76] proceeded by arguing that if one allows n → ∞, e.g., by considering all clones in the repertoire, then the sums in Eq. (26) can be replaced by integrals, and one can employ specific distributions to define the relative sizes, αi, of the various subpopulations. For instance, assuming that the turnover rates, di, are distributed according to a gamma distribution, the model given by Eq. (26) can be solved, yielding
| (27) |
where d̄ is the average rate of cell turnover in the population, and k is the shape parameter of the gamma distribution. For k = 1, the gamma distribution becomes an exponential distribution, and the fraction of labeled DNA is simply
| (28) |
This is an interesting model in which the average turnover rate, d̄, determines the non-exponential labeling curve, and in which d̄ and tend together define the de-labeling curve. Being based on Eq. (26) there is no asymptote and ultimately all cells would become labeled. In agreement with the findings of Asquith et al. [8], this model predicts that the logarithmic down-slope depends on the length of the labeling period, tend. The initial rate, d*, at which the fraction of labeled DNA decreases can be found by taking the derivative of ln[L(t)] at t → tend, which can then be approximated by , such that after short labeling experiments, i.e., d̄tend ≪ 1, the initial logarithmic down-slope, d* ≈ 2d̄, will be 2-fold faster than that after long labeling experiments where d* ≈ d̄. Generally, the maximum difference between d* and d̄ need not be 2-fold, and is determined by the variance of the distribution [76]. Being based on Eq. (26) this model is very general, but unfortunately we do not know the distribution of turnover rates in lymphocyte populations.
Explicit temporal heterogeneity
Another form of heterogeneity that can possibly complicate the interpretation of labeling data is the simple fact that within any homogeneous population a recently divided cell may have a faster death rate than a quiescent cell [84]. Cells that have just completed a phase of clonal expansion during an immune response are indeed known to die rapidly by a process called activation induced cell death, which allows for the contraction of the response (see Eqs. (11-12)). Cells involved in clonal expansion during the labeling phase are therefore expected to contribute with an atypically high death rate to the down-slope of the de-labeling phase [84]. Although Eq. (23) proposed by Asquith et al. [8] was developed as a model for a kinetically heterogeneous population, it can also be interpreted as a model for temporal heterogeneity because it allows labeled cells to die faster than the average cell. It is not known whether the two daughter cells that result from a rare stochastic division of a cell from an otherwise quiescent population, e.g., a single renewal division of a naive or memory T cell [36], also have a transient fast death rate. Even is this is the case, it remains unclear whether or not the fast time scale of such recently divided cells would affect the up- and down-slopes in a population that is homogeneous with respect to the division rates, and only heterogeneous because the daughter cells resulting from a single division have a transient faster death rate. It has recently been shown that as CD8+ memory T cells proliferate they generate a sub-population of “death-intermediate memory cells” that exhibit apoptotic markers [167]. Thus, presumably some CD8+ memory T cells acquire a more rapid death rate following homeostatic division. It is not known whether this subset results from asymmetric division, or whether daughter cells randomly acquire this “death-intermediate” phenotype [167].
De Boer et al. [53] developed a mechanistic model for temporal heterogeneity that was inspired by the stochastic division of CD8+ memory T cells described by Choo et al. [36]. Surprisingly, this model is a simplification of the more general two compartment model for kinetic heterogeneity proposed by Ribeiro et al. [188, 189], and given in Eqs. (19-20). Thus, allowing for a transiently increased death rate of recently divided cells in a otherwise kinetically homogeneous population, we write
| (29) |
For c = 2, every resting cell, R, that is triggered to divide at a homogeneous rate a, produces two daughter cells that have an increased death rate, dA > dR, until they revert (r) to the resting state [53]. Since this is a simplification of the similar two-compartment model of Ribeiro et al. [189], one can use their general solutions for the number of deuterium labeled DNA strands to see that the up- and down-slopes of Eq. (29) involve two exponentials [53]. Thus temporal heterogeneity can account for biphasic accrual and loss of deuterium. Note that interpreting the “Asquith model” of Eq. (23) as a phenomenological model for temporal heterogeneity would not allow for biphasic up- or down-slopes because that model is based upon a single exponential.
The values of the two exponentials in the labeling and de-labeling curves predicted by Eq. (29) are determined by several parameters of the model [189], and have no bearing on the turnover rates, dR and dA, of the two subpopulations of Eq. (29) [53]. Choosing c = 2, i.e., considering single divisions with an exponentially distributed interdivision time, 1/a, Eq. (29) has four parameters. Using A + R = 1, the steady steady dA/dt = 0 gives that the fraction of divided cells f = ca/(ca + r + dA), and the steady state of dR/dt = 0 can be used to eliminate another parameter, e.g., r = dA(a + dR)/([c − 1]a − dR), leaving three free parameters (a, dR and dA), which is the proper number to describe labeling data with two exponentials [188]. The average turnover rate of the model is defined as d̄= fdA +(1 − f)dR. For c = 2, and the requirement dR < a, the reversion rate, r, will always be larger than the death of the daughter cells, dA, and most of the labeled short-lived daughter cells will revert to the quiescent stage and become long-lived. Thus, for c = 2 the effect of having dA > dR will be relatively minor, and one expects labeling and de-labeling curves that look relatively monophasic (Fig. 5a).
Figure 5.

Deuterium labeling curves expected for the temporal heterogeneity model of Eq. (29) for c = 2 (a) and c = 32 (b) taken from De Boer et al. [53]. The model is parameterized for the slowly renewing LCMV specific memory CD8+ T cells described by Choo et al. [36]. During the labeling phase one writes for the unlabeled fraction of DNA isolated from resting and activated cells, respectively, dUR=dt = rUA−(dR+a)UR and dUA=dt = aUR−(dA+r)UA, whereas during the de-labeling phase one writes the same equation for the labeled fraction dLR=dt = rLA (dR +a)LR and dLA=dt = aLR − (dA + r)LA [189], with the total fraction labeled defined as L = −LR + LA = 1−UR−LR. Parameters in Panel (a): c = 2; a = 0.02 and hence f = 0.01865; r = 1.105 day−1, and an average turnover rate of d̄ = 0.01963 day−1 (which is close to fdA). The fraction of activated cells, f, and the average turnover rate, d̄, are the same in both panels by setting the parameters in Panel (b) as: c = 32; a = 0.02/31 = 0.0006452 and hence r = 0.08658 [53]. Other parameters: dR = 0.001 day−1 and dA = 1 day−1. The up and down-slopes are technically biphasic [189], but this is hardly visible when c = 2 (a).
Setting c > 2, Eq. (29) can also be used to study the effect of temporal heterogeneity due to clonal expansion [84]. From the same steady state expressions one can now see that dA can become much larger than r, arguing that most recently divided cells die before they revert to quiescence. This increases the impact of the rapid time scale on the labeling curves and hence allows for truly biphasic labeling and de-labeling curves [53] (see Fig. 5b). Thus, clonal expansion is required to expect markedly biphasic curves from temporal heterogeneity only, and if one were to study the slowly renewing LCMV specific memory T cells of Choo et al. [36] with deuterium labeling, one expects fairly monophasic labeling and de-labeling curves.
Disturbingly, the solution of the total labeled fraction of labeled cells of Eq. (29) is very similar to the sum of the two exponentials described by Eq. (26) for n = 2 [53]. Data generated with the explicit temporal heterogeneity of Eq. (29) can therefore be extremely well described with the general kinetic heterogeneity model of Eq. (26). The parameters estimated by fitting Eq. (26) with n = 2, i.e., α1, d1 and d2, to biphasic labeling curves generated with temporal heterogeneity will reflect complicated combinations of all parameters of Eq. (29) [189], and will not reflect the relative size and the turnover rate of any two kinetically different subpopulations. As a consequence, the only parameter that can reliably be estimated from biphasic labeling data is the average turnover rate [53]. Although the average turnover rate in the two panels in Fig. 5 is the same, label accrual is approximately twice as fast when c = 2 because most labeled daughter cells survive. Fitting the in silico data in Fig. 5a with the kinetic heterogeneity model of Eq. (26) tends to underestimate the true average turnover rate [53]. Indeed, for dA > dR the model of Eq. (29) corresponds to the situation where cell death is linked to cell division [181], which is expected to change the estimated division times (see below in Eq. (48)), and apparently also the rate of label accrual.
4.1.1 Biological interpretations of deuterium data
The current estimates for the average turnover rates of T cells as determined by deuterium labeling vary widely, and depend strongly on whether deuterated glucose or water has been used [28]. One possible explanation for this is that labeling periods with deuterated glucose are typically much shorter, i.e., one day to one week, than those using deuterated water. During a short labeling period one largely labels cells turning over rapidly, and by the kinetic heterogeneity models of Eq. (26), one expects faster loss rates, d*, after shorter labeling periods [8, 76]. The observed up-slope is determined by the average turnover rate, and should not depend on the length of the labeling period [8, 76]. Nevertheless, using the up-slopes as estimates for the average T cell turnover rates, a recent review [28] reveals that turnover rates based on glucose can be more than 10-fold faster than those based upon heavy water (see also Tables 1 & 2).
Table 1.
Expected in vivo life span of human CD4+ T cells in healthy volunteers.
| Life span | Median: range | n | Period | Method | Model | Ref. | Remarks |
|---|---|---|---|---|---|---|---|
| Naive CD4+ T cells | |||||||
| 169 d | 273: 65–476 d | 8 | 1 d | 2H2-gl | Eq. (23) | Macallan et al. [148] | de-labeling only |
| 521 d | 625: 270–909 d | 5 | 1 d | 2H2-gl | Eq. (23) | Macallan et al. [150] | de-labeling only |
| 172 d | 268: 65–476 d | 8 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; young |
| 265 d | 321: 114–1000 d | 6 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; elderly |
| 270 d | — | 5 | 1–2 d | 2H2O | L = 1 − e−kt | McCune et al. [157] | maximal enrichment L only |
| 868 d | — | 10 | 63 d | 2H2O | 0.07=1−e−k63 | Hellerstein et al. [105] | 9 week point, no de-labeling |
| 1851 d | 2000: 1111–3333 d | 5 | 63 d | 2H2O | Eq. (23) | Vrisekoop et al. [223] | up- and down-curves |
|
| |||||||
| Memory CD4+ T cells | |||||||
| 38 d | 51: 13–75 d | 8 | 1 d | 2H2-gl | Eq. (23) | Macallan et al. [148] | de-labeling only |
| 69 d | 96: 27–135 d | 6 | 1 d | 2H2-gl | Eq. (23) | Macallan et al. [150] | de-labeling only; CM cells |
| 21 d | 25: 13–44 d | 6 | 1 d | 2H2-gl | Eq. (23) | Macallan et al. [150] | de-labeling only; EM cells |
| 41 d | 46: 22–69 d | 8 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; young |
| 52 d | 50: 38–87 d | 7 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; elderly |
| 115 d | — | 8 | 1–2 d | 2H2O | L = 1 − e−kt | McCune et al. [157] | maximal enrichment L only; EM cells |
| 289 d | — | 15 | 35 d | 2H2O | 0.114=1−e−k35 | Hellerstein et al. [105] | 5 week point |
| 334 d | — | 15 | 63 d | 2H2O | 0.172=1−e−k63 | Hellerstein et al. [105] | 9 week point, no de-labeling |
| 226 d | 222: 149–588 d | 5 | 63 d | 2H2O | Eq. (23) | Vrisekoop et al. [223] | up- and down-curves |
| 230 d | 164: 71–500 d | 5 | 63 d | 2H2O | Eq. (26) | Westera et al. [231] | up- and down-curves |
|
| |||||||
| Total CD4+ T cells | |||||||
| 122 d | 125: 56—333 d | 9 | 2 d | 2H2-gl | L = 1 − e−kt | Hellerstein et al. [103] | maximal enrichment L only |
| 117 d | 141: 45–286 d | 12 | 1–2 d | 2H2O | L = 1 − e−kt | McCune et al. [157] | maximal enrichment L only |
| 250 d | 250: 200–333 d | 4 | 7 d | 2H2-gl | Eq. (22) | Mohri et al. [163] | up- and down-curves |
| 222 d | 225: 167–333 d | 4 | 7 d | 2H2-gl | Eq. (25) | Ribeiro et al. [188] | data: Mohri et al. [163] |
| 222 d | 225: 167–333 d | 4 | 7 d | 2H2-gl | Eq. (26) or (29) | De Boer et al. [53] | data: Mohri et al. [163] |
| 497 d | — | 15 | 35 d | 2H2O | 0.068=1−e−k35 | Hellerstein et al. [105] | 5 week point |
| 611 d | — | 16 | 63 d | 2H2O | 0.098=1−e−k63 | Hellerstein et al. [105] | 9 week point, no de-labeling |
| 484 d | 455: 311–1245 d | 5 | 63 d | 2H2O | Eq. (23) | Vrisekoop et al. [223] | Recalculated from fraction naive |
Abbreviations: Life span: average life span calculated from the inverse of the average turnover rate, n: number of individuals, 2H2-gl: 2H2-glucose, L = 1 − e−kt: precursor product model, where L is enrichment at time t, EM: effector memory cells, CM: central memory cells, d: days.
This table is an extension of the one published in Borghans & De Boer [28].
Table 2.
Expected in vivo life span of human CD8+ T cells in healthy volunteers.
| Life span | Median: range | n | Period | Method | Model | Ref. | Remarks |
|---|---|---|---|---|---|---|---|
| Naive CD8+ T cells | |||||||
| 221 d | 323: 95–∞ d | 6 | 1 d | 2H2-gl | Eq. (23) | Macallan et al. [148] | de-labeling only |
| 188 d | 223: 91–∞ d | 8 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; young |
| 162 d | 123: 94–5000 d | 7 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; elderly |
| 294 d | — | 4 | 1–2 d | 2H2O | L = 1 − e−kt | McCune et al. [157] | maximal enrichment L only |
| 1018 d | — | 9 | 63 d | 2H2O | 0.06=1−e−k63 | Hellerstein et al. [105] | 9 week point |
| 2778 d | 3333: 2000–3333 d | 5 | 63 d | 2H2O | Eq. (23) | Vrisekoop et al. [223] | up- and down-curves |
|
| |||||||
| Memory CD8+ T cells | |||||||
| 20 d | 52: 6–179 d | 7 | 1 d | 2H2-gl | Eq. (23) | Macallan et al. [148] | de-labeling only |
| 26 d | 68: 6–179 d | 8 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; young |
| 34 d | 97: 11–213 d | 7 | 1 d | 2H2-gl | Eq. (23) | Wallace et al. [225] | de-labeling only; elderly |
| 57 d | — | 5 | 1–2 d | 2H2O | L = 1 − e−kt | McCune et al. [157] | maximal enrichment L only; ME cells |
| 339 d | — | 9 | 35 d | 2H2O | 0.098=1−e−k35 | Hellerstein et al. [105] | 5 week point |
| 347 d | — | 11 | 63 d | 2H2O | 0.166=1−e−k63 | Hellerstein et al. [105] | 9 week point, no de-labeling |
| 308 d | 357: 167–526 d | 5 | 63 d | 2H2O | Eq. (23) | Vrisekoop et al. [223] | up- and down-curves |
| 162 d | 157: 113–231 d | 5 | 63 d | 2H2O | Eq. (26) | Westera et al. [231] | up- and down-curves |
| 100 d | — | 5 | 49 d | 2H2O | L = L(70)e−dt | Ladell et al. [134] | de-labeling only; EM and CM cells |
| >36 y | — | 5 | 49 d | 2H2O | L = L(70)e−dt | Ladell et al. [134] | de-labeling only; TEMRA cells |
|
| |||||||
| Total CD8+ T cells | |||||||
| 107 d | 196: 25—1000 d | 8 | 2 d | 2H2-gl | L = 1 − e−kt | Hellerstein et al. [103] | maximal enrichment L only |
| 200 d | 222: 100–∞ d | 12 | 1–2 d | 2H2O | L = 1 − e−kt | McCune et al. [157] | maximal enrichment L only |
| 400 d | 500: 250–500 d | 4 | 7 d | 2H2-gl | Eq. (22) | Mohri et al. [163] | up- and down-curves |
| 400 d | 500: 250–500 d | 4 | 7 d | 2H2-gl | Eq. (25) | Ribeiro et al. [188] | data: Mohri et al. [163] |
| 400 d | 500: 250–500 d | 4 | 7 d | 2H2-gl | Eq. (29) or (37) | De Boer et al. [53] | data: Mohri et al. [163] |
| 642 d | — | 12 | 35 d | 2H2O | 0.053=1−e−k35 | Hellerstein et al. [105] | 5 week point |
| 586 d | — | 15 | 63 d | 2H2O | 0.102=1−e−k63 | Hellerstein et al. [105] | 9 week point |
Abbreviations: Life span: average life span calculated from the inverse of the average turnover rate, n: number of individuals, 2H2-gl: 2H2-glucose, L = 1 − e−kt: precursor product model, where L is enrichment at time t, EM: effector memory cells, CM: central memory cells, d: days, and y: years.
This table is an extension of the one published in Borghans & De Boer [28].
It is not known why these seemingly similar labeling techniques deliver different results. One problem with very short labeling periods of, say one day, and the subsequent measurements in the blood, is that there is a delay of a few days between the end of labeling and the peak fraction of labeled DNA observed in the blood [148, 151]. In humans labeled with deuterated glucose for one week, the deuterium enrichment measured in the blood becomes detectable after about one day of labeling [163]. In labeling experiments involving one day of deuterated glucose labeling, the first published data point at day three corresponded to the observed peak enrichment, as the fraction of labeled DNA declined monotonically thereafter [148, 151]. Unpublished measurements at day one and two suggest that the enrichment in the blood is gradually increasing towards this peak value at day three (Derek Macallan, personal communication), but these early data points have not been included in the modeling because the mechanisms underlying the delayed peak are not completely understood. One possible explanation is that cells typically divide in lymphoid tissues, and stay there until they have completed their cascade of divisions. Unfortunately, it is not well understood how rapidly recently divided cells migrate to the blood. Kovacs et al. [132] measured BrdU+ T cells in blood and lymphoid tissue in HIV-1 infected patients at several time points after an in vivo pulse of half an hour of BrdU labeling. For their first time point at 6 hours after the pulse, they found a two to three-fold higher fraction of labeled T cells in lymphoid tissue. At the second time point at 24 hours they found similar fractions of BrdU+ T cells in blood and lymphoid tissue [132], suggesting that recently divided cells egress to the blood within one day, consistent with the findings of Mohri et al. [163].
In the studies involving one day of deuterated-glucose labeling it was assumed that the true peak occurs at the end of day one, and the exponential de-labeling curve that was fitted from the monotonic decline phase was extrapolated backward to estimate the peak value, L(1), at day one [148, 150, 151, 225]. Thus, the estimated peak at day one was higher than the observed peak at day three. Using the estimated L(1), the average turnover rate was estimated from Eq. (23), which would be correct if there is no more label accrual after day one, and labeled cells have to survive for two days before they appear in the blood. If recently divided labeled cells were to divide several times before they exit to the blood, and/or still have an intracellular source of deuterium, this simple extrapolation procedure could overestimate the average turnover rate (Drylewicz et al. work in progress). Proper modeling of such short-term labeling studies may therefore require mathematical models allowing for the migration of cells from the compartment where they divide to the blood where their enrichment is measured. The differences between glucose and water labeling also call for new experiments directly comparing these techniques in one system, and for simultaneously measuring the enrichment in blood and lymphoid tissue.
Currently there are three long-term labeling studies in healthy human volunteers, which have data in the labeling phase. There is a one week study using deuterated glucose [163], and there are two nine week heavy water studies [105, 223]. The turnover rate is again highest in the shortest study using glucose [28]. The one week deuterated glucose study found expected life spans, 1/d, of 250 (range: 200-333) and 400 (range 250-500) days for CD4+ T cells and CD8+ T cells, respectively (using Eq. (22) to fit the data). In this experiment the T cells were not separated into naive and memory subpopulations. Surprisingly, after nine weeks of heavy water labeling, Vrisekoop et al. [223] report similar median expected life spans of 226 (range: 149-588) and 308 (range: 167-526) days for CD4+ and CD8+ memory T cells, but almost 10-fold longer expected life spans of 1851 (range: 1111-3333) and 2778 (range: 2000-3333) days for naive CD4+ and CD8+ T cells (fitting an extension of Eq. (23) to the data; see Tables 1 & 2). Westera et al. [231] report that these estimates for the average life span of memory T cells reduce considerably when the same data is fitted with a two-compartment version of Eq. (26), and estimate median expected life spans of 164 (range: 71-500) and 157 (range: 113-231) days for CD4+ and CD8+ memory T cells, respectively.
Because this two-compartment model fitted the data significantly better than the extension of Eq. (23) did in Vrisekoop et al. [223], they conclude that one-compartment models tend to overestimate expected life spans of kinetically heterogeneous populations. The other study using nine weeks of heavy water labeling [105], also reported enrichments corresponding to longer expected life spans of 500-600 days for total CD4+ and CD8+ T cells, and around 300 and 340 days, for memory CD4+ and CD8+ T cells (using the one-compartment precursor product model to fit the data; see Tables 1 & 2). Reading the percentages of labeled naive T cells after 9 weeks of labeling from the figure in Hellerstein et al. [105] suggests that CD4+ and CD8+ naive T cells have expected life spans of 868 and 1018 days respectively (see Tables 1 & 2). One consistent finding in all of these studies is that CD4+ T cells turn over somewhat more rapidly than CD8+ T cells, [105, 163, 188, 223], and this seems true for both naive and memory T cells [223]. The deuterium studies separating naive from memory T cells consistently find that memory T cells have a much faster turnover rate than naive T cells [105, 223, 231]. This is consistent with findings obtained with several other techniques [36, 73, 159, 209, 244] and implies that the long-lived immunological memory is carried by relatively short-lived cells that maintain a relatively stable population size by self-renewal [167].
In young human adults typically half of the T cells have a naive phenotype. Given the slow turnover of naive T cells [223], it is not surprising that Hellerstein et al. [105] found that the turnover rate of memory T cells is almost 2-fold faster than that of total T cells. From the supplemental information in Vrisekoop et al. [223], we recalculated the average turnover rate in the total CD4+ T cell compartment, i.e., d̂= fNpN + (1 −fN)pM, where fN is the fraction of naive T cells in the CD4+ T cell pool, and pN and pM are the estimated average proliferation rates of naive and memory CD4+ T cells for every subject in Table 1 of Vrisekoop et al. [223]. This can only be done for CD4+ T cells because in the CD8+ compartment the fractions of naive and memory T cells do not sum up to one, as a relatively large population of CD45RA+CD27− effector cells was excluded. To compare these average turnover rates with the four 1/p average lifespan estimates from Table 1 in Mohri et al. [163], who measured average turnover rates in healthy adults using deuterated glucose, we take the inverses of the d̂ values and depict them as a function of the CD4 or CD8 T cell count of the subject (Fig. 6). The inverse d̂ of the CD4+ T cells from Vrisekoop et al. [223] had a mean of 484 days (see Table 1). Thus, the estimates from nine weeks of heavy water labeling are approximately 2-fold longer than those from one week of deuterated glucose labeling. This 2-fold difference cannot be attributed to uncertainty in the estimated timing of the peak, nor to the choice of the model, because the models used to fit these data sets are mathematically identical to Eq. (24). Note that the inverse average turnover rate, d̂, is not the same as the average life span if one averages over subpopulations. The true average life span would be defined as fN/pN + (1 − fN)/pM, which is much longer than 1/d̂ because the long expected life span of the naive T cells, 1/pN, dominates.
Figure 6.

T cell turnover rates estimated by deuterium labeling. Panel (a): Expected life spans of total T cells estimated by one week of deuterated glucose labeling in Mohri et al. [163] versus 9 weeks of deuterated water labeling in Vrisekoop et al. [223]. Each symbol represents a healthy human volunteer and is plotted at the CD4 or CD8 T cell count (per l blood) of that subject. The horizontal lines depict the average expected life spans, i.e., 250 and 484 days for CD4+ T cells, and 400 days for CD8+ cells. The vertical lines depict the 95% confidence intervals; since the Vrisekoop et al. [223] data was recalculated from the naive and memory T cell enrichment, we have no confidence intervals for those data points. Note that the CD4+ T cells of one volunteer in the Vrisekoop et al. [223] data have an expected life span that is about 2-fold larger than the mean, which is largely due to an approximately 2-fold lower deuterium enrichment in this subject’s CD4+ memory T cell compartment (and not to a poor fitting of the data). Judging the CD4 data on either the mean, or the median to exclude the outlier, the difference between the two techniques is about 2-fold. Westera et al. [231] perform a similar comparison of these two data sets by re-fitting the data with a two-compartment version of Eq. (26), and find that the difference remains but becomes somewhat smaller. Panel (b): Mohri et al. [163] also measured the fraction of dividing cells by staining with the Ki67 antibody, and we plot for each individual the estimated average turnover rates, i.e., the p values in their Table 1, as a function of the Ki67 measurements in CD4+ and CD8+ T cells. The line in Panel (b) results from fitting the linear regression line y = ax to the data, and suggest that the daily turnover is approximately one fifth of the fraction of Ki67+ cells.
Since the two labeling techniques seem so similar it remains puzzling why they deliver different outcomes. One possibility is that it is due to the length of the labeling period, and that during the first few days of labeling the fastest subpopulations become completely labeled. If this were the case the labeling curve should be biphasic with an early rapid phase, picked up in short-term labeling studies, and a late slow phase, largely picked up in long-term labeling studies (Asquith, personal communication). Such kinetic heterogeneity partly explains the discrepancy between the one-week Mohri et al. [163] and the nine-week Vrisekoop et al. [223] data, because the differences between the estimated turnover rates of CD4+ and CD8+ T cells become smaller if both sets of data are re-fitted with a two-compartment version of Eq. (26) [231], see Tables 1 & 2.
Another possibility is a difference in the normalization factor. In both approaches one corrects for the measured extracellular enrichment in plasma (2H2-glucose) or urine (2H2O) of the precursor molecule in body fluid, and one needs another intracellular dilution factor for glucose [149], or intracellular amplification factor for water [166], to correct for the maximum possible enrichment. For deuterated glucose labeling this dilution factor is a fixed fraction of 0.65 validated by a number of measurements [149]. In heavy water studies the enrichment of the DNA becomes larger than that in the body water because deuterium can be incorporated in several positions of the sugar moiety in which the enrichment is detected [166]. The amplification factor varies between 3 to 5 and is measured per individual from the maximum enrichment estimated in another population with a rapid turnover, such as granulocytes [105, 179, 223] or thymocytes [223]. This difference in the correction factor, i.e., fixed dilution versus estimated enrichment, may explain part of the difference between the heavy water and the deuterated glucose studies.
Comparing average life spans we have largely used the information in the data from the labeling phases fitted with Eqs. (22-23). These two models are mathematically identical to Eq. (24), and the initial up-slope of Eq. (24), αd, defines the average death rate of the cells [45, 46]. In a population at steady state, one intuitively expects that the initial rate of label accrual reflects the average replacement rate of the cells because the fraction of unlabeled DNA is lost with the average death rate of the cells. In most of the models the de-labeling phase should provide most information about the death rate of labeled cells, i.e., recently produced cells. Surprisingly, Vrisekoop et al. [223] found very flat de-labeling curves for human naive T cells, suggesting that recently produced naive T cells live at least as long as the average naive T cell (using an extension of Eq. (23) to fit the data). This observation is in good agreement with the similar flat de-labeling curves of naive T cells labeled with BrdU in monkeys [46, 162] (see below).
Vrisekoop et al. [223] applied Eq. (23) to fit their data. For fitting label accrual in naive T cells this deserves some further discussion because (1) that model was originally derived for proliferating cells, and (2) the model requires that the asymptote p/d 1 [8]. Above we derived the model writing dL/dt = p(U + L) − dL = p − dL, giving L(t) = (p/d)(1−e−dt) for the uplabeling phase (see Eq. (23)). Since most of the de novo production of naive T cells probably occurs in the thymus, one could instead write dL/dt = σ − dL for the labeled fraction in the uplabeling phase. Switching σ with p this remains mathematically the same equation, however. This illustrates that when Eq. (23) is used for naive T cells, the p parameter obtains the interpretation of a total production rate rather than a per capita proliferation rate [223]. However, the other constraint, i.e., p d required because the asymptote in the fraction of labeled cells is maximally one, was≤violated by the slow estimated death rates of labeled naive T cells in [223]. The same problem occurred in a study of B cell turnover in leukemia patients [214], where in all volunteers it was found that p < d, while in some of the patients p was estimated to be larger than d. Although technically incorrect, this will not have affected their estimates on the average life spans because the labeling curves were straight, i.e., remained far from the asymptote, and because the initial up-slope of (p/d)(1 − e−dt) remains p even if d → 0. However, the interpretation of Vrisekoop et al. [223] that recently produced naive T cells → are preferentially incorporated in the repertoire is an artifact of their incorrect p > d estimate.
Fitting the deuterium data with Eq. (23), one should always test whether p and d are required to be different. We recently found that these labeling data from human naive T cells are well described by the single compartment version of Eq. (21), arguing that human naive T cells form a homogeneous population of long-lived cells [224]. However, the data from the memory T cells in that study [223] required at least two compartments to obtain a good fit to the labeling data, suggesting that memory T cells form a heterogeneous population [231]. This could be due to the temporal heterogeneity that we discussed above when modeling the renewal dynamics of CD8+ LCMV specific memory T cells [36, 53]. Additionally, memory T cell populations are known to be kinetically heterogeneous as central-memory and effector-memory T cells that were labeled with 2H2-glucose [150] and with 2H2O [134] have different de-labeling curves. Peripheral memory T cell populations might even include quiescent memory T cells residing in the bone marrow [206-208], and/or the intestine [154] that are transient in the blood (although there is probably very little migration between these two compartments and the blood in the absence of an infection).
Current consensus holds that naive T cells that have recently emigrated from the thymus have a short expected life span [21, 22, 70, 110], and hence that the naive T cell population should be kinetically heterogeneous. Transplanting an additional thymus to mice and tracking the fate of the recent thymic emigrants (RTE) originating from that thymus it was reported that RTE are short-lived, i.e., have a life-span of 3 weeks [21, 22]. One potential problem is that the recipients of the embryonic thymic transplants were at an age of 5-6 weeks when the naive T cell pool is at its maximal density [57, 87]. If the death rate of naive T cell were to increase with T cell density [57], one would expect such a high death rate for all naive T cells at that age. Recently, other experiments co-transferring RTE and resident naive T cells into recipient mice confirmed that in normal mice RTE do have a shorter expected life-span than the average resident naive T cell [70, 110]. The ratio of RTE to resident naive T cells halved in about four weeks. If both transferred populations are declining exponentially, this halving in four weeks suggests a difference in the death rate of 0.17 week−1. If resident naive T cells in mice live about 10 weeks [176], this would suggest that RTE have a death rate of 0.27 week−1, and hence an expected life span of 3-4 weeks, which is close to the original estimates of Berzins et al. [21, 22]. Deuterium labeling experiments of human naive T cell populations fail to pick up such a kinetic heterogeneity in the population, which is probably due to the fact that in adult humans the fraction of RTE is so small that we fail to detect their contribution to the labeling curves [57]. One week labeling experiments of naive T cells in mice do provide evidence for kinetic heterogeneity [231], and this disappears in longer labeling studies [57], suggesting that most recently produced naive T cells in mice are short-lived RTE. We are repeating the thymus transplantation experiments in 12 week old recipients to estimate the life span of RTE in adult mice [work in progress]. Interpreting 2H2O labeling in young adult mice with Eq. (26), the expected life spans of CD4+ and CD8+ naive T cells were estimated to be 47 (range: 41-54) and 80 (range: 67-92) days, respectively [57], whereas those of CD4+ and CD8+ memory T cells were estimated to be 15 (range: 11-15) and 20 (range 12-22) days, respectively [231] (see Table 3).
Table 3.
Expected in vivo life span of T cells in other species. The ranges indicate the reported 95% confidence intervals (CI) or the range over all animals in the study (n).
| Life span | Range | T cell type | Method | Model | Ref. | Remarks | |
|---|---|---|---|---|---|---|---|
|
mouse
| |||||||
| 68 d | 65–71 d | CI | naive CD8+ | BrdU | Eq. (13) | Parretta et al. [176] | thymectomized mice |
| 47 d | 41–54 d | CI | naive CD4+ | 2H2O | Eq. (23) | Den Braber et al. [57] | young adult mice |
| 80 d | 67–92 d | CI | naive CD8+ | 2H2O | Eq. (23) | Den Braber et al. [57] | young adult mice |
| 41 d | 36–47 d | CI | naive CD4+ | 2H2O | Eq. (23) | Den Braber et al. [57] | old mice |
| 116 d | 94–139 d | CI | naive CD8+ | 2H2O | Eq. (23) | Den Braber et al. [57] | old mice |
|
| |||||||
| 90 d | 64-133 d | CI | memory CD8+ | BrdU | Eq. (18) | Parretta et al. [176] | no source: σ = 0, no de-labeling |
| 50 d | — | memory CD8+ | CFSE | Eq. (15) | Choo et al. [36] | LCMV specific memory cells | |
| 14–22 d | — | memory CD4+ | BrdU | * | Younes et al. [244] | memory phenotype cells | |
| 50 d | — | memory CD4+ | Ki67 | — | Younes et al. [244] | LCMV specific memory cells | |
| 15 d | 11–15 d | CI | memory CD4+ | 2H2O | Eq. (26) | Westera et al. [231] | 3 different labeling periods |
| 20 d | 12–22 d | CI | memory CD8+ | 2H2O | Eq. (26) | Westera et al. [231] | 3 different labeling periods |
|
| |||||||
|
rhesus macaque
| |||||||
| 106 d | — | total CD4+ | BrdU | * | Pitcher et al. [182] | relationship p and Ki67 | |
| 111 d | 83–200 d | n = 4 | total CD4+ | BrdU | Eq. (32) | De Boer et al. [46] | data: Mohri et al. [162] |
| 93 d | 77–125 d | n = 4 | total CD4− | BrdU | Eq. (32) | De Boer et al. [46] | data: Mohri et al. [162] |
| 167 d | 83–200 d | n = 4 | naive CD4+ | BrdU | Eq. (32) | De Boer et al. [46] | p = 0, same data |
| 93 d | 77–125 d | n = 4 | naive CD4− | BrdU | Eq. (32) | De Boer et al. [46] | p = 0, same data |
| 95 d | 67–143 d | n = 4 | memory CD4+ | BrdU | Eq. (32) | De Boer et al. [46] | same data |
| 87 d | 71–100 d | n = 4 | memory CD4− | BrdU | Eq. (32) | De Boer et al. [46] | same data |
| 154 d | 111–200 d | n = 4 | memory CD4+ | BrdU | Eq. (37) | Ganusov & De Boer [77] | same data |
| 125 d | 100-143 d | n = 4 | memory CD4− | BrdU | Eq. (37) | Ganusov & De Boer [77] | same data |
|
| |||||||
|
sooty mangabye
| |||||||
| 83 d | 63-111 d | CI | total CD4+ | BrdU | Eq. (32) | Kaur et al. [121] | n = 5 animals |
| 125 d | 200–1000 d | CI | total CD8+ | BrdU | Eq. (32) | Kaur et al. [121] | n = 5 animals |
| 100 d | 56–500 d | CI | naive CD4+ | BrdU | Eq. (32) | Kaur et al. [121] | n = 4 animals |
| 83 d | 67–111 d | CI | memory CD4+ | BrdU | Eq. (32) | Kaur et al. [121] | CD45RA−; n = 5 animals |
| 56 d | 42–83 d | CI | memory CD4+ | BrdU | Eq. (32) | Kaur et al. [121] | CD45RA+; n = 5 animals |
| 100 d | 67–167 d | CI | memory CD8+ | BrdU | Eq. (32) | Kaur et al. [121] | CD45RA−; n = 5 animals |
These studies report the percentage of BrdU+ T cells after several days, which can be translated into a daily turnover rate using Eq. (32), i.e., L(t) = 1 − e−2pt (assuming σ = 0, α = 1 and p = d because this is a self-renewing population [77]). From the 7.25% BrdU+ CD4+ T cells after 4 days of labeling in Pitcher et al. [182] one obtains p = 0:0094 day−1, or an expected life span of 106 days. Younes et al. [244] find 35% and 60% BrdU+ memory CD4+ T cells after 3 and 10 days of labeling, respectively, translating into 0:046 ≤ p ≤ 0:071 day−1, and an expected life span between 14 ≤ 1/p ≤ 22 days. Interestingly, Pitcher et al. [182] report Ki67 measurements varying around 4.3%, suggesting that the average turnover rate (p=0.0094) day−1 is 0.22 times the fraction of Ki67+ cells.
In individuals labeled with deuterated glucose Mohri et al. [163] also measured the fraction of dividing cells by staining with the monoclonal antibody Ki67. Although Ki67 is only expressed by cells that are undergoing cell division [199], Ki67 measurements only provide an estimate of the fraction of cells in division but not the rate of division. Taking the estimated average turnover rates and the Ki67 measurements from the Mohri et al. [163] study, and fitting the linear relation, y = ax, between the turnover rate, y, and the fraction of Ki67+ cells, x, in CD4+ and CD8+ T cells, suggests that the daily turnover rate is approximately one fifth of the fraction of Ki67+ T cells (Fig. 6b). For B cells, Van Gent et al. [214] depict a similar linear relationship, albeit for a small set of low Ki67 expression levels, and there the slope suggests that the daily turnover rate is about one tenth of the fraction of Ki67+ B cells. It would be interesting to test the generality of this relationship in other deuterium labeling experiments, and for various cell types, because this would allow one to estimate average turnover rates from single snapshots of Ki67 expression. In the legend of Table 3 we discuss that a similar relationship between the daily turnover rate and the fraction of Ki67+ cells is obtained with BrdU labeling.
Deuterium de-labeling curves
Despite the potential problem that labeled cells are expected to be enriched in cells with a more rapid turnover, several papers have characterized T lymphocyte turnover by concentrating on the data in the de-labeling phase. Kovacs et al. [133] labeled volunteers and HIV-1 infected patients for five days with 2H2-glucose, and observing that the de-labeling curves were not single exponentials, fitted their data with a semi-empirical model with a log-normal distribution of death rates. Because in this study IL-2 treatment disrupted the steady state in T cell numbers, the model was fitted to the percentage of labeled DNA. However, whenever a population is not at steady state during the de-labeling phase, the decline of the enrichment is also a function of the proliferation rate, since cell division in the absence of deuterium dilutes the percentage of labeled DNA strands. Considering the de-labeling phase of a single population, and defining N as the total number of DNA strands in that population, and NL < N as the number of labeled strands in that population, one would write
| (30) |
When the total number of cells is declining from a peak value induced by the IL-2 treatment, and there is a relatively low production of new cells, i.e., when p ≪ d, the f = NL/N is hardly declining because N and NL are declining at similar rates, even though all cells may have a high death rate d. Mathematically one can write the differential equation for the enrichment as
| (31) |
were the prime denotes differentiation. Thus, the enrichment is expected to decline at a rate representing the rate of proliferation, p, and should not reflect the death rate d. The slow decline in the enrichment reported by Kovacs et al. [133] therefore indicates a slow proliferation rate in between IL-2 treatment cycles, rather than a long survival of the cells.
Ladell et al. [134] studied the de-labeling of CD8+ T cells after seven weeks of 2H2O labeling in four HIV− volunteers and five HIV+ patients. Allowing for an additional three weeks for the washout of 2H2O from the body, the enrichment at week ten was taken as the initial value, and the loss of enrichment in subpopulations of central-memory and effector-memory CD8+ T cells was fitted by a simple exponential decay over two subsequent time points. Sorting the CD8+ T cells based on their CD45RA, CCR7, and CD28 expression, Ladell et al. [134] reported half-lives varying between 50-100 days for effector-memory and central-memory CD8+ T cells in healthy volunteers, and a half-life of more than 25 years for a small subpopulation of CD45RA+CCR7−CD28− TEMRA cells (see Table 2), which is a population of CD45RA+ effector-memory CD8+ T cells, the majority of which express the senescence marker CD57. This long live span was estimated by pooling the loss of enrichment of several volunteers, but could nevertheless be an overestimate because the maximum enrichment of 0.5-1% in this subpopulation was only several-fold lower than the 2-3% enrichment observed in the other subpopulations. Ladell et al. [134] also recorded the enrichment in CD8+CD45RA+CCR7+CD28+ naive T cells, but could not estimate a half-life because the enrichment continued to increase during the eight week de-labeling phase of healthy volunteers. Although labeled naive T cells are expected to be produced by the thymus for several weeks after the withdrawal of the 2H2O, eight weeks is a surprisingly long period. Measuring over a de-labeling period of 16 weeks, Vrisekoop et al. [223] found very slow death rates for human CD8+ naive T cells corresponding a half-life of more than 7 years (i.e., an expected life span of 2778 days or 10.5 years; see Table 2).
4.2 BrdU labeling
BrdU is a nucleoside analogue that is incorporated instead of thymidine into the DNA of cells that divide. BrdU has been used for decades in mice [209, 210], and more recently in monkeys [162]. Because of potential problems with toxicity it has been used infrequently in humans [58, 132, 133, 138, 202], and only over short periods. The mathematical model for BrdU labeling differs from that for deuterium labeling because one measures the BrdU intensity of individual cells, rather than the enrichment in DNA extracted from a population of cells. In the presence of BrdU, any unlabeled cell that divides will give rise to two labeled daughter cells, and a labeled cell that divides increases the number of BrdU+ cells by one, i.e., U → 2L and L → 2L. During the first part of the de-labeling phase a BrdU+ positive cell that divides will give rise to two BrdU+ cells, each expressing half of the parent’s BrdU intensity [162]. Employing the same general models as used above for deuterium labeling, one would write for the labeling phase that dU/dt = −(p+d)U, i.e., unlabeled cells disappear by proliferation and death (assuming any source that is present gives rise to labeled cells). During the de-labeling phase one would write dL/dt = (p − d)L because labeled cells divide into labeled daughter cells (and assuming that the source yields unlabeled cells after the label is removed). Solving these equations one finds
| (32) |
where α ≤ 1 was introduced to define a possible asymptote in the labeling phase [46].
Estimating average life spans from BrdU data is more difficult than from deuterium data because the initial up-slope of Eq. (32), α(p + d), contains not only the death rate but also the proliferation rate. If one is labeling naive T cells, that are probably largely produced in the thymus and have very little peripheral proliferation, the unlabeled fraction would disappear according to dU/dt = −dU. While labeling memory T cells, that are probably largely maintained by renewal, the unlabeled fraction would disappear according to dU/dt = −(p + d)U. Thus, even if naive and memory T cells were to have the same life span, 1/d, label accrual would be faster in memory T cells. Hitherto, this difference has typically been neglected, and faster up-labeling in memory T cells was taken as evidence for their shorter life spans. BrdU data resemble deuterium data in the sense that the fraction of labeled cells increases during the labeling phase and tends to decrease during the de-labeling phase. The fraction of BrdU+ cells typically declines during the de-labeling phase, and according to Eq. (32), the initial down-slope, L(tend)(p − d), and the loss rate of labeled cells (i.e., the logarithmic down-slope), p − d, can only be negative when there is a source to compensate for the fact that the average death rate exceeds the average proliferation rate [162]. Below we argue that BrdU dilution is also expected to contribute to the down-slope.
Labeling various cell types, including naive and memory CD4+ and CD8+ T cells in monkeys for three weeks with BrdU, Mohri et al. [162] found significant down-slopes for most cell types, and suggested that there should be a significant source of cells from other compartments to allow for p ≪ d. These data have been modeled using variants of Eq. (32). Like with the deuterium labeling above, there are two possible explanations for having an asymptote. First there could be a source of unlabeled cells during the labeling phase [162], or there could be a slowly turning over subpopulation with hardly any label accrual during the experiment [45, 46]. Fitting Eq. (32) to the data revealed that most data sets could best be described with two parameters, i.e., α and d, because p ≃ 0 allows for the largest possible down-slope [45, 46]. Fortunately, it has been suggested that the average turnover rate, αd, estimated from Eq. (32) is fairly independent of the particular model chosen to fit the data [45, 46]. Again, one could argue that the up-slope contains most of the information to estimate the average turnover rate, and that the down-slopes tell us more about the death rate of recently produced cells (including potential toxicity problems), heterogeneity, and the dilution of BrdU by subsequent cell divisions during the de-labeling phase (see below).
Grossman et al. [84] and Debacq et al. [54] explicitly invoked heterogeneity to argue that labeled cells are lost more rapidly than unlabeled cells as an alternative explanation for a source of unlabeled cells during the de-labeling phase. Debacq et al. [54] described the fraction of labeled cells after a pulse of BrdU as
| (33) |
where b(t) denotes the probability that a dividing cell becomes BrdU+, p is the average proliferation rate, and d is the death rate of labeled, i.e., recently divided cells. Because BrdU decays exponentially after it is administered, b(t) was chosen as b(t) = b0e−kt, with k constant. Like Eq. (23) this model is phenomenological: the division rate p of labeled and unlabeled cells is identical, but the death rate of labeled cells is larger than that of unlabeled cells. The corresponding equation for the unlabeled cells was not written, and should initially be dU/dt = p[1−2b(t)]U−pU, where the death rate has to be equal to the proliferation rate, p, to allow for steady state. Since, the death rate should ultimately approach the average turnover rate, this model seems most appropriate for short-term labeling experiments.
For self-renewing populations without a source, i.e., dMi/dt = (pi − di)Mi, we discussed above that the kinetic heterogeneity model of Eq. (26) readily accounts for biphasic de-labeling curves in deuterium labeling. The equivalent kinetic heterogeneity model however fails to explain the non-zero down-slopes in BrdU labeling because one should have an equation like Eq. (32) for every subpopulation i, and for each of them one would have an up-slope of αi(pi + di) = 2αidi and a down-slope Li(tend)(pi − di) = 0 if there is no source [77]. The population as a whole should therefore also have a zero down-slope, which is not what was observed for most cell types [162]. Thus, it seems that kinetic heterogeneity cannot explain the loss of BrdU+ cells in the de-labeling phase. Temporal heterogeneity, i.e., recently produced cells die faster than average, would obviously work [84] but remains a controversial explanation in some circumstances. For example, in SIV infected monkeys half of the memory T cells become BrdU+ after three weeks of BrdU labeling [162], showing that half of the population has recently divided implying that the average death rate and that of recently divided cells cannot be too different.
BrdU dilution
After BrdU administration has ended BrdU+ cells will become BrdU− after several rounds of division due to label dilution [26, 77, 83, 123, 176, 237]. If most of the division occurs in clonal expansion bursts as defined by Eqs. (11-12), a single BrdU+ cell could have a large number progeny that are BrdU− cells [84, 191]. The mechanisms underlying the loss of BrdU could therefore again differ between normal healthy subjects, and infected subjects mounting an immune response, which complicates the comparison of cell turnover rates between healthy and chronically infected subjects. Another complication is that BrdU may not label cells with 100% efficacy. Bonhoeffer et al. [26] thus extended a variant of Eq. (32) to allow for labeling efficacy, 0 ≤ ∊ ≤ 1, and label dilution, 0 ≤ υ ≤ 1 by writing dU/dt = ([2∊ − 1]p + d)U for the loss of unlabeled cells during the labeling phase, and dL/dt = ([1 − 2υ]p − d)L during the de-labeling phase. Here, ∊ is the probability that a dividing cell becomes labeled in the presence of BrdU, and υ is the probability that a BrdU+ cell divides into two BrdU− daughter cells in the absence of BrdU. Since Eq. (32) with a source of unlabeled cells sufficed to describe the BrdU data that they were examining, Bonhoeffer et al. [26] did not pursue the effects of efficacy and dilution any further. Combining CFSE with BrdU data, Parretta et al. [176] estimated that ∊ = 0.8 during their mouse BrdU labeling regime. If the same labeling efficacy were to apply to the monkeys studied by Mohri et al. [162], the estimated asymptotes α would be 20% lower, which would require a 20% increase in the estimated turnover rate to match the data.
Parretta et al. [176] used a truncated form of Eq. (13) to keep track of the total number of cells in division classes 0, 1, and 2, by writing dP2/dt = 2pP1 + (p − d)P2, and fitted this model to BrdU labeling and de-labeling data of naive and memory CD8+ T cells in thymectomized mice. Similar models have been used for tracking BrdU labeling in populations of hematopoietic stem cells [83, 123, 237]. Since total memory T cell numbers remained constant over the course of the experiment, the memory data were fitted with the parameter constraint p = d. Naive T cell numbers were slowly declining in these thymectomized mice, which was fitted by an exponential loss to constrain the value p − d [176]. The labeling phase was described very well by this model, and provided estimates of p ≃ 0.002 day−1 and d = 0.015 day−1 for the naive CD8+ T cells in mice, and p = d = 0.01 day−1, for their memory CD8+ T cells (see Table 3). To estimate the number of divisions that are required for a BrdU+ T cell to become BrdU−, these parameter estimates were fixed when fitting the de-labeling phase, which had relatively slow down-slopes (with the naive T cells having the slowest down-slope). The initial condition of the model, P0(0), for the de-labeling phase was either the total number of BrdU+ naive T cells, or BrdU+ memory T cells. Interestingly, while fixing the p and d parameters Parretta et al. [176] were able to fit the naive and memory de-labeling data by assuming that BrdU+ CD8 T cells become BrdU− upon the second division. Fewer or more divisions gave too slow and too rapid down-slopes, respectively. The slow down-slope of the BrdU+ naive T cells was therefore naturally explained by their slow division rate p. Thus, in these data BrdU dilution was a sufficient explanation for the down-slope during the de-labeling phase, even under the p = d constraint.
Becoming BrdU− during the second division is not the same as having a constant dilution probability 0 < υ < 1 as in the model of Bonhoeffer et al. [26], because none of the cells would be BrdU− after the first division, suggesting υ = 0, and all of them would be BrdU− after the second division, suggesting υ = 1. Additionally, note that the naive and memory CD8+ T cells divide slowly in these normal unimmunized mice, which implies that the BrdU+ cells in these experiments may have completed just one division in the presence of BrdU, and will have just half of their DNA labeled (ι = 1/2). The Parretta et al. [176] analysis therefore suggests that cells with a quarter of their DNA labeled, ι = 1/4, are still BrdU+, whereas those with ι = 1/8 are BrdU−. A similar argument holds for the monkeys that were labeled with BrdU for three weeks [162]. In uninfected monkeys memory T cells are not expected to complete more than one division in three weeks, arguing that BrdU+ memory cells would have half of the DNA labeled, whereas BrdU+ naive T cells coming out of the thymus are expected to have completed several divisions over a period of three weeks, and would hence be brighter (ι → 1). Thus, it seemed very natural to also invoke BrdU dilution to explain the BrdU data from both uninfected and infected monkeys.
Studying self-renewing populations lacking a source, Ganusov & De Boer [77] used the simple cascade model of Eq. (13) to keep track of the number of divisions cells have completed during and after BrdU administration. Because none of the cells have divided in the presence of BrdU at the onset of BrdU administration, the initial condition is the total T cell number, i.e., P0(0) = T (0), and the general solution is given by Eq. (14). Since DNA is replicated during cell division, cells having completed one division, P1, have half of their DNA strands labeled. After two divisions 3/4 of the DNA strands are labeled, and so on. Ganusov & De Boer [77] defined ιn = 1 – 2−n as the fraction of labeled DNA strands after n divisions, and assuming that the measured fluorescence intensity increases with the fraction of DNA strands labeled, one can use Eq. (14) to define the number of labeled cells in the labeling phase as
| (34) |
P (t) is the total number of cells at time t, 0.125 < ιθ < 0.25 is the threshold BrdU intensity above which a cell is measured as BrdU+, and H() is a Heaviside function.
For the de-labeling phase Eq. (14) is generalized into Pn,m(t) for the number of cells having completed n divisions during labeling and m divisions during de-labeling,
| (35) |
where the middle term gives the Poisson distribution at the end of the labeling phase (see Eq. (34)), and the latter term is the Poisson distribution after labeling (t > tend), respectively. Noting that each cell on average loses half of its labeled DNA strands per division, one knows the fluorescence intensity, ιn,m = (1 − 2−n)/2m, and by summing over all n and m, one obtains for the de-labeling phase
| (36) |
Ganusov & De Boer [77] combined this mechanistic BrdU dilution model with the kinetic heterogeneity of Eq. (26), by again considering k different subpopulations i at steady state, each with a turnover rate pi = di, and wrote that
| (37) |
where αi is the fraction of cells with turnover rate pi = di, and fn(t, p) is the Poisson distribution defined by Eq. (15). Due to the kinetic heterogeneity the labeled cells will be enriched in cells with a fast turnover rate, and the de-labeling curve need not be a single exponential and can account for data that appear to have an at least biphasic de-labeling curve. We have fitted Eq. (37) to the BrdU data of Mohri et al. [162] and illustrate a biphasic example from a monkey infected with SIV in Fig. 7.
Figure 7.

Three weeks of BrdU labeling of a monkey infected with SIV. The left and right panels show the percentage of BrdU+ cells in CD4+ and CD4− memory T cells from monkey H1348 in the study of Mohri et al. [162]. Fitting Eq. (37) to these data required at least two compartments (i.e., n = 2), and restricting ιθ = 0.25, i.e., two divisions to become BrdU−, we find for CD4+ T cells an average turnover rate of 0.025 day−1 (with α1 = 0.34, α2 = 1 − α1; d1 = 0.072 and d2 = 0.0016 day−1), and for CD4− T cells 0.019 day−1 (with α1 = 0.36, α2= 1−α1, d1 = 0.048 and d2 = 0.0028 day−1). The fitting of the same data with the source model of Eq. (32) is shown in De Boer et al. [46].
The fact that a model that is based upon a realistic combination BrdU dilution and kinetic heterogeneity provides a good description of the Mohri et al. [162] data, demonstrates that an unlabeled source is not required to explain the down-slope in BrdU data. Importantly, this would suggest that fitting BrdU data from populations that are largely maintained by a source requires a different model, i.e., a source death model with an up-slope reflecting the average turnover rate, than fitting data from self-renewing populations, which would require a model like Eq. (37), with an up-slope that is twice the average turnover rate.
Mean fluorescence intensity
The best approach to study BrdU dilution would be to model the changes in the BrdU intensity profiles, or in the mean fluorescence intensity (MFI), because that contains more information than just the fraction of BrdU+ cells [26, 77]. Bonhoeffer et al. [26] proposed a simple model for the total, I, and the mean,Î, fluorescence intensity of BrdU, in a population of labeled cells. The total BrdU intensity is not changed by cell division, which yields two cells with approximately half the intensity each. Thus, the total fluorescence intensity can only decrease by cell death, i.e., dI/dt = −dI. If total cell numbers obey dT/dt = (p d)T, the average BrdU intensity,Î = I/T obeys dÎ/dt = −pÎ [26]. Speirs et al. [200] developed a very similar model (for the dilution of another label called CFSE, see below), allowing for unequal distribution of the label between the two daughter cells. In the limit of a large number of labeled molecules per cell, where the fluorescence intensity is approximately equally divided between the two daughter cells, their model simplifies into dÎ/dt = −2 log[2]pÎ, which is also proportional to the division rate, and just has a different scaling of the intensity.
As the fluorescence intensity is typically represented on a log scale, there is ambiguity on the meaning of the term MFI as one could take the arithmetic mean, the geometric mean, or the median. Ganusov & De Boer [77] therefore extended the BrdU cascade model of Eqs. (34) and (36) and defined the total, IT, and mean BrdU content (MBC) of cells, IM, as
| (38) |
because . Here, IM, is a well-defined measure of the MFI. Eq. (38) suggests that the rate at which the MBC increases during BrdU labeling reflects the division rate p. For the de-labeling one obtains
| (39) |
| (40) |
which confirms the result of Bonhoeffer et al. [26] that during de-labeling the MBC (or MFI) decreases with the proliferation rate, whereas the total fluorescence intensity decreases with the death rate. Since the BrdU MFI is typically only measured for cells in the labeled fraction, Ganusov & De Boer [77] also provide equations for the MBC of BrdU+ cells. Importantly, the MBC of labeled cells need not change much when the fraction of BrdU+ cells is changing markedly during a labeling experiment [77].
Combining CFSE with BrdU labeling experiments Takizawa et al. [205] showed that the BrdU intensities of the cells saturate with the number of divisions they have completed (their Fig. 1b), which seems in reasonable agreement with the definition ιn = 1 − 2−n. Even for cells that have apparently completed precisely one division in the presence of BrdU there is a wide distribution of BrdU intensities, overlapping with the BrdU intensities of cells that failed to divide in the presence of BrdU [205]. This calls for a novel class of models extending Eqs. (34) and (36) with a probability, ∊, of picking up BrdU upon division, or for models defining the change in the distributions of BrdU intensities with cell division.
4.2.1 Biological interpretations of BrdU data
In their now classic studies Von Boehmer & Hafen [221] and Tough & Sprent [209] labeled normal and thymectomized mice with BrdU in the drinking water and established that memory T cells turn over more rapidly than naive T cells. Additionally, they showed that the turnover of naive T cells in mice with a normal functional thymus is much faster than that in thymectomized mice, which confirms that in mice the thymus plays a substantial role in the production of naive T cells [57]. As discussed above, Parretta et al. [176] recently estimated life spans of naive and memory CD8+ T cells in mice by fitting non-equilibrium models keeping track of the number of divisions cell have completed. To avoid the complications of having to deal with a source of naive T cells mice were thymectomized, after which naive T cell numbers were slowly declining. The expected life span of memory CD8+ T cell was about 90 (range: 64-133) days, and that of naive CD8+ T cells was 68 (range: 65-71) days [176], which being shorter than that of memory cells was unexpected, but is similar to the 80 (range: 67-92) day life span estimated by Den Braber et al. [57] using deuterium labeling (see Table 3). Interestingly, Parretta et al. [176] also studied division rates and suggested that the expected interdivision time of memory cells is the same 90 days, i.e., p = d for CD8+ memory T cells, whereas the interdivision time of naive T cells is 1.4 years, which implies that most naive T cells in mice never divide over their 68 day life span [57].
Rhesus monkeys were labeled with BrdU in their drinking water for three weeks, and label accrual was measured in naive and memory, CD4+ and CD4− T cells, B cells and NK cells [162]. These data were fit with Eq. (32), either keeping all parameters free, or fixing some parameters. For every data set which parameters were required to vary to fit the data was tested statistically [46]. Because the model had to fit both the labeling and the de-labeling phase the required number of parameters depended strongly on the difference between the up and down-slopes. For instance, the B cell data from normal healthy monkeys could typically be fit without proliferation, p = 0, because the exponentials describing the labeling and de-labelling curves tended to be similar in B cells (i.e., p + d ≃ d − p), whereas the NK cell data could be fit with p free and the asymptote fixed at α = 1 because the exponential describing the labeling curve (i.e., p + d) were steeper than the the exponential describing the de-labeling curve (i.e., d − p) in NK cells [46]. Biologically, this would suggest that the maintenance of NK cells involves peripheral proliferation whereas B cells are largely produced in the bone marrow [46]. Both cell types were estimated to have an average life span of approximately 50 days in normal healthy rhesus macaques. Surprisingly, most memory T cell data could be described by Eq. (32) while restricting p = 0, i.e., having no explicit proliferation [46], with expected life spans of 95 (range: 67-143) and 87 (range: 71-100) days, respectively. The expected life spans of CD4+ and CD4− T cells were 111 (range: 83-200) and 93 (range: 77-125) days, respectively (remember that in humans CD4+ T cells have a shorter life expectancy than CD8+ T cells; see Tables 1 & 2). For fitting the naive T cells the proliferation rate was naturally restricted to zero, and expected life spans of 167 (range: 83-200) and 93 (range: 77-125) days were found for CD4+ and CD4− naive T cells, respectively [46] (see Table 3). Sooty mangabeys have been labeled with BrdU in their drinking water for two weeks, and these data were also fit with Eq. (32). In this species the expected life span of CD4+ T cells was approximately 83 (range 67-111) days and that of CD8+ T cells was 125 (range: 200-1000) days [121], resembling the difference in humans and not in macaques (see Table 3). Interestingly there was no significant difference in the average turnover rates between naturally SIV infected and uninfected sooty mangabeys, despite significantly lower total B and T cell counts in the infected animals [121].
A problem with these previous interpretations is that they were fitted with models lacking the combination of BrdU dilution and heterogeneity. The biphasic de-labeling curves of some of the data sets could previously not be accounted for because they were using variants of Eq. (32) [46, 162], but can now be explained with the kinetic heterogeneity of Eq. (37), as illustrated for the memory CD4+ and CD4− T cells from one SIV infected monkey in Fig. 7. Ganusov & De Boer [77] refitted all memory T cell data from Mohri et al. [162] with the new model of Eq. (37) and showed that it tends to describe that data with equal or superior quality as Eq. (32) did. On average a somewhat better quality fit was to obtained with θι = 0.25 (i.e., BrdU− after two divisions), but θι = .0125 (i.e., BrdU− after three divisons) also allowed for good fits. Allowing for kinetic heterogeneity may affect the estimated average turnover rates, as Ganusov & De Boer [77] found a somewhat increased turnover when θι = 0.25 (see Table 3), but not when θι = 0.125. For instance, in monkey 1348 the average turnover rate of memory T cells went from 0.037 day−1 and 0.033 day−1 in De Boer et al. [46] to 0.025 day−1 and 0.019 day−1 in Fig. 7, for CD4+ and CD4− T cells, respectively, which corresponds to an increase by 50% in the expected life span (from 30 to 40–50 days).
Although BrdU dilution in combination with kinetic heterogeneity can explain the loss in the fraction of BrdU+ cells during the de-labeling phase without requiring a source of unlabeled cells (Fig. 7), it remains controversial whether there is any evidence for BrdU dilution in this particular data [162, 177, 191]. Since the BrdU MFI is typically defined for labeled cells, Ganusov & De Boer [77] defined the mean BrdU content (MBC) using Eq. (40), and predicted that the MBC of the monkeys shown in Fig. 7 was hardly declining during the de-labeling phase, whereas their fraction of BrdU+ cells is declining markedly, which reconciles the controversy. Note that BrdU labeling studies in mice have provided direct evidence for BrdU dilution during the de-labeling phase [176, 209].
Surprisingly, BrdU intensity profiles lack the peaks (fingers) that the model of Eq. (34) predicts to be present (and which actually are present in CFSE data). At the peak of labeling cells should have either none, 1/2, 3/4, 7/8, … of their DNA strands labeled with BrdU, and if the staining of BrdU labeled DNA with the specific monoclonal antibody were exact, one could precisely determine the number of divisions the cells have completed. BrdU staining is too noisy for this [205], and one typically sets a threshold to define the fraction of BrdU+ cells. In the end deuterium labeling may remain superior, however, because some studies have reported that BrdU is toxic for various cell types, and may trigger an injury response leading to activation and division [205, 237], which would perturb the normal population dynamics.
Kovacs et al. [132, 202] studied cellular turnover rates in HIV-infected patients after a 30 min in vivo pulse of BrdU, using a semi-empirical model for describing the dynamics of BrdU+ cells in the peripheral blood. Like in most other studies involving HIV-infected patients they find higher peak values for labeled CD4+ T cells than for CD8+ T cells, and higher peak values for memory than for naive T cells. Having a few samples of BrdU labeling in lymph nodes they observed that initially the fraction of labeled cells is higher in the lymphoid tissue than that in the blood, but that this difference vanished in about a day. Despite the short pulse of BrdU labeling, BrdU+ cells continued to accumulate in the blood for several days, and after the peak the wash-out seemed at least biphasic. The height and the timing of the peak was fitted from the data, and the de-labeling curve was modeled independently as the sum of two decaying exponentials [132]. Disturbingly, each exponential was interpreted to reflect the death rate within one subpopulation, whereas we have seen above that with BrdU labeling the de-labeling curve is determined by the difference between the proliferation and death rate (Eq. (32)), in combination with the effect of dilution (Eq. (37)). This could explain why the authors found a correlation between the peak values and the viral load, and not between the estimated decay rate and the viral load [132, 202], as in more mechanistic models the peak value at the end of a short labeling phase should be proportional to the average turnover rate of the population [45, 54, 77, 162]. Another surprising finding was the biphasic decline of BrdU+ naive T cells, with an early phase of short-lived cells having an average life span of approximately five days [202]. Even if these cells were RTE this is unexpectedly short-lived, and it seems likely that BrdU dilution, preferential homing to lymphoid tissue, or death of HIV infected naive T cells, was playing a role.
Finally, biphasic BrdU data can also be explained with temporal heterogeneity, because BrdU data can successfully be described with models like Eq. (29) [45].
4.3 Differences between BrdU and 2H2O labeling
Above we have pointed out that the interpretation of BrdU labeling experiments is much more difficult than that of 2H2O labeling data because the equations for the fraction of BrdU+ cells contain more parameters than those describing the 2H2O enrichment. This argument was made for the situation where total cell numbers are not changing over time, allowing us to remove one parameter by scaling the total cell numbers, and hence the total number of DNA strands, to one. Ganusov & De Boer [77] develop a similar argument in terms of the total cell numbers. Starting with Eq. (18) they follow Mohri et al. [162] to write for a BrdU labeling experiment that the number of unlabeled and labeled cells, TU and TL, respectively, should obey
| (41) |
where TU + TL = T. For simplicity, assume that the source of σ cells per day consists of BrdU+ cells during the labeling phase, and of BrdU− cells during the de-labeling phase. Defining the fraction of labeled cells as L = TL/T one obtains dL/dt = TL′/T − (T′/T)L, or
| (42) |
during the labeling and de-labeling phases, respectively. The s(t) term can be interpreted as the daily fractional replacement by the source. In the absence of a source, e.g., for self-renewing memory T cells, the initial up-slope therefore corresponds to 2p, and in the absence of proliferation the initial up-slope represents the daily fractional replacement by the source. If BrdU dilution were to play no role, the rate at which labeled cells are lost, s(t), would reflect the daily fractional replacement by the unlabeled source. If the total cell number T (t) is changing during the experiment, one would have to know, or estimate, T (t) to be able to estimate the two parameters of Eq. (42). Reconsidering Eq. (42) for the case where the total cell number is not changing over the experiment, one can substitute T̄ = σ/(d − p) to “rediscover” that dL/dt = (p + d)(1 − L) during the labeling phase, and that dL/dt = (p − d)L during the de-labeling phase. In the absence of a source the initial up-slope would be p + d = 2p = 2d, i.e., twice the average turnover rate, and in the absence of proliferation the initial up-slope would be p + d = d, i.e., the average turnover rate [77]. This reconfirms that, if naive and memory T cells were to have the same turnover rate d, one expects a 2-fold higher initial up-slope for self-renewing memory T cells than for the non-dividing naive T cells. Similarly, Hellerstein [104] pointed out that BrdU labeling curves depend on the distribution of cell division over the population, i.e., curves will be different when a few cells are expanding as a clone, or when the same number of cell divisions is distributed diffusively. Comparing n cell divisions under clonal expansion, i.e., U → 2L followed by (n−1) × (L → 2L) gives 2 + (n−1) = n + 1 novel labeled cells, with n divisions under diffuse cell division, i.e., n × (U → 2L) gives 2n new labeled cells, to difference factor leading a maximal of a two between the expected up-slopes for large n.
Under deuterium labeling Eq. (18) can be taken to represent the total number of DNA strands in the population, and because unlabeled DNA-strands are now conserved, i.e., during labeling U → U + L and L → 2L, the corresponding equations for the total numbers become
| (43) |
where TU +TL = T are the number of un-labeled and labeled DNA strands in the population [163]. For simplicity, again assume that the source is completely labeled or un-labeled during the two phases of the experiment. Defining L = TL/T as the fraction of labeled strands one readily arrives at the
| (44) |
during labeling and de-labeling, respectively [77]. Here s(t) is the same daily fractional replacement by the source, and in situations where the total cell number is not at a steady state one would have to know the total cell numbers, T (t), to be able to fit the two parameters of Eq. (44). When total cell numbers are changing the models for the fraction of labeled cells, Eq. (42), and of labeled DNA-strands, Eq. (44), differ by the p terms in the labeling and de-labeling phases, but they contain the same number of parameters, i.e., p and σ, because d disappears when total cell numbers T (t) are known.
Importantly, assuming steady state the expressions for the fraction of labeled DNA-strands, Eq. (44), become the simple dL/dt = d(1 − L) and dL/dt = −dL that were also derived above when we generalized the precursor-product relationship in Eq. (21). This expression only contains d. Under steady state conditions, it apparently does not matter whether cells are produced by a source or cell divisions, as the up-slope and the loss rate of the deuterium enrichment can correctly be interpreted as the average turnover rate, d, of the population. Thus, even if we ignore the problems with BrdU dilution [77], and with the distribution of the cell division events over the population [104], 2H2O labeling experiments under steady state conditions are still easier to interpret than the corresponding BrdU labeling curves. Interestingly, combining BrdU and deuterium labeling would allow one to estimate the contributions of cell division and the source. Since the increase in the fraction of BrdU+ cells occurs at the initial slope of 2p + σ/T̄, while the deuterium enrichment during labeling will increase at an initial slope p + σ/T̄, the difference between the slopes provides the division rate p [77]. Once p is known the fractional source rate can be computed from either slope.
5 CFSE
Carboxyfluorescin succinimidyl ester (CFSE) is an intracellular fluorescent dye that dilutes 2-fold when a cell divides [145]. Cells are typically labeled with CFSE in vitro, and labeled cells can be followed thereafter in vitro or in vivo. Harvesting the cells and sorting them by the CFSE intensity generates profiles with maximally 7 or 8 peaks, each reflecting the number of divisions the cells have undergone (see Fig. 8). The limit of 7 or 8 divisions is caused by the dilution of the dye: after 8 divisions the CFSE intensity is 28 fold lower than the original intensity. CFSE labeling is currently the most informative technique for characterizing the kinetics of cells in the immune system. A number of reviews address the experimental procedures [94, 175, 183] and protocols for the interpretation of CFSE data [94]. The interpretation of CFSE data is far from trivial however, which has resulted in many different mathematical approaches to this problem. Here we attempt to give a balanced overview of these.
Figure 8.
Basic features of a CFSE profile of dividing B cells four days after polyclonal stimulation. The dashed line at the right illustrates the CFSE intensity of unstimulated B cells. These cells serve as the control to locate the undivided cell position. The solid line shows the dividing B cell population revealing the typical asynchronous profile. Progressive divisions are apparent by the accurate two-fold dilutions of the fluorescence intensity, which on the log scale appear as even spacings. The dashed line to the left illustrates the position of an equivalent population that was not labelled with CFSE, allowing the position of the autoflourescence intensity to be determined. This is Figure 1a in Hasbold et al. [91]; reprinted with permission from the Nature Publishing Group.
Wells et al. [227] pioneered the field of analyzing CFSE data, counting the number of cells in each peak of the CFSE profile, and normalizing these by the 2-fold population expansion that is associated with each division. This normalization gives the distribution of the number of “precursor cells” having completed n divisions, which has the immediate advantage of allowing one to see the distribution of the cells from the original starting population over the various division numbers not confounded by their clonal expansion. CFSE data have indeed been misinterpreted by arguing that the large number of cells in the highest division number means that most cells have proceeded through this many divisions over the time of the experiment [120, 217]. The first kinetic models that were fitted to CFSE data used the same normalization to obtain “precursor cohort distributions” at various time points in order to estimate the death and division rates implied by the CFSE data [81, 91, 168].
Normalized CFSE profiles can be described by the normalized cascade model of Eq. (16), and thanks to its simple solution one can estimate the death rate, d, from the exponential slope by which the total normalized cell number decreases [51, 79, 168], and estimate the division rate, p, from the linear slope by which the mean (and the variance) of the distribution increases over time [51, 79, 81, 168]. One can extend the model of Eq. (16) by incorporating a time delay to allow for the extra time, Δ0, non-divided cells may require to complete the first division [51]. One can shift time, and allow for cell death during this extra time period by defining ρ(Δ0) = T(0)e−dΔ0, where T(0) is the original number of precursor cells, and e−dΔ0 is the fraction that survived the extra time period. After shifting time P(0) = T(0)e−dΔ0 is the new initial condition for the total precursor population ρ(t) = P(0)e−dt. The parameter Δ0 can be estimated by fitting μ(t) in Eq. (17) by linear regression, and solving Δ0 + p−1 = μ(t) = 1, i.e., the time point at which the mean division number is one [51]. A sensible first analysis of CFSE data would therefore be to plot versus time the total cell number, P(t) = P(0)e(p−d)t, the number of undivided cells P0(t) = P(0)e−(p+d)t, and the normalized cell number ρ(t) = P (0)e−dt on a logarithmic scale, and the mean and variance of the distribution of Eq. (17) on a linear scale, which should give straight lines with slopes that should all be consistent with each other [43, 51, 79, 81, 91, 94, 126, 168]. Lines that are not straight may indicate changes in the culture conditions, or changes of cell behavior with the number of divisions they have completed.
Choo et al. [36] have fitted the random birth death model of Eq. (13) to CFSE data obtained with slowly renewing populations of CD8+ memory T cells, and Takizawa et al. [205] have fitted it to CFSE data obtained from hematopoietic stem cells. In both cases the division rate was slow, and this ODE model seemed sufficient to describe the data. Importantly, Choo et al. [36] confirmed that the observed CFSE profiles are in good agreement with the Poission distribution of Eq. (14), that the undivided cells decay exponentially, and that the mean and variance increase linearly in time, in good agreement with Eq. (15).
There is an interesting difference between the mean of the Poisson distribution of Eq. (17), and the mean of the normalized data when the non-divided cells, P0(t) = ρ0(t), are excluded (as was originally proposed by Gett & Hodgkin [81]). First, extend the model with a parameter ϕ for the fraction of precursor cells that will ultimately divide. For the cells that will ultimately divide one can still use the solution of Eq. (16) when one replaces the initial condition T(0) by ϕT(0). For the cells that fail to divide one has (1 − ϕ)T(0)e−dt. The normalized frequency distribution and fi(t) = ϕρi(t)/ρ(t), for i = 1, …, ∞, becomes
| (45) |
Thus, the mean division number increases linearly in time but with slope ϕp, which would argue that one cannot simply estimate the division time from the slope. However, if one also computes a mean excluding the non-divided cells by defining [81], one obtains
| (46) |
which equals one when t → 0, and which approaches a slope pt after an initial transient corresponding to a few cell cycles [51]. Comparing the slopes of both means for the same data set, one therefore obtains information about the fraction of precursor cells that are recruited into division, ϕ.
If cells are dividing rapidly, a major problem arises because the random birth death ODE model assumes an exponential distribution of cell cycle times, for which the probability of division is highest at t = 0, i.e., as soon as a cell has completed a prior division. This allows cells to proceed too fast through the division cascade [51]. The faster the proliferation rates the larger the deviation between the behavior of Eq. (13) and that of models allowing for an explicit time delay corresponding to the minimal length of the cell cycle [51, 79]. Thus proper fitting of CFSE data from rapidly expanding populations requires models with a delay corresponding to the minimal length of the cell cycle, which casts doubt on the some of the cell cycle times estimated by fitting ODE models to CFSE data [25, 186, 219]. Despite these serious problems with this simple ODE approach when cells divide rapidly, the various estimates based on Eqs. (16) and (46) can always be used as a check on the quality of the CFSE data, e.g., to check whether conditions are changing over time, and provide excellent starting points for fitting more realistic models of cell division.
Another problem is that models which explicitly consider the cell cycle and allow for different death rates during the different phases of the cell cycle can give quite different estimates of the cell cycle time than models assuming a constant death rate [79, 181]. This can be illustrated by comparing the conventional model having a constant death rate throughout the cell cycle with a model where death occurs upon division [181]. The first case is the conventional random birth-death model of Eq. (13) with solution P(t) = T(0)e(p−d)t, whereas the latter is
| (47) |
where f defines the fraction of cells dying upon cell division [181]. For the initial condition P0(0) = T(0) and Pn(0) = 0 for n = 1, …, ∞, the mathematical solution is
| (48) |
where the first term gives the total population size, and the second and third together gives the Poisson distribution over the division numbers [181].
Importantly, in both models the distribution over the division classes is Poisson, but with different means μ(t) = 2pt and μ(t) = 2p(1 − f)t, respectively. Moreover, both populations grow exponentially with a natural rates of increase of p−d and p(1−2f), respectively. Thus, if division rates are estimated from the increase in the mean division number [51, 81, 126], the outcome may depend on the distribution of death rates over the age of the cell [181]. For the case of a stable population, f = 0.5, one would have a 2-fold difference in the estimated division time between the two models. This difference becomes larger if populations contract, f > 0.5, and vanishes when populations expand [181].
Despite these problems, a final important lesson that can be learned from these simple ODE models is that one obtains a Poisson precursor cohort distribution from a model having a (shifted) exponential distribution of the times to first division. Thus, one cannot infer the distribution of times to first division from the precursor cohort distribution. For example for an apparently normal or log-normal precursor cohort plot [56, 81], one should not conclude that the time to first division is normally or log-normally distributed, because for sufficiently large t the Poisson distribution will resemble a normal distribution. Instead, the distribution of times to first division should be measured separately [56, 90], and be explicitly implemented in the model [43, 78, 96, 137].
5.1 More realistic models
More realistic models for the cell cycle have been proposed and have been used to interpret CFSE data. Let us write a general model and show how various simpler models in the literature can be derived from this. Since a major problem with the ODE model of Eq. (13) is its exponential distribution of division times, allowing too many cells to have unrealistically short division times [51], one can formulate an age-structured population model [20, 43, 59, 181] in which the rates of cell division and death can be any function, pn(a) and dn(a) of a cell’s age a since the previous division, and division number n,
| (49) |
where Pn(t, a) is defined as the density of cells of age a, having completed n divisions at time t, and with boundary conditions
| (50) |
where R(t) is a recruitment function describing the time to complete the first division. The proliferation rate, pn(a), and the death rate, dn(a), can typically be computed [248] from the underlying probability density functions for a cell to divide or die at age a, p̂n(a) and d̂n(a), by
| (51) |
Depending on the form of each probability distribution, and the number of different distributions for the different division numbers, this model can have few or many parameters.
Although written in a completely different notation this model with its age and division number dependent division and death functions, Eqs. (49-51), is also known as the cyton model [96, 204]. The cyton model is written as a set of nested integrals, and is based on a large number of experiments showing that death and division tend to be independently controlled in cells, that cellular survival times are not exponentially distributed, and that recruitment into the first division tends to obey a normal or log-normal distribution [56, 65, 81, 96, 204]. An important part of the work with the cyton model is to prove experimentally that its explicit assumptions on the independent death and division terms are biologically correct. Similar assumptions are made implicitly when writing an age-structured model like Eq. (49).
Formulating the cyton model in the same notation as above, one would take p̂n(a) and d̂n(a) as the probability for a cell having completed n divisions, to divide or die at age a, respectively (where the age is reset to zero at each division). In the cyton model p̂n(a) and d̂n(a) are typically log-normal distributions [96]. Defining the number of cells dividing and dying at any point in time, one can write the model in the form of a set of nested integrals
| (52) |
| (53) |
| (54) |
| (55) |
where T (0) is the initial cell number, and ϕn is the fraction of cells that will ultimately divide at each division number n. Here the () and the () terms provide the probability that a cell has reached aged a without having died or divided, respectively. Thus, although the changes of dividing and dying are independent, these events still censor each other because cells cannot divide after they have died, and since they reset their age, cell division changes the probability to die. From these expressions one can calculate the number of cells in each division class as an integral over all cells that have entered due to their previous division minus the cells that have left by division or death
| (56) |
| (57) |
One can fit Eqs. (52-57) to CFSE data using a publicly available general cyton solver (GCytS) that was coded in Matlab [96]. To reduce the number of parameters one typically considers unique distributions, p0(a) and d0(a), for the first division number, and assumes that cells in subsequent divisions sample their division and death events from the same distributions, i.e., p̂n(a) = p̂(a) and d̂n(a) = d̂(a), for n = 1, …, nmax. The progression fraction, ϕn, can be used to allow for a fraction, 1 − ϕ0, of precursor cells that fails to divide (see above, where we called this fraction 1 − ϕ), and/or to define the expected “division destiny” of cells, which allows cells to stop dividing, ϕn → 0, after a particular number of divisions [96]. If the latter is ignored, i.e., ϕn = 1 for n = 1, …, nmax, the model has nine parameters (, , μdiv, σdiv, , , μdie, σdie, ϕn), where the μdi and the σdi. parameters define the mean and standard deviation of the four log-normal distributions. One can add on more parameters by giving the non-recruited cells, (1 − ϕ0)T (0), a different death rate, and/or by allowing for a division destiny, ϕn < 1, for n = 1, …, nmax. Typically, CFSE data is not rich enough to estimate even the basic nine parameters reliably, as one needs data on the number of dead cells per division number, which is experimentally much more difficult to obtain [96, 115]. This cyton model has been fitted to CFSE data using log-normal distributions for the division and death rates, and even though not all death rate parameters could be estimated, it was claimed to fit the data better than other models, including the Smith-Martin model [96]. An interesting property of the model is that slight variations in the means of the four distributions have a marked impact on the behavior of the model, such that small quantitative differences can have a qualitative effect [90, 96].
Leon et al. [139] developed a general framework similar to the structure of the cyton model by writing nested integrals over division dependent probability distributions, p̂n(t), defining the likelihood of undergoing the nth division at time t after completing a previous division. They analyzed two data sets of Gett & Hodgkin [81] who studied CD4+ T cell division after polyclonal stimulation in vitro. Since one of the data sets had no information on total cell numbers, cell death was ignored in the modeling, or was assumed to obey a conventional exponential distribution [139]. Allowing for a difference in mean and variance between the distributions for the first and all subsequent divisions, they showed that a model with two gamma distributions allowed for better fits than the model of Hasbold et al. [91], where the time to first division was determined by a normal distribution and the subsequent cell divisions were of a fixed length [139]. Biologically, the results remained in reasonable agreement because the standard deviation of the gamma distribution for the first division was much larger than that of the later divisions, implying that most of the variation between the cells was due to time in took to complete the first division. In retrospect it is not too surprising that a model with two gamma distributions allowed for superior fits because we now know that the cyton model with log normal distributions for division and death provides good fits to CFSE data from lymphocytes after polyclonal stimulation in vitro [96], and that the gamma distribution can approach the shape of a log normal distribution, making fine distinction difficult. Indeed Zilman et al. [248] proved mathematically that the nested integral models like the cyton model [96] and that of Leon et al. [139] are special cases of Eq. (49), which in turn is similar to the model originally proposed by Bernard et al. [20]. Interestingly, the best fits of Leon et al. [139] were obtained when the shape of the gamma distribution was fairly similar to that of an exponential distribution, although their distributions still defined a minimal time to complete the division division. Finally, note that later experiments measuring the time to the first cell division directly by thymidine incorporation demonstrate that this is best described by a (log) normal distribution [56, 94, 96, 108].
There is an interesting difference between integrating over probability distributions for division and death and solving PDEs with division and death rates, in cases where the local environment of the cells is changing over time. One example is the in vitro culture of T cells under various concentrations of the growth factor IL-2, which has been modeled by an increase of the death rate of cells as a consequence of the decreasing concentrations of IL-2 due to consumption of IL-2 by the dividing cells [78]. Having a model with proliferation and death rates, pn(a) and dn(a), one can multiply these rates with a dimensionless function representing the environmental conditions, like the relative concentration of IL-2 [78]. Working with nested integrals over probability distributions, p̂n(a) and d̂n(a) (see Eq. (51)), one has the choice of changing the mean and variance of the distribution as a function of the environmental conditions, and/or multiplying the integrals with a fraction like the progressor fraction discussed above.
5.1.1 Smith-Martin model
The model for the cell cycle developed by Smith & Martin [198] has proven useful for analyzing the population dynamics of dividing cells as it prevents too rapid progression through the cell cycle by introducing the equivalent of a time delay, i.e., a fixed length for the S, G2 and M phases of the cell cycle (see Fig. 9a & b). The Smith-Martin model allows for two phases of the cell cycle: cells in the “A” state, which approximately corresponds to the G0 or G1 phase of the cell cycle, are randomly activated to divide, and dividing cells in the “B” phase remain in this phase for a fixed time Δ, after which they yield two daughter cells in the A state. Cells in the A state and B phase have death rates dA and dB, respectively. Cells in the A state are triggered to enter the B phase at a rate p and divide when they exit the B phase. The Smith-Martin model can be formulated in terms of PDEs [20] or as a set of delayed ODEs [43]. Assuming uniform proliferation and death rates across all divisions the model can be written as
| (58) |
where An(t) and Bn(t) are the number of cells in the A-state and the B-phase, respectively, having undergone n divisions at time t [78]. This Smith-Martin model has four parameters, with the length of the cell cycle defined as p−1 + Δ, and two different death rates. The death rates, dA and dB, cause similar parameter identification problems as discussed above using Eq. (48), and the Smith-Martin model will only give unique fits to CFSE data if one simplifies the model to three parameters, e.g., by assuming that dA = dB, dA = 0, or dB = 0 [79, 181]. Note that the similar problems with the uniqueness of fits exist in the cyton model [96], and that one needs more information, like the number of dead cells per division, to resolve these parameter identification problems.
Figure 9.

A simple representation of the Smith-Martin model (a) and a cartoon (b) of the mathematical model of Eq. (58). Panel (c) shows the fit of Eq. (67) to CFSE data fitted with various models in De Boer et al. [43]. Here n is the number of divisions CD4+ T cells have completed after polyclonal stimulation, and n = 6+ refers to all cells having completed six or more divisions. Panels (a & b) are adapted from Figure 1 in Ganusov et al. [79].
Ganusov et al. [79] analyzed the properties of the uniform Smith-Martin model of Eq. (58). Since cells in the B-phase do not influence the dynamics of those in the A-state, one can sum over n to obtain the total growth, dA(t)/dt, or the 2−n-normalized total growth, dÂ(t)/dt, i.e.,
| (59) |
| (60) |
showing that after an initial transient, the total number of proliferating cells in the A-state increases exponentially at a rate r = 2pe−(dB+r)Δ − (p + dA), and the normalized total of cells in the A-state declines exponentially at a rate d = (p + dA) − pe−(dB–d)Δ. Assuming exponential growth, A(t) ∝ ert, the mean of the division number of the cells in the A-state and its variance increase linearly with respect to time, i.e.,
| (61) |
where k = r + p + dA = 2pe−(r+dB)Δ. In the absence of the time delay, i.e., if Δ = 0, the Smith-Martin model becomes similar to the random birth death model of Eq. (13), and indeed μ(t) = σ2(t) = kt = 2pt. Thus, a difference between the rates at which mean and variance increase should provide information on the length of the B phase. Importantly, r and d are not independent in the Smith-Martin model, and the decline rate of undivided cells, p + dA = k − r, is not an independent parameter. Ganusov et al. [79] fitted this uniform Smith-Martin model to in vivo data on the CFSE dilution of naive CD8+ T cells, and demonstrated that this data maximally allow one to estimate three of the four parameters of this particular Smith-Martin model.
Pilyugin et al. [181] proposed to solve these parameter identification problems with a rescaling method that estimates two invariant parameters, i.e., the fraction of cells that die in one generation, and the mean generation time of surviving cells. This was a clever proposal because these parameters are independent of the functional form of the proliferation and death rates. Unfortunately, these measures are not necessarily the biological quantities that we are interested in. The method works by rescaling Eq. (58) such that each parent cell produces 2a daughter cells (instead of two). With this rescaling the exponential growth rate of the Smith-Martin model becomes r(a) = 2ape−(dB+r(a))Δ−(p + dA) [79, 181]. One can easily solve for a from this expression when r(a) = 0, i.e., for zero growth. Defining a* as the scaling factor that removes the expansion from the data one obtains
| (62) |
where r′(a*) is the slope of r(a) at a = a* [181]. One can solve for the probability that a cell divides before dying in the A-state, p/(p + dA), and does not die during the B-phase, e−dBΔ, from
| (63) |
Thus, 1 − (2a*)−1 gives the fraction of cells that die per generation. Similarly, the mean generation time of surviving cells can be obtained from
| (64) |
One still needs to determine a* from the data. To do this one rescales the data for various values of a by multiplying the number of cells in each division class with an. The exponential growth rate r(a) of the total rescaled cell number P (t) = Σ Pn(t)an is estimated by fitting to the exponential growth equation P(0)er(a)t. Plotting the estimated r(a) as a function of a one searches numerically for the scaling factor that removes the expansion from the data. The estimated a* can then be used to evaluate Eqs. (63) and (64) [181]. Here we illustrated the rescaling method for the Smith-Martin model [79], but that these two invariant parameters can be estimated for any cell age dependent form of the proliferation and death rates [181].
Luzyanina et al. [143] compare fits obtained with a classical Smith-Martin model, with fits obtained with a heterogeneous random birth data model, i.e., Eq. (13) extended with division and death rates, pn and dn, that depend on the division number, n, and find that the random birth death model fits their data better. This is not a fair comparison, however, because the heterogeneous model has many more parameters, that could compensate for the absence of the time delay, Δ, of the Smith-Martin model.
We have seen above that modeling experiments where quiescent cells are activated to proliferate in a programmed cascade, one needs different parameters to describe the first division. Quiescent cells are in the G0 state of the cell cycle, and need more time to enter the G1 state of the cell cycle, and their first B phase could take longer than subsequent B phases. The Smith-Martin model can be extended with a longer first division by implementing a recruitment function R(t), see Eq. (49), defining the distribution of times to complete the first division [43, 78, 137].
Assuming dA = dB = d to solve the parameter identification problem, but allowing for different division and death rates for each division number, a heterogeneous Smith-Martin model can be written as
| (65) |
where pn and dn are the division and death rates at the nth division, respectively [78, 137]. Fitting either a time-shifted log-normal [78] or a gamma distribution [78, 137] for R(t) to experiments explicity measuring the time to first division, this heterogeneous Smith-Martin model was successfully fitted to CFSE data from T cells stimulated in vitro with various concentrations of the cytokine IL-2 [56]. The magnitude of clonal expansion increased with the IL-2 concentration [56]. At the lowest IL-2 concentrations an initial phase of expansion was followed by a phase of contraction [78]. Explaining the data therefore required a heterogeneous model, where proliferation rates decrease, or death rates increase, over time or at higher division numbers [78, 137]. One possibility is to increase the death rate linearly with the division number, e.g., dn = d0 + αn, [78]. Alternatively, the length of the B-phase could increase with the division number, and/or the fraction of cells proceeding to the next division class could decrease at higher division numbers [137]. See below for a discussion on how these models describe the data.
Leon et al. [139] fit another approximation of the Smith-Martin model to the CFSE data of Hasbold et al. [91], by allowing cells at the end of the B-phase to skip the A-stage with a certain probabililty, and immeditately enter the next B-phase. For rapidly expanding cells with short A-stages this may be a reasonable approximation. There was no death in the B-phase of their model, however, which side stepped the problem of estimating both dA and dB from CFSE data [79, 181]. Since all of these models tend to have more parameters than can reliably be estimated from CFSE data, it remains unclear whether it is a good choice to introduce a new parameter for the likelihood of skipping the next A-stage. To allow cells to proceed quickly through a series of B-phases, one can also allow for a very high rate of exit from the A-state. Also, if the A-stage corresponds to G1 it cannot be skipped in reality.
Deterministic model
In circumstances where quiescent cells are triggered to proliferate rapidly for several divisions, most of the variation between the cells is due to differences in the recruitment into the first division [43, 56, 78, 81, 96, 127]. Rapidly dividing cells seem to proceed quite deterministically through several rounds of division. To describe this one can eliminate the exponential A phase of the Smith-Martin model by assuming a proliferation rate pn(a) → ∞, where a is the age of the cell. For a homogeneous model one arrives at the model proposed by Deenick et al. [56] that can be written as a single ODE for the first division class, and a set of algebraic scaling equations for subsequent divisions
| (66) |
where H(t) is again a Heaviside function. The middle term in the ODE describes the cells that have not died during the division time Δ, and thus have successfully completed their second division, and proceed to the next division stage [43]. The algebraic equation is based on the fact that the cells in the nth division class are those that have completed n divisions without dying, and have taken a time Δ for each division. The shape of the solution of the later divisions is identical to the first one, except for a shift in time and a scaling for the total area under the curve by doubling through division and the death rate. Using a log-normal or gamma-distribution for the recruitment function, R(t), this model reasonably describes CFSE data of T cells stimulated in vitro with high concentrations of the T cell growth factor IL-2 [43]. For lower concentrations of IL-2 the monotonic scaling of Eq. (66) was inconsistent with the data because the second cohort, P2(t), was larger than the first and the third cohort. Apparently, the parameters of Eq. (66) need to change over time, or change with the division number. Choosing for a linearly increasing death rate, dn = d + α(n−1), where d is the death rate of the first cohort, and α is the slope with which the death rate changes with the division number, and writing the model as a system of ODEs, the model becomes
| (67) |
for n = 2, …, ∞. This model can be shown to be identical to Eq. (66) when one restricts dn = d by setting α = 0 [43]. The model fits the same IL-2 data with good quality (see e.g. Fig. 9), and one can show statistically by an F-test that allowing α > 0 markedly improves the quality of the fits [43]. Because Eq. (67) has only a limited number of parameters, it seems an excellent choice for describing the dynamics of cells involved in rapid deterministic clonal expansion.
Fluorescence intensity
CFSE experiments are typically performed by labeling cells in vitro and following their division history in vitro or in vivo after injecting the cells back into animals. This in vitro labeling with CFSE allows for uniform labeling of the cells, such that one can readily distinguish the two-fold dilutions associated with each division. CFSE can also be injected in vivo which has the advantage that the labeled cells remain in their natural environment, but the disadvantage that the labeling tends to be heterogeneous, and consequently that the CFSE profiles typically lack the typical fingers corresponding to each two-fold dilution (which was not the case in the Choo et al. [36] data). To estimate division and death rates from CFSE data that do not allow one to classify the division number of each cell, the data has been described by changes in the mean fluorescence intensity (MFI) of CFSE labeled cells and unlabeled cells [7, 55, 72]. Asquith et al. [7] wrote a random birth-death model like Eq. (13), and estimated the number of divisions that were required for a CFSE+ cells to become CFSE− from the ratio of the MFI of all CFSE+ cells over all CFSE− cells. Finding a 25-fold ratio, they truncated Eq. (13) at the fifth division,
| (68) |
for n = 1, …, 4, and included a possible source, σ, of CFSE− cells, P5 [7]. Since in vivo CFSE administration may label only a fraction, 0 f 1, of the cells, one can define the initial condition of the model as P0(0) = f and P5(0) ≤ = 1 − f to directly scale the system into fractions of labeled and unlabeled cells. One obtains the fraction, P, of labeled cells from the solution of Eq. (68), i.e.,
| (69) |
CFSE is not lost by cell division, and only diluted into the two daughter cells. Thus, the total amount of CFSE label, L, in the population is
| (70) |
where the factor 32 comes from the initial 32-fold ratio in the MFI of labeled cells over unlabeled cells. Note that we have not used the equation for the unlabeled fraction, dP5/dt, with the source. Defining the MFI of the labeled cells as L/P one arrives at
| (71) |
for the ratio of the MFI of the CFSE+ population to the CFSE− population [7].
Thus, this model predicts two observables, the fraction of CFSE+ cells (Eq. (69)) and the ratio of the MFIs of CFSE+ to CFSE− cells. These two observables were successfully fit to B cell data from sheep, where sheep were injected with CFSE, and blood was collected at regular time intervals thereafter [7, 55, 72], providing median estimates of d = 0.09 day−1 and p = 0.03 day−1 of B cells in normal unimmunized sheep. Given the criticism of using the random birth-death model for fitting CFSE data due to the assumed exponential distributions of cell cycle times and life spans [51, 79, 181], the MFI method was also tested on artificial data generated with the Smith-Martin model [7]. Probably, because normal unstimulated B cells proliferate rather slowly, the MFI method correctly predicted the proliferation and death rates in the artificial data [7]. Finally, note that B cells are largely produced in the bone marrow, and that a random birth-death model need not be the most realistic choice. Instead one could use Eq. (2) with a large source and little or no renewal, rN 0, to write a new MFI model for unstimulated B cells.
Luzyanina et al. [144] defined a model directly describing the kinetics of the CFSE intensity profile using a label-structured population model similar to the age and volume-structured population models developed by Bell & Anderson [17]. Their models is comprised of a CFSE-structured PDE allowing for cell death, for the 2-fold dilution per division, and for CFSE loss by normal catabolism. This has the immediate advantage of not having to classify CFSE profiles into individual peaks, which is particularly helpful when the data is not nicely fingered. Assuming that each CFSE peak represents a cohort of cells that entered their first division at approximately the same time, Luzyanina et al. [144] wrote a label-structured population model for the density of cells with CFSE intensity x
| (72) |
where the v(x) term is an advection term describing the natural decay of the CFSE intensity, the proliferation p(x) and death d(x) rates depend on the CFSE expression of the cell, and γ is the CFSE dilution factor. One would expect γ = 2 if cells divide into two daugther cells each expressing half the amount of CFSE of the parent. Cells expressing a CFSE fluorescence intensity γx divide into two cells expressing approximately half that intensity, x. Eq. (72) therefore considers two ranges of CFSE intensities, split at approximately half the maximum CFSE intensity, xmax/γ, to exclude the division into daugther cells with a CFSE intensity higher than half the maximal intenstity. The 2γp(γx)n(t, γx) term describes that a cell with CFSE intensity γx, divides into two cells with intensity x, at a rate p(γx), where one needs another factor γ ≃ 2 to account for the doubling in the density if cells from a CFSE intensity range [γx, γ(x + dx)] divide into a approximately 2-fold smaller range [x, x + dx] [17, 144].
Taking a cell’s CFSE intensity as an approximate measure for the number of divisions the cell has completed, proliferation and death rates depended on a cell’s CFSE intensity, x, i.e., proliferation and death rates were approximately dependent on the division number like the pn and dn parameters used above. This dependence was described by piecewise cubic interpolation functions, each requiring a number of parameters. The advection term, v(x), was either described by an exponential loss term, or by assuming a constant loss of CFSE intensity. Fitting this PDE model directly to CFSE intensity profiles required smoothing of the data, and required non-trivial numerical integration methods for solving the PDEs [144]. Two data sets obtained from in vitro proliferation of T cells following polyclonal activation were fit with this model. The loss rate of CFSE, v(x), surprisingly was not exponential. The death rate hardly dependend on the CFSE intensity, whereas the division rate was found to be a bell-shaped function of the CFSE intensity x, with relatively slow maximum division rates of 0.55 day−1 and 0.8 day−1 at the third or fourth division. Finally, the dilution factor, γ, was less than two in both data sets [144].
Fitting the PDE of Eq. (72) directly to the CFSE profile circumvents the sometimes difficult problem of assigning all measured CFSE intensities in the fluorescence profile to a particular division number. The major drawback of the model is that the CFSE fluorescence of a cell is not a direct measure of the number of divisions a cell has completed, and that one may need complex dependencies to describe division and death rates that depend on the division number. The general label-structured population approach of Luzyanina et al. [144] has been extended by several authors [13-16, 92, 194]. Banks et al. [15] address the paradoxical parameter estimate, γ < 2, which suggested that CSFE was being created at cell division. After extending the original model with cellular autofluorescence, and with a biphasic natural loss of CFSE by replacing the exponential loss of the fluorescence by a Gompertz decay process, they can describe the same CFSE data reasonably well with the expected γ = 2 [15]. Biphasic loss of fluorescence in non-dividing CFSE labeled cells had been observed before [146], but then the first phase had a time scale of about a week, whereas in Banks et al. [15] the much more rapid first phase takes less than a day. Their interpretation of the biphasic loss also differs, as Lyons et al. [146] argue that the slow phase is due to the CFSE that is bound to long-lived proteins, and Banks et al. [15] explain their much more rapid first phase by the time it takes for CFSE to become stably incorporated in the cell. Because the time scales are so different, both could be true, suggesting a triphasic loss of CFSE in the absence of cell division. Importantly, in both papers [15, 146] the last phase is so slow that labeled cells will remain well above the autofluorescence level for long periods of time.
Schittler et al. [194] and Hasenauer et al. [92] extend the Luzyanina et al. [144] model with discrete populations for each division, and this extension leads to the much more intuitive model
| (73) |
for n = 1, …, nmax, and where x is the amount (or concentration) of CFSE in each cell, which decreases at a rate v(x). The number of cells contained in the nth subpopulation is defined as , and the number of cells having an amount x of CFSE is given by . After adding on the autofluorescence the latter can be fitted directly to measured CFSE profiles, whereas the total cell number in the data is predicted by P (t) = Σ Pn(t) [92]. Because the cellular dynamics are now decoupled from the CFSE fluorescence, this system of PDEs can be simplified into a simple set of ODEs for the cell numbers,
| (74) |
for n = 1, …, nmax, and simple linear PDEs for the loss of the normalized fluorescence. Solving the PDEs, Hasenauer et al. [92] derive a model that markedly speeds up the fitting of the model to CFSE profiles. Having a combined division and fluorescence structured model, it is much more natural to incorporate division and death rates that depend on the number of divisions the cells have completed [92, 194]. Banks & Clayton Thompson [13] take this model further, by choosing an appropriate v(x) enabling them to restrict γ = 2 [15], and rewriting Eq. (73) into the age-structured approach of the cyton model Eqs. (52-57), where division and death rates depend on the time since the last division:
| (75) |
for n = 1, …, nmax. This is a cyton model that can directed be fitted to CFSE profiles, i.e., without having to assign each fluorescence measurement to a particular division number. Starting with the basic cyton model of Eqs. (52-57) with nine parameters, they add on various assumptions and find that their most complex cyton model having 13 parameters describes this one particular set of data best [13].
We have seen above that the assumption of exponentially distributed inter-division times that is made implicitly by ODEs performs poorly at describing the proliferation of rapidly dividing cells. The fluorescence and/or division structured PDEs derived from Eq. (72) make the same assumption and should suffer from similar problems. Since the CFSE data were obtained after polyclonal stimulation of the cells, which typically triggers rapid proliferation, it could be that the bell-shaped dependence of the division rate on the division number that was found in these studies [15, 16, 92, 144] is an artifact that is compensating for the too fast progress through the division cascade in these PDEs. As yet it also remains unclear whether the bell-shaped dependence of the division rate on the division number can be replaced by a bell-shaped recruitment function, R(t), and a linearly increasing death rate, which was sufficient to describe other CFSE data [78, 137]. Finally, although the PDEs derived from Eq. (72) provide a powerful approach to model the MFI or poorly fingered CFSE data, one should remain careful and check whether the data contains sufficient information to reliably estimate all the parameters of such a model. Fitting complex models to simple data calls for estimating confidence intervals, and comparing different dependencies of recruitment, division and death on age and/or division number [158].
Branching process models
One advantage of using branching process theory is that it allows one to calculate not only the mean number of cells in different division classes, but also the probability of a given number of cells in a given division class. Comparison of the theoretical predictions with the observed statistical variance can help tease apart different mechanisms behind the variability in population behavior. Zilman et al. [248] review a number of the models that have been used to interpret CFSE data, and conclude that the cyton model [96], the age structured model of Eq. (49), and continuous branching process models, can all yield formally identical systems of equations. They provide simple analytical solutions for a model in which the distribution of interdivision times follows a gamma distribution, and consider examples where the division rates within lineages are correlated. Because a gamma distribution can adopt the shape of an exponential distribution, and can look very similar to a lognormal distribution, this seems an excellent general model for fitting CFSE data. Disturbingly, they also show that the estimates of some critical kinetic parameters, such as the average interdivision time, depend on the assumed distribution of interdivision times [248]. Determining the shape of the distributions describing how death and division depend on a cell’s age since the last division is therefore of crucial importance for properly understanding of cell kinetics. This has recently been achieved by following B cells and their daughters in vitro over extended periods of time while they are dividing and dying by video microscopy [95]. These imaging experiments suggest further complications in the modeling of CFSE data because division and death times are strongly correlated within the lineages descending from a single cell [67, 96, 152, 226]. Dependencies between the life spans of parent and daughter cells are expected to affect the interpretation of CFSE data [115].
Hyrien and Zand et al. [35, 114-117] devised a series of age-dependent branching process to model CFSE data, allowing for arbitrary probability distributions for the age at which cells die, divide, revert to rest, or differentiate. Cell death was left out from their earlier models [117], but was accounted for in their later models [35, 114, 115]. Their models allow for lineages of cells to account for the possible correlations between daugther cells and their parent cells [67, 96, 152, 226], and importantly they show that most of these dependencies are not expected to change the interpretation of the CFSE data [114]. Hyrien et al. [115] argue that the age-structured population model of Eq. (49) and the cyton model of Eq. (57) are based upon a “competing risk approach”, where the expected life-span of cell is completely determined by the distributions of the time to division and time to death, and that this need not reflect the actual biology properly. One example would be a cell that inherits the decision to die from a previous generation, and another example is a cell that needs additional time after the decision to divide or die has become irreversible, to actually complete the cell division or the process of apoptosis [115]. They therefore extend the model with a probability to divide, pn, at generation n, and let cells die with a probability 1 − pn. Cells that divide have a distribution of times to division, p̂n(a), and cells that die sample their life-span from a distribution of times to death, d̂n(a). Thus, the life-span of a live cell at generation n is determined by p̂n(a) if the cell divides and by d̂n(a) if the cell dies, whereas in the cyton model the expected life-span is determined by the combination of p̂n(a) and d̂n(a), and does not depend on the actual event type.
When the model is fitted to CFSE data obtained by polyclonal stimulation of human CD8+ T cells, it is further extended with a probability that a cell neither dies, nor divides, but returns to rest and become long-lived [115]. The CFSE profiles, i.e., the fraction of live and dead cells expressing each particular CFSE fluorescence intensity were fitted directly to the corresponding probablilty density functions of the model [115, 117]. The data consisted of ten time points taken between 40 hours and 112 hours, but there was no separate data estimating the distribution of the time to complete the first division. The proliferation of undivided cells was modeled as a gamma distribution, p̂0(a), and had to be estimated from the CFSE profiles. Allowing for different parameters for the undivided cells (n = 0) and activated cells (n > 0), and no further dependencies on the division number, the model fitted the CFSE data of live and dead cells well [115]. The mean time to division of activated cells was 12.9 hours and the mean time to death was 1.5 hours. Thus, cells that are going to die, do so rapidly. Simplifying the model by not allowing cells to revert to rest markedly decreased the quality of the fit [115]. Another simplification of the model was made by adopting the competing risk approach of the cyton model, and this decreased the quality of the fit even further. Hyrien et al. [115] argue that this poor fit suggests that the competing risk approach cannot properly describe the biology because decisions of cell fate are made earlier than the realization of the actual event. Indeed, it could be difficult in the cyton model to combine a short time to cell death, probably required to explain the CFSE profile of the dead cells, with a long time to division estimated from the whole CFSE profile, and remain consistent with the observed increase in the cell numbers. Alternatively, one could argue that it was not tested whether a cyton model where p̂n(a), d̂n(a), and/or the progression fraction, ϕn, depend on the division number for n > 1, would be able to explain this data. This remains undecided as we do not know whether all the parameters of models of such complexity are estimable from CFSE data [115]. Importantly, in vitro imaging studies of individual B cells provide strong statistical evidence that cell fates like division and death, can be described by the competing risk approach assumed by the cyton model [66, 67, 95].
Miao et al. [158] also allow cell fates to be determined before the actual events and extended the age-dependent branching process of [117] to allow for cell death. They developed an agent based model to generate artificial CFSE data to compare how the ODE of Eq. (14), the simple Smith-Martin model of Eq. (58), the cyton model in [96], and two variants of their novel branching process models perform in describing that data. To allow for fair comparisons they also allowed for exponential distributions in some of the simulations of the agent based model. In general the two models based on branching processes performed best [158]. It is perfectly understandable that general models based upon age-dependent branching process outcompete the simple ODE and Smith-Martin models; we expect that the additional states in the new models bring about additional parameters that allow for the superior fits.
Yates et al. [241] fit the CFSE dilution of dividing cells by describing the cellular kinetics with a discrete time branching process lasting N generations until the cells have diluted their CFSE fluorescence to background levels. At every time step, or generation, of the model cells have a particular probability to divide, p, a probability to die, d, and hence a probabily, 1 − p − d to survive without division. Similar to what is assumed explicitly in the cyton model [96] and implicitly in Eqs. (13-49), cells retain no memory of the events in previous divisions, other than their division number [241]. All parameters of this model are identifiable because there are only three parameters, i.e., the length of the generation, and p and d. Moreover, the time delay that is implied with cell division is naturally accounted for by the generation time of the branching process, i.e., for any finite time step the population will expand slower than one that is based on the continuous time random birth death model of Eq. (13). Finally, a branching process allows one to estimate the process noise [161] originating from the stochastic processes of division and death, and to compare that to the measurement noise in the CFSE data [241]. Fitting the model to T cell proliferation data it was found that the best fits were obtained with different probabilities of division and death in the first division, in divisions 1-3, and in the subsequient divisions. Having a fixed generation time and a fixed probability for the first division implies that the time to complete the first division obeys a binomial distribution. Since the times to first division typically follow a time-shifted normal or log-normal (or gamma) distributions [56, 81, 96], and because this binomial distribution would approach a normal distribution only when both the probability to divide and the generation time are small, it is not completely clear whether this model can deliver a realistic distribution for the time to first division.
Many different models share the problem that current CFSE data is not rich enough to estimate all parameters reliably. Moreover in most of the CFSE data sets total cell numbers have not been measured, and one only knows the frequency distribution over the division classes. Cell death rates can only be estimated when total cell numbers are known. Although directly fitting CFSE profiles would seem very helpful, it is not obvious that the CFSE-structured PDE of Eq. (72) [144] is the best approach. Rates of cell division and death would depend on a cell’s CFSE intensity when division and death rates depend on the division number (like in Eq. (67)), but division and death rates may also depend on the time since the last division, i.e., a cells age, see Eq. (49) and Refs [43, 96, 248], which is a period during which a cell’s CFSE intensity should hardly decline. Thus, one could develop more realistic models by structuring the population by age and division number, and on top of that keep track of the CFSE loss over time and dilution by division. For instance, one could allow for an exponential loss of the mean CFSE fluoresence intensity of undivided cells over time, allow for a mean and variance of the CFSE intensity of undivided cells, and calculate mean and variance of divided cells by propagating the increase in the variance with every division. After estimating the loss rate, mean and variance from the data, such a model would allow one to calculate the corresponding CFSE profile from the precursor distribution, and hence would allow one to fit Eq. (49), the cyton model [96], or any other continuous branching process [115, 158, 248] directly to CFSE data.
5.1.2 Some examples of biological interpretation of CFSE data
The slow renewal of CD8+ memory T cells specific for particular epitopes from LCMV was recently characterized by labeling memory P14 CD8+ T cells in vitro with CFSE and transferring these cells into naive recipients [36]. Recipient mice were then serially bled at various time points posttransfer and both the number and the CFSE profiles of the transferred memory cells were longitudinally assessed in individual mice. Transferred memory CD8 T cells were stably maintained in the recipient for the entire duration of the experiment. The percentage of undivided cells decreased exponentially with time, suggesting that this was a homogeneous population of memory cells, and that the recruitment into division was stochastic. Since the CFSE dilution was slow, the data was described with the cascade model of Eq. (13). As expected from Eq. (15), the mean number of divisions and the variance in the number of divisions both increased linearly with time. Fitting the CFSE distribution in the number of cells over time, in each mouse, to the Poisson distribution of Eqs. (14) and (15), the estimated rate of division was in agreement with that estimated from the rate of increase in the mean number of divisions [36]. These observations implied that the homeostatic turnover of memory CD8 T cells occurred stochastically, and that the probability that a memory cell divided did not depend on its previous division history. This stochastic turnover resulted in an average rate of division of p = 0.02 day−1, or an intermitotic time (1/p) of approximately 50 days (see Table 3).
The homeostatic proliferation that naive T cells undergo following adoptive transfer into an environment with low T cell numbers was studied by Yates et al. [242]. They labeled F5 TCR transgenic naive CD8+ T cells, which are specific for an influenza peptide, with CFSE and transferred these cells into Rag1 knockout mice that have no endogenous T cells. At different time points lymph nodes were recovered from the recipient mice to record the CFSE profiles. In the presence of cognate antigen, i.e., the influenza virus, CFSE dilution was rapid due to the vigorous clonal expansion of the F5 T cells. In its absence, the F5 cells started to grow exponentially after a few days. The mean division number (as defined by Eq. (15)) increased linearly with time, with some evidence for a slowing-down after about two weeks. Fitting the Smith-Martin model to the data obtained in the absence of cognate antigen, Yates et al. [242] estimate an average time between divisions of 1/p + Δ ≃ 5 days (with Δ ≃ 7 hours). Comparing the deterministic model of Eq. (66) with the Smith-Martin model, having an exponential recruitment into division, on this data they concluded that homeostatic proliferation involves stochastic recruitment into division. To account for the reduction in the expansion rate after two weeks, the Smith-Martin model was extended with an exponentially decreasing proliferation rate. The extended model fitted the data significantly better and estimated interdivision times starting at 3.4 days and declining to 11.3 days after two weeks [242], which remains much slower than what is observed during immune responses to cognate antigen.
To investigate the role of IL-2 in T lymphocyte proliferation, CFSE-labeled naive CD4+ T cells were stimulated in vitro with anti-CD3 antibodies at different concentrations of exogenous IL-2 [56]. This data was originally interpreted with Eq. (66), i.e., by assuming a lognormal distribution, R(t), of division times for the first division, and deterministic expansion with a fixed interdivision time for the divided cells [56]. This analysis suggested that IL-2 mainly affects the fraction of cells recruited into the response, the interdivision time, and the probability of cell death during the division for divided cells. Since visual inspection of the CFSE data suggested that there should also be some stochasticity during the later divisions, the same data was later analyzed with extended Smith-Martin models [78, 137]. Assuming either a delayed gamma distribution or a lognormal distribution for the recruitment function, R(t), the new analyses confirmed that IL-2 affects the fraction of cells recruited (the recruitment data were slightly better explained by the delayed gamma distribution [137]). Ganusov et al. [78] fitted Eq. (65) to the data and found that having an increased rate of death at the higher division numbers significantly improved the quality of the fit, which led to their interpretation that the main effect of IL-2 is a reduction of the cellular death rate after a few divisions. This is in good agreement with independent in vitro data [220]. Lee & Perelson [137] instead made the assumption that the length of the B phase increases with the division class, i.e., Δn = Δ0 + nΔ, and found that this heterogeneity also improved the quality of the fit to the data, leading to their result that a main effect of IL-2 is a change in the interdivision time. Unfortunately, it was never tested which of these two explanations is most realistic, and/or if both are valid. Collectively, this illustrates how the choice of the mathematical model may determine the results one obtains, and that it is important to understand the modeling and study various possibilities.
The proliferation of B cells was studied in a similar fashion by stimulating naive B cells in vitro for different periods of time with various concentrations of different stimuli [212]. T cell-dependent stimulation was mimicked using an anti-CD40 mAb and IL-4, whereas the Toll-like receptor (TLR) agonists LPS and CpG were used as T cell-independent stimuli. The CFSE data was analyzed by computing the change in the mean division number (defined by Eq. (46)), and the total cell numbers over time. The analysis suggested that for all stimuli the fraction of cells recruited and the rate of population growth increased with the concentration of the stimulus. Similarly, the duration of the stimulus correlated with better expansion and a larger fraction recruited. Thus, both the concentration and the duration of the stimulus appear to play a key role in the overall proliferative outcome. The type of stimulus determined at which time point proliferation would stop, which caused the populations to decline, suggesting a unique intrinsic limit to B cell proliferation for any given stimulus, even when stimulation conditions were improved by diluting the population [212]. Additionally, proliferating B cells were sorted according to the number of divisions they had completed, and were transferred into separate cultures. Tracking the subsequent divisions revealed that cells having completed more divisions proliferate less, suggesting that that a division-linked limit is the key regulator of the extent of B cell proliferation [212].
Similar B cell data from the same laboratory were analyzed by fitting an analytical cyton formulation of the extended Smith-Martin model of Eq. (65) to the data [136]. In these experiments naive B cells were stimulated with LPS in the presence or the absence of IL-4. The recruitment into the first division was measured with thymidine labeling, and was fitted with a recruitment function, R(t), assuming a delayed gamma distribution of the division times. Although here a lognormal recruitment function explained the data slightly better, the very similar gamma distribution allowed for analytical solutions [136]. When IL-4 was present, a greater proportion of cells were recruited into division, but with a longer average time to complete the first division. Similar to the protective effect of IL-2 on proliferating T cells [78], it was observed that IL-4 has more of an effect on the death rate of B cells than on the rate of proliferation. The most profound effect of IL-4 was to decrease death rates for smaller division classes [136]. As an alternative for the inhomogeneous death rates in Eq. (65), the possibility of the above-mentioned increase in the length of the B phase depending on the division class was tested on this data. This analysis showed that for proliferating B cells, Eq. (65) with the increase of death rate provides a better fit than the model with an increase of cell cycle length [136].
The fitting of the CFSE data from human CD8+ T cells after polyclonal stimulation by the extended age-dependent branching process model suggested that cell division takes approximately 12.9 hours and cell death about 1.5 hours in human CD8+ T cells [115]. The activated cells die with a probability 0.13 per generation, they divide with a probability 0.66, and they revert to rest with a probability 0.21 per generation. The fact that about 20% of the cycling cells reverts to a quiescent state at each generation could account for the generation of separate lineages of memory cells and effector cells during clonal expansion [78, 115, 245]. The fact that cells die so rapidly suggests that the decision to die is made in preceding generations, which we would predict that sister cells are expected to die at similar times [115]. This prediction is born out by the experiments where individual B cells were followed in vitro by imaging [67, 95].
6 TRECs and telomeres
In addition to labeling populations to characterize their population dynamics one can study particular markers that reflect the division history of cells. Two such markers have been studied in the past: (1) telomeres, which are the non-coding ends of chromosomes that shorten every cell division, and (2) T cell receptor excision circles (TRECs), which are small circles of DNA that are formed when T cells rearrange the gene segments coding for their antigen receptors in the thymus. Since TRECs are not duplicated when cells divide, the fraction of TREC+ cells in a population provides information about the frequency of cell division. Similar information is provided by the average telomere length of a population because cell division shortens the telomeric ends of chromosomes. Note that the expected number of TRECs per cell, here called the TREC content of a population, declines geometrically with cell division, since the TREC content halves with every division, whereas the telomere lengths decline linearly with division, because every division removes 50-100 nucleotides [88, 218]. Remarkably, in the literature the use of telomeres was typically restricted to measuring cell division [192, 229], while TREC data were originally used to measure thymic output [62], even though both should be influenced by de novo production and peripheral division.
6.1 TRECs
TRECs have been used to quantify the output of newly produced naive T cells from the thymus. This is an important parameter to estimate because the size of the thymus declines with age [203], and the reduced production of novel naive T cells with unique new antigen receptors is thought to play an important role in aging [165]. It was therefore a major step forward when thymic output could be quantified by the introduction of the TREC assay [62, 130]. Since TRECs are not copied during peripheral proliferation, each TREC remains a true marker of thymic origin, and the number of TREC+ cells in a population reflects the number of cells that were originally produced by the thymus at any point in time and that are still present in the periphery. Conversely, the number of TREC− naive T cells reflects the number of cells in the population that have been produced by peripheral proliferation. The average TREC content of a naive T-cell population can therefore be used to estimate the fraction of cells that were originally produced by the thymus. When the average number of TRECs per CD4+ or CD8+ T cell was measured in healthy individuals of different ages, an exponential loss of the TREC content was observed [62], reminiscent of the supposedly exponential decay of thymus output with age [203]. The TREC content of T lymphocytes has therefore been widely used to measure thymus output. For example, the fact that the TREC content of CD4+ and CD8+ T cells tend to be reduced in HIV+ patients, has been taken as evidence for HIV-induced loss of thymus output [62].
TRECs are usually measured as the fraction of the amount of DNA analyzed, and are therefore typically expressed as TREC content, i.e., the average TREC number per cell. Reviewing TREC data one needs to be careful about the population that is being sampled, and the best data measure TREC content within naive T cell populations [89] and/or even within subsets of naive T cells [124, 125]. Measurements that have lumped the naive and memory T cell subsets may be biased by shifts in the naive and memory ratios, as memory T cells tend to contain few TRECs [140]. Another difficulty in the interpretation of TREC data is that TRECs are long-lived, and are thus not a direct marker of current thymus output. Indeed, in patients who had been fully thymectomized, TRECs could still be identified in CD4+ and CD8+ T cells up to 39 years after thymectomy [62]. Intuitive interpretation of TREC data may therefore easily lead to false conclusions [41, 99, 102, 140], and mathematical modeling is required for proper interpretation.
There are several ways to formulate models for the TREC dynamics in naive T cell populations. One approach is to write equations for both the TREC+ and TREC− naive T cells [140], and another is to extend cascade models like Eq. (13) realizing that the TREC content of each population halves with every cell division [213]. The latter has the advantage that it can also be used for tracking the average telomere length of the population (see below). Hazenberg et al. [102] proposed a very simple TREC model, simplifying Eq. (2) for naive T cells by lumping death and activation into a single loss rate d, and adding one equation for the total number of TRECs in that population, i.e.,
| (76) |
where σ(a) is an age-dependent thymic production rate, p is the renewal rate, and d is the loss rate of naive T cells. Note here age refers to the age of an individual, not the age of a cell. The corresponding dynamics of the total number of TRECs, T, was described as:
| (77) |
where c is the average TREC content of a cell appearing from the thymus (i.e., a recent thymic emigrant). Since TREC can only be produced in the thymus, the total number of TREC is not affected by peripheral proliferation, i.e., Eq. (77) lacks a proliferation term. Thymocytes that have formed their TREC(s) by rearranging their T cell receptor on average complete a few divisions before emigrating from the thymus [62], and the expected value of the TREC content of a recent thymic emigrant is approximately 1/8 c 1/4 [11, 243]. Because a T cell can rearrange its T cell receptor genes on both chromosomes, ≤ ≤ a thymocyte may contain two TRECs. However, because of subsequent divisions in the thymus very few recent thymic emigrants will contain more than one TREC. Naive T cells will typically have either zero or one TREC and Eq. (77) should approximately reflect the number of TREC+ naive T cells in the system. From these two equations one can derive that the TREC content (C = T/N) changes according to:
| (78) |
One can immediately see that the total number, T, of TRECs in the system provides a much better estimate for thymic production than the TREC content, C, because the latter is confounded by peripheral proliferation [41, 140, 187]. For estimating thymus output it would therefore be good practice to analyze total TREC numbers in addition to TREC content [41, 140].
Assuming that the TREC content is in quasi steady state, i.e., assuming dC/dt = 0, the TREC content is equally affected by thymic production, σ(a), and peripheral proliferation, P,
| (79) |
This equation has various interesting implications. First, the TREC content can only decline with age if naive T cells proliferate, i.e., if p > 0. The experimental data demonstrating that the TREC content of human naive T cells declines one to two orders of magnitude over one’s lifespan [89], whereas the TREC content of thymocytes, and probably that of RTEs (c), remains constant [118], “proves” that human naive T cells divide without switching to the memory phenotype (provided that TRECs are stable) [68, 102]. Second, if the system were in quasi steady state, and if there were no density dependent regulation in the naive cell compartment, that is, if the number of naive T cells was simply proportional to the thymic output, i.e., if N(t) ∝ σ(a), the average TREC content would approach a constant value (provided TRECs are stable). Thus, the fact that the TREC content declines provides evidence for homeostasis within the naive T cell compartment [68, 102]. Third, Eq. (79) shows that the scaled TREC content, Ĉ ≡ C/c, of the naive T cell population reflects the fraction of cells that were originally produced in the thymus (because the σ(a) + pN term in the denominator reflects the total production) [57], which makes sense because TRECs remain a marker for cells that were originally produced in the thymus. Human TREC contents measured in thymocytes, cord blood cells, and naive T cells taken from volunteers of various different ages, suggest that CD4+CD8− thymocytes and CD4+ cord blood cells have an indistinguishable TREC content of c ≈ 0.2/cell [57], and that 30 year old adults have a TREC content of C ≈ 0.04/naive CD4+ ≈ T cell [57, 89]. This would argue that in a 30 year old healthy human adult the scaled TREC content Ĉ ≈ 0.2, i.e., that about 20% of their circulating naive CD4+ T cells have originally been produced in the thymus [57]. Finally, note that the reported decline in TREC content with age is reasonably well described by C = 0.2e−0.055a, where a is age in years, which agrees surprisingly well with the yearly 5% loss of productive thymus tissue estimated by Steinmann et al. [203].
These results can also be used to understand the mechanisms by which the population densities of CD4+ and CD8+ naive T cells in HIV+ patients are reduced [190], and their TRECs are diluted [89]. The most likely explanation for the reduction in naive T numbers is increased priming by immune activation [101], taking cells from the naive into the memory compartment, which in the model for naive T cells corresponds to increasing d. Lowering the number of naive T cells, N, by increasing d would however increase the TREC content (see Eq. (79), Hazenberg et al. [102] and Dutilh & De Boer [68]). Low TREC content calls for increased proliferation (see Eq. (79)), which would however increase N. Because this is intuitively difficult to understand, let us define the division rate as p = αd, where 0 α 1 because p ≤ d. According to this definition a fraction 1/(α + 1) of the cells are expected ≤ ≤to die before they divide. Then use the steady expression of Eq. (79), and the steady state of Eq. (76), i.e., N = σ(a)/(d[1 − α]), to compute from the observed scaled TREC content, Ĉ, and the actual number of naive T cells, N, i.e.,
| (80) |
This shows that 1 − Ĉ directly estimates “the likelihood of cell division over the expected life span of a cell”, α, and that to explain decreased naive T cell counts given a particular thymic output the death rate has to increase more than the TREC content decreases.
Estimates of the death rate are available from studies using deuterium labeling of CD4+ naive T cells in healthy volunteers [223] and HIV+ patients [224], which suggested average loss rates of d = 0.0005 day−1 and d = 0.00152 day−1, respectively (i.e., life spans of 5.6 and 1.8 years, respectively; just exceeding a 3-fold difference). Naive T cell counts are depleted during HIV-1 infection, and after one or two years of HIV-1 infection one readily observes a 5-fold TREC dilution and a 2-fold reduction of the number of naive CD4+ T cells in the blood. Given that Ĉ and d are known, Eq. (80) can be used to estimate the impact of HIV-1 on thymic output. For instance, for a normal individual with 500 naive CD4+ T cells per μl blood, a death rate of d = 0.0005 day−1, and a scaled TREC content of Ĉ = 0.2 TREC cell−1, one estimates that σ = 500 × 0.2 × 0.0005 = 0.05 cells μl−1 blood day−1. A “typical” HIV+ patient with an approximately 3-fold faster loss rate of d = 0.00152 day−1, a 2-fold reduction of its naive T cell numbers (N = 250 cells), and a 5-fold lower scaled TREC content (Ĉ = 0.04), would therefore have a thymic production of σ = 250 × 0.04 × 0.00152 = 0.0152 cells μl−1 blood day−1, which is approximately 30% of the normal thymic output. Summarizing, to explain the TREC dilution in HIV+ patients one has to invoke increased division rates of the naive T cells [102], which compensates for their increased loss rate d. To explain severe naive T cell depletion in combination with significant TREC dilution, one has to invoke decreased thymic production, and the more TREC dilution (i.e., the more the division), the lower the estimated thymic production that is required to explain marked naive T cell depletion. Note, that this reasoning is based upon steady state behavior, and that the dynamics of naive T cells are very slow. A numerical simulation over 20 years of Eqs. (76) and (77) reveals that the 5-fold TREC dilution occurs much faster than the 2-fold depletion of the naive T cells (Fig. 10), which argues that the quasi steady state of Eq. (78) is a better approximation than that of Eq. (76).
Figure 10.
The decline of the naive T cell numbers, the total number of TRECs, and the TREC content after infection with HIV-1. The steady state before time zero represents a healthy individual with N = 500 naive CD4+ T cells per μl blood, a death rate of d = 0.0005 day−1, and a scaled TREC content of Ĉ = 0.2 TREC cell−1, suggesting that p = 0.8d, and σ = 0.5 cells μl−1 blood day−1. After time zero we set σ = 0.0152 cells l−1 blood day−1, p = 0.96d, and d = 0.00152 day−1 to represent HIV-1 infection. Note that the TREC dynamics are much faster than the depletion of the naive T cells because naive T cells also maintain themselves by proliferation.
It has been observed that both HIV+ patients under successful treatment [89], and human stem-cell transplantation patients [64], have TREC contents that are higher than normal. This has been interpreted as evidence for increased thymic production (“thymus rebound”) [64]. Employing similar mathematical models, Ribeiro & De Boer [187] show these higher than normal TREC contents may in fact reflect the normal influx of recent thymus emigrants into a virtually empty peripheral T cell pool. Indeed, according to Eqs. (76-77) the TREC content will approach its maximum, C → c, when the peripheral pool largely consists of recent thymic emigrants, even if thymic output is normal.
Cascade models like Eq. (13) have been used to model the TREC dynamics of the serial compartments of thymocytes, recent thymic emigrants, and naive T cells [213]. One choice is to model the dynamics of TREC+ and TREC− cells in each compartment, i.e.,
| (81) |
for n = 1, 2, …, l, where the source σ(t) is the inflow from the preceding compartment, and where the plus and minus superscripts denote TREC+ and TREC− cells, respectively. Upon the lth division cells are assumed to mature into the next compartment, e.g., transform from a thymocyte into an RTE, where they then appear as a source σ(t) weighted by their TREC content c. Here c obtains the interpretation of the fraction of TREC+ cells in the source (i.e., we assume that cells cannot harbor more than one TREC). Note that the division of a TREC+ cell preserves the TREC+ cell and leads to one new TREC− cell. Alternatively, one can model the total number of TRECs in the cascade, T, with one equation, i.e.,
| (82) |
where , and the last term is the cell division of the last stage Nl of the cascade in this compartment weighted by its expected TREC content 2−l, and define the TREC content as C = T/N [213].
Bains et al. [11, 12] generalize Eqs. (76-77) by letting all parameters depend on time, i.e., on the age of the individual, to investigate the contribution of peripheral renewal, p(t)N(t), to the maintenance of naive CD4+ T cells during childhood. Their analysis is based on TREC measurements in T cells in young adults from Douek et al. [61], who recalculate their TREC data into TREC content of naive T cells by assuming that memory cells contain no TRECs, and by dividing the measured TREC content in individuals of different ages by the measured fractions of naive T cells. Because the recalculated data suggest that the TREC content does not decline up to an age of 20 years, Bains et al. [11] argue from Eq. (79) (their Eq. (4)) that the relative contribution of thymic production and peripheral renewal should not change with age. Thus, because thymic production is decreasing with age, the total production by peripheral renewal should decline similarly when youngsters mature. Total naive CD4+ T cell numbers in the body, N(t), tend to increase during the first 20 years of life, and were computed by multiplying the measurements in the blood with the dependences of blood volume with body weight [141], and of body mass with age, and by assuming that 2% of the naive T cells resides in the blood [11].
In Bains et al. [11] thymic production, σ(t), was assumed to be proportional to the volume of productive thymic tissue, which has been measured, and declines with age [203]. Using an estimate for the TREC content of a recent thymic emigrant similar to that defined above, i.e., c = 0.25, and having estimates for the thymic output, σ(t), and the total number of naive T cells, N(t), they estimate the division rate p(t) from Eq. (79). The interdivision time, 1/p(t), in children between 1 than 5 years was about 125 days, which increased to 1/p(t) = 500 days at the age of twenty. Similarly, substituting T (t) = CN(t) into Eq. (77) they computed the death rate from
| (83) |
and find expected life spans of naive T cells of 1/d = 70 days between the ages of 1 to 5 years, increasing to approximately 400 days at the age of 20 years [11]. These life spans would become longer if lower estimates of c were used. This expected life span of about one year for naive CD4+ T cells in young adults is in good agreement with the short term deuterated glucose labeling study of Macallan et al. [150], but is over 5-fold shorter than the life spans estimated in the long term deuterated water study of Vrisekoop et al. [223]. Finally, finding that C/c ≃ 0.08/0.25 ≃ 0.32 the authors calculate from Eq. (79) that up to an age of 20 years only 32% of the total naive T cell production is due to the thymus [11].
In their second study, Bains et al. [12] used published measurements on the fraction of Ki67+ naive T cells in individuals of 0–30 years, which decreased with age and approximately obeyed 0.02e−0.1a, where a is age in years, to estimate how the fraction of dividing naive T cells decreases with age. To translate Ki67 expression into a division rate it was assumed that a dividing naive T cell is Ki67+ for about half a day (note that Fig. 6b would suggest that five days is a more appropriate estimate). Combining the estimated proliferation rate, the stable TREC content, with the observed naive T cell densities per μl of blood, the thymic output was computed from Eq. (79) (their Eq. (10)). Using this approach, they estimated that at birth the average human thymus exports 6.9×108 CD4+ T cells day−1, which approximately doubles during the first year of life to 1.4 × 109 CD4+ T cells day−1. After this peak thymic export declines in a biphasic manner with a decline of 12% per year between one to eight years, and 4% per year later on [12]. These rates are reasonably consistent with those predicted by the classical histological study of Steinmann et al. [203], except for the decline of 12% per year in one to eight year olds, which is somewhat too fast. The two studies are not entirely consistent on the relative contributions of thymic production and peripheral renewal because the estimated thymic output in Bains et al. [12] is several-fold higher than that in Bains et al. [11]. The particular translation of Ki67 expression into a division rate in Bains et al. [12] could be responsible for this discrepancy because increasing the estimate for the duration of Ki67 expression changes the estimate of thymic output. In both studies the relative contribution of the thymus in the maintenance of naive CD4+ T cells remains smaller than that of peripheral renewal, even in these relatively young individuals [27], which is in good agreement with the even smaller contribution of the thymus estimated later in life [57].
6.2 Telomeres
Chromosomes have unique structures at their ends consisting of non-coding tandem DNA repeats that are called telomeres. Due to the incapability of DNA polymerases to copy the very ends of chromosomes, telomeres shorten with each cell division [23, 88]. Since each cell division leads to the loss of 50-100 terminal nucleotides from each chromosome, the average telomere lengths of all chromosomes in a cell provides a record of a cell’s proliferation history. Telomere shortening also has functional consequences, as it limits the replication capacity of cells when the telomeres become too short [1, 97, 98]. The implications of this “Hayflick limit” on the senescence of immune responses has been addressed by mathematical modelling [180]. Activated T cells may express the enzyme telomerase that elongates the telomeric ends of the chromosomes [106, 228, 230].
One can develop a model for the average telomere length of a naive T population by adding a source to Eq. (13), i.e.,
| (84) |
where n is the division number. Summing these equations yields Eq. (76) for the total naive T cell population. When L0 is the average telomere length of recent thymic emigrant N0, and LΔ is the telomere loss per division, one can obtain for the average telomere length
| (85) |
Taking the derivative gives
| (86) |
where the ′ denotes differentiation with respect to time. Thus, in the absence of a source the average telomere length declines with twice the division rate [47], times the telomere loss per division (the factor two is due the fact that cell division gives two daughter cells with shortened telomeres). This has the quasi steady state
| (87) |
at the steady state of Eq. (76). Interesting, these equations confirm that the average telomere length declines linearly with the proliferation rate, as opposed to the TREC content which declines geometrically with p.
In an earlier paper of a cascade model without a source, the mean division number μN = ΣnNn/N of Eq. (84), was differentiated to derive that for σ(t) = 0 the change of the mean obeys dμN/dt = −2pN [47]. Because the change in the mean division number should be proportional to the rate of telomere erosion, this was also interpreted to argue that the rate of telomere loss reflects twice the proliferation rate. Note that we showed above that such a cascade model generates a Poisson distribution of cells in the different division classes, i.e., Eq. (15), with mean μ(t) = 2pt, yielding the same dμ/dt = 2p. A second contribution of that paper [47] was the study of telomere lengths in a cascade model coupling naive, N, and memory, M, T cells, i.e.,
| (88) |
where aN is the activation rate of naive T cells, cN is their clonal expansion, and K is the average telomere loss during clonal expansion. Telomere erosion during clonal expansion may be reduced due to telomerase expression in activated T cells, i.e., 2K ≪ cN [47]. Differentiating the mean division index, μM, of Eq. (88) it was shown that
| (89) |
arguing that the rate of telomere erosion in memory T cells is less than proportional to 2pM because it is bounded by the influx of naive T cells having a lower average division number. Subtracting dμN/dt = −2pN from Eq. (89) gives an ODE for the difference between the mean naive and memory division indices
| (90) |
which will ultimately approach the steady state
| (91) |
From this equation one can see that the average telomere lengths of naive and memory T cells should approach a fixed distance, and thus ultimately decline at the same rate 2pN [47], despite the fact that memory T cell divide more frequently than naive T cells, i.e., pM > pN.
This is perfectly consistent with experimental results showing than the average telomere lengths of naive and memory T cells decline at the same rate with age [229], and unfortunately argues that the rate at which telomeres erode says more about the division rate of the precursor population than about that of the population itself. The same holds for naive T cells, because they are formed from progenitor populations in the bone marrow, that are also eroding their telomeres [192]. Thus, Eq. (86) allowing for a source of cells with telomere length L0, that could be declining over time, seems a good general model. From its steady state Eq. (87) one can indeed see that the average telomere length would follow L0 with a fixed distance. This is probably the explanation of why the telomeres of granulocytes, naive and memory T cells all erode at a rate that is set by the telomere erosion of their common precursor, the hematopoietic stem cell [192].
7 Outlook
This review started by arguing that we know too little about the production rates, division rates, and death rates of lymphocytes during health and disease. Although we have discussed several papers estimating these kinetic parameters in various circumstances in mice, monkeys and men, we have also shown that reliable quantitative interpretation of experimental data in immunology remains challenging. In several cases the biological interpretations depended strongly on the particular assumptions underlying the mathematical model that was used to fit to the data. It is of utmost importance therefore to interpret experimental data with the most appropriate mathematical models that are currently available, to know which models are most appropriate for what experimental setup, to compare the outcome of the different models, and to fully understand the assumptions underlying the different mathematical models. Reliable modeling of experimental data therefore requires close collaboration between the immunologists performing the experiments and the theoreticians developing the mathematical models for interpreting their data. These modelers should be fully aware of the intricacies of the experiments and should help design them to optimize the statistics of their fitting procedures. The immunologists have to fully appreciate the precise assumptions underlying the various mathematical models and help to ensure that these assumptions are biologically realistic. These requirements are increasingly being met in modern systems immunology [69].
Despite these technical difficulties of enriching immunology with quantitative estimates, several reliable kinetic parameter estimates have been obtained over the past decade. In healthy human adults naive T cells have expected life spans of almost a decade [223], and are largely maintained by peripheral renewal, leaving a fairly minimal role of thymic production [11, 12, 57]. In mice, which have expected life spans of about two years, naive T cells are expected to live for a few months and the thymus plays the major role in their maintenance throughout life [57, 231]. Total memory T cell populations tend to be stable, but turn over much more rapidly than naive T cell populations, with expected life spans of 30 to 52 weeks in humans [223] and about two weeks in mice [231]. In mice memory T cells specific for LCMV have longer expected life spans of 50 days [36, 244], and it is not known why the other memory phenotype cells in mice tend to have shorter life spans [231, 244]. The difference in the expected life span of naive and memory T cells is smaller in mice than it is in men, which is at least partly due to the relatively short life span of naive T cells in mice caused by their high thymic production throughout life. Indeed the life spans of naive T cells tend to be longer in thymectomized mice [57, 176, 209, 221].
Overall, the scaling in the expected life spans of naive T cells between adult mice and men is almost a factor fifty, from approximately ten weeks (i.e., 7 to 13 weeks [231]) to almost ten years (i.e., 8.4 to 9.4 years [223]), which is not so far from the ten-fold difference that is expected from basic scaling laws [109]. For memory T cells this scales from about two weeks in mice to 30 to 52 weeks in humans, i.e., an average factor of about twenty. During normal homeostasis CD4+ T cells tend to be turning over more rapidly than CD8+ T cells, and this is true for both naive and memory T cells, in mice, men and sooty mangabeys [57, 121, 223] but not in rhesus macaques [46, 162]. Memory T cell populations are heterogeneous and consist of several subpopulations with markedly different rates of turnover, whereas naive T cells tend to be homogeneous [231].
Quantitative interpretation of CFSE experiments has taught us that in mice the first division of recently activated cells typically takes several days, and is followed by a fairly deterministic clonal expansion phase during which cells divide much more rapidly, e.g., with cell cycle times of about half a day both in vitro [43, 78, 81, 96] and in vivo [2, 44, 107]. During the clonal expansion triggered by an acute infection in mice, CD8+ T cells divide somewhat faster than CD4+ T cells, i.e., with doubling times of 8 vs. 11 hours, over approximately the same time period, thus allowing for larger expansion of CD8+ T cells [44]. After the peak of the response activated CD8+ T cells contract much faster than activated CD4+ T cells [44], but afterwards approach a stable memory phase comprised of self-renewing memory T cells [36]. In the much larger rhesus macaques the rate of clonal expansion is about one per day, as estimated from the growth rate of antigen specific CD8+ T cells responding to SIV infection [39]. This one per day corresponds to a doubling time of 16 hours, which is only 2-fold slower than that in mice. Since there are so few data on acute T cell reactions in humans (but see Turnbull et al. [211] for an exceptional, but yet difficult to quantify example suggesting growth rates of 0.2 day−1, or doubling times of 3.5 days), and/or any other large vertebrates, we know little about the maximum expansion rates of T cells in large species. It has been argued that acute immune responses should not obey the general scaling laws because all species need to mount a large adaptive immune response on a time scale of days to a week [33] (although pathogens do replicate somewhat slower in larger host species). Nonetheless, in mice, T cell expansion is observed to start within one to two days after infection [44, 131], whereas it has been shown that in vaccinated macaques antigen-specific T cell expansion may not start until one or two weeks after infection [39, 40]. Scaling aspects of the immune response have also been studied by Perelson and Wiegel [178, 234].
Although this review has focused on quantifying T cell turnover in normal healthy immune systems, much of the current interest in estimating turnover rates comes from the increased cellular turnover rates observed during chronic infection with HIV-1 and HIV-2 in humans, and with SIV in macaques. A large variety of techniques, varying from Ki67 staining [37, 71, 193, 247], BrdU labeling [46, 121, 132, 162], deuterium labeling [103, 105, 134, 163, 224], TREC analysis [60, 62, 102, 140, 187], telomere analysis [173, 238, 239] and various combinations thereof [61, 89, 172] have unequivocally established that T lymphocytes are turning over more rapidly in chronically infected patients and macaques than in healthy controls. It has been difficult to precisely quantify the fold increase in T lymphocyte turnover because (1) the estimation of turnover rates from this data can be challenging, (2) studies have not always separated naive from memory T cells, and (3) the rates of cell division, i.e., the fraction of Ki67+ T cells, depend on the viral load and the density of CD4+ T cells [37, 193]. Long-term deuterium labeling in volunteers and HIV-1 infected patients suggests that the turnover rate of memory CD4+ and CD8+ T cells is approximately 3-fold increased in patients with CD4+ T cell counts between 180 to 450 cells per μl blood [224]. The variation in the turnover rate of naive T cells was higher, with a similar 3-fold increase in the naive CD4+ T cell compartment, and a 12-fold increase for CD8+ naive T cells [224]. Note that such data are typically interpreted with mathematical models assuming steady state, which seems reasonable because the time scale of CD4+ T cell depletion is much slower than the estimated turnover rates. Indeed during labeling experiments in chronically infected patients there is no evidence for a decline of the CD4+ T cell population. This is not surprising because if the CD4+ T cell count falls from 1000/μl to 200/μl, the definition of AIDS, over 10 years, the average decline is 6.7 cells/μl per month, which is extremely difficult to detect over a short labeling period.
Similar several-fold increases in T cell turnover seem consistent with most of the studies cited above, and collectively these observations form the basis of the “immune activation” hypothesis arguing that this perturbation of the normal T lymphocyte kinetics is mechanistically responsible for the slow depletion of CD4+ T cells [19, 63, 85, 101]. The other basis of this hypothesis is the lack CD4+ T cell depletion in chronically infected natural hosts of SIV, like sooty mangabeys and African green monkyes, which do have high viral loads, but no signs of immune activation [30, 34, 121, 174, 195, 196]. Patients with very low viral loads and very slow disease progression, i.e., the long term non progressors or elite controllers, do have evidence for some immune activation [3, 18, 112, 171]. In HIV-1 infected patients the turnover rates of CD4+ and CD8+ T cells tend correlate positively with the viral load in the plasma, positively with LPS levels in the plasma, and negatively with the CD4+ T cell numbers in peripheral blood [37, 112, 193]. The increased T cell turnover in patients with low CD4+ T cell counts is not, or hardly, due to homeostatic response however, because T cell activation markers decline dramatically after the initiation of anti-retroviral therapy long before the recovery of the CD4+ T cell pool [100]. Moreover, immune activation is not restricted to CD4+ T cells, as various other populations like NK cells, CD8+ T cells, and B cells are also turning over several-fold more rapidly in SIV infected monkeys [46]. Despite the indisputable evidence that HIV infected patients suffer from this several-fold increased turnover in various cell types of the immune system, we currently lack a full mechanistic understanding of how this generalized immune activation causes depletion, and particularly the depletion of CD4+ T cells only.
highlights.txt.
we review the modeling approaches for estimating T cell turnover
we aim at an audience of both modelers and biologists
we illustrate how modeling assumptions affect biological interpretations.
we present a large number of different models in one common notation
we cover acute immune responses, labeling, TREC and telomere erosion.
Acknowledgments
We thank José Borghans, Vitaly Ganusov, Andrew Yates and Ruy Ribeiro for discussions and helpful comments on various parts of this review. Portions of this work were done under the auspices of the U. S. Department of Energy under contract DE-AC52-06NA25396 and supported by NIH grants AI028433, OD011095, P01-AI071195, and P20-RR018754, and contract HHSN272201000055C. RdB thanks the Netherlands Organisation for Scientific Research NWO (VICI grant 016.048.603) for financial support. Part of this paper was written at the Santa Fe Institute and it was finished at the KITP at UCSB. This research was supported in part by the National Science Foundation under Grant No. NSF PHY11-25915.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Allsopp RC, Vaziri H, Patterson C, Goldstein S, Younglai EV, Futcher AB, Greider CW, Harley CB. Telomere length predicts replicative capacity of human fibroblasts. Proc. Natl. Acad. Sci. U.S.A. 1992;89:10114–10118. doi: 10.1073/pnas.89.21.10114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Althaus CL, Ganusov VV, De Boer RJ. Dynamics of CD8+ T cell responses during acute and chronic lymphocytic choriomeningitis virus infection. J. Immunol. 2007;179:2944–2951. doi: 10.4049/jimmunol.179.5.2944. [DOI] [PubMed] [Google Scholar]
- [3].Andrade A, Bailey JR, Xu J, Philp FH, Quinn TC, Williams TM, Ray SC, Thomas DL, Blankson JN. CD4+ T cell depletion in an untreated HIV type 1-infected human leukocyte antigen-B*5801-positive patient with an undetectable viral load. Clin. Infect. Dis. 2008;46:e78–e82. doi: 10.1086/529387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Antia R, Bergstrom CT, Pilyugin SS, Kaech SM, Ahmed R. Models of CD8+ responses: 1. What is the antigen-independent proliferation program. J. theor. Biol. 2003;221:585–598. doi: 10.1006/jtbi.2003.3208. [DOI] [PubMed] [Google Scholar]
- [5].Antia R, Ganusov VV, Ahmed R. The role of models in understanding CD8+ T-cell memory. Nat. Rev. Immunol. 2005;5:101–111. doi: 10.1038/nri1550. [DOI] [PubMed] [Google Scholar]
- [6].Asquith B, Bangham CR. An introduction to lymphocyte and viral dynamics: the power and limitations of mathematical analysis. Proc. R. Soc. Lond., B, Biol. Sci. 2003;270:1651–1657. doi: 10.1098/rspb.2003.2386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Asquith B, Debacq C, Florins A, Gillet N, Sanchez-Alcaraz T, Mosley A, Willems L. Quantifying lymphocyte kinetics in vivo using carboxyfluorescein diacetate succinimidyl ester (CFSE) Proc. R. Soc. Lond., B, Biol. Sci. 2006;273:1165–1171. doi: 10.1098/rspb.2005.3432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Asquith B, Debacq C, Macallan DC, Willems L, Bangham CR. Lymphocyte kinetics: the interpretation of labelling data. Trends Immunol. 2002;23:596–601. doi: 10.1016/s1471-4906(02)02337-2. [DOI] [PubMed] [Google Scholar]
- [9].Badovinac VP, Haring JS, Harty JT. Initial T cell receptor transgenic cell precursor frequency dictates critical aspects of the CD8+ T cell response to infection. Immunity. 2007;26:827–841. doi: 10.1016/j.immuni.2007.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Badovinac VP, Porter BB, Harty JT. Programmed contraction of CD8+ T cells after infection. Nat. Immunol. 2002;3:619–626. doi: 10.1038/ni804. [DOI] [PubMed] [Google Scholar]
- [11].Bains I, Antia R, Callard R, Yates AJ. Quantifying the development of the peripheral naive CD4+ T-cell pool in humans. Blood. 2009;113:5480–5487. doi: 10.1182/blood-2008-10-184184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Bains I, Thiebaut R, Yates AJ, Callard R. Quantifying thymic export: combining models of naive T cell proliferation and TCR excision circle dynamics gives an explicit measure of thymic output. J. Immunol. 2009;183:4329–4336. doi: 10.4049/jimmunol.0900743. [DOI] [PubMed] [Google Scholar]
- [13].Banks HT, Clayton Thompson W. A division-dependent compartmental model with cyton and intracellular label dynamics. Intl. J. Pure and Appl. Math. 2012;77:119–147. [Google Scholar]
- [14].Banks HT, Clayton Thompson W, Peligero C, Giest S, Argilaguet J, Meyerhans A. A division-dependent compartmental model for computing cell numbers in CFSE-based lymphocyte proliferation assays. Math. Biosci. Eng. 2012;9:699–736. doi: 10.3934/mbe.2012.9.699. [DOI] [PubMed] [Google Scholar]
- [15].Banks HT, Sutton KL, Thompson WC, Bocharov G, Doumic M, Schenkel T, Argilaguet J, Giest S, Peligero C, Meyerhans A. A new model for the estimation of cell proliferation dynamics using CFSE data. J. Immunol. Methods. 2011;373:143–160. doi: 10.1016/j.jim.2011.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Banks HT, Sutton KL, Thompson WC, Bocharov G, Roose D, Schenkel T, Meyerhans A. Estimation of cell proliferation dynamics using CFSE data. Bull. Math. Biol. 2011;73:116–150. doi: 10.1007/s11538-010-9524-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Bell GI, Anderson EC. Cell growth and division. I. A mathematical model with applications to cell volume distributions in mammalian suspension cultures. Biophys. J. 1967;7:329–351. doi: 10.1016/S0006-3495(67)86592-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Bello G, Velasco-de Castro CA, Bongertz V, Rodrigues CA, Giacoia-Gripp CB, Pilotto JH, Grinsztejn B, Veloso VG, Morgado MG. Immune activation and antibody responses in non-progressing elite controller individuals infected with HIV-1. J. Med. Virol. 2009;81:1681–1690. doi: 10.1002/jmv.21565. [DOI] [PubMed] [Google Scholar]
- [19].Bentwich Z, Kalinkovich A, Weisman Z, Grossman Z. Immune activation in the context of HIV infection. Clin. Exp. Immunol. 1998;111:1–2. doi: 10.1046/j.1365-2249.1998.00483.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Bernard S, Pujo-Menjouet L, Mackey MC. Analysis of cell kinetics using a cell division marker: mathematical modeling of experimental data. Biophys. J. 2003;84:3414–3424. doi: 10.1016/S0006-3495(03)70063-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Berzins SP, Boyd RL, Miller JF. The role of the thymus and recent thymic migrants in the maintenance of the adult peripheral lymphocyte pool. J. Exp. Med. 1998;187:1839–1848. doi: 10.1084/jem.187.11.1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Berzins SP, Godfrey DI, Miller JF, Boyd RL. A central role for thymic emigrants in peripheral T cell homeostasis. Proc. Natl. Acad. Sci. U.S.A. 1999;96:9787–9791. doi: 10.1073/pnas.96.17.9787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Blackburn EH. Structure and function of telomeres. Nature. 1991;350:569–573. doi: 10.1038/350569a0. [DOI] [PubMed] [Google Scholar]
- [24].Blattman JN, Antia R, Sourdive DJ, Wang X, Kaech SM, Murali-Krishna K, Altman JD, Ahmed R. Estimating the precursor frequency of naive antigen-specific CD8 T cells. J. Exp. Med. 2002;195:657–664. doi: 10.1084/jem.20001021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Bocharov G, Quiel J, Luzyanina T, Alon H, Chiglintsev E, Chereshnev V, Meier-Schellersheim M, Paul WE, Grossman Z. Feedback regulation of proliferation vs. differentiation rates explains the dependence of CD4 T-cell expansion on precursor number. Proc. Natl. Acad. Sci. U.S.A. 2011;108:3318–3323. doi: 10.1073/pnas.1019706108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Bonhoeffer S, Mohri H, Ho D, Perelson AS. Quantification of cell turnover kinetics using 5-bromo-2′-deoxyuridine. J. Immunol. 2000;164:5049–5054. doi: 10.4049/jimmunol.164.10.5049. [DOI] [PubMed] [Google Scholar]
- [27].Borghans JA, Tesselaar K. Be fruitful, multiply, and replenish. Blood. 2009;113:5369–5370. doi: 10.1182/blood-2009-03-207266. [DOI] [PubMed] [Google Scholar]
- [28].Borghans JAM, De Boer RJ. Quantification of T-cell dynamics: From telomeres to DNA labelling. Immunol. Reviews. 2007;216:35–47. doi: 10.1111/j.1600-065X.2007.00497.x. [DOI] [PubMed] [Google Scholar]
- [29].Borrow P, Evans CF, Oldstone MB. Virus-induced immunosuppression: immune system-mediated destruction of virus-infected dendritic cells results in generalized immune suppression. J. Virol. 1995;69:1059–1070. doi: 10.1128/jvi.69.2.1059-1070.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Broussard SR, Staprans SI, White R, Whitehead EM, Feinberg MB, Allan JS. Simian immunodeficiency virus replicates to high levels in naturally infected African green monkeys without inducing immunologic or neurologic disease. J. Virol. 2001;75:2262–2275. doi: 10.1128/JVI.75.5.2262-2275.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Busch R, Neese RA, Awada M, Hayes GM, Hellerstein MK. Measurement of cell proliferation by heavy water labeling. Nat. Protoc. 2007;2:3045–3057. doi: 10.1038/nprot.2007.420. [DOI] [PubMed] [Google Scholar]
- [32].Busch R, Siah IM, Gee TA, Hellerstein MK. Heavy water labeling of DNA for measurement of cell proliferation and recruitment during primary murine lymph node responses against model antigens. J. Immunol. Methods. 2008;337:24–34. doi: 10.1016/j.jim.2008.05.014. [DOI] [PubMed] [Google Scholar]
- [33].Cable JM, Enquist BJ, Moses ME. The allometry of host-pathogen interactions. PLoS. One. 2007;2:e1130. doi: 10.1371/journal.pone.0001130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Chakrabarti LA, Lewin SR, Zhang L, Gettie A, Luckay A, Martin LN, Skulsky E, Ho DD, Cheng-Mayer C, Marx PA. Normal T-Cell turnover in sooty mangabeys harboring active simian immunodeficiency virus infection. J. Virol. 2000;74:1209–1223. doi: 10.1128/jvi.74.3.1209-1223.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Chen R, Hyrien O, Noble M, Mayer-Proschel M. A composite likelihood approach to the analysis of longitudinal clonal data on multitype cellular systems under an age-dependent branching process. Biostatistics. 2011;12:173–191. doi: 10.1093/biostatistics/kxq050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Choo DK, Murali-Krishna K, Anita R, Ahmed R. Homeostatic turnover of virus-specific memory CD8 T cells occurs stochastically and is independent of CD4 T cell help. J. Immunol. 2010;185:3436–3444. doi: 10.4049/jimmunol.1001421. [DOI] [PubMed] [Google Scholar]
- [37].Cohen Stuart JW, Hazenberg MD, Hamann D, Otto SA, Borleffs JC, Miedema F, Boucher CA, De Boer RJ. The dominant source of CD4+ and CD8+ T-cell activation in HIV infection is antigenic stimulation. J. Acquir. Immune Defic. Syndr. 2000;25:203–211. doi: 10.1097/00126334-200011010-00001. [DOI] [PubMed] [Google Scholar]
- [38].Corbin GA, Harty JT. Duration of infection and antigen display have minimal influence on the kinetics of the CD4+ T cell response to Listeria monocytogenes infection. J. Immunol. 2004;173:5679–5687. doi: 10.4049/jimmunol.173.9.5679. [DOI] [PubMed] [Google Scholar]
- [39].Davenport MP, Ribeiro RM, Chao DL, Perelson AS. Predicting the impact of a nonsterilizing vaccine against human immunodeficiency virus. J. Virol. 2004;78:11340–11351. doi: 10.1128/JVI.78.20.11340-11351.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Davenport MP, Zhang L, Bagchi A, Fridman A, Fu TM, Schleif W, Shiver JW, Ribeiro RM, Perelson AS. High-potency human immunodeficiency virus vaccination leads to delayed and reduced CD8+ T-cell expansion but improved virus control. J. Virol. 2005;79:10059–10062. doi: 10.1128/JVI.79.15.10059-10062.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].De Boer RJ. Estimating the role of thymic output in HIV infection. Curr. Opin. HIV AIDS. 2006;1:16–21. doi: 10.1097/01.COH.0000194105.12816.6a. [DOI] [PubMed] [Google Scholar]
- [42].De Boer RJ. Which of our modeling predictions are robust? PLoS. Comput. Biol. 2012;8:e1002593. doi: 10.1371/journal.pcbi.1002593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].De Boer RJ, Ganusov VV, Milutinovic D, Hodgkin PD, Perelson AS. Estimating lymphocyte division and death rates from CFSE data. Bull. Math. Biol. 2006;68:1011–1031. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- [44].De Boer RJ, Homann D, Perelson AS. Different dynamics of CD4+ and CD8+ T cell responses during and after acute lymphocytic choriomeningitis virus infection. J. Immunol. 2003;171:3928–3935. doi: 10.4049/jimmunol.171.8.3928. [DOI] [PubMed] [Google Scholar]
- [45].De Boer RJ, Mohri H, Ho DD, Perelson AS. Estimating average cellular turnover from BrdU measurements. Proc. R. Soc. Lond., B, Biol. Sci. 2003;270:849–858. doi: 10.1098/rspb.2002.2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].De Boer RJ, Mohri H, Ho DD, Perelson AS. Turnover rates of B cells, T cells, and NK cells in simian immunodeficiency virus-infected and uninfected rhesus macaques. J. Immunol. 2003;170:2479–2487. doi: 10.4049/jimmunol.170.5.2479. [DOI] [PubMed] [Google Scholar]
- [47].De Boer RJ, Noest AJ. T cell renewal rates, telomerase, and telomere length shortening. J. Immunol. 1998;160:5832–5837. [PubMed] [Google Scholar]
- [48].De Boer RJ, Oprea M, Antia R, Krishna K, Murali-Ahmed R, Perelson AS. Recruitment times, proliferation, and apoptosis rates during the CD8+ T-cell response to lymphocytic choriomeningitis virus. J. Virol. 2001;75:10663–10669. doi: 10.1128/JVI.75.22.10663-10669.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].De Boer RJ, Perelson AS. How diverse should the immune system be? Proc. R. Soc. Lond., B, Biol. Sci. 1993;252:171–175. doi: 10.1098/rspb.1993.0062. [DOI] [PubMed] [Google Scholar]
- [50].De Boer RJ, Perelson AS. Towards a general function describing T cell proliferation. J. theor. Biol. 1995;175:567–576. doi: 10.1006/jtbi.1995.0165. [DOI] [PubMed] [Google Scholar]
- [51].De Boer RJ, Perelson AS. Estimating division and death rates from CFSE data. J. Comp. Appl. Math. 2005;184:140–164. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- [52].De Boer RJ, Perelson AS. Reduction in primary response cd4+ T cell expansion at high precursor T cell densities explained by an increased loss of peptide-MHC complexes. 2012. submitted. [Google Scholar]
- [53].De Boer RJ, Perelson AS, Ribeiro RM. Modelling deuterium labelling of lymphocytes with temporal and/or kinetic heterogeneity. J. R. Soc. Interface. 2012;9:2191–2200. doi: 10.1098/rsif.2012.0149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Debacq C, Asquith B, Kerkhofs P, Portetelle D, Burny A, Kettmann R, Willems L. Increased cell proliferation, but not reduced cell death, induces lymphocytosis in bovine leukemia virus-infected sheep. Proc. Natl. Acad. Sci. U.S.A. 2002;99:10048–10053. doi: 10.1073/pnas.142100999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Debacq C, Gillet N, Asquith B, Sanchez-Alcaraz MT, Florins A, Boxus M, Schwartz-Cornil I, Bonneau M, Jean G, Kerkhofs P, Hay J, Thewis A, Kettmann R, Willems L. Peripheral blood B-cell death compensates for excessive proliferation in lymphoid tissues and maintains homeostasis in bovine leukemia virus-infected sheep. J. Virol. 2006;80:9710–9719. doi: 10.1128/JVI.01022-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Deenick EK, Gett AV, Hodgkin PD. Stochastic model of T cell proliferation: A calculus revealing IL-2 regulation of precursor frequencies, cell cycle time, and survival. J. Immunol. 2003;170:4963–4972. doi: 10.4049/jimmunol.170.10.4963. [DOI] [PubMed] [Google Scholar]
- [57].Den Braber I, Mugwagwa T, Vrisekoop N, Westera L, Mogling R, De Boer AB, Willems N, Schrijver EH, Spierenburg G, Gaiser K, Mul E, Otto SA, Ruiter AF, Ackermans MT, Miedema F, Borghans JA, De Boer RJ, Tesselaar K. Maintenance of peripheral naive T cells is sustained by thymus output in mice but not humans. Immunity. 2012;36:288–297. doi: 10.1016/j.immuni.2012.02.006. [DOI] [PubMed] [Google Scholar]
- [58].Di Mascio M, Sereti I, Matthews LT, Natarajan V, Adelsberger J, Lempicki R, Yoder C, Jones E, Chow C, Metcalf JA, Sidorov IA, Dimitrov DS, Polis MA, Kovacs JA. Naive T-cell dynamics in human immunodeficiency virus type 1 infection: effects of highly active antiretroviral therapy provide insights into the mechanisms of naive T-cell depletion. J. Virol. 2006;80:2665–2674. doi: 10.1128/JVI.80.6.2665-2674.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Diekmann O, Gyllenberg M, Huang H, Kirkilionis M, Metz JA, Thieme HR. On the formulation and analysis of general deterministic structured population models. II. Nonlinear theory. J. Math. Biol. 2001;43:157–189. doi: 10.1007/s002850170002. [DOI] [PubMed] [Google Scholar]
- [60].Dion ML, Poulin JF, Bordi R, Sylvestre M, Corsini R, Kettaf N, Dalloul A, Boulassel MR, Debre P, Routy JP, Grossman Z, Sekaly RP, Cheynier R. HIV infection rapidly induces and maintains a substantial suppression of thymocyte proliferation. Immunity. 2004;21:757–768. doi: 10.1016/j.immuni.2004.10.013. [DOI] [PubMed] [Google Scholar]
- [61].Douek DC, Betts MR, Hill BJ, Little SJ, Lempicki R, Metcalf JA, Casazza J, Yoder C, Adelsberger JW, Stevens RA, Baseler MW, Keiser P, Richman DD, Davey RT, Koup RA. Evidence for increased T cell turnover and decreased thymic output in HIV infection. J. Immunol. 2001;167:6663–6668. doi: 10.4049/jimmunol.167.11.6663. [DOI] [PubMed] [Google Scholar]
- [62].Douek DC, McFarland RD, Keiser PH, Gage EA, Massey JM, Haynes BF, Polis MA, Haase AT, Feinberg MB, Sullivan JL, Jamieson BD, Zack JA, Picker LJ, Koup RA. Changes in thymic function with age and during the treatment of HIV infection. Nature. 1998;396:690–695. doi: 10.1038/25374. [DOI] [PubMed] [Google Scholar]
- [63].Douek DC, Picker LJ, Koup RA. T cell dynamics in HIV-1 infection. Annu. Rev. Immunol. 2003;21:265–304. doi: 10.1146/annurev.immunol.21.120601.141053. [DOI] [PubMed] [Google Scholar]
- [64].Douek DC, Vescio RA, Betts MR, Brenchley JM, Hill BJ, Zhang L, Berenson JR, Collins RH, Koup RA. Assessment of thymic output in adults after haematopoietic stem-cell transplantation and prediction of T-cell reconstitution. Lancet. 2000;355:1875–1881. doi: 10.1016/S0140-6736(00)02293-5. [DOI] [PubMed] [Google Scholar]
- [65].Dowling MR, Milutinovic D, Hodgkin PD. Modelling cell lifespan and proliferation: is likelihood to die or to divide independent of age? J. R. Soc. Interface. 2005;2:517–526. doi: 10.1098/rsif.2005.0069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Duffy KR, Hodgkin PD. Intracellular competition for fates in the immune system. Trends Cell Biol. 2012;22:457–464. doi: 10.1016/j.tcb.2012.05.004. [DOI] [PubMed] [Google Scholar]
- [67].Duffy KR, Wellard CJ, Markham JF, Zhou JH, Holmberg R, Hawkins ED, Hasbold J, Dowling MR, Hodgkin PD. Activation-induced B cell fates are selected by intracellular stochastic competition. Science. 2012;335:338–341. doi: 10.1126/science.1213230. [DOI] [PubMed] [Google Scholar]
- [68].Dutilh B, De Boer RJ. Decline in excision circles is no evidence for homeostatic renewal of naive T cells. J. theor. Biol. 2003;224:351–358. doi: 10.1016/s0022-5193(03)00172-3. [DOI] [PubMed] [Google Scholar]
- [69].Feinerman O, Jentsch G, Tkach KE, Coward JW, Hathorn MM, Sneddon MW, Emonet T, Smith KA, Altan-Bonnet G. Single-cell quantification of IL-2 response by effector and regulatory T cells reveals critical plasticity in immune response. Mol. Syst. Biol. 2010;6:437. doi: 10.1038/msb.2010.90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Fink PJ, Hendricks DW. Post-thymic maturation: young T cells assert their individuality. Nat. Rev. Immunol. 2011;11:544–549. doi: 10.1038/nri3028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Fleury S, De Boer RJ, Rizzardi GP, Wolthers KC, Otto SA, Welbon CC, Graziosi C, Knabenhans C, Soudeyns H, Bart PA, Gallant S, Corpataux JM, Gillet M, Meylan P, Schnyder P, Meuwly JY, Spreen W, Glauser MP, Miedema F, Pantaleo G. Limited CD4+ T-cell renewal in early HIV-1 infection: effect of highly active antiretroviral therapy. Nat. Med. 1998;4:794–801. doi: 10.1038/nm0798-794. [DOI] [PubMed] [Google Scholar]
- [72].Florins A, Gillet N, Asquith B, Debacq C, Jean G, Schwartz-Cornil I, Bonneau M, Burny A, Reichert M, Kettmann R, Willems L. Spleen-dependent turnover of CD11b peripheral blood B lymphocytes in bovine leukemia virus-infected sheep. J. Virol. 2006;80:11998–12008. doi: 10.1128/JVI.01447-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Freitas AA, Rocha B. Population biology of lymphocytes: the flight for survival. Annu. Rev. Immunol. 2000;18:83–111. doi: 10.1146/annurev.immunol.18.1.83. [DOI] [PubMed] [Google Scholar]
- [74].Ganusov VV. Discriminating between different pathways of memory CD8+ T cell differentiation. J. Immunol. 2007;179:5006–5013. doi: 10.4049/jimmunol.179.8.5006. [DOI] [PubMed] [Google Scholar]
- [75].Ganusov VV, Barber DL, De Boer RJ. Killing of targets by CD8 T cells in the mouse spleen follows the law of mass action. PLoS. One. 2011;6:e15959. doi: 10.1371/journal.pone.0015959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Ganusov VV, Borghans JA, De Boer RJ. Explicit kinetic heterogeneity: mathematical models for interpretation of deuterium labeling of heterogeneous cell populations. PLoS Comput. Biol. 2010;6:e1000666. doi: 10.1371/journal.pcbi.1000666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Ganusov VV, De Boer RJ. A mechanistic model for bromodeoxyuridine dilution naturally explains labelling data of self-renewing T cell populations. J R Soc Interface. 2012 doi: 10.1098/rsif.2012.0617. 0, O. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Ganusov VV, Milutinovic D, De Boer RJ. IL-2 regulates expansion of CD4+ T cell populations by affecting cell death: insights from modeling CFSE data. J. Immunol. 2007;179:950–957. doi: 10.4049/jimmunol.179.2.950. [DOI] [PubMed] [Google Scholar]
- [79].Ganusov VV, Pilyugin SS, De Boer RJ, Murali-Krishna K, Ahmed R, Antia R. Quantifying cell turnover using CFSE data. J. Immunol. Methods. 2005;298:183–200. doi: 10.1016/j.jim.2005.01.011. [DOI] [PubMed] [Google Scholar]
- [80].Gerlach C, Van Heijst JW, Schumacher TN. The descent of memory T cells. Ann. N. Y. Acad. Sci. 2011;1217:139–153. doi: 10.1111/j.1749-6632.2010.05830.x. [DOI] [PubMed] [Google Scholar]
- [81].Gett AV, Hodgkin PD. A cellular calculus for signal integration by T cells. Nat. Immunol. 2000;1:239–244. doi: 10.1038/79782. [DOI] [PubMed] [Google Scholar]
- [82].Gillespie D. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- [83].Glauche I, Moore K, Thielecke L, Horn K, Loeffler M, Roeder I. Stem cell proliferation and quiescence-two sides of the same coin. PLoS. Comput. Biol. 2009;5:e1000447. doi: 10.1371/journal.pcbi.1000447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Grossman Z, Herberman RB, Dimitrov DS. T cell turnover in SIV infection. Science. 1999;284:555a–555b. [Google Scholar]
- [85].Grossman Z, Meier-Schellersheim M, Sousa AE, Victorino RM, Paul WE. CD4+ T-cell depletion in HIV infection: are we closer to understanding the cause? Nat. Med. 2002;8:319–323. doi: 10.1038/nm0402-319. [DOI] [PubMed] [Google Scholar]
- [86].Hairer E. Springer Series in Computational Mathematics. Springer; Berlin: 1993. Solving Ordinary Differential Equations I. Nonstiff Problems. [Google Scholar]
- [87].Hale JS, Boursalian TE, Turk GL, Fink PJ. Thymic output in aged mice. Proc. Natl. Acad. Sci. U.S.A. 2006;103:8447–8452. doi: 10.1073/pnas.0601040103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Harley CB, Futcher AB, Greider CW. Telomeres shorten during ageing of human fibroblasts. Nature. 1990;345:458–460. doi: 10.1038/345458a0. [DOI] [PubMed] [Google Scholar]
- [89].Harris JM, Hazenberg MD, Poulin JF, Higuera-Alhino D, Schmidt D, Gotway M, McCune JM. Multiparameter evaluation of human thymic function: interpretations and caveats. Clin. Immunol. 2005;115:138–146. doi: 10.1016/j.clim.2004.12.008. [DOI] [PubMed] [Google Scholar]
- [90].Hasbold J, Corcoran LM, Tarlinton DM, Tangye SG, Hodgkin PD. Evidence from the generation of immunoglobulin G-secreting cells that stochastic mechanisms regulate lymphocyte differentiation. Nat. Immunol. 2004;5:55–63. doi: 10.1038/ni1016. [DOI] [PubMed] [Google Scholar]
- [91].Hasbold J, Gett AV, Rush JS, Deenick E, Avery D, Jun J, Hodgkin PD. Quantitative analysis of lymphocyte differentiation and proliferation in vitro using carboxyfluorescein diacetate succinimidyl ester. Immunol. Cell. Biol. 1999;77:516–522. doi: 10.1046/j.1440-1711.1999.00874.x. [DOI] [PubMed] [Google Scholar]
- [92].Hasenauer J, Schittler D, Allgower F. Analysis and simulation of division- and label-structured population models: a new tool to analyze proliferation assays. Bull. Math. Biol. 2012;74:2692–2732. doi: 10.1007/s11538-012-9774-5. [DOI] [PubMed] [Google Scholar]
- [93].Hataye J, Moon JJ, Khoruts A, Reilly C, Jenkins MK. Naive and memory CD4+ T cell survival controlled by clonal abundance. Science. 2006;312:114–116. doi: 10.1126/science.1124228. [DOI] [PubMed] [Google Scholar]
- [94].Hawkins ED, Hommel M, Turner ML, Battye FL, Markham JF, Hodgkin PD. Measuring lymphocyte proliferation, survival and differentiation using CFSE time-series data. Nat. Protoc. 2007;2:2057–2067. doi: 10.1038/nprot.2007.297. [DOI] [PubMed] [Google Scholar]
- [95].Hawkins ED, Markham JF, McGuinness LP, Hodgkin PD. A single-cell pedigree analysis of alternative stochastic lymphocyte fates. Proc. Natl. Acad. Sci. U.S.A. 2009;106:13457–13462. doi: 10.1073/pnas.0905629106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Hawkins ED, Turner ML, Dowling MR, Van Gend C, Hodgkin PD. A model of immune regulation as a consequence of randomized lymphocyte division and death times. Proc. Natl. Acad. Sci. U.S.A. 2007;104:5032–5037. doi: 10.1073/pnas.0700026104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Hayflick L. Why do we live so long? Geriatrics. 1988;43:77–79. [PubMed] [Google Scholar]
- [98].Hayflick L. Antecedents of cell aging research. Exp. Gerontol. 1989;24:355–365. doi: 10.1016/0531-5565(89)90043-0. [DOI] [PubMed] [Google Scholar]
- [99].Hazenberg MD, Borghans JA, De Boer RJ, Miedema F. Thymic output: a bad TREC record. Nat. Immunol. 2003;4:97–99. doi: 10.1038/ni0203-97. [DOI] [PubMed] [Google Scholar]
- [100].Hazenberg MD, Cohen Stuart JW, Otto SA, Borleffs JC, Boucher CA, De Boer RJ, Miedema F, Hamann D. T-cell division in human immunodeficiency virus (HIV)-1 infection is mainly due to immune activation: a longitudinal analysis in patients before and during highly active antiretroviral therapy (HAART) Blood. 2000;95:249–255. [PubMed] [Google Scholar]
- [101].Hazenberg MD, Hamann D, Schuitemaker H, Miedema F. T cell depletion in HIV-1 infection: how CD4+ T cells go out of stock. Nat. Immunol. 2000;1:285–289. doi: 10.1038/79724. [DOI] [PubMed] [Google Scholar]
- [102].Hazenberg MD, Otto SA, Stuart JW, Verschuren MC, Borleffs JC, Boucher CA, Coutinho RA, Lange JM, De Wit TF, Tsegaye A, Van Dongen JJ, Hamann D, De Boer RJ, Miedema F. Increased cell division but not thymic dysfunction rapidly affects the T-cell receptor excision circle content of the naive T cell population in HIV-1 infection. Nat. Med. 2000;6:1036–1042. doi: 10.1038/79549. [DOI] [PubMed] [Google Scholar]
- [103].Hellerstein M, Hanley MB, Cesar D, Siler S, Papageorgopoulos C, Wieder E, Schmidt D, Hoh R, Neese R, Macallan D, Deeks S, McCune JM. Directly measured kinetics of circulating T lymphocytes in normal and HIV-1-infected humans. Nat. Med. 1999;5:83–89. doi: 10.1038/4772. [DOI] [PubMed] [Google Scholar]
- [104].Hellerstein MK. Measurement of T-cell kinetics: recent methodologic advances. Immunol. Today. 1999;20:438–441. doi: 10.1016/s0167-5699(99)01529-7. [DOI] [PubMed] [Google Scholar]
- [105].Hellerstein MK, Hoh RA, Hanley MB, Cesar D, Lee D, Neese RA, McCune JM. Subpopulations of long-lived and short-lived T cells in advanced HIV-1 infection. J. Clin. Invest. 2003;112:956–966. doi: 10.1172/JCI17533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Hodes RJ, Hathcock KS, Weng NP. Telomeres in T and B cells. Nat. Rev. Immunol. 2002;2:699–706. doi: 10.1038/nri890. [DOI] [PubMed] [Google Scholar]
- [107].Homann D, Teyton L, Oldstone MB. Differential regulation of antiviral T-cell immunity results in stable CD8+ but declining CD4+ T-cell memory. Nat. Med. 2001;7:913–919. doi: 10.1038/90950. [DOI] [PubMed] [Google Scholar]
- [108].Hommel M, Hodgkin PD. TCR affinity promotes CD8+ T cell expansion by regulating survival. J. Immunol. 2007;179:2250–2260. doi: 10.4049/jimmunol.179.4.2250. [DOI] [PubMed] [Google Scholar]
- [109].Hou C, Zuo W, Moses ME, Woodruff WH, Brown JH, West GB. Energy uptake and allocation during ontogeny. Science. 2008;322:736–739. doi: 10.1126/science.1162302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110].Houston EG, Jr, Higdon LE, Fink PJ. Recent thymic emigrants are preferentially incorporated only into the depleted T-cell pool. Proc. Natl. Acad. Sci. U.S.A. 2011;108:5366–5371. doi: 10.1073/pnas.1015286108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [111].Huang JF, Yang Y, Sepulveda H, Shi W, Hwang I, Peterson PA, Jackson MR, Sprent J, Cai Z. TCR-Mediated internalization of peptide-MHC complexes acquired by T cells. Science. 1999;286:952–954. doi: 10.1126/science.286.5441.952. [DOI] [PubMed] [Google Scholar]
- [112].Hunt PW, Brenchley J, Sinclair E, McCune JM, Roland M, Page-Shafer K, Hsue P, Emu B, Krone M, Lampiris H, Douek D, Martin JN, Deeks SG. Relationship between T cell activation and CD4+ T cell count in HIV-seropositive individuals with undetectable plasma HIV RNA levels in the absence of therapy. J. Infect. Dis. 2008;197:126–133. doi: 10.1086/524143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Hwang I, Ki D. Receptor-mediated T cell absorption of antigen presenting cell-derived molecules. Front. Biosci. 2011;16:411–421. doi: 10.2741/3695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Hyrien O, Chen R, Mayer-Proschel M, Noble M. Saddlepoint approximations to the moments of multitype age-dependent branching processes, with applications. Biometrics. 2010;66:567–577. doi: 10.1111/j.1541-0420.2009.01281.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Hyrien O, Chen R, Zand MS. An age-dependent branching process model for the analysis of CFSE-labeling experiments. Biol. Direct. 2010;5:41. doi: 10.1186/1745-6150-5-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Hyrien O, Mayer-Proschel M, Noble M, Yakovlev A. A stochastic model to analyze clonal data on multi-type cell populations. Biometrics. 2005;61:199–207. doi: 10.1111/j.0006-341X.2005.031210.x. [DOI] [PubMed] [Google Scholar]
- [117].Hyrien O, Zand MS. A mixture model with dependent observations for the analysis of CFSE-labeling experiments. J. Am. Stat. Assoc. 2008;103:222–239. [Google Scholar]
- [118].Jamieson BD, Douek DC, Killian S, Hultin LE, Scripture-Adams DD, Giorgi JV, Marelli D, Koup RA, Zack JA. Generation of functional thymocytes in the human adult. Immunity. 1999;10:569–575. doi: 10.1016/s1074-7613(00)80056-4. [DOI] [PubMed] [Google Scholar]
- [119].Jones LE, Perelson AS. Opportunistic infection as a cause of transient viremia in chronically infected HIV patients under treatment with HAART. Bull. Math. Biol. 2005;67:1227–1251. doi: 10.1016/j.bulm.2005.01.006. [DOI] [PubMed] [Google Scholar]
- [120].Kaech SM, Ahmed R. Memory CD8+ T cell differentiation: initial antigen encounter triggers a developmental program in naive cells. Nat. Immunol. 2001;2:415–422. doi: 10.1038/87720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Kaur A, Di Mascio M, Barabasz A, Rosenzweig M, McClure HM, Perelson AS, Ribeiro RM, Johnson RP. Dynamics of T- and B-lymphocyte turnover in a natural host of simian immunodeficiency virus. J. Virol. 2008;82:1084–1093. doi: 10.1128/JVI.02197-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [122].Kedl RM, Schaefer BC, Kappler JW, Marrack P. T cells down-modulate peptide-MHC complexes on APCs in vivo. Nat. Immunol. 2002;3:27–32. doi: 10.1038/ni742. [DOI] [PubMed] [Google Scholar]
- [123].Kiel MJ, He S, Ashkenazi R, Gentry SN, Teta M, Kushner JA, Jackson TL, Morrison SJ. Haematopoietic stem cells do not asymmetrically segregate chromosomes or retain BrdU. Nature. 2007;449:238–242. doi: 10.1038/nature06115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [124].Kilpatrick RD, Rickabaugh T, Hultin LE, Hultin P, Hausner MA, Detels R, Phair J, Jamieson BD. Homeostasis of the naive CD4+ T cell compartment during aging. J. Immunol. 2008;180:1499–1507. doi: 10.4049/jimmunol.180.3.1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Kimmig S, Przybylski GK, Schmidt CA, Laurisch K, Mowes B, Radbruch A, Thiel A. Two subsets of naive T helper cells with distinct T cell receptor excision circle content in human adult peripheral blood. J. Exp. Med. 2002;195:789–794. doi: 10.1084/jem.20011756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Ko KH, Odell R, Nordon RE. Analysis of cell differentiation by division tracking cytometry. Cytometry. A. 2007;71:773–782. doi: 10.1002/cyto.a.20437. [DOI] [PubMed] [Google Scholar]
- [127].Koch AL, Schaechter M. A model for statistics of the cell division process. J. Gen. Microbiol. 1962;29:435–454. doi: 10.1099/00221287-29-3-435. [DOI] [PubMed] [Google Scholar]
- [128].Kohler B. Mathematically modeling dynamics of T cell responses: predictions concerning the generation of memory cells. J. theor. Biol. 2007;245:669–676. doi: 10.1016/j.jtbi.2006.10.017. [DOI] [PubMed] [Google Scholar]
- [129].Kohlmeier JE, Reiley WW, Perona-Wright G, Freeman ML, Yager EJ, Connor LM, Brincks EL, Cookenham T, Roberts AD, Burkum CE, Sell S, Winslow GM, Blackman MA, Mohrs M, Woodland DL. Inflammatory chemokine receptors regulate CD8+ T cell contraction and memory generation following infection. J. Exp. Med. 2011;208:1621–1634. doi: 10.1084/jem.20102110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130].Kong F, Chen CH, Cooper MD. Thymic function can be accurately monitored by the level of recent T cell emigrants in the circulation. Immunity. 1998;8:97–104. doi: 10.1016/s1074-7613(00)80462-8. [DOI] [PubMed] [Google Scholar]
- [131].Kotturi MF, Scott I, Wolfe T, Peters B, Sidney J, Cheroutre H, Von Herrath MG, Buchmeier MJ, Grey H, Sette A. Naive precursor frequencies and MHC binding rather than the degree of epitope diversity shape CD8+ T cell immunodominance. J. Immunol. 2008;181:2124–2133. doi: 10.4049/jimmunol.181.3.2124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132].Kovacs JA, Lempicki RA, Sidorov IA, Adelsberger JW, Herpin B, Metcalf JA, Sereti I, Polis MA, Davey RT, Tavel J, Falloon J, Stevens R, Lambert L, Dewar R, Schwartzentruber DJ, Anver MR, Baseler MW, Masur H, Dimitrov DS, Lane HC. Identification of dynamically distinct subpopulations of T lymphocytes that are differentially affected by HIV. J. Exp. Med. 2001;194:1731–1741. doi: 10.1084/jem.194.12.1731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [133].Kovacs JA, Lempicki RA, Sidorov IA, Adelsberger JW, Sereti I, Sachau W, Kelly G, Metcalf JA, Davey RT, Jr, Falloon J, Polis MA, Tavel J, Stevens R, Lambert L, Hosack DA, Bosche M, Issaq HJ, Fox SD, Leitman S, Baseler MW, Masur H, Di Mascio M, Dimitrov DS, Lane HC. Induction of prolonged survival of CD4+ T lymphocytes by intermittent IL-2 therapy in HIV-infected patients. J. Clin. Invest. 2005;115:2139–2148. doi: 10.1172/JCI23196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [134].Ladell K, Hellerstein MK, Cesar D, Busch R, Boban D, McCune JM. Central memory CD8+ T cells appear to have a shorter lifespan and reduced abundance as a function of HIV disease progression. J. Immunol. 2008;180:7907–7918. doi: 10.4049/jimmunol.180.12.7907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [135].Lau LL, Jamieson BD, Somasundaram T, Ahmed R. Cytotoxic T-cell memory without antigen. Nature. 1994;369:648–652. [PubMed] [Google Scholar]
- [136].Lee HY, Hawkins E, Zand MS, Mosmann T, Wu H, Hodgkin PD, Perelson AS. Interpreting CFSE obtained division histories of B cells in vitro with Smith-Martin and cyton type models. Bull. Math. Biol. 2009;71:1649–1670. doi: 10.1007/s11538-009-9418-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137].Lee HY, Perelson AS. Modeling T cell proliferation and death in vitro based on labeling data: generalizations of the Smith-Martin cell cycle model. Bull. Math. Biol. 2008;70:21–44. doi: 10.1007/s11538-007-9239-4. [DOI] [PubMed] [Google Scholar]
- [138].Lempicki RA, Kovacs JA, Baseler MW, Adelsberger JW, Dewar RL, Natarajan V, Bosche MC, Metcalf JA, Stevens RA, Lambert LA, Alvord WG, Polis MA, Davey RT, Dimitrov DS, Lane HC. Impact of HIV-1 infection and highly active antiretroviral therapy on the kinetics of CD4+ and CD8+ T cell turnover in HIV-infected patients. Proc. Natl. Acad. Sci. U.S.A. 2000;97:13778–13783. doi: 10.1073/pnas.250472097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139].Leon K, Faro J, Carneiro J. A general mathematical framework to model generation structure in a population of asynchronously dividing cells. J. theor. Biol. 2004;229:455–476. doi: 10.1016/j.jtbi.2004.04.011. [DOI] [PubMed] [Google Scholar]
- [140].Lewin SR, Ribeiro RM, Kaufmann GR, Smith D, Zaunders J, Law M, Solomon A, Cameron PU, Cooper D, Perelson AS. Dynamics of T cells and TCR excision circles differ after treatment of acute and chronic HIV infection. J. Immunol. 2002;169:4657–4666. doi: 10.4049/jimmunol.169.8.4657. [DOI] [PubMed] [Google Scholar]
- [141].Linderkamp O, Versmold HT, Riegel KP, Betke K. Estimation and prediction of blood volume in infants and children. Eur. J. Pediatr. 1977;125:227–234. doi: 10.1007/BF00493567. [DOI] [PubMed] [Google Scholar]
- [142].Linskens MH, Harley CB, West MD, Campisi J, Hayflick L. Replicative senescence and cell death. Science. 1995;267:17. doi: 10.1126/science.7848496. [DOI] [PubMed] [Google Scholar]
- [143].Luzyanina T, Mrusek S, Edwards JT, Roose D, Ehl S, Bocharov G. Computational analysis of CFSE proliferation assay. J. Math. Biol. 2007;54:57–89. doi: 10.1007/s00285-006-0046-6. [DOI] [PubMed] [Google Scholar]
- [144].Luzyanina T, Roose D, Schenkel T, Sester M, Ehl S, Meyerhans A, Bocharov G. Numerical modelling of label-structured cell population growth using CFSE distribution data. Theor. Biol. Med. Model. 2007;4:26. doi: 10.1186/1742-4682-4-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [145].Lyons AB. Analysing cell division in vivo and in vitro using flow cytometric measurement of CFSE dye dilution. J. Immunol. Methods. 2000;243:147–154. doi: 10.1016/s0022-1759(00)00231-3. [DOI] [PubMed] [Google Scholar]
- [146].Lyons AB, Hasbold J, Hodgkin PD. Flow cytometric analysis of cell division history using dilution of carboxyfluorescein diacetate succinimidyl ester, a stably integrated fluorescent probe. Methods. Cell. Biol. 2001;63:375–398. doi: 10.1016/s0091-679x(01)63021-8. [DOI] [PubMed] [Google Scholar]
- [147].Ma CS, Hodgkin PD, Tangye SG. Automatic generation of lymphocyte heterogeneity: Division-dependent changes in the expression of CD27, CCR7 and CD45 by activated human naive CD4+ T cells are independently regulated. Immunol. Cell Biol. 2004;82:67–74. doi: 10.1046/j.0818-9641.2003.01206.x. [DOI] [PubMed] [Google Scholar]
- [148].Macallan DC, Asquith B, Irvine AJ, Wallace DL, Worth A, Ghattas H, Zhang Y, Griffin GE, Tough DF, Beverley PC. Measurement and modeling of human T cell kinetics. Eur. J. Immunol. 2003;33:2316–2326. doi: 10.1002/eji.200323763. [DOI] [PubMed] [Google Scholar]
- [149].Macallan DC, Fullerton CA, Neese RA, Haddock K, Park SS, Hellerstein MK. Measurement of cell proliferation by labeling of DNA with stable isotope-labeled glucose: studies in vitro, in animals, and in humans. Proc. Natl. Acad. Sci. U.S.A. 1998;95:708–713. doi: 10.1073/pnas.95.2.708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [150].Macallan DC, Wallace D, Zhang Y, De Lara C, Worth AT, Ghattas H, Griffin GE, Beverley PC, Tough DF. Rapid turnover of effector-memory CD4+ T cells in healthy humans. J. Exp. Med. 2004;200:255–260. doi: 10.1084/jem.20040341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [151].Macallan DC, Wallace DL, Irvine AJ, Asquith B, Worth A, Ghattas H, Zhang Y, Griffin GE, Tough DF, Beverley PC. Rapid turnover of T cells in acute infectious mononucleosis. Eur. J. Immunol. 2003;33:2655–2665. doi: 10.1002/eji.200324295. [DOI] [PubMed] [Google Scholar]
- [152].Markham JF, Wellard CJ, Hawkins ED, Duffy KR, Hodgkin PD. A minimum of two distinct heritable factors are required to explain correlation structures in proliferating lymphocytes. J. R. Soc. Interface. 2010;7:1049–1059. doi: 10.1098/rsif.2009.0488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [153].Marquardt DW. Finite difference algorithm for curve fitting. J. Soc. Ind. Appl. Math. 1963;11:431–441. [Google Scholar]
- [154].Masopust D, Choo D, Vezys V, Wherry EJ, Duraiswamy J, Akondy R, Wang J, Casey KA, Barber DL, Kawamura KS, Fraser KA, Webby RJ, Brinkmann V, Butcher EC, Newell KA, Ahmed R. Dynamic T cell migration program provides resident memory within intestinal epithelium. J. Exp. Med. 2010;207:553–564. doi: 10.1084/jem.20090858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [155].Matloubian M, Kolhekar SR, Somasundaram T, Ahmed R. Molecular determinants of macrophage tropism and viral persistence: importance of single amino acid changes in the polymerase and glycoprotein of lymphocytic choriomeningitis virus. J. Virol. 1993;67:7340–7349. doi: 10.1128/jvi.67.12.7340-7349.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [156].Matloubian M, Somasundaram T, Kolhekar SR, Selvakumar R, Ahmed R. Genetic basis of viral persistence: single amino acid change in the viral glycoprotein affects ability of lymphocytic choriomeningitis virus to persist in adult mice. J. Exp. Med. 1990;172:1043–1048. doi: 10.1084/jem.172.4.1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [157].McCune JM, Hanley MB, Cesar D, Halvorsen R, Hoh R, Schmidt D, Wieder E, Deeks S, Siler S, Neese R, Hellerstein M. Factors influencing T-cell turnover in HIV-1-seropositive patients. J. Clin. Invest. 2000;105:R1–8. doi: 10.1172/JCI8647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [158].Miao H, Jin X, Perelson AS, Wu H. Evaluation of multitype mathematical models for CFSE-labeling experiment data. Bull. Math. Biol. 2012;74:300–326. doi: 10.1007/s11538-011-9668-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [159].Michie CA, McLean A, Alcock C, Beverley PC. Lifespan of human lymphocyte subsets defined by CD45 isoforms. Nature. 1992;360:264–265. doi: 10.1038/360264a0. [DOI] [PubMed] [Google Scholar]
- [160].Miller NE, Bonczyk JR, Nakayama Y, Suresh M. Role of thymic output in regulating CD8 T-cell homeostasis during acute and chronic viral infection. J. Virol. 2005;79:9419–9429. doi: 10.1128/JVI.79.15.9419-9429.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [161].Milutinovic D, De Boer RJ. Process noise: an explanation for the fluctuations in the immune response during acute viral infection. Biophys. J. 2007;92:3358–3367. doi: 10.1529/biophysj.106.094508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162].Mohri H, Bonhoeffer S, Monard S, Perelson AS, Ho DD. Rapid turnover of T lymphocytes in SIV-infected rhesus macaques. Science. 1998;279:1223–1227. doi: 10.1126/science.279.5354.1223. [DOI] [PubMed] [Google Scholar]
- [163].Mohri H, Perelson AS, Tung K, Ribeiro RM, Ramratnam B, Markowitz M, Kost R, Hurley A, Weinberger L, Cesar D, Hellerstein MK, Ho DD. Increased turnover of T lymphocytes in HIV-1 infection and its reduction by antiretroviral therapy. J. Exp. Med. 2001;194:1277–1288. doi: 10.1084/jem.194.9.1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [164].Moon JJ, Chu HH, Pepper M, McSorley SJ, Jameson SC, Kedl RM, Jenkins MK. Naive CD4(+) T cell frequency varies for different epitopes and predicts repertoire diversity and response magnitude. Immunity. 2007;27:203–213. doi: 10.1016/j.immuni.2007.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [165].Naylor K, Li G, Vallejo AN, Lee WW, Koetz K, Bryl E, Witkowski J, Fulbright J, Weyand CM, Goronzy JJ. The influence of age on T cell generation and TCR diversity. J. Immunol. 2005;174:7446–7452. doi: 10.4049/jimmunol.174.11.7446. [DOI] [PubMed] [Google Scholar]
- [166].Neese RA, Misell LM, Turner S, Chu A, Kim J, Cesar D, Hoh R, Antelo F, Strawford A, McCune JM, Christiansen M, Hellerstein MK. Measurement in vivo of proliferation rates of slow turnover cells by 2H2O labeling of the deoxyribose moiety of DNA. Proc. Natl. Acad. Sci. U.S.A. 2002;99:15345–15350. doi: 10.1073/pnas.232551499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [167].Nolz JC, Rai D, Badovinac VP, Harty JT. Division-linked generation of death-intermediates regulates the numerical stability of memory CD8 T cells. Proc. Natl. Acad. Sci. U.S.A. 2012;109:6199–6204. doi: 10.1073/pnas.1118868109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [168].Nordon RE, Nakamura M, Ramirez C, Odell R. Analysis of growth kinetics by division tracking. Immunol. Cell. Biol. 1999;77:523–529. doi: 10.1046/j.1440-1711.1999.00869.x. [DOI] [PubMed] [Google Scholar]
- [169].Nowak MA, Bangham CR. Population dynamics of immune responses to persistent viruses. Science. 1996;272:74–79. doi: 10.1126/science.272.5258.74. [DOI] [PubMed] [Google Scholar]
- [170].Nowak MA, May RM. Mathematical principles of immunology and virology. Oxford U.P.; Oxford: 2000. Virus dynamics. [Google Scholar]
- [171].O’Connell KA, Bailey JR, Blankson JN. Elucidating the elite: mechanisms of control in HIV-1 infection. Trends Pharmacol. Sci. 2009;30:631–637. doi: 10.1016/j.tips.2009.09.005. [DOI] [PubMed] [Google Scholar]
- [172].Okoye A, Meier-Schellersheim M, Brenchley JM, Hagen SI, Walker JM, Rohankhedkar M, Lum R, Edgar JB, Planer SL, Legasse A, Sylwester AW, Piatak M, Jr, Lifson JD, Maino VC, Sodora DL, Douek DC, Axthelm MK, Grossman Z, Picker LJ. Progressive CD4+ central memory T cell decline results in CD4+ effector memory insufficiency and overt disease in chronic SIV infection. J. Exp. Med. 2007;204:2171–2185. doi: 10.1084/jem.20070567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [173].Palmer LD, Weng N, Levine BL, June CH, Lane HC, Hodes RJ. Telomere length, telomerase activity, and replicative potential in HIV infection: analysis of CD4+ and CD8+ T cells from HIV-discordant monozygotic twins. J. Exp. Med. 1997;185:1381–1386. doi: 10.1084/jem.185.7.1381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [174].Pandrea I, Ribeiro RM, Gautam R, Gaufin T, Pattison M, Barnes M, Monjure C, Stoulig C, Dufour J, Cyprian W, Silvestri G, Miller MD, Perelson AS, Apetrei C. Simian immunodeficiency virus SIVagm dynamics in African green monkeys. J. Virol. 2008;82:3713–3724. doi: 10.1128/JVI.02402-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [175].Parish CR, Glidden MH, Quah BJ, Warren HS. Use of the intracellular fluorescent dye CFSE to monitor lymphocyte migration and proliferation. Curr Protoc Immunol. 2009;4:4.9.1–4.9.13. doi: 10.1002/0471142735.im0409s84. [DOI] [PubMed] [Google Scholar]
- [176].Parretta E, Cassese G, Santoni A, Guardiola J, Vecchio A, Di Rosa F. Kinetics of in vivo proliferation and death of memory and naive CD8 T cells: parameter estimation based on 5-bromo-2′-deoxyuridine incorporation in spleen, lymph nodes, and bone marrow. J. Immunol. 2008;180:7230–7239. doi: 10.4049/jimmunol.180.11.7230. [DOI] [PubMed] [Google Scholar]
- [177].Perelson AS, Bonhoeffer S, Mohri H, Ho D. T cell turnover in SIV infection. Science. 1999;284:555b–555d. [Google Scholar]
- [178].Perelson AS, Wiegel FW. Scaling aspects of lymphocyte trafficking. J. theor. Biol. 2009;257:9–16. doi: 10.1016/j.jtbi.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [179].Pillay J, Den Braber I, Vrisekoop N, Kwast LM, De Boer RJ, Borghans JA, Tesselaar K, Koenderman L. In vivo labeling with 2H2O reveals a human neutrophil lifespan of 5.4 days. Blood. 2010;116:625–627. doi: 10.1182/blood-2010-01-259028. [DOI] [PubMed] [Google Scholar]
- [180].Pilyugin S, Mittler J, Antia R. Modeling T-cell proliferation: an investigation of the consequences of the Hayflick limit. J. theor. Biol. 1997;186:117–129. doi: 10.1006/jtbi.1996.0319. [DOI] [PubMed] [Google Scholar]
- [181].Pilyugin SS, Ganusov VV, Murali-Krishna K, Ahmed R, Antia R. The rescaling method for quantifying the turnover of cell populations. J. theor. Biol. 2003;225:275–283. doi: 10.1016/s0022-5193(03)00245-5. [DOI] [PubMed] [Google Scholar]
- [182].Pitcher CJ, Hagen SI, Walker JM, Lum R, Mitchell BL, Maino VC, Axthelm MK, Picker LJ. Development and homeostasis of T cell memory in rhesus macaque. J. Immunol. 2002;168:29–43. doi: 10.4049/jimmunol.168.1.29. [DOI] [PubMed] [Google Scholar]
- [183].Quah BJ, Warren HS, Parish CR. Monitoring lymphocyte proliferation in vitro and in vivo with the intracellular fluorescent dye carboxyfluorescein diacetate succinimidyl ester. Nat. Protoc. 2007;2:2049–2056. doi: 10.1038/nprot.2007.296. [DOI] [PubMed] [Google Scholar]
- [184].Quiel J, Caucheteux S, Laurence A, Singh NJ, Bocharov G, BenSasson SZ, Grossman Z, Paul WE. Antigen-stimulated CD4 T-cell expansion is inversely and log-linearly related to precursor number. Proc. Natl. Acad. Sci. U.S.A. 2011;108:3312–3317. doi: 10.1073/pnas.1018525108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [185].Raue HP, Slifka MK. CD8+ T cell immunodominance shifts during the early stages of acute LCMV infection independently from functional avidity maturation. Virology. 2009;390:197–204. doi: 10.1016/j.virol.2009.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [186].Revy P, Sospedra M, Barbour B, Trautmann A. Functional antigen-independent synapses formed between T cells and dendritic cells. Nat. Immunol. 2001;2:925–931. doi: 10.1038/ni713. [DOI] [PubMed] [Google Scholar]
- [187].Ribeiro RM, De Boer RJ. The contribution of the thymus to the recovery of peripheral naive T-cell numbers during antiretroviral treatment for HIV infection. J. Acquir. Immune Defic. Syndr. 2008;49:1–8. doi: 10.1097/QAI.0b013e318184fb28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [188].Ribeiro RM, Mohri H, Ho DD, Perelson AS. In vivo dynamics of T cell activation, proliferation, and death in HIV-1 infection: Why are CD4+ but not CD8+ T cells depleted? Proc. Natl. Acad. Sci. U.S.A. 2002;99:15572–15577. doi: 10.1073/pnas.242358099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [189].Ribeiro RM, Mohri H, Ho DD, Perelson AS. Modeling deuterated glucose labeling of T-lymphocytes. Bull. Math. Biol. 2002;64:385–405. doi: 10.1006/bulm.2001.0282. [DOI] [PubMed] [Google Scholar]
- [190].Roederer M, Dubs JG, Anderson MT, Raju PA, Herzenberg LA, Herzenberg LA. CD8 naive T cell counts decrease progressively in HIV-infected adults. J. Clin. Invest. 1995;95:2061–2066. doi: 10.1172/JCI117892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [191].Rouzine IM, Coffin JM. T cell turnover in SIV infection. Science. 1999;284:555b. [Google Scholar]
- [192].Rufer N, Brummendorf TH, Kolvraa S, Bischoff C, Christensen K, Wadsworth L, Schulzer M, Lansdorp PM. Telomere fluorescence measurements in granulocytes and T lymphocyte subsets point to a high turnover of hematopoietic stem cells and memory T cells in early childhood. J. Exp. Med. 1999;190:157–168. doi: 10.1084/jem.190.2.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [193].Sachsenberg N, Perelson AS, Yerly S, Schockmel GA, Leduc D, Hirschel B, Perrin L. Turnover of CD4+ and CD8+ T lymphocytes in HIV-1 infection as measured by Ki-67 antigen. J. Exp. Med. 1998;187:1295–1303. doi: 10.1084/jem.187.8.1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [194].Schittler D, Hasenauer J, Allgower F. Proc. 8 th Int. Workshop on Computational Systems Biology (WCSB) Zürich; Switzerland: 2011. A generalized population model for cell proliferation: Integrating division numbers and label dynamics; pp. 165–168. TICSP series # 57. [Google Scholar]
- [195].Silvestri G, Fedanov A, Germon S, Kozyr N, Kaiser WJ, Garber DA, McClure H, Feinberg MB, Staprans SI. Divergent host responses during primary simian immunodeficiency virus SIVsm infection of natural sooty mangabey and nonnatural rhesus macaque hosts. J. Virol. 2005;79:4043–4054. doi: 10.1128/JVI.79.7.4043-4054.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [196].Silvestri G, Sodora DL, Koup RA, Paiardini M, O’Neil SP, McClure HM, Staprans SI, Feinberg MB. Nonpathogenic SIV infection of sooty mangabeys is characterized by limited bystander immunopathology despite chronic high-level viremia. Immunity. 2003;18:441–452. doi: 10.1016/s1074-7613(03)00060-8. [DOI] [PubMed] [Google Scholar]
- [197].Slifka MK, Whitton JL. Functional avidity maturation of CD8(+) T cells without selection of higher affinity TCR. Nat. Immunol. 2001;2:711–717. doi: 10.1038/90650. [DOI] [PubMed] [Google Scholar]
- [198].Smith JA, Martin L. Do cells cycle? Proc. Natl. Acad. Sci. U.S.A. 1973;70:1263–1267. doi: 10.1073/pnas.70.4.1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [199].Soares A, Govender L, Hughes J, Mavakla W, De Kock M, Barnard C, Pienaar B, Janse van Rensburg E, Jacobs G, Khomba G, Stone L, Abel B, Scriba TJ, Hanekom WA. Novel application of Ki67 to quantify antigen-specific in vitro lymphoproliferation. J. Immunol. Methods. 2010;362:43–50. doi: 10.1016/j.jim.2010.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [200].Speirs C, Van Nimwegen E, Bolton D, Zavolan M, Duvall M, Angleman S, Siegel R, Perelson AS, Lenardo MJ. Analysis of human immunodeficiency virus cytopathicity by using a new method for quantitating viral dynamics in cell culture. J. Virol. 2005;79:4025–4032. doi: 10.1128/JVI.79.7.4025-4032.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [201].Sprent J. Swapping molecules during cell-cell interactions. Sci. STKE. 2005;2005:pe8. doi: 10.1126/stke.2732005pe8. [DOI] [PubMed] [Google Scholar]
- [202].Srinivasula S, Lempicki RA, Adelsberger JW, Huang CY, Roark J, Lee PI, Rupert A, Stevens R, Sereti I, Lane HC, Di Mascio M, Kovacs JA. Differential effects of HIV viral load and CD4 count on proliferation of naive and memory CD4 and CD8 T lymphocytes. Blood. 2011;118:262–270. doi: 10.1182/blood-2011-02-335174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [203].Steinmann GG, Klaus B, Muller-Hermelink HK. The involution of the ageing human thymic epithelium is independent of puberty. A morphometric study. Scand. J. Immunol. 1985;22:563–575. doi: 10.1111/j.1365-3083.1985.tb01916.x. [DOI] [PubMed] [Google Scholar]
- [204].Subramanian VG, Duffy KR, Turner ML, Hodgkin PD. Determining the expected variability of immune responses using the cyton model. J. Math. Biol. 2008;56:861–892. doi: 10.1007/s00285-007-0142-2. [DOI] [PubMed] [Google Scholar]
- [205].Takizawa H, Regoes RR, Boddupalli CS, Bonhoeffer S, Manz MG. Dynamic variation in cycling of hematopoietic stem cells in steady state and inflammation. J. Exp. Med. 2011;208:273–284. doi: 10.1084/jem.20101643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [206].Tokoyoda K, Hauser AE, Nakayama T, Radbruch A. Organization of immunological memory by bone marrow stroma. Nat. Rev. Immunol. 2010;10:193–200. doi: 10.1038/nri2727. [DOI] [PubMed] [Google Scholar]
- [207].Tokoyoda K, Zehentmeier S, Chang HD, Radbruch A. Organization and maintenance of immunological memory by stroma niches. Eur. J. Immunol. 2009;39:2095–2099. doi: 10.1002/eji.200939500. [DOI] [PubMed] [Google Scholar]
- [208].Tokoyoda K, Zehentmeier S, Hegazy AN, Albrecht I, Grun JR, Lohning M, Radbruch A. Professional memory CD4+ T lymphocytes preferentially reside and rest in the bone marrow. Immunity. 2009;30:721–730. doi: 10.1016/j.immuni.2009.03.015. [DOI] [PubMed] [Google Scholar]
- [209].Tough DF, Sprent J. Turnover of naive- and memory-phenotype T cells. J. Exp. Med. 1994;179:1127–1135. doi: 10.1084/jem.179.4.1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [210].Tough DF, Sprent J. Lifespan of γ/δ T cells. J. Exp. Med. 1998;187:357–365. doi: 10.1084/jem.187.3.357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [211].Turnbull EL, Wong M, Wang S, Wei X, Jones NA, Conrod KE, Aldam D, Turner J, Pellegrino P, Keele BF, Williams I, Shaw GM, Borrow P. Kinetics of expansion of epitope-specific T cell responses during primary HIV-1 infection. J. Immunol. 2009;182:7131–7145. doi: 10.4049/jimmunol.0803658. [DOI] [PubMed] [Google Scholar]
- [212].Turner ML, Hawkins ED, Hodgkin PD. Quantitative regulation of B cell division destiny by signal strength. J. Immunol. 2008;181:374–382. doi: 10.4049/jimmunol.181.1.374. [DOI] [PubMed] [Google Scholar]
- [213].Van den Dool C, De Boer RJ. The effects of age, thymectomy, and HIV infection on α and β TCR excision circles in naive T cells. J. Immunol. 2006;177:4391–4401. doi: 10.4049/jimmunol.177.7.4391. [DOI] [PubMed] [Google Scholar]
- [214].Van Gent R, Kater AP, Otto SA, Jaspers A, Borghans JA, Vrisekoop N, Ackermans MA, Ruiter AF, Wittebol S, Eldering E, Van Oers MH, Tesselaar K, Kersten MJ, Miedema F. In vivo dynamics of stable chronic lymphocytic leukemia inversely correlate with somatic hypermutation levels and suggest no major leukemic turnover in bone marrow. Cancer Res. 2008;68:10137–10144. doi: 10.1158/0008-5472.CAN-08-2325. [DOI] [PubMed] [Google Scholar]
- [215].Van Heijst JW, Gerlach C, Swart E, Sie D, Nunes-Alves C, Kerkhoven RM, Arens R, Correia-Neves M, Schepers K, Schumacher TN. Recruitment of antigen-specific CD8+ T cells in response to infection is markedly efficient. Science. 2009;325:1265–1269. doi: 10.1126/science.1175455. [DOI] [PubMed] [Google Scholar]
- [216].Van Kampen NG. Stochastic processes in physics and chemistry. North-Holland Publishing; Amsterdam: 1992. [Google Scholar]
- [217].Van Stipdonk MJ, Lemmens EE, Schoenberger SP. Naive CTLs require a single brief period of antigenic stimulation for clonal expansion and differentiation. Nat. Immunol. 2001;2:423–429. doi: 10.1038/87730. [DOI] [PubMed] [Google Scholar]
- [218].Vaziri H, Dragowska W, Allsopp RC, Thomas TE, Harley CB, Lansdorp PM. Evidence for a mitotic clock in human hematopoietic stem cells: loss of telomeric DNA with age. Proc. Natl. Acad. Sci. U.S.A. 1994;91:9857–9860. doi: 10.1073/pnas.91.21.9857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [219].Veiga-Fernandes H, Walter U, Bourgeois C, McLean A, Rocha B. Response of naive and memory CD8+ T cells to antigen stimulation in vivo. Nat. Immunol. 2000;1:47–53. doi: 10.1038/76907. [DOI] [PubMed] [Google Scholar]
- [220].Vella AT, Dow S, Potter TA, Kappler J, Marrack P. Cytokine-induced survival of activated T cells in vitro and in vivo. Proc. Natl. Acad. Sci. U.S.A. 1998;95:3810–3815. doi: 10.1073/pnas.95.7.3810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [221].Von Boehmer H, Hafen K. The life span of naive α/β T cells in secondary lymphoid organs. J. Exp. Med. 1993;177:891–896. doi: 10.1084/jem.177.4.891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [222].Voogt JN, Awada M, Murphy EJ, Hayes GM, Busch R, Hellerstein MK. Measurement of very low rates of cell proliferation by heavy water labeling of DNA and gas chromatography/pyrolysis/isotope ratio-mass spectrometric analysis. Nat. Protoc. 2007;2:3058–3062. doi: 10.1038/nprot.2007.421. [DOI] [PubMed] [Google Scholar]
- [223].Vrisekoop N, Den Braber I, De Boer AB, Ruiter AF, Ackermans MT, Van der Crabben SN, Schrijver EH, Spierenburg G, Sauerwein HP, Hazenberg MD, De Boer RJ, Miedema F, Borghans JA, Tesselaar K. Sparse production but preferential incorporation of recently produced naive T cells in the human peripheral pool. Proc. Natl. Acad. Sci. U.S.A. 2008;105:6115–6120. doi: 10.1073/pnas.0709713105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [224].Vrisekoop N, Van Gent R, Mugwagwa T, De Boer AB, Otto S, Ruiter AFC, Ackermans MT, Vermeulen JN, Huidekoper HH, Gaiser K, Sauerwein HP, Prins JM, Miedema F, De Boer RJ, Tesselaar K, Borghans JAM. Qualitative changes in T cell turnover during HIV-1 infection. 2012. submitted. [Google Scholar]
- [225].Wallace DL, Zhang Y, Ghattas H, Worth A, Irvine A, Bennett AR, Griffin GE, Beverley PC, Tough DF, Macallan DC. Direct measurement of T cell subset kinetics in vivo in elderly men and women. J. Immunol. 2004;173:1787–1794. doi: 10.4049/jimmunol.173.3.1787. [DOI] [PubMed] [Google Scholar]
- [226].Wellard C, Markham J, Hawkins ED, Hodgkin PD. The effect of correlations on the population dynamics of lymphocytes. J. theor. Biol. 2010;264:443–449. doi: 10.1016/j.jtbi.2010.02.019. [DOI] [PubMed] [Google Scholar]
- [227].Wells AD, Gudmundsdottir H, Turka LA. Following the fate of individual T cells throughout activation and clonal expansion. Signals from T cell receptor and CD28 differentially regulate the induction and duration of a proliferative response. J. Clin. Invest. 1997;100:3173–3183. doi: 10.1172/JCI119873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [228].Weng N, Levine BL, June CH, Hodes RJ. Regulation of telomerase RNA template expression in human T lymphocyte development and activation. J. Immunol. 1997;158:3215–3220. [PubMed] [Google Scholar]
- [229].Weng NP, Levine BL, June CH, Hodes RJ. Human naive and memory T lymphocytes differ in telomeric length and replicative potential. Proc. Natl. Acad. Sci. U.S.A. 1995;92:11091–11094. doi: 10.1073/pnas.92.24.11091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [230].Weng NP, Palmer LD, Levine BL, Lane HC, June CH, Hodes RJ. Tales of tails: regulation of telomere length and telomerase activity during lymphocyte development, differentiation, activation, and aging. Immunol. Rev. 1997;160:43–54. doi: 10.1111/j.1600-065x.1997.tb01026.x. [DOI] [PubMed] [Google Scholar]
- [231].Westera L, Drylewicz J, Den Braber I, Mugwagwa T, Van der Maas I, Kwast L, Volman T, Schrijver EHR, Bartha I, Spierenburg G, Gaiser K, Ackermans MT, Asquith B, De Boer RJ, Tesselaar K, Borghans JAM. Reliable quantification of leukocyte life spans from stable isotope labeling data. 2012. submitted. [Google Scholar]
- [232].Wetzel SA, McKeithan TW, Parker DC. Peptide-specific intercellular transfer of MHC class II to CD4+ T cells directly from the immunological synapse upon cellular dissociation. J. Immunol. 2005;174:80–89. doi: 10.4049/jimmunol.174.1.80. [DOI] [PubMed] [Google Scholar]
- [233].Wetzel SA, Parker DC. MHC transfer from APC to T cells following antigen recognition. Crit. Rev. Immunol. 2006;26:1–21. doi: 10.1615/critrevimmunol.v26.i1.10. [DOI] [PubMed] [Google Scholar]
- [234].Wiegel FW, Perelson AS. Some scaling principles for the immune system. Immunol. Cell Biol. 2004;82:127–131. doi: 10.1046/j.0818-9641.2004.01229.x. [DOI] [PubMed] [Google Scholar]
- [235].Williams MA, Bevan MJ. Shortening the infectious period does not alter expansion of CD8 T cells but diminishes their capacity to differentiate into memory cells. J. Immunol. 2004;173:6694–6702. doi: 10.4049/jimmunol.173.11.6694. [DOI] [PubMed] [Google Scholar]
- [236].Willis RA, Kappler JW, Marrack PC. CD8 T cell competition for dendritic cells in vivo is an early event in activation. Proc. Natl. Acad. Sci. U.S.A. 2006;103:12063–12068. doi: 10.1073/pnas.0605130103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [237].Wilson A, Laurenti E, Oser G, Van der Wath RC, Blanco-Bose W, Jaworski M, Offner S, Dunant CF, Eshkind L, Bockamp E, Lio P, Macdonald HR, Trumpp A. Hematopoietic stem cells reversibly switch from dormancy to self-renewal during homeostasis and repair. Cell. 2008;135:1118–1129. doi: 10.1016/j.cell.2008.10.048. [DOI] [PubMed] [Google Scholar]
- [238].Wolthers KC, Noest AJ, Otto SA, Miedema F, De Boer RJ. Normal telomere lengths in naive and memory CD4+ T cells in HIV type 1 infection: a mathematical interpretation. AIDS Res. Hum. Retroviruses. 1999;15:1053–1062. doi: 10.1089/088922299310340. [DOI] [PubMed] [Google Scholar]
- [239].Wolthers KC, Wisman GBA, Otto SA, De Roda Husman AM, Schaft N, De Wolf F, Goudsmit J, Coutinho RA, Van der Zee AG, Meyaard L, Miedema F. T cell telomere length in HIV-1 infection: no evidence for increased CD4+ T cell turnover. Science. 1996;274:1543–1547. doi: 10.1126/science.274.5292.1543. [DOI] [PubMed] [Google Scholar]
- [240].Yarke CA, Dalheimer SL, Zhang N, Catron DM, Jenkins MK, Mueller DL. Proliferating CD4+ T cells undergo immediate growth arrest upon cessation of TCR signaling in vivo. J. Immunol. 2008;180:156–162. doi: 10.4049/jimmunol.180.1.156. [DOI] [PubMed] [Google Scholar]
- [241].Yates A, Chan C, Strid J, Moon S, Callard R, George AJ, Stark J. Reconstruction of cell population dynamics using CFSE. BMC. Bioinformatics. 2007;8:196. doi: 10.1186/1471-2105-8-196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [242].Yates A, Saini M, Mathiot A, Seddon B. Mathematical modeling reveals the biological program regulating lymphopenia-induced proliferation. J. Immunol. 2008;180:1414–1422. doi: 10.4049/jimmunol.180.3.1414. [DOI] [PubMed] [Google Scholar]
- [243].Ye P, Kirschner DE. Reevaluation of T cell receptor excision circles as a measure of human recent thymic emigrants. J. Immunol. 2002;168:4968–4979. doi: 10.4049/jimmunol.168.10.4968. [DOI] [PubMed] [Google Scholar]
- [244].Younes SA, Punkosdy G, Caucheteux S, Chen T, Grossman Z, Paul WE. Memory phenotype CD4 T cells undergoing rapid, nonburst-like, cytokine-driven proliferation can be distinguished from antigen-experienced memory cells. PLoS. Biol. 2011;9:e1001171. doi: 10.1371/journal.pbio.1001171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [245].Zand MS, Briggs BJ, Bose A, Vo T. Discrete event modeling of CD4+ memory T cell generation. J. Immunol. 2004;173:3763–3772. doi: 10.4049/jimmunol.173.6.3763. [DOI] [PubMed] [Google Scholar]
- [246].Zehn D, Lee SY, Bevan MJ. Complete but curtailed T-cell response to very low-affinity antigen. Nature. 2009;458:211–214. doi: 10.1038/nature07657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [247].Zhang ZQ, Notermans DW, Sedgewick G, Cavert W, Wietgrefe S, Zupancic M, Gebhard K, Henry K, Boies L, Chen Z, Jenkins M, Mills R, McDade H, Goodwin C, Schuwirth CM, Danner SA, Haase AT. Kinetics of CD4+ T cell repopulation of lymphoid tissues after treatment of HIV-1 infection. Proc. Natl. Acad. Sci. U.S.A. 1998;95:1154–1159. doi: 10.1073/pnas.95.3.1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [248].Zilman A, Ganusov VV, Perelson AS. Stochastic models of lymphocyte proliferation and death. PLoS One. 2010;5:e12775. doi: 10.1371/journal.pone.0012775. [DOI] [PMC free article] [PubMed] [Google Scholar]