Iterative Refinement of a Binding Pocket Model: Active Computational Steering of Lead Optimization

Abstract

Computational approaches for binding affinity prediction are most frequently demonstrated through cross-validation within a series of molecules or through performance shown on a blinded test set. Here, we show how such a system performs in an iterative, temporal lead optimization exercise. A series of gyrase inhibitors with known synthetic order formed the set of molecules that could be selected for “synthesis.” Beginning with a small number of molecules, based only on structures and activities, a model was constructed. Compound selection was done computationally, each time making five selections based on confident predictions of high activity and five selections based on a quantitative measure of three-dimensional structural novelty. Compound selection was followed by model refinement using the new data. Iterative computational candidate selection produced rapid improvements in selected compound activity, and incorporation of explicitly novel compounds uncovered much more diverse active inhibitors than strategies lacking active novelty selection.

Introduction

The field of computational structure–activity modeling in medicinal chemistry has a long history, going back at least 40 years.¹ Methods-oriented papers have generally analyzed statistical performance in terms of numerical prediction accuracy, and application-oriented papers have described predictions made based upon QSAR models built from a particular training set. The present study considers these aspects of predictive activity modeling but adds new dimensions. Rather than focus purely on how well a method can predict activity based on a fixed, particular set of compounds, we instead ask how a method can guide a trajectory of chemical exploration in a protocol that incorporates iterative model refinement. Further, in addition to considering prediction accuracy and the efficiency of discovering active compounds, we consider how selection strategies and modeling methods affect the structural diversity of the chemical space that is uncovered over time. We show that there is a direct benefit for active selection of molecules that will “break” a model by venturing into chemical and physical space that is poorly understood. We also show that modeling methods that are accurate within a narrow range of structural variation can appear to be highly predictive but guide molecular selection toward a structurally narrow end point. Conservative selection strategies and conservative modeling methods can lead to active compounds, but these may represent just a fraction of the space of active compounds that exist.

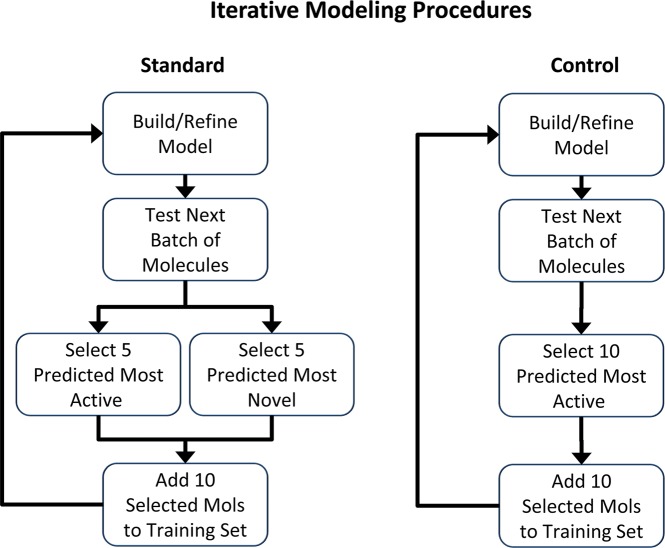
The primary method used to explore these issues is a relatively new one for binding affinity prediction, called Surflex QMOD (Quantitative MODeling), which constructs a physical binding pocket into which ligands are flexibly fit and scored to predict both a bioactive pose and binding affinity.²⁻⁴ Our initial work focused on demonstrating the feasibility of the approach, with a particular emphasis on addressing cross-chemotype predictions, as well as the relationship between the underpinnings of the method to the physical process of protein ligand binding. Those studies considered receptors (5HT1a and muscarinic), enzymes (CDK2), and membrane-bound ion channels (hERG). The present work addresses two new areas. First, we examined the performance of QMOD in an iterative refinement scenario, where a large set of molecules from a lead-optimization exercise⁵ was used as a pool from which selections were made using model predictions. Multiple “rounds” of model building, molecule selection, and model refinement produced a trajectory of molecular choices. Second, we considered the effect of active selection of structurally novel molecules that probed parts of three-dimensional space that were unexplored by the training ligands for each round’s model. Figure 1 shows a diagram of the iterative model refinement procedure. Selection of molecules for “synthesis” for the first round took place from a batch of molecules made after the initial training pool had been synthesized. Subsequent rounds allowed for choice from later temporal batches, along with previously considered but unselected molecules. The approach was designed to limit the amount of “look-ahead” for the procedure. The space for molecular selections within each round formed a structural window that reflected the changing chemical diversity that was explored over the course of the project. The iterative procedure was carried out until all molecules were tested. The primary procedural variations involved use of different modeling and selection methods, and the analyses focused on the characteristics of the selected molecular populations, and the relationship of the models to the experimentally determined structure of the protein binding pocket.

Figure 1.

Inhibitors first synthesized were used for initial training. All subsequent molecules were divided into sequential batches of 50 candidates each. At the completion of each build/refine iteration, the next sequential batch and all previously considered but unchosen molecules formed a “window” for molecular selections. Based upon model predictions, ten molecules were selected and added to the training set for each round of model refinement. Two selection schemes were employed. The standard method selected molecules based on high-confidence predictions of high activity or based on 3D structural novelty. The control procedure made selections purely based on activity predictions.

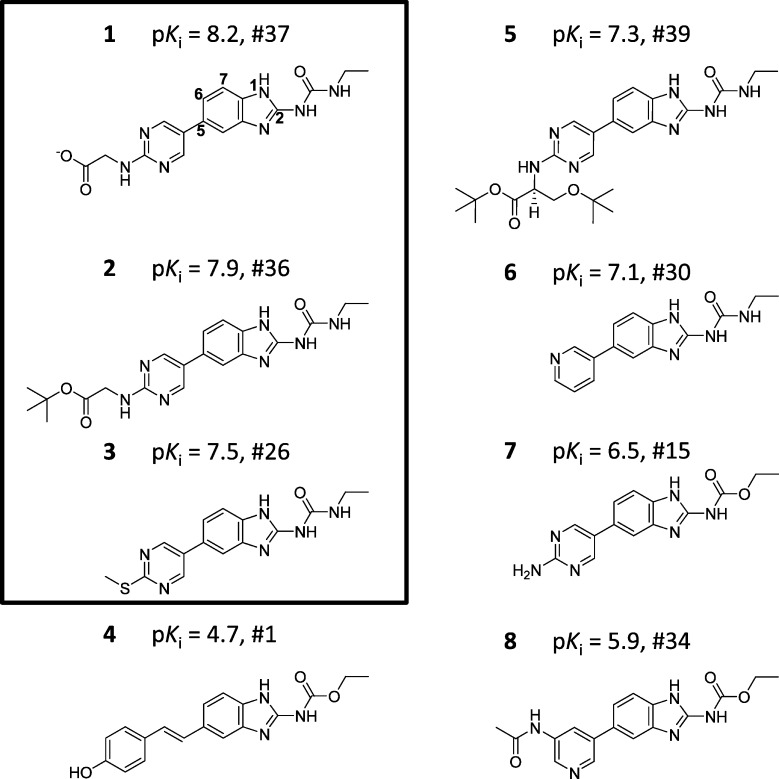
All of the molecules used in this study were taken from a lead optimization program conducted at Vertex Pharmaceuticals. This program involved the optimization of benzimidazole based inhibitors of the bacterial gyrase heterotetramer.⁵ The enzyme is a type II topoisomerase that alters chromosome structure through modification of double stranded DNA. Antibacterials such as the fluoroquinolones target the non-ATP catalytic sites of gyrase. In contrast, the benzimidazole inhibitors were discovered in a high-throughput ATPase assay of the GyrB subunit. These were then optimized for activity against the ATP-binding site of GyrB, with an eye toward activity against the ATP site of the ParE subunit (topoisomerase IV) as well. Both of these subunits are responsible for supplying energy for catalysis. In the present study, only activity data from GyrB assays were used for modeling and compound selection. Figure 2 shows typical examples of structures and GyrB activities from the initial training set. The position 2 substituents of all inhibitors used in this study were either alkyl-urea (e.g., compound 1) or alkyl-carbamate (e.g., 4). Structural exploration was predominated by variation in the position 5 substituent of the benzimidazole, with some substitutions also being made at other positions on the central scaffold (especially position 7). The series used in this study consisted of 426 compounds.

Figure 2.

Examples of gyrase ligands in the initial training set, which contained the first 39 made from a total of 426 gyrase inhibitors (both pK_i and synthetic sequence number are given). Training molecule activities ranged from a pK_i of 8.2 to 4.7. The 3 most active compounds of the training set (boxed) were used to generate the initial alignment hypotheses.

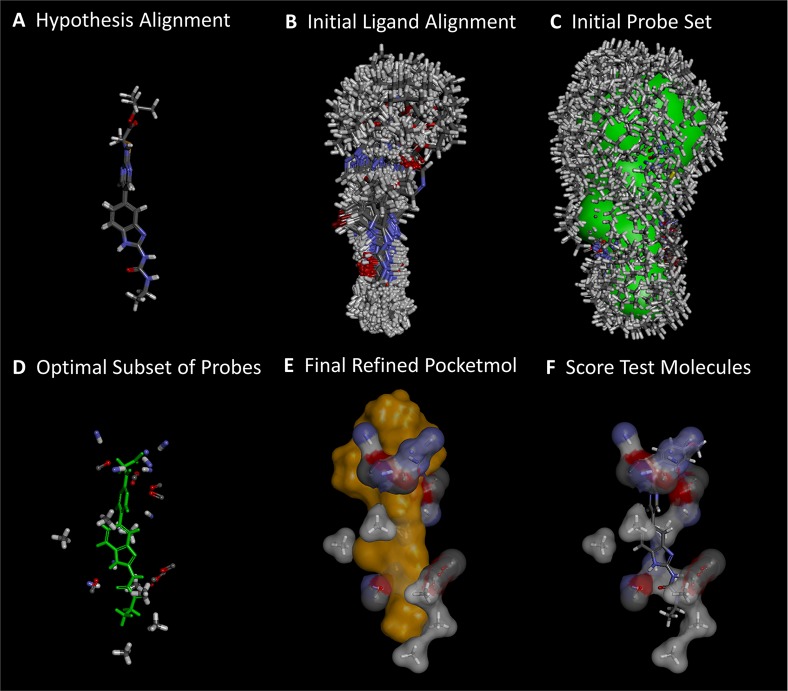
For the present study, the most interesting aspect of the QMOD approach is that it constructs a physical model of a protein binding site based purely on structure–activity data, and it produces predictions of both binding affinity and bound ligand pose. Because the optimal molecular poses depend directly on the physical pocket model, multiple-instance machine-learning is used for model induction.^2,3,6−12 Figure 3gives a brief overview of the process, which begins with selection of a small number of molecules to form a seed alignment hypothesis (the boxed inhibitors from Figure 2) and ends with a physical representation of a binding pocket, to which we refer as a “pocketmol.” New molecules are docked into the pocketmol and scored, yielding predictions of activity and binding mode. By considering the differences between the predicted bound poses of molecules with known activity (training molecules) and novel candidates, it is possible to quantify the degree to which a new molecule “probes” part of a modeled binding cavity differently than has been probed before. This computational definition of molecular novelty offers a visualizable means to actively consider synthetic choices that specifically probe beyond the established and explored 3D space of a particular model. As a comparator, we also made use of a descriptor-based QSAR approach that constructs a purely statistical model of activity prediction based on topological molecular features.

Figure 3.

Derivation and testing of a QMOD pocketmol proceeds in six automated steps: (A) an alignment seed hypothesis is constructed from 2 to 3 ligands; (B) 100–200 alignments for each training ligand are produced; (C) a large set of probes (many thousands) is created where interactions may exist; (D) a small near-optimal set is selected based on fit to experimental binding data and model parsimony; (E) probe positions and ligand poses are refined iteratively; (F) new molecules are tested by flexible alignment into the pocket to optimize score. The final pocketmol is used in a fixed configuration, but conformational flexibility within the corresponding protein pocket is represented by probes being places in multiple positions.

There were four primary results of the study. First, the iterative QMOD procedure rapidly converged on models that reliably identified highly active molecules. By the final two model refinement rounds, 70–80% of molecules selected based on predicted activity fell into the highest category of experimental activity (pK_i > 7.9, which represented all molecules having activity within 3-fold of the most active inhibitors). Second, explicit computational selection of novel molecules lead to a much more structurally diverse pool of active inhibitors than resulted from a control procedure that made selections purely based on activity considerations. Both procedures produced similar performance in terms of the distributions of experimental activity for selected molecules. Third, the induced binding site model showed strong concordance with the experimentally determined gyrase binding site. This was true both in terms of predicted ligand poses as well as similarities in contact patterns between ligand/pocketmol and ligand/protein. Fourth, direct comparison with descriptor-based QSAR methods showed that while such models yielded similar distributions of activity among selected molecules, the structural diversity of selected active molecules was much lower than for QMOD. In particular, while QMOD identified examples of active molecules across the entire arc of the project’s chemical exploration, the descriptor-based approach failed to select a particularly attractive set of inhibitors made toward the end of the project.

The basic Surflex QMOD methodology has been validated in prior studies.²⁻⁴ The significance here relates to systematic application in the context of a virtual lead optimization exercise. There is a dramatic benefit in making use of an active-learning paradigm in which exploration of unknown space is explicitly made through the selection of structurally novel molecules. In addition, apart from the obvious benefits of providing a physical model along with accurate predictions of binding modes, the physically realistic modeling approach of QMOD showed a surprising benefit: great structural diversity among the set of discovered active inhibitors. In particular, the procedure identified ligands that showed strong activity against GyrB but also against ParE (topoisomerase IV). Activity of ligands against ParE was an indirect consequence of spatial probing through active selection of compounds. These ligands had large 7-position substituents that represented a clearly new structural direction when compared with the bulk of inhibitors made.

In the case of the congeneric chemical series studied here, it was not surprising that descriptor-based QSAR methods performed competitively in a purely numeric sense with respect to identification of active GyrB inhibitors. However, the narrow domain of applicability of such models manifested itself by predicting high activity based only upon very close structural similarity to pre-existing active inhibitors. The resulting trajectory of selected molecules failed to identify the pool of active ParE inhibitors that the QMOD approach found, even when a procedure to increase novelty was employed in conjunction with the descriptor-based method. Models that are fundamentally correlative machines may appear to work well, but they may sharply limit the space of compound exploration over the course of time. Structural conservatism would appear to be a hidden cost of reliance upon modeling methods that directly depend upon the existence of near-neighbors to make accurate predictions on new molecules.

We believe that this approach of studying trajectories through chemical space, subject to different prediction and selection methods, offers a very different means by which to assess the real-world behavior of modeling systems. The results clearly encourage the use of physically sensible approaches that move beyond purely correlative modeling and also support the active incorporation of chemical possibilities that are clearly beyond the knowledge of a model at a given time.

Results and Discussion

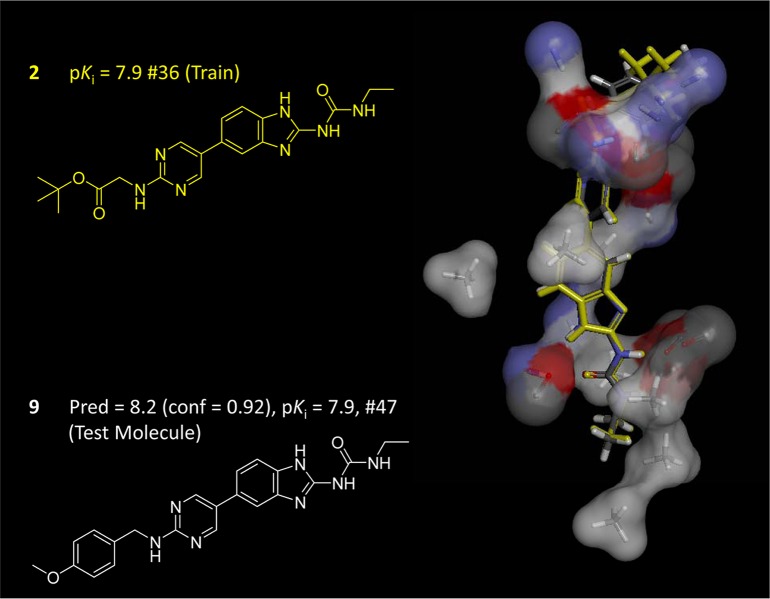
Figure 4 shows the initial QMOD pocketmol derived from 39 training molecules (atom-color thin sticks with surface). The pose of compound 2, which was part of the initial training set, is shown along with the optimal pose of compound 9 (the 47th molecule in the synthetic series). Molecule 9 was predicted with high confidence (0.92/1.0) to have high activity (predicted pK_i of 8.2), yielding an error of 0.3 log units when compared with experimental activity. The confidence measure is defined as the maximal 3D molecular similarity between a test molecule and any of the training molecules (each in its optimal pose according to fit within the pocketmol). Here, the most similar training compound to 9 was 2, with the high similarity obvious in the 2D representations, and with the optimal poses of both molecules being concordant, even including volume overlap of the differing left-hand side substituents.

Figure 4.

Initial QMOD binding site model is shown (right), derived from 39 training molecules. The probes comprising the pocket are shown in atom-colored thin sticks with surfaces. Training compound 2 is shown in yellow, with 2D at left and in its predicted optimal pose at right. Compound 9 (number 47 in the synthetic series) was predicted with high confidence to have a pK_i of 8.2, very close to the experimental value of 7.9 (shown at right in atom colored sticks).

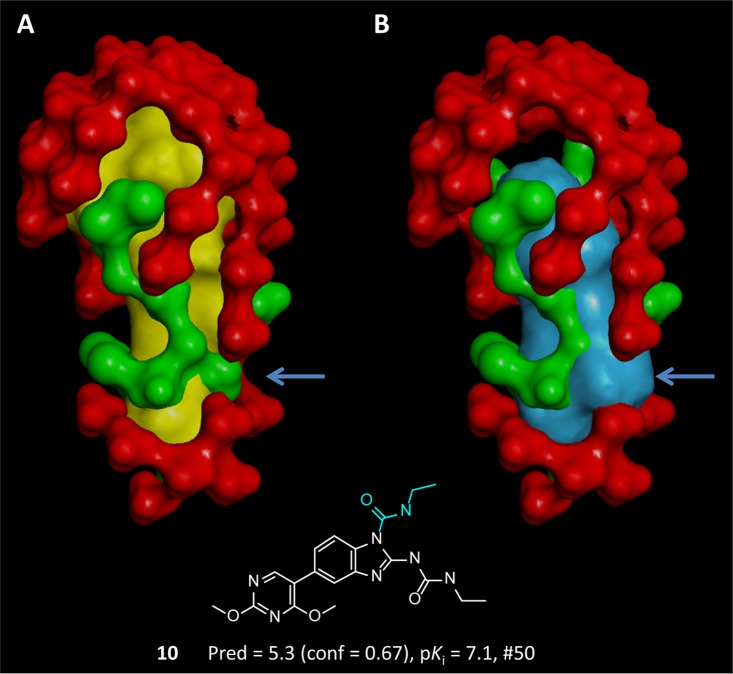
As described above (and shown in Figure 1), this initial model formed the root of two branches for molecular choice: one making use of a novelty computation and the other focusing only on activity. Figure 5 depicts an example of the novelty computation relating to a substitution at position 1 of the benzimidazole scaffold. Molecular novelty is a quantitative measure of the degree to which a new molecule explores the space of the binding pocket with new chemical functionality. It is defined using statistics based on the interactions of training molecules with the pocketmol and the interactions with unoccupied space near the pocketmol (termed the antipocketmol). The statistics characterize the scores for each probe against the optimal poses for each training molecule and additional poses that sample ligand configurations that are close to optimal (see the Experimental Section for details). The antipocketmol is constructed such that it borders on the explored pose pool but excludes the space immediately around the pocketmol. Novelty is quantified by comparing the interactions made with the pocketmol/antipocketmol to those made by the training ligands. Compound 10 had the highest novelty score among all 50 molecules in the first batch of compounds from which selections were made. Compound 10 was predicted incorrectly to have low activity, and it was correctly flagged as a low-confidence prediction. Its novelty score was 51.6, corresponding to a normalized Z-score of 5.7 standard deviation units greater than the mean of the remaining pool from those molecules upon which the initial model was tested. The extreme relative magnitude highlights the novelty of the pattern of interaction scores associated with the substitution at position 1 of the central scaffold.

Figure 5.

Molecular novelty computation compares the interaction score profile of the training molecules in their explored poses (yellow surface, Panel A) to that of a new molecule’s probable poses (blue surface, Panel B). The scoring profiles are computed against the pocketmol (green surface) and antipocketmol (red surface), which occupies space that would otherwise be empty. Compound 10, from the initial batch of 50 candidate ligands, contained a novel substitution (shown in blue). This substituent has a natural clash with the pocketmol when aligned to training molecules (blue arrow). The pocketmol incorrectly placed a “wall” there due to inadequate exploration within the training set. The clash produced a tilted pose (not shown), resulting in a low-confidence prediction that was significantly lower than the experimental value.

Effects of Selection Strategy on Experimental Activities of Chosen Molecules

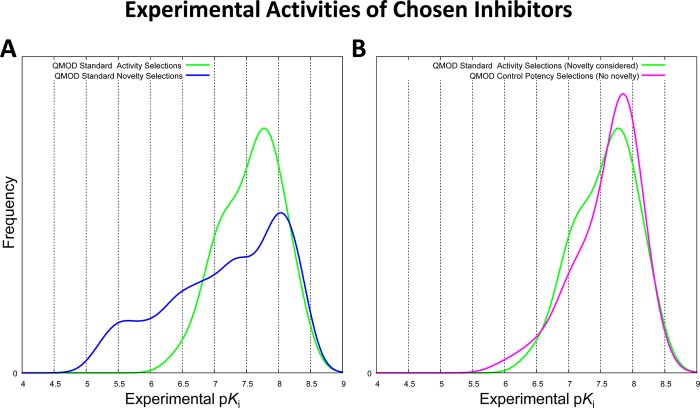
The ideal experiment in which to assess different design strategies for lead optimization would require independent synthetic teams of equivalent capabilities, each totally isolated from the other. Given an initial starting point, the teams would make a fixed number of compounds over a set time period, with common protocols involving compound testing and provision of assay feedback to the design teams. While we do not have the resources to perform the ideal experiment, we have tried to perform a balanced comparison. Here the 39 initial training molecules and their GyrB activities form a common initial starting point, and it is interesting to consider the effects of different computational approaches in terms of the properties of the molecules that are selected from among the remaining 387 that were part of the series. In the standard procedure, half of the molecules selected were chosen to maximize predicted activity and half were chosen as being structurally novel in order to inform the model in areas that had not been explored. In the control procedure, all of the molecules were chosen to maximize activity. Figure 6 shows the distributions of experimental activities of molecules chosen using the QMOD standard procedure compared with the QMOD control procedure (recall Figure 1). The two distributions within the standard procedure were very different (p ≪ 0.01 by Kolmogorov–Smirnov (KS)),with the novelty-driven selections exhibiting a wider dispersion of experimental activity and a much larger proportion of poorly active molecules (roughly 30% with pK_i < 6.5 compared with <5% from the activity-driven selections). Despite being informed quite differently in terms of structure–activity data, the distribution of activities for molecules selected for activity under the standard protocol were not different than those selected in the control procedure (see Figure 6b). The structural characteristics of the resulting pools were very different, and this will be discussed in the next section.

Figure 6.

(A) Distribution of experimentally measured activity for the QMOD standard procedure, comparing the 40 molecules chosen based on predictions of high activity (green curve) and the 40 molecules chosen based on structural novelty (blue curve). (B) Comparison between the QMOD standard procedure (green curve) and the control procedure (magenta curve), which made selections based solely on activity predictions.

The comparison between the two QMOD procedure variations fits our Gedanken ideal, with fully independent “synthetic teams” employing different design strategies in isolation. Beginning with the same initial set of 39 training molecules, the two procedures each made eight rounds of molecular selections, each consisting of ten molecules, with the single difference being the selection strategy. If we consider the distribution of experimental activities of the next 80 molecules actually made after the initial 39 in the training set, we deviate from the ideal comparison. First, the project chemists were interested in addressing issues beyond just activity against GyrB. The considerations included activity against ParE, physical properties of compounds, complexities of synthesis given existing routes and materials, and a host of other items. Clearly, however, they were interested in maximizing activity against GyrB. Second, the project chemists had access to information well beyond what the QMOD modeling procedures had, including crystallographic guidance and knowledge of other inhibitors of the ATP binding sites of gyrase. Bearing this in mind, it is interesting to consider the comparison between the QMOD selections in the standard procedure and the activities of the next 80 molecules actually synthesized after the initial 39. Figure 7 shows the three distributions, each of which is highly statistically different from one another. The QMOD activity selections (green curve) were enriched for highly active compounds, the QMOD novelty selections (blue curve) showed a wide range of activities, and the next 80 project-synthesized compounds (red curve) had high variance in activity but lacked a significant fraction of highly active selections. This comparison is not meant to suggest that the QMOD selection approach is definitively “better” in some sense than the efforts of human designers. The comparison provides context for what the space of designable compounds looked like within a fixed frame of temporal exploration measured in numbers of compounds made.

Figure 7.

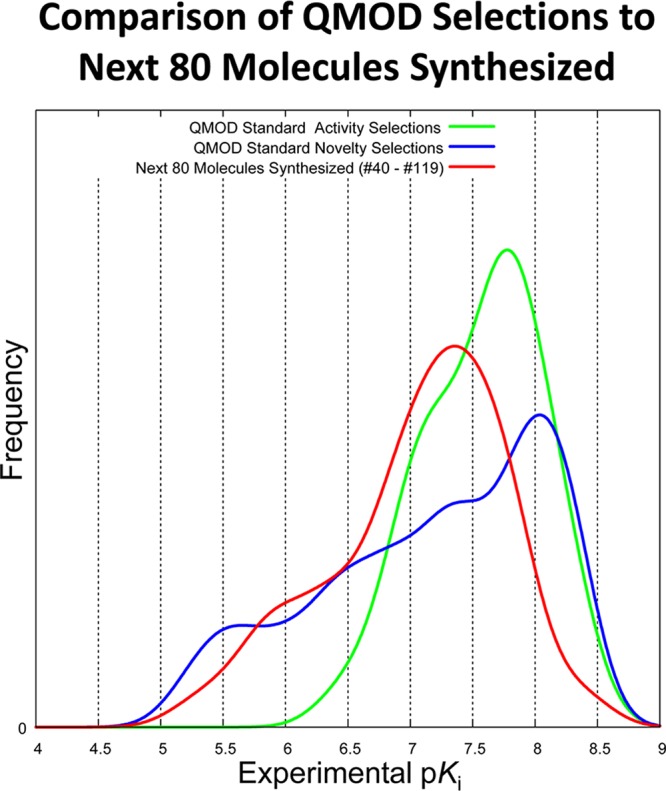
Three distributions of experimental activities shown are all highly significantly different from one another: 40 compounds selected for activity (green), 40 selected for novelty (blue), and the next 80 actually synthesized after the 39 that formed the QMOD initial training set (red).

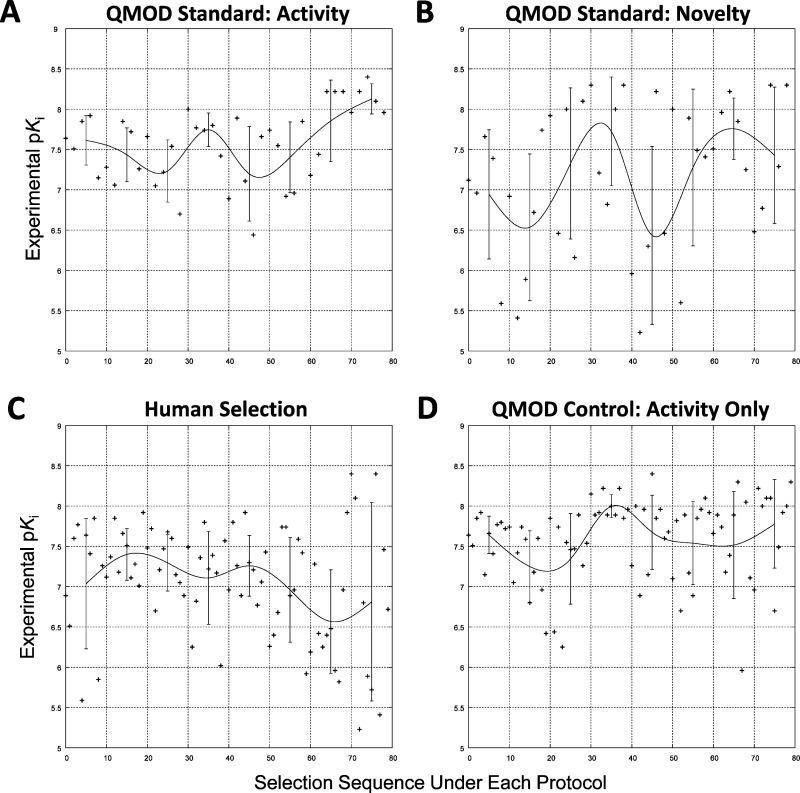
Figure 8 provides additional detail, showing the experimental activities in temporal selection order for the QMOD standard protocol, the control protocol with no novelty bias, and the next 80 molecules synthesized. Figure 8a shows the trajectory of activity observed with the 40 QMOD standard activity-based selections, nearly all of which had activity greater than 7.0 pK_i. Toward the end of the eight rounds of selection, nearly all molecules had potencies of 8.0 or higher. The corresponding novelty selections (Figure 8b) exhibit much wider dispersion, with both high- and low-activity molecules being selected across the entire sequence. Notably, maximally active molecules were chosen earlier through novelty-based selection than through activity-based selection in the standard procedure. Again, for contextual purposes, and with the caveats described above, Figure 8c shows the sequence of experimental activities for molecules in the synthetic sequence numbered 40–119. The high dispersion and downward trend were probably driven by many factors, but clearly there were challenges in meeting multiple design criteria while maintaining or increasing activity against GyrB. The QMOD control procedure (Figure 8d) exhibited stable performance, reliably picking a preponderance of molecules with activity greater than a pK_i of 7.5. Recall that while the distributions corresponding to plots A–C were all significantly different, conditions A and D produced indistinguishable distributions in a statistical sense.

Figure 8.

Experimental activity of molecules selected is plotted against selection order under different protocols. The bars indicate standard deviations within local windows, and the curves represent a smoothed window-average for each trajectory.

Effects of Selection Strategy on Structural Diversity of Chosen Winners

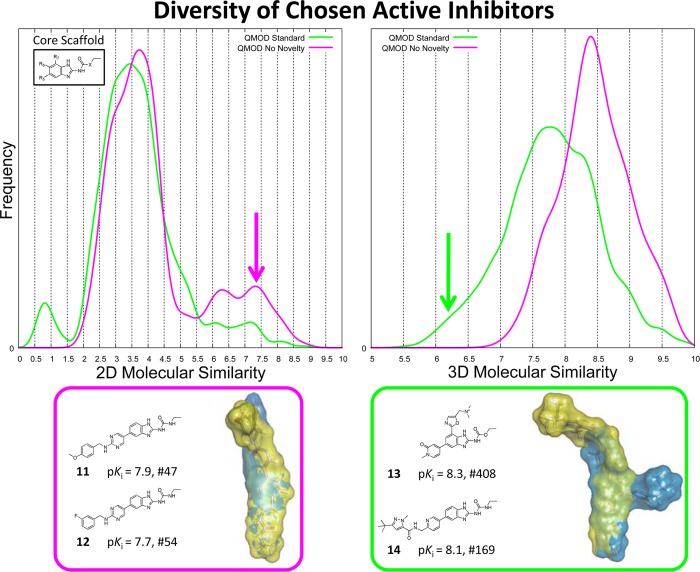
The molecular pools selected with and without a novelty bias exhibited indistinguishable distributions of GyrB activity. However, the actual value of a given pool of active inhibitors is affected by chemical composition. A single active inhibitor along with several nearly identical variants will generally be less useful that the same inhibitor along with several equipotent but structurally different variants. We defined a threshold of pK_i ≥ 7.5 to identify molecules with desirably high activity (“winners”) and compared the structural diversity of the winners chosen within the different selection procedures. The standard selection procedure that included novelty and activity found structurally diverse active molecules. The plots in Figure 9 show the distribution of pairwise 2D (left) and 3D (right) similarities of the winners. The diversity of winners resulting from the standard QMOD procedure is shown in green, and that resulting from the control procedure without novelty is shown in magenta. The distributions of 2D similarity differed primarily in the tails, with the standard procedure showing very few highly similar winning pairs compared with the control procedure. Also, the standard procedure identified a small population of divergent pairs that were missed by the control procedure. The 3D similarity distributions exhibited much more substantial differences, with a very significant shift toward lower mutual similarity within the population of winners from the standard procedure. Figure 9 shows an example of a typical highly similar pair (compounds 11 and 12) from the control procedure along with a structurally divergent pair (compounds 13 and 14) from the standard procedure. The protrusion of 13 (lower right, in blue) is particularly stark. Notably, inhibitors containing 7-position substitutions also possessed markedly improved activity against ParE,⁵ with dual-inhibition of GyrB and ParE being desirable in the context of antibacterial development.

Figure 9.

Structural diversity among the molecules selected using the QMOD procedure that included an active novelty component was significantly higher in both 2D (left) and 3D (left). At bottom, example pairs of molecules are given from the control procedure (left) and the standard procedure (right). This comparison considered all molecular selections from each procedure, whether derived from an activity prediction or one from novelty, a total 80 molecules each for the standard procedure and the control procedure.

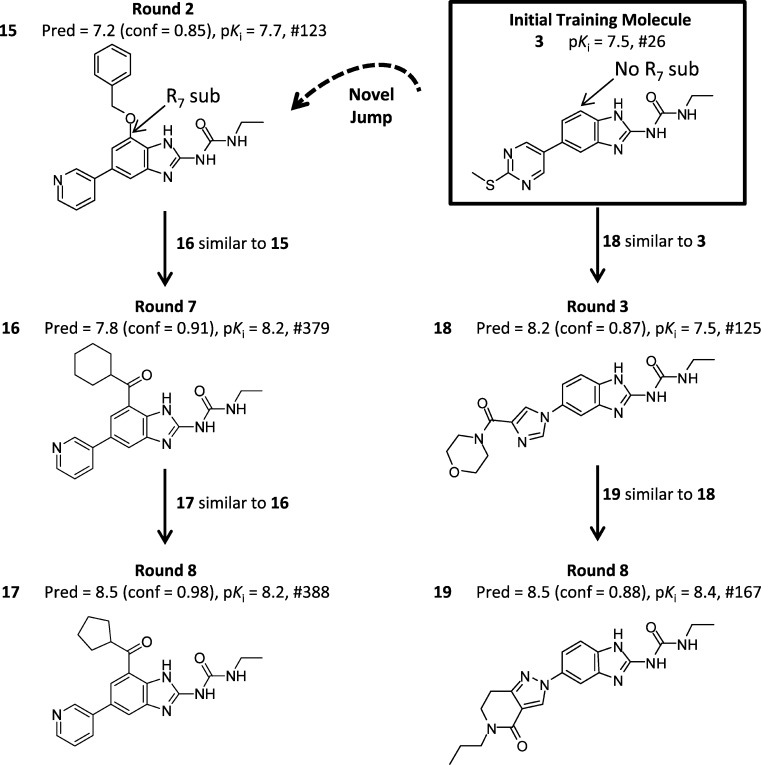
The use of a novelty bias in compound selection drove the computational exploration of structural diversity. This is easily seen in the evolutionary design tree shown in Figure 10. Two selection pathways are depicted that led to two structurally different, yet active, gyrase inhibitors. In round 2 (left side of Figure 10), 15 (dashed arrow) was selected for novelty because of the new interactions made with the model from the benzyl-ester substitution at position 7 of the benzimidazole. In round 7, 16 was selected for activity, where confidence was derived from 15. In round 8, 17 was selected confidently based on similarity to 16. By the final round, QMOD had converged on making confident and accurate predictions for position 7-substituted molecules (e.g., the prediction error for 17 was just 0.3 log units and was predicted with a confidence value of 0.98). On the right-hand side of Figure 10, a separate branch of selections without a substituent at position 7 was also elaborated. In round 3, 18 was selected for activity (similar to 3). In round 8, QMOD identified one of the most active compounds in the entire set. Compound 19 was accurately predicted with high confidence (similar to 18). Molecules 17 and 19 are examples of the most active and structurally dissimilar molecules in the entire pool.

Figure 10.

Examples of molecular selection based on novelty or on high-confidence predictions of high activity give rise to a branched pattern of chemical exploration.

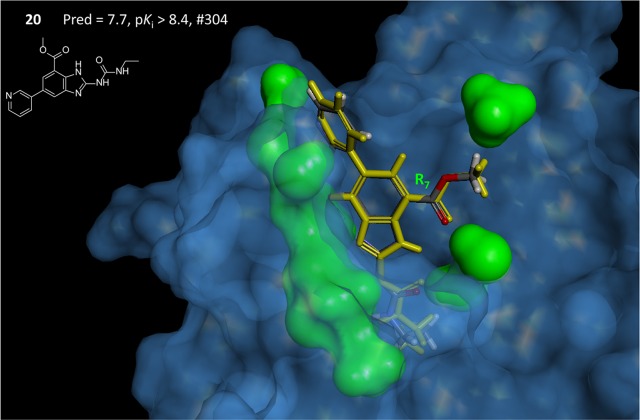
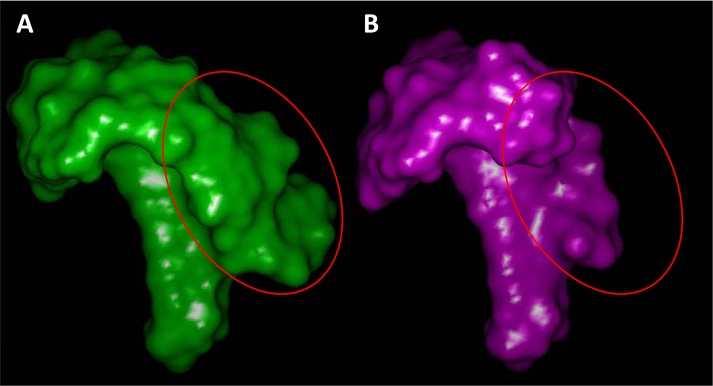
A significant driver of the 3D structural diversity in the standard procedure arose based on the discovery of multiple active inhibitors (e.g., compound 13) with significant 7-position substituents. Figure 11 shows the surface envelope of the winners from the standard selection procedure (green) along with that from the control procedure (magenta). These poses were derived by docking into an experimentally determined GyrB protein structure to provide a common target for visualization of the spatial exploration of the binding pocket. The corresponding circled areas identify the binding pocket space that was explored based on active selection of novel molecules that was missed when focusing solely on activity. One of the pitfalls in exploring a binding pocket without the benefit of an experimentally determined protein structure is that the degree to which the pocket can be defined is driven purely based on synthesis and assay of compounds. In this purely apples-to-apples comparison of two computationally driven selection procedures, it was clear that a quantitatively driven strategy to explore space beyond what had been mapped led to the discovery of a cavity capable of offering increases in inhibitor activity. The class of 7-position substituted inhibitors showed notably better dual-inhibition profiles,⁵ illustrating a concrete biological benefit of this type of structural diversity.

Figure 11.

Structural diversity among the molecules selected using the QMOD procedure that included an active novelty component was significantly higher in both 2D (left) and 3D (right).

In addition to considering the two variants of the QMOD approach, we also ran a descriptor-based QSAR approach that combined 2D molecular fingerprints with the random forest learning method (termed “RF”).¹³⁻¹⁵ Two procedures using the RF approach were run, paralleling the two procedures used by QMOD (see Figure 1). Selection of novel molecules with the RF approach was done by clustering compounds in the selection pool based on their fingerprints and identifying cluster centers. Among the pools of molecules selected for activity by either the QMOD or RF method, whether or not active novelty bias was employed, no significant differences in the distributions of experimental activities were found (KS test p-value >0.05 in all pairwise comparisons).

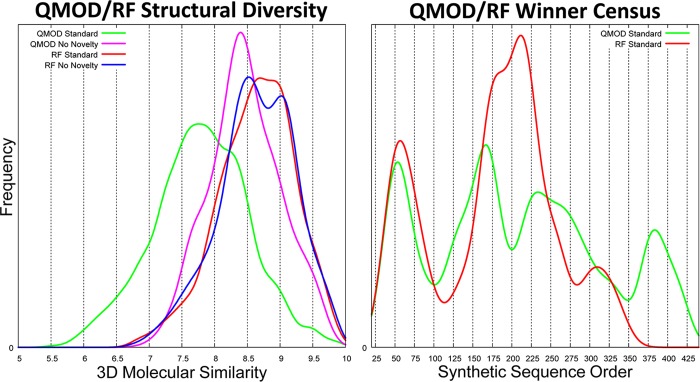
However, the RF approach, either with or without a novelty component within the selection procedure, produced far less diverse pools of winners. Figure 12 (left plot) shows the 3D similarity distributions of pairwise winner comparisons for the two QMOD variants and the two RF variants. Use of diverse fingerprint cluster centers failed to make an impact on the structural diversity of winners for the RF approach (KS test p-value = 0.33). However, while the QMOD standard approach produced a much more diverse pool of winners than the control approach without active novelty selections, the QMOD control approach produced a significantly more structurally diverse pool of winners than either RF procedure (KS p-value ≪ 0.01). The lack of diversity is directly evident in the histogram of synthetic sequence numbers shown in Figure 12 (right plot), with the RF approach exhibiting just two primary peaks corresponding to early- and midproject. The QMOD approach exhibited four peaks, including a set of active inhibitors from late in the project. Compounds 13, 16, and 17 (Figures 9 and 10) all corresponded to the rightmost peak, and all of which were made after any experimentally active selections from the RF procedures.

Figure 12.

Structural diversity among the winners chosen by the RF procedures was much lower than for QMOD (left plot). This lack of diversity stemmed from the lack of diverse selections from the overall project chemical population (right plot).

From the middle peak of winners in the synthetic sequence order was a winner shared between the QMOD and RF approaches (sequence #219). Among the winners from the RF protocol, 55% had extremely high 3D similarity to that single compound (≥8.50), compared with just 12% of the QMOD control winners. The RF procedure was certainly successful in identifying active inhibitors, but the procedure, even with a novelty bias, ended up strongly over-represented with multiple examples of highly similar molecules.

One property of sophisticated regression methods such as random forest learning is that many aspects of the population statistics of a training set are well-modeled in order to reduce errors when tested on new data. The models are explicitly affected by both the prevalence of output values and particular features. In a molecular modeling application, it is frequently the case that one specifically designs molecules that literally reach beyond those whose behavior has been modeled. Consider two design candidate molecules, both of which will turn out to be highly active. Suppose that one of the molecules is highly similar to a pre-existing training molecule in terms of its computed features and one is not. A sophisticated correlative machine such as a random forest predictor will correctly assign a high activity to the former active ligand. But, it will tend to predict a value for the latter ligand that is close to the maximum likelihood value based on the distribution of training molecules’ activities (typically close to the mean or median activity). A midrange prediction for an “unknown” is a wise play in a probabilistic sense, but it reflects no knowledge of the structure–activity relationship. This “near neighbor” effect manifested itself here very directly. The compounds that were correctly ranked highly during the selection process for the RF method tended to be structurally similar to pre-existing active compounds.

To test this directly, we constructed an RF model using the same final training molecules as were used for the final QMOD standard model. Both methods identified active compounds among their top 10 ranked predictions (mean experimental pK_i in both cases of 8.0). However, the 2D structural similarity of the top-ranked RF molecules to the training molecules was much higher than for the QMOD approach (KS p-value ≪ 0.001). This was also seen in the reverse direction. Among the test compounds with pK_i ≥ 7.9 (the most active group of compounds), there was significant variation in the 2D similarity of each compound to its nearest training neighbor. The set of 10 furthest neighbors from the training set were arguably the most interesting compounds from the perspective of requiring an accurate computational prediction. They had a mean experimental activity of 8.2. For these, the RF predictions averaged just 7.0, with just a single compound predicted to have pK_i ≥ 7.5. For QMOD, the predictions averaged 7.8, with 7/10 compounds predicted to have pK_i ≥ 7.5. The full set of training compounds had experimental activity with mean 6.9 ± 0.92 and median activity of 7.1. The RF prediction simply regressed to the wisest guess of activity for the most difficult compounds, making use of information on the population of potencies of the training molecules. The QMOD predictive methodology has no ability to make use of population-based information, but despite that, for these difficult compounds, made predictions that correctly identified most as highly active.

One of the surprising aspects of the results is that multiple approaches yielded quite similar population and correlation statistics in terms of the activities of the molecules chosen under different selection protocols. These approaches would all be reasonably characterized as working well on that basis. However, when considering the characteristics of the structures of the pool of active selected molecules, very sharp differences arose.

Active Learning: Abstract versus Physical Models

What we have described in terms of explicit design bias toward novel compounds is related to other active learning approaches, both in the broader machine learning field as well as within computer-aided drug discovery (see the review by Kell¹⁶ for a broad overview). Warmuth et al.¹⁷ used active learning in combination with support-vector machine (SVM) classifiers to iteratively construct QSAR models with the goal of identifying active compounds quickly. They found that a selection strategy of seeking highly confident actives (similar to our potency selections) was effective for finding active ligands and that a strategy of decision-boundary selections was most effective for improving the QSAR models themselves. The study treated activity as a binary variable and did not structure the selection task temporally to mirror lead optimization. The focus was on activity alone and did not assess questions of structural diversity. Fujiwara et al.¹⁸ studied active learning in the context of virtual screening and considered the question of structural diversity. As with the Warmuth study, compound activity was considered as a binary variable and temporal considerations were not taken into account. They showed advantages for combining a diversity-driven model building strategy with a selection method that sought new ligands on which different models produced maximally divergent predictions.

We have explicitly focused on procedures designed to mimic the constraints of a lead optimization exercise, with real-valued compound activities and temporally ordered chemical space exploration. Our direct comparison of the QMOD approach with a parallel random-forest approach exposed differences that relate to the assumptions underpinning a physical QMOD model compared with an abstract mathematical model. The central assumption made by machine-learning methods such as the random-forest approach or support-vector machines is that training and testing examples are drawn randomly from the same population. So, the distributional characteristics of the activities of molecules and of the structural descriptorsare assumed to be the same. Under conditions where these assumptions are true, such methods can produce reliably accurate predictions, where the distribution of test errors will match estimates made by techniques such as cross-validation. The detailed algorithmic underpinnings of such methods actively “game” these assumptions, in order, for example, to reduce the effect of putative outliers in a training set on learned decision boundaries. However, in a lead optimization exercise, both the structural characteristics and activity profiles of compounds made later will be quite different (by design!) than those of compounds made earlier. With the RF approach, even when making active selection of structurally diverse molecules, no increase in structural diversity among the highly active selected molecules was observed (see Figure 12, red and blue curves in the left-hand plot).

In order for the iterative selection/test/refinement procedure to identify a pool of highly active molecules that are also structurally diverse, two things must be true. First, the selection strategy should incorporate structural diversity. Second, the predictive modeling method must be able to incorporate information from novel compounds so as to correctly identify new compounds that are both active and structurally novel compared with previously known actives. Recall from Figure 6, the structurally novel molecules included significant numbers with low activity. It is not enough merely to seek novelty in a selection procedure. The predictive models must be capable of making risky “bets” in order to discover a pool of highly active molecules that exhibit a wide range of structural characteristics. A pro-diversity bias alone, as with the novelty-biased RF method, does not guarantee a diverse pool of actives at the end of iterative lead optimization. The QMOD approach makes use of each training molecule to come up with a single physical model. A molecule whose high activity and unusual descriptors might be essentially “shrugged off” by an RF or SVM learning machine will be incorporated into a QMOD pocketmol in a manner that maximizes model parsimony while also explaining the high activity. Because the QMOD model is capable of correctly predicting activity values at or beyond the extremum observed during training, and because it may do so for structurally novel molecules, the iterative procedure that combined predictions of potency with selections of novel molecules produced a diverse pool of winners.

Relationship of the Induced Binding Pockets with the GyrB ATP Binding Site

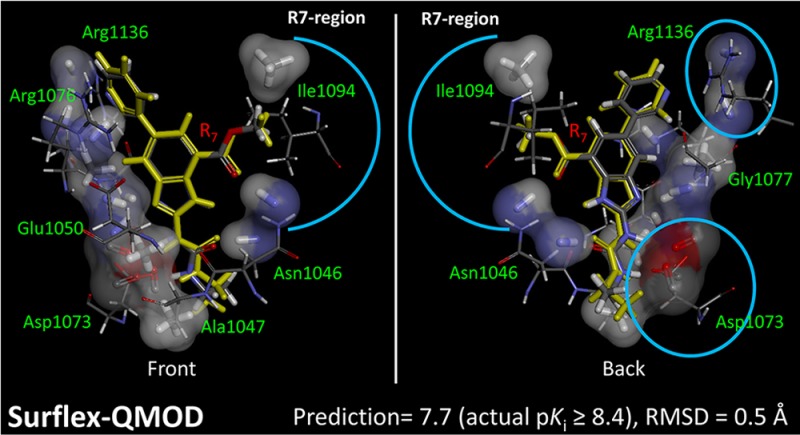
The foregoing discussion has addressed questions about the numerical and structural qualities of the ligands produced by different selection schemes. While there were clearly benefits to the QMOD approach over the pure machine-learning RF method, perhaps the most salient advantage from a molecular design perspective is depicted in Figure 13. The QMOD approach induces the structure of an actual binding pocket, and that pocket has a direct relationship to the true biological active site that was responsible for the activity patterns observed. The QMOD pocket forms a funnel-like shape, with an open area corresponding to where solvent exists. Compound 20 is shown in its predicted conformation along with the experimentally determined one, reflecting no significant deviations and capturing all pendant conformational flips correctly.

Figure 13.

Relationship of the final QMOD standard pocket model to the GyrB binding site. Compound 20 in its optimal predicted QMOD pose (atom color) had rmsd of 0.5 Å from the experimentally determined bound state (yellow). Alignment of the QMOD pocketmol and optimal ligand poses to the protein structure was done with a single alignment transformation that produced a close alignment of the benzimidazole inhibitor core. Configurational deviations are reflected primarily in the pendant moieties.

In total, 11 structures of bound inhibitors were aligned to one another based on protein pocket similarity,¹⁹ and the predicted poses from the QMOD approach were compared to the bound configurations using the alignment from Figure 13. The predicted poses from the QMOD final pocketmol had mean rmsd of 1.2 Å, with all but 2 having rmsd less than 1.5 Å. Note that rms deviation is somewhat difficult to interpret here. Barring a grossly different QMOD prediction of the benzimidazole core, which moved very little in the GyrB structures, the measured rmsd would tend to be relatively small. Another measurement of concordance between the pocketmol and protein compares the contact patterns for each ligand to the pocketmol or to the protein. The degree of concordance can be quantified by permutation of atom numbers. Given that a particular set of a ligand’s atoms have contact with the pocketmol and another set has contact with the protein, we can count the number of contacts that are shared. If we randomize the atom numbering order many times for the pocketmol-bound ligand, we can count the number of times that the number of shared contacts is greater than or equal to the observed number in order to estimate the likelihood of this occurring by chance. In all but three of the eleven cases, there was a statistically significant relationship in the contact patterns (p < 0.05).

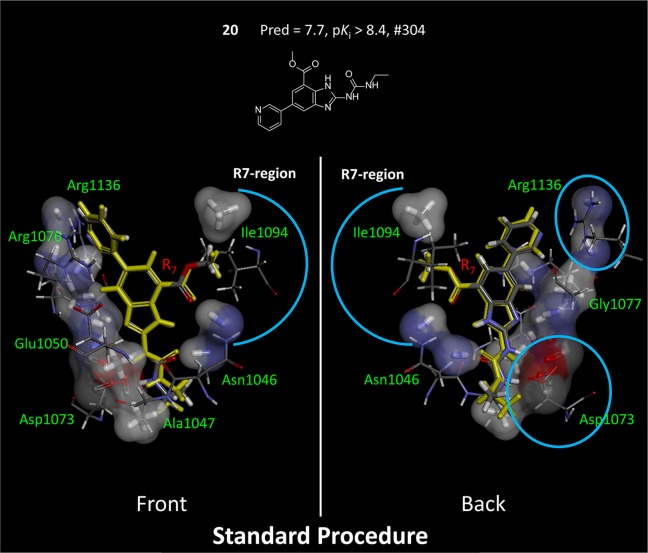
Figure 14 shows additional detail, illustrating the direct correspondence between pocketmol probes and key moieties on the protein. The left-hand view highlights the reason behind the conformational choice for the methyl-ester substituent of compound 20, which was correctly predicted (marked with a blue arc). The carbonyl ester oxygen makes a hydrogen bond with the N–H probe of the pocketmol, which parallels the same interaction with Asn-1046. The terminal methyl of the ester makes a hydrophobic interaction with a methane pocketmol probe, paralleling an interaction with Ile-1094. The right-hand view highlights two carbonyl probes that mimic the effect of Asp-1073 and two N–H probes that mimic Arg-1136. This degree of qualitative correspondence between pocketmol and protein is typical of our previous work.^2,3

Figure 14.

QMOD standard procedure yielded a pocket model where there was a direct correspondence of many probes to particular atoms in the actual GyrB binding pocket. Pocketmol probes that do not interact with compound 20 (atom color) have been omitted from the display for clarity, and the protein has been trimmed to highlight areas of correspondence. The two views shown are flipped front to back.

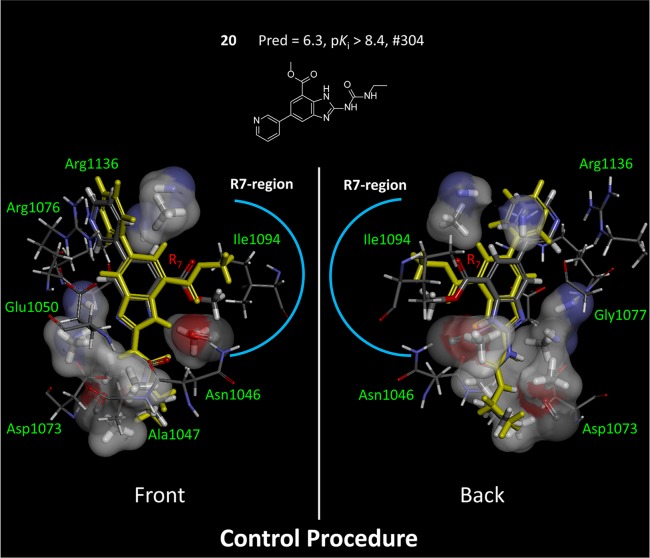
Figure 15 shows the analogous depiction of compound 20, but using the final QMOD pocketmol that arose from the control procedure. Recall that the structural variation of the final pool of active selected ligands was much reduced and that the spatial probing of the binding pocket bordered by Asn-1046 and Ile-1094 was shallow (see Figure 11). The prediction for 20 was both numerically poor (low by 2.1 log units) and predicted the incorrect orientation of the 7-position methyl ester. The induced pocket here was unable to correctly accommodate the substituent, also showing a shift of the central scaffold away from its optimal position. While there were areas of good correspondence, especially with respect to the surface shape of the base of the binding pocket, the model induction process is sharply limited by the set of selected compounds. For the 11 inhibitors for which we had bound structures, just 3/11 had concordant contact patterns (compared with 8/11 for the QMOD standard predictions). In operational use of such modeling methods during lead optimization, mindful production of chemical variations that explicitly probe the “edges” of a model can produce significant improvements in the correspondence of refined models with biological reality.

Figure 15.

QMOD pocket model that resulted from the procedure lacking an explicit novelty bias produced a poor prediction for compound 20 (atom color). The depiction here is analogous to that from Figure 14.

For completeness, because we had bona fide structures of the GyrB binding pocket, we also made a comparison of the QMOD predictions to docking and scoring the final pool of unselected molecules. Using a single structure and the score of the top-ranked docking pose for each inhibitor did not produce a significant rank correlation. It is conceivable that a more sophisticated procedure such as MM-PBSA²⁰ might have yielded a reasonable correlation. Brown and Muchmore reported an average RMSE for predicted pK_i using MM-PBSA on three targets of 0.75 (range 0.66–0.89) using linearly rescaled predictions to account for extreme slope and intercept deviations between computation and experimental values. The QMOD final standard model yielded 0.76 RMSE with no scaling correction on the 317 remaining unselected molecules, which is clearly comparable. Molecules pairs whose activity was different by 0.5 pK_i units or greater were correctly ranked more than 70% of the time (p ≪ 0.001). Rank correlation of this quality is challenging because over 80% of the experimental activity values fell within 1.5 log units of one another and over 90% within 2.0 units. It is encouraging that a method such as QMOD, with no information of any kind regarding either the bound configuration of ligands or of the actual binding site composition and geometry, could produce predictions of both activity and bound pose that are competitive with sophisticated structure-based methods.

Conclusions

We believe that this study has approached the QSAR modeling question in a novel manner. We explored how different computational selection strategies shaped and produced different synthetic trajectories. There were four primary results. First, the iterative QMOD procedure rapidly converged on models that reliably identified highly active molecules. Second, explicit computational selection of novel molecules directly lead to a much more structurally diverse pool of active inhibitors, despite not producing a pool with a different distribution of experimental activities than a control procedure with no novelty focus. Third, the induced binding site model showed strong concordance with the experimentally determined binding site, both in terms of absolute predicted poses as well as ligand/pocket contact patterns. Fourth, direct comparison with descriptor-based QSAR methods showed that while such models yielded similar distributions of activity among selected molecules, the structural diversity of selected active molecules was much lower than for QMOD. QMOD identified examples of active molecules across the entire arc of the project’s chemical exploration, while the descriptor-based approaches instead produced many examples of highly similar minor variants clustered around the midpoint of the project’s history.

There are two major lessons to be learned from this work, which we hope to further validate on additional systems in the future. First, there appears to be a significant hidden cost to reliance upon molecular design strategies that do not actively seek to probe new chemical functionality in a spatial sense. While such strategies may well identify compounds with desirable properties, they may completely miss the identification of entire classes of active compounds. Here, for example, strong activity against GyrB and ParE was exhibited by compounds discovered through the selection procedure that sought three-dimensional structural novelty in order to test the physical boundaries of the evolving models. Second, statistical regression methods whose fundamental basis for prediction relies upon correlations between features and desired output values impose hidden costs. They do so by being strongly dependent upon the existence of near-neighbors with known activity in order to accurately predict a new compound to have similar activity. In molecular activity optimization, effort is often placed on design goals toward or even beyond the extreme end of the distribution of known molecular activities. Truly active molecules that are structurally novel in the descriptor space being used by a correlative machine will be underpredicted as a consequence of the gaming strategy employed by statistical regression methods.

The issues of confirmation bias and correlation fallacies discussed in a recent perspective⁴ appear naturally in the iterative application of predictive modeling for design of active molecules. Given a method that depends on noncausative correlations to predict activity, selection of the molecules predicted to be active will tend to automatically self-confirm, because only those candidate molecules that are highly similar to known molecules with high activity will tend to be top-ranked. The structurally novel compounds that would have been shown to be active remain invisible in practice, because they will have been predicted to have middling activity. In typical machine-learning problems, inductive bias issues will show up in the distribution of prediction errors on different types of test objects. In the case of medicinal chemistry lead optimization, such bias issues may altogether suppress the synthesis of molecules that do not confirm the hypothesis, so no errors may become apparent.

By making use of a different molecular selection strategies, each of which is nominally equally accurate in aggregate behavior, very different outcomes will arise from repeated temporal iteration. The resulting molecules having the high activity sought during optimization will reflect the hidden or explicit biases embedded in the predictive modeling approaches. An approach whose basis for prediction mimics the protein ligand binding process, coupled with an explicit selection strategy designed to expand model coverage, will tend to identify a diverse pool of molecules. The structural diversity will most likely manifest itself in properties that were not directly optimized. When making use of purely correlative learning machines, the unseen cost can manifest itself as a numerous but narrow pool of molecules. Given the challenging problem of drug discovery, we would argue that generation of a diverse pool is generally the more desirable outcome.

Experimental Section

Molecular and Activity Data

Overall, 426 compounds formed the data set for the study. All were previously synthesized and tested as part of a lead optimization project.⁵ Three-dimensional molecule structures were provided as an SDF file. The standard Surflex procedure was used to protonate, ring-search, and minimize the ligands (“sf-sim +misc_ring -misc_outconfs 5 +fp prot gyrasemols.sdf gyr”). This resulted in up to five conformations per inhibitor, which were then provided to the QMOD procedure, in which all molecular poses were produced. Assays were performed as reported in Charifson et al.,⁵ and assay values were converted into molar pK_i units (9.0 being equivalent to a K_i of 1 nM). The molecules were named based on the actual lead optimization project’s synthetic sequence order (e.g., “gyrase000001 to gyrase000426”).

Computational Procedures

The QMOD procedure is fully automatic, requiring no human choice points. For this work, default parameters were used, employing Surflex QMOD version 1.5. There were two significant algorithmic introductions in this version, compared with that reported in the last methodologically focused study.³ First, the notion of model parsimony has been included directly in the search for optimal binding pocket models. Second, a procedure for computing molecular novelty for candidate models was implemented (see Figure 5).

QMOD defines model parsimony based on the degree to which training molecules that have similar potencies also quantitatively share similar optimal bound poses. This is expressed in terms of a weighted sum of pairwise similarities of all final ligand poses, where molecule pairs with similar activity receive higher weight than those with different activity values. Parsimony was introduced as a means to choose from among models of nominally equivalent residual training errors.³ Here, model parsimony has been made part of the model generation process itself. The procedure that is used to select probes for inclusion in a pocketmol simultaneously optimizes the fit to experimental data as well as model parsimony. The standard procedure for producing a de novo pocketmol requires a single command (“sf-qmod.exe runsetup SetupFile”) that produces a script that will generate initial alignment hypotheses, full alignments of training ligands, and final pocketmols. The setup file contains information on pathnames to training ligands and their activities, which ligands to use for hypothesis generation, and modifications to default parameters for model building if desired. By default, three models are generated, each using different probe densities. The model with the highest parsimony was selected for iterative refinement.

The initial induced model was then used for testing the next window of molecules and selections were made automatically based on two criterion: molecules predicted with high confidence to be the most active, and molecules predicted as the most novel. The transition between rounds involved the addition of selected molecules to the training data and a series of automated steps required for preparation of the next model refinement round (as with initial model building, QMOD produces a script based on the list of new molecules and activities). The automated preparation involved compression of the training ligand poses explored during model induction and testing. The compression scheme seeks the highest scoring poses against the pocketmol while enforcing conformational diversity among the retained poses. As with the initial model, alignments are produced for the new molecules along with a corresponding pool of new probes. The new molecules’ alignments and the new probes are added to the pose and probe pools, respectively. The next round of model refinement begins with the previous optimal pocketmol and repeats the standard learning procedure using the amended probe and pose pools.

Novelty is quantified in a three-dimensional sense by measuring the degree to which a new molecule explores the space of the binding pocket with new chemical functionality. Statistics are computed based on the interactions between the explored pool of training ligand poses with the pocketmol and the unoccupied space near the pocketmol (termed the antipocketmol). The explored pool of training ligand poses encompasses the final optimal poses of each training ligand and also includes all poses for each that are highly 3D similar to the final pose of any training molecule. The antipocketmol is constructed such that it borders the explored pose pool and provides a symmetrical nonoverlapping representation of the pocketmol, highlighting regions of the binding pocket that have not been explored or modeled. For each pocketmol and antipocketmol probe, the mean and standard deviation of scores of the explored training pose pool are computed. These statistics form a baseline interaction profile of the induced model for each probe. Upon fitting a new test molecule into the pocketmol, pose variations that share high 3D similarity to any of the optimal training poses are cached, and the mean score for each probe is computed. Molecular novelty for a test molecule is the average of the Z-scores for the test molecule probe mean scores, using the statistics derived from the training data to provide the mean and standard deviation for each probe’s Z-score normalization. So, molecules that interact with the pocketmol and surrounding region differently than the training ligands receive a higher novelty score than otherwise. This definition of novelty is highly context dependent and quite different from pure molecular similarity computations. For example, a single methyl group addition to a training molecule will generally have very low impact on a similarity computation. However, if the methyl group pushes into unexplored space (which may or may not contain a pocketmol probe), the novelty score will tend to be high.

By default (and for all experiments reported), QMOD makes use of the highest-scoring alignment hypothesis upon which to base alignments of other training ligands. Additional controls were carried out using alternative hypothesis alignments used for seeding the initial ligand alignment during de novo model induction. We identified the five most dissimilar hypothesis alignments (data not shown) from the original alignment used in the standard run (see Figure 3 Panel A) and repeated the iterative modeling protocol as described above (see Figure 1). Results from these alternative starting points revealed similar performance with respect to enrichment of highly active molecules from those compounds selected, convergence on selecting active inhibitors over time, and identifying structurally diverse active compounds when actively selecting for structurally novel molecules. QMOD’s performance proved to be robust in the presence of alternate initial alignment conditions.

As a control procedure, we employed the random forest machine learning technique.¹³⁻¹⁵ It is an ensemble classification approach that constructs multiple decision trees using a random sampling approach in order to minimize generalization errors. We used the Random Forest method implemented in version 4.6–2 of the randomForest package for the R software (version 2.12.2). MDL 320 fingerprints²¹ were generated using the fingerprint packages implemented by Mesa Analytics (www.mesaac.com). The iterative procedure paralleled that used for QMOD, making use of default parameters for the RF learning procedure. To mimic the novelty procedure, we performed K-means clustering (with K = 5) among the pool of molecules from which selections could be made and chose the cluster centers. This provided diverse structures according to the features employed by the classifier.

Glossary

Abbreviations

QMOD

Surflex Quantitative Modeling

GyrB

DNA gyrase

ParE

Topisomerase IV

RF

random forest classifier

SVM

support-vector machine

The authors declare the following competing financial interest(s): Dr. Jain has a financial interest in BioPharmics LLC, a biotechnology company whose main focus is in the development of methods for computational modeling in drug discovery. Tripos Inc. has exclusive commercial distribution rights for the Surflex platform, licensed from BioPharmics LLC.

Funding Statement

National Institutes of Health, United States