Abstract
In this paper, we describe some central mathematical problems in medical imaging. The subject has been undergoing rapid changes driven by better hardware and software. Much of the software is based on novel methods utilizing geometric partial differential equations in conjunction with standard signal/image processing techniques as well as computer graphics facilitating man/machine interactions. As part of this enterprise, researchers have been trying to base biomedical engineering principles on rigorous mathematical foundations for the development of software methods to be integrated into complete therapy delivery systems. These systems support the more effective delivery of many image-guided procedures such as radiation therapy, biopsy, and minimally invasive surgery. We will show how mathematics may impact some of the main problems in this area, including image enhancement, registration, and segmentation.
Keywords: Medical imaging, artificial vision, smoothing, registration, segmentation
1. Introduction
Medical imaging has been undergoing a revolution in the past decade with the advent of faster, more accurate, and less invasive devices. This has driven the need for corresponding software development, which in turn has provided a major impetus for new algorithms in signal and image processing. Many of these algorithms are based on partial differential equations and curvature driven flows, which will be the main topics of this survey paper.
Mathematical models are the foundation of biomedical computing. Basing those models on data extracted from images continues to be a fundamental technique for achieving scientific progress in experimental, clinical, biomedical, and behavioral research. Today, medical images are acquired by a range of techniques across all biological scales which go far beyond the visible light photographs and microscope images of the early 20th century. Modern medical images may be considered to be geometrically arranged arrays of data samples which quantify such diverse physical phenomena as the time variation of hemoglobin deoxygenation during neuronal metabolism or the diffusion of water molecules through and within tissue. The broadening scope of imaging as a way to organize our observations of the biophysical world has led to a dramatic increase in our ability to apply new processing techniques and to combine multiple channels of data into sophisticated and complex mathematical models of physiological function and dysfunction.
A key research area is the formulation of biomedical engineering principles based on rigorous mathematical foundations in order to develop general-purpose software methods that can be integrated into complete therapy delivery systems. Such systems support the more effective delivery of many image-guided procedures such as biopsy, minimally invasive surgery, and radiation therapy.
In order to understand the extensive role of imaging in the therapeutic process and to appreciate the current usage of images before, during, and after treatment, we focus our analysis on four main components of image-guided therapy (IGT) and image-guided surgery (IGS): localization, targeting, monitoring, and control. Specifically, in medical imaging we have four key problems:
Segmentation - automated methods that create patient-specific models of relevant anatomy from images;
Registration - automated methods that align multiple data sets with each other;
Visualization - the technological environment in which image-guided procedures can be displayed;
Simulation - softwares that can be used to rehearse and plan procedures, evaluate access strategies, and simulate planned treatments.
In this paper, we will consider only the first two problem areas. However, it is essential to note that in modern medical imaging, we need to integrate these technologies into complete and coherent image-guided therapy delivery systems and validate these integrated systems using performance measures established in particular application areas.
We should note that in this survey we touch upon only those aspects of the mathematics of medical imaging reflecting the personal tastes (and prejudices) of the authors. Indeed, we do not discuss a number of very important techniques, such as wavelets, which have had a significant impact on imaging and signal processing; see [59] and the references therein. Several articles and books are available which describe various mathematical aspects of imaging processing, such as [66] (segmentation), [83] (curve evolution), and [70], [87] (level set methods).
Finally, it is extremely important to note that all the mathematical algorithms which we sketch lead to interactive procedures. This means that in each case there is a human user in the loop (typically a clinical radiologist) who is the ultimate judge of the utility of the procedure and who tunes the parameters either on- or off-line. Nevertheless, there is a major need for further mathematical techniques which lead to more automatic and easier-to-use medical procedures. We hope that this paper may facilitate a dialogue between the mathematical and medical imaging communities.
2. Outline
We briefly outline the subsequent sections of this paper.
Section 3 reviews some of the key imaging modalities. Each one has certain advantages and disadvantages, and algorithms tuned to one device may not work as well on another device. Understanding the basic physics of the given modality is often very useful in forging the best algorithm.
In Section 4, we describe some of the relevant issues in computer vision and image processing for the medical field as well as sketch some of the partial differential equation (PDE) methods that researchers have proposed to deal with these issues.
Section 5 is the heart of this survey paper. Here we describe some of the main mathematical and engineering problems connected with image processing in general and medical imaging in particular. These include image smoothing, registration, and segmentation (see Sections 5.1, 5.2, and 5.3). We show how geometric partial differential equations and variational methods may be used to address some of these problems as well as illustrate some of the various methodologies.
Finally, in Section 6, we summarize the survey as well as point out some possible future research directions.
3. Medical imaging
3.1. Generalities
In 1895, Roentgen discovered X-rays and pioneered medical imaging. His initial publication [82] contained a radiograph (i.e., an X-ray generated photograph) of Mrs. Roentgen’s hand; see Figure 3.1(b). For the first time, it was possible to visualize non-invasively (i.e., not through surgery) the interior of the human body. The discovery was widely publicized in the popular press, and an “X-ray mania” immediately seized Europe and the United States [30], [80]. Within only a few months, public demonstrations were organized, commercial ventures created and innumerable medical applications investigated; see Figure 3.1(a).The field of radiography was born with a bang!1
Figure 3.1.
X-ray radiography at the end of the 19th century.
Today, medical imaging is a routine and essential part of medicine. Pathologies can be observed directly rather than inferred from symptoms. For example, a physician can non-invasively monitor the healing of damaged tissue or the growth of a brain tumor and determine an appropriate medical response. Medical imaging techniques can also be used when planning or even while performing surgery. For example, a neurosurgeon can determine the “best” path in which to insert a needle and then verify in real time its position as it is being inserted.
3.2. Imaging Modalities
Imaging technology has improved considerably since the end of the 19th century. Many different imaging techniques have been developed and are in clinical use. Because they are based on different physical principles [41], these techniques can be more or less suited to a particular organ or pathology. In practice they are complementary in that they offer different insights into the same underlying reality. In medical imaging, these different imaging techniques are called modalities.
Anatomical modalities provide insight into the anatomical morphology. They include radiography, ultrasonography or ultrasound (US, Section 3.2.1), computed tomography (CT, Section 3.2.2), and magnetic resonance imagery (MRI, Section 3.2.3). There are several derived modalities that sometimes appear under a different name, such as magnetic resonance angiography (MRA, from MRI), digital subtraction angiography (DSA, from X-rays), computed tomography angiography (CTA, from CT), etc.
Functional modalities, on the other hand, depict the metabolism of the underlying tissues or organs. They include the three nuclear medicine modalities, namely, scintigraphy, single photon emission computed tomography (SPECT) and positron emission tomography (PET, Section 3.2.4), as well as functional magnetic resonance imagery (fMRI). This list is not exhaustive, as new techniques are being added every few years as well [13]. Almost all images are now acquired digitally and integrated in a computerized picture archiving and communication system (PACS).
In our discussion below, we will give only very brief descriptions of some of the most popular modalities. For more details, a very readable treatment (together with the underlying physics) may be found in the book [43].
3.2.1. Ultrasonography (1960s)
In this modality a transmitter sends high-frequency sound waves into the body, where they bounce off the different tissues and organs to produce distinctive patterns of echoes. These echoes are acquired by a receiver and forwarded to a computer that translates them into an image on a screen. Because ultrasound can distinguish subtle variations among soft, fluid-filled tissues, it is particularly useful in imaging the abdomen. In contrast to X-rays, ultrasound does not damage tissues with ionizing radiation. The great disadvantage of ultrasonography is that it produces very noisy images. It may therefore be hard to distinguish smaller features (such as cysts in breast imagery). Typically quite a bit of image preprocessing is required. See Figure 3.2(a).
Figure 3.2.
Examples of different image modalities.
3.2.2. Computed Tomography (1970s)
In computed tomography (CT), a number of 2D radiographs are acquired by rotating the X-ray tube around the body of the patient. (There are several different geometries for this.) The full 3D image can then be reconstructed by computer from the 2D projections using the Radon transform [40]. Thus CT is essentially a 3D version of X-ray radiography and therefore offers high contrast between bone and soft tissue and low contrast between different soft tissues. See Figure 3.2(b). A contrast agent (some chemical solution opaque to the X-rays) can be injected into the patient in order to artificially increase the contrast among the tissues of interest and so enhance image quality. Because CT is based on multiple radiographs, the deleterious effects of ionizing radiation should be taken into account (even though it is claimed that the dose is sufficiently low in modern devices so that this is probably not a major health risk issue). A CT image can be obtained within one breath hold, which makes CT the modality of choice for imaging the thoracic cage.
3.2.3. Magnetic Resonance Imaging (1980s)
This technique relies on the relaxation properties of magnetically excited hydrogen nuclei of water molecules in the body. The patient under study is briefly exposed to a burst of radio-frequency energy, which, in the presence of a magnetic field, puts the nuclei in an elevated energy state. As the molecules undergo their normal, microscopic tumbling, they shed this energy into their surroundings in a process referred to as relaxation. Images are created from the difference in relaxation rates in different tissues. This technique was initially known as nuclear magnetic resonance (NMR), but the term “nuclear” was removed to avoid any association with nuclear radiation.2 MRI utilizes strong magnetic fields and non-ionizing radiation in the radio frequency range and according to current medical knowledge, is harmless to patients. Another advantage of MRI is that soft tissue contrast is much better than with X-rays, leading to higher-quality images, especially in brain and spinal cord scans. See Figure 3.2(c). Refinements have been developed, such as functional MRI (fMRI), which measures temporal variations (e.g., for detection of neural activity), and diffusion MRI, which measures the diffusion of water molecules in anisotropic tissues such as white matter in the brain.
3.2.4. Positron Emission Tomography (1990s)
The patient is injected with radioactive isotopes that emit particles called positrons (anti-electrons). When a positron meets an electron, the collision produces a pair of gamma ray photons having the same energy but moving in opposite directions. From the position and delay between the photon pair on a receptor, the origin of the photons can be determined. While MRI and CT can only detect anatomical changes, PET is a functional modality that can be used to visualize pathologies at the much finer molecular level. This is achieved by employing radioisotopes that have different rates of intake for different tissues. For example, the change of regional blood flow in various anatomical structures (as a measure of the injected positron emitter) can be visualized and relatively quantified. Since the patient has to be injected with radioactive material, PET is relatively invasive. The radiation dose however is similar to a CT scan. Image resolution may be poor and major preprocessing may be necessary. See Figure 3.2(d).
4. Mathematics and imaging
Medical imaging needs highly trained technicians and clinicians to determine the details of image acquisition (e.g., choice of modality, of patient position, of an optional contrast agent, etc.), as well as to analyze the results. The dramatic increase in availability, diversity, and resolution of medical imaging devices over the last 50 years threatens to overwhelm these human experts.
For image analysis, modern image processing techniques have therefore become indispensable. Artificial systems must be designed to analyze medical datasets either in a partially or even a fully automatic manner. This is a challenging application of the field known as artificial vision (see Section 4.1). Such algorithms are based on mathematical models (see Section 4.2). In medical image analysis, as in many practical mathematical applications, numerical simulations should be regarded as the end product. The purpose of the mathematical analysis is to guarantee that the constructed algorithms will behave as desired.
4.1. Artificial Vision
Artificial Intelligence (AI) was initiated as a field in the 1950’s with the ambitious (and so-far unrealized) goal of creating artificial systems with human-like intelligence.3 Whereas classical AI had been mostly concerned with symbolic representation and reasoning, new subfields were created as researchers embraced the complexity of the goal and realized the importance of sub-symbolic information and perception. In particular, artificial vision [32, 44, 39, 91] emerged in the 1970s with the more limited goal to mimic human vision with man-made systems (in practice, computers).
Vision is such a basic aspect of human cognition that it may superficially appear somewhat trivial, but after decades of research the scientific understanding of biological vision remains extremely fragmentary. To date, artificial vision has produced important applications in medical imaging [18] as well as in other fields, such as Earth observation, industrial automation, and robotics [91].
The human eye-brain system evolved over tens of millions of years, and at this point no artificial system is as versatile and powerful for everyday tasks. In the same way that a chess-playing program is not directly modelled after a human player, many mathematical techniques are employed in artificial vision that do not pretend to simulate biological vision. Artificial vision systems will therefore not be set within the natural limits of human perception. For example, human vision is inherently two dimensional.4 To accommodate this limitation, radiologists must resort to visualizing only 2D planar slices of 3D medical images. An artificial system is free of that limitation and can “see” the image in its entirety. Other advantages are that artificial systems can work on very large image datasets, are fast, do not suffer from fatigue, and produce repeatable results. Because artificial vision system designers have so far been unsuccessful in incorporating high-level understanding of real-life applications, artificial systems typically complement rather than replace human experts.
4.2. Algorithms and PDEs
Many mathematical approaches have been investigated for applications in artificial vision (e.g., fractals and self-similarity, wavelets, pattern theory, stochastic point process, random graph theory; see [42]). In particular, methods based on partial differential equations (PDEs) have been extremely popular in the past few years [20, 35]. Here we briefly outline the major concepts involved in using PDEs for image processing.
As explained in detail in [17], one can think of an image as a map ; i.e., to any point x in the domain , I associates a “color” I(x) in a color space . For ease of presentation we will mainly restrict ourselves to the case of a two-dimensional grayscale image which we can think of as a function from a domain to the unit interval .
The algorithms all involve solving the initial value problem for some PDE for a given amount of time. The solution to this PDE can be either the image itself at different stages of modification or some other object (such as a closed curve delineating object boundaries) whose evolution is driven by the image.
For example, introducing an artificial time t, the image can be deformed according to
| (4.1) |
where is the evolving image, is an operator which characterizes the given algorithm, and the initial condition is the input image I0. The processed image is the solution I(x, t) of the differential equation at time t. The operator usually is a differential operator, although its dependence on I may also be nonlocal.
Similarly, one can evolve a closed curve representing the boundaries of some planar shape (Γ need not be connected and could have several components). In this case, the operator specifies the normal velocity of the curve that it deforms. In many cases this normal velocity is a function of the curvature κ of Γ and of the image I evaluated on Γ. A flow of the form
| (4.2) |
is obtained, where N is the unit normal to the curve Γ.
Very often, the deformation is obtained as the steepest descent for some energy functional. For example, the energy
| (4.3) |
and its associated steepest descent, the heat equation,
| (4.4) |
correspond to the classical Gaussian smoothing (see Section 5.1.1).
The use of PDEs allows for the modelling of the crucial but poorly understood interactions between top-down and bottom-up vision.5 In a variational framework, for example, an energy is defined globally, while the corresponding operator F will influence the image locally. Algorithms defined in terms of PDEs treat images as continuous rather than discrete objects. This simplifies the formalism, which becomes grid independent. On the other hand, models based on nonlinear PDEs may be much harder to analyze and implement rigorously.
5. Imaging problems
Medical images typically suffer from one or more of the following imperfections:
low resolution (in the spatial and spectral domains),
high level of noise,
low contrast,
geometric deformations,
presence of imaging artifacts.
These imperfections can be inherent to the imaging modality (e.g., X-rays offer low contrast for soft tissues, ultrasound produces very noisy images, and metallic implants will cause imaging artifacts in MRI) or the result of a deliberate trade-off during acquisition. For example, finer spatial sampling may be obtained through a longer acquisition time. However, that would also increase the probability of patient movement and thus blurring. In this paper, we will be interested only in the processing and analysis of images, and we will not be concerned with the challenging problem of designing optimal procedures for their acquisition.
Several tasks can be performed (semi)-automatically to support the eye-brain system of medical practitioners. Smoothing (Section 5.1) is the problem of simplifying the image while retaining important information. Registration (Section 5.2) is the problem of fusing images of the same region acquired from different modalities or putting in correspondence images of one patient at different times or of different patients. Finally, segmentation (Section 5.3) is the problem of isolating anatomical structures for quantitative shape analysis or visualization. The ideal clinical application should be fast, robust with regards to image imperfections, simple to use, and as automatic as possible. The ultimate goal of artificial vision is to imitate human vision, which is intrinsically subjective.
Note that for ease of presentation, the techniques we present below are applied to two-dimensional grayscale images. The majority of them, however, can be extended to higher dimensions (e.g., vector-valued volumetric images).
5.1. Image Smoothing
Smoothing is the action of simplifying an image while preserving important information. The goal is to reduce noise or useless details without introducing too much distortion so as to simplify subsequent analysis.
It was realized that the process of smoothing is closely related to that of pyramiding, which led to the notion of scale space. This was introduced by Witkin [97] and formalized in such works as [52, 46]. Basically, a scale space is a family of images {St | t ≥ 0} in which S0 = I is the original image and St, t > 0, represent the different levels of smoothing for some parameter t. Larger values of t correspond to more smoothing.
In Alvarez et al. [2], an axiomatic description of scale space was proposed. These axioms, which describe many of the methods in use, require that the process Tt which computes the image St = Tt[I] from I should have the following properties:
Causality/Semigroup: T0[I] ≡ I and for all t, s ≥ 0, Tt[Ts[I]] = Tt+s[I]. (In particular, if the image St has been computed, all further smoothed images {Ss | s ≥ t} can be computed from St, and the original image is no longer needed.)
Generator: The family St = Tt[I] is the solution of an initial value problem ∂tSt = A[St], in which A is a non-linear elliptic differential operator of second order.
Comparison Principle: If for all , then pointwise on . This property is closely related to the Maximum Principle for parabolic PDEs.
Euclidean invariance: The generator A and the maps T t commute with Euclidean transformations6 acting on the image S0.
The requirement that the generator A of the semigroup be an elliptic differential operator may seem strong and even arbitrary at first, but it is argued in [2] that the semigroup property, the Comparison Principle, and the requirement that A act locally make this axiom quite natural. One should note that already in [52], it is shown that in the linear case a scale space must be defined by the linear heat equation. (See our discussion below.)
5.1.1. Naive, linear smoothing
If is a given image which contains a certain amount of noise, then the most straightforward way of removing this noise is to approximate I by a mollified function S; i.e., one replaces the image function I by the convolution Sσ = Gσ * I, where
| (5.1) |
is a Gaussian kernel with covariance the diagonal matrix σ2 Id. This mollification will smear out fluctuations in the image on scales of order σ and smaller. This technique had been in use for quite a while before it was realized7 by Koenderink [52] that the function S2σ = G2σ * I satisfies the linear diffusion equation
| (5.2) |
Thus, to smooth the image I the diffusion equation (5.2) is solved with initial data S0 = I. The solution St at time t is then the smoothed image.
The method of smoothing images by solving the heat equation has the advantage of simplicity. There are several effective ways of computing the solution St from a given initial image S0 = I, e.g., using the fast Fourier transform. Linear Gaussian smoothing is Euclidean invariant and satisfies the Comparison Principle. However, in practice one finds that Gaussian smoothing blurs edges. For example, if the initial image S0 = I is the characteristic function of some smoothly bounded set so that it represents a black and white image with no gray regions, then for all but very small t > 0 the image St will resemble the original image in which the sharp boundary ∂Ω has been replaced with a fuzzy region of varying shades of gray. (See Section 5.3.1 for a discussion on edges in computer vision.)
Figure 5.1(a) is a typical MRI brain image. Specular noise is usually present in such images, and so edge-preserving noise removal is essential. The result of Gaussian smoothing implemented via the linear heat equation is shown in Figure 5.1(b). The edges are visibly smeared. Note that even though 2D slices of the 3D image are shown to accommodate human perception, the processing was actually performed in 3D and not independently on each 2D slice.
Figure 5.1.
Linear smoothing smears the edges.
We now discuss several methods which have been proposed to avoid this edge blurring effect while smoothing images.
5.1.2. Anisotropic smoothing
Perona and Malik [74] replaced the linear heat equation with the non-linear diffusion equation
| (5.3) |
with
Here g is a non-negative function for which . The idea is to slow down the diffusion near edges, where the gradient |∇S| is large. (See Sections 5.3.1 and 5.3.2 for a description of edge detection techniques.)
The matrix aij of diffusion coefficients has two eigenvalues: one, λ∥, for the eigenvector ∇S, and one, λ⊥, for all directions perpendicular to ∇S. They are
While λ⊥ is always non-negative, λ∥ can change sign. Thus the initial value problem is ill-posed if sg′(s) + g(s) < 0, i.e., if sg(s) is decreasing, and one actually wants g(s) to vanish very quickly as s → ∞ (e.g., g(s) = e−s). Even if solutions St could be constructed in the ill-posed regime, they would vary strongly and unpredictably under tiny perturbations in the initial image S0 = I, while it is not clear if the Comparison Principle would be satisfied.
In spite of these objections, numerical experiments [74] have indicated that this method actually does remove a significant amount of noise before edges are smeared out very much.
5.1.3. Regularized Anisotropic Smoothing
Alvarez, Lions and Morel [3] proposed a class of modifications of the Perona-Malik scheme which result in well-posed initial value problems. They replaced (5.3) with
| (5.4) |
which can be written as
| (5.5) |
with
Thus the stopping function g in (5.3) has been set equal to g(s) = 1/s, and a new stopping function h is introduced. In addition, a smoothing kernel Gσ which averages ∇S in a region of order σ is introduced. One could let Gσ be the standard Gaussian (5.1), but other choices are possible. In the limiting case σ ↘ 0, in which Gσ * ∇S simply becomes ∇S, a PDE is obtained.
5.1.4. Level Set Flows
Level set methods for the implementation of curvature driven flows were introduced by Osher and Sethian [71] and have proved to be a powerful numerical technique with numerous applications; see [70, 87] and the references therein.
Equation (5.4) can be rewritten in terms of the level sets of the image S. If S is smooth, and if c is a regular value of (in the sense of Sard’s Theorem), then is a smooth curve in . It is the boundary of the region with gray level c or less. As time goes by, the curve Γt(c) will move about, and as long as it is a smooth curve one can define its normal velocity V by choosing any local parametrization and declaring V to be the normal component of ∂tΓ.
If the normal component is chosen to be in the direction of ∇S (rather than −∇S), then
The curvature of the curve Γt(c) (also in the direction of ∇S) is
| (5.6) |
Thus (5.4) can be rewritten as
which in the special case h ≡ 1 reduces to the curve shortening equation8
| (5.7) |
So if h ≡ 1 and if is a family of images which evolve by (5.4), then the level sets Γt(c) evolve independently of each other.
This leads to the following simple recipe for noise removal: given an initial image S0 = I, let it evolve so that its level curves (St)−1(c) satisfy the curve shortening equation (5.7). For this to occur, the function S should satisfy the Alvarez-Lions-Morel equation (5.4) with h ≡ 1, i.e.,
| (5.8) |
It was shown by Evans and Spruck [25] and Chen, Giga and Goto [21] that, even though this is a highly degenerate parabolic equation, a theory of viscosity solutions can still be constructed.
The fact that level sets of a solution to (5.8) evolve independently of each other turns out to be desirable in noise reduction, since it eliminates the edge blurring effect of the linear smoothing method. E.g., if I is a characteristic function, then St will also be a characteristic function for all t > 0.
The independent evolution of level sets also implies that besides obeying the axioms of Alvarez, Lions and Morel [2] mentioned above, this method also satisfies their axiom on:
Gray scale invariance: For any initial image S0 = I and any monotone function , one has .
One can easily verify that (5.8) formally satisfies this axiom, and it can in fact be rigorously proven to be true in the context of viscosity solutions. See [21, 25].
5.1.5. Affine Invariant Smoothing
There are several variations on curve shortening which will yield comparable results. Given an initial image , one can smooth it by letting its level sets move with normal velocity given by → some function of their curvature,
| (5.9) |
instead of directly setting V = κ as in curve shortening. Using (5.6), one can turn the equation V = Φ(κ) into a PDE for S. If is monotone, then the resulting PDE for S will be degenerate parabolic, and existence and uniqueness of viscosity solutions has been shown [21, 2].
A particularly interesting choice of Φ leads to affine curve shortening [1, 2, 86, 84, 85, 9],
| (5.10) |
(where we agree to define (−κ)1/3 = −(κ)1/3).
While the evolution equation (5.9) is invariant under Euclidean transformations, the affine curve shortening equation (5.10) has the additional property that it is invariant under the action of the Special Affine group . If Γt is a family of curves evolving by (5.10) and , , then also evolves by (5.10).
Non-linear smoothing filters based on mean curvature flows respect edges much better than Gaussian smoothing; see Figure 5.1(c) for an example using the affine filter. The affine smoothing filter was implemented based on a level set formulation using the numerics suggested in [4].
5.1.6. Total Variation
Rudin et al. presented an algorithm for noise removal based on the minimization of the total first variation of S, given by
| (5.11) |
(See [54] for the details and the references therein for related work on the total variation method.) The minimization is performed under certain constraints and boundary conditions (zero flow on the boundary). The constraints they employed are zero mean value and given variance σ2 of the noise, but other constraints can be considered as well. More precisely, if the noise is additive, the constraints are given by
| (5.12) |
Noise removal according to this method proceeds by first choosing a value for the parameter σ and then minimizing subject to the constraints (5.12). For each σ > 0 there exists a unique minimizer satisfying the constraints.9 The family of images {Sσ | σ > 0} does not form a scale space and axioms does not satisfy the set forth by Alvarez et al. [2]. Furthermore, the smoothing parameter σ does not measure the “length scale of smoothing” in the way the parameter t in scale spaces does. Instead, the assumptions underlying this method of smoothing are more statistical. One assumes that the given image I is actually an ideal image to which a “noise term” N(x) has been added. The values N(x) at each are assumed to be independently distributed random variables with average variance σ2.
The Euler-Lagrange equation for this problem is
| (5.13) |
where λ is a Lagrange multiplier. In view of (5.6) we can write this as κ = −λ(S-I); i.e., we can interpret (5.13) as a prescribed curvature problem for the level sets of S. To find the minimizer of (5.11) with the constraints given by (5.12), start with the initial image S0 = I and modify it according to the L2 steepest descent flow for (5.11) with the constraint (5.12), namely
| (5.14) |
where λ(t) is chosen so as to preserve the second constraint in (5.12). The solution to the variational problem is given when S achieves steady state. This computation must be repeated ab initio for each new value of σ.
5.2. Image Registration
Image registration is the process of bringing two or more images into spatial correspondence (aligning them). In the context of medical imaging, image registration allows for the concurrent use of images taken with different modalities (e.g., MRI and CT) at different times or with different patient positions. In surgery, for example, images are acquired before (pre-operative), as well as during (intra-operative) surgery. Because of time constraints, the real-time intra-operative images have a lower resolution than the pre-operative images obtained. Moreover, deformations which occur naturally during surgery make it difficult to relate the high-resolution pre-operative image to the lower-resolution intra-operative anatomy of the patient. Image registration attempts to help the surgeon relate the two sets of images.
Registration has an extensive literature. Numerous approaches have been explored, ranging from statistics to computational fluid dynamics and various types of warping methodologies. See [58, 93] for a detailed description of the field as well as an extensive set of references, and [37, 76] for recent papers on the subject.
Registration typically proceeds in several steps. First, one decides how to measure similarity between images. One may include the similarity among pixel intensity values, as well as the proximity of predefined image features such as implanted fiducials or anatomical landmarks.10 Next, one looks for a transformation which maximizes similarity when applied to one of the images. Often this transformation is given as the solution of an optimization problem where the transformations to be considered are constrained to be of a predetermined class C. In the case of rigid registration (Section 5.2.1), C is the set of Euclidean transformations. Soft tissues in the human body typically do not deform rigidly. For example, physical deformation of the brain occurs during neurosurgery as a result of swelling, cerebrospinal fluid loss, hemorrhage and the intervention itself. Therefore a more realistic and more challenging problem is elastic registration (Section 5.2.2), where C is the set of smooth diffeomorphisms. Due to anatomical variability, non-rigid deformation maps are also useful when comparing images from different patients.
5.2.1. Rigid Registration
Given some similarity measure S on images and two images I and J, the problem of rigid registration is to find a Euclidean transformation T*x = Rx + a (with and ) which maximizes the similarity between I and T*(J), i.e.,
| (5.15) |
A number of standard multidimensional optimization techniques are available to solve (5.15).
Many similarity measures have been investigated [73], e.g., the normalized cross correlation
| (5.16) |
Information-theoretic similarity measures are also popular. By selecting a pixel x at random with uniform probability from the domain and computing the corresponding grey value I(x), one can turn any image I into a random variable. If we write pI for the probability density function of the random variable I and pIJ for the joint probability density of I and J, then one can define the entropy of the difference and the mutual information of two images I and J:
| (5.17) |
| (5.18) |
The normalized cross correlation (5.16) and the entropy of the difference (5.17) are maximized when the intensities of the two images are linearly related. In contrast, the mutual information measure (5.18) assumes only that the co-occurrence of the most probable values in the two images is maximized at registration. This relaxed assumption explains the success of mutual information in registration [57, 77].
5.2.2. Elastic Registration
In this section, we describe the use of optimal mass transport for elastic registration. Optimal mass transport ideas have already been used in computer vision to compare shapes [27] and have appeared in econometrics, fluid dynamics, automatic control, transportation, statistical physics, shape optimization, expert systems, and meteorology [79]. We outline below a method for constructing an optimal elastic warp as introduced in [27, 62, 10]. We describe in particular a numerical scheme for implementing such a warp for the purpose of elastic registration following [38]. The idea is that the similarity between two images is measured by their L2 Kantorovich-Wasserstein distance, and hence finding “the best map” from one image to another then leads to an optimal transport problem.
In the approach of [38] one thinks of a grayscale image as a Borel measure11 μ on some open domain , where, for any , the “amount of white” in the image contained in E is given by μ(E). Given two images (, μ0) and (, μ1) one considers all maps which preserve the measures, i.e., which satisfy12
| (5.19) |
and one is required to find the map (if it exists) which minimizes the Monge-Kantorovich transport functional (see the exact definition below). This optimal transport problem was introduced by Gaspard Monge in 1781 when he posed the question of moving a pile of soil from one site to another in a manner which minimizes transportation cost. The problem was given a modern formulation by Kantorovich [49], and so now is known as the Monge-Kantorovich problem.
More precisely, assuming that the cost of moving a mass m from to is m. Φ(x, y), where is called the cost function, Kantorovich defined the cost of moving the measure μ0 to the measure μ1 by the map to be
| (5.20) |
The infimum of M(u) taken over all measure preserving is called the Kantorovich-Wasserstein distance between the measures μ0 and μ1. The minimization of M(u) constitutes the mathematical formulation of the Monge-Kantorovich optimal transport problem.
If the measures μi and Lebesgue measure are absolutely continuous with respect to each other so that we can write for certain strictly positive densities , and if the map u is a diffeomorphism from to , then the mass preservation property (5.19) is equivalent with
| (5.21) |
The Jacobian equation (5.21) implies that if a small region in is mapped to a larger region in , there must be a corresponding decrease in density in order to comply with mass preservation. In other words, expanding an image darkens it.
The L2 Monge-Kantorovich problem corresponds to the cost function . A fundamental theoretical result for the L2 case [12, 29, 51] is that there is a unique optimal mass-preserving u and that this u is characterized as the gradient of a convex function p, i.e., u = ∇p. General results about existence and uniqueness may be found in [6] and the references ∇ therein.
To reduce the Monge-Kantorovich cost M(u) of a map , in [38] the authors consider a rearrangement of the points in the domain of the map in the following sense: the initial map u0 is replaced by a family of maps ut for which one has ut ∘ st = u0 for some family of diffeomorphisms . If the initial map u0 sends the measure μ0 to μ1, and if the diffeomorphisms st preserve the measure μ0, then the maps ut = u0 ∘ (st)−1 will also send μ0 to μ1.
Any sufficiently smooth family of diffeomorphisms is determined by its velocity field, defined by ∂tst = vt ∘ st.
If ut is any family of maps, then, assuming ut#μ0 = μ1 for all t, one has
| (5.22) |
The steepest descent is achieved by a family , whose velocity is given by
| (5.23) |
Here is the Helmholtz projection, which extracts the divergence-free part of vector fields on ; i.e., for any vector field w on one has .
From u0 = ut ∘ st one gets the transport equation
| (5.24) |
where the velocity field is given by (5.23). In [8] it is shown that the initial value problem (5.23), (5.24) has short time existence for C1,α initial data u0, and a theory of global weak solutions in the style of Kantorovich is developed.
For image registration, it is natural to take and to be a rectangle. Extensive numerical computations show that the solution to the unregularized flow converges to a limiting map for a large choice of measures and initial maps. Indeed, in this case, we can write the minimizing flow in the following “nonlocal” form:
| (5.25) |
The technique has been mathematically justified in [8] to which we refer the reader for all of the relevant details.
5.2.3. Optimal Warping
Typically in elastic registration, one wants to see an explicit warping which smoothly deforms one image into the other. This can easily be done using the solution of the Monge-Kantorovich problem. Thus, we assume now that we have applied our gradient descent process as described above and that it has converged to the Monge-Kantorovich mapping .
Following the work of [10, 62] (see also [29]), we consider the following related problem:
over all time varying densities m and velocity fields v satisfying
| (5.26) |
| (5.27) |
It is shown in [10, 62] that this infimum is attained for some mmin and vmin and that it is equal to the L2 Kantorovich-Wasserstein distance between and . Further, the flow X = X(x, t) corresponding to the minimizing velocity field vmin via
is given simply as
| (5.28) |
Note that when t = 0, X is the identity map and when t = 1, it is the solution to the Monge-Kantorovich problem. This analysis provides appropriate justification for using (5.28) to define our continuous warping map X between the densities m0 and m1.
This warping is illustrated on MR heart images, Figure 5.2. Since the images have some black areas where the intensity is zero, and since the intensities define the densities in the Monge-Kantorovich registration procedure, we typically replace m0 by some small perturbation m0 + ε for 0 < ε ≪ 1 to ensure that we have strictly positive densities. Full details may be found in [98]. We should note that the type of mixed L2/Wasserstein distance functionals which appear in [98] were introduced in [11].
Figure 5.2.
Optimal Warping of Myocardium from Diastolic to Systolic in Cardiac Cycle. These static images become much more vivid when viewed as a short animation. (Available at http://www.bme.gatech.edu/groups/minerva/publications/papers/medicalBAMS2005.html).
Specifically, two MR images of a heart are given at different phases of the cardiac cycle. In each image the white part is the blood pool of the left ventricle. The circular gray part is the myocardium. Since the deformation of this muscular structure is of great interest, we mask the blood pool and consider only the optimal warp of the myocardium in the sense described above. Figure 5.2(a) is a diastolic image, and Figure 5.2(f) is a systolic image.13 These are the only data given. Figures 5.2(b) to Figure 5.2(e) show the warping using the Monge-Kantorovich technique between these two images. These images offer a very plausible deformation of the heart as it undergoes its diastole/systole cyle. This is remarkable considering the fact that they were all artificially created by the Monge-Kantorovich technique. The plausibility of the deformation demonstrates the quality of the resulting warping.
5.3. Image Segmentation
When looking at an image, a human observer cannot help seeing structures which often may be identified with objects. However, digital images as the raw retinal input of local intensities are not structured. Segmentation is the process of creating a structured visual representation from an unstructured one. The problem was first studied in the 1920s by psychologists of the Gestalt school (see Kohler [53] and the references therein) and later by psychophysicists [48, 95].14 In its modern formulation, image segmentation is the problem of partitioning an image into homogeneous regions that are semantically meaningful, i.e., that correspond to objects we can identify. Segmentation is not concerned with actually determining what the partitions are. In that sense, it is a lower level problem than object recognition.
In the context of medical imaging, these regions have to be anatomically meaningful. A typical example is partitioning an MRI image of the brain into the white and gray matter. Since it replaces continuous intensities with discrete labels, segmentation can be seen as an extreme form of smoothing/information reduction. Segmentation is also related to registration in the sense that if an atlas15 can be perfectly registered to a dataset at hand, then the registered atlas labels are the segmentation. Segmentation is useful for visualization,16 allows for quantitative shape analysis, and provides an indispensable anatomical framework for virtually any subsequent automatic analysis.
Indeed, segmentation is perhaps the central problem of artificial vision, and accordingly many approaches have been proposed (for a nice survey of modern segmentation methods, see the monograph [66]). There are basically two dual approaches. In the first, one can start by considering the whole image to be the object of interest and then refining this initial guess. These “split and merge” techniques can be thought of as somewhat analogous to the top-down processes of human vision. In the other approach, one starts from one point assumed to be inside the object and adds other points until the region encompasses the object. Those are the “region growing” techniques and bear some resemblance to the bottom-up processes of biological vision.
The dual problem to segmentation is that of determining the boundaries of the segmented homogeneous regions. This approach has been popular for some time, since it allows one to build upon the well-investigated problem of edge detection (Section 5.3.1). Difficulties arise with this approach because noise can be responsible for spurious edges. Another major difficulty is that local edges need to be connected into topologically correct region boundaries. To address these issues, it was proposed to set the topology of the boundary to that of a sphere and then deform the geometry in a variational framework to match the edges. In 2D, the boundary is a closed curve, and this approach was named snakes (Section 5.3.2). Improvements of the technique include geometric active contours (Section 5.3.3) and conformal active contours (Section 5.3.4). All these techniques are generically referred to as active contours. Finally, as described in [66], most segmentation methods can be set in the elegant mathematical framework proposed by Mumford and Shah [68] (Section 5.3.7).
5.3.1. Edge detectors
Consider the ideal case of a bright object on a dark background. The physical object is represented by its projections on the image I. The characteristic function of the object is the ideal segmentation, and since the object is contrasted on the background, the variations of the intensity I are large on the boundary . It is therefore natural to characterize the boundary as the locus of points where the norm of the gradient |∇I| is large. In fact, if is piecewise smooth, then |∇I| is a singular measure whose support is exactly .
This is the approach taken in the 60’s and 70’s by Roberts [81] and Sobel [90], who proposed slightly different discrete convolution masks to approximate the gradient of digital images. Disadvantages with these approaches are that edges are not precisely localized and may be corrupted by noise. See Figure 5.3(b) is the result of a Sobel edge detector on a medical image. Note the thickness of the boundary of the heart ventricle as well as the presence of “spurious edges” due to noise. Canny [14] proposed to add a smoothing pre-processing step (to reduce the influence of the noise) as well as a thinning post-processing phase (to ensure that the edges are uniquely localized). See [26] for a survey and evaluation of edge detectors using gradient techniques.
Figure 5.3.
Result of two edge detectors on a heart MRI image.
A slightly different approach initially motivated by psychophysics was proposed by Marr and Hildreth [61, 60] where edges are defined as the zeros of ∇Gσ * I, the Laplacian of a smooth version of the image. One can give a heuristic justification by assuming that the edges are smooth curves; more precisely, assume that near an edge the image is of the form
| (5.29) |
where S is a smooth function with ∇S = O(1) which vanishes on the edge, ε is a small parameter proportional to the width of the edge, and is a smooth increasing function with .

The function φ describes the profile of I transverse to its level sets. We will assume that the graph of φ has exactly one inflection point.
The assumption (5.29) implies ∇I = φ′(S/ε)∇S, while the second derivative ∇2I is given by
| (5.30) |
Thus ∇2I will have eigenvalues of moderate size (O(ε−1)) in the direction perpendicular to ∇I, while the second derivative in the direction of the gradient will change from a large O(ε−2) positive value to a large negative value as one crosses from small I to large I values.
From this discussion of ∇2I, it seems reasonable to define the edges to be the locus of points where |∇I| is large and where either (∇I)t · ∇2I · ∇I or ΔI or det ∇2I changes sign. The quantity (∇I)T · ∇2I · ∇I vanishes at if the graph of the function I restricted to the normal line to the level set of I ∈passing through x has an inflection point at x (assuming ). In general, zeros of ΔI and det ∇2I do not have a similar description, but since the first term in (5.30) will dominate when ε is small, both (∇I)T · ∇2I · ∇I and det ∇2I will tend to vanish at almost the same places.
Computation of second derivatives is numerically awkward, so one prefers to work with a smoothed out version of the image, such as Gσ * I instead of I itself.
See Figure 5.3(c) for the result of the Marr edge detector. In these images the edge is located precisely at the zeroes of the Laplacian (a thin white curve).
While it is now understood that these local edge detectors cannot be used directly for the detection of object boundaries (local edges would need to be connected in a topologically correct boundary), these techniques proved instrumental in designing the active contour models described below and are still being investigated [36, 7].
5.3.2. Snakes
A first step toward automated boundary detection was taken by Witkin, Kass and Terzopoulos [56] and later by a number of researchers (see [23] and the references therein). Given an image , they subject an initial parametrized curve to a steepest descent flow for an energy functional of the form17
| (5.31) |
The first two terms control the smoothness of the active contour Γ. The contour interacts with the image through the potential function which is chosen to be small near the edges and large everywhere else (it is a decreasing → function of some edge detector). For example one could take:
| (5.32) |
Minimizing will therefore attract Γ toward the edges. The gradient flow is the fourth order non-linear parabolic equation
| (5.33) |
This approach gives reasonable results. See [64] for a survey of snakes in medical image analysis. One limitation however is that the active contour or snake cannot change topology; i.e., it starts out being a topological circle, and it will always remain a topological circle and will not be able to break up into two or more pieces, even if the image would contain two unconnected objects and this would give a more natural description of the edges. Special ad hoc procedures have been developed in order to handle splitting and merging [63].
5.3.3. Geometric Active Contours
Another disadvantage of the snake method is that it explicitly involves the parametrization of the active contour Γ, while there is no obvious relation between the parametrization of the contour and the geometry of the objects to be captured. Geometric models have been developed by [15, 78] to address this issue.
As in the snake framework, one deforms the active contour Γ by a velocity which is essentially defined by a curvature term and a constant inflationary term weighted by a stopping function W. By formulating everything in terms of quantities which are invariant under reparametrization (such as the curvature and normal velocity of Γ), one obtains an algorithm which does not depend on the parametrization of the contour. In particular, it can be implemented using level sets.
More specifically, the model of [15, 78] is given by
| (5.34) |
where both the velocity V and the curvature κ are measured using the inward normal N for Γ. Here, as previously, W is small at edges and large everywhere else, and c is a constant, called the inflationary parameter. When c is positive, it helps push the contour through concavities and can speed up the segmentation process. When it is negative, it allows expanding “bubbles”, i.e., contours which expand rather than contract to the desired boundaries. We should note that there is no canonical choice for the constant c, which has to be determined experimentally.
In practice Γ is deformed using the Osher-Sethian level set method descibed in Section 5.1.4. One represents the curve Γt as the zero level set of a function ,
| (5.35) |
For a given normal velocity field, the defining function Φ is then the solution of the Hamilton-Jacobi equation
which can be analyzed using viscosity theory [55].
Geometric active contours have the advantage that they allow for topological changes (splitting and merging) of the active contour Γ. The main problem with this model is that the desired edges are not steady states for the flow (5.34). The effect of the factor W (x) is merely to slow the evolution of Γt down as it approaches an edge, but it is not the case that the Γt will eventually converge to anything like the sought-for edge as t → ∞. Some kind of artificial intervention is required to stop the evolution when Γt is close to an edge.
5.3.4. Conformal Active Contours
In [50, 16], the authors propose a novel technique that is both geometric and variational. In their approach one defines a Riemannian metric gW on from a given image by conformally changing the standard Euclidean metric to →
| (5.36) |
Here W is defined as above in (5.32). The length of a curve in this metric is
| (5.37) |
Curves which minimize this length will prefer to be in regions where W is small, which is exactly where one would expect to find the edges. So, to find edges, one should minimize the W-weighted length of a closed curve Γ rather than some “energy” of Γ (which depends on a parametrization of the curve).
To minimize , one computes a gradient flow in the L2 sense. Since the first variation of this length functional is given by
where V is the normal velocity measured in the Euclidean metric and N is the Euclidean unit normal, the corresponding L2 gradient flow is
| (5.38) |
Note that this is not quite the curve-shortening flow in the sense of [33, 34] on given the Riemannian manifold structure defined by the conformally Euclidean metric gW. Indeed, a simple computation shows that in that case one would have
| (5.39) |
Thus the term “geodesic active contour” used in [16] is a bit of a misnomer, and so we prefer the term “conformal active contour” as in [50].
Contemplation of the conformal active contours leads to another interpretation of the concept “edge”. Using the landscape metaphor one can describe the graph of W as a plateau (where |∇I| is small) in which a canyon has been carved (where |∇I| is large). The edge is to be found at the bottom of the canyon. Now if W is a Morse function, then one expects the “bottom of the canyon” to consist of local minima of W alternated by saddle points. The saddle points are connected to the minima by their unstable manifolds for the gradient flow of W (the ODE x′ = −∇W (x)). Together these unstable manifolds form one or more closed curves which one may regard as the edges which are to be found.
Comparing (5.38) to the evolution of the geometric active contour (5.34), we see that we have the new term −N · ∇W, the normal component of −∇W. If the contour Γt were to evolve only by V = −N·∇W, then it would simply be deformed by the gradient flow of W. If W is a Morse function, then one can use the λ-lemma from dynamical systems [72, 65] to show that for a generic choice of initial contour the Γt will converge to the union of unstable manifolds “at the bottom of the canyon”, possibly with multiplicity more than one. The curvature term in (5.34) counteracts this possible doubling up and guarantees that Γt will converge smoothly to some curve which is a smoothed out version of the heteroclinic chain in Figure 5.4.
Figure 5.4.

A conformal active contour among unstable manifolds.
5.3.5. Conformal Area Minimizing Flows
Typically, in order to get expanding bubbles, an inflationary term is added in the model (5.38) as in (5.34). Many times segmentations are more easily performed by seeding the image with bubbles rather than contracting snakes. The conformal active contours will not allow this, since very small curves will simply shrink to points under the flow (5.38). To get a curve evolution which will force small bubbles to expand and converge toward the edges, it is convenient to subtract a weighted area term from the length functional , namely
where dx is 2D Lebesgue measure and RΓ is the region enclosed by the contour Γ.
The first variation of this weighted area is [89, 88, 75]):
| (5.40) |
where, as before, V is the normal velocity of Γt measured with the inward normal.
The functional which one now tries to minimize is
| (5.41) |
where is a constant called the inflationary parameter.
To obtain steepest descent for one sets
| (5.42) |
For c = 1 this is a conformal length/area miminizing flow (see [88]). As in the model of [15, 78] the inflationary parameter c may be chosen as positive (snake or inward moving flow) or negative (bubble or outward moving flow).
In practice, for expanding flows (negative c, weighted area maximizing flow), one expands the bubble just using the inflationary part
until the active contour is sufficiently large and then “turns on” the conformal part Vconf which brings the contour to its final position. Again as in [15, 78], the curvature part of Vact also acts to regularize the flow. Finally, there is a detailed mathematical analysis of (5.42) in [50] as well as extensions to the 3 dimensional space, in which case the curvature κ is replaced by the mean curvature H in Equation (5.42).
5.3.6. Examples of Segmentation via Conformal Active Contours
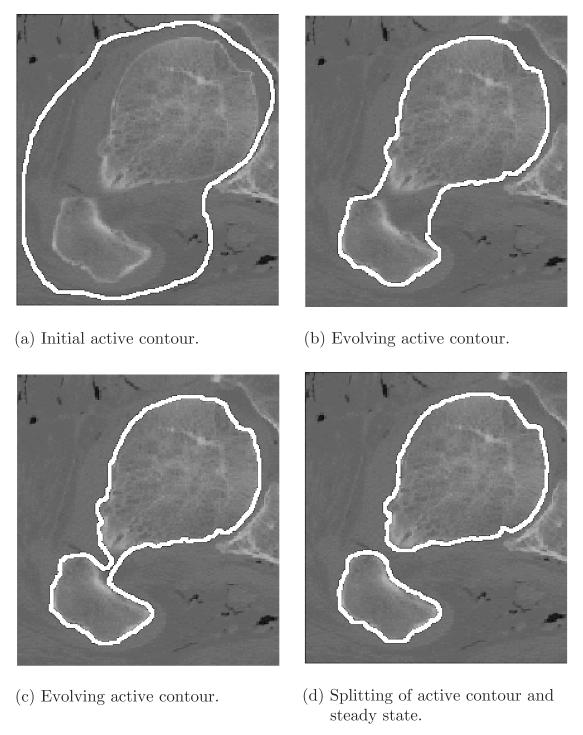
This technique can also be implemented in the level set framework to allow for the splitting and merging of evolving curves. Figure 5.5 shows the ventricle of an MR image of the heart being captured by a conformal active contour Vconf. We can also demonstrate topological changes. In Figure 5.6, we show two bubbles, which are evolved by the full flow Vact with c < 0 and which merge to capture the myocardium of the same image. Conformal active contours can be employed for the segmentation of images from many modalities. In Figure 5.7, the contour of a cyst was successfully captured in an ultrasound image. This again used the full flow Vact with c < 0. Because that modality is particularly noisy, the image had been pre-smoothed using the affine curve shortening non-linear filter (see Section 5.1.5). In Figure 5.8, the contracting active contour splits to capture two disconnected osseous regions on a CT image.
Figure 5.5.
Ventricle segmentation in MRI heart image via shrinking conformal active contour.
Figure 5.6.
Myocardium segmentation in MRI heart image with two merging expanding conformal active contours.
Figure 5.7.
Cyst segmentation in ultrasound breast image with three merging expanding conformal active contours.
Figure 5.8.
Bone segmentation in CT image with splitting shrinking conformal active contour.
5.3.7. Mumford-Shah Framework
Mumford and Shah [69] define segmentation as a joint smoothing and edge detection problem. In their framework, given an image , the goal is to find a set of discontinuities and a piecewise smooth image S(x) on that minimize
| (5.43) |
where is the Euclidean length or, more generally, the 1-dimensional Hausdorff measure of K.
The first term ensures that any minimizer S is smooth (except across edges), while the second term ensures that minimizers approximate I. The last term will cause the set K to be regular. It is interesting to note, as argued in the book [66], that many segmentation algorithms (including some of the most common) can be formulated in the Mumford-Shah framework. Further the Mumford-Shah functional can be given a very natural Bayesian interpretation [67].
The functional itself is very difficult to analyze mathematically even though there have been some interesting results. The book [66] gives a very nice survey on the mathematical results concerning the Mumford-Shah functional. For example, Ambrosio [5] has found a weak solution to the problem in the class of Special Bounded Variation functions. The functional itself has influenced several different segmentation techniques, some connected with active contours, including [94, 19].
6. Conclusion
In this paper, we sketched some of the fundamental concepts of medical image processing. It is important to emphasize that none of these problem areas has been satisfactorily solved, and all of the algorithms we have described are open to considerable improvement. In particular, segmentation remains a rather ad hoc procedure, with the best results being obtained via interactive programs with considerable input from the user.
Nevertheless, progress has been made in the field of automatic analysis of medical images over the last few years thanks to improvements in hardware, acquisition methods, signal processing techniques, and of course mathematics. Curvature driven flows have proven to be an excellent tool for a number of image processing tasks and have definitely had a major impact on the technology base. Several algorithms based on partial differential equation methods have been incorporated into clinical software and are available in open software packages such as the National Library of Medicine Insight Segmentation and Registration Toolkit (ITK) [47] and the 3D Slicer of the Harvard Medical School [92]. These projects are very important in disseminating both standard and new mathematical methods in medical imaging to the broader community.
The mathematical challenges in medical imaging are still considerable, and the necessary techniques touch just about every major branch of mathematics. In summary, we can use all the help we can get!
Acknowledgments
The authors would like to thank Steven Haker, Ron Kikinis, Guillermo Sapiro, Anthony Yezzi, and Lei Zhu for many helpful conversations on medical imaging and to Bob McElroy for proofreading the final document.
This research was supported by grants from the NSF, NIH (NAC P41 RR-13218 through Brigham and Women’s Hospital), and the Technion, Israel Institute of Technology. This work was done under the auspices of the National Alliance for Medical Image Computing (NAMIC), funded by the National Institutes of Health through the NIH Roadmap for Medical Research, Grant U54 EB005149.
Biography
Sigurd Angenent is a professor of mathematics at the University of Wisconsin at Madison. He is currently (2005/06) on leave at the math department of the Vrije Universiteit Amsterdam.
Allen Tannenbaum is currently a professor of electrical, computer, and biomedical engineering at the Georgia Institute of Technology.
Eric Pichon is currently a graduate student in the Electrical and Computer Engineering Department at the Georgia Institute of Technology.
Footnotes
It was not understood at that time that X-rays are ionizing radiations and that high doses are dangerous. Many enthusiastic experimenters died of radio-induced cancers.
The nuclei relevant to MRI exist whether the technique is applied or not.
The definition of “intelligence” is still very problematic.
Stereoscopic vision does not allow us to see inside objects. It is sometimes described as “2.1 dimensional perception”.
“Top-down” and “bottom-up” are loosely defined terms from computer science, computation and neuroscience. The bottom-up approach can be characterized as searching for a general solution to a specific problem (e.g. obstacle avoidance) without using any specific assumptions. The top-down approach refers to trying to find a specific solution to a general problem, such as structure from motion, using specific assumptions (e.g., rigidity or smoothness).
Because an image is contained in a finite region , the boundary conditions which must be imposed to make the initial value problem well-posed will generally keep the Tt from obeying Euclidean invariance even if the generator A does so.
This was of course common knowledge among mathematicians and physicists for at least a century. The fact that this was not immediately noticed shows how disjoint the imaging/engineering and mathematics communities were.
There is substantial literature on the evolution of immersed plane curves, or immersed curves on surfaces by curve shortening and variants thereof. We refer to [24, 28, 33, 45, 96, 22], knowing that this is a far-from-exhaustive list of references.
BV() is the set of functions of bounded variation on . See [31].
Registration or alignment is most commonly achieved by marking identifiable points on the patient with a tracked pointer and in the images. These points, often called fiducials, may be anatomical or artificially attached landmarks, i.e., “implanted fiducials”.
This can be physically motivated. For example, in some forms of MRI the image intensity is the actual proton density.
If X and Y are sets with σ-algebras and , and if f : X → Y is a measurable map, then we write f#μ for the pushforward of any measure μ on (X, ); i.e., for any measurable E ⊂ Y we define f#μ(E) = μ(f−1(E)).
Diastolic refers to the relaxation of the heart muscle, while systolic refers to the contraction of the muscle.
Segmentation was called “perceptual grouping” by the Gestaltists. The idea was to study the preferences of human beings for the grouping of sets of shapes arranged in the visual field.
An image from a typical patient that has been manually segmented by some human expert.
As discussed previously, human vision is inherently two dimensional. In order to “see” an organ we therefore have to resort to visualizing its outside boundary. Determining this boundary is equivalent to segmenting the organ.
We present Cohen’s [23] version of the energy.
2000 Mathematics Subject Classification. Primary 92C55, 94A08, 68T45; Secondary 35K55, 35K65.
Contributor Information
SIGURD ANGENENT, Department of Mathematics, University of Wisconsin-Madison, Madison, Wisconsin 53706, angenent@math.wisc.edu.
ERIC PICHON, Department of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0250, eric@ece.gatech.edu.
ALLEN TANNENBAUM, Departments of Electrical and Computer and Biomedical Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0250, tannenba@ece.gatech.edu.
References
- 1.Alvarez L, Guichard F, Lions PL, Morel J-M. Axiomes etéquations fondamentales du traitement d’images. C. R. Acad. Sci. Paris. 1992;315:135–138. MR1197224 (94d:47066) [Google Scholar]
- 2.Alvarez L. Axioms and fundamental equations of image processing. Arch. Rat. Mech. Anal. 1993;123(3):199–257. MR1225209 (94j:68306) [Google Scholar]
- 3.Alvarez L, Lions PL, Morel J-M. Image selective smoothing and edge detection by nonlinear diffusion. SIAM J. Numer. Anal. 1992;29:845–866. MR1163360 (93a:35072) [Google Scholar]
- 4.Alvarez L, Morel J-M. Formalization and computational aspects of image analysis. Acta Numerica. 1994;3:1–59. MR1288095 (95c:68229) [Google Scholar]
- 5.Ambrosio L. A compactness theorem for a special class of functions of bounded variation. Boll. Un. Math. It. 1989;3:857–881. MR1032614 (90k:49005) [Google Scholar]
- 6.Ambrosio L. CIME Series of Springer Lecture Notes. Springer; Jul, 2000. Lecture notes on optimal transport theory, Euro Summer School, Mathematical Aspects of Evolving Interfaces. [Google Scholar]
- 7.Ando S. Consistent gradient operators. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000;22(3):252–265. [Google Scholar]
- 8.Angenent S, Haker S, Tannenbaum A. Minimizing flows for the Monge-Kantorovich problem. SIAM J. Math. Anal. 2003;35(1):61–97. (electronic). MR2001465 (2004g:49070) [Google Scholar]
- 9.Angenent S, Sapiro G, Tannenbaum A. On the affine heat flow for non-convex curves. J. Amer. Math. Soc. 1998;11(3):601–634. MR1491538 (99d:58039) [Google Scholar]
- 10.Benamou J-D, Brenier Y. A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem. Numerische Mathematik. 2000;84:375–393. MR1738163 (2000m:65111) [Google Scholar]
- 11.Benamou J-D. Mixed L2-Wasserstein optimal mapping between prescribed density functions. J. Optimization Theory Applications. 2001;111:255–271. MR1865668 (2002h:49069) [Google Scholar]
- 12.Brenier Y. Polar factorization and monotone rearrangement of vector-valued functions. Comm. Pure Appl. Math. 1991;44:375–417. MR1100809 (92d:46088) [Google Scholar]
- 13.Brooks D. Emerging medical imaging modalities. IEEE Signal Processing Magazine. 2001;18(6):12–13. [Google Scholar]
- 14.Canny J. Computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1986;8(6):679–698. [PubMed] [Google Scholar]
- 15.Caselles V, Catte F, Coll T, Dibos F. A geometric model for active contours in image processing. Numerische Mathematik. 1993;66:1–31. MR1240700 (94k:65195) [Google Scholar]
- 16.Caselles V, Kimmel R, Sapiro G. Geodesic active contours. International Journal of Computer Vision. 1997;22(11):61–79. [Google Scholar]
- 17.Caselles V, Morel J, Sapiro G, Tannenbaum A. Introduction to the special issue on partial differential equations and geometry-driven diffusion in image processing and analysis. IEEE Trans. on Image Processing. 1998;7(3):269–273. doi: 10.1109/TIP.1998.661176. [DOI] [PubMed] [Google Scholar]
- 18.Chabat F, Hansell DM. and Guang-Zhong Yang, Computerized decision support in medical imaging. IEEE Engineering in Medicine and Biology Magazine. 2000;19(5):89–96. doi: 10.1109/51.870235. [DOI] [PubMed] [Google Scholar]
- 19.Chan T, Vese L. Active contours without edges. IEEE Trans. Image Processing. 2001;10:266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- 20.Chan TF, Shen J, Vese L. Variational PDE models in image processing. Notices of AMS. 2003;50(1):14–26. MR1948832 (2003m:94008) [Google Scholar]
- 21.Chen YG, Giga Y, Goto S. Uniqueness and existence of viscosity solutions of generalized mean curvature flow equations. J. Differential Geometry. 1991;33:749–786. MR1100211 (93a:35093) [Google Scholar]
- 22.Chou K-S, Zhu X-P. The curve shortening problem. Chapman & Hall/CRC; Boca Raton: 2001. MR1888641 (2003e:53088) [Google Scholar]
- 23.Cohen LD. On active contour models and balloons. CVGIP: Image Understanding. 1991;53(2):211–218. [Google Scholar]
- 24.Epstein CL, Gage M. In: The curve shortening flow, Wave Motion: Theory, Modeling and Computation. Chorin A, Majda A, editors. Springer-Verlag; New York: 1987. MR0920831 (89f:58128) [Google Scholar]
- 25.Evans LC, Spruck J. Motion of level sets by mean curvature, I. J. Differential Geometry. 1991;33(3):635–681. MR1100206 (92h:35097) [Google Scholar]
- 26.Fram JR, Deutsch ES. On the quantitative evaluation of edge detection schemes and their comparisions with human performance. IEEE Transaction on Computers. 1975;24(6):616–627. [Google Scholar]
- 27.Fry D, Harvard University . Ph.D. thesis. 1993. Shape recognition using metrics on the space of shapes. [Google Scholar]
- 28.Gage M, Hamilton RS. The heat equation shrinking convex plane curves. J. Differential Geometry. 1986;23:69–96. MR0840401 (87m:53003) [Google Scholar]
- 29.Gangbo W, McCann R. The geometry of optimal transportation. Acta Math. 1996;177:113–161. MR1440931 (98e:49102) [Google Scholar]
- 30.Gerson ES. Scenes from the past: X-Ray mania, the X-Ray in advertising, circa 1895. Radiographics. 2004;24:544–551. doi: 10.1148/rg.242035157. [DOI] [PubMed] [Google Scholar]
- 31.Giusti E. Minimal surfaces and functions of bounded variation. Birkḧauser-Verlag; 1984. MR0775682 (87a:58041) [Google Scholar]
- 32.Gonzalez R, Woods R. Digital image processing. Prentice Hall; 2001. [Google Scholar]
- 33.Grayson M. The heat equation shrinks embedded plane curves to round points. J. Differential Geometry. 1987;26:285–314. MR0906392 (89b:53005) [Google Scholar]
- 34.Grayson M. Shortening embedded curves. Annals of Mathematics. 1989;129:71–111. MR0979601 (90a:53050) [Google Scholar]
- 35.Guichard F, Moisan L, Morel JM. A review of PDE models in image processing and image analysis. Journal de Physique. 2002;IV(12):137–154. [Google Scholar]
- 36.Gunn SR. On the discrete representation of the Laplacian of Gaussian. Pattern Recognition. 1999;32(8):1463–1472. [Google Scholar]
- 37.Hajnal J, Hawkes DJ, Hill D, Hajnal JV, editors. Medical image registration. CRC Press; 2001. [Google Scholar]
- 38.Haker S, Zhu L, Tannenbaum A, Angenent S. Optimal mass transport for registration and warping. Int. Journal Computer Vision. 2004;60(3):225–240. [Google Scholar]
- 39.Haralick R, Shapiro L. Computer and robot vision. Addison-Wesley; 1992. [Google Scholar]
- 40.Helgason S. The Radon transform. Birkḧauser; Boston, MA: 1980. MR0573446 (83f:43012) [Google Scholar]
- 41.Hendee W, Ritenour R. Medical imaging physics. 4th ed. Wiley-Liss; 2002. [Google Scholar]
- 42.Hero AO, Krim H. Mathematical methods in imaging. IEEE Signal Processing Magazine. 2002;19(5):13–14. [Google Scholar]
- 43.Hobbie R. Intermediate physics for medicine and biology. third edition Springer; New York: 1997. [Google Scholar]
- 44.Horn BKP. Robot vision. MIT Press; 1986. [Google Scholar]
- 45.Huisken G. Flow by mean curvature of convex surfaces into spheres. J. Differential Geometry. 1984;20:237–266. MR0772132 (86j:53097) [Google Scholar]
- 46.Hummel R. Representations based on zero-crossings in scale-space. IEEE Computer Vision and Pattern Recognition. 1986:204–209. [Google Scholar]
- 47.Insight Segmentation and Registration Toolkit. http:itk.org.
- 48.Julesz B. Textons, the elements of texture perception, and their interactions. Nature. 1981;12(290):91–97. doi: 10.1038/290091a0. [DOI] [PubMed] [Google Scholar]
- 49.Kantorovich LV. On a problem of Monge. Uspekhi Mat. Nauk. 1948;3:225–226. [Google Scholar]
- 50.Kichenassamy S, Kumar A, Olver P, Tannenbaum A, Yezzi A. Conformal curvature flows: from phase transitions to active vision. Arch. Rational Mech. Anal. 1996;134(3):275–301. MR1412430 (97j:58023) [Google Scholar]
- 51.Knott M, Smith C. On the optimal mapping of distributions. J. Optim. Theory. 1984;43:39–49. MR0745785 (86a:60026) [Google Scholar]
- 52.Koenderink JJ. The structure of images. Biological Cybernetics. 1984;50:363–370. doi: 10.1007/BF00336961. MR0758126. [DOI] [PubMed] [Google Scholar]
- 53.Köhler W. Gestalt psychology today. American Psychologist. 1959;14:727–734. [Google Scholar]
- 54.Osher S, Rudin LI, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D. 1992;60:259–268. [Google Scholar]
- 55.Ishii H, Crandall MG, Lions PL. User’s guide to viscosity solutions of second order partial differential equations. Bulletin of the American Mathematical Society. 1992;27:1–67. MR1118699 (92j:35050) [Google Scholar]
- 56.Witkin A, Kass M, Terzopoulos D. Snakes: active contour models. Int. Journal of Computer Vision. 1987;1:321–331. [Google Scholar]
- 57.Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Transactions on Medical Imaging. 1997;16(2):187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- 58.Maintz J, Viergever M. A survey of medical image registration. Medical Image Analysis. 1998;2(1):1–36. doi: 10.1016/s1361-8415(01)80026-8. [DOI] [PubMed] [Google Scholar]
- 59.Mallat S. A wavelet tour of signal processing. Academic Press; San Diego, CA: 1998. MR1614527 (99m:94012) [Google Scholar]
- 60.Marr D. Vision. Freeman; San Francisco: 1982. [Google Scholar]
- 61.Marr D, Hildreth E. Theory of edge detection. Proc. Royal Soc. Lond. B. 1980;(207):187–217. doi: 10.1098/rspb.1980.0020. [DOI] [PubMed] [Google Scholar]
- 62.McCann R, Princeton University . Ph.D. Thesis. 1994. A convexity theory for interacting gases and equilibrium crystals. [Google Scholar]
- 63.McInerney T, Terzopoulos D. Topologically adaptable snakes. Int. Conf. on Computer Vision (Cambridge, MA) 1995 Jun;:840–845. [Google Scholar]
- 64.McInerney T. Deformable models in medical image analysis: a survey. Medical Image Analysis. 1996;1(2):91–108. doi: 10.1016/s1361-8415(96)80007-7. [DOI] [PubMed] [Google Scholar]
- 65.Milnor J. Morse theory. Princeton University Press; 1963. MR0163331 (29:634) [Google Scholar]
- 66.Morel J-M, Solimini S. Variational methods in image segmentation. Birkḧauser; Boston: 1995. MR1321598 (96b:68184) [Google Scholar]
- 67.Mumford D. ch. The Bayesian Rationale for Energy Functionals. Kluwer Academic Publishers; 1994. Geometry-driven diffusion in computer vision; pp. 141–153. MR1339987 (97e:68147) [Google Scholar]
- 68.Mumford D, Shah J. Boundary detection by minimizing functionals. IEEE Conference on Computer Vision and Pattern Recognition. 1985:22–26. [Google Scholar]
- 69.Mumford D. Optimal approximations by piecewise smooth functions and associated variational problems. Comm. Pure Appl. Math. 1989;42(5):577–685. MR0997568 (90g:49033) [Google Scholar]
- 70.Osher S, Fedkiw RP. Level set methods: An overview and some recent results. Journal of Computational Physics. 2001;169:463–502. MR1836523 (2002c:65255) [Google Scholar]
- 71.Osher SJ, Sethian JA. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Computational Physics. 1988;79:12–49. MR0965860 (89h:80012) [Google Scholar]
- 72.Palis Jacob, Jr., de Melo Welington. An introduction. Springer-Verlag; New York: 1982. Geometric theory of dynamical systems. Translated from the Portuguese by A. K. Manning. MR0669541 (84a:58004) [Google Scholar]
- 73.Penney GP, Weese J, Little JA, Desmedt P, Hill DLO, Hawkes DJ. A comparison of similarity measures for use in 2-D-3-D medical image registration. IEEE Transactions on Medical Imaging. 1998;17(4):586–595. doi: 10.1109/42.730403. [DOI] [PubMed] [Google Scholar]
- 74.Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Machine Intell. 1990;12:629–639. [Google Scholar]
- 75.Pichon E, Tannenbaum A, Kikinis R. Statistically based flow for image segmentation. Medical Imaging Analysis. 2004;8:267–274. doi: 10.1016/j.media.2004.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Pluim JPW, Fitzpatrick JM, editors. Special issue on image registration. IEEE Transactions on Medical Imaging. 2003;22(11) doi: 10.1109/tmi.2003.819272. [DOI] [PubMed] [Google Scholar]
- 77.Pluim JPW, Maintz JBA, Viergever MA. Mutual-information-based registration of medical images: a survey. IEEE Transactions on Medical Imaging. 2003;22(8):986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- 78.Sethian J, Malladi R, Vemuri B. Shape modeling with front propagation: a level set approach. IEEE Trans. Pattern Anal. Machine Intell. 1995;17:158–175. [Google Scholar]
- 79.Rachev S, Rüschendorf L. Mass transportation problems. Springer; 1998. [Google Scholar]
- 80.Radiology Centennial Inc. A century of radiology. http:www.xray.hmc.psu.edu/rci/centennial.html. [Google Scholar]
- 81.Roberts L. ch. Machine perception of 3-D solids. MIT Press; 1965. Optical and electro-optical information processing. [Google Scholar]
- 82.Roentgen WC. Ueber eine neue Art von Strahlen. Annalen der Physik. 1898;64:1–37. [Google Scholar]
- 83.Sapiro G. Geometric partial differential equations and image analysis. Cambridge University Press; Cambridge: 2001. MR1813971 (2002a:68142) [Google Scholar]
- 84.Sapiro G, Tannenbaum A. Affine invariant scale-space. International Journal of Computer Vision. 1993;11(1):25–44. [Google Scholar]
- 85.Sapiro G. On invariant curve evolution and image analysis. Indiana Univ. Math. J. 1993;42(3):985–1009. MR1254129 (94m:58048) [Google Scholar]
- 86.Sapiro G. On affine plane curve evolution. Journal of Functional Analysis. 1994;119(1):79–120. MR1255274 (94m:58049) [Google Scholar]
- 87.Sethian JA. Levelset methods and fast marching methods. Cambridge University Press; 1999. MR1684542 (2000m:65125) [Google Scholar]
- 88.Siddiqi K, Lauziere Y, Tannenbaum A, Zucker S. Area and length minimizing flows for shape segmentation. IEEE TMI. 1998;7:433–443. doi: 10.1109/83.661193. [DOI] [PubMed] [Google Scholar]
- 89.Simon L. Proceedings of the Centre for Mathematical Analysis. Australian National University; Canberra: 1983. Lectures on geometric measure theory. MR0756417 (87a:49001) [Google Scholar]
- 90.Sobel IE, Stanford Univ. Ph.D. thesis. 1970. Camera models and machine perception. [Google Scholar]
- 91.Sonka M, Hlavac V, Boyle R. Image processing: Analysis and machine vision. 2nd ed. Brooks Cole; 1998. [Google Scholar]
- 92.3D Slicer. http://slicer.org.
- 93.Toga A. Brain warping. Academic Press; San Diego: 1999. [Google Scholar]
- 94.Tsai A, Yezzi A, Willsky A. A curve evolution approach to smoothing and segmentation using the Mumford-Shah functional. CVPR. 2000:1119–1124. [Google Scholar]
- 95.von de Heydt R, Peterhans E. Illusory contours and cortical neuron responses. Science. 1984;224(4654):1260–1262. doi: 10.1126/science.6539501. [DOI] [PubMed] [Google Scholar]
- 96.White B. Some recent developments in differential geometry. Mathematical Intelligencer. 1989;11:41–47. MR1016106 (90k:53003) [Google Scholar]
- 97.Witkin AP. Scale-space filtering. Int. Joint. Conf. Artificial Intelligence. 1983:1019–1021. [Google Scholar]
- 98.Zhu L. Ph.D. thesis. Department of Biomedical Engineering, Georgia Institute of Technology; 2004. On visualizing branched surfaces: An angle/area preserving approach. [Google Scholar]