Abstract
Nitric oxide (NO) consumption by red blood cell (RBC) hemoglobin (Hb) in vasculature is critical in regulating the vascular tone. The paradox of NO production at endothelium in close proximity of an effective NO scavenger Hb in RBCs is mitigated by lower NO consumption by RBCs compared to that of free Hb due to transport resistances including membrane resistance, extra- and intra- cellular resistances for NO biotransport to the RBC. Relative contribution of each transport resistance on NO-RBC interactions is still not clear. We developed a mathematical model of NO transport to a single RBC to quantify the contributions from individual transport barriers by analyzing the effect of RBC membrane permeability (Pm), hematocrit (Hct) and NO-Hb reaction rate constants on NO-RBC interactions. Our results indicated that intracellular diffusion of NO was not a rate limiting step for NO-RBC interactions. The extracellular diffusion contributed 70–90% of total transport resistance for Pm >1 cm/s whereas membrane resistance accounts for 50–75% of total transport resistance for Pm < 0.1 cm/s. We propose a narrow Pm range of 0.21–0.44 cm/s for 10–45% Hct, respectively, below which membrane resistance is more significant and above which extracellular diffusion is a dominating transport resistance for NO-RBC interactions.
Keywords: Nitric oxide, red blood cells, biotransport, permeability, extracellular diffusional resistance, internal diffusion
Introduction
Nitric oxide (NO) acts as a potent vasodilator in vasculature (Furchgott and Zawadzki, 1980; Ignarro et al., 1987) and is a key player in physiological and pathophysiological processes (Moncada et al., 1991). In vasculature, NO homeostasis is maintained with its production by endothelial cells and consumption by smooth muscle cells and red blood cell (RBC) hemoglobin (Hb). It is established that Hb is an effective scavenger of NO (kHb-NO ~ 107 M−1 s−1) (Cassoly and Gibson, 1975; Doyle and Hoekstra, 1981; Eich et al., 1996; Moncada et al., 1991). This has raised an important question about how NO is able to escape its potent scavenger Hb to maintain NO bioavailability in the vasculature. The paradox of vasoactive nitric oxide (NO) production in the close proximity of an effective NO scavenger Hb encapsulated in red blood cells has resulted in multitude of theoretical and experimental studies to examine NO interaction with RBCs (Deonikar and Kavdia, 2010a; Han and Liao, 2005; Huang et al., 2007; Liao et al., 1999; Vaughn et al., 2000).
The NO consumption by RBCs is much lower than that of NO consumption by equivalent amount of free Hb (Carlsen and Comroe, 1958; Deonikar and Kavdia, 2010b; Vaughn et al., 2001). A series of transport resistances are reported to slow the NO-RBC interactions. In blood vessels, a red blood cell-free layer near the vessel wall provides diffusional resistance for NO transport (Liao et al., 1999). Furthermore, an unstirred layer surrounding an RBC can provide additional diffusional resistance (Liu et al., 2002; Liu et al., 1998b). The membrane of the RBC can also act as a resistance for NO transport into the RBC. Sakai et al. (Sakai et al., 2008) recently reported that a diffusional transport resistance is also present inside the RBC. Although it is established that RBCs consume NO at a lower rate than free Hb, the mechanisms that lead to the lower consumption are still under intense investigation.
Several experimental studies have reported that RBC membrane permeability plays a critical role in the NO-RBC interactions. In the literature, RBC membrane permeability for NO varies four orders of magnitude from 0.0415 –40 cm/s (Liu et al., 2007; Tsoukias and Popel, 2002; Vaughn et al., 2001). Han et al. (Han and Liao, 2005) observed an increase in NO diffusion into the RBCs when they reduced the submembrane cytoskeleton compared to that with an intact submembrane cytoskeleton. Additionally, a study by Huang et al. (Huang et al., 2001) reported that the NO-RBC interaction increased and decreased when RBC membrane was chemically modified with azide and bis(sulfosuccinimidul)-suberate, respectively. Recently, we reported that a RBC membrane permeability of 0.0415–0.4 cm/s is required to maintain sufficient NO bioactivity (Deonikar and Kavdia, 2010a). In a computational analysis of an earlier experimental study by Azarov et al. (Azarov et al., 2005), Huang et al. (Huang et al., 2007) suggested that the binding of deoxygenated hemoglobin at the band-3 protein in submembrane cytoskeleton increased the membrane permeability NO by approximately ~10 fold than that under oxygenated conditions, thereby allowing more NO under deoxygenated conditions and less NO under oxygenated conditions through the RBC membrane for NO-RBC interactions.
Experimental and theoretical analyses have proposed that the extracellular diffusional resistance plays a major role in slowing NO-RBCs interactions (Liu et al., 2002; Liu et al., 1998b). Given that the extracellular diffusional resistance lowers the oxygen uptake by RBCs (Huxley and Kutchai, 1981), it is extrapolated that the transport of similar sized gaseous molecule NO is also limited to the RBCs by the extracellular diffusional resistance (Huxley and Kutchai, 1981; Liu et al., 2002). By comparing the measured rate of NO disappearance in presence of RBCs and oxyHb, Liu et al. (Liu et al., 2002) concluded that the lower consumption of NO by RBCs is due to extracellular diffusional resistance.
The understanding of NO-RBC interactions is also critical in developing and optimizing the Hb based oxygen carriers (HBOC) because the NO bioavailability at smooth muscle cell layer for vasodilatation is dependent on NO consumption in the vascular lumen by the HBOC. Diffusional resistance and permeability are important design parameters for HBOC. Sakai et al. (Sakai et al., 2008) reported that the internal diffusional resistance and not the lipid membrane barrier is responsible for lowering the consumption of NO by the Hb vesicles designed to carry oxygen, and they extrapolated this to NO-RBC interactions. A recent study by Azarov et al. (Azarov et al., 2011) concluded that extracellular diffusion was the rate limiting step for NO-RBC and NO-Hb vesicle interactions while NO membrane permeability was the rate limiting step for NO-RBC microparticle interactions.
The understanding of NO-RBC interactions will also provide insight into the mechanisms of NO export out of the RBCs. RBCs have been reported to preserve NO bioactivity in the form of S-nitrosohemoglobin (SNOHb) (Jia et al., 1996; Stamler et al., 1997). In addition, deoxyHb can act as a nitrite reductase to form NO under deoxygenated conditions (Crawford et al., 2006; Gladwin et al., 2006). Export of NO from either SNOHb or nitrite reductase pathway would strongly depend on the transport resistances in the RBC and vascular lumen.
Thus, the quantification of individual transport resistance can provide useful insights in NO-RBC interactions. To understand the individual contributions of transport resistances including membrane permeability, extra-, and intra- cellular resistances on NO-RBC interactions, we developed a computational model of NO transport to a single RBC. We predicted the NO concentration profile across the unstirred plasma layer, the RBC membrane and the RBC core for different values of NO concentration outside the unstirred plasma layer, Hct and RBC membrane permeability. We also estimated the NO concentrations inside and outside the RBC membrane as a function of extracellular diffusional resistance and RBC membrane permeability.
Mathematical model
Model Geometry
The NO biotransport to a single RBC at steady state was modeled in spherical geometry as shown in Fig. 1. The spherical model consisted of three concentric spheres representing the RBC core, the RBC membrane, and an unstirred plasma layer (PL). The inner sphere represents the RBC-hemoglobin and the outer sphere represents the unstirred plasma layer. The RBC membrane separates the inner sphere to the outer sphere and has a thickness of δ. NO diffuses from the unstirred plasma layer into the RBC membrane and reaches the RBC core to react rapidly with Hb. We simulated how NO-RBC interactions are affected from various hemodynamic, biophysical and biochemical parameters.
Figure 1. Model Geometry.
NO biotransport to a single RBC is modeled in spherical geometry. The model consists of three concentric spheres. The inner sphere represents the RBC enclosed by an outer sphere representing unstirred plasma layer surrounding the RBC. NO concentration outside the unstirred plasma layer is considered constant.
Model Equation
The steady state NO biotransport in the spherical geometry is represented as follows:
| (1) |
where, CNO represents the NO concentration, represents the diffusivity of NO in the respective region. Ri represents the net reaction rate to describe the NO consumption in each region. In the RBC core NO reacts with Hb. The reaction rate is given as Rcyt = kNO–Hb C NO CHb. kNO–Hb is the reaction rate constant for NO-Hb reaction in the RBC core and CHb represents the hemoglobin concentration inside the RBC. No reaction is considered in the RBC membrane, hence Rm = 0. In the unstirred plasma layer surrounding the RBC, NO autooxidation reaction is considered and the reaction rate is given as Rpl = kNO–O2 CNO 2CO2, where kNO–O2 represents the reaction rate constant for auto-oxidation reaction of NO in the unstirred plasma layer and CO2 represents the oxygen concentration in the unstirred plasma layer.
Boundary Conditions
A zero flux boundary condition was assumed at the center of the RBC to represent the symmetry of NO concentration. Thus,
At the center of the RBC (r = 0):
| (2a) |
Continuous flux boundary conditions were assumed at the membrane- unstirred plasma layer and the membrane-RBC core interfaces.
At the unstirred plasma layer –membrane interface:
| (2b) |
are the NO diffusivities in unstirred plasma layer and the membrane, respectively. rrbc is the radius of the RBC.
At the membrane–RBC core interface:
| (2c) |
is the NO diffusivity in the RBC core, δ is the thickness of the RBC membrane. NO concentration at the outer edge of unstirred plasma layer was assumed constant.
At the outer surface of unstirred plasma layer (r = rpl)
| (3) |
Model Parameters
Parameter values used to solve the model equation are listed in Table 1. The radius of the RBC, rrbc, is 2.8 µm and was based on a RBC volume of ~90 µm3 (Fung, 1997). The thickness of the RBC membrane (δ) is 7 × 10−3 µm (Malinski et al., 1993). To understand the effect of Hct and consequently the diffusional resistance provided by the unstirred plasma layer surrounding the RBC on the NO transport to RBC, we used Hct values ranging from 1 to 45%. The thickness of the unstirred plasma layer surrounding the RBCs is dependent on the local Hct. Hct is the volumetric ratio of RBC to the blood. For a single RBC, the radius of the unstirred plasma layer surrounding it is obtained by taking the ratio of RBC volume to blood volume. Since the RBC in this study is approximated to a spherical shape, the Hct can be rewritten as where rrbc is the RBC radius and rpl is the unstirred layer (outer sphere) radius. Thus,
| (4) |
is 3.3 × 10−5 cm2/s (Malinski et al., 1993; Vaughn et al., 1998). was obtained from the permeability (Pm) values of NO in the RBC membrane by using following equation.
| (5) |
In the cytosol of RBC, was considered to be 1.6×10−5 cm2/s (Goldstick et al., 1976; Malinski et al., 1993). To study the effect of RBC membrane permeability on steady state NO concentrations inside and outside the RBC membrane, we used Pm values ranging from 0.0415 – 40 cm/s (Liu et al., 2007; Tsoukias and Popel, 2002; Vaughn et al., 2001).
Table 1.
Model Parameters
| Parameter | Description | Value/Expression | |
|---|---|---|---|
| Pm | NO permeability in RBC membrane | 0.0415, 0.4, 1 and 40 cm/s (Liu et al., 2007; Tsoukias and Popel, 2002; Vaughn et al., 2001) | |
| δ | Thickness of RBC membrane | 7×10−3 µm (Malinski et al., 1993) | |
| NO diffusivity in plasma | 3.3×10−5 cm2 s−1 (Malinski et al., 1993; Vaughn et al., 1998) | ||
| NO diffusivity in RBC membrane | Pm × δ | ||
| NO diffusivity in RBC core | 1.6×10−5 cm2 s−1(Goldstick et al., 1976; Malinski et al., 1993) | ||
| kHb–NO | NO-Hb reaction rate constant | 2.5×107 and 8.9×107 M−1s−1(Cassoly and Gibson, 1975; Eich et al., 1996; Herold et al., 2001) | |
| kNO–O2 | NO autooxidation rate constant | 9.6×106 M−2 s−1 | |
| rrbc | Radius of RBC | 2.8 µm (Fung, 1997) | |
| CHb | Hemoglobin concentration in RBC | 20.3 mM (Altman and Katz, 1971) | |
| CO2 | Oxygen concentration | 27 µM (Kavdia and Popel, 2003) | |
|
|
NO concentration outside unstirred plasma layer | 1, 10, 100 and 1000 nM |
The NO concentration outside the unstirred plasma layer was kept constant and was varied from 1, 10, 100 and 1000 nM for the simulations conducted in this study. To analyze the effect of NO-Hb reaction rate on NO-RBC interactions, simulations were performed for NO-Hb reaction rate constants of 2.5 × 107 and 8.9 × 107 M−1 s−1(Cassoly and Gibson, 1975; Eich et al., 1996; Herold et al., 2001). In the unstirred plasma layer surrounding the RBC, the NO transport was assumed to be due to diffusion and convective NO transport was neglected.
Estimation of diffusional resistances for NO transport to RBC
As shown in Fig. 1, NO encounters three transport resistances extracellular diffusion in the plasma, RBC membrane, and intracellular diffusion as it approaches the Hb encapsulated in the RBC. We evaluated the significance of each of the resistances as follows. To estimate the significance of intracellular diffusional resistance, we evaluated the internal effectiveness factor (η) for NO-RBC diffusion/reaction inside the RBC cytoplasm. η is an indicator of relative significance of diffusion and reaction for the overall reaction rate. Internal effectiveness is defined as the ratio of actual reaction rate to the reaction rate obtained if the entire interior surface of the spherical body was exposed to the outside surface concentration. The value of η ranges from 0 to 1. If η is close to 0, it indicates that the reaction rate is diffusion limited and a value close to 1 indicates reaction rate to be limited by surface-reaction.
The RBC core was considered a homogenous medium. For a spherical particle, η is calculated as follows (Fogler, 1986):
ϕ is the Thiele modulus and is calculated as follows:
where, (rrbc −δ) is the radius of the RBC core and CNO, core–m is the NO concentration at the RBC core – membrane interface.
In order to determine the relative contributions of transport resistance from RBC membrane and extracellular diffusion in unstirred plasma layer on NO transport to RBCs, we evaluated the mass transfer coefficients in the unstirred layer by equating the mass transfer of NO from outside the unstirred plasma layer to the RBC membrane- unstirred plasma layer interface and unstirred plasma layer-membrane interface to membrane-RBC core interface. A mass balance of NO in the unstirred plasma layer and RBC membrane is given as follows.
| (6) |
where, kec is the mass transfer coefficient in the unstirred plasma layer, is the NO concentration outside the unstirred layer, CNO, core–pl is the NO concentration at the RBC membrane–unstirred plasma layer interface, Pm is the RBC membrane permeability. kec was evaluated using Eq. 6 for all the Hct and Pm values used in this study. The total transport resistance for NO-RBC interactions was calculated by adding the extracellular diffusion, RBC membrane and internal diffusion resistances in series as follows equation.
| (7) |
where kcyt is the mass transfer coefficient in the RBC cytosol. Percent contributions from individual resistances were calculated as follows.
Numerical Solution
Equation 1 was solved numerically using appropriate boundary conditions to estimate the NO concentration profiles across the model geometry using FlexPDE5 software (PDESolutions Inc., Antioch, CA). The adaptive mesh finite element algorithm used in this software allows mesh generation in proportion to the concentration gradients in respective regions. The relative accuracy used in this study was 0.0005 for all simulations.
Results
Effect of RBC membrane permeability on NO biotransport to the RBC
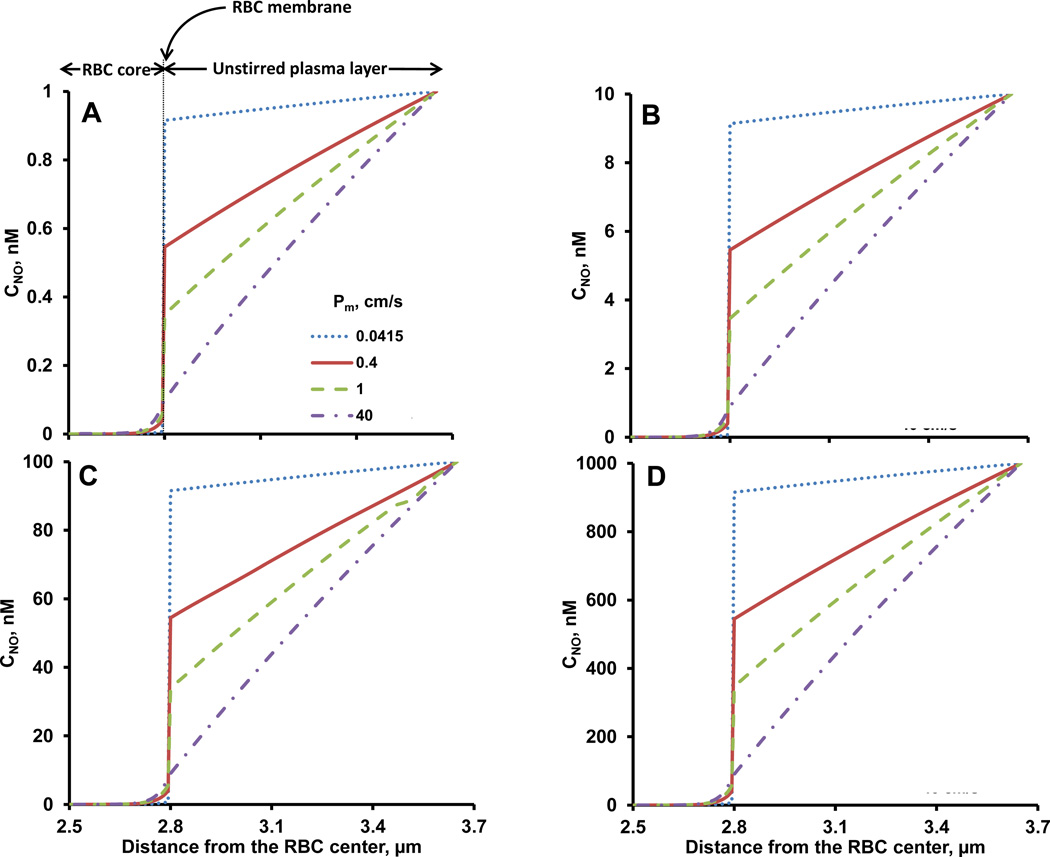
The role of resistance from RBC membrane in reducing the NO consumption by RBCs is under intense investigation (Deonikar and Kavdia, 2010a; Han and Liao, 2005; Huang et al., 2007; Liu et al., 2002; Liu et al., 1998b; Tsoukias and Popel, 2002). We studied the NO-RBC interactions for RBC membrane NO permeability of 0.0415, 0.4, 1 and 40 cm/s at physiological Hct of 45%. Fig. 2 shows the steady state NO concentration profiles as a function of distance from the RBC center (center at zero) for values of 1, 10, 100 and 1000 nM (panel A–D, respectively).
Figure 2. NO concentration profiles.
NO concentrations across the model geometry are plotted as a function of distance from the center of the RBC at different Pm values. Panels A, B, C and D represent the NO concentration profiles for unstirred plasma layer NO concentrations values of 1, 10, 100 and 1000 nM, respectively. The Hct used for these simulations was 45% and NO-Hb reaction rate constant was 8.9×107 M−1s−1.
Steady NO concentrations across the model geometry were predicted by solving Eq (1) numerically using appropriate boundary conditions given in Eq (2a, 2b, 2c) and (3). The concentration gradient arise from NO consumption by RBC encapsulated Hb or oxygen and the NO diffusion across the model geometry. Before NO reaches the RBC core and reacts with RBC bound Hb, NO has to cross the unstirred layer and the membrane. As expected, the steady state NO concentrations decreased as NO diffused towards the center of the RBC for all the and Pm values used in the simulations. The steady state NO concentrations across the model geometry decreased with increased in Pm. This is due to the fact that at low Pm values, less amount of NO would pass through the membrane and as the Pm increases, more NO can pass through the membrane. Hence, the steady state NO concentrations will be higher at lower Pm and the steady state NO decrease with increase in Pm.
Three gradients of NO concentrations were observed across the model geometry. The NO concentrations gradients include between 1) the edge of the unstirred plasma layer and the outside RBC membrane; 2) the out and in- side RBC membrane; and 3) the inside RBC membrane and the RBC core. As the RBC membrane permeability increased, NO concentration gradients across the unstirred plasma layer and from inside membrane to the RBC core increased whereas NO concentration gradients across the membrane decreased (Fig. 2). For all the simulations, NO concentrations reached zero close to the membrane inside the RBC core. The RBC membrane permeability of 40 cm/s did not have significant transport resistance as demonstrated by almost linear NO profile across the whole geometry.
Relationship between RBC membrane NO concentration, RBC membrane permeability
In order to understand the effect of membrane permeability on NO availability across RBC membrane, NO concentrations as a function of RBC membrane permeability on the either side of the RBC membrane are shown in the Figure 3. CNO, core-m increased with permeability. The highest CNO, core-m were observed at Pm of 40 cm/s and the lowest CNO, core-m were observed at Pm of 0.0415 cm/s. A logarithmic relationship was observed between CNO, core–m and Pm which is given by , where concentrations are in nM and Pm is in cm/s. The steady state CNO, pl–m (Fig. 3B) decreased with RBC membrane permeability. For a given , CNO, pl–m were highest for Pm = 0.0415 cm/s and lowest for Pm = 40 cm/s. The logarithmic relationship between CNO, pl–m and Pm is given by , where concentrations are in nM and Pm is in cm/s.
Figure 3. NO concentrations at the RBC membrane.
CNO, core–m, NO concentration at the RBC core-RBC membrane interface, (panel A) and CNO, pl–m, NO concentrations at the RBC membrane-plamsa interface (panel B), are plotted as a function of Pm for values of 1, 10, 100 and 1000 nM. The Hct used for these simulations was 45% and NO-Hb reaction rate constant was 8.9×107 M−1s−1.
NO concentrations at the RBC membrane increased with Hct in a membrane permeability dependent manner
Unstirred plasma layer thickness surrounding the RBC offers diffusional resistance for NO transport to the RBC and is a function of Hct (Liu et al., 2002; Liu et al., 1998b). We performed simulations for Hct ranging from 1 to 45% to examine the contribution of extracellular diffusional resistance on NO transport to RBC. was kept constant at 100 nM. Steady state CNO, core–m and CNO, pl–m were estimated and plotted in Fig. 4A and B, respectively.
Figure 4. NO concentrations at the membrane as a function of Hct.
CNO, core–m, NO concentration at the RBC core-RBC membrane interface (panel A), and CNO, pl–m, NO concentrations at the RBC membrane-plasma interface (panel B), are plotted as a function of Hct for . NO-Hb reaction rate constant used was 8.9×107 M−1s−1, Hct ranged from 1–45%.
Increasing Hct increased both CNO, core–m and CNO, pl–m for all the RBC membrane permeability values. The increase in membrane NO concentration was linear for Hct ≥ 10%. The linear relationships between membrane NO concentrations and Hct are provided in Table 2. For Hct ≤ 10%, the membrane NO concentrations increased non-linearly with Hct. At higher Pm values of 1 and 40 cm/s, the steady state NO concentrations inside and outside the RBC membrane increased linearly with Hct. For a given Hct, we observed that CNO, pl–m decreased whereas CNO, core–m increased with increase in membrane permeability.
Table 2.
Membrane NO concentration and Hct relationship for Hct>10%
| Pm, cm/s | RBC core-membrane NO conc., nM |
R2 | Plasma-membrane NO conc., nM |
R2 |
|---|---|---|---|---|
| 0.0415 | CNO, core–m = 0.36 Hct + 75.75 | 0.98 | CNO, pl–m = 0.0028 Hct + 0.58 | 0.98 |
| 0.4 | CNO, core–m = 0.71 Hct + 22.62 | 0.99 | CNO, pl–m = 0.049 Hct + 1.56 | 0.99 |
| 1 | CNO, core–m = 0.54 Hct + 9.84 | 0.99 | CNO, pl–m = 0.085 Hct + 1.57 | 0.99 |
| 40 | CNO, core–m = 0.15 Hct + 1.46 | 0.99 | CNO, pl–m = 0.14 Hct + 1.29 | 0.99 |
CNO, core–m is the NO concentration at the RBC core-RBC membrane interface; CNO, pl–m is the NO concentration at the RBC membrane- unstirred plasma layer interface; Hct units are in %
Effect of NO-Hb reaction rate constant on membrane NO concentrations
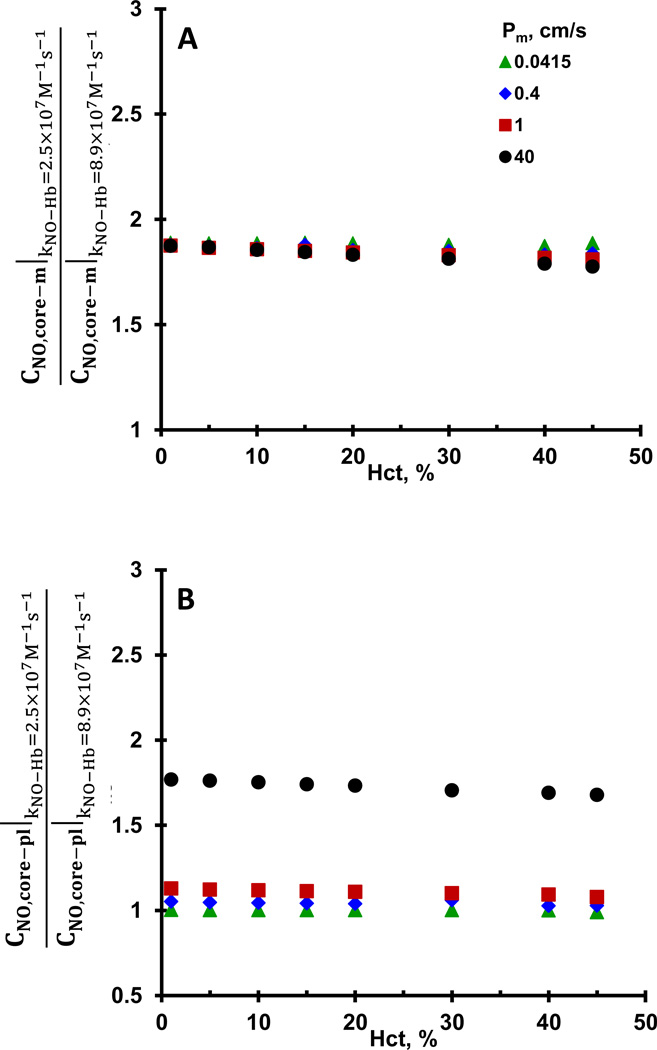
The reaction rate constant of NO-Hb reaction has been reported in the range of 2.5–8.9 × 107 M−1 s−1 (Cassoly and Gibson, 1975; Eich et al., 1996; Herold et al., 2001; Vaughn et al., 1998). To assess the effect of NO consumption rate by Hb on NO transport to the RBCs, we estimated CNO, core–m and CNO, pl–m for NO-Hb reaction rate constants of 2.5 × 107 M−1 s−1 and 8.9× 107 M−1 s−1. Ratios of CNO, core–m and CNO, pl–m estimated for 2.5 × 107 M−1 s−1 w.r.t. CNO, core–m and CNO, pl–m estimated for 8.9 × 107 M−1 s−1 are plotted as a function of Hct in Fig. 5A and B, respectively. CNO, core–m were ~1.8 fold higher for NO-Hb reaction rate constant of 2.5× 107 M−1 s−1 than those for 8.9× 107 M−1 s−1 and remained similar for all Hct and Pm. For membrane permeability of 0.0415 cm/s, CNO, pl–m for NO-Hb reaction rate constants 2.5 and 8.9 × 107 M−1 s−1 were similar to each other and did not change with Hct. However, for membrane permeability of to 0.4, 1 and 40 cm/s, CNO, pl–m for NO-Hb reaction rate constant 2.5 × 107 M−1 s−1 were ~1.05, 1.1 and 1.7-fold higher than those at NO-Hb reaction rate constant of 8.9 × 107 M−1 s−1, respectively.
Figure 5. Effect of NO-Hb reaction rate constants on NO membrane concentrations.
CNO, core–m and CNO, pl–m were estimated for NO-RBC reaction rate constants of 2.5 and 8.9×107 M−1s−1. Ratios of CNO, core–m at 2.5×107 M−1s−1 to CNO, core–m at 8.9×107 M−1s−1 are plotted as a function of Hct in panel A and ratios of CNO, pl–m at 2.5×107 M−1s−1 to CNO, pl–m at 8.9×107 M−1s−1 are plotted in panel B as a function of Hct.
Relative contribution of intracellular diffusion, extracellular diffusion and RBC membrane permeability on NO transport to the RBC
To determine the relative importance of internal diffusional transport resistance on overall NO reaction rate with RBCs, we estimated the internal effectiveness factor. The internal effectiveness factor is the ratio of actual reaction rate and the rate of reaction if the entire interior of the RBC were to be exposed to the surface NO concentration, which will indicate the rate limiting step for NO reaction with RBCs. The internal effectiveness factor along with the Thiele modulus (a ratio of characteristic diffusion time to characteristic reaction time (Fogler, 1986)) was also evaluated for different NO-Hb reaction rate constants and membrane permeability values for physiological Hct of 45 and listed in Table 3. As the Pm increased from 0.0415 to 40 cm/s, the Thiele modulus changed from ~0.01 to 0.05 and 0.01 to 0.03 for NO-Hb reaction rate constants of 8.9 and 2.5 × 107 M−1 s−1, respectively. The internal effectiveness factor approached ~1 for all the RBC membrane permeability values for both the NO-Hb reaction rate constants at 45% Hct. Based on the internal effectiveness (~1) and Thiele modulus values (≪1) estimates, the NO reaction with Hb and not the internal diffusion is the rate limiting step in the RBC core (Fogler, 1986). We observed similar Thiele modulus and internal effectiveness factor values for 1, 5, 10, 15, 20, 30 and 40% Hct values (data not shown).
Table 3.
Internal Effectiveness factors and Thiele modulus for 45% Hct
| Thiele Modulus | Internal Effectiveness | |||
|---|---|---|---|---|
| Pm, cm/s | kHb-NO=8.9×107 M−1s−1 | kHb-NO=2.5×107 M−1s−1 | kHb-NO=8.9×107 M−1s−1 | kHb-NO=2.5×107 M−1s−1 |
| 0.0415 | 0.0177 | 0.0129 | 0.999979 | 0.999989 |
| 0.4 | 0.0410 | 0.0295 | 0.999888 | 0.999942 |
| 1 | 0.0488 | 0.0352 | 0.999841 | 0.999917 |
| 40 | 0.0581 | 0.0308 | 0.999775 | 0.999937 |
Pm is the NO permeability of the RBC membrane; kHb-NO is the reaction rate constant for NO-Hb reaction.
Individual contributions from membrane permeability and extracellular diffusion in the unstirred layer towards the overall transport resistance for NO transport to RBCs were calculated for all the Hct and membrane permeability values. The percentage of each individual transport resistance with respect to the overall NO transport resistances were calculated using Eq 8a and 8b and plotted as a function of RBC membrane permeability for all the Hct values in Fig 6. Our results showed that contributions from extracellular diffusion and RBC membrane resistance toward total transport resistance increased and decreased, respectively, with RBC membrane permeability for all Hct. At a Hct of 1%, the extracellular diffusion and RBC membrane resistance contributions were ~84% and ~16%, respectively, of the total transport resistance for NO consumption by RBCs for RBC membrane permeability of 0.4 cm/s. On the other hand, for the same membrane permeability value of 0.4 cm/s at higher Hct of 45%, we observed that the transport resistance from the membrane accounted for ~52% whereas the extracellular diffusion resistance accounted for 47% of the total transport resistance. For all the Hct values used in this study, the contribution from membrane resistance was more for Pm values in the 0.0415–0.4 cm/s range whereas the extracellular diffusion resistance contribution was higher for the higher Pm in the 1–40 cm/s. Our results indicate that under physiological Hct, the membrane resistance is more significant if the Pm were in the range of 0.0415–0.4 cm/s whereas extracellular resistance was the major transport resistance for Pm in the range of 1–40 cm/s. Note that the most significant aspect of these results is that the extracellular diffusion contribution to overall transport resistance overtakes the membrane resistance contribution at Pm value over a narrow range from 0.21–0.44 cm/s for hematocrit range of 10–45%, respectively.
Figure 6. Relative contributions of transport resistances.
Contribution of membrane permeability and extracellular resistance in NO-RBC interaction was plotted for Hct ranging from 1–45% and Pm values ranging from 0.0415–40 cm/s.
Validation of modeling approach
To validate the effects of unstirred plasma layer diffusional resistances on the modeling approach used in this study, we estimated NO concentrations for extreme values of diffusion coefficient for NO. We used 2 orders of magnitude higher diffusion coefficient of 3.3×10−3 cm2·s−1 and a membrane permeability of 40 cm·s−1 to estimate NO concentrations across the model geometry. In addition, As shown in Fig. 7, we observed that for the high diffusion coefficient of 3.3×10−3 cm2·s−1, the gradient in steady state NO concentrations in the unstirred plasma layer was much lower as compared to that of low diffusion coefficient of 3.3×10−5 cm2·s−1 for the same RBC membrane permeability of 40 cm·s−1. Additionally, the steady state concentrations were almost identical to those obtained at the low RBC membrane permeability value of 0.0415 cm·s−1. When we increased the diffusion coefficient to 3.3×10−2 cm2·s−1, we observed that the effect of unstirred plasma layer on NO transport was negligible as evidenced by a nearly flat NO concentration profile. This indicates that the unstirred plasma layer does not offer significant diffusional resistance for NO transport and is not a major limitation for NO-RBC interactions when the NO diffusivity is very high.
Figure 7. Validation of model.
NO concentration profiles are plotted as a function of distance from the RBC center. NO concentrations were estimated for diffusion coefficients of 3.3×10−5, 3.3×10−3 and 3.3×10−2 at high Pm of 40 cm·s−1, and compared with NO profiles at diffusion coefficient of 3.3×10−5 cm2·s−1 at low Pm of 0.0415 cm·s−1.
Discussion
It is established that NO consumption by Hb in RBCs is much lower than that of free Hb and this lower rate of consumption is attributed to transport resistances from cell free layer (Liao et al., 1999), extracellular diffusion in unstirred layer surrounding the RBCs (Liu et al., 2002), RBC membrane (Vaughn et al., 2000) and intracellular diffusion inside the RBCs (Sakai et al., 2008). However, the relative contribution of these transport resistances is still not clear. The analysis of the relative contribution from individual transport resistance has proven more difficult due to lack of direct physical measurements of parameters like RBC membrane permeability. Computational modeling of NO biotransport can provide useful insights into quantifying the relative contributions of the individual transport resistances. Towards this end, we present a computation analysis of NO biotransport to a single RBC to analyze the role of intracellular diffusion resistance in the RBC core, RBC membrane permeability, extracellular diffusion resistance from unstirred layer surrounding the RBC and NO consumption rates by Hb in lowering the NO-RBC interactions.
Role of intracellular diffusional resistance in NO-RBC interactions
A number of recent studies have analyzed the contribution of intracellular diffusional resistance in the RBC cytosol. A recent study involving NO interactions with polyethylene glycol conjugated with liposome encapsulated Hb (PEG-LEH) by Rameez et al. (Rameez and Palmer, 2011) attributed the lower NO consumption by PEG-LEH to the intracellular diffusional resistance. In an experimental analysis of NO transport to Hb vescicles (HbV), Sakai et al. (Sakai et al., 2008) reported that as the concentration of Hb inside the HbV and the size of the HbV increased, the NO binding to Hb was reduced. They concluded that the NO binding to Hb in the HbV is dependent on the Hb concentration indicating a role for intracellular diffusion in reducing the NO binding to Hb. They further postulated that the intracellular diffusion may also play a role reducing the NO consumption by Hb in the RBC cytosol.
To understand the significance intracellular diffusional resistance, we estimated the Thiele modulus and internal effectiveness factor, indicators of rate limiting mechanisms (Fogler, 1986) in a spherical particle (RBC). Based on our results of Thiele modulus and internal effectiveness factor, the rate limiting step for NO transport to the RBCs is the reaction of NO with the Hb in RBCs. In other words, the NO consumption rate by RBC is determined by how fast the RBC encapsulated Hb consumes NO rather than how fast NO can reach Hb. It is worth noting that the internal effectiveness factor remained ~1 and the Thiele modulus was << 1 for all the RBC membrane permeability and NO-Hb reaction rate constant values used in this study. These results suggest that internal diffusional resistance in the RBC cytosol may not play a significant role in the NO consumption by RBCs.
Role of membrane resistance in NO-RBC interactions
Resistance from the RBC membrane for the transport of small gaseous molecules such as O2 was shown to be much lesser than that from the unstirred layer surrounding the RBCs (Coin and Olson, 1979; Huxley and Kutchai, 1981). Since NO is similar in size to O2, RBC membrane was shown to provide insignificant resistance for NO transport into the RBCs (Liu et al., 2002; Liu et al., 1998b). However, some studies have estimated a low Pm value for NO in the RBC membrane indicating a significant role for RBC membrane in NO-RBC interactions (Han and Liao, 2005; Vaughn et al., 2000). Additionally, oxygen tension in the RBCs was also shown to affect the Pm, and hence the NO-RBC interactions (Huang et al., 2007).
The value of Pm is a critical factor in determining the impact of membrane resistance in NO-RBC interactions. Lack of direct experimental measurement for Pm value adds to the complexity of determining the role of RBC membrane resistance in NO-RBC interactions. In this model, we estimated steady state NO concentrations at the inside and outside membrane using Pm range of 0.0415–40 cm/s (Liu et al., 2002; Tsoukias and Popel, 2002; Vaughn et al., 2000). For physiological Hct of 45% (Fig.2), as the Pm increased, the steady state NO concentrations inside the membrane increased. This indicates that the transport resistance for NO from the RBC membrane decreased thereby allowing more NO inside the RBC. The decrease in steady state NO concentrations outside the membrane with an increase in Pm further corroborates that the RBC membrane transport resistance decreased as the Pm values increased. An increase in NO auto-oxidation rate was reported by Liu et al. in the biological membranes (Liu et al., 1998a). To understand the effect of increased NO auto-oxidation reaction rate, we incorporated the NO auto-oxidation reaction in the RBC membrane. We observed that the estimated NO concentrations across the model geometry remained the same as those without NO auto-oxidation reaction in the membrane (data not shown).
For lower Pm of 0.0415 cm/s, the membrane NO concentrations for Hct >10% remained similar indicating that NO consumption by RBCs remained similar despite an increase in the Hct. In an experimental and theoretical analysis of NO-RBC interactions using a novel flow system, we also previously observed that the NO consumption by RBCs remained similar for Hct values >10% (Deonikar and Kavdia, 2010b) which indicates a significant role for transport resistance from the RBC membrane at higher Hct.
Role of extracellular diffusion in unstirred layer on NO-RBC interactions
The unstirred layer surrounding the RBC has been reported to be a major barrier for NO transport to the RBC (Liu et al., 2002; Liu et al., 1998b; Tsoukias and Popel, 2002). The unstirred layer surrounding the RBCs is reported to exist even in rapid mixing devices (Coin and Olson, 1979; Rice, 1980). The thickness of the unstirred layer around the RBC indicates the diffusional distance NO has to overcome before it reaches RBCs. The thickness of the unstirred layer is dependent on the Hct (Deonikar and Kavdia, 2010a; Liu et al., 2002; Tsoukias and Popel, 2002) as shown in Eq. (4). To determine the influence of the thickness of unstirred layer, we estimated the steady state NO concentrations at the inside and outside RBC membrane for Hct values ranging from 1–45%. As shown in the Fig. 3, the inside and outside steady state NO concentrations increased with the Hct in a Pm dependent manner. For Hct>10%, we observed a linear increase in membrane concentrations w.r.t. Hct (Table 2). For a given Pm, the diffusional distances for NO should decrease with an increase in Hct, thereby increasing NO availability at the inside and outside RBC membrane at steady state. It is worth noting that the inside membrane concentrations at steady state were higher for high Pm and vice versa, as NO receives little membrane resistance at high Pm values. On the other hand, the outside membrane NO concentrations were higher for lower Pm and vice versa.
Decrease in NO consumption by changing the NO-Hb reaction rate constant from 8.9 to 2.5×107 M−1s−1 increased the inside as well as outside membrane steady NO concentrations. However, the fold increase in the membrane NO concentrations remained unaffected by Hct as well as membrane permeability. These results indicate that the steady state NO concentrations are less sensitive to the change in the NO consumption inside the RBC.
Relative contributions of individual transport resistances on NO-RBC interactions
We estimated the contributions from membrane transport resistance and the resistance from unstirred layer by equating the fluxes in the unstirred layer and the RBC membrane. The transport resistance from the internal diffusion inside the RBC was deemed negligible based on the internal effectiveness factor and Thiele modulus. As shown in Fig. 6, the transport resistance from the extracellular resistance increased while the transport resistance from membrane decreased with membrane permeability for all the Hct.
Our results indicate that the resistance from the RBC membrane plays a dominant role if the Pm was very low. The threshold value of Pm below which RBC membrane resistance is dominant over extracellular resistance is dependent on Hct. For a low Hct of 1%, the fraction of transport resistance was ~16% for RBC membrane and 84% from extracellular resistance at a low membrane permeability value was 0.4 cm/s. Liu et al. (Liu et al., 2002) also found that at lower Hct, the extracellular resistance was a significant resistance for NO transport to RBCs. We recently reported that the Pm should be in the range of 0.0415–0.4 cm/s so that sufficient NO bioactivity is maintained at the smooth muscle cell layer for vasodilation (Deonikar and Kavdia, 2010a). In that case, at physiological Hct of 45%, the RBC membrane resistance would account for ~50–90% of the total transport resistance for NO-RBC interactions. If the Pm was in the range of 1–40 cm/s, the contribution of membrane resistance towards the overall transport resistance would be in the range of ~1–30%.
NO transport models proposed by Liu et al. (Liu et al., 2002; Liu et al., 1998b) and Tsoukias et al. (Tsoukias and Popel, 2002) reported that extracellular diffusion resistance was a major transport resistance for NO-RBC reaction indicating no resistance from the RBC membrane and a high Pm value. On the other hand, modeling and experimental studies from Liao group reporting a significant role for membrane resistance have indicated very low values of Pm (0.0415–0.4 cm/s) (Han and Liao, 2005; Vaughn et al., 2000; Vaughn et al., 2001). One of the key findings of our study is the narrow range of RBC membrane permeability values of 0.21–0.44 cm/s for Hct range of 10–45% which provides a conclusive criteria in determining the significance of extracellular and membrane transport resistances in NO-RBC interaction. We predict that RBC membrane is significant transport resistance if the Pm value is lower than Pm range of 0.21–0.44 cm/s range, consistent with findings of Liao group (Han and Liao, 2005; Vaughn et al., 2000; Vaughn et al., 2001). The extracellular diffusion and membrane resistance both play significant role if the Pm is ~ 0.21–0.44 cm/s. Extracellular diffusion is the dominating transport resistance if the Pm is higher than the 0.21–0.44 cm/s range consistent with findings of Liu et al. (Liu et al., 2002; Liu et al., 1998b) and Tsoukias et al. (Tsoukias and Popel, 2002).
Although not analyzed in this study, along with extracellular diffusion from unstirred layer RBC membrane, cell free layer near the vessel wall also provides a significant source of resistance for NO diffusion in the vascular lumen and can lower the NO-RBC interactions (Deonikar and Kavdia, 2012; Kavdia and Popel, 2003; Kavdia et al., 2002; Kim et al., 2007). RBCs under flow tend to migrate towards the center of the vessel leaving an almost RBC free layer near the vessel wall consisting mainly of plasma. The width of cell free layer plays a significant role in modulating the effective blood viscosity thereby modulating the wall shear stress dependent NO production from the endothelium, in small arterioles (Ong et al., 2011).
Physiological Significance
The computational model developed in this study provides a unique tool for quantification of individual transport resistances involved in lowering NO-RBC interactions. We report a logarithmic relationship between steady state membrane NO concentrations and Pm, which is dependent on the NO concentration outside the unstirred layer. This relationship, in conjunction with experimental data, can be utilized to determine NO scavenging rates for HBOCs and help optimize the design parameters like the size, Hb concentration inside HBOC, thickness of HBOC membrane for developing HBOCs. RBCs have been reported to preserve NO bioactivity in the form of either S-nitrosohemoglobin (SNOHb) (Jia et al., 1996; Stamler et al., 1997). Nitrite reductase activity of deoxyHb in the RBCs is also reported to release NO and the NO bioactivity can be transported out of RBCs to cause vasodilation (Crawford et al., 2006; Gladwin et al., 2006). The relationship between Pm and NO concentrations at the membrane obtained in this study can be used to quantify the amount of NO exported out of RBCs from SNOHb/nitrite pathways.
Highlkight.
We developed a model of nitric oxide (NO) transport to a red blood cell (RBC)
Effect of diffusion transport resistances on NO-RBC interaction was analysed
Intracellular diffusion of NO does not affect NO-RBC interaction
Membrane transport resistance is dominant if membrane permeability (Pm)<0.21 cm/s
Extracellular diffusion transport resistance is dominant if Pm>0.44 cm/s
Acknowledgements
This study is supported by NIH grants R01 HL084337 and R15 HL087287.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Altman PL, Katz DD. Federation of American Societies for Experimental Biology. Bethesda, Md: 1971. Respiration and circulation. [Google Scholar]
- Azarov I, Huang KT, Basu S, Gladwin MT, Hogg N, Kim-Shapiro DB. Nitric oxide scavenging by red blood cells as a function of hematocrit and oxygenation. J Biol Chem. 2005;280:39024–39032. doi: 10.1074/jbc.M509045200. [DOI] [PubMed] [Google Scholar]
- Azarov I, Liu C, Reynolds H, Tsekouras Z, Lee JS, Gladwin MT, Kim-Shapiro DB. Mechanisms of slower nitric oxide uptake by red blood cells and other hemoglobin-containing vesicles. J Biol Chem. 2011;286:33567–33579. doi: 10.1074/jbc.M111.228650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlsen E, Comroe JH., Jr The rate of uptake of carbon monoxide and of nitric oxide by normal human erythrocytes and experimentally produced spherocytes. J Gen Physiol. 1958;42:83–107. doi: 10.1085/jgp.42.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassoly R, Gibson Q. Conformation, co-operativity and ligand binding in human hemoglobin. J Mol Biol. 1975;91:301–313. doi: 10.1016/0022-2836(75)90382-4. [DOI] [PubMed] [Google Scholar]
- Coin JT, Olson JS. The rate of oxygen uptake by human red blood cells. J Biol Chem. 1979;254:1178–1190. [PubMed] [Google Scholar]
- Crawford JH, Isbell TS, Huang Z, Shiva S, Chacko BK, Schechter AN, Darley-Usmar VM, Kerby JD, Lang JD, Jr, Kraus D, Ho C, Gladwin MT, Patel RP. Hypoxia, red blood cells, and nitrite regulate NO-dependent hypoxic vasodilation. Blood. 2006;107:566–574. doi: 10.1182/blood-2005-07-2668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deonikar P, Kavdia M. Extracellular diffusion and permeability effects on NO-RBCs interactions using an experimental and theoretical model. Microvasc Res. 2010a;79:47–55. doi: 10.1016/j.mvr.2009.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deonikar P, Kavdia M. An integrated computational and experimental model of nitric oxide-red blood cell interactions. Ann Biomed Eng. 2010b;38:357–370. doi: 10.1007/s10439-009-9823-x. [DOI] [PubMed] [Google Scholar]
- Deonikar P, Kavdia M. Low micromolar intravascular cell-free hemoglobin concentration affects vascular NO bioavailability in sickle cell disease: a computational analysis. J Appl Physiol. 2012;112:1383–1392. doi: 10.1152/japplphysiol.01173.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle MP, Hoekstra JW. Oxidation of nitrogen oxides by bound dioxygen in hemoproteins. J Inorg Biochem. 1981;14:351–358. doi: 10.1016/s0162-0134(00)80291-3. [DOI] [PubMed] [Google Scholar]
- Eich RF, Li T, Lemon DD, Doherty DH, Curry SR, Aitken JF, Mathews AJ, Johnson KA, Smith RD, Phillips GN, Jr, Olson JS. Mechanism of NO-induced oxidation of myoglobin and hemoglobin. Biochemistry. 1996;35:6976–6983. doi: 10.1021/bi960442g. [DOI] [PubMed] [Google Scholar]
- Fogler HS. Elements of Chemical Reaction Engineering. Englewood Cliffs, New Jersey: Prentice-Hall Inc.; 1986. [Google Scholar]
- Fung YC. Biomechanics: Circulation. New York: Springer-Verlag; 1997. [Google Scholar]
- Furchgott RF, Zawadzki JV. The obligatory role of endothelial cells in the relaxation of arterial smooth muscle by acetylcholine. Nature. 1980;288:373–376. doi: 10.1038/288373a0. [DOI] [PubMed] [Google Scholar]
- Gladwin MT, Raat NJ, Shiva S, Dezfulian C, Hogg N, Kim-Shapiro DB, Patel RP. Nitrite as a vascular endocrine nitric oxide reservoir that contributes to hypoxic signaling, cytoprotection, and vasodilation. Am J Physiol Heart Circ Physiol. 2006;291:H2026–H2035. doi: 10.1152/ajpheart.00407.2006. [DOI] [PubMed] [Google Scholar]
- Goldstick TK, Ciuryla VT, Zuckerman L. Diffusion of oxygen in plasma and blood. Adv Exp Med Biol. 1976;75:183–190. doi: 10.1007/978-1-4684-3273-2_23. [DOI] [PubMed] [Google Scholar]
- Han TH, Liao JC. Erythrocyte nitric oxide transport reduced by a submembrane cytoskeletal barrier. Biochim Biophys Acta. 2005;1723:135–142. doi: 10.1016/j.bbagen.2005.01.013. [DOI] [PubMed] [Google Scholar]
- Herold S, Exner M, Nauser T. Kinetic and mechanistic studies of the NO*-mediated oxidation of oxymyoglobin and oxyhemoglobin. Biochemistry. 2001;40:3385–3395. doi: 10.1021/bi002407m. [DOI] [PubMed] [Google Scholar]
- Huang KT, Huang Z, Kim-Shapiro DB. Nitric oxide red blood cell membrane permeability at high and low oxygen tension. Nitric Oxide. 2007;16:209–216. doi: 10.1016/j.niox.2006.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang KT, Han TH, Hyduke DR, Vaughn MW, Van Herle H, Hein TW, Zhang C, Kuo L, Liao JC. Modulation of nitric oxide bioavailability by erythrocytes. Proc Natl Acad Sci U S A. 2001;98:11771–11776. doi: 10.1073/pnas.201276698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley VH, Kutchai H. The effect of the red cell membrane and a diffusion boundary layer on the rate of oxygen uptake by human erythrocytes. J Physiol. 1981;316:75–83. doi: 10.1113/jphysiol.1981.sp013773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ignarro LJ, Buga GM, Wood KS, Byrns RE, Chaudhuri G. Endothelium-derived relaxing factor produced and released from artery and vein is nitric oxide. Proc Natl Acad Sci U S A. 1987;84:9265–9269. doi: 10.1073/pnas.84.24.9265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia L, Bonaventura C, Bonaventura J, Stamler JS. S-nitrosohaemoglobin: a dynamic activity of blood involved in vascular control. Nature. 1996;380:221–226. doi: 10.1038/380221a0. [DOI] [PubMed] [Google Scholar]
- Kavdia M, Popel AS. Wall shear stress differentially affects NO level in arterioles for volume expanders and Hb-based O2 carriers. Microvasc Res. 2003;66:49–58. doi: 10.1016/s0026-2862(03)00008-6. [DOI] [PubMed] [Google Scholar]
- Kavdia M, Tsoukias NM, Popel AS. Model of nitric oxide diffusion in an arteriole: impact of hemoglobin-based blood substitutes. Am J Physiol Heart Circ Physiol. 2002;282:H2245–H2253. doi: 10.1152/ajpheart.00972.2001. [DOI] [PubMed] [Google Scholar]
- Kim S, Kong RL, Popel AS, Intaglietta M, Johnson PC. Temporal and spatial variations of cell-free layer width in arterioles. Am J Physiol Heart Circ Physiol. 2007;293:H1526–H1535. doi: 10.1152/ajpheart.01090.2006. [DOI] [PubMed] [Google Scholar]
- Liao JC, Hein TW, Vaughn MW, Huang KT, Kuo L. Intravascular flow decreases erythrocyte consumption of nitric oxide. Proc Natl Acad Sci U S A. 1999;96:8757–8761. doi: 10.1073/pnas.96.15.8757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Samouilov A, Lancaster JR, Jr, Zweier JL. Nitric oxide uptake by erythrocytes is primarily limited by extracellular diffusion not membrane resistance. J Biol Chem. 2002;277:26194–26199. doi: 10.1074/jbc.M201939200. [DOI] [PubMed] [Google Scholar]
- Liu X, Yan Q, Baskerville KL, Zweier JL. Estimation of nitric oxide concentration in blood for different rates of generation. Evidence that intravascular nitric oxide levels are too low to exert physiological effects. J Biol Chem. 2007;282:8831–8836. doi: 10.1074/jbc.M611684200. [DOI] [PubMed] [Google Scholar]
- Liu X, Miller MJ, Joshi MS, Thomas DD, Lancaster JR., Jr Accelerated reaction of nitric oxide with O2 within the hydrophobic interior of biological membranes. Proc Natl Acad Sci U S A. 1998a;95:2175–2179. doi: 10.1073/pnas.95.5.2175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Miller MJ, Joshi MS, Sadowska-Krowicka H, Clark DA, Lancaster JR., Jr Diffusion-limited reaction of free nitric oxide with erythrocytes. J Biol Chem. 1998b;273:18709–18713. doi: 10.1074/jbc.273.30.18709. [DOI] [PubMed] [Google Scholar]
- Malinski T, Taha Z, Grunfeld S, Patton S, Kapturczak M, Tomboulian P. Diffusion of nitric oxide in the aorta wall monitored in situ by porphyrinic microsensors. Biochem Biophys Res Commun. 1993;193:1076–1082. doi: 10.1006/bbrc.1993.1735. [DOI] [PubMed] [Google Scholar]
- Moncada S, Palmer RM, Higgs EA. Nitric oxide: physiology, pathophysiology, and pharmacology. Pharmacol Rev. 1991;43:109–142. [PubMed] [Google Scholar]
- Ong PK, Jain S, Kim S. Modulation of NO bioavailability by temporal variation of the cell-free layer width in small arterioles. Ann Biomed Eng. 2011;39:1012–1023. doi: 10.1007/s10439-010-0216-y. [DOI] [PubMed] [Google Scholar]
- Rameez S, Palmer AF. Simple method for preparing poly(ethylene glycol)-surface-conjugated liposome-encapsulated hemoglobins: physicochemical properties, long-term storage stability, and their reactions with O2, CO, and NO. Langmuir. 2011;27:8829–8840. doi: 10.1021/la201246m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice SA. Hydrodynamic and diffusion considerations of rapid-mix experiments with red blood cells. Biophys J. 1980;29:65–77. doi: 10.1016/S0006-3495(80)85118-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakai H, Sato A, Masuda K, Takeoka S, Tsuchida E. Encapsulation of concentrated hemoglobin solution in phospholipid vesicles retards the reaction with NO, but not CO, by intracellular diffusion barrier. J Biol Chem. 2008;283:1508–1517. doi: 10.1074/jbc.M707660200. [DOI] [PubMed] [Google Scholar]
- Stamler JS, Jia L, Eu JP, McMahon TJ, Demchenko IT, Bonaventura J, Gernert K, Piantadosi CA. Blood flow regulation by S-nitrosohemoglobin in the physiological oxygen gradient. Science. 1997;276:2034–2037. doi: 10.1126/science.276.5321.2034. [DOI] [PubMed] [Google Scholar]
- Tsoukias NM, Popel AS. Erythrocyte consumption of nitric oxide in presence and absence of plasma-based hemoglobin. Am J Physiol Heart Circ Physiol. 2002;282:H2265–H2277. doi: 10.1152/ajpheart.01080.2001. [DOI] [PubMed] [Google Scholar]
- Vaughn MW, Kuo L, Liao JC. Estimation of nitric oxide production and reaction rates in tissue by use of a mathematical model. Am J Physiol. 1998;274:H2163–H2176. doi: 10.1152/ajpheart.1998.274.6.H2163. [DOI] [PubMed] [Google Scholar]
- Vaughn MW, Huang KT, Kuo L, Liao JC. Erythrocytes possess an intrinsic barrier to nitric oxide consumption. J Biol Chem. 2000;275:2342–2348. doi: 10.1074/jbc.275.4.2342. [DOI] [PubMed] [Google Scholar]
- Vaughn MW, Huang KT, Kuo L, Liao JC. Erythrocyte consumption of nitric oxide: competition experiment and model analysis. Nitric Oxide. 2001;5:18–31. doi: 10.1006/niox.2000.0328. [DOI] [PubMed] [Google Scholar]