Time-scale invariance as an emergent property in a perceptron with realistic, noisy neurons

Abstract

In most species, interval timing is time-scale invariant: errors in time estimation scale up linearly with the estimated duration. In mammals, time-scale invariance is ubiquitous over behavioral, lesion, and pharmacological manipulations. For example, dopaminergic drugs induce an immediate, whereas cholinergic drugs induce a gradual, scalar change in timing. Behavioral theories posit that time-scale invariance derives from particular computations, rules, or coding schemes. In contrast, we discuss a simple neural circuit, the perceptron, whose output neurons fire in a clockwise fashion (interval timing) based on the pattern of coincidental activation of its input neurons. We show numerically that time-scale invariance emerges spontaneously in a perceptron with realistic neurons, in the presence of noise. Under the assumption that dopaminergic drugs modulate the firing of input neurons, and that cholinergic drugs modulate the memory representation of the criterion time, we show that a perceptron with realistic neurons reproduces the pharmacological clock and memory patterns, and their time-scale invariance, in the presence of noise. These results suggest that rather than being a signature of higher-order cognitive processes or specific computations related to timing, time-scale invariance may spontaneously emerge in a massively-connected brain from the intrinsic noise of neurons and circuits, thus providing the simplest explanation for the ubiquity of scale invariance of interval timing.

Time-scale invariance is ubiquitous in many species

Interval timing is the ability of perceiving and using the passage of time in the seconds-to-minutes range. Interval timing is essential for psychological processes critical for survival and adaptation, such as decision making and rate estimation, and its impairment leads to severe cognitive and motor dysfunctions (Buhusi & Meck, 2005; Gallistel, 1990). In most species interval timing is not only accurate but also time-scale invariant, or simply scalar, in that the errors in time estimation scale-up with the estimated duration (Gibbon, 1977; Gibbon, Church, & Meck, 1984; Meck, Penney, & Pouthas, 2008). For example, the left panel of Figure 1A shows that when timing different durations (2s, 4s, 6s, and 8s), human adults distribute their responses quasi-Gaussian around the target durations, indicating that they acquired an accurate representation of the target intervals (Wearden, Denovan, Fakhri, & Haworth, 1997). Most important for this paper, the width of these distributions scale-up with the estimated duration, such that when the timing functions are displayed in time units relative to the timed criterion, as shown in the right panel of Figure 1A, the timing functions superimpose. In other words, interval timing is increasingly less precise as the interval being timed lengthens, i.e., it is time-scale invariant.

Figure 1. The ubiquity of scale-invariant timing in humans.

(A) In human adults, interval timing functions peak at the target duration, and their width increases with duration (left), such that they superimpose in relative time units, indicating scale-invariant timing (right) (adapted from Wearden, et al., 1997). (B) Scale-invariant timing is ubiquitous throughout human development, in 3-year old (left), 5-year old (center), and 8-year old children (right) (adapted from Droit-Volet, et al., 2001). (C) Scale-invariance of timing does not depend on the modality of the timed stimulus (adapted from Zarco, et al., 2009). (D) Scale-invariant timing is ubiquitous in both explicit (generalization) and implicit (estimation) timing tasks (adapted from Piras & Coull, 2011). (E) Scale-invariant timing is ubiquitous in timing tasks with different motor requirements, and number of to-be-timed signals: production of single (STT) or multiple time intervals (MTT), temporal categorization (CAT) and discrimination (DIS) (adapted from Merchant, et al., 2008).

The time-scale invariance of interval timing is ubiquitous in many species from invertebrates such as bees (Boisvert & Sherry, 2006), to many vertebrates, such as fish (Talton, Higa, & Staddon, 1999), birds (Cheng & Westwood, 1993), and mammals such as rats (Dews, 1962), mice (Buhusi et al., 2009) and humans (Rakitin et al., 1998). For example, in humans, time-scale invariance can be observed throughout development, as shown in Figure 1B: In similarity to human adults (Figure 1A), the response of children trained to timed multiple durations follow a quasi-Gaussian distribution around the target durations (here, 4s and 8s), and their response functions superimpose when displayed in time units relative to the target interval (Droit-Volet, Clement, & Wearden, 2001). Moreover, the linear relationship between estimation error and estimated duration does not depend on the modality of the timed stimulus (Figure 1C, Zarco, Merchant, Prado, & Mendez, 2009), on whether human participants time implicitly or explicitly (Figure 1D, Piras & Coull, 2011), on sensorimotor processes involved, or on the number of intervals timed (Figure 1E, Merchant, Zarco, & Prado, 2008).

Time-scale invariance is resilient to behavioral, sensorimotor, and pharmacological manipulations

In similarity to human adults (Figure 2A–B, Rakitin, et al., 1998), rodents trained in a peak-interval procedure produce quasi-Gaussian distributions of responses around the criterion durations, whose width scale up with the estimated intervals (Figure 2C, Matell, King, & Meck, 2004). In similarity to humans and rodents, estimation errors increase linearly with estimated duration in Rhesus monkeys (Figure 2D, Zarco, et al., 2009). Interestingly, time-scale invariance is particular to timing in the seconds-to-minutes range, but not to circadian timing, which is far more accurate than interval timing, and whose estimation errors increase very little with the mean of the interval (Gibbon, 1977; Hinton & Meck, 1997).

Figure 2. Time-scale invariance in primates and rodents.

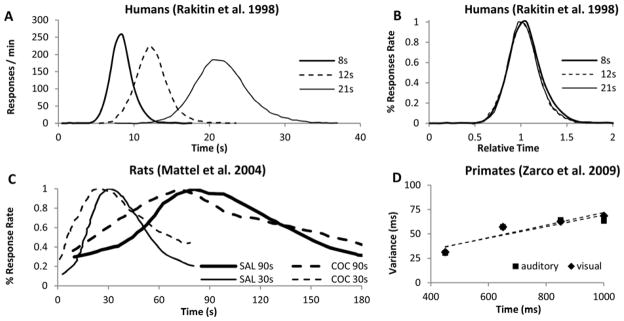
(A) Response rate in peak-interval experiments with human adults trained with three target durations (8s, 12s, 21s) (Rakitin, et al., 1998). (B) Responses from (A) rescaled both relative to the target duration and the maximum response rate. (C) Percent maximum response rate in peak-interval experiments with rats trained with two target durations (30s, 90s); administration of indirect dopamine agonist cocaine (COC) results in an immediate, scalar (proportional) leftward shift in response functions, relative to saline (SAL) (adapted from Matell, et al., 2004). (D) Scalar timing in Rhesus monkeys (adapted from Zarco, et al., 2009).

The ubiquity of scalar timing extends over behavioral, lesion (Meck, Church, Wenk, & Olton, 1987), and pharmacological manipulations of interval timing (Buhusi & Meck, 2010). Considerable progress has been made in recent years towards elucidating the neural bases of time perception in the seconds-to-minutes range (Buhusi & Meck, 2005; Mauk & Buonomano, 2004; Meck, et al., 2008). Recent studies consistently point towards the cortico-striatal circuits as being critical for interval timing both, in animals (Matell & Meck, 2000; Matell, Meck, & Nicolelis, 2003; Meck, 2006) and humans (Coull, Cheng, & Meck, 2011; Coull, Vidal, Nazarian, & Macar, 2004; Stevens, Kiehl, Pearlson, & Calhoun, 2007). These studies also consistently indicate that the dopaminergic system is crucial for interval timing, and for its time-scale invariance. For example, severe deficiencies in reproducing temporal intervals were found in various neuropsychiatry disorders, such as Parkinson’s (Harrington & Haaland, 1991), characterized by loss of dopaminergic cells. With few notable exceptions (Malapani, Deweer, & Gibbon, 2002; Malapani et al., 1998), time-scale invariance is resilient to behavioral, lesion and pharmacological manipulations.

For example, acute administration of dopaminergic (DA) agonists, such as cocaine, result in a characteristic immediate leftward shift of response functions (Figure 2C), consistent with the speeding up of an internal clock (Matell, et al., 2004). At the same dose, cocaine speeds up timing of a 90s interval three times more than when timing a 30s interval (Figure 2C), suggesting that the effect of the drug is proportional -- scalar -- to the timed interval. On the other hand, pharmacological manipulations (Meck, 1983, 1996; Meck & Church, 1987a, 1987b) and lesions (Meck, et al., 1987) aimed at the cholinergic (ACh) systems produce gradual (rather than immediate) effects on the memory storage. Importantly, time-scale invariance of both the clock pattern of DA drugs and the memory pattern of ACh drugs is not restricted to the drug state, but that the linear relationship between estimation error and estimated duration extends over the estimated durations and drugs states (vehicle v. drug) (Figure 2C) (Matell, et al., 2004).

How does time-scale invariance, including the scalar effect of DA and ACh drugs, emerge from unreliable, noisy neurons firing in the milliseconds range? Here we discuss a biologically plausible neural circuit, the perceptron, in which large numbers of inputs activate a relatively small number of output neurons. Due to its simple yet general architecture, the perceptron has long been considered a suitable model for information storage and organization in the brain (Rosenblatt, 1958). Here we discuss the biological support for the perceptron architecture in interval timing, and we show computer simulations suggesting that in a perceptron, time scale invariance emerges naturally from neural noise, ubiquitous in the form of small fluctuations in the intrinsic frequencies of input neurons, and in the encoding and decoding errors at output neurons. These results suggest that time-scale invariance is a general property naturally emerging in a massively-connected brain from the intrinsic noise of neurons and circuits, and not necessarily from intricate computations specific to temporal processing.

The perceptron

A current neurobiological model of interval timing, the Striatal Beat Frequency (SBF) model (Buhusi & Meck, 2005; Matell & Meck, 2004) assumes that time is coded by the coincidental activation of a large number of cortical neurons projecting onto spiny neurons in the striatum, which act as perceptrons, and selectively respond to particular reinforced patterns (Beiser & Houk, 1998a; Houk, Adams, & Barto, 1995) (Figure 3A). Indeed, each striatal spiny neuron integrates a very large number of cortical afferents (between 10,000 and 30,000) (Wilson, 1995), of which a vast majority are cortical (about 70%) (Doig, Moss, & Bolam, 2010). Support for the involvement of the fronto-striatal dopaminergic system in timing comes from imaging studies in humans (Coull, et al., 2004; Harrington & Haaland, 1999; Stevens, et al., 2007), lesion studies in humans and rodents (Gibbon, Malapani, Dale, & Gallistel, 1997; Malapani, et al., 1998; Meck, 1983), and drug studies in rodents (Meck, 1996; Neil & Herndon Jr., 1978) all pointing towards the basal ganglia as having a central role in interval timing. Striatal firing patterns are peak-shaped around a trained criterion time, a pattern consistent with substantial striatal involvement in interval timing processes (Matell, et al., 2003). Lesions of striatum result in deficiencies in both temporal-production and temporal-discrimination procedures (Jin & Costa, 2010). Elsewhere we (Oprisan & Buhusi, 2011) implemented an SBF model which included the fronto-striatal perceptron, along with dopaminergic and cholinergic modulatory circuits in order to model the psychopharmacology of interval timing (Figure 3A).

Figure 3. The perceptron.

(A) Schematic representation of the neurobiological structures involved in interval timing in the Striatal Beat Frequency model (SBF) model (Matell & Meck, 2004). Frontal oscillators are implemented as biophysically realistic ML neurons. ACh: acetylcholine; FC: frontal cortex; BG: basal ganglia; DA: dopamine; Glu: glutamate; GP_E: globus pallidus external; GP_I: globus pallidus internal; STn: subthalamic nucleus; SNc/r: substantia nigra pars compacta/reticulata; TH: thalamus; VTA: ventral tegmental area. (B) The basic structure of the perceptron used to implement the SBF-ML model. Dashed lines in panel (A) signify couplings that were not implemented in our SBF-ML version (Oprisan & Buhusi, 2011).

To mimic the spiny neurons in the striatum, which integrate a very large number of different inputs and respond selectively to particular reinforced patterns (Beiser & Houk, 1998b; Houk, 1995; Houk, Davis, & Beiser, 1995), one may implement a perceptron as follows: Let’s assume N_osc neural (input) oscillators with intrinsic frequencies f_i (i = 1… N_osc) uniformly distributed over the interval [f_min; f_max], projecting onto N_mem output neurons (Figure 3B). The memory for the criterion time can be modeled by the activity pattern w_ij of input neuron i projecting onto the output neuron j. At the onset of each trial, the oscillators are reset (0 phase), and the N_osc neurons are set to fire with frequencies f_i. During reinforced trials, upon delivery of the reinforcement at criterion time T, a linear combination of oscillators’ membrane potential in the current trial at the criterion time T was stored in long-term memory as criterion pattern w_ij(T). In a perceptron the output neurons act as coincidence detectors (Figure 3B),: They fire when the pattern of activity w_ij(t) at the current time t matches the reference activity pattern w_ij(T) which encode the criterion duration T. Thus, the vector w_*,j(t) represents the activity patterns connecting the cortical oscillators to output neuron j at the current (running) time t, and the vector w_*,j(T) represent the activity patterns of cortical oscillators projecting on output neuron j at reinforcement time T. Therefore, the activation of output neuron j at time t is the dot product of the above activity vectors, i.e.,

$$w_{\ast ,j}(t)w_{\ast ,j}(T)=\sum _{i=1}^{N_{\mathit{osc}}}{w}_{ij}(t)w_{ij}(T).$$

The response function of the SBF implementation is the sum of activation over all output neurons:

$$\mathit{response}(t)=\sum _{j=1}^{N_{\mathit{mem}}}{w}_{\ast ,j}(t)w_{\ast ,j}(T)=\sum _{j=1}^{N_{\mathit{mem}}}\sum _{i=1}^{N_{\mathit{osc}}}{w}_{ij}(t)w_{ij}(T)$$

Here we investigate the role of noise in the emergence of time-scale invariance. Biological noise and background neural activity in the neural oscillators can be modeled by allowing the parameters of the model to fluctuate, e.g., by small variations of conductances and half-activation voltages for specific ionic channels, variations in the background neural activity, or in overall synaptic inputs, or variations in the intrinsic frequencies f_i, according to specified probability density functions pdf, e.g., Gaussian, Poisson, etc. This will generate a specific probability density function of the stored criterion T, pdf_T, e.g., Gaussian, Poisson, etc. Here we explore the behavior of a perceptron with and without parameter variability (noise) under several assumptions: First, that input neurons are phase oscillators (sine waves) (Matell & Meck, 2004). Second, that neural oscillators are biophysically realistic Morris-Lecar (ML) model neurons (Morris & Lecar, 1981a; Rinzel & Ermentrout, 1998). Third, that DA projections from the ventral tegmental area (VTA) to the frontal cortex modulate the intrinsic firing frequency of cortical oscillators. To further explore the latter assumption, more specifically the fact that the system can store/retrieve in separate drug states (vehicle v. drug), we allowed the encoding and retrieval of the criterion time to and from the N_mem neurons to be affected by trial-to-trial variability. Fourth, that the cholinergic system modulates the basal ganglia activity, memory storage and retrieval (Figure 3A). The cumulative effect of variability in the memory storage (at encoding and/or retrieval time), was modeled by allowing the activity patterns w_ij(T) that code a particular criterion time T to be randomly distributed according to a probability density function pdf_T (Oprisan & Buhusi, 2011). We show that under all four conditions, time-scale invariance does not emerge in the absence of noise, but rather emerges when the circuits/neurons are noisy, which allows time-scale invariance to be resilient to both behavioral and pharmacological manipulations.

Time-scale invariance does not depend on the type on input neuron, but rather on whether input neurons are “noise-free” or “noisy”

The impracticality of perfect oscillators questions the robustness of an SBF model in a brain with real, noisy neurons, particularly after pharmacological manipulations. Therefore, we first explored the biological details required for time-scale invariance at the level of the neural oscillators. First, we explored the case in which the cortical neurons of the perceptron (Figure 3B) are implemented as plain phase oscillators (sine waves). As such, activity patterns w_ij, which represent the state of the neural (input) oscillator i projecting on output neuron j, are given by a normalized linear combination of input neuron states, i.e., w_ij(T) is proportional to cos(2πf_iT_j), where f_i is the frequency of neural oscillator i, T_j is the criterion time stored in the memory cell j. In the absence of noise, T_j = T for all j =1,…,N_mem. Using the definition of the output function and simple trigonometric manipulations, the response(t) is proportional to sin(πN_osc df (t−T))/sin(πdf (t−T)), where df is the frequency increment (f_max−f_min)/N_osc. The envelope of the above response(t) function peaks at t=T, but its width does not depend on T, i.e., it is not scale invariant.

Figure 4A shows numerical simulations with a perceptron with “noise-free” (deterministic) phase oscillators (sine waves); the inset shows the theoretically predicted response(t) function. These simulations indicate that response of the perceptron peaks when w_ij(t) “lines-up” or “coincides” with w_ij(T), i.e., at t=T. On the other hand, when we conducted multiple simulations with various to-be-timed criteria T (Figure 4B), results indicated that the estimation errors do not scale-up with the estimated durations, but that, as theoretically predicted, the response functions were rather fixed in width (Figure 4B). In other words, a perceptron with “noise-free” sine-wave cortical inputs is accurate (responds maximally at the criterion time T, Figure 4A), but it does not exhibit time-scale invariance (its estimated errors do not scale-up with the estimated durations, Figure 4B).

Figure 4. An SBF model with phase oscillators and no variance does not exhibit time-scale invariance.

(A) Normalized output function in numerical simulations of the SBF model versus theoretical predictions (inset). (B) The standard deviation of the Gaussian envelope of the normalized output function is independent of the criterion time in the absence of any variability in model parameters, indicating lack of time-scale invariance.

On the other hand, as soon as noise (small fluctuations in intrinsic oscillation frequencies, f_i) was implemented, time-scale invariance immediately emerged in the perceptron. Figure 5A shows the response functions for three criteria, T₁ = 15s, T₂ = 30s, and T₃ = 45s. The perceptron was accurate in that the response function peaked about the criterion times. Moreover, upon using “noisy” sine-wave oscillators, the response functions’ widths scaled-up with the estimated duration, i.e., the perceptron exhibited time-scale invariance. We therefore conducted multiple simulations with various to-be-timed criteria T, as shown in Figure 5B, in which each dot represents a separate simulation with a particular to-be-timed criterion T. Results indicated that the estimation errors increase linearly with the timed criterion. Furthermore, Figure 5B shows that the time-scale invariance emerges both for Gaussian (solid squares) and uniform (solid triangles) distribution of noise. In summary, a perceptron with “noisy” sine-wave cortical oscillators is accurate (it responds maximally at the criterion time T, Figure 5A), and it exhibits time-scale invariance regardless of the distribution of criterion time noise (its estimated errors scale-up with the estimated durations, Figure 5B).

Figure 5. Time scale invariance emerges in an SBF model with phase oscillators upon introducing noise.

(A) Normalized output functions (continuous line) in numerical simulations of the SBF model with phase oscillators affected by uniform noise for three different criteria show a significant increase in the standard deviation with the criterion time (T₁ = 15s, T₂ = 30s, and T₃ = 45s). The corresponding Gaussian envelopes are shown with dashed lines. (B) Standard deviation varies linearly with criterion time, indicating the noisy SBF model exhibits scale-invariant timing, both for Gaussian (solid squares) and uniform (solid triangles) distribution of noise.

Time-scale invariance emerges in a perceptron with realistic ML neurons, in the presence of noise

Since action potential recordings from real neurons are never phase oscillators, i.e., sine waves, we further explored the role of noise in a perceptron in which the cortical “oscillators” are implemented by biophysically realistic Morris-Lecar (ML) neurons (Morris & Lecar, 1981b; Rinzel & Ermentrout, 1998). ML neurons are biophysically realistic models that include fundamental conductance-based mechanisms involving potassium and calcium channels. By tuning model’s parameters, the ML model neuron can mimic both the firing pattern of a spiking neuron with very brief (less than 1 ms) action potentials and the membrane voltage envelope of a bursting neuron with a very long depolarization (hundreds of ms) that can last over half the duration of the firing period (Morris & Lecar, 1981b; Rinzel & Ermentrout, 1998). Biological noise was modeled by allowing the frequency of oscillators to vary according to a pdf_f. Additionaly, biological noise influence on output neurons was mimicked by variations in the stored criterion T, which can cumulatively be modeled as a specific probability density function of the stored criterion T, pdf_T, e.g., Gaussian, Poisson, etc. (see Oprisan & Buhusi, 2011 for details of simuations).

Our simulations revealed time scale-invariant behavior of the perceptron when the noisy sine-wave oscillators were replaced with noisy biophysically plausible Morris-Lecar (ML) neurons (Figure 6). For very small fluctuations in parameters, which generated low memory storage/retrieval variability -- 0.1% standard deviation in Figure 6A, and 1% standard deviation in Figure 6B -- the standard deviation of the Gaussian fit of the response function (shaded area) varied very little with criterion time (Figure 6D), indicating that the perceptron did not exhibit scale-invariant timing. However, the standard deviation of the response (shaded area) increased significantly when variability increased to about 10%, as seen in Figure 6C. As seen in Figure 6D, at this level of noise the perceptron exhibited a linear relationship between estimation errors and estimated duration, i.e., time-scale invariance (Figure 6D). In summary, a perceptron with “noisy” ML cortical neurons is accurate (it responds maximally at the criterion time T, Figure 6A-C), and it exhibits time-scale invariance (its estimated errors scale-up with the estimated durations, Figure 6D), in the presence of noise.

Figure 6. Time-scale invariance in an SBF-ML model with noisy Morris-Lecar neurons.

(A–C) For very low memory variance, the standard deviation of the Gaussian fit (shaded area in panels AC) varies very little with criterion time failing to indicate scale-invariant timing. (D) The scalar property emerges only when the system is noisy (at large variances). All simulations used 600 cortical oscillators in the frequency range from 5.5 Hz to 11.5 Hz.

Time-scale invariance of the pharmacological clock pattern

In mammals, manipulations involving dopaminergic (DA) drugs such as cocaine induce a particular pattern of response -- clock pattern -- characterized by several features exemplified by the data presented in Figure 7 (Meck, 1996). First, DA drugs produce an immediate, scalar change in the perceived time when administered either systemically (Maricq & Church, 1983; Maricq, Roberts, & Church, 1981; Matell, et al., 2004; Meck, 1983, 1996), or directly into the anterior portion of the striatum (Neil & Herndon Jr., 1978); the pattern is often taken to be suggestive of a change in the speed of an internal clock, and thus is known as a clock pattern (Meck, 1996). For example, an immediate, scalar (proportional), leftward shift in perceived time (responding earlier in time than under control conditions) is evident following systemic DA agonist administration, e.g., methamphetamine or cocaine (black squares in Figure 7). Similarly, an immediate, proportional, rightward shift in perceived time (responding later in time than under control conditions) occurs following systemic administration of DA antagonist, e.g., haloperidol (red circles in Figure 7). Second, the magnitude of the shift in the temporal response scales with the timed duration, and the response functions on and off-drug overlap when normalized in amplitude and duration. Third, upon chronic administration of DA drugs, the timing functions recalibrate, i.e., they shift back to the values prior to drug administration, an effect often interpreted as a relearning of the clock value associated with a particular duration (left side of the Figure 7). Fourth, upon discontinuing the drug regimen, the timing functions rebound (in a scalar manner) in the opposite direction from the initial effects of the drug (Meck, 1983) (right side of Figure 7). This rebound effect is a signature of the clock pattern. Finally, the magnitude of the shift in the temporal response scales roughly linearly with the dose (Meck, 1996; Meck et al., 2011), suggesting a tight relationship between synaptic dopamine levels and clock speed.

Figure 7. The clock pattern is time-scale invariant.

The clock pattern of dopaminergic (DA) drugs (adapted from Meck, 1996): Two groups of rats were trained off-drug to time a criterion time of either 40s (upper pattern) or 20s (lower pattern); they were then administered either DA agonists or antagonists for 7 sessions, followed by 7 session off drug. The first administration of DA drugs results in an immediate, dose-dependent shift in timing, leftward (faster timing) for DA agonists (solid squares, methamphetamine), and rightward (slower timing) for DA antagonists (solid circles, haloperidol). Under continuous training with the pre-drug criterion time and despite continuing the drug administration, the timing functions recalibrate to the pre-drug criterion time. Upon discontinuing the drug, timing functions immediately rebound in the opposite direction, then gradually recalibrate to the pre-drug criterion time (Meck, 1996). Solid triangles indicate numerical simulations with the SBF-ML model (Oprisan & Buhusi, 2011). Insets: The insets indicate the response function generated by the SBF-ML model throughout the clock pattern (indicated by arrows, and by a triangle symbol of the color of the inset) (Oprisan & Buhusi, 2011). (A1) Immediate rebound from T = 40 s to T^** = 48 s upon discontinuing methamphetamine. (A2) Recalibration under methamphetamine. (A3) Immediate shift under methamphetamine from T = 40 s to T^* = 32 s. (A4) Immediate shift under haloperidol from T = 20 s to T^* = 24 s. (A5) Recalibration under haloperidol. (A6) Immediate rebound upon discontinuing haloperidol. The dashed (panels A1–A3), respectively, continuous (panels A4–A6) smooth lines represent Gaussian fits. Note that the effect of the same dose of drug is twice as large in the 40s rats (upper pattern) than in the 20s rats (lower pattern); also, in all insets, the width of the function is proportional to the peak time, indicative of time-scale invariance in both the behavioral and pharmacological dimensions of the experiment. Reproduced from (Oprisan & Buhusi, 2011).

The above pharmacological manipulations were conducted in the peak-interval procedure, in which subjects -- rats (Matell, et al., 2004), mice (Buhusi, et al., 2009) or human participants (Rakitin, et al., 1998) -- receive two types of trials: In fixed-interval (FI) trials, subjects are reinforced for the first response after the to-be-timed interval has elapsed; it is in FI trials that subjects store the to-be-timed duration. Due to variability in responding, the actual reinforced duration is usually different from the theoretical one (Gibbon, et al., 1984). On the other hand, in peak-interval trials, subjects are never reinforced, this is a test trial in which subjects produce a near-Gaussian distribution of responses centered at the acquired criterion. Therefore, to explore the role of noise in time-scale invariance under the above pharmacological manipulations, we considered further sources of variability (noise), such as the variance with which the to-be-timed criterion is stored in/retrieved from memory in on- and off-drug sessions. For example, this may involve variations in both the encoding and the recall of the criterion time due to the current (on- or off-drug) frequencies f_i. Therefore, in the following we need to differentiate between within- and between-trial variability.

Our modeled experimental setting for pharmacological manipulations included both reinforced and non-reinforced trials (see Oprisan & Buhusi, 2011 for details of simuations). At the onset of each trial, the neurons were reset (0 phase), then neurons were set to fire with frequencies f_i, fixed during each trial, but variable from trial to trial. During reinforced trials, upon delivery of the reinforcement at criterion time T, a linear combination of oscillators’ membrane potential in the current trial at the criterion time T was stored in long-term memory as criterion pattern w_ij(T) (Matell & Meck, 2004). During non-reinforced (test) trials, spiny neurons were assumed to act as coincidence detectors by computing the product of the running activity patterns w_ij(t) stored in the working memory onto the retrieved reference activity patterns w_ij(T) stored in the long-term memory. We assumed that both the storage and retrieval of the criterion time -- stored as criterion pattern w_ij(T) -- to and from long term memory is affected by random biological noise, modeled as follows: Criterion time variability was modeled by randomly distributing the criterion time T according to a normal density probability function pdf_T. This assumption accounts for the randomness in learned sample times (reinforced times), as explained in the previous paragraph. Therefore, sample times stored in memory were assumed to be distributed around T.

We further assumed that phasic release of dopamine from VTA to FC modulates the firing rate of cortical neural oscillators. A change in drug state induced an immediate change in oscillator frequencies from the off-drug frequencies f_i to the on-drug frequencies f_i*, respectively, from the on-drug frequencies f_i* to the off-drug frequencies f_i. In our numerical implementation of the SBF-ML, the ML neural oscillators fire off-drug in the frequency range [f_min, f_max] and that the criterion time T is represented off-drug as a set of activity patterns w_ij(T). The DA drugs alter the frequency of the cortical oscillators to f_i* = (1+ α)f_i such that the on-drug frequency range changes to [f*_min, f*_max], where a positive α accounted for the action of dopamine agonists, such as methamphetamine or cocaine, and a negative α accounted for the effect of dopamine antagonists, such as haloperidol (Meck, 1996). As a result, the projection (coincidence detection) of the current on-drug activity patterns w*_ij(t) to the reference off-drug activity patterns w_ij(T) peaks at a time T* that differs from T (see Oprisan & Buhusi, 2011 for details of simuations).

Simulations shown in Figure 7 indicate that the clock pattern of DA drugs can be understood as the interplay between storage and retrieval of the criterion time w_ij(T), on and off drug. Indeed, our implementation of the SBF-ML model showed the major features of the clock pattern effect: immediate, scalar shift in timing and recalibration on-drug, followed by an immediate, scalar rebound and recalibration off-drug (solid triangles in Figure 7). Systemic administration of DA agonists produced an immediate, leftward shift of the response function to T* < T (inset A3 in Figure 7), in agreement with experimental data for DA agonists methamphetamine and cocaine (Buhusi & Meck, 2002; Matell, et al., 2004; Meck, 1996). On the other hand, systemic administration of DA antagonists produced an immediate rightward shift due to a slowdown of cortical oscillators during retrieval T* > T (inset A4 in Figure 7), in agreement with experimental observation of the effect of DA antagonist haloperidol (Buhusi & Meck, 2005; Meck, 1996).

According to the clock pattern (Meck, 1996), chronic drug administration results in a gradual recalibration, such that the response time on-drug gradually approaches the response time off-drug drug, an effect which is not due to receptor desensitisation, but rather attributed to relearning of the criterion time using the drug-altered cortical frequencies (Meck, 1996). In our implementation, the repeated drug administration resulted in the criterion time T – which is represented in memory by a distribution of learned patterns w_ij(T) – to be gradually re-written with new samples of reinforced duration, samples which are computed using drug-altered oscillator frequencies. During drug sessions, a fraction of the activity patterns w_ij(T) originally stored off-drug, are replaced with new running activity patterns w(T*), stored on-drug, such that gradually the activity patterns stored in the reference (long-term) memory are characteristic of the on-drug state. Similarly, when discontinuing the drug, we assumed that the criterion time, stored in long-term memory as a distribution of w_ij(T*) samples, stored on-drug, is replaced with a fraction during each off-drug session, such that with sufficient training, the activity patterns w_ij stored in the reference (long-term) memory will be characteristic of the off-drug state. Under these assumptions, simulation presented in Figure 7 indicate that our SBF-ML model exhibited recalibration of the criterion time T* back to T under repeated methamphetamine administration (inset A2 of Figure 7) as well as under repeated haloperidol administration (inset A5 of Figure 7). A similar recalibration occurs after the drug is discontinued, when the model re-learns the activity patterns w_ij(T) for the criterion T off-drug (see right-side of Figure 7).

An interesting property of the SBF-ML model is that discontinuing the drug results in a scalar rebound of the response in the opposite direction, due to the sudden change from on-drug cortical frequencies f* to the off-drug cortical frequencies f = (1− β)f*. For example, an immediate leftward shift from T = 40 s (inset A2 in Figure 7) to T* = 32 s (inset A3 in Figure 7) under methamphetamine is followed by relearning of the criterion on-drug; discontinuing the drug results in an immediate rightward displacement to T** = 48 s (inset A1 in Figure 7), followed again by a slow recalibration back to the original criterion time T = 40 s due to relearning of the criterion time with the new cortical frequencies.

Most importantly for this paper, in our implementation of the SBF-ML model, time-scale invariance is preserved throughout the clock pattern, as shown by the insets in Figure 7. The variance in the response rate (width of response function), throughout the pharmacological manipulation remains proportional to the current response time, either off-drug or off-drug. Although to address the effect of drugs required supplemental assumptions, time-scale invariance did not require any supplemental assumptions; it emerged as a result of noisy processing by the perceptron.

Time-scale invariance of the pharmacological memory pattern

Pharmacological manipulations (Meck, 1983, 1996; Meck & Church, 1987a, 1987b) and lesions (Meck, et al., 1987) aimed at the cholinergic (ACh) systems produce gradual, scalar (proportional) effects on the memory storage, as shown in data from Figure 8: First, administration of ACh drugs produced a gradual (rather than immediate), scalar temporal shift (Meck, 1996); ACh lesions produce permanent effects (Malapani & Fairhurst, 2002). Second, chronic administration amplifies (rather than recalibrates) the temporal shift (left side of Figure 8). Third, upon discontinuing the drug administration, the timing functions gradually return to the original criterion time (Figure 8, right side). Finally, the magnitude of the shift in the temporal response scales with the timed duration (Meck, 1996), twice as large for the 40s group (upper pattern in Figure 8) than for the 20s group (lower pattern in Figure 8). This memory pattern is consistent with alterations of the internal representation of the memorized criterion time (Meck, 1996).

Figure 8. The memory pattern is time-scale invariant.

The memory pattern of cholinergic (ACh) drugs (adapted from Meck, 1996): Two groups of rats were trained off-drug to time a criterion time of either 40s (upper pattern) or 20s (lower pattern); they were then administered either ACh agonists or antagonists for 7 sessions, followed by 7 session off-drug. The first administration of ACh drugs results in a minimal effect; repeated ACh drug administration results in a gradual, dose-dependent shift in timing, leftward for ACh agonists (solid circles, physostigmine), and rightward for ACh antagonists (solid squares, atropine). Upon discontinuing the drug, timing functions gradually recalibrate to the initial criterion time (Meck, 1996). Solid triangles indicate numerical simulations obtained with the SBF-ML model (Oprisan & Buhusi, 2011). Insets: The insets indicate the output function generated by the SBF-ML model with biophysically realistic ML neurons throughout the memory pattern (indicated by arrows, and by a triangle symbol of the color of the inset) (Oprisan & Buhusi, 2011). (A1) Gradual shift from T = 40 s to T^* = 50 s under atropine. (A2) Gradual recalibration upon discontinuing atropine. (A3) Gradual recalibration upon discontinuing physostigmine. (A4) Gradual recalibration under physostigmine. The dashed (panels A1–A2), respectively, continuous (panels A3–A4) smooth lines represent Gaussian fits. Note that the effect of the same dose of drug is twice as large in the 40s rats (upper pattern) than in the 20s rats (lower pattern); also, in all insets, the width of the function is proportional to the peak time, indicative of time-scale invariance in both the behavioral and pharmacological dimensions of the experiment. Reproduced from (Oprisan & Buhusi, 2011).

Systemic administration of ACh agonist physostigmine results in a gradual, dose-dependent leftward shift of the response (solid circles in Figure 8) (Meck, 1996). Similarly, administration of ACh blocker atropine leads to a gradual and dose-dependent rightward shift of the psychophysical functions (solid squares in Figure 8) (Meck, 1996). Moreover, the magnitudes of the temporal shifts observed are dose-dependent and proportional to the intervals being timed (Meck, 1996). To address this issue, it was proposed that training under the influence of the ACh drug produces a gradually re-learning of an altered criterion time T* = k*T (Buhusi & Meck, 2010; Gibbon, et al., 1984; Meck, 1996).

Our numerical implementation assumes that criterion time T is coded in long-term memory as a set of activity patterns w_ij(T), and that administration of ACh drugs alter the processes involved in memorizing this distribution. Every session, new samples are learned; the new samples are assumed to represent an altered, on-drug representation of the criterion time, T^* = k^* T, where the multiplicative coefficient k^* is both drug and dose-dependent (Gibbon, et al., 1984; Meck, 1996), with k^* > 1 for ACh antagonists, such as atropine, and k^* < 1 for ACh agonists, such as physostigmine (see Oprisan & Buhusi, 2011 for details of simuations). Under these assumptions, the dynamics of memory pattern (Figure 8) is significantly different from that of the clock pattern (Figure 7): The memory pattern is determined by a gradual alteration of representation of the criterion time in the long-term memory that affects a growing number of memorized sample activity patterns. Relearning the criterion under the ACh drug eventually overwrites the entire long-term memory with the altered representation k^*T of the criterion time T. This induces a gradual change in the content of the long-term memory that leads to an increasing mismatch between the contents of the working and the long-term memory (Figure 8).

As shown in Figure 8 (solid triangles), the gradual change in memory samples under atropine gradually shifts the peak of the output function from the initial value, T = 20s (inset A3 in Figure 8), to the altered value T^* = k^*T = 15s (inset A4 in Figure 8). A similar shift takes place for ACh antagonists, say from T = 40s (inset A2 in Figure 8) to T* = 50s (inset A1 in Figure 8). Most importantly, both the amplitude of the gradual shift on-drug and the amplitude of the recalibration when the ACh drug is discontinued are proportional to the criterion interval T. Moreover, the width of the response remains scalar, i.e., proportional to the current peak time, either between the 20s and 40s criterion durations, as well as off-drug or on-drug, i.e., throughout the memory pattern (see insets in Figure 8).

An interesting question concerns how can such a k* effect be implemented within SBF? For example, in SET, which has one numerical value for T, this value could indeed be multiplicatively scaled by k*. On the other hand, in SBF, T is represented by a vector of activations w(T). In fact in our implementation, T was represented by a set (of 1000) such activation vectors w(T) (see Oprisan & Buhusi, 2011 for details). How is this activation vector w(T) shifted by a k* effect? This is not a trivial question. One possibility is that, at a cellular-level, each element of the vector that codes T would be changed in similar ways by the k*factor. The only requirement for this solution to work would be to preserve the ordinal scale of T values, such that a particular k* would always produce an increase in T, or always a decrease in T. Another possibility, is that, at a behavioral level, the pattern w(T) would be updated based upon the organism perceiving that it got food earlier or later than it objectively did. However, this is likely to generate an immediate shift in responding, similar to a clock effect. This clearly does not happen for cholinergic drugs. Finally, a systems-level solution to this problem would be to have separate circuits for updating memories versus generating behavior (Dr. Matthew S. Matell, personal communication). For example, the memory system could be updated (and thus, altered) during sleep, when memories are replayed by a fronto-hippocampal circuit (Bendor & Wilson, 2012). Further work is necessary to theoretically dissociate the benefits and drawbacks of these solutions, and to experimentally test these possibilities.

Discussion: Time-scale invariance as an emergent property, rather than an assumption of timing models

By and large, to address scale invariance behavioral theories make convenient assumptions. The putative mechanisms of timing were proposed to rely on pacemaker/accumulator processes (Gibbon, 1977; Gibbon, et al., 1984), sequences of behaviors (Killeen & Fetterman, 1988), pure sine-wave oscillators (Church & Broadbent, 1990; Matell & Meck, 2000, 2004), memory traces (Buhusi & Schmajuk, 1999; Grossberg & Merrill, 1992; Grossberg & Schmajuk, 1989; Machado, 1997; Staddon & Higa, 1999), or cell and network-level models (Resnick, 2006; Rizzuto et al., 2003). All these models share a basic feature: They explain time-scale invariance by making convenient assumptions relative to the computations, rules, or coding schemes. For example, the Scalar Expectancy Theory (Gibbon, 1977) assumes a linear relationship between time and the number of clock ticks of the pacemaker-accumulator model, and a linear increase in estimation errors, thus explaining time-scale invariance. Unfortunately, these computations, rules, or coding schemes have been rarely tested experimentally or computationally (but see Shea-Brown, Rinzel, Rakitin, & Malapani, 2006). Also unfortunately, upon test, the results were inconclusive because either other computations in the same models could be changed to address the results, or because the biological assumptions are difficult to test at this time, thus leaving these explanations of time-scale invariance unfalsifiable in practice.

Some neurobiological models share computational assumptions with behavioral models and continue to address time-scale invariance by specific computations or embedded linear relationships. Some assume that timing involves neural integrators capable of linearly ramping up their firing rate in time (Simen, Balci, de Souza, Cohen, & Holmes, 2011), while others assume LTP/LTD processes whose balance leads to a linear decay of the firing rate in time (Reutimann, Yakovlev, Fusi, & Senn, 2004). It is unclear whether such models can account for time-scale invariance in a large range of behavioral or neurophysiological manipulations. For example, both neurometric functions from single neurons and ensemble of neurons successfully paralleled the psychometric functions for the to-be-timed intervals shorter than one second (Rizzuto, et al., 2003). Reutimann et al. (2004) also considered interacting populations that are subject to neuronal adaptation and synaptic plasticity based on the general principle of firing rate modulation in single-cell. Balancing LTP and LTD mechanisms are thought to modulate the firing rate of neural populations with the net effect that the adaptation leads to a linear decay of the firing rate in time. Therefore, the linear relationship between time and the number of clock ticks of the pacemaker-accumulator model in the Scalar Expectancy Theory (SET) of interval timing (Gibbon, 1977) was successfully translated into a linearly decaying firing rate model that maps time and variable firing rate.

In contrast to these approaches, here we show that a simple neural circuit, the perceptron, allows the emergence of time-scale invariance without any assumptions other than that the circuits are noisy. We also show that the level of detail in regard to implementing the cortical neurons is not a factor in regard to time-scale invariance. In the absence of noise (Figure 4), and when the noise levels are relatively low (Figure 6, panels A and B), implementing the perceptron with either unrealistic sine-wave neural oscillators or with biologically realistic ML neurons does not allow the emergence of time-scale invariance. In contrast, introduction of noise (small fluctuations in the parameters) for both unrealistic sine-wave neural oscillators and biologically realistic ML neurons allow the emergence of time-scale invariance. Interestingly, the level of noise required for time-scale invariance to emerge is not very high, in the range of 5–10% (Figure 6C–D).

Indeed, the level of noise (variance) in timed responses is just about 10% in human participants (Rakitin, et al., 1998), but significantly higher, about 40% in rats (Matell, et al., 2004), or even higher, about 60%, in mice (Buhusi, et al., 2009). Thus, it is reasonable to believe that other sources of variation contribute to the timing of the response. Although not detailed here, we (Oprisan & Buhusi, 2011) also considered the combined effect of multiple sources of variance. Additional randomness was included in our SBF-ML implementation by a Gaussian noise added to the intrinsic frequencies f_i of the neural oscillators within and between trails. The within-trial variability in frequencies f_i accounts for the randomness in response (e.g., for the first response reinforced), while the between-trial variability accounts for the observed differences in response between trials (Church, Meck, & Gibbon, 1994; Swearingen & Buhusi, 2010). Interestingly enough, when variability in the intrinsic frequencies f_i of the neural oscillators was introduced, the SBF-ML model’s response started showing a characteristic long tail (skewness) (Oprisan & Buhusi, 2011), a characteristic which pervades the human and animal timing literature (see Figures 1 and 2), suggesting that other properties of timing may also be an expression of noisy neural processing.

The suggestion that time-scale invariance is a result of (neural) noise is not new. The first to propose that time-scale invariance derives from neural noise was Shadlen, who suggested that timing of sub-second intervals may be addressed at the level of single noisy neurons (Leon & Shadlen, 2003), though how such a mechanism accounts for timing of supra-second durations is yet unclear. A similar “noisy” solution to timing by counting was offered by Killeen and Taylor (Killeen & Taylor, 2000a, 2000b) who explained timing in terms of information transfer between noisy counters, although the biological mechanisms were not addressed. Indeed, both timing and counting are scale-invariant, and they may share biological mechanisms (Buhusi & Cordes, 2011). Following Miall’s binary oscillator model (Miall, 1989), the Striatal Beat Frequency (SBF) model proposes that timing is the result of coincidental activation of striatal spiny neurons by patterns of cortical activity (Matell & Meck, 2004). Although the SBF model makes no assumptions relative to time-scale invariance, Matell and Meck (2004) noted that time-scale invariance does not emerge in this model in the absence of noise (parameter variability). Finally, although time-scale invariance in a “noisy” SBF model was first reported by Matell and Meck (2004), their implementation seems much more complex than our perceptron. Here we showed that a rather simple perceptron exhibits time-scale invariance, in the presence of noise; thus, this property may not depend on other details of the SBF model.

Was scalar property really emerging in our simulations, or was its emergence promoted by some assumptions we made? This is highly unlikely. For example, it may have been that using Gaussian noise may have prompted the “emergence” of scalar property. This is unlikely, since Figure 5B suggests that scalar property emerges for other types of noise as well, like uniform noise. Did scalar property “emerge” because the assumptions hidden within the ML model neurons? This is unlikely, because it also emerged in a noisy perceptron with sine wave inputs. Finally, might its emergence be due to assuming a multiplicative k* effect for the memory pattern of ACh drugs (Figure 8 insets). This is again unlikely, since scalar property also emerged throughout the clock pattern (Figure 7 insets). Moreover, the k* feature indicates the assumed effect of ACh drugs on estimated time T, and not a relationship between estimated time and estimation errors. For example, the k* assumption allows SET (Gibbon et al. 1984) to address the ACh memory pattern, but it is not the reason SET shows scalar property. SET shows scalar property because it has the supplemental assumption that variability increase linearly with the criterion time. Similarly, in our model, the k* addresses the ACh memory pattern, but it is not the reason our model shows the scalar property. In fact our model has no supplemental assumption to address the scalar property. Scalar property simply emerges in the presence of noise. Here we showed that the only variable capable of eliminating scalar property in our model is lack of noise (Figure 4), and that scalar property emerges in the presence of various types of noise (Figure 5). The work shown here suggests the clear possibility that, should indeed time be computed in the brain in a manner vaguely similar to SBF, that its scalar property may simply be a property of the brain, rather than a feature of timing per se.

In summary, we reviewed simulations with the SBF-ML model (Oprisan & Buhusi, 2011) which successfully exhibits time-scale invariance in regard to both behavioral and pharmacological manipulations (Gibbon, 1977; Gibbon, et al., 1984; Meck, 1996). Such a range of scale-invariant effects was previously addressed by only a handful of behavioral models in the field, such as SET (Gibbon, 1977; Gibbon, et al., 1984) and STM (Buhusi & Schmajuk, 1999; Grossberg & Schmajuk, 1989). However, while SET and STM explain time-scale invariance by convenient computations of time representations, the perceptron (and models which incorporate perceptrons, like SBF) explain time-scale invariance without unnecessary assumptions. For example, SET (Gibbon, 1977; Gibbon, et al., 1984) explains time-scale invariance based on convenient computations (ratios) of specific time representations (linear) (Gibbon, 1977; Gibbon, et al., 1984). Similarly, STM (Buhusi & Schmajuk, 1999; Grossberg & Schmajuk, 1989) explains time-scale invariance based on specific computations (linear algebra of Rescorla-Wagner rules) upon conveniently-chosen time representations (time-scale invariant memory traces). In contrast, the only (realistic) assumption required for time-scale invariance to emerge in a perceptron, is noise, or imprecise computations. Together with previous studies (Buhusi & Meck, 2005; Matell & Meck, 2000, 2004; Oprisan & Buhusi, 2011), these results establish the SBF model as a biologically-realistic model of interval timing capable of explaining a large range of phenomena, from behavior, to lesions, and pharmacology, with the potential to provide insight into the neurobiological bases on interval timing.

Highlights.

• Time-scale invariance emerges spontaneously in a noisy perceptron

• Emergence of time-scale invariance does not depend on the type on input neuron

• Emergence of time-scale invariance does not depend on the type of noise

• Time-scale invariance emerges in pharmacological manipulations of noisy perceptrons