Evaluation of Shear-Induced Platelet Activation Models Under Constant and Dynamic Shear Stress Loading Conditions Relevant to Devices

Abstract

The advent of implantable blood-recirculating devices such as left ventricular assist devices and prosthetic heart valves provides a viable therapy for patients with end-stage heart failure and valvular disease. However, device-generated pathological flow patterns result in thromboembolic complications that require complex and lifelong anticoagulant therapy, which entails hemorrhagic risks and is not appropriate for certain patients. Optimizing the thrombogenic performance of such devices utilizing numerical simulations requires the development of predictive platelet activation models that account for variations in shear-loading rates characterizing blood flow through such devices. Platelets were exposed in vitro to both dynamic and constant shear stress conditions emulating those found in blood-recirculating devices in order to determine their shear-induced activation and sensitization response. Both these behaviors were found to be dependent on the shear loading rates, in addition to shear stress magnitude and exposure time. We then critically examined several current models and evaluated their predictive capabilities using these results. Shear loading rate terms were then included to account for dynamic aspects that are either ignored or partially considered by these models, and model parameters were optimized. Independent optimization for each of the two types of shear stress exposure conditions tested resulted in different sets of best-fit constants, indicating that universal optimization may not be possible. Inherent limitations of the current models require a paradigm shift from these integral-based discretized power law models to better address the dynamic conditions encountered in blood-recirculating devices.

Introduction

Implantable cardiovascular blood-recirculating devices are rapidly becoming a viable long term solution for patients with congestive heart failure or valvular disease, particularly among the growing elderly population. Platelets are known to activate and aggregate in response to shear stress conditions in these devices.^7,11,20 However, blood-recirculating device manufacturers mostly test and optimize these devices for hemolysis, which occurs at shear stress levels ten-fold higher than those for platelet activation.^27,31 Thus, blood-recirculating devices are hardly optimized for this lower level flow-induced thrombogenicity.^4,5 This is exacerbated by the relative paucity of shear-induced platelet activation models developed and experimentally validated for the dynamic, time-dependent flow conditions found in such devices.

Several studies have focused on the formulation of platelet “stimulation” (i.e. activation) functions based on experimental observations. Ramstack et al. derived a geometry-dependent function to predict platelet factor 3 (PF3) activity in response to constant flow.²⁷ The Platelet Stimulation Function (PSF) derived by Boreda et al. states that platelet stimulation is due to a combination of shear stress and exposure time, based on flow velocities in experimental models of coronary stenoses.⁸ This formula is based on a model of fractional platelet lysis, as measured by lactate dehydrogenase (LDH) release¹⁴, which in turn is based on a previous model of red blood cell (RBC) hemolysis.³ More recent studies utilized these LDH-based models, as well as linear “level of activation” or stress accumulation (SA) formulations^6,12,32, to predict platelet activation response to flow through mechanical heart valve hinge regions and stenoses.^30,33 This concept originated from the observation that platelet activation was dependent on the product of shear stress and exposure time¹⁸, and was utilized in both numerical simulations^6,12,32 and experimental validation.³³ These models were developed for experiments where blood is exposed to constant shear stresses, but they do not address well, if at all, dynamic shear stress conditions (i.e. accelerating and decelerating flow).

A more recent model by our group¹ addressed the transient nature of the flow field and senescence, or past damage history, of platelets under dynamic recirculating conditions. This formulation was based on an RBC damage model³⁶, where a phenomenological damage index, dependent only on shear stress and time and applied to individual cells, increases as the cell passes through the circulation, culminating in a critical value reflecting the destruction or removal of the cell. This model accounted for the transient nature of the flow field and prior damage history, and assumes a “perfect memory” of previous platelet damage. It required the computation of individual platelet trajectories within the device flow field and their corresponding stress loading histories.

Another recent platelet activation model²⁵ was adapted from the RBC hemolysis power law model of Grigioni et al.¹⁷ The latter was derived by making an earlier RBC damage power law model¹⁶ mechanical loading dose-dependent. This approach allowed the shear-exposed RBC to retain its previous damage history, a feature lacking from prior RBC damage models, with the exception of Yeleswarapu et al.³⁶ Nobili et al. adapted this approach to predict platelet activation state (PAS) in response to dynamic shear stress waveforms. While this phenomenological model accounted for the prior shear loading history of the platelet, like prior models it neglected the role of the shear loading rate, or the acceleration and deceleration phases of the shear stress. Prior studies have shown that the shear stress gradients due to spatial orientation or change in flow conditions are often neglected in shear induced platelet damage studies and have a significant impact on platelet response.^6,26 We hypothesize that this shear loading rate, or even turbulent flow effects, may have a significant impact on the platelet activation behavior.

The present study exposes platelets to both constant and dynamic shear stress conditions, where the duration of high shear stress pulses and the acceleration/deceleration times are within serve as a proxy to those encountered in blood-recirculating devices. Several commonly used platelet activation and damage models are optimized using experimental PAS results. These models are then evaluated to determine their robustness in describing shear-induced platelet activation and whether they are appropriate for assisting in the design and optimization of blood-recirculating devices in a way that may significantly reduce their thrombogenicity.

Materials and Methods

In Vitro Experiments

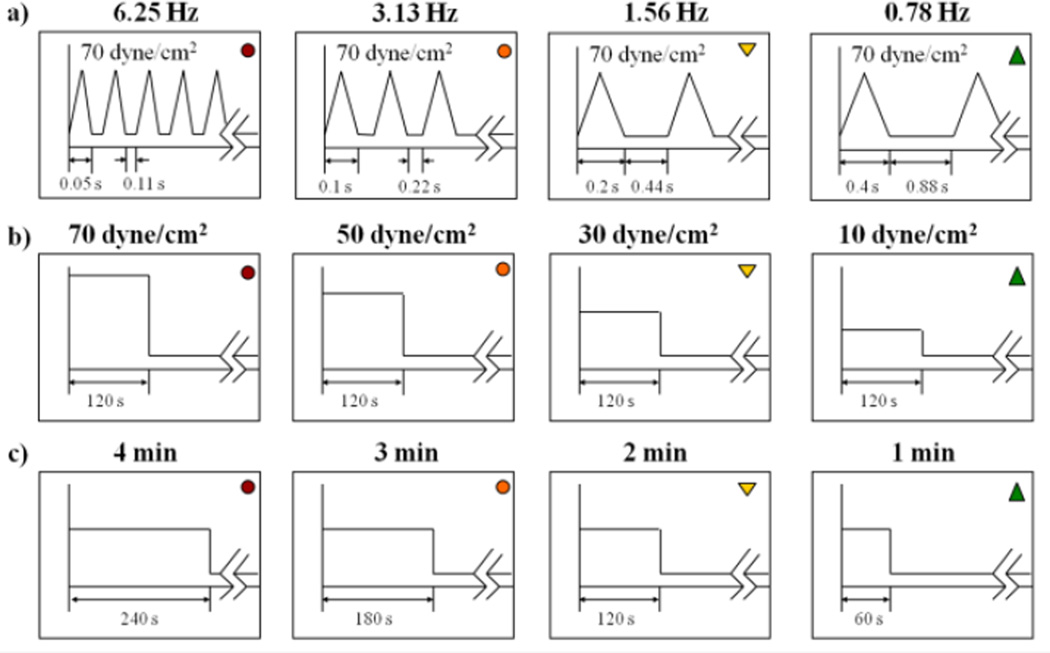
Whole blood, 30 ml, was drawn via venipuncture, in accordance with Stony Brook University IRB-approved protocol, from consenting healthy adult volunteers of both sexes who had not taken aspirin or ibuprofen for two weeks. Purified gel-filtered platelets (GFP) were prepared as previously described^28,29 and diluted to a count of 20,000/µl in HEPES-modified Tyrode’s buffer. A computer-controlled hemodynamic shearing device (HSD)^25,35 was utilized for shear stress exposure. Prior experimental and numerical observations show that the shear stress is homogeneous in all fluid regions of the HSD, except for the small corner regions, and motor response time is ~ 3 ms.³⁵ GFP were exposed to constant and dynamic shear stress waveforms (Fig. 1), which include:

1. repeated triangular peaks of accelerating and decelerating flow with different shear stress rates, ranging from 345 dyne s⁻¹ cm⁻² (frequency of 0.78 Hz) to 2760 dyne s⁻¹ cm⁻² (frequency of 6.25 Hz), for 4 min, followed by a 10 min exposure to 1 dyne/cm² (n = 7). Peak stress was 70 dyne/cm². These shear stress rates represent the range that platelets encounter during passage through blood-recirculating devices, such as mechanical heart valves^2,35, and stenoses.

2. constant shear stress of variable magnitude (70, 50, 30 and 10 dyne/cm²) for 2 min (with acceleration and deceleration times of 0.025 s) followed by 12 min exposure to 1 dyne/cm² (n = 9);

3. constant shear stress of 30 dyne/cm² for variable durations (1, 2, 3 and 4 min, with acceleration and deceleration times of 0.025 s) followed by exposure to 1 dyne/cm² (n = 8);

Figure 1. Dynamic and constant shear stress waveforms.

Platelets were exposed to (a) dynamic waveforms with variable loading rates, (b) variable magnitudes of constant shear stress for 2 min, and (c) 30 dyne/cm² shear stress for variable durations.

Total duration of all experiments was 14 min. Exposure of GFP to 1 dyne/cm² for 14 min served as the negative control for all waveforms. Samples for the prothrombinase-based platelet activation state (PAS) assay^19,29 were drawn every min from 0 to 4 min and every 2.5 min from 4 to 14 min using a LabView-controlled syringe pump (PSD/8, Hamilton, Reno, NV) connected to the HSD via a 30-gauge PTFE tube. PAS values were normalized against those obtained by sonicating unsheared platelets at 10 W for 10 s with a Branson Sonifier 150 with a microprobe (Branson, MO). The sonication step yields platelets that are fully activated, and thus normalized PAS values represent the bulk activity as a fraction of this full activation state. Change in PAS (ΔPAS) was calculated over the duration of high shear stress exposure. Sensitization platelet activation rates (PAR) were determined by performing linear least squares regression analysis on PAS values from the subsequent low shear period and computing the slope. It is important to note that ΔPAS is used instead of a linear PAR for the shear stress exposure periods, but this does not imply that PAS increases linearly during this period. The sensitization PAR assumes that the PAS values subsequent to shear stress exposure fall along a straight line, and post hoc chi-square goodness-of-fit tests validate this assumption. Loading ΔPAS and sensitization PAR values for each type of shear stress waveform (dynamic, variable magnitude, and variable duration) were analyzed and compared to their respective controls using one-way ANOVA with Dunnett’s T3 post hoc test, where p < 0.05 established significance.

Platelet Activation Model Analysis

The objective of this study was to determine if current platelet activation models are robust enough to accurately describe the phenomenological (i.e. based on shear stress and time) response of platelets to both constant and dynamic shear stress conditions. We adapted the power law model derived to fit LDH release from red blood cells³, and later platelets¹⁴, exposed to very high constant shear stresses for fixed durations. This “original power law (OPL)” model was redefined for the PAS:

$${\mathit{\text{PAS}}}_{\mathit{\text{OPL}}}(\tau ,t)=C{\tau }^{\alpha }{t_{\text{exp}}}^{\beta }$$ (1)

where the platelet activation state, PAS, is dependent on the shear stress, τ, and exposure time, t_exp. The value of the constants C, α, and β were originally obtained for platelet LDH release and cannot be used for PAS. Therefore, the constants were optimized for PAS by minimizing the difference between Eq. 1 and the experimental data as described later (in Optimization Approach for the Model Parameters).

This model was discretized by Grigioni et al. to allow fitting of experimental hemolysis data at additional time points^16,17 and adapted by Nobili et al. for PAS measurements.²⁵ Since these models were originally developed for constant shear stress conditions, they were derived again from basic principles to account for the shear loading rate τ̇ (Appendix). Each expansion of these models results in constants C₁ and C₂, which represent C for the constant and dynamic shear stress parts of the equations, respectively. When C₂ = 0, the models revert back to their originally presented forms.^16,17,25

Cumulative Power Law Model

The cumulative power law model (CPL) developed by Grigioni et al. was adapted to PAS by expanding Eq. 1 to account for dynamic conditions and derived utilizing their approach for a prior blood damage model¹⁶ (Appendix):

$${\mathit{\text{PAS}}}_{\mathit{\text{CPL}}}(\tau (t),t)=C_1{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\beta \tau {(t)}^{\alpha }{t}^{\beta -1}\mathit{\text{dt}}+C_2{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\alpha \tau {(t)}^{\alpha -1}{t}^{\beta }\frac{|d\tau (t)|}{\mathit{\text{dt}}}\mathit{\text{dt}}+\mathit{\text{PAS}}(t_0)$$ (2)

where t_total is the total duration of the experiment. The platelet activation state at the start of the experiments is given by PAS(t₀). The absolute value of the change in shear stress, dτ(t), is taken to avoid violating the principle of causality¹⁷, where decrease in shear stress does not cause a decrease in PAS. We assume that platelets activate the same regardless of whether dτ(t) is due to acceleration or deceleration. In discrete form, Eq. 2 becomes:

$${\mathit{\text{PAS}}}_{\mathit{\text{CPL}}}\mathit{(}\tau ,t\mathit{)}=C_{\mathit{1}}\beta {\displaystyle \sum _{i=\mathit{1}}^n}{t_i}^{\beta -\mathit{1}}{{\tau }_i}^{\alpha }\mathrm{\Delta }{t}_i+C_{\mathit{2}}\alpha {\displaystyle \sum _{i=\mathit{1}}^n}{{\tau }_i}^{\alpha -\mathit{1}}{t_i}^{\beta }|{\tau }_i-{\tau }_{i-\mathit{1}}|+\mathit{\text{PAS}}\mathit{(}{t}_{\mathit{0}}\mathit{)}$$ (3)

All 3 power law conditions defined by Grigioni et al.¹⁷ are satisfied. Eq. 3 is similar to a previously derived model³⁵ but does not assume that the constants C, α, and β are equal to 1. If Δt_i included a linear ramping of τ(t), τ_i over this interval was approximated using the trapezoidal rule.

Linear Model

The simplest form of the power law model assumes that shear stress and exposure time have equal weight, and that α = β = 1. Simplifying Eq. 2 yields the linear (L) model:

$${\mathit{\text{PAS}}}_L(\tau (t),t)=C_1{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\tau (t)\mathit{\text{dt}}+C_2{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}t\frac{|d\tau (t)|}{\mathit{\text{dt}}}\mathit{\text{dt}}+\mathit{\text{PAS}}(t_0)$$ (4)

When C₂ = 0, Eq. 4 relates the stress accumulation (SA) of particular platelet shear histories⁶ to PAS through multiplication with constant C₁. In discrete form, Eq. 4 becomes:

$${\mathit{\text{PAS}}}_L\mathit{(}\tau ,t\mathit{)}=C_{\mathit{1}}{\displaystyle \sum _{i=\mathit{1}}^n}{\tau }_i\mathrm{\Delta }{t}_i+C_{\mathit{2}}{\displaystyle \sum _{i=\mathit{1}}^n}{t}_i|{\tau }_i-{\tau }_{i-\mathit{1}}|+\mathit{\text{PAS}}\mathit{(}{t}_{\mathit{0}}\mathit{)}$$ (5)

If Δt_i included a linear ramping of τ(t), τ_i over this interval was approximated using the trapezoidal rule.

Modified Cumulative Power Law Model

While Eq. 2 addresses the shear loading rate that previous models neglect, it does not truly satisfy the prior damage history condition for power law models: PAS(t₀) was taken into account, however it did not include the effect of loading at each interval in which an experimental observation is made. Thus, the modified cumulative power law (MPL), adapted by Nobili et al. for PAS,²⁵ was expanded to include the shear loading rate (Appendix):

$${\mathit{\text{PAS}}}_{\mathit{\text{MPL}}}(\tau (t),t)=C_1\beta \left[{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{tot}}}}{\int }}}{({\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\xi )}^{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}d\xi +\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.{\displaystyle \underset{\tau (t_0)}{\overset{\tau (\varphi )}{\int }}}\xi ·\tau {(\xi )}^{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.-1}d\tau +{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.})}^{\beta -1}{\tau }^{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}d\varphi \right]$$ (6)

C₁, α, and β are constants, while dτ is the change in shear stress for a given time interval. The inner integrals represent mechanical stress loading dose D (Appendix) divided into constant and dynamic shear stress terms and applied over a time ξ, where dξ is the interval over which an elemental dose of shear stress is applied and Γ is the shear stress at time ξ. The outer integral is the summation of these doses over the duration of the experiment, with ϕ and dϕ as the observation time points and the interval between them, respectively. In discrete form, Eq. 6 becomes:

$${\mathit{\text{PAS}}}_{\mathit{\text{MPL}}}(\tau ,t)=C_1\beta {\displaystyle \sum _{i=1}^{\mathrm{N}}}{({\displaystyle \sum _{j=1}^i}\tau {(t_j)}^{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}\mathrm{\Delta }{t}_j+\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.{\displaystyle \sum _{j=1}^i}{t}_j·\tau {(t_j)}^{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.-1}|\mathrm{\Delta }{\tau }_j|+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.})}^{\beta -1}\tau {(t_i)}^{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}\mathrm{\Delta }{t}_i$$ (7)

The i-th interval refers to experimental observation time points, while the j-th interval refers to time points where the mechanical loading changes. For example, in the constant shear stress experiments included in the model parameters optimization, the initial high shear stress loading had three distinct phases: a linear ramping of shear stress, constant high shear stress, followed by a linear decrease in shear stress. Experimental PAS values were measured at the start of the first ramping phase (PAS(t₀)) and at the end of the decreasing shear stress phase (PAS(t₁)). Thus, there are 3 mechanical stress loading dose intervals (j) for the single observation interval (i) in this case. The absolute value of the shear loading term Δτ_j was taken to avoid violating the principle of causality, and to ensure that a reduction in shear stress does not cause a decrease in PAS. As before, if Δt_i and Δt_j included a linear ramping of τ(t), the integrals of τ_i and τ_j over these intervals were determined using the trapezoidal rule. Eqs. 6 and 7 revert to the prior model²⁵ when only constant shear stress conditions are considered.

Optimization Approach for the Model Parameters

Where appropriate, constants were optimized for the cases where (1) only constant shear effects are considered (C₂ = 0); (2) constant and dynamic shear effects have equal weights (C₁ = C₂); and (3) constant and dynamic shear effects have unequal weights (C₁ ≠ C₂). Optimization was performed for PAS values from 0 to 4 min, as sensitization was not considered in the models evaluated.

Constants for Eqs. 1, 3, 5, and 7 were optimized using a Levenberg-Marquardt (L-M)^21,22 optimization scheme in MATLAB 7.13 (MathWorks, Natick, MA), where the difference between the model prediction and experimental results was minimized:

$$\underset{\theta }{\mathit{\text{min }}}f\mathit{(}x\mathit{)}=\mathit{\text{min}}\mathit{(}{\mathit{\text{PAS}}}_{\mathit{\text{exp}}}-{\mathit{\text{PAS}}}_{\mathit{\text{num}}}\mathit{)}$$ (8)

$$s.t.\theta =\mathit{\{}{C}_{\mathit{1}},C_{\mathit{2}},\alpha ,\beta \mathit{\}}$$

PAS_num refers to the discrete forms of the models examined. For constant shear stress waveforms, PAS_num includes the initial and final transient phases of the high shear exposure regardless of the shear loading term. Experimental PAS values, PAS_exp, were taken from the results at each time point during constant and dynamic shear stress loading for each condition tested. Shear stress, exposure time, and shear loading rate were inputted into the discrete forms of the models for each experimental sampling point, with each successive equation inclusive of the prior equations for each condition tested. Optimization included experimental values for the 1 dyne/cm² negative control that indicated no significant increase in PAS over the course of the experiment.

In order to reduce the dependence of the optimized constants on the initial values, the following iterative procedure was followed: C₁ and C₂ were initialized at values between 0.005 and 0.1, with increments of 0.005, and α and β were initialized between 0.5 and 10, with increments of 0.5 between each value, such that:

$$C_{\mathit{1}}=C_{\mathit{2}}=\mathit{[}\mathit{0.005},\mathit{0.1}\mathit{]}\mathit{;}\alpha =\beta =\mathit{[}\mathit{0.5},\mathit{10}\mathit{]}$$ (9)

This range of values was based on the results of a previous platelet activation model optimization study.²⁵ This resulted in 20 initial values for each constant, generating up to 160,000 unique sets of these three constants. For each combination of constants, iterations were performed until the cumulative least square error (LSE) between the experimental and numerical PAS values was below 1 × 10⁻⁵ or when 2 × 10⁴ iterations were exceeded. In the event that the number of iterations was exceeded, the set of constants were discarded and the program initialized at a new set of constants. The combination of constants that yielded the lowest cumulative error was selected for the final formulation of the model.²⁵ If there were several combinations of constants that yielded the lowest error, the mean values for all such constants were calculated.

Results

In Vitro Experiments

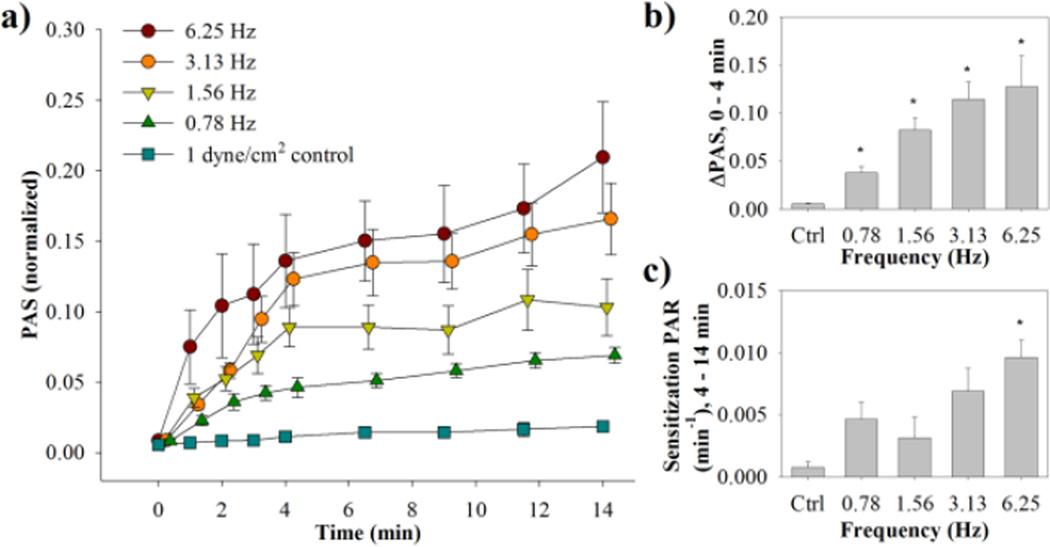
A general increasing trend was observed for both the change in the high shear platelet activation state (ΔPAS) and sensitization platelet activation rate (PAR) for the dynamic waveforms (Fig. 1a), correlating with an increase in frequency of 70 dyne/cm² peaks (Fig. 2, Table 1, n = 7). Furthermore, the evolution of PAS over the 4 min high shear stress exposure was different for the four waveforms, despite having identical stress accumulations (SA) of 2800 dyne s cm⁻². This increase in high shear PAS was observed to be non-linear, contrasting with a linear increase in PAS for the subsequent sensitization phase. For the 4 min shear stress exposure, ΔPAS is significantly higher than the control for all waveforms, whereas the sensitization PAR is only significant for 6.25 Hz (τ̇ = 2760 dyne s⁻¹ cm⁻², p < 0.05). In addition, ΔPAS for 6.25 Hz and 3.13 Hz (τ̇ = 1380 dyne s⁻¹ cm⁻²) was significantly higher than for 0.78 Hz (τ̇= 345 dyne s⁻¹ cm⁻²).

Figure 2. Dynamic waveforms PAS and PAR results.

(a) Normalized PAS results were obtained for both the dynamic phase (0–4 min) and sensitization phase (4–14 min) (standard error bars, n = 7). (b) ΔPAS was measured over the dynamic phase, while (c) PAR was measured for the sensitization phase (*p <0.05 vs. control).

Table 1.

Platelet activation response to dynamic shear stress experiments

Frequency (Hz)	Integral Shear Stress (dyne s cm−2)	Loading activation state (ΔPAS) (× 10−2)	p vs. control	Sensitization rate (PAR) (× 10−3 min−1)	p vs. control
6.25	2800	12.7 ± 3.0	0.04	9.6 ± 1.3	0.001
3.13	2800	11.4 ± 1.7	0.005	6.9 ± 1.7	0.07
1.56	2800	8.2 ± 1.2	0.004	3.2 ± 1.5	0.74
0.78	2800	3.8 ± 0.8	0.04	4.7 ± 1.6	0.3
1 dyne/cm2 (control)	240	0.6 ± 0.1	-	0.8 ± 0.4	-

Loading activation states are means ± S.E.M and are determined from the change in PAS values from 0 min to the end of dynamic shear stress exposure (4 min, n = 7). Sensitization rates are obtained from the slope of a line fit to PAS values from 4 min to the end of the experiment.

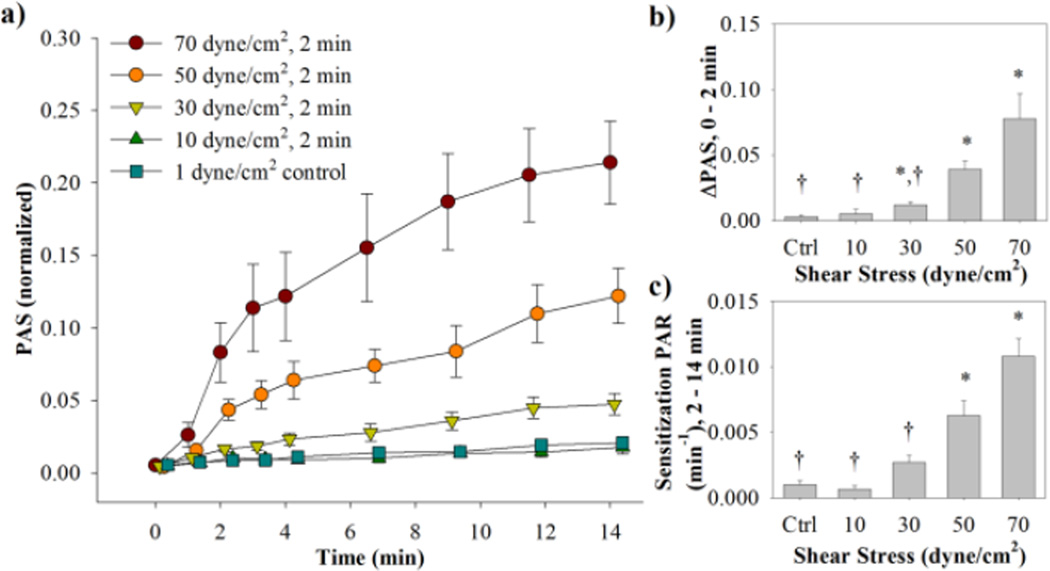
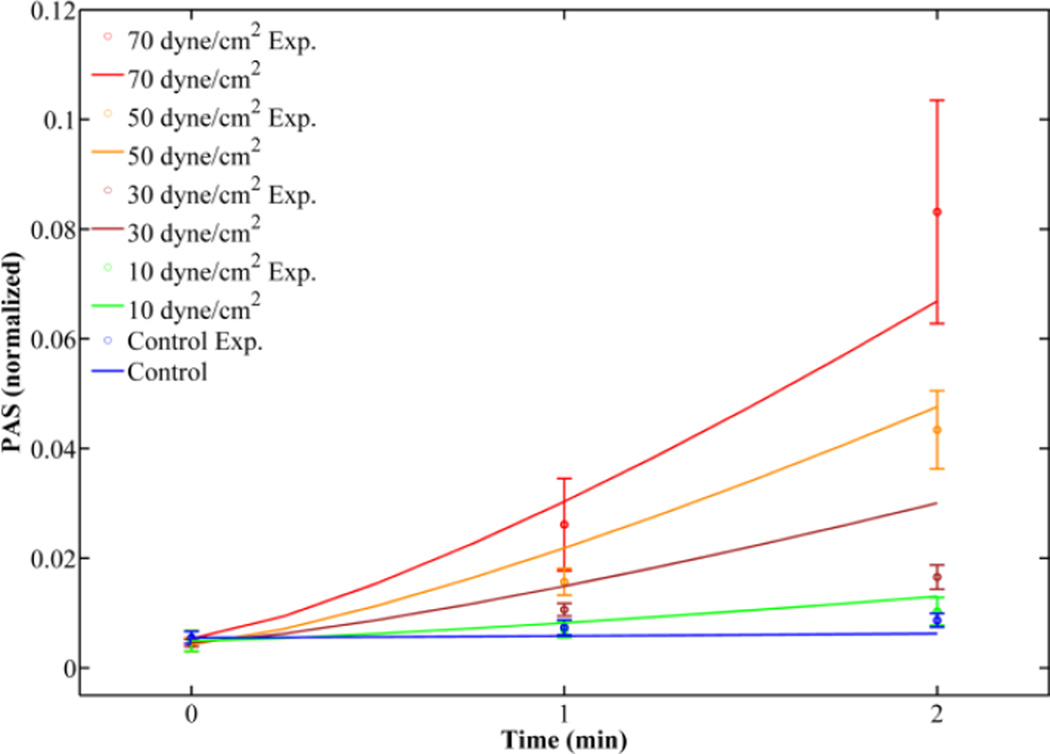
For the constant shear stress waveforms with variable magnitudes (Fig. 1b), there was a general increasing trend for both ΔPAS and sensitization PAR with an increase in shear stress magnitude (Fig. 3, Table 2a, n = 9). Similar to the dynamic waveforms, a non-linear increase in PAS is observed for the 2 min high shear exposure, followed by a linear increase in PAS for the subsequent sensitization phase. For the 2 min shear stress exposure, ΔPAS is significantly higher than the control for 70, 50, and 30 dyne/cm², and ΔPAS for the 30 and 10 dyne/cm² waveforms is significantly lower than for the 70 dyne/cm² waveform (p < 0.05). The sensitization PAR is significantly higher than the control for 70 and 50 dyne/cm², whereas it is significantly lower than the 70 dyne/cm² PAR for the 30 and 10 dyne/cm² conditions (p < 0.05).

Figure 3. Variable magnitude waveforms PAS and PAR results.

(a) Normalized PAS results were obtained for both the high shear stress phase (0–2 min) and sensitization phase (2–14 min) (standard error bars, n = 9). (b) ΔPAS was measured over the high shear stress phase, while (c) PAR was measured for the sensitization phase (*p <0.05 vs. control, ^†p < 0.05 vs. 70 dyne/cm²).

Table 2.

Platelet activation response to constant shear stress experiments

Shear Stress (dyne/cm2)	Duration (s)	Integral Shear Stress (dyne s cm−2)	Loading activation state (ΔPAS) (× 10−2)	p vs. control	Sensitization rate (PAR) (× 10−3 min−1)	p vs. control
a) Variable Magnitude
70	120	8400	7.8 ± 1.8	0.02	10.8 ± 1.3	< 0.001
50	120	6000	3.9 ± 0.6	0.002	6.3 ± 1.0	0.007
30	120	3600	1.2 ± 0.2	0.02	2.7 ± 0.5	0.07
10	120	1200	0.5 ± 0.3	> 0.5	0.7 ± 0.3	> 0.5
1 (control)	120	120	0.3 ± 0.1	-	1.0 ± 0.3	-
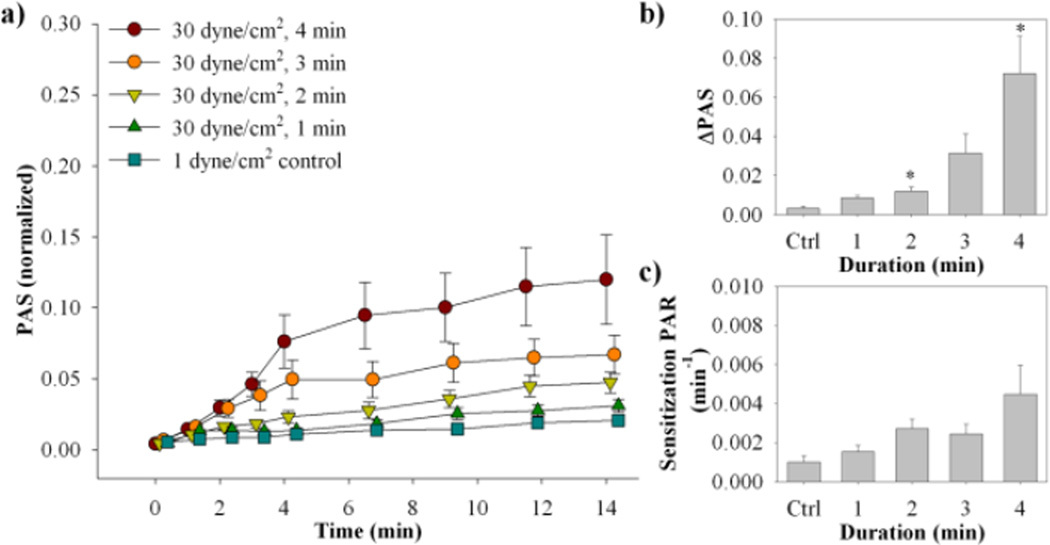
b) Variable Duration
30	240	7200	7.2 ± 1.8	0.03	4.5 ± 1.4	0.25
30	180	5400	3.1 ± 0.9	0.12	2.5 ± 0.5	0.17
30	120	3600	1.2 ± 0.2	0.02	2.7 ± 0.5	0.07
30	60	1800	0.9 ± 0.1	0.06	1.5 ± 0.3	> 0.5
1 (control)	120	120	0.3 ± 0.1	-	0.7 ± 0.3	-

Loading activation rates are means ± S.E.M and are determined from the change in PAS values from 0 min to the end of higher shear stress exposure for the (a) variable magnitude (2 min, n = 9) and (b) duration (1, 2, 3, or 4 min, n = 8) experiments. Sensitization rates are obtained from the slope of a line fit to PAS values from the end of high shear stress exposure to the end of the experiment.

For the constant 30 dyne/cm² shear stress waveforms with variable durations (Fig. 1c), there was a general increasing trend for both ΔPAS and sensitization PAR with an increase in exposure duration (Fig. 4, Table 2b, n = 8). As observed previously, the increase in PAS is non-linear over the initial high shear stress exposure, followed by a linear increase in PAS during the subsequent sensitization phase. Significantly higher ΔPAS is observed only for the 2 and 4 min exposure times when compared to the control (p < 0.05). No significance is observed for the sensitization PAR when compared to the control.

Figure 4. Variable exposure time waveforms PAS and PAR results.

(a) Normalized PAS results were obtained for both the high shear stress phase and sensitization phase (standard error bars, n = 8). (b) ΔPAS was measured over the high shear stress phase, while (c) PAR was measured for the sensitization phase (*p <0.05 vs. control).

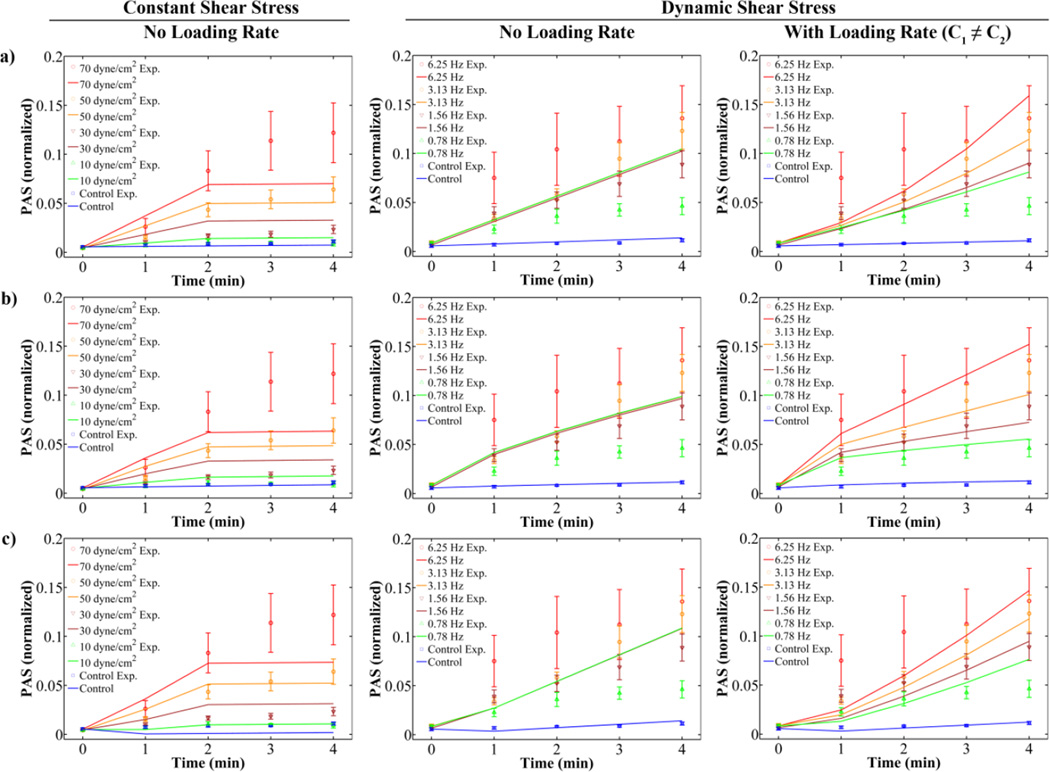
Platelet Activation Model Analysis

The OPL model (Eq. 1), optimized with experimental results for both sets of constant shear stress waveforms (Fig. 1b,c), provides a good fit for experimental PAS for both the 1 and 2 min time points for the variable magnitude waveforms (Fig. 5, LSE = 1.0 × 10⁻³). To account for intermediate time points, 3 discrete models were analyzed: the linear (L, Eq. 4), cumulative power law (CPL, Eq. 2), and modified cumulative power law (MPL, Eq. 6) models. For all 3 models, when τ̇ is not considered, the fit yields lower LSE values for constant than dynamic shear stress waveforms (Fig. 6, Table 3). In addition, the lack of a term for τ̇ in these 3 models yields an identical fit for the 4 dynamic waveforms from 0 to 4 min, despite experimental values showing different PAS values for each during the intermediate time points (Fig. 2). Including this loading rate term generally yields lower LSE, with lowest errors obtained when constants C₁ ≠ C₂ (Table 3). For the dynamic shear stress waveforms, the lowest LSE and concave activation behavior representative of the experimental response are obtained with the CPL model where C₁ ≠ C₂ (Fig. 6b). For the constant shear stress waveforms, the lowest LSE is achieved for the L model (Fig. 6a, Table 3). However, both the L and CPL models with C₁ ≠ C₂ yield lower LSE compared to models with C₁ = C₂ when including the loading rate due to acceleration to and deceleration from the peak shear stress condition (Table 3). While C₂, the constant preceding the loading rate term, is on the same order of magnitude as C₁, the constant preceding the constant shear stress term, for the constant shear stress L model, it is 3 to 4 orders of magnitude lower in all the other cases. Furthermore, setting C₁ ≠ C₂ increases α and β to values markedly larger than 0 compared to C₁ = C₂ for the CPL model under both dynamic and combined conditions.

Figure 5. Giersiepen original power law (OPL) fit for variable magnitude constant shear stress experiments.

Fits for 1 and 2 min experimental values (open circles with standard error bars) were obtained with constants C = 1.47 × 10⁻⁶, α = 1.04, and β = 1.30.

Figure 6. Linear and power law model fits for constant and dynamic shear stress experiments (constants in Table 3a–b).

PAS results for constant and dynamic shear stress experiments were fit to (a) L, (b) CPL, and (c) MPL power law models. These models fit the high shear period (0–2 min) well for constant shear stress experiments without a loading rate term (left), but do not differentiate between the different loading frequencies (middle, 0 – 4 min) until addition of a loading rate term (right).

Table 3.

Optimized model constants for constant and dynamic shear stress experiments

Model		C1	C2	α	β	LSE (× 10−3)
a) Constant only
L		7.59 × 10−6	-	-	-	1.9
OPL		1.47 × 10−6	-	1.0400	1.3000	1.0
CPL		5.35 × 10−5	-	0.8240	0.7620	2.1
MPL		7.30 × 10−2	-	1.0300	0.0063	33.4
L w/ loading rate	C1=C2	4.36 × 10−6	-	-	-	1.7
	C1≠C2	5.78 × 10−6	2.65 × 10−6	-	-	1.5
CPL w/ loading rate	C1=C2	3.40 × 10−5	-	0.5280	0.9700	3.0
	C1≠C2	2.07 × 10−5	2.14 × 10−9	0.8720	0.9000	1.5
MPL w/ loading rate		6.19 × 10−7	-	1.0400	1.4400	32.2
b) Dynamic only
L		3.39 × 10−5	-	-	-	12.4
CPL		1.30 × 10−4	-	1.0293	0.7249	11.7
MPL		7.85 × 10−8	-	1.2600	2.0700	114.0
L w/ loading rate	C1=C2	7.52 × 10−9	-	-	-	17.6
	C1≠C2	2.17 × 10−5	3.59 × 10−9	-	-	6.9
CPL w/ loading rate	C1=C2	9.10 × 10−2	-	0.0002	0.0468	2.7
	C1≠C2	9.84 × 10−3	4.15 × 10−6	0.4291	0.1628	2.4
MPL w/ loading rate		6.86 × 10−6	-	0.3120	1.3200	83.9
c) Constant and dynamic
L		1.23 × 10−5	-	-	-	48.6
CPL		5.59 × 10−1	-	0.3940	0.0068	17.1
MPL		1.46 × 10−2	-	0.1500	0.2810	149.0
L w/ loading rate	C1=C2	7.53 × 10−9	-	-	-	35.2
	C1≠C2	8.65 × 10−6	5.95 × 10−9	-	-	13.0
CPL w/ loading rate	C1=C2	6.97 × 10−3	-	0.0004	0.3710	10.8
	C1≠C2	2.58 × 10−3	7.43 × 10−7	0.6890	0.2430	5.5
MPL w/ loading rate		8.30 × 10−7	-	1.2200	1.2600	91.7

Constants are optimized values corresponding to the lowest least square errors (LSE) for the linear (L), cumulative power law (CPL), and modified cumulative power law (MPL) models. Constants were optimized for (a) constant shear stress waveforms only, (b) dynamic shear stress waveforms only, and (c) constant and dynamic shear stress waveforms in combination.

PAS values predicted by the discretized CPL models and the OPL model were compared with experimental PAS values (PAS_exp) for the 1 and 2 min time points of the variable magnitude constant shear stress waveforms (Fig. 1b) to determine which yields the highest accuracy. The CPL models included the forms with C₂ = 0 (PL0) and C₁ ≠ C₂ (PL2). The OPL model yields the lowest difference between model predictions and PAS_exp for all but the 2 min value for the 70 dyne/cm² experiment (Table 4), indicating that the OPL model is still valid for constant shear stress conditions. However, this model only accounts for initial PAS value (PAS(t₀)) and the final observed PAS value, and cannot be used for intermediate time points.

Table 4.

Comparison of power law models for variable shear stress magnitude experiments

	Time (min)
Shear Stress (dyne/cm2)	0	1				2
	PASexp	PASexp	PASOPL	PASPL0	PASPL2	PASexp	PASOPL	PASPL0	PASPL2
10	0.0049	0.0069	0.0082	0.0111	0.0104	0.0103	0.0130	0.0212	0.0205
30	0.0045	0.0106	0.0149	0.0198	0.0190	0.0166	0.0300	0.0372	0.0369
50	0.0042	0.0157	0.0218	0.0274	0.0267	0.0434	0.0476	0.0513	0.0519
70	0.0053	0.0261	0.0303	0.0360	0.0355	0.0831	0.0669	0.0673	0.0690

Comparison of power law model predictions of PAS with mean experimental results (PAS_exp) at 1 and 2 min for constant shear stress experiments with variable magnitudes. Models selected for comparison are the Giersiepen original power law (OPL), cumulative power law (CPL) with no loading rate (PL0), and cumulative power law (CPL) with constants C₁ ≠ C₂ (PL2).

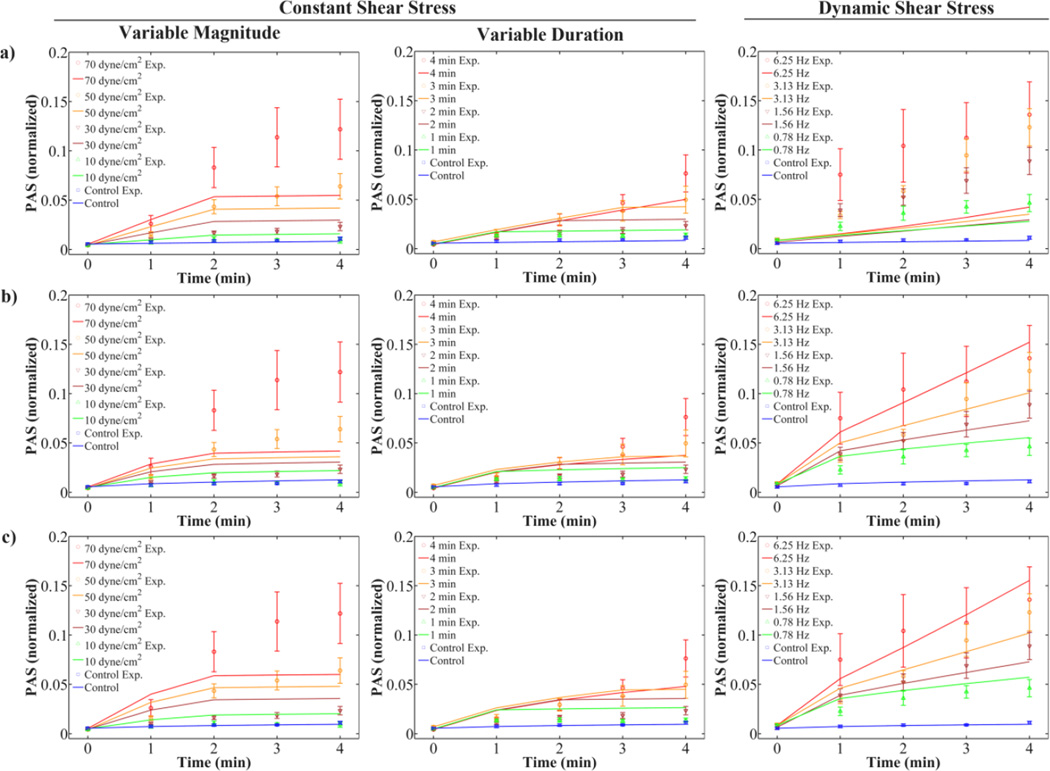
However, the fits described earlier utilized different sets of constants C₁, C₂, α, and β for each type of model depending on whether constant or dynamic shear stress waveforms were optimized. Constants obtained from optimization of the CPL model with C₁ ≠ C₂ were fit simultaneously to constant and dynamic shear stress PAS values in order to evaluate the predictive capability of the model. This model was selected as it yielded the lowest LSE for the optimization of the constant and dynamic shear stress waveforms (Table 3). As expected, model fits for the variable magnitude and variable duration waveforms agree well with experimental PAS values when using constants obtained from optimization of only the constant shear stress waveforms (Fig. 7a). However, these constants cause underestimation of PAS for the dynamic shear stress waveforms. Conversely, model fits for the dynamic waveforms agree well with PAS values using constants obtained from optimization of only the dynamic waveforms, while underestimating the PAS values for the constant shear stress waveforms (Fig. 7b). Optimizing the CPL model with C₁ ≠ C₂ simultaneously for the constant and dynamic shear stress waveforms restores some of the behavior observed for the individual optimizations (Fig. 7c), but the LSE increased (Table 3).

Figure 7. Cumulative power law (CPL) model fits for constant and dynamic shear stress experiments (constants in Table 3a–c).

Variable magnitude and duration constant shear stress, and dynamic shear stress experiments were fit using the CPL model including the loading rate term and C₁ ≠ C₂. The fits use constants optimized for (a) constant shear stress results only, (b) dynamic shear stress results only, and (c) combined constant and dynamic shear stress results.

Discussion

While several researchers explored the concept of predictive platelet activation models, few developed such models based on direct experimental results.^8,25,27 Moreover, these models were developed using either constant shear stress experiments, or approximated using formulations originally developed for constant shear stress conditions. The overwhelming majority of these models and their predecessors were either developed or optimized based on experiments where samples were taken at the start and end of shear stress exposure.^{8,14,18,27,34} However, these models neglect shear loading rate or turbulent flow effects, which may have a significant impact on the platelet activation behavior.^6,26

In this study, platelets were exposed to tightly-controlled constant and dynamic shear stress waveforms (Fig. 1), which serve as a proxy to conditions found in mechanical circulatory support (MCS) devices and prosthetic heart valves (PHVs). The exposure time in these waveforms is generally longer than found in vivo, but these conditions allow the development of models which can later be validated under more realistic conditions. While platelets are only briefly exposed to shear stresses up to 3000 dyne/cm² in such devices,³⁷ repeated exposure to these conditions may result in persistent platelet activation despite anticoagulation therapy.^9,10 This may be partially explained by our observation that residual activation response (sensitization) subsequent to high shear stress exposure correlates well with the shear stress-time product, or stress accumulation (SA), encountered by the platelets.²⁹ As expected, change in PAS for the constant shear stress experiments showed a positive correlation with increases in both shear stress magnitude and exposure time (Figs. 3a–b, 4a–b). This trend was also observed in the sensitization response subsequent to high shear stress exposure, with more significant results observed for the variable shear stress magnitude experiments (Fig. 3c). Positive correlations were also observed for both ΔPAS and the sensitization PAR with increasing frequency in the dynamic shear stress waveforms (Figs. 1a, 2), but SA, maintained at 2800 dyne s cm⁻² for all waveforms, had no correlation with PAS observations. Constant shear stress waveforms result in a convex platelet activation response during high shear stress exposure (0 –2 min in Fig. 3 and 0–4 min in Fig. 4), whereas the dynamic shear stress waveforms result in a concave response during dynamic loading (0 – 4 min, Fig. 2). This is particularly apparent for the higher shear stresses or exposure times in all 3 types of exposure examined.

While the results of the constant and dynamic shear stress experiments were not directly compared, it is interesting to note the mean ΔPAS for the most dynamic waveform (6.25 Hz, Fig. 2b) is greater than the 2 min, 70 dyne/cm² constant shear stress exposure (Fig. 3b), even though the SA for the former is 33% of the latter waveform. The mean sensitization PAR values for the dynamic (Fig. 2c) and constant (Fig. 3c) shear stress waveforms are similar, despite the 1:3 ratio in SA. Thus, frequency, and shear loading rate by extension, has a significant effect on platelet activation and subsequent sensitization, confirming previous observations that secondary flow effects, which include acceleration and deceleration, may be more damaging than constant shear stress effects.²⁶ These observations suggest that while SA has been successfully applied in experimental¹⁸ and numerical^6,12,33 approaches, it is more relevant for constant shear stress exposures. Therefore, researchers using SA in computational fluid dynamics (CFD) simulations as a benchmark of thrombogenic performance of blood-recirculating devices may need to additionally account for flow acceleration and deceleration that platelets encounter.

Initial platelet damage models were correlated with experimental measurements of platelet lysis but only at the end of the experiments.¹⁴ This Giersiepen formulation (OPL) fit constant shear stress platelet activation experiments well and yielded lower LSE when compared with other power law models (Fig. 5, Table 3a). Our results show a lower C₁ and α, and higher β than the original OPL constants of C = 3.31 × 10⁻⁶, α = 3.075, and β = 0.77 obtained for platelet lysis.¹⁴ In addition to our constants being optimized for platelet activation, differences between these two sets of constants may be due to Giersiepen et al. using shear stresses 2 orders of magnitude higher and exposures times 1 to 2 orders of magnitude lower than our experimental conditions. However, this model cannot be used for dynamic waveforms with variable conditions, such as those found in blood-recirculating devices. We expanded this basic formulation following the approach of several recent studies^16,17,25 to predict the PAS value due to cumulative stress over time for dynamic, time-dependent, stress loading waveforms, while incorporating the effect of the shear loading rate. The resulting models were integral functions of time and dynamic shear stress rather than the original algebraic formulation based on constant shear stress exposure.¹⁴ Furthermore, these models were optimized with experimental PAS results obtained at intermediate time points to obtain a more robust fit.

In the first use of the MPL model for platelet activation²⁵, it was observed that fits for square waveforms yielded lower root-mean-square errors than for triangular waveforms.²⁵ This indicates that earlier power law models may predict platelet activation or damage levels with greater accuracy for constant, rather than dynamic, shear stress conditions. In the present study, optimizing these models with both constant and dynamic shear stress conditions confirm this observation: power law-based models (Fig. 6b–c) and the modified linear model (Fig. 6a) without consideration of the loading rate term τ̇ yields a better fit for the constant shear stress conditions (Table 3). These models account for the acceleration and deceleration preceding and succeeding the high shear stress phase, and the loading rate term does not become trivial. Furthermore, incorporation of a loading rate term that accounts for acceleration and deceleration of flow in the dynamic shear stress waveforms (Fig. 6, right column) yields a more accurate reflection of the different activation rates observed experimentally (Fig. 2a), since the original models only consider the impact of exposure to constant shear stress present from the beginning to the end of experiments and do not differentiate between the different loading frequencies (Fig. 6, center).

Inclusion of shear loading rate terms yielded model constants that are different from prior models derived for constant shear stress conditions. The CPL model optimized for both constant and dynamic shear stress conditions yields C₁ which was higher, and α and β which were lower, than the Giersiepen constants (Table 3). The constants for the original MPL model for platelet activation prediction were: C = 10⁻⁵, α = 0.6256, and β = 1.3198, where α and β correspond to b and a, respectively, in the original model.²⁵ In comparison, the MPL model with a loading rate term yields constants C and β that were lower and α that was higher than the original MPL constants (Table 3). Unlike the CPL, the MPL modeled the concave PAS response of the dynamic waveforms (Fig. 6, right) with a convex fit. While this convex behavior is more appropriate for the constant shear stress waveforms (Fig. 6, left), the MPL largely under predicted PAS for the earlier time points for the lower shear stresses and exposure times. These factors, combined with error accumulation over 32 and 20 unique observation time points for the constant dynamic waveforms, respectively, may explain why the MPL model yields the highest LSE (Table 3). For dynamic shear stress waveforms, the CPL model accounting for loading rate and with C₁≠ C₂ yields the lowest LSE between predicted and experimental PAS, and reflects the experimental response of PAS over time (Fig. 6b). In addition, the reduction in LSE associated with the different weights on the constants preceding the constant shear stress and shear loading terms (C₁ and C₂, respectively) indicate that these models are improved when separately accounting for transient effects such as flow acceleration and deceleration. It is expected that C₂ is several magnitudes smaller than C₁, as observed, since the shear loading term includes the time t at which the shear stress is computed. Incorporating the condition that C₁≠ C₂ also ensures that α and β for the CPL model with loading rate for the dynamic and combined conditions (Table 3) do not approach 0, which would imply that the effect of shear stress or time is negligible. This issue can also be resolved by using global nonlinear least squares (NLS) optimization techniques, such as the genetic algorithm (GA) method²⁴, over local NLS minimization approaches, such as the Levenberg-Marquardt^21,22, although the latter is less computationally expensive. The strengths of these 2 approaches can also be harnessed in tandem to provide both a global solution and space and fast convergence to optimized parameters in the local domain.¹³

In adding a loading rate term, it was necessary to take the absolute value of the change in shear stress, dτ(t), to avoid violating the principle of causality.¹⁷ While several researchers examined the effect of loading rate on platelet activation^26,38, the directional effects of stress change are not well understood and the effect of fluid acceleration and deceleration have not been directly compared. In our modeling approach, we assumed that the platelet response to either acceleration or deceleration is identical, as our experiments are unable to separately examine these behaviors.

These discretized power law models are hindered by the observation that application of these models to different types of shear stress conditions (i.e. constant or dynamic) results in different sets of constants (Fig. 7). These issues need to be addressed with regards to prediction of platelet activation in response to potentially thousands of shear stress trajectories extracted from CFD simulations of blood-recirculating devices. Utilizing a universal set of constants will not only lower the computational expense of such simulations, and researchers will not have to subjectively determine what constitutes a “constant” or “dynamic” shear stress condition.

In addition to the requirement of different sets of constants for the type of shear stress exposure, the CPL model¹⁶ is prone to accumulation of error resulting from the utilization of time steps in discrete form due to the use of powers on time (Appendix). The mechanical dose function D in the MPL model was redefined to remove the power on time, with the specification that the model was appropriate for constant shear stress conditions.¹⁷ However, the precision of this model and its subsequent adaptation for PAS^23,25 is still dependent on the discretization of the time intervals (Appendix). Other researchers have attempted to tackle the effect arising from the nonlinear dependence on exposure time by introducing “virtual time points” that are force-fitted back into the model¹⁵, but the resulting algebraic formulation is cumbersome. The accuracy of these models may be improved by using higher-order methods of approximation for integral functions (i.e. trapezoidal rule, as utilized in this study, Simpson’s rule, and finite difference methods), reducing the discrete time step size in the models, and increasing the number of temporal experimental data points, although the latter is limited by time required for sampling and performing the PAS assay. However, the errors arising from time-dependent discretization of these power law models have yet to be addressed.

The expanded platelet activation models presented herein provide improved descriptive capabilities as compared to prior platelet activation models^8,17,25 by introducing shear loading rate terms that account for the dynamic nature of shear stress waveforms, such as those found in blood-recirculating devices.⁵ However, these models have yet to incorporate sensitization, where platelets continue to activate in response to high shear stress exposure even in subsequent low shear stress regions.²⁹ A robust shear-induced platelet activation prediction tool will be of great benefit to device optimization techniques, such as our Device Thrombogenicity Emulator (DTE) methodology³⁵, which combines highly resolved CFD simulations of blood flows in devices, experimental emulation of these conditions, and measurement of the resultant platelet activation in the HSD to map device-specific thrombogenicity footprints.

Our analysis indicates that a paradigm shift is required in the development of models that eliminate errors arising from discretization of the power law and allows universal prediction of platelet response to varying shear conditions. Our group is concurrently developing ordinary differential equation-based models that may better address the dynamic stress loading conditions encountered in blood-recirculating devices. Further studies are needed to expand the robustness and range of these models to include device-specific conditions.

Appendix

Derivation of the Cumulative Power Law Model (CPL) with Loading Rate

We wish to derive a power-law formulation that includes a shear loading term, τ̇, that accounts for the change in shear stress as opposed to assuming the shear stress is applied in a stepwise manner. The following approach utilizes the derivation method for a prior blood damage model.¹⁶ We start with the simple equation that accounts for shear stress and time (Eq. A1):

$$\mathit{\text{PAS}}({\tau }_{\mathit{\text{const}}},t)=C{\tau }^{\alpha }{t_{\text{exp}}}^{\beta }$$ (A1)

This is the simple extrapolation of the Giersiepen expression for platelet damage to predict the instantaneous value of the platelet activation state (PAS) at a given time point (“original power law – OPL”). For the dynamic case where shear stress is a function of time, τ = τ(t), we consider the integral form of the quantities τ and t. We first differentiate Eq. A1 to obtain the loading rate term, yielding:

$$\frac{d}{\mathit{\text{dt}}}\left(C\tau {(t)}^{\alpha }{t}^{\beta }\right)=C\beta \tau {(t)}^{\alpha }{t}^{\beta -1}+C\alpha \tau {(t)}^{\alpha -1}{t}^{\beta }\frac{d\tau (t)}{\mathit{\text{dt}}}$$ (A2)

The final term $\frac{d\tau (t)}{\mathit{\text{dt}}}$ is the shear loading rate term. We substitute this into Eq. A1, and then integrate to obtain the form presented in Eq. A2:

$${\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\frac{d}{\mathit{\text{dt}}}\left(C\tau {(t)}^{\alpha }{t}^{\beta }\right)\mathit{\text{dt}}={\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}(C\beta \tau {(t)}^{\alpha }{t}^{\beta -1}+C\alpha \tau {(t)}^{\alpha -1}{t}^{\beta }\frac{d\tau (t)}{\mathit{\text{dt}}})\mathit{\text{dt}}$$ (A3)

Therefore, taking the integral yields the following without loss of generality:

$$\mathit{\text{PAS}}(\tau (t),t){|}_{t_0}^{t_{\mathit{\text{total}}}}=C\tau {(t)}^{\alpha }{t}^{\beta }{|}_{t_0}^{t_{\mathit{\text{total}}}}=C{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\beta \tau {(t)}^{\alpha }{t}^{\beta -1}\mathit{\text{dt}}+C{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\alpha \tau {(t)}^{\alpha -1}{t}^{\beta }\frac{d\tau (t)}{\mathit{\text{dt}}}\mathit{\text{dt}}+C_0$$ (A4)

The constant of integration, C₀, is defined as the non-zero initial platelet activation state at t = 0, or PAS(t₀). The absolute value of dτ(t) is taken to avoid violating the principle of causality. The cumulative power law PAS model (CPL) with loading rate then becomes:

$${\mathit{\text{PAS}}}_{\mathit{\text{CPL}}}(\tau (t),t){|}_{t_0}^{t_{\mathit{\text{total}}}}=C_1{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\beta \tau {(t)}^{\alpha }{t}^{\beta -1}\mathit{\text{dt}}+C_2{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\alpha \tau {(t)}^{\alpha -1}{t}^{\beta }\frac{|d\tau (t)|}{\mathit{\text{dt}}}\mathit{\text{dt}}+\mathit{\text{PAS}}(t_0)$$ (A5)

The constants C₁ and C₂ represent C for the constant and dynamic shear stress parts of the model, respectively. For constant shear stress conditions, where τ̇= 0, Eq. A5 can be rewritten:

$${\mathit{\text{PAS}}}_{\mathit{\text{CPL}}}(\tau (t),t){|}_{t_0}^{t_{\mathit{\text{total}}}}=C_1{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}\beta \tau {(t)}^{\alpha }{t}^{\beta -1}\mathit{\text{dt}}+\mathit{\text{PAS}}(t_0)$$ (A6)

This is the original CPL model¹⁶ adapted to PAS. For utilization in a computational tool, such as MATLAB, Eq. A5 is discretized:

$${\mathit{\text{PAS}}}_{\mathit{\text{CPL}}}\mathit{(}\tau ,t\mathit{)}=C_{\mathit{1}}\beta {\displaystyle \sum _{i=\mathit{1}}^n}{t}_i^{\beta -\mathit{1}}{\tau }_i^{\alpha }\mathrm{\Delta }t+C_{\mathit{2}}\alpha {\displaystyle \sum _{i=\mathit{1}}^n}{\tau }_i^{\alpha -\mathit{1}}{t}_i^{\beta }\frac{|\mathrm{\Delta }{\tau }_i|}{\mathrm{\Delta ̸}t}\mathrm{\Delta ̸}t+\mathit{\text{PAS}}\mathit{(}{t}_{\mathit{0}}\mathit{)}$$

Rewriting Δτ_i, we get Eq. A7:

$${\mathit{\text{PAS}}}_{\mathit{\text{CPL}}}\mathit{(}\tau ,t\mathit{)}=C_{\mathit{1}}\beta {\displaystyle \sum _{i=\mathit{1}}^n}{t}_i^{\beta -\mathit{1}}{\tau }_i^{\alpha }\mathrm{\Delta }t+C_{\mathit{2}}\alpha {\displaystyle \sum _{i=\mathit{1}}^n}{\tau }_i^{\alpha -\mathit{1}}{t}_i^{\beta }|{\tau }_i-{\tau }_{i-\mathit{1}}|+\mathit{\text{PAS}}\mathit{(}{t}_{\mathit{0}}\mathit{)}$$ (A7)

Similarly, Eq. A6 is discretized:

$${\mathit{\text{PAS}}}_{\mathit{\text{CPL}}}\mathit{(}\tau ,t\mathit{)}=C_{\mathit{1}}\beta {\displaystyle \sum _{i=\mathit{1}}^n}{t}_i^{\beta -\mathit{1}}{\tau }_i^{\alpha }\mathrm{\Delta }t+\mathit{\text{PAS}}\mathit{(}{t}_{\mathit{0}}\mathit{)}$$ (A8)

Derivation of the Modified Cumulative Power Law (MPL) Model with Loading Rate

As in the previous section, we want to derive a power-law formulation that includes a shear loading term, τ̇, that accounts for the change in shear stress as opposed to assuming the shear stress is applied in a stepwise manner. However, we want to truly account for loading history, where two groups of platelets exposed to different mechanical loadings are expected to show different responses in a subsequent loading, even if the latter is the same for both groups. That means that the PAS at each loading stage is dependent on the PAS of a previous loading scheme. Equations A5 and A6 do not satisfy these requirements, since only the initial activation, PAS(t₀), is considered. Thus, we need to follow the Grigioni approach¹⁷, with adaptation for PAS.²⁵ This approach is different from that utilized for the earlier CPL formulation¹⁶ in that the latter does not consider the loading history of the platelet (i.e. a mechanical dose function). We start with the simple equation that accounts for shear stress and time (Eq. A9):

$$\mathit{\text{PAS}}({\tau }_{\mathit{\text{const}}},t)=C{\tau }^{\alpha }{t}^{\beta }$$ (A9)

Grouping the independent variables τ and t on one side, we get:

$$\frac{\mathit{\text{PAS}}(\tau ,t)}{C}={\tau }^{\alpha }{t}^{\beta }$$ (A10)

Here, we define a mechanical dose function, D:

$$D=\sqrt[\beta ]{\frac{\mathit{\text{PAS}}(\tau ,t)}{C}}={\tau }^{\alpha /\beta }t$$ (A11)

Thus, the function for PAS can be rewritten as:

$$\mathit{\text{PAS}}(\tau ,t)=C·D^{\beta }$$ (A12)

Applying the chain rule, we get the form:

$$\frac{\mathit{\text{dD}}}{\mathit{\text{dt}}}=\frac{\partial D}{\partial t}+\frac{\partial D}{\partial \tau }·\frac{d\tau }{\mathit{\text{dt}}}={\tau }^{\alpha /\beta }+\frac{\alpha }{\beta }t·{\tau }^{\alpha /{\beta }^{-1}}\mathrm{\tau ̇}$$ (A13)

Grigioni et al. neglected τ̇, claiming that it violates the principle of causality and causes a reduction in damage if shear stress is decreasing.¹⁷ We diverge from this approach by accounting for the shear loading rate and taking its absolute value so that its effect is always additive. In partial differential form, the above equation becomes:

$$\mathit{\text{dD}}={\tau }^{\alpha /\beta }\mathit{\text{dt}}+\frac{\alpha }{\beta }t·{\tau }^{\alpha /{\beta }^{-1}}d\tau$$ (A14)

Integrating with respect to time and shear stress, the above equation becomes:

$$D(t)-D(t_0)={\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\varphi )}^{\alpha /\beta }d\varphi +\alpha /\beta {\displaystyle \underset{\tau (t_0)}{\overset{\tau (\varphi )}{\int }}}\varphi ·\tau {(\varphi )}^{\alpha /{\beta }^{-1}}d\tau$$ (A15)

We must rewrite D(t₀) in terms of the initial platelet activation state, PAS(t₀):

$$\mathit{\text{PAS}}(t_0)=C·D{(t_0)}^{\beta }$$ (A16)

$$D(t_0)={\left(\frac{\mathit{\text{PAS}}(t_0)}{C}\right)}^{1/\beta }$$

Taking the derivative of the PAS function in terms of the dose D, we obtain:

$$d(\mathit{\text{PAS}})=d(C·D^{\beta })=\mathit{\text{Cd}}(D^{\beta })=C\beta D^{\beta -1}\mathit{\text{dD}}$$ (A17)

Putting this equation in integral form yields:

$$d(\mathit{\text{PAS}})=C\beta {({\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\xi )}^{\alpha /\beta }d\xi +\alpha /\beta {\displaystyle \underset{\mathrm{\Gamma }(t_0)}{\overset{\mathrm{\Gamma }(\varphi )}{\int }}}\xi ·\tau {(\xi )}^{\alpha /{\beta }^{-1}}d\tau +D(t_0))}^{\beta -1}\mathit{\text{dD}}$$ (A18)

The inner integrals represent the total mechanical stress loading dose D divided into constant and dynamic shear stress terms and applied over a time ξ, where dξ is the interval over which an elemental dose of shear stress is applied and Γ is the shear stress at time ξ. The outer integral is the summation of these doses over the duration of the experiment, with ϕ and dϕ as the observation time points and the interval between them, respectively. Substituting Eq. A14 for dD yields:

$$d(\mathit{\text{PAS}})=C\beta {({\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\xi )}^{\alpha /\beta }d\xi +\alpha /\beta {\displaystyle \underset{\tau (t_0)}{\overset{\tau (\varphi )}{\int }}}\xi ·\tau {(\xi )}^{\alpha /{\beta }^{-1}}d\tau +D(t_0))}^{\beta -1}({\tau }^{\alpha /\beta }d\varphi +\frac{\alpha }{\beta }t·{\tau }^{\alpha /{\beta }^{-1}}d\tau )$$ (A19)

Expressing the platelet activation state (PAS) as the integral sum of the infinitesimal contributions represented by the above equation yields:

$$\mathit{\text{PAS}}=C\beta [{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}{({\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\xi )}^{\alpha /\beta }d\xi +\alpha /\beta {\displaystyle \underset{\tau (t_0)}{\overset{\tau (\varphi )}{\int }}}\xi ·\tau {(\xi )}^{\alpha /{\beta }^{-1}}d\tau +D(t_0))}^{\beta -1}{\tau }^{\alpha /\beta }d\varphi +{\displaystyle \underset{\tau (t_0)}{\overset{\tau (t_{\mathit{\text{total}}})}{\int }}}\alpha /\beta {({\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\xi )}^{\alpha /\beta }d\xi +\alpha /\beta {\displaystyle \underset{\tau (t_0)}{\overset{\tau (\varphi )}{\int }}}\xi ·\tau {(\xi )}^{\alpha /{\beta }^{-1}}d\tau +D(t_0))}^{\beta -1}t·{\tau }^{\alpha /{\beta }^{-1}}d\tau ]$$ (A20)

PAS can be numerically computed by adding the mechanical doses acting on a platelet trajectory. The discrete elemental dose Δ(PAS)_i is sustained by a platelet in the i-th interval, from the instant t_i−1 to t_i, and is expressed as:

$$\mathrm{\Delta }{(\mathit{\text{PAS}})}_i=C\beta [{({\displaystyle \sum _{j=1}^i}\tau {(t_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+\alpha /\beta {\displaystyle \sum _{j=1}^i}{t}_j·\tau {(t_j)}^{\alpha /{\beta }^{-1}}|\mathrm{\Delta }{\tau }_j|+D(t_0))}^{\beta -1}\tau {(t_i)}^{\alpha /\beta }\mathrm{\Delta }{t}_i+\alpha /\beta {({\displaystyle \sum _{j=1}^i}\tau {(t_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+\alpha /\beta {\displaystyle \sum _{j=1}^i}{t}_j·\tau {(t_j)}^{\alpha /{\beta }^{-1}}|\mathrm{\Delta }{\tau }_j|+D(t_0))}^{\beta -1}{t}_i·\tau {(t_i)}^{\alpha /{\beta }^{-1}}|\mathrm{\Delta }{\tau }_i|]$$ (A21)

The time period Δt_i refers to the duration between experimental observations. Unlike previous derivations of this formula, we no longer assume the shear stress is constant in this interval, as we now have a shear loading term. The starting observation time, t₀, is conventionally assumed to be equal to 0. The mechanical dose, due to dynamic behavior, is broken into multiple sub-intervals (referred to as the j-th interval in the above equation). Each sub-interval can be a constant shear stress dose if applied as such, or an approximation, where the dose is approximated as a constant shear stress part and a linearly ramped part, which includes the change in shear stress Δτ_j. Note that for the latter, the absolute value is taken in order not to violate the principle of causality.¹⁷ Thus, for each i-th interval, multiple j-th intervals may be present. From the integral form for the PAS function (Eq. A20), we derive the discrete form:

$$\mathit{\text{PAS}}=C\beta {\displaystyle \sum _{i=1}^N}[{({\displaystyle \sum _{j=1}^i}\tau {(t_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+\alpha /\beta {\displaystyle \sum _{j=1}^i}{t}_j·\tau {(t_j)}^{\alpha /{\beta }^{-1}}|\mathrm{\Delta }{t}_j|+D(t_0))}^{\beta -1}\tau {(t_i)}^{\alpha /\beta }\mathrm{\Delta }{t}_i+\alpha /\beta {({\displaystyle \sum _{j=1}^i}\tau {(t_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+\alpha /\beta {\displaystyle \sum _{j=1}^i}{t}_j·\tau {(t_j)}^{\alpha /{\beta }^{-1}}|\mathrm{\Delta }{\tau }_j|+D(t_0))}^{\beta -1}{t}_i·\tau {(t_i)}^{\alpha /{\beta }^{-1}}|\mathrm{\Delta }{t}_i|]$$ (A22)

This represents the sum of PAS values over N intervals. In our experiments, PAS measurements are only taken during constant shear stress phases. Therefore, we can neglect the second part of the above equation. In addition, the term for D(t₀) can also be substituted, yielding the discrete form of the modified cumulative power law model (MPL) with loading rate:

$${\mathit{\text{PAS}}}_{\mathit{\text{MPL}}}(\tau ,t)=C\beta {\displaystyle \sum _{i=1}^{\mathrm{N}}}{({\displaystyle \sum _{j=1}^i}\tau {(t_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+\alpha /\beta {\displaystyle \sum _{j=1}^i}{t}_j·\tau {(t_j)}^{\alpha /{\beta }^{-1}}|\mathrm{\Delta }{\tau }_j|+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C}\right)}^{1/\beta })}^{\beta -1}\tau {(t_i)}^{\alpha /\beta }\mathrm{\Delta }{t}_i$$ (A23)

Making a similar simplification for Eq. A20 yields:

$${\mathit{\text{PAS}}}_{\mathit{\text{MPL}}}(\tau ,t)=C\beta \left[{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}{({\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\xi )}^{\alpha /\beta }d\xi +\alpha /\beta {\displaystyle \underset{\tau (t_0)}{\overset{\tau (\varphi )}{\int }}}\xi ·\tau {(\xi )}^{\alpha /{\beta }^{-1}}d\tau +{\left(\frac{\mathit{\text{PAS}}(t_0)}{C}\right)}^{1/\beta })}^{\beta -1}{\tau }^{\alpha /\beta }d\varphi \right]$$ (A24)

For constant shear stress conditions, where τ̇ = 0, Eqs. A23 and A24 can be rewritten as Eqs. A25 and A26, respectively. To allow comparison with other models in this study, we set C = C₁. These 2 equations are the original MPL model for PAS:

$${\mathit{\text{PAS}}}_{\mathit{\text{MPL}}}(\tau ,t)=C_1\beta {\displaystyle \sum _{i=1}^{\mathrm{N}}}{({\displaystyle \sum _{j=1}^i}\tau {(t_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta })}^{\beta -1}\tau {(t_i)}^{\alpha /\beta }\mathrm{\Delta }{t}_i$$ (A25)

$${\mathit{\text{PAS}}}_{\mathit{\text{MPL}}}(\tau ,t)=C_1\beta \left[{\displaystyle \underset{t_0}{\overset{t_{\mathit{\text{total}}}}{\int }}}{({\displaystyle \underset{t_0}{\overset{\varphi }{\int }}}\tau {(\xi )}^{\alpha /\beta }d\xi +{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta })}^{\beta -1}{\tau }^{\alpha /\beta }d\varphi \right]$$ (A26)

Equation A24 provides a model that accounts for previous shear stress history and platelet activation, as well as the effect of the shear loading rate, the latter which was not addressed in prior models.^8,25,27

Errors in Power Law Models Due to Discretization

The CPL model (Eq. A8)¹⁶ is prone to accumulation of error resulting from the utilization of time steps in discrete form due to the use of powers on time. Consider the initial condition of PAS(t₀)=PAS₀ at t = t₀, after which platelets are subjected to a constant shear stress, including at two subsequent times separated by Δt. These time points are given at t₁ = t₀ + Δt and t₂ = t₀ + 2Δt. Substituting into the OPL (Eq. A1) and rewriting yields:

$${\mathit{\text{PAS}}}_1=\mathit{\text{PAS}}(t_1)={\mathit{\text{PAS}}}_0+C{\tau }^{\alpha }{(t_1-t_0)}^{\beta }={\mathit{\text{PAS}}}_0+C{\tau }^{\alpha }\mathrm{\Delta }{t}^{\beta }$$ (A27)

$${\mathit{\text{PAS}}}_2=\mathit{\text{PAS}}(t_2)={\mathit{\text{PAS}}}_0+C{\tau }^{\alpha }{(t_2-t_0)}^{\beta }={\mathit{\text{PAS}}}_0+C{\tau }^{\alpha }{(2\mathrm{\Delta }t)}^{\beta }$$ (A28)

Alternatively, PAS₂ can be obtained by substituting the time of exposure from t₁ to t₂ into Eq. A1 and adding PAS₁:

$${\mathit{\text{PAS}}}_2={\mathit{\text{PAS}}}_1+C{\tau }^{\alpha }{(t_2-t_1)}^{\beta }={\mathit{\text{PAS}}}_0+2C{\tau }^{\alpha }\mathrm{\Delta }{t}^{\beta }$$ (A29)

Eqs. A28 and A29 are not equivalent if β ≠ 1, and therefore this form of the power law model¹⁶ is inconsistent.

While the mechanical dose term was redefined in the MPL¹⁷ to remove the power on time (Eq. A11), errors due to the discretization of the time intervals Δt_i and Δt_j are still present. Consider the case where shear stress, τ, is constant over the time period t₀ to t₂. Thus, Δt = t₂ − t₁ = t₁ − t₀ and 2Δt = t₂ − t₀, as described earlier. We set |Δτ_j| = 0 in Eq. 7, since the loading is instantaneous. For simplicity, we consider a single i-th interval, from t₀ to t₂, and set the i-th and j-th intervals equivalent in size. Substituting these values into Eq. 7, we obtain:

$${\mathit{\text{PAS}}}_{0-2}={\displaystyle \sum _{i=1}^1}{C}_1\beta {[{\displaystyle \sum _{j=1}^1}{({\tau }_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{\beta -1}{({\tau }_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_i=2C_1\beta {(\tau )}^{\alpha /\beta }\mathrm{\Delta }t{[2{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{\beta -1}$$ (A30)

Alternatively, we consider 2 i-th and j-th intervals with the same sizes, from t₀ to t₁ and from t₁ to t₂. Substituting into Eq. A21, and setting |Δτ_i| = |Δτ_j| = 0, we obtain:

$$\mathrm{\Delta }{(\mathit{\text{PAS}})}_{0-1}=C_1\beta {[{\displaystyle \sum _{j=1}^1}{({\tau }_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{\beta -1}{({\tau }_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_i=C_1\beta {[{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{\beta -1}{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t$$ (A31)

$$\mathrm{\Delta }{(\mathit{\text{PAS}})}_{1-2}=C_1\beta {[{\displaystyle \sum _{j=1}^2}{({\tau }_j)}^{\alpha /\beta }\mathrm{\Delta }{t}_j+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{a-1}{({\tau }_i)}^{\alpha /\beta }\mathrm{\Delta }{t}_i=C_1\beta {[{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t+{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{a-1}{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t$$ (A32)

Adding Eqs. A31 and A32, we obtain:

$${\mathit{\text{PAS}}}_{0-2}=\mathrm{\Delta }{(\mathit{\text{PAS}})}_{0-1}+\mathrm{\Delta }{(\mathit{\text{PAS}})}_{1-2}=C_1\beta {(\tau )}^{\alpha /\beta }\mathrm{\Delta }t({[{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{\beta -1}+{[2{(\tau )}^{\alpha /\beta }\mathrm{\Delta }t+{\left(\frac{\mathit{\text{PAS}}(t_0)}{C_1}\right)}^{1/\beta }]}^{\beta -1})$$ (A33)

We see Eqs. A30 and A33 are not equivalent since the first bracket of Eq. A33 is missing an additional (τ)^α/β Δt, and therefore, accuracy of the MPL model is still heavily dependent on discretization of time intervals.