INTRODUCTION
Actin-myosin crossbridge (XB) formation is the fundamental source of force generation and contraction in cardiac muscle. These interactions are initiated by Ca2+ activation of the thin filament, and are modulated by sarcomere length (SL) [1, 2]. Furthermore, XBs modulate thin filament activation through cooperative mechanisms of activation [3-7]. Therefore, these two intrinsic properties of the sarcomere allow cardiac function to be modulated through structural changes imposed by either changes in SL or changes in cooperative activation. However, whether there is interplay between these mechanisms of cooperative and SL-mediated activation is unclear.
SL modulates inotropy by sensitizing the myofilaments to Ca2+ and by increasing the tension developed in cardiac muscle during activation. These phenomenon are thought to occur by two widely-accepted mechanisms: 1) a SL-dependent increase in thick and thin myofilament overlap, which coincides with a decrease in myofilament lattice spacing in the intact sarcomere; and 2) a SL-dependent change in the structure of the myofilaments, which promotes Ca2+ binding to the troponin complex and acto-myosin interactions. The latter is supported by the findings that the structure of thin-filament regulatory proteins is important determinants of the length-dependence of contractile activation (LDA) [8-11]. Thick-filament myosin binding to actin also plays a modulatory role in determining the SL dependence of Ca2+-activated tension development [12-14]. The structure of thick-filament proteins, such as myosin regulatory light chain, have been recently linked to LDA [15] and the strain-dependence of myosin XB turnover [16]. Furthermore, titin, which interacts with both thick and thin myofilaments [17], has been linked to LDA (reviewed in [18]). However, whether the SL-dependent structural changes in the thin and thick myofilaments confer a difference in isoform-dependent kinetics of XB cycling remains poorly understood.
We sought to test our hypothesis that XB cycling kinetics are influenced by SL in a myosin heavy chain (MHC)-dependent manner. The rationale for this study is that the different isoforms of MHC – despite sharing a high degree of homology (e.g. [19, 20]) – possess intrinsically different acto-myosin cycling kinetics. For example, cardiac α-MHC possesses faster XB cycling kinetics than does β-MHC, and imparts much faster contractile dynamics in mammalian hearts [21-25]. This implies that the kinetics of the XB cycle are highly-dependent on the structure of MHC. Therefore, it is conceivable that muscle length may also alter the kinetics of the XB cycle via SL-induced changes in myofilament structure. Consequently, we hypothesized that effects of SL may have a different outcome depending on structure of the MHC isoform. This follows that β-MHC XBs possess a longer XB dwell time than α-MHC XBs, and thus the kinetics of β-MHC may have a greater sensitivity of structural changes imposed by changes in SL.
To test our hypothesis, we measured a broad range of contractile parameters in fibers from the ventricles of normal and PTU-treated mice (expressing α-MHC or β-MHC, respectively) at both SL 2.0 and 2.2 μm. We measured Ca2+-activated maximal tension, ATPase activity, tension cost, and used model-predicted estimates of force responses to changes in muscle length to characterize contractile dynamic behavior from cardiac muscle fiber preparations. In addition, we studied nonlinear length-dependent contractile behavior at SL 2.2 μm in α-MHC and β-MHC fibers. Differences in nonlinear behavior indicated whether the underlying allosteric mechanisms, whereby length-mediated XB strain affects XB recruitment dynamics, were different in α-MHC and β-MHC fibers.
Our results provide a novel characterization of how SL mediates contractile dynamics, and further how MHC isoform influences the SL effect on contractile dynamics, which is poorly understood. Our findings suggest that the heterogeneity in cardiac MHC isoforms confers unique differences in the SL-dependence of contractile dynamics in α-MHC and β-MHC fibers. We conclude that these differences in SL-dependent contractile dynamics may be due to the difference in XB dwell time in α-MHC and β-MHC fibers, such that β-MHC XBs are more sensitive to length-induced structural changes in the myofilament that mediate XB cycling dynamics.
MATERIAL AND METHODS
PTU treatment
All mice were housed and treated in accordance to the procedures and guidelines set by the Washington State University Institutional Animal Care and Use Committee. Young adult (3-4 months in age) friend virus B-type (FVB) mice were either untreated controls or were treated with propylthiouracil (PTU), administered in drinking water (0.2 g L-1) and in feed for five weeks. PTU treatment has been shown to induce a shift ventricular MHC isoform from predominantly α-MHC to predominantly β-MHC without altering other myofilament proteins [26-28].
Preparation of cardiac muscle samples for protein analysis
Ventricular samples for protein analysis were prepared as described previously [29]. After excision, hearts were submerged in liquid nitrogen and pulverized using a mortar and pestle. The tissue was then resuspended in 10 μL of a protein extraction buffer per 1 mg of pulverized tissue. The protein extraction buffer contained the following: 2.5% SDS, 10% glycerol, 50 mM tris base (pH 6.8 at 4 C), 1 mM DTT, 1mM PMSF, 4 mM benzamidine HCl, and contained a fresh cocktail of phosphatase inhibitors (PhosSTOP, Roche Applied Science) and protease inhibitors (E-64, leupeptin, and bestatin). Resuspended tissue was further homogenized on ice using a “Tissue Tearor” (Model 985370-395 Biospec Products, Inc.), sonicated in a water bath at 4°C, and then centrifuged at 10K rpm.
Analysis of MHC content and phosphorylation status in cardiac muscle following PTU treatment
Loading amounts were standardized between each sample by estimating total protein concentration and further optimized based on relative actin concentrations. Equal amounts of protein were loaded and separated on 6.5% SDS gels for analysis of MHC composition or 12.5% gels for analysis of myofilament protein phosphorylation. 12.5% gels were stained with Pro-Q Diamond staining solution (Invitrogen P33300, stain; P33310, destain) to determine the levels of phosphorylated protein in ventricular samples. Bands corresponding to phosphorylated proteins were visualized by UV transillumination and a BioRad Chemi Doc XRS camera. Following Pro-Q visualization, 12.5% gels were stained with coomassie brilliant blue staining solution to visualize the isoform expression profiles of myofilament regulatory proteins other than MHC. Relative MHC content was quantified by densitometric analysis using ImageJ software (NIH, acquired at http://rsbweb.nih.gov/ij/) for coomassie stained gel images.
Preparation of detergent-skinned cardiac muscle bundles
Papillary bundles from control and PTU-treated mice were prepared using procedures described previously [22]. Mice were deeply anaesthetized using isoflurane and hearts were quickly excised and placed into an ice-cold high relaxing (HR) solution. The HR solution contained the following (in mM): 20 2,3-butanedione monoxime (BDM), 50 N,N-bis (2-hydroxyethyl)-2-amino-ethane-sulfonic acid (BES), 30.83 potassium propionate (K- propionate), 10 sodium azide, 20 ethylene glycol tetra-acetic acid (EGTA), 6.29 magnesium chloride, 6.09 Na2ATP, 4 benzamidine-HCl, and 1 mM of DTT. pH was carefully adjusted to 7.0 using KOH and the following protease inhibitors are added (in μM): 5 of bestatin, 2 of E-64, 10 of leupeptin, 1 of pepstatin and 200 of PMSF. Papillary bundles were extracted from the left ventricle in the HR solution, from which thin muscle fiber bundles (~2-2.5 mm in length and ~150-200 μm in width) were dissected. Thin muscle fiber bundles (fibers) were chemically demembranated overnight at 4 C in HR solution containing 1% Triton X-100.
pCa solutions and compositions
Each fiber was bathed in different solutions with pCa levels ranging from 4.3 to 9.0. Maximal Ca2+ activating solution (pCa 4.3) contained the following (in mM): 50 BES, 5 NaN3,10 phosphoenol pyruvate (PEP), 10 EGTA, 10.11 CaCl2, 6.61 MgCl2, 5.95Na2ATP and 31 K-propionate, whereas the relaxing solution (pCa 9.0) has the following: 50 BES, 5 NaN3,10 PEP, 10 EGTA, 0.024 CaCl2, 6.87 MgCl2, 5.83 Na2ATP and 51.14 K-propionate. In addition, the maximal activating and relaxing solutions contained 0.5 mg/ml pyruvate kinase (PK), 0.05 mg/ml lactate dehydrogenase (LDH), with the following cocktail of protease inhibitors (in μM): 10 leupeptin, 1000 pepstatin, 100 PMSF, 20 μM A2P5, 10 μM oligomycin. The reagent concentrations for all intermediate pCa solutions were calculated based on the program by Fabiato (1988) [30] and the pCa solutions were prepared accordingly.
Simultaneous measurement of isometric steady-state tension and ATPase activity
Simultaneous measurements of isometric steady-state tensions and the ATPase activity in various pCa solutions were conducted using methods described previously [10, 22, 31]. Briefly, muscle fibers were clipped using aluminum clips and the fiber was then attached between a servo motor (322C, Aurora Scientific Inc., Ontario, Canada) and to a force transducer (AE801, Sensor One Technologies, Sausalito, CA). The sarcomere length (SL) of the fiber was adjusted to 2.0 or 2.2 μm in HR solution using a He-Ne laser diffraction system. The fiber was then subjected to two cycles of activation and relaxation and the SL of the fiber was readjusted to the respective SL, if necessary. The fiber was then activated with a series of pCa solutions starting from pCa 4.3 to pCa 9.0. Simultaneous tension and ATPase measurements from each fiber in various pCa solutions were used to determine tension cost. Tension values at various pCa were normalized to steady-state maximal tension (measured at pCa 4.3) and were used to construct pCa-tension relationships. Normalized pCa-tension relationships were fitted using the Hill equation:
| (Eq. 1) |
In the equation above, TMax is the maximal isometric tension at pCa 4.3 and TpCa is the tension elicited by a fiber at a given pCa.
The ATPase activity during steady-state isometric tension production was measured using an assay described previously [10, 31]. In brief, a near-UV light (340 nm) was projected through the muscle chamber which was split (50:50) for intensity detection at 340 nm and 400 nm wavelengths. Light intensity of the beam at 340 nm was sensitive to NADH and thus a change in the UV absorbance at 340 nm could be directly correlated to the oxidation of NADH (i.e., ATP usage) through enzymatically-coupled reactions. NADH was added drop-wise to each activating solution to produce a signal substantially low at 340 nm to detect changes produced by the following reactions. Pyruvate kinase converts PEP and the ADP generated from the steady-state ATP hydrolysis of actomyosin to ATP and pyruvate, which is subsequently converted to lactate by LDH in a reaction that is coupled to the oxidation of NADH to NAD+. Light intensity of the beam at 400 nm was insensitive to NADH and therefore served as the reference signal. An analog divider and log amplifier produced a signal proportional to the amount of ATP consumed (i.e., amount of NADH oxidized) in the muscle chamber solution. Changes in the UV absorbance signal for NADH were calibrated by multiple injections of 0.25 nmol of ADP into the activation solution.
Mechano-dynamic studies
We applied sinusoidal muscle length (ML) changes of constant amplitude (±0.5% of ML), with increasing frequency over time (chirp) on maximally-activated muscle fibers (i.e. at pCa 4.3) to measure the dynamic force-length relationship as described previously [10, 21]. Two chirps, one with frequencies ranging from 0.1 to 4 Hz for a time period of 40 s, and the other with frequencies ranging from 1 to 40 Hz for a time period of 5 s, were administered to emphasize low and high frequency components of the force response. Representative chirp responses and corresponding length-perturbation data are shown in Figs. 1A and 1B, respectively. The overall force response (including both low- and high-frequency components) elicited by the fiber was fitted to a three-component, linear recruitment-distortion (LRD) model which was successfully used previously to elicit the dynamic features of constantly activated muscle fibers [22]. In brief, the LRD model predicts a change in muscle force, ΔF(t), corresponding to a change in ML, ΔL(t), in a constantly activated muscle fiber, as follows:
| (Eq. 2) |
Figure 1.
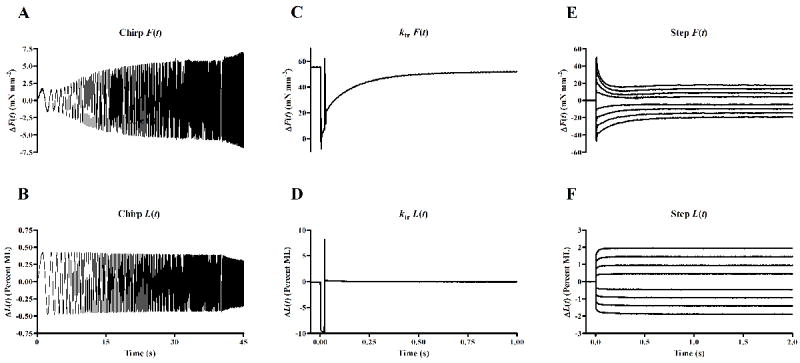
Representative data from mechanical perturbation studies conducted at maximal activation. The chirp force response (A) is shown corresponding to the constant-amplitude (0.5% initial muscle length, ML), sinusoidal length perturbation of increasing frequency over time (B). Two frequency sweeps were administered; a low frequency, 0.1-4 Hz sweep over a span of 40 seconds, and a high frequency, 2-40 Hz sweep over a span of 5 seconds. Tension redevelopment (C) following a rapid slack, restretch protocol (D) was used to determine ktr. Force responses (E) to step-like length changes (F) were fitted using the nonlinear recruitment-distortion model to characterize nonlinear contractile behavior.
In the equation above, η(t) is a variable that describes the dynamic changes in XB recruitment with changes in length, whereas x1(t) and x2(t) represent XB distortion variables, and each possess the units of length. E0, E∞, and D are scaling coefficients and carry the units of stiffness. E0 is a measure of newly-recruited XBs, whereas E∞ and D are stiffness coefficients proportional to the number of XBs in strongly- or weakly-bound states, respectively. The dynamic relationships of η(t), x1(t), and x2(t) with ΔL(t) are governed by the following differential equations:
| (Eq. 3) |
| (Eq. 4) |
| (Eq. 5) |
where b represents the rate constant governing the XB recruitment, c and d represent rate constants that govern the distortion dynamics of strongly- and weakly-bound XBs, respectively.
The LRD model was fitted to by minimizing the least squared errors between the simulated and experimental force responses using nonlinear regression techniques in order to estimate the six model parameters, E0, b, E∞, c, D and d. The LRD model allowed us to uniquely separate recruitment dynamics (E0, b) from distortion dynamics (E∞, c, D and d). The distortion component, Dx2(t) in Eq.’s 2, 5 contributed very little to the force response within the frequency range of interest (e.g., ~0.1-2 Hz), and therefore, we only reported b, E0, c, E∞ parameters in this study. A low standard error (<1% of the parameter value) in each of these model parameters indicated that these estimates were robust and reliable for comparisons in this study.
Rate constant of tension redevelopment (ktr)
The rate constant associated with the tension redevelopment following rapid slack/restretch, ktr was estimated based on the protocol described previously [22, 32]. In this protocol, the maximally activated fiber (i.e. at pCa 4.3) was rapidly slackened by 10% of its preset ML in a step-like fashion. After 25 ms, the motor arm was commanded to swing past its original set point backward thereby stretching it by 10% from its set point. The muscle fiber was then rapidly brought back to its set point at which point the muscle fiber was allowed to redevelop force. This method was done in order to break any strongly-bound XBs to minimize residual force from which tension starts to redevelop force. Figs. 1C and 1D respectively illustrate a representative force response to the rapid slack-restretch protocol. ktr was estimated by fitting a mono-exponential function given by, , where Fo is the steady state isometric force and Fres is the residual force from which the fiber starts to redevelop tension. All the fiber records measured during the tension redevelopment were well fitted by a mono-exponential relation with R2 ≥ 0.9.
Determination of nonlinear length-dependent contractile behavior in muscle
Once the muscle fiber attained steady-state maximal activation (i.e. pCa 4.3), step-like length changes were applied to the fibers as described previously [33]. In brief, ML was rapidly stretched (by 0.5%, 1.0%, 1.5%, and 2.0% of ML) and held at the increased length for 5 seconds. The motor arm was then commanded to rapidly return (representing release by 0.5%, 1.0%, 1.5%, and 2.0% of ML) to the initial ML where it was held for another 5 seconds. Representative force responses and corresponding step-length perturbation data are shown in Figs. 1E and 1F, respectively. A previously-developed nonlinear formulation of the recruitment distortion (NRD) model [33] was fitted to the entire family of force responses (Fig 1E) to characterize the XB cycling dynamics in the muscle fiber. The force responses, F(t), to step-like length changes were represented as a product of the net stiffness of the fiber, η(t), times the distortion of the fiber, x(t):
| (Eq. 6) |
η(t) represents the stiffness of the fiber, and is proportional to the number of XBs bound at time t. The change in ML, ΔL(t), due to the step perturbation, results in a change in recruitment of the number of bound XBs, and η(t) changes with time as shown in Eq. 7. b is a rate constant that determines the speed at which the recruitment variable η(t) changes and γ is a parameter that represents how XB distortion, x(t), influences XB recruitment. x(t) represents the mean distortion of bound XBs, and changes with respect to the velocity of ML change, , as shown in Eq. 8. c is a rate constant that determines the speed at which XB distortion dissipates, as XBs that were distorted due to detach and repopulate into a non-distorted state. Therefore, c is considered a measure of the rate of XB detachment and b is considered a measure of the rate of XB recruitment. γ is described as a parameter that characterizes how XB strain influences the dynamics of XB recruitment. Therefore, γ may be considered a measure of thin filament-based cooperative/allosteric mechanisms that modulate XB-mediated effects on other XBs.
| (Eq. 7) |
| (Eq. 8) |
Eq. 7 contains a variation of the formulation described in Ford et al. (2010). γ was estimated in the model fits with a high degree of confidence, similar to that reported in Ford et al. (2010).
Data analysis
Measurements of contractile function and dynamics from untreated or PTU-treated mouse muscle fibers were compared using two-way ANOVA, with one factor being MHC isoform (α-MHC vs. β-MHC) and the other being SL (2.0 μm vs. 2.2 μm). The interaction effects were evaluated to test the hypothesis that MHC isoform altered the effects of sarcomere length on cardiac function. Subsequent post hoc multiple pairwise comparisons were planned and made using Fisher s LSD method. Statistical significance was assumed for p < 0.05.
RESULTS
We sought to understand whether length-dependent effects on cardiac contractile function and dynamics were different in fibers containing α-MHC and β-MHC. To better understand this relationship, we compared the sarcomere length-dependence of maximal tension and ATPase, tension and ATPase activity at varying levels of Ca2+ activation, and contractile dynamic behaviors (i.e. those elicited in chirp responses) in cardiac muscle fibers isolated from normal (α-MHC) or PTU-treated (β-MHC) mice. We also investigated whether cooperative/allosteric mechanisms that underlie nonlinear behavior in step responses differ in α- or β-MHC fibers. Results were interpreted using two-way ANOVA, with significant interaction implying that the SL-dependence of a given contractile function parameter is dependent on MHC isoform.
MHC isoform expression in non-treated and PTU-treated mouse ventricular myocardium
Ventricular samples were prepared from non-treated and PTU-treated mice, and protein compositions were separated by SDS PAGE (Fig. 2). MHC isoform expression was shifted from predominantly α-MHC to predominantly β-MHC following five weeks of PTU treatment (Fig. 2A). This shift was quantified using densitometric analysis; non-treated mice expressed α-MHC as ~95% of total MHC, whereas PTU-treated mice expressed β-MHC as ~90% of total MHC. Due to this near-complete shift in MHC expression, we refer to non-treated fibers as α-MHC fibers, and PTU-treated fibers as β-MHC fibers throughout the rest of the manuscript. In agreement with previous studies [34, 35], PTU-treatment did not affect the phosphorylation status of sarcomeric proteins (e.g. cardiac myosin binding protein C (MyBPC), desmin, troponin T (TnT) cardiac α-tropomyosin (α-Tm), troponin I (TnI) myosin light chain-1 (MLC1), or myosin light chain-2 (MLC2); Fig. 2B). Also in agreement with previous studies [23], we found that PTU treatment did not affect the expression profile of other sarcomeric proteins (e.g. actin, TnT, α-Tm, TnI, MLC1, MLC2 or troponin C (TnC); Fig 2C).
Figure 2.
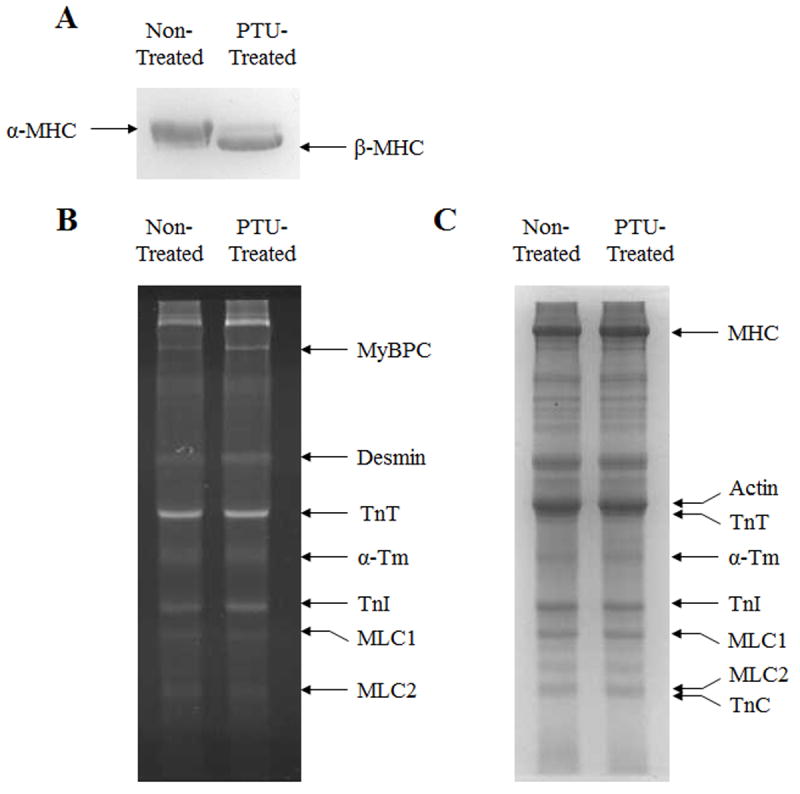
Effect of five weeks of PTU treatment on isoform expression of MHC and other myofilament proteins, and on myofilament protein phosphorylation status in mouse ventricular preparations. Separation of α-MHC and β-MHC isoforms was done on 6.5% SDS polyacrylamide gels, as shown in panel A. Separation of other myofilament proteins was done on 12.5% gels. After separation, protein phosphorylation of myofilament proteins was visualized by UV-transilluminescence following Pro-Q diamond staining of 12.5% gels, as shown in panel B. After Pro-Q imaging, gels were stained with coomassie blue to visualize whether the isoform expression profiles of proteins other than MHC were altered by PTU treatment, as shown in panel C.
Effects of SL on tension production and ATPase activity at varying levels of Ca2+ activation in α- vs. β-MHC containing fibers
The SL-dependent effects on maximal tension development or ATPase activity were not different in α-MHC or β-MHC fibers. For example, the increase in SL from 2.0 to 2.2 μm gave rise to a 14% or 13% increase in maximal tension in α-MHC or β-MHC fibers, respectively (Fig. 3A). Two-way ANOVA revealed that the interaction effect of SL and MHC did not have a significant impact on maximal tension. Therefore, the SL-dependence of maximal tension development was the same for α-MHC or β-MHC fibers. The main effects of an increase in SL (p = 0.0005) or β-MHC expression (p < 0.0001) significantly increased tension production. Two-way ANOVA also revealed that the interaction effect of SL and MHC on maximal ATPase activity was not significant. Main effects of β-MHC (p < 0.0001), but not SL, significantly reduced the rate of ATPase activity. Post hoc analysis further revealed that ATPase activity was significantly lower at SL 2.2 μm vs. 2.0 μm in β-MHC fibers (p < 0.05), but not in α-MHC fibers.
Figure 3.
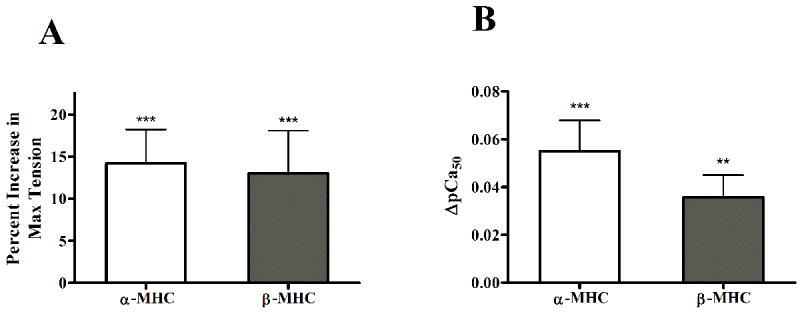
Effect of increase in SL on contractile activation, as estimated by the percent increase in tension development (A), or the increase myofilament Ca2+ sensitivity (ΔpCa50, B). Estimates of myofilament Ca2+ sensitivity (pCa50) were determined by fitting Hill’s model to pCa-tension relationships. Values are mean + SEM. Number of determinants is 10 for each group. ** - p < 0.01; *** - p < 0.001, when comparing tension or pCa50 values at SL 2.0 μm vs. 2.2 μm within α-MHC or β-MHC fibers groups.
We measured tension production at various levels of Ca2+ activation to construct pCa-tension relationships in muscle fibers. Hill s equation was fitted to pCa-tension relationships to get estimates of myofilament calcium sensitivity (pCa50, Table 1) and cooperativity of tension development (nH, Table 1). The SL-MHC interaction effect was not significant on pCa50. This suggests that SL-dependent increase on myofilament Ca2+ sensitivity (ΔpCa50, Fig. 3B) and cooperativity was not different in α-MHC or β-MHC fibers. As was seen with max tension, the main effects of an increase in SL (p = 0.0005) or β-MHC expression (p < 0.0001) significantly increased pCa50. Along with our finding that SL dependence of tension development was not different, these data suggest that the length-dependence of myofilament activation were not different in α-MHC or β-MHC fibers. The SL-MHC interaction effect on nH was significant (p < 0.05); post-hoc analysis revealed that the SL-mediated effect on nH was less pronounced in β-MHC fibers than in α-MHC fibers. At SL 2.0 or 2.2 μm, nH was 3.08 ± 0.22 or 2.16 ± 0.09 (ΔnH = 0.92, p < 0.01) in α-MHC fibers, whereas nH was 2.81 ± 0.07 or 2.46 ± 0.06 (ΔnH = 0.35, p < 0.01), respectively.
Table 1.
Maximal tension (mN mm-2) and rate of ATPase activity (pmol mm-3 s-1) estimated in fibers from normal or PTU-treated mice at SL 2.0 or 2.2 μm. Hill s equation was fitted to pCa-tension relationships to estimate myofilament Ca2+ sensitivity (pCa50) and cooperativity (nH) parameter estimates. Values are mean ± SEM. Number of determinants is at least 10 for each group.
| Fibers from Normal Mice (α -MHC) | Fibers from PTU-Treated Mice (β -MHC) | |||
|---|---|---|---|---|
| SL | 2.0 μm | 2.2 μm | 2.0 μm | 2.2 μm |
| Max Tension | 38.01±0.62 | 43.75±1.53* | 46.75±0.90 α | 52.84±2.37*α |
| Max ATPase | 319.72±8.99 | 319.83±18.60 | 163.67±5.15 α | 145.90±5.19 α |
| pCa50 | 5.73±0.01 | 5.78±0.01* | 5.81±0.01 α | 5.85±0.01* α |
| nH | 3.08±0.22 | 2.16±0.09* | 2.81±0.07 α | 2.46±0.06* α |
- p < 0.05 vs. short SL in same (α-MHC or β-MHC) group of fibers;
- p < 0.05 vs. α-MHC fibers at same SL.
The slope of the relationship between tension development and ATPase activity at various pCa is reported as tension cost (Fig. 4). The SL-MHC interaction effect on tension cost was not significant, but the main effects of SL or MHC were both significant; an increase in SL (p = 0.0012) and β-MHC (p < 0.0001) significantly decreased tension cost. Further analysis revealed that the SL-dependent decrease in tension cost was slightly more pronounced in β-MHC (~14% decrease, p < 0.01) than in α-MHC (~11% decrease, p < 0.05) fibers.
Figure 4.
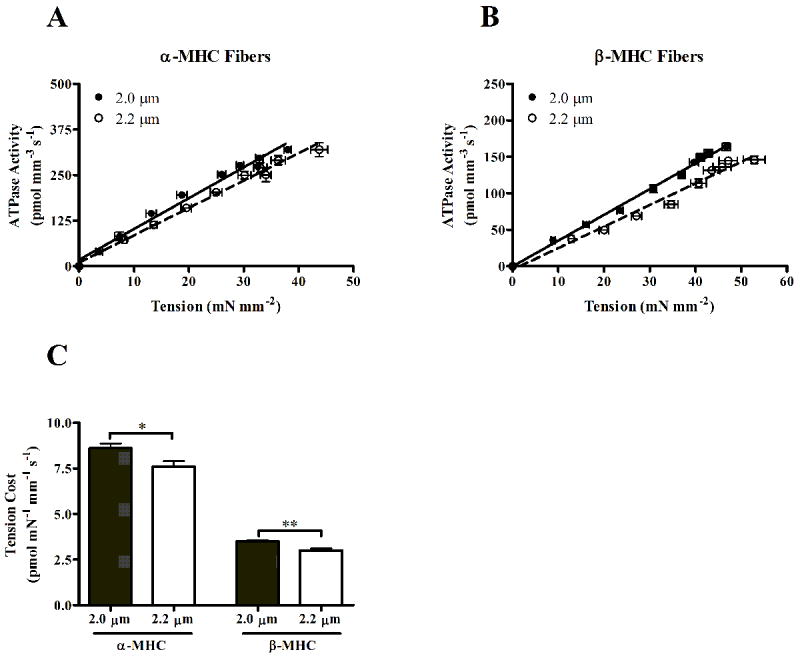
Relationship between the rate of ATP hydrolysis and corresponding tension development at varying levels of Ca2+ activation in normal (A) and PTU-treated (B) mouse fibers. Tension cost is determined by the slope of this linear relationship, and the slope values are represented in C. Values are mean ± SEM. Number of determinants is 10 for each group. * - p < 0.05; ** - p < 0.01.
Effects of SL on XB recruitment and distortion dynamics in α- vs. β-MHC fibers
Contractile dynamic parameters of α-MHC and β-MHC fibers at different SLs were characterized by fitting a linear recruitment-distortion (LRD) model to force responses to chirp length perturbations. Fitted model predictions determined from α-MHC or β-MHC (shown in Figs. 5A and 5B), illustrate an apparent difference in the contractile dynamics at SL 2.0 and 2.2 μm. Figs. 5C-5F are shown to illustrate the SL effects on the XB recruitment or XB distortion model components. SL did not have an apparent influence on XB recruitment dynamics in either α-MHC (Fig. 5C) or β-MHC (Fig. 5D) fibers. An increase in SL did have an apparent effect of slowing XB distortion dynamics in α-MHC fibers (Fig. 5E), but this effect seemed more pronounced in β-MHC fibers (Fig. 5F).
Figure 5.
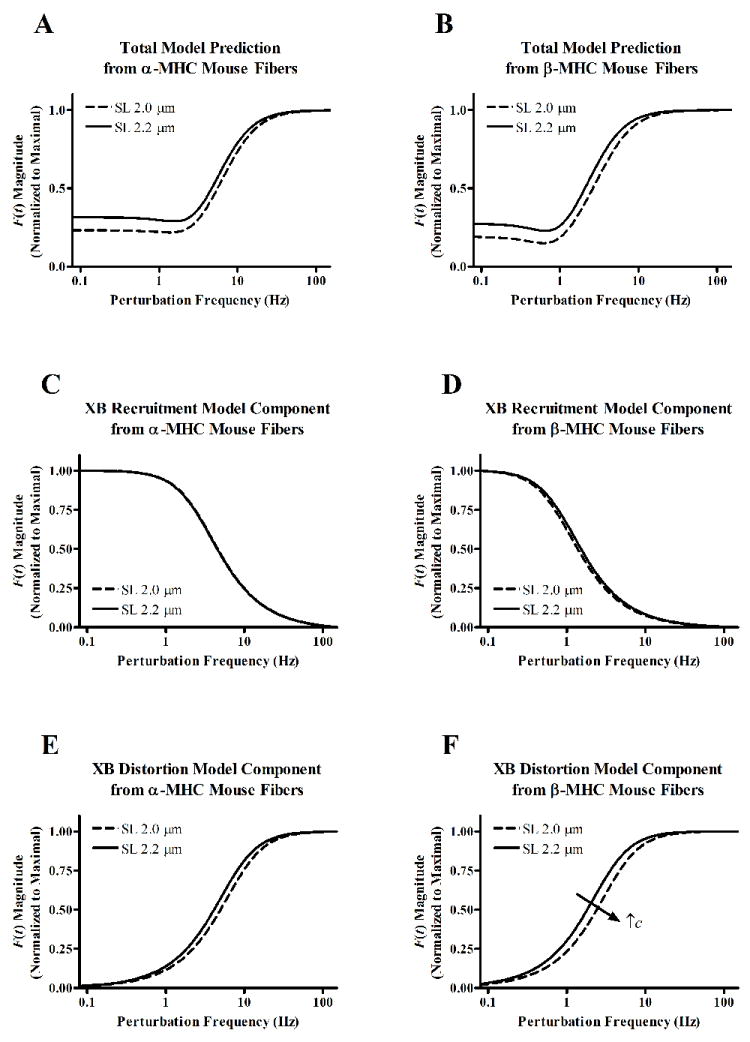
Linear recruitment-distortion (LRD) model-predicted force responses to sinusoidal length perturbations of increasing frequency in α-MHC (A) and β-MHC (B) fibers at SL 2.0 or 2.2 μm. Model components are shown in panels C-F to illustrate the SL-based effects on XB recruitment or XB distortion dynamics. Low-frequency model components are shown for fibers from α-MHC (C) or β-MHC (D) fibers. High-frequency model components are shown for fibers from α-MHC (E) or β-MHC (F) fibers. Plotted model predictions are determined based on average model fits to each group of chirp data.
LRD model parameters b and c were used to quantify these SL-dependent effects on XB recruitment or XB distortion dynamics, respectively. The effect of SL on b was not different in α-MHC or β-MHC fibers (Fig. 6A). The SL-MHC interaction effect did not have a significant effect on b, suggesting that the SL-mediated effect on XB recruitment dynamics was not different in α-MHC or β-MHC fibers. β-MHC expression, but not SL, had a significant effect (p < 0.0001) on slowing b.
Figure 6.
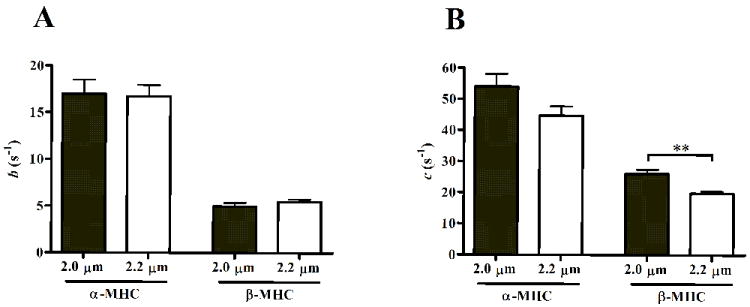
Model-predicted estimates of the rate constant of length-mediated XB recruitment, b (A), and the rate constant associated with XB distortion, c (B). b approximates the rate of XB recruitment in response to length change. c approximates XB detachment rate and correlates well with tension cost. Parameter values are mean + SEM. Number of determinants is 10 for each group. ** - p < 0.01.
Interestingly, the effect of SL on c was different in α-MHC or β-MHC fibers (Fig. 6B). Although the SL-MHC interaction effect was not significant, post-hoc analysis revealed differences in the SL-dependence of c in α-MHC and β-MHC fibers. At SL 2.0 or 2.2 μm, c decreased from 54 s-1 to 47 s-1 (~17% slower, not significant) in α-MHC fibers, whereas c decreased from 26 s-1 to 19 s-1 (~25% slower, p < 0.001) in β-MHC fibers. Since the rate of XB detachment is considered to be a major demining factor for c [21, 22], these data suggest that XB detachment rate is sensitive to SL in β-MHC, but not α-MHC fibers.
Effects of SL on the rate constant of tension redevelopment (ktr) in α- vs. β-MHC fibers
The rate of tension redevelopment following rapid slack and restretch was approximated by the monoexponential rate constant, ktr. We examined the effects of SL on the rate of tension development by estimating ktr at both SL 2.0 and 2.2 μm. Tension redevelopment traces measured from α-MHC or β-MHC fibers, at both SL, are shown in Figs. 7A and 7B, respectively. The SL-MHC interaction did not have a significant effect on ktr, however post-hoc analysis suggest differences in the SL-dependence of ktr in α-MHC and β-MHC fibers. When comparing ktr at SL 2.0 vs. 2.2 μm, ktr was not different in α-MHC fibers, but an increase in SL caused ktr to significantly decrease (~13% decrease, p < 0.01) in β-MHC fibers. These findings further suggest that contractile dynamics are more dependent on SL in β-MHC fibers than in α-MHC fibers.
Figure 7.
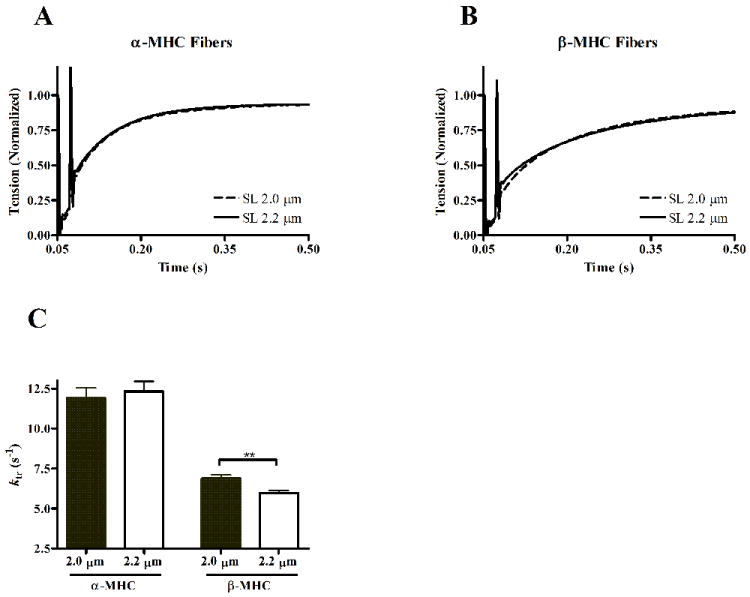
Tension redevelopment following rapid slack and restretch protocol in α-MHC (A) or β-MHC (B) fibers. Data are normalized to isometric tension attained prior to length change, and are shown as ensemble averages of at least 10 data records. Tension redevelopment traces at long SL (solid lines) and short SL (dashed lines) are shown to illustrate any length-dependence of the rate of tension redevelopment. The rate of tension redevelopment was determined by the monoexponential rate constant, ktr (C). ktr values are shown as mean + SEM. Number of determinants is 10 for each group. ** - p < 0.01; *** - p < 0.001.
Nonlinear XB strain-dependent effect on XB recruitment dynamics in α- vs. β-MHC fibers
Nonlinear contractile behavior was characterized by fitting the nonlinear recruitment-distortion (NRD) model to a family of force responses to various amplitude step-length changes. The NRD model is formulated with a parameter, γ, to reproduce the nonlinearity observed in the family of force responses to various amplitude quick stretches and releases [33]. Physiologically, γ interprets how XB strain negatively impacts the dynamics of XB recruitment. Because such XB-XB interactions are indirect, γ is thought to interpret allosteric/cooperative mechanisms in the myofilaments. The force responses to step perturbations elicited a nonlinear behavior that was more pronounced in β-MHC fibers than was in α-MHC fibers (Fig. 8A). This gave rise to a significant (p < 0.0001) increase in the NRD model parameter γ in β-MHC fibers. This suggests that the allosteric mechanisms, through which XB strain influences XB recruitment, are more prominent in β-MHC fibers than in α-MHC fibers.
Figure 8.
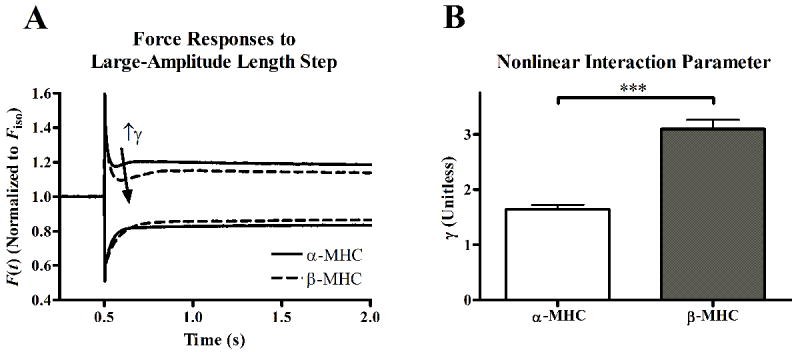
Force responses to large-amplitude step-like stretch or release (A) in α-MHC (solid lines) or β-MHC (dashed lines) fibers. Data are normalized to isometric tension (FIso) attained prior to length change, and are shown as ensemble averages of at least 10 data records. Nonlinearity in the responses to stretch or release is seen in both α-MHC and β-MHC fibers; the difference in the shape of the transient and presence of a nadir in the responses to large amplitude stretch, but not release, illustrates this nonlinearity. This nonlinearity is ascribed to effects that XB strain has on recruitment of other XB, and is thus a measure of allosteric mechanisms of myofilament activation. The nadir in the response to stretch was more prominent in β-MHC fiber than in α-MHC fibers, demonstrating a more prominent nonlinearity in β-MHC fibers. The nonlinear recruitment-distortion (NRD) model was fitted to the family of force responses to various amplitude stretch or release to quantify this nonlinearity with the parameter γ. As illustrated in panel B, γ predicted that the nonlinear behavior was significantly higher in β-MHC fibers. γ values are shown as mean + SEM. Number of determinants is 10 for each group. *** - p < 0.001.
DISCUSSION
We sought to determine whether the length-dependence of contractile function and XB cycling dynamics would be different in cardiac fibers containing α-MHC or β-MHC. The rationale for this study was that: 1) α-MHC and β-MHC impart very different contractile dynamics in cardiac muscle [21, 22, 24, 25]; and 2) α-MHC and β-MHC are expressed differently across different species [36, 37], during development and aging [37-42], and in cardiac disease [43-47], where contractile function is widely varied. The mechanisms behind this correlation, while unclear, may be linked to differences in XB cycling rates. The slower cycling, and thus, longer dwell time of β-MHC XBs, may allow for allosteric length-sensing mechanisms of the myofilaments to impart different contractile function. We hypothesized that the length-sensing mechanisms that regulate contractile function were different in α-MHC or β-MHC fibers. To test our hypothesis, we approximated contractile dynamics in fibers from normal (α-MHC) or PTU-treated (β-MHC) mice at SL 2.0 or 2.2 μm. Interestingly, we found that β-MHC, but not α-MHC, exhibited an apparent length-dependence of XB detachment dynamics. Furthermore, an increased γ was suggestive of increased strain-dependent allosteric/cooperative effects in fibers containing β-MHC XBs.
Length-dependence of tension production and myofilament Ca2+ is not affected by β-MHC
Length-dependent activation (LDA) is a well-documented phenomenon whereby an increase in SL results in an increase in myofilament tension production and Ca2+ sensitivity [1, 2]. LDA is an important phenomenon of healthy heart function, and underlies the Frank-Starling Law of the heart. Therefore, the mechanisms that contribute to LDA are hallmark in understanding healthy heart function, but currently remain unclear. However, two underlying themes are widely accepted to contribute to LDA: 1) changes in myofilament overlap and lattice spacing in response to changes in SL; and 2) changes in the structure of the thin and thick myofilaments in response to changes in SL. The former theme suggests proximity effects that allow for an increase in probability of XB binding as SL increases, whereas the latter theme suggests allosteric changes that allow the sarcomeres to become more sensitive to activation at longer lengths. The latter is supported by the fact that changes in the thin-filament structure influences LDA [8-11]. Furthermore, the structure of thick filament proteins appears to play a role in LDA. For example, the presence of XBs influence LDA [12-14], and furthermore, alterations in myosin regulatory light chain have been linked to modulating LDA [15] and the strain-dependence of myosin XB cycling [16]. However, whether α-MHC or β-MHC isoform expression leads to differences in length-dependent XB cycling dynamics is not currently understood.
We investigated whether the SL dependence of tension and pCa50 were different in α-MHC or β-MHC fibers. Interestingly, we found that maximal tension development and pCa50 were slightly, but significantly higher in β-MHC fibers than was in α-MHC fibers. These findings are different than results published earlier [23-25, 47, 48], but these discrepancies could be attributed to differences in preparation procedures. For example, results obtained in previous studies were from samples dissected using mincing – vs. microdissection in our study – and included both right- and left-ventricular preparations [23-25, 48] – vs. only left ventricle preparations in our study. Regardless of this discrepancy, we observed no difference in the SL-dependence of tension development (Fig. 3A) in α-MHC or β-MHC fibers. Similarly, there was no difference in the SL-dependence of pCa50 (Fig. 3B), suggesting that the SL-dependence of contractile activation was not different between α-MHC and β-MHC fibers. Thus, the inotropic responses of tension and myofilament Ca2+ sensitivity to an increase in SL were not different in α-MHC or β-MHC fibers.
Length-dependence of contractile dynamics is more sensitive in β-MHC
It is well-documented that β-MHC imparts slower contractile dynamic behaviors in cardiac muscle when compared to α-MHC [21-24]. However, whether contractile dynamics are sensitive to length, and whether the length-dependence of the contractile dynamics is different in α-MHC and β-MHC cardiac muscle is not well understood. This may hold physiological significance, as changes in preload, and thus change in SL may allow the heart to impart different contractile dynamics on a beat-to-beat basis. Thus, we sought to determine whether changes in SL could influence contractile dynamics, and further, whether MHC isoform played a role in the determination of length-dependent dynamics.
LRD model parameters were fitted to force responses to sinusoidal length perturbations (as in [21, 22]) to determine effects of SL and MHC isoform on contractile dynamics. Consistent with previous findings, MHC isoform had a major impact on slowing both LRD model predicted rates of XB recruitment, b (Figs. 5C, 5D and 6A), and XB distortion, c (Figs. 5E, 5F and 6B). We observed no significant SL dependence on the model-predicted rate constant of XB recruitment, b, whether fibers were of α-MHC or β-MHC background (Fig. 6A). This indicates that SL does not alter the speed of XB recruitment in response to length in either α-MHC or β-MHC fibers. Interestingly, however, an increase in SL significantly slowed c in β-MHC fibers, but not α-MHC fibers (Fig. 6B). This finding was corroborated by our measurement of tension cost (Fig. 4), whereby tension cost decreased as SL increased, a trend that was more pronounced in β-MHC fibers. Both c and tension cost are limited by the rate constant of XB detachment, and are considered parameters that can infer XB detachment kinetics [21, 49]. Therefore, our findings suggest that an increase in SL speeds XB detachment kinetics in β-MHC, but not α-MHC fibers.
In a two state XB model, ktr estimated at maximal activation can be approximated as the sum of XB cycling forward, f, plus detachment, g, rate constants [32]. At maximal activation, ktr was not different in α-MHC fibers, but was significantly lower at the longer SL in β-MHC fibers (Fig. 7C). These findings correlate well with those reported by Korte and McDonald (2007) [50], where a length-dependent decrease in ktr in β-MHC, but not in α-MHC fibers, was also observed. Taken together with findings of decreased c and tension cost – and the finding that b was not affected – suggest that an increase in SL decreases the apparent rate of XB detachment, g in β-MHC fibers, without affecting f.
β-MHC exhibits a greater XB strain effect on XB recruitment; implications for cooperative and/or allosteric mechanisms that underlie nonlinear contractile behavior
The NRD model parameter γ is a nonlinear interaction term that represents the effect that strained XBs have on the recruitment of other XBs [33]. The XB strain effect on recruitment of other XBs is assumed to transmit through cooperative and allosteric mechanisms of the thin and thick filaments. For example, the slowing effect of XB strain on XB recruitment may be due, in part, to the compliant realignment of myosin binding sites on actin relative to myosin heads [51]. Therefore, γ reflects cooperative and/or allosteric mechanisms operating within sarcomeres. We performed step perturbation analysis at SL 2.2 μm and found that the nonlinearity in the shape of the curves was much more pronounced in β-MHC fibers (Fig. 8A), which gave rise to a significantly higher γ (Fig. 8B). Similarly, b and c from the NRD model predictions were slowed by ~2 fold in the β-MHC fibers (data not shown), which matched the trends seen in b and c from the chirp LRD model. These trends also correlate well with the trends reported for kdf and k1 by Stelzer et al. (2007), which are determined by the same phases of the F(t) response to step-length changes that principally determine c and b, respectively.
The significant finding of an increased γ indicates that allosteric and/or cooperative mechanisms within the myofilaments are more pronounced in β-MHC fibers. This change may be due to XB feedback effects on the regulatory units (RU), whose activation is tightly coupled to both Ca2+- and XB-induced changes in the thin filament (for review, see [52]). Because XBs themselves affect the balance between RU “on” and “off” states through cooperative activation, β-MHC may have a more prominent strain-dependent effect on XB recruitment dynamics due to its slower cycling. This suggests that the higher duty time of β-MHC XBs imparts a greater effect of XB-strain feedback on RU on/off dynamics, shifting the equilibrium more so toward the RU off state when XBs are strained.
In conclusion, our data suggest that cardiac MHC isoforms differently influence the outcome of how SL influences contractile dynamics. We report a SL-dependent decrease in the rate of XB detachment and ktr, in fibers containing β-MHC, but not α-MHC. Furthermore, the nonlinear effect that XB strain has on XB recruitment was greater in β-MHC fibers, as approximated by γ. These findings are suggestive of a more prominent cooperative mechanism involved in mediating XB cycling dynamics in β-MHC fibers. We attribute this increased cooperative effect to the slower cycling, and thus higher duty time of XBs in β-MHC fibers. The higher duty time of β-MHC XBs may cause the strain-dependent allosteric changes, imposed by a change in SL, to have a longer residual time allowing transduction of cooperative feedback from one XB to another. Collectively, these findings imply that kinetics of the β-MHC XB cycle are more dependent on allosteric length-sensing mechanisms in cardiac muscle than the α-MHC XB cycle. These results suggest that larger mammals possess different SL-dependencies of contractile dynamics than smaller mammals that express different isoform compositions of MHC. Therefore, our data suggests that animals expressing predominantly β-MHC would be a better model in understanding the Frank-Starling law of the human heart.
RESEARCH HIGHLIGHTS.
Propylthiouracil-treated adult mice expressed cardiac β-myosin heavy chain (MHC)
We studied length dependence of crossbridge dynamics of α- and β-MHC cardiac muscle
No length dependence of XB detachment was found in control, α-MHC cardiac muscle
XB detachment kinetics were significantly length dependent in β-MHC cardiac muscle
Cooperative/allosteric effects on XB recruitment dynamics were increased by β-MHC
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Kentish JC, ter Keurs HE, Ricciardi L, Bucx JJ, Noble MI. Circ Res. 1986;58:755–768. doi: 10.1161/01.res.58.6.755. [DOI] [PubMed] [Google Scholar]
- 2.Dobesh DP, Konhilas JP, de Tombe PP. Am J Physiol Heart Circ Physiol. 2002;282:H1055–1062. doi: 10.1152/ajpheart.00667.2001. [DOI] [PubMed] [Google Scholar]
- 3.Bacchiocchi C, Graceffa P, Lehrer SS. Biophys J. 2004;86:2295–2307. doi: 10.1016/S0006-3495(04)74287-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bacchiocchi C, Lehrer SS. Biophys J. 2002;82:1524–1536. doi: 10.1016/S0006-3495(02)75505-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vibert P, Craig R, Lehman W. J Mol Biol. 1997;266:8–14. doi: 10.1006/jmbi.1996.0800. [DOI] [PubMed] [Google Scholar]
- 6.Xu C, Craig R, Tobacman L, Horowitz R, Lehman W. Biophys J. 1999;77:985–992. doi: 10.1016/S0006-3495(99)76949-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McKillop DF, Geeves MA. Biophys J. 1993;65:693–701. doi: 10.1016/S0006-3495(93)81110-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Farman GP, Allen EJ, Schoenfelt KQ, Backx PH, de Tombe PP. Biophys J. 2010;99:2978–2986. doi: 10.1016/j.bpj.2010.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Konhilas JP, Irving TC, Wolska BM, Jweied EE, Martin AF, Solaro RJ, de Tombe PP. J Physiol. 2003;547:951–961. doi: 10.1113/jphysiol.2002.038117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chandra M, Tschirgi ML, Rajapakse I, Campbell KB. Biophys J. 2006;90:2867–2876. doi: 10.1529/biophysj.105.076950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tachampa K, Wang H, Farman GP, de Tombe PP. Circ Res. 2007;101:1081–1083. doi: 10.1161/CIRCRESAHA.107.165258. [DOI] [PubMed] [Google Scholar]
- 12.Fitzsimons DP, Moss RL. Circ Res. 1998;83:602–607. doi: 10.1161/01.res.83.6.602. [DOI] [PubMed] [Google Scholar]
- 13.Fukuda N, Kajiwara H, Ishiwata S, Kurihara S. Circ Res. 2000;86:E1–6. doi: 10.1161/01.res.86.1.e1. [DOI] [PubMed] [Google Scholar]
- 14.Fukuda N, J OU, Sasaki D, Kajiwara H, Ishiwata S, Kurihara S. J Physiol. 2001;536:153–160. doi: 10.1111/j.1469-7793.2001.00153.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cazorla O, Szilagyi S, Le Guennec JY, Vassort G, Lacampagne A. FASEB J. 2005;19:88–90. doi: 10.1096/fj.04-2066fje. [DOI] [PubMed] [Google Scholar]
- 16.Greenberg MJ, Kazmierczak K, Szczesna-Cordary D, Moore JR. Proc Natl Acad Sci U S A. 2010;107:17403–17408. doi: 10.1073/pnas.1009619107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jin JP. J Biol Chem. 1995;270:6908–6916. [PubMed] [Google Scholar]
- 18.Campbell KS. Pflugers Arch. 2011;462:3–14. doi: 10.1007/s00424-011-0952-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kurabayashi M, Tsuchimochi H, Komuro I, Takaku F, Yazaki Y. J Clin Invest. 1988;82:524–531. doi: 10.1172/JCI113627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McNally EM, Kraft R, Bravo-Zehnder M, Taylor DA, Leinwand LA. J Mol Biol. 1989;210:665–671. doi: 10.1016/0022-2836(89)90141-1. [DOI] [PubMed] [Google Scholar]
- 21.Campbell KB, Chandra M, Kirkpatrick RD, Slinker BK, Hunter WC. Am J Physiol Heart Circ Physiol. 2004;286:H1535–1545. doi: 10.1152/ajpheart.01029.2003. [DOI] [PubMed] [Google Scholar]
- 22.Chandra M, Tschirgi ML, Ford SJ, Slinker BK, Campbell KB. Am J Physiol Regul Integr Comp Physiol. 2007;293:R1595–1607. doi: 10.1152/ajpregu.00157.2007. [DOI] [PubMed] [Google Scholar]
- 23.Fitzsimons DP, Patel JR, Moss RL. J Physiol. 1998;513(Pt 1):171–183. doi: 10.1111/j.1469-7793.1998.171by.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rundell VL, Manaves V, Martin AF, de Tombe PP. Am J Physiol Heart Circ Physiol. 2005;288:H896–903. doi: 10.1152/ajpheart.00407.2004. [DOI] [PubMed] [Google Scholar]
- 25.Stelzer JE, Brickson SL, Locher MR, Moss RL. J Physiol. 2007;579:161–173. doi: 10.1113/jphysiol.2006.119719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pope B, Hoh JF, Weeds A. FEBS Lett. 1980;118:205–208. doi: 10.1016/0014-5793(80)80219-5. [DOI] [PubMed] [Google Scholar]
- 27.Palmer BM, Noguchi T, Wang Y, Heim JR, Alpert NR, Burgon PG, Seidman CE, Seidman JG, Maughan DW, LeWinter MM. Circ Res. 2004;94:1615–1622. doi: 10.1161/01.RES.0000132744.08754.f2. [DOI] [PubMed] [Google Scholar]
- 28.Krenz M, Sadayappan S, Osinska HE, Henry JA, Beck S, Warshaw DM, Robbins J. J Biol Chem. 2007;282:24057–24064. doi: 10.1074/jbc.M704574200. [DOI] [PubMed] [Google Scholar]
- 29.Ford SJ, Mamidi R, Jimenez J, Tardiff JC, Chandra M. J Mol Cell Cardiol. 2012 doi: 10.1016/j.yjmcc.2012.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fabiato A. Methods Enzymol. 1988;157:378–417. doi: 10.1016/0076-6879(88)57093-3. [DOI] [PubMed] [Google Scholar]
- 31.de Tombe PP, Stienen GJ. Circ Res. 1995;76:734–741. doi: 10.1161/01.res.76.5.734. [DOI] [PubMed] [Google Scholar]
- 32.Brenner B, Eisenberg E. Proc Natl Acad Sci U S A. 1986;83:3542–3546. doi: 10.1073/pnas.83.10.3542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ford SJ, Chandra M, Mamidi R, Dong W, Campbell KB. J Gen Physiol. 2010;136:159–177. doi: 10.1085/jgp.201010467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ford SJ, Chandra M. J Physiol. 2012 doi: 10.1113/jphysiol.2012.240085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Locher MR, Razumova MV, Stelzer JE, Norman HS, Patel JR, Moss RL. Am J Physiol Heart Circ Physiol. 2009;297:H247–256. doi: 10.1152/ajpheart.00922.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Clark WA, Jr, Chizzonite RA, Everett AW, Rabinowitz M, Zak R. J Biol Chem. 1982;257:5449–5454. [PubMed] [Google Scholar]
- 37.Lompre AM, Mercadier JJ, Wisnewsky C, Bouveret P, Pantaloni C, D’Albis A, Schwartz K. Dev Biol. 1981;84:286–290. doi: 10.1016/0012-1606(81)90396-1. [DOI] [PubMed] [Google Scholar]
- 38.Chizzonite RA, Zak R. J Biol Chem. 1984;259:12628–12632. [PubMed] [Google Scholar]
- 39.Lompré AM, Nadal-Ginard B, Mahdavi V. J Biol Chem. 1984;259:6437–6446. [PubMed] [Google Scholar]
- 40.Siedner S, Krüger M, Schroeter M, Metzler D, Roell W, Fleischmann BK, Hescheler J, Pfitzer G, Stehle R. J Physiol. 2003;548:493–505. doi: 10.1113/jphysiol.2002.036509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lyons GE, Schiaffino S, Sassoon D, Barton P, Buckingham M. J Cell Biol. 1990;111:2427–2436. doi: 10.1083/jcb.111.6.2427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Metzger JM, Lin WI, Johnston RA, Westfall MV, Samuelson LC. Circ Res. 1995;76:710–719. doi: 10.1161/01.res.76.5.710. [DOI] [PubMed] [Google Scholar]
- 43.Mercadier JJ, Bouveret P, Gorza L, Schiaffino S, Clark WA, Zak R, Swynghedauw B, Schwartz K. Circ Res. 1983;53:52–62. doi: 10.1161/01.res.53.1.52. [DOI] [PubMed] [Google Scholar]
- 44.Nadal-Ginard B, Mahdavi V. J Clin Invest. 1989;84:1693–1700. doi: 10.1172/JCI114351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Miyata S, Minobe W, Bristow MR, Leinwand LA. Circ Res. 2000;86:386–390. doi: 10.1161/01.res.86.4.386. [DOI] [PubMed] [Google Scholar]
- 46.Nakao K, Minobe W, Roden R, Bristow MR, Leinwand LA. J Clin Invest. 1997;100:2362–2370. doi: 10.1172/JCI119776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rundell VL, Geenen DL, Buttrick PM, de Tombe PP. Am J Physiol Heart Circ Physiol. 2004;287:H408–413. doi: 10.1152/ajpheart.00049.2004. [DOI] [PubMed] [Google Scholar]
- 48.Herron TJ, Korte FS, McDonald KS. Am J Physiol Heart Circ Physiol. 2001;281:H1217–1222. doi: 10.1152/ajpheart.2001.281.3.H1217. [DOI] [PubMed] [Google Scholar]
- 49.Brenner B. Proc Natl Acad Sci U S A. 1988;85:3265–3269. doi: 10.1073/pnas.85.9.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Korte FS, McDonald KS. J Physiol. 2007;581:725–739. doi: 10.1113/jphysiol.2007.128199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Daniel TL, Trimble AC, Chase PB. Biophys J. 1998;74:1611–1621. doi: 10.1016/s0006-3495(98)77875-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gordon AM, Homsher E, Regnier M. Physiol Rev. 2000;80:853–924. doi: 10.1152/physrev.2000.80.2.853. [DOI] [PubMed] [Google Scholar]


