Limited plasticity in the phenotypic variance-covariance matrix for male advertisement calls in the black field cricket, Teleogryllus commodus

Abstract

Phenotypic integration and plasticity are central to our understanding of how complex phenotypic traits evolve. Evolutionary change in complex quantitative traits can be predicted using the multivariate breeders’ equation, but such predictions are only accurate if the matrices involved are stable over evolutionary time. Recent work, however, suggests that these matrices are temporally plastic, spatially variable and themselves evolvable. The data available on phenotypic variance-covariance matrix (P) stability is sparse, and largely focused on morphological traits. Here we compared P for the structure of the complex sexual advertisement call of six divergent allopatric populations of the Australian black field cricket, Teleogryllus commodus. We measured a subset of calls from wild-caught crickets from each of the populations and then a second subset after rearing crickets under common-garden conditions for three generations. In a second experiment, crickets from each population were reared in the laboratory on high- and low-nutrient diets and their calls recorded. In both experiments, we estimated P for call traits and used multiple methods to compare them statistically (Flury hierarchy, geometric subspace comparisons and random skewers). Despite considerable variation in means and variances of individual call traits, the structure of P was largely conserved among populations, across generations and between our rearing diets. Our finding that P remains largely stable, among populations and between environmental conditions, suggests that selection has preserved the structure of call traits in order that they can function as an integrated unit.

Introduction

Phenotypic traits seldom evolve independently and responses to selection are often correlated due to shared genetic effects such as pleiotropy and linkage (Lande & Arnold, 1983). The phenotypes expressed in a population may further covary because traits arise from shared developmental processes or are influenced by the same environmental factors (West-Eberhard, 2003). The resulting non-independence of traits is generally referred to as ‘phenotypic integration’ (e.g. Zelditch et al., 1992; Cheverud, 1995; Olson & Miller, 1999; Merilä & Björklund, 1999; Pigliucci & Kolodynska, 2002b) and can be quantified as the pattern of phenotypic variance in and covariances between traits in a population.

Much of quantitative genetic theory on how complex traits evolve is based on the assumption that the phenotypic (P) and genetic (G) variance-covariance matrices will remain stable over evolutionary time (Lande, 1980; Turelli, 1988), or vary only proportionally (Roff et al., 2000; Stirling & Roff, 2000). However, there is now a substantial body of theoretical and empirical work suggesting that these matrices may vary (Roff & Mousseau, 1999; Agrawal et al., 2001; Eroukhmanoff, 2009; de Oliveira et al., 2009), and that they can themselves evolve, both in response to selection (Blows & Higgie, 2003), as a result of mutation (Camara et al., 2000) and through random genetic drift (Phillips, P. C. et al., 2001). Thus it is important to study empirically the extent to which P varies, and to quantify the scale over which this variation occurs (Arnold & Phillips, 1999; Ackermann & Cheverud, 2000; Bégin et al., 2004; Roff et al., 2004; Game & Caley, 2006; de Oliveira et al., 2009).

The issue of the stability of P is of importance to evolutionary biology because the response of complex traits to selection is modelled by the multivariate extension of the breeders’ equation: Δz̄ =GP⁻¹s, where Δz̄ is the vector of change in trait means, and s is the vector of selection differentials (Lande, 1979). Following the breeders’ equation, P is expected to play an important role in the trajectory of phenotypic evolution, since selection (s) may only act on trait combinations that are expressed (P). However, most organisms encounter heterogeneity in their environment and phenotypes are often plastic in their expression. As P has an environmental component, an understanding of the plasticity of P is required for prediction of the capacity for complex phenotypes to evolve in response to selection (Lande & Arnold, 1983; Schluter, 2001).

Sexually selected signals are expected to show a high degree of plasticity if their expression is to accurately reflect an individuals’ condition and therefore communicate information about mate quality to the choosing sex (Zahavi, 1975; Andersson, 1982). However, there are conflicting predictions about the level of integration between individual traits that comprise a complex sexual signal, as well as between the sexual signal and other traits expressed by the organism (Badyaev, 2004). On one hand, if sexual signals function as an honest indicator of male quality or general vigour, we might predict strong integration between signals and the traits that are advertised by those signals (Wedekind, 1992; Johnstone, 1995; Bischoff et al., 2009). On the other, when selection favours the expression of sexual signals to become more exaggerated, we might predict that this should minimise the integration between sexual signals and other elements of the phenotype, as this would allow the sexual signal to evolve independently of traits that are not subject to sexual selection (Emlen & Nijhout, 2000).

From the state of current research it is not clear at what taxonomic level we ought to predict divergence in P. Empirical work has shown stability of P among populations of garter snakes (Phillips & Arnold, 1999) and among populations of a number of different species of coral reef fishes (Game & Caley, 2006) and New World monkeys (de Oliveira et al., 2009). Conversely, studies have shown P to vary between populations of house finches (Badyaev & Hill, 2000), and there is some evidence for stability of P at the species level in tamarins (Ackermann & Cheverud, 2000). The relationship between integration and plasticity has also been investigated, most prominently in the morphology of Arabidopsis (Pigliucci & Kolodynska, 2002a; b; Kolodynska & Pigliucci, 2003; Bossdorf & Pigliucci, 2009). In addition to differences in P that have been documented across populations of Arabidopsis (Pigliucci & Kolodynska, 2002a; Bossdorf & Pigliucci, 2009), a number of studies have also examined patterns of phenotypic integration under experimentally induced stress. Despite finding plastic responses (in terms of trait means and variances) associated with changes in soil moisture content (Pigliucci & Kolodynska, 2002a), light intensity (Pigliucci & Kolodynska, 2002b) and wind speed (Bossdorf & Pigliucci, 2009), these studies found that patterns of phenotypic covariance tended to remain stable. This work has been focused on morphology, and we know of no study examining the plasticity of integration in sexual signals. Such data is needed, given that the stability of (co)variance structures is of particular relevance to how complex sexual signals evolve (Badyaev, 2004).

The advertisement call produced by male black field crickets (Teleogryllus commodus) is a complex sexual signal. It commences with a single chirp sequence, which is followed by a variable number of trill sequences (Bentley & Hoy, 1972; Hill et al., 1972). Female preference for this call structure has been studied, and females have been shown to be sensitive to both temporal (Pollack, 1979) and spectral (Hennig & Weber, 1997) call properties. The selection imposed by these female preferences has been measured both in the laboratory (Brooks et al., 2005) and in the field (Bentsen et al., 2006), and the dominant form of selection on call structure was found to be multivariate stabilising. If persistent, this is a selection regime that would be predicted to facilitate trait integration (Lande, 1980; Cheverud, 1984; McGlothlin et al., 2005).

Here we present estimates of P for the structure of the advertisement call of T. commodus from 6 geographically isolated populations across the southern distribution of this species in Australia. We demonstrate that the advertisement calls vary among populations, and compare P estimated from call recordings of wild-caught males and from males reared under common garden conditions. Using a suite of statistical analyses (Flury hierarchy, geometric subspace comparisons and random skewers), we evaluate the stability of P among populations and between rearing environments. The sexual advertisement calls of some crickets are also know to show phenotypic plasticity in response to environmental conditions, most famously relating to temperature (e.g. Elliott & Koch, 1985; Olvido & Mousseau, 1995). Additionally, call plasticity has been measured in a number of cricket species in response to diet, both in terms of calling effort (Wagner & Hoback, 1999; Hunt et al., 2004; Hedrick, 2005; Judge et al., 2008; Zajitschek et al., 2009) and in the structure of the call (Scheuber, Jacot, & Brinkhof, 2003a; b), thought this result is not ubiquitous (Gray & Eckhardt, 2001; Hartbauer et al., 2006). In a second experiment, we reared crickets from the same six populations on high- and low-nutrient diets. We then employ the same suite of approaches to test for plasticity of P for the advertisement call of this species across diets. In this study, we therefore compare the stability of P between allopatric populations, across generations and in response to different rearing environments.

Materials and methods

Experiment 1. Collection and common-garden rearing of crickets from six populations

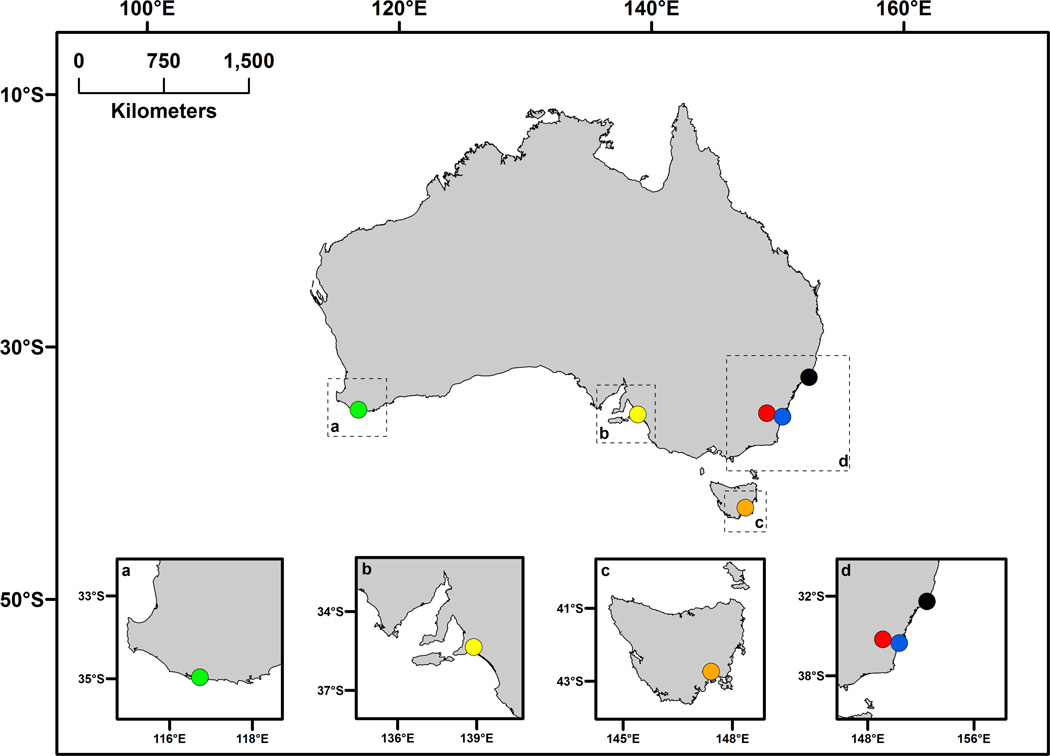
Approximately 400 adult T. commodus were collected from each of six populations spanning the southern distribution of this species in Australia: Western Australia (WA), South Australia (SA), Tasmania (TAS), Kioloa (KL), Australian Capital Territory (ACT) and Smith’s Lake (SL) (Figure 1). These populations are widely distributed across both latitude and longitude in southern Australia, and the abiotic (e.g. rainfall, temperature) and abiotic (e.g. species composition and amount of vegetation) environmental conditions they experience (Pitchers, personal observation). However, these populations do not vary according to a simple environmental cline. Crickets were collected between January and April in 2004 and air-freighted back to the University of New South Wales. In the laboratory, each population was established in a separate 80L culture container and provided with Go-Cat Senior cat pellets as food (Purina, Croydon, UK) and water ad libitum, and an abundance of egg cartons for shelter. Cultures were maintained in a constant temperature room at 28° ± 1°C with a 14L:10D light regime. A random sample of males from each population was recorded within 3 nights of being established in the laboratory. As this sample of males had completed their development and reached sexual maturity in the field, we refer to these as field males.

Figure 1.

The location of the six populations that crickets were collected. Populations are colour coded: Western Australia (WA, green), South Australia (SA, yellow), Tasmania (TAS, orange), Australian Capital Territory (ACT, red), Kioloa (KL, blue) and Smith’s Lakes (SL, black).

In each generation, populations were maintained by randomly pairing 100 males each with a virgin female. Each pair was placed in an individual clear plastic container (5cm × 5cm × 5cm) for 3 days to mate. Males were then removed and females provided with food, water and a 4cm Petri-dish of moist cotton wool for a week to lay eggs. At hatching, approximately 25 nymphs were randomly selected from each mating pair and reared in a small clear plastic container (15 × 10 × 15cm) until they reached 4th instar. Nymphs were then sexed and 5 crickets of each sex per container were randomly selected to contribute to the next generation. These crickets were reared to eclosion in a single, large plastic container (80L) for each population. Containers were checked daily and adults removed and maintained in sex-specific containers (80L) until sexually mature. When sexually mature, these crickets were used to propagate the next generation following the protocol outlined above.

These populations were maintained in this fashion under common environmental conditions for 3 generations prior to measuring the calls of a random sample from each population for a second time. As this sample of males has been maintained in the laboratory for 3 generations, we refer to them as laboratory males. Even in the absence of genetic differences among populations, maternal effects are known to induce adaptive plastic responses that can resemble local adaptation (Agrawal et al., 1999), but after 3 generations of rearing under lab-standard conditions any such effects are predicted to be reduced to a negligible level (Roach & Wulff, 1987).

Experiment 2. The plasticity of P under dietary manipulation

Between February and March, 2007, we collected approximately 400 adult crickets from each of the same six populations outlined above. Crickets were air-freighted to the Australian National University in Canberra, where they were maintained in 80L culture containers and provided with moist cotton wool to oviposit. These egg-pads were then air-freighted to the University of Exeter in Cornwall (UK) to establish the new cultures for each population. The laboratory populations derived from these egg-pads were maintained in common-garden conditions following the same protocol outlined above for 5 generations before we began our diet manipulation study.

In each population, a total of 300 nymphs on their day of hatching were established in individual plastic containers (5 × 5 × 5cm) and provided with a small water bottle (small plastic vial, 4cm long × 1cm diameter plugged with cotton wool) and a piece of cardboard egg carton for shelter. Half of the nymphs per population were provided with a high nutrient diet and the remaining half with a low nutrient diet (n = 900 nymphs per diet, total n = 1800 nymphs). The high-nutrient diet consisted of Go-Cat Senior cat pellets (Purina, Croydon, UK) that were used to maintain our stock cultures, whereas the low-nutrient diet consisted of a 50:50 mixture (by dry weight) of ground cat pellets and ground oats. Cat food and oats were ground to a fine powder using a food processor (BL10450H model, Black and Decker, London, UK) and sieved to remove larger particles. Each diet was then mixed with a small quantity of water and stirred to make a paste, which was then spread across a 1cm thick rigid polymer sheet perforated with 4cm holes. After drying for 24hrs at 30°C, the dried diet was pushed out from each hole in pellet form. Pellets were stored in sealed containers at room temperature. Both diets were presented as powder (in the lid of a 1.5ml centrifuge tube) for the first 4 weeks of feeding because small nymphs can have difficulty feeding on the larger food pellets. Food and water were replaced and containers cleaned weekly. Upon reaching final instar, crickets were checked daily for eclosion to adulthood to determine development time. Since some aspects of some cricket calls have been found to covary with body size (e.g. Bennet-Clark, 1999), we measured the body weight of each cricket at eclosion to adulthood on an analytic balance (Mettler-Toledo, 345G). We also measured the width of the pronotum, another commonly used measure of size in crickets, using an eyepiece graticule on a binocular dissecting microscope (Leica, MZ5). All crickets were maintained in a constant temperature room set to 28° ± 1°C with a 14L:10D light regime.

Call Recording and Analysis

At 10 days of age post-eclosion, all males were moved to a separate constant temperature room set to 28° ± 1°C to record their advertisement call. Each male remained housed in their original plastic container that they were reared in through development but the lid of the container was replaced with one that had a small condenser microphone (C1163, Dick Smith, Chullora, Australia) mounted onto its underside. Prior to recording, each container housing a male was placed inside a foam box (15 × 15 × 15cm) to minimise interference from other calling males when recording. The calls of field and laboratory males in Experiment 1 were recorded at the University of New South Wales using a Sony Professional Walkman (WM-D6C) on high quality chrome tapes (BASF CEII, Germany). Calls were recorded opportunistically between 21:00 and 03:00 each night by scanning recording chambers hourly. The recordings were then digitized for measurement and analysis. In total, we measured the calls of 142 males (WA=20, SA=25, TAS=17, ACT=25, KL=25, SL=30) collected from the field and 173 males (WA=25, SA=35, TAS=32, ACT=26, KL=28, SL=27) after 3 generations of common garden rearing in the laboratory.

The calls of the high- and low-nutrient males reared under common garden conditions at the University of Exeter were recorded using an automated multi-channel digital recorder with a NI-DAQ digital acquisition interface running at 48K samples-s (NI USB-6009, National Instruments, www.uk.ni.com) controlled by software written in LabView (National Instruments, www.uk.ni.com) using the full sampling speed of the interface to record at 48KHz. This system automatically monitored up to 256 channels and made 1-minute digital recordings only when the sound amplitude on a channel exceeds a user-defined threshold. In total, we measured the calls of 174 males (WA=34, SA=27, TAS=28, ACT=28, KL=25, SL=31) reared on the high-nutrient diet and 183 males (WA=31, SA=26, TAS=30, ACT=31, KL=27, SL=37) reared on the low-nutrient diet.

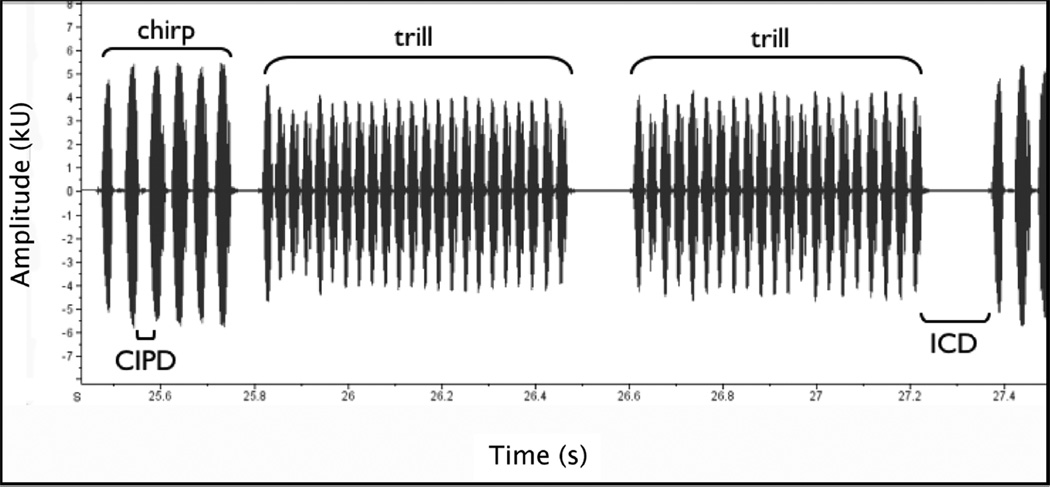
All calls were measured using ‘Raven’ software version 1.1 (Bioacoustics Research Group: Cornell Lab of Ornithology). We measured the following properties of six randomly selected calls per male: the number of pulses in the chirp (CPN, chirp pulse number), the interval between pulses in the chirp (CIPD, chirp inter-pulse duration (ms)), the number of trills in the call (TN, trill number), the interval between the last trill pulse of one call and the first chirp pulse of the next call (ICD, inter-call duration (ms)) and the dominant frequency of the call (DF, dominant frequency (mHz)) (Figure 2). We used the mean of these call properties for each male in all subsequent analyses.

Figure 2.

Screen capture from ‘Raven’ analysis software (v1.1), with annotations to show the main features of the call. Measures recorded from each call were the number of pulses in the chirp (CPN), the interval between pulses in the chirp (CIPD), the number of trills in the call (TN), the interval between the last trill and the next call (ICD) and the dominant frequency of the call (DF – not shown).

Statistical Analysis

Unless otherwise stated, analyses were conducted in R (version 2.13.0). To determine if the structure of the advertisement call had genetically diverged across our populations, we analysed our call data using a multivariate analysis of covariance (mancova) using the ‘Manova’ function from the ‘car’ package. We used a model including population, generation (i.e. field and common-garden males) and their interaction as fixed effects and the 5 call traits as the response variables. Male size (measured as the maximum width of the pronotum) differed significantly across populations (anova: F_5,303 =4.61, P <0.001), between rearing environments (F_1,303 =221.16, P <0.001) and there was a significant interaction between population and rearing environment (F_5,303 =15.19, P <0.001). As body size is known to influence the structure of the advertisement call in other field cricket species (e.g. Simmons, 1995; Simmons & Zuk, 1992), we included male size as a covariate in our mancova of call traits. Our model was therefore: Y=μ+β_p+β_r+β_p×r+β_s+ε, where Y is the matrix of call variables, β_p is the vector of coefficients for population, β_r is that for rearing environment (field or lab), β_p×r is that for the interaction of population and rearing and β_s is that vector of coefficients for size. The model was the same for the second experiment, with diet treatment in place of rearing environment. All call structure parameters, as well as male size, were log transformed prior to analysis. Some of the call data from Experiment 2 were not normally distributed and could not be transformed to normal, so we used a permutation test to determine the significance of terms in our model. Briefly, for each of 10,000 iterations we resampled Y (without replacement), ran a mancova and retained the P values. These P values then give us an expected distribution under the null hypothesis, and the permuted P value is obtained as the proportion of iterations wherein the null P is smaller than the P value obtained from a mancova of the original data.

We visualized the results of our mancova’s by using linear discriminant analysis (‘lda’ function from the ‘MASS’ package), to find the rotation that best separated the call structure data by both population and generation or diet. We then calculated means and standard errors for each population/rearing environment combination. In order to determine which call traits were driving the patterns revealed by these multivariate analyses, we also ran post-hoc anova’s for each trait. The right-hand side of each post-hoc model was the same as the corresponding multivariate model. For the data from experiment 2 we used the same permutation approach as above to assign P values, and post-hoc tests were also run for 10,000 permutations. For Experiment 2 we also ran anova’s to test for effects of population, diet and population × diet interaction on development time (number of days from hatching to eclosion), weight and pronotum width (measured at elcosion).

We calculated P matrices for the five call traits of each population and rearing environment in Experiment 1 and for each population and diet in Experiment 2, using the ‘cov’ function from the ‘stats’ package. With six populations and 2 treatments in each experiment, we had 12 call P matrices for each experiment. Though our focus was to compare the P matrices for call traits, we were also able to calculate a second set of P matrices for the life-history traits (development time, weight and pronotum width) that we measured in Experiment 2. There is currently no single best method of comparing matrices, with each available technique testing slightly different aspects of the matrices being compared (Roff et al., 2012). We therefore used a suite of complementary methods to test whether P differed across populations and our treatments (generation and diet).

Firstly, we used Common Principal Component (CPC) analysis (Phillips & Arnold, 1999). CPC analysis sequentially tests for differences between matrices in a hierarchical manner (Phillips & Arnold, 1999). We used the ‘CPC’ program (Phillips, 1997) to perform analyses and evaluated the results using the ‘jump-up’ approach; evaluating each model against the null model of unrelated matrices. CPC analysis is quite well-used in the field (e.g. Bégin & D. A. Roff, 2001; Game & Caley, 2006; Sherrard et al., 2009), but is not without problems. In particular, CPC analysis compares all principal components between matrices, but does not take account of their relative eigenvalues, meaning that similarity may be inferred between principal components that have a small eigenvalue in one matrix but a large eigenvalue in another (Blows et al., 2004).

We also compared the eigenstructure of the P matrices using geometric subspace analysis (Krzanowski, 1979). Krzanowski’s geometric method compares k-dimensional subspaces, where k is the number of eigenvectors being compared in each sample, by calculating the angles between the most similar pairs of orthogonal components. In order to be meaningful, no more than half the eigenvectors of an n-dimensional matrix can be included in any comparison because to do so would constrain the analysis to recover common dimensions (Blows et al., 2004). In the extreme case, including all eigenvectors will, by definition, recover identical subspaces. In our analyses we are therefore only able to include the first 2 eigenvectors (of our 5-dimensional matrices) in the subsets. However these account for greater than 99% of the variation in the structure of the advertisement call. For a pair of matrices to be compared (in our case; two 5 × 5 (co)variance matrices) the subset of eigenvectors to be compared are designated as matrices A & B (in our case; two 5 × 2 matrices), and used to calculate a new matrix (S) as: S = A^TBB^TA. The angle between most closely aligned vectors can be then be found as ${\text{cos}}^{-1}\sqrt{{\lambda }_1}$, where λ₁ is the largest eigenvalue of S. Additionally, the sum of S matrix eigenvalues, which is equal to the sum of squares of the cosines of the angles between the two sets of orthogonal axes, can be used as a metric of similarity. This metric will have a possible range from 0 (orthogonal subspaces) to k (identical subspaces). Since our estimates of P contain may be influenced by sampling error we boostrapped our Krzanowski tests (10,000 iterations) to place confidence intervals on the resulting statistics. Krzanowski comparisons were made using the ‘krzanowski.test’ function in the ‘MCMCglmm’ package of R (Hadfield, 2010).

As discussed above, one of the main reasons that P is of interest is their potential to influence a population’s evolutionary response to selection. The ‘random skewers’ method developed by Cheverud (1996) is intuitive, in that it compares matrices by comparing the direction of ‘response’ to set of randomly drawn ‘skewers’. These are sometimes described as hypothetical vectors of selection and so are represented as β_R. The elements of the random skewers are randomly drawn from a uniform distribution from −1 to +1, and each vector is then standardized so that the sum of the squares of its elements is equal to 1 (Cheverud & Marroig, 2007). For each pair of matrices (A and B) and each random skewer, ‘response’ vectors are computed as R_A=Aβ_R and R_B=Bβ_R, and the vector correlation between R_A and R_B are calculated following Calsbeek & Goodnight (2009). As we are testing P matrices, the skewers are not directly analogous to the vector of standardised selection gradients (β, sensu Lande & Arnold, 1983). We report the mean vector correlation from the application of 1000 random skewers as a measure of matrix similarity. We used a randomization approach in order to assess statistical differences between matrices (Roff et al., 2000). After estimating a mean vector correlation for each pair of matrices, we randomized our data among populations to generate two new matrices and computed their vector correlation. This process was also iterated 1000 times. Following Calsbeek & Goodnight (2009) and Roff et al. (2000), we took the null hypothesis to be that matrices A and B are identical. P values are therefore assigned as P=n/R, where n is the number of r_rand ≥ r_obs and R is the number of randomizations. Random skewers analyses were performed using R code adapted from Roff et al. (2000).

Lastly, we used the Bayesian ‘d method’ of matrix comparison as described by Ovaskainen et al (2008). Briefly, P matrices were estimated from centred data using an MCMCglmm and compared pairwise. We calculated the divergence metric ‘d’ using the ‘Ddivergence’ function (‘MCMCglmm’ package for R) at each position in the posterior distributions. The posterior mean and standard deviation from the distribution of d values provide an estimate of the magnitude of the difference between matrices in each pairwise comparison. We also calculated posterior distributions for Ovaskainen’s Ψ_d measure by resampling from the posterior distributions. Drawing 2 random samples from the posterior distribution for each matrix (P^A and P^B), we calculated the difference over 10,000 resampling iterations as:

$$\Psi d(\mathbf{A},\mathbf{B})=\mathbf{\left[}d\mathbf{\right(}{\mathbf{P}}_1^{\mathbf{A}},{\mathbf{P}}_2^{\mathbf{A}}\mathbf{)}+d\mathbf{(}{\mathbf{P}}_1^{\mathbf{B}},{\mathbf{P}}_2^{\mathbf{B}}\mathbf{\left)}\mathbf{\right]}-$$

$$\mathbf{\left[}d\mathbf{\right(}{\mathbf{P}}_1^{\mathbf{A}},{\mathbf{P}}_2^{\mathbf{B}}\mathbf{)}+d\mathbf{(}{\mathbf{P}}_1^{\mathbf{B}},{\mathbf{P}}_2^{\mathbf{A}}\mathbf{\left)}\mathbf{\right]}$$

The proportion of the posterior Ψ_d distribution where Ψ_d(A,B)<0 can then be used to infer statistical support for difference between the two matrices.

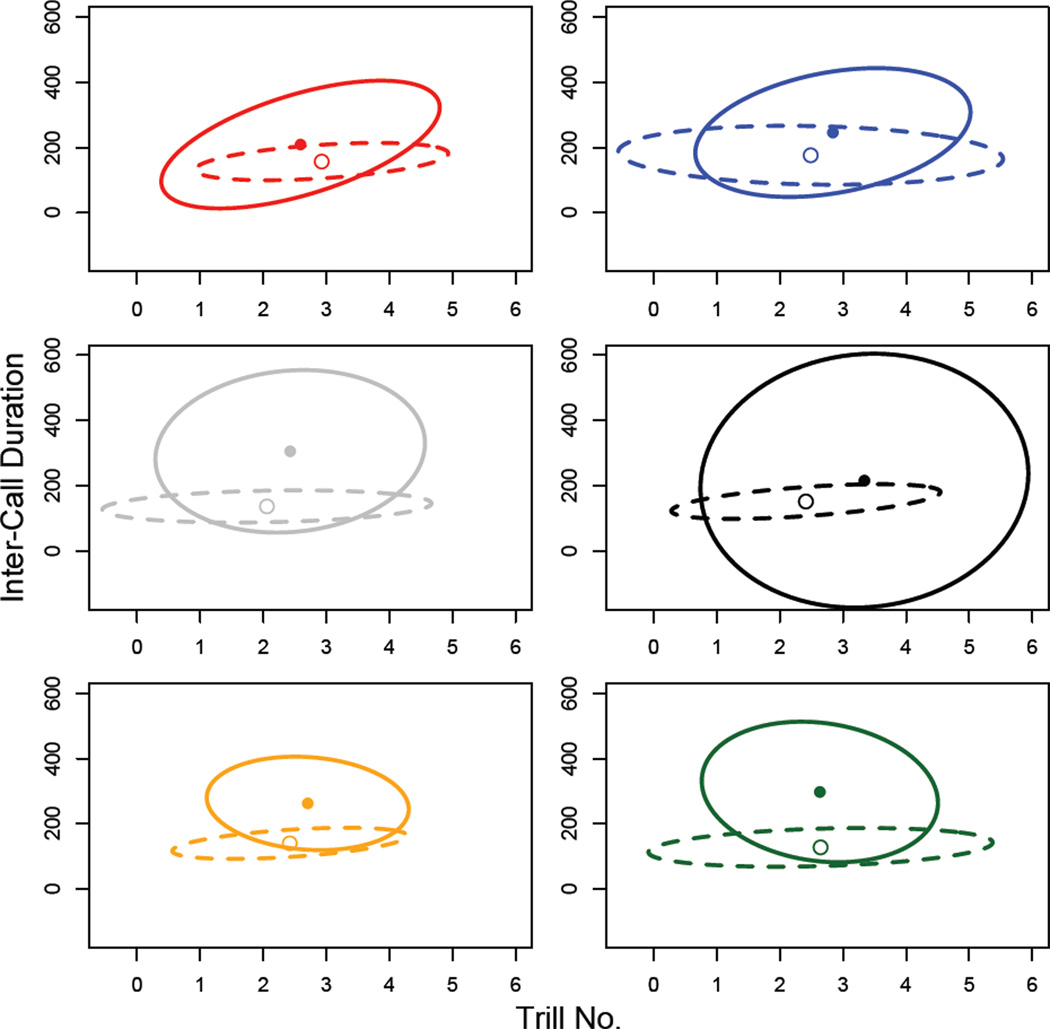
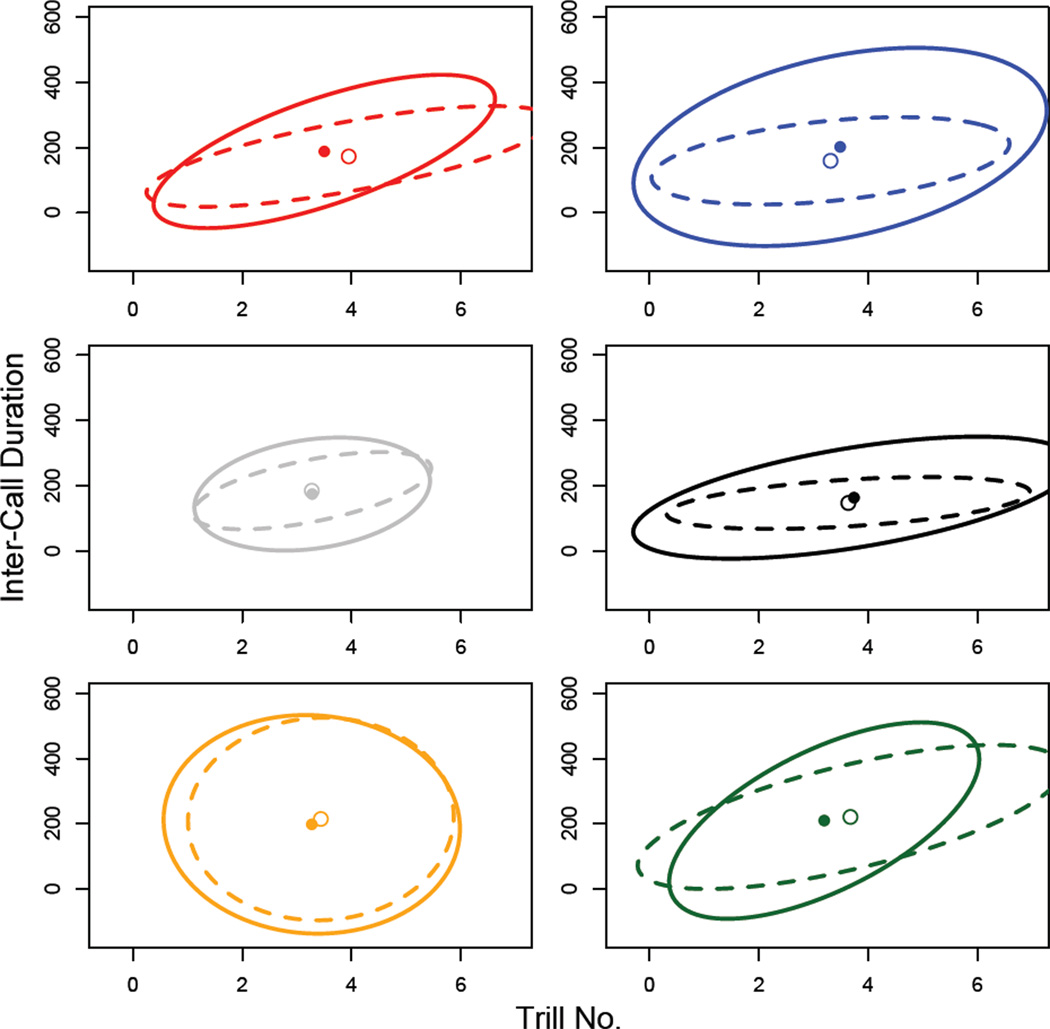
In order to illustrate the covariance matrices in 2 dimensions we extracted principal components from the data for the 5 call traits (i.e. populations, generation and diet treatments were pooled to give 1 set of PCs for each experiment) using the ‘prcomp’ function from the ‘stats’ package in R. As the call traits are measured in a number of different units and therefore are quite different in magnitude, extractions were performed on correlation matrices. Inter-call duration and trill number were the two traits with the highest loadings on PC1 and PC2 respectively, and so PC1 and PC2 were projected onto these traits to draw 95% confidence ellipses for Figures 4 and 6.

Figure 4.

Ellipses representing the first two dimensions of the call-trait P matrices from experiment 1. The ellipses show the first two principal components projected onto the ICD and TN traits. These traits were chosen for illustration since they had the highest loadings for PC1 and PC2, respectively. The solid point and ellipse represent the call structure of the wild-caught males; the open point and the dashed ellipse represent the call structure of common-garden-reared males. Population colours and abbreviations are as shown for Figure 1.

Figure 6.

Ellipses representing the first two dimensions of the call-trait P matrices from experiment 2. The ellipses show the first two principal components projected onto the ICD and TN traits. These traits were chosen for illustration since they had the highest loadings for PC1 and PC2, respectively. The solid point and ellipse represent the call structure of the males reared on the high-nutrient diet; the open point and the dashed ellipse represent the call structure of males reared on the low-nutrient diet. Population colours and abbreviations are as shown for Figure 1.

Results

Experiment 1: Common-garden rearing of crickets from six populations

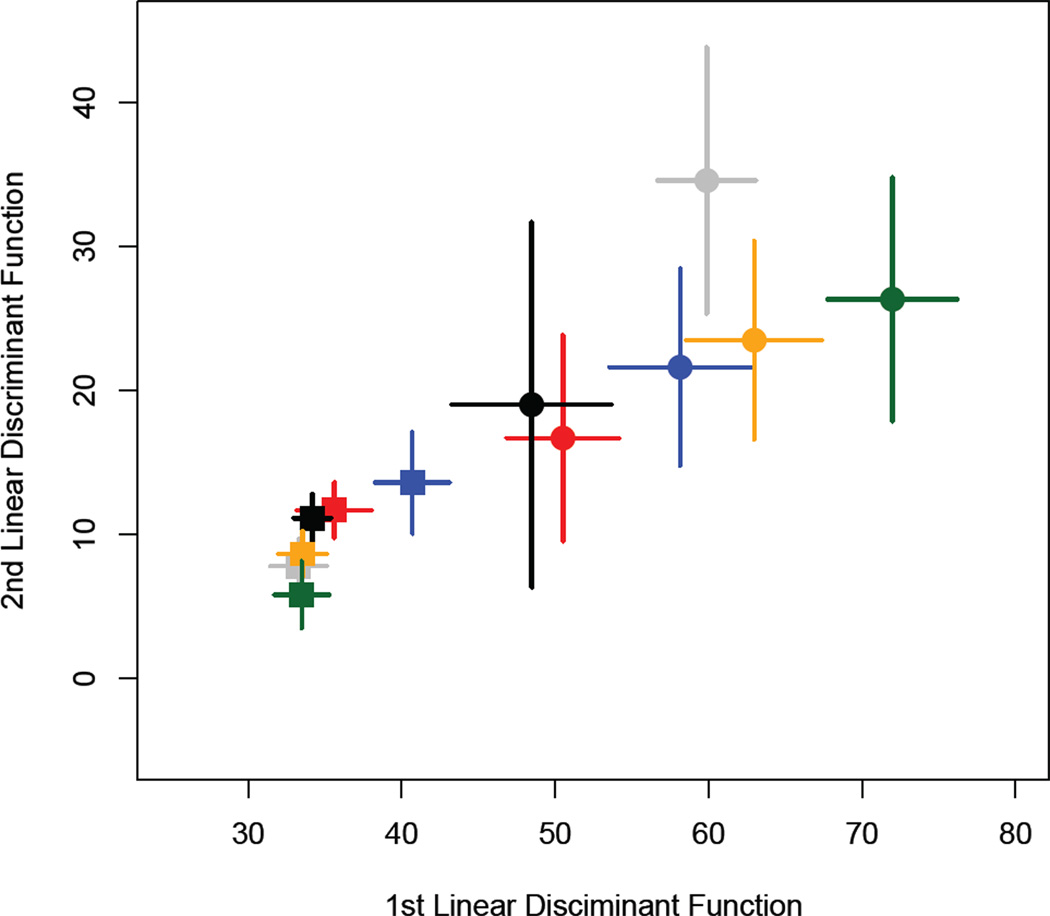
A mancova (Table 1) revealed significant differences in the structure of the advertisement call in T. commodus both among populations and between rearing environments and there was also a significant interaction effect of population × rearing environment. Male body size (pronotum width) was also a significant predictor of call traits and the inclusion of this term in our model ensures that the differences in the main effects are not driven solely by allometric relationships with body size. Among the crickets collected in the wild, males from the WA and TAS populations were most distinct from the other populations in call structure (Figure 3). Differences between populations were dramatically reduced when the environmental component of these differences were minimised by laboratory rearing, while the effect of lab rearing differed between populations. The KL population was the most distinct under laboratory conditions. The maintenance of detectable differences across populations under common-garden rearing conditions is indicative that the divergence in advertisement calls has a heritable genetic basis as opposed to being the result of maternal effects. Post-hoc ancova’s revealed a significant effect of population on CPN (F_5,302 = 3.51, P = 0.004), DF (F_5,302 = 5.41, P = 0.0001) and CIPD (F_5,302 =13.47, P = 0.001) and a significant effect of generation on all 5 call traits (CPN: F_1,302 =66.63, P = 0.0001; TN: F_1,302 =5.87, P = 0.016; DF: F_1,302 =172.78, P = 0.0001; ICD: F_1,302 =126.03, P = 0.0001; CIPD: F_1,302 =602.48, P <0.0001). Body size, included in these analyses as pronotum width, only significantly influenced CIPD (F_1,302 =13.30, P <0.001), but the interaction effect of population × generation was found to be significant for all 5 call traits (CPN: F_5,302 =6.74, P = 0.0001; TN: F_5,302 =2.23, P = 0.05; DF: F_5,302 =20.19, P = 0.0001; ICD: F_5,302 =6.24, P = 0.0001; CIPD: F_5,302 =14.68, P = 0.0001).

Table 1.

MANCOVA statistics from experiment 1.

Effect		Pillai	F approx.	hypoth. df	resid. df	p value
Population (A)		0.38	5.01	25	1510	<0.0001
Rearing Environment (B)		0.66	117.86	5	298	<0.0001
A × B		0.58	7.90	25	1510	<0.0001
Size (PW)		0.05	3.14	5	298	<0.01
		Trait Means (±SE) by Population
Wild-Caught		CPN (#)	TN (#)	DF (MHz)	ICD (ms)	CIPD (ms)
ACT		6.43 (0.30)	2.59 (0.21)	3.87 (0.03)	209.29 (18.25)	26.67 (0.94)
KL		6.73 (0.25)	2.84 (0.20)	3.78 (0.03)	246.09 (18.40)	30.33 (1.19)
SA		6.73 (0.26)	2.43 (0.20)	3.66 (0.05)	305.33 (23.21)	29.28 (0.71)
SL		6.02 (0.20)	3.34 (0.22)	4.00 (0.04)	215.4 (33.11)	25.32 (0.83)
TAS		6.95 (0.21)	2.7 (0.18)	3.49 (0.04)	262.54 (16.19)	32.75 (1.43)
WA		8.15 (0.48)	2.63 (0.20)	3.89 (0.08)	297.56 (22.45)	37.4 (0.87)
Common-Garden		CPN (#)	TN (#)	DF (MHz)	ICD (ms)	CIPD (ms)
ACT		5.59 (0.14)	2.93 (0.18)	4.06 (0.02)	157.15 (5.13)	18.97 (0.75)
KL		6.08 (0.17)	2.49 (0.28)	4.04 (0.03)	176.44 (8.42)	21.5 (0.76)
SA		5.79 (0.15)	2.06 (0.23)	4.15 (0.03)	136.42 (4.34)	18.08 (0.61)
SL		5.77 (0.12)	2.41 (0.17)	3.97 (0.03)	151.52 (4.19)	18.1 (0.38)
TAS		5.79 (0.12)	2.42 (0.16)	4.08 (0.03)	140.17 (4.00)	18.13 (0.49)
WA		5.56 (0.14)	2.64 (0.24)	4.15 (0.03)	127.78 (5.32)	18.63 (0.57)
Post-hoc P<0.05		A, B, A×B	B, A×B	A, B, A×B	B, A×B	A, B, A×B, PW

Significant p values are italicized.

Figure 3.

Call structure variation between populations and between rearing environments in experiment 1. Population mean linear discriminant scores for the first and second linear discriminant functions of call phenotype calculated with population and rearing environment as grouping variables. Populations are colour-coded as per the legend of Figure 1. The round points are for calls measured from wild-collected males, whereas the square points represent common-garden males. The bars represent the standard error around the mean.

Comparing the covariance matrices for the wild collected crickets from all six populations using CPC analysis found the most parsimonious model among the three approaches (step-up, model building and jump-up) was that for 2 common principal components (‘CPC(2)’). This model implies that 2 of the 5 eigenvectors of each matrix are closely aligned among all six matrices (Phillips & Arnold, 1999). When we performed a similar comparison of matrices from the common-garden reared crickets, we found that the best fitting model was for 3 common principal components (’CPC(3)’). We also performed pairwise tests between rearing environments within each population, and again found the proportional model to be most parsimonious in the majority of cases. The only exception to this was the comparison of calls from field and lab-reared crickets from the ACT population, where the most parsimonious model was found to be that of ‘common principal components’; the next model down Flury’s hierarchy, also indicating differences confined to eigenvalues, but in this case the eigenvalues do not differ proportionately. These comparisons suggest that while these matrices have a conserved structure, they differ in the overall magnitude of variation they contain (Figure 4). The comparative reduction in the amount of variation contained in P after common-garden rearing suggests an important role for environmental variance in P for wild-caught crickets.

We also compared P from Experiment 1 using Krzanowski’s geometric subspace comparison method (Krzanowski, 1979). This approach can only compare 2 matrices at a time and therefore all comparisons are pairwise (Table 2). Population comparisons of P in the wild collected males found all sums of Sλ values to ≥0.56 (where the maximum possible value of 2 would indicate identical subspaces). Closest eigenvector angles were all ≤ 44.4º, indicating strong similarity of matrices. The results of P comparisons among populations in the lab reared males were somewhat more similar, with the sum of Sλ values all being ≥ 0.89 and the closest eigenvector angles all being ≤18.8º. We found that P matrices compared between field and lab-reared males within populations were of an intermediate level of similarity; with the sum of Sλ values all being ≥0.80 and the closest eigenvector angles all being ≤ 27.9º. The consistency of these results and those of the common principal analyses indicate that, although not identical, P is very similar in structure across populations and generations

Table 2.

The results of geometric matrix comparisons among P matrices from the experiment 1.

	ACT	KL	SA	SL	TA	WA
ACT	0.92	0.74	1.06	1.66	1.31	0.72	Common-Garden Males
	0.41 – 1.36	0.29 – 1.29	0.55 – 1.85	0.90 – 1.91	0.62 – 1.74	0.18 – 1.34
KL	1.00	0.78	1.02	0.57	1.16	1.22
	0.69 – 1.59	0.20 – 1.33	0.34 – 1.63	0.13 – 1.14	0.42 – 1.65	0.27 – 1.68
SA	1.24	1.01	1.62	0.97	1.05	0.99
	0.60 – 1.71	0.66 – 1.76	0.62 – 1.90	0.46 – 1.91	0.37 – 1.77	0.12 – 1.40
SL	1.47	1.15	0.98	0.87	1.55	0.99
	0.87 – 1.81	0.76 – 1.61	0.67 – 1.63	0.35 – 1.36	0.67 – 1.83	0.22 – 1.55
TA	0.79	0.63	1.16	0.65	0.69	1.53
	0.26 – 1.56	0.14 – 1.30	0.40 – 1.80	0.21 – 1.51	0.26 – 1.38	0.48 – 1.84
WA	0.65	0.93	0.55	1.01	1.26	0.91
	0.26 – 1.30	0.61 – 1.49	0.19 – 1.29	0.31 – 1.54	0.29 – 1.60	0.02 – 1.42
ACT	16.95	34.96	8.88	12.83	13.38	36.54
	1.70 – 46.6	3.94 – 56.9	0.89 – 43.5	0.96 – 27.7	1.21 – 39.2	4.85 – 60.2
KL	3.63	29.57	12.02	49.20	19.32	6.46
	0.37 – 29.5	2.06 – 57.8	1.01 – 50.7	14.3 – 69.5	1.48 – 48.5	2.17 – 55.5
SA	14.71	7.15	11.88	11.69	3.59	6.82
	0.91 – 39.4	0.29 – 34.1	0.93 – 42.0	0.69 – 48.1	0.60 – 50.7	2.14 – 63.0
SL	8.78	6.13	8.83	24.76	11.41	39.98
	0.96 – 28.9	0.73 – 30.7	0.34 – 36.0	3.94 – 49.8	1.62 – 40.7	3.19 – 59.5
TA	30.71	40.51	11.58	40.87	35.54	8.20
	2.66 – 55.6	2.45 – 58.6	1.13 – 49.8	3.62 – 58.1	4.35 – 57.0	1.23 – 47.6
WA	40.34	22.30	47.81	22.86	18.88	27.94
	4.21 – 55.7	4.49 – 39.2	8.02 – 61.0	2.36 – 50.9	3.31 – 52.4	4.15 – 67.2
	Wild-Caught Males

The upper matrix contains the sum of S matrix eigenvalues (a value between 0 & 2 in this case – 2 indicating that matrices span an identical subspace, with their 95% confidence interval below them. The lower italicized matrix contains the closest angles between principal vectors describing the shared subspace between matrices (in degrees), with 95% confidence intervals. Within each matrix, cells on the diagonal (bold) are within-population comparisons between wild-caught and common-garden calls. Cells below the diagonal are between-population comparisons of wild-caught calls – between-population comparisons of common-garden are calls above the diagonal. Population abbreviations are as for Figure 1.

Matrix comparison by random skewers is also a pairwise procedure. The random skewers vector correlations among populations in the field cohort were all ≥ 0.57 (mean ± SE = 0.81 ± 0.06), and 9 of the 15 comparisons were found to be significantly different from identical in randomization tests (Table 3). Among populations in the common-garden cohort random skewers vector correlations were all ≥ 0.44 (mean ± SE = 0.73 ± 0.06), with 9 of 15 comparisons again being different from identical (Table 3). Within populations between rearing environments, random skewer vector correlations were all ≥0.83 (mean ± SE = 0.92 ± 0.03), but P for the KL and WA populations were significantly different from identical between cohorts.

Table 3.

Random skewers correlations between and within populations in experiment 1.

	ACT	KL	SA	SL	TA	WA
ACT	0.96	0.54	0.97	0.88	0.91	0.70	Common-Garden Males
	0.25	0.00	0.35	0.05	0.06	0.00
KL	0.77	0.89	0.58	0.69	0.47	0.63
	0.01	0.04	0.00	0.00	0.00	0.00
SA	0.94	0.74	0.96	0.90	0.94	0.70
	0.19	0.00	0.28	0.10	0.17	0.00
SL	0.82	0.96	0.71	0.90	0.71	0.92
	0.01	0.38	0.00	0.12	0.00	0.26
TA	0.93	0.76	0.98	0.72	0.98	0.44
	0.13	0.00	0.64	0.00	0.51	0.00
WA	0.66	0.94	0.57	0.94	0.64	0.83
	0.00	0.23	0.00	0.22	0.00	0.03
	Wild-Caught Males

Correlations between populations in the wild-caught cohort are below the diagonal, and between the common-garden cohort are above the diagonal. Correlations along the diagonal are within population and between cohorts. Below each correlation is its associated p-value in italics, where a significant value indicates difference from equality.

Finally, we tested for differences between matrices using the Bayesian approach of Ovaskainen et al. (2008). The resulting ‘d’ divergence statistics were small for all comparisons. The mean ‘d’ value among within-population tests between rearing treatments was 0.08 (SD = 0.01), with a similar mean value (mean = 0.05, SD = 0.01) for between-population comparisons among wild-caught males. The mean ‘d’ value for between-population comparisons among common-garden reared males was slightly higher, at 0.16 (SD = 0.03). However, the ψ_d statistics for all comparisons were high (all > 0.95) which implies a lack of statistical support for these matrices being different. A table of results for individual tests is available in Online Supplement 1.

Experiment 2. The plasticity of P under dietary manipulation

We used anova’s to test for the influence of diet treatment on the development time and size of crickets from all six populations. Males reared on the low-nutrient diet took 2.6 (±1.2) days longer to reach eclosion than those on the high-nutrient diet (F_1,719 = 21.97, P = 0.0001). Development time varied significantly among populations (F_5,719 = 61.17, P = 0.0001), but there was no significant interaction effect of population × diet. In addition to developing more slowly, males reared on the low-nutrient diet also weighed 0.03g (± 0.01) more and were 0.22mm (± 0.01) wider in the pronotum (weight: F_1,719 = 49.87, P = 0.0001; PW: F_1,719 =43.52, P = 0.0001). Weight and pronotum width also varied significantly among populations (weight: F_5,719 = 30.03, P = 0.001; PW: F_5,719 = 32.56, P = 0.0001). However, unlike development time, weight and pronotum width did show a significant interaction between population and diet (weight: F_5,719 = 5.08, P = 0.0001; PW: F_5,719 = 3.36, P = 0.005). Given that these effects were measured in common-garden conditions, this suggests genotype × environment interactions for these phenotypic traits.

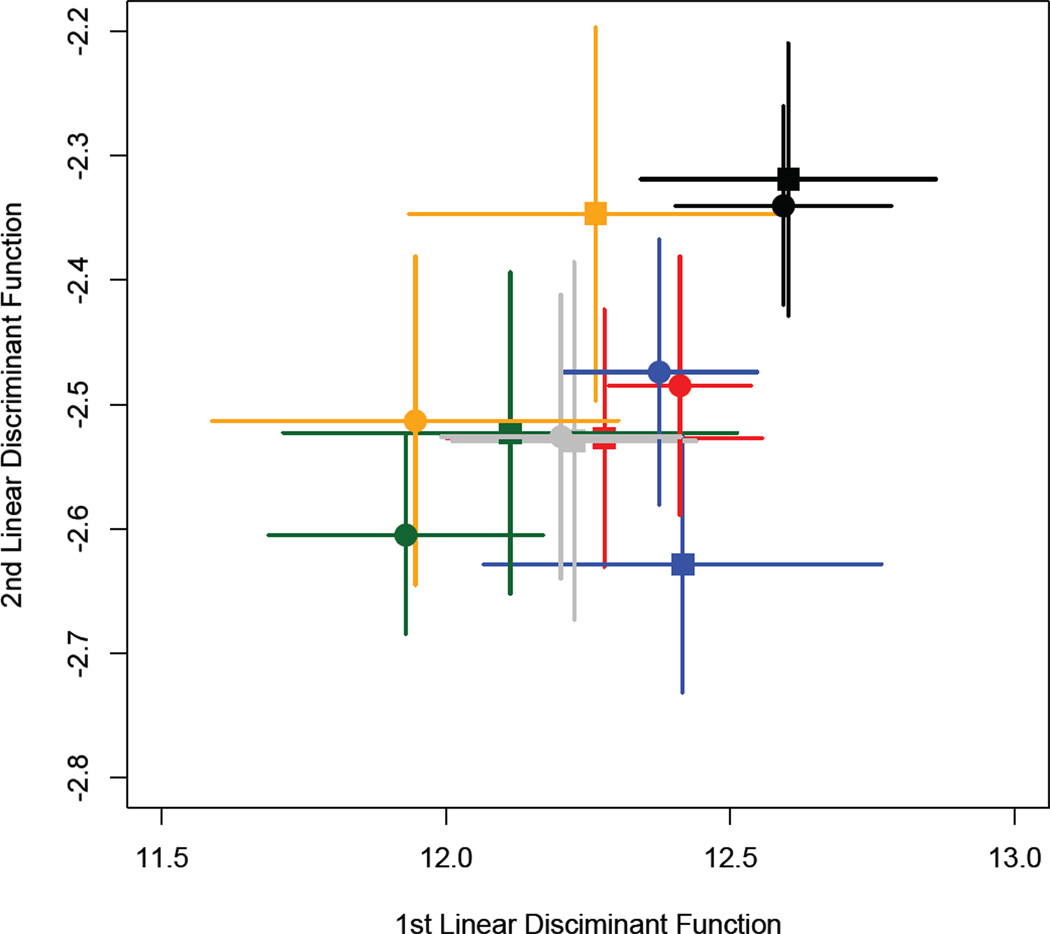
We tested the effects of population, diet and their interaction on male call structure using the same model as specified for Experiment 1. However, due to the distribution of the call data we obtained P values using a permutation test rather than from the parametric mancova (Table 4). As in Experiment 1, we found that the call traits showed significant differences among populations. These among-population differences (Figure 6) appear to be similar to the pattern found in the common-garden reared cohort from experiment 1 (dashed ellipses in Figure 4), with the distributions being of similar size and shape among populations. There is no evidence for a diet effect on call traits. Though the between-diet differences in population means appear to be in different directions (Figure 5), the population × diet effect is also non-significant. As in Experiment 1, pronotum width was also a significant predictor of call traits. Post-hoc ANOVAs, with P values again assigned by permutation, showed that the among-population differences were driven by significant differences in ICD, CIPD and DF (10,000 permutations; ICD P = 0.001; CIPD P = 0.002; DF P = 0.048) and the effect of pronotum width was driven by CPN, CIPD and DF (10,000 permutations; CPN P = 0.003; CIPD P = 0.008; DF P = 0.001).

Table 4.

Statistics from the randomisation tests on the data from the experiment 2.

Effect		# permutations		# permutations Pp ≤ P		p value
Population (A)		10,000		0		<0.0001
Diet (B)		10,000		4952		0.50
A × B		10,000		1696		0.17
Size (PW)		10,000		276		0.03
		Trait Means (±SE) by Population
High-Nutrient Diet		CPN	TN	DF	ICD	CIPD
ACT		5.64 (0.38)	3.5 (0.25)	4.81 (0.30)	188.11 (19.36)	17.37 (1.22)
KL		6.19 (0.50)	3.48 (0.32)	5.25 (0.35)	202.05 (25.84)	20.70 (1.40)
SA		6.00 (0.39)	3.73 (0.32)	4.49 (0.22)	163.37 (15.17)	17.32 (1.21)
SL		5.22 (0.28)	3.27 (0.18)	4.36 (0.18)	174.35 (15.25)	18.40 (1.87)
TAS		6.27 (0.30)	3.27 (0.22)	4.19 (0.17)	198.31 (28.04)	18.57 (1.50)
WA		5.69 (0.23)	3.19 (0.22)	4.10 (0.11)	209.88 (23.38)	20.26 (0.87)
Low-Nutrient Diet		CPN	TN	DF	ICD	CIPD
ACT		5.7 (0.35)	3.94 (0.29)	4.74 (0.27)	172.87 (12.3)	19.74 (1.43)
KL		5.26 (0.27)	3.31 (0.28)	4.32 (0.19)	159.41 (11.5)	16.95 (0.89)
SA		5.8 (0.33)	3.27 (0.19)	4.52 (0.25)	184.79 (10.4)	20.57 (2.04)
SL		5.48 (0.19)	3.63 (0.24)	4.42 (0.18)	146.94 (5.92)	16.59 (0.96)
TAS		5.72 (0.34)	3.43 (0.20)	4.31 (0.21)	214.72 (25.5)	18.31 (1.34)
WA		5.90 (0.31)	3.67 (0.30)	4.41 (0.22)	220.96 (17.3)	22.30 (1.33)
Post-hoc P<0.05		PW	-	A, PW	A	A, PW

Significant P values are italicized.

Figure 5.

Variation in call structure among populations and between diet treatments in experiment 2. Population mean linear discriminant scores for the first and second linear discriminant functions were calculated for call structure using population and rearing environment as grouping variables. Populations are colour-coded and abbreviated according to the legend of Figure 1. The round points represent calls measured from males reared on the high-nutrient diet, whereas the square points represent males reared on the low-nutrient diet, and the bars represent the standard error around the mean.

Our CPC analysis of P from Experiment 2 found that for males reared on both diets, the most parsimonious model comparing P among populations was the proportional model. This result is in agreement with the finding from Experiment 1 that these P matrices differ in their eigenvalues, but not in the direction of their eigenvectors. When we compared P within populations across our diet treatments, the most parsimonious model was that of proportional matrices for all populations, with the exception of the KL population whose best model was for the common principal components. These results indicate that the structure of P for call structure was largely unaffected by the difference between the diet treatments, with only the KL population showing evidence of change but this was for eigenvalues only and the eigenvectors remained the same across diets.

Results from matrix comparison by Krzanowski’s geometric method (Table 5) were similar to those for Experiment 1. Among-population comparisons between males reared on the high-nutrient diet revealed differences of a similar scale to those found in the common-garden cohort in Experiment 1: sums of Sλ values were ≥ 0.99 (identical matrices would return a value of 2), and the angles between most closely aligned vectors were ≤ 13.8º. The among-population differences between P matrices were of similar magnitude when reared on the low-nutrient diet, with sum of Sλ values ≥ 1.14, and all maximum angles between closest vectors ≤ 17.1º. The between-diet differences within populations were somewhat smaller than the inter-population differences within either diet treatment, with sum of Sλ values ≥ 1.26 and angles between most closely aligned vectors ≤ 7.79º.

Table 5.

The results of geometric matrix comparisons among P matrices from experiment 2.

	ACT	KL	SA	SL	TA	WA
ACT	1.63	1.53	1.52	1.26	0.99	1.87	Low-Nutrient Diet
	1.28 – 1.91	1.04 – 1.98	0.36 – 1.90	0.99 – 1.82	0.31 – 1.94	0.99 – 1.99
KL	1.73	1.03	1.01	1.70	1.23	1.20
	0.84 – 1.99	0.75 – 1.98	0.35 – 1.96	0.98 – 1.96	0.32 – 1.94	0.74 – 1.99
SA	1.80	1.60	1.63	1.02	1.43	1.68
	1.05 – 1.99	0.80 – 1.99	0.51 – 1.99	0.27 – 1.85	0.49 – 1.88	0.38 – 1.98
SL	1.03	1.00	1.05	1.16	1.02	1.04
	0.95 – 1.37	0.78 – 1.43	0.93 – 1.77	0.96 – 1.93	0.30 – 1.79	0.61 – 1.97
TA	1.32	1.26	1.03	1.71	1.94	1.04
	0.94 – 1.96	0.52 – 1.84	0.73 – 1.96	0.60 – 1.97	0.59 – 1.96	0.38 – 1.95
WA	1.08	1.04	1.45	1.74	1.29	1.24
	0.97 – 1.72	0.73 – 1.59	0.97 – 1.90	0.99 – 1.96	0.56 – 1.98	0.70 – 1.80
ACT	0.72	3.62	1.41	3.68	6.61	4.73
	0.13 – 4.83	0.15 – 10.2	0.04 – 53.1	0.13 – 8.06	0.15 – 58.8	0.01 – 16.9
KL	1.92	5.21	3.62	1.58	3.24	7.76
	0.12 – 30.6	0.10 – 32.0	0.02 – 55.2	0.10 – 9.58	0.07 – 58.1	0.08 – 36.7
SA	3.29	4.21	3.19	3.54	7.55	1.20
	0.06 – 7.73	0.02 – 31.1	0.02 – 47.2	0.12 – 54.7	0.14 – 45.1	0.06 – 53.8
SL	4.14	4.59	6.79	0.40	4.07	7.50
	0.23 – 11.2	0.17 – 25.3	0.40 – 13.5	0.01 – 11.6	0.03 – 52.6	0.08 – 41.2
TA	5.45	5.19	1.47	1.66	3.66	6.85
	0.23 – 22.4	0.15 – 43.2	0.04 – 36.0	0.08 – 42.5	0.20 – 41.9	0.12 – 54.6
WA	1.51	3.15	3.77	1.23	5.94	5.44
	0.09 – 6.93	0.07 – 27.8	0.10 – 11.6	0.05 – 8.64	0.09 – 46.3	0.15 – 34.0
	High-Nutrient Diet

The upper matrix contains the sum of S matrix eigenvalues (a value between 0 & 2 in this case – 2 indicating that matrices span an identical subspace, with their 95% confidence interval below them. The lower italicized matrix contains the closest angles between principal vectors describing the shared subspace between matrices (in degrees), with 95% confidence intervals. Within each matrix, cells on the diagonal (bold) are within-population comparisons between males reared on the high-nutrient diet and those reared on the low-nutrient diet. Cells below the diagonal are between-population comparisons of calls from the high-nutrient diet treatment – between-population comparisons of calls from the low-nutrient treatment are above the diagonal. Population abbreviations are as for Figure 1.

We compared matrices in a pairwise fashion by the application of random skewers. The random skewers vector correlations among populations in the cohort reared on the high-nutrient diet were all ≥ 0.83 (mean ± SE = 0.93 ± 0.06), and only 4 of 15 comparisons tested as significantly different from identical (Table 6). Among populations in the cohort reared on the low-nutrient diet random skewer vector correlations were all ≥ 0.78 (mean ± SE = 0.92 ± 0.06), and 5 of 15 comparisons were significantly different from identical (Table 6). Within populations between diet treatments, random skewer vector correlations were all ≥ 0.85 (mean ± SE = 0.95 ± 0.03), and only populations KL and SA tested as different from identical between treatments.

Table 6.

Random skewers correlations between and within populations in experiment 2.

	ACT	KL	SA	SL	TA	WA
ACT	0.97	0.90	0.86	0.99	0.99	0.90	Low-Nutrient Diet
	0.33	0.05	0.01	0.63	0.86	0.05
KL	0.91	0.85	0.94	0.93	0.93	0.93
	0.02	0.00	0.12	0.11	0.11	0.12
SA	0.99	0.87	0.90	0.86	0.90	0.78
	0.71	0.01	0.04	0.01	0.04	0.00
SL	0.97	0.97	0.94	0.99	0.99	0.96
	0.31	0.27	0.11	0.74	0.74	0.25
TA	1.00	0.92	0.98	0.96	0.99	0.92
	0.89	0.05	0.49	0.27	0.73	0.10
WA	0.91	0.83	0.95	0.89	0.88	0.97
	0.06	0.00	0.24	0.03	0.05	0.44
	High-Nutrient Diet

Correlations between populations reared on the high-nutrient diet are below the diagonal, and between those on the low-nutrient diet are above the diagonal. Correlations along the diagonal are within population and between diets. Below each correlation is its associated P value in italics, where a significant value indicates difference from equality.

Lastly, we tested for differences between P matrices using the Bayesian ‘d’ method (see supplementary material for full details). Divergence (‘d’) values were somewhat higher than for Experiment 1. The mean ‘d’ value for within-population comparisons between diet treatments was 1.22 (SD= 0.21), with a mean of 1.32 (SD= 0.25) for between population tests on the high-nutrient diet and 0.86 (SD= 0.15) for between population tests on the low-nutrient diet. However, as with Experiment 1 these differences lacked statistical support, with ψ_d statistics for all tests being > 0.98.

We also applied the same suite of matrix comparisons to P matrices estimated for the three life-history traits we measured in Experiment 2. These analyses provided little evidence to suggest that the life-history P matrices differed among populations or between diet treatments (see Online Supplement 2).

Discussion

Quantifying the scale of variation in the phenotypic variance-covariance matrix (P) is vital to our understanding of the evolution of complex traits (Roff et al., 2000). Over short timescales, G is predicted to influence the direction of response to selection (Lande, 1979; Schluter, 1996), but over longer timescales selection is expected to influence the structure of G (Steppan et al., 2002). Since P comprises G, this is also true of P, but with the added complication that we must also consider changes due to the environment (E). Comparisons of P have sometimes found substantial changes between divergent populations (Badyaev & Hill, 2000), although more frequently P has been found to be stable at this level of comparison (Arnold & Phillips, 1999; Game & Caley, 2006; de Oliveira et al., 2009). Notably, we are not aware of any previous comparisons of P for a sexual signal. In this study, we compared P for the advertisement call of six allopatric populations of the field cricket T. commodus, as well as estimating P from the recorded calls of both wild-caught and common-garden-reared males in each population to assess population divergence in P. We then re-measured advertisement calls from an independent collection of these populations after rearing them on high- and low-nutrient diets in order to assess the plasticity of P. We found that call structure varied among populations, with evidence for only small changes in P that were of a similar degree in wild-caught and common-garden-reared males. While our manipulation of diet was sufficient to measurably affect the life-history of crickets (i.e. development time and body size), it did not result in a plastic response in the mean structure of advertisement calls nor did it alter the structure of P. Together, the results of our two experiments suggest that although minor differences in the structure of P were detected on various scales (i.e. populations, generations or diets), the overarching pattern was that P remained relatively stable in each of these comparisons. P matrix stability has potential consequences for the evolution of advertisement call, depending on the nature of selection. If the structure of P is stable, then it has the potential to influence the rate of response to selection; allowing a stronger response if P and G are aligned, and slowing the response if P and G are poorly aligned.

We identified differences in the five call traits across populations and between generations, and these differences remained after common-garden rearing, indicating that the divergence in call structure observed across of our six populations has a genetic basis. This pattern is not altogether surprising as geographic variation in the call structure of Gryllids has been demonstrated before (Ferreira & Ferguson, 2002; Jang & Gerhardt, 2006), including in the genus Teleogryllus (Simmons et al., 2001), and these structural components of T. commodus call are known to have a strong genetic basis (Hunt et al., 2007). The effect of generation (wild-caught vs. common-garden reared) indicates a plastic developmental response in addition to the inferred genetic differences. The calls of the six populations were less variable and more similar to each other after rearing in common-garden, but as the interaction between generation and population demonstrates, the six populations responded differently to the common-garden conditions of the laboratory. Though not conclusive, this pattern suggests a genotype × environment interaction for advertisement call traits in T. commodus (Olvido & Mousseau, 1995; Tolle & Wagner, 2011). Male body size was also a significant predictor of calling traits, but differing body size between rearing environments or among populations does not appear to be driving all the differences in call traits, since we find that body size is predictive only of CIPD (Table 1). This finding does not fit the general hypothesis that dominant call frequency signals body size in Orthopterans (e.g. (Bennet-Clark, 1999). Thus, to summarise we find convincing evidence that the call traits we measured differ among populations, and are responsive to common garden rearing environment in the laboratory.

As all the call traits were affected by the interaction of population and generation, it is perhaps not surprising that we detect differences among P matrices for advertisement call structure. However the evidence suggests that these differences are small and therefore unlikely to lead to biologically significant differences in the evolution of call structure under a given regime of selection. Among the wild-caught cohort, the general outcome from CPC analysis was for 2 common principal components, which fits well with the results from the Krzanowski test where the mean closest eigenvector angle was 25.2º, indicating that the subspaces are closer to alignment than to being orthogonal. These results indicate a comparable level of among-population divergence to that found between populations of house finches by (Badyaev & Hill, 2000), with partial common principal components and statistical support for some differences (Tables 3 and 5). Somewhat smaller differences have been reported from other inter-population matrix comparison, for example in garter snake morphology (Arnold & Phillips, 1999) and in the body shape of six species of reef fish (Game & Caley, 2006) where all principal components were found to be common. However, despite this evidence of differences among populations, the mean random skewers correlation was high (0.81) and there was statistical support for matrices being different in only 60% of pairwise comparisons. Among the common-garden reared cohort, there is some evidence that P matrices were slightly more similar, with the consensus CPC verdict being a step higher on Flury’s hierarchy (i.e.CPC(3)), Kzanowski tests giving a lower mean closest eigenvector angle (10.2º) and a slightly lower mean correlation of random skewers (0.73), but with only 60% of pairwise comparison showing statistical support for divergence on P. The within population differences in P across generations were of a similar magnitude to the between population differences, with a consensus verdict of 3 common PCs, a mean closest eigenvector angle of 22.5º and a high mean random skewers correlation (0.92). This indicates that the P matrices for advertisement calls have a very similar structure in both the wild and the laboratory. Together, these results show small but detectable differences among populations in P matrices and illustrate the value of using multiple tests to assess matrix similarity (Roff et al., 2012).

When we re-collected from these same populations three years later (Experiment 2), we once again detected the significant inter-population differences in advertisement call. However, the differences were confined to DF, TN and CIPD, as opposed to Experiment 1 where we found evidence for inter-population differences in all five call traits. Notably, in addition to its association with CIPD in Experiment 1, body size is a significant predictor of both CPN and DF. The relationship between size and call traits appears to have changed and this suggests that the link between call frequency and body size (Simmons, 1995; Brown et al., 1996; Simmons & Ritchie, 1996; Scheuber, Jacot, & Brinkhof, 2003a; b) may be mediated, in part, by some other additional factors. We know from Experiment 1 that the call traits we measured are responsive to the number of generations of laboratory common-garden rearing, and a number of other studies have found call trait plasticity in response to diet (e.g. Wagner & Hoback, 1999; Scheuber, Jacot, & Brinkhof, 2003b; Hedrick, 2005). Our manipulation of diet had effects on body size and development time, in line with what has been observed in other field crickets (Scheuber, Jacot, & Brinkhof, 2003a; b), but we found no evidence of differences in P for these life-history traits, nor any associated changes in call structure. This is not unprecedented, since diet manipulations have previously been shown to result in body size effects without affecting advertisement calls in bushcrickets (Hartbauer et al., 2006), and dietary effects on call structure without differences in body size have been found in a field cricket (Wagner & Hoback, 1999). Therefore, it seems that the relative magnitudes of change in diet required to affect calling behaviour and body size may be somewhat species-specific.

Overall, the results of Experiment 2 found that P matrices for advertisement call structure were relatively more stable than those estimated from Experiment 1. At all three levels of comparison: among-populations within the low and high-nutrient diets and within-populations between diets, the consensus verdict from our CPC analysis was that all principal components were common. The mean random skewers correlations were also very high, although some of the pairwise comparisons on both diets were significantly different from identical and the Krzanowski test also indicated a greater degree of similarity for comparisons than in Experiment 2. Taken together these results strongly suggest that P for the structure of the advertisement call, like the individual trait means, were robust in response to the diet manipulation. This was in strong contrast to the plasticity in development time and body size shown in this experiment.

Plasticity in the face of a heterogeneous environment is an extremely common adaptation in a variety of species (West-Eberhard, 2003; DeWitt & Scheiner, 2004), and the advertisement calls of numerous cricket species are known to exhibit this kind of plasticity (Elliott & Koch, 1985; Wagner & Hoback, 1999; Scheuber, Jacot, & Brinkhof, 2003b; Hunt et al., 2004; Grace & Shaw, 2004; Hedrick, 2005; Jacot et al., 2005; Judge et al., 2008; Zajitschek et al., 2009). If sexual signals are too readily plastic, however, their reliability as signals is predicted to break down (Greenfield & Rodriguez, 2004; Ingleby et al., 2010). When considering complex traits that function as sexual signals, this leads to somewhat paradoxical predictions (Badyaev, 2004): they should be integrated with the rest of the phenotype in order that any variability may function as an honest indicator of physiological quality, yet response to sexual selection is also expected to uncouple sexual signals from the rest of the phenotype to enable them to become plastic in their expression and evolve independently from the rest of the phenotype (Emlen & Nijhout, 2000). Natural selection can be expected to favour integration as it contributes to the development of robust and functionally resilient body-plans (Pigliucci, 2003), but this does not mean that the processes of plasticity and integration need be thought of as mutually exclusive (Phillips & McGuigan, 2006).

The plasticity we measured in T. commodus advertisement calls between field conditions and common-garden rearing involved both shifts in the position of the population means and changes in some of the eigenvectors of P (Figures 3 and 4). The eigenvector angles show small to intermediate changes between wild and common-garden matrices (confidence intervals in Table 2), but the strong random skewers correlations (Table 3) suggest that these effects are relatively unimportant. The plastic response was similar in magnitude to the differences found among populations. In comparison, in most other cases where the stability of integration has been assessed by comparing covariance matrices between populations they have often found intermediate levels of difference (Cowley & Atchley, 1990; Shaw & Billington, 1991; Platenkamp & Shaw, 1992; Brodie, 1993; Fenster, 1994; Jernigan et al., 1994) or more recently, detected conserved eigenstructure (Roff et al., 2004; Game & Caley, 2006). In general, we might predict that inter-population differences would be predominantly described by changes in means and variances, with changes in covariances being less important.

A number of researchers studying multivariate evolution have recently used the concept of modularity (Wagner & Altenberg, 1996; Hansen et al., 2003; Mezey & Houle, 2003; Badyaev, 2004; Kraft et al., 2006; Bossdorf & Pigliucci, 2009; de Oliveira et al., 2009). A phenotypic module is a suite of traits that display enhanced integration with each other and reduced integration with the rest of the organism (Wagner & Altenberg, 1996). In light of the limited plasticity we observe in P and the apparent insensitivity of call traits to the plasticity of the animals’ life-history, it seems reasonable to suggest that the structure of the advertisement call in T. commodus meets this criterion. Badyaev (2004) specifically addressed the issue of modularity and integration in sexual signals and made three predictions: that sexual traits should exhibit (1) weakened developmental integration with other traits, (2) strengthened functional integration and modularity, and (3) weaker genetic integration with the rest of the organism. We found evidence supporting prediction (1). Although pronotum width was a significant predictor of call traits in both experiments (Table 1 and 4), the correlations between call traits and pronotum width were consistently low (Experiment 1, r = 0.20; Experiment 2, r = 0.17). This contrasts the tight correlations observed between body size and body weight (Experiment 1, r = 0.79; Experiment 2, r = 0.87) and between body size and development time (Experiment 1, r = 0.49; Experiment 2, r = 0.54). Our finding of limited plasticity in the structure of P for call traits also provides support for prediction (2). Although the structure of P varied across populations and time in Experiment 1, the magnitude of these differences was small. This pattern was even more pronounced in Experiment 2 where body size, weight and development time showed a plastic response to diet, but neither mean call structure nor the structure of P for call traits differed across diets. This finding suggests that call structure is unlikely to signal a male’s underlying condition (i.e. condition-dependence) but instead represents a tightly integrated functional module. Taken collectively, this suggests that call structure is tightly integrated in T. commodus and largely independent of other elements of the phenotype which should, in theory, allow call structure to evolve independently of traits that are not subject to sexual selection (Badyaev, 2004). Unfortunately, as our work consists of phenotypic measurements only, we are unable to directly test prediction (3), although our current work is addressing this question.

Sexual selection imposed by female mate choice on the structure of advertisement call has been measured in our study populations and there are significant differences in linear, quadratic and correlational selection gradients across populations (Hunt et al. unpublished data). Given these differences in sexual selection it is therefore not surprising that populations also differ in the call traits that are the target of female choice. However, we found little evidence to suggest that the differences between populations in the structure of P was any greater in magnitude that the response of P to common garden rearing in the laboratory. This is surprising as a regime of both quadratic and correlational selection is likely to influence the evolution of phenotypic integration and thus the structure of P (Cheverud, 1984). Although not conclusive, this finding is further evidence of the constraining influence that the integration of P has on phenotypic evolution, enabling some divergence and plasticity in call traits but ultimately conserving the underlying structure of P.