MULTIVARIATE VARYING COEFFICIENT MODEL FOR FUNCTIONAL RESPONSES

Abstract

Motivated by recent work studying massive imaging data in the neuroimaging literature, we propose multivariate varying coefficient models (MVCM) for modeling the relation between multiple functional responses and a set of covariates. We develop several statistical inference procedures for MVCM and systematically study their theoretical properties. We first establish the weak convergence of the local linear estimate of coefficient functions, as well as its asymptotic bias and variance, and then we derive asymptotic bias and mean integrated squared error of smoothed individual functions and their uniform convergence rate. We establish the uniform convergence rate of the estimated covariance function of the individual functions and its associated eigenvalue and eigenfunctions. We propose a global test for linear hypotheses of varying coefficient functions, and derive its asymptotic distribution under the null hypothesis. We also propose a simultaneous confidence band for each individual effect curve. We conduct Monte Carlo simulation to examine the finite-sample performance of the proposed procedures. We apply MVCM to investigate the development of white matter diffusivities along the genu tract of the corpus callosum in a clinical study of neurodevelopment.

1. Introduction

With modern imaging techniques, massive imaging data can be observed over both time and space [41, 17, 37, 4, 19, 25]. Such imaging techniques include functional magnetic resonance imaging (fMRI), electroencephalography (EEG), diffusion tensor imaging (DTI), positron emission tomography (PET), and single photon emission-computed tomography (SPECT) among many other imaging techniques. See, for example, a recent review of multiple biomedical imaging techniques and their applications in cancer detection and prevention in Fass [17]. Among them, predominant functional imaging techniques including fMRI and EEG have been widely used in behavioral and cognitive neuroscience to understand functional segregation and integration of different brain regions in a single subject and across different populations [19, 18, 29]. In DTI, multiple diffusion properties are measured along common major white matter fiber tracts across multiple subjects to characterize the structure and orientation of white matter structure in human brain in vivo [2, 3, 54].

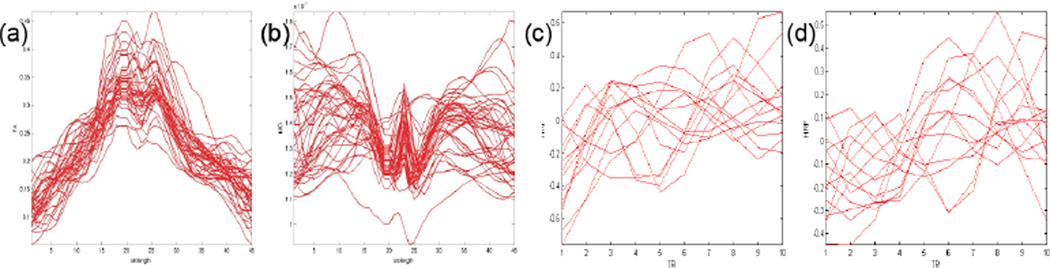
A common feature of many imaging techniques is that massive functional data are observed/calculated at the same design points, such as time for functional images (e.g., PET and fMRI). As an illustration, we present two smoothed functional data as an illustration and a real imaging data in Section 6, that we encounter in neuroimaging studies. First, we plot two diffusion properties, called fractional anisotropy (FA) and mean diffusivity (MD), measured at 45 grid points along the genu tract of the corpus callosum (Figs. 1 (a) and (b)) from 40 randomly selected infants from a clinical study of neurodevelopment with more than 500 infants. Scientists are particularly interested in delineating the structure of the variability of these functional FA and MD data and their association with a set of covariates of interest, such as age. We will systematically investigate the development of FA and MD along the genu of the corpus callosum tract in Section 6. Secondly, we consider the BOLD fMRI signal, which is based on hemodynamic responses secondary to neural activity. We plot the estimated hemodynamic response functions (HRF) corresponding to two stimulus categories from 14 randomly selected subjects at a selected voxel of a common template space from a clinical study of Alzheimer’s disease with more than 100 infants. Although the canonical form of the HRF is often used, when applying fMRI in a clinical population with possibly altered hemodynamic responses (Figs. 1 (c) and (d)), using the subject’s own HRF in fMRI data analysis may be advantageous because HRF variability is greater across subjects than across brain regions within a subject [34, 1]. We are particularly interested in delineating the structure of the variability of the HRF and their association with a set of covariates of interest, such as diagnostic group [33].

Fig 1.

Representative functional neuroimaging data: (a) and (b) FA and MD along the genu tract of the corpus callosum from 40 randomly selected infants; and (c) and (d) the estimated hemodynamic response functions (HRF) corresponding to two stimulus categories from 14 subjects.

A varying-coefficient model, which allows its regression coefficients to vary over some predictors of interest, is a powerful statistical tool for addressing these scientific questions. Since it was systematically introduced to statistical literature by Hastie and Tibshirani [24], many varying-coefficient models have been widely studied and developed for longitudinal, time series, and functional data [13, 48, 12, 15, 44, 26, 38, 28, 27, 51, 23]. However, most varying-coefficient models in the existing literature are developed for univariate response. Let y_i(s) = (y_i1(s), …, y_iJ (s))^T be a J-dimensional functional response vector for subject i, i = 1, …, n, and x_i be its associated p × 1 vector of covariates of interest. Moreover, s varies in a compact subset of Euclidean space and denotes the design point, such as time for functional images and voxel for structural and functional images. For notational simplicity, we assume s ∈ [0, 1], but our results can be easily extended to higher dimensions. A multivariate varying coefficient model (MVCM) is defined as

$$y_{\mathit{\text{ij}}}(s)={\mathbf{x}}_i^T{B}_j(s)+{\eta }_{\mathit{\text{ij}}}(s)+{\epsilon }_{\mathit{\text{ij}}}(s)\text{ for }j=1,\dots ,J,$$ (1.1)

where B_j(s) = (b_j1(s), …, b_jp(s))^T is a p × 1 vector of functions of s, ε_ij(s) are measurement errors, and η_ij(s) characterizes individual curve variations from ${\mathbf{x}}_i^T{B}_j(s)$. Moreover, {η_ij(s) : s ∈ [0, 1]} is assumed to be a stochastic process indexed by s ∈ [0, 1] and used to characterize the within-curve dependence. For image data, it is typical that the J functional responses y_i(s) are measured at the same location for all subjects and exhibit both the within-curve and between-curve dependence structure. Thus, for ease of notation, it is assumed throughout this paper that y_i(s) was measured at the same M location points s₁ = 0 ≤ s₂ ≤ … ≤ s_M = 1 for all i.

Most varying coefficient models in the existing literature coincide model (1.1) with J = 1 and without the within-curve dependence. Statistical inferences for these varying coefficient models have been relatively well studied. Particularly, Hoover et al. [26] and Wu, Chiang and Hoover [47] were among the first to introduce the time-varying coefficient models for analysis of longitudinal data. Recently, Fan and Zhang [15] gave a comprehensive review of various statistical procedures proposed for many varying coefficient models. It is of particular interest in data analysis to construct simultaneous confidence bands (SCB) for any linear combination of B_j instead of point-wise confidence intervals and to develop global test statistics for the general hypothesis testing problem on B_j. For univariate varying coefficient models without the within-curve dependence, Fan and Zhang [14] constructed SCB using the limit theory for the maximum of the normalized deviation of the estimate from its expected value. Faraway [16], Chiou, Muller and Wang [8], and Cardot [5] proposed several varying coefficient models and their associated estimators for univariate functional response, but they did not give functional central limit theorem and simultaneous confidence band for their estimators. It has been technically difficult to carry out statistical inferences including simultaneous confidence band and global test statistic on B_j in the presence of the within-curve dependence.

There have been several recent attempts to solve this problem in various settings. For time series data, which may be viewed as a case with n = 1 and M → ∞, asymptotic SCB for coefficient functions in varying coefficient models can be built by using local kernel regression and a Gaussian approximation result for non-stationary time series [52]. For sparse irregular longitudinal data, Ma, Yang and Carroll [35] constructed asymptotic SCB for the mean function of the functional regression model by using piecewise constant spline estimation and a strong approximation result. For functional data, Degras [9] constructed asymptotic SCB for the mean function of the functional linear model without considering any covariate, while Zhang and Chen [51] adopted the method of “smoothing first, then estimation” and propose a global test statistic for testing B_j, but their results cannot be used for constructing SCB for B_j. Recently, Cardot et al. [7], Cardot and Josserand [6] built asymptotic SCB for Horvitz-Thompson estimators for the mean function, but their models and estimation methods differ significantly from ours.

In this paper, we propose an estimation procedure for the multivariate varying coefficient model (1.1) by using local linear regression techniques, and derive a simultaneous confidence band for the regression coefficient functions. We further develop a test for linear hypotheses of coefficient functions. The major aim of this paper is to investigate the theoretical properties of the proposed estimation procedure and test statistics. The theoretical development is challenging but of great interest for carrying out statistical inferences on B_j. The major contributions of this paper are summarized as follows. We first establish the weak convergence of the local linear estimator of B_j, denoted by B̂_j, by using advanced empirical process methods [42, 31]. We further derive the bias and asymptotic variance of B̂_j. These results provide insight into how the direct estimation procedure for B_j using observations from all subjects outperforms the estimation procedure with the strategy of “smoothing first, then estimation.”. After calculating B̂_j, we reconstruct all individual functions η_ij and establish their uniform convergence rates. We derive uniform convergence rates of the proposed estimate for the covariance matrix of η_ij and its associated eigenvalue and eigenvector functions by using related results in Li and Hsing [32]. Using the weak convergence of the local linear estimator of B_j, we further establish the asymptotic distribution of a global test statistic for linear hypotheses of the regression coefficient functions, and construct an asymptotic SCB for each varying coefficient function.

The rest of this paper is organized as follows. In Section 2, we describe MVCM and its estimation procedure. In Section 3, we propose a global test statistic for linear hypotheses of the regression coefficient functions and construct an asymptotic SCB for each coefficient function. In Section 4, we discuss the theoretical properties of estimation and inference procedures. Two sets of simulation studies are presented in Section 5 with the known ground truth to examine the finite sample performance of the global test statistic and SCB for each individual varying coefficient function. In Section 6, we use MVCM to investigate the development of white matter diffusivities along the genu tract of the corpus callosum in a clinical study of neurodevelopment.

2. Estimation Procedure

Throughout this paper, we assume that ε_i(s) = (ε_i1(s), …, ε_iJ (s))^T and η_i(s) = (η_i1(s), …, η_iJ (s))^T are mutually independent, and η_i(s) and ε_i(s) are independent and identical copies of SP(0, Σ_η) and SP(0, Σ_ε), respectively, where SP(μ, Σ) denotes a stochastic process vector with mean function μ(t) and covariance function Σ(s, t). Moreover, ε_i(s) and ε_i(t) are assumed to be independent for s ≠ t and Σ_ε(s, t) takes the form of S_ε(t)1(s = t), where S_ε(t) = (s_ε,jj′(t)) is a J × J matrix of functions of t and 1(·) is an indicator function. Therefore, the covariance structure of y_i (s), denoted by Σ_y(s, t), is given by

$${\mathrm{\Sigma }}_y(s,t)=\text{Cov}({\mathbf{y}}_i(s),{\mathbf{y}}_i(t))={\mathrm{\Sigma }}_{\eta }(s,t)+S_{\epsilon }(t)\mathbf{1}(s=t).$$ (2.1)

2.1. Estimating varying coefficient functions

We employ local linear regression [11] to estimate the coefficient functions B_j. Specifically, we apply the Taylor expansion for B_j(s_m) at s as follows

$$B_j(s_m)\approx B_j(s)+{Ḃ}_j(s)(s_m-s)=A_j(s){\mathbf{z}}_{h_{1j}}(s_m-s),$$ (2.2)

where z_h (s_m − s) = (1, (s_m − s)/h)^T and A_j(s) = [B_j(s) h_1j Ḃ_j(s)] is a p × 2 matrix, in which Ḃ_j(s) = (ḃ_j1(s), …, ḃ_jp(s))^T is a p × 1 vector and ḃ_jl(s) = db_jl(s)/ds for l = 1, …, p. Let K(s) be a kernel function and K_h(s) = h⁻¹K(s/h) be the rescaled kernel function with a bandwidth h. We estimate A_j(s) by minimizing the following weighted least squares function:

$${\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{m=1}^M}{[y_{\mathit{\text{ij}}}(s_m)-{\mathbf{x}}_i^T{A}_j(s){\mathbf{z}}_{h_{1j}}(s_m-s)]}^2{K}_{h_{1j}}(s_m-s).$$ (2.3)

Let us now introduce some matrix operators. Let a^⊗2 = aa^T for any vector a and C⊗D be the Kronecker product of two matrices C and D. For an M₁ × M₂ matrix C = (c_jl), denote vec(C) = (c₁₁, …, c_1M2, …, c_M11, …, c_M1M2)^T. Let Â_j(s) be the minimizer of (2.3). Then

$$\text{vec}({Â}_j(s))=\mathrm{\Sigma }{(s,h_{1j})}^{-1}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{m=1}^M}{K}_{h_{1j}}(s_m-s)[{\mathbf{x}}_i\otimes {\mathbf{z}}_{h_{1j}}(s_m-s)]y_{\mathit{\text{ij}}}(s_m),$$ (2.4)

where $\mathrm{\Sigma }(s,h_{1j})={\displaystyle {\sum }_{i=1}^n}{\displaystyle {\sum }_{m=1}^M}{K}_{h_{1j}}(s_m-s)[{\mathbf{x}}_i^{\otimes 2}\otimes \mathbf{z}{h}_{1j}(s_m-s){\otimes }^2]$. Thus, we have

$${\mathrm{B̂}}_j(s)={({\mathrm{b̂}}_{j1}(s),\dots ,{\mathrm{b̂}}_{\mathit{\text{jp}}}(s))}^T=[I_p\otimes (1,0)]\text{vec}({Â}_j(s)),$$ (2.5)

where I_p is a p × p identity matrix.

In practice, we may select the bandwidth h_1j by using leave-one-curve-out-cross-validation. Specifically, for each j, we pool the data from all n subjects and select a bandwidth h_1j, denoted by ĥ_1j, by minimizing the cross-validation score given by

$$\text{CV}(h_{1j})={(\mathit{\text{nM}})}^{-1}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{m=1}^M}{[y_{\mathit{\text{ij}}}(s_m)-{\mathbf{x}}_i^T{\mathrm{B̂}}_j{(s_m,h_{1j})}^{(-i)}]}^2,$$ (2.6)

where B̂_j(s, h_1j)⁽⁻ⁱ⁾ is the local linear estimator of B_j(s) with the bandwidth h_1j based on data excluding all the observations from the i-th subject.

2.2. Smoothing individual functions

By assuming certain smoothness conditions on η_ij(s), we also employ the local linear regression technique to estimate all individual functions η_ij(s) [11, 43, 49, 38, 45, 51]. Specifically, we have the Taylor expansion for η_ij(s_m) at s:

$${\eta }_{\mathit{\text{ij}}}(s_m)\approx {\mathbf{d}}_{\mathit{\text{ij}}}{(s)}^T{\mathbf{z}}_{h_{2j}}(s_m-s),$$ (2.7)

where d_ij(s) = (η_ij(s), h_2jη̇_ij(s))^T is a 2 × 1 vector. We develop an algorithm to estimate d_ij(s) as follows. For each i and j, we estimate d_ij(s) by minimizing the weighted least squares function.

$${\displaystyle \sum _{m=1}^M}{[y_{\mathit{\text{ij}}}(s_m)-{\mathbf{x}}_i^T{\mathrm{B̂}}_j(s_m)-{\mathbf{d}}_{\mathit{\text{ij}}}{(s)}^T{\mathbf{z}}_{h_{2j}}(s_m-s)]}^2{K}_{h_{2j}}(s_m-s).$$ (2.8)

Then, η_ij(s) can be estimated by

$${\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)=(1,0){\mathbf{d̂}}_{\mathit{\text{ij}}}(s)={\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{h_{2j}}(s_m-s)[y_{\mathit{\text{ij}}}(s_m)-{\mathbf{x}}_i^T{\mathrm{B̂}}_j(s_m)],$$ (2.9)

where K̃_h2j (s) are the empirical equivalent kernels and d̂_ij(s) is given by

$${\mathbf{d̂}}_{\mathit{\text{ij}}}(s)={[{\displaystyle \sum _{m=1}^M}{K}_{h_{2j}}(s_m-s){\mathbf{z}}_{h_{2j}}{(s_m-s)}^{\otimes 2}]}^{-1}\times {\displaystyle \sum _{m=1}^M}{K}_{h_{2j}}(s_m-s){\mathbf{z}}_{h_{2j}}(s_m-s)[y_{\mathit{\text{ij}}}(s_m)-{\mathbf{x}}_i^T{\mathrm{B̂}}_j(s_m)].$$

Finally, let S_ij be the smoother matrix for the j-th measurement of the i-th subject [11], we can obtain

$${\mathit{\eta ̂}}_{\mathit{\text{ij}}}={({\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s_1),\dots ,{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s_M))}^T=S_{\mathit{\text{ij}}}{R}_{\mathit{\text{ij}}},$$ (2.10)

where $R_{\mathit{\text{ij}}}={(y_{\mathit{\text{ij}}}(s_1)-{\mathbf{x}}_i^T{\mathrm{B̂}}_j(s_1),\dots ,y_{\mathit{\text{ij}}}(s_M)-{\mathbf{x}}_i^T{\mathrm{B̂}}_j(s_M))}^T$.

A simple and efficient way to obtain h_2j is to use generalized cross-validation method. For each j, we pool the data from all n subjects and select the optimal bandwidth h_2j, denoted by ĥ_2j, by minimizing the generalized cross-validation score given by

$$\text{GCV}(h_{2j})={\displaystyle \sum _{i=1}^n}\frac{R_{\mathit{\text{ij}}}^T{(I_M-S_{\mathit{\text{ij}}})}^T(I_M-S_{\mathit{\text{ij}}})R_{\mathit{\text{ij}}}}{{[1-M^{-1}\text{tr}(S_{\mathit{\text{ij}}})]}^2}.$$ (2.11)

Based on ĥ_2j, we can use (2.9) to estimate η_ij(s) for all i and j.

2.3. Functional principal component analysis

We consider a spectral decomposition of Σ_η(s, t) = (Σ_η,jj′(s, t)) and its approximation. According to Mercer’s theorem [36], if Σ_η(s, t) is continuous on [0, 1] × [0, 1], then Σ_η,jj(s, t) admits a spectral decomposition. Specifically, we have

$${\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)={\displaystyle \sum _{l=1}^{\mathrm{\infty }}}{\lambda }_{\mathit{\text{jl}}}{\psi }_{\mathit{\text{jl}}}(s){\psi }_{\mathit{\text{jl}}}(t)$$ (2.12)

for j = 1, …, J, where λ_j1 ≥ λ_j2 ≥ … ≥ 0 are ordered values of the eigenvalues of a linear operator determined by Σ_η,jj with ${\displaystyle {\sum }_{l=1}^{\mathrm{\infty }}}{\lambda }_{\mathit{\text{jl}}}<\mathrm{\infty }$ and the ψ_jl(t)’s are the corresponding orthonormal eigenfunctions (or principal components) [32, 50, 22]. The eigenfunctions form an orthonormal system on the space of square-integrable functions on [0, 1] and η_ij(t) admits the Karhunen-Loeve expansion as ${\eta }_{\mathit{\text{ij}}}(t)={\displaystyle {\sum }_{l=1}^{\mathrm{\infty }}}{\xi }_{\mathit{\text{ijl}}}{\psi }_{\mathit{\text{jl}}}(t),\text{ where }{\xi }_{\mathit{\text{ijl}}}={\displaystyle {\int }_0^1}{\eta }_{\mathit{\text{ij}}}(s){\psi }_{\mathit{\text{jl}}}(s)\mathit{\text{ds}}$ is referred to as the (jl)-th functional principal component scores of the i-th subject. For each fixed (i, j), the ξ_ijls are uncorrelated random variables with E(ξ_ijl) = 0 and $E({\xi }_{\mathit{\text{ijl}}}^2)={\lambda }_{\mathit{\text{jl}}}$. Furthermore, for j ≠ j′, we have

$${\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}\prime }(s,t)={\displaystyle \sum _{l=1}^{\mathrm{\infty }}}{\displaystyle \sum _{l\prime =1}^{\mathrm{\infty }}}E({\xi }_{\mathit{\text{ijl}}}{\xi }_{\mathit{\text{ij}}\prime l\prime }){\psi }_{\mathit{\text{jl}}}(s){\psi }_{j\prime l\prime }(t).$$

After obtaining η̂_i(s) = (η̂_i1(s), …, η̂_iJ (s))^T, we estimate Σ_η(s, t) by using the empirical covariance of the estimated η̂_i(s) as follows:

$${\mathrm{\Sigma ̂}}_{\eta }(s,t)={(n-p)}^{-1}{\displaystyle \sum _{i=1}^n}{\mathit{\eta ̂}}_i(s){\mathit{\eta ̂}}_i{(t)}^T.$$

Following Rice and Silverman [39], we can calculate the spectral decomposition of Σ̂_η,jj(s, t) for each j as follows:

$${\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}(s,t)={\displaystyle \sum _l}{\mathrm{\lambda ̂}}_{\mathit{\text{jl}}}{\mathrm{\psi ̂}}_{\mathit{\text{jl}}}(s){\mathrm{\psi ̂}}_{\mathit{\text{jl}}}(t),$$ (2.13)

where λ̂_j1 ≥ λ̂_j2 ≥ … ≥ 0 are estimated eigenvalues and the ψ̂_jl(t)’s are the corresponding estimated principal components. Furthermore, the (j, l)-th functional principal component scores can be computed using ${\mathrm{\xi ̂}}_{\mathit{\text{ijl}}}={\displaystyle {\sum }_{m=1}^M}{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s_m){\mathrm{\psi ̂}}_{\mathit{\text{jl}}}(s_m)(s_m-s_{m-1})$ for i = 1, …, n. We further show the uniform convergence rate of Σ̂_η(s, t) and its associated eigenvalues and eigenfunctions. This result is useful for constructing the global and local test statistics for testing the covariate effects.

3. Inference Procedure

In this section, we study global tests for linear hypotheses of coefficient functions and SCB for each varying coefficient function. They are essential for statistical inference on the coefficient functions.

3.1. Hypothesis test

Consider the linear hypotheses of B(s) as follows:

$$H_0:\mathbf{C}\text{vec}(\mathbf{B}(s))={\mathbf{b}}_0(s)\text{ for all }s\text{ vs}.H_1:\mathbf{C}\text{vec}(\mathbf{B}(s))\ne {\mathbf{b}}_0(s),$$ (3.1)

where B(s) = [B₁(s),…,B_J (s)], C is a r × Jp matrix with rank r, and b₀(s) is a given r ×1 vector of functions. Define a global test statistic S_n as

$$S_n={\displaystyle {\int }_0^1}\mathbf{d}{(s)}^T{[\mathbf{C}({\mathrm{\Sigma ̂}}_{\eta }(s,s)\otimes {\mathrm{\Omega ̂}}_X^{-1}){\mathbf{C}}^T]}^{-1}\mathbf{d}(s)\mathit{\text{ds}},$$ (3.2)

where ${\mathrm{\Omega ̂}}_X={\displaystyle {\sum }_{i=1}^n}{\mathbf{x}}_i^{\otimes 2}$ and d(s) = Cvec(B̂(s) − bias(B̂(s))) − b₀(s).

To calculate S_n, we need to estimate the bias of B̂_j (s) for all j. Based on (2.5), we have

$$\text{bias}({\mathrm{B̂}}_j(s))=[I_p\otimes (1,0)]\text{vec}(\mathrm{\Sigma }{(s,h_{1j})}^{-1}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{m=1}^M}{K}_{h_{1j}}(s_m-s)\times [{\mathbf{x}}_i\otimes {\mathbf{z}}_{h_{1j}}(s_m-s)]{\mathbf{x}}_i{(s_m)}^T[B_j(s_m)-{Â}_j(s){\mathbf{z}}_{h_{1j}}(s_m-s)]).$$ (3.3)

By using Taylor’s expansion, we have

$$B_j(s_m)-{Â}_j(s){\mathbf{z}}_{h_{1j}}(s_m-s)\approx 2^{-1}{\mathrm{B̈}}_j(s){(s_m-s)}^2+6^{-1}{\mathrm{B⃛}}_j(s){(s_m-s)}^3,$$

where B̈_j(s) = d²B_j(s)/ds² and B⃛_j(s) = d³B_j(s)/ds³. Following the preasymptotic substitution method of Fan and Gijbels [11], we replace B_j(s_m) − Â_j(s)z_h1j (s_m − s) by $2^{-1}{\widehat{\ddot{B}}}_j(s){(s_m-s)}^2+6^{-1}{\widehat{\stackrel{⃛}{B}}}_j(s){(s_m-s)}^2$, in which ${\widehat{\ddot{B}}}_j(s)\text{ and }{\widehat{\stackrel{⃛}{B}}}_j(s)$ are estimators obtained by using local cubic fit with a pilot bandwidth selected in (2.6).

It will be shown below that the asymptotic distribution of S_n is quite complicated and it is difficult to directly approximate the percentiles of S_n under the null hypothesis. Instead, we propose using a wild bootstrap method to obtain critical values of S_n. The wild bootstrap consists of the following three steps.

Step 1. Fit model (1.1) under the null hypothesis H₀, which yields B̂* (s_m), ${\mathit{\eta ̂}}_{i,0}^{*}(s_m)\text{ and }{\mathit{\epsilon ̂}}_{i,0}^{*}(s_m)$ for i = 1, …, n and m = 1, …, M.

Step 2. Generate a random sample ${\tau }_i^{(g)}$ and τ_i(s_m)^(g) from a N(0, 1) generator for i = 1, …, n and m = 1, …, M and then construct

$${\mathbf{ŷ}}_i{(s_m)}^{(g)}={\mathrm{B̂}}^{*}{(s)}^T{\mathbf{x}}_i+{\tau }_i^{(g)}{\mathit{\eta ̂}}_{i,0}^{*}(s_m)+{\tau }_i{(s_m)}^{(g)}{\mathit{\epsilon ̂}}_{i,0}^{*}(s_m).$$

Then, based on ŷ_i(s_m)^(g), we recalculate B̂(s)^(g), bias(B̂(s)^(g)), and d(s)^(g) = Cvec(B̂(s)^(g) − bias(B̂(s)^(g))) − b₀(s). We also note that Cvec(B̂(s)^(g)) ≈ b₀ and Cvec(bias(B̂(s)^(g))) ≈ 0. Thus, we can drop the term bias(B̂(s)^(g)) in d(s)^(g) for computational efficiency. Subsequently, we compute

$$S_n^{(g)}=n{\displaystyle {\int }_0^1}\mathbf{d}{(s)}^{(g)T}{[\mathbf{C}({\mathrm{\Sigma ̂}}_{\eta }(s,s)\otimes {\mathrm{\Omega ̂}}_X^{-1}){\mathbf{C}}^T]}^{-1}\mathbf{d}{(s)}^{(g)}\mathit{\text{ds}}.$$

Step 3. Repeat Step 2 G times to obtain $\{S_n^{(g)}:g=1,\dots ,G\}$ and then calculate $p=G^{-1}{\displaystyle \sum _{g=1}^G}1(S_n^{(g)}\ge S_n)$. If p is smaller than a pre-specified significance level α, say 0.05, then one rejects the null hypothesis H₀.

3.2. Simultaneous confidence bands

Construction of SCB for coefficient functions is of great interest in statistical inference for model (1.1). For a given confidence level α, we construct SCB for each b_jl(s) as follows:

$$P({\mathrm{b̂}}_{\mathit{\text{jl}}}^{L,\alpha }(s)<b_{\mathit{\text{jl}}}(s)<{\mathrm{b̂}}_{\mathit{\text{jl}}}^{U,\alpha }(s)\text{ for all }s\in [0,1])=1-\alpha ,$$ (3.4)

where ${\mathrm{b̂}}_{\mathit{\text{jl}}}^{L,\alpha }(s)\text{ and }{\mathrm{b̂}}_{\mathit{\text{jl}}}^{U,\alpha }(s)$ are the lower and upper limits of SCB. Specifically, it will be shown below that a 1 − α simultaneous confidence band for b_jl(s) is given as follows:

$$({\mathrm{b̂}}_{\mathit{\text{jl}}}(s)-\text{bias}({\mathrm{b̂}}_{\mathit{\text{jl}}}(s))-\frac{C_{\mathit{\text{jl}}}(\alpha )}{\sqrt{n}},{\mathrm{b̂}}_{\mathit{\text{jl}}}(s)-\text{bias}({\mathrm{b̂}}_{\mathit{\text{jl}}}(s))+\frac{C_{\mathit{\text{jl}}}(\alpha )}{\sqrt{n}}),$$ (3.5)

where C_jl(α) is a scalar. Since the calculation of b̂_jl(s) and bias(b̂_jl(s)) has been discussed in (2.5) and (3.3), the next issue is to determine C_jl(α).

Although there are several methods of determining C_jl(α) including random field theory [46, 40], we develop an efficient resampling method to approximate C_jl(α) as follows [53, 30].

• We calculate ${\mathrm{r̂}}_{\mathit{\text{ij}}}(s_m)=y_{\mathit{\text{ij}}}(s_m)-{\mathbf{x}}_i^T{\mathrm{B̂}}_j(s_m)$ for all i, j, and m.

• For g = 1, …, G, we independently simulate $\{{\tau }_i^{(g)}:i=1,\dots ,n\}$ from N(0, 1) and calculate a stochastic process G_j(s)^(g) given by

  $$\sqrt{n}[I_p\otimes (1,0)]\text{vec}(\mathrm{\Sigma }{(s,h_{1j})}^{-1}{\displaystyle \sum _{i=1}^n}{\tau }_i^{(g)}{\displaystyle \sum _{m=1}^M}{K}_{h_{1j}}(s_m-s)[{\mathbf{x}}_i\otimes {\mathbf{z}}_{h_{1j}}(s_m-s)]{\mathrm{r̂}}_{\mathit{\text{ij}}}(s_m)).$$

• We calculate sup_{s∈[0, 1]} |e_lG_j(s)^(g)| for all g, where e_l be a p × 1 vector with the l-th element 1 and 0 otherwise, and use their 1 − α empirical percentile to estimate C_jl(α).

4. Asymptotic Properties

In this section, we systematically examine the asymptotic properties of B̂(s), η̂_ij(s), Σ̂_η(s, t), and S_n developed in Sections 2 and 3. Let us first define some notation. Let u_r(K) = ∫ t^r K(t)dt and υ_r(K) = ∫ t^r K²(t)dt, where r is any integer. For any smooth functions f(s) and g(s, t), define ḟ(s) = df(s)/ds, f̈(s) = d²f(s)/ds², f⃛ (s) = d³f(s)/ds³, and g^(a,b)(s, t) = ∂^a+bg(s, t)/∂^as∂^bt, where a and b are any nonnegative integers. Let H = diag(h₁₁, …, h_1J), B(s) = [B₁(s), …, B_J (s)], B̂ (s) = [B̂₁(s), …, B̂_J (s)] and B̈(s) = [B̈₁(s), …, B̈_J (s)], where B̈_j(s) = (b̈_j1(s), …, b̈_jp(s))^T is a p × 1 vector. Let S = {s₁, …, s_M}.

4.1. Assumptions

Throughout the paper, the following assumptions are needed to facilitate the technical details, although they may not be the weakest conditions. We need to introduce some notation. Let N(μ, Σ) be a normal random vector with mean μ and covariance Σ. Let Ω₁(h, s) = ∫(1, h⁻¹(u − s))^⊗2 K(u − s, h)π(u)du. Moreover, we do not distinguish the differentiation and continuation at the boundary points from those in the interior of [0, 1]. For instance, a continuous function at the boundary of [0, 1] means that this function is left continuous at 0 and right continuous at 1.

Assumption (C1). For all j = 1, …, J, sup_sm E[|ε_ij(s_m)|^q] < ∞ for some q > 4 and all grid points s_m.

Assumption (C2). Each component of {η (s) : s ∈ [0, 1]}, {η(s)η(t)^T : (s, t) ∈ [0, 1]²}, and {xη^T (s) : s ∈ [0, 1]} are Donsker classes.

Assumption (C3). The covariate vectors x_is are independently and identically distributed with Ex_i = μ_x and ‖x_i‖_∞ < ∞. Assume that $E[{\mathbf{x}}_i^{\otimes 2}]={\mathrm{\Omega }}_X$ is positive definite.

Assumption (C4). The grid points 𝒮 = {s_m, m = 1, …, M} are randomly generated from a density function π(s). Moreover, π(s) > 0 for all s ∈ [0, 1] and π(s) has continuous second-order derivative with the bounded support [0, 1].

Assumption (C4b). The grid points 𝒮 = {s_m, m = 1, …, M} are prefixed according to π(s) such that ${\displaystyle {\int }_0^{s_m}}\pi (s)\mathit{\text{ds}}=m/M$ for M ≥ m ≥ 1. Moreover, π(s) > 0 for all s ∈ [0, 1] and π(s) has continuous second-order derivative with the bounded support [0, 1].

Assumption (C5). The kernel function K (t) is a symmetric density function with a compact support [−1, 1], and is Lipschitz continuous. Moreover, 0 < inf_{h∈(0,h0],s∈[0, 1]} det(Ω₁(h, s)), where h₀ > 0 is a small scalar and det(Ω₁(h, s)) denotes the determinant of Ω₁(h, s).

Assumption (C6). All components of B(s) have continuous second derivatives on [0, 1].

Assumption (C7). Both n and M converge to ∞, max_j h_1j = o(1), Mh_1j → ∞, and ${\text{max}}_j{h}_{1j}^{-1}{|\text{log }{h}_{1j}|}^{1-2/q_1}\le M^{1-2/q_1}$ for j = 1, …, J, where q₁ ∈ (2, 4).

Assumption (C7b). Both n and M converge to ∞, max_j h_1j = o(1), Mh_1j → ∞, and log(M) = o(Mh_1j). There exists a sequence of γ_n > 0 such that γ_n → ∞, ${\text{max}}_j{n}^{1/2}{\gamma }_n^{1-q}{h}_{1j}^{-1}=o(1)$ and n^−1/2γ_n log(M) = o(1).

Assumption (C8). For all j, max_j(h_2j)⁻⁴(log n/n)^1−2/q₂ = o(1) for q₂ ∈ (2, ∞), max_j h_2j = o(1), and Mh_2j → ∞ for j = 1, …, J.

Assumption (C9a). The sample path of η_ij(s) has continuous second-order derivative on [0, 1] and $E[{\text{sup}}_{s\in [0,1]}{\Vert \mathit{\eta }(s)\Vert }_2^{r_1}]<\mathrm{\infty }$ and E{sup_s∈[0,1][‖η̇ (s)‖₂+‖η̈(s)‖₂]^r₂} < ∞ for some r₁, r₂ ∈ (2,∞), where ‖·‖₂ is the Euclidean norm.

Assumption (C9b). $E[{\text{sup}}_{s\in [0,1]}{\Vert \mathit{\eta }(s)\Vert }_2^{r_1}]<\mathrm{\infty }$ for some r₁ ∈ (2, ∞) and all components of Σ_η(s, t) have continuous second-order partial derivatives with respect to (s, t) ∈ [0, 1]² and inf_s∈[0,1] Σ_η(s, s) > 0.

Assumption (C10). There is a positive fixed integer E_j < ∞ such that λ_j,1 > … > λ_j,Ej > λ_j,Ej+1 ≥ … ≥ 0 for j = 1, …, J.

Remark. Assumption (C1) requires the uniform bound on the high-order moment of ε_ij(s_m) for all grid points s_m. Assumption (C2) avoids smoothness conditions on the sample path η(s), which are commonly assumed in the literature [9, 51, 22]. Assumption (C3) is a relatively weak condition on the covariate vector and the boundedness of ‖x_i‖₂ is not essential. Assumption (C4) is a weak condition on the random grid points. In many neuroimaging applications, M is often much larger than n and for such large M, a regular grid of voxels is fairly well approximated by voxels generated by a uniform distribution in a compact subset of Euclidean space. For notational simplicity, we only state the theoretical results for the random grid points throughout the paper. Assumption (C4b) is a weak condition on the fixed grid points. We will prove several key results for the fixed grid point case in Lemma 8 of the supplementary document. The bounded support restriction on K(·) in Assumption (C5) is not essential and can be removed if we put a restriction on the tail of K(·). Assumption (C6) is the standard smoothness condition on B(s) in the literature [13, 48, 12, 15, 44, 26, 38, 28, 27, 51, 23]. Assumptions (C7)–(C8) on bandwidths are similar to the conditions used in [32, 10]. Assumptions (C7b) is a weak condition on n, M, h_1j, and γ_n for the fixed grid point case. For instance, if we set γ_n = n^1/2 log(M)^−1−c₀ for a positive scalar c₀ > 0, then we have $n^{1/2}{\gamma }_n^{1-q}{h}_{1j}^{-1}=n^{1-q/2}\text{log}{(M)}^{(1+c_0)(q-1)}{h}_{1j}^{-1}=o(1)$ and n^−1/2γ_n log(M) = log(M)^−c₀ = o(1). As shown in Theorem 1 below, if h_1j = O((nM)^−1/5) and γ_n = n^1/2 log(M)^−1−c₀, $n^{1/2}{\gamma }_n^{1-q}{h}_{1j}^{-1}$ reduces to n^6/5−q/2 log(M)^{(1+c₀)(q−1)}M^1/5. For relatively large q in Assumption (C1), n^6/5−q/2 log(M)^{(1+c₀)(q−1)}M^1/5 can converge to zero. Assumptions (C9a) and (C3) are sufficient conditions of assumption (C2). Assumption (C9b) on the sample path is the same as Condition C6 used in [32]. Particularly, if we use the method for estimating Σ_η(s, s′) considered in Li and Hsing [32], then the differentiability of η(s) in Assumption (C9a) can be dropped. Assumption (C10) on simple multiplicity of the first E_j eigenvalues is only needed to investigate the asymptotic properties of eigenfunctions.

4.2. Asymptotic properties of B̂(s)

The following theorem establishes the weak convergence of {B̂(s), s ∈ [0, 1]}, which is essential for constructing global test statistics and SCB for B(s).

Theorem 1. Suppose that Assumptions (C1)–(C7) hold. The following results hold:

1. $\sqrt{n}\{\mathit{\text{vec}}(\mathbf{B̂}(s)-\mathbf{B}(s)-0.5\mathbf{B̈}(s){\mathbf{U}}_2(K;s,\mathbf{H}){\mathbf{H}}^2[1+o_p(1)]):s\in [0,1]\}$ converges weakly to a centered Gaussian process G(·) with covariance matrix ${\mathrm{\Sigma }}_{\eta }(s,s\prime )\otimes {\mathrm{\Omega }}_X^{-1}$ , where Ω_X = E[x^⊗2] and U₂(K; s, H) is a J × J diagonal matrix, whose diagonal elements will be defined in Lemma 5 in Appendix.

2. The asymptotic bias and conditional variance of B̂_j(s) given 𝒮 for s ∈ (0, 1) are given by $0.5h_{1j}^2{u}_2(K){\mathrm{B̈}}_j(s)[1+o_p(1)]\text{ and }{n}^{-1}{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,s){\mathrm{\Omega }}_X^{-1}[1+o_p(1)]$ , respectively.

Remarks. 1. The major challenge in proving Theorem 1 (i) is dealing with within-subject dependence. This is because the dependence between η(s) and η(s′) in the newly proposed multivariate varying coefficient model does not converge to zero due to the within-curve dependence. It is worth noting that for any given s, the corresponding asymptotic normality of B̂(s) may be established by using related techniques in Zhang and Chen [51]. However, the marginal asymptotic normality does not imply the weak convergence of B̂(s) as a stochastic process in [0, 1], since we need to verify the asymptotic continuity of {B̂(s) : s ∈ [0, 1]} to establish its weak convergence. In addition, Zhang and Chen [51] considered “smoothing first, then estimation”, which requires a stringent assumption such that n = O(M^4/5). Readers are referred to Condition A.4 and Theorem 4 in Zhang and Chen [51] for more details. In contrast, directly estimating B(s) using local kernel smoothing avoids such stringent assumption on the numbers of grid points and subjects.

2. Theorem 1 (ii) only provides us the asymptotic bias and conditional variance of B̂_j(s) given 𝒮 for the interior points of (0, 1). The asymptotic bias and conditional variance at the boundary points 0 and 1 are given in Lemma 5. The asymptotic bias of B̂_j(s) is of the order $h_{1j}^2$, as the one in nonparametric regression setting. Moreover, the asymptotic conditional variance of B̂_j(s) has a complicated form due to the within-curve dependence. The leading term in the asymptotic conditional variance is of order n⁻¹, which is slower than the standard nonparametric rate (nMh_1j)⁻¹ with the assumption h_1j → 0 and Mh_1j → ∞.

3. Choosing an optimal bandwidth h_1j is not a trivial task for model (1.1). Generally, any bandwidth h_1j satisfying the assumption h_1j → 0 and Mh_1j → ∞ can ensure the weak convergence of {B̂(s) : s ∈ [0, 1]}. Based on the asymptotic bias and conditional variance of B̂(s), we can calculate an optimal bandwidth for estimating B(s), h_1j = O_p((nM)^−1/5). In this case, $n^{-1}{h}_{1j}^2$ and (nM)⁻¹h_1j reduce to O_p(n^−7/5M^−2/5) and (nM)^−6/5, respectively, and their contributions depend on the relative size of n over M.

4.3. Asymptotic properties of η ^_ij(s)

We next study the asymptotic bias and covariance of η̂_ij(s) as follows. We distinguish between two cases. The first one is conditioning on the design points in 𝒮, X, and η. The other is conditioning on the design points in 𝒮 and X. We define K^* ((s − t)/h) = ∫ K(u)K(u + (s − t)/h)du.

Theorem 2. Under Assumptions (C1) and (C3)–(C8), the following results hold for all s ∈ (0, L).

1. Conditioning on (𝒮, X, η), we have

   $$\mathit{\text{Bias}}[{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)|𝒮,\mathit{\eta },{\mathbf{x}}_i]=0.5u_2(K)[{\mathrm{\eta ̈}}_{\mathit{\text{ij}}}(s)h_{2j}^2+{\mathbf{x}}_i^T{\mathrm{B̈}}_j(s_m)h_{1j}^2][1+o_p(1)]+O_p(n^{-1/2}),$$

   $$\mathit{\text{Cov}}[{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s),{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(t)|𝒮,\mathit{\eta },{\mathbf{x}}_i]=K^{*}((s-t)/h_{2j})\pi {(t)}^{-1}{({\mathit{\text{Mh}}}_{2j})}^{-1}{O}_p(1)-{\mathbf{x}}_i^T{\mathrm{\Omega }}_X^{-1}{\mathbf{x}}_i{({\mathit{\text{nMh}}}_{1j})}^{-1}{O}_p(1).$$
2. The asymptotic bias and covariance of η̂_ij(s) conditioning on 𝒮 and X are given by

   $$\mathit{\text{Bias}}[{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)|𝒮,\mathbf{X}]=0.5u_2(K){\mathbf{x}}_i^T{\mathrm{B̈}}_j(s_m)h_{1j}^2[1+o_p(1)],$$

   $$\mathit{\text{Cov}}({\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)-{\eta }_{\mathit{\text{ij}}}(s),{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(t)-{\eta }_{\mathit{\text{ij}}}(t)|𝒮,\mathbf{X})=[1+o_p(1)][0.25u_2{(K)}^2{h}_{2j}^4{\displaystyle {\sum }_{\eta ,\mathit{\text{jj}}}^{(2,2)}}(s,t)+K^{*}((s-t)/h_{2j})\times \pi {(t)}^{-1}{({\mathit{\text{Mh}}}_{2j})}^{-1}{O}_p(1)+n^{-1}{\mathbf{x}}_i^T{\mathrm{\Omega }}_X^{-1}{\mathbf{x}}_i{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)].$$
3. The mean integrated squared error (MISE) of all η̂_ij(s) is given by

   $$n^{-1}{\displaystyle \sum _{i=1}^n}{\displaystyle {\int }_0^1}E\{{[{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)-{\eta }_{\mathit{\text{ij}}}(s)]}^2|𝒮\}\pi (s)\mathit{\text{ds}}=[1+o_p(1)]\times \{O({({\mathit{\text{Mh}}}_{2j})}^{-1})+n^{-1}{\displaystyle {\int }_0^1}{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,s)\pi (s)\mathit{\text{ds}}+0.25u_2^2(K){\displaystyle {\int }_0^1}[{\mathrm{B̈}}_j{(s)}^T{\mathrm{\Omega }}_X{\mathrm{B̈}}_j(s)h_{1j}^4+{\displaystyle {\sum }_{\eta ,\mathit{\text{jj}}}^{(2,2)}}(s,s)h_{2j}^4]\pi (s)\mathit{\text{ds}}\}.$$ (4.1)
4. The optimal bandwidth for minimizing MISE (4.1) is given by

   $${ĥ}_{2j}=O(M^{-1/5}).$$ (4.2)
5. The first order LPK reconstructions η̂_ij(s) using ĥ_2j in (4.2) satisfy

   $$\underset{s\in [0,1]}{\text{sup}}|{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)-{\eta }_{\mathit{\text{ij}}}(s)|=O_p(|\text{log}(M){|}^{1/2}{M}^{-2/5}+h_{1j}^2+n^{-1/2})$$ (4.3)

   for i = 1, …, n.

Remark. Theorem 2 characterizes the statistical properties of smoothing individual curves η_ij(s) after first estimating B_j(s). Conditioning on individual curves η_ij(s), Theorem 2 (a) shows that Bias[η̂_ij(s)|𝒮,X,η] is associated with $0.5u_2(K){\mathbf{x}}_i^T{\mathrm{B̈}}_j(s_m)h_{1j}^2$, which is the bias term of B̂_j(s) introduced in the estimation step, and $0.5u_2(K){\mathrm{\eta ̈}}_{\mathit{\text{ij}}}(s)h_{2j}^2$ is introduced in the smoothing individual functions step. Without conditioning on η_ij(s), Theorem 2 (b) shows that the bias of η̂_ij(s) is mainly controlled by the bias in the estimation step. The MISE of η̂_ij(s) in Theorem 2 (c) is the sum of $O_p(n^{-1}+h_{1j}^4)$ introduced by the estimation of B_j(s) and $O_p({({\mathit{\text{Mh}}}_{2j})}^{-1}+h_{2j}^4)$ introduced by the reconstruction of η_ij(s). The optimal bandwidth for minimizing the MISE of η̂_ij(s) is a standard bandwidth for LPK. If we use the optimal bandwidth in Theorem 2 (d), then the MISE of η̂_ij(s) can achieve the order of $n^{-1}+h_{1j}^4+M^{-4/5}$.

4.4. Asymptotic properties of Σ̂_η(s, t)

In this section, we study the asymptotic properties of Σ̂_η(s, t) and its spectrum decomposition.

Theorem 3. (i) Under Assumptions (C1) and (C3)–(C9a), it follows that

$$\underset{(s,t)\in {[0,1]}^2}{\text{sup}}|{\mathrm{\Sigma ̂}}_{\eta }(s,t)-{\mathrm{\Sigma }}_{\eta }(s,t)|=O_p({({\mathit{\text{Mh}}}_{2j})}^{-1}+h_{1j}^2+h_{2j}^2+{(\text{log}n/n)}^{1/2}).$$

(ii) Under Assumptions (C1) and (C3)–(C10), if the optimal bandwidths h_mj for m = 1, 2 are used to reconstruct B̂_j(s) and η̂_ij(s) for all j, then for l = 1, …,E_j, we have the following results:

1. ${\displaystyle {\int }_0^1}{[{\mathrm{\psi ̂}}_{\mathit{\text{jl}}}(s)-{\psi }_{\mathit{\text{jl}}}(s)]}^2\mathit{\text{ds}}=O_p({({\mathit{\text{Mh}}}_{2j})}^{-1}+h_{1j}^2+h_{2j}^2+{(\text{log }n/n)}^{1/2})$;

2. $|{\mathrm{\lambda ̂}}_{\mathit{\text{jl}}}-{\lambda }_{\mathit{\text{jl}}}|=O_p({({\mathit{\text{Mh}}}_{2j})}^{-1}+h_{1j}^2+h_{2j}^2+{(\text{log }n/n)}^{1/2})$.

Remark. Theorem 3 characterizes the uniform weak convergence rates of Σ̂_η(s, t), ψ̂_jl, and λ̂_jl for all j. It can be regarded as an extension of Theorems 3.3–3.6 in Li and Hsing [32], which established the uniform strong convergence rates of these estimates with the sole presence of intercept and J = 1 in model (1.1). Another difference is that Li and Hsing [32] employed all cross products y_ijy_ik for j ≠ k and then used the local polynomial kernel to estimate Σ_η(s, t). As discussed in Li and Hsing [32], their approach can relax the assumption on the differentiability of the individual curves. In contrast, following Hall, Müller and Wang [22] and Zhang and Chen [51], we directly fit a smooth curve to η_ij(s) for each i and estimate Σ_η(s, t) by the sample covariance functions. Our approach is computationally simple and can ensure that all Σ̂_η,jj(s, t) are positive semi-definite, whereas the approach in Li and Hsing [32] cannot. This is extremely important for high-dimensional neuroimaging data, which usually contains a large number of locations (called voxels) on a two-dimensional (2D) surface or in a 3D volume. For instance, the number of M can number in the tens of thousands to millions, and thus it can be numerically infeasible to directly operate on Σ̂_η(s, s′).

We use Σ̃_η(s, s′) to denote the local linear estimator of Σ_η(s, s′) proposed in Li and Hsing [32]. Following the arguments in Li and Hsing [32], we can easily obtain the following result.

Corollary 1. Under Assumptions (C1)–(C8) and (C9b), it follows that

$$\underset{(s,t)\in {[0,1]}^2}{\text{sup}}|{\mathrm{\Sigma ̃}}_{\eta }(s,t)-{\mathrm{\Sigma }}_{\eta }(s,t)|=O_p(h_{1j}^2+h_{2j}^2+{(\text{log}n/n)}^{1/2}).$$

4.5. Asymptotic properties of the inference procedures

In this section, we discuss the asymptotic properties of the global statistic S_n and the critical values of SCB. Theorem 1 allows us to construct SCB for coefficient functions b_jl(s). It follows from Theorem 1 that

$$\sqrt{n}[{\mathrm{b̂}}_{\mathit{\text{jl}}}(s)-b_{\mathit{\text{jl}}}(s)-\text{Bias}({\mathrm{b̂}}_{\mathit{\text{jl}}}(s))]\Rightarrow G_{\mathit{\text{jl}}}(s),$$ (4.4)

where ⇒ denotes weak convergence of a sequence of stochastic processes and G_jl(s) is a centered Gaussian process indexed by s ∈ [0, 1]. Therefore, let X_C(s) be a centered Gaussian process, we have

$${[\mathbf{C}({\mathrm{\Sigma ̂}}_{\eta }(s,s)\otimes {\mathrm{\Omega ̂}}_X^{-1}){\mathbf{C}}^T]}^{-1/2}\mathbf{d}(s)\Rightarrow X_{\mathbf{C}}(s),$$ (4.5)

$$\underset{s\in [0,1]}{\text{sup}}|\sqrt{n}[{\mathrm{b̂}}_{\mathit{\text{jl}}}(s)-b_{\mathit{\text{jl}}}(s)-\text{Bias}({\mathrm{b̂}}_{\mathit{\text{jl}}}(s))]|\Rightarrow \underset{s\in [0,1]}{\text{sup}}|G_{\mathit{\text{jl}}}(s)|.$$

We define C_jl(α) such that P(sup_s∈[0,1] |G_jl(s)| ≥ C_jl(α)) = 1 − α. Thus, the confidence band given in (3.5) is a 1 − α simultaneous confidence band for b_jl(s).

Theorem 4. If Assumptions (C1)–(C9a) are true, then we have

$$S_n\Rightarrow {\displaystyle {\int }_0^1}{X}_{\mathbf{C}}{(s)}^T{X}_{\mathbf{C}}(s)\mathit{\text{ds}}.$$ (4.6)

Remark. Theorem 4 is similar to Theorem 7 of Zhang and Chen [51]. Both characterize the asymptotic distribution of S_n. In particular, Zhang and Chen [51] delineate the distribution of ${\displaystyle {\int }_0^1}{X}_C{(s)}^T{X}_C(s)\mathit{\text{ds}}$ as a χ²-type mixture. All discussions associated Theorem 7 with Zhang and Chen [51] are valid here and therefore, we do not repeat them for the sake of space.

We consider conditional convergence for bootstrapped stochastic processes. We focus on the bootstrapped process {G_j(s)^(g) : s ∈ [0, 1]} as the arguments for establishing the wild bootstrap method for approximating the null distribution of S_n and the bootstrapped process {G_j(s)^(g) : s ∈ [0, 1]} are similar.

Theorem 5. If Assumptions (C1)–(C9a) are true, then G_j(s)^(g)(s) converges weakly to G_j(s) conditioning on the data, where G_j(s) is a centered Gaussian process indexed by s ∈ [0, 1].

Remark. Theorem 5 validates the bootstrapped process of G_j(s)^(g). An interesting observation is that the bias correction for B̂_j(s) in constructing G_j(s)^(g) is unnecessary. It leads to substantial computational saving.

5. Simulation Studies

In this section, we present two simulation example to demonstrate the performance of the proposed procedures.

Example 1. This example is designed to evaluate the Type I error rate and power of the proposed global test S_n using Monte Carlo simulation. In this example, the data were generated from a bivariate MVCM as follows:

$$y_{\mathit{\text{ij}}}(s_m)={\mathbf{x}}_i^T{B}_j(s_m)+{\eta }_{\mathit{\text{ij}}}(s_m)+{\epsilon }_{\mathit{\text{ij}}}(s_m)\text{ for }j=1,2,$$ (5.1)

where s_m ~ U[0, 1], (ε_i1(s_m), ε_i2(s_m))^T ~ N((0, 0)^T, $S_{\epsilon }(s_m)=\text{diag}({\sigma }_1^2,{\sigma }_2^2))$, and x_i = (1, x_i1, x_i2) for all i = 1, …, n and m = 1, …, M. Moreover, (x_i1, x_i2)^T ~ N((0, 0)^T, diag(1−2^−0.5, 1−2^−0.5)+2^−0.5(1, 1)^⊗2) and η_ij(s) = ξ_ij1 ψ_j1(s) + ξ_ij2 ψ_j2(s), where ξ_ijl ~ N(0, λ_jl) for j = 1, 2 and l = 1, 2. Furthermore, s_m, (x_i1, x_i2), ξ_i11, ξ_i12, ξ_i21, ξ_i22, ε_i1(s_m), and ε_i2(s_m) are independent random variables.We set $({\lambda }_{11},{\lambda }_{12},{\sigma }_1^2,{\lambda }_{21},{\lambda }_{22},{\sigma }_2^2)=(1.2,0.6,0.2,1,0.5,0.1)$ and the functional coefficients and eigenfunctions as follows:

$$b_{11}(s)=s^2,b_{12}(s)={(1-s)}^2,b_{13}(s)=4s(1-s)-0.4;$$

$${\psi }_{11}(s)=\sqrt{2}\text{ sin}(2\pi s),{\psi }_{12}(s)=\sqrt{2}\text{ cos}(2\pi s);$$

$$b_{21}(s)=5{(s-0.5)}^2,b_{22}(s)=s^{0.5},b_{23}(s)=4s(1-s)-0.4;$$

$${\psi }_{21}(s)=\sqrt{2}\text{ cos}(2\pi s),{\psi }_{22}(s)=\sqrt{2}\text{ sin}(2\pi s).$$

Then, except for (b₁₃(s), b₂₃(s)) for all s, we fixed all other parameters at the values specified above, whereas we assumed (b₁₃(s), b₂₃(s)) = c(4s(1 − s) − 0.4, 4s(1 − s) − 0.4), where c is a scalar specified below.

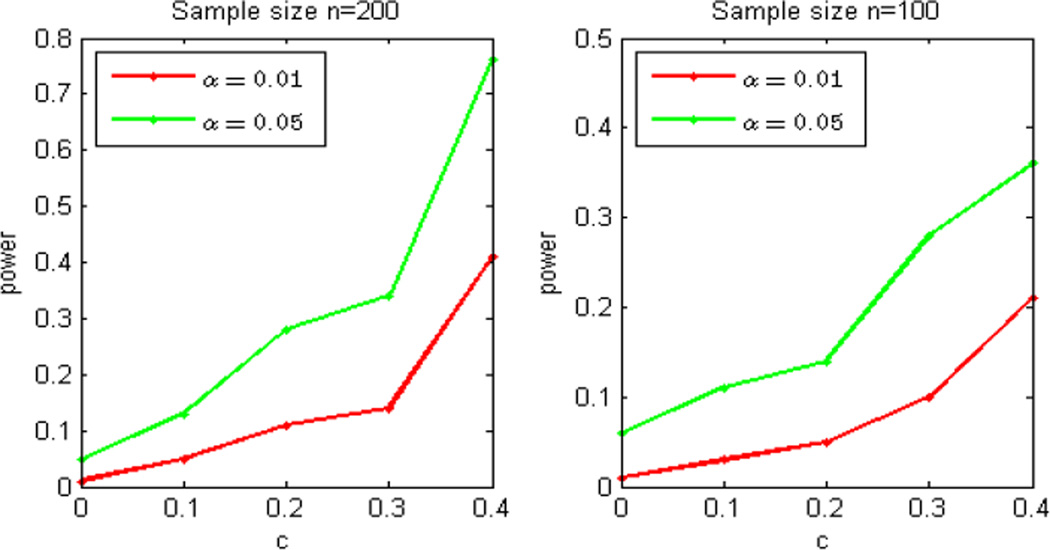
We want to test the hypotheses H₀ : b₁₃(s) = b₂₃(s) = 0 for all s against H₁ : b₁₃(s) ≠ 0 or b₂₃(s) ≠ 0 for at least one s. We set c = 0 to assess the Type I error rates for S_n, and set c = 0.1, 0.2, 0.3, and 0.4 to examine the power of S_n. We set M = 50, n = 200 and 100. For each simulation, the significance levels were set at α = 0.05 and 0.01, and 100 replications were used to estimate the rejection rates.

Fig. 2 depicts the power curves. It can be seen from Fig. 2 that the rejection rates for S_n based on the wild bootstrap method are accurate for moderate sample sizes, such as (n = 100, or 200) at both significance levels (α = 0.01 or 0.05). As expected, the power increases with the sample size.

Fig 2.

Plot of Power Curves. Rejection rates of S_n based on the wild bootstrap method are calculated at five different values of c (0, 0.1, 0.2, 0.3, and 0.4) for two sample sizes of n (100 and 200) subjects at 5% (green) and 1% (red) significance levels.

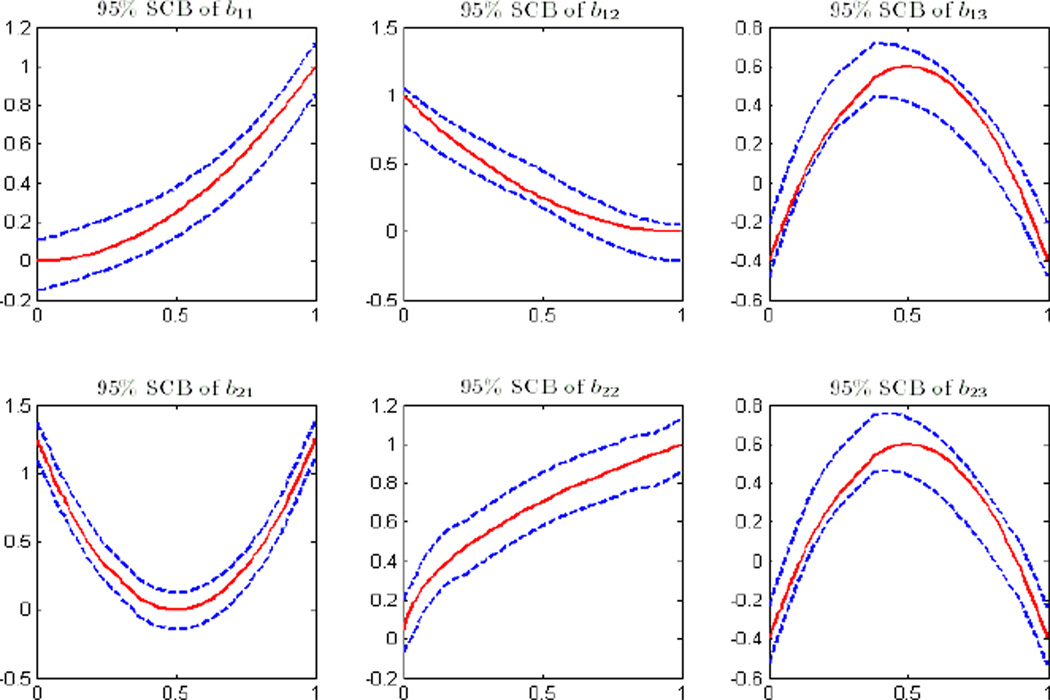
Example 2. This example is used to evaluate the coverage probabilities of SCB of the functional coefficients B(s) based on the wild bootstrap method. The data were generated from model (5.1) under the same parameter values. We set n = 500 and M = 25, 50, and 75 and generated 200 datasets for each combination. Based on the generated data, we calculated SCB for each component of B₁(s) and B₂(s). Table 1 summarizes the empirical coverage probabilities based on 200 simulations for α = 0.01 and α = 0.05. The coverage probabilities improve with the number of grid points M. When M = 75, the differences between the coverage probabilities and the claimed confidence levels p are fairly acceptable. The Monte Carlo errors are of size $\sqrt{0.95\times 0.05/200}\approx 0.015$ for α = 0.05. Fig. 3 depicts typical simultaneous confidence bands, where n = 500 and M = 50. Additional simulation results are given in the supplementary document.

Table 1.

Empirical coverage probabilities of 1 − α SCB for all components of B₁(·) and B₂(·) based on 200 simulated data sets.

	α = 0.05
M	b11	b12	b13	b21	b22	b23
25	0.915	0.930	0.945	0.920	0.915	0.945
50	0.925	0.940	0.945	0.930	0.925	0.950
75	0.945	0.950	0.955	0.945	0.945	0.955
	α = 0.01
25	0.985	0.965	0.985	0.985	0.990	0.980
50	0.995	0.980	0.985	0.985	0.995	0.985
75	0.990	0.985	0.990	0.995	0.990	0.990

Fig 3.

Typical simultaneous confidence bands with n = 500 and M = 50. The red solid curves are the true coefficient functions, and the blue dashed curves are the confidence bands.

6. Real Data Analysis

The data set consists of 128 healthy infants (75 males and 53 females) from the neonatal project on early brain development. The gestational ages of these infants range from 262 to 433 days and their mean gestational age is 298 days with standard deviation 17.6 days. The DTIs and T1-weighted images were acquired for each subject. For the DTIs, the imaging parameters were as follows: the six non-collinear directions at the b-value of 1000 s/mm² with a reference scan (b = 0), the isotropic voxel resolution=2 mm, and the in-plane field of view=256 mm in both directions. A total of five repetitions were acquired to improve the signal-to-noise ratio of the DTIs.

The DTI data were processed by two key steps including a weighted least squares estimation method [2, 54] to construct the diffusion tensors and a DTI atlas building pipeline [20, 55] to register DTIs from multiple subjects to create a study specific unbiased DTI atlas, to track fiber tracts in the atlas space, and to propagate them back into each subject’s native space by using registration information. Subsequently, diffusion tensors (DTs) and their scalar diffusion properties were calculated at each location along each individual fiber tract by using DTs in neighboring voxels close to the fiber tract. Fig. 1 (a) displays the fiber bundle of the genu of the corpus callosum (GCC), which is an area of white matter in the brain. The GCC is the anterior end of the corpus callosum, and is bent downward and backward in front of the septum pellucidum; diminishing rapidly in thickness, it is prolonged backward under the name of the rostrum, which is connected below with the lamina terminalis. It was found that neonatal microstructural development of GCC positively correlates with age and callosal thickness.

The two aims of this analysis are to compare diffusion properties including FA and MD along the GCC between the male and female groups and to delineate the development of fiber diffusion properties across time, which is addressed by including the gestational age at MRI scanning as a covariate. FA and MD, respectively, measure the inhomogeneous extent of local barriers to water diffusion and the averaged magnitude of local water diffusion. We fitted model (1.1) to the FA and MD values from all 128 subjects, in which x_i = (1, G, Age)^T, where G represents gender. We then applied the estimation and inference procedures to estimate B(s) and calculate S_n for each hypothesis test. We approximated the p-value of S_n using the wild bootstrap method with G = 1, 000 replications. Finally, we constructed the 95% simultaneous confidence bands for the functional coefficients of B_j(s) for j = 1, 2.

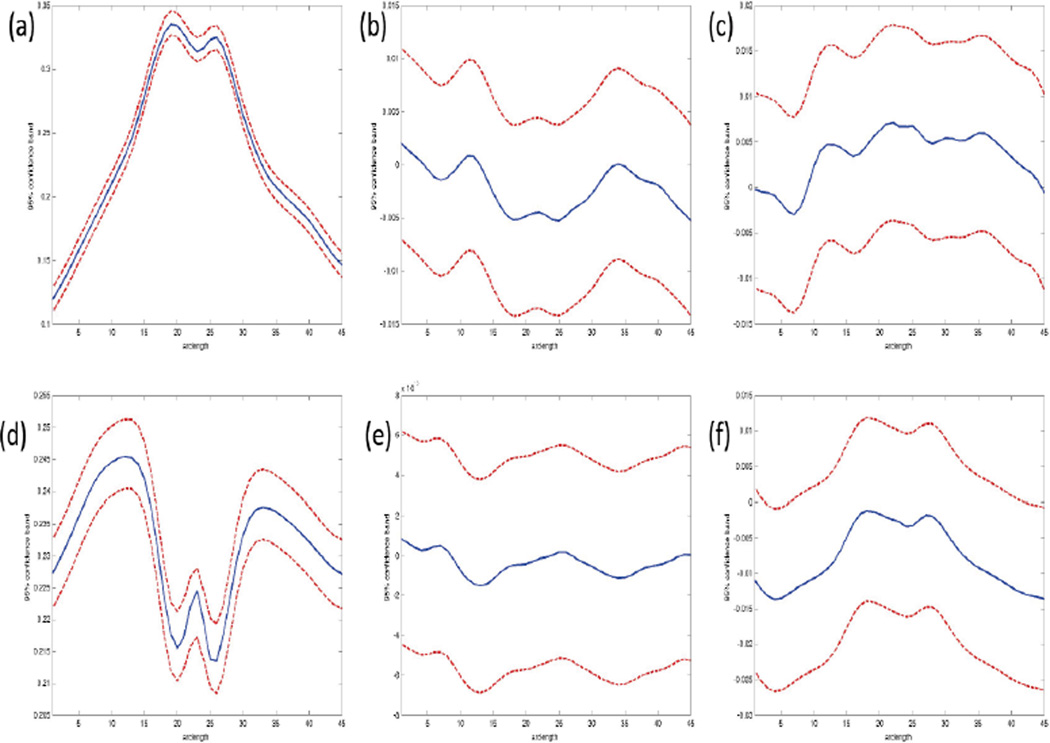
Fig. 4 presents the estimated coefficient functions corresponding to 1, G, and Age associated with FA and MD (blue solid lines in all panels of Fig. 4). The intercept functions (all panels in the first column of Fig. 4) describe the overall trend of FA and MD. The gender coefficients for FA and MD in the second column of Fig. 4 are negative at most of the grid points, which may indicate that compared with female infants, male infants have relatively smaller magnitudes of local water diffusivity along the genu of the corpus callosum. The gestational age coefficients for FA (panel (c) of Fig. 4) are positive at most grid points, indicating that FA measures increase with age in both male and female infants, whereas those corresponding to MD (panel (f) of Fig. 4) are negative at most grid points. This may indicate a negative correlation between the magnitudes of local water diffusivity and gestational age along the genu of the corpus callosum.

Fig 4.

Plot of estimated effects of intercept, gender, and age (from left to right) and their 95% confidence bands. The upper panels are for FA and the lower panels are for MD. The blue solid curves are the estimated coefficient functions and the red dashed curves are the confidence bands.

We statistically tested the effects of gender and gestational age on FA and MD along the GCC tract. To test the gender effect, we computed the global test statistic S_n = 144.63 and its associated p-value (p = 0.078), indicating a weakly significant gender effect, which agrees with the findings in panels (b) and (e) of Fig. 4. A moderately significant age effect was found with S_n = 929.69 (p-value< 0.001). This agrees with the findings in panel (f) of Fig. 4, indicating that MD along the GCC tract changes moderately with gestational age. Furthermore, for FA and MD, we constructed the 95% simultaneous confidence bands of the varying-coefficients for G_i and age_i (Fig. 4).

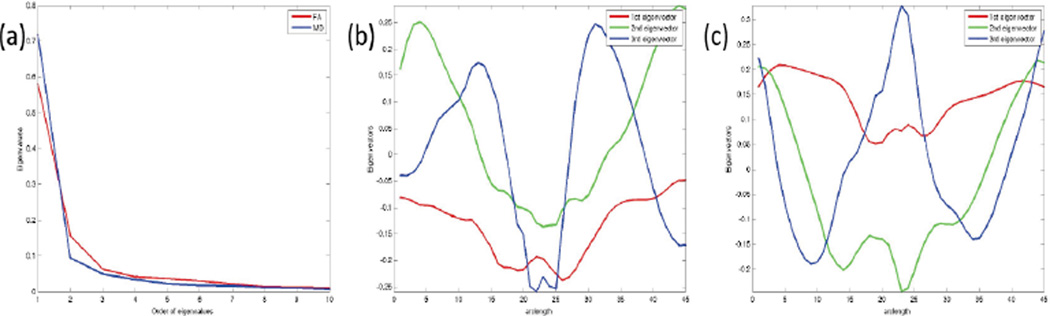
Fig. 5 presents the first 10 eigenvalues and 3 eigenfunctions of Σ̂_η,jj(s, t) for j = 1, 2. The relative eigenvalues of Σ̂_η,jj defined as the ratios of the eigenvalues of Σ̂_η,jj(s, t) over their sum have similar distributional patterns (panel (a) of Fig. 5). We observe that the first three eigenvalues account for more than 90% of the total and the others quickly vanish to zero. The eigenfunctions of FA corresponding to the largest three eigenvalues (Fig. 5 (b)) are different from those of MD (Fig. 5 (c)).

Fig 5.

Plot of the first 10 eigenvalues (a) and the first 3 eigenfunctions for FA (b) and MD (c).

In the supplementary document, we further illustrate the proposed methodology by an empirical analysis of another real data set.

Appendix

We introduce some notation. We define

$$T_{B,j}(h,s)={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{m=1}^M}{K}_h(s_m-s)[{\mathbf{x}}_i\otimes {\mathbf{z}}_h(s_m-s)]{\mathbf{x}}_i^T{B}_j(s_m),$$

$$T_{\eta ,j}(h,s)={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{m=1}^M}{K}_h(s_m-s)[{\mathbf{x}}_i\otimes {\mathbf{z}}_h(s_m-s)]{\eta }_{\mathit{\text{ij}}}(s_m),$$ (6.1)

$$T_{\epsilon ,j}(h,s)={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{m=1}^M}{K}_h(s_m-s)[{\mathbf{x}}_i\otimes {\mathbf{z}}_h(s_m-s)]{\epsilon }_{\mathit{\text{ij}}}(s_m),$$

$$r_u(K;s,h)=\frac{u_2{(K;s,h)}^2-u_1(K;s,h)u_3(K;s,h)}{u_0(K;s,h)u_2(K;s,h)-u_1{(K;s,h)}^2},$$

$$H_h(s_m-s)=K_h(s_m-s){\mathbf{z}}_h(s_m-s),$$

$${\mathrm{\Delta }}_j(s;{\mathit{\eta }}_i,h_{1j})=M^{-1}{\displaystyle \sum _{m=1}^M}{H}_{h_{1j}}(s_m-s){\eta }_{\mathit{\text{ij}}}(s_m)-{\displaystyle {\int }_0^1}{H}_{h_{1j}}(u-s){\eta }_{\mathit{\text{ij}}}(u)\pi (u)\mathit{\text{du}}.$$

where $u_r(K;s,h)={\displaystyle {\int }_0^1}{h}^{-r}{(u-s)}^r{K}_h(u-s)\mathit{\text{du}}$. Throughout the proofs, C_ks stand for a generic constant, and it may vary from line to line.

The proofs of Theorems 1–5 rely on the following lemmas whose proofs are given in the supplementary document.

Lemma 1. Under Assumptions (C1), (C3)–(C5), and (C7), we have that for each j,

$$\underset{s\in [0,1]}{\text{sup}}{n}^{-1/2}{h}_{1j}|T_{\epsilon ,j}(h_{1j},s)|=O_p(\sqrt{{\mathit{\text{Mh}}}_{1j}|\text{log }{h}_{1j}|})=o_p({\mathit{\text{Mh}}}_{1j}).$$ (6.2)

Lemma 2. Under Assumptions (C1), (C4), (C5), and (C7), we have that for any r ≥ 0 and j,

$$\underset{s\in [0,1]}{\text{sup}}|{\displaystyle \int }{K}_{h_{1j}}(u-s)\frac{{(u-s)}^r}{h_{1j}^r}d[{\mathrm{\Pi }}_M(u)-\mathrm{\Pi }(u)]|=O_p({({\mathit{\text{Mh}}}_{1j})}^{-1/2}),$$

$$\underset{s\in [0,1]}{\text{sup}}|{\displaystyle \int }{K}_{h_{1j}}(u-s)\frac{{(u-s)}^r}{h_{1j}^r}{\epsilon }_{\mathit{\text{ij}}}(u)d{\mathrm{\Pi }}_M(u)|=O_p({({\mathit{\text{Mh}}}_{1j})}^{-1/2}\sqrt{|\text{log }{h}_{1j}|}),$$

where Π_M(·) is the sampling distribution function based on 𝒮 = {s₁,…, s_M} and Π(·) is the distribution function of s_m.

Lemma 3. Under Assumptions (C2)–(C5), we have

$$\underset{s\in [0,1]}{\text{sup}}|n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i\otimes {\mathrm{\Delta }}_j(s;{\mathit{\eta }}_i,h_{1j})|=o_p(1).$$ (6.3)

Lemma 4. If Assumptions (C1) and (C3)–(C6) hold, then we have

$$\mathrm{E}[{\mathrm{B̂}}_j(s)|𝒮]-B_j(s)=0.5h_{1j}^2{u}_2(K){\mathrm{B̈}}_j(s)[1+o_p(1)],$$ (6.4)

$$\text{Var}[{\mathrm{B̂}}_j(s)|𝒮]=n^{-1}{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,s){\mathrm{\Omega }}_X^{-1}[1+o_p(1)],$$

where e_n(s) = O_p((Mh_1j)^−1/2) with E[e_n(s)] = 0.

Lemma 5. If Assumptions (C1) and (C3)–(C6) hold, then for s = 0 or 1, we have

$$E[{\mathrm{B̂}}_j(s)|𝒮]-B_j(s)=0.5h_{1j}^2{r}_u(K;s,h_{1j}){\mathrm{B̈}}_j(s)[1+o_p(1)],$$ (6.5)

$$\text{Var}[{\mathrm{B̂}}_j(s)|𝒮]=n^{-1}{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,s){\mathrm{\Omega }}_X^{-1}[1+o_p(1)].$$

Lemma 6. Under Assumptions (C1)–(C9a), we have

$$\underset{(s,t)}{\text{sup }}{n}^{-1}|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)|=O_p(n^{-1/2}{(\text{log }n)}^{1/2}),$$

$$\underset{(s,t)}{\text{sup }}{n}^{-1}|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s)\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(t)|=O_p(n^{-1/2}{(\text{log }n)}^{1/2}),$$

$$\underset{s}{\text{sup }}{n}^{-1}|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\mathbf{x}}_i|=O_p(n^{-1/2}{(\text{log }n)}^{1/2}),$$

$$\underset{s}{\text{sup }}{n}^{-1}|{\displaystyle \sum _{i=1}^n}\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s){\mathbf{x}}_i|=O_p(n^{-1/2}{(\text{log }n)}^{1/2}).$$

Lemma 7. Under Assumptions (C1)–(C9a), we have

$$\underset{(s,t)}{\text{sup }}{n}^{-1}|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(t)|=O({({\mathit{\text{Mh}}}_{2j})}^{-1}+{(\text{log }n/n)}^{1/2})=o_p(1).$$

We present only the key steps in the proof of Theorem 1 below.

Proof of Theorem 1. Define

$${\mathbf{U}}_2(K;s,\mathbf{H})=\text{diag}(r_u(K;s,h_{11}),\dots ,r_u(K;s,h_{1J})),$$

$$X_n(s)=\sqrt{n}\{\mathbf{B̂}(s)-E[\mathbf{B̂}(s)|𝒮]\},X_{n,j}(s)=\sqrt{n}\{{\mathrm{B̂}}_j(s)-E[{\mathrm{B̂}}_j(s)|𝒮]\}.$$

According to the definition of vec(Â_j(s)), it is easy to see that

$$\text{vec}({Â}_j(s))=\mathrm{\Sigma }{(s,h_{1j})}^{-1}[T_{B,j}(h_{1j},s)+T_{\epsilon ,j}(h_{1j},s)+T_{\eta ,j}(h_{1j},s)].$$ (6.6)

$$X_{n,j}(s)=\sqrt{n}[{\mathbf{I}}_p\otimes (1,0)]\mathrm{\Sigma }{(s,h_{1j})}^{-1}[T_{\epsilon ,j}(h_{1j},s)+T_{\eta ,j}(h_{1j},s)].$$ (6.7)

The proof of Theorem 1 (i) consists of two parts.

• Part 1 is to show that $\sqrt{n}\mathrm{\Sigma }{(s,h_{1j})}^{-1}{T}_{\epsilon ,j}(h_{1j,}s)=o_p(1)$ holds uniformly for all s ∈ [0, 1] and j = 1, …, J.

• Part 2 is to show that $\sqrt{n}\mathrm{\Sigma }{(s,h_{1j})}^{-1}{T}_{\eta ,j}(h_{1j,}s)=o_p(1)$ converges weakly to a Gaussian process G(·) with mean zero and covariance matrix ${\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,s\prime ){\mathrm{\Omega }}_X^{-1}$ for each j.

In part 1, we show that

$$\sqrt{n}[{\mathbf{I}}_p\otimes (1,0)]\mathrm{\Sigma }{(s,h_{1j})}^{-1}{T}_{\epsilon ,j}(h_{1j},s)=o_p(1).$$ (6.8)

It follows from Lemma 1 that

$$n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i\otimes \{M^{-1}{\displaystyle \sum _{m=1}^M}{K}_{h_{1j}}(s_m-s){\mathbf{z}}_{h_{1j}}(s){\epsilon }_{i,j}(s_m)\}=o_p(1)$$

hold uniformly for all s ∈ [0, 1]. It follows from Lemma 2 that

$${(\mathit{\text{nM}})}^{-1}\mathrm{\Sigma }(s,h_{1j})={\mathrm{\Omega }}_X\otimes {\mathrm{\Omega }}_1(h_{1j},s)+o_p(1)$$ (6.9)

hold uniformly for all s ∈ [0, 1]. Based on these results, we can finish the proof of (6.8).

In part 2, we show the weak convergence of $\sqrt{n}[{\mathbf{I}}_p\otimes (1,0)]\mathrm{\Sigma }{(s,h_{1j})}^{-1}{T}_{\eta ,j}(h_{1j,}s)$ for j = 1, …, J. The part 2 consists of two steps. In Step 1, it follows from the standard central limit theorem that for each s ∈ [0, 1],

$$\sqrt{n}[{\mathbf{I}}_p\otimes (1,0)]\mathrm{\Sigma }{(s,h_{1j})}^{-1}{T}_{\eta ,j}(h_{1j},s){\to }^{L}N(\mathbf{0},{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,s){\mathrm{\Omega }}_X^{-1}),$$ (6.10)

where →^L denotes convergence in distribution.

Step 2 is to show the asymptotic tightness of $\sqrt{n}[{\mathbf{I}}_p\otimes (1,0)]\mathrm{\Sigma }{(s,h_{1j})}^{-1}{T}_{\eta ,j}(h_{1j,}s)$. By using (6.9) and (6.1), $\sqrt{n}\mathrm{\Sigma }{(s,h_{1j})}^{-1}{T}_{\eta ,j}(h_{1j,}s)[1+o_p(1)]$ can be approximated by the sum of three terms (I), (II), and (III) as follows:

$$(\mathrm{I})=n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathrm{\Omega }}_X^{-1}{\mathbf{x}}_i\otimes {\mathrm{\Omega }}_1{(h_{1j},s)}^{-1}{\mathrm{\Delta }}_j(s;{\mathit{\eta }}_i,h_{1j}),$$ (6.11)

$$(\text{II})=n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathrm{\Omega }}_X^{-1}{\mathbf{x}}_i\otimes {\mathrm{\Omega }}_1{(h_{1j},s)}^{-1}{\eta }_{\mathit{\text{ij}}}(s){\displaystyle {\int }_{\text{max}(-{\mathit{\text{sh}}}_{1j}^{-1},-1)}^{\text{min}((1-s)h_{1j}^{-1},1)}}K(u){(1,u)}^T\pi (s+h_{1j}u)\mathit{\text{du}},$$

$$(\text{III})=n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathrm{\Omega }}_X^{-1}{\mathbf{x}}_i\otimes {\mathrm{\Omega }}_1{(h_{1j},s)}^{-1}$$

$${\displaystyle {\int }_{\text{max}(-{\mathit{\text{sh}}}_{1j}^{-1},-1)}^{\text{min}((1-s)h_{1j}^{-1},1)}}K(u)(\begin{array}{c}\hfill 1\hfill \\ \hfill u\hfill \end{array})[{\eta }_{\mathit{\text{ij}}}(s+h_{1j}u)-{\eta }_{\mathit{\text{ij}}}(s)]\pi (s+h_{1j}u)\mathit{\text{du}}.$$

We investigate the three terms on the right hand side of (6.11) as follows. It follows from Lemma 3 that the first term on the right hand side of (6.11) converges to zero uniformly. We prove the asymptotic tightness of (II) as follows. Define

$${\mathrm{X̂}}_{n,j}(s)=n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathrm{\Omega }}_X^{-1}{\mathbf{x}}_i\otimes (1,0){\mathrm{\Omega }}_1{(h_{1j},s)}^{-1}{\eta }_{\mathit{\text{ij}}}(s){\displaystyle {\int }_{\text{max}(-{\mathit{\text{sh}}}_{1j}^{-1},-1)}^{\text{min}((1-s)h_{1j}^{-1},1)}}K(u){(1,u)}^T\pi (s+h_{1j}u)\mathit{\text{du}}.$$

Thus, we only need to prove the asymptotic tightness of X̂_n,j(s). The asymptotic tightness of X̂_n,j(s) can be proved using the empirical process techniques [42]. It follows that

$$(1,0){\mathrm{\Omega }}_1{(h_{1j},s)}^{-1}{\displaystyle {\int }_{\text{max}(-{\mathit{\text{sh}}}_{1j}^{-1},-1)}^{\text{min}((1-s)h_{1j}^{-1},1)}}K(u){(1,u)}^T\pi (s+h_{1j}u)\mathit{\text{du}}=\frac{u_2(K;s,h_{1j})u_0(K;s,h_{1j})-u_1{(K;s,h_{1j})}^2+o(h_{1j})}{u_2(K;s,h_{1j})u_0(K;s,h_{1j})-u_1{(K;s,h_{1j})}^2+o(h_{1j})}=1+o(h_{1j}).$$

Thus, X̂_n,j(s) can be simplified as

$${\mathrm{X̂}}_{n,j}(s)=[1+o(h_{1j})]n^{-1/2}{\displaystyle \sum _{i=1}^n}{\eta }_{\mathit{\text{ij}}}(s){\mathrm{\Omega }}_X^{-1}{\mathbf{x}}_i.$$

We consider a function class ${ℰ}_{\eta }=\{f(s;\mathbf{x},{\eta }_{·,j})={\mathrm{\Omega }}_X^{-1}\mathbf{x}{\eta }_{·,j}(s):s\in [0,1]\}$. Due to Assumption C2, ℰ_η is a P−Donsker class.

Finally, we consider the third term (III) on the right hand side of (6.11). It is easy to see that (III) can be written as

$${\mathrm{\Omega }}_X^{-1}\otimes {\mathrm{\Omega }}_1{(h_{1j},s)}^{-1}{\displaystyle {\int }_{\text{max}(-{\mathit{\text{sh}}}_{1j}^{-1},-1)}^{\text{min}((1-s)h_{1j}^{-1},1)}}K(u)$$

$$[n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i\{{\eta }_{\mathit{\text{ij}}}(s+h_{1j}u)-{\eta }_{\mathit{\text{ij}}}(s)\}]\otimes (\begin{array}{c}\hfill 1\hfill \\ \hfill u\hfill \end{array})\pi (s+h_{1j}u)\mathit{\text{du}}.$$

Using the same argument of proving the second term (II), we can show the asymptotic tightness of $n^{-1/2}{\displaystyle {\sum }_{i=1}^n}{\mathbf{x}}_i{\eta }_{\mathit{\text{ij}}}(s)$. Therefore, for any h_1j → 0,

$$\underset{s\in [0,1],|u|\le 1}{\text{sup}}|n^{-1/2}{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i\{{\eta }_{\mathit{\text{ij}}}(s+h_{1j}u)-{\eta }_{\mathit{\text{ij}}}(s)\}|=o_p(1).$$ (6.12)

It follows from Assumptions (C5) and (C7) and (6.12) that (III) converges to zero uniformly. Therefore, we can finish the proof of Theorem 1 (i). Since Theorem 1 (ii) is a direct consequence of Theorem 1 (i) and Lemma 4, we finish the proof of Theorem 1.

Proof of Theorem 2. Proofs of Parts (a)—(d) are completed by some straightforward calculations. Detailed derivation is given in the supplemental document. Here we prove Part (e) only. Let K̃_M,h(s) = K̃_M(s/h)/h, where K̃_M(s) is the empirical equivalent kernels for the first-order local polynomial kernel [11]. Thus, we have

$${\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)-{\eta }_{\mathit{\text{ij}}}(s)={\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{M,h_{2j}}(s_m-s){\mathbf{x}}_i^T[B_j(s_m)-{\mathrm{B̂}}_j(s_m)]+{\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{M,h_{2j}}(s_m-s)[{\eta }_{\mathit{\text{ij}}}(s_m)+{\epsilon }_{\mathit{\text{ij}}}(s_m)-{\eta }_{\mathit{\text{ij}}}(s)].$$ (6.13)

We define

$${\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s)={\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{M,h_{2j}}(s_m-s){\epsilon }_{\mathit{\text{ij}}}(s_m),$$

$$\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s)={\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{M,h_{2j}}(s_m-s)[{\eta }_{\mathit{\text{ij}}}(s_m)-{\eta }_{\mathit{\text{ij}}}(s)],$$

$$\mathrm{\Delta }{B}_j(s)={\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{M,h_{2j}}(s_m-s)[B_j(s_m)-{\mathrm{B̂}}_j(s_m)],$$

$${\mathrm{\Delta }}_{\mathit{\text{ij}}}(s)={\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s)+\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s)+{\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s).$$

It follows from (6.13) that

$${\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)-{\eta }_{\mathit{\text{ij}}}(s)={\mathrm{\Delta }}_{\mathit{\text{ij}}}(s)={\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s)+\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s)+{\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s).$$ (6.14)

It follows from Lemma 2 and a Taylor’s expansion that

$$\underset{s\in [0,1]}{\text{sup}}|{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s)|=O_p(\sqrt{\frac{|\text{log}(h_{2j})|}{{\mathit{\text{Mh}}}_{2j}}})\text{ and }\underset{s\in [0,1]}{\text{sup}}|\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s)|=O_p(1)\underset{s\in [0,1]}{\text{sup}}|{\mathrm{\eta ̈}}_{\mathit{\text{ij}}}(s)|h_{1j}^{(2)2}.$$

Since $\sqrt{n}\{{\mathrm{B̂}}_j(·)-B_j(·)-0.5u_2{(K)}^2{h}_{1j}^2{\mathrm{B̈}}_j(·)[1+o_p(1)]\}$ weakly converges to a Gaussian process in ℓ^∞([0, 1]) as n → ∞, $\sqrt{n}\{{\mathrm{B̂}}_j(·)-B_j(·)-0.5u_2{(K)}^2{h}_{1j}^2{\mathrm{B̈}}_j(·)[1+o_p(1)]\}$ is asymptotically tight. Thus, we have

$$\mathrm{\Delta }{B}_{\mathit{\text{ij}}}(s)=-{\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{M,h_{2j}}(s_j-s)0.5u_2{(K)}^2{h}_{1j}^2{\mathrm{B̈}}_j(s_m)[1+o_p(1)]+{\displaystyle \sum _{m=1}^M}{\mathrm{K̃}}_{M,h_{2j}}(s_j-s)\{0.5u_2{(K)}^2{h}_{1j}^2{\mathrm{B̈}}_j(s_m)[1+o_p(1)]+B_j(s_m)-\mathrm{B̂}(s_m)\},\underset{s\in [0,1]}{\text{sup}}\Vert \mathrm{\Delta }{B}_j(s)\Vert =O_p(n^{-1/2})+O_p(h_{1j}^2).$$

Combining these results, we have

$$\underset{s\in [0,1]}{\text{sup}}|{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s)-{\eta }_{\mathit{\text{ij}}}(s)|=O_p(|\text{log}(h_{2j}){|}^{1/2}{({\mathit{\text{Mh}}}_{2j})}^{-1/2}+h_{1j}^{(2)2}+h_{1j}^2+n^{-1/2}).$$

This completes the proof of Part (e).

Proof of Theorem 3. Recall that η̂_ij(s) = η_ij(s) + Δ_i,j(s), we have

$$n^{-1}{\displaystyle \sum _{i=1}^n}{\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(s){\mathrm{\eta ̂}}_{\mathit{\text{ij}}}(t)=n^{-1}{\displaystyle \sum _{i=1}^n}{\mathrm{\Delta }}_{\mathit{\text{ij}}}(s){\mathrm{\Delta }}_{\mathit{\text{ij}}}(t)+n^{-1}{\displaystyle \sum _{i=1}^n}{\eta }_{\mathit{\text{ij}}}(s){\mathrm{\Delta }}_{\mathit{\text{ij}}}(t)+n^{-1}{\displaystyle \sum _{i=1}^n}{\mathrm{\Delta }}_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)+n^{-1}{\displaystyle \sum _{i=1}^n}{\eta }_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t).$$ (6.15)

This proof consists of two steps. The first step is to show that the first three terms on the right hand side of (6.15) converge to zero uniformly for all (s, t) ∈ [0, 1]² in probability. The second step is to show the uniform convergence of $n^{-1}{\displaystyle {\sum }_{i=1}^n}{\eta }_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)$ to Σ_η(s, t) over (s, t) ∈ [0, 1]² in probability.

We first show that

$$\underset{(s,t)}{\text{sup}}{n}^{-1}|{\displaystyle \sum _{i=1}^n}{\mathrm{\Delta }}_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)|=O_p(n^{-1/2}+h_{1j}^2+h_{2j}^2+{(\text{log }n/n)}^{1/2}).$$ (6.16)

Since

$${\displaystyle \sum _{i=1}^n}{\mathrm{\Delta }}_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)\le n^{-1}\{|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)|+|{\displaystyle \sum _{i=1}^n}\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)|+|{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s){\eta }_{\mathit{\text{ij}}}(t)|\},$$ (6.17)

it is sufficient to focus on the three terms on the right-hand side of (6.17). Since

$$|{\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s){\eta }_{\mathit{\text{ij}}}(t)|\le {\Vert {\mathbf{x}}_i\Vert }_2\underset{s\in [0,1]}{\text{sup}}{\Vert \mathrm{\Delta }{B}_k(s)\Vert }_2\underset{t\in [0,1]}{\text{sup}}|{\eta }_{\mathit{\text{ij}}}(t)|,$$

we have

$$n^{-1}|{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s){\eta }_{\mathit{\text{ij}}}(t)|\le \underset{s\in [0,1]}{\text{sup}}{\Vert \mathrm{\Delta }{B}_k(s)\Vert }_2{n}^{-1}{\displaystyle \sum _{i=1}^n}{\Vert {\mathbf{x}}_i\Vert }_2|{\eta }_{\mathit{\text{ij}}}(t)|=O_p(n^{-1/2}+h_{1j}^2).$$

Similarly, we have

$$n^{-1}|{\displaystyle \sum _{i=1}^n}\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)|\le n^{-1}{\displaystyle \sum _{i=1}^n}\underset{s,t\in [0,1]}{\text{sup}}|\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)|=O_p(h_{1j}^{(2)2})=o_p(1).$$

It follows from Lemma 6 that ${\text{sup}}_{(s,t)}{n}^{-1}\{|{\displaystyle {\sum }_{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)|=O({(\text{log }n/n)}^{1/2})$. Similarly, we can show that ${\text{sup}}_{(s,t)}{n}^{-1}|{\displaystyle {\sum }_{i=1}^n}{\mathrm{\Delta }}_{\mathit{\text{ij}}}(t){\eta }_{\mathit{\text{ij}}}(s)|=O_p(n^{-1/2}+h_{1j}^2+h_{2j}^2+{(\text{log }n/n)}^{1/2})$.

We can show that

$$\underset{(s,t)}{\text{sup}}|n^{-1}{\displaystyle \sum _{i=1}^n}[{\eta }_{\mathit{\text{ij}}}(s){\eta }_{\mathit{\text{ij}}}(t)-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)]|=O_p(n^{-1/2}).$$ (6.18)

Note that

$$|{\eta }_{\mathit{\text{ij}}}(s_1){\eta }_{\mathit{\text{ij}}}(t_1)-{\eta }_{\mathit{\text{ij}}}(s_2){\eta }_{\mathit{\text{ij}}}(t_2)|\le 2(|s_1-s_2|+|t_1-t_2|)\underset{s\in [0,1]}{\text{sup}}|{\mathrm{\eta ̇}}_{\mathit{\text{ij}}}(s)|\underset{s\in [0,1]}{\text{sup}}|{\eta }_{\mathit{\text{ij}}}(s)|$$

holds for any (s₁, t₁) and (s₂, t₂), the functional class {η_j(u)η_j(υ) : (u, υ) ∈ [0, 1]²} is a Vapnik and Cervonenkis (VC) class [42, 31]. Thus, it yields that (6.18) is true.

Finally, we can show that

$$\underset{(s,t)}{\text{sup}}{n}^{-1}|{\displaystyle \sum _{i=1}^n}{\mathrm{\Delta }}_{\mathit{\text{ij}}}(s){\mathrm{\Delta }}_{\mathit{\text{ij}}}(t)|=O_p({({\mathit{\text{Mh}}}_{2j})}^{-1}+{(\text{log }n/n)}^{1/2}+h_j^4+h_{1j}^{(2)4}).$$ (6.19)

With some calculations, for a positive constant C₁, we have

$$|{\displaystyle \sum _{i=1}^n}{\mathrm{\Delta }}_{\mathit{\text{ij}}}(s){\mathrm{\Delta }}_{\mathit{\text{ij}}}(t)|\le C_1\underset{(s,t)}{\text{sup}}[|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(t)|+|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s)\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(t)|+|{\displaystyle \sum _{i=1}^n}\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(t){\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s)|+|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(t)|+|{\displaystyle \sum _{i=1}^n}\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s)\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(t)|+|{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s)\mathrm{\Delta }{B}_j(t){\mathbf{x}}_i|].$$

It follows from Lemma 7 that

$$\underset{(s,t)}{\text{sup}}{n}^{-1}|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(t)|=O_p({({\mathit{\text{Mh}}}_{2j})}^{-1}+{(\text{log }n/n)}^{1/2}),$$

$$\underset{(s,t)}{\text{sup}}{n}^{-1}[|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s)\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(t)|+|{\displaystyle \sum _{i=1}^n}\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(t){\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s)|+|{\displaystyle \sum _{i=1}^n}{\mathrm{\epsilon ̅}}_{\mathit{\text{ij}}}(s){\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(t)|]=O_p({(\text{log }n/n)}^{1/2}).$$

Since ${\text{sup}}_{s\in [0,1]}|\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s)|=C_2{\text{sup}}_{s\in [0,1]}|{\mathrm{\eta ̈}}_{\mathit{\text{ij}}}(s)|h_{2j}^2$ we have ${\text{sup}}_{(s,t)}{n}^{-1}|{\displaystyle {\sum }_{i=1}^n}\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(s)\mathrm{\Delta }{\eta }_{\mathit{\text{ij}}}(t)|=O(h_{1j}^{(2)4})$. Furthermore, since ${\text{sup}}_{s\in [0,1]}\Vert \mathrm{\Delta }\mathbf{B}(s)\Vert =O_p(n^{-1/2}+h_j^2)$, we have

$$n^{-1}|{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i^T\mathrm{\Delta }{B}_j(s)\mathrm{\Delta }{B}_j(t){\mathbf{x}}_i|=O_p(n^{-1}+h_j^4).$$

Note that the arguments for (6.16)–(6.19) hold for Σ̂_η,jj′(·, ·) for any j ≠ j′. Thus, combining (6.16)–(6.19) leads to Theorem 3 (i).

To prove Theorem 3 (ii), we follow the same arguments in Lemma 6 of Li and Hsing [32]. For completion, we highlight several key steps below. We define

$$(\mathrm{\Delta }{\psi }_{j,j})(s)={\displaystyle {\int }_0^1}[{\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}(s,t)-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)]{\psi }_{j,j}(t)\mathit{\text{dt}}.$$ (6.20)

Following Hall and Hosseini-Nasab [21] and the Cauchy-Schwarz inequality, we have

$${\{{\displaystyle {\int }_0^1}{[{\mathrm{\psi ̂}}_{j,j}(s)-{\psi }_{j,j}(s)]}^2\mathit{\text{ds}}\}}^{1/2}\le C_2\{{[{\displaystyle {\int }_0^1}{(\mathrm{\Delta }{\psi }_{j,j})(s)]}^2\mathit{\text{ds}}]}^{1/2}+{\displaystyle {\int }_0^1}{\displaystyle {\int }_0^1}{[{\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}(s,t)-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)]}^2\mathit{\text{dsdt}}\}\le C_2{\{{\displaystyle {\int }_0^1}{\displaystyle {\int }_0^1}{[{\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}(s,t)-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)]}^2\mathit{\text{dsdt}}\}}^{1/2}{\{{\displaystyle {\int }_0^1}{[{\psi }_{j,j}(t)]}^2\mathit{\text{dt}}\}}^{1/2}+{\displaystyle {\int }_0^1}{\displaystyle {\int }_0^1}{[{\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}(s,t)-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)]}^2\mathit{\text{dsdt }}\le C_3\underset{(s,t)\in {[0,1]}^2}{\text{sup}}|{\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}(s,t)-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)|,$$

which yields Theorem 3 (ii.a).

Using (4.9) in Hall, Müller and Wang [22], we have

$$|{\mathrm{\lambda ̂}}_{j,j}-{\lambda }_{j,j}|\le |{\displaystyle {\int }_0^1}{\displaystyle {\int }_0^1}[{\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}](s,t){\psi }_{j,j}(s){\psi }_{j,j}(t)\mathit{\text{dsdt}}+O({\displaystyle {\int }_0^1}(\mathrm{\Delta }{\psi }_{j,j}){(s)}^2\mathit{\text{ds}})\le C_4\underset{(s,t)\in {[0,1]}^2}{\text{sup}}|{\mathrm{\Sigma ̂}}_{\eta ,\mathit{\text{jj}}}(s,t)-{\mathrm{\Sigma }}_{\eta ,\mathit{\text{jj}}}(s,t)|,$$

which yields Theorem 3 (ii.b). This completes the proof.

Proof of Theorem 5. The proof of Theorem 5 is given in the supplementary material of this paper.