Evidence of Abnormal Lower-Limb Torque Coupling After Stroke

Abstract

Background and Purpose

Although stroke survivors often display abnormal joint torque patterns, studies of torque-coupling in the lower limb are lacking, despite their potential impact on gait abnormalities.

Methods

Twenty-two chronic ambulating stroke subjects and 11 age-matched control subjects produced isometric hip torques in the frontal and sagittal planes with the hemiparetic leg (or randomly selected leg for the control group) in postures that resemble stages of gait. The involuntary knee torques were also recorded although no feedback or instructions were given.

Results

In the toe-off and midswing postures, the stroke group had a significant torque bias toward extension and adduction, whereas the control group had a symmetric torque space. The stroke group also produced significantly smaller torques than the control group in the flexion and abduction/flexion directions. Finally, the stroke group displayed abnormal coupling of knee extension with hip adduction, unique to the toe-off position.

Conclusions

Whereas gait abnormalities after stroke have been attributed to a number of factors, including sagittal plane strength impairments at the hip, knee, and ankle, our findings indicate that neuromechanical changes after stroke may play a significant role in determining the nature of the movement abnormality. Specifically, abnormal hip adduction and knee extension torque coupling was observed, in addition to direction-specific hip torque weakness. Future studies are needed to delineate the differential contributions of each potential factor to gait abnormalities. Understanding the underlying neuromechanical changes after stroke may aid the development of rehabilitation strategies.

Coordinated lower-limb movements require the intact nervous system to master redundancy in the musculo-skeletal system, which can be accomplished through neurophysiological constraints to reduce the degrees-of-freedom.^1,2 These constraints are likely influenced by brain injury, resulting in abnormal walking patterns. For example, some individuals poststroke use circumduction (a combination of pelvic obliquity³ and thigh abduction⁴) to clear the toe during swing.⁵ Although these movement adaptations may be successful in improving independence, weight support, and speed,^4,6 such maladaptive strategies increase energy expenditure during ambulation⁷ and can result in unstable walking patterns.⁸

Abnormal lower-limb kinematics during the swing phase of walking may be due to the manifestation of detrimental multijoint isometric torque-coupling. In the upper extremity, abnormal coupling of shoulder and elbow torques have been identified in chronic stroke subjects during isometric force production protocols.⁹ Moreover, stroke subjects produce abnormal trajectories during free reaching in directions that require elbow and shoulder torques that deviate from the torque-couplings found under isometric conditions.¹⁰ These findings suggest that upper-extremity movement abnormalities may be a manifestation of additional neural constraints on motor outflow that can be evaluated under isometric conditions.¹¹ However, similar findings in the lower limb are described only anecdotally.¹²

Given that disturbances of natural hip movements after stroke are found in the frontal and sagittal planes (eg, circumduction), we seek to investigate the frontal and sagittal plane kinetics at the hemiparetic hip joints of chronic stroke subjects under isometric conditions. In this study, stroke and control subjects produced voluntary hip torques in 8 target directions using real-time visual feedback. We hypothesize that stroke survivors will exhibit a reduction in the kinetic output of the hip compared with healthy controls. The kinetic output is defined by the area of the isometric hip torques in the transverse plane (flexion/extension, abduction/adduction and combination torques) and will be defined herein as the hip torque workspace. Based on previous findings,^13,14 we further hypothesize that this reduction in hip-torque work-space will be asymmetric with larger reductions in specific directions, including flexion. Given that gait abnormalities poststroke involve the hip frontal plane and knee sagittal plane kinematics, we hypothesize that lower limb, across-joint torque coupling between the hip frontal and knee sagittal torques will also be observed. Consistent with clinical observations,¹⁵ we further hypothesize that this coupling will be dependent on limb posture. The nature of this coupling will be explored by examining the unintended knee torques measured during the hip isometric tasks. By clarifying the underlying impairments of the lower extremity, more efficacious methods of improving poststroke gait performance may be developed.

Materials and Methods

Experimental Set-Up and Protocol

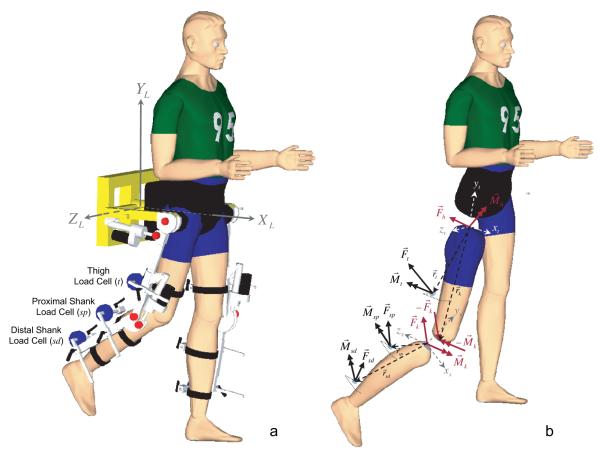
Subjects were secured in a computer-controlled, motorized, instrumented exoskeleton (see Figure 1a). The orthosis’ dimensions were adjusted for each participant to align the orthosis joint centers with those of the subject. The subject’s lower extremities were secured to the orthosis via cuffs instrumented with six-degree-of-freedom load cells to measure the interaction forces/moments between the subject and the orthosis. The pelvis was also strapped to the exoskeleton. The unloaded test limb was completely supported by the experimental set-up; subjects did not have to actively support the limb before or during the torque production tasks. In light of our preliminary results, to provide functionally relevant, yet comfortable, load-bearing levels on the contralateral limb during a relatively long experiment (45 to 90 minutes), 30% to 40% body-weight support was provided via a harness.

Figure 1.

a, Testing setup. Motorized, instrumented exoskeletal orthosis with three 6-degrees of freedom load cells (JR3, Woodland, CA) on the leg attachment. b, Free body diagram of forces and torques acting on the human leg segments (shank and thigh) during the hip torque generation tasks.

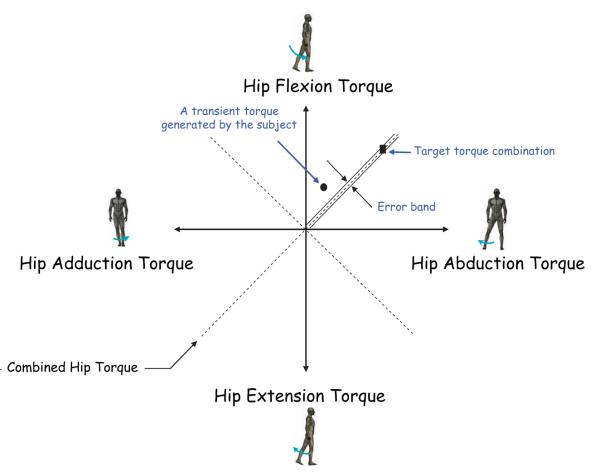
Before the initiation of a trial, subjects were instructed to relax and the load cells were zeroed such that any measured torques reflected muscle activation only. Participants were familiarized with the set-up and the experimental protocol. Subjects were asked to produce voluntary isometric hip torques in 8 directions (flexion, extension, abduction, adduction, flexion/abduction, flexion/adduction, extension/abduction, and extension/adduction) as shown in Figure 2. The hip torques were presented in real-time by the position of a cursor on a computer display (see Figure 2). These hip torques were defined as the primary (intended) torques and were calculated from the thigh, proximal shank, and distal shank load cell signals (Figure 1a; acquired at 1000 Hz sampling rate) using static equilibrium (see Figure 1b). See Supplemental section at http://stroke.ahajournals.org for further details.

Figure 2.

Schematic of target matching 2-D display. The circular cursor (●) shows the torque produced by the subject en route to the target (■).

The experimental procedure consisted of 2 parts: (1) measurement of the maximum voluntary hip torques (MVHT) along 8 torque directions and (2) testing at 50% of the MVHT. Subjects were given three 30-second opportunities to achieve a MVHT within ±5° of the target torque direction and hold it for 200 ms. The largest value was used to calculate the magnitude of target torques in part 2. In the target-matching phase of the experiment, subjects were presented with targets (50% MVHT) in the 8 directions, in the order the MVHT were collected. Subjects were instructed to produce the hip-target torque and hold for 200 ms. A successful trial was defined when ±5% of the magnitude and ±5° of the target direction were reached.

To investigate the influence of biomechanics on the torque-producing capabilities of stroke and control subjects, 2 test postures were examined. The first posture, defined in this study as the “toe-off” posture, was at 15° hip extension and 45° knee flexion. The second posture was at 10° hip flexion and 65° knee flexion and was defined in this study as the “midswing” posture. The toe-off posture was selected to examine the lower-limb torques at the initiation point of the swing phase, where abnormal gait behavior is observed in stroke subjects. The control gait hip- and knee-joint angles were chosen because, unlike stroke gait,⁴ lower-limb joint angles are fairly consistent across subjects. The second posture (midswing) was chosen to study the influence of biomechanics on the torque output. While the hip target-matching torques were produced, subjects were unaware that the knee flexion/extension torque measurements were recorded simultaneously. Specific instruction regarding the kinetic outflow at the knee joint would have confounded the ability to investigate the intrinsic across-joint coupling during the hip-joint torque generation tasks and hence no instructions/feedback of knee torque was provided.

Data Analysis

The load cell signals were filtered off-line using a 4th order Butterworth, low-pass, and zero-phase digital filter with a 50-Hz cutoff frequency. The effect of height and weight were accounted for by normalizing the measured torques to the subject’s lower extremity inertias. See Supplemental section for further details.

Circular statistics provide quantitative measures of the orientation and focus of a distribution in space and are quantified by mean vector direction and dispersion about the mean.^12,16 In this case, the hip sagittal plane/frontal plane workspaces of normalized torque amplitudes as a function of posture were analyzed. The resultant vector, R, is the vector sum of normalized torque magnitudes T_i over all target directions:

$$R=\sum _1^n{T}_i\cdot \left[\begin{array}{c}\hfill x_i\hfill \\ \hfill y_i\hfill \end{array}\right],$$

where x_i and y_i are the direction cosines of the moment vector direction. The dispersion of data about the mean direction is defined by the normalized magnitude of the resultant vector. This is equivalent to the resultant vector magnitude divided by the sum of the magnitudes in all directions:

$$q=\frac{R}{\sum _1^n{T}_i},$$

where q ranges from 0 to 1. A value close to 0 indicates torque is achievable in all directions, whereas q=1 means the subject’s torque is primarily biased in a specific direction indicating an extremely limited torque workspace. The torque spaces were tested for directionality using the Rayleigh Test. The null hypothesis is the data are uniformly distributed around the circle. If the distribution is nonuni-form and unimodal, the resultant vector direction is termed the achievable torque direction.^12,16

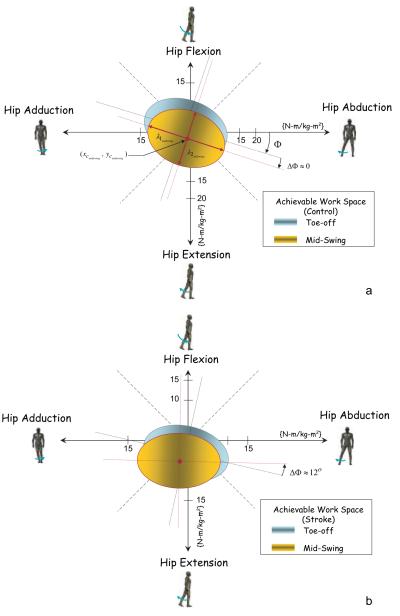
In addition to the statistical analysis, a geometric summary of the achievable workspace at both postures was created using an elliptical least squares fit¹⁷ of the measured torque data across all subjects. Each ellipse was identified by 5 quantities: two principal directions (λ₁; λ₂) with the largest value (maximum (λ₁; λ₂)) representing the bias in the torque production; an angular orientation defining the direction of the bias (Φ); and two centroidal coordinates (x_c; y_c).

The distributions of the knee torque (flexion or extension) produced during each frontal plane hip torque task (abduction and adduction) were tested for differences between groups using a χ² test.¹⁸ As the χ² test distinguishes inhomogeneity of distributions, but not specific differences in group behaviors, nonparametric tests on the knee torques were also performed to determine whether the observed torques differed significantly from zero. For both the χ² analysis and the nonparametric tests, statistical significance was set at P=0.05.

Results

Twenty-two ambulating stroke survivors and 11 age-matched controls were tested (see Table, a and b). The mean age of the stroke group (15 males) was 56.3 years (SD 9.1) and 49.9 years (SD 11.8) for the control group (5 males; P>0.05). The hemiparetic limb was tested for the stroke subjects, whereas a randomly assigned limb was evaluated for the control subjects. Experimental procedures were approved by the Institutional Review Board of Northwestern University and informed consent was obtained before testing. See Supplemental section for further inclusion/exclusion criteria.

Table. Demographic Data for the Hemiparetic (a) and Control (b) Groups.

a. Subject	Age	Gender	Race/Ethnicity	Affected Side	Time Since Stroke, mo	Height, cm	Weight, kg
S1	55	M	White	R-Hemi	28	175.26	70.5
S2	75	M	White	R-Hemi	49	185.4	94.1
S3	40	M	Black	L-Hemi	83	165.1	88.6
S4	49	M	White	R-Hemi	26	182.9	102.3
S5	57	F	White	R-Hemi	47	172.7	90.5
S6	57	F	Black	R-Hemi	20	158.8	54.5
S7	56	F	White	L-Hemi	109	160	47.7
S8	56	M	Black	R-Hemi	156	167.6	92.3
S9	70	M	White	L-Hemi	94	175.3	78.6
S10	60	F	White	L-Hemi	34	172.72	72.7
S11	57	M	White	R-Hemi	24	175.3	79.5
S12	37	M	Asian	R-Hemi	41	180.34	113.6
S13	53	F	White	R-Hemi	226	171.5	61.4
S14	60	M	White	R-Hemi	60	180.3	111.4
S15	65	M	Black	L-Hemi	148	162.6	75.5
S16	59	M	Black	R-Hemi	103	167.6	76.8
S17	58	M	White	L-Hemi	18	180.34	77.3
S18	51	M	Black	R-Hemi	24	180.3	84.1
S19	39	M	White	R-Hemi	33	180.3	79.5
S20	57	F	Black	L-Hemi	156	152.4	53.6
S21	62	M	Hispanic	L-Hemi	172	167.6	93.2
S22	59	F	Black	L-Hemi	43	154.9	60
Average	56.3	M=15		R=13	77	171.3	79.9
SD	9.1				60.3	9.4	17.8
b. Subject	Age	Gender	Race/Ethnicity	Tested	Side	Height, cm	Weight, kg
C1	59	M	White	R		180.3	79.5
C2	51	M	White	R		157.5	93.2
C3	31	M	White	L		185.4	79.5
C4	62	F	White	R		171.5	66.4
C5	59	F	White	R		167.6	65.9
C6	60	F	White	R		160	59.1
C7	55	F	Black	L		162.6	57.3
C8	41	F	White	R		165.1	51.8
C9	47	M	White	L		180.3	95.5
C10	28	F	White	R		157.5	61.4
C11	56	M	Black	R		177.8	81.8
Average	49.9	M=5		R=8		169.6	71.9
SD	11.8					10.0	14.8

Stroke subjects had more variability in strength levels contingent on torque direction compared with controls. The average maximum normalized hip torques for the stroke subjects at toe-off were 10.23 Nm/Kgm² for flexion, 17.52 Nm/Kgm² for extension, 13.50 Nm/Kgm² for abduction, and 13.67 Nm/Kgm² for adduction. There was no statistical difference between torque magnitude in the abduction and adduction directions. However, the flexion torque was significantly less than the extension torque in the stroke group (P<0.005). The controls exhibited more symmetric strength patterns in the flexion, extension, abduction and adduction directions. The average maximum normalized hip torques for the control subjects at toe-off posture were 19.58 Nm/Kgm² for flexion, 19.20 Nm/Kgm² for extension, 18.53 Nm/Kgm² for abduction, and 22.35 Nm/Kgm² for adduction. The hip torques produced by the controls were significantly larger than those developed by the stroke population in the flexion and adduction directions at toe-off and the flexion direction at midswing (P<0.05). See Supplemental Table I, available online at http://stroke.ahajournals.org.

Torque space data from a representative control (dashed line) and 7 randomly selected stroke subjects illustrate the asymmetry during the target matching experiments (see Figure 3). The data exemplify the significant weakness in the flexion direction observed in the stroke subjects. Additionally, compared with controls, stroke subjects had limited ability to generate torques that combined flexion/abduction torques in the toe-off and midswing postures (P<0.005).

Figure 3.

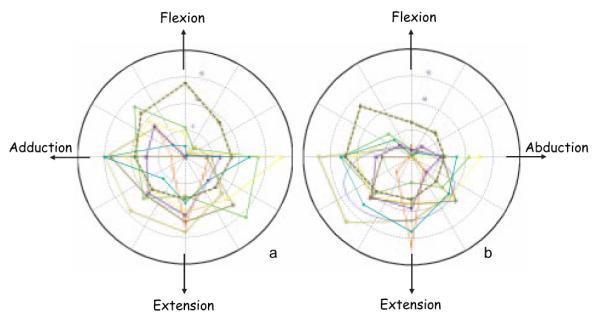
Examples of normalized torque (N-m/kg m²) output by 7 randomly selected stroke subjects and a control subject (dashed line) at the toe-off (a) midswing (b) postures.

The circular statistics (Rayleigh Test) of the asymmetry (or unimodality) of the hip torque space revealed that the stroke subjects had a significant grouping of the torque biases (P<0.05) and a small 95% CI (±24°), whereas the control group showed an insignificant grouping and a large 95% CI (±94°). Further analysis of the stroke data revealed that the hip torque bias was in the adduction and extension quadrant at both the toe-off and midswing postures.

The ability of the stroke group to produce torque in some directions was influenced by limb posture, as revealed by within-group paired t tests. More specifically, the maximum hip torque decreased with the increased hip flexion angle from the toe-off to midswing posture in 4 of the 8 directions (abduction, flexion, adduction/flexion, and abduction/extension). On the contrary, controls had postural torque dependence in only 2 of the 8 target directions (flexion and adduction/extension, P<0.05). Specifically, control subjects generated larger hip flexion torque at toe-off and greater adduction/extension at midswing (P<0.05). See Supplemental Table II, available online at http://stroke.ahajournals.org.

A geometric summary of the achievable workspace at both postures was also created using elliptical least squares fit of the torque data (Figure 4). The control group showed symmetry at both postures with a torque workspace bias occurring along the same direction (Φ≈18°). The mean centroidal coordinates (x_c, y_c) of the control group (−1.46, 0.85 Nm/Kgm²) and (−1.1, −1.9 Nm/Kgm²) at the toe-off and midswing postures, respectively) were not statistically different from 0. On the other hand, the stroke hip torque data fits revealed that the y coordinate of the ellipse center at the toe-off posture (−3.2 Nm/Kgm²) and both centroidal coordinates at the midswing posture (−2.3, −5.1 Nm/kgm²) were significantly different than 0 (P<0.05). Additionally, the stroke group’s hip workspace was consistently smaller (P<0.05) than that of the control group at both postures (36% and 33% for the toe-off and midswing, respectively). As a function of posture, both the control and stroke groups had moderate but statistically significant (P<0.05) decreases in workspace area from toe-off to midswing (12% and 7%, respectively). The stroke workspace exhibited a significant rotational change of 12° (ΔΦ≈12°), whereas the control group had an insignificant change in the angular orientation (ΔΦ≈0°).

Figure 4.

Geometric summaries of the achievable workspaces for the control (a) and stroke (b) groups.

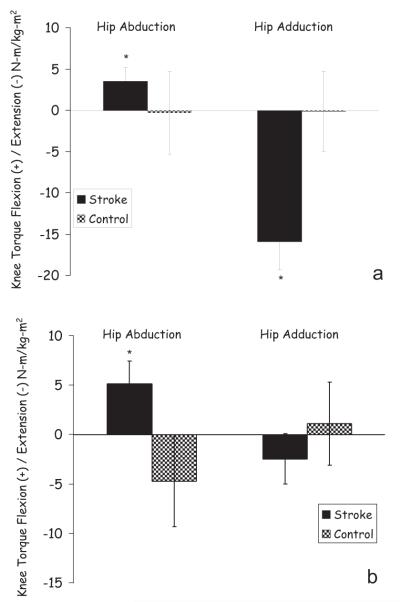
At the toe-off posture, the χ² analysis showed a significant group effect on the knee torque direction for the hip adduction task (P<0.001). Specifically, 19/22 (86%) stroke subjects coupled knee extension with hip adduction torque, whereas only 2/11 (18%) control subjects produced similar torque patterns. The 2 control subjects generated not only the same direction of knee torque (extension) but also similar torque magnitudes as compared with the stroke group (24.05 Nm/Kgm² compared with 18.88 Nm/Kgm² for the stroke group). On the other hand, the 3 stroke subjects who produced knee flexion during the hip adduction task generated a small torque (average 2.55 Nm/Kgm² knee flexion compared with an average of 18.88 Nm/Kgm² knee extension for the other 19 stroke subjects). The observed knee torque behavior during the hip adduction task was further analyzed with 1-sample t tests to identify the intensity of the knee torque produced at the toe-off posture. A significant knee extension torque (P<0.05; −15.31 [SE 3.45] Nm/Kgm²) was generated by the stroke group whereas the knee torque generated by the control group was not statistically different than 0 (P>0.05; −0.12 [SE 4.64] Nm/Kgm²; see Figure 5a).

Figure 5.

Mean knee torque produced during the hip abduction and adduction target matching tasks at toe-off by the stroke and control group. *significantly different from 0 by nonparametric test (P<0.05).

Unlike in the hip adduction task case, the knee torque behavior was not consistent within each group during the hip abduction torque generation task at toe-off, and therefore no group differences were revealed by the χ² analysis. Specifically, 12/22 stroke and 7/11 control subjects produced knee flexion torque during the hip abduction task. Despite the decreased consistency in the knee torque direction within the group, as a whole the stroke subjects produced significant (P<0.05) knee flexion torque during the hip abduction target-matching task (4.86 [SE 2.05] Nm/Kgm²), whereas the control group generated a statistically insignificant knee torque (P>0.05; −0.26 [SE 5.02] Nm/Kgm²; see Figure 5a).

Similar analyses were performed to explore the potential associations between the hip and knee torque behaviors at the midswing posture. The distribution of the knee torque behavior was not significantly influenced by group during both the hip abduction and adduction tasks, as determined by the χ² analysis (P>0.05). Subsequent nonparametric analysis showed that the knee torques produced by the control group were not statistically significant from 0 (P>0.05) during either the hip abduction or adduction target matching tasks. As expected, a nonparametric test revealed that the differential change in posture had no significant effect on knee torque generated by the control group during hip adduction/abduction tasks (P>0.05).

Contrary to the significant knee extension torque generated during the hip adduction task at the toe-off posture, statistically insignificant knee torque was generated by the stroke group during the same task at the midswing posture (−1.87 [SE 2.55] Nm/Kgm²; see Figure 5b). Hence, a nonparametric test revealed that the change in posture from toe-off to midswing resulted in a significant decrease in the knee extension torque generated by the stroke group during the hip adduction task (P<0.05). In addition, the stroke group continued to produce significant knee flexion torque (5.20 [SE 2.41 Nm/Kgm²]) during hip abduction in the midswing posture (see Figure 5b). A nonparametric test revealed that the change in posture from toe-off to midswing resulted in no change of the knee extension/flexion torque generated by the stroke group during the hip abduction task (P>0.05).

Discussion

This investigation revealed that stroke subjects exhibit directionally dependent weakness during isometric hip torque production. Stroke subjects produced diminished hip flexion torque at both the toe-off and midswing postures, which is consistent with reported clinical and experimental observations.^15,19 Our data indicated that the stroke group exhibited abduction strength comparable to their control counterpart, but had significantly reduced abduction/flexion torque. Despite the significant reduction, the stroke group did retain ≈50% of the control group flexion strength. The directional weakness resulted in a stroke hip torque workspace biased toward adduction and extension. The data also revealed an abnormal coupling between the sagittal plane knee torque and the frontal plane hip torque by the stroke group. Specifically, the hip adduction torque generated by the stroke participants was strongly coupled with knee extension torque at the toe-off posture. Conversely, the distribution of knee torque direction during hip abduction was not influenced by group, and therefore no abnormal across joint coupling was observed. Moreover, change in posture from toe-off to midswing prompted similar knee torque distributions by both groups during both hip-torque tasks, meaning that the likelihood of producing knee flexion or extension was the same in both groups. Therefore, the only abnormal across-joint–coupling displayed by the stroke group was between hip adduction and knee extension in the toe-off posture. These findings are in contrast to previous upper extremity studies reporting a persistent across-joint coupling independent of posture.²⁰ In light of the abnormal gait patterns involving the hip frontal plane and knee sagittal plane kinematics after stroke, our data suggest that it is likely that poststroke gait impairments can be attributed to the individual hip, knee, and ankle weakness, as well as the observed abnormal within- and across-joint torque patterns.

Whereas similar experimental set-ups have been used in lower²¹ extremity studies, it can be argued that the observed torque couplings may be attributed to the intrinsic design of our experimental set-up. In this case, one would expect the “set-up” effect to be independent of group (control versus stroke). On the contrary, our analysis of the across-joint torque coupling data revealed a consistent behavior within the stroke group and basic differences between groups. Given that basic group differences where also observed in the within-joint torque pattern, it is highly unlikely that the observed torque behaviors are experimental artifacts attributed to the design of the set-up used.

Our results indicated that a minority of the control subjects (2 of 11) exhibited stroke like across joint torque coupling at the toe-off posture (hip adduction/knee extension). This crossover behavior by a minority of the control participants has been observed in data derived from a number of earlier investigations of across-joint coupling in the neurologically impaired populations.^9,21 Others have suggested that abnormal torque coupling in stroke population may be caused by the exploitation of lower-level neural circuits, such as the bulbospinal tracts, circuitry that also present in healthy controls.²² Given that the task is volitional, it is conceivable that some control subjects can activate these pathways and hence present stroke-like behaviors.

Our results revealed that a significant knee flexion torque was produced during the hip abduction task in the stroke group, a finding consistent with Brunnstrom’s¹⁵ clinical observation. This difference in frequency distribution between groups was, however, not statistically significant. The absence of the flexion-coupling is not unique to this investigation. Indeed, torque-coupling studies on stroke subjects and other neurologically diseased states have found that extension coupling is more prevalent than flexion coupling.^21,23

Although selective weakness may have contributed to the decrease in achievable torque space at the hip after stroke, it does not explain the observed hip/knee-coupling. Although some researchers presume that torque coupling is predominantly due to abnormal neural coupling between motorneuron pools,²⁴ Lum et al propose that torque couplings are a manifestation of strength imbalances.²² It is unlikely that a strength disparity at the knee joint is responsible for the observed across-joint coupling seen in this data because there were no statistical differences in the extension-to-flexion knee strength ratios across groups and postures. Based on the strength imbalance hypothesis, a bias toward knee extension torque at the midswing posture would be expected. However, our results revealed that the hip adduction/knee extension coupling did not exist at midswing, despite the same knee extension bias across postures.

To examine the potential effect of moment arm changes due to posture, a musculoskeletal model (SIMM, Musculo-Graphics, Inc) was used to estimate the moment arms of the hamstrings (semimembranosus, semitendinosus, and biceps femoris [long head]), and rectus femoris at the knee at the toe-off and midswing postures. A greater increase in the extension moment arm of the rectus femoris than the increase in flexion moment arms of the hamstrings was found, suggesting that if purely biomechanical factors were being used, then the adduction with knee extension torque coupling observed in toe-off would be exaggerated in the midswing posture. Therefore, neither the changes in strength ratio nor moment arm would explain the lack of connectivity between the hip adduction and knee extension torque, a coupling found in the toe-off posture. Hence, whereas differential weakness may have contributed to the observed hip joint torque changes, we argue that intrinsic neural coupling between hip frontal plane musculature and uni-articular knee extensors are largely responsible for the observed across-joint torque coupling after stroke.

Our goal in this study was to systematically compare between stroke survivors and control subjects the within and across-joint torque patterns obtained during a sub-maximal, voluntary, isometric hip torque generation task in postures similar to those of overground gait. Whereas basic differences in torque patterns were observed between groups, these torque patterns may be manifestations of different muscle activation patterns across participants, irrespective of neurological state (stroke versus control). Indeed, redundancy in the musculature at the hip and knee joints allows for different combinations of muscle activity (EMG) to achieve the observed torques.²⁵ Given that some hip muscles also cross the knee joint, the across-subject variability in the observed knee torques provides indirect evidence that subjects may have used different activation patterns during the target matching tasks. Further investigations to quantify the within-group consistency of the EMG patterns responsible for the observed torque behaviors are, therefore, warranted. Such investigation would also facilitate the comparison of these patterns to the muscle recruitment during overground walking. Although the lower limb configurations were compatible to postures observed during normal overground walking, it is conceivable that the EMG patterns identified during the current task may not relate simply to the dynamic muscular activity that is presumably responding to the specific force demands during locomotion.²⁶

The absence of torque coupling at the midswing posture may be due to the influence of limb posture on motorneuron pool excitability. For example, hip posture significantly effects the H-reflex intensity of the soleus muscle,²⁷ possibly via connections between the motorneuron pools of the hip and ankle muscles.²⁸ It is plausible that posture-mediated changes in group Ia afferents may have contributed to the change in across-joint synergistic behaviors observed in this study by altering the excitability of the motorneuron pools of the knee flexors and extensors. Alternatively, postural changes may be mediated by other sensory proprioceptive components (group II, group Ib, and joint afferents).²⁹ Systematic studies in reduced animal preparations to investigate the effect of changing descending drive on the reflex are warranted.

Stroke survivors commonly exhibit excessive thigh abduction with respect to the laboratory coordinate system and reduced knee flexion during the swing phase of gait.⁴ Therefore, coupling of the hip abduction torque with knee extension torque was expected, not the hip adduction/knee extension-coupling reported in this study. On closer inspection, circumduction is a combination of pelvic obliquity and hip abduction/adduction measured with respect to the pelvis.⁵ Preliminary gait analysis on a subset of the participants in this study³⁰ revealed larger hip abduction angles in swing by the controls compared with the stroke group. Additionally, stroke subjects exhibited excessive up-pelvic obliquity, presumably to compensate for reduced knee flexion to achieve toe clearance. We suggest that the observed reduction in hip abduction angle seen in the stroke group may have been mediated by the hip adduction/knee extension torque-coupling observed in this study. Further experimental investigation correlating our isometric data to functional behaviors seen at similar postures would validate this conclusion.

Reduced ankle dorsiflexion, knee flexion, or hip flexion torques are postulated causes of compensatory frontal plane motion to clear the toe during the swing phase of gait.⁵ Simulation studies attribute the reduced knee flexion angle at toe-off to a failure to achieve the required knee flexion velocity before toe-off,³¹ which is further ascribed to reduced iliopsoas and gastrocnemius activity or overactive vasti activity.²⁵ Our findings suggest that abnormal across-plane synergistic action may also be a contributing component. Given our findings and recent developments in musculoskeletal simulations, an investigation of the differential role of lower extremity muscles kinetic-coupling might provide insights for rehabilitation interventions. See Supplemental section for further discussion.