The Effect of Connective Tissue Material Uncertainties on Knee Joint Mechanics under Isolated Loading Conditions

Abstract

Although variability in connective tissue parameters is widely reported and recognized, systematic examination of the effect of such parametric uncertainties on predictions derived from a full anatomical joint model is lacking. As such, a sensitivity analysis was performed to consider the behavior of a three-dimensional, non-linear, finite element knee model with connective tissue material parameters that varied within a given interval. The model included the coupled mechanics of the tibio-femoral and patellofemoral degrees of freedom. Seven primary connective tissues modeled as nonlinear continua, articular cartilages described by a linear elastic model, and menisci modeled as transverse isotropic elastic materials were included. In this study, a multi-factorial global sensitivity analysis is proposed, which can detect the contribution of influential material parameters while maintaining the potential effect of parametric interactions. To illustrate the effect of material uncertainties on model predictions, exemplar loading conditions reported in a number of isolated experimental paradigms were used. Our findings illustrated that the inclusion of material uncertainties in a coupled tibio-femoral and patello-femoral model reveals biomechanical interactions that otherwise would remain unknown. For example, our analysis revealed that the effect of anterior cruciate ligament parameter variations on the patello-femoral kinematic and kinetic response sensitivities were significantly larger, over a range of flexion angles, when compared to variations associated with material parameters of tissues intrinsic to the patello-femoral joint. We argue that the systematic sensitivity framework presented herein will help identify key material uncertainties that merit further research, as well as provide insight on those uncertainties that may not be as relative to a given response.

1. INTRODUCTION

Biomechanical models of articular joints are highly useful for understanding joint functions in normal and pathological states (c.f. Cohen et al., 2003; Fernandez and Hunter, 2005). However, the predictive power of a model depends on its structure/formulation (number of degrees of freedom) and the uncertainties associated with its constituents (properties of the soft tissues and connective tissues). Previous studies have provided extensive experimental quantification of knee joint connective tissue properties for use in developing and validating numerical models (Quapp and Weiss, 1998; Song et al., 2004). A wide range of resulting values have been reported (c.f. Woo and Buckwalter, 1988), which may be explained in part by differences in the donor's activity level (c.f. Blevins et al., 1994), age (c.f. Woo et al., 1986), gender (c.f. Chandrashekar et al., 2005), and species (Butler et al., 1984). Differences in experimental procedures such as storage methods (Woo et al., 1986), biases due to imprecise calibration/gripping (Abrahams, 1967), and inaccuracies in assumptions regarding specimen orientation (Mommersteeg et al., 1995; Woo et al., 1991) may also contribute to variability.

During the past three decades, a number of analytical finite element (FE) models of the knee joint with varying degrees of complexity have been proposed (c.f. D'Lima et al., 2003; Pena et al., 2005). While the majority of these models have investigated the patello-femoral (PF) or tibio-femoral (TF) joints in isolation, only a few have examined the coupled actions of the PF and TF joints (Beillas et al., 2004; Halloran et al., 2005; Pena et al., 2006; Piazza and Delp, 2001). The models of Halloran et al. and Piazza and Delp focused on specific knee joint implants, while Beillas and colleagues work overlooked some of the major joint connective tissues, including the joint's lateral stabilizers. A number of simplifying assumptions on the mechanical behaviors of both the menisci and the connective tissues were also used. For example, the joint's connective tissues were described by linear discrete elements while the menisci were modeled as isotropic continua. The exact effect of these simplifying assumptions in model complexity on the coupled PF and TF model predictions are not well understood. Accordingly, in this study, the complexity of a coupled PF and TF model was sufficiently increased to include most of the connective tissues with their nonlinear behaviors in an attempt to isolate the effect of connective tissue material uncertainty on model predictions.

While several parametric sensitivity studies have reported the effect of soft tissue material properties on the mechanics of the knee joint sub-structures (c.f. Haut Donahue et al., 2004; Yao et al., 2006), systematic examination of the effect of their parametric uncertainties on predictions derived from a coupled TF and PF formulation of the anatomical joint are lacking. In a recent study by Beillas and colleagues (2007), a direct sensitivity analysis scheme (SA) was employed to analyze simulation outcomes derived from a three-dimensional FE knee model (Beillas et al., 2001). One limitation of the study outcomes is that they were restricted to a limited number of stiffness variations (a total of three) of the model's connective tissues (anterior and posterior cruciate ligaments). The conclusion derived from these simulations may not necessarily be generalized over the entire parameter space associated with these tissues.

The SA method described by Beillas et al. was used to estimate changes in model output when material parameters were shifted within a given range while all other factors remained constant. Specifically, the material parameters of the anterior and posterior cruciate ligaments were equally and simultaneously changed. It is plausible that a change in the material property of the anterior cruciate ligament (ACL) may be associated with a concurrent or divergent change in the material properties of other connective tissues of the joint, a co-variation overlooked with the “one-variable-at-a-time” SA method. As a robust alternative to this type of analysis, we propose a multi-factorial global sensitivity scheme, which can detect the contribution of influential parameters while maintaining the potential effect of parametric interactions (c.f. Ibrahim, 1987). Such approaches are typically used to determine how the uncertainty in a model output can be apportioned to sources of variability in the model parameters and to ascertain which parameters are important in contributing to the variability in the outcome measure (Iman and Helton, 1988). Alternatively, the apportioned sensitivity may also indicate the variance in the measured kinematic/kinetic outcomes that may be attributed to differences in the material properties of a given tissue across specimens.

Accordingly, we implemented the global sensitivity approach by considering the response of a three-dimensional, non-linear, FE knee model with soft tissue material parameters that varied within a given interval. To illustrate the effect of material uncertainties on model predictions using the current sensitivity analysis framework, exemplar loading conditions reported in a number of isolated experimental paradigms (e.g., passive knee flexion in the presence of a quadriceps muscle force; see Table 1) were used. Our analysis focused on the PF kinematics and contact properties to highlight the effect of material uncertainties on simulation outcomes for a coupled formulation.

Table 1.

Summary of in vitro experiments published in the literature and used to test the current FE model. A subset of the PF and TF kinematics where chosen for comparison with model simulations to illustrate the model performance.

Experimental Study (Cadavers)	Kinematic Inputs	Loading Conditions	Preparations	Outputs
Sakai et. al. 2000 (7 specimens)	Passive flexion	150 N quadriceps force (60 N, rectus femoris; 50 N vastus lateralis; 40 N vastus medialis)	Skin and subcutaneuos soft tissues and superficial fascia were resected; the quadriceps, patellar retinaculum, iliotibial tract and patellofemoral ligaments remained intact.	Kinematics Patello-femoral
Nagamine et. al., 1995 (9 specimens, normal)	Passive flexion	Constant 30 N vertical load bearing force balanced by a constant 30 N quadriceps tendon force (no internal/external tibial torque)	The skin and muscles were resected 5 cm above and below the tibiofemoral joint line. Insertions of all tendons and ligaments were left intact.	Kinematics Patello-femoral
VanKampen & Huiskes, 1990 (4 specimens,)	Passive flexion	112 N quadriceps force (28 N per muscle) (no internal/external tibial torque)	All soft tissue circumferentially above and below the joint line including ligaments were intact.	Kinematics Tibio-femoral
Beck et al. 2007 (8 specimens)	Passive flexion	178 N quadriceps force	Soft tissue circumferentially 10 cm proximal to the superior pole of the patella and 5 cm distal to the tibial tubercle were removed leaving all ligaments intact.	Kinetics Patello-femoral
Zavatsky et. al. 2004 (12 specimens)	Passive flexion	~200 N quadriceps force at full extension (estimated)	Soft tissue circumferentially 15 cm above and below the joint line were removed, leaving all ligaments intact.	Kinematics Patello-femoral / Tibio-femoral

2. MATERIALS AND METHODS

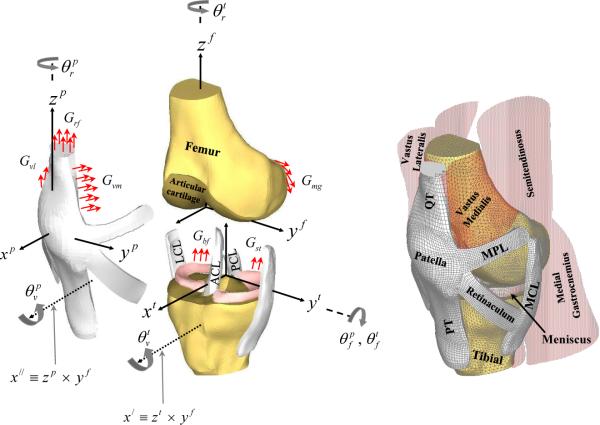
An anatomically accurate FE model of the PF and TF joints that included muscles, major ligaments, cartilages, menisci, and bones was developed (see Figure 1 and Appendix A for details and abbreviations).

Figure 1.

An anterior-medial view of the three dimensional finite element model of the knee shows the corresponding soft tissues, muscles and articular surfaces acting on the bones. In the figure, ACL and PCL are the anterior and posterior cruciate ligaments, MCL and LCL are the medial and lateral collateral ligaments, MPL and LPL (not shown) are the medial and lateral patello-femoral ligaments, and PT and QT are the patellar and quadriceps tendons, respectively. In all three coordinate systems (patellar, tibial and femoral), the medial (y), anterior (x), and superior (z) directions were chosen to be positive. The femoral and tibial z-axes were in the direction of the long axis of both bones. The patellar z-axis was along the line connecting the center of the patellar coordinates with the lowest point on the apex of the patella. The three dimensional sequential rotations defining TF and PF joint motions shown in the figure, have been described in detail elsewhere (Dhaher and Khan, 2002). For both joints, the first rotation is through an angle ${\theta }_f^{\left(•\right)}$ about the femoral medio-lateral axis (y^f -axis) followed by rotations about the tibial and patellar zaxis (z^t and z^p) through ${\theta }_r^t$ and ${\theta }_r^p$ respectively. Finally, the last rotation is about an anterior/posterior-floating axis (χ^| and χ^∥), through ${\theta }_v^t$ and ${\theta }_v^p$ respectively. Finally, G_rf, G_vm, G_vl, G_bf, G_mg, G_lg, and G_st represent the net muscle force distributed across the common nodes of the muscle-bone junctions.

To describe the constitutive behavior of fiber-reinforced connective tissues, a transversely isotropic hyperelastic material model, assumed to be nearly incompressible (Pena et al., 2005; Pioletti et al., 1998; Song et al., 2004), was derived from an uncoupled representation of the strain energy function (W) defined as follows (Limbert et al., 2004):

$$\begin{array}{cc}\hfill W& ={\stackrel{‒}{W}}_{ISO}({\stackrel{‒}{I}}_1,{\stackrel{‒}{I}}_4)+W_{VOL}\left(J\right)\hfill \\ \hfill W& =\{\begin{array}{c}{c}_1({\stackrel{‒}{I}}_1-3)+\frac{1}{D_1}{(J-1)}^2{I}_4<1.0\hfill \\ c_1({\stackrel{‒}{I}}_1-3)+\frac{c_2}{2c_3}({\text{exp}}^{c_3{({\stackrel{‒}{I}}_4-1)}^2}-1)+\frac{1}{D_1}{(J-1)}^2{I}_4\ge 1.0\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (1)

where ${\stackrel{‒}{W}}_{ISO}$, W_VOL are the isotropic and volumetric parts, respectively. In these equations, ${\stackrel{‒}{I}}_1=tr\left(\stackrel{‒}{C}\right)$, ${\stackrel{‒}{I}}_4=\stackrel{‒}{C}:a_0\otimes a_0$ (a₀ is a unit vector specifying the fiber direction in the reference configuration), $\stackrel{‒}{C}={\stackrel{‒}{F}}^T\stackrel{‒}{F}$ is the modified right Cauchy-Green tensor, $F=(J^{2∕3}\cdot 1)\cdot \stackrel{‒}{F}$ is the deformation gradient tensor, J = detF, $I_4=J^{2∕3}{\stackrel{‒}{I}}_4$, and $I_4={\lambda }_f^2$ (λ_f is the fiber stretch). The incompressibility penalty function is (J - 1)² and D₁ is chosen to be 0.001 to simulate the near incompressibility of ligaments. For completeness, the stress and elasticity tensors from Equation (1) are presented in Appendix B1. More detailed derivations can be found in (Prot and Skallerud, 2009).

In this framework, the fibers were assumed to be extensible and uniformly distributed in the ground substance and perfectly bonded to the matrix, while the matrix was assumed to be isotropic and hyperelastic. With the proposed strain energy function, the typical non-linear stiffening behavior of the collagen fibers under tension is provided by an exponential form and the collagen fibers are assumed not to support any compressive loads in the case of I₄ <1.0.

The mean values of the material coefficients presented in Equation (1) (c₁, c₂, and c₃) were identified by fitting experimentally reported uni-axial tension test data on the ACL, PCL (Pioletti, 1997) and MCL (Bonifasi-Lista et al., 2005). Due to a lack of experimental data, we assumed the mechanical behavior of the LCL was identical to the MCL. The preliminary calibration showed that c₁, which controls the matrix mechanical response, was almost identical for each ligament and c₂ and c₃, representing fiber characteristics, could be linearly related with sufficient accuracy. Table 2 shows the fixed c₁ value and linear correlation between c₂ and c₃ for each ligament. Accordingly, the resulting material model was a function only of a single coefficient (c₂). This indicates that it is possible to generate a probability density function of c₃ from a given density function of c₂.

Table 2.

Summary of the material coefficients of the model given in Equation (1) and used in the sensitivity study.

	C1 (fixed for each ligament)	C2 (normal distribution)		C3
		Mean	S.D.
MCL (= LCL)	1.0	35	17.5	C3 = 0.4 C2
ACL	0.5	2.0	1.0	C3 = 2.4 C2 + 7.6
PCL	0.2	1.2	0.6	C3 = 15.7 C2 − 4.7

Unfortunately, these tension tests (Pioletti, 1997) were conducted on a limited number of specimens (n = 4), limiting our ability to develop a statistical distribution of the material coefficients. Ideally, the parametric variability of the transverse isotropic model (Equation (1)) can be quantified through basic specimen experiments, which are designed to isolate and characterize each of the model coefficients (fiber and matrix). However, examination of the literature revealed only this set of experimental data on key knee ligaments (MCL, ACL, and PCL) derived from a testing paradigm applicable to the identification of material coefficients. Hence, to guide our choice of the statistical characteristics of the material coefficients, a simple neo-Hookean model was used to estimate variations of soft tissue properties from a cohort of structural tests on connective tissues of the human knee. These estimates indicated that variations of soft tissue properties take a Gaussian distribution (Figure 2) with a normalized standard deviation (σ* = σ /μ;σis the standard deviation and μ is the mean) of 0.56, 0.605, 0.56, and 0.4178 for the ACL, LCL, MCL, and PCL respectively. In this study, we assumed a similar probability density function for the material coefficients of the transverse isotropic model. Thus, a Gaussian distribution was used with σ* of 0.5 for the MCL, LCL, ACL, and PCL (Table 2). Again, due to the lack of experimental data, the range of the material coefficients for the MPL and LPL were assumed to be similar to those reported for the MCL and LCL, respectively.

Figure 2.

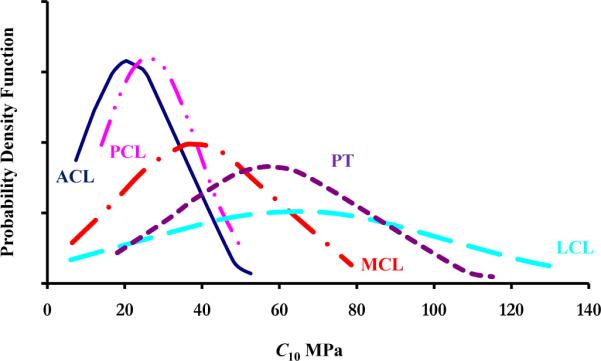
Based on experimental data, the figure shows the probability density function of the neo-Hookean coefficient (C₁₀) of the ACL (Butler et al., 1992; Butler et al., 1986; Chandrashekar et al., 2005; Hagena et al., 1989; Jones et al., 1995; Marinozzi et al., 1983; Mommersteeg et al., 1995; Noyes et al., 1984; Noyes and Grood, 1976; Trent et al., 1976; Woo et al., 1991), PCL (Butler et al., 1986; Hagena et al., 1989; Marinozzi et al., 1983; Mommersteeg et al., 1995; Moon et al., 2006; Prietto et al., 1988; Race and Amis, 1992; Race and Amis, 1994; Trent et al., 1976), MCL (Bonifasi-Lista et al., 2005; Bull, 1998; Claes et al., 1987; Marinozzi et al., 1983; Mommersteeg et al., 1995; Quapp and Weiss, 1998; Robinson et al., 2005; Trent et al., 1976), LCL (Butler et al., 1986; Ciccone et al., 2006; Claes et al., 1987; Espregueira and Vieira da Silva, 2006; LaPrade et al., 2005; Marinozzi et al., 1983; Maynard et al., 1996; Meister et al., 2000; Mommersteeg et al., 1995; Sugita and Amis, 2001; Trent et al., 1976), andPT (Blevins et al., 1994; Butler et al., 1986; Cooper et al., 1993; Flahiff et al., 1995; Haraldsson et al., 2005; Hashemi et al., 2005; Haut and Powlison, 1990; Johnson et al., 1994; Noyes et al., 1984; Paulos et al., 1988; Staubli et al., 1999; Wilson et al., 1999). In this study, it was assumed that the range of the MPL and LPL was similar to those reported for the MCL and LCL, respectively. The strain energy function used to describe the neo-Hookean model was given in the form C₁₀(I₁ – 3).

While all material coefficients of the connective tissues (MCL, LCL, PCL, ACL, MPL, and LPL) were varied, the meniscal and cartilage parameters were kept constant for all simulations. The PT and QT (see Appendix A and Figure 2 for definitions) were assumed to be neo-Hookean with material coefficients representing the mean value of the reported experimental data: 55.9 MPa for the PT and 65.9 MPa for the QT (Staubli et al., 1999). The articular cartilages were assumed to be linear isotropic with constant coefficients. Consistent with earlier static finite element simulation studies, the cartilage equilibrium compression modulus was set at 12 MPa (Haut Donahue et al., 2003) with a Poisson's ratio of 0.45 (Park et al., 2004; Shepherd and Seedhom, 1999). The menisci were modeled as a transversely isotropic, linearly elastic, homogeneous material (Haut Donahue et al., 2003). The circumferential modulus was set at 120 MPa (c.f. Tissakht and Ahmed, 1995). The axial and transverse moduli were assumed identical and were set at 20 MPa (c.f. Skaggs et al., 1994). The circumferential, radial, and axial Poisson's ratios were set at 0.45, 0.3, and 0.3, respectively. Comparable values have been used in other simulation studies (c.f. Yao et al., 2006). The meniscal parameters used in the current simulations satisfied the positive definiteness inequality constraints of the elasticity tensor (Batra, 2006). Finally, since the material properties of the meniscal horns are poorly understood (Yao et al., 2006), an isotropic linear elastic model was used with modulus of 120 MPa and Poisson's ratio of 0.45. Comparable horn moduli values have been used in earlier FE models of meniscal mechanics (Donahue et al., 2002).

A 0.001 g/mm³ density was assigned to all soft tissues (Penrose et al., 2002) while the bony segments were assigned a density of 0.002 g/mm³ (Cochran, 1982). It has been shown that the joint's connective tissues exhibit spatial initial stretches in their neutral state (Blankevoort and Huiskes, 1996). Hence, using the reported experimental initial stretches in the LCL, MCL, and ACL, the previous approach of the multiplicative decomposition of deformation gradients by (Weiss et al., 1995) is applied to introduce the initial stretch field to the FE model (see Appendix B). Due to the lack of experimental data, initial stretches were set to zero for the rest of the connective tissues included in the model.

FE simulations were performed in two steps. In the first step, the initial stretches were enforced in search of equilibrium with zero muscle forces at a flexion angle of zero degrees (see Appendix B). In the second step, the TF flexion angle was imposed along with muscle loading conditions: quadriceps forces of 56 N for the combined effect of the RF and VI muscles, 20 N for the VM, and 38 N for the VL (see Appendix A for definitions). The muscle forces were applied as uniformly distributed tractions at the muscle-bone junctions. The two steps were implemented with a user defined material model in Abaqus 6.9 (Simulia, Providence, RI) and were repeated for each of 50 sets of material parameters chosen at random from an admissible set using a conventional Monte Carlo sampling procedure. A single simulation required approximately 2.0 hr for the range of flexion angles specified (0–80°) using an Intel Xeon E5520 2.27 GHz dual processor, 12.0 GB of RAM, Dell Precision T5500 machine.

The variance-based measures of sensitivity were built on the Sobol' decomposition of a response surface model function of the form f (x) into summands of increasing dimensionality (Sobol', 1990 (in Russian), 1993 (in English)):

$$Y=f(x_1\cdots x_m)=f_1+\sum _i{f}_i\left(x_i\right)+\sum _i\sum _{j>1}{f}_{ij}(x_i,x_j)\cdots$$ (2)

Where x_i is the i^th material parameter (a total of six parameters were changed in this study, m = 6). Using the decomposing in equation (2), it can be shown (See Materials and Methods on line supplement for further details) that the first order sensitivity indices, also known as importance measures can be written in the form:

$$S_i\left(x_i\right)=\frac{V\left(E(Y\mid x_i)\right)}{V\left(Y\right)},i=1,\cdots ,k$$ (3)

which are used to rank the factors (material coefficients) according to the amount of output variance removed when the true values of $x_i^{\ast }$ of a given factor x_i are known (traditionally known as a factor prioritization setting). Since we do not know $x_i^{\ast }$ for each x_i, the most reliable result is achieved by considering E(V(Y|x_i)) When E(V(Y|x_i)) is small, the factor x_i is more influential. Since V(Y) = E(V(Y|x_i)) + V(E(Y|x_i)), focusing on the lowest E(V(Y|x_i)) is equivalent to focusing on the highest V_i = V(E(Y|x_i)) (i.e. on the highest S_i). S_i can be interpreted as the proportion of the total variance attributable to variable x_i and is an appropriate measure of sensitivity for ranking the importance of the given factors, even if they are correlated (Saltelli and Tarantola, 2002).

3. RESULTS

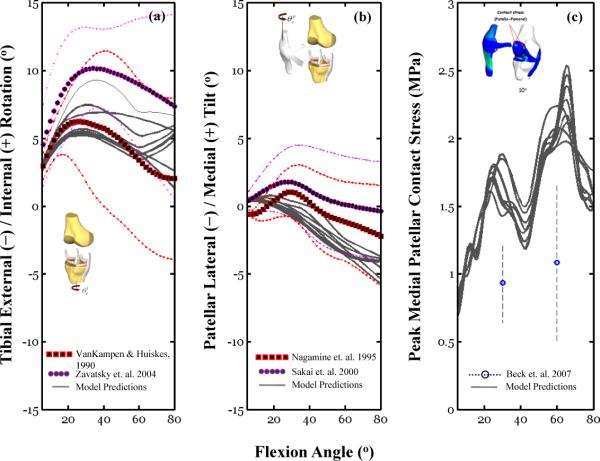
To illustrate the potential effect of material model variations on simulation outcomes, results of a subset of 10 different simulations conducted with different material coefficients selected at random from the 50 total Monte Carlo simulations are shown in Figure 3. Using exemplar TF and PF DOF, variation of c₂ for the six ligaments induced differences in the predicted overall internal/external TF rotation (Figure 3a), patellar tilt (Figure 3b), and patellar peak contact stress (Figure 3c) profiles. The peak contact stress increased progressively from 5° to 80°, going from 0.2–0.3 to 1.0–2.5 MPa depending on the value of c₂. This trend is consistent with reported cadaveric data (Beck et al., 2007) obtained under similar loading conditions (quadriceps force of 178 N).

Figure 3.

This figure illustrates the effect of material model variations on simulation outcomes. Finite element simulation results (gray lines) obtained for 10 random set of six material properties (c₂) are compared to experimental data collected under similar loading conditions. Table 1 provides an overview of the experimental conditions for the data shown in these figures. Model simulations were obtained using simultaneous quadriceps forces; 56 N for the combined effect of the RF and VI muscles, 20 N for the VM and 38 N for the VL. Figure 3b shows the mean peak contact stress (with standard deviation bars) for the medial patellar facet reported recently by Beck and colleagues (Beck et al., 2007) using a single quadriceps force of 178 N (see Table 1 for experimental description of the Beck et al study).

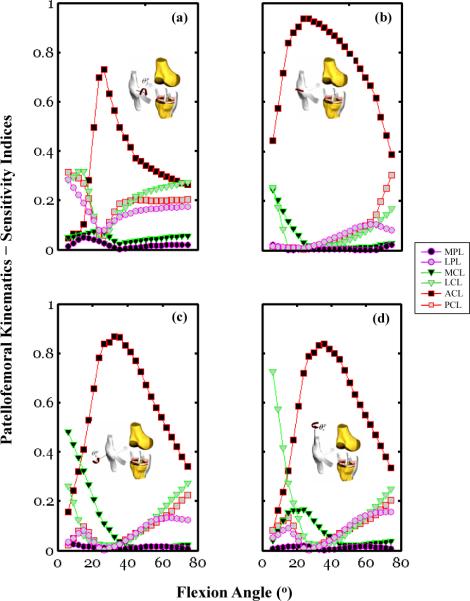
Our sensitivity analysis illustrated the significant effect of varying the material parameters of soft tissues extrinsic to the PF joint on the response sensitivities of the patellar DOFs (Figure 4). For example, the patellar flexion response sensitivity was larger than 40% of the ACL c₂ variability between 20° and 40° of flexion. This result indicates that about 40% of the patellar flexion variance would persist if only the ACL material parameter were to remain undetermined. Alternatively, this may also indicate that 40% of the variance in the measured patellar flexion may be attributed to differences in the ACL material properties across specimens. Moreover, for the 40–80° flexion range, over 75% of the patellar flexion response sensitivity was attributed to the combined effect of the LCL, PCL, and ACL c₂ variability. Our analysis also revealed that the patellar flexion response sensitivity was multi-factorial, including the parameter variability of the LPL, a soft tissue intrinsic to the PF joint (Figure 4a). Specifically, 20–35% of the patellar flexion sensitivity was due to the LPL c₂ variability for angular amplitudes less than 20° of flexion. This is consistently larger than the contribution of the MPL c₂ variability (with peak value < 10%) over the same angular range (Figure 4a). The flexion response sensitivity associated with the LPL parametric variability remained at a constant level, near 20%, for all flexion angles larger than 40°.

Figure 4.

Sensitivity indices calculated using Equation (4) and plotted as a function of the knee flexion angle for the PF DOF: (a) flexion, (b) medial/lateral translation, (c) rotation, (d) tilt. Kinematic values of the patella were obtained for each of the 50 Monte Carlo simulations using the coupled PF and TF knee model. Simulations were conducted under simultaneous quadriceps forces of 56 N for the combined effect of the RF and VI muscles, 20 N for the VM and 38 N for the VL. For each sub-figure, six traces are shown that corresponds to the response sensitivity of a given degree of freedom for each of the six parameter variations, ACL, PCL, MCL, LCL, MPL, and LPL.

The patellar medial/lateral response sensitivity was dominated by the ACL parametric variability, which accounted for 75–95% of the response sensitivity over the 20° to 60° flexion range. Over the same angular range, the combined parametric variability of the joint's intrinsic tissues, MPL and LPL, was insignificant, accounting for less than 10% of the response sensitivity. The role that collateral ligament (MCL, LCL) parametric variability played on the patellar medial/lateral response sensitivity was most pronounced at flexion angles near full extension (< 15°). Our data indicates that at the larger angular excursions (flexion angles > 60°), the overall patellar medial/lateral response sensitivity can be attributed to the combined effect of the parametric variability of the cruciate ligaments (Figure 5b).

Figure 5.

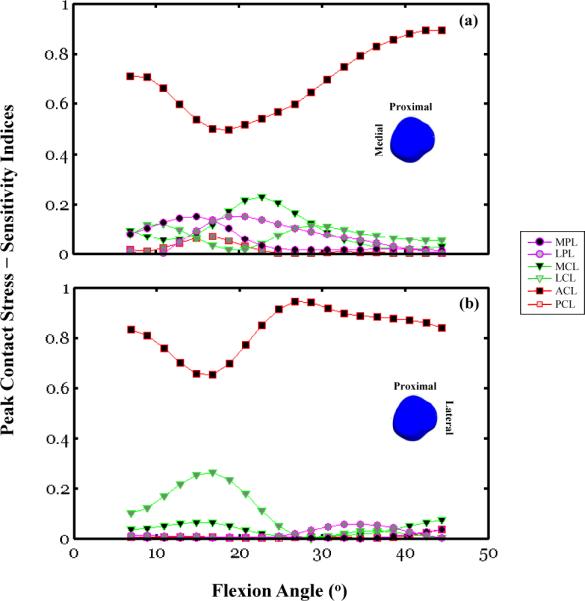
Sensitivity indices calculated using Equation (4) and plotted as a function of the knee flexion angle for the patellar peak contact stresses:(a) medial facet, (b) lateral facet. The peak contact stress amplitudes and locations are associated with the same simulation outputsfor which Figure 3 shows the response sensitivity curves of the PF DOF. For each subfigure, six traces are shown that correspond to the response sensitivity of a given degree of freedom for each of the six parameter variations, ACL, PCL, MCL, LCL, MPL, and LPL.

The patellar rotation and tilt response sensitivities were largely attributable to the ACL c₂ variability (Figure 4c & 4d). Specifically, between 20° and 60° of flexion, the response sensitivity associated with the ACL c₂ variability ranged from 55–90% and 60–85% for the tilt and rotation DOFs, respectively. At lower flexion angles (less than 20°), the MCL parameter significantly influenced patellar rotation with sensitivity indices ranging from 50-30% (Figure 4c). The sensitivity indices were equal to 50% for the MCL calculated at the near full extension posture (~5°). This indicates that about 50% of the variance in the patellar rotation would persist if only the MCL c₂ were to remain undetermined. At a similar posture (~5°) the patellar tilt response sensitivity was 75% of the LCL parameter variability (Figure 4c). Both the tilt and rotational DOFs response sensitivities showed moderate dependence on the parametric variability of the LPL and MPL, intrinsic tissues of the PF joint (Figure 4c & 4b).

The biomechanical significance of the coupled TF/PF mechanics is illustrated by the effect of the ACL, MCL, and LCL c₂ variation on the medial and lateral facet peak contact stress sensitivity responses (Figure 5a & 5b). To illustrate this effect on the medial and lateral facets separately, sensitivity analyses were conducted for a range of flexion angles (5° to 45°). This angular range was associated with two distinct contact locations at both patellar facets for the loading condition considered in this study. Here, the uncertainty in the ACL material property had a considerable impact on the medial and lateral peak contact stress response sensitivity across the full range of flexion angles (Figure 5c). This effect was the smallest between 15° and 20° with 50% and 65% sensitivity indices for the medial and lateral contact stress, respectively. Over the same angular range, two other parameters, MCL and LCL, had a significant influence on the medial and lateral facet peak contact stress response sensitivity. The largest sensitivity indices were equal to 25% and 28% for the MCL and LCL when calculated over this angular range. In general, over the full range of flexion angles considered here, the effect of the MCL, LCL, and PCL parameter variations on the medial facet peak contact stress response sensitivity was comparable to variations associated with material parameters of connective tissues intrinsic to the PF joint, the MPL and LPL. The LPL parameter variation, while a relatively important contributor to the peak medial facet stress response sensitivity, did not account for any of the response sensitivity of the lateral facet peak contact stress (Figure 5b).

4. DISSCUSION

We investigated the effect of uncertainty in connective tissue intrinsic properties on the predicted kinematics and kinetics of the human knee joint under combined quadriceps loading during a knee flexion task. Our findings illustrated that the inclusion of material uncertainties in a coupled TF and PF DOF model reveals biomechanical interactions that otherwise would remain unknown. For example, our analysis indicated that the effects of ACL parameter variation on the PF kinematic and kinetic response sensitivities were more influential than variations associated with material parameters of connective tissues intrinsic to the PF joint. Furthermore, the framework presented herein can be replicated to examine the relative soft tissue contributions during loading conditions associated with a number of joint pathologies (example: a valgus moment for the study of ACL injury).

Our goal was to investigate the effect of uncertainties in joint connective tissue parameters on knee joint mechanics under loading conditions traditionally used in experimental examination of normal and pathological joint mechanics (Sakai et al., 2000; Wilson et al., 2000; Zavatsky et al., 2004). The method described herein presents a framework to evaluate the potential effect of material uncertainty on the outcomes of such investigations. It is noted, however, that the current model predicted physiological kinematics and kinetics under a 114 N quadriceps force (Figure 3), which is lower than loading magnitudes estimated for functional tasks such as walking (Besier et al., 2009). One could argue that under weight-bearing conditions, the observed in situ strain levels in key ligaments may be attenuated. In these cases, the relative effect of the connective tissue material parameters may be different than the contributions reported in the current study. To estimate the relative contribution of connective tissue uncertainty under these conditions, the model predictions should be cross-validated against knee responses observed during physiological loading conditions associated with daily activities. Thus, despite the advantages of using the current three-dimensional computational knee joint model and analysis framework, there are certainly limitations in the generalizability of the current findings to other loading paradigms.

For the current loading conditions, our analysis revealed that the patellar medial/lateral response sensitivity is multi-factorial and includes the effects of parameter variability of connective tissues extrinsic to the PF joint, namely the ACL, MCL, and LCL (Figure 3b). These contributions were angle-specific and were manifestations of the coupled formulation of the TF and PF DOF. Biomechanically, the combined changes in ACL, MCL, and LCL parameters resulted in TF internal/external, varus/valgus, and anterior/posterior translation (data not shown). These motions can lead to changes in the mechanical state of the PT which will influence patellar motion. Based on the simulation results, the effect of the extrinsic tissues on the PF motion and peak contact stress was not symmetric. That is, the lateral facet peak contact stress response sensitivity was dependent on the ACL parameter variation only, a variation comparable to those contributed by the joint's intrinsic tissues, the MPL and LPL.

According to Kondo et al. (2003), an injury or partial tear to the ACL may be estimated as a change in the material parameter of the tissue. Our sensitivity analysis showed a significant effect of such changes on the PF DOF. These findings are consistent with reported in vitro studies examining PF kinematic abnormalities associated with experimentally induced ACL injuries (Hsieh et al., 1998; Steiner et al., 2001). It has been hypothesized that the PF abnormalities are an indirect manifestation of abnormal anterior tibial translation induced by an ACL excision. It remains to be seen if such association will reemerge under more realistic loading conditions that would include larger muscle forces and externally applied three-dimensional loads (e.g., applied varus/valgus and internal/external torques).

Irrespective of the knee model complexity, model validations are traditionally based on comparisons between the output from single deterministic simulations and single or repeated experiments. However, a wide range of joint kinematics has been reported during similar experimental conditions as illustrated in the examples used in this study (Figures 3a & 3b). These inter-specimen variations have been attributed to differences in the coordinate system used, specimen fixation, and difference in loading conditions. Our data suggests that variations in connective tissue properties across specimens (material uncertainties) may also contribute to these differences. Although recent model validation approaches for mechanical systems have focused on propagating the uncertainty in model predictions, little work has been accomplished in this area of musculoskeletal modeling. Using connective tissue properties as an example, we have presented a framework for model synthesis via uncertainty propagation using a global sensitivity analysis. We argue that by understanding the sensitivity of a knee model output to the connective tissue parameters contained in the model, it is possible to place confidence limits on the model kinematics and kinetic predictions. Furthermore, sensitivity analyses can be used to guide experimental efforts aimed at determining soft tissue properties; high priority should be placed on accurately estimating those parameters which most influence experimental outputs.

For more discussion on issues related to the initial strain assumption and the Monte Carlo simulation formwork, please see Discussion online supplement.

Figure B1.

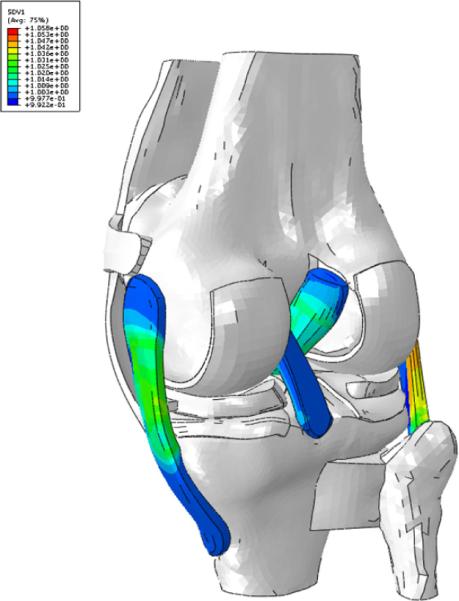
The initial stretch (SVD1 in the legend) in the fibers after the equilibrium step. For clarity, only the ligaments with initial stretch imposed are displayed.

Table B1.

Initial stretch for MCL in full extension as reported by (Gardiner et al., 2001). In this table as well as Tables B2 and B3, the numerical value 1.0 indicates a strain-free initial state.

Location	Inferior	Middle	Superior
Anterior	1.015	1.026	1.024
Middle	1.02	1.039	1.052
Posterior	1.027	1.048	1.058

Table B2.

Initial stretch for ACL in full extension as reported by (Pena et al., 2006)

Location	Inferior	Middle	Superior
Anterior	1.014	1.020	1.004
Posterior	1.027	1.024	1.004

Table B3.

Initial stretch for LCL in full extension as reported by (Pena et al., 2006)

Location	Initial Stretch
Anterior	1.0
Middle	1.0
Posterior	1.08