Abstract
Dendrites of many types of neurons contain voltage-dependent conductances that are active at subthreshold membrane potentials. To understand the computations neurons perform it is key to understand the role of active dendrites in the subthreshold processing of synaptic inputs. We examine systematically how active dendritic conductances affect the time course of postsynaptic potentials propagating along dendrites, and how they affect the interaction between such signals. Voltage-dependent currents can be classified into two types that have qualitatively different effects on subthreshold input responses: regenerative dendritic currents boost and broaden EPSPs, while restorative currents attenuate and narrow EPSPs. Importantly, the effects of active dendritic currents on EPSP shape increase as the EPSP travels along the dendrite. The effectiveness of active currents in modulating the EPSP shape is determined by their activation time constant: the faster it is, the stronger the effect on EPSP amplitude, while the largest effects on EPSP width occur when it is comparable to the membrane time constant. We finally demonstrate that the two current types can differentially improve precision and robustness of neural computations: restorative currents enhance coincidence detection of dendritic inputs, whereas direction selectivity to sequences of dendritic inputs is enhanced by regenerative dendritic currents.
Keywords: Synaptic integration, Voltage-dependent currents, Dendrites, Quasi-active cable
1 Introduction
Neuronal dendritic trees are complex structures that endow the cell with powerful computing capabilities (London and Häusser 2005) and allow for high neural interconnectivity (Chklovskii 2004). A large body of data has demonstrated the presence of voltage-dependent conductances in the dendrites of various types of neurons (Migliore and Shepherd 2002). These currents can be involved in excitable voltage dynamics, such as dendritic spikes (Stuart et al. 1997) and somatic action potential bursting (Schwartzkroin and Slawsky 1977), but several voltage-dependent dendritic currents are also active at subthreshold membrane potentials and can significantly affect the integration of synaptic inputs. For example, the hyperpolarization-activated inward current, Ih, can actively decrease temporal summation of trains of dendritic excitatory postsynaptic potentials (EPSPs) (Magee 1999), and the persistent sodium current, INaP, and the low voltage activated calcium current, IT, can amplify EPSP amplitude (Schwindt and Crill 1995; Lipowsky et al. 1996; Gillessen and Alzheimer 1997). To understand the computations that neurons perform it is central to understand what role active dendrites have in the subthreshold processing of synaptic inputs.
Here, we examine systematically how active dendritic conductances affect the time course of postsynaptic potentials that ‘propagate’ (without generating spikes) along dendrites. We subsequently study the interaction between such signals, focussing on coincidence detection of synaptic inputs and direction selectivity to inputs that are activated sequentially along the dendrite.
Coincidence detection is one of the most basic operations that a neuron can perform, requiring the neuron to respond to the occurrence of two or more EPSPs in a short time interval. Neurons of the medial superior olivary nucleus (MSO) are specialized in performing this task, being able to distinguish between extremely short (~10 μs) EPSP intervals (Joris et al. 1998). Coincidence detection is expected to benefit from EPSPs that are as brief as possible. However, we know from theory and experiments that EPSPs propagating along passive dendrites not only decrease in amplitude, but also increase in width, hence reducing temporal precision (Rall 1967; Rall et al. 1967; Jack et al. 1971; Jack and Redman 1971a, b). Indeed, it was recently shown that MSO cell dendrites possess a low voltage activated potassium current (IKLT) that actively decreases EPSP width, thereby enhancing coincidence selectivity (Mathews et al. 2010). Such findings provide further motivation to study the effects of active dendritic currents on subthreshold input integration and coincidence detection.
Sequential activation of EPSPs along a passive dendrite toward the soma leads to larger amplitude somatic responses than sequences away from the soma (Rall 1964). This mechanism can underlie direction selective responses and has been put forward in the context of, for example, direction selectivity to visual stimuli of V1 pyramidal neurons (Livingstone 1998) and retinal starburst amacrine cells (Tukker et al. 2004). The consequences of cable filtering for the response to input sequences along a dendrite were first investigated by Rall (1964) using passive cables. However, active dendritic conductances are likely to play an important role in the response to such stimuli.
To systematically study the effects of active dendritic conductances on synaptic inputs, we make use of the so-called quasi-active description of dendritic cables (Sabah and Leibovic 1969; Koch 1984), an extension of classical passive cable theory. This approach relies on linearizing voltage-dependent cable conductances. Though the linearized description naturally does not capture the full dynamics of voltage-dependent currents, the results can serve as a solid reference for the effects of active dendritic currents on the subthreshold propagation of EPSPs. The approach allows us to classify the active dendritic currents into two types. First, restorative currents, which function as a negative feedback and counteract changes of the membrane potential. This negative feedback can be realized by outward currents that activate upon depolarization, such as IKLT, or by inward currents that activate upon hyperpolarization, like Ih. Second, regenerative currents, which act as a positive feedback and amplify membrane potential changes, for example, INaP. The two current types have qualitatively different effects on the subthreshold propagation of EPSPs. In general, regenerative dendritic currents make the cell electrotonically more compact—decreasing the attenuation of EPSPs along dendrites—and slow the membrane response. In contrast, restorative currents make the cell electrotonically larger and the membrane response faster. Compared to a passive cable response, EPSP amplitude and halfwidth are decreased by restorative currents and increased by regenerative currents. Moreover, these effects increase as the EPSP propagates along the active cable. The activation time constant of the active current also plays an important role: the strongest effects on EPSP amplitude occur for currents that activate much faster than the membrane time constant, while maximum effects on duration occur when the activation time constant is comparable to the membrane time constant. Since narrow EPSPs will only summate on short intervals, coincidence detection of dendritic inputs is enhanced by restorative currents, creating a narrow coincidence window. Direction selectivity benefits from strong summation of EPSPs and is therefore enhanced by regenerative dendritic currents. Finally, we demonstrate that the linear quasi-active approximation can give very good predictions of the response of nonlinear cable models to synaptic inputs that evoke large amplitude EPSPs.
2 Methods
2.1 Quasi-active description of a dendritic cable
Our model describes a dendritic cable with a single voltage-dependent conductance. We consider an infinite cable, hence not taking into account the effects of sealed or killed end boundary conditions. We let V(x, t) denote the membrane potential (in millivolts) along the cable at position x (in centimeters) and time t (in milliseconds). The passive properties of the cable are determined by membrane time constant τ (in milliseconds) and space constant λ (in centimeters). The cable expresses a voltage-dependent conductance with gating variable w(x, t), which has activation function w∞(V) and time constant τw(V) (in milliseconds). The equations governing V(x, t) and w(x, t) are
| (1) |
where EL is the leak reversal potential, Ew is the reversal potential of the active current, and γw is the ratio of the maximal conductance of the active current to the leak conductance. Note that, where possible, we use parameter naming conventions as in Goldberg et al. (2007).
To obtain the quasi-active approximation of the nonlinear cable we linearize Eq. (1) about membrane potential VR (Sabah and Leibovic 1969; Koch 1984). We define U(x, t) as the difference between V(x, t) and VR and we define m(x, t) analogously as m(x, t) ≡ w(x, t) − w∞(VR). Using a Taylor series expansion of Eq. (1) we can write
where F(x, t) and G(x, t) are the right-hand sides of Eq. (1) divided by the respective time constants. By dropping the higher-order terms (h.o.t.) we obtain the linear equations describing the quasi-active cable:
| (2) |
where τw = τw(VR) and γR = 1 + γww∞(VR), i.e., the total membrane conductance of the cable at VR divided by the cable membrane leak conductance. It is worth noting that linearizing Eq. (1) does not yield terms that involve the derivative of τw(V).
In order to determine the response of the quasi-active cable to external input we use its impulse response function or Green’s function. This function can be obtained by first writing the Fourier transform of Eq. (2):
| (3) |
where Ũ(x, ω) is the Fourier transform of U(x, t) with respect to time, ω = 2πf with frequency f (in Hz), and
| (4) |
with
| (5) |
The parameter μ is central in characterizing the effect of the active membrane current, denoting the strength of the positive or negative feedback that the current provides. Solving Eq. (3) when a δ-current impulse is injected at the origin of the infinite cable gives the Fourier transform of the Green’s function (i.e., the transfer function):
| (6) |
where R∞ is the input resistance (in ohm) of a passive infinite cable: , with specific membrane resistance Rm (in ohm cm2), intracellular resistivity Ra (in ohm cm), and cable diameter d (in centimeters).
2.1.1 Quasi-active cable with multiple gating variables
Throughout most of this study we use the above dendritic cable model Eq. (1), which includes one active membrane current Iact(x, t) with a single gating variable:
In Section 3.7 we also consider quasi-active cables with an additional gating variable that either functions as an inactivation gate or as an activation gate of a second active current. When the active current includes an inactivation gating variable z(x, t), we have
with density γwz, reversal potential Ewz, and where z(x, t) evolves according to a first-order differential equation with activation function z∞(V) and time constant τz(V). After linearizing the cable equation with this inactivating current, we obtain the Green’s function Eq. (6) with
| (7) |
where , τw = τw(VR), τz = τz(VR), and γR = 1 + γwzw∞(VR) z∞(VR). Note that parameters μw and μz have opposite signs.
When extending Eq. (1) with a second active current with gating variable z(x, t), we have
where the additional current has density γz, activation function z∞(V), reversal potential Ez, and its gating evolves according to a first-order differential equation with time constant τz(V). After linearizing the cable equation with these two active currents, we obtain the Green’s function Eq. (6), where the factor b2(ω) is given by Eq. (7), with , and γR = 1 + γww∞(VR) + γz z∞(VR). More active currents can be easily included in the model, each leading to further increases of γR and to two additional terms in Eq. (7).
2.1.2 Response to sinusoidal input currents
With the Fourier transform of the Green’s function Eq. (6) we can describe the frequency-dependent filtering by the cable. The amplitude of the signal at location x resulting from a sinusoidal input current with frequency ω at the origin is
| (8) |
where |z| is the modulus and Re{z} is the real part of the complex number z. Hence, a sinusoidal signal decays exponentially along the cable with frequency-dependent space constant
| (9) |
The phase shift of the signal at location x is
| (10) |
where arg{z} is the argument and Im{z} is the imaginary part of the complex number z. Thus, the delay of the signal along the cable (i.e., the reciprocal of the signal velocity) increases linearly with slope
| (11) |
Note that the expressions for the real and imaginary part of b(ω) can be written as and , where sgn q is the sign of q and the parameters p and q are given by, respectively, the real and the imaginary part of b2(ω). For the cable model with one gating variable we obtain for ω = 0
| (12) |
and
| (13) |
2.1.3 Response to synaptic input
Synaptic current input is described by an alpha function: Isyn(t) = wsyn t/τsyn exp(1 − t/τsyn) for t > 0 with synaptic time constant τsyn (in milliseconds) and peak synaptic current wsyn (in picoamperes). The response of a cable to such an input cannot be solved analytically but can be computed by convolving the input with the Green’s function of the system (see Eq. (6)). The response of the linear quasi-active cable to two synaptic inputs (see Section 3.5) or to a sequence of synaptic inputs (see Section 3.6) is equal to the sum of the individual responses. When we compute the response to an input sequence, the sequence is truncated at an electrotonic distance X = x/λ from the recording site at which the amplitude of a synaptic input does not contribute significantly (<1%) to the composite EPSP amplitude and halfwidth that result from summation of the inputs, yielding input sequences that are at most 3 space constants long. The synaptic inputs in a sequence are spaced equally along the cable with electrotonic distance ΔX ~ 0.02 space constants between the inputs, such that a smooth composite EPSP response is obtained.
2.2 Models of voltage-dependent membrane currents
We use three examples of voltage-dependent currents to illustrate how the parameter μ defined by Eq. (5) depends on the voltage VR (see Section 3.1): the persistent sodium current INaP (from pyramidal neurons, Traub et al. 2003), the low threshold potassium current IKLT (auditory brainstem MSO cells, Mathews et al. 2010), and the hyperpolarization-activated inward current Ih (pyramidal neurons, Magee 1998). We also use the models of INaP and IKLT to simulate nonlinear cables (see Section 3.8). The currents are described by
with reversal potentials ENa = 55 mV, EK = −106 mV and Eh = −30 mV. Dynamics of the gating variables p, n, z and r satisfy first-order differential equations: dx/dt = (x∞(V) − x)/τx(V). Functions of INaP activation p∞(V), IKLT activation n∞(V) and inactivation z∞(V), and Ih activation r∞(V) are given by
Voltage-dependent activation time constants (in milliseconds) of INaP activation τp(V), IKLT activation τn(V), and IKLT inactivation τz(V) are
Steady state current-voltage relationships and corresponding values of μ shown in Fig. 1 use peak conductances ḡNaP = 6 nS, ḡKLT = 300 nS and ḡh = 70 nS. Computing μ requires specification of the leak conductance, which is set to gL = 15 nS. Values of μ for INaP and Ih are computed using Eq. (5), and the value of μ associated with IKLT activation is given by .
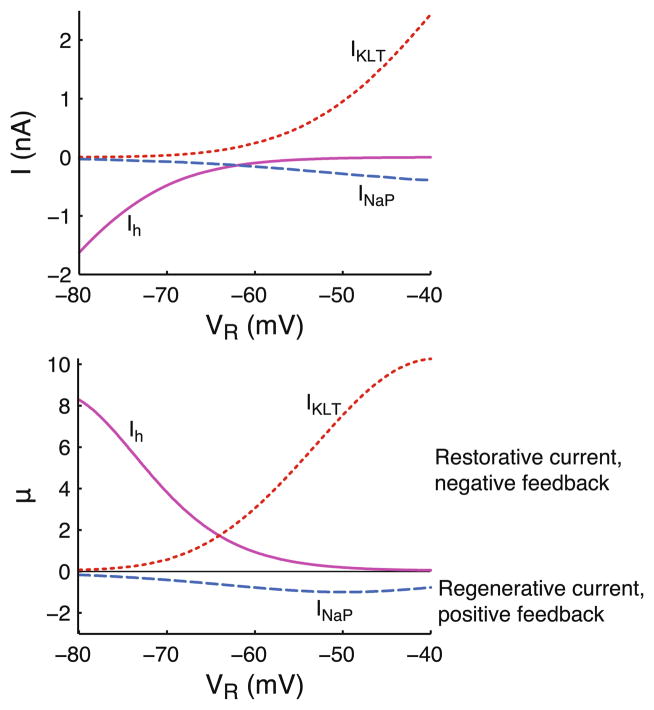
Fig. 1.
Parameter μ denotes strength of the feedback and classifies active currents into regenerative and restorative type. Steady state current-voltage relationships of a persistent sodium current, INaP, a hyperpolarization-activated inward current, Ih, and a low threshold potassium current, IKLT (top panel), and the corresponding values of μ at the voltage VR around which the current is linearized (bottom panel). Negative values of μ indicate that a current functions as a positive feedback (regenerative current) and positive μ denotes negative feedback (restorative current). See Section 2 for current descriptions and computing μ (see Eq. (5))
2.3 Numerical simulations of cables with voltage-dependent currents
We perform numerical simulations (see Section 3.8) of a cable with a persistent sodium current, INaP, or a cable with a low threshold potassium current, IKLT. To illustrate different parameter regimes and relate the models to experimental findings, the models use different sets of membrane and synaptic time constants. The persistent sodium current has been demonstrated, for example, in dendrites of neocortical pyramidal neurons (Schwindt and Crill 1995), and therefore the cable with INaP uses synaptic and membrane parameters similar to those in pyramidal neurons. The cable with IKLT has membrane and synaptic time constants based on MSO neurons whose dendrites indeed possess a prominent IKLT (Mathews et al. 2010). Conductance densities for the two models are ḡNaP = 0.04 mS/cm2 and leak conductance gL = 0.1 mS/cm2, or ḡKLT = 20 mS/cm2 and gL = 1 mS/cm2. The leak reversal potential EL is set such that we obtain resting potential Vrest = −53.9 mV or −57.6 mV for the model with INaP or IKLT, respectively. The linearized active current parameters at these resting potentials are μ = −1.0, γR = 1.14 and τw = 0.08 msec for the INaP model, and μ = 4.0, γR = 1.48 and τw = 1.05 msec for the IKLT model. Note that inactivation of IKLT is very slow (τz ~ 150 msec) compared to the EPSP time scale (~1 msec). For simplicity we therefore do not include its dynamics in the quasi-active approximation.
The simulated cable has diameter d = 2 μm, intracellular resistivity Ra = 150 ohm cm, and capacitance Cm = 1 μF/cm2. This yields a membrane time constant τ = 10 msec or 1 msec, and space constant λ = 577 μm or 183 μm for the model with INaP or IKLT, respectively, where both τ and λ are computed using only the leak conductance gL (as is the convention in our quasi-active description). Results from numerical simulations are compared to semi-analytical results from the quasi-active cable. Because we consider an infinite quasi-active cable, the length of the simulated cable is set to ~10 space constants such that the finite length does not significantly affect the results. The cable is discretized into compartments of 0.05 λ.
Synaptic inputs are modeled as described in Section 2.1.3, with synaptic time constant τsyn = 2 msec (cable with INaP) or 0.2 msec (cable with IKLT). To obtain an EPSP amplitude of 20 mV, the peak synaptic current is set to wsyn = 258 pA (cable with INaP) or 1022 pA (cable with IKLT). Numerical simulations were performed using the NEURON simulation environment (Hines and Carnevale 1997).
3 Results
3.1 Voltage-dependent currents are either regenerative (μ < 0) or restorative (μ > 0)
We explore the effects of an active current on the sub-threshold propagation of signals along a cable. The central parameters that qualitatively determine the effects of the active (non-spiking) current on signal propagation are the current-type μ (defined by Eq. (5)) and the activation time constant τw. The parameter μ determines the strength of the feedback that the active current provides. For negative μ, the current functions as a positive feedback and is called a regenerative or amplifying current, for example, a persistent sodium current, INaP (see e.g., Hutcheon and Yarom 2000). When μ is positive, the current provides a negative feedback and is called a restorative or resonating current, for example, the hyperpolarization-activated inward current, Ih, or the low threshold potassium current, IKLT. Note that μ = 0 indicates the current shows no voltage-dependence, i.e., it is passive. The value of μ can be readily computed from an ion current model. Its value at membrane potential VR is determined by the slope of the current’s activation curve, its driving force, and its membrane density (see Eq. (5)). Computing μ over a range of subthreshold potentials for three example currents based on experimental data from pyramidal neurons and auditory brainstem cells (see Section 2) yields values ranging up to 8–10 for Ih and activation of IKLT and down to ~−1 for INaP (Fig. 1). Note that since we consider subthreshold and not excitable dynamics, regenerative currents cannot be too strong: the positive feedback makes the system unstable when μ + γR ≤ 0, where γR denotes the relative density of the active current at VR. In the following sections we will typically use the values μ = −1 and μ = 4 (with γR = 2) to illustrate the effects of regenerative and restorative currents, respectively.
3.2 Regenerative and restorative currents differentially modulate the frequency-dependent space constant and signal delay
Filtering of subthreshold current inputs by dendritic cables leads to attenuation and delays along the cable. We first briefly focus on the subthreshold propagation of a sinusoidal signal. Although this has been explored previously (see Koch 1984), it will highlight certain central effects of active dendritic currents. Using sinusoidal inputs we can get explicit expressions for the steady state signal attenuation and delay as a function of the signal’s angular frequency ω (see Section 2). The decay of the signal amplitude along the cable is exponential with frequency-dependent space constant λ(ω) (see Eq. (9)). For a passive cable the space constant decreases as the input frequency increases, hence making the cable electrotonically larger (Fig. 2(a), μ = 0). A cable with a regenerative current (μ = −1) increases the space constant when input frequencies are low compared to the current’s activation time constant τw, which we set equal to the membrane time constant τ. Regenerative currents boost the input signal for such frequencies, making the cable electrotonically more compact. In contrast, restorative cable currents (μ = 4) decrease the space constant for sufficiently low input frequencies. Note that such currents can produce membrane potential resonances and that this is also expressed in a peak of the space constant at a nonzero frequency (~0.4/τ Hz in Fig. 2(a)). Hence, the cell is electrotonically more compact for signals at this resonant frequency than at other frequencies (see also Koch 1984).
Fig. 2.
Frequency-dependent space constant and signal delay are increased by regenerative currents and decreased by restorative currents. (a) Frequency-dependent space constant of a cable with regenerative (μ = −1), passive (μ = 0) or restorative (μ = 4) currents. The frequency-dependent space constant is normalized by the space constant λ of a passive cable with μ = 0 and γR = 1 (see Eq. (9)). Note that the three cases use γR = 2, including the passive cable, such that the total membrane conductance is equal for all conditions. Activation time constant τw = τ. Frequency of the sinusoidal input is expressed in units of 1/τ. (b) Frequency-dependent delay θ(ω) (i.e., the reciprocal of signal velocity) of a sinusoidal signal along a cable for the same conditions as in A, computed using Eq. (11)
The delay along the cable of the sinusoidal signal increases linearly with slope θ(ω) (i.e., the reciprocal of velocity, see Eq. (11)). For a passive cable the delay decreases as the input frequency increases (Fig. 2(b), μ = 0). When input frequencies are sufficiently slow compared to τw, the delay is increased by regenerative cable currents (μ = −1), while it is decreased by restorative currents (μ = 4). Restorative currents can make the delay along the cable zero for a particular input frequency (~0.2/τ Hz in Fig. 2(b)). Thus, the voltage along the cable oscillates synchronously for sinusoidal input at this frequency. Below this input frequency θ(ω) is negative, meaning that (in steady state) voltage peaks occur later at the injection site than at the adjacent parts of the cable.
Summarizing, regenerative and restorative currents have opposite effects on both signal attenuation and signal delay along dendritic cables. Regenerative currents make dendrites electrotonically more compact and increase signal delays. Restorative currents increase electrotonic size and counteract signal delays that result from passive cable filtering.
3.3 EPSPs are attenuated and sharpened by restorative currents, and amplified and broadened by regenerative currents, effects increasing along cable
In the next sections we systematically examine how voltage-dependent dendritic currents affect the response to synaptic input. We compare the passive cable response with that of a cable with either restorative or regenerative currents. Synaptic input is described by an alpha function with time constant τsyn (see Section 2).
The response of a passive cable to a single EPSC has been studied extensively (Rall 1967; Rall et al. 1967; Jack and Redman 1971a, b): recording the EPSP at increasing electrotonic distance X from the injection site (Fig. 3(a), μ = 0) shows a strongly decreasing amplitude (left column, “EPSP”) accompanied by an increasing EPSP duration and time to peak (right column, “Normalized EPSP”). We next introduce voltage-dependent currents to the cable, setting the activation time constant τw = τ/2. Note that we keep the total membrane conductance equal for all conditions (i.e., γR = 2), including the passive cable, such that differences in the response are solely due to voltage-dependent current dynamics. The most noticeable effect of adding a regenerative current to the cable is the strong broadening of the EPSP (μ = −1). In contrast, adding restorative currents to the cable narrows or sharpens the EPSP (μ = 4). Note that this type of current can also produce an afterhyperpolarization (AHP) following the EPSP.
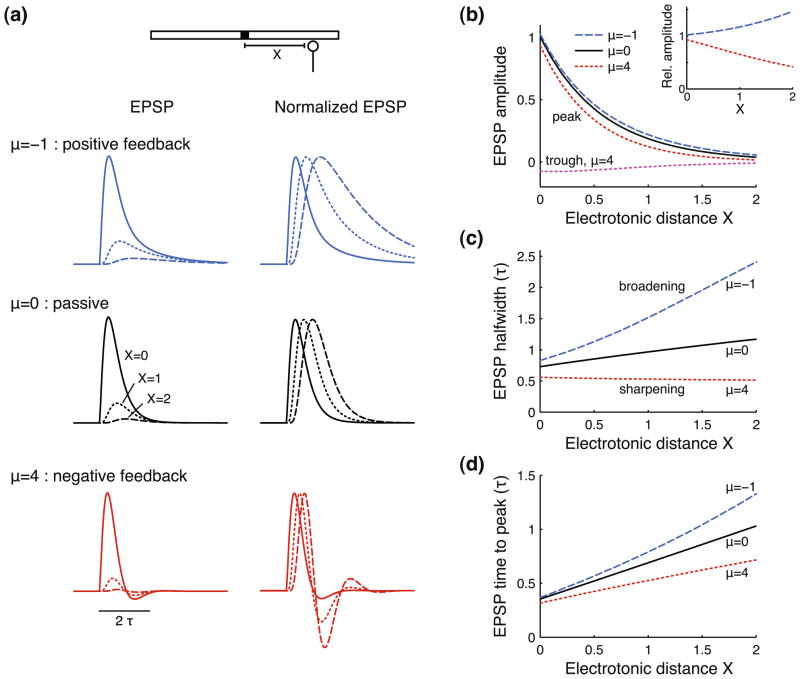
Fig. 3.
Regenerative currents amplify and broaden EPSPs, restorative currents attenuate and sharpen EPSPs, with effects increasing as the EPSP propagates along the cable. (a) EPSC response of a cable with regenerative (top, μ = −1), passive (middle, μ = 0) or restorative (bottom, μ = 4) currents. Traces are recorded at X = 0 (solid lines), X = 1 (dotted lines), and X = 2 (dashed lines) space constants from the injection site. Right column gives normalized responses to facilitate comparison of EPSP shapes. Note that all cables use γR = 2, including the passive cable, such that the total membrane conductance is equal for all conditions. (b) EPSP peak and trough (only for μ = 4) as a function of electrotonic distance X along the cable, shown for the same three cables as in panel (a). EPSP amplitude is normalized with respect to the maximal passive (μ = 0) cable response at X = 0. Inset shows the EPSP peak amplitude for the quasi-active cables relative to the response of the passive cable for all X. (c) EPSP halfwidth as a function of X. EPSP halfwidth is the EPSP width at half-maximal amplitude. (d) EPSP time to peak as a function of X. EPSP time to peak is computed from the EPSC onset at t = 0 until the time of maximal EPSP amplitude. Halfwidth and time to peak are expressed in units of τ, and electrotonic distance X is expressed in units of λ. Note that τ and λ are based on the passive cable properties (see Eq. (1)) and do not include the added active or passive current. Active currents use activation time constant τw/τ = 0.5. The EPSC is described by an alpha function with time constant τsyn/τ = 0.2 (see Section 2)
We computed EPSP amplitude, halfwidth (i.e., the EPSP width at half-maximal amplitude) and time to peak as the signal travels along the cable (Fig. 3(b–d)). In absolute terms the EPSP peak amplitude shows a fairly similar attenuation with electrotonic distance X for all three conditions (Fig. 3(b), “peak”). However, relative to the passive response (μ = 0), the regenerative current (μ = −1) gives an amplification that grows up to 50% at X = 2, while the restorative current (μ = 4) attenuates the response by 60% (see inset in Fig. 3(b)). Furthermore, the restorative current produces an AHP that attenuates with increasing X (“trough”). Regenerative currents strongly increase EPSP halfwidth, and this effect grows with distance X, in Fig. 3(c) up to a factor 2 compared to a passive cable. Interestingly, restorative currents actively decrease the halfwidth and can thereby make it independent of X, or even make the halfwidth decrease with distance travelled along the cable. Finally, the time for the EPSP to reach its peak is also increased by regenerative currents and shortened by restorative currents (Fig. 3(d)).
In summary, subthreshold dendritic voltage-dependent currents greatly affect EPSP shape. Regenerative currents amplify and broaden EPSPs, whereas restorative currents attenuate and sharpen them, and these effects increase with distance traveled along the cable.
3.4 EPSP width is most affected when the activation time constant is comparable to the membrane time constant
The activation time constant of the voltage-dependent current is central in determining the degree to which active currents affect EPSP shape. A relatively slow current (τw ≫ τ) is not able to react to voltage transients. It will simply act as a passive current on the time scale of an EPSP and will decrease τ, λ2 and the input current by a factor 1/γR (see Eq. (2), setting m(x, t) = 0). A very fast current (τw ≪ τ) is continuously in steady state with the voltage and will therefore effectively also act as a passive current (over the voltage range where the current-voltage relationship is approximately linear), scaling τ, λ2 and the input current by a factor 1/(γR + μ) (see Eq. (2), setting . Hence, the voltage response of a cable with a regenerative current (Fig. 4(a), μ = −1, “EPSP”) looks more similar to a passive response when the activation time constant is slow (τw/τ = 10) or fast (τw/τ = 0.1), than when it is intermediate (τw/τ = 1). The faster active current gives a stronger boost of the EPSP amplitude, but also produces a faster decay than the current with intermediate τw. Similarly, the responses of a cable with slow or fast restorative currents (μ = 4, “EPSP”) look fairly similar to passive responses, with fast currents more strongly attenuating the EPSP, while not producing an AHP.
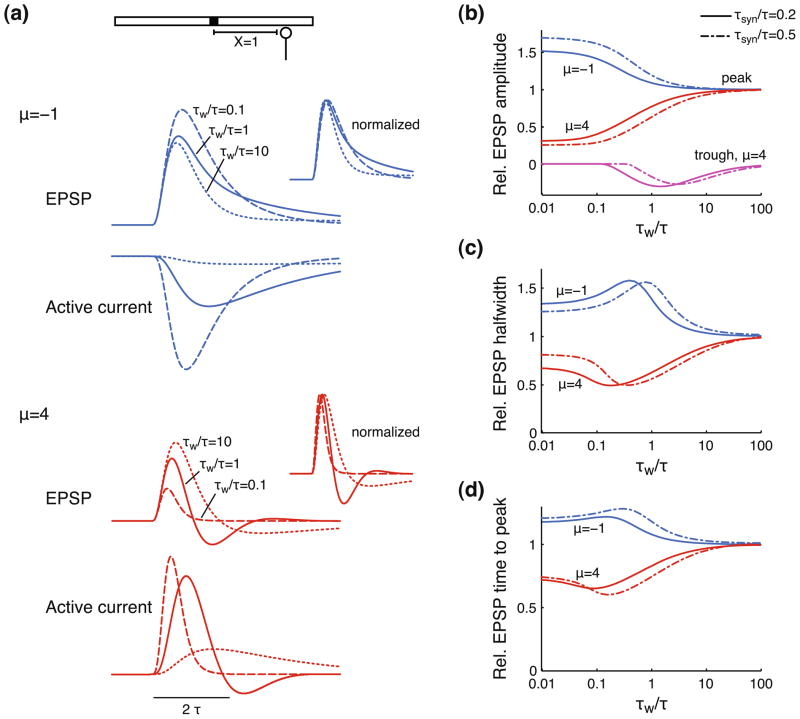
Fig. 4.
Activation time constant determines how strongly active dendritic currents affect propagating EPSPs. (a) EPSP and active current recorded at an electrotonic distance X = 1 from the injection site. The active current is regenerative (top, μ = −1) or restorative (bottom, μ = 4) with activation time constant τw/τ = 0.1 (dashed lines), τw/τ = 1 (solid lines) or τw/τ = 10 (dotted lines). Insets show normalized EPSPs. Other parameters are as in Fig. 3. (b-c-d) Shape of the EPSP after propagating over an electrotonic distance X = 1 as a function of the activation time constant τw/τ for a cable with regenerative (μ = −1) or restorative currents (μ = 4). EPSP amplitude peak and trough (only for μ = 4) (b), halfwidth (c), and time to peak (d) are computed relative to the response of a cable with μ = 0. The EPSC is described by an alpha function with time constant τsyn/τ = 0.2 (solid lines) or τsyn/τ = 0.5 (dash-dotted lines). All conditions use γR = 2
We varied the activation time constant over four orders of magnitude and computed EPSP amplitude, halfwidth, and time to peak (Fig. 4(b–d)). The values are normalized with respect to the response of a passive cable, hence, all three variables approach 1 for large τw. The faster the active currents, the stronger their effects on EPSP amplitude, with regenerative currents amplifying EPSPs and restorative currents attenuating EPSPs (Fig. 4(b), “peak”). The AHPs generated by restorative currents only occur over a limited range of τw (“trough”) and notably not for fast activation time constants.
The relationships between τw and the EPSP halfwidth (Fig. 4(c)) or time to peak (Fig. 4(d)) are non-monotonic. For very small or very large τw, the halfwidth and time to peak are equal to a passive cable response with λ and τ modified as described above. For intermediate values, however, active currents have stronger effects on EPSP halfwidth and time to peak. The largest effects occur when the active current feedback acts predominantly during the falling phase of the EPSP (see Fig. 4(a), “Active current”), hence typically when τw is comparable to τ. Though slow active currents affect the EPSP time course over a longer time, the amplitude of the active current is also smaller. In contrast, fast active currents have larger amplitude and also affect the rising phase of the EPSP. However, their effects last shorter and wear off during the falling phase.
The range of τw over which the maximum effects on amplitude, halfwidth and time to peak occur also depends on the synaptic time constant τsyn. We considered two values: τsyn/τ = 0.2 (Fig. 4(b–d), solid lines) and τsyn/τ = 0.5 (dash-dotted lines). Note that the faster time constant corresponds to typical values for AMPA currents in cortical pyramidal cells, but also for auditory brainstem MSO cells, which have membrane time constants that are ~10 times faster than those of pyramidal cells (see, for example, Povysheva et al. 2006; Scott et al. 2005). The slower synaptic time constant shifts the relationships between τw and EPSP amplitude, halfwidth and time to peak rightwards. Hence, maximal effects on EPSP amplitude, halfwidth and time to peak, require slightly slower active currents.
Summarizing, the faster the kinetics of voltage-dependent currents, the stronger their effects on EPSP amplitude. However, the strongest effects on EPSP halfwidth and time to peak occur when the activation time constant is such that the active currents operate mostly during the peak and falling phase of the EPSP.
3.5 Summation of synaptic inputs: restorative currents narrow the coincidence window
The response to combinations of synaptic inputs is key to dendritic computations. We next focus on the summation of two EPSCs activated at an interval ΔT with both inputs at a distance X from the recording site. The response to multiple inputs in the linearized system is equal to the sum of the individual responses. Hence, the voltage response to two synchronous inputs (Fig. 5(a), ΔT = 0, solid lines) has the same shape as a single EPSP, but twice the amplitude. When the second EPSC is activated with a delay ΔT = τ (dotted lines), summation (i.e., the maximal voltage) is decreased. A cable with regenerative currents shows stronger input summation (μ = −1, dotted line) than a passive cable (μ = 0, dotted line), resulting from the increased EPSP halfwidth. In contrast, we find no summation when ΔT = τ for the cable with restorative currents (μ = 4, dotted line), because the second EPSP arrives when the first EPSP is in its AHP phase.
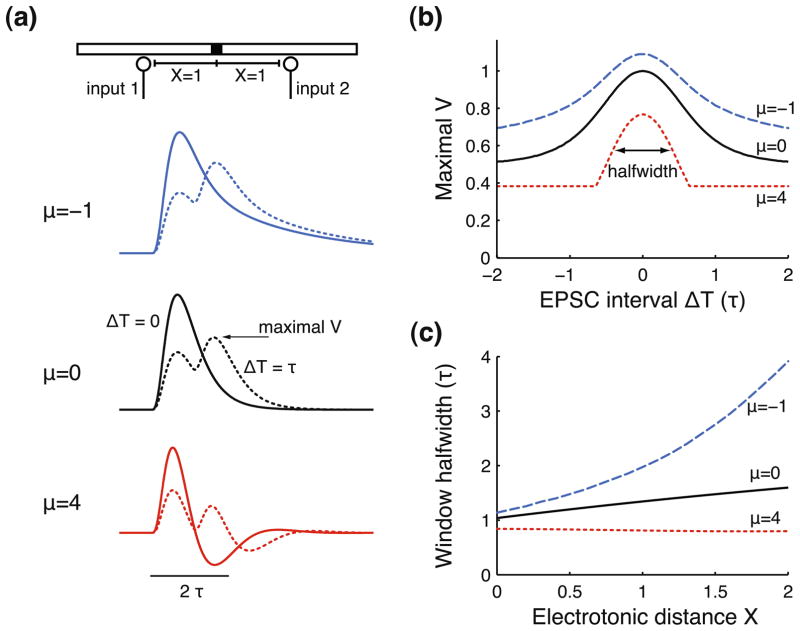
Fig. 5.
Coincidence window is narrowed by restorative dendritic currents. (a) Examples of responses to two EPSCs injected at an electrotonic distance X = 1 from the recording site with EPSC interval ΔT = 0 (solid lines) or ΔT = τ (dotted lines), shown for a cable with regenerative (μ = −1), passive (μ = 0) or restorative currents (μ = 4). EPSC and cable parameters are as in Fig. 3 with τw = τ. (b) Coincidence window for a pair of EPSCs with interval ΔT. The window amplitude is normalized by the maximal voltage response of the passive cable (μ = 0) to two coincident EPSCs (i.e., ΔT = 0). (c) Halfwidth of the coincidence window for two EPSCs injected at electrotonic distance X from the recording site. Window halfwidth is defined as the width of the window at half-maximal amplitude (between the baseline and the peak, see panel (b))
We determined the ‘coincidence window’ for two excitatory inputs: the maximal response to two EPSCs as a function of the interval ΔT (Fig. 5(b)). Note that for the neuron to actually perform coincidence detection, we could simply add a spike generation mechanism with a fixed threshold. The coincidence window is symmetrical because the two identical inputs are at equal distance X = 1 from the recording site. The window is much narrower for a cable with restorative currents (μ = 4) than for a cable with regenerative currents (μ = −1), differing more than a factor 2 when expressing the window width by its halfwidth. Hence, restorative dendritic currents allow for more precise coincidence detection. The shape of the coincidence window is closely related to the EPSP shape: the decay of the window from maximum to minimum is determined by the decay of the EPSP from peak to zero. Thus, for increasing ΔT the coincidence window gradually decays back to the amplitude of a single EPSP for a cable with passive or regenerative currents. However, restorative currents can produce an abrupt end to the coincidence window, due to the AHPs that these currents can generate (see also Fig. 5(a)).
The halfwidth of the coincidence window is determined by the time for the EPSP to move from its peak to its half-maximal amplitude and is thus closely related to the EPSP halfwidth. Varying the electrotonic distance X of the inputs to the recording site affects the EPSP halfwidth (see Fig. 3(c)) and should therefore also affect the window halfwidth. Indeed, window halfwidth (Fig. 5(c)) increases strongly with X for cables with regenerative currents, whereas restorative currents counteract the passive broadening of the window, thereby allowing for more precise coincidence detection.
3.6 Response to input sequences: regenerative currents enhance direction selectivity
Some types of neurons are thought to detect sequences of synaptic inputs along their dendrites. In particular this has been suggested to explain direction selective responses of neurons in the visual system (Livingstone 1998; Tukker et al. 2004). Responses to input sequences were first investigated by Rall (1964) using compartmental models of passive cables. We next examine how active cable properties affect subthreshold integration of synaptic inputs that are activated sequentially with input delays θinp (in units of τ per λ, the reciprocal of sequence velocity, Fig. 6). Positive values of θinp indicate sequences toward the recording site (centripetal) and negative values indicate sequences away from the recording site (centrifugal). Note that θinp = 0 indicates that all inputs are activated synchronously.
Fig. 6.
Direction selectivity to input sequences is enhanced by regenerative currents. (a) A sequence of EPSPs with input delay θinp (i.e., the reciprocal of input sequence velocity) results in a composite EPSP at the recording site (filled square in diagram). Positive θinp indicates sequences toward the recording site. Example composite EPSPs are shown for a passive cable using θinp = 1 τ/λ (solid line) and θinp = −1 τ/λ (dotted line). (b) Peak amplitude of composite EPSP for a range of input delays θinp, computed for a cable with regenerative (μ = −1), passive (μ = 0) or restorative currents (μ = 4). (c) Direction selectivity as a function of the absolute input delays |θinp|, computed as the ratio of composite EPSP peak amplitude in positive direction to the peak amplitude in negative direction. (d) Halfwidth of composite EPSP for a range of input delays θinp. EPSC and cable parameters are as in Fig. 3 with τw = τ. See Section 2 for more details on computing the composite EPSP
The shape of the composite EPSP that results from summation of the EPSP sequence depends strongly on the sequence direction and input delay (Fig. 6(a)). First note that the maximal amplitude of the composite EPSP (Fig. 6(b)) does not occur when all inputs are activated synchronously, but when input delays match the EPSP travel-delay along the cable, such that all EPSP peaks arrive at the recording site at the same time (see Fig. 3(d)). Peak amplitude in the passive cable (μ = 0) occurs when θinp = 0.33 τ/λ. The cable withregenerative currents (μ = −1) needs slower sequences to achieve maximal amplitude (θinp = 0.39 τ/λ), while the cable with restorative currents (μ = 4) requires faster sequences (θinp = 0.23 τ/λ).
Importantly, the composite EPSP has larger amplitude for centripetal sequences than for centrifugal sequences for both passive and active cables. We define direction selectivity as the ratio of the composite EPSP amplitude for centripetal sequences with input delay θinp with respect to centrifugal sequences with input delay −θinp (Fig. 6(c)). Clearly, direction is not relevant to synchronous inputs (θinp = 0), giving a ratio of 1. Maximal direction selectivity for a passive cable (μ = 0) is found when θinp ≈ 0.9 τ/λ, giving 56% larger composite EPSP amplitude for centripetal sequences than for centrifugal sequences. Regenerative cable currents (μ = −1) increase direction selectivity to a maximum of 76% (when θinp ≈ 1.6 τ/λ) and extend the input delay range over which direction selectivity occurs. Restorative currents (μ = 4) decrease direction selectivity, limiting it to a small range of input delays, and decreasing its maximum to 36% (when θinp ≈ 0.5 τ/λ).
Enhancement of direction selectivity by regenerative currents results from the strong increase of EPSP halfwidth with distance travelled along the cable. As a consequence EPSPs summate efficiently for centripetal sequences since wide, small amplitude EPSPs are followed by gradually narrower, larger EPSPs, resulting in a relatively narrow and large amplitude composite EPSP (Fig. 6(b–d), μ = −1). In contrast, summation is not efficient in centrifugal direction, since narrow, large EPSPs are followed by wider, smaller EPSPs, resulting in a wide, small amplitude response. Direction selectivity is reduced by restorative cable currents, because EPSP halfwidth is small and varies little along the cable, making summation practically equally inefficient in both sequence directions (Fig. 6(b–d), μ = 4).
3.7 Combined effects of regenerative and restorative currents on the shape of propagating EPSPs
In the previous sections we focussed on how dendritic input integration is affected by a restorative or a regenerative current. We next consider a dendritic cable with either two active currents or with a single current that both activates and inactivates. Both cases use two gating variables, w(t) and z(t), which—in the quasi-active cable approximation—introduce two parameters to denote the feedback that they produce: μw and μz, respectively. The difference between the two cases is that μw and μz are independent when considering two active currents, but not when considering an inactivating current (see Section 2). For example, if w(t) represents the activation of a potassium current and z(t) its inactivation, then activation functions as a negative feedback (i.e., restorative, μw > 0) and inactivation as a positive feedback (i.e., regenerative, μz < 0).
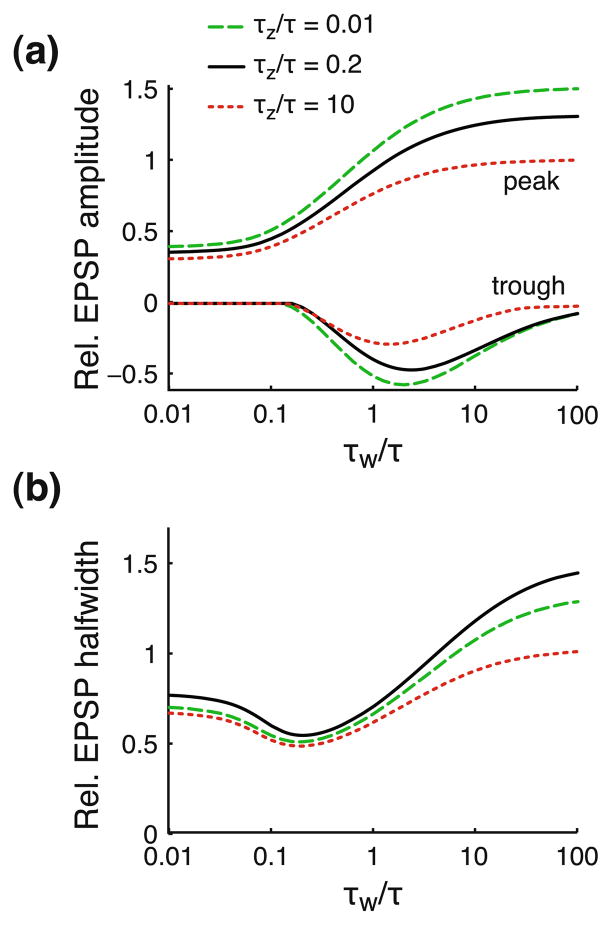
To illustrate the combined effects on EPSP shape, we consider the same parameters as in the previous sections, with μw = 4 and μz = −1, but note again that the two components can represent either two active currents or one current that activates and inactivates. If both components have the same time constant, τw = τz, we effectively have a single component producing a feedback that is determined by the sum μw + μz = 3 (see Eq. (7)), hence functioning as a restorative current. We thus computed the EPSP shape for combinations of time constants τw and τz (Fig. 7). The faster the restorative component (τw), the stronger the decrease in EPSP amplitude (Fig. 7(a)), similar to our results in Fig. 4(b). Also, the faster the additional regenerative component (τz), the larger the EPSP peak and trough (compare solid and dashed lines with dotted lines). The regenerative component also modifies the non-monotonic relationship between halfwidth and τw (Fig. 7(b)): halfwidth is increased most strongly when τz has intermediate values (τz = 0.2, solid line), in line with results in Fig. 4(c).
Fig. 7.
Combining restorative and regenerative components can differentially affect EPSP amplitude and width. Peak amplitude, trough (a) and halfwidth (b) of the EPSP after propagating over an electrotonic distance X = 1 along a cable with both restorative and regenerative components. Shape parameters are shown as a function of the activation time constant of the restorative component τw/τ, and for three values of the time constant of the regenerative component τz/τ: 0.01 (dashed line), 0.2 (solid line), and 10 (dotted line). The restorative and regenerative components use μw = 4 and μz = −1, respectively, and γR = 2. EPSP amplitude peak, trough and halfwidth are computed relative to the response of a passive cable with μ = 0 and γR = 2. The EPSC is described by an alpha function with time constant τsyn/τ = 0.2
Because EPSP amplitude depends monotonically on the (in)activation time constants, while there is a non-monotonic relationship between EPSP halfwidth and these time constants, a combination of restorative and regenerative components allows them to differentially affect EPSP amplitude and halfwidth. For example, consider that τw is comparable to the membrane time constant and τz is fast (τz/τ = 0.01, dashed lines). In this case the relative EPSP amplitude is ~1, meaning that the attenuation is the same as in a passive cable. The EPSP is, however, still strongly sharpened by ~30%.
3.8 Responses of linear quasi-active cables agree well with responses of nonlinear models
Finally, we test the validity of the linear quasi-active approximation by comparing its predictions with the results of numerical simulations of nonlinear models. Two cable models are used: one with a persistent sodium current, INaP, and one with a low threshold activated potassium current, IKLT (see Section 2). To explore different parameter regimes and relate the models to experimental findings we use two different sets of membrane and synaptic time constants. The cable with INaP has membrane time constant τ = 10 msec and synaptic time constant τsyn = 2 msec, similar to values found in pyramidal neurons. The cable with IKLT uses the much faster membrane and synaptic time constants found in auditory brainstem MSO cells, with τ = 1 msec and τsyn = 0.2 msec.
The linear quasi-active models (Fig. 8(a), solid lines) give very good predictions of the amplitude (top panels) and halfwidth (bottom panels) of an EPSP traveling along the cable in the nonlinear models (circles), even while the synaptic inputs evoke large amplitude EPSPs (20 mV). Note that such large EPSPs sample a considerable range of the nonlinearities of the voltage-dependent currents (see Fig. 1). The linearized IKLT-model (right panels) gives slightly larger EPSP amplitude and halfwidth than the nonlinear model. This results because μ is considered constant during the EPSP in the linear model, whereas the negative feedback by this restorative current increases for depolarized membrane potentials in the nonlinear model (see bottom panel Fig. 1). Freezing the dynamics of the active currents by setting the activation time constants to infinity results in a linear model (“passive”, dashed lines) and reveals that the effects of the active currents on EPSP amplitude are modest whereas they strongly affect the EPSP halfwidth.
Fig. 8.
Quasi-active cable models give good predictions of the response of nonlinear models to large amplitude inputs. (a) Panels show amplitude (top) and halfwidth (bottom) of an EPSP propagating along a cable over an electrotonic distance X. Responses are determined using numerical simulations of nonlinear models (circles) or using the linear quasi-active approximation (solid lines). Left and right columns show the response of a cable with INaP or with IKLT, respectively, and also when the dynamics of these active currents are frozen (“passive”, dashed lines). See Section 2 for model descriptions. (b, c) Halfwidth of the EPSP as a function of the local EPSP amplitude (b) or the synaptic time constant τsyn (c) for the cable with IKLT. EPSP halfwidth is determined with the nonlinear model (circles and squares) and the quasi-active approximation (solid and dotted lines) at an electrotonic distance X = 0 or X = 1 from the injection site. Peak amplitude of the synaptic input in panel (b) is varied from 10 to 2,600 pA. In panel (c) the peak amplitude is fixed at 1,022 pA resulting in EPSP amplitudes ranging over 14–22 mV at X = 0 and over 1.6–3.6 mV at X = 1
To illustrate that the EPSP amplitude is a central parameter determining the error of the linear prediction, we simulated the response of the IKLT-model to a large range of input amplitudes (Fig. 8(b), squares and circles). While the EPSP halfwidth is necessarily independent of amplitude in the linear quasi-active model (solid and dotted lines), it decreases when input amplitude is increased in the nonlinear model (“voltage-dependent sharpening”, Mathews et al. 2010). Also note that the halfwidth decrease is more pronounced for a propagated EPSP (X = 1, circles) than for the EPSP at the input site (X = 0, squares), increasing the error of the linear prediction.
Another important factor determining the error of the linear approximation is the duration of the input. A slower synaptic time constant τsyn allows an active current to more fully express its voltage-dependent nonlinearities. Therefore, the error of the linear approximation typically increases as inputs last longer (Fig. 8(c)).
4 Discussion
We systematically examined how active dendritic conductances affect postsynaptic potentials that propagate along dendrites and how they affect the interaction between such signals. Using the quasi-active description of dendritic cables we could classify voltage-dependent dendritic currents into two types that have qualitatively different effects on subthreshold input responses: regenerative dendritic currents boost and broaden EPSPs, while restorative currents attenuate and narrow EPSPs. Importantly, these effects on EPSP shape increase as the EPSP travels along the dendrite. The activation time constant of the active current determines its effectiveness in modulating EPSP shape: the strongest effects on EPSP amplitude occur for currents that activate much faster than the membrane time constant, while maximum effects on EPSP width occur when the activation time constant is comparable to the membrane time constant. Finally, we showed that the two current types can differentially improve precision and robustness of neural computations: restorative currents enhance coincidence detection of dendritic inputs, whereas direction selectivity to sequences of dendritic inputs is enhanced by regenerative dendritic currents.
4.1 The two classes of active dendritic currents have qualitatively different effects on EPSP shape
By making use of the quasi-active cable approximation we obtain three parameters to describe voltage-dependent currents: the current type μ, the activation time constant τw, and the relative current density γR. The parameter μ denotes the strength of the feedback and its sign classifies active currents into two types: regenerative currents, which implement a positive feedback (μ < 0), and restorative currents, which function as a negative feedback (μ > 0). It is important to realize that both types of currents can be either inward or outward currents, for example, negative feedback results from both an inward current that deactivates (e.g., Ih) or an outward current that activates upon depolarization (e.g., IKLT). The two types of feedback result in qualitatively different effects on the integration of a synaptic input (see Fig. 3). We showed that regenerative dendritic currents increase both the EPSP amplitude and duration. Examples of such currents are the persistent sodium current, INaP, and the low voltage activated calcium current, IT, and experiments have indeed demonstrated that blocking these currents decreases the amplitude and duration of dendritic inputs (Schwindt and Crill 1995; Lipowsky et al. 1996; Gillessen and Alzheimer 1997). Restorative currents have the opposite effect, decreasing the amplitude and duration of dendritically evoked EPSPs. Examples of this class of currents are the Kv1 channel-mediated potassium current, IKLT, that is present in many cell types of the auditory brainstem, and Kv3 channel-mediated potassium currents in fast-spiking hippocampal interneurons. And indeed, experiments in which these currents are blocked show an increased EPSP amplitude and duration (Hu et al. 2010; Mathews et al. 2010).
While the above effects also hold for input integration in a single compartment model, a key finding in our study is that the effects of active currents on EPSP shape increase as the EPSP travels along the dendrite (see Fig. 3(c)). This results because the active current amplitude only depends on the local voltage, hence the EPSP transient will be locally amplified or attenuated by active currents that provide positive or negative feedback, respectively. At each point along the dendrite the active current operates on an increasingly amplified (or attenuated) voltage transient and further increases this amplification (or attenuation). For example, restorative dendritic currents can counteract the passive EPSP broadening along the cable in this way, and maintain a constant halfwidth or even gradually narrow it further. Recent data from auditory brainstem MSO neurons showed that the soma and dendrites of these cells contain IKLT and can thereby actively decrease EPSP halfwidth (Mathews et al. 2010). It is clear that accumulation of these active current effects along the dendrite cannot be achieved in a single compartment neuron model. As a consequence, the effects of active dendritic currents on subthreshold input processing will typically be underestimated in such models.
The effects of subthreshold active currents on the EPSP shape also depend crucially on the current’s activation time constant. EPSP amplification or attenuation is strongest for currents that are at least an order of magnitude faster than the membrane time constant τ (see Fig. 4(b)). The effects of such fast currents on the membrane dynamics can be simply described by scaling τ, λ2, and the input current by a factor 1/(γR + μ), that is, as long as a linearized approximation of the active current is appropriate (see below). Note that this clearly illustrates that restorative currents (μ > 0) lead to smaller but also faster membrane responses, whereas regenerative currents (μ < 0) result in larger but slower membrane responses compared to a passive current (μ = 0). Interestingly, the largest effects on EPSP width occur when the activation time constant is comparable to the membrane time constant (see Fig. 4(c)) such that the feedback operates mostly during the falling phase of the EPSP and therefore also has relatively little effect on the EPSP amplitude.
The only effect a slowly-gated active current has on the EPSP shape is due to its contribution to the membrane conductance, thereby scaling τ, λ2 and the input current by a factor 1/γR. An example of such a current is the hyperpolarization-activated h-type current Ih. The activation time constant of this current is typically too slow (e.g., ~ 50 msec at resting potential in pyramidal neurons, Magee 1998) for its dynamics to significantly affect the shape of a single EPSP (but see Williams and Stuart 2000). However, its dynamics will have a role in longer lasting inputs. For example, during trains of EPSCs, the negative feedback resulting from Ih dynamics (expressed in a so-called “sag-like” response) can equalize the amount of summation for EPSC trains injected at different distances from the soma (Magee 1999; Angelo et al. 2007).
4.2 Subthreshold active dendritic currents can improve robustness and precision of neural computations
A central question is what role active dendritic currents have in the computations a neuron performs. One of the most basic computations is coincidence detection, which requires the neuron to detect the occurrence of two or more EPSPs in a short time interval. Coincidence detection will be more precise when EPSPs are as brief as possible, however, passive spread of dendritic inputs increases EPSP width and hence leads to loss of temporal precision (Rall 1967; Rall et al. 1967; Jack et al. 1971; Jack and Redman 1971a, b). We showed that restorative currents narrow the EPSP and thereby enhance coincidence detection of dendritic inputs since inputs will only summate for very short intervals (see Fig. 5(b)). In contrast, coincidence detection is diminished by regenerative currents because these currents increase the EPSP duration. This suggests that dendrites of neurons performing precise coincidence detection of subthreshold dendritic inputs are likely to possess restorative currents. Indeed, neurons from the auditory brainstem MSO nucleus, which are specialized in performing coincidence detection of binaural inputs (Joris et al. 1998), show a prominent restorative current (IKLT) in soma and dendrites (Mathews et al. 2010), whereas a small, regenerative (sodium) current is restricted to the soma (Scott et al. 2010). The cost for cells using a restorative current to increase temporal precision is the stronger attenuation of dendritic signals arriving at the soma (though note that an appropriate activation time constant can have large effects on EPSP width, while effects on amplitude are relatively small, see Figs. 3(b, c) and 4(b, c)). In small dendritic trees—such as those of MSO cells—this attenuation can be overcome by a sufficiently large amplitude of dendritic EPSPs or by combining the restorative current with a fast regenerative current (see Fig. 7). However, in large dendritic trees attenuation can be too strong to be overcome in these ways. It was shown by Softky (1994) that temporally precise coincidence detection can still be achieved by mechanisms that involve fast, large amplitude dendritic spikes, hence requiring strong regenerative currents.
A second elementary neural computation that we investigated is direction selectivity. Neurons at different levels of the visual system respond strongly to stimuli moving in one direction, while stimuli moving in the opposite direction lead to small responses. A role for subthreshold dendritic input processing has been proposed based on the mechanism that sequential activation of EPSPs along the dendrites toward the soma (centripetal) leads to larger amplitude somatic responses than sequences away from the soma (centrifugal) (Rall 1964; Livingstone 1998; Tukker et al. 2004). We showed that regenerative dendritic currents increase this direction selectivity (see Fig. 6(c)). This results from the increase in EPSP halfwidth with distance travelled along the dendrite, leading to more efficient input summation for centripetal sequences than for centrifugal sequences. In contrast, responses of cell models with restorative dendritic currents show limited direction selectivity. Hence, if direction selective cells make use of this mechanism, one expects such cells to have regenerative rather than restorative dendritic currents. Interestingly, the above mechanism has been proposed to explain direction selective responses of retinal starburst amacrine cells (Tukker et al. 2004), and indeed, the dendrites of these cells contain a prominent regenerative (calcium) current that is active at sub-threshold potentials (Hausselt et al. 2007). However, there is currently no strong support for the role of the sequence-based mechanism in direction-selective responses.
4.3 Use of quasi-active cables to describe subthreshold membrane dynamics
A central element in the present study is the use of quasi-active cables, an extension of passive cable theory that includes the dynamics of voltage-dependent cable currents by linearizing those currents. The method was first employed to study the subthreshold behavior of the squid giant axon, focussing on the generation and propagation of damped oscillations in response to small perturbations (Sabah and Leibovic 1969; Mauro et al. 1972; Sirovich and Knight 1977). Further work by Koch (1984) elucidated certain general principles of quasi-active cables, such as the consequences of active currents for the membrane impedance and the frequency-dependent space constant and delays along the cable (see also Fig. 2). Note that we use the term ‘quasi-active’ for any cable with linearized active currents, while Koch (1984) originally applied the term only to cables whose membrane impedance shows bandpass behavior, which occurs when the cable contains large phenomenological inductances (i.e., restorative currents). More recent studies have used the approach, for example, for examining how active dendritic currents affect phase-locking of neural oscillators receiving dendritic inputs (Bressloff 1999; Goldberg et al. 2007; Remme et al. 2009, 2010), in which case the effects on signal delays play a central role.
In the present work, we used the quasi-active approximation to systematically study the effect of active dendritic conductances on the shape of propagating EPSPs. By using this approach we could obtain general results that do not rely on the specifics of a particular voltage-dependent current. However, several aspects of the active current are lost when it is linearized: the nonlinearity of the current’s activation function, the voltage-dependence of its driving force, and the voltage-dependence of the activation time constant. The linear approximation is valid for small voltage changes; the larger the voltage changes, the more the linearized system will deviate from the nonlinear system. However, depending on the specific current and the type of stimulus, these voltage changes can actually be quite large. Our results from numerical simulations of two very different nonlinear systems producing 20 millivolt EPSPs matched very well with the response of the linear system (see Fig. 8(a)). The steady state current-voltage relationship of a voltage-dependent current gives an indication of how strongly nonlinear the current is over a particular voltage range. When a current is very nonlinear, e.g., when the foot of the activation curve lies near the voltage around which the current is linearized (i.e., typically the resting potential), the linearized approximation will quickly under- or overestimate the effect of the current’s dynamics (see Fig. 8(b)). It is such nonlinear behavior that underlies the recently reported voltage-dependent sharpening of EPSPs in MSO cells (Mathews et al. 2010). These strong nonlinearities will be particularly important when considering inputs that are relatively long compared to the membrane time constant and the activation time constant. In such cases the voltage-dependent current will fully adapt to the time-varying membrane potential, thereby changing the current’s response to the ongoing stimulus (see Fig. 8(c)).
Another type of nonlinearity that is not included in our approach results from describing synaptic input as current injections rather than conductance changes, thus considering the driving force of the synaptic current as constant. However, this does not significantly affect the response to a single EPSC, since the reversal potential for excitatory inputs is typically about 60 mV above the resting potential. While the present manuscript focuses on the response to excitatory input, the same results hold for inhibitory input. For example, the restorative KLT-type current will also sharpen dendritic IPSPs, resulting from deactivation of this inward current. Note, however, that the voltage-dependence of the driving force is particularly relevant to inhibitory input, since the synaptic reversal potential can be close to the resting potential. Hence, describing inhibitory inputs as current injections may not be appropriate. Note also that nonlinear interactions between synaptic inputs do not occur when considering synaptic inputs as current injections. For example, when two conductance inputs are located close to each other on a dendrite, responses will summate sublinearly, whereas segregation of the inputs onto different dendrites avoids such effects and inputs can summate linearly (see, for example, Agmon-Snir et al. 1998).
Finally, we chose to focus on the behavior of infinite quasi-active cables and did not consider the effects of the boundary conditions that are imposed by finite cable lengths. This was done in order to obtain general results that do not depend on the specifics of the dendritic morphology. Note that a recent study by Coombes et al. (2007) shows how to derive the Green’s function of quasi-active dendrites with arbitrary branched geometries. The effects of various boundary conditions on EPSP shape have been thoroughly investigated for passive cables (see, e.g., Rall 1967; Jack and Redman 1971a, b). In general, sealed end boundary conditions lead to an increased EPSP amplitude and duration, in particular near the sealed ends through which charge cannot leave.
In summary, the quasi-active cable approximation serves as a solid reference for the effects of voltage-dependent currents on subthreshold input integration. Depending on the system under consideration, this approach can, in fact, give very good predictions of the response of the nonlinear system. The linearized system not only makes it possible to apply analytical techniques, it also reduces the system to the essential parameters, thereby aiding in the understanding and further study of the role of active dendrites in neural computations.
Acknowledgments
This work was supported by a grant from the US National Institutes of Health: DC008543 to JR.
Contributor Information
Michiel W. H. Remme, Email: michiel.remme@nyu.edu, Center for Neural Science, New York University, 4 Washington Place, New York, NY 10003, USA
John Rinzel, Center for Neural Science, New York University, 4 Washington Place, New York, NY 10003, USA. Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, USA.
References
- Agmon-Snir H, Carr CE, Rinzel J. The role of dendrites in auditory coincidence detection. Nature. 1998;393(6682):268–272. doi: 10.1038/30505. [DOI] [PubMed] [Google Scholar]
- Angelo K, London M, Christensen SR, Häusser M. Local and global effects of Ih distribution in dendrites of mammalian neurons. Journal of Neuroscience. 2007;27(32):8643–8653. doi: 10.1523/JNEUROSCI.5284-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressloff PC. Resonantlike synchronization and bursting in a model of pulse-coupled neurons with active dendrites. Journal of Computational Neuroscience. 1999;6(3):237–249. doi: 10.1023/a:1008853805855. [DOI] [PubMed] [Google Scholar]
- Chklovskii DB. Synaptic connectivity and neuronal morphology: Two sides of the same coin. Neuron. 2004;43(5):609–617. doi: 10.1016/j.neuron.2004.08.012. [DOI] [PubMed] [Google Scholar]
- Coombes S, Timofeeva Y, Svensson CM, Lord GJ, Josić K, Cox SJ, et al. Branching dendrites with resonant membrane: A “sum-over-trips” approach. Biological Cybernetics. 2007;97(2):137–149. doi: 10.1007/s00422-007-0161-5. [DOI] [PubMed] [Google Scholar]
- Gillessen T, Alzheimer C. Amplification of EPSPs by low Ni2+- and amiloride-sensitive Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. Journal of Neurophysiology. 1997;77(3):1639–1643. doi: 10.1152/jn.1997.77.3.1639. [DOI] [PubMed] [Google Scholar]
- Goldberg JA, Deister CA, Wilson CJ. Response properties and synchronization of rhythmically firing dendritic neurons. Journal of Neurophysiology. 2007;97(1):208–219. doi: 10.1152/jn.00810.2006. [DOI] [PubMed] [Google Scholar]
- Hausselt SE, Euler T, Detwiler PB, Denk W. A dendrite-autonomous mechanism for direction selectivity in retinal starburst amacrine cells. PLoS Biology. 2007;5(7):e185. doi: 10.1371/journal.pbio.0050185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The neuron simulation environment. Neural Computation. 1997;9(6):1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hu H, Martina M, Jonas P. Dendritic mechanisms underlying rapid synaptic activation of fast-spiking hippocampal interneurons. Science. 2010;327(5961):52–58. doi: 10.1126/science.1177876. [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends in Neurosciences. 2000;23(5):216–222. doi: 10.1016/s0166-2236(00)01547-2. [DOI] [PubMed] [Google Scholar]
- Jack JJ, Redman SJ. An electrical description of the motoneurone, and its application to the analysis of synaptic potentials. Journal of Physiology. 1971a;215(2):321–352. doi: 10.1113/jphysiol.1971.sp009473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack JJ, Redman SJ. The propagation of transient potentials in some linear cable structures. Journal of Physiology. 1971b;215(2):283–320. doi: 10.1113/jphysiol.1971.sp009472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack JJ, Miller S, Porter R, Redman SJ. The time course of minimal excitory post-synaptic potentials evoked in spinal motoneurones by group Ia afferent fibres. Journal of Physiology. 1971;215(2):353–380. doi: 10.1113/jphysiol.1971.sp009474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joris PX, Smith PH, Yin TC. Coincidence detection in the auditory system: 50 years after Jeffress. Neuron. 1998;21(6):1235–1238. doi: 10.1016/s0896-6273(00)80643-1. [DOI] [PubMed] [Google Scholar]
- Koch C. Cable theory in neurons with active, linearized membranes. Biological Cybernetics. 1984;50(1):15–33. doi: 10.1007/BF00317936. [DOI] [PubMed] [Google Scholar]
- Lipowsky R, Gillessen T, Alzheimer C. Dendritic Na+ channels amplify EPSPs in hippocampal CA1 pyramidal cells. Journal of Neurophysiology. 1996;76(4):2181–2191. doi: 10.1152/jn.1996.76.4.2181. [DOI] [PubMed] [Google Scholar]
- Livingstone MS. Mechanisms of direction selectivity in macaque V1. Neuron. 1998;20(3):509–526. doi: 10.1016/s0896-6273(00)80991-5. [DOI] [PubMed] [Google Scholar]
- London M, Häusser M. Dendritic computation. Annual Review of Neuroscience. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- Magee JC. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. Journal of Neuroscience. 1998;18(19):7613–7624. doi: 10.1523/JNEUROSCI.18-19-07613.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee JC. Dendritic Ih normalizes temporal summation in hippocampal CA1 neurons. Nature Neuroscience. 1999;2(6):508–514. doi: 10.1038/9158. [DOI] [PubMed] [Google Scholar]
- Mathews PJ, Jercog PE, Rinzel J, Scott LL, Golding NL. Control of submillisecond synaptic timing in binaural coincidence detectors by Kv1 channels. Nature Neuroscience. 2010;13(5):601–609. doi: 10.1038/nn.2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauro A, Freeman AR, Cooley JW, Cass A. Propagated subthreshold oscillatory response and classical electrotonic response of squid giant axon. Biophysik. 1972;8(2):118–132. doi: 10.1007/BF01188562. [DOI] [PubMed] [Google Scholar]
- Migliore M, Shepherd GM. Emerging rules for the distributions of active dendritic conductances. Nature Reviews Neuroscience. 2002;3(5):362–370. doi: 10.1038/nrn810. [DOI] [PubMed] [Google Scholar]
- Povysheva NV, Gonzalez-Burgos G, Zaitsev AV, Kröner S, Barrionuevo G, Lewis DA, et al. Properties of excitatory synaptic responses in fast-spiking interneurons and pyramidal cells from monkey and rat prefrontal cortex. Cerebral Cortex. 2006;16(4):541–552. doi: 10.1093/cercor/bhj002. [DOI] [PubMed] [Google Scholar]
- Rall W. Theoretical significance of dendritic trees for neuronal input–output relations. In: Reiss RF, editor. Neural theory and modeling. Palo Alto: Stanford University Press; 1964. pp. 122–146. [Google Scholar]
- Rall W. Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input. Journal of Neurophysiology. 1967;30(5):1138–1168. doi: 10.1152/jn.1967.30.5.1138. [DOI] [PubMed] [Google Scholar]
- Rall W, Burke RE, Smith TG, Nelson PG, Frank K. Dendritic location of synapses and possible mechanisms for the monosynaptic EPSP in motoneurons. Journal of Neurophysiology. 1967;30(5):1169–1193. doi: 10.1152/jn.1967.30.5.1169. [DOI] [PubMed] [Google Scholar]
- Remme MWH, Lengyel M, Gutkin BS. The role of ongoing dendritic oscillations in single-neuron dynamics. LoS Computational Biology. 2009;5(9):e1000, 493. doi: 10.1371/journal.pcbi.1000493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remme MWH, Lengyel M, Gutkin BS. Democracy-independence trade-off in oscillating dendrites and its implications for grid cells. Neuron. 2010;66(3):429–437. doi: 10.1016/j.neuron.2010.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabah NH, Leibovic KN. Subthreshold oscillatory responses of the Hodgkin-Huxley cable model for the squid giant axon. Biophysical Journal. 1969;9(10):1206–1222. doi: 10.1016/S0006-3495(69)86446-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartzkroin PA, Slawsky M. Probable calcium spikes in hippocampal neurons. Brain Research. 1977;135(1):157–161. doi: 10.1016/0006-8993(77)91060-5. [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Crill WE. Amplification of synaptic current by persistent sodium conductance in apical dendrite of neocortical neurons. Journal of Neurophysiology. 1995;74(5):2220–2224. doi: 10.1152/jn.1995.74.5.2220. [DOI] [PubMed] [Google Scholar]
- Scott LL, Mathews PJ, Golding NL. Posthearing developmental refinement of temporal processing in principal neurons of the medial superior olive. Journal of Neuroscience. 2005;25(35):7887–7895. doi: 10.1523/JNEUROSCI.1016-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott LL, Mathews PJ, Golding NL. Perisomatic voltage-gated sodium channels actively maintain linear synaptic integration in principal neurons of the medial superior olive. Journal of Neuroscience. 2010;30(6):2039–2050. doi: 10.1523/JNEUROSCI.2385-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirovich L, Knight BW. On subthreshold solutions of the Hodgkin–Huxley equations. Proceedings of the National Academy of Sciences of the United States of America. 1977;74(12):5199–5202. doi: 10.1073/pnas.74.12.5199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Softky W. Sub-millisecond coincidence detection in active dendritic trees. Neuroscience. 1994;58(1):13–41. doi: 10.1016/0306-4522(94)90154-6. [DOI] [PubMed] [Google Scholar]
- Stuart G, Spruston N, Sakmann B, Häusser M. Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends in Neurosciences. 1997;20(3):125–131. doi: 10.1016/s0166-2236(96)10075-8. [DOI] [PubMed] [Google Scholar]
- Traub RD, Buhl EH, Gloveli T, Whittington MA. Fast rhythmic bursting can be induced in layer 2/3 cortical neurons by enhancing persistent Na+ conductance or by blocking BK channels. Journal of Neurophysiology. 2003;89(2):909–921. doi: 10.1152/jn.00573.2002. [DOI] [PubMed] [Google Scholar]
- Tukker JJ, Taylor WR, Smith RG. Direction selectivity in a model of the starburst amacrine cell. Visual Neuroscience. 2004;21(4):611–625. doi: 10.1017/S0952523804214109. [DOI] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ. Site independence of EPSP time course is mediated by dendritic Ih in neocortical pyramidal neurons. Journal of Neurophysiology. 2000;83(5):3177–3182. doi: 10.1152/jn.2000.83.5.3177. [DOI] [PubMed] [Google Scholar]