Subthreshold K⁺ Channel Dynamics Interact With Stimulus Spectrum to Influence Temporal Coding in an Auditory Brain Stem Model

Abstract

Neurons in the auditory brain stem encode signals with exceptional temporal precision. A low-threshold potassium current, I_KLT, present in many auditory brain stem structures and thought to enhance temporal encoding, facilitates spike selection of rapid input current transients through an associated dynamic gate. Whether the dynamic nature of I_KLT interacts with the timescales in spectrally rich input to influence spike encoding remains unclear. We examine the general influence of I_KLT on spike encoding of stochastic stimuli using a pattern classification analysis between spike responses from a ventral cochlear nucleus (VCN) model containing I_KLT, and the same model with the dynamics removed. The influence of I_KLT on spike encoding depended on the spectral content of the current stimulus such that maximal I_KLT influence occurred for stimuli with power concentrated at frequencies low enough (<500 Hz) to allow I_KLT activation. Further, broadband stimuli significantly decreased the influence of I_KLT on spike encoding, suggesting that broadband stimuli are not well suited for investigating the influence of some dynamic membrane nonlinearities. Finally, pattern classification on spike responses was performed for physiologically realistic conductance stimuli created from various sounds filtered through an auditory nerve (AN) model. Regardless of the sound, the synaptic input arriving at VCN had similar low-pass power spectra, which led to a large influence of I_KLT on spike encoding, suggesting that the subthreshold dynamics of I_KLT plays a significant role in shaping the response of real auditory brain stem neurons.

INTRODUCTION

Auditory brain stem neurons encode signals with exceptional temporal precision. The relaying of precise temporal information is important for birds and low-frequency– hearing mammals in localizing sounds based on the encoding of very small interaural time differences of acoustic signals arriving at the two ears (Goldberg and Brown 1969; Moiseff and Konishi 1981; Spitzer and Semple 1995; Yin and Chan 1990). Several biophysical mechanisms in the auditory brain stem enable high temporal precision, including calyceal synaptic inputs (Jhaveri and Morest 1982), fast adapting synaptic currents (Gardner et al. 1999; Raman and Trussell 1992; Smith et al. 2000), short (<1 ms) membrane time constants (Scott et al. 2005), and the subject of our study: the fast, low-threshold potassium current (I_KLT) (Manis and Marx 1991; Rathouz and Trussell 1998; Reyes et al. 1994). Neurons with large densities of I_KLT have been found to fire phasically in response to step-current stimuli (Manis and Marx 1991; Reyes et al. 1994; Smith 1995); have increased phase-locking to strong sinusoidal current stimuli (Oertel 1983; Reyes et al. 1996; Rothman and Young 1996); and have an increased signal-to-noise ratio for detecting small current signals in noise (Svirskis et al. 2002). Some of these phenomena, including the ability to enhance detection of coincident synaptic input, may be attributed, in part, to the simple passive properties associated with I_KLT decreasing the resting membrane time constant. However, it remains unclear to what extent the active, dynamic properties of I_KLT influence spike train encoding in the auditory brain stem.

The influence of I_KLT has been investigated by observing the voltage response of cells and models of cells to simple current stimuli such as steps, ramps, pulse trains, and sinusoids in the presence and absence of I_KLT channel blockers (Brew and Forsythe 1995; Cai et al. 2000; Ferragamo and Oertel 2002; Svirskis et al. 2002, 2004). Alternatively, I_KLT has also been investigated by observing changes in spike encoding of a dynamic stimulus with application of I_KLT channel blockers (Slee et al. 2005; Svirskis et al. 2002, 2004). These latter studies used spike-triggered reverse correlation on stochastic current signals, such as summated excitatory and inhibitory postsynaptic currents and broadband stochastic currents, to characterize spike encoding. Here, the influence of I_KLT has been assessed with a qualitative comparison of the shape of the spike-triggered average (STA) (Svirskis et al. 2002, 2004) or the principal components of the spike-triggered covariance (STC) (Slee et al. 2005) in the presence and absence of I_KLT channel blockers. Furthermore, since these studies do not correct for any change in passive membrane properties after a pharmacological I_KLT block, and do not vary the spectral content of stimuli in a systematic fashion, it is then difficult to quantify the exclusive influence that the dynamic nature of I_KLT has on spike train coding.

In this study, we examine the influence of I_KLT on spike encoding in a Hodgkin–Huxley-like model of VCN neurons (Rothman and Manis 2003b) using stochastic current stimuli. In contrast to the above-cited STA/STC approaches, we use a linear pattern classifier (Duda et al. 2001) to more accurately quantify how much influence I_KLT has on spike encoding, without assuming a specific representation of the code. We apply the pattern classifier in a novel way to assess the difference in spike encoding caused by the interaction of the spectral content of a stimulus and I_KLT dynamics. By comparing a model with dynamic I_KLT to a model with I_KLT conductance fixed to its level at resting membrane potential, we find that dynamic I_KLT has a significant influence on the stimulus current selectivity of the spiking model only when the stimulus has sufficiently low-frequency power or when a broadband stimulus is sufficiently weak. Further, we specifically investigate whether the spectral content of realistic synaptic input interacts with the dynamics of I_KLT to affect spike encoding.

METHODS

Model

The model used to simulate neurons with I_KLT was the same as the Type II VCN model developed by Rothman and Manis (2003b). The Rothman–Manis model (here abbreviated “RM03”) is a Hodgkin–Huxley-type point neuron model consisting of a standard fast-inactivating sodium current (I_Na), a high-threshold potassium current (I_KHT), and leak currents (I_lk), as well as a low-threshold potassium current (I_KLT) and a hyperpolarization-activated cation current (I_h). These currents are combined in the current-balance equation

$$C_{\text{m}}\frac{\text{d}V}{\text{d}t}=-I_{\text{Na}}-I_{\text{KHT}}-I_{\text{KLT}}-I_{\text{h}}-I_{\text{lk}}+s(t)$$ (1)

where C_m is the membrane capacitance, V is the membrane potential, and s(t) is the external stimulating current. Expressing each current I_x in terms of its activation and inactivation gating variables rewrites Eq. 1 as

$$\begin{array}{l}{C}_{\text{m}}\frac{\text{d}V}{\text{d}t}=-{\overline{g}}_{\text{Na}}{m}^{3}h(V-E_{\text{Na}})-{\overline{g}}_{\text{KHT}}(0.85n^2+0.15p)(V-E_{\text{K}})\\ -{\overline{g}}_{\text{KLT}}{w}^{4}z(V-E_{\text{K}})-{\overline{g}}_{\text{h}}r(V-E_{\text{h}})-{\overline{g}}_{\text{lk}}(V-E_{\text{lk}})+s(t)\end{array}$$ (2)

where g_x and E_x are the respective maximal conductance and reversal potential for ionic species x. For all simulations, C_m =12 pF, E_K =70 mV, E_Na = +55 mV, E_h =−43 mV, and E_lk = −65 mV. Maximal conductances are: ḡ_Na = 1,000 nS, ḡ_KHT = 150 nS, ḡ_KLT = 200 nS, ḡ_h = 20 nS, and g_lk = 2 nS. The voltage- and time dependencies of the activation/inactivation variables, x, are described by the equation

$$\frac{\text{d}x}{\text{d}t}=\frac{[x_{\infty }(V)-x]}{{\tau }_x(V)}$$ (3)

where x_∞ (V) is the steady-state value of x at potential V and τ_x(V) is the time constant of x. The functions x_∞ (V) and τ_x(V) are empirically derived from voltage-clamped responses of cochlear nucleus neurons and may be found in Rothman and Manis (2003b). Additionally, all time constants were multiplied by 0.17 and maximal conductances were multiplied by 3.03 to adjust model dynamics to normal body temperature (38°C) (Rothman and Manis 2003b).

Integration of the preceding equations was carried out using the forward Euler method with a time step of 0.01 ms. This first-order, single-step integration scheme proved adequately efficient for our long simulations to collect many spikes and was accurate due to the small step size. Halving the time step produced no noticeable differences in voltage traces. Spike times were recorded when the membrane potential crossed upward through our selected threshold, V_Th = 0 mV.

We examined responses of two versions of the RM03 model. The dynamic KLT model was the unaltered RM03 model, with no change in the dynamics of I_KLT. The frozen KLT model had the activation and inactivation gating variables of I_KLT, w and z, fixed to their resting values. This eliminated the voltage- and time dependencies of I_KLT in the frozen KLT model, yet maintained the same resting conductance and membrane time constant in both models.

Stimuli

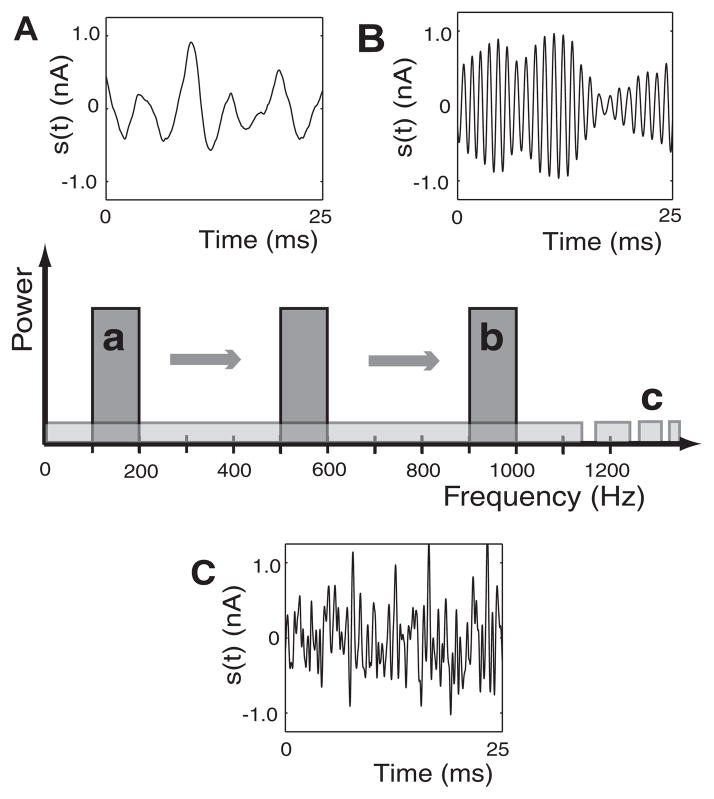
All random stimuli, s(t), were filtered Gaussian white-noise currents digitized at the integration time step. We implemented a fourth-order Butterworth filter (MATLAB, The MathWorks) to create narrowband (approximately rectangular power spectrum) and broadband stimuli (Fig. 1). For narrowband stimuli, upper and lower cutoff frequencies were chosen to create a bandwidth of 100 Hz. The center frequency of the narrowband was chosen to create signals that spanned nonoverlapping intervals 0 –100 Hz, 100 –200 Hz, and so on to ≤1,100 –1,200 Hz. For broadband stimuli the spectrum was uniform between 0 and 2,000 Hz. Stimulus currents were scaled such that the SD of the stimulus amplitude was set to a value chosen between 0.3 and 0.8 nA. Simulations were continued long enough to obtain 10,000 spikes for a given stimulus.

FIG. 1.

Current stimuli. Center: power spectra of the current stimuli used in the study. Narrowband stimuli were 100 Hz wide with center frequency varied along the frequency axis. The broadband stimulus had a cutoff frequency off the axis at 2 kHz. Sample time courses are shown for 2 narrowband stimuli with center frequencies of 150 Hz (A) and 950 Hz (B), respectively. C: sample time course of the broadband stimulus.

Pattern classification analysis

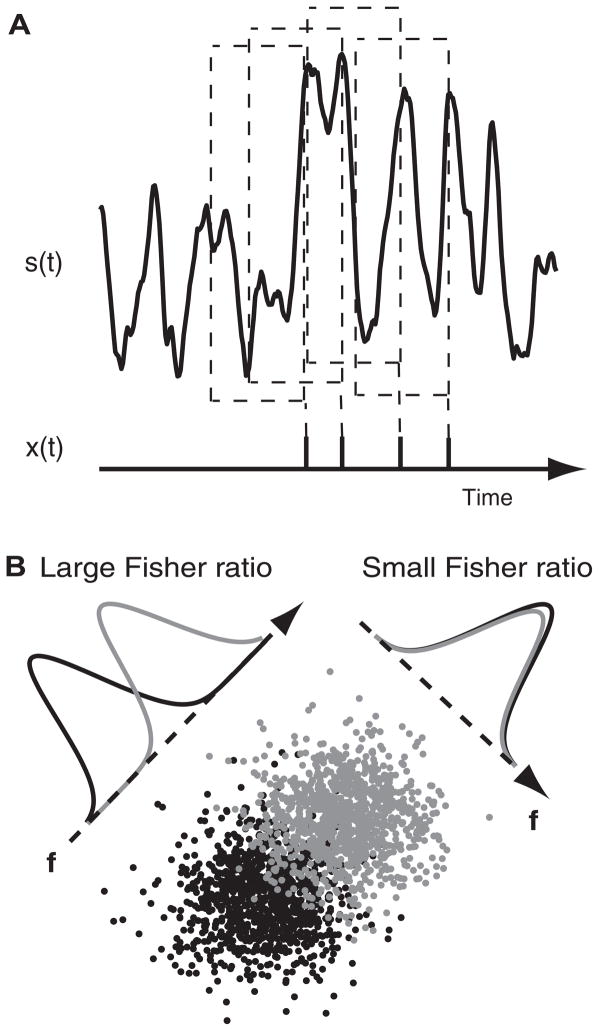
For every stimulus, 10,000 spike times were collected each from the dynamic and frozen KLT models. To develop a putative spike code we used reverse-correlation techniques (Rieke et al. 1997; Slee et al. 2005) on the simulated data. Specifically, for every spike time,, we recorded the preceding stimulus as the vector s = {s[t_sp − (K − 1)Δt], s[t_sp − (K − 2)Δt], …, s(t_sp − Δt), s(t_sp)}, where K = T/Δt, with T being the time interval of the reverse correlation and Δt the time discretization (Fig. 2A). In practice Δt = 0.2 ms and T = 30 ms. The collection of these spike-triggered stimulus vectors for a given model—the spike-triggered ensemble (STE)—formed a cloud of points in 150-dimensional stimulus space. The STE was a finite sample of all possible stimuli that caused the model to spike. The spike-triggered average m is the mean of the STE

FIG. 2.

Schematic of Fisher linear discrimination on spike-triggered stimulus waveforms. A: for every spike event in the spike train x(t) the 30 ms of stimulus current s(t) preceding the spike is collected as a spike-triggered current waveform. B: example of Fisher linear discrimination on dynamic and frozen KLT (low-threshold potassium) model spike-triggered ensembles (STEs), idealized in 2 dimensions. Here, a line instead of a hyperplane may be visualized to separate the 2 ensembles, if oriented properly. The orientation of the normal vector f, perpendicular to the separating line, changes the Fisher ratio of the projected ensemble probability densities. f is chosen to maximize the Fisher ratio.

$${\mathbf{m}}_{d,f}={\langle \mathbf{s}\rangle }_{d,f}$$ (4)

where the subscripts d and f represent the dynamic and frozen KLT models, respectively, and the brackets 〈〉 represent an average over the corresponding ensemble, not over time.

STAs were compared between the dynamic and frozen KLT models as a means of visually observing the difference in stimulus selection (or equivalently, spike encoding). However, STAs assume a mean representation of stimulus selection and, further, do not themselves quantify the difference in stimulus selection between the two models. The problem of quantifying stimulus selection difference between models was addressed as a standard pattern classification problem (Duda et al. 2001). Given large samples of two pattern classes (e.g., STEs), the question was posed as to how accurately a classifier could correctly classify a given spike-triggered stimulus as either causing the dynamic KLT model to spike or the frozen KLT model to spike. The accuracy of such a classifier depended on how distinct the STEs from each model were from one another. If the STEs largely overlapped, meaning most spike-triggered stimuli caused spiking in both models, then the classifier would have poor accuracy in correctly classifying a stimulus.

In K-dimensional stimulus space, the STEs exist as two partially overlapping clouds of points. A linear classifier attempts to optimally separate the two STE clouds with an appropriate hyperplane. This hyperplane may be defined by its normal vector f. We used a linear discriminant classifier function, h(s), of the form

$$h(\mathbf{s})=\mathbf{f}·\mathbf{s}-\theta$$ (5)

where the projection of the stimulus vector s onto f is compared with a threshold value θ. Spike-triggered stimuli that gave a positive value of h(s) were classified as causing the dynamic KLT model to spike; otherwise, the stimulus was classified as causing the frozen KLT model to spike.

The separating hyperplane was chosen using the Fisher method (Metzner et al. 1998). This method chooses f such that when the STEs are projected onto it, creating two distributions of projected values, the ratio of the squared difference of means of the distributions to the sum of the variances of the distributions is maximized (see Fig. 2B for a schematic illustration). The Fisher ratio F(f) takes the form

$$F(\mathbf{f})=\frac{{[\mathbf{f}·({\mathbf{m}}_f-{\mathbf{m}}_d)]}^2}{{\mathbf{f}}^T\left(1/2{\sum }_d+1/2{\sum }_f\right)\mathbf{f}}$$ (6)

where m_d and m_f are the STAs of the dynamic and frozen KLT models, respectively, and Σ_d and Σ_f are the covariance matrices. The covariance matrix is

$${\sum }_{d,f}={\langle (\mathbf{s}-{\mathbf{m}}_{d,f}){(\mathbf{s}-{\mathbf{m}}_{d,f})}^T\rangle }_{d,f}$$ (7)

where the vector product is averaged over the STE. The f that maximizes the Fisher ratio has a relatively simple closed-form solution (Duda et al. 2001)

$${\mathbf{f}}_{max}=2{\left({\sum }_d+{\sum }_f\right)}^{-1}({\mathbf{m}}_f-{\mathbf{m}}_d)$$ (8)

Most often, the sum of the covariance matrices in Eq. 8 was not invertible, and thus the inverse was replaced with the pseudoinverse using the MATLAB function pinv.

After solving for f_max, both STEs were projected onto it, creating two probability densities of projected values (e.g., Fig. 4A, a and b). Each probability density was approximated by combining projected values into a histogram with 200 bins, then dividing by the total number of spike-triggered stimuli. The misclassification error ε(θ) of the classifier was determined by

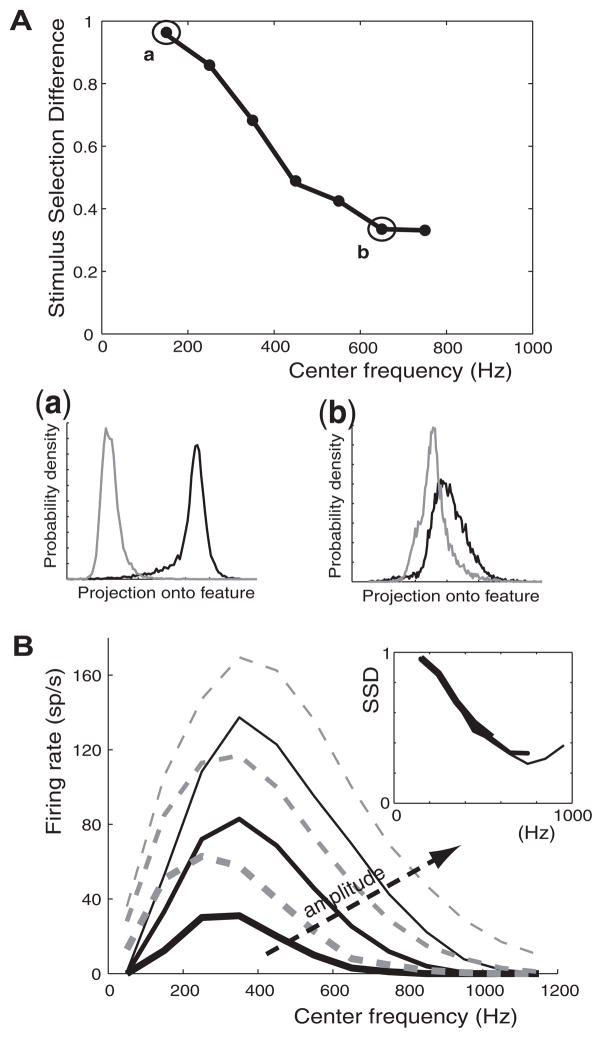
FIG. 4.

Difference between dynamic and frozen KLT spike encoding to narrowband stimuli at different center frequencies. A: stimulus selection difference (SSD) between models in response to narrowband stimuli as a function of center frequency (100-Hz bandwidth; 0.4-nA intensity). The probability densities of the projected STEs are shown for 2 narrowband stimuli with center frequencies 150 Hz (a) and 650 Hz (b), respectively. B: firing rates of the dynamic (black) and frozen (gray dashed) KLT models in response to narrowband stimuli. Intensity of the stimulus was varied: 0.3 nA (thick lines); 0.4 nA (medium lines); 0.5 nA (thin lines). Inset: SSD curves for the same stimuli at 0.3-nA (thick), 0.4-nA (medium), and 0.5-nA (thin) intensities.

$$\epsilon (\theta )=1/2P_{Fd}(\theta )+1/2P_{Ff}(\theta )$$ (9)

where P_Fd(θ) is the probability that, for a fixed θ, a stimulus is falsely classified with the dynamic KLT model; and P_Ff (θ) is the probability that it is falsely classified with the frozen KLT model. The threshold was varied through the complete range of projected values, effectively parameterizing ε. The optimal linear classifier was constructed using the θ that minimized ε, denoted ε_min. A linear transformation of ε_min motivated a simple definition of the stimulus selection difference (SSD) between the two models

$$\text{SSD}=1-2{\epsilon }_{min}$$ (10)

The SSD takes a value between 0 and 1. An SSD of 0 occurs when the STEs of each model completely overlap, meaning that the dynamic and frozen KLT models spiked to the same stimulus waveforms. Conversely, an SSD of 1 occurs when the STEs are completely separable, in which case the dynamic and frozen KLT models spiked to distinctly different stimuli.

The Fisher method is ideal when the projection of the STEs along any f forms two Gaussian distributions, although the projection of the STEs in this study were not Gaussian. Nevertheless, projecting the STEs onto f_max resulted in probability distributions that were unimodal and could be described largely by the first two moments (Fig. 4A, a and b). Therefore Fisher linear discrimination was assumed to be adequate in quantifying SSD. The accuracy of SSD computations was checked with a bootstrap procedure. The STEs collected in response to the narrowband stimulus with center frequency 150 Hz were resampled with replacement 100 times, creating 100 bootstrap estimates of the SSD. The 95% bootstrap confidence interval surrounding the SSD was ±0.0034.

Physiological conductance stimuli

The narrowband and broadband current stimuli described earlier were useful artificial stimuli to compare spike encoding between the dynamic and frozen KLT models. However, these stimuli were not physiologically realistic examples of the input that VCN neurons likely receive from convergent AN synapses. To compare the dynamic and frozen KLT model spike encoding of physiological stimuli, realistic inputs were approximated using the output of an appropriate AN model (Fig. 8A).

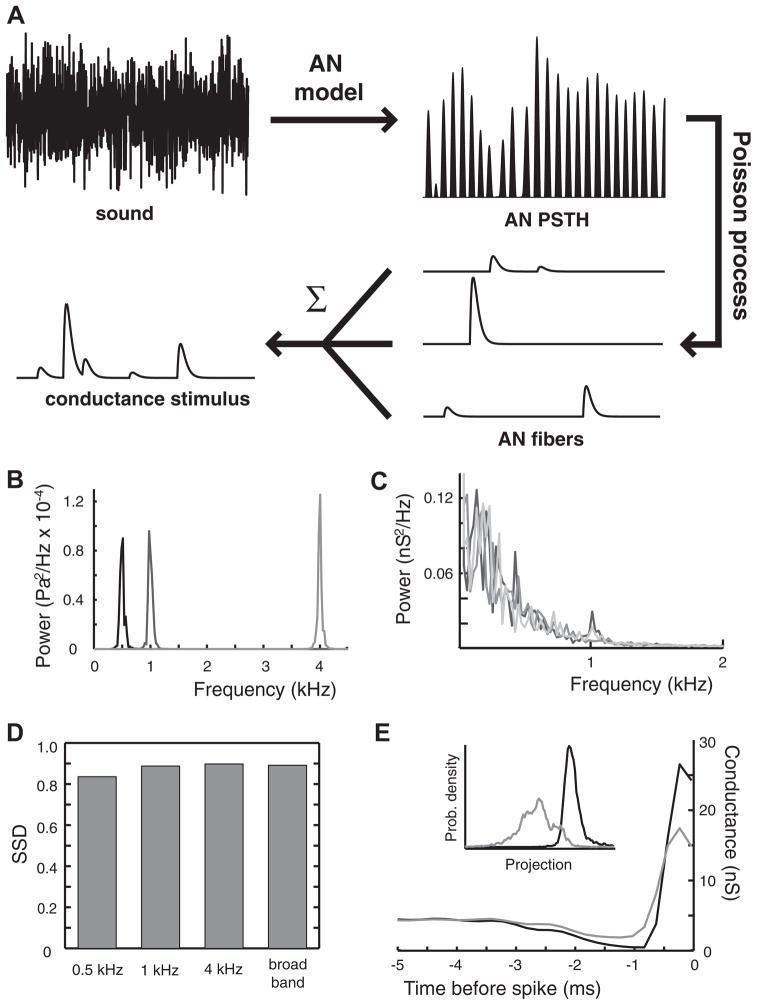
FIG. 8.

Difference between dynamic and frozen KLT model responses to physiological conductance stimuli. A: schematic of the transformation of a sound into a conductance stimulus. A sound pressure waveform is input into an auditory nerve (AN) model to produce a poststimulus time histogram (PSTH). Three spike trains are randomly obtained from the PSTH via an inhomogeneous Poisson process. The spike trains are convolved with an excitatory postsynaptic conductance waveform with randomized peak conductance, then summated to produce the conductance stimulus. B: power spectra of the initial sounds. The sounds are narrowband waveforms centered at 500 Hz (black), 1 kHz (dark gray), and 4 kHz (light gray). The power spectrum of the broadband sound is flat and not visible at this scale. C: power spectra of the conductance stimuli. Regardless of the initial sound, the stimuli arriving at ventral cochlear nucleus (VCN) have approximately the same power spectrum: 500 Hz (black); 1 kHz (dark gray); 4 kHz (medium gray); broadband (light gray). D: SSD between model responses to the different sounds. E: STAs of the dynamic KLT model (black) and the frozen KLT model (gray) in response to the broadband sound. STAs in response to the other sounds look similar. Inset: probability densities of the STEs projected onto the normal vector. These densities led to the SSD for broadband sound in D.

To this end, stochastic narrowband and broadband sound waveforms were created as described earlier for current stimuli (see Stimuli). Sound waveforms were scaled to have a SD pressure level of 70 dB SPL. The waveforms were then input into an AN model (Tan and Carney 2003) with the characteristic frequency of the model set to match the center frequency of the input band. The AN model produced in response to the input waveform a poststimulus time histogram (PSTH). Three separate spike trains were randomly extracted from the PSTH assuming an inhomogeneous Poisson process where the probability of spike occurrence in each time bin was set to the firing probability of the corresponding time in the PSTH. Spike times within a hard refractory period of 1 ms were eliminated, yielding the final AN spike trains. Each AN spike train was convolved with an α-function with a time constant of 0.3 ms, yielding an excitatory postsynaptic potential with a decay time of about 0.4 ms (Gardner et al. 1999). Furthermore, each synaptic event was randomly assigned a peak conductance from a Gaussian distribution, modeling a strong reliability of event occurrence of the end bulb of Held synapse. Mean peak conductance was set to 15 nS and SD of 3.75 nS. The three conductance time courses were summated to produce a single conductance stimulus, s(t). The summation of the three AN fibers modeled the synapsing of a small number of end bulbs of Held onto spherical bushy cells (Sento and Ryugo 1989). Globular bushy cells, on the other hand, receive a large number of convergent AN inputs (Spirou et al. 2005). This study focused on the case of spherical bushy cells, which are known to project to medial and lateral superior olive (MSO and LSO, respectively).

Finally, since s(t) was a conductance stimulus, not a current stimulus, the current stimulus term in Eq. 2 was replaced with s(t)(V − E_exc), where E_exc = 0 mV was the excitatory synaptic reversal potential. As with the artificial current stimuli, simulation was continued long enough to collect 10,000 spikes for each sound waveform.

RESULTS

We conducted this study to investigate whether subthreshold I_KLT dynamics influences the stimulus selectivity exhibited by spike train responses. We compared the spike train responses of the RM03 model (dynamic KLT) to responses from an altered version of the model (frozen KLT) in which the time-and voltage-varying activation gating of I_KLT was removed, effectively freezing the gating variable to its value at the resting potential (see METHODS). This alteration kept the input resistance and membrane time constant the same in the two models, ensuring any difference in response between models would be due to the loss of time- and voltage-varying properties of I_KLT and not due to the passive filtering that I_KLT automatically adds just by increasing the resting conductance.

Differential voltage response to current ramps and random stimuli of different timescales

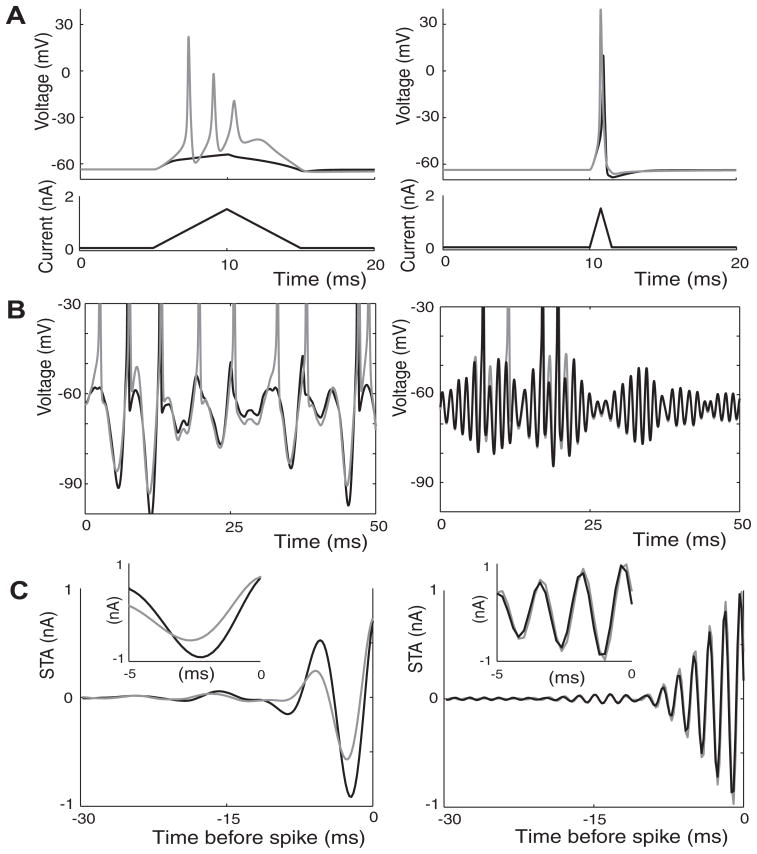
As an introduction to the dynamic stimulus selectivity that I_KLT imparts to excitable membrane, we compared the voltage responses of dynamic and frozen KLT models to two triangular current ramps (Fig. 3A). Each current ramp had the same peak current (1.5 nA), but different rates of rise up to peak (0.3 and 2 nA·ms⁻¹). In response to the slow current ramp, the frozen KLT model spiked several times, whereas the dynamic KLT model responded with only a subthreshold depolarization. In contrast, both models spiked in response to the fast current ramp.

FIG. 3.

Comparison of model responses to stimuli with slow and fast timescales. A: response of the dynamic (black) and frozen (gray) KLT models (top) to triangular current ramps (bottom). Current ramps have equal peak amplitude but different ramp speeds (left, slow; right, fast). B: response of the 2 models to a narrowband stimulus with center frequency 150 Hz (left) and a narrowband stimulus with center frequency 750 Hz (right). Note how the subthreshold voltage trajectories of the 2 models deviate from each other more in response to the low-frequency stimulus. C: spike-triggered averages (STAs) of the 2 models in response to low- (left) and high-frequency (right) narrowband stimuli, same as in B. The STAs are oscillatory due to temporal correlations inherent in the stochastic stimulus. Inset: STAs plotted at a finer timescale.

Next, we compared the models’ membrane voltage responses to two random current stimuli: one with low-frequency content (100 –200 Hz) and the other with high-frequency content (700 – 800 Hz) (Fig. 3B). In a sense, these stimuli were stochastic analogs of the slow and fast current ramps. The slow rate of rise of the current upswings in the low-frequency stimulus was similar to the rate of rise of the slow current ramp, and likewise for the high-frequency stimulus and fast current ramp. In response to the low-frequency stimulus, the models’ voltage responses were visibly different in the subthreshold regime, and the frozen KLT model fired more often than the dynamic KLT model. However, in response to the high-frequency stimulus, the frozen KLT model fired only slightly more often and the subthreshold voltage trajectories were almost identical.

Differential activation of I_KLT in response to stimuli with slow and fast timescales can be understood from the dynamics of I_KLT’s activation gating variable (Svirskis and Rinzel 2003). As voltage rises, the steady-state value of the I_KLT gate also rises. The dynamic gate approaches this new value with a time constant, τ_KLT, that is also voltage dependent. At resting potential, τ_KLT = 1.1 ms and decreases to 0.25 ms near spike threshold (see Table 1). The membrane time constant, τ_m = 0.3 ms, is faster than τ_KLT at rest, thus allowing fast stimulus upswings, such as fast current ramps or high-frequency stochastic stimuli, to drive the membrane potential up to spike threshold before I_KLT has time to fully activate. For slower stimulus fluctuations, the membrane potential changes at a slow enough rate to allow the I_KLT gate to fully activate its rectifying current, making it more difficult to depolarize the cell to spike threshold.

TABLE 1.

Summary of model properties

Membrane time constant	τm	0.3 ms
Time constant of IKLT activation at resting potential	τKLT	1.1 ms
Time constant of IKLT activation near spike threshold	τKLT	0.25 ms
Time constant of INa inactivation at resting potential	τNainact.	1.1 ms
Resting membrane resistance	Rrest	23 MΩ
Contribution of IKLT to membrane conductance at Vrest = −64 mV		65%

Differences in STAs

We investigated I_KLT’s effect on spike encoding by comparing the stimulus waveforms that caused each model to spike. For each spike response to the random time-varying stimulus, we recorded the 30 ms of the stimulus waveform preceding the spike (see METHODS). We collected a large number of these spike-triggered stimuli, yet due to the large dimension of the stimulus waveforms this still gave only a sparse sample of all possible stimuli that elicit spikes in a given model. One way to examine how I_KLT changes spike encoding is to visually compare the averages of the STEs between dynamic and frozen KLT models (Slee et al. 2005; Svirskis et al. 2002). Figure 3C shows the STAs of the two models in response to the same low- and high-frequency inputs of Fig. 3B. On comparison of the two model STAs two major observations are made.

1. In response to low-frequency inputs the dynamic KLT model spiked to stimuli with on-average sharper upswings than those of the frozen KLT model (Svirskis et al. 2002). In contrast, there was no discernable difference between the two models’ STAs in response to high-frequency stimuli. This conditional influence of I_KLT on the STA shape is expected from the earlier voltage response results showing dynamic KLT model selectivity for fast current ramps.

2. The dynamic KLT model exhibited a larger preceding hyperpolarization in its STA than the frozen KLT model in response to low-frequency stimuli, yet not in response to high-frequency stimuli. A preceding stimulus downswing before a stimulus upswing enhances the probability of the dynamic KLT model to fire. This enhancement is because the downswing temporarily hyperpolarizes the model below the resting potential, permitting a deactivation of the resting I_KLT conductance before the subsequent upswing toward spike threshold. For high-frequency stimuli, upswings were fast enough not to require a deactivation of I_KLT to enhance spike discharge probability, leading to no visible differences between STAs computed from frozen and dynamic KLT models.

We remark that both models display oscillatory STAs due to the correlative timescale inherent in the stimulus itself. Nevertheless, the preceding hyperpolarization is on average reduced for the frozen KLT model, similar to experimental STAs of MSO bathed in dendrotoxin (DTX, an I_KLT channel blocker) (Svirskis et al. 2002). Any preceding hyperpolarization in the frozen KLT model STA (beyond the one induced by a stimulus oscillation) is likely due to the spike probability-enhancing effect of removing latent I_Na inactivation before a stimulus upswing (Svirskis et al. 2004). The timescale of I_Na inactivation is 1.1 ms, the same as τ_KLT; therefore low-frequency stimuli contain downswings that are slow enough for I_Na to deinactivate, thus promoting spike discharge in either model.

The combination of these two observations qualitatively ex-poses the influence of I_KLT on spike stimulus selectivity, conditional on the stimulus power spectrum being low-frequency dominated. However, a visual comparison of STAs of the two models, as mean representations of two ensembles of spike-triggered stimuli, may not accurately assess how different the two ensembles are from each other (or, conversely, how similar). In the next section we offer a quantitative analysis to better expose the stimulus dependence of I_KLT’s influence on spike encoding.

Stimulus selection difference for narrowband stimuli

We performed pattern classification on spike-triggered stimulus ensembles (STEs) collected from the dynamic and frozen KLT models using reverse correlation. To assess the amount of STE overlap we first project both STEs onto a vector determined by the Fisher ratio (see METHODS). This transforms the task of measuring the amount of overlap between two multidimensional densities into the simpler task of measuring the overlap of two single-variable probability densities of projected values (see METHODS; Fig. 2). The classifier sets a threshold between the two probability densities by which spike-triggered stimuli are classified as causing either the dynamic or the frozen KLT models to spike. The SSD (see METHODS) is a measure of how accurately the classifier performs and, equivalently, a measure of the difference in spike encoding between the models. The SSD takes a value between 0 and 1: an SSD of 0 means the models fire to completely distinguishable stimulus features; an SSD of 1 means the models fire to the same stimulus features.

In Fig. 4A, we show the SSD in response to narrowband stimuli (0.4-nA intensity) as the center frequency is shifted along the frequency axis. I_KLT had a large influence on the spike train response to low-frequency stimuli, which lessened as the center frequency shifted to higher frequencies. This result confirmed our intuition gained from a visual comparison of the dynamic and frozen KLT model STAs for low- and high-frequency stimuli (Fig. 3).

An SSD value could not be computed for the narrowband stimulus with a center frequency of 50 Hz, even for large stimulus amplitudes. For this lowest-frequency content, stimulus fluctuations were always slow enough to allow time for I_KLT to fully activate near spike threshold and reduce the spike probability to very low values (≪ 1 spike/s). Without sufficient spike-triggered events from the dynamic KLT model, SSD could not be reliably computed. In contrast, the frozen KLT model did fire in response to narrowband stimuli with 50-Hz center frequency (Fig. 4B). This comparison again demonstrates that the phasic nature of the dynamic KLT model (i.e., no firing to lowest frequencies and phasic firing to current step onset) is due to the dynamic properties of I_KLT (see Fig. 3). In terms of frequency-response, the dynamic KLT model is a band-pass filter, responding only to stimuli in an intermediate frequency range due to a combination of the phasic I_KLT reducing the spike response to low-frequency stimuli and the passive membrane filtering reducing the spike response to high-frequency stimuli. However, the frozen KLT model is not completely band-pass due to its firing even at the lowest frequencies. Both the frozen and dynamic KLT models had a resonance of firing rate in the intermediate frequency range (Hutcheon and Yarom 2000; Izhikevich 2001). At all frequencies, the dynamic KLT model fired less than the frozen KLT model. Curiously, the quantitative relationship between SSD and center frequency was maintained at three stimulus intensities: 0.3, 0.4, and 0.5 nA (Fig. 4B, inset). This is true even though the range of stimulus intensities used was quite large given that Fig. 4B shows an increase of firing rate by up to a factor of 5. This demonstrates that the influence of I_KLT on spike encoding is very dependent on the center frequency of the narrowband yet is roughly independent of the stimulus amplitude or firing rate.

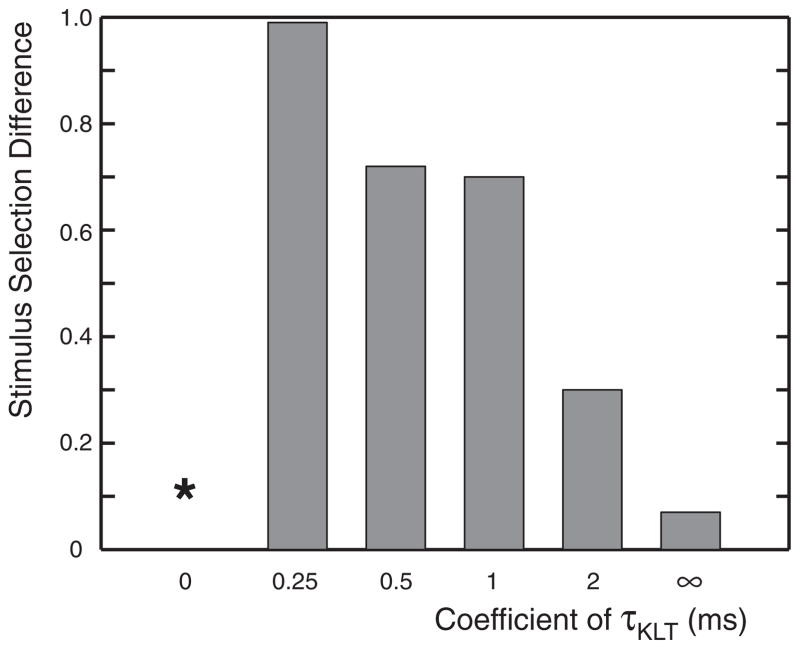
Alternatively, while fixing the stimulus spectrum we observed that the SSD was dependent on the time constant of the I_KLT activation gate, τ_KLT (Fig. 5). Specifically, we computed the response to a narrowband stimulus with a center frequency of 350 Hz for dynamic KLT models having different values ofτ_KLT. When τ_KLT was reduced by a factor of 4, the SSD rose from 0.70 to 0.99, an SSD value that represents nearly complete distinction between model coding. When τ_KLT was reduced to zero (equivalent to matching the I_KLT activation gate instantaneously to its steady-state value at a given voltage) the dynamic KLT model ceased to fire since for reasonable stimulus intensities the membrane potential was not capable of escaping I_KLT activation. Conversely, SSD decreased when τ_KLT was increased. When τ_KLT was set to infinity, implying that the dynamic and frozen KLT models are identical, the SSD settled to a lower limit of about 0.07. In total, the smaller τ_KLT is, the larger the influence of I_KLT is on spike encoding. This is because the faster I_KLT activates, stimulus upswings must be faster and stronger to overcome its dampening effect.

FIG. 5.

The change in the influence of I_KLT on spike encoding as the time constant of I_KLT activation, τ_KLT, is varied. SSDs were computed for model responses to a narrowband stimulus with a center frequency of 350 Hz (0.4-nA intensity) as τ_KLT was varied. The SSD measure could not be computed for τ_KLT = 0 (*) because the instantaneous activation of I_KLT completely prevented the dynamic KLT model from firing at this stimulus intensity.

Stimulus selection difference for broadband stimuli

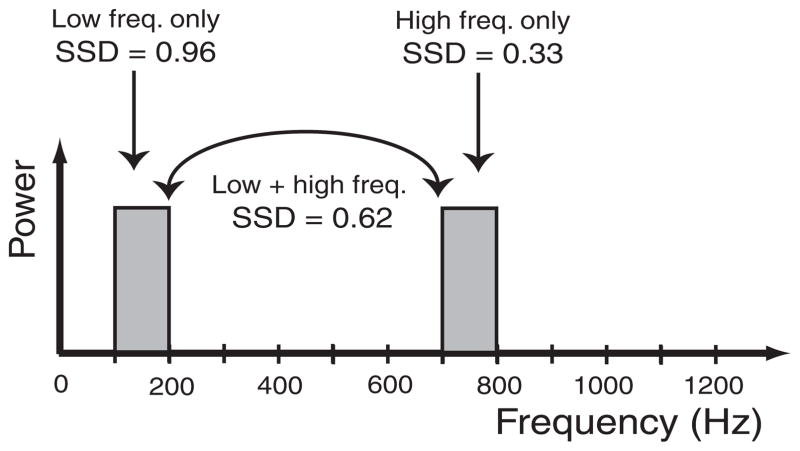
The stimulus-dependent influence of I_KLT on spike encoding was evident as the center frequency of a narrowband stimulus was varied. We next examined the influence that I_KLT had on the encoding of stimuli with more complex power spectra. As shown in Fig. 6, the SSD in response to a stimulus generated from the addition of two narrowband stimuli was 0.62, an SSD value in between the values for isolated presentation of the frequency bands. In other words, the addition of high-frequency components to the low-frequency stimulus deteriorated the influence of I_KLT on spike encoding. This decrease in the influence of I_KLT held true if the total power of the combined stimulus was allowed to increase, as in Fig. 6, or if the total power of the combined stimulus was normalized to that of the isolated narrowband presentation (SSD = 0.60).

FIG. 6.

Difference in spike encoding between dynamic and frozen KLT models to a stimulus with combined low- and high-frequency content. SSD was computed in response to a stimulus consisting of a combination of a narrowband stimulus with center frequency of 150 Hz and another narrowband with center frequency of 750 Hz. Note that SSD decreases with the addition of high-frequency stimulus components in comparison to an exclusively low frequency stimulus.

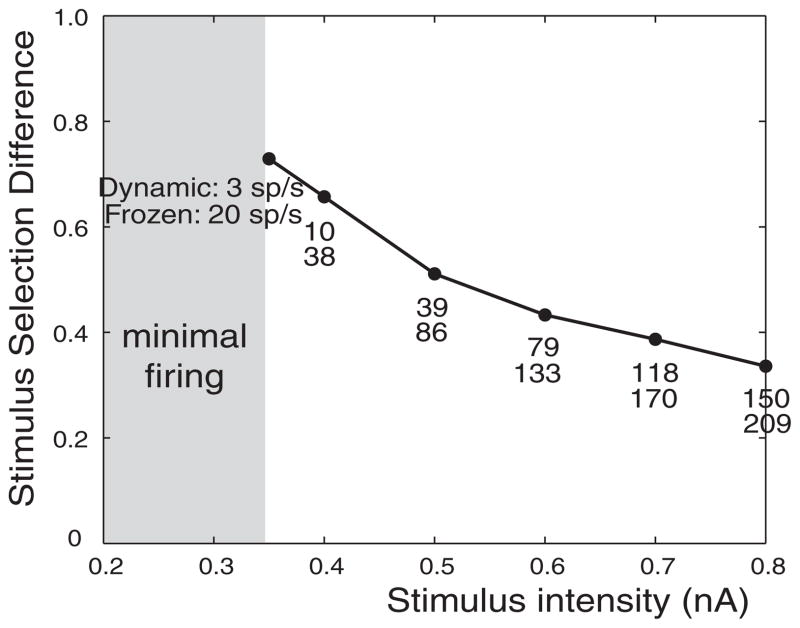
A broadband stimulus is a linear combination of many narrowband stimuli with power spread equally over the components. The majority of these frequency components contain fluctuations that are too fast to allow I_KLT time to influence the membrane potential, whereas fewer frequency components at the lowest end of the spectrum allow significant influence of I_KLT. In response to a broadband stimulus of an intensity of 0.4 nA we found the SSD to be 0.66, a value significantly less than that in response to a lower-frequency narrowband of the same intensity (Fig. 4A), yet higher than that in response to a high-frequency narrowband. Unlike the SSD for narrowband stimuli, the SSD in response to the broadband stimulus was dependent on the intensity of the stimulus (Fig. 7). The tendency for the models to become more similar as the intensity of the broadband stimulus is increased is likely due to the “linearizing” effect of a strong broadband input on a weakly nonlinear system (see DISCUSSION).

FIG. 7.

Difference in spike encoding between dynamic and frozen KLT models to a broadband stimulus. SSD was computed in response to a broadband stimulus as intensity was varied. The firing rates of both models are listed for each stimulus intensity tested. Note that at <0.35-nA intensity the dynamic KLT model fired minimally (<1 spike/s) and thus SSD could not be computed.

Stimulus selection difference for physiological conductance stimuli

Up to this point we have used rather artificial current stimuli to investigate I_KLT’s influence on spike encoding: current ramps and both narrowband and broadband stochastic currents with a Gaussian distribution. From the responses to artificial stimuli, one can predict how the system might respond to real synaptic input. Yet in reality, neurons receive conductance, not current stimuli, as well as stimuli shaped by a synaptic filter, not current steps, ramps, or flat-spectrum Gaussian noise. To investigate whether I_KLT could influence the spike train encoding of more realistic synaptic inputs in a manner similar to that found for artificial stimuli, we re-created synaptic stimuli based on what is known of the input feeding into VCN (Fig. 8A; see METHODS). In brief, a sound pressure waveform was fed into an AN firing rate model (Tan and Carney 2003). This model produced a PSTH from which we created three separate spike trains (AN fibers) via an inhomogeneous Poisson process with a dynamic rate defined by the AN PSTH. Finally, the spike trains were convolved with an excitatory postsynaptic conductance waveform and summed to create the final conductance stimulus.

We performed pattern classification analysis on conductance stimuli derived from four sound waveforms: stochastic narrow-band sounds centered at 500 Hz, 1 kHz, and 4 kHz; and a broadband waveform (Fig. 8B). The power spectra of the corresponding conductance stimuli were all low-pass and nearly identical between all sound waveforms (Fig. 8C), being essentially dominated by the synaptic filter associated with the excitatory postsynaptic conductance. Additionally, the AN model phase-locks to the 500-Hz narrowband, to a lesser extent to the 1-kHz narrowband, and not at all to the 4-kHz narrowband and broadband sound waveforms. Therefore the power spectrum of the synaptic response to the 500-Hz narrowband waveform shows a slight additional increase of power at 500 Hz.

The SSD between dynamic and frozen KLT model responses was between 0.8 and 0.9 for all sound waveforms (Fig. 8D). This means that I_KLT had a large influence on the spike encoding of synaptic stimuli derived from all of these very different sounds. The majority of spectral power of conductance stimuli derived from sound input came from frequencies well below 1/τ_KLT (~1 kHz). As we showed in Fig. 4A, it is stimulus frequencies well below 1/τ_KLT that best recruit I_KLT. Since the physiological conductance stimuli had spectra dominated at those frequencies, there then was a significant influence of I_KLT on spike train encoding. Like the STAs in response to low-frequency current stimuli (Fig. 3C), the dynamic KLT model fired on average to a physiological conductance stimulus with a sharper upswing and greater preceding hyperpolarization (Fig. 8E). Further, the dynamic KLT model required a greater peak conductance to fire. Altogether, the resultant stimulus selectivity of the dynamic KLT model is nearly equivalent to a detection of precisely coincident (monaural) AN fiber input.

An extensive influence of I_KLT occurred when we drove the model with a reasonable strength of input (creating a dynamic KLT firing rate of ~35 spikes/s). When we increased the mean peak conductance of synaptic events by one third, the dynamic KLT model firing rate increased to about 100 spikes/s and the SSD lowered to 0.74 (1-kHz narrowband sound). This may, again, be interpreted in light of the stimulus power spectrum. Although most power in the conductance stimulus was concentrated at frequencies well below 1/τ_KLT, there was a contribution of power near to and above 1/τ_KLT. In this respect the physiological conductance stimulus was similar to broadband current in having some power at frequencies that activate I_KLT, and some at those that do not. Like the broadband current stimulus (Fig. 7), the SSD of the physiological conductance stimulus was intensity dependent because the model became input driven when presented with strong stimuli that overwhelmed the weak I_KLT nonlinearity.

DISCUSSION

We used a pattern classifier methodology to quantify the degree to which the dynamic properties of I_KLT influences the spike encoding of stimuli in an auditory brain stem neuron model. We compared STEs in response to various stochastic stimuli when the conductance for I_KLT was voltage and time dependent against when the conductance was frozen at its resting level. The classifier evidenced a significant encoding contribution by dynamic I_KLT for stimuli with dominant low-frequency content, including physiologically realistic synaptic input. Conversely, I_KLT’s contribution to spike encoding was diluted when substantial high-frequency power was present in the stimulus. In total, the influence of I_KLT on response to stochastic inputs was dependent on the spectrum of the stimulus.

Comparison to previous experimental studies

The selective recruitment of I_KLT in response to stimuli with slow fluctuations has been qualitatively shown previously. Like the dynamic KLT model’s response to current ramps (Fig. 3A), MSO cells (Svirskis et al. 2002) and VCN octopus cells (Ferragamo and Oertel 2002) fire selectively to fast current ramps, and will not fire to slow ramps of equal peak amplitude, due to the activation of low-threshold outward current. When I_KLT channel blockers were applied the MSO cells (in gerbils, age P14 –P17) and VCN cells fired to both stimuli, similar to the frozen KLT model. Gerbil MSO has also been shown to produce STAs similar to Fig. 3C (left) in response to a stimulus with high power at low frequencies (Svirskis et al. 2002). The STAs in that study demonstrated a decreased preceding hyper-polarization and a slower upswing when the cell was bathed in DTX.

We note that the difference between our dynamic and frozen KLT models is not equivalent to the blocking of I_KLT in experimental studies. I_KLT contributes a substantial conductance to cells at resting potential (Reyes et al. 1994; Rothman and Manis 2003a; Scott et al. 2005). The removal of this conductance with I_KLT channel block depolarizes the cell, decreases the resting membrane conductance, and increases the membrane time constant. In our comparison, by freezing I_KLT’s gating variables to their resting values, we ensure that the resting conductance and membrane time constant are unaltered compared with the dynamic KLT model. The difference between the dynamic and frozen KLT models’ responsiveness therefore lies with the extra filtering properties in the dynamic KLT model conferred by a voltage- and time-dependent I_KLT. The frozen KLT model spiked to stimuli with slow or fast timescales (Fig. 3), similar to experimental performance of cells with I_KLT channel block. Therefore the selectivity of cells with I_KLT for stimuli with fast timescales is not solely dependent on these cells’ decreased membrane time constant, but crucially depends on the dynamic properties of I_KLT, as also noted in previous modeling studies (Cai et al. 2000; Svirskis et al. 2002). The specific effects of the dynamic properties of I_KLT could be experimentally verified in vitro by comparing cell responses under control conditions with responses in the presence of I_KLT channel blockers while maintaining the control resting conductance by simulating a frozen I_KLT with dynamic clamp.

I_KLT influence on spike encoding is largely bypassed with broadband stimuli, especially for strong stimuli

Our pattern classification analysis showed that the dynamic properties of I_KLT greatly altered spike encoding for stochastic input with dominant low-frequency spectral content. This ef- fect of I_KLT was eroded when high frequencies were introduced into the stimulus (Figs. 6 and 7). Moreover, the eroding effect of the broadband stimulus on I_KLT’s influence became more dramatic as the intensity of the stimulus increased. This can be understood by examining the current-balance equation (Eq. 2) in the subthreshold potential regime. Only the currents I_KLT, I_h, I_lk, and s(t) contribute to subthreshold integration. Further, the inactivation gate of I_KLT and the activation gate of I_h have very long time constants, and may be approximated as constant over the short time periods used in the reverse-correlation analysis. Thus in this regime, the right-hand side of Eq. 2 may be reduced to three current terms: one which is linear with respect to voltage; the nonlinear I_KLT term; and the stimulus s(t). For weak-intensity broadband stimuli, the I_KLT nonlinearity plays a role in shaping the distribution of output voltage. However, for strong broadband inputs, the s(t) term becomes much more dominant in shaping output voltage than the weaker I_KLT nonlinearity. It is known that strong broadband inputs effectively “linearize” the response of systems with weak nonlinearities (Chialvo et al. 1997). Therefore strong broadband inputs make the dynamic KLT model more like the frozen KLT model, reducing the SSD between them.

Erosion of the influence of I_KLT on spike encoding in response to broadband stimuli creates a problem for functional models of I_KLT-expressing cells derived from traditional reverse correlation using white-noise stimuli (Slee et al. 2005). Our results suggest that such models should be more similar to our frozen KLT model—a model with a short membrane time constant but without the function conferred by a voltage- and time-dependent I_KLT. Further, our results from physiological conductance stimuli suggest that functional models constructed from reverse correlation on realistic synaptic input (instead of white-noise currents) could more accurately exhibit the functional contribution of I_KLT. Consistent with this idea, a change in a functional model derived from an avian auditory brain stem neuron under pharmacological blockade of low-threshold K⁺ current was demonstrable only when synaptic waveform-filtered currents were used, and not white-noise currents (Slee et al. 2005).

Pattern classification on spike-triggered stimuli

Pattern classification has been used previously to analyze spike-triggered stimuli from periphery electrosensory processing in weakly electric fish. Gabbiani et al. (1996) performed Fisher linear discrimination to discriminate between stimuli that produced spikes (or bursts) versus stimuli that did not produce spikes (or bursts) as a means to assess the quality of coding of cells in the electrosensory pathway. Later, Oswald et al. (2007) used Fisher linear discrimination to discriminate between stimuli that created bursts of different lengths in current-driven in vitro electrosensory pyramidal neurons (for similar work in model cells also see Kepecs and Lisman 2003). We demonstrate a novel use for the Fisher linear discriminant by discriminating between spike-triggered events from different neuronal models (i.e., different membrane properties) in response to the same stimulus. This allowed us to quantify the influence that a particular biophysical mechanism (dynamic I_KLT) had on spike encoding. We mention that pattern classification did not give any information about how I_KLT changed spike encoding. This information was obtained using various experimental paradigms such as response to current ramps and band-limited stochastic stimuli. Instead, pattern classification provided an answer as to how much I_KLT changed spike encoding. This quantification of coding change through pattern classification was more sophisticated than a simple comparison of firing rates or STAs of the two models for a given stimulus. For instance, it is possible for two models to fire at the same rate to a given stochastic input, yet be firing to quite different features within the input. Further, it is possible for two models to have similar STAs, yet one model to be more selective in its firing than the other.

Our pattern classification method could be adapted to investigate the effect on spike encoding of other ion channels in the nervous system. As an example, in vitro experiments on stellate cells in entorhinal cortex have shown how persistent Na⁺ currents and the inward rectifier I_h combine to influence spike encoding in a stimulus-dependent manner (Haas et al. 2007). Further, calcium-activated K⁺ channels have been shown to change the frequency tuning of spike response in primary electrosensory neurons through an influence on the burst discharge in these cells (Ellis et al. 2007). In both of these examples, when the stimulus timescale is chosen appropriately, the channel dynamics is such that the measured spike train encoding is distinct from that when the channel is pharmacologically blocked. It would be straightforward to use the pattern classification methodology presented here to quantify the stimulus-dependent coding influence of the various ion channels in these, and many other, single-neuron coding schemes.

Generality of results across auditory brain stem areas and models

We computed all results in this study using the RM03 model, a Hodgkin–Huxley-like model of Type II cells in the guinea pig VCN (Rothman and Manis 2003b). Many studies have used VCN models for the MSO (Brand et al. 2002; Brughera et al. 1996; Zhou et al. 2005) because of the high prevalence of I_KLT in both areas, similar firing characteristics between Type II VCN neurons and MSO neurons, and the absence of voltage-clamped kinetics data for currents in MSO. The RM03 model, when adjusted for a body temperature of 38°C, has a very fast membrane time constant of 0.3 ms, like that found in gerbil MSO (Scott et al. 2005). Other I_KLT variants also exist in the avian nucleus magnocellularis (Rathouz and Trussell 1998; Reyes et al. 1994), in the mammalian MNTB (Brew and Forsythe 1995), and in VCN octopus cells (Cai et al. 2000), each of which transmits precise timing information. Although our results were based on the RM03 model, we believe the finding that the dynamic properties of I_KLT influence spike encoding dependent on stimulus spectrum is general for any auditory brain stem neuron that has a large density of currents in the I_KLT family. Correspondingly, our approach if applied to other models that include phasic-firing properties would yield similar results. For example, contributions to spike encoding by other biophysical phasic-inducing mechanisms should demonstrate an interaction between the timescale of the mechanism and the power spectrum of the input. We have previously demonstrated such stimulus-dependent spike encoding for an idealized, phasic-spiking, leaky integrate-and-fire model with a dynamic V- and t-gated rectification (Day et al. 2006). Many of our conclusions about stimulus-dependent encoding should also generalize to other non-I_KLT, subthreshold, dynamic negative feedback mecha- nisms (such as the inactivation of sodium current) that contribute to phasic behavior (Svirskis and Rinzel 2003; Svirskis et al. 2004).