A NEW FRACTURE ASSESSMENT APPROACH COUPLING HR-pQCT IMAGING AND FRACTURE MECHANICS-BASED FINITE ELEMENT MODELING

Abstract

A new fracture assessment approach that combines HR-pQCT imaging with fracture mechanics-based finite element modeling was developed to evaluate distal radius fracture load. Twenty distal radius images obtained from postmenopausal women (fracture, n = 10; nonfracture, n = 10) were processed to obtain a cortical and a whole bone model for each subject. The geometrical properties of each model were evaluated and the corresponding fracture load was determined under realistic fall conditions using cohesive finite element modeling. The results showed that the whole bone fracture load can be estimated based on the cortical fracture load for nonfracture (R² = 0.58, p = 0.01) and pooled data (R² = 0.48, p < 0.001) but not for the fracture group. The portion of the whole bone fracture load carried by the cortical bone increased with increasing cortical fracture load (R² ≥ 0.5, p < 0.05) indicating that a more robust cortical bone carries a larger percentage of whole bone fracture load. Cortical thickness was found to be the best predictor of both cortical and whole bone fracture load for all groups (R² range: 0.49–0.96, p < 0.02) with the exception of fracture group whole bone fracture load showing the predictive capability of cortical geometrical properties in determining whole bone fracture load. Fracture group whole bone fracture load was correlated with trabecular thickness (R² = 0.4, p < 0.05) whereas the nonfracture and the pooled group did not show any correlation with the trabecular parameters. In summary, this study introduced a new modeling approach that coupled HR-pQCT imaging with fracture mechanics-based finite element simulations, incorporated fracture toughness and realistic fall loading conditions in the models, and showed the significant contribution of the cortical compartment to the overall fracture load of bone. Our results provide more insight into the fracture process in bone and may lead to improved fracture load predictions.

1. INTRODUCTION

Osteoporosis is one of the prominent public health problems affecting millions of people and leading to high medical costs in the United States and the world (Cooper et al., 1992; Melton, 2003; Ray et al., 1997). Accurate identification of individuals under high fracture risk is important for decreasing the prevalence and negative impact of fractures.

High resolution peripheral computed tomography (HR-pQCT) has recently been proposed as a possible alternative to the current clinical fracture risk assessment approach, dual energy X-ray absorptiometry (DXA), based on several studies which demonstrated that bone mineral density (BMD) measured by DXA is not sufficient to predict future fractures (Cummings et al., 1990; Hui et al., 1988; Ott, 1993). HR-pQCT provides three-dimensional in vivo images combining BMD, geometry and architecture of both cortical and trabecular bone compartments exclusively at distal radius and tibia that can be used as early detection sites for future hip and spine fractures (Cuddihy et al., 1999; Lauritzen et al., 1993; Mallmin et al., 1993; Owen et al., 1982). The detailed noninvasive bone measurements by HR-pQCT may provide additional information which can lead to a better assessment of fracture risk.

The bone images obtained by HR-pQCT can also be converted to finite element models to improve the mechanistic understanding of the failure process in bone. The current state of the art in HR-pQCT-based finite element modeling utilizes axial compressive loading of the clinical scan region at the distal radius or tibia and evaluates the failure load based on the percentage of elements that exceed a certain level of strain (Pistoia et al., 2002). This approach has been used to evaluate the structural and mechanical properties of distal radius and tibia (Liu et al., 2010; Varga et al., 2010), to compare bone properties between patients with and without fracture (Boutroy et al., 2008; Melton et al., 2007), and to determine the load distribution between the cortical and trabecular bone (Boutroy et al., 2008; Burghardt et al., 2010; MacNeil and Boyd, 2007).

Although these studies were successful at several fronts, development of new modeling techniques that can provide a better understanding of the fracture process in bone will be beneficial. This can be achieved by introducing a fracture mechanics-based failure criterion and by incorporating loading conditions that represent fall orientations in the finite element models. The use of a fracture mechanics-based approach instead of a strength-based approach will provide a more robust failure criterion by explicitly modeling the crack formation process and by integrating fracture toughness, a parameter that directly influences the bone fracture behavior (Nalla et al., 2004; Vashishth et al., 1997) in the models. Previous studies on bone test specimens and idealized radius geometries by one of the authors demonstrated the promise of this finite element technique (Buchanan and Ural, 2010; Ural, 2009; Ural and Vashishth, 2006). Incorporating loading conditions that represent fall orientations instead of pure axial compression in the models will provide more accurate assessment of the fracture load and location. In addition, the new modeling approach will make it possible to systematically evaluate the mechanical behavior of the cortical compartment of the bone which has been shown to contribute significantly to the distal radius fracture load in experimental studies (Ashe et al., 2006; Augat et al., 1998; Augat et al., 1996; Lochmuller et al., 2002; Muller et al., 2003; Myers et al., 1993; Myers et al., 1991; Spadaro et al., 1994).

In summary, the goals of this study were (i) to introduce a new fracture load prediction method that couples HR-pQCT imaging with fracture mechanics-based finite element modeling, (ii) to incorporate realistic fall loading conditions in fracture load assessment, and (iii) to assess the contribution of the cortical compartment to the overall fracture load at the distal radius.

2. MATERIALS AND METHODS

2.1 HR-pQCT Scans and Finite Element Models

The distal radius of 20 postmenopausal women ranging from 60–90 years old (mean age: 68.4 ± 7.2 years) was scanned using HR-pQCT (XtremeCT, Scanco Medical AG, Brüttisellen, Switzerland) at the standard human in vivo scan location at 82 µm isotropic voxel size resulting in a 9.02 mm section composed of 110 slices. Ten of these scans were obtained from individuals with a prior vertebral fracture (mean age: 70.2 ± 9.0 years) and the remaining ten of the scans were from individuals with no prior fracture history (mean age: 66.5 ± 4.6 years). The cortical and trabecular compartments were separated using a manual tracing method to accurately capture the cortical compartment at thinner regions based on previous studies (Buie et al., 2007; Mueller et al., 2009). This resulted in two models for each patient one of which is the whole bone model (Figure 1a) including both the trabecular and cortical bone compartments and the cortical bone model (Figure 1b) that only includes the cortical compartment of the bone.

Figure 1.

A sample HR-pQCT bone image from a 63-year-old subject for (a) whole bone (b) cortical bone. Finite element mesh for (c) whole bone (d) cortical bone. The crack plane tiled with cohesive elements in (e) whole bone (f) cortical bone.

The segmented images were converted to finite element meshes using the ScanFE software (Simpleware, Exeter, UK) (Figure 1c, 1d). The models used a geometry-based meshing technique that generated finite element meshes using tetrahedral elements. This approach provided smoother meshes eliminating artificial stress concentration locations compared to voxel-based meshes while preserving the accuracy of the geometry of the bone. The meshes generated by ScanFE were then imported into the finite element program ABAQUS (version 6.11, 2011, Simulia, Providence, RI). The total number of elements in cortical and whole bone models ranged between 0.99–1.32 million and 1.63–3.95 million elements, respectively. The simulations were run on a parallel cluster using 60 and 96 processors for cortical and whole bone models, respectively. The simulation run time for cortical bone models ranged between 3–6 hours and 5.5–16 hours for whole bone models.

A crack plane with cohesive elements (Section 2.2) that represent the fracture behavior was inserted at the mid-height of all models corresponding to the average location of the distal forearm fractures (Figure 1e, 1f) (Eastell, 1996). The models were assigned isotropic properties following previous studies (Liu et al., 2010) with an elastic modulus of 15 GPa and a Poisson’s ratio of 0.3. The fracture properties for the cohesive elements were taken from the literature (Section 2.2). The bone sections were fixed in all directions at the proximal end and were loaded at the distal surface in a fall loading orientation that accounts for 75° dorsiflexion of the wrist and 10° internal rotation used in previous studies (Augat et al., 1996; Myers et al., 1991). The load was incrementally increased and the fracture load was identified at the point where the first cohesive element broke. This fracture criterion was chosen based on our previous study that showed only 1–4% increase in fracture load if failure of all cohesive elements were considered (Ural, 2009). The simulations were run on 40 models including 20 whole bone models and 20 cortical bone models to obtain the whole bone fracture load (F^W) and cortical bone fracture load (F^C). In addition, in order to assess the influence of crack location on the fracture load, three randomly selected bone models were simulated with a crack at the distal and proximal quarter of the bone section. These simulations determined the whole and cortical bone fracture loads at the distal (F^W_d, F^C_d) and proximal (F^W_p, F^C_p) crack locations.

Geometrical properties for all models were evaluated at the most distal, most proximal, and the crack surfaces for both whole and cortical bone models using the ScanIP software (Simpleware, Exeter, UK). The parameters that were evaluated included the cortical thickness, bone area, volume, and moment of inertia in palmar-dorsal and medial-lateral directions (Table 2). In addition, trabecular bone parameters including trabecular bone volume fraction, trabecular number, trabecular thickness, and trabecular separation were evaluated for each bone (Table 2).

Table 2.

Mean values and standard deviations of the geometrical and trabecular parameters and the predicted fracture loads for fracture and nonfracture groups as well as the pooled data. Note that the statistically different (p < 0.05) properties between nonfracture and fracture groups are shown in bold.

Parameters		Nonfracture	Fracture	Pooled
		Mean ± SD	Mean ± SD	Mean ± SD
FW	N	4066 ± 1530	3619 ± 883	3842 ± 1237
FC	N	2225 ± 1191	1884 ± 745	2055 ± 982
FC/FW		0.538 ± 0.207	0.526 ± 0.181	0.532 ± 0.189
CTh	mm	0.890 ± 0.210	0.794 ± 0.112	0.842 ± 0.169
VC	mm3	466 ± 74	482 ± 59	474 ± 66
DAC	mm2	44.1 ± 8.1	43.9 ± 4.9	44.0 ± 6.5
PAC	mm2	55.3 ± 10.1	60.7 ± 9.3	58.0 ± 9.9
CAC	mm2	52.6 ± 9.0	53.5 ± 6.5	53.1 ± 7.6
DIxxC	mm4	274 ± 73	294 ± 69	284 ± 70
PIxxC	mm4	194 ± 67	232 ± 90	213 ± 80
CIxxC	mm4	240 ± 76	264 ± 74	252 ± 74
DIyyC	mm4	172 ± 74	93.4 ± 39.7	133 ± 71
PIyyC	mm4	49.6 ± 20.6	65.2 ± 31.6	57.4 ± 27.2
CIyyC	mm4	61.8 ± 23.7	78.8 ± 41.4	70.3 ± 34.0
DJC	mm4	446 ± 139	388 ± 105	417 ± 123
PJC	mm4	243 ± 84	298 ± 111	270 ± 100
CJC	mm4	302 ± 94	343 ± 107	322 ± 100
VW	mm3	844 ± 137	814 ± 157	829 ± 144
DAW	mm2	107 ± 18	102 ± 20	105 ± 19
PAW	mm2	81.5 ± 13.1	77.3 ± 12.5	79.4 ± 12.6
CAW	mm2	90.9 ± 15.0	85.1 ± 16.9	88.0 ± 15.8
DIxxW	mm4	492 ± 171	517 ± 155	504 ± 159
PIxxW	mm4	250 ± 101	268 ± 100	259 ± 98
CIxxW	mm4	347 ± 140	351 ± 113	349 ± 124
DIyyW	mm4	146 ± 62	169 ± 103	158 ± 84
PIyyW	mm4	61.3 ± 24.6	76.9 ± 46.2	69.1 ± 36.9
CIyyW	mm4	84.0 ± 34.0	106 ± 70	94.8 ± 54.6
DJW	mm4	638 ± 222	686 ± 247	662 ± 230
PJW	mm4	312 ± 118	345 ± 131	328 ± 123
CJW	mm4	431 ± 163	457 ± 168	444 ± 162
Tb.Th	mm	0.065 ± 0.014	0.053 ± 0.007	0.059 ± 0.013
Tb.Sp	mm	0.492 ± 0.057	0.581 ± 0.163	0.537 ± 0.127
Tb.N	1/mm	1.818 ± 0.218	1.661 ±0.372	1.740 ± 0.307
BV/TV		0.117 ± 0.018	0.088 ± 0.025	0.103 ± 0.026

Whole (F^W) and cortical (F^C) bone fracture load; cortical thickness at the crack surface (CTh); cortical bone volume (V^C); cortical bone area at the distal (DA^C), proximal (PA^C), crack (CA^C) surfaces; cortical bone moment of inertia in palmar-dorsal direction at the distal (DI_xx^C), proximal (PI_xx^C), crack (CI_xx^C) surfaces; cortical bone moment of inertia in medial-lateral direction at the distal (DI_yy^C), proximal (PI_yy^C), crack (CI_yy^C) surfaces; cortical bone polar moment of inertia at the distal (DJ^C), proximal (PJ^C), crack (CJ^C) surfaces; whole bone volume (V^W); whole bone area in distal (DA^W), proximal (PA^W), crack (CA^W) surfaces; whole bone moment of inertia in palmar-dorsal direction at the distal (DI_xx^W), proximal (PI_xx^W), crack (CI_xx^W) surfaces; whole bone moment of inertia in medial-lateral direction at the distal (DI_yy^W), proximal (PI_yy^W), crack (CI_yy^W) surfaces; whole bone polar moment of inertia at the distal (DJ^W), proximal (PJ^W), crack (CJ^W) surfaces; trabecular thickness (Tb.Th); trabecular separation (Tb.Sp); trabecular number (Tb. N); trabecular bone volume fraction (BV/TV).

2.2 Cohesive Finite Element Modeling

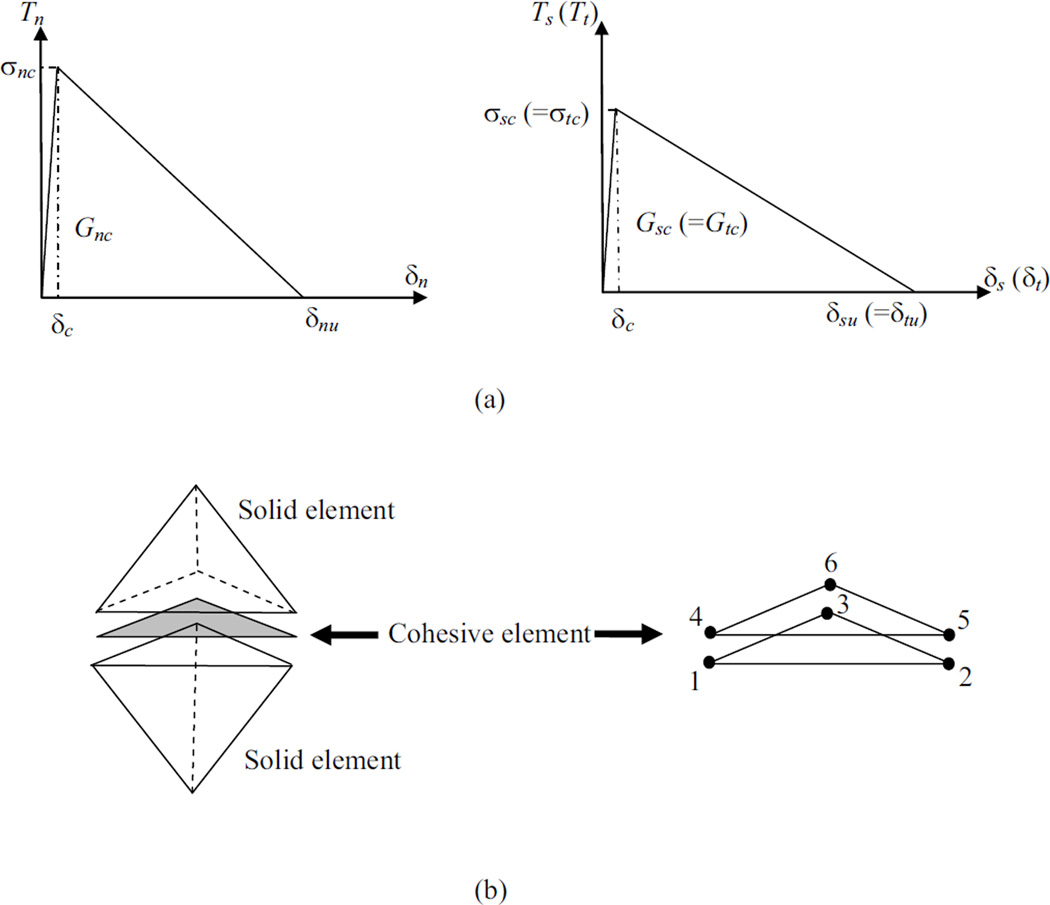
The fracture process was modeled with cohesive finite element modeling which is a phenomenological traction-displacement relationship that captures the nonlinear fracture behavior of bone. In the current study, we employed a bilinear cohesive relationship (Figure 2a) since the model parameters are the most important contributors to the results rather than the shape of the traction-displacement curve (Tvergaard and Hutchinson, 1992). The initial ascending slope of the curve is a penalty stiffness in the numerical formulation and is generally chosen to be as high as possible in order to obtain a very small δ_c value, satisfying numerical convergence (Camanho et al., 2003). The cohesive model captures the material softening via the descending part of the curve (Figure 2a), where the traction transferred between the material surfaces decreases as the crack opening displacement increases. For the current study, the model has both normal (opening) and shear components representing the mixed mode behavior that occurs due to the load application direction. As a result, both the normal and shear cohesive behavior needs to be defined considering the critical energy release rate and strength denoted by G_nc, G_sc, G_tc, and σ_nc, σ_sc, σ_tc, respectively (Figure 2a), where subscript n refers to normal and subscripts s and t refer to in-plane shear directions. The in-plane shear response is assumed to be the same in both directions (G_sc = G_tc and σ_sc = σ_tc).

Figure 2.

Traction-displacement relationship defining the cohesive zone model in normal (n) and shear modes (t, s). Note that T_i are the tractions, σ_ic are the critical strengths, δ_i are the crack opening displacements, and δ_iu are the ultimate values of the crack opening displacements (i = n, t and s). (b) Tetrahedral solid elements and the compatible wedge shaped cohesive element with six nodes.

The cohesive models are formulated as interface finite elements that have zero initial thickness and are compatible with solid elements (Figure 2b). The damage initiation in a cohesive element occurs when the traction on the surfaces of the cohesive elements reach a critical value defined by (Camanho et al., 2003):

$${\left(\frac{T_n}{{\sigma }_{nc}}\right)}^2+{\left(\frac{T_s}{{\sigma }_{sc}}\right)}^2+{\left(\frac{T_t}{{\sigma }_{tc}}\right)}^2=1$$

where T_n, T_s, T_t are the current stress values in normal and shear directions and σ_nc, σ_sc, σ_tc are critical normal and shear strengths. In each cohesive element, damage accumulates following the traction-displacement profile. An element forms a full crack based on the mixed mode fracture criterion (Camanho et al., 2003),

$$\frac{G_n}{G_{nc}}+\frac{G_s}{G_{sc}}+\frac{G_t}{G_{tc}}=1$$

where G_n, G_s, and G_t are the current values of energy release rate and G_nc, G_sc, and G_tc are the critical energy release rates in normal and shear modes. The material properties that are used to define the traction-displacement relationship are based on experimental properties reported in the literature (Table 1) (Brown et al., 2000; Cezayirlioglu et al., 1985; McCalden et al., 1993; Zioupos and Currey, 1998).

Table 1.

Cohesive model parameters used in the simulations based on experimental data in the literature (Brown et al., 2000; Cezayirlioglu et al., 1985; McCalden et al., 1993; Zioupos and Currey, 1998). Note that σ_nc, σ_sc (=σ_tc), G_nc, and G_sc (=G_tc) are the normal strength, the shear strength, the critical energy release rate for opening mode, and the critical energy release rate for shear mode, respectively.

Cohesive Model Properties
σnc	104MPa
σsc	68 MPa
Gnc	1.16 N/mm
Gsc	2.97 N/mm

2.3 Statistical Analysis

The statistical analyses were performed using MATLAB (MathWorks, Natick, MA). Linear correlation coefficients (R²) and the statistical significance of the correlations (p < 0.05) were calculated between the whole and cortical bone fracture loads. The correlations were reported for fracture and nonfracture groups separately in addition to the pooled data from both groups. In addition, statistically significant differences (p < 0.05) in geometrical and trabecular parameters as well as the fracture loads between fracture and nonfracture groups were assessed using paired Student’s t-test.

Forward stepwise multiple regression analysis was performed to find the best predictors of the whole, cortical, and the ratio of whole to cortical bone fracture load among the geometrical and trabecular parameters investigated. In this analysis approach, at each step, the most significant term was added or the least significant term was removed based on an entrance tolerance of p < 0.05 and an exit tolerance of p > 0.10. The analysis was terminated when the root-mean-square error reached a local minimum.

3. RESULTS

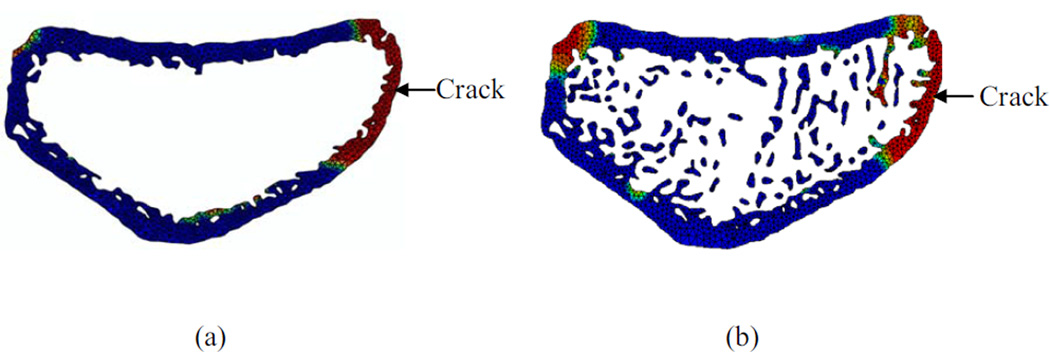
Finite element simulations performed on whole and cortical bone models successfully simulated the crack formation and failure (Figure 3a, 3b). The whole bone fracture loads ranged between 2374–5024 N for the fracture group and 1945–6283 N for the nonfracture group. For cortical bone, fracture and nonfracture groups exhibited fracture loads between 1020–3443 N and 498–4196 N, respectively. The ratios of the fracture loads between the cortical and whole bone models ranged between 0.33–0.84 for nonfracture group and between 0.25–0.90 for the fracture group. The mean values of the cortical and whole bone fracture loads and their ratios were larger for the nonfracture group, however, the differences did not reach statistical significance (Table 2). In addition, the geometrical and trabecular parameters showed statistically significant differences between fracture and nonfracture groups only in the distal cortical moment of inertia in the medial lateral direction, trabecular thickness, and trabecular bone volume fraction (Table 2).

Figure 3.

Crack plane showing the damage accumulation and crack formation for (a) cortical and (b) whole bone model for a 63-year-old subject. Note that the arrows indicate the initial location of crack formation. Red color indicates high level of damage and blue color indicates no damage.

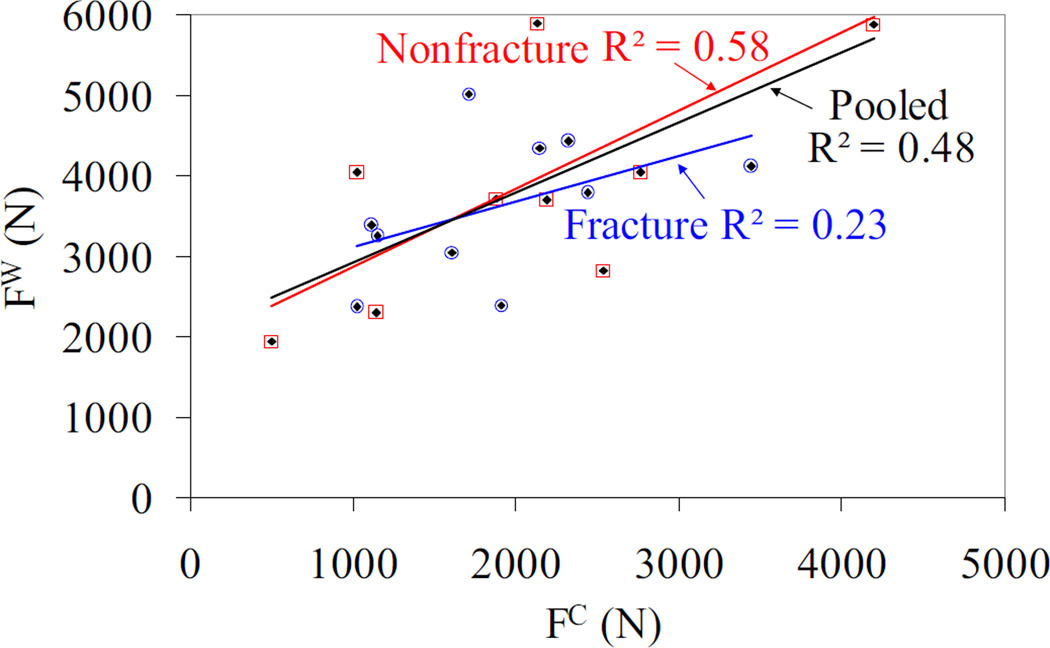
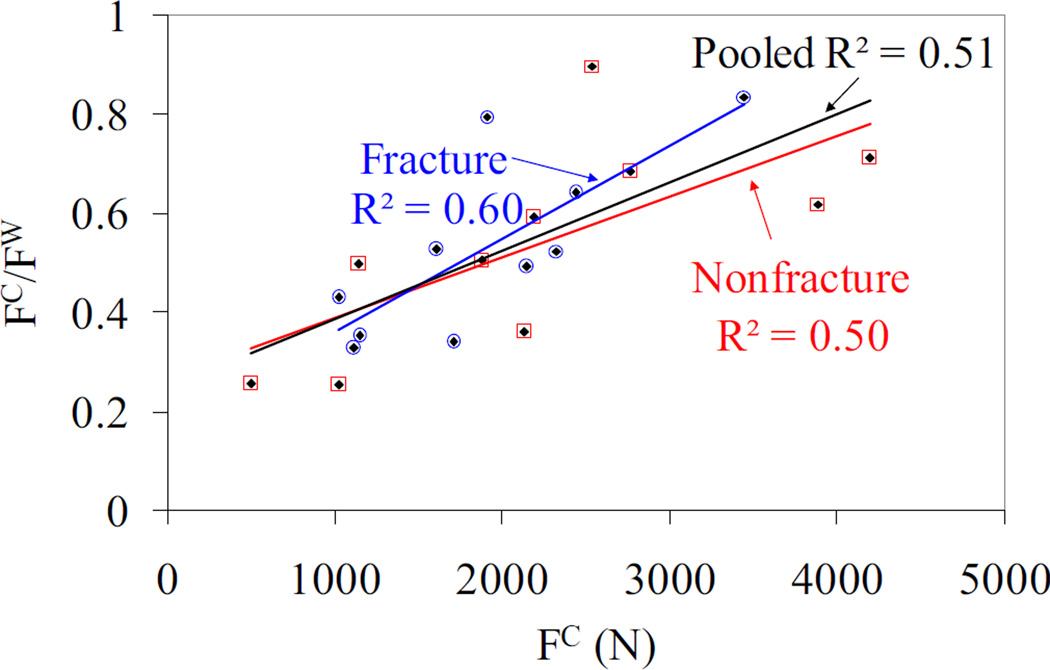
The fracture loads obtained from cortical and whole bone models exhibited statistically significant correlations for the nonfracture group and pooled data with R² = 0.58 (p = 0.01) and R² = 0.48 (p < 0.001), respectively, whereas the correlation was not significant for the fracture group (Figure 4). In addition, when the cortical fracture load was plotted with respect to the cortical to whole bone fracture load ratio, positive and statistically significant correlations (R² ≥ 0.5, p < 0.05) were observed for all groups (Figure 5).

Figure 4.

Cortical bone vs. whole bone fracture loads for fracture, nonfracture and pooled data. Note that the blue hollow circles, red hollow squares, and black diamonds correspond to fracture, nonfracture and pooled data, respectively. The nonfracture and pooled data has a statistically significant correlation with p = 0.01, and p < 0.001, respectively. The fracture group data did not exhibit significant correlation between the cortical and whole bone load.

Figure 5.

Cortical bone fracture load vs. ratio of cortical to whole bone fracture load for fracture, nonfracture and pooled data. Note that the blue hollow circles, red hollow squares, and black diamonds correspond to fracture, nonfracture and pooled data, respectively. The nonfracture, fracture and pooled data has a statistically significant correlation with p = 0.02, p < 0.01 and p < 0.001, respectively.

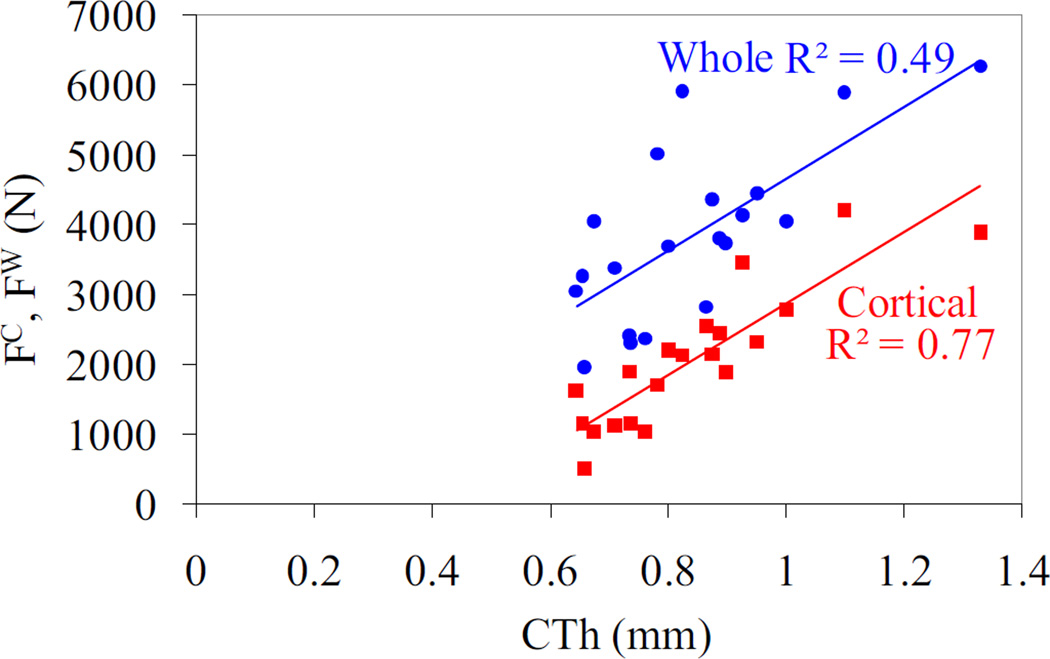
The stepwise multiple regression analysis between the geometrical properties and the cortical and whole bone fracture loads demonstrated that cortical thickness is the best and only predictor for whole bone fracture load with the exception of the fracture group that exhibited no correlation (Table 3, Figure 6). Cortical thickness was the common predictor of cortical fracture load for all groups (Figure 6) with additional terms of distal cortical polar moment of inertia and cortical crack area for the pooled and fracture groups, respectively (Table 3). The fracture load ratios were predicted by a single geometric ratio including the ratio of cortical to whole bone crack area for pooled and fracture groups and the ratio of cortical to whole bone moment of inertia in the medial-lateral direction at the crack plane for the nonfracture group (Table 3).

Table 3.

Stepwise multiple regression models between the fracture loads and the geometrical and trabecular properties and the corresponding R² and p values.

Stepwise Multiple Regression Models	R2	p
Pooled whole bone fracture load vs. Geometric properties
FW = 5144.8 CTh – 488.6	0.49	< 0.001
Fracture group whole bone fracture load vs. Geometric properties :
none	-	-
Nonfracture group whole bone fracture load vs. Geometric properties:
FW = 5339.1 CTh – 684.3	0.52	0.019
Pooled cortical bone fracture load vs. Geometric properties:
FC = 4807.0 CTh – 2.34 DJC – 1017.1	0.86	< 0.001
Fracture group cortical bone fracture load vs. Geometric properties:
FC = 6815.5 CTh – 71.6 CAC + 306.5	0.96	< 0.001
Nonfracture group cortical bone fracture load vs. Geometric properties:
FC = 5255.6 CTh – 2450.4	0.83	< 0.001
Pooled cortical/whole bone fracture load ratio vs. Geometric properties:
FC/FW = 1.30 (CAC/CAW) – 0.270	0.47	< 0.001
Fracture group cortical/whole bone fracture load ratio vs. Geometric properties:
FC/FW = 1.56 (CAC/CAW) – 0.476	0.67	0.004
Nonfracture group cortical/whole bone fracture load vs. Geometric properties:
FC/FW = 1.41 (CIxxC/ CIxxW) – 0.474	0.45	0.034
Pooled whole bone fracture load vs. Trabecular properties:
none	-	-
Fracture group whole bone fracture load vs.Trabecular properties:
FW = 78861.9 Tb.Th – 521.7	0.40	< 0.05
Nonfracture group whole bone fracture load vs. Trabecular properties:
none	-	-

Whole (F^W) and cortical (F^C) bone fracture load; cortical thickness at the crack surface (CTh); cortical bone polar moment of inertia at the distal surface (DJ^C); cortical bone area at the crack surface (CA^C); whole bone area at the crack surface (CA^W); cortical bone moment of inertia in medial-lateral direction at the crack surface (CI_xx^C); whole bone moment of inertia in medial-lateral direction at the crack surface (CI_xx^W); trabecular thickness (Tb.Th). Note that the units of F^W and F^C are in N, CTh and Tb.Th are in mm, CA^C and CA^W are in mm², DJ^C, CI_xx^C, and CI_xx^W are in mm⁴.

Figure 6.

Correlation between pooled cortical and whole bone fracture load vs. the cortical thickness at the crack location (p < 0.001). The cortical thickness was the best single predictor for the cortical and whole bone fracture loads.

The stepwise multiple regression analysis between trabecular parameters and the whole bone fracture loads showed that trabecular thickness was a predictor of fracture group whole bone fracture load (Table 3). However, the nonfracture group and pooled whole bone fracture load exhibited no correlation with the trabecular variables.

The studies on models that investigated the influence of crack location demonstrated higher fracture loads for the proximal crack plane and lower fracture loads for the distal crack plane (Table 4). The predicted load ratio between cortical and whole bone at the mid-height was closely replicated in the distal crack plane. However, at the proximal crack plane the contribution of the cortical bone was higher for the two models which had much thicker cortical thickness at the proximal region (Table 4). The ratio of fracture loads between distal, proximal and mid-height crack planes varied in proportion to the ratio of cortical thickness on the corresponding crack surfaces.

Table 4.

Fracture load and cortical thickness ratios between distal and proximal crack surfaces and the average crack surface of three bone models. Ratios of cortical to whole bone fracture load at the average, distal and proximal crack surfaces. Bone Model 1, 2, and 3 refer to the three randomly selected bone models that were used to evaluate the influence of the crack location.

Fracture Load and Cortical Thickness Ratio
	FWd/FW	FWp/FW	FCd/FC	FCp/FC	CThd/CTh	CThp/CTh
Bone Model 1	0.72	1.02	0.77	1.07	0.90	1.03
Bone Model 2	0.65	1.64	0.71	2.94	0.98	1.86
Bone Model 3	0.67	1.13	0.63	1.32	0.68	1.32
Cortical to Whole Bone Fracture Load Ratio
	FC/FW	FCd/FWd	FCp/FWp
Bone Model 1	0.36	0.38	0.38
Bone Model 2	0.33	0.36	0.59
Bone Model 3	0.49	0.46	0.57

Whole bone fracture load at the average crack surface (F^W); whole bone fracture load at the distal crack surface (F^W_d); whole bone fracture load at the proximal crack surface (F^W_p); cortical bone fracture load at the average crack surface (F^C); cortical bone fracture load at the distal crack surface (F^C_d); cortical bone fracture load at the proximal crack surface (F^C_p); cortical thickness at the average crack surface (CTh); cortical thickness at the distal crack surface (CTh_d); cortical thickness at the proximal crack surface (CTh_p)

4. DISCUSSION

This study presented a new approach for evaluating the fracture load at the distal radius that combines in vivo human images with nonlinear fracture mechanics-based finite element modeling. Although, this technique was utilized previously on idealized radius models (Buchanan and Ural, 2010; Ural, 2009), this is the first study that combines HR-pQCT imaging with cohesive finite element modeling.

Previous studies utilized only strength-based parameters and pure axial compression loading for assessing fracture load (Boutroy et al., 2008; Burghardt et al., 2010; MacNeil and Boyd, 2007; Melton et al., 2007; Pistoia et al., 2002; Varga et al., 2010). Our current model determined the fracture load based on both strength and fracture toughness and incorporated a more realistic loading direction that represents a fall to prevent overestimation of the fracture load due to pure axial compression loading (Buchanan and Ural, 2010; Troy and Grabiner, 2007). In addition, pure axial compression simulations that we ran on six sample bone models for comparison purposes showed a narrower range of cortical to whole bone fracture load ratios than predicted by our modeling approach. Furthermore, the ratio of fracture loads obtained from both approaches did not exhibit a constant value and showed variation from model to model indicating the possibility that the axial compression loading may not be fully capturing the failure mechanisms in distal radius fracture.

One of the goals of our study was to provide better insight into the contribution of cortical bone to the overall bone fracture load by direct evaluation instead of extraction from whole bone models (Boutroy et al., 2008; MacNeil and Boyd, 2007; Pistoia et al., 2003). The results of our simulations showed a positive and significant correlation between the cortical and whole bone fracture load (Figure 4) highlighting the possibility of estimating whole bone fracture load based on cortical bone fracture load with substantially less computational cost. Patients to whom this approach can be applied may be identified by the distal cortical moment of inertia in the medial-lateral direction that exhibited a statistically significant difference between fracture and nonfracture groups. In addition, a significant and positive correlation between the cortical bone fracture load and the cortical to whole bone fracture load ratio showed that the portion of the whole bone fracture load carried by the cortical bone increases with cortical bone fracture load. This relationship indicates that a more robust cortical bone structure carries a larger percentage of the whole bone fracture load (Figure 5) which may be an evidence for the importance of the integrity of the cortical compartment on fracture risk.

The simulation results showed that the cortical geometrical properties can identify not only the cortical fracture load but also the whole bone fracture load (Table 3). The cortical thickness was found to be the most important predictor of whole bone fracture load with the exception of the fracture group. Previous studies also found cortical thinning to be the most influential factor on bone strength compared to trabecular bone properties (Pistoia et al., 2003). In addition, it was shown that the thicker cortical thickness may enable the cortical compartment to carry a higher percentage of the load applied to the bone and may lead to lower rates of fracture (Walker et al., 2011). The lack of any single geometrical predictor for the fracture group whole bone fracture load may be due to the compromised cortical structure that cannot contribute significantly to the overall mechanical response of bone. As a result, the fracture group may try to derive its fracture resistance from the trabecular compartment as highlighted by the correlation between the whole bone fracture load and trabecular thickness in the fracture group. This observation is also supported by our simulations that did not find any significant correlation between the cortical and whole bone fracture load in the fracture group.

In the current study, both the average cortical and whole bone fracture load were larger in the nonfracture group compared to the fracture group. Although the differences did not reach statistical significance, most likely due to the small sample group used in the study, the difference may indicate a more robust bone structure for the nonfracture group. On the other hand, the fracture group in this study is composed of women who had prior vertebral fractures. The current results may also support previous findings in the literature that showed a weak predictive capability of vertebral fractures in women based on distal bone strength (Vilayphiou et al., 2010).

One of the limitations of the current study is the sample size used for fracture and nonfracture subgroups. In this study, our main goal was to establish a new HR-pQCT-based cohesive finite element modeling approach and to demonstrate the feasibility of using this approach for fracture risk assessment. Due to the computational time involved in the simulations particularly with the whole bone models, we selected a limited subgroup sample size to demonstrate the novel components of our approach compared to previous studies. In the future studies based on this approach, larger subgroup sizes will need to be utilized to further confirm the observed group differences.

The simulations were performed using a predetermined crack plane which corresponds to the average location of distal forearm fractures reported in the literature (Eastell, 1996). Investigation of the influence of crack location on the results at proximal and distal locations showed that the fracture load varied proportional to the ratio of cortical thickness between the corresponding crack location and the average crack location. This indicates that the limiting distal radius fracture load can be estimated based on the average crack location used in the current simulations and the ratio of the cortical thickness at the distal and proximal locations to the cortical thickness at the crack plane. Selection of the predetermined crack plane provides a good estimate of the fracture load while avoiding the selection of the whole bone section as a crack domain that is computationally very expensive and that may lead to convergence issues based on the possible activation of cohesive elements at various sites.

In this study, homogeneous material properties were utilized for both elastic and cohesive properties. Various relationships that relate the elastic modulus to densitometric measures (Helgason et al., 2008) or attenuation values of bone (Homminga et al., 2001) have been proposed in the literature. However, there is substantial site and specimen specific variation between these relationships (Austman et al., 2008; Helgason et al., 2008; Morgan et al., 2003). Furthermore, the fracture toughness and strength variation with attenuation have not been reported in the literature. As a result, a systematic study is needed to establish reliable relationships between HR-pQCT attenuation values and elastic modulus, strength and fracture toughness to incorporate spatial variation of these values in finite element simulations. Further advancement on the local material measurements can easily be incorporated in our model to represent spatial and age-related material and fracture property changes in future studies. The additional information on densitometric parameters can also be combined with structural and microarchitectural parameters in the multiple regression analysis for predicting fracture load.

In summary, this study introduced a new modeling approach that coupled HR-pQCT imaging with nonlinear fracture mechanics-based finite element simulations, incorporated a realistic loading direction that mimic fall conditions, and showed the significant contribution of the cortical compartment to the overall fracture load of bone. The results provide more insight into the fracture process and evaluation of fracture load at the distal radius.