Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 May 3.
Published in final edited form as: Addict Behav. 2011 Jan 20;36(5):543–546. doi: 10.1016/j.addbeh.2011.01.010

Prevention of Alcohol Use in Middle School Students: Psychometric Assessment of the Decisional Balance Inventory

Steven F Babbin 1, Magdalena Harrington 1, Caitlin Burditt 1, Colleen Redding 1, Andrea Paiva 1, Kathryn Meier 1, Karin Oatley 1, Heather McGee 1, Wayne F Velicer 1
PMCID: PMC3642983  NIHMSID: NIHMS463385  PMID: 21316862

Abstract

A measurement model should be equivalent across the different subgroups of a target population. The Decisional Balance Inventory for the Prevention of Alcohol Use is a 2- factor correlated model with 3 items for Pros of alcohol use and 3 items for Cons. The measure is part of a tailored intervention for middle school students. This study evaluated the important psychometric assumptions of factorial invariance and scale reliability with a large sample of sixth grade students (N = 3565) from 20 schools. A measure is factorially invariant when the model is the same across subgroups. Three levels of invariance were assessed, from least restrictive to most restrictive: 1) Configural Invariance (unconstrained nonzero factor loadings); 2) Pattern Identity Invariance (equal factor loadings); and 3) Strong Factorial Invariance (equal factor loadings and measurement errors). Structural equation modeling was used to assess invariance over two levels of gender (male and female), race (white and black), ethnicity (Hispanic and non-Hispanic), and school size (large, indicating >200 students per grade, or small). The strongest level of invariance, Strong Factorial Invariance, was a good fit for the model across all of the subgroups: gender (CFI: 0.94), race (CFI: 0.96), ethnicity (CFI: 0.93), and school size (CFI: 0.97). Coefficient alpha was 0.61 for the Pros and 0.67 for Cons. Together, invariance and reliability provide strong empirical support for the validity of the measure.

Keywords: Factorial invariance, Decisional Balance, Transtheoretical Model, Alcohol Prevention, Middle school students

Alcohol use by middle-school aged students is common and must be recognized as a public health concern. Despite negative health and legal consequences, 39% of eighth graders have tried alcohol (Johnston, O’Malley, Bachman, & Schulenberg, 2009). Recent heavy drinking, defined as consumption of five or more drinks in a row at least once in the past two weeks (NIH guideline), is also a problem for middle school students; 8% of eighth graders report heavy drinking (Johnston et al., 2009). As students mature this problem becomes worse as rates of heavy drinking increase throughout high school, with 16% of tenth graders and 25% of twelfth graders reporting heavy drinking (Johnston et al., 2009). To alleviate this problem, prevention programs for middle school students need to effectively intervene before alcohol use begins. The present study assesses the psychometric properties of a key component of a tailored intervention designed to prevent alcohol acquisition in middle school students.

Computer-based tailored interventions have been effective for a wide variety of behaviors (Noar, Benac, & Harris, 2007; Velicer, Prochaska, & Redding, 2006). Tailoring interventions requires the development of short, psychometrically sound measures. The Decisional Balance Inventory for the Prevention of Alcohol Use was developed as part of a tailored intervention based on the Transtheoretical Model of Behavior Change (TTM). In order for the measure to be meaningful and useful for intervention purposes, it must be valid. The factorial invariance and scale reliability of this measure were evaluated in the present study.

The TTM is an integrative framework that consists of multiple dimensions (Prochaska & Velicer, 1997; Velicer, Prochaska, Fava, Rossi, Redding, Laforge, & Robbins, 2000). The Decisional Balance component of TTM assesses an individual’s weighing of the pros and cons of engaging in a behavior (Velicer, DiClemente, Prochaska, & Brandenburg, 1985). The relation between the decisional balance and the stages has been shown to replicate across more than 48 different behaviors (Hall & Rossi, 2008). A decisional balance measure for alcohol use has been explored and validated in adolescent populations (Migneault, Pallonen, & Velicer, 1997) and college students (Migneault, Velicer, Prochaska, & Stevenson, 1999). The Decisional Balance Inventory for Prevention of Alcohol Use was developed for middle-school aged students, and the measure has six items, three Pros of Alcohol Use and three Cons of Alcohol Use. A short inventory with three items each for pros and cons has been demonstrated to be psychometrically valid for smoking in an adult sample (Ward, Velicer, Rossi, Fava, & Prochaska, 2004).

Decisional balance is important for intervention purposes because the responses to the inventory lead to different interventions for alcohol use; in the tailored intervention, students receive individualized feedback. The aim of this study is to confirm the psychometric assumptions of measurement invariance and scale reliability. A measurement model is called factorially invariant when the structural model is the same for different subgroups of a population. Three levels of factorial invariance, from the least restrictive to the most restrictive, were assessed. Each level adds more restraints to the model. The weakest level is Configural Invariance, which states that subgroups have zero loadings on the same constructs and that nonzero factor loadings are unconstrained (Ward et al., 2004; Meredith, 1993). Next is Pattern Identity Invariance, which requires the factor loadings to be equal. Finally, Strong Factorial Invariance requires factor loadings and error terms to be equivalent across subgroups. Factorial invariance is crucial to assessing the validity of the measure. If a scale is factorially invariant across groups, then comparisons between groups on the measure of interest can confidently be attributed to true differences in the construct and not to variance on the measure.

The present study was a secondary data analysis of a sample of sixth grade Rhode Island middle school students (N = 3565), and the factorial invariance was examined across gender, racial identity, ethnicity, and school size. Reliability of the scales was assessed with Cronbach’s Coefficient Alpha.

Method

Participants

The participants were N = 3543 subjects where complete data was available (total sample = 3565). The data is from the baseline assessment of sixth grade students from 20 Rhode Island middle schools who were involved in an intervention project based on TTM. The overall sample was 82% white and 48% female.

Decisional balance inventory

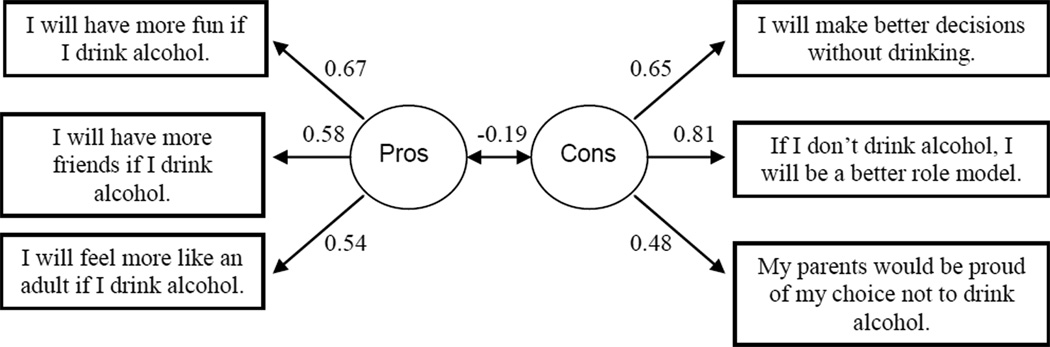
The Decisional Balance Inventory for Prevention of Alcohol Use was developed for middle school students using the sequential method of scale development (Jackson, 1971). The structure of the inventory is a two-factor correlated model with six items: three items for Pros of Alcohol Use and three items for Cons of Alcohol Use (see Figure 1). For each item, participants are asked to rate how much they agree or disagree on a 5- point Likert scale, from 1 = “strongly disagree” to 5 = “strongly agree.”

Figure 1.

Figure 1

Open in a new tab

CFA Model with standardized parameter estimates for the total sample.

Analysis

Three levels of invariance were tested in sequential order, with each level requiring more constraints: 1) Configural Invariance (unconstrained nonzero factor loadings); 2) Pattern Identity Invariance (equal factor loadings); and 3) Strong Factorial Invariance (equal factor loadings and measurement errors). Each invariance procedure required specific subgroups. In the creation of these subgroups, non-responders were deleted. For the analysis of gender, the subgroups were male (n = 1822) and female (n = 1708). For the analysis of racial identity, the subgroups were white (n = 2345) and black (n = 97). While the demographic questions included more racial identities (American Indian or Alaskan Native, Asian, Native Hawaiian or other Pacific Islander, other), no other racial identities had enough responses (roughly > 100) to be compared. For the analysis of ethnicity, the subgroups were Hispanic (n = 471) and non-Hispanic (n = 2991). For the analysis of school size, the subgroups were students from a small school, meaning less than 200 students (n = 1240) and large, meaning greater than 200 students (n = 2403).

Results

Factorial invariance

To test for factorial invariance, structural equation modeling (SEM) was employed using EQS 6.1 software (Bentler, 2007). The following indices were used to analyze the fit of the invariance: Comparative Fit Index (CFI), Normed Fit Index (NFI), Nonnormed Fit Index (NNFI), and Root Mean Squared Error of Approximation (RMSEA). CFI, NFI, and NNFI indicate how well a model fits the data with values from 0 to 1, with larger values indicating a better fit. Values greater than .90 indicate good fit and values greater than .95 indicate very good fit (Kline, 2005; Bentler, 1992). For RMSEA, smaller values indicate better fit, with values less than 0.1 indicating good fit and values less than 0.05 indicating very good fit (Kline, 2005, Browne & Cudeck, 1993). The indicators of fit considered in the present study (CFI, NFI, NNFI, RMSEA) were the same indices utilized by Ward et al. (2004) in a paper evaluating the psychometric properties of a six-item decisional balance inventory for cigarette smoking. Additionally, the difference in CFI between the model and the previous (lower) level of invariance (ΔCFI) was calculated to indicate whether the null hypothesis of invariance should be rejected; a value of −0.01 or less indicates it should not be rejected and that the model demonstrates invariance (Cheung & Rensvold, 2002). Chi-squared statistics are not reported in the present study due to the issue of large sample sizes frequently resulting in statistically significant but practically insignificant values (Kline, 2005; Hu & Bentler, 1999; Bentler & Bonett, 1980). No constraints were dropped in any of the models to achieve a better fit.

Gender

Sample size was adequate for male (n = 1822) and female (n = 1708) subgroups. The highest level of invariance, Strong Factorial Invariance, was a good fit for the model for gender (CFI: 0.944; NFI: 0.937; NNFI: 0.923; RMSEA: 0.063; see Table 1).

Table 1.

Goodness-of–Fit Statistics for Three Invariance Models.

Model NFI NNFI CFI Δ CFI RMSEA
Gender
Configural Invariance 0.969 0.951 0.974 - 0.053
Pattern Identity Invariance 0.968 0.962 0.975 0.001 0.047
Strong Factorial Invariance 0.937 0.923 0.944 −0.031 0.063
Race
Configural Invariance 0.968 0.952 0.974 - 0.054
Pattern Identity Invariance 0.964 0.959 0.973 −0.001 0.050
Strong Factorial Invariance 0.945 0.938 0.955 -0.018 0.057
Ethnicity
Configural Invariance 0.969 0.951 0.974 - 0.053
Pattern Identity Invariance 0.962 0.953 0.968 −0.006 0.052
Strong Factorial Invariance 0.926 0.907 0.933 −0.035 0.069
School
Configural Invariance 0.972 0.956 0.977 - 0.051
Pattern Identity Invariance 0.970 0.964 0.976 −0.001 0.046
Strong Factorial Invariance 0.960 0.955 0.968 −0.008 0.047
Open in a new tab

Race

Sample size was adequate for white (n = 2345) and black (n = 97) subgroups. Strong Factorial Invariance was a good fit for racial identity (CFI: 0.955; NFI: 0.945; NNFI: 0.938; RMSEA: 0.057; see Table 1).

Ethnicity

Sample size was adequate for Hispanic (n = 471) and non-Hispanic (n = 2991) subgroups. Strong Factorial Invariance was a good fit for ethnicity (CFI: 0.933; NFI: 0.926; NNFI: 0.907; RMSEA: 0.069; see Table 1).

School size

Sample size was adequate for small schools (n = 1240) and large schools (n = 2403). Strong Factorial Invariance provided a very good fit for school size (CFI: 0.968; NFI: 0.960; NNFI: 0.955; RMSEA: 0.047; see Table 1).

Scale reliabilities

Since Strong Factorial Invariance held for each of the four cross-sample comparisons, the structure is reported only for the total sample (see Figure 1). In the total sample, Coefficient Alpha was 0.61 for Pros and 0.67 for Cons, suggesting that additional items would strengthen the scales for this age level. The limited number of students who are currently using or experimenting with alcohol may also have reduced the reliability estimates.

Discussion

The Decisional Balance Inventory for Prevention of Alcohol Use demonstrates a high level of factorial invariance. Strong Factorial Invariance requires that factor loadings and error terms are constrained in the model, and this provided a good fit across gender, racial identity, ethnicity, and school size. These analyses demonstrate a consistent relationship between the factors (Pros and Cons), and the six items that measure the factors.

When considering the criteria for Strong Factorial Invariance, NFI, NNFI, CFI, and RMSEA consistently showed good fit across all subgroups. In contrast, the ΔCFI indicator was less consistent, with the comparisons for gender, ethnicity, and race slightly larger than the suggested cut-off value of −0.01. This suggests that there could be some minor differences in the factor model within these subgroups, but this does not indicate an unacceptable level of fit for Strong Factorial Invariance. While the change in CFI is important to consider, the final CFI values still consistently demonstrate good fit.

Greater coefficient alphas for the pros and cons would be desirable. There is room for an improvement in reliability of the scales. Cronbach’s coefficient alpha could be improved by adding more pros and more cons to the scale. This would result in a longer, more reliable scale but a less parsimonious model.

Factorial invariance does not mean that subgroup means are equivalent. Mean differences should be investigated separately, and they would have a different interpretation. This could be the focus of a future study.

One limitation of this study involves the racial demographics. The current analyses do not provide comprehensive coverage of all races; a larger, more diverse sample would enable the inclusion of other racial identities as opposed to just white and black. The ethnicity aspect could also be improved. The invariance for Hispanic versus non-Hispanic shows the lowest degree of fit, compared to the other subgroup comparisons, but all of the values are still adequate. A larger sample of individuals that identify themselves as Hispanic could improve fit. Additionally, the level of acculturation may explain the lower degree of fit.

Confirming the invariance of a factor model is beneficial to conducting valid research. Unless the sample consists of individuals that are homogenous in every way, there is inevitably some variation among subgroups that is extraneous to the research question. With a factorially invariant model, these differences among subgroups will not distort the results. The validity of the research is increased because the measurement should be the same regardless of the sample taken from the target population.

The consistency of the measurement model across subgroups provides strong empirical support for the construct validity of the scale. Despite only having three items for Pros and three items for Cons, the model is consistent and reliable. Short, psychometrically sound measures such as the Decisional Balance Inventory for Prevention of Alcohol Use are important for developing effective tailored prevention interventions.

Research highlights.

  • Measurement models should be equivalent across the different subgroups of a target population.

  • Decisional Balance Inventory for the Prevention of Alcohol Use is a 2-factor correlated model with 3 items for Pros of alcohol use and 3 items for Cons.

  • Measure is part of a tailored prevention intervention for middle school students.

  • The strongest level of invariance, Strong Factorial Invariance, was a good fit for the model across all of the subgroups: gender, race, ethnicity, and school size.

  • Coefficient alpha was 0.61 for the Pros and 0.67 for Cons.

Acknowledgments

This paper was partially supported by Grant CA11919 from NCI and Grant DA020112 from NIDA.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bentler PM. On the fit of models to covariances and methodology to the Bulletin. Psychological Bulletin. 1992;112:400–404. doi: 10.1037/0033-2909.112.3.400. [DOI] [PubMed] [Google Scholar]
  2. Bentler PM. EQS 6.1 structural equations program manual. Encino, CA: Multivariate Software; 2007. [Google Scholar]
  3. Bentler PM, Bonett DG. Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin. 1980;88:588–606. [Google Scholar]
  4. Browne MW, Cudeck R. Alternative ways of assessing model fit. In: Bollen KA, Long JS, editors. Testing structural equation models. Newbury Park, CA: Sage; 1993. pp. 445–455. [Google Scholar]
  5. Cheung GW, Rensvold RB. Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling. 2002;9:233–255. [Google Scholar]
  6. Hall KL, Rossi JS. Meta-analytic examination of the strong and weak principles across 48 health behaviors. Preventive Medicine. 2008;46:266–276. doi: 10.1016/j.ypmed.2007.11.006. [DOI] [PubMed] [Google Scholar]
  7. Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
  8. Jackson DN. The dynamics of structured personality tests: 1971. Psychological Review. 1971;78:229–248. [Google Scholar]
  9. Johnston LD, O’Malley PM, Bachman JG, Schulenberg JE. Monitoring the future: National survey results on drug use, 1975–2008: Volume I, Secondary school students (NIH Publication No. 09-7402) Bethesda, MD: National Institute on Drug Abuse; 2009. [Google Scholar]
  10. Kline RB. Principles and Practice of Structural Equation Modeling. 2nd ed. New York: The Guilford Press, NY; 2005. [Google Scholar]
  11. Meredith W. Measurement invariance, factor analysis, and factorial invariance. Psychometrika. 1993;58:521–543. [Google Scholar]
  12. Migneault JP, Pallonen UE, Velicer WF. Decisional balance and stage of change for adolescent drinking. Addictive Behaviors. 1997;22:339–351. doi: 10.1016/s0306-4603(96)00252-3. [DOI] [PubMed] [Google Scholar]
  13. Migneault JP, Velicer WF, Prochaska JO, Stevenson JF. Decisional balance for immoderate drinking in college students. Substance Use and Misuse. 1999;34:1325–1346. doi: 10.3109/10826089909029387. [DOI] [PubMed] [Google Scholar]
  14. Noar SM, Benac C, Harris M. Does tailoring matter? Meta-analytic review of tailored print health behavior change interventions. Psychological Bulletin. 2007;133:673–693. doi: 10.1037/0033-2909.133.4.673. [DOI] [PubMed] [Google Scholar]
  15. Prochaska JO, Velicer WF. The Transtheoretical Model of Behavior Change. American Journal of Health Promotion. 1997;12:38–48. doi: 10.4278/0890-1171-12.1.38. [DOI] [PubMed] [Google Scholar]
  16. Velicer WF, DiClemente CC, Prochaska JO, Brandenberg N. Decisional balance measure for assessing and predicting smoking status. Journal of Personality and Social Psychology. 1985;48:1279–1289. doi: 10.1037//0022-3514.48.5.1279. [DOI] [PubMed] [Google Scholar]
  17. Velicer WF, Prochaska JO, Fava JL, Rossi JS, Redding CA, Laforge RG, Robbins ML. Using the transtheoretical model for population-based approaches to health promotion and disease prevention. Homeostasis in Health and Disease. 2000;40:174–195. [Google Scholar]
  18. Velicer WF, Prochaska JO, Redding CA. Tailored communications for smoking cessation: Past successes and future directions. Drug and Alcohol Review. 2006;25:47–55. doi: 10.1080/09595230500459511. [DOI] [PubMed] [Google Scholar]
  19. Ward R, Velicer WF, Rossi JS, Fava JL, Prochaska JO. Factorial Invariance and internal consistency for the decisional Balance inventory – short form. Addictive Behaviors. 2004;29:953–958. doi: 10.1016/j.addbeh.2004.02.042. [DOI] [PubMed] [Google Scholar]

RESOURCES