Short-Term Integration of Cdc25 Dynamics Controls Mitotic Entry during Drosophila Gastrulation

SUMMARY

Cells commit to mitosis by abruptly activating the mitotic cyclin-Cdk complexes. During Drosophila gastrulation, mitosis is associated with the transcriptional activation of cdc25^string, a phosphatase that activates Cdk1. Here, we demonstrate that the switch-like entry into mitosis observed in the Drosophila embryo during the 14^th mitotic cycle is timed by the dynamics of Cdc25^string accumulation. The switch operates as a short-term integrator, a property that can improve the reliable control of timing of mitosis. The switch is independent of the positive feedback between Cdk1 and Cdc25^string and of the double negative feedback between Cdk1 and Wee1. We propose that the properties of the mitotic switch are established by the out-of-equilibrium properties of the covalent modification cycle controlling Cdk1 activity. Such covalent modification cycles, triggered by transcriptional expression of the activating enzymes, might be a widespread strategy to obtain reliable and switch-like control of cell decisions.

INTRODUCTION

During the cell cycle, a series of biochemical switches govern a cell’s progression through major regulatory checkpoints (Morgan, 2007). At the onset of mitosis, the final G2/M checkpoint induces a reorganization of the cytoskeleton, nuclear membrane and chromatin structure to prepare for sister chromatids segregation. All these processes depend on a single group of master regulators: the mitotic cyclin-Cdk complexes.

In most cell types, entry into mitosis is triggered by an abrupt switch-like activation of cyclin-Cdk1 complexes (Morgan, 2007; O’Farrell, 2001). Cdk1 complexes are initially held in an inactive state by inhibitory phosphorylation of the Cdk1 subunit (mediated by the kinases Wee1 and Myt1). At the onset of mitosis, the abrupt removal of this phosphorylation (mediated by the phosphatase Cdc25) leads to the activation of Cdk1 (Morgan, 2007; O’Farrell, 2001). In human cells activation of Cdk1 triggers different mitotic events at different levels of kinase activity (Gavet and Pines, 2010). Although these mechanisms are well conserved among eukaryotes, the strategies that cells use to trigger Cdk1 activation and entry into mitosis differ in various organisms (Morgan, 2007).

During Drosophila gastrulation, entry into mitosis is associated with and requires transcriptional activation of cdc25^string (Edgar and O’Farrell, 1989, 1990). cdc25^string expression is sufficient to induce dephosphorylation of Cdk1 and to trigger mitosis (Edgar and O’Farrell, 1990). Mitosis 14 in the Drosophila embryo is executed in a reproducible and accurate spatiotemporal pattern consisting of 25 spatially distinct domains (Foe, 1989), providing a dramatic example of the precision with which the cell cycle can be programmed during development (Edgar and O’Farrell, 1990; O’Farrell, 2001). However, how expression of cdc25^string results in abrupt activation of Cdk1 and precise timing of cell division in Drosophila remains unknown. It has been proposed from experiments in Xenopus egg extract and mammalian cells that the abrupt activation of Cdk1 at the onset of mitosis is controlled by two feedback loops: a positive feedback loop between Cdc25 and Cdk1 and a double negative feedback loop between Wee1 and Cdk1. Cdc25 activity is stimulated by Cdk1-dependent phosphorylation (Hoffmann et al., 1993; Izumi and Maller, 1993; Kumagai and Dunphy, 1992; Trunnell et al., 2011), whereas Wee1 activity is inhibited by Cdk1-dependent phosphorylation (McGowan and Russell, 1995; Mueller et al., 1995). Positive feedback between Cdc25^string and Cdk1 and double negative feedback between Wee1 and Cdk1 can produce the switch-like control of mitosis observed in the Xenopus egg extract (Izumi and Maller, 1993; Kim and Ferrell, 2007; Novak and Tyson, 1993; Pomerening et al., 2003, 2005; Sha et al., 2003; Solomon et al., 1990; Trunnell et al., 2011). These feedbacks might facilitate the unidirectionality of the transition by creating a hysteretic bistable system (Pomerening et al., 2003; Sha et al., 2003). Recent experiments in somatic cell extracts (Deibler and Kirschner, 2010) indicate that Wee1 activity might be stimulated by phosphorylation by low Cdk1 levels (Deibler and Kirschner, 2010; Harvey et al., 2005) and inhibited by high levels (Deibler and Kirschner, 2010), suggesting a more complicated control mechanism.

In fission yeast, it is possible to engineer a functional cell cycle oscillator lacking Cdc25 and Wee1 dependent controls, as well as other controls (Coudreuse and Nurse, 2010). However, the timing of such cell cycles is very noisy (Coudreuse and Nurse, 2010), reminiscent of the extremely variable quantized cell cycles observed in cells mutant for both cdc25 and wee1 (Sveiczer et al., 1996). These results suggest that, similarly to fission yeast, inputs from Cdc25 and Wee1 might be required to obtain the reliable timing of cell division observed during embryonic development. The role of positive feedback and other molecular mechanisms in ensuring such temporal precision remains unclear.

To characterize the molecular switch controlling entry into mitosis during Drosophila embryonic development we focused on the control of the 14^th mitotic division that happens after the embryo has cellularized and gastrulation has begun. The pattern of mitosis is associated with the expression of cdc25^string that is established by the developmental program regulating overall patterning of the embryo (Edgar et al., 1994a; Edgar and O’Farrell, 1989, 1990).

We find that cell divisions inside individual mitotic domains are controlled in a precise and reproducible wave-like pattern. This wave-like pattern reflects the transcriptional activation of cdc25^string and is unlikely to depend on other cellular or developmental inputs. The rate of accumulation of Cdc25^string determines the time of cell division in a switch-like manner. The switch operates as a short-term integrator, so that the decision of mitosis is effectively controlled by the concentration of Cdc25^string integrated over a timescale of 2 min. Cdc25^string activates Cdk1 in an ultrasensitive manner and this ultrasensitivity does not require the positive feedback between Cdc25^string and Cdk1 or the double negative feedback between Wee1 and Cdk1. Mathematical modeling and theoretical analysis suggest that ultrasensitive activation of Cdk1 is controlled by a covalent modification cycle operating in the first-order regime and far from steady state. The predicted signaling properties of such a covalent modification cycle reproduce well the measured signaling properties of the mitotic switch.

RESULTS

cdc25^string Transcriptional Activation Controls the Timing of Cell Division in Individual Cells

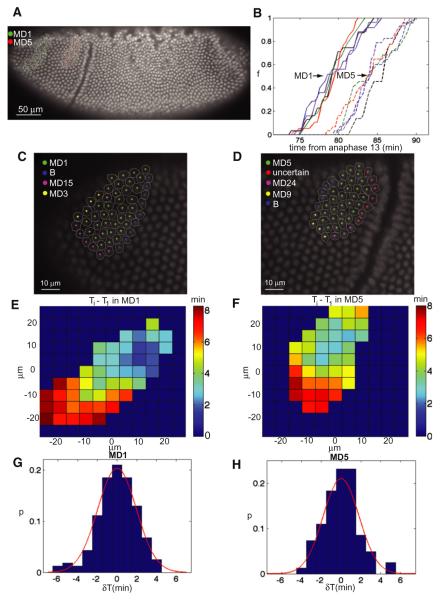
Within a mitotic domain, cell divisions are not absolutely synchronous. This asynchrony may reflect inherent variability and noise, but could also in part arise from the fact that within each domain, mitosis starts in a single cell or in a small number of interior cells then spreads wave-like, in all directions, until it stops at the domain boundary (Foe, 1989). To characterize the properties of the wave-like divisions inside mitotic domains, we imaged embryos expressing His2Av-GFP with 20-s frame rate to determine the time of mitosis inside domains 1 and 5 (Figure 1A). We developed algorithms to track the coordinates of each cell at the onset of gastrulation and the time at which it divided (Figures 1C and 1D). On average, cells in mitotic domain 1 divide ~5 min before those in mitotic domain 5 (Figure 1B), but each domain shows a reproducible wave-like pattern (Figures 1E and 1F). In both domains 1 and 5, the pattern begins in the center of the domain and extends radially. Most of the variability in division within each domain is attributable to this wave-live pattern. Although it takes ~10 min for all the cells in either domain to divide, on a cell-to-cell basis, the deviation from the expected (smoothed) wave-like pattern in either domain is only 2 min (Figures 1G and 1H).

Figure 1. Mitosis inside Domains 1 and 5 Follow Reproducible Wave-Like Pattern.

(A) Confocal image of His2Av-GFP embryo. Cells belonging to mitotic domain 1 (MD1) and mitotic domain 5 (MD5) are highlighted in green and red, respectively.

(B) Fraction of cells that have divided inside MD1 and MD5 as a function of time from anaphase 13.

(C and D) Enlarged view of a region around MD1 (C) and MD5 (D).

(E and F) A map of the average pattern of mitosis inside MD1 (E) and MD5 (F). Data show the time of cell division relative to the first cell that divides in the domain. The coordinates are relative to the centroid of the domain. Embryos were oriented laterally.

(G and H) Probability distribution of the difference (δT) between the time when a cell divides and the time when it was predicted to divide based on the average pattern; MD1 (G), MD5 (H). The data in both histograms are well described by a Gaussian (red lines) of standard deviation of ~2 min.

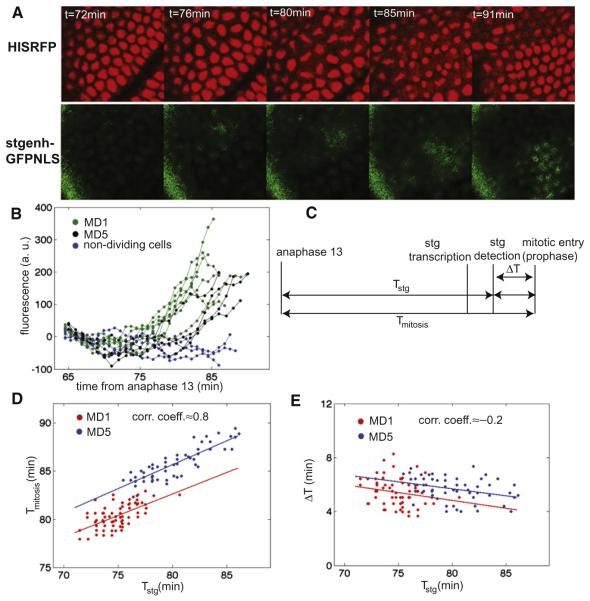
The wave may represent a secondary control of mitotic timing, independent of Cdc25^string, or it might be produced if cdc25^string expression were initiated within each domain in a wave-like pattern corresponding to the final progression of mitosis. To distinguish between these possibilities, we examined the dynamics of cdc25^string expression in living embryos using a transcriptional reporter expressing nuclear localized GFP (GFP-NLS, Figure 2A and Movie S1 available online) under the control of a cdc25^string enhancer that drives expression in mitotic domains 1 and 5 (Lehman et al., 1999) (Figure S1). We developed algorithms to track individual nuclei and to quantify in each the nuclear fluorescence intensity (Figure 2B) from the early phase of gastrulation to the entry into mitosis (see Figure 2C for the definition of timing of cellular events). Using a numerical fitting procedure (Skotheim et al., 2008), we could estimate the time of activation of cdc25^string transcription for most cells belonging to domain 1 and 5. This analysis shows that for each cell the timing of its division correlates with the timing of its activation of cdc25^string (Figure 2D). The time from cdc25^string activation to entry into mitosis is similar in all the cells inside the two domains regardless of when cdc25^string expression is activated (Figure 2E). These results imply that the wave-like pattern of mitosis observed inside domain 1 and 5 reflect the pattern of activation of cdc25^string rather than any additional control process that intervenes between cdc25^string expression and division. Therefore, we conclude that it is very unlikely that other cellular and developmental inputs play an important role in setting the timing of mitosis in these cells.

Figure 2. Transcriptional Activation of cdc25^string Controls the Wave-Like Pattern of Cell Divisions inside Mitotic Domain 1 and 5.

(A) Confocal images of an embryo expressing His2Av-RFP and the transcriptional reporter for cdc25^string expression (stgenh-GFPNLS). The region displayed is the one surrounding MD5.

(B) Quantification of fluorescence intensity from stgenh-GFPNLS in individual cells.

(C) Diagram of the measured time intervals.

(D) Correlation between T_stg and T_mitosis for cells in mitotic domain 1 (MD1, red circles) and in mitotic domain 5 (MD5, blue circles).

(E) Correlation between T_stg and ΔT for cells in mitotic domain 1 (MD1, red circles) and in mitotic domain 5 (MD5, blue circles). See also Figure S1 and Movie S1.

Cdc25^string Dynamics Controls the Timing of Entry into Mitosis

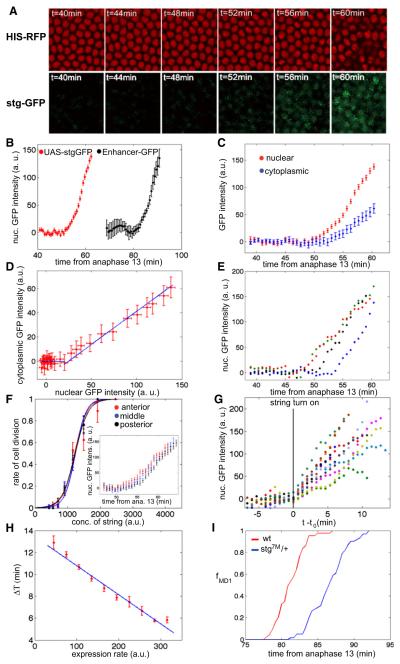
The wave-like pattern of initial cdc25^string expression does not explain the remaining variability in division pattern and does not provide insight into how Cdc25^string ultimately controls entry into mitosis. To investigate the relationship between mitotic entry and Cdc25^string levels, we used a Gal4/UAS expression system to drive Cdc25^stringGFP uniformly in the embryo. Under our experimental conditions, Cdc25^stringGFP begins to accumulate uniformly in all cells ~50 min after the 13^th anaphase (Figures 3A and 3B and Movie S3) preceding the time when endogenous Cdc25^string is first detectable by about 20 min (Figures 2C and 3B). Cdc25^stringGFP accumulates proportionally in the cytoplasm and inside nuclei (Figures 3C and 3D), indicating that measurements of nuclear concentrations are proportional to cytoplasmic and cellular concentrations.

Figure 3. Cdc25^string Dynamics Controls Entry into Mitosis.

(A) Confocal images of His2Av-RFP and UAS-Cdc25^stringGFP (stgGFP) embryo.

(B) Average expression of UAS-Cdc25^stringGFP and of stgenh-GFPNLS reporter as a function of time from anaphase 13 (the two data sets are from two separate embryos).

(C) Nuclear and cytoplasmic concentration of Cdc25^stringGFP as a function of time from anaphase 13 (average of all the cells).

(D) Correlation between nuclear and cytoplasmic concentration derived from (C).

(E) Quantification of fluorescence intensity for individual cells.

(F) Rate of cell division as a function of Cdc25^stringGFP concentration for cells in different positions along the anterior-posterior axis. Inset shows the average expression of UAS-Cdc25^stringGFP for cells in different positions along the anterior-posterior axis.

(G) Quantification of fluorescence intensity of UAS-Cdc25^stringGFP for individual cells with time rescaled to the beginning of Cdc25^stringGFP accumulation (stg turn on, t₀).

(H) Correlation between ΔT (see Figure 2 for a definition) and the average expression rate of UAS-Cdc25^stringGFP.

(I) Fraction of cells that have divided inside mitotic domain 1 as a function of time from anaphase 13 for WT embryos (red line) and embryos heterozygous for cdc25^string (blue line). Each curve is the average of data from five different embryos. Error bars are standard error of the mean. See also Figure S2 and Movie S2.

Uniform Cdc25^stringGFP expression overrides the more complicated spatiotemporal pattern of endogenous Cdc25^string and all ectodermal cells in the embryo enter mitosis at about the same time (Movie S2). Similar results have been reported by Edgar and O’Farrell (1990). Because Gal4 levels vary between embryos, there is some variability in the rate of Cdc25^string accumulation and, consequently, in when cell division occurs (Figure S2J). Approximately half of the embryos express Cdc25^string at level similar to WT, so that the interval from the beginning of Cdc25^stringGFP accumulation to mitosis is similar to the interval between GFP accumulation and mitosis observed for the previously described reporter strains for mitotic domains 1 and 5 (Figure 3B). We restrict our analysis to these cases.

Using algorithms to track nuclei, measure fluorescence in individual cells (Figure 3E, n = 198) and to reconstruct the total concentration of Cdc25^stringGFP from the fluorescence measurements (see Experimental Procedures, Supplemental Experimental Procedures, and Figure S2) we find that in a given embryo cells in different positions along the anterior-posterior axis accumulate Cdc25^stringGFP at the same rate and respond very similarly to expression of Cdc25^stringGFP (Figure 3F and Experimental Procedures). To determine if variability in the timing of mitotic entry correlates with the rate of accumulation of Cdc25^stringGFP, we plot the duration of the period from the beginning of Cdc25^string accumulation to mitotic entry (defined as ΔT) as a function of the Cdc25^stringGFP accumulation rate. We find that ΔT varies subtly in individual cells and correlates inversely with the rate of Cdc25^stringGFP accumulation in that cell (Figures 3G and 3H). We also analyzed the timing of cell division in wild-type (WT) embryos and embryos heterozygous for cdc25^string (see Experimental Procedures). We detected a delay of ~5 min in the timing of cell division in embryos heterozygous for cdc25^string compared to WT embryos (Figure 3I), supporting the observation that Cdc25^string accumulation rate determines the timing of cell division. These results argue that the dynamics of Cdc25^string accumulation may account for the remaining variability in the control of entry in mitosis.

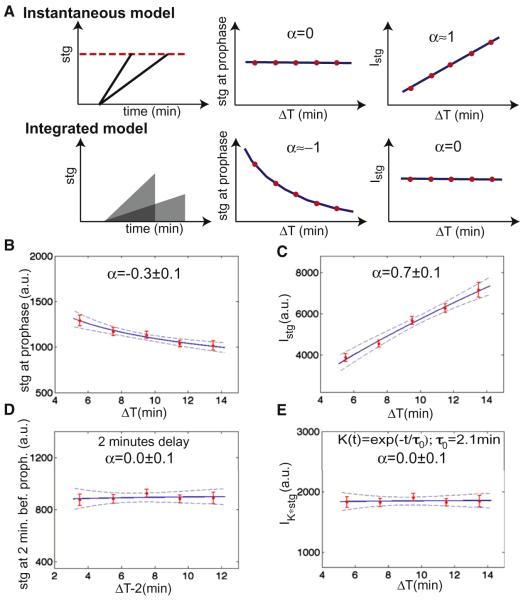
We then use this variability to investigate how Cdc25^string controls mitotic entry. We consider two simple models: mitotic entry might be triggered instantaneously in a given cell once Cdc25^string levels reach a specific threshold, or Cdc25^string activity might be integrated over time to regulate mitosis (Figure 4A). An instantaneous model predicts that the value of Cdc25^string at entry into mitosis is the same for all the cells independently of ΔT, whereas the integral is an increasing function of ΔT (that should scale linearly with ΔT). An integrated model predicts that the integral of Cdc25^string should be a constant, whereas the value of Cdc25^string at entry into mitosis should scale approximately as ΔT⁻¹. We measured the correlation between the concentration of Cdc25^string at the time of mitotic entry and the interval ΔT (Figures 4B and S3). We also measured the correlation between the integral of Cdc25^string concentration from the beginning of accumulation and the interval ΔT (Figures 4C and S3). Neither the instantaneous model, nor integrating levels from the beginning of expression can account for the control of entry into mitosis (Figures 4B and 4C and S3). The decision of entering mitosis can be fitted by an instantaneous model assuming that for each cell there is a 2 min delay between the decision of entering mitosis and chromosome condensation (Figures 4D and S3). An equivalently good fit is obtained if cells integrate the concentration of Cdc25^stringGFP over timescales of ~2 min to make their decision of entering mitosis (Figure 4E; integration time = 2.1 ± 0.9min, see Figure S3). We favor the short-term integration model for reasons that we will elucidate below.

Figure 4. Two Models for the Control of Entry into Mitosis.

(A) Correlation analysis to distinguish between an instantaneous and an integrated model for cell cycle control. Data were fitted with the function AΔT^α (predicted value of α are reported; dashed lines are 95% confidence intervals on the fit).

(B) Concentration of Cdc25^string at the time of chromosome condensation as a function of ΔT.

(C) Integral of the concentration of Cdc25^string as a function of ΔT.

(D) Concentration of Cdc25^string 2 min before chromosome condensation as a function of ΔT.

(E) Convolution between the concentration of Cdc25^string and an exponential kernel K(t) as a function of ΔT $(l_{k^{\ast }\mathit{stg}}={\int }_0^{\Delta T}\mathit{stg}(t^{\prime }\left)e^{-(\Delta T-t^{\prime })∕{\tau }_0}{\mathit{dt}}^{\prime }\right)$, where t = 0 is the beginning of Cdc25^string accumulation. Error bars are standard error of the mean. See also Figure S3.

The Decision of Entering Mitosis Depends on Cdc25^string in an Ultrasensitive Manner

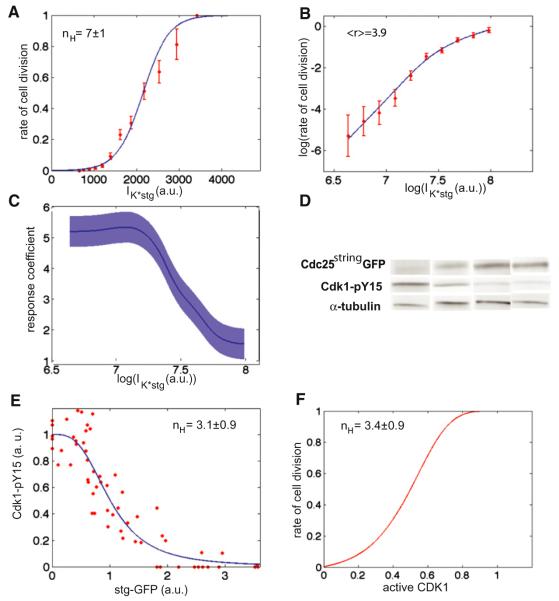
To gain further insights into the molecular mechanisms by which Cdc25^string regulates the cell cycle, we analyzed how the rate of cell division is determined by the “short-term” integrated concentration of Cdc25^string: I_K*stg. Similar results are obtained using Cdc25^string concentration (or the concentration 2 min before chromosome condensation, Figure S4). In all cases, we find that Cdc25^string controls entry into mitosis in an ultrasensitive manner (Figure 5A).

Figure 5. Cdc25^string Controls Entry into Mitosis and Cdk1 Activation in a Switch-like Manner.

(A) Rate of cell division as a function of I_K*stg. The fit gives an apparent Hill coefficient n_H = 7 ± 1.

(B) Log-log plot of the rate of cell division as a function of I_K*stg.

(C) Response coefficient r as a function of I_K*stg.

(D) Detection of Cdc25^stringGFP and Cdk1-pY15 by western blot of individual embryos.

(E) Quantification of Cdk1-pY15 amount as a function of Cdc25^stringGFP (stgGFP) amount. The line is a Hill function with coefficient n_H = 3.1 ± 0.9.

(F) Rate of cell division as a function of Cdk1 activity. This dependency was derived using the dependency of the rate of cell division (A) and of Cdk1 activity (D) on Cdc25^string concentration (a relation between the two different measurements of Cdc25^string was inferred by measuring Cdc25^stringGFP and Cdk1-pY15 levels in embryos in which approximately half of the cells were in mitosis). Error bars are standard error of the mean. See also Figure S4.

We used two standard procedures to obtain quantitative parameters describing the ultrasensitive control of mitosis by Cdc25^string. In the first procedure, we fit the rate of cell division with a logistic function and then estimate the values of Cdc25^string concentration at which the rate of cell division is 0.1 (S_0.1) and 0.9 (S_0.9). We then use these two numbers (Koshland et al., 1966) to determine an apparent Hill coefficient:

$$n_H=\frac{\log \left(81\right)}{\log \left(\frac{S_{0.9}}{S_{0.1}}\right)}$$

Apparent Hill coefficients close to 1 are indicative of a hyperbolic response, whereas coefficients much larger than 1 indicate ultrasensitivity. We also use an alternative definition of sensitivity (Fell, 1992). Given a system for which one measures how a quantity y depends on a signal S, one can define the response coefficient, r, as:

$$r=\frac{d\log \left(y\right)}{d\log \left(S\right)}=\frac{\mathit{Sdy}}{\mathit{ydS}}$$

For a linear system: r = 1, whereas ultrasensitive systems are characterized by r > 1.

We find that the rate of division moves from 0.1 to 0.9 over a change in I_K*stg of only 1.95, giving an apparent Hill coefficient: n_H = 7 ± 1 (Figure 5A) and by an average response coefficient (<r > = 3.9) much larger than 1 (r range: 1.5–5.3, Figures 5B and 5C).

Part of the ultrasensitivity reflects the direct effect of Cdc25^string on the phosphorylated state of Cdk1. We characterized how Cdc25^string activates Cdk1, performing western blots of 59 individual embryos expressing uniform UAS-Cdc25^stringGFP to measure the amount of inactive Cdk1, i.e., Cdk1-pY15, as a function of Cdc25^stringGFP levels (Figure 5D). The amount of Cdk1-pY15 decreases sharply as the concentration of Cdc25^stringGFP increases (Figure 5E), indicating that Cdc25^string activates Cdk1 in an ultrasensitive manner. Activation of Cdk1 by Cdc25^string can be well described by a Hill function with a coefficient n_H = 3.1 ± 0.9 (Figure 5E). We attribute the remaining switch-like behavior of the division to a nonlinear dependency on Cdk1 activity (apparent Hill coefficient = 3.4 ± 0.9) (Figure 5F).

Ultrasensitive Control of Mitosis Does Not Require Positive Feedback

The phosphorylated state of Cdk1 depends on the balance between the phosphatase activity of Cdc25 and the kinase activity of Wee1, responsible for the inhibitory phosphorylation of Cdk1. Both Cdc25 and Wee1 are thought to be subject to feedback (see Introduction). To test the role of these feedbacks in the ultrasensitivity of the response, we constructed transgenic flies expressing mutant Cdc25^string and Wee1 (Cdc25^string-9AGFP and Wee1-9ACFP both under the control of the Gal4/UAS system) in which the Cdk1 consensus sites were mutated (S/TP mutated to AP). Mutation of Cdk1 consensus sites have been shown to affect the feedback between Cdk1 and Cdc25^string in Xenopus and mammalian cells (Izumi and Maller, 1993; Strausfeld et al., 1994) and the feedback between Cdk1 and Wee1 in Xenopus and budding yeast (Harvey et al., 2011; Kim et al., 2005; Okamoto and Sagata, 2007).

To analyze if the phosphorylatable and nonphosphorylatable forms of both proteins are functional and if mutation of the Cdk1 consensus sites altered the activity of Cdc25^string and Wee1 as expected, we analyzed the effect of zygotic expression of these proteins. Zygotic overexpression of both Wee1-CFP and Wee1-9ACFP cause delays in the timing of mitotic domains (Figures 6A and 6B), indicating that both proteins are functional. Wee1-9ACFP overexpression causes a longer delay than overexpression of Wee1-CFP (Figure 6B), as expected because mutation of the Cdk1 consensus sites should prevent Cdk1-dependent inactivation of Wee1 (Kim et al., 2005; Okamoto and Sagata, 2007). When expressed zygotically Cdc25^string-9AGFP induced uniform mitoses in a manner similar to Cdc25^string (Movies S3 and S4), indicating that this mutant form is functional. The mutant probably impairs the ability of Cdk1 to phosphorylate and activate Cdc25^string, as Cdc25^string-9AGFP is less effective than Cdc25^stringGFP at driving mitosis in the presence of high levels of Wee19A-CFP (Figures 6C and 6D; to avoid complication from expression of endogenous Cdc25^string, we analyzed the mitotic timing in amnioserosa cells, which never express cdc25^string and thus normally never divide after the completion of cellularization).

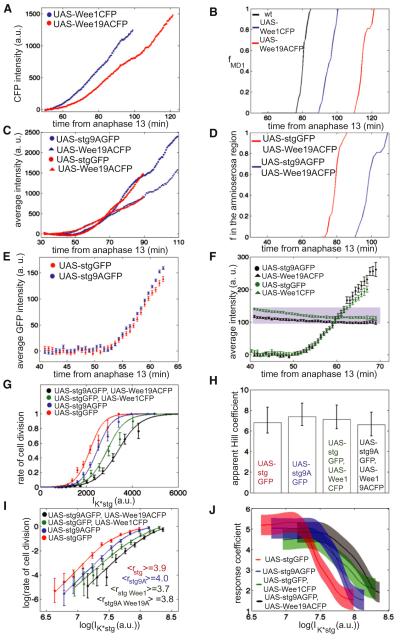
Figure 6. Switch-like Control of Mitotic Entry Is Independent of Feedbacks.

(A) Fluorescence intensity of zygotically expressed UAS-Wee1CFP (blue points) and UAS-Wee19ACFP (red points) as a function of the time from anaphase 13.

(B) Fraction of UAS-Wee1CFP (blue line), UAS-Wee19ACFP (red line), and WT (black line) cells that have divided inside mitotic domain 1 as a function of time from anaphase 13.

(C) Fluorescence intensity of zygotically expressed UAS-Wee19ACFP UAS-Cdc25^stringGFP (red triangles and circles, respectively) and UAS-Wee19ACFP UAS-Cdc25^string9AGFP (blue triangles and circles, respectively) as a function of the time from anaphase 13.

(D) Fraction of UAS-Wee19ACFP UAS-Cdc25^stringGFP (red line) and UAS-Wee19ACFP UAS-Cdc25^string9AGFP (blue line) cells that have divided in the amnioserosa region as a function of the time from anaphase 13.

(E) Average expression of UAS-Cdc25^stringGFP (red circles) and of UAS-Cdc25^string9AGFP (blue circles) as a function of time from anaphase 13.

(F) Average expression of UAS-Cdc25^stringGFP (green circles), UAS-Wee1CFP (green squares), UAS-Cdc25^string9AGFP (black circles), and UAS-Wee19ACFP (black squares) as a function of time from anaphase 13. Shaded region indicates the expression levels of endogenous Wee1.

(G) Rate of cell division as a function of I_K*stg (UAS-Cdc25^stringGFP, red circles; UAS-Cdc25^stringGFP UAS-Wee1CFP green circles; UAS-Cdc25^string9AGFP, blue circles; UAS-Cdc25^string9AGFP, UAS-Wee19ACFP, black circles).

(H) Bar graph reporting the apparent Hill coefficients for all four data sets reported in (G).

(I) Log-log plot of the rate of cell division as a function of I_K*stg (UAS-Cdc25^stringGFP, red circles; UAS-Cdc25^stringGFP, UAS-Wee1CFP, green circles; UAS-Cdc25^string9AGFP, blue circles; UAS-Cdc25^string9AGFP, UAS-Wee19ACFP, black circles). The numbers reported in the graph are the average response coefficients.

(J) Response coefficient r as a function of I_K*stg for all four data sets reported in (I). Error bars are standard error of the mean, with exception of (H) where the 95% confidence interval is reported. See also Figure S5 and Movies S3, S4, S5, and S6.

To test the effect of the mutants on ultrasensitivity under physiological conditions, we selected embryo expressing Cdc25^stringGFP and Cdc25^string-9AGFP at similar rate (and at a rate similar to WT; see Figures 3D and 6E) and compared the dependency of the rate of cell division on the concentration of either form of Cdc25^stringGFP. Control of mitotic entry has a similar ultrasensitive dependency on Cdc25^stringGFP and Cdc25^string-9AGFP (apparent Hill coefficients ≈7 ± 1, average response coefficients ≈4 ± 1 for both curves; Figures 6G and 6J, S4 and S5, and Movie S4, N_stgGFP = 198 and N_stg9AGFP = 233), indicating that the positive feedback between Cdc25^string and Cdk1 is not required for switch-like entry into mitosis. A slightly higher concentration of Cdc25^string-9AGFP (12%) is required for entry into mitosis.

To test the properties of the mitotic switch in the absence of both feedbacks, we analyzed the control of mitosis in embryos expressing Wee1CFP and Cdc25^stringGFP or Wee1-9ACFP and Cdc25^string-9AGFP at levels similar to WT (Figure 6F; these embryos also express endogenous Wee1). We selected embryos that express Wee1CFP (or Wee1-9ACFP) only maternally and also express Cdc25^stringGFP (or Cdc25^string-9AGFP) zygotically. In these conditions, Wee1CFP (or Wee1-9ACFP) concentration is almost constant during cycle 14, whereas Cdc25^stringGFP (or Cdc25^string-9AGFP) accumulates as observed previously (Figure 6F). The rate of cell division shows a similar ultrasensitive dependency on Cdc25^string and Cdc25^string9A in embryos that express Cdc25^string and Wee1 or Cdc25^string9A and Wee19A (apparent Hill coefficients ≈7 ± 1, average response coefficients ≈4 ± 1 for both curves; Figures 6G–6J, S4 and S5, and Movies S5 and S6, N_{stgGFPWee1CFP} = 148 and N_{stg9AGFPWee19ACFP} = 110). The concentration of Cdc25^string-9AGFP required for entry into mitosis in embryos expressing both mutant proteins is slightly higher (17%) than the concentration of Cdc25^stringGFP in embryos expressing both WT proteins (Figures 6G and S4). We interpret this shift (compatible with the existence of feedback; see also Figures 6A–6D) as a minor change in the properties of cell cycle control. These results, therefore, argue that switch-like activation of mitosis in response to Cdc25^string expression does not require any feedback mechanism between Cdk1 and Cdc25 and/or Wee1.

An Out-of-Equilibrium Covalent Modification Cycle Can Explain Feedback-Independent Ultrasensitivity

In the absence of feedbacks, the control of Cdk1 activity by Cdc25^string and Wee1 resembles a simple covalent modification cycle in which Cdk1 exists in unmodified and modified forms with the interconversion catalyzed by two converter enzymes (Cdc25^string and Wee1). An important question is how such a covalent modification cycle can produce switch-like changes in Cdk1 activity in the absence of feedbacks.

Although covalent modification cycles are widespread in signaling modules (Kholodenko, 2006), their properties have largely been analyzed at steady state where, in the absence of feedback loops, the cycle gives a hyperbolic activation of the substrate if the enzymes operate in the first-order regime but a switch-like activation if the enzymes are saturated (zero-order ultrasensitivity) (Goldbeter and Koshland, 1981). To investigate which regime might be relevant during activation of Cdk1, we measured the concentrations of Cdk1, Cdc25^string, and Wee1, because in zero-order kinetics substrate concentration should be in excess relative to that of enzymes and to the K_m of enzyme/substrate reaction (Goldbeter and Koshland, 1981). Using western blots of embryos and recombinant proteins we estimated the concentration of Cdk1 to be 240 ± 24 nM (Figure 7A), Cdk1 is saturated with cyclins in G2 of cycle 14 as indicated by its complete modification and the fact that Wee1-dependent phosphorylation requires cyclin association (Edgar et al., 1994b; Parker et al., 1991; Solomon et al., 1990). We, therefore, assume that the measured Cdk1 concentration approximates well the concentration of cyclin-bound Cdk1.

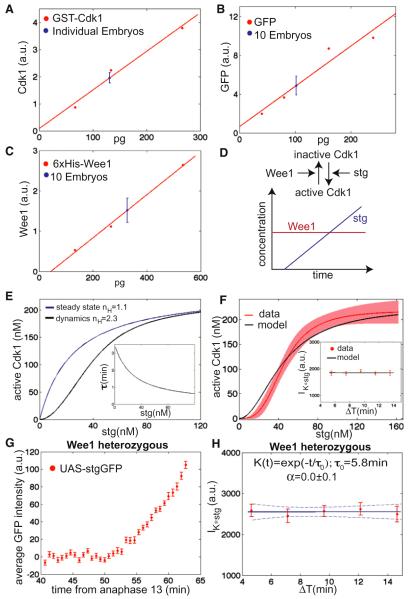
Figure 7. A Covalent Modification Cycle Operating Out-of-Equilibrium and as a Short-Term Integrator Controls Entry into Mitosis.

(A) Quantification of western blot of individual embryos and recombinant GST-Cdk1.

(B) Quantification of western blot of ten UAS-Cdc25^stringGFP embryos and recombinant GFP. Fraction of inactive Cdk1 (Cdk1-pY15) was measured comparing the ratio of Cdk1-pY15 over tubulin to the same ratio measured in embryos in G2 of cycle 14 (mid cellularization).

(C) Quantification of western blot of ten embryos in G2 of cycle 14 and recombinant 6xHis-Wee1.

(D) Schematic representation of the mathematical model.

(E) Simulations of Cdk1 activation by a covalent modification cycle controlled by Cdc25^string and Wee1. Inset shows the response time (τ) as a function of Cdc25^string concentration.

(F) Measured (Figure 5D) and simulated Cdk1 activation as a function of Cdc25^string concentration (shaded region indicates the 95% confidence interval of the fit of the experimental data). Inset shows I_K*stg (as defined in Figure 4) as a function of ΔT for experimental data and numerical simulations.

(G) Average nuclear intensity of UAS-Cdc25^stringGFP as a function of time from anaphase 13 for an embryo heterozygous for wee1.

(H) I_K*stg (computed using an integration time τ₀ = 5.8 min) as a function of ΔT for the wee1 heterozygous embryo. Dashed lines are 95% confidence intervals on the fit. Error bars are standard error of the mean.

The concentrations of Wee1 (50 ± 10 nM) and Cdc25^string (45 ± 10 nM, measured under conditions when half of Cdk1 is active) are only 5-fold lower than that of their substrate Cdk1 (Figures 7A–7C). Whether this is enough for zero-order ultrasensitivity depends on the enzymatic properties (K_m) of Cdc25^string and Wee1. Estimates for human Cdc25s suggest that the measured concentration of Cdk1 is much lower than the K_m for the Cdc25/Cdk1 reaction (K_m > 1 μM; see Experimental Procedures). These results imply that the dynamics of Cdk1 activation by Cdc25^string should be well described by first-order kinetics. We lack precise measurements of the enzymatic properties of Wee1. However, as the concentration of Cdk1 is relatively low it is likely that Wee1 phosphorylation of Cdk1 also operates in the first-order regime. We, therefore, suggest that both enzymes operate in the first-order regime and that switch-like activation of Cdk1 cannot be attributed to zero-order kinetics.

One special feature of cell cycle control in Drosophila gastrula is that mitotic entry is driven by rapid accumulation of Cdc25^string and may not be near equilibrium. To take this into account, we built a mathematical model of Cdk1 activation consisting of a covalent modification cycle in which Cdc25^string is accumulating over time (Figure 7D). The unknown parameters of the model, relevant in the first-order regime, are the k_cat/K_m of Wee1 and Cdc25^string. Using the data of Cdk1 activation (Figure 5D) and numerical simulations, we estimated these parameters (Wee1: k_cat/K_m = 10⁵ M⁻¹s⁻¹, Cdc25^string: k_cat/K_m = 2 × 10⁵ M⁻¹s⁻¹). Simulations of the model using these parameters indicate that the rapid accumulation of Cdc25^string can produce switch-like activation of Cdk1 even when operating in the first-order regime (Figure 7E). Linear response theory indicates that this is at least in part due to the fact that the response time decreases as Cdc25^string concentration increases (see below, Figure 7E, and Supplemental Experimental Procedures). To compare the model to the experimental data of Cdk1 activation (Figure 5E), we simulated it using the measured variable rates (and times) of Cdc25^string accumulation (Figure 3). The model reproduces reasonably the curve of Cdk1 activation and the signaling properties of the mitotic switch (Figure 7F).

A Short-Term Integrator Controls Entry into Mitosis

The level of activated Cdk1 changes whenever the concentration of Cdc25^string and Wee1 vary, but these changes are not instantaneous. The time required for Cdk1 to respond to changes in the concentration of Cdc25^string and Wee1 reflects a property of the dynamical system controlling Cdk1 activity, termed response time (τ, Figure 7E). At every instant, the level of Cdk1 reflects in part its levels prior to the change and, therefore, the response time can be thought of as a time interval for temporal averaging. Tau can also be related to the typical time intervals that individual molecules of Cdk1 spend in a given phosphorylation state (see Supplemental Experimental Procedures). From the standpoint of cellular decision-making, the response time is essentially analogous to an integration time, as shown by numerical simulations (Figures 7E and 7F).

Because the response time is determined by the time required for Cdc25^string and Wee1 to act on Cdk1, it should depend on the concentrations of Cdc25^string and Wee1. In the first-order regime the response time of a covalent modification cycle is well approximated by the expression: τ = (k_wee1[Wee1] + k_Cdc25[Cdc25])⁻¹, where k_Wee1 and k_Cdc25 are the k_cat/K_m of Wee1 and Cdc25 (Detwiler et al., 2000; Gomez-Uribe et al., 2007). The model, therefore, predicts that it should be possible to change the response time (and as a consequence the integration time) by altering the levels of Wee1 (and as a result the levels of Cdc25^string required for mitosis). Using embryos heterozygous for wee1, we analyzed the dependency of the integration time on Wee1 levels. The integration time is significantly increased in such embryos (Figures 7G and 7H, integration time = 5.8 ± 1.2 min) compatibly with the predictions of the model. Such an increase argues against a delay between the decision of entering mitosis and detectable chromosome condensation (which should only depend on pathways downstream of Wee1 and Cdc25^string). We also observe that the integration time is similar in embryos with or without feedback and slightly reduced by increase in Wee1 concentration as expected (Figure 8). This suggests that feedback does not play a role in setting the integration time and is unlikely to explain the change in integration time observed in wee1 heterozygous embryos. Based on the above results, we propose that a short-term integrator controls the decision of entering mitosis and that the integration time is set by the time required for Cdk1 to respond to changes in Cdc25^string.

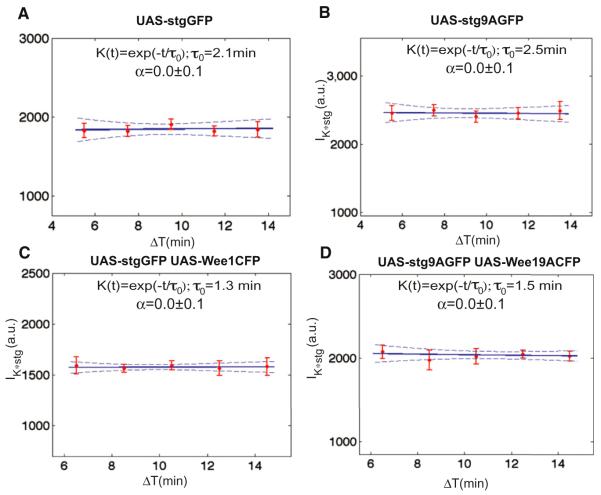
Figure 8. The Integration Time Does Not Depend on Positive Feedback.

Convolution between the concentration of Cdc25^string and an exponential kernel K(t) as a function of ΔT $(l_{k^{\ast }\mathit{stg}}={\int }_0^{\Delta T}\mathit{stg}(t^{\prime }\left)e^{-(\Delta T-t^{\prime })∕{\tau }_0}{\mathit{dt}}^{\prime }\right)$ for UAS-Cdc25^stringGFP (A), UAS-Cdc25^string9AGFP (B), UAS-Cdc25^stringGFP UAS-Wee1CFP (C), and UAS-Cdc25^string9AGFP UAS-Wee19ACFP (D). The data are from the same embryos shown in Figure 6. Expression of either Cdc25^string or Cdc25^string9A produces comparable integration times. Compare (A) and (B) integration times: 2.1 ± 0.9 min and 2.5 ± 0.9 min, respectively. The integration time decreases with ectopic Wee1 expression (compare C and D with A and B), but is very similar in embryos expressing either the WT and mutant Wee1 protein (integration times: 1.3 ± 0.7 min and 1.5 ± 0.8 min respectively), indicating that the relative contribution of positive feedback is minor compared to the contribution of the balance between the two components. Error bars are standard error of the mean, dashed lines are 95% confidence interval on the fit.

DISCUSSION

Control of Mitotic Entry by Cdc25^string

During Drosophila gastrulation, transcriptional activation of cdc25^string is associated with entry into mitosis (Edgar and O’Farrell, 1989, 1990). Here, we have investigated how Cdc25^string accumulation results in abrupt switch-like activation of Cdk1 and entry into mitosis. The time interval between cdc25^string transcriptional activation and entry into mitosis is controlled by the rate of Cdc25^string expression. The concentration of Cdc25^string integrated over 2 min is the quantity that best correlates with the decision of entering mitosis and such integration time might be determined by the response time of Cdk1 activity to changes in Cdc25^string concentration.

Two ultrasensitive steps (activation of Cdk1 by Cdc25^string and entry into mitosis by Cdk1) control mitosis. Such a cascade can provide high ultrasensitivity from two moderately ultrasensitive steps. Positive feedback does not play an important role in the control of entry into mitosis in the Drosophila gastrula and we propose that the ultrasensitivity is rather due to the out-of-equilibrium properties of the covalent modification cycle controlling Cdk1. We observe that feedback mechanisms are conserved in Drosophila as it can be shown that mutants (Cdc25^string9A and Wee19A) that disable feedbacks have the expected effects on cell cycle control when overexpressed. This raises the question of why feedbacks do not play a role in WT cells. We propose that activation of mitosis in Drosophila is too rapid for feedback to make a significant contribution to Cdk1 activation. In Xenopus egg extract, positive feedback introduces a 10 min delay between the accumulation of cyclin to a critical threshold concentration and the activation of Cdk1 (Solomon et al., 1990). This delay has been interpreted as the time required to activate the feedback mechanism (Deibler and Kirschner, 2010; Solomon et al., 1990). Controlling entry into mitosis through rapid accumulation of Cdc25^string is, therefore, likely to make the contribution of feedback irrelevant. When Cdc25^string9A (Cdc25^string) and Wee19A (Wee1) are overexpressed, the time between Cdc25^string activation and mitosis can become significantly longer providing enough time for feedback to contribute to activation of Cdk1. We speculate that the molecular network controlling entry into mitosis is highly flexible (O’Farrell, 2001) and can operate as cyclin-driven switch dependent on feedback or as Cdc25-driven switch with the properties described in this article. These two different strategies to control the cell cycle might reflect different selective pressures on the control of mitosis and might be utilized at different stages during development.

Precise Control of the Timing of Cell Divisions during Embryonic Development

The control of cell division during Drosophila gastrulation provides an extraordinary example of the temporal precision with which cell behaviors can be timed during embryonic development (Foe, 1989). This precision might be required to avoid incompatible cell behaviors that might easily arise due to the fast timescales of Drosophila embryonic development (Johnston, 2000). We suggest that controlling entry into mitosis by transcriptional expression of cdc25^string rather than accumulation of cyclins avoids the possible delay due to activation of the positive feedback (Solomon et al., 1990). Such a delay might be incompatible with the precise control of cell divisions observed during Drosophila gastrulation. Positive feedback also has the potential of amplifying noise in the expression of cdc25^string and could in principle deteriorate the precision of cdc25^string transcriptional control. We speculate that Cdc25^string-driven switches similar to the one that we have described might be a preferred solution for the precise temporal control of mitosis (O’Farrell, 2001). Such switches, when operating as short-term integrators, have the ability to filter out the probably unavoidable fast fluctuations in the expression of cdc25^string.

Transcriptionally Driven Covalent Modification Cycle as a Mechanism to Precisely Control Cell Decisions

Covalent modification cycles are widespread signaling modules that can generate ultrasensitivity when operating in the zero-order regime (Goldbeter and Koshland, 1981; Kholodenko, 2006). Our theoretical work shows that transcriptionally driven covalent modification cycle can effectively generate an ultrasensitive response when they operate in the first-order regime as long as they are not close to steady state. In this regime, these cycles also display interesting signaling properties (Detwiler et al., 2000; Gomez-Uribe et al., 2007). They act as low-pass filters dampening fluctuations that happen on time scales faster than the response time (Detwiler et al., 2000; Gomez-Uribe et al., 2007). Effectively, they resemble short-term integrators with an integration time that is determined by the response time. Because the response time depends on the concentration of the two opposing enzymes, the filtering properties of the cycle can be easily tuned to the desired frequency (Detwiler et al., 2000; Gomez-Uribe et al., 2007). We propose that by driving the cycle with cdc25^string expression, Drosophila is able to achieve switch-like behavior while maintaining the robust filtering properties of covalent modification cycles. Positive feedback driven circuits that have similar integration properties and therefore achieve both ultrasensitive and precise control of cell decision might be much harder to design. We speculate that covalent modification cycles, triggered by transcriptional expression of the activating enzymes, might be a widespread strategy to obtain reliable and switch-like control of cell decisions.

EXPERIMENTAL PROCEDURES

Fly Stocks and Plasmids

Standard methods were used all throughout. To distinguish cdc25^string heterozygous embryos from WT embryos, we crossed His2Av-RFP females to males carrying the cdc25^string amorphic allele stg^7M53 on one chromosome and a cdc25^string enhancer driving GFP-NLS on the other. This cross produces WT embryos (GFP positive) and embryos heterozygous for cdc25^string (GFP negative).

Microscopy

Live imaging of His2Av-GFP embryos was performed on a CARV spinning disk confocal microscope (Nikon) using a X-Cite120Q light source and a CCD camera (Hamamatsu ORCA-ER). Images were acquired every 20 s. The other live imaging experiments were performed with a Leica SP5 confocal microscope, a 20×/0.7 numerical aperture glycerol-immersion objective, an argon ion laser and a 594-nm diode laser. Detection was performed using photomultiplier tubes. For embryos expressing GFP and RFP every acquired image was the average of 30 subsequent images (acquired with a scanning time slightly larger than 1 s for an image 1,024 × 512 pixels, giving a frame rate of 40 s). For embryos expressing CFP, GFP, and RFP every acquired image was the average of 20 subsequent images (acquired with a scanning time of about 2 s for an image 1,024 × 512 pixels, giving a frame rate of 40 s). Averaging was used to obtain a good signal-to-noise ratio and minimize photobleaching.

Image Analysis

Using MATLAB (MathWorks) we developed software to track nuclei and measure fluorescence intensity. Mitotic events were scored manually.

Data Analysis

The time of transcriptional activation of cdc25^stringenh-GFP (Figure 2) was evaluated using the method described in Skotheim et al. (2008).

We used the UAS/Gal4 system to uniformly express fluorescently tagged Cdc25^string or Cdc25^string9A (in some experiments coexpressed with Wee1 and Wee19A respectively) and obtain quantitative dynamical data on how the rate of entering mitosis depends on Cdc25^string dynamics. We imaged various embryos of the appropriate genotypes and obtained all our quantitative data from single embryos in order to avoid possible global differences between the embryos (e.g., different transcription\translation rates in different embryos). We developed an algorithm to segment and track individual nuclei. The number of cells analyzed for each genotype was: UAS-Cdc25^stringGFP 198 cells, UAS-Cdc25^string9AGFP 233 cells, UAS-Cdc25^stringGFP UAS-Wee1CFP 148 cells, UAS-Cdc25^string9AGFP UAS-Wee19ACFP 110 cells, UAS-Cdc25^stringGFP in wee1 heterozygous (see Figure 7) 173 cells.

The measured fluorescence intensity of Cdc25^stringGFP is not strictly proportional to its concentration because GFP does not mature instantaneously or on time scales significantly shorter than the time scale over which Cdc25^string accumulation controls entry into mitosis. Therefore, to estimate the concentration of Cdc25^stringGFP from the measured fluorescence traces (i.e., correct for the maturation time of GFP), we used the following mathematical model:

$$\begin{array}{cc}\hfill \frac{\mathit{ds}}{\mathit{dt}}=\beta \left(t\right)& -\frac{1}{\tau }s-\frac{1}{{\tau }_1}s\hfill \\ \hfill \frac{{\mathit{ds}}^{\ast }}{\mathit{dt}}=& \frac{1}{\tau }s-\frac{1}{{\tau }_1}{s}^{\ast }\hfill \end{array}$$

where s indicates immature Cdc25^stringGFP, s* indicates fluorescent Cdc25^stringGFP, τ describes the pseudo-first-order kinetics of GFP maturation (Heim et al., 1995; Sniegowski et al., 2005), τ₁ describes the degradation dynamics of Cdc25^stringGFP, assumed also to be first-order and β(t) indicates the translation rate of Cdc25^string.

The total amount of Cdc25^stringGFP, indicated as s_T, can be estimated from the measured fluorescence signal s* by the following expression: s_T = s + s* = s*(1 + (τ/τ₁)) + τ(ds^*/dt). Algebraic conversion yields: s_T ~ s* + γ(ds*/dt), where γ = ττ₁/(τ + τ₁). This equation implies that it is possible to infer Cdc25^string dynamics from the data without a detailed knowledge of the translation rate β(t) (note that: min (τ,τ₁)/2 ≤ γ ≤ min (τ,τ₁) and that γ = 0 min would correspond to not applying any correction to the measured intensities).

The measurement of Cdc25^stringGFP fluorescence intensity displayed appreciable variability (Figure S2A). We used the smoothing spline in MATLAB (De Boor, 2001) with a parameter p = 0.1 to obtain Cdc25^stringGFP intensity at any given time point rather than using the value directly measured. Figures S4A and S4B show that control of the cell cycle by Cdc25^string is switch-like regardless of the value of γ and thus very robust to changes in the parameters used to reconstruct Cdc25^stringGFP concentration. Similarly, it can be shown that our conclusion that positive feedback does not play an important role in the control of mitosis is also very robust to the parameters used to reconstruct Cdc25^string dynamics (Figure S5).

To determine the integration time for the decision to enter mitosis, we reconstructed the dynamics of Cdc25^string using various values of γ and then studied how the integration time depends on this parameter. We found that there is a small range of parameters (γ < 3.5 min, see Figures S3A and S3B) compatible with an instantaneous model. For larger values of γ, the integration time sharply increases to a plateau of about 3.5 min (Figures S3A and S3B). Effectively values of γ between 8 and 360 min predict integration times that differ by less than a factor two (1.8–3.5 min). These results suggest that, as long as γ is larger than 8 min, the integration time for the decision of entering mitosis should be ~2–3 min and that such estimate is very robust to changes in the parameters used to reconstruct Cdc25^string dynamics.

To estimate γ experimentally, we measured the maturation time of GFP and the lifetime of Cdc25^stringGFP (see Supplemental Experimental Procedures). We obtained a maturation time for GFP of 41 ± 6 min and a lifetime for Cdc25^string of 31 ± 4 min. From these estimates, we obtain γ = 18 ± 5 min (integration time = 2.6 ± 1.0, Figures S3A and S3B) and thus conclude that 2–3 min is a reasonable estimate of the integration time relevant for the decision of entering mitosis.

Binning was performed by separating data in nonoverlapping bins and plotting the mean and the standard error for each bin. The rate of cell division as function of × was defined as the probability that a cell that has not yet divided would divide at a given value of × (× indicates Cdc25^stringGFP or Cdc25^string-9AGFP). Operatively, we start from a histogram of × at entry into mitosis and then compute the ratio between the number of cells that divide within a given concentration interval and the total number of cells that had not divided yet. The error bars on the rate of cell division are standard errors, estimated assuming that the number of cells that divide within a given concentration interval follows a Bernoulli distribution.

For the analysis presented in Figure 3F, we separated cells in three subgroups according to their position along the anterior-posterior axis (anterior: cells occupying the region between 5% and 20%, middle: cells occupying the region between 43% and 58%, posterior: cells occupying the region between 80% and 95%).

Error bars for Hill coefficients and integration time represent 95% confidence intervals.

Western Blots

Standard methods (Maniatis et al., 1982) were used with the following primary antibodies: mouse anti-GFP antibody (1:1,000, Roche), rabbit anti-Cdk1pY15 antibody (1:1,000, Cell Signaling), Cdk1 p34(PSTAIRE) (1:200, Santa Cruz), mouse anti-αtubulin antibody (1:5,000, Sigma-Aldrich), and rat anti-Wee1 (1:1,000). A FluorChem HD2 system (AlphaInnotech) was used to image and quantify the signals from the chemiluminescence reactions.

Recombinant Proteins and Estimate of Cdc25 Enzymatic Properties

GST-Cdk1 was expressed in Escherichia coli and purified using the method described in Frangioni and Neel (1993). Wee1 protein was purified by GenScript, purified recombinant GFP was purchased from Clontech.

To estimate the enzymatic properties of Cdc25^string, we observe that the k_cat of human Cdc25s and of their catalytic domains has been measured for various substrates and is close to 1 s⁻¹ (Gottlin et al., 1996; McCain et al., 2002; Wilborn et al., 2001). Because on-rate for efficient enzymes range between 10⁵–10⁶ M⁻¹s⁻¹ (Chen et al., 2010), one can deduce that K_m = (k_cat + k_off)/k_on > 1 μM.

Antibody Production

Rat anti-Wee1 antisera were raised against purified full-length Wee1 protein by Panigen. Specificity of the antibodies was tested by comparing western blots of WT and wee1-null embryos.

Simulations

Differential equations describing the mitotic switch (Supplemental Experimental Procedures) were solved in MATLAB.