Evaluation of affine fiber kinematics in human supraspinatus tendon using quantitative projection plot analysis

Abstract

Structural constitutive modeling approaches are often based on the assumption of affine fiber kinematics, even though this assumption has rarely been evaluated experimentally. We are interested in applying mathematical models to understand the mechanisms responsible for the inhomogeneous, anisotropic, and non-linear properties of human supraspinatus tendon (SST); however, the relationship between macroscopic and fiber-level deformation in this tendon remains unknown and current methods for making this assessment are inadequate. Therefore, the purpose of this study was to develop an improved method for quantitatively assessing agreement between two distributions and to examine the affine assumption in SST by comparing experimental fiber alignment to affine model predictions using this analysis approach. Measured fiber angle values of SST samples in uniaxial tensile tests were compared with predictions of affine fiber deformation using modified projection plots, which provide a method for qualitative and quantitative comparisons of two distributions. The projection plot metrics of offset and range, which were developed in this study, are of particular benefit by providing a quantitative representation of agreement that can be subjected to statistical comparisons. For SST, offset and range values varied by tendon location and test orientation, with more affine deformation evidenced for tendon regions of higher alignment. Results suggest that non-affine fiber behavior is dependent on specific tissue, orientation of the applied stretch relative to the fiber organization, and length scale of the observation. In addition, this study has established a method for evaluating the affine assumption in other tissues.

1 Introduction

Mathematical modeling approaches are frequently used to characterize and predict the mechanics of biological soft tissues. Structurally based continuum models, which describe the relationship of the constituents’ properties (i.e., collagen fibers, matrix) to overall tissue properties, require knowledge of the relationship between microscopic (fiber) and macroscopic (tissue) deformation. The most common and straightforward approach is the use of an affine model, which assumes that local fiber kinematics follow the macroscopic tissue deformation. In other words, the affine assumption posits that each fiber is subjected to stretch and rotation that is the tensor transformation of the overall tissue strain field. Although affine fiber kinematics are frequently assumed in constitutive model approaches, very few studies have evaluated the affine assumption empirically. As a result, its validity in most modeling studies remains largely unknown and untested. Importantly, the few studies that have examined this assumption reported non-affine fiber behavior in fiber-reinforced soft tissue testing (Billiar and Sacks 1997; Hepworth et al. 2001; Gilbert et al. 2006; Guerin and Elliott 2006). Taken together, the limited number of studies that have evaluated fiber kinematics during soft tissue testing, and the evidence for non-affine kinematics presented in those few studies that have, indicates that the relationship between macroscopic deformation and fiber-level kinematics is poorly understood. Further investigation is necessary to determine whether the frequently used affine assumption is valid.

The most common analysis approach for determining whether fiber kinematics are affine consists of comparing two distributions of fiber orientation angles: (1) the experimentally measured angles of fibers under an applied strain and (2) the affine-predicted angles calculated by applying the macroscopic strain field to the undeformed angle distribution. An important consideration in this analysis is the use of an appropriate comparison technique and statistical approach. Qualitatively, raw distributions can be compared visually or data can be plotted using cumulative distribution functions. While several studies have made these types of qualitative comparisons (Billiar and Sacks 1997; Stella et al. 2008; Guerin and Elliott 2006), such an approach is limited in scope because it lacks a quantitative or statistical comparison that describes the degree to which distributions differ. The simplest quantitative method is a comparison of mean and standard deviation values; however, unless both distributions follow a normal distribution, these metrics can be misleading. The two-sample Kolmogorov–Smirnov test (Massey 1951) presents an appropriate statistical analysis; however this test’s high sensitivity may detect differences that are too small to have physiological meaning and, importantly, this statistical test only indicates whether two distributions differ but not how they differ. Another approach is the use of quantile–quantile (Q-Q) plots, which are created by plotting quantile-grouped data for the two distributions on opposing axes (Wilk and Gnanadesikan 1968). Advantages of Q-Q plots are that there are no assumptions about distribution shape and no data smoothing, and the graphs present comparisons of location, spread, and shape of two distributions simultaneously. A further development of this approach was achieved with projection plots (Jones 1997), where quantile differences are plotted against average quantile values. Projection plots retain all the advantages of Q-Q plots but are better suited for quantitative analysis since they provide a symmetric treatment of data on the x- and y-axes. As initially proposed, projection plots, which allow for the assessment of agreement between two data sets similar to Bland–Altman plots (Bland and Altman 1986), were assessed in a mostly qualitative manner. In this study, we have modified projection plots to include two metrics (offset and range) to quantify agreement between distributions and used these plots to evaluate the affine assumption in test samples of human supraspinatus tendon, one of the tendons of the rotator cuff in the shoulder.

The biomechanics of the supraspinatus tendon (SST) is of significant interest due to a high rate of degeneration and injury and its poor healing capacity. In addition, the inhomogeneous, anisotropic, and non-linear properties of this tissue suggest that a mathematical model could be of great use in further quantifying the interrelationships between its structural organization and tensile mechanical behavior. Our recent work quantified the mechanical and organizational properties of human SST in uniaxial tensile testing (Lake et al. 2009, 2010). Highly inhomogeneous collagen fiber alignment in SST, including regions of very disperse fiber orientation unique to this tendon, was found to correlate significantly with modulus values of samples tested in the longitudinal and transverse directions. While several regions of SST demonstrated strong anisotropy typical of other tendons, surprisingly, superior regions near the tendon to bone insertion demonstrated mechanical planar isotropy. In an effort to elucidate the structural mechanisms responsible for these mechanical properties, our group has evaluated different formulations of structurally based fiber dispersion models by incorporating fiber alignment using angular integrals or generalized structure tensors (Cortes et al. 2010). To date, however, the relationship between macroscopic and fiber-level deformation (i.e., whether local deformation is affine) in this tendon remains unknown. This is of vital importance in developing an appropriate model formulation for SST, since many models assume affine fiber kinematics. Therefore, the purpose of this study was to develop a modified projection plot method for quantitatively assessing agreement between two distributions and to examine the affine assumption in human SST fiber kinematics by comparing experimentally measured fiber alignment to affine model-predicted distributions.

2 Methods

2.1 Sample preparation

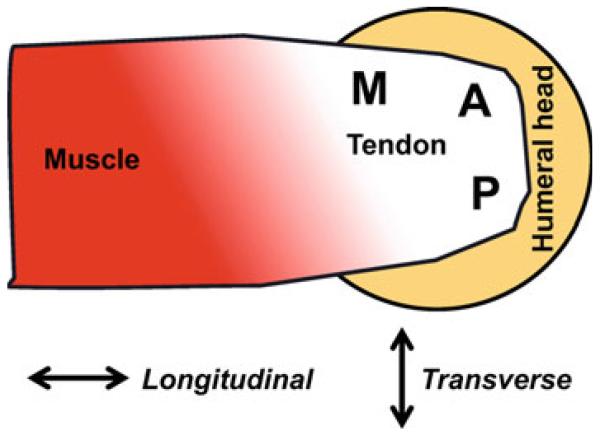
Human supraspinatus tendons (SST) were dissected from cadaver shoulders (n = 27; average age = 55.7 ± 13.8 years) and subjected to tensile mechanical testing and structural analysis using polarized light imaging. The methods and results of this experimental testing have been published previously (Lake et al. 2009, 2010); however, brief summaries are provided here to provide sufficient background to clarify the novel aspects of the current study, namely the utilization of these experimental data to assess the validity of the affine assumption in SST. Full-thickness rectangular samples (20 mm × 5 mm) were cut from three different locations across the length-width of the SST, which were defined as anterior (A), posterior (P), and medial (M). From each of these, the outer fascia of the top and bottom surfaces was removed and thin samples (~400 μm thick) representing the bursal (B) and joint (J) layers of the tendon were cut using a sliding stage cryomicrotome, yielding a total of six test samples from each SST (Fig. 1). The cross-sectional area (CSA) of each sample was measured with a laser-based device (Favata 2006).

Fig. 1.

Superior view of the musculotendinous supraspinatus anatomy (right shoulder shown); samples were harvested from anterior (A), posterior (P), and medial (M) length-width locations, as well as bursal (B) and joint (J) layers through the tendon thickness (bursal side visible, joint side not shown), yielding six total samples per shoulder (AB, AJ, PB, PJ, MB, and MJ) in either the longitudinal or transverse orientation (direction indicated by arrows)

2.2 Experimental testing and analysis

Samples were placed in custom grips, loaded in an Instron test machine, and tested in uniaxial tension parallel (longitudinal, n = 16) and perpendicular (transverse, n = 11) to the tendon long axis. The testing protocol consisted of a quasi-static ramp to failure at 0.1% strain/second. Prior to testing, a grid of small beads (0.5 mm diameter, 4-8 per sample) was adhered to the tendon surface using cyanoacrylate. Images were acquired at 5-second intervals throughout testing and were analyzed post-test with a custom Matlab program to quantify marker coordinates. Reference ($X_1^i$, $X_2^i$) and deformed ($x_1^i$, $x_2^i$) marker coordinates were used to calculate the two-dimensional deformation gradient (F) and translation vector (p):

$$\begin{array}{cc}\hfill \left[\begin{array}{cccc}\hfill x_1^1\hfill & \hfill x_1^2\hfill & \hfill \cdots \hfill & \hfill x_1^n\hfill \\ \hfill x_2^1\hfill & \hfill x_2^2\hfill & \hfill \cdots \hfill & \hfill x_2^n\hfill \end{array}\right]=& \left[\begin{array}{ccc}\hfill F_{11}\hfill & \hfill F_{12}\hfill & \hfill p_1\hfill \\ \hfill F_{21}\hfill & \hfill F_{22}\hfill & \hfill p_2\hfill \end{array}\right]\hfill \\ \hfill & \times \left[\begin{array}{cccc}{X}_1^1\hfill & X_1^2\hfill & \hfill \cdots \hfill & X_1^n\hfill \\ X_2^1\hfill & X_2^2\hfill & \hfill \cdots \hfill & X_2^n\hfill \\ 1\hfill & 1\hfill & \hfill \dots \hfill & 1\hfill \end{array}\right]\hfill \end{array}$$ (1)

where n = number of beads on the surface of each sample. Using the deformation gradient F, two-dimensional Lagrangian strain (E) was calculated:

$$\mathbf{E}=\frac{1}{2}({\mathbf{F}}^T\mathbf{F}-\mathbf{I})$$ (2)

where I is the identity matrix and the components of E are normal strain E₁₁ and E₂₂, and shear strain E₁₂. Stress was computed as load divided by undeformed CSA. A bilinear curvefit using a least squares approach was applied to stress–strain data in order to calculate the transition strain or the strain value corresponding to the breakpoint between the toe region and linear-region. Then, linear-region strain (ε_L) was defined as 2X transition strain, allowing the evaluation of experimental and affine-predicted strain values at a consistent, mathematically repeatable strain level across all test samples. Preliminary work also evaluated the affine assumption at the transition strain with similar overall observations as will be shown at the linear region strain. For space considerations, and because the overall observations were the same, we selected a single strain condition as our evaluation point. The selection of linear-region strain allows for the comparisons of our results to previous (and future) experimental and computational studies, which commonly evaluate and report properties of tissues in the linear region (i.e., modulus), and provides a sub-failure and, under full SST function, physiologically relevant strain condition.

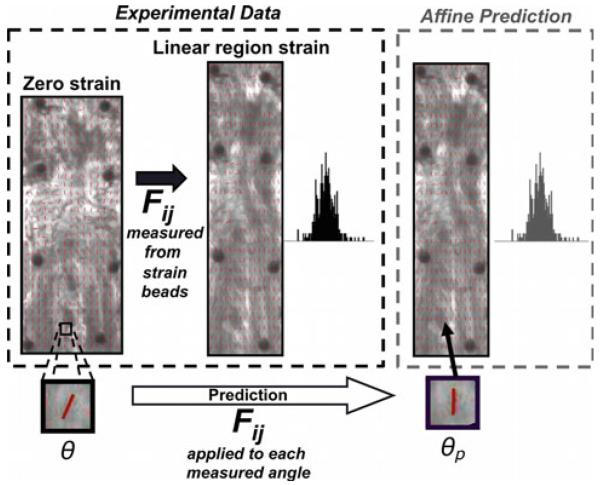
Taking advantage of the natural birefringence of collagen, a polarized light imaging system was used to quantify collagen fiber orientation (averaged through the sample thickness) during testing (Lake et al. 2009). Orientation values across the sample were used to create fiber alignment maps and corresponding histograms (Fig. 2), which were computed at ε₀ (zero strain) and at ε_L (linear-region strain). Circular variance (VAR) values were calculated to quantify the spread of each histogram, where VAR = 0 indicates uniform alignment and VAR = 0.5 corresponds to isotropic fiber alignment (for a π–periodic distribution). To evaluate repeatability of polarized light imaging data, a subset of highly aligned samples was analyzed five times each and projection plots were used to compare the five sets of histogram data. Very small average range and offset values (0.2° and 0°, respectively) indicated a high degree of repeatability for our polarized light measurements of collagen fiber orientation.

Fig. 2.

To evaluate the proximity of the affine prediction to experimental data, components of the deformation matrix (F_ij) calculated using changes in bead coordinates between zero and linear-region strain are applied to measured orientation angle values θ to compute affine-predicted angle values θ_p; linear-region strain (left) and affine-predicted (right) histograms containing all angle values are then compared to evaluate the affine prediction

2.3 Affine model predictions

The analysis methods described below were utilized in the current study and applied to the experimental data described above. For each sample, the fiber orientation data at ε₀ were used to calculate the predicted distribution of fiber orientations at ε_L, with the assumption of affine fiber kinematics (Fig. 2). Specifically,

$${\theta }_p={\tan }^{-1}\left[\frac{F_{22}\sin \theta +F_{21}\cos \theta }{F_{11}\cos \theta +F_{12}\sin \theta }\right]$$ (3)

where θ is the experimental fiber orientation angle at ε₀, θ_p is the predicted orientation angle at ε_L, and F₁₁, F₂₂, F₂₁ and F₁₂ are components of the 2D deformation gradient. The loading axis for all samples was in the 2-direction resulting in very small F₁₂ values, which were therefore set to be zero. Predicted angle values (θ_p) were computed for each area in a 30 × 15 grid overlaid on the surface of the sample, which were then compiled to create affine-predicted histogram distributions for each sample at ε_L.

2.4 Comparison between experimental data and affine predictions

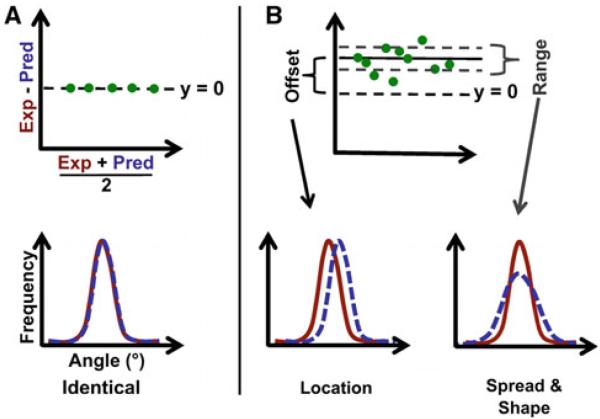
Experimentally determined fiber orientation histograms from our previous study at ε_L were compared with corresponding affine-predicted histograms using projection plots (Jones 1997). For each histogram, fiber orientation values were grouped into 100 quantiles (at increments of 1%) and projection plots were created by plotting average quantile values (of paired experimental and predicted data) on the x-axis and difference quantile values (experimental – prediction) on the y-axis (Fig. 3). When two non-identical distributions are compared to determine the level of agreement, they can vary in terms of location (i.e., biased shift in angle), spread (i.e., degree of isotropy/uniformity), and shape (i.e., differences in skewness, kurtosis, and/or modality). The appearance of a projection plot provides a qualitative description of how two distributions compare. For example, two identical distributions will yield projection plot data that fall along the line y = 0 (Fig. 3a), while distributions without complete agreement (Fig. 3b) will yield vertically shifted data (indicating a location difference) and/or vertically scattered data (indicating differences in spread and/or shape).

Fig. 3.

a The points in a projection plot, which is constructed by plotting quantile difference (y-axis) vs. quantile average (x-axis) for experimental (exp) and predicted (pred) distributions, fall along the line y = 0 when the distributions are identical; b With unequal distributions,=the offset indicates a difference in location, while the range value corresponds to differences in spread and shape

To obtain a quantitative comparison, projection plots were modified as follows. Three horizontal lines are added to each projection plot representing the median quantile difference (solid line, Fig. 3b) and the median difference ±34.1% of the spread of quantile differences (dashed lines, Fig. 3b). The value of 34.1% was selected such that these two additional lines represent ± standard deviation for normally distributed quantile difference values; for non-normally distributed values, these lines represent an equivalent portion of the total data set. In this manner, there are no assumptions made about how the quantile difference data are distributed. From this set of three horizontal lines, two numerical values are calculated to quantify the agreement between distributions: the “offset” is the amount the median is offset from y = 0 (more simply, offset = median value), and the “range” is the vertical distance between the two dashed lines (i.e., range encompasses the middle 68.2% of the quantile difference values). Importantly, the projection plot values of offset and range provide a quantitative measure of location, spread, and shape distribution differences, allowing for an analysis and comparison of grouped data that would be difficult to assess using qualitative data only. Specifically, offset values represent differences in location, while range values quantify differences in distribution spread and shape.

2.5 Statistical analysis

Data were found to be non-normally distributed, so nonparametric statistical tests were used. Range and offset values were compared across tendon location (AB, AJ, PB, PJ, MB, MJ) using Kruskal-Wallis and Mann–Whitney post hoc tests with Bonferroni corrections made for number of comparisons. Within each tendon location, these values were also compared across test orientation (longitudinal and transverse) using Mann–Whitney tests with Bonferroni corrections. Correlations between spread of fiber alignment at ε₀ (VAR values) and offset and range values were evaluated for both test orientations by computing Spearman rank correlation coefficients. For all statistical analyses, significance was set as p < 0.05.

3 Results

3.1 Comparison of experimental data and affine predictions

Range and offset values varied with test orientation and across tendon locations. The histograms and corresponding projection plots for two representative samples demonstrate the level of agreement for a relatively affine sample (Fig. 4, top) and a less affine sample (Fig. 4, bottom). Qualitatively, the close agreement between the experimental and predicted distributions in the top sample is demonstrated by the nearly horizontal data that lie near y = 0 on the corresponding projection plot. In contrast, the leftward shift (i.e., location difference) of the predicted distribution for the bottom sample is represented by a negative vertical shift of the data on the projection plot, while the vertical scatter of the data indicates a difference in spread and/or shape between the experimental and predicted distributions. Quantitatively, the more affine sample (Fig. 4, top) yields very small range and offset values, while the less affine sample (Fig. 4, bottom) presents much larger range and offset values corresponding with differences in spread/shape and location, respectively. Simply stated, the larger the range and offset values, the poorer the affine assumption.

Fig. 4.

Histograms (left) and projection plots (right) from two samples: (top) close agreement between experimental and predicted distributions represented by small offset and range values of the projection plot; (bottom) less overall agreement and a location shift are indicated by larger range and offset values, respectively

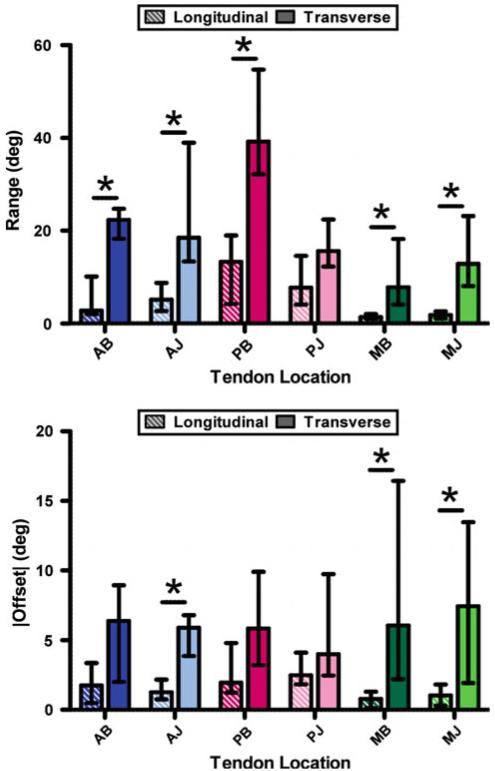
Range values were greater in transverse testing than longitudinal testing (Fig. 5, top), with five of the six tendon locations (AB, AJ, PB, MB, MJ) demonstrating differences that were statistically significant (p ≤ 0.003). Offset values were also greater in transverse samples (Fig. 5, bottom), with three of the six locations (AJ, MB, MJ) showing statistical significance (p ≤ 0.01). Taken together, larger range and offset values indicate less affine behavior in transverse compared with longitudinal testing directions.

Fig. 5.

Agreement between experimental data and affine predictions, represented by projection plot values of range (top) and offset (bottom), varies by tendon location and test orientation; greater values for transverse samples suggest less affine behavior than longitudinal tests (asterisk indicate statistical difference between longitudinal/transverse values)

In longitudinal tests (Fig. 5, striped bars), across tendon location, medial range values (“M” prefix) were smaller than both anterior and posterior values (“A” and “P” prefix). Specifically, medial-bursal (MB) range values were smaller than AB (p = 0.019) and PB (p < 0.001), and medial-joint (MJ) values were smaller compared with AJ (p = 0.0036) and PJ (p < 0.001). In addition, longitudinal MB offset values were significantly less than PB (p = 0.048). Thus, in longitudinal testing, medial samples follow more affine fiber deformation than anterior/posterior samples, as demonstrated by smaller range/offset values. In transverse tests (Fig. 5, solid bars), the only difference due to tendon location was larger PB range values, which were significantly larger than PJ (p < 0.001), AB (p = 0.0054), and MB (p = 0.011) values; there were no differences across tendon location for offset values in transverse test samples. Therefore, the relative success of the affine prediction was less dependent on tendon location in transverse compared with longitudinal testing.

3.2 Correlation between fiber alignment and affine prediction

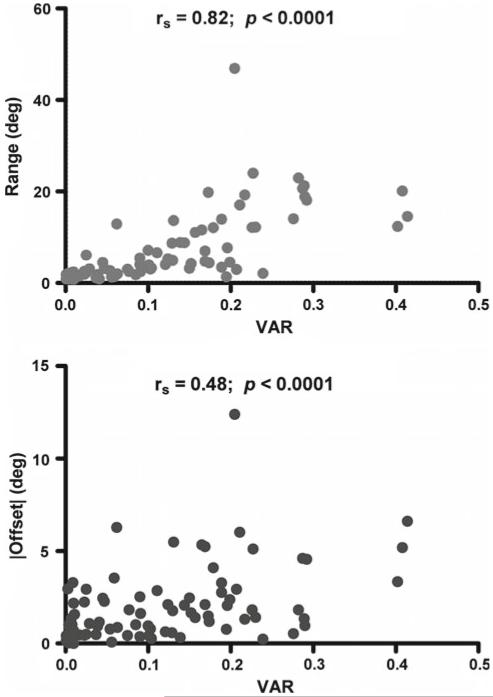
In evaluating the relationship between the degree of initial fiber alignment and the affine prediction, the ε₀ fiber alignment (VAR) was found to be significantly correlated with both range (r_s = 0.82, p < 0.0001, Fig. 6a) and offset (r_s = 0.48, p < 0.0001, Fig. 6b) values in longitudinal tests. Since small VAR values correspond to a high degree of collagen fiber alignment, positive correlations (+r_s) here demonstrate increasingly affine fiber behavior (smaller offset and range) with increasingly uniform alignment (small VAR). In transverse samples, range values also exhibited a significant correlation with VAR values (r_s = 0.58, p < 0.0001), while the correlation was not statistically significant (p = 0.83) for transverse offset values and VAR (transverse correlations not shown graphically).

Fig. 6.

Range (top) and offset values (bottom) for longitudinal samples are significantly correlated with degree of fiber alignment at zero strain (VAR); increased alignment (decreased VAR) corresponds to more affine fiber behavior demonstrated by decreased range and offset values (r_s = Spearman rank correlation coefficient)

4 Discussion

This study compared measured collagen fiber kinematics (using polarized light imaging during tensile testing) and affine model predictions using a new quantitative projection plot analysis of alignment distributions. Projection plots allow for a qualitative and quantitative evaluation of agreement in location, shape, and spread between two distributions (Jones 1997). Projection plots, which are used specifically to compare distributions, represent an analysis similar to that of Bland–Altman plots (Bland and Altman 1986), which provide a measure of agreement for more general data sets. One additional advantage over Bland–Altman plots is that projection plots, by grouping data using quantiles, can compare distributions with unequal sample numbers and still include all of the data set. Other approaches for comparing two distributions (e.g., comparing mean, median, variance, and/or standard deviation values, or using Kolmogorov–Smirnov statistical tests) can be misleading because similar mean and variance values may exist for distributions with unequal modes, they provide little detail on how distributions differ, and they may show significant differences when meaningful differences are not present. In contrast, projection plots provide both a qualitative comparison, through the appearance of plotted data, and quantitative comparison, through range and offset values, that can be evaluated statistically. Importantly, projection plots provide detailed analysis for how two distributions differ, not just that they differ. Detailed descriptions of how affine-predicted and experimental fiber distributions differ, obtained via projection plots, could be particularly useful in developing models to better understand microstructural kinematic behavior and incorporate such knowledge into macroscale tissue and/or joint models. For example, vertically scattered projection plot data (e.g., Fig. 4, bottom) represent a difference in distribution spread and/or shape, suggesting mechanistically that fibers rotated to a greater (or lesser) degree than predicted by the affine prediction, thereby providing insight into how fibers are able to move through the matrix and informing hypotheses on the nature of fiber–matrix interactions. Thus, projection plots, first proposed by Jones (1997) and modified in this study to include the quantitative measures of range and offset, provide a method for evaluating agreement between two distributions, and when used to examine collagen fiber kinematics, can deepen the understanding of how tissues deform under load and improve modeling efforts by providing insight into microstructural mechanisms of soft tissues.

In this study, the relative success of the affine prediction of fiber kinematics in human supraspinatus tendon was dependent on both test orientation and tendon location. In terms of test orientation, affine predictions were more closely matched to the longitudinal than transverse experimental data. In other words, the collagen fiber network follows a more affine deformation when samples were stretched parallel to the tendon long axis than perpendicular to it. This was demonstrated by significantly decreased range and offset values for longitudinal samples compared with transverse (Fig. 5). Since the load is applied perpendicular to the predominant fiber direction in transverse testing, fibers are required to reorient to a greater extent in order to support tensile load. The highlighted dark fiber (Fig. 7), for example, is required to reorient toward the direction of loading to a much greater extent in the transverse sample than in the longitudinal sample in order to support load. It is possible that increased reorientation in transverse samples results in more interactions between tissue constituents, resulting in local fiber deformations different from what are predicted via the macroscopic tissue deformation. Alternatively, or perhaps complementary to this, the increased initial dispersion of collagen fibers in transverse samples may be responsible for less affine kinematics compared with longitudinal tests. The strain values at which the affine prediction was evaluated were different for longitudinal and transverse samples, which may also contribute to the differences between projection plot values for the two test orientations. Specifically, transition strain (and by definition linear-region strain) was larger for transverse samples (~0.06 – 0.26; Lake et al. 2010) than longitudinal (~0.03–0.06; Lake et al. 2009). In order to be consistent, we utilized the same definition for the strain at which to evaluate the affine prediction, irrespective of sample location or test orientation. This is consistent with the common practice of comparing material properties in the “linear region” across different groups, even though the strain at which that region occurs may vary.

Fig. 7.

As compared with the fibers in longitudinal samples (a), collagen fibers in transverse samples (b) are required to reorient to a greater extend in order to support tensile load (e.g., dark fiber in each sample)

Location-dependent differences provide further evidence of the effect of initial fiber alignment on collagen fiber kinematics. Specifically, test samples from tendon locations that are more highly aligned, such as the medial samples (Lake et al. 2009), exhibit lower range and offset values compared to locations with more initially disperse collagen fiber distributions (e.g., posterior samples; Fig. 5). For range values in particular, differences by tendon location were observed in a similar pattern as for ε₀ fiber alignment (Lake et al. 2009, 2010), suggesting that inhomogeneous local properties affect fiber kinematics. Furthermore, with data from all tendon locations considered together, statistically significant correlations of range/offset with zero-strain fiber alignment (Fig. 6) indicate that local tissue structure affects the deformation of the collagen fiber network under tensile load. As the initial fiber distributions of samples become increasingly disperse, the range and offset values increase. Thus, samples more highly aligned at zero strain exhibit more affine behavior than less aligned samples. Interestingly, these correlations were less pronounced in the transverse data, suggesting that the effect of test orientation dominates over effects due to sample location. This may be because changing orientation (i.e., from longitudinal to transverse) causes the collagen fibers to be pulled toward (longitudinal) or away from (transverse) the predominant fiber direction, which is a much larger effect than changing to a different tendon location within the same orientation, where the direction of loads remain constant.

While the affine assumption is important for interpreting mechanical test data and applying these data to constitutive models, it has received very little experimental validation. A small number of studies have evaluated collagen fiber kinematics in stretched soft biological tissues and presented evidence for non-affine deformation (Billiar and Sacks 1997; Gilbert et al. 2006; Guerin and Elliott 2006; Hepworth et al. 2001). Bovine pericardium and porcine aortic valve leaflets subjected to biaxial stretch demonstrated non-affine fiber kinematics that were highly tissue specific, suggesting that conclusions regarding affine behavior for one tissue may not be applicable to others (Billiar and Sacks 1997). Extending this logic further, separate regions within a highly heterogeneous tissue (e.g., varying degrees of collagen fiber alignment) may present different fiber kinematics when subjected to similar levels of tensile load. The location-dependent results for the highly inhomogeneous supraspinatus tendon in this study provide supporting evidence (Fig. 5). In addition, for both pericardium and aortic valve samples, the proximity of the affine prediction to the experimentally measured collagen fiber distributions was qualitatively greater when samples were stretched in a direction near the predominant fiber direction than for samples tested in an orthogonal direction (Billiar and Sacks 1997). Further evidence of test orientation dependence is provided by small intestinal submucosa (SIS) samples tested under uniaxial and biaxial stretches: affine behavior was observed in equibiaxial tests, but non-affine behavior was seen for uniaxial tensile tests where, again, samples tested transverse to the preferred fiber direction demonstrated less affine deformation than samples tested parallel (Gilbert et al. 2006). These studies corroborate the results of the current work, where longitudinal samples exhibited more affine behavior than transverse samples (Fig. 5), thereby demonstrating test orientation dependence for the relative success of affine model predictions.

Further evidence for non-affine behavior in soft biological tissues, observed by overestimates of fiber orientation at higher strains, has been shown in human annulus fibrosus tensile tests (Guerin and Elliott 2006). Another study reported length scale dependence to fiber kinematics, with non-affine behavior on the microscale and affine kinematics on the millimeter scale of porcine skin under compression testing (Hepworth et al. 2001); however, large variation in the data complicates its interpretation. A theoretical study of deformation of random fiber networks supports this conclusion, where the degree of affine deformation was increased with increasing scale of observation (Hatami-Marbini and Picu 2009). The limit of this relationship, of course, is when the scale of observation is equal to the macroscopic tissue deformation, resulting in equivalent (and hence, affine) measures of deformation. Together with the current work, previous studies of collagen fiber kinematics in soft biological tissues demonstrate a complex microstructural response to strain with evidence for non-affine fiber behavior that may be dependent on specific tissues, heterogeneous regions within a tissue, orientation of the applied stretch relative to the fiber organization, and length scale of the microstructural observation.

This study is not without limitations. First, while non-affine behavior was observed, a cut-off point at which to define a material as non-affine was not selected. As shown in Fig. 6, there is a continuous progression toward non-affinity and, together with previous studies, the results of this study demonstrate that fiber kinematics depend on test orientation, degree of alignment, and length scale of observation. Thus, the choice of when a tissue is sufficiently affine must be addressed on a case-by-case basis for the application being considered. While we do not define an affine vs. non-affine cutoff, the projection plot metrics of range and offset defined in this study present a method to make relative comparisons of how affine a tissue behaves, where larger offset and range values indicate a less affine response.

A second limitation is that the affine predictions computed in this study are based on the assumption of a homogeneous experimental strain field. In order to assess homogeneity, localized strain values were computed in several sub-regions of each sample. The interquartile range of the strain values at ε_L was divided by the median strain value at ε_L, thus giving a measure of normalized strain variation (or NSV), which was compared across test orientation and tendon location to identify any dependence due to these factors. Importantly, NSV was relatively uniformly distributed across both test orientation and tendon location, with one exception being a larger variation for longitudinal MB samples (Fig. 8). In addition, correlations between offset and range values and NSV yielded only two significant comparisons and all r² were less than or equal to 0.16, suggesting no meaningful effects. Thus, the measured strain variation (NSV) is not dependent on test orientation or tendon location and has no meaningful correlation with the affine model prediction of fiber kinematics. The variation in strain, which may be due to natural variation in biological tissue, appears to be largely consistent, unbiased noise in the data and suggests that the large differences observed in the relative success of the affine predictions are not due to inhomogeneity of the experimental strain field.

Fig. 8.

Normalized E₁₁ strain variation shows little dependence on test orientation and tendon location: MB was the only group with significant tendon location and test orientation differences; no other comparisons were significantly different (asterisk indicate statistically significant)

The final limitation is that the polarized light imaging technique used in this study (Lake et al. 2009) measures collagen fiber orientation averaged over a small region rather than for individual collagen fibers. However, since our regions are small, the polarized light approximation is reasonable.

In this study, we have evaluated the collagen fiber kinematics of human supraspinatus tendon under longitudinal and transverse uniaxial tensile testing. Experimentally measured fiber angle values were compared with predictions of affine fiber deformation using modified projection plots, which provide a method for qualitative and quantitative comparisons of two distributions. The projection plot metrics of offset and range, which we have developed and utilized in this study, are of particular benefit by allowing for a quantitative representation of agreement that can be subjected to statistical comparisons. In this study, the validity of the affine prediction varied by tendon location and test orientation, which is consistent with previous studies that reported evidence of non-affine behavior in other soft tissues (albeit with less rigorous comparison techniques). Non-affine behavior of the SST and other soft tissues also has implications for efforts in developing models for these tissues, in particular when utilizing structurally based continuum models that are based on the assumption of affine deformation. Finally, the results of this study agree with previous assessments of other fiber-reinforced soft tissues and suggest that non-affine fiber behavior may be dependent on specific tissues, heterogeneous regions within a tissue, orientation of the applied stretch relative to the fiber organization, and length scale of the observation.