Radiation damping in modern NMR experiments: Progress and challenges

1. Introduction

The ability to resolve as many resonances as possible in the nuclear magnetic resonance (NMR) spectra of large biomolecules is an important goal in facilitating the assignment of chemical shifts, and for ultimately determining the structure and measuring multiple time scale dynamics in the solution state [1–3]. The application of NMR spectroscopic methods designed to narrow the line widths of crowded spectra of large molecules contributes to the ongoing efforts to extend the upper size limits in their structure determination [4–6]. Increasing the magnetic field strength (B₀) greater than 21.1 T (ν_H > 900 MHz) can increase the spectral resolution. Isotopic labeling of mid-sized biomolecules (~50 kD) using ¹⁵N, ¹³C and ²H [7,8] have successfully moved NMR from a routine analytical technique to a powerful tool capable of structure determination of large molecules in solution. The limitations arising from increased line widths have partially been tackled by altering the relaxation pathways by using samples labeled with deuterium isotopes and applying NMR methodology that utilizes additional cross-relaxation pathways which yield narrowing of line widths (e.g. TROSY experiments [9,10]). In addition, the sensitivity of the NMR experiments is improved by the use of digital signal processing and over-sampling techniques [11–13]. The quest for increased sensitivity and resolution of the NMR spectra and simultaneous reduction of the amount of sample requirements continues to fuel new developments in biomolecular NMR spectroscopy.

In most NMR experimental methods, protons are detected in the acquisition dimension to take advantage of the inherent high sensitivity of these spins. The free induction decay (FID) collected at the end of each experiment is a mixture of signals from the protons in the molecule of interest and in the solvent molecules. The concentration of protons in the solvent can be thousands of times higher than those in the solute. This in turn affects the NMR spectra of the solute significantly. It is important to dissolve the molecules in aqueous buffers consisting of 90–95%H₂O (the rest being D₂O) when observing signals from the exchangeable amide protons in protein and imino and amino protons in nucleic acids, under biologically relevant conditions. The concentration of water protons is approximately 100 M, whereas the sample solute is typically less than one millimolar. Standard NMR methods overlook the possibility that individual spins can influence the bulk nuclear magnetization of the whole sample, predominantly those of the water spins. Detection of the water resonances through a tuned circuit introduces an effect commonly known as radiation damping (RD), which is a manifestation of the combined spin system and the electronic resonance circuit assembly.

The phenomenon of RD has been known for almost as long as nuclear magnetic resonance has been studied. As far back as 1949, Suryan [14] first proposed the interaction of an RF coil with the bulk magnetization of a sample as an explanation for the discrepancy between theoretical predictions of relaxation times and experimental observations. Bloembergen and Pound [15] formulated Suryan’s hypothesis mathematically by combining the Bloch and Maxwell equations, coining the phrase “radiation damping.” Bruce et al. [16] highlighted an erroneous assumption in the original Bloembergen paper, however the steady-state limit is the same as the original description by Bloembergen and Pound. Building on the previous work, Bloom [17] published modified Bloch equations in which the effects of RD are included; directly in a set of non-linear differential equations describing the motion of bulk magnetization. Bloom successfully described the effects of RD on the line shapes of continuous wave (CW) experiments with and without relaxation, and highlighted the effects on adiabatic rapid passage. Though often discussed in the pulsed-NMR experiments, Bruce et al. [18] and Sanders et al. [19] have shown the RD effect is a crucial component in continuous wave magnetic resonance experiments.

The term “radiation damping” does not accurately describe the effect. Szöke and Meiboom [20] showed that following a single pulse between flip-angles 90° and 270°, the NMR signal passes through a maximum before decaying and thus drawing attention to the fact that the term “radiation damping” is something of a misnomer. According to Abragam [21], this process results in the vanishing of the transverse magnetization, yet it does not reduce (or damp) the length of the magnetization vector. Jeener and coworkers [22] reinforced this concept and confirmed that it is rather ‘unfortunate’ to describe this phenomenon as radiation damping. Radiation feedback or Suryan’s broadening effect would have been a more suitable name. However to be consistent with the literature for over 50 years, the magnetic resonance community refers to this phenomenon as radiation damping (RD).

Although RD is an intrinsic physical phenomenon in all NMR experiments, the magnitude of the damping field depends on the Q_c (quality factor) value, the filling factor of the probe, and the bulk magnetic moment of the sample in correlation with the static field strength. RD is thus normally observed in experiments with high proton or fluorine concentrations at high fields. In order to make their observations at 0.704 T (proton frequency ~30 MHz), Szöke and Meiboom artificially increased the Q_c of their receiver coil using positive feedback or “Q-multiplication” [20]. After an initial flurry of interest, little work was published on RD, because at static field strengths being used the RD effects were generally negligible. As technology has advanced and both static field strengths and probe Q_c values have increased, a renewed interest in RD has developed. In 1989 Warren et al. [23] described the effects of RD during soft pulse irradiation. Since, then articles have appeared describing RD effects on multiplet shape [24], solvent suppression [25], spin–lattice and spin–spin relaxation measurements [26,27], the use of RD to determine chemical exchange rates [28,29], and radiation damping-induced spurious peaks in 2D spectroscopy [30]. Several aspects of the theoretical framework of RD both in homogenous and inhomogeneous fields [31,32] as well as review articles covering many other related aspects of the field have been presented [33–37].

Radiation damping can be best described in the following fashion. The precessing transverse magnetization of the water protons after a radio frequency pulse induces an electromagnetic field (emf) in the receiver coil. This creates an oscillating current that generates a transverse magnetic field at the same frequency. This induced field rotates the magnetization of the solvent spins to its equilibrium toward the direction of the applied magnetic field, before other relaxation mechanisms can take effect. The rate, at which the solvent magnetization is rotated to equilibrium, is given by a characteristic time constant known as the radiation damping time (τ_rd). For example, a sample of water in an NMR spectrometer operating at 400 MHz will have a τ_rd value of around 20 ms. In contrast, the expected spin lattice (T₁) and spin–spin relaxation (T₂) times of water have durations on the order of more than hundreds of milliseconds. The decay of the time domain signal is dominated by the much shorter τ_rd, rather than the longer T₂. Despite the importance of this effect in causing a broadening of the NMR signals, a literature search shows that the total number of papers that discuss RD with reference to NMR during the time period from the date of its discovery in 1949 to 1985 is only 15. This number has increased to100 s in the last two decades indicating the awareness of RD affecting spectral quality in experiments performed with macromolecules in aqueous solutions using higher field spectrometers. Several powerful solutions based on either hardware (probe engineering) modifications or pulse sequences have developed effective suppression of RD in biomolecular NMR applications. In the last four decades, there has been a continuous evolution in solvent suppression techniques that attempt to meet new and increasingly stringent requirements (e.g., lower solute concentration, multiple signals, and greater selectivity). Although only a few techniques have been developed for the suppression of RD, simple pulse sequences based on RD suppression methods are compatible for use with common solvent suppression schemes. Radiation damping has also been shown to influence magnetic resonance spectroscopy (MRS) and magnetic resonance imaging (MRI) [38–45]. This article focuses only on RD effects in high-resolution solution NMR experiments.

The purpose of this article to provide a comprehensive introduction to radiation damping with particular focus on the effects of RD in performing high-resolution solution state NMR experiments. First, the radiation damping effects are described using phenomenological Bloch equations followed by modifications to include multiple resonances and other effects such as chemical exchange. Upon description of the experimental measurement of radiation damping, the rest of the sections focus on its influence in NMR experiments and the kinds of artifacts introduced. Methods used to control radiation damping effects using both hardware and software modifications are provided. The article concludes with a description of the constructive use of radiation damping in biological applications.

2. Theoretical aspects

Several papers appeared in the late 1950s on the topic of RD based on the equations of Bloembergen and Pound [15]. Burce et al. [16] had experimentally shown the effect of RD on the broadening of the resonance line shape, and Bloom [17] has described the analytical solutions of the Bloch equations including RD for slow and fast passage experiments. Szöke et al. [20] had demonstrated experimentally the effect on RD of tuning the receiver coil of the probe. Hobson et al. [46] simulated the effect with an explicit computer algorithm. Most features of RD effects can be well understood with the modified phenomenological Bloch equations. However, when other effects are present such as the dipolar fields in the presence of pulsed field gradients (PFGs, the RD effects need a more complex description [22,32,47–49]. In this section, we briefly describe the phenomenological approach as well as a method to integrate the effect of solute spins into the calculations.

2.1. Phenomenological description of RD using the Bloch equation

In the absence of collective effects, Bloch’s differential equations for the components of average spin magnetization are linear. The presence of an induced magnetic field, such as RD, is explicitly dependent on the average spin magnetization, making these equations to be non-linear. The mathematical analysis of RD with the modified Bloch–Maxwell equations proposed by Bloembergen and Pound [15], in the rotating frame is given by

$$\frac{d}{dt}\left[\begin{array}{c}\langle I_x\rangle \\ \langle I_y\rangle \\ \langle I_z\rangle \end{array}\right]=\left[\begin{array}{ccc}-R_2& -\omega & 0\\ \omega & -R_2& 0\\ 0& 0& -R_1\end{array}\right]\left[\begin{array}{c}\langle I_x\rangle \\ \langle I_y\rangle \\ \langle I_z\rangle \end{array}\right]-\frac{1}{{\tau }_{rd}}\left[\begin{array}{c}\langle I_x\rangle \langle I_z\rangle \\ \langle I_y\rangle \langle I_z\rangle \\ {\langle I_x\rangle }^2+{\langle I_y\rangle }^2\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ R_1\langle I_z^{eq}\rangle \end{array}\right]$$ (1)

〈I_x〉, 〈I_y〉 and 〈I_z〉 are the expectation values of the x, y and z components with z along B₀ of the magnetization and $\langle I_z^{eq}\rangle$ is the equilibrium value, given by the Boltzmann distribution at the high field and high temperature approximations. ω is the frequency of a spin in the frame rotating at an angular frequency Ω, given by $\omega =\sqrt{{\mathrm{\Omega }}_o^2-{\mathrm{\Omega }}^2}$, and Ω_o is the applied static magnetic field in frequency units. $R_1(T_1^{-1})$ and $R_2(T_2^{-1})$ are the spin–lattice and spin–spin relaxation rates, respectively. ${\tau }_{rd}^{-1}$ is the classical radiation damping rate given in SI units by [15,21]

$${\tau }_{rd}^{-1}=2\pi \eta Q_c\gamma M_0$$ (1)

The filling factor η is defined as the ratio of the probe coil volume to the sample volume enclosed. The Q_c is the quality factor of the resonance circuit (Q_c = ΩL/C); Ω, L and C are frequency, conductance, and capacitance of the resonance circuit, respectively and γ is the gyromagnetic ratio of the observed spin. Substituting for $M_o(\langle I_z^{eq}\rangle )$ the thermal equilibrium magnetization for spin half nuclei [50,21], Eq. (2) can be rewritten as

$${\tau }_{rd}^{-1}=\frac{\eta Q_c{\gamma }^3{h}^2{N}_o{B}_o}{8\pi k_{B}T}$$ (3)

where h is Plank’s constant (6.6262 × 10⁻³⁴ m² kg s⁻¹), N_o is the number of spins per unit volume (typically 1.3 × 10²² protons per 200 μL of water [50]), B_o is the strength of the magnetic field in Tesla, k_B is the Boltzmann constant (1.3806 × 10⁻²³ m² kg s⁻² K⁻¹) and T is the temperature of the sample in K. Eq. (3) indicates that the rate at which the magnetization vector is rotated is proportional to the experimental parameters, quality factor, and the choice of the spectrometer frequency. Eqs. (2) and (3) are valid only when the probe is tuned to the resonance frequency of the spins of interest. Detuning the probe will decrease the effect of RD sensitivity on the signals, in addition to the frequency shifts in high-sensitivity probes, such as cold probes [32] (vide infra).

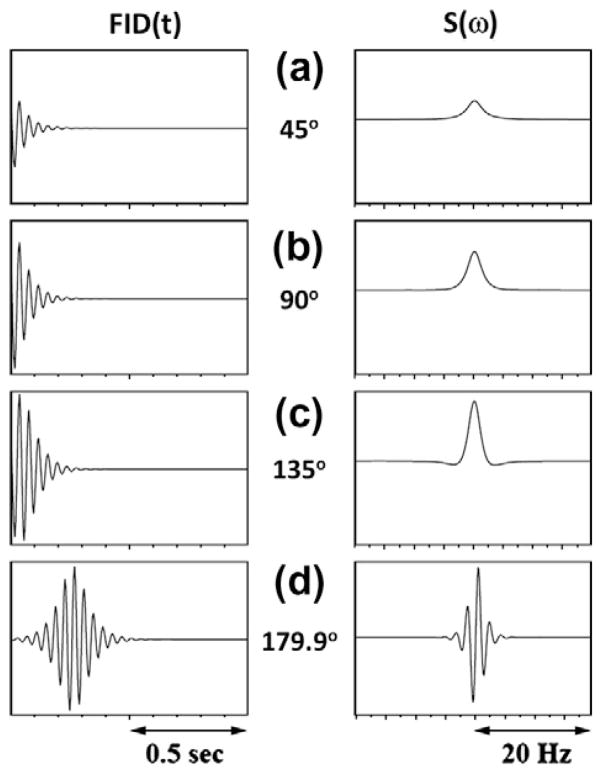
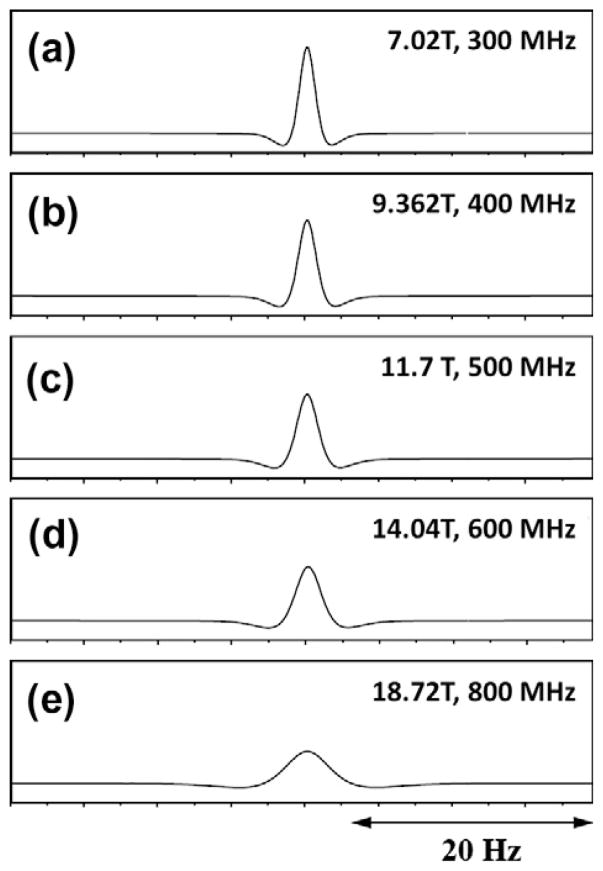
The modified phenomenological Bloch equations (Eq. (1)) for a system of single spins with RD, by itself are one of the sets of challenging equations to solve. Many attempts have been made to obtain an analytical solution for the most general case. One such solution was presented by Barbara [51] using a projection technique. Often a numerical integration procedure provides an easier way to solve Eq. (1). Self-consistent numerical integration procedures [52], can adjust the step size of the integration used in the calculations. In order to demonstrate the effect of RD as a function of the excitation pulse angle, Fig. 1 indicates the calculated plots of the time domain signal as the water spins are flipped increasingly away from their equilibrium positions along B₀ (along the Z-axis). The FID in Fig. 1c, which was obtained after a 135° pulse, already shows the effects of RD. The echo-like shape of the FID in Fig. 1d after near inversion (pulse angle ~179°) is typical of a strongly radiation damped signal. The effect of applied magnetic field on RD can be easily seen in the simulated spectra shown in Fig. 2. For a flip angle of 150°, the line width of the water signal increases with a corresponding linear decrease in τ_rd as the magnetic field is increased. For example, τ_rd decreases from 40 ms to 15 ms by increasing the field from 300 MHz (Fig. 2a) to 800 MHz (Fig. 2e), respectively.

Fig. 1.

Dependence of signals of nuclear spins (water) on flip-angles from thermal equilibrium. Panels on the left show the free induction decays (FID) calculated after a 45°, 90°, 135° or 179.9° pulse to equilibrium magnetization and the panels on the right show the respective Fourier transformed spectra. FIDs are simulated by numerical integration of Eq. (1) with the parameters: τ_rd = 25 ms, R₁ = R₂ = 10 Hz and ω = 50 Hz. The calculations were performed over 1024 complex points with a spectral width of 250 Hz and the time domain data were fast Fourier transformed without any apodization. The vertical scales of FID and spectrum are normalized with reference to 179.9° pulse data (figure made using information presented in Ref. [35]).

Fig. 2.

Simulation of radiation damping effect on signal as a function of the spectrometer frequency. Proton frequencies and spectrometer field strengths are marked in each panel. Radiation damping time constant (τ_rd) at 300 MHz is assumed to be 40 ms, the rest being scaled according to Eq. (3). The tip angle of the read pulse is 150°, while the rest of the simulation parameters remain the same as in Fig. 1, ignoring the field dependency of relaxation rates (figure made using information presented in Ref. [35]).

Eq. (1) and the respective solutions of the Bloch equations are for a system of single spins. A more realistic representation of the experimental system must include a spatial distribution of the water spins. Eq. (1) can be rewritten, for a homogeneous ensemble irradiated on resonance in the rotating frame as [17,33],

$$\frac{d}{dt}\left[\begin{array}{c}\langle I_x\rangle \\ \langle I_y\rangle \\ \langle I_z\rangle \end{array}\right]=\left(\begin{array}{c}-{\omega }_y\langle I_z\rangle \\ -{\omega }_x\langle I_z\rangle \\ {\omega }_x\langle I_y\rangle -{\omega }_y\langle I_x\rangle \end{array}\right)+\left(\begin{array}{c}\langle I_x\rangle R_2\\ -\langle I_y\rangle R_2\\ (\langle I_z^{eq}\rangle -\langle I_z\rangle )R_1\end{array}\right)+\frac{1}{\langle I_z^{eq}\rangle {\tau }_{rd}}\left[\begin{array}{c}\langle I_x\rangle \langle I_z\rangle \\ \langle I_y\rangle \langle I_z\rangle \\ {\langle I_x\rangle }^2+{\langle I_y\rangle }^2\end{array}\right]$$ (4)

In the case of an inhomogeneous ensemble with different resonance offsets ω, each isochromat is characterized by a Bloch vector I(ω) = [I_x(ω), I_y(ω), I_x(ω)]^t (superscript ‘t’ represents transpose operation). Following the approach Augustine and Hahn [34], the transverse magnetization components of the isochromats are collectively coupled to the RF coil to produce a unique field that can be included in the Bloch equation as follows:

$$\frac{d}{dt}\left[\begin{array}{c}\langle I_x\rangle (\omega )\\ \langle I_y\rangle (\omega )\\ \langle I_z\rangle (\omega )\end{array}\right]=\left(\begin{array}{c}-\omega \langle I_y\rangle (\omega )+{\omega }_y\langle I_z\rangle (\omega )\\ \omega \langle I_x\rangle (\omega )-{\omega }_x\langle I_z\rangle (\omega )\\ {\omega }_x\langle I_y\rangle (\omega )-{\omega }_y\langle I_x\rangle (\omega )\end{array}\right)+\left(\begin{array}{c}-\langle I_x\rangle (\omega )R_2\\ -\langle I_y\rangle (\omega )R_2\\ (\langle I_z^{eq}\rangle -\langle I_z\rangle (\omega ))R_1\end{array}\right)+\frac{1}{\langle I_z^{eq}\rangle {\tau }_{rd}}\left(\begin{array}{c}-\langle {\overline{I}}_x\rangle \langle I_z\rangle (\omega )\\ -\langle {\overline{I}}_y\rangle \langle I_z\rangle (\omega )\\ \langle {\overline{I}}_x\rangle \langle I_x\rangle (\omega )+\langle {\overline{I}}_y\rangle \langle I_y\rangle (\omega )\end{array}\right)$$ (5)

〈Ī〉 represents the average Bloch vector for the entire inhomogeneous ensemble and is defined as

$$\langle \overline{I}\rangle ={(\langle {\overline{I}}_x\rangle ,\langle {\overline{I}}_y\rangle ,\langle {\overline{I}}_z\rangle )}^t={\int }_{\omega =-\infty }^{+\infty }g(\omega )\langle \overline{I}\rangle (\omega )d\omega$$ (6)

where g(ω) is a weighting function specifying the relative weight of the magnetization vectors 〈I〉(ω) and could be assumed to follow a specific distribution such as a Lorentzian or Gaussian. Zhang et al. [53] have established a time optimal control of a homogeneous as well as an inhomogeneous ensemble of dissipative spin 1/2 particles in the presence of RD. This approach is expected to be particularly powerful in designing RF pulses and sequences for the distribution of the water spins in the active volume of the probe as well as other shape related effects.

It is worth noting that recently Tropp and Van Criekinge [54] have provided an alternative description of the radiation feedback phenomenon. These authors argue that the filling factor η, a parameter that directly affects RD (Eq. (3)) is neither uniquely defined nor easily measured, and thus the basic equation to describe RD should be rewritten to remove the dependence of η. It has been shown that the experimental measurements using this approach provide estimates of the RD constant close to that of the conventional methods.

2.2. Quantum mechanical description

The RD phenomenon can also be explained by using a quantum mechanical treatment of the spin system. Shrivastava [55] first described Suryan’s line broadening (RD effects) using a quantum mechanical treatment. The induced magnetization process of RD is one of two collective effects, which can result from placing a high density of protons in an external magnetic field. The other effect, known as a dipolar field [56,57] is sometimes confused with RD [58–63]. Therefore, a brief description of the dipolar field is included here to complete the discussion on RD, and the reader is referred to articles by Jeener and co-workers [22,32,48,49] and Levitt [64] for further details about the differences between these two effects. A dipolar field refers to the presence of additional magnetic field at the site of each spin due to the presence of its neighbors. As in the case of RD, a dipolar field is proportional to the nuclear spin density and the strength of the external magnetic field. However, unlike RD, it has a strong dependency on the shape of the sample and the spatial distribution of the magnetic field [32,33,49,56,57,64]. In addition, dipolar effects are independent of the quality factor (Q_c) of the resonance coil [32,33,49,56,57,64]. More importantly, RDdiminishes the quality of the spectra to a greater extent than does the dipolar field. For example, a typical 600 μL sample of water in a 5 mm diameter cylindrical tube placed in a 600 MHz spectrometer produces a dipolar field resulting in a shift of the NMR signal of the protons on the order of 1 Hz while ${\tau }_{rd}^{-1}$ is on the order of 100 Hz [32,49].

2.3. Radiation damping effects on multiplet structures

The dynamics of RD effects arising from resonances with multiplet structures is not only interesting, but also complex. Barjat et al. [24] noted several interesting features of resonances with multiplet structures. In the case of a doublet, each of the resonances creates its own RD effects (own rotating radio frequency magnetic field). However, the motion of the magnetization is perturbed by both fields leading to a rather complex trajectory of the motion of the magnetization vectors. This study noted three major effects: (a) the doublet signals broaden asymmetrically but remain well-resolved (b) the appearance of extra satellite peaks and (c) changes in the relative intensities of the components of the doublet with further line shape distortions where the probe coil is not tuned on resonance. In order to understand these effects, the Bloch equation (Eq. (1)) for N independent resonances (labeled i, j, k, etc.) can be modified as follows [24]:

$$\frac{d}{dt}\left[\begin{array}{c}\langle I_x^i\rangle \\ \langle I_y^i\rangle \\ \langle I_z^i\rangle \end{array}\right]=\left[\begin{array}{ccc}-R_2^i& -{\omega }_i& 0\\ {\omega }_i& -R_2^i& 0\\ 0& 0& -R_1^i\end{array}\right]\left[\begin{array}{c}\langle I_x^i\rangle \\ \langle I_y^i\rangle \\ \langle I_z^i\rangle \end{array}\right]-\alpha \left[\begin{array}{c}\sum _j^N\langle I_x^j\rangle \langle I_z^i\rangle \\ \sum _j^N\langle I_y^j\rangle \langle I_z^i\rangle \\ \sum _j^N\langle I_x^j\rangle \langle I_x^i\rangle +\sum _j^N\langle I_y^j\rangle \langle I_y^i\rangle \end{array}\right]+\left[\begin{array}{c}0\\ 0\\ R_1\langle I_z^{i,eq}\rangle \end{array}\right]$$ (7)

The above equation reduces to Eq. (1), when N = 1 and $\alpha ({\tau }_{rd}^{-1})$ is the radiation damping constant. Following the approach by Barjat et al. [24], Eq. (7) is modified to include the effect of detuning as

$$\frac{d}{dt}\left[\begin{array}{c}\langle I_x^i\rangle \\ \langle I_y^i\rangle \\ \langle I_z^i\rangle \end{array}\right]=\left[\begin{array}{ccc}-R_2^i& -{\omega }_i& 0\\ {\omega }_i& -R_2^i& 0\\ 0& 0& -R_1^i\end{array}\right]\left[\begin{array}{c}\left(\begin{array}{c}\alpha {cos}^2\beta \langle I_z^i\rangle \sum _j^N\langle I_y^j\rangle +\\ \alpha cos\beta sin\beta \langle I_z^i\rangle \sum _j^N\langle I_y^j\rangle \end{array}\right)\\ \left(\begin{array}{c}\alpha {cos}^2\beta \langle I_z^i\rangle \sum _j^N\langle I_y^j\rangle -\\ \alpha cos\beta sin\beta \langle I_z^i\rangle \sum _j^N\langle I_x^j\rangle \end{array}\right)\\ \left(\begin{array}{c}\alpha cos\beta (cos\beta \langle I_x^i\rangle -sin\beta \langle I_y^i\rangle )\sum _j^N\langle I_x^j\rangle +\\ \alpha cos\beta (cos\beta \langle I_y^i\rangle +sin\beta \langle I_x^i\rangle )\sum _j^N\langle I_y^j\rangle \end{array}\right)\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ R_1\langle I_z^{i,eq}\rangle \end{array}\right]$$ (8)

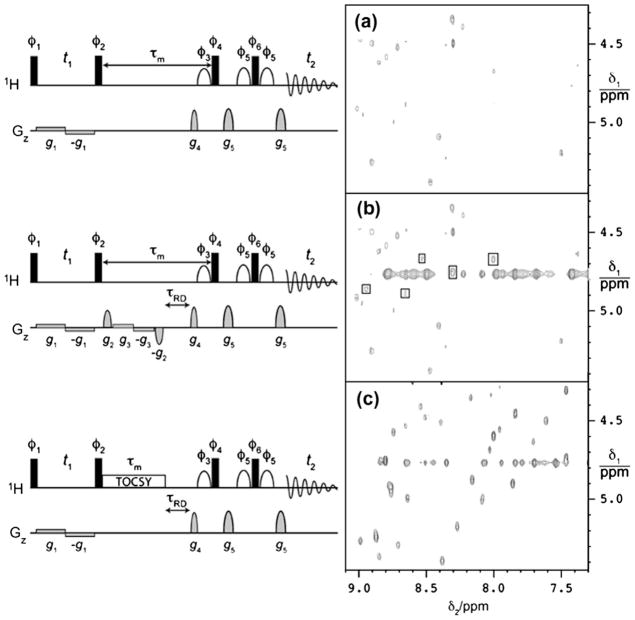
where δ = (Ω − Ω_o)/Ω_o is the relative effect of detuning to a frequency (Ω) from the resonance frequency (Ω_o), with phase (β = tan⁻¹(Q_cδ(δ + 2)/(δ + 1))) and amplitude (cos β = (i/i_o)). In Eq. (8), the offset angular frequency ω_i is typically in kHz relating to the difference between the center of the applied radio frequency and the Larmor frequency while δ refers to the offset in MHz. Eq. (8) accounts for the effects of RD, by considering the rotating magnetic field shifted by a phase β and reduced in amplitude by cos(β). Fig. 3 shows the experimental and simulated spectra (solving Eq. (8)) using numerical integration procedures) in the case of the isopropyl methyl proton doublet from a 80% v/v solution of isopropyl alcohol in CDCl₃.

Fig. 3.

Radiation damping effects on doublets. 500 MHz proton NMR spectra of the isopropyl methyl ¹H doublet in a 80% v/v solution of isopropyl alcohol in CDCl₃ as a function of the probe detuning as defined by β β = tan⁻¹(Q_cδ(δ + 2)/(δ + 1)), below Eq. (8)). Experimental (left) and simulated spectra (right) show results from perfect tuning (β = 0) and detuned in either negative (β = +52°) or negative offset (β = −43°) (Eq. (8)). Reproduced with permission from [24].

2.4. Including radiation damping effects on the solute

In the earlier sections, the RD effect of water alone is treated by implementing the phenomenological Bloch equations. In addition to solvent effects produced by RD, solute spin magnetization is known to be affected by RD in an aqueous solution. These include selective modulations of the J-coupling constants [65] and intermolecular exchange between water and dissolved solutes [28,29,66]. Miao et al. [65] have shown that in the natural abundant ¹³C NMR spectrum of acetate, the two-bond heteronuclear coupling constant seen in the ¹³C–¹²C–¹H₃ systems (~1% of the sample) is strongly modulated by the RD of the methyl protons from the abundant ¹²C–¹²C–¹H₃ molecules (~99% of the sample). The RD field is considered as a selective RF pulse in explaining the observed experimental line shape modulations. To describe chemical exchange effects systematically, it is necessary to develop an equation of motion that includes solvent and solute spins. In this section we describe a procedure to extend the Bloch equations with RD to include intermolecular exchange effects (Krishnan and Rance, unpublished results and Chen and Mao [28]).

The approach taken here is still phenomenological in nature and follows the assumptions of the Bloch equation. The equation of motion described above has four different time constants; (a) the relaxation rates (R₁ and R₂) of the solvent spins, (b) RD time (τ_rd) as defined by Eq. (3) and (c) other dynamic parameters related to solute spins such as chemical exchange rate τ_ex as well as self- and cross-relaxation rates. The modifications of Bloch equations are valid based on the assumption that all dynamic processes with solutions to the equation of motion, takes place at a time scale such that τ_cir ≪ τ < τ_rd, τ_ex < T₂, where τ_cir is the time constant of the electric circuit of the probe defined by the ratio of quality factor of the coil (Q_c) to the resonance frequency (Ω_o). These equations are developed further under the assumption that the spins are in a tuned circuit. A schematic representation of the spin system is shown in Fig. 4. The solute portion is represented by two protons, ‘a’ and ‘b’ are the ¹Hα and the amide proton (¹HN) resonances in a protein. The amide proton undergoes a chemical exchange with the water spins as well as intermolecular relaxation with other protons of the protein. For a three spin system consisting of two protein protons and a water (chemical equivalence of the two water protons allows them to be treated as a single proton), the X, Y and Z components of the magnetization are given by Bloch equations in the rotating frame as

Fig. 4.

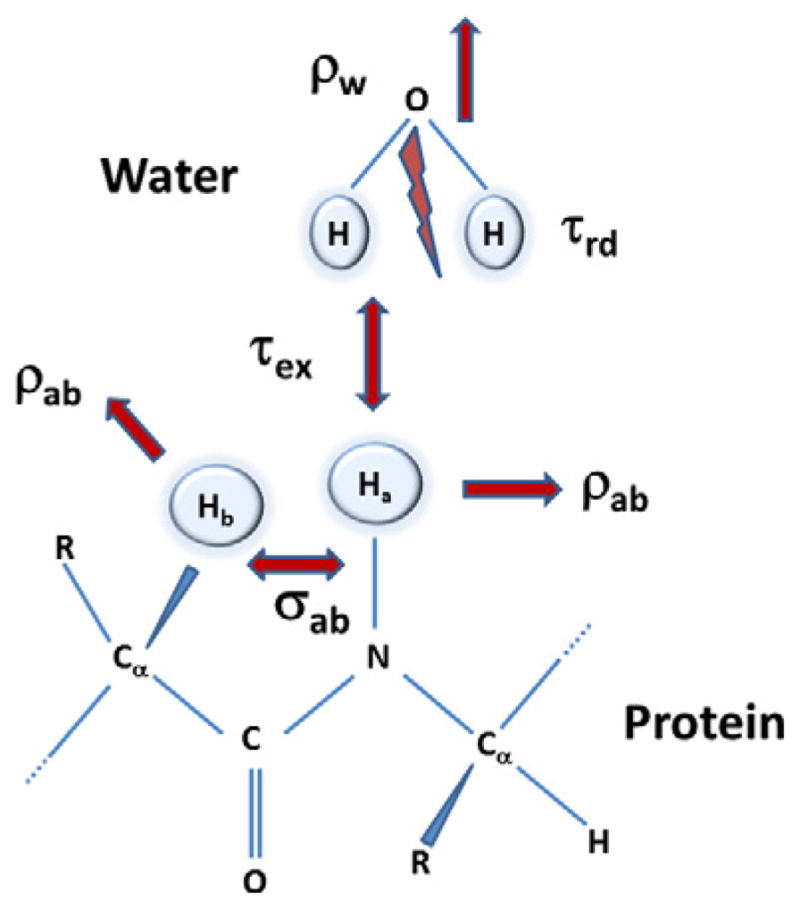
Schematic representation of the spin system considered in developing a system of equations to consider radiation damping effects of the water as well as its chemical exchange with a labile proton in a protein. Spins ‘a’ and ‘b’ are the amide proton and a proton in a protein, respectively. Water and the protein spins have their respective relaxation mechanism given by ρ_w and by the self-relaxation (ρ_ab) and cross relaxation rates (σ_ab). The radiation damping of the water spins are characterized by a time constant τ_rd and the intermolecular exchange between the water and the amide proton is given by τ_ex. The protein concentration is considered too low to have any radiation damping effects of its own.

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)=-\left(\begin{array}{ccc}{\omega }_a& ·& ·\\ ·& {\omega }_b& ·\\ ·& ·& {\omega }_w\end{array}\right)\left(\begin{array}{c}\langle I_y^a\rangle \\ \langle I_y^b\rangle \\ \langle I_y^w\rangle \end{array}\right)-\left(\begin{array}{ccc}{R}_2^a& ·& ·\\ ·& R_2^b& ·\\ ·& ·& R_2^w\end{array}\right)\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)-\gamma \left(\begin{array}{ccc}{B}_y^a& ·& ·\\ ·& B_y^b& ·\\ ·& ·& B_y^w\end{array}\right)\left(\begin{array}{c}\langle I_z^a\rangle \\ \langle I_z^b\rangle \\ \langle I_z^w\rangle \end{array}\right)$$ (9)

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_y^a\rangle \\ \langle I_y^b\rangle \\ \langle I_y^w\rangle \end{array}\right)=\left(\begin{array}{ccc}{\omega }_a& ·& ·\\ ·& {\omega }_b& ·\\ ·& ·& {\omega }_w\end{array}\right)\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)-\left(\begin{array}{ccc}{R}_2^a& ·& ·\\ ·& R_2^b& ·\\ ·& ·& R_2^w\end{array}\right)\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)-\gamma \left(\begin{array}{ccc}{B}_x^a& ·& \mathit{cdot}\\ ·& B_x^b& ·\\ ·& ·& B_x^w\end{array}\right)\left(\begin{array}{c}\langle I_z^a\rangle \\ \langle I_z^b\rangle \\ \langle I_z^w\rangle \end{array}\right)$$ (10)

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_z^a\rangle \\ \langle I_z^b\rangle \\ \langle I_z^w\rangle \end{array}\right)=\gamma \left(\begin{array}{ccc}{B}_y^a& ·& ·\\ ·& B_y^b& ·\\ ·& ·& B_y^w\end{array}\right)\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)-\gamma \left(\begin{array}{ccc}{B}_x^a& ·& ·\\ ·& B_x^b& ·\\ ·& ·& B_x^w\end{array}\right)\left(\begin{array}{c}\langle I_y^a\rangle \\ \langle I_y^b\rangle \\ \langle I_y^w\rangle \end{array}\right)-\left(\begin{array}{ccc}{\rho }_a& ·& ·\\ ·& {\rho }_b& ·\\ ·& ·& {\rho }_w\end{array}\right)\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^b\rangle -\langle I_o^b\rangle \\ \langle I_z^w\rangle -\langle I_o^w\rangle \end{array}\right)$$ (11)

For the spin “I” (a, b or w), $\langle I_{x,y,z}^i\rangle$ is the expectation values of the X, Y or Z components of the magnetization with $\langle I_0^i\rangle$ given by the thermal equilibrium value. ω_i is the resonance frequency of the spin “i” in the rotating frame rotating at an angular frequency Ω_i such that ω_i = Ω_o − Ω_i, and Ω_o is the applied magnetic field in frequency units. The terms ρ_I and $R_2^i$ are spin–lattice and spin–spin relaxation rate constants with $B_{x,y}^i$ is the RF field along the X, Y axes.

If the spins “i” and “j” of the protein are relaxation coupled to each other, the Z-components of the spin magnetizations can be described by the Solomon equation of motion [67]:

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^b\rangle -\langle I_o^b\rangle \end{array}\right)=-\left(\begin{array}{cc}{\rho }_{ab}& {\sigma }_{ab}\\ {\sigma }_{ab}& {\sigma }_{ab}\end{array}\right)\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^b\rangle -\langle I_o^b\rangle \end{array}\right)$$ (12)

where ρ_ab and σ_ab are the self- and cross-relaxation rates of the dipole–dipole relaxation and for ¹H–¹H interactions are defined as

$$\begin{array}{l}{\rho }_{ab}=\frac{k_{ab}{\tau }_c}{r_{ab}^6}\left(1+\frac{3}{(1+{\mathrm{\Omega }}_o^2{\tau }_c^2)}+\frac{3}{(1+4{\mathrm{\Omega }}_o^2{\tau }_c^2)}\right)\text{and}\\ {\sigma }_{ab}=\frac{k_{ab}{\tau }_c}{r_{ab}^6}\left(\frac{6}{(1+4{\mathrm{\Omega }}_o^2{\tau }_c^2)}-1\right)\end{array}$$ (13)

where τ_c, r_ab and Ω_o are the rotational correlation time (in nanosecond), the internuclear distance between the spins (in Angstroms) and spectrometer frequency (in radians), respectively. The constant k_ab is calculated for a homonuclear ¹H–¹H dipole–dipole interaction.

As the amide proton (spin ‘a’) of the protein undergoes an exchange process with the water spin ‘w’, assuming a two-site exchange process with a rate constant $k_{ex}(={\tau }_{ex}^{-1})$, the time evolution of the Z-components of spins ‘a’ and ‘w’ can be described by McConnell’s equation [68] as

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^w\rangle -\langle I_o^w\rangle \end{array}\right)=-\left(\begin{array}{cc}{k}_{ex}& -k_{ex}\\ -k_{ex}& k_{ex}\end{array}\right)\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^w\rangle -\langle I_o^w\rangle \end{array}\right)$$ (14)

Combination of Eqs. (12) and (14) describes the equation of motion of the Z-components of three spins in the absence of radiation damping.

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^b\rangle -\langle I_o^b\rangle \\ \langle I_z^w\rangle -\langle I_o^w\rangle \end{array}\right)=-\left(\begin{array}{ccc}{\rho }_{ab}+k_{ex}& {\sigma }_{ab}& -k_{ex}\\ {\sigma }_{ab}& {\rho }_{ab}& ·\\ -k_{ex}& ·& {\rho }_w+k_{ex}\end{array}\right)\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^b\rangle -\langle I_o^b\rangle \\ \langle I_z^w\rangle -\langle I_o^w\rangle \end{array}\right)$$ (15)

Following the classical description of RD effects by defining the transverse components B_x,y in Eqs. (11) and (12) as

$$B_{x,y}=\pm \langle I_{y,x}\rangle {\tau }_{rd},$$ (16)

where τ_rd is the radiation damping time (Eq. (3)). RD effects in terms of B_x,y from Eq. (16) can be included in Eq. (9)–(11). Similarly, including the effect of cross-relaxation and chemical exchange from Eq. (15), a modified equation of motion incorporates RD effects on water, chemical exchange between water and amide protons with cross relaxation effects can be written as

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)=-\left(\begin{array}{ccc}{\omega }_a& ·& ·\\ ·& {\omega }_b& ·\\ ·& ·& {\omega }_w\end{array}\right)\left(\begin{array}{c}\langle I_y^a\rangle \\ \langle I_y^b\rangle \\ \langle I_y^w\rangle \end{array}\right)-\left(\begin{array}{ccc}{R}_2^a& ·& ·\\ ·& R_2^b& ·\\ ·& ·& R_2^w\end{array}\right)\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)-{\tau }_{rd}^{-1}\left(\begin{array}{c}\langle I_x^w\rangle \langle I_z^a\rangle \\ \langle I_x^w\rangle \langle I_z^b\rangle \\ \langle I_x^w\rangle \langle I_z^w\rangle \end{array}\right)$$ (17)

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_y^a\rangle \\ \langle I_y^b\rangle \\ \langle I_y^w\rangle \end{array}\right)=-\left(\begin{array}{ccc}{\omega }_a& ·& ·\\ ·& {\omega }_b& ·\\ ·& ·& {\omega }_w\end{array}\right)\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)-\left(\begin{array}{ccc}{R}_2^a& ·& ·\\ ·& R_2^b& ·\\ ·& ·& R_2^w\end{array}\right)\left(\begin{array}{c}\langle I_x^a\rangle \\ \langle I_x^b\rangle \\ \langle I_x^w\rangle \end{array}\right)+{\tau }_{rd}^{-1}\left(\begin{array}{c}\langle I_y^w\rangle \langle I_z^a\rangle \\ \langle I_y^w\rangle \langle I_z^b\rangle \\ \langle I_y^w\rangle \langle I_z^w\rangle \end{array}\right)$$ (18)

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_z^a\rangle \\ \langle I_z^b\rangle \\ \langle I_z^w\rangle \end{array}\right)={\tau }_{rd}^{-1}\left(\begin{array}{c}\langle I_x^w\rangle \langle I_x^a\rangle +\langle I_y^w\rangle \langle I_y^a\rangle \\ \langle I_x^w\rangle \langle I_x^b\rangle +\langle I_y^w\rangle \langle I_y^b\rangle \\ {\langle I_x^w\rangle }^2+{\langle I_y^w\rangle }^2\end{array}\right)\left(\begin{array}{ccc}{\rho }_{ab}+k_{ex}& {\sigma }_{ab}& -k_{ex}\\ {\sigma }_{ab}& {\rho }_{ab}& ·\\ -k_{ex}& ·& {\rho }_{ab}+k_{ex}\end{array}\right)\times \left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^b\rangle -\langle I_o^b\rangle \\ \langle I_z^w\rangle -\langle I_o^w\rangle \end{array}\right)$$ (19)

This model assumes that the transverse component of magnetization created by the intense water spins resulting from RD is similar to a transient and time dependent RF signal that is highly selective to the water frequency. The selective nature of this phenomenon and the RD field from the protein is negligible, unless there is an overlap of the signals from the water and one of the protein spins, the transverse components of spins ‘a’ and ‘b’ (Eqs. (17) and (18)) will be negligible. However, the dynamics of the Z-magnetization of the labile proton can be altered because of the RD of water. Analytical solutions to solve simultaneously the above equation of motion may not be feasible because of the non-linear nature of the equations. However, it is straightforward to adopt a numerical integration procedure (results not shown). In the absence of relaxation effects, the Z-components of water with RD effect and amide protons undergoing intermolecular exchange, Eq. (19) reduces to

$$\frac{d}{dt}\left(\begin{array}{c}\langle I_z^a\rangle \\ \langle I_z^w\rangle \end{array}\right)={\tau }_{rd}^{-1}\left(\begin{array}{c}\langle I_x^w\rangle \langle I_x^a\rangle +\langle I_y^w\rangle \langle I_y^a\rangle \\ {\langle I_x^w\rangle }^2+{\langle I_y^w\rangle }^2\end{array}\right)-\left(\begin{array}{cc}{\rho }_{ab}+k_{ex}& -k_{ex}\\ -k_{ex}& {\rho }_w+k_{ex}\end{array}\right)\left(\begin{array}{c}\langle I_z^a\rangle -\langle I_o^a\rangle \\ \langle I_z^w\rangle -\langle I_o^w\rangle \end{array}\right)$$ (20)

In the absence of RD, analytical solution of Eq. (20) is straightforward [69]. Even though the analytical solution of Eq. (20) is difficult for a general case, the reader is referred to the solutions derived by Chen and Mao [28] under the assumption of strong RD conditions. Recently, a simplified version has been presented by Fan et al. [70] to measure amide exchange rates with the use of RD (vide infra).

3. Measurement of radiation damping

Following the formulation provided by Mao and Ye [71], the value of τ_rd can be evaluated from the water line width, Δν_1/2 (full-width at half height in Hz) measured in the spectrum obtained using a non-selective 90° pulse as:

$${\tau }_{rd}^{-1}=\frac{\mathrm{\Delta }{\nu }_{1/2}}{0.8354}$$ (21)

The magnitude of the RD field can be calculated using the equation provided by Abragam [21] as

$$B_{rd}=\frac{-sin\theta }{\gamma {\tau }_{rd}}$$ (22)

For example, a magnetic field of 11.7 T (500 MHz for ¹H), ηQ_c of 10, and pulse-angle, θ = 90, yield a RD field of 16 Hz [36]. This field is significantly smaller than the radio frequency field of 25 kHz, generated by a typical 90° pulse (pulse width of 10 μs) in a high field NMR spectrometer. Though fairly precise measurement of τ_rd is possible using Eq. (21), line-width measurements are affected by relaxation, inhomogeneous broadening, susceptibility effects, and dipolar or scalar couplings.

Chen et al. [72] proposed an alternative method that involves fitting experimental data to an analytical description. In this approach, the recovery of the inverted magnetization is dominated by RD, in the absence of relaxation effects. In this situation, ${\tau }_{rd}^{-1}$ following the recovery of the Z-magnetization can be written as

$${\tau }_{rd}^{-1}(t-{\tau }_0)=\frac{1}{2}ln\left[\frac{\langle I_z^{eq}\rangle -\langle I_z(t)\rangle }{\langle I_z^{eq}\rangle +\langle I_z(t)\rangle }\right],$$ (23)

where τ₀ is referred to as the ‘latency interval’, the time required for RD to rotate the nearly inverted magnetization onto the transverse plane, This term could be written as

$${\tau }_0=ln\left[tan\left(\frac{{\theta }_0}{2}\right)\right]{\tau }_{rd}$$ (24)

with θ₀ as the azimuthal angle of the magnetization relative to B₀ following the inversion pulse [71]. Fig. 5 shows the results obtained using this method [72].

Fig. 5.

Recovery of the water magnetization in an inversion recovery experiment (180°–τ–90°–acq) used to measure the radiation damping time constant. A sample of sucrose (2 mM) either in 90%H₂O/10%D₂O (continuous line) or 50%H₂O/50%D₂O (dotted line) at proton frequency of 600 MHz. Panel (a) shows the actual recovery of magnetization to equilibrium due to radiation damping, while panel (b) shows the linearization of the data according to Eq. (23). Linear regression was used to determine R_RD = 130.0 ± 0.8 s⁻¹ and t₀ = 22.4 ± 0.2 ms for 90%H₂O (solid line), whereas R_RD = 75.8 ± 0.6 s⁻¹ and t₀ = 41.2 ± 0.3 ms for 50%H₂O (dashed line). Reproduced with permission [72].

The RD time constant sometimes is defined as α (in frequency units ${\tau }_{rd}^{-1}$) [24]. Following this approach, the transverse component of the RD of a single NMR signal can be described as

$${\omega }_{+}^{rd}(t)=-i\alpha I_{+}(t)e^{-i\beta }cos(\beta )$$ (25)

where ${\omega }_{+}^{rd}(t)={\omega }_x^{rd}(t)+i{\omega }_y^{rd}(t)$ and $I_{+}(t)=I_x^{rd}(t)+i{I}_y^{rd}(t)$ are the complex forms of the RD and transverse magnetization, respectively.

The α term is the coefficient of proportionality between the transverse magnetization and the resulting RD field, while β is the phase angle between a vector orthogonal to the precessing magnetization and the RF field induced in the coil. When the probe is tuned exactly at electrical resonance, the RD field is at perfect quadrature with the transverse magnetization, i.e. β = 0. Since probe tuning minimizes reflected power rather than leaving the probe at exact electrical resonance [73], β can be nonzero. Measurement of RD parameters, either in terms of ${\tau }_{rd}^{-1}$ and τ_o (Eqs. (3) and (24)) or α and β are equivalent (Eq. (25)).

3.1. Microcoil NMR probes

Increasing sensitivity, resolution, or both is the fundamental driving force seen by NMR spectroscopy over the last 60 years. Being naturally an insensitive method (low gyromagnetic ratio and small nuclear spin polarization at room temperature) [21], NMR spectroscopy demands large sample volume (500–800 μL) and fairly high concentrations that scares collaborating molecular biologists. However, over the last decade the availability of high-field super-conducting magnets (>14 T) and a steady improvement in NMR probe technology have notably improved the sensitivity of detection [74]. In particular, two kinds of probe technology have been developed recently: (a) probes with cryogenically cooled detector coils [75] that have 2–4 times better sensitivity than standard probes, and (b) small volume probes [76] that are capable of acquiring good quality NMR spectra from microliter [76] down to picoliter [77] sample volumes. Cryogenically cooled probes lower the temperature of the probe detector coil and preamplifiers to increase the sensitivity. In addition, small volume probes utilize the sensitivity improvement from decreasing the diameter of the NMR detector coil.

Although the microcoil probes are optimized for increased sensitivity, the sample volume in these probes is 1–2 orders of magnitude less than the standard probes, suggest that the RD effects may be minimal. A detailed investigation by Krishnan, however, suggests otherwise [78]. There are few differences between the standard NMR probes and microcoil NMR probes; most detectors with probe volumes greater than 50 μL described in the literature, are based on Helmholtz saddle coils [79,80]. This allows sample exchange by commercially available NMR glass tubes. For sample volumes of less than 45 μL the detector is typically a solenoid coil [76,81]. The microcoil probe has a solenoidal detection coil, which must be orthogonal to the B₀ field. Furthermore, the use of conventional NMR sample tubes for sample exchange is not possible. Inherently, solenoidal microcoil NMR probes have a higher intrinsic sensitivity [82] than saddle coils (Helmholtz coils) by a factor of 2–3, because of stronger coil-sample coupling. The sensitivity of solenoidal coils is given by [79,80]

$$\frac{B_1}{i}=\frac{{\mu }_{0}n}{\sqrt{1+{\left(\frac{h}{d}\right)}^2}}$$ (26)

where B₁ is the applied radio frequency field, i is the current unit, μ₀ is the permeability in a vacuum, n is the number of turns, d is the diameter of the coil, and h is the length of the coil. Microcoil probes take advantage of decreasing ‘d’ to increase the sensitivity. The reduction in ‘d’ subsequently leads to a significant increase in the filling factor (η) of the probe. Typically, microcoil probes are able to achieve improved values (η ~ 0.64), whereas the standard 5 mm saddle coil probes are able to achieve only η ~ 0.3 [81]. The microcoil probes also have exceptional RF homogeneity and small coils that lead to short RF pulses. These factors allow the ability to attain an excellent control of the water magnetization in comparison with standard probes.

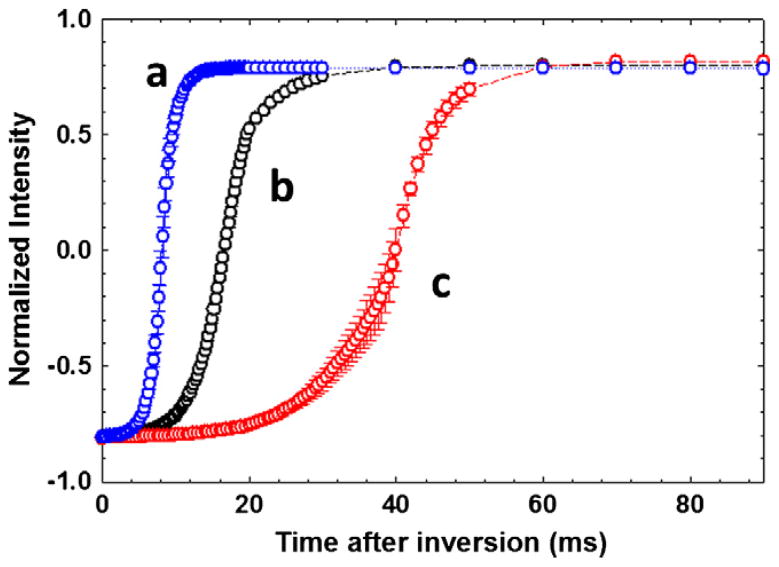
Fig. 6 summarizes the experimental data obtained to measure the ${\tau }_{rd}^{-1}$ using the method above [72] in a microcoil solenoid probe (black), a 5 mm saddle (blue), and 8 mm saddle probe (red). Table 1 lists the radiation-damping rate constant ( ${\tau }_{rd}^{-1}$); t₀ and the correlation coefficient of the linear fit of the data to Eq. (6) for each probe. Results in Table 1 show a significant amount of RD in the microcoil probe (rate constant of 114.1 s⁻¹, which corresponds to a RD time of 8.76 ms). The 5 mm and 8 mm probes indicated RD rate constants at 108.7 and 554.8 s⁻¹, and with RD times of 9.2 and 1.8 ms, respectively. These results compare well with the results of Chen et al. [72], as seen with ${\tau }_{rd}^{-1}$ ranges from 75.8 s⁻¹ to 130.0 s⁻¹and τ₀ ranges from 41.2 ms to 22.4 ms. These ranges are dependent on the amount of H₂O in the sample at the proton resonating frequency of 600 MHz. RD in the microcoil probe is slightly stronger than in the 5 mm probe, but weaker in the 8 mm probe.

Fig. 6.

Plot of the recovery of water magnetization after inversion due to radiation damping in (a) standard 5 mm (saddle) indirect detection probe (5 mm IDPFG, 550 mL, blue), (b) microcoil (solenoid) NMR probe (25 μL, black) and (c) standard 8 mm (saddle) triple resonance probe (8 mm TR-PFG, 730 mL, red). The Intensity along the Y-axis is the area under the water resonance and the recovery time is along the X-axis. The error bars determine the standard deviation over four consecutive measurements. (remade using the data presented in [78]. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Radiation damping rate constants in microcoil NMR probe at 600 MHza.

NMR Probeb	${\tau }_{rd}^{-1}(s^{-1})$	τ0 (ms)	Sample (active) volume (μL)
Microcoil (S/N: 32:1)	114.10 ± 1.50	1.28 ± 0.03	25 (5)
5mm (S/N: ~900:1)	108.72 ± 5.80	9.09 ± 1.12	550 (222)
8mm (~1, 400:1)	554.84 ± 12.34	26.14 ± 4.18	730 (325)

^aTable adopted from reference [78]. ${\tau }_{rd}^{-1}(s^{-1})$ and t₀ (ms) are estimated using non-linear least squared fit to Eq. (23) (R₂ > 0.98).

The much smaller standard errors in the magnetization recoveries in Fig. 6 and τ₀ values in Table 1 show that the water magnetization recovers mainly though radiation-damping effects in the microcoil probe and the effects are observed in a cleaner fashion than in the 5 mm and 8 mm probes. The latency interval (τ₀, Eq. (24)) is related to the initial azimuthal angle θ₀ of the magnetization relative to B₀ following the imperfect inversion pulse, and is given by rewriting Eq. (24) as,

$$\frac{{\theta }_0}{2}={tan}^{-1}(exp({\tau }_0{\tau }_{rd}^{-1})).$$ (27)

Upon using Eq. (27), the azimuthal angles θ₀ for the microcoil, 5 mm and 8 mm probes are 26°, 31° and 44°, respectively. This variation in θ₀ is directly proportional to the external influences (B₀ or RF inhomogeneity) within a metastable state of the inverted magnetization of the water magnetization. Lower values of θ₀ indicate that there is less influence from destabilizing factors, such as RF inhomogeneity.

Radiation damping for the protons at a given probe temperature is directly proportional to the filling factor η, quality factor Q_c and the concentration of protons within the sample volume (Eq. (3)). The quantities Q_c and η are often optimized to increase the sensitivity of the NMR probe. Thus, it is natural to expect the RD effects also to increase sensitivity. In fact, Guéron and Leroy [50] suggest that ${\tau }_{rd}^{-1}$ can be used as a measure of the absolute sensitivity of the probe, as it is directly proportional to both η and Qc. For the RD effects in the microcoil probe to be comparable to those in a standard 5 mm probe, the increase in ηQ_c must be of the same order of magnitude as the reduction in the number of water protons.

To determine which factor (η or Q_c) has the greater contribution to the RD effects, we can use the measured ${\tau }_{rd}^{-1}$ values from Table 1, along with other known probe specifications The ratio of ${\tau }_{RD}^{-1}$ between the 5 mm and microcoil probe is 0.95 (108.72 s⁻¹/114.1 s⁻¹), while the volume ratio is 44.4 (222/5) [81]. The filling factor values are 0.3 and 0.64 for the 5 mm and microcoil probes, respectively, and the ratio of the quality factors ( $Q_C^{\mathit{cap}}/Q_c^{5\text{mm}}$) of the probes is estimated to be 19.7. This estimate assumes that Eq. (2) provides a valid description of the RD effects in 5 mm (Helmholtz coil) and the solenoid microcoil (capillary) probes. One of the major inferences from this rough estimate is the effects of RD in the microcoil probe is due to an increase in the filling factor, η, rather than the quality factor, Q_c. The RD time constant of the microcoil probe is approximately the same as that of the 5 mm probe, and 1/4 that of the 8 mm probe at the same spectrometer field strength and sample temperature. Therefore, it is important to optimize the water suppression and water-selective pulses, when using samples with large amounts of water in the microcoil probes. Due to an increased RF performance (short pulse widths with good B₀ and B₁ homogeneity), the water selection and control will be more efficient in microcoil probes in comparison with other standard probes, including the cryogenically cooled detector coil probes (see below).

3.2. Cryogenic NMR probes

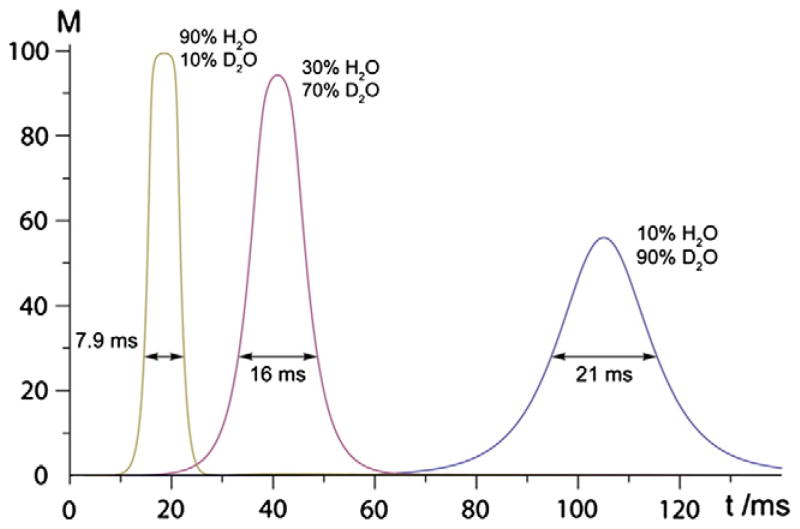
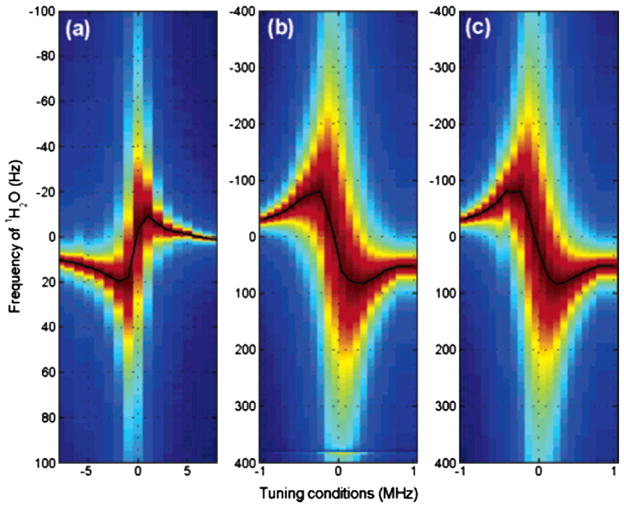
Cryogenic probes achieve improved sensitivity partially by the increased quality factor of the RF coil and therefore one would expect significant increase of RD as well. Extending the studies with microcoil probes, to probes with cryogenically cooled detector coils that have approximately 3 times more sensitivity than a standard probe would also increase the RD effects. However, the increased effect will be primarily due to increase in the Q_c, rather than η (in cryogenic probes the filling factor is usually less than the normal probes). This estimation has been confirmed in a preliminary investigation of the RD effects in a cryogenically cooled detector coil probe and its impact on heteronuclear experiments [83]. Recently, Shishmarev and Otting [84] presented a detailed study on the RD effects in cryogenic probes at spectrometer frequencies of 600 MHz and 800 MHz. Fig. 7 shows free induction decays for three different v/v ratios of H₂O/D₂O (9:1,3:7 and 9:1) with the corresponding τ_rd listed in each case. The results from this study [84] provide the following conclusions: (a) RD parameters obtained directly (measured using the FID) and indirectly (from data fit to x, y and z components by simulation of Bloch equations with RD, Eq. (1) and Fig. 1) can be different from observed magnetization trajectories, and (b) inspection of the FID observed after an inversion pulse easily leads one to underestimate the actual RD-field strength acting during a pulse sequence, especially if the most intense part of the signal is attenuated by preamplifier overload. Though the strong RD field associated with the cryoprobe makes it harder to control intense solvent signals, it opens new opportunities for convenient water flip-back incorporations in biomolecular NMR experiments. The enhanced RD requires careful optimization of selective water flip-back pulses and water flipdown pulses. The power requirement for a 180 flip-back pulse is somewhat less than that of the flip-down pulse. In the former case the magnetization rotation towards the +z-axis is aided by the RD field and in the latter the rotation towards −z-axis is made by the RD field. Such fine optimizations have been incorporated in bio- NMR pulse sequences (for example in BioPack sequences in Varian/Agilent NMR systems).

Fig. 7.

Radiation damping effects of water signal in a cryogenically cooled probe at 800 MHz. Each FID is acquired after inversion of the thermal equilibrium water magnetization followed by pulsed-field- gradient (PFG) of 40 G cm⁻¹ for period of 0.9 ms. Reproduced with permission from [84].

4. Influence of radiation damping in diffusion and relaxation experiments

Radiation damping can affect a wide multitude of NMR experimental measurements from self-diffusion coefficients to relaxations times. In this section, we present some of the methods described in recent literature to circumvent its effect.

4.1. Diffusion coefficient measurements

Pulsed field gradient spin echo NMR is generally the method of choice for making diffusion measurements on liquid samples. With modern high field instruments, however, severe problems can arise when applied to samples with very high proton concentrations as a result of RD. The problems may be reduced by choosing suitable experimental parameters. In particular, the use of modified stimulated echo pulse sequences, with a reduced flip angle for the first pulse. However, if sensitivity is an issue then use of small-flip angle pulses can result in an unacceptable reduction in the signal to the noise level of the resonances.

Krishnan et al. [85] introduced a simple modification that uses the RD effects of the water in an advantageous manner. The pulse sequence, designated as BPP-SED, is an optimized combination of the bipolar-gradient pulse pair longitudinal-eddy-current delay (BPP-LED) sequence proposed by Wu et al. [86] to measure diffusion coefficients and the selective echo dephasing (SED or also known as MEGA)sequence [87]. BPP-LED is an excellent method for measuring self-diffusion coefficients because the bipolar-gradients can reduce the effects of inhomogeneous background gradients, cancel more than 95% of the eddy current, combine bipolar-gradients with the 180° pulses to reduce the active sample volume to regions where both RF and gradient fields are homogeneous [86]. Fig. 8 indicates the modified pulse sequence in the following manner. In the original design of the BPP-LED pulse sequence, a 0°/180° phase shift of the second 90° pulse is required to minimize the relaxation of the protein signal during the diffusion period ‘T’. Although, the water and the protein magnetization undergo the same pulses and delays, only the water magnetization that is along the −z axis at the end of the 180° phase shift is highly susceptible to RD effects. In measurements of self-diffusion coefficients of proteins using ¹H NMR a diffusion delay typically around 100–150 ms can be used, which is sufficient time for the RD effect to selectively flip the water spins to +z axis. Thus, at the end of the ‘T’ period of the sequence, the water and protein spins are along the −Z and +Z axes, respectively. The rest of the sequence after the ‘T’ period does not differentiate between the water and protein spin magnetizations, allowing for an appropriate receiver phase cycle to be used to reduce effective water signaling. The resulting phase cycle, employing constructive use of RD to suppress water magnetization, is given in the caption of Fig. 8.

Fig. 8.

The time sequence of radio frequency (RF) pulses and pulsed field gradients (G_x, G_y and G_z along X, Y and Z-axis respectively) in filled and hatched bars respectively used in the PFG experiments to measure diffusion coefficients [85]. Thick and thin filled bars are the 180° and 90° hard pulses, respectively while the pulses marked as ‘S’ are single lobe sinc shaped pulses used to selectively invert water magnetization and of length 4 ms. The various delays used in the sequence are; τ = 0.1 ms, δ2 = 7 ms, and T = 130 ms. Gradients for the diffusion coefficient measurement (long hatched bars) are varied from 1 G cm⁻¹ to 32 G cm⁻¹ in units of 0.5 G cm⁻¹, while the other gradients (small hatched bars) are applied at a strength of 30 G cm⁻¹ for 1 ms each, yielding a total echo time (τ₁ + τ₂) of 14.026 ms. The phase cycling required to advantageously utilize the RD effects for water suppression is; ϕ₁ = 2(x), 2(y), 2(−x), 2(−y); ϕ₂ = 2(y), 2(−x), 2(−y), 2(x); ϕ₃ = −x, x, −y, y, x, −x, y, −y; ϕ₄ = 2(x), 2(y), 2(−x), 2(−y); ϕ₅ = 2(y), 2(−x), 2(−y), 2(x); ϕ₄ = 2(x), 2(y), 2(−x), 2(−y), 2(−x), 2(−y), 2(x), 2(y); receiver phase ϕ_r = −y, y, x, −x, y, −y, −x, x. Reproduced with permission from [85].

Price et al. [88] investigated the effect of both macroscopic gradient and RD effects on diffusion coefficient measurements. The dynamics of water magnetization was examined under various modifications of the pulsed-gradient spin-echo (PGSE) sequence. The authors concluded that RD greatly complicates the performance of diffusion measurements involving strong NMR resonances and can cause effects similar to those caused by background gradients. Apart from using a very small sample, accurate PGSE based diffusion experiments can be conducted either by keeping all transverse magnetization spatially encoded during as much of the sequence as possible or by allowing part of the magnetization to (reproducibly) decay before starting the diffusion part of the sequence. The authors extended the approach to a Q-switched sequence [89] that was effective in suppressing RD effects.

4.2. Relaxation, NOE and exchange measurements

Wu and Johnson [90] first addressed the effect of RD on inversion recovery experiments, with the suggestion of using homospoiled-pulses (pulsed field gradient) to dephase the residual transverse magnetization at the beginning of the recovery period.

Radiation damping effects can alter homonuclear NOESY experiments of biomolecules in aqueous solutions. Several experimental methods have been developed over the years to suppress water resonances in an NMR experiment, although only a few have explicitly focused on controlling RD all through the pulse sequence. “Water flip-back” sequences in heteronuclear NMR have been described [91,92] in the context of minimally saturating water and simultaneously minimizing effects of RD and increase the sensitivity of the coherence transfer between ¹H-¹⁵N spins. Lippens et al. [93] have demonstrated, that the combination of a water flip-back selective pulse at the end of the NOE mixing time with a water suppression scheme before the detection period can provide an overall good water suppression by keeping the water magnetization close to equilibrium. This approach has been adopted in performing ROESY experiments [94] and using cryoprobes [84]. In a comprehensive article Hiller et al. [95] provides a recipe for managing and optimizing water polarization in order to obtain an improved NMR spectra of large biomolecules. This paper presents a formalism to follow the propagation of water polarization during the course of the NMR experiments and demonstrates the optimization process.

The radiation damping time in cryoprobes is in the order of 1–2 ms, which is shorter than a typical water-selective pulse than a water-flip back pulse sequence. Shishmarev and Otting [84] improved the performance of NOESY and TOCSY experiments by incorporating RD-driven water flip backs at the end of the mixing time. This allows the water magnetization to return to the positive z-axis regardless of its previous orientation, while any other transverse component is dephased by pulsed field gradients. The pulse sequences and the corresponding spectra are shown in Fig. 9. These new developments use a combination of RD-compensated water-selective 90° pulses, such as WATERGATE sequence for selecting protein magnetization while maintaining water flip-back conditions with weak bipolar gradient pulses [96,97]. One of the ways to minimize the RD delay is to keep the water magnetization far away from the inversion by placing the carrier frequency on the water resonance and applying a phase shift of 45° between the two 90° pulses surrounding the evolution time (t₁ period of the 2D experiment) [98]. These authors further note that RD-driven water flip-back can be more efficient if placed towards the end of the mixing time rather than at the start. As mentioned earlier, constructive use of radiation damping is more effective in cryoprobes with robust water suppression than it is in the active manipulation of the water magnetization by a series of phase-cycled water-selective 90° pulses, with each selective pulse being compensated separately for radiation damping effects.

Fig. 9.

(a) NOESY pulse sequence and the spectrum with RD-driven water flip-back at the start of the mixing time τ_m. (b) Improved NOESY pulse sequence and spectrum where RD-driven water flip-back occurs only at the end of the mixing time during the delay τ_rd. (c) TOCSY pulse sequence and corresponding spectrum with RD-driven water flip-back at the end of the mixing time. NMR experiments were performed at 800 MHz using a cryoprobe and a sample of 0.5 mM solution of ubiquitin fused to a 15-residue peptide in 90%H₂O/10%D₂O at pH 7.0 and 25 °C. The NOESY and TOCSY mixing times were 60 ms. Refer to [84] for additional details. Pulses sequence and spectral data are adopted from [84] (reproduced with permission).

5. Artifacts and surprises of radiation damping

Radiation damping is commonly assumed to affect signals only in a narrow frequency range close to the solvent resonance. In addition to the complications it poses in selective excitation of solvents [99] and solvent signal suppression [100], Sobol et al. [101] have demonstrated how RD can influence signals with frequencies differing by several kHz from the solvent signal. During multi-pulse NMR experiments, the magnetic fields caused by the RD related field can become time dependent enabling the system to be nonlinear and influence the resonance frequency positions of all the nuclei in the sample. This feature is of particular importance in pulse sequences that are designed to study macromolecular hydration effects [101]. Investigation of the hydration of biological macromolecules in solution, is an application unique for NMR spectroscopy [64,102–105] and these experiments are highly prone to artifacts from the effects of RD. The pulse sequences for these techniques rely heavily on detection of weak signals in the presence of intense water resonances. Sobol et al. [101] demonstrated that in certain biological hydration experiments, the small magnitude of the RD field (15–30 Hz at 700–800 MHz) can disturb the nuclei that resonate from 2 to 3 kHz away from the solvent signal. Particularly, in exchange mediated experiments the effect of pre-saturation eliminates the water magnetization during the initial portion of the experiment [23,63,103]. Methods to reduce these artifacts involve careful optimization of a range of parameters that need to be tested for each sample individually. The general test include a cancelation tests for the relay step, a difference test with pre-saturation of the solvent signal experiments to evaluate the building up of solvent-protein NOEs, either a short mixing time (<5 ms) experiment or preferably a build-up curve with short mixing steps (<100 μs). In contrast to the RD effects, the demagnetization effects tend to introduce ‘dispersion-like’ subtraction artifacts.

5.1. Radiation damping induced frequency shifts

One topic that has received rather less attention is the effect of RD when a probe is not at exact electrical resonance [32]. Traditionally, detuning of the probe has been used as a method of reducing the effects of RD, in a trade-off against signal-to-noise ratio. Detuning reduces the line broadening effects of RD both by reducing the induced current, and by reducing the angle between the precessing magnetization, and the secondary radiofrequency field generated by the coil. Even slight detuning has been shown to introduce unexpected effects in multiplet patterns [24]. In a comprehensive simulation study, Vlassenbroek et al. [32], described the RD phenomenon using an ideal tuning circuit of the NMR probe with the aid of the Maxwell–Bloch equations. The particular solution to these equations includes all aspects of radiation feedback to the circuit [32]. The time dependent solution of the magnetization vector indicated a frequency shift to the observed resonance line that is directly influenced by the circuit properties. Accordingly, the frequency shift is given as

$$\mathrm{\Delta }\mathrm{\Omega }(t)=\frac{\langle {\stackrel{\sim }{I}}_z\rangle (t)}{\langle I_z^0\rangle }\frac{Q}{{\tau }_{rd}}\frac{{\mathrm{\Omega }}_{LC}^2}{{\mathrm{\Omega }}_o^2}\left(\frac{{\mathrm{\Omega }}_o^2-{\mathrm{\Omega }}_{LC}^2}{{\mathrm{\Omega }}_o^2}\right),$$ (28)

where ΔΩ (t) is the time-dependent frequency shift and 〈Ĩ_z〉(t) is the expectation value of the z-magnetization having a Larmor frequency Ω₀ and a corresponding equilibrium value of 〈I₀〉. Q_c and τ_rd are the quality factor and RD time (Eq. (3)), respectively while Ω_LC is the resonance frequency of the idealized LC circuit. Eq. (28) shows that there will be a non-zero frequency shift when the probe is detuned (|Ω_o − Ω_LC| ≠ 0) which is directly proportional to the RD time constant ( ${\tau }_{rd}^{-1}$). This measurement of the signal in a pulsed NMR experiment creates a small change in the magnetic field experienced by the spins. At higher magnetic field strengths (>10 T), the equilibrium proton magnetization of concentrated solutions generates a dipolar field (Section 2.2). Edzes [106] has demonstrated that these effects change the line shape of the observed signals to non-Lorenzian and can induce a measurable shift in the resonant frequency. The frequency shift predicted by Eq. (28) is not due to the demagnetization field but is a direct consequence of RD as well as mistuning of the probe. The frequency shift is negligible when the concentration of spins is low or when the probe is tuned to the resonance frequency of the circuit (Ω_o ≅ Ω_LC).

Huang et al. [107] demonstrated these effects in high-resolution solution NMR systematically for various probe configurations and as a function of the flip-angle of the read pulse to 〈Ĩ_z〉(t). Fig. 10 shows the dependence of ΔΩ (Eq. (28)) on the probe tuning conditions in a sample of 95%H₂O (5%CH₂Cl₂) after a small flip-angle pulse. The frequency shift plotted along the Y-axis is symmetrical with respect to the probe tuning (center of the X-axis). Consequently, the resulting RD induced frequency shift as a function of probe detuning exhibits maximum shifts, the positions of which depend on the particular probe design. This work leads to an important optimization that may be required in pre-saturation experiments to set the saturation irradiation frequency to the frequency of the residual solvent magnetization signal following suppression by other means.

Fig. 10.

Frequency shifts induced by the combined effects of radiation damping and probe detuning. Frequency changes of the 95%H₂O/5%CH₂Cl₂ in the ¹H spectra (normalized to the peak) at 300 K as a function of probe detuning. Spectra were acquired after applying a 10° pulse to the sample. (a) Standard 5 mm probe (b) cryoprobe and (c) simulations using experimental data in (b). Note the small detuning (±1 MHz) in the cryoprobe to introduce large frequency shifts, while the conventional probes need to much more out of tune (±8 MHz) Reproduced after permission from [107].

Recently Torchia [108] extended this work to multiple spectrometer frequencies (including ^1Hν = 900 MHz) using cryoprobes at each frequency. The measured frequency shifts as a function of detector circuit tuning offset from 500 to 900 MHz are in agreement with the predicted shifts (Eq. (28)). This study highlights that even a small degree of mistuning, can significantly influence the performance of a pulse sequence: mistuning the probe detector circuit by only ca. 0.01% of the carrier frequency (50 or 100 kHz at 500 or 900 MHz, respectively) can lead to shift in the water resonance frequency of ±0.03 ppm. The author suggests that the proton chemical shifts of two spectra, in reference to water, could suffer a difference of 0.06 ppm. This is a consequence of small fractional differences (positive or negative) between ω_o and ω_LC. Such an error in chemical shift referencing would negatively influence many types of NMR experiments that focus on measuring small changes in chemical shifts. These errors can be important in measurements of small residual anisotropic chemical shifts [109] related to structure determination of proteins [110] and nucleic acids [111–113].

6. Controlling radiation damping

Pulse sequences designed to suppress strong solvent signals in NMR spectra can alter the dynamics of the RD. Solvent suppression schemes can be divided into pre- and post-incorporation of pulsed field gradients with shielded gradient coils. Of the several review articles on solvent suppression before the use of PFG [114–117] the one by Gueron et al. [118,119] considered RD in all aspects of solvent signal suppression. Recently Price et al. [120] and McKay [121,122] provide detailed accounts of the current state of the field including applications to biomolecules and metabolomics. In this section, we focus exclusively on solvent suppression schemes that address the effects of RD. Following the traditional description of NMR experiments according to Ernst [123], the pulse sequence can be divided into four periods: preparation, evolution, mixing and detection. Methods used for control of RD are often optimized to work mostly during the preparation period of an experiment, such as in the solvent suppression schemes.

Radiation damping effects may be eliminated from the NMR spectrum either using hardware (probe) modifications or by modifications in the pulse-sequences. Two major hardware based approaches have been proposed: RF feed-circuit [124,125] and Q-factor switches [99,126]. Both these hardware based approaches are successful in eliminating RD to a large extent. Pulse sequence based eliminations include use of selective pulses to compensate for noise modulations [72,127,128]. In general all these approaches are fairly successful in their respective applications, yet none of them seems to have been adopted for use on a routine basis.

6.1. Hardware modifications

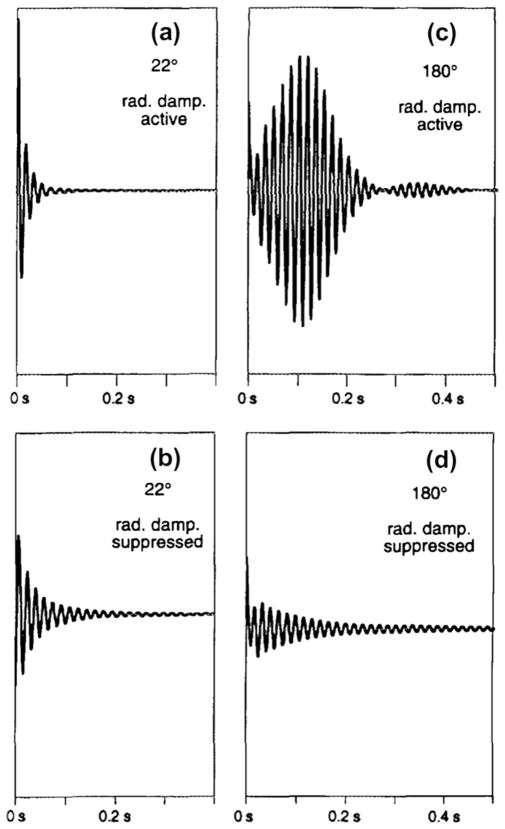
In a historical perspective, the very first experimental method for reducing RD was provided by Chidambaram in 1959 [125]. The author suggested that by applying negative feedback to the resonant circuit containing the sample, the RD effect can be reduced without deterioration in the signal-to-noise ratio. Broekaert and Jeener [124] demonstrated that the RD effects can be strongly suppressed by RF feedback on the tuned probe circuit, without appreciable degradation of the signal-to-noise ratio for the detection of small signals. The logic behind this idea is the fact that RD acts akin to a self-soft pulse and in a tuned probe causes the spin magnetization to rotate to its equilibrium. The idea is to keep the RF current in the sample coil very small, except during the RF pulses, by counteracting the EMF induced by the nuclear precession with a feedback signal derived from the output of the RF amplifier of the spectrometer. Fig. 11 demonstrates the effect of the RF feedback on the observed signals. Louis-Joseph et al. [129] showed that the solvent suppression of a conventional jump and return pulse sequence [130] can be enhanced by feeding a fraction of the residual solvent signal into the NMR probe. This results in amplifying the RD between consecutive transients, but not during signal acquisition.

Fig. 11.

Demonstration of the effect of feed-back loop to control radiation damping effects. Panels (a) and (c) show the free induction decay (FID) after a 22° and 180° pulse to spins in thermal equilibrium using standard NMR probe configuration. Panels (b) and (d) show same experiments using the active electronic feedback modification of the probe. Vertical scale is all the panels. All the experiments were performed in a 300 MHz ((¹H) solid-state spectrometer. Reproduced after permission from [124].

In most NMR experiment the pulse widths are in the order in μs, while the rest of the delays are in the range of milliseconds. RD effects can be neglected during the RF pulses, but is dominant during the delays, switching the Q_c of the coil to a smaller value during the delay time can significantly reduce RD effects. Therefore, the idea behind the Q-switch, is to have a large Q-factor of the RF coil only during the pulses and signal acquisition. The high Q-factor contributes to a short pulse length and high sensitivity while the Q-factor can be set low during free-precision delays in the NMR sequence by the grounding of the RF coil. Anklin et al. [99] described a “Q-switch probe’, in which the Q_c of the resonant circuit is rapidly switched back and forth (time constant of <2 μs) between a high value (regular operation) and low-Q mode (close to zero) where the radiation damping is effectively eliminated. In this implementation the probe was switched to a low-Q mode during the evolution time of a 2D experiment or during the recovery delay during the inversion-recovery experiment to measure T₁ values. In a modified implementation Maas et al. [126] demonstrated the ability to perform Q-switching during the acquisition time as well. In spite of the advantages offered by this approach, only limited applications have been noted in the literature [89,131].

6.2. Pulse sequence modifications

Instead of altering the dynamics of RD using probe circuit switching as discussed above, some authors have suggested modifications in the pulse sequences and data acquisition schemes [132–134]. These methods in general require only software modifications, with no alterations to the probe, and no significant loss of spectrometer sensitivity. Barjat et al. [133] suggested the application of a DANTE sequence [135] of hard pulses of small flip angle to nudge the solvent magnetization back again to +z-axis by means of a series of tiny rotations about the +x axis. As the DANTE sequence behaves like a soft radiofrequency pulse, this can provide a suitably long duration for RD to show effects on the solvent resonance. Instead of controlling RD during acquisition, Böckmann and Guittet [134] incorporated long selective pulses at the water frequency along with gradient echoes inserted between the single pulses of a DANTE train. This approach was referred to as the WANTED (water-selective DANTE using gradients). Chen et al. [132] presented a method for compensating radiation damping during the application of selective RF pulses prior to beginning the pulse sequence. This method has also been used to measure amide proton exchange rates in proteins [127].

Recently Michal [128] developed a method to control radiation damping with spatially-encoded noise. The method is based upon the encoding of a structured pattern of noise into the spatial distribution of magnetization and was inspired by an optical spectroscopy technique known as noise autocorrelation spectroscopy with coherent Raman scattering (NASCARS) [136]. This provided a similar excitation-imposed noise structure imprinted upon broad optical spectra to improve resolution. Experimental demonstration showed that this approach can be applied to both radiation damping and one-dimensional field inhomogeneity with improvement in line widths of more than a factor of 40, with possible applications to two-dimensional NMR.

Use of bipolar gradient pulses in both homonuclear and heteronuclear experiments to control radiation damping, suggested by Sklenar [97] has been a frequently used approach. This is an easy to implement method when used with correctly positioned water flip-back pulses [84,137] and has produced consistent results in a large number of biomolecular NMR experiments.

7. Constructive use of radiation damping effects

7.1. Solvent suppression schemes

Excellent review articles [25,119,120,122,138] describe in detail the wide range of schemes available for the control of water magnetization in biological NMR experiments. In this section we present an overview of the techniques that use RD as part of the active design for the desired purpose. Price et al. [139,140] introduced a water-pre-sequence suppression (Water-PRESS) in which the longitudinal relaxation behavior of the water is manipulated by a train of homo-spoil pulses to differentiate the water from the protein resonances. Water-PRESS sequences perform an optimization between the RD time, spin–lattice relaxation times of the water and the proteins to reduce the relative intensity of water resonance. Recently, Xiao-Hong et al. [141] have adopted a similar approach to optimize only the RD effects.

7.2. Exchange measurements

Chen and Mao provided a detailed account on the effects of RD on chemical exchange [28,29] and later the effects were demonstrated by Rodriguez et al., in NMR studies on the osmolyte solution of glycine [66]. In a seminal work related to exchange mechanisms, Williamson et al. [142] investigated the effect of RD in Z-spectroscopy, which refers to the measurement of the perturbation of a solvent’s Z-magnetization as a function of the frequency of a long off-resonance saturation pulse [143,144]. Asymmetric Z-spectra were shown to be the consequence of both RD and probe tuning in a theoretical and experimental study of a one-pool system and an exchanging two-pool model.

Measurement of amide hydrogen exchange with water is fundamental to understanding protein dynamics as it directly relates to accessibility to solvent, early protein folding events as well as to local and global dynamics [145–148]. A large number of heteronuclear NMR experiments have been developed to measure amide exchange rates [149,150]. In typical amide hydrogen-exchange experiment the non-equilibrium magnetization of water (typically inversion) created in the preparation period is allowed to undergo intermolecular exchange with the protein amide protons for a given mixing time. At the end of mixing, normally the transferred magnetization is detected using a ¹⁵N-edited heteronuclear correlation spectrum such as HSQC [151,152]. As the inherent property of the RD of water selectively returns the water magnetization to the +z axis after a non-selective pulse to all the resonances in the spectrum, it can be constructively utilized in measuring amide exchange rates. Although, careful choice of pulse phases can be used to optimize the water magnetization prior to the exchange experiment [153], radiation damping mechanism can alter water’s position during the exchange period which might in turn affect the measured exchange rates. Radiation damping effects allow only the water to align in an opposite direction with respect to other proton magnetizations. Though it conveniently sets the initial conditions, quantification of exchange rates with water gets complicated because, during the mixing periods, the water recovery is modulated by RD. Fan et al. [70] recently introduced a method that accounts for these effects in measuring the exchange rates. In order to account for the RD effects in solutions where water is undergoing chemical exchange with amide protons (Eq. (20)), a latency delay (Eq. (24)) due to RD is introduced. The sample dependent delay was experimentally measured from the RD recovery curves and empirically adjusted to provide the best fit to the exchange process [70]. The magnetization transfer process was shown to fit to the following equation:

$$\langle I_z^a\rangle (t)=\langle I_z^{\mathit{ref}}\rangle \frac{k_{ex}}{{\rho }_{ab}-{\rho }_w+k_{ex}}(e^{-{\rho }_w(t-{\tau }_o)-e^{-({\rho }_{ab}+k_{ex})(t-{\tau }_o)}})$$ (29)

Eq. (29) is solution to the two-spin exchange system [69] and τ₀ is the latency delay introduced due to RD.

7.3. Weak radiation damping effects

Most of the techniques discussed above focus on strong RD effects and their influence on the NMR spectra. In a notable review article, Szantay and Demeter [37] point out that weak RD effects are seldom detected, although they can appreciably influence the recovery of non-equilibrium magnetization to thermal equilibrium as in relaxation-time measurements. The authors observe that in spin–lattice relaxation time measurements, weak RD does not alter the shape of the recovery curve when a near 180° pulse (inversion recovery) is used. However for a near 90° pulse (saturation recovery), the RD effects can appreciably shorten the time to recover to thermal equilibrium even if the RD time (τ_rd) is an order of magnitude longer than the effective spin–spin relaxation time ( $T_2^{\ast }$). A new experimental scheme, RD difference spectroscopy (RADDSY) was proposed to reveal the effect of weak RD [37]. For high sensitivity probes it is reasonable to assume that these effects might influence magnetization-transfer processes such as found in experiments involving cross-relaxation or chemical exchange and in particular for dynamical events occurring at time scales < $T_2^{\ast }$.

8. Summary and challenges

In summary, we have presented an overview of radiation damping (which should perhaps be known as Suryan’s line broadening effect) with an historic perspective and by revisiting the phenomenon’s impact on the quality of the spectra of samples in aqueous solutions obtained using high field NMR spectrometers. The classical description of RD based on the Bloch–Maxwell equation has presented and solved by numerical integration methods. The ultimate goal of obtaining high resolution, accurate structures of biomolecules in solution depends on obtaining high quality NMR data. Consideration of methods that can either eliminate or beneficially use RD will enable researchers to reach this goal.

Re-examining the effect of RD on the quality of NMR spectra opens up several new avenues of research in high field NMR spectroscopy, since optimization of the sample signals alone does not guarantee an improvement in the quality of the data. Techniques to suppress, utilize and control RD during the entire course of an experiment need to be developed. Examples of techniques to suppress RD include simple pre-saturation technique [154,155] of the water signal, using multiple excitation pulses [25,119], in combination with pulsed field gradients [120,121]. Radiation damping is difficult to control during the course of a multiple pulse experiment since the water spins undergo the same set of pulses as that of the sample protons. It is inevitable that RD will affect the spectrum of molecules in solvents containing a high concentration of protons. The increased sensitivity of high field NMR spectrometers is a double edged sword. On the one edge, the increased sensitivity allows the acquisition of NMR data for samples at lower concentrations, but at the other, it makes it possible to observe RD effects, which were considered negligible only a short time ago.

^b Microcoil (capillary microcoil NMR probe, microcoil, MRM corporation, Savoy, USA); 5 mm: standard 5 mm inverse detection probe (Varian Inc., Palo Alto, California, purchase year 1997); 8 mm: standard 8 mm triple resonance probe (Varian Inc., Palo Alto, California, purchase year 1997); the probe has an S/N ratio estimated using a 10 mM sucrose (anomeric proton) sample in D₂O (4 scans, no presaturation, and no line broadening).

Abbreviations

NMR

nuclear magnetic resonance

NOESY

nuclear overhauser effect

PFG

pulsed field gradient

PGSE

pulsed gradient spin echo

RD

radiation damping

ROESY

rotating frame nuclear overhauser effect spectroscopy

TOCSY

total correlation spectroscopy

TROSY

transverse relaxation optimized spectroscopy