Sherlock: Detecting Gene-Disease Associations by Matching Patterns of Expression QTL and GWAS

Abstract

Genetic mapping of complex diseases to date depends on variations inside or close to the genes that perturb their activities. A strong body of evidence suggests that changes in gene expression play a key role in complex diseases and that numerous loci perturb gene expression in trans. The information in trans variants, however, has largely been ignored in the current analysis paradigm. Here we present a statistical framework for genetic mapping by utilizing collective information in both cis and trans variants. We reason that for a disease-associated gene, any genetic variation that perturbs its expression is also likely to influence the disease risk. Thus, the expression quantitative trait loci (eQTL) of the gene, which constitute a unique “genetic signature,” should overlap significantly with the set of loci associated with the disease. We translate this idea into a computational algorithm (named Sherlock) to search for gene-disease associations from GWASs, taking advantage of independent eQTL data. Application of this strategy to Crohn disease and type 2 diabetes predicts a number of genes with possible disease roles, including several predictions supported by solid experimental evidence. Importantly, predicted genes are often implicated by multiple trans eQTL with moderate associations. These genes are far from any GWAS association signals and thus cannot be identified from the GWAS alone. Our approach allows analysis of association data from a new perspective and is applicable to any complex phenotype. It is readily generalizable to molecular traits other than gene expression, such as metabolites, noncoding RNAs, and epigenetic modifications.

Introduction

Recent application of genome-wide association studies (GWASs) to complex human diseases led to the discovery that the majority of disease-associated variants (estimated to be as high as 88%) are located in noncoding sequences, potentially affecting gene expression rather than protein function.^1,2 Because of the complexity of gene regulation, the expression of a gene can be modulated by mutations in cis (proximal to the gene) and/or in trans (distal to the gene or on different chromosomes, such as upstream transcription/chromatin factors, distal regulatory elements, etc.).^3,4 As a result of a large mutational target size (primarily because of mutations in trans) and the buffering of gene regulatory systems that helps tolerate expression changes, genetic variants altering expression levels are common in populations.⁵ Indeed, many studies of expression quantitative trait loci (eQTL) demonstrate that the expression of most genes is influenced by multiple loci, most of which act in trans.^6–9 Despite their individually small effect sizes, trans eQTL are collectively important for variation of gene expression and by some estimates account for a larger proportion of the heritability of gene expression than do cis eQTL.^8,10

Because of their prevalence in the human population, expression variations, especially those in trans, provide systematic perturbations of the gene regulatory networks underlying various complex phenotypes, and as such might reveal important information about the genetic basis of these phenotypes. Thus there is a pressing need to develop a general framework to mine the collective information in both cis- and trans-expression QTL in the context of association studies. So far, information from trans variations has largely been ignored because only cis variants can be assigned to their target genes based on proximity by using the GWAS data alone. The growing collection of eQTL data for various human tissues makes it possible to associate trans variants with target genes.⁸ Although previous studies demonstrated the utility of eQTL data for aiding the analysis of association studies,^9,11 most of these used only cis eQTL located close to the genes. This reflects some fundamental difficulties of utilizing information in trans. Because trans eQTL are usually much weaker than those in cis, the statistical signal of an individual trans eQTL is difficult to detect—it may fall far below the genome-wide threshold.⁹ Another major challenge is the pleiotropic effect of trans variation. A gene’s trans perturbation may come from the mutation of a regulatory molecule, but this mutation may also affect multiple other genes.

Here we present a general strategy to infer genes whose perturbations contribute to the etiology of complex diseases by tapping into statistical information provided by both cis and trans variations affecting gene expression. Although individual variants are often weak and not particularly informative, the overall pattern of expression variants of a gene can provide a strong statistical signal. A unique aspect of this strategy is that because we utilize trans variants far from target genes, it is possible to identify important genes distal to any GWAS association signals and thus impossible to detect with GWAS alone.

To illustrate the basic concept, we consider a gene whose expression level may influence the risk of a complex disease. There may be multiple variants in the genome that affect the expression of this gene in a disease-related tissue (these are expression SNPs, or eSNPs; technically eSNPs are only in linkage disequilibrium with the causal variants, though we do not make the distinction here). A change of genotype at any of these eSNPs will lead to a change of expression level, which could in turn alter the disease risk (Figure 1A). Therefore, many of these eSNPs are likely to be associated with the disease as well. In general, each gene has a different set of eSNPs across the genome, with different effect sizes, reflecting the unique regulatory program governing the expression of this gene. The characteristic pattern of all genetic associations with the expression of a gene thus constitutes a unique “genetic signature” of this gene (Figure 1B, top). Similarly, we can define the genetic signature of a phenotype as the statistical association of all the loci in the genome to the phenotype. If the expression level of a gene influences the disease risk, the genetic signature of this gene should match, at least partially, the genetic signature of the disease (Figure 1B, bottom).

Figure 1.

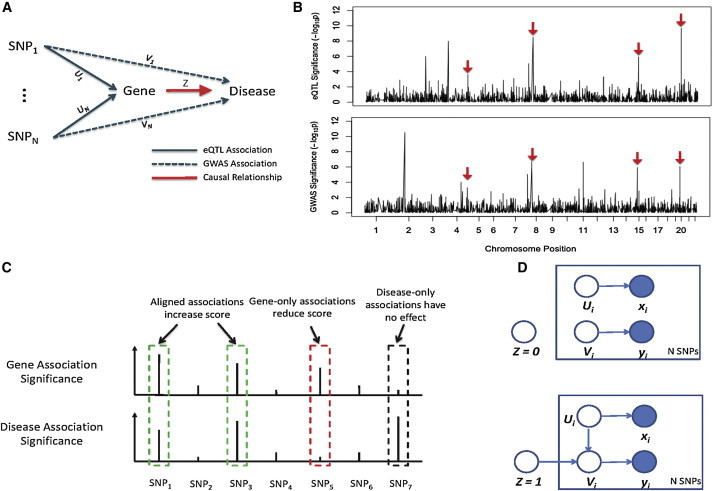
The Sherlock Algorithm: Matching Genetic Signatures of Gene Expression Traits to that of the Disease to Identify Gene-Disease Associations

(A) Perturbation of the expression level of a disease-associated gene at any of its eQTL changes the disease risk, and thus the eQTL tend to be associated with the complex disease as well (the dashed lines). The eQTL associations may contain false positives, so we use binary indicator variables, U, to represent the true SNP-gene expression relationship; similarly we use indicator variables, V, for the SNP-disease relationship. Z is a binary variable indicating whether the expression trait influences the disease risk.

(B) Hypothetic genome-wide association plots of the causal expression trait (top) and a complex disease (bottom). The genetic signature of the gene expression trait partially overlaps with that of the disease. Red arrows indicate the matched loci.

(C) Alignment of genetic signatures of a gene expression trait and the phenotype. Three different scenarios are shown, represented by the green, red, and black boxes.

(D) The probabilistic model representing the dependency of the variables. The semantics of the variables U, V, and Z are shown in (A). When Z = 0, U and V are independent (top). When Z = 1, V depends on both Z and U; if U = 1, then V is also likely to be 1 (bottom). The association statistics of a SNP with respect to the gene expression trait and the disease (x and y) depend on the hidden variables U and V. Shaded and open circles indicate observed and latent variables, respectively.

Our analysis identifies potential gene-disease association by matching the genetic signature of a gene to that of the disease, using the GWAS data of the disease and the eQTL data of a related tissue. It is worth emphasizing that we do not directly test the statistical relationships between genotypes, gene expression, and phenotypes, as done by earlier methods.¹² Thus, the eQTL and GWAS data do not have to come from the same subjects. Instead, the eQTL data provide information of the genetic signatures of many genes, and then in an independent GWAS of some phenotype, the match of a gene’s signature with the GWAS would suggest that the gene plays a role in that phenotype. This is much like how a detective works (hence the name of our algorithm, “Sherlock”): he compares the fingerprint from a crime scene (like our GWAS association data) against a database of fingerprints (like our eQTL data) to determine the real culprit (the genes whose expression levels influence the disease risk).

We implement this idea of genetic signature matching by using a Bayesian statistical framework. Instead of applying a stringent cutoff, we utilize both strong and moderate SNPs in the eQTL and GWAS data. The statistical model allows us to access information in the moderate SNPs without introducing many false signals. Application to two well-studied diseases shows the promise of our approach. We predicted ten genes associated with Crohn disease (MIM 266600), six of which are highly plausible based on literature evidence. With an independent GWAS data set, all but one gene were replicated. Among our four predicted genes associated with type 2 diabetes (T2D [MIM 125853]), three are supported by experimental evidence from literature, and the other is a promising candidate based on a combined analysis of multiple genomic data sets.

In summary, our approach allows the analysis of association studies from a different perspective and, as we demonstrate, enables the discovery of genes and pathways missed by the traditional GWAS analysis. We have constructed a web-based resource to facilitate the application of our method. We collected eQTL data sets from multiple human tissues and provided the software to search for gene-disease associations with the disease GWAS as a query (only p values are needed). With the increasing collection of eQTL data (as well as QTL of other molecular phenotypes), we expect that these resources/tools will become an important platform for interpreting the results from association studies.

Material and Methods

Statistical Model

Given a gene and the disease of interest, our method tests whether the expression change of the gene has any effect on the risk of the disease, using the information of N putative eSNPs of the gene (passing some low significance threshold in the eQTL data). We define binary indicator variables U_i and V_i to represent whether the i^th SNP is associated with the expression and the disease trait, respectively, and a binary indicator variable Z to represent whether the gene is associated with the disease (Figure 1A). Our data consist of the p values of SNPs relative to the gene expression trait (eQTL profile), denoted as vector x, and the p values of the SNPs relative to the phenotypic trait (GWAS profile), denoted as y. Although U_i and V_i are not observed, they are related to x_i and y_i: when x_i(y_i) is small (i.e., the SNP is highly significant), it is likely that U_i(V_i) is true. We use the data x and y to test the hypothesis H₀ (i.e., Z = 0) that the gene is not associated with the disease versus the alternative hypothesis (H₁). The dependencies of the statistical variables are shown in Figure 1D. We describe some intuitions of our model. Under H₀, the gene is irrelevant to the phenotype, and thus U_i and V_i, are independent in a statistical sense (Figure 1D, top). Under H₁, a true eSNP of the gene is expected to be associated with the phenotype (Figure 1A). In other words, whenever U_i is true, V_i should also be true under H₁ (Figure 1D, bottom).

Our inference is based on the posterior ratio, defined as:

$$\frac{P\left(Z=1|x,y\right)}{P\left(Z=0|x,y\right)}=\frac{P\left(Z=1\right)}{P\left(Z=0\right)}\times \frac{P\left(x,y|Z=1\right)}{P\left(x,y|Z=0\right)}.$$ (Equation 1)

The first term in the right side is the ratio of the prior probabilities of H₁ and H₀. Typically, the prior ratio is small because only a small fraction of all genes are expected to be associated with a disease. The second term is the ratio of model evidence (i.e., the probability of data under H₁ or H₀) called the Bayes factor (BF). The BF is similar to the familiar likelihood ratio test and does not depend on the prior probabilities. We will focus on computing the BF for the inference task.

We assume all SNPs are unlinked (see below for LD blocks). The BF of the gene expression trait is the product of the BF of all SNPs:

$$B=\prod _i{B}_i=\prod _i\frac{P\left(x_i,y_i|Z=1\right)}{P\left(x_i,y_i|Z=0\right)}.$$ (Equation 2)

The likelihood function at each SNP at a given Z is computed by summing over the hidden variables U_i and V_i:

$$P\left(x_i,y_i|Z\right)=\sum _{U_i,V_i}P\left(U_i\right)P\left(V_i|Z,U_i\right)P\left(x_i|U_i\right)P\left(y_i|V_i\right).$$ (Equation 3)

U_i is a Bernoulli random variable with the success probability α (the prior probability of a SNP being associated with the expression trait). The information about the gene-disease relationship is encoded in the conditional probability P(V_i | Z, U_i). When Z = 0 or when Z = 1 and U_i = 0 (a false eSNP), V_i is a Bernoulli random variable with the success probability β (the prior probability of a SNP being associated the phenotype). When Z = 1 and U_i = 1, according to our discussion before, V_i should also be 1. The probability terms P(x_i | U_i) and P(x_i | V_i) reflect the distribution of p values under the null or alternative hypothesis, and we derive these distributions in Appendix A.

The Bayes factor defined in Equation 2 can be expressed in terms of the following variables:

$$B_{i,x}=\frac{P\left(x_i|U_i=1\right)}{P\left(x_i|U_i=0\right)}{B}_{i,y}=\frac{P\left(y_i|V_i=1\right)}{P\left(y_i|V_i=0\right)}.$$ (Equation 4)

These are the Bayes factors measuring the association of the i^th SNP with the expression and the phenotypic trait, respectively. We show, in Appendix B, that the BF of the i^th SNP in Equation 2 is given by

$$B_i=\frac{1-\alpha }{1-\alpha +\alpha B_{i,x}}+\frac{\alpha B_{i,x}}{1-\alpha +\alpha B_{i,x}}\frac{B_{i,y}}{1-\beta +\beta B_{i,y}}.$$ (Equation 5)

Thus the Bayes factor of the gene being tested depends only on the parameters α, β, and the SNP-level Bayes factors. If Bayesian inference has been performed in both the eQTL and GWAS analysis, it is straightforward to combine the resulting BFs to obtain the BF for the gene.

Dealing with Linkage Disequilibrium

For multiple adjacent SNPs, we use a block-level BF in Equation 2. According to Duan et al.,¹³ a block is defined as a region of the genome containing one or more eSNPs associated with the same gene and having a between-eSNP interval of <500 Kb. Although this criterion appears somewhat arbitrary, it does not have a large impact on our analysis primarily because by defining eSNPs with a certain threshold (p < 10⁻⁵), most eSNPs naturally fall into blocks. To combine the BFs of individual SNPs in a block, we follow Servin and Stephens:¹⁴ the block-level BF is the mean of the BFs of all SNPs in that block. It has been shown that this simple averaging is a reasonable way of dealing with dependent SNPs in a region.¹⁴

Model Analysis

To gain some intuition into our method, we show that it leads to a scoring scheme that is similar to sequence alignment but with an inherent asymmetry (Figure 1C).¹⁵ According to Equation 2, the total score (logarithm of BF, or LBF) of a gene is the sum of LBF of each SNP, written as S_i = logB_i. We discuss the value of S_i for different types of SNPs. We first note that in Equation 5, both α and β are small numbers (prior probabilities, typically less than 0.01). For a SNP not associated with the gene expression trait, B_i,x < 1, thus αB_i,x ≪ 1, according to Equation 5, S_i ≈ 0. These SNPs are not informative, regardless of their association status with the phenotype. For the informative SNPs, we consider only very strong eSNPs for simplicity of analysis, αB_i,x ≫ 1, and we have this approximation:

$$S_i=\log B_i\approx \log \frac{B_{i,y}}{1+\beta B_{i,y}}.$$ (Equation 6)

We analyze three possible cases depending on the strength of association of a SNP with the phenotype. (1) The SNP is strongly associated with the phenotype βB_i,y ≫ 1, and thus we have S_i ≈ log(1/β). This is a positive number and represents the reward when the signatures of the two traits match at this SNP. (2) The SNP is moderately associated with the phenotype B_i,y > 1 but βB_i,y ≪ 1, and thus we have S_i ≈ logB_i,y > 0, representing the positive but smaller contribution of the SNP. (3) The SNP is not associated with the phenotype B_i,y < 1, and thus we have the approximation S_i ≈ logB_i,y < 0. The negative score represents the evidence against the gene.

This analysis allows us to understand some properties of the model. First, the score of any SNP is always bounded by log(1/β), even if the SNP reaches extremely low p values. Thus the LBF of a gene is generally not dominated by a single SNP (except for genes with relatively few eSNPs). Another property of the model is that the score of a SNP moderately associated with the phenotype (S_i ≈ logB_i,y) is not sensitive to the parameter β. Thus we see that β determines the relative contribution of strong versus weak SNPs: a smaller value of β favors a single strong SNP over multiple weaker ones. In general, we believe that genes supported by multiple SNPs are more interesting than those supported by single strong SNPs, which are probably due to the pleiotropic effects of SNPs (SNPs independently associated with gene expression and the phenotype). This suggests that we should use a relatively high value of β. Meanwhile, this would lead to a conservative estimate of the Bayes factor (because the maximum LBF per SNP is log(1/β)).

Statistical Significance of Bayes Factors

We use simulation to compute the p values of the BFs, a procedure known as Bayes/non-Bayes compromise.¹⁴ To generate the null distribution of the BFs, we fix the eQTL profiles (the p values of putative eSNPs) of all the genes and randomize the GWAS data K times (see below for the details of randomization). The resulting BFs of all genes over all the K-simulated GWAS data sets then form the genome-wide null distribution. The p value of each gene is estimated from the ranking of its BF in this null distribution. We used K = 50 in our experiments.

To create a randomized GWAS data set, we follow the procedure described in Liu et al.¹⁶ Note that we need to generate randomized GWAS data only for all the putative eSNPs across all genes, because other SNPs will not enter the BF calculation. For each gene, we first divide all its putative eSNPs into blocks, then the p values of each block are sampled independently: within each block, a multivariate normal (MVN) random vector is sampled with the covariance matrix matching the LD structure of the block, and the vector is then converted to p values of SNPs. It has been shown that this MVN-based approach is a very good approximation of the full permutation procedure (random swapping of cases and controls).¹⁶

We choose not to perform permutation of eQTL data because our statistical procedure depends on the alignment of the eQTL and GWAS profiles, which are relative to each other. Thus permuting GWAS data should be equivalent to permuting eQTL data. In practice, permuting eQTL data is more difficult to implement, because there are correlated structures in eQTL data that are difficult to account for and the genotype data of eQTL are generally not available.

Choice of Parameters

The parameters α and β specify the prior probabilities of a SNP being associated with an expression and a phenotypic trait, respectively. We further distinguish between cis and trans eSNPs: α should be higher for cis eSNPs (within 1 Mb of the gene) than for trans eSNPs. As per the guidelines in literature,¹⁷ we chose these values: α = 1.0 × 10⁻³ (cis) and 5.0 × 10⁻⁵ (trans), β = 1.0 × 10⁻³. We provide some intuitive explanation of these parameters. If we assume there are a total of one million SNPs, the number of SNPs close to a gene (within 1 Mb of the coding sequence) is roughly 1,000,000/3,000,000,000 × 2,000,000 = 1,000 (only order-of-magnitude estimate is made here). Assuming a gene has one cis eSNP, the prior probability α for SNPs in cis is 1/1,000 = 10⁻³. For trans eSNP, we assume that a gene may have a relatively large number of eSNPs across the genome, say 50, then the prior probability for SNPs in trans is 50/1,000,000 = 5.0 × 10⁻⁵. Our selection of the value of β is based on the following: (1) complex traits are known to be associated with hundreds of loci,¹⁸ and (2) according to the discussion in the section “Model Analysis,” a somewhat high value of β is preferred for our model. We chose β = 10⁻³ in our experiments.

For a SNP associated with a trait, we assume that its effect size follows a prior normal distribution $N\left(0,{\mathrm{\sigma }}_a^{\mathrm{2}}\right)$. The default value of the prior variance parameter is 0.5 for expression traits and 0.2 for phenotypic traits, based on earlier studies.^14,17 We note that these parameters are not necessary if the Bayes factors of SNP associations are available from eQTL and GWAS analysis, according to Equation 5. In addition to these prior parameters, the method also requires the disease prevalence (5.0 × 10⁻⁴ for Crohn disease and 0.1 for type 2 diabetes) and allele frequencies for each SNP (from HapMap).

Computational Experiments

The eQTL and GWAS data were downloaded from their respective sources. Because only putative eSNPs are informative, we applied a weak cutoff to eQTL based on p values: p < 10⁻⁵ for trans associations and p < 10⁻⁴ for cis associations. Each gene with at least one putative eSNP is scored by our program.

In the replication experiment for Crohn disease, we took the meta-analysis data from IBD Genetics Consortium.¹⁹ Because this data set includes some data we used for predicting disease genes, we removed it by using the weighted subtraction algorithm in Zhong et al.,²⁰ and this gave about 2,000 cases and 7,000 controls.

Coexpression Analysis of PURB

The gene expression data were taken from several studies in humans^21–23 and various mouse crosses.^12,24,25 The weighted coexpression networks were constructed with previously described methods to derive subnetworks or modules containing highly coregulated genes from each tissue.²⁶ We retrieved all network modules that contain PURB from all coexpression networks and then extracted all genes that share module membership with PURB as PURB-coexpressed genes. These genes are then ranked by how often they appear with PURB in the same modules.

Results

Genetic Signature Matching Algorithm: Sherlock

Our algorithm takes as input the association results from independent eQTL and GWAS experiments and aims to identify genes whose expression levels may influence the disease risk. It uses summary statistics (p values of the associations), but does not require the genotype and phenotype data. As discussed previously, it assumes that such genes will have multiple, coincident loci with elevated significance in both the GWAS and eQTL data sets (Figures 1A and 1B). The algorithm scores the significance of the overlap by the statistical model described in Material and Methods.

To see why significant overlap supported by multiple loci may imply causality, we consider two alternative scenarios.¹² In the first scenario, a SNP may affect the disease and also happen to affect the expression of a gene that has nothing to do with the disease. However, the likelihood that multiple disease-associated SNPs happen to affect the expression of the same gene by chance is very small. In the second scenario, the disease may compromise the gene expression patterns of relevant cells, causing some expression traits to share loci with the disease. This scenario is also unlikely because the eQTL mapping used for our analysis is usually performed in individuals unrelated to the GWAS phenotype, and thus the disease loci generally should not affect gene expression in these samples.

Intuitively, our algorithm performs an alignment of the genetic signature of one phenotypic trait against an expression trait. For any SNP, there are potentially three scenarios, depending on the association of the SNP with the two traits (Figure 1C). Any SNP that appears to be associated with both traits contributes a positive score to the gene (Figure 1A). Any SNP associated with the expression trait but not the disease is evidence against the role of the gene, contributing a negative score. The third type of SNPs are associated with the disease but not the expression of the gene being tested. Because they are not informative for this gene at the expression level, they will not contribute to the score of the gene.

We compute the Bayes factor (or its logarithm, LBF) for each gene (see Material and Methods), which evaluates evidence supporting that the gene is associated versus not associated with the disease. Specifically, we first compute the LBF score of each putative eSNP of the gene being tested, which represents how strongly the SNP supports a functional role of this gene (see Material and Methods). The LBF score of a SNP is analogous to the nucleotide matching scores in sequence alignment, with the sign of the score corresponding to the three situations described above (also see Material and Methods, “Model Analysis”). For the cases where multiple SNPs in LD are associated with a gene, we define a block-level LBF and treat them as if they were a single SNP (see Material and Methods, “Dealing with Linkage Disequilibrium”). Herein, the set of all eSNPs of a gene are represented by a set of independent eSNPs, each of which may actually represent a block of adjacent SNPs. The total LBF score of a gene is the sum of LBFs of all SNPs. The value of the LBF score of a gene reflects the strength of evidence: for example, a LBF of 2.3 means that the posterior probability of the gene being associated with the disease is exp(2.3) = 10 times more likely than the opposite hypothesis assuming that the two hypotheses are equally likely a priori. In practice, a gene is a priori far more likely to be unrelated to the disease, so we generally demand a high LBF (e.g., at least 4.0).

Although BFs can be directly used for inference under a purely Bayesian framework,²⁷ we take an approach, known as Bayes/non-Bayes compromise, to compute the p values of the BFs based on simulations. This has the advantage that the results are less sensitive to the prior assumptions.¹⁴ Ideally, the simulation procedure would permute the case/control labels of the subjects in the GWAS data to obtain the null distribution of the BFs (we discuss in Material and Methods why permutation is applied only to the GWAS and not to the eQTL data). In practice, this requires genotype data (which is generally not publicly available) and is computationally intensive. We use an approximation scheme to generate randomized GWAS data by modeling the LD structure in the genome with multivariate normal (MVN) distributions.¹⁶ We correct for multiple hypothesis testing by using the standard Benjamini-Hochberg procedure.²⁸

It is important to emphasize the use of SNPs that fail to reach traditional thresholds for genome-wide statistical significance. For both gene expression and phenotypic traits, recent studies suggest that a large number of loci may have small effects and fall below the statistical threshold.^8,18 Rather than excluding modest GWAS and eQTL associations up front, our statistical method takes them into account and relies on the unlikely occurrence of chance overlap to assign strong significance at the gene level. For example, consider a hypothetical gene with four independent eSNPs, each having a p value of 0.001 in the GWAS of a disease. Individually, these SNPs are far from achieving genome-wide significance. However, the chance that all four eSNPs achieve such p values in GWAS is extremely low: 0.001⁴ = 10⁻¹². Hence, by combining multiple weak signals, it is possible to achieve strong statistical confidence.

Overview of Experiments

In each experiment, a GWAS data set (summary statistics or p values) of some trait is provided and the program runs the analysis against eQTL data of a relevant tissue in unrelated subjects. For all experiments, the program uses a default set of parameters. For each gene, a LBF score and its p value based on simulation are computed. The distribution of the p values of all genes is analyzed to determine the false discovery rate (FDR) of the predictions. For both Crohn disease and type 2 diabetes, we reported statistically significant findings. We further assessed the predictions by a combination of literature search, replication with independent GWAS, and analysis of additional genomic data sets.

Application to Crohn Disease

Our first experiment is on a GWAS meta-analysis of Crohn disease (3,230 cases and 4,829 controls)²⁹ uses the eQTL data from lymphoblast B cells (LBL).¹³ Crohn disease is an autoimmune disease of the intestines, one of two major forms of inflammatory bowel disease (IBD). The LBL eQTL (mainly cis eQTL) has been widely used to support the analysis of GWAS data of immune-related diseases including Crohn disease.^9,11,30 The original GWAS data suffers from modest population stratification (λ = 1.17), so we applied the genomic control procedure before further analysis.³¹ With only cis eSNPs, we identified a single SNP, close to ORMDL3 (MIM 610075), that passes the respective thresholds in both GWAS and eQTL, consistent with the previous findings.²⁹ In contrast, Sherlock identified a number of significant genes: the Q-Q plot of our predictions for all genes shows a clear excess of genes with small p values (Figure 2A). To rule out p value inflation, we created randomized GWAS data by randomly assigning individuals from the 1000 Genomes Project to “case” and “control” groups.³² We then performed the same analysis on this randomized data with the real LBL eQTL data set. The p values from this experiment closely follow the uniform distribution, suggesting that our test is well calibrated (Figure S1 available online).

Figure 2.

Quantile-Quantile Plots of the p Values at the Log. Scale of All Genes Calculated by Sherlock

(A) Analysis of GWAS data of Crohn disease with the eQTL of lymphoblast B cells.

(B) Analysis of T2D GWAS data with the liver eQTL.

At p < 10⁻⁴ (the FDR at this p value threshold is 0.09), we predicted ten genes (Table 1). Three of the ten, PTGER4 (MIM 601586), ORMDL3, and SLC22A5 (MIM 603377), were reported in the original GWAS paper and supported by additional studies.^29,33 Below we discuss the remaining genes and additional analyses. Except for UBE2L3 (MIM 603721), which is supported by a combination of cis and trans eSNPs, all the remaining genes are supported only by trans-acting SNPs (Table 2, full results in Table S1). Importantly, most of these supporting SNPs have moderate p values in both eQTL and GWAS data and therefore are generally ignored in the traditional GWAS analyses.

Table 1.

Top Predicted Genes for Crohn Disease

Gene	LBF	p Value	GWAS Hit	Supporting Evidence	p Value (Rep.)
UBE2L3	7.78	2.2 × 10−6	no	associated with celiac disease, rheumatoid arthritis, and lupus34	4.2 × 10−6
ORMDL3	5.72	3.3 × 10−5	yes	associated with Crohn disease and ulcerative colitis29,33	1.0 × 10−6
PTGER4	5.57	3.7 × 10−5	yes	associated with Crohn disease33	3.4 × 10−5
IK	5.43	4.3 × 10−5	no	regulates class II MHC antigen, which is associated with autoimmune diseases38	0.75
LYNX1	5.34	4.8 × 10−5	no	agonist of nonneuronal nAchR pathway, which may be important for IBD39–41	0.014
NUDT4	5.32	4.8 × 10−5	no	NA	3.4 × 10−5
EFS	5.23	6.1 × 10−5	no	knockout mice exhibit symptoms similar to Crohn disease36,37	0.039
FAM96A	5.19	6.3 × 10−5	no	NA	4.2 × 10−6
SLC22A5	5.17	6.3 × 10−5	yes	associated with Crohn disease29,33	3.8 × 10−5
ANAPC2	4.87	9.2 × 10−5	no	NA	0.0006

The LBF column is the logarithm of the Bayes Factor for the genes. The p values refer to the p values of LBFs, calculated from simulations. The “GWAS hit” column shows whether a gene has been implicated as a candidate gene in previous GWASs. The last column shows the p value of the genes using an independent GWAS data set of Crohn disease (replication). See the text for details of the supporting evidence.

Table 2.

Supporting SNPs for Some of the Predicted Genes of Crohn Disease

Gene	SNP	SNP Location	Proximity	eQTL p Value	GWAS p Value	LBF
UBE2L3 (7)	rs2283790	chr22: 20,286,653	cis	6.0 × 10−6	8.9 × 10−6	6.7
	rs7735799	chr5: 84,248,096	trans	3.0 × 10−6	7.2 × 10−4	1.3
EFS (16)	rs2154490	chr21: 29,837,833	trans	6.0 × 10−6	3.5 × 10−4	2.6
	rs8044972	chr16: 75,957,583	trans	1.0 × 10−6	2.0 × 10−2	1.9
	rs6843282	chr4: 32,433,817	trans	9.0 × 10−6	2.0 × 10−3	1.4
	rs2210054	chr14: 33,091,890	trans	1.0 × 10−5	5.9 × 10−3	0.8
LYNX1 (5)	rs921719	chr8: 126,615,379	trans	1.0 × 10−5	7.8 × 10−5	3.7
	rs11205709	chr1: 50,581,881	trans	1.0 × 10−5	2.8 × 10−3	1.1
	rs1998564	chr13: 107,034,232	trans	1.0 × 10−6	1.2 × 10−2	0.7

A SNP is called in cis of a gene if it is located within 1 Mb of the transcription start site of this gene. Each SNP in the table actually represents a block of adjacent eSNPs (chosen to be the one with the highest LBF). The number in parentheses in the Gene column shows the total number of putative eSNP blocks (defined as p < 10⁻⁵ in the eQTL data) of that gene. The LBF column shows the LBF of individual SNP (see Material and Methods). Only SNPs with LBF greater than 0.5 are shown.

Notably, the genetic and experimental evidence strongly suggest possible roles for UBE2L3 and EFS (MIM 609906) in Crohn disease. UBE2L3 was associated with several autoimmune diseases, including systemic lupus erythematosus (MIM 152700), celiac disease (MIM 212750), and rheumatoid arthritis (MIM 180300).³⁴ Because autoimmune diseases often share genetic risk loci,³⁵ the combined evidence supports the role of UBE2L3 in Crohn disease. EFS has not been associated with autoimmune diseases in previous GWASs. However, in mouse studies, Efs overexpression was shown to inhibit T lymphocyte development³⁶ and Efs knockout mice exhibit exaggerated T-cell-mediated immune responses.³⁷ Remarkably, the knockout mice develop tissue-specific inflammatory lesions in their small intestine, a pattern very similar to Crohn disease.³⁷ Additionally, the target of EFS, the kinase FYN (MIM 137025), is marginally significant (p = 9.6 × 10⁻⁴, FDR < 0.25). Together, this evidence suggests that EFS is a strong candidate gene for Crohn disease.

Two other genes in our list have well-established immune functions and are possibly related to autoimmune diseases and IBD. IK (MIM 600549) encodes a cytokine that downregulates class II MHC antigen whose aberrant expression has been associated with autoimmune diseases.³⁸ LYNX1 (MIM 606110) encodes a signaling peptide of nicotinic acetylcholine receptors (nAChR).³⁹ The nonneuronal cholinergic system plays an important function in regulating the development and activation of T and B cells.⁴⁰ Smoking (nicotine) affects both types of IBD, and it was recently found that these effects are mediated through alpha7 nAChR,⁴⁰ a target of LYNX1.³⁹ Furthermore, agonists of alpha7 nAChR affect the disease condition in experimental colitis (a model of IBD) in mice.⁴¹ This evidence suggests a likely role for LYNX1 in Crohn disease through its effect on nAChR-mediated signaling pathway.

Next, we performed a replication experiment with an independent GWAS data set for Crohn disease¹⁹ and the same eQTL data set. All genes, except IK, are replicated at p < 0.05 (Table 1). The extent of replication is highly significant (p = 1.8 × 10⁻¹¹, binomial test).

In summary, of the ten genes predicted by our method at FDR < 0.1, six are known to be associated with Crohn disease and/or IBD or are strong candidates supported by both independent discoveries from literature and replication (UBE2L3, ORMDL3, PTGER4, LYNX1, EFS, and SLC22A5). One concern is that the genes in the lymphoblasts eQTL data are enriched with immune-related functions,¹¹ and thus even a randomly chosen set will hit some plausible candidate genes. We performed some estimation and a computational experiment to rule out this possibility. In this eQTL data set, a total of ∼9,200 genes have at least one putative eSNP (defined by the same thresholds used for the predicted genes). Assuming there are 1,000 risk genes of Crohn disease (probably an overestimate), and even if they all belong to this list of 9,200 genes, the chance that a randomly chosen gene is associated with Crohn disease is only 1,000/9,200 = 11%, a ratio far below that of our predictions (6 out of 10, p = 2.5 × 10⁻⁴, binomial test). Next we randomly sampled two dozen genes from the set of ∼9,200 genes and manually judged their relevance to Crohn disease by searching literature in the same way as we did for our candidate genes (Table S2). Only three genes were found to have some immune function, but none specifically related to IBD, compared with seven immunity-related genes (the six candidates plus IK) out of ten in our predictions (p = 0.002, Fisher’s exact test). Despite some limitations (e.g., manual judgment is inherently unreliable), the very conservative nature of our estimation and the strong statistical trends in both analyses suggest that the eQTL data alone cannot explain the results.

Finally, we explore gene networks underlying Crohn disease by using information from trans eSNPs that might reveal potential upstream regulatory genes. We found an interesting group of genes with moderate statistical support (nominal p values from .001 to .003; Table S3) that are associated with the same two independent SNPs in trans (Figure S2). Most of these genes are related to some aspects of autoimmunity (Table S3). Because they are all affected by the same two eSNPs, this group may be involved in the same molecular pathway affecting Crohn disease. Interestingly, one of the two SNPs, rs10248053, is located inside RELN (MIM 600514), which is associated with the age of onset of multiple sclerosis (MIM 126200), an autoimmune disease,⁴² and may also be involved in a subtype of T cell leukemia.⁴³

Application to Type 2 Diabetes

We next performed an experiment on the GWAS of T2D from DIAGRAM (4,549 cases and 5,579 controls)⁴⁴ by using liver eQTL.⁴⁵ Previous studies that used the liver data have provided insights on T2D, though only cis eSNPs were utilized.^20,45 The p values of the vast majority of the genes closely track the uniform distribution, with about a dozen genes significantly above the diagonal line in the Q-Q plot (Figure 2B). The analysis using permuted GWAS data confirmed the absence of p value inflation (Figure S1). At p < 10⁻⁴ (FDR 0.3 at this p value cutoff), we predicted four genes (Tables 3 and 4). Two of the four, PURB (MIM 608887) and GNB5 (MIM 604447), are supported only by trans-acting SNPs. Similar to Crohn disease, most of the supporting SNPs have only moderate statistical significance in both the GWAS and eQTL data sets.

Table 3.

Top Predicted Genes for Type 2 Diabetes

Gene	LBF	p Value	GWAS Hit	Supporting Evidence
TSPAN8	6.08	9.4 × 10−6	yes	associated with T2D in GWAS48
PURB	6.07	9.4 × 10−6	no	expression is causal to T2D-related phenotypes (see text)
GNB5	4.97	8.9 × 10−5	no	deletion leads to T2D symptoms46,47
JAZF1	4.93	9.5 × 10−5	yes	deletion leads to T2D symptoms;49 GWAS association48

The LBF column is the logarithm of the Bayes Factor for the genes. The p values refer to the p values of LBFs, calculated from simulations. The “GWAS Hit” column shows whether a gene has been implicated as a candidate gene in previous GWAS. See the text for details of the supporting evidence.

Table 4.

Supporting SNPs for the Predicted Genes for Type 2 Diabetes

Gene	SNP	SNP Location	Proximity	eQTL p Value	GWAS p Value	LBF
TSPAN8 (5)	rs7298255	chr12: 69,714,336	cis	2.7 × 10−9	1.3 × 10−6	6.4
PURB (14)	rs319598	chr5: 134,268,134	trans	4.5 × 10−6	3.9 × 10−5	4.9
	rs11022347	chr11: 12,391,558	trans	7.3 × 10−6	2.2 × 10−3	1.3
	rs2028967	chr2: 142,990,138	trans	6.4 × 10−6	5.0 × 10−3	0.9
GNB5 (7)	rs2021910	chr6: 85,141,735	trans	1.8 × 10−6	3.0 × 10−4	3.8
	rs13105547	chr4: 52,974,359	trans	5.5 × 10−7	2.1 × 10−2	1.0
JAZF1 (10)	rs1635852	chr7: 28,155,936	cis	3.6 × 10−6	2.2 × 10−5	4.8
	rs885720	chr12: 12,139,366	trans	2.1 × 10−6	2.7 × 10−2	0.6

A SNP is called in cis of a gene if it is located within 1 Mb of the transcription start site of this gene. Each SNP in the table actually represents a block of adjacent eSNPs (chosen to be the one with the highest LBF). The number in parentheses in the Gene column shows the total number of putative eSNP blocks (defined as p < 10⁻⁵ in the eQTL data) of that gene. The LBF column shows the LBF of individual SNP (see Material and Methods). Only SNPs with LBF greater than 0.5 are shown.

We found literature evidence supporting three of our predicted genes. TSPAN8 (MIM 600769) is reported in the original DIAGRAM study and replicated by subsequent GWASs.⁴⁴ In an experimental mouse study, haploinsufficiency (deletion of a single copy) of Gnb5 (the mouse homolog of GNB5) caused late-onset obesity, insulin resistance, and liver steatosis on a normal diet, phenotypes strongly resembling human metabolic syndrome and T2D.⁴⁶ In addition, a closely related gene, GNB3 (MIM 139130), is shown to be associated with obesity, insulin resistance, and glucose tolerance in several studies.⁴⁷ A SNP close to JAZF1 (MIM 606246) was associated with T2D,^44,48 and deletion of Jazf1 in mice leads to increased fat mass and insulin resistance.⁴⁹ Interestingly, the SNP rs849134 (close to the supporting cis eSNP rs1635852 of JAZF1, Table 4) was reported to be strongly associated with both T2D and the expression of JAZF1 in adipose tissue in the DIAGRAM study.⁴⁸ The replication of this finding in liver (rs1635852, associated with T2D and liver expression of JAZF1) along with the additional trans eSNP from our analysis provides independent evidence of JAZF1.

We assembled genomic data from a number of mouse studies to assess the putative role of PURB in T2D. The expression of Purb in multiple tissues (liver, adipose, muscle, and islet) has been previously found to influence a number of metabolic phenotypes including fat mass, fat to body weight ratio, glucose level, insulin level, glucose to insulin ratio, and oral glucose tolerance test in six mouse crosses via a genetic causality test (FDR 10%).^12,24,25,50 The fact that this relationship was consistently discovered in different tissues and in different genetic backgrounds provides good evidence of a putative role of PURB in T2D. We also surveyed genes coexpressed with PURB by using previously described tissue-specific coexpression networks constructed from expression data in human and various mouse crosses (see Material and Methods). Genes within a given network module have been found to share similar biological functions. The top gene coexpressed with PURB is SERPINF1 (MIM 172860, appeared in >30% of the 128 coexpression modules containing PURB), a strong candidate gene for T2D.^51,52 The strong coexpression between the two genes thus lends further support to PURB as a possible T2D-associated gene.

We also analyzed the supporting trans eSNPs of the predicted genes of T2D. One supporting eSNP of PURB, rs319598 (Table 4), is located in the promoter of PCBD2 (MIM 609836), which is a cofactor of HNF1A (MIM 142410), a liver-specific transcription factor. Mutations of HNF1A are responsible for 30%–70% of the cases of maturity-onset diabetes of the young (MODY [MIM 606391]), a rare form of T2D.⁵³ In another example, we focused on NDRG2 (MIM 605272), a gene slightly below our threshold (p = 3.0 × 10⁻⁴, ranked sixth, not shown in Table 3) but biologically interesting because of its role in β cell protection.⁵⁴ One of the two supporting eSNPs of NDRG2, rs7334, is close to the 3′ end of EGFR (MIM 131550). The EGFR signaling pathway plays a key role in pancreatic beta cell development: even a modest attenuation leads to a severe defect in β cells, causing diabetes.⁵⁵ These analyses thus further support PURB and NDRG2 as T2D candidate genes and suggest the possible mechanism of their actions, by linking them to the well-established diabetes pathways.

Discussion

We have proposed a general strategy for genetic mapping that integrates information from GWAS with eQTL data. Instead of testing individual variants close to a gene, we pool the information in all variants, mostly in trans, that perturb the expression of the gene to infer its role in a complex disease. The major difficulties for utilizing trans variants to date are their relatively small effects and the pleiotropicity of their influences. We overcome these by utilizing the statistical pattern of multiple trans variants, much like a detective using a fingerprint to identify a suspect. Our experiments in Crohn disease and T2D demonstrate the benefits of this approach. Our predictions are often supported by moderate SNPs acting in trans (Tables 2 and 4) and thus are not possible to identify by the traditional methods. We believe this general framework significantly extends existing approaches to genetic mapping of complex phenotypes. Both theoretical considerations (complexity of gene regulatory networks) and empirical studies support the importance of trans variants affecting gene expression traits. By accessing this large amount of so-far unutilized information, our method could greatly expand our ability to derive new insights from association studies.

Application of our method to two complex diseases led to findings that are supported by multiple lines of evidence. First, for both Crohn disease and T2D, there are clear enrichments of candidate genes from the overall p value distributions (Figure 2). Second, in the study of Crohn disease, we show that all but one of ten predicted genes are replicated in an independent GWAS data set. Third, among our predictions not implicated in human studies before, genetic manipulations of Efs and Gnb5 in experimental mice lead to phenotypes highly consistent with the roles in Crohn disease and T2D, respectively. The collective evidence thus supports our approach as a promising strategy to extract insights from GWASs.

From a population genetic perspective, our strategy provides a significant addition to existing paradigms for genetic mapping. Selection pressure generally keeps proximal, large-effect variants at very low frequencies in the population.⁵⁶ This largely explains the observation that most common variants identified in GWASs have small effect sizes.⁵⁷ Major efforts are underway to identify rare variants with larger effects by using exome or whole-genome sequencing. Although this has led to a number of discoveries for Mendelian diseases, its success in complex diseases is modest,⁵⁸ presumably reflecting large sample size requirements for rare variants. Our strategy is based on the notion that distal variations that only weakly perturb the expression of a gene may survive at significant frequencies in the population because of weaker selection and that there could be many such variations across the genome. Although such weak genetic perturbations may manifest as only modest associations in both the eQTL analysis and the GWAS of a disease, the genes they perturb can play an important role in the disease. In our analysis, although the supporting SNPs of EFS and GNB5 are all in trans with modest associations, genetically manipulated mice exhibit severe abnormalities resembling Crohn disease and T2D, respectively.^37,46 Thus our strategy of genetic mapping is capable of finding hidden gene-disease associations by leveraging the collective signals of multiple modest perturbations across the genome.

Our work laid down a general framework for using data from association studies of quantitative molecular traits to interpret GWASs of complex diseases. Many eQTL studies in human have been performed,^9,30 but the vast amount of information in the trans eQTL remains unutilized. There are also efforts on mapping QTL of other molecular traits, such as metabolites⁵⁹ and epigenetic modifications.⁶⁰ Misregulation in these aspects could be important drivers of complex diseases.⁶¹ Our method is readily generalizable to these data sets, by defining the genetic signatures of molecular traits and by matching these signatures to that of the disease.

Our method employs a rigorous statistical framework, leading to major advantages over simple, heuristic methods (e.g., count the number of SNPs shared by the expression and disease traits, defined via some p value threshold). First, both strong and weak loci are taken into account with proper weighting. We incorporate all GWAS associations into the analysis without relying on arbitrary significance thresholds. This is crucial because most of the supporting SNPs in our findings are moderately associated with the expression trait and phenotype but fail to reach genome-wide significance threshold (Tables 2 and 4). Second, our method in general does not permit individual SNPs to dominate the results (see “Model Analysis” in Material and Methods), a common issue when testing association of a set of SNPs in GWASs.⁶² Third, the inherent asymmetry of the relationship between the gene and the disease is reflected in our model. A SNP associated with gene expression but not the disease is used as evidence against the gene, and a SNP associated with the disease but not gene expression is treated as noninformative.

An important decision to make when using our tool is the selection of phenotype-appropriate eQTL data sets. For some common diseases, it may be straightforward to choose relevant disease tissues, e.g., brain for psychiatric diseases. The results of our method also provide a quantitative measure of success (the number of significant genes above a certain FDR) and hence an indication of how informative a particular eQTL data set is. In general, we believe that there is probably not a single “correct” tissue; rather, multiple tissues may be informative to different degrees. For instance, it was reported recently that skin, adipose, and blood cells share a substantial fraction of eQTL.⁶³ Thus, it is possible that skin or blood eQTL may provide information for metabolic diseases. An important future challenge is to characterize the similarity and difference of eQTL across tissues and to develop an analytic framework to integrate information from multiple tissues.

Schadt et al. pioneered the use of eQTL for understanding genetics of complex traits.^12,61 In experimental animals, it is possible to perform genotyping, expression profiling, and phenotyping on the same individuals, allowing researchers to analyze patterns of correlation and dependency among variables to infer causal relationships.¹² It is difficult, however, to apply this strategy to human studies. Expression profiling of disease-related tissues in human subjects is generally costly and often not feasible. Another difficulty is the challenge of mapping trans eQTL in human;⁹ as a result, most of the existing studies utilizing human eQTL data focus on associations in cis,^9,11 with only a few exceptions.^64,65 With our approach, we have circumvented these problems and demonstrated that, even without all three types of data in the same samples, it is possible to infer associations between expression traits and diseases.

In our experiments with T2D, unlike Crohn disease, we predicted a small number of genes at a relatively high error rate (four genes at FDR < 0.3). Several factors might contribute to this lower level of statistical evidence: (1) our T2D analysis is based on liver eQTL data, although more relevant tissues for T2D are probably adipose and pancreatic tissues; and (2) we were unable to perform imputation because of lack of genotype data, thus reducing the overlap between eQTL and GWAS data sets and the power of our method. We believe the results still provide valuable information from existing data. The predictions create a short list of candidate genes; when combining with additional evidence, some interesting hypotheses may emerge. One of our predictions, PURB, for instance, is supported by multiple human and mouse genomic data sets, and therefore is an interesting candidate for follow-up analysis.

Although current GWASs typically use only common SNPs measured by array-based genotyping platforms, next-generation sequencing (NGS) technologies provide a window into other types of genetic variation, including rare SNPs, copy-number variants, and indels. Our strategy of matching genetic signatures is based on very general principles and therefore can be easily adapted to these new forms of genetic variations.

Appendix A: The Null and Alternative Distributions of the Association Statistics of SNPs

For a given SNP, let T be its association test statistic (p value can be converted to T, assuming a standard normal distribution) for a trait, either an expression trait or phenotype. We use M to denote the model: M = 0 corresponds to the null model of no association between the SNP and the trait, and M = 1 corresponds to the alternative model. We need to compute the probability distribution, P(T | M). In the null model, typically, P(T | M = 0) follows the standard normal distribution. In the alternative model, the distribution P(T | M = 1) depends on the statistical test through which T is derived and the effect size of the SNP, as explained below.

Binary Trait

We assume the Armitage trend test was used to derive the test statistics. We follow the notations in Slager and Schaid:⁶⁶ for a given SNP, there are two alleles, A for the high-risk allele and a for the other. The frequency of the i^th genotype (i = 0,1,2 is the number of A alleles) in cases is p_i, and its frequency in controls is q_i. The number of case and control individuals with each genotype are shown in Table A1.

Table A1.

The Number of Individuals with Given Genotypes

Genotype	aa	aA	AA	Total
Cases	r0	r1	r2	R
Controls	s0	s1	s2	S
Total	n0	n1	n2	N

We define a variable x_i = i, the number of A alleles in a genotype, the Armitage trend test can be written as $T=U/\sqrt{Var\left(U\right)}$, where

$$U=\sum _i{x}_i\left(\frac{S}{N}{r}_i-\frac{R}{N}{s}_i\right).$$ (Equation A1)

Under the null hypothesis of no association, the mean of U(μ₀) is 0 and its variance is given by⁶⁶

$${\sigma }_0^2=N\varphi \left(1-\varphi \right)\left[\sum _i{x}_i^2{q}_i-{\left(\sum _i{x}_i{q}_i\right)}^2\right],$$ (Equation A2)

where ϕ = R/N is the fraction of cases in the sample. Based on the central limit theorem, the asymptotic distribution, $T=U/{\mathrm{\sigma }}_0\sim N\left(0,1\right)$.

Under the alternative hypothesis of association, the mean and variance of U are given by⁶⁶

$${\mu }_1=N\varphi \left(1-\varphi \right)\sum _i{x}_i\left(p_i-q_i\right)$$ (Equation A3)

$${\sigma }_1^2=N\varphi {\left(1-\varphi \right)}^2\left[\sum _i{x}_i^2{p}_i-{\left(\sum _i{x}_i{p}_i\right)}^2\right]+N{\varphi }^2\left(1-\varphi \right)\left[\sum _i{x}_i^2{q}_i-{\left(\sum _i{x}_i{q}_i\right)}^2\right].$$ (Equation A4)

Thus, T follows normal distribution:

$$T=\frac{U}{{\sigma }_0}\mathrm{\sim }N\left(\frac{{\mu }_1}{{\sigma }_0}\mathrm{,}\frac{{\sigma }_1^2}{{\sigma }_0^2}\right).$$ (Equation A5)

The parameters p_i and q_i are unknown, but they are related to the effect size and allele frequency of the SNP in the population. For the i^th genotype, let f_i be its penetrance (the probability of disease given the genotype) and g_i be its frequency in the population. Then p_i and q_i are related to f_i and g_i through the Bayes theorem:

$$p_i=\frac{f_i{g}_i}{\sum _i{f}_i{g}_i},q_i=\frac{\left(1-f_i\right)g_i}{\sum _i\left(1-f_i\right)g_i}.$$ (Equation A6)

The sum Σ_if_ig_i is also called disease prevalence, K. Assuming Hardy-Weinberg equilibrium, the genotype frequencies are simply related to p, the frequency of the risk allele (assumed known, e.g., from HapMap). Suppose the effect size (the logarithm of the odds ratio of the risk allele) is β, the relative risk is then approximately γ = e^β. Assuming the multiplicative genetic model, we have f₁ = γf₀ and f₂ = γ²f₀. With the fact K = Σ_if_ig_i, we could solve f₀:

$$f_0=\frac{K}{{\left[\gamma p+\left(1-p\right)\right]}^2}$$ (Equation A7)

In summary, given K and p, p_i and q_i can be expressed as functions of β. Plug in p_i and q_i to equations of μ₁, σ₁, we can write μ₁, σ₁ as functions of β as well: μ₁(β; K, p) and σ₁(β; K, p). Because β is unknown, we assume a prior distribution of β: $\mathrm{\beta }|M=1\sim N\left(0,{\mathrm{\sigma }}_a^2\right)$ and integrate out β in the distribution P(T | M = 1):

$$P\left(t|M=1\right)=\int P\left(t|\beta \right)P\left(\beta |M=1\right)d\beta =\int N\left(t|\frac{{\mu }_1\left(\beta \right)}{{\sigma }_0}\mathrm{,}\frac{{\sigma }_1^2\left(\beta \right)}{{\sigma }_0}\right)N\left(\beta |0,{\sigma }_a^2\right)d\beta ,$$ (Equation A8)

Where N(t|.) is the p.d.f. of the normal distribution. A common choice of the prior distribution is ${\mathrm{\sigma }}_a^2=0.2$.¹⁷

Quantitative Trait

For an association study of a quantitative trait, we assume a z-test of the linear regression coefficient is used. Specifically, we have the following regression:

$$y_i=\mathrm{\mu +\beta }{x}_i+{\mathrm{\epsilon }}_i,$$ (Equation A9)

where x_i and y_i are the genotype and phenotype of the i^th subject in the sample, respectively, and ε_i ∼ N(0,σ²) is the error term. The statistic test of whether β = 0 is: T = b₁/σ(b₁), where b₁ is the MLE of β. The variance of b₁ is given by

$${\sigma }^2\left(b_1\right)=\frac{{\sigma }^2}{\sum {\left(x_i-\overline{x}\right)}^2}=\frac{{\sigma }^2}{2Np\left(1-p\right)},$$ (Equation A10)

where N is sample size and p is the allele frequency (assuming HWE). T follows standard normal distribution under M = 0: T = b₁/σ(b₁) ∼ N(0,1). In this calculation, we assume that σ² is known. If this is not true, we need to replace σ² with its MLE, σ² in T. However, with large sample size (which is often the case in large GWASs), the two are close, so for simplicity, we will use σ² instead. Under M = 1, we assume the prior distribution $\mathrm{\beta }\sim N\left(0,{\mathrm{\sigma }}_a^{\mathrm{2}}{\mathrm{\sigma }}^{\mathrm{2}}\right)$, according to Servin and Stephens,¹⁴ where σ_a reflects the typical effect size compared with the standard deviation of the quantitative trait. With the distribution b₁ ∼ N(β,σ²(b₁)), we have

$$P\left(b_1|M=1\right)=\int P\left(b_1|\beta \right)P\left(\beta |M=1\right)d\beta =\int N\left(b_1|\beta \mathrm{,}{\sigma }^2\left(b_1\right)\right)N\left(\beta |0,{\sigma }_a^2{\sigma }^2\right)d\beta$$ (Equation A11)

It is easy to show that b₁ under M = 1 follows the normal distribution $b_1\mathrm{\sim }N\left(0,{\mathrm{\sigma }}^2\left(b_1\right)+{\mathrm{\sigma }}_a^{\mathrm{2}}{\mathrm{\sigma }}^{\mathrm{2}}\right)$, thus

$$T=\frac{b_1}{\sigma \left(b_1\right)}\mathrm{\sim }N\left(\mathrm{0,1}+2Np\left(1-p\right){\sigma }_a^2\right).$$ (Equation A12)

The hyperparameter of the prior distribution, σ_a, is fixed at 0.5 in our experiments, based on the earlier study of Bayesian association mapping of quantitative traits.¹⁴

Appendix B: Relating the Bayes Factors of Genes to the SNP-Level Bayes Factors in eQTL and GWAS Data

Under the null hypothesis of no gene-disease relationship (Z = 0), the eQTL and GWAS data are independent (Figure 1D), and we thus have the model evidence of the null hypothesis:

$$P\left(x,y|H_0\right)=\prod _{i=1}^{N}P\left(x_i|H_0\right)P\left(y_i|H_0\right)=\prod _{i=1}^N{f}_0\left(x_i\right)g_0\left(y_i\right),$$ (Equation A13)

where the two functions describe the probability of eQTL and GWAS summary statistics, respectively:

$$f_0\left(x_i\right)=P\left(x_i|H_0\right)=\left(1-\alpha \right)P\left(x_i|U_i=0\right)+\alpha P\left(x_i|U_i=1\right)$$ (Equation A14)

$$g_0\left(y_i\right)=P\left(y_i|H_0\right)=\left(1-\beta \right)P\left(y_i|V_i=0\right)+\beta P\left(y_i|V_i=1\right).$$ (Equation A15)

Under the alternative hypothesis (Z = 1), we plug in the relevant terms to Equation 3:

$$P\left(x_i,y_i|H_1\right)=\left(1-\alpha \right)P\left(x_i|U_i=0\right)g_0\left(y_i\right)+\alpha P\left(x_i|U_i=1\right)P\left(y_i|V_i=1\right).$$ (Equation A16)

Divide the model evidence of H₁ at the i^th SNP over that of H₀, we have

$$B_i=\frac{P\left(x_i,y_i|H_1\right)}{P\left(x_i,y_i|H_0\right)}=\frac{\left(1-\alpha \right)P\left(x_i|U_i=0\right)g_0\left(y_i\right)+\alpha P\left(x_i|U_i=1\right)P\left(y_i|V_i=1\right)}{f_0\left(x_i\right)g_0\left(y_i\right)}.$$ (Equation A17)

Eliminate the common terms in the numerator and the denominator, and we have Equation 5 shown in the main text. The gene level BF is simply the product of B_is.

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes, http://browser.1000genomes.org

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/

• Sherlock, http://sherlock.ucsf.edu/