Accuracy of measurements of mandibular anatomy in cone beam computed tomography images

Abstract

Objectives

Cone beam computed tomography (CBCT) images of ideally positioned and systematically mispositioned dry skulls were measured using two-dimensional and three-dimensional software measurement techniques. Image measurements were compared with caliper measurements of the skulls.

Study design

Cone beam computed tomography volumes of 28 skulls in ideal, shifted, and rotated positions were assessed by measuring distances between anatomic points and reference wires by using panoramic reconstructions (two-dimensional) and direct measurements from axial slices (three-dimensional). Differences between caliper measurements on skulls and software measurements in images were assessed with paired t tests and analysis of variance (ANOVA).

Results

Accuracy of measurement was not significantly affected by alterations in skull position or measurement of right or left sides. For easily visualized orthodontic wires, measurement accuracy was expressed by average errors less than 1.2% for two-dimensional measurement techniques and less than 0.6% for three-dimensional measurement techniques. Anatomic measurements were significantly more variable regardless of measurement technique.

Conclusions

Both two-dimensional and three-dimensional techniques provide acceptably accurate measurement of mandibular anatomy. Cone beam computed tomography measurement was not significantly influenced by variation in skull orientation during image acquisition.

Diagnosis and treatment of facial asymmetry requires accurate measurement of a variety of osseous and soft tissue landmarks. Measurement of mandibular anatomy is problematic when using panoramic radiography.¹ Previous studies suggest that projection geometry, focal plane shape, differential vertical and horizontal magnification factors, and operator error in patient positioning affect the utility of panoramic images to provide accurate measurements.^1–9 Although medical computed tomography (CT) imaging provides higher accuracy with no significant difference between measurement of actual landmarks or CT images,^10–11 its relatively high x-ray dose and examination costs make medical CT undesirable for routine orthodontic diagnosis. The introduction of low-dose, low-cost cone beam CT for oral and maxillofacial imaging holds the promise of overcoming these obstacles while providing more accurate craniometric and orthodontic diagnostic information than conventional radiographic techniques.¹² Because conventional medical CT technology differs from cone beam computed tomography (CBCT) in the choice of x-ray sources, detectors, and reconstruction algorithms, performance characteristics may differ.¹³ Few studies have investigated the accuracy of CBCT for craniometric measurement.¹⁴ This study uses multiple positions of multiple dry skulls to assess the accuracy of planer and three-dimensional measurements of mandibular anatomy.

MATERIAL AND METHODS

Skull preparation and landmark identification

While a number of anatomical landmarks may be chosen to evaluate image fidelity in the assessment of mandibular symmetry, a combination of investigator-applied radiopaque markers and natural anatomic landmarks that could be employed in making caudal-cranial and anterior-posterior measurements were chosen for this study. Superior condylar surface (condylion), gonial angle (gonion), and mental foramen were selected as anatomic landmarks. Condylion to gonion measurement (C-G) provides an assessment of the vertical dimension of the ramus and its contribution to posterior facial height. Gonion to mental foramen measurement (G-MF) permits horizontal assessment of mandibular dimension. These dimensions are commonly affected by mandibular asymmetry. Fixed-length straight orthodontic wires, affixed to the mandible in vertical and horizontal orientations, provided external references for image measurement accuracy.

Thirty dry skulls were borrowed from the Anatomy Department at the University of North Carolina at Chapel Hill. Radiopaque .018-inch straight orthodontic wires, trimmed to precise lengths of 40.0 mm and 20.0 mm, were attached to the right and left sides of each mandible. The 40-mm markers were oriented approximately parallel to C-G and affixed to the lateral surface of the mandibular ramus by using clear adhesive tape. The 20-mm markers were oriented approximately parallel to G-MF and similarly attached to the lateral surface of the mandibular body.

Paper adhesive labels were placed on the anterior skull and marked with lines to facilitate skull positioning for radiographic images. These labels were placed on the anterior nasal spine, nasion, and anatomical pogonion. The labels were also marked 7 mm to the left of each of these anatomic points. Graph paper was placed over the area on the skull where the calvarium had been removed. A line representing the midsagittal plane was drawn on the graph paper. A second line was drawn 7 mm to the left of midsagittal. A third line was scribed that was at 10° to midsagittal as measured with a protractor by using a vertex located 7 cm posterior to the most anterior point on the midsagittal line.

Skull measurement

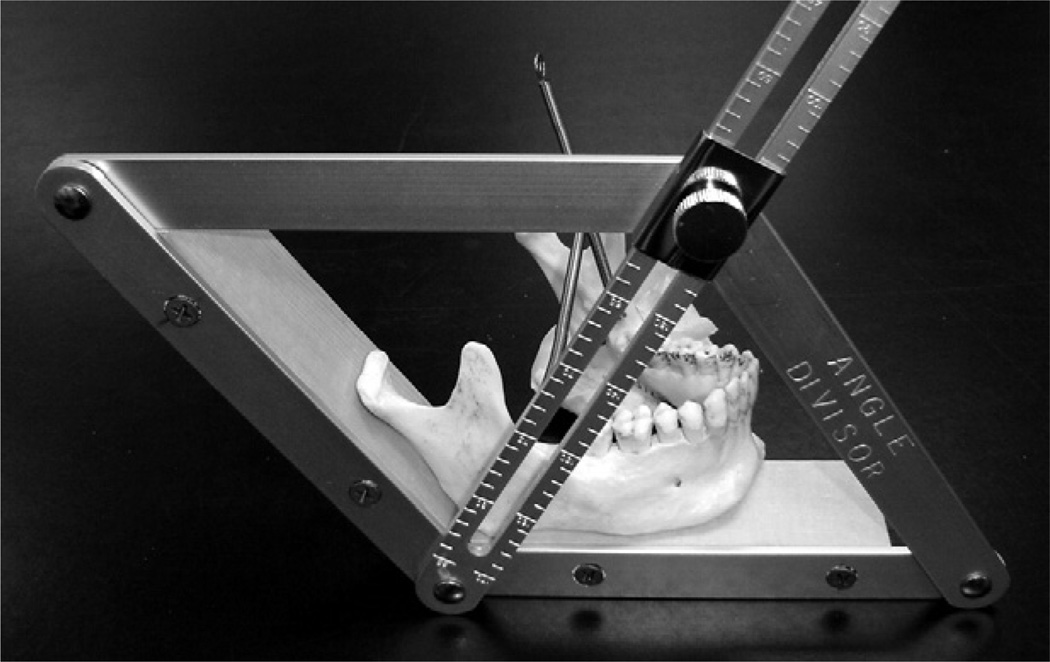
Accurate determination of gonion is challenging. The problem is related to the curving transition between the posterior ramus margin and the inferior mandibular border. It is difficult to locate the most posterior and inferior point on this curved surface without the aid of surface tangents and angle bisectors. In an approach that permitted the application of tangents and bisectors, an angle-forming tool (Angle Divider No. 19050, Big Horn Corporation, Littleton, Colo) was modified with the addition of wood block extensions (Fig. 1). Each side of the mandible was positioned in the angle divisor such that the extensions simultaneously contacted 2 points on the posterior ramus edge and 2 points on the inferior border of the mandible. Using the tip of a pencil, the bisector of this gonial angle was marked where it visually intersected the cortical border of the mandible. Marking of gonion was facilitated by a groove in the center of the bisector arm through which the pencil point was inserted. If a continuously curving lower mandibular border was encountered, a tangent to this surface at the middle of the body of the mandible was used. A digital caliper (Absolute Digimatic No. 500-172, Mitutoyo America Corporation, Aurora, Ill) was used to measure the distances between C-G and G-MF. Distances were recorded to the nearest 0.1 mm.

Fig. 1.

Modified angle divisor tool with right mandible seated and ready for marking of gonial angle. A pencil will be placed in the groove of the bisector arm to mark gonion.

Cone beam computed tomography images

Cone beam computed tomography images were acquired with a NewTom 9000 CBCT scanner (NIM S.r.l., Verona, Italy) using a 9-inch field of view. To maintain their dry condition while immersed in water, skulls were placed in plastic bags and oriented in a supine position in an acrylic immersion box (20 cm × 20 cm × 20 cm) for image acquisition. The box design incorporated vertical lines marking the midsagittal plane of the box. The aforementioned skull labels were used to orient the skull midsagittal plane relative to the box midsagittal plane. The box midsagittal plane was then aligned with respect to the midsagittal-positioning laser of th CBCT unit. A laterally placed anterior-posterior positioning laser on the unit was used to adjust the height of the patient table until the laser was centered on the ramus. For ideal position, midsagittal planes of the skull and box were centered in the midsagittal-positioning beam. For shifted position, skull orientation remained the same, but the box was shifted to the right until the midsagittal positioning beam aligned with the marks on the skull labels corresponding to the 7-mm lateral shifted position. For rotated position, the skull was removed from the box and repositioned in such a way that the rotated line on the graph paper covering the cranial vault now corresponded to the midsagittal plane of the box. After the skull was secured in place using a combination of rigid fasteners and elastic bands, the box was filled with water to simulate the attenuation of soft tissues that would be present in clinical imaging. Computed tomography data were imported into NewTom 3G software for primary reconstruction of images. Primary reconstructions were made using the large window setting with .5-mm axial slices. Axial slicing was oriented parallel to the Frankfort plane.

Cone beam computed tomography measurement using panoramic slice and two-dimensional tool

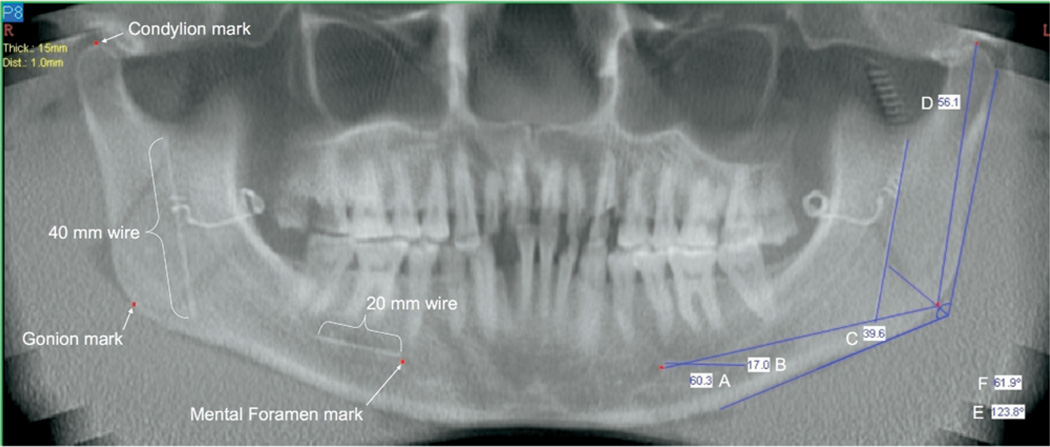
Secondary reconstruction and measurement of the CBCT images was accomplished using the NewTom 3G software package. With operator-selected 15- or 20-mm slice thicknesses, the panoramic tool was used on a representative axial slice to reconstruct the CBCT data in the form of a panoramic image. Initial mapping of the panoramic path was adjusted as needed to ensure that all anatomical points of interest could be easily located within the slice. Once the reconstruction had taken place, axial views of the data were used to locate specific anatomical points. Superior condyle and the posterior edge of the mental foramen on each side were marked using the software marking tool. These marks were centered on each landmark and were extended approximately 2 cm mediolaterally. In the case of the condyle, the mark extended parallel to the long axis of the condyle. In the case of the mental foramen, the mark was extended perpendicular to the long axis of the body of the mandible at this point. These marks were automatically displayed in the panoramic image at the point where each intersected the center of the image layer. Gonial angle was defined using the software angle tool. In a manner analogous to the physical determination of gonion on the skull, the arms of the angle were placed in contact with the surface of the posterior ramus border and inferior mandibular body border. A second angle was placed at the vertex of the first angle to form a bisecting angle. The contact of the bisector with the cortical border was defined as gonion (Fig. 2).

Fig. 2.

Example of 15-mm panoramic image layer used for two-dimensional measures. Condylion, gonion, and mental foramen marks are projections from the axial slice at the center of the image layer location (see Fig. 3). Measurement values: A = gonion-mental foramen distance, B = horizontal reference wire, C = vertical reference wire, D = condylion-gonion distance, E = gonial angle, and F = gonial angle bisector.

Measurements were made using a computer mouse to position the two-dimensional measurement tool cursor at one and then the other end of the landmarks of interest. The distance between landmarks along the curved plane at the center of the panoramic image layer was automatically calculated and displayed. Lengths of the vertical and horizontal markers as well as C-G and G-MF distances were measured for each side. The image reconstruction software and measuring tools are calibrated by the manufacturer for 1:1 measurement.

Cone beam computed tomography measurement using axial slices and three-dimensional tool

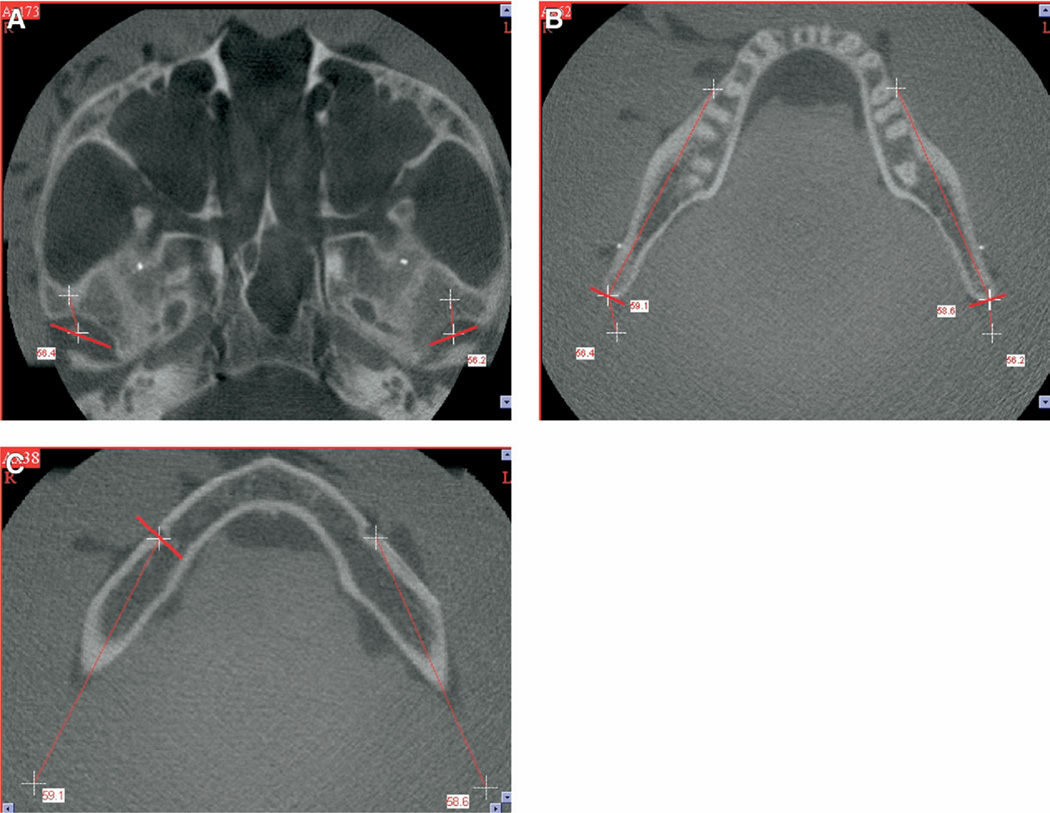
The NewTom CBCT software allows the user to measure linear distances in 3 dimensions by using 2 different axial slices. Vertical and horizontal markers were measured by mouse clicking the three-dimensional measurement tool on the marker in the first axial slice in which it appeared, as well as the last axial slice before it disappeared. Due to their radiopaque nature and finite size, the ends of the markers were easily identified in the axial slices. Condylion to gonion measurement and G-MF measurements were made after first marking gonion in the axial slice by using the marker tool. Gonion location was determined iteratively. By double-clicking the cursor location on the gonion region in the lateral scout view, the axial slice associated with this area is displayed. In this axial slice, the marker tool was used to draw a short line tangent to the posterior ramus surface and perpendicular to the long axis of the ramus. The location of this mark was checked in the panoramic image layer. If the mark was not coincident with the intersection point of the gonial angle bisector line with the ramus border, the mark was erased and a different axial slice was selected and marked. After gonion was marked, the cursor of the three-dimensional measuring tool was positioned on the mark for 1 of the 2 desired landmarks. The operator then scrolled through the stack of axial slices until the mark for the other landmark was located. After selecting this landmark, the linear distance between the points was automatically calculated. Fig. 3 provides examples of axial slices containing condylion, gonion, and mental foramen. Measured distance and pairs of crosshairs indicating the trajectory between points are automatically recorded on the images.

Fig. 3.

Axial slices and marked measuring points. Red lines are placed perpendicular to the panoramic image path and tangent to the landmark. Crosshairs represent measuring points placed by the three-dimensional measuring tool. Crosshairs are displayed in every axial slice between the actual measurement point locations. A, Marking of superior condylar surfaces bilaterally and measurement of condylion-gonion distance. B, Marking of the ramus cortex at gonion bilaterally. Inner values represent gonion-mental foramen measurements. Outer values depict condylion to gonion measurement distance. C, Marking of the inner cortical surface of the posterior aspect of the right mental foramen. Measurements are gonion to mental foramen measurement distances.

Observers

Skull dimensions were measured twice by observer A and once by observer B. Wire segments were measured twice in two-dimensional and three-dimensional images by observer C. Condylion to gonion measurement and G-MF distances were measured in CBCT images once each by observers A and B. Observer A was an experienced oral and maxillofacial radiologist. Observer B was a third-year dental student having little prior experience with skull or image measurement techniques. Observer C was a third-year orthodontic resident.

Statistical analysis

Interobserver variation was determined by paired t tests for skull, two-dimensional, and three-dimensional measurements. Intraobserver measurement variation was determined by paired t tests of first and second measurements. To compensate for multiple comparisons, significance was set at α = 0.01. Averages of the 2 measurements of observer A were used for further comparisons of imaging method and anatomic feature. Paired t tests were used to determine statistical significance between measurements of CT and photographic images. Again, an alpha level of .01 was selected for statistical significance. Analysis of variance (ANOVA) was performed on the subset of measurements common to both two-dimensional and three-dimensional measurement techniques. The ANOVA model included main effects of two-dimensional versus three-dimensional measurements (2), skull orientation (3), skull side (2), and skull measurement feature (C-G, G-MF), as well as the interactions of these variables. The threshold for statistical significance was set at α = .05.

RESULTS

Two of the original 30 skulls had 1 or more image volumes where a condyle was shifted or rotated out of the image volume, limiting the image data to 28 skulls. These skulls and images were excluded from the data analysis. Images from the 28 skulls were used to calculate interobserver measurement variation. In addition, these skull images were used to determine measurement accuracy of horizontal and vertical reference wires. Following initial skull measurement, 3 of the skulls were unavailable for interobserver and intraobserver measurement. Therefore, complete data was available for 25 skulls. Because an average of first and second measurements of the skull features was used as “truth,” assessment of C-G and G-MF measurement accuracy was constrained to the 25 skulls with complete data. Table I shows the reproducibility of repeated measurement of skulls. Measurements were reproducible for observer A with a mean difference of −0.08 mm for C-G and 0.12 mm for G-MF between second and first measurements. These differences were not statistically significant. Interobserver variation was greater with a difference of −0.89 mm for C-G and 0.87 mm for G-MF between observer A and observer B. These differences were statistically significant.

Table I.

Intraobserver and interobserver variation in measuring condylion-gonion and gonion-mental foramen distances on 25 skulls

		C-G	G-MF
Intraobserver reading 2-1	Mean difference	−0.08	0.12
	Standard error	0.17	0.13
	Probability of > |t|	0.6317	0.3627
Interobserver observer A, B	Mean difference	−0.89	0.87
	Standard error	0.25	0.26
	Probability of > |t|	0.0009	0.0018

C-G, condylion-gonion; G-MF, gonion-mental foramen; prob, author queried.

Repeated measurements of horizontal and vertically oriented wires seen in Table II were not different for two-dimensional measurements and were on average within 0.25 mm of each other. First and second three-dimensional measurements were also not statistically different and were on average within 0.07 mm with repeated measurement. Interobserver variation in the measurement of skeletal landmarks is seen in Table III. While significant differences in measurement were seen with the 2 observers, the means of these differences were less than 0.9 mm.

Table II.

Repeated measurements accuracy. Difference between first and second measurements for 28 skulls

		2D measurement			3D measurement
Wire orientation	Skull side	Mean Difference (Mean Abs Diff)	SD	P value	Mean Difference (Mean Abs Diff)	SD	P value
Horizontal	Left	0.25	0.99	0.02	−0.02	0.56	0.71
		(0.50)	0.39		(0.34)	0.23
	Right	−0.24	1.01	0.03	−0.05	0.42	0.24
		(0.47)	0.34		(0.19)	0.14
Vertical	Left	0.02	0.84	0.8	0.07	0.38	0.08
		(0.56)	0.39		(0.25)	0.19
	Right	0.22	1.01	0.04	0.03	0.36	0.46
		(0.61)	0.47		(0.37)	0.23

2D, two dimensional; 3D, three-dimensional; mean abs diff, mean absolute value of difference (measurement–truth).

Table III.

Interobserver variation in measuring gonion-mental foramen and condylion-gonion distances using two-dimensional and three-dimensional measurement techniques on 28 skulls imaged in 3 positions: difference observers A and B

Landmarks	Side	Measurement	2D	3D
G-MF	Left	Mean difference	0.17	−0.78
		Standard error	0.27	0.20
		Probability of > |t|	0.5185	0.0002
	Right	Mean difference	0.29	−0.75
		Standard error	0.20	0.19
		Probability of > |t|	0.1651	0.0002
C-G	Left	Mean difference	−0.90	−0.62
		Standard error	0.19	0.19
		Probability of > |t|	<.0001	0.0017
	Right	Mean difference	−0.41	0.24
		Standard error	0.18	0.24
		Probability of > |t|	0.0314	0.2029

2D, two-dimensional; 3D, three dimensional; G-MF, gonion-mental foramen; C-G, condylion-gonion; prob, author queried.

Table IV shows ANOVA model factors and P values resulting from the assessment of difference and absolute value of difference between CT measurements and direct skull measurements for observer A. Difference and magnitude of difference (absolute value) measurements were not significant for measuring technique or skull position. The magnitude of difference in measuring right or left sides was significantly different; however, on average, there was neither significant underestimation nor overestimation due to skull side. An interaction of anatomic feature and skull side was significant for measurement difference, but not for measurement magnitude.

Table IV.

Assessment of difference and absolute value of difference between image measurements and skull measurements: ANOVA model and resulting P values

Source	Factors	Difference Probability of > F	Absolute difference Probability of > F
Modality	2D, 3D	0.7107	0.0682
Feature	G-MF, C-G	<.0001	<.0001
Position	Ideal, rotated, shifted	0.2510	0.5585
Side	Right, left	0.1382	<.0001
Modality*position		0.7772	0.9244
Modality*feature		0.0338	0.6808
Modality*side		0.5779	0.1942
Position*feature		0.2633	0.1701
Position*side		0.6556	0.6268
Feature*side		<.0001	0.3748

2D, two-dimensional; 3D, three-dimensional; G-MF, gonion-mental foramen; C-G, condylion-gonion.

^*indicates interaction term.

The sources of significant measurement differences between CT and known wire dimensions or skull measurements can be seen in Tables V and VI. The data from wire measurements using either two-dimensional or three-dimensional techniques demonstrate excellent accuracy regardless of wire orientation, measurement side, or skull position. Average magnitude of differences in wire measurements was less than 0.5 mm for two-dimensional CT, and less than 0.3 mm for three-dimensional CT. For the two-dimensional measurement technique, consistent undermeasurement of wires averaged approximately 1.2% of the actual distance, while the average magnitude of error was approximately 2.0%. For three-dimensional measurement, horizontal wire length was slightly overestimated, whereas vertical wire length was underestimated. Average measurement error was approximately 0.7%, and the average magnitude of individual errors was approximately 1%.

Table V.

Wire landmarks: comparison of differences between two-dimensional and three-dimensional measurements of 20-mm horizontal wires and 40-mm vertical wires for 28 skulls imaged in 3 positions

Wire orientation	Skull side	Measurement	Difference*		Absolute value of difference†
			2D	3D	2D	3D
Horizontal	Left	Mean error (mm)	−0.28	0.18	0.5	0.34
		% error	1.4%	0.9%	2.5%	1.7%
		SD	(0.58)	(0.38)	(0.39)	(0.23)
	Right	Mean error (mm)	−0.20	0.03	0.47	0.19
		% error	1.0%	0.2%	2.4%	1.0%
		SD	(0.56)	(0.24)	(0.34)	(0.14)
Vertical	Left	Mean error (mm)	−0.47	−0.23	0.56	0.25
		% error	1.2%	0.6%	1.4%	0.6%
		SD	(0.50)	(0.23)	(0.39)	(0.19)
	Right	Mean error (mm)	−0.50	−0.36	0.61	0.37
		% error	1.3%	0.9%	1.5%	0.9%
		SD	(0.60)	(0.26)	(0.47)	(0.23)

2D, two-dimensional; 3D, three-dimensional.

^*Average of 84 measurements (measurement in image–known length).

^†Average of 84 measurements |measurement in image–known length|.

Table VI.

Skull landmarks: comparison of differences between two-dimensional and three-dimensional measurements of gonion-mental foramen (G-MF) and condylion-gonion (C-G) distances for 25 skulls imaged in 3 positions

Landmarks	Skull side	Measurement	Difference*		Absolute value of difference†
			2D	3D	2D	3D
G-MF	Left	Mean error (mm)	1.66	1.26	1.77	1.37
		% error	3.0%	2.3%	3.2%	2.5%
		SD	(1.78)	(1.28)	(1.68)	(1.15)
	Right	Mean error (mm)	0.26	0.13	0.97	0.96
		% error	0.5%	0.2%	1.7%	1.7%
		SD	(1.34)	(1.33)	(0.95)	(0.92)
C-G	Left	Mean error (mm)	−2.1	−1.89	2.12	1.94
		% error	−3.7%	−3.4%	3.8%	3.5%
		SD	(1.24)	(1.27)	(1.21)	(1.19)
	Right	Mean error (mm)	−1.13	−0.96	1.3	1.21
		% error	−2.0%	−1.7%	2.3%	2.2%
		SD	(1.05)	(1.13)	(0.83)	(0.84)

G-MF, gonion-mental foramen; C-G, condylion-gonion.

^*Average of 75 measurements (measurement in image–skull length).

^†Average of 75 measurements |measurement in image–skull length|.

Anatomical measurements were more variable regardless of measurement technique. Using two-dimensional measurement techniques, G-MF was overestimated by 3.8%, whereas C-G was underestimated by 2.9%. Using three-dimensional techniques, G-MF and C-G were both overestimated by 2.5% and 3.1%, respectively. The average magnitude of error for all measurements was 2.8% for two-dimensional techniques and 2.5% for three-dimensional techniques.

DISCUSSION

There are a number of potential sources for measurement error in this study. The CBCT unit actually rotates with a slight wobble that is a potential source of image distortion. A correction algorithm is used to remove that distortion prior to reconstruction of images. Errors in the algorithm or changes in the wobble pattern over time may result in residual distortion. Precision of measurement is limited by the resolution of the system. The reconstruction pixel size of 0.5 mm chosen for this study limits accuracy of individual measurements to ±0.5 mm. In addition, partial volume averaging may reduce the visibility of a structure within an image layer. This would tend to result in underestimation of the edges of structures such as cortical bone surfaces or the orthodontic wire ends measured in this study. Although primary and secondary slice reconstruction thickness will also influence measurement, narrower slices should result in better measurement accuracy. Measurement of wire markers in this study suggest that the NewTom 9000 performed well in providing volumes that are relatively free from distortion in vertical and horizontal dimensions.

Measuring features within a reconstructed image layer is analogous to making measurements on conventional transmission radiographs such as cephalometric or panoramic images. While predictable anatomic distortions due to projection geometry and panoramic image layer formation characteristics are present, their effect on actual anatomic structures is dependent on the shape and orientation of the structure. Because of this, true anatomical variation or asymmetry in a patient may be difficult to distinguish from projective distortion in the image. Cone beam computed tomography volumes provide the radiologist with the flexibility of choosing the orientation of reconstructed image layer. The operator has the advantage of constructing the image layer after studying a volume of axial slices. In this way, the image layer can be adapted to the anatomy of interest.

But the image layer may not fully conform to the anatomy in all directions. Panoramic image layers in this study were mapped using representative axial slices. Generation of the reformatted panoramic image extended the mapping perpendicular to the axial slice through the complete stack of axial slices. To be sure that relevant anatomy was contained in the panoramic view, a finite image layer of 15 or 20 mm was chosen. This means that anatomy anywhere within the image layer would be projected in the displayed panoramic image on lines parallel to the axial slice plane and perpendicular to the mapping line. For a linear anatomic feature such as an orthodontic wire, oriented at an angle with respect to the reconstruction axis (the axis is perpendicular to the axial slice), and in a plane perpendicular to the panoramic mapping line, the image of the feature will appear smaller than the feature’s actual size. This size reduction will be a function of the cosine of the angle formed by the feature with respect to the reconstruction axis. Angular deviations less than 18° result in image size reductions less than 5%.

The situation in measuring gonion-mental foramen is somewhat different. The panoramic image layer approximates the curve of the mandible between gonion and the mental foramen. However, the caliper measurement of gonion-mental foramen on the skull represents a straight line, which is a secant to the curve represented by the panoramic image layer. Based on the preceding theoretical arguments, it would be expected that two-dimensional measurements of a panoramic image layer would overestimate gonion-mental foramen distances and underestimate condylion-gonion distances. This is supported by the data seen in Table VI. The measurement errors seen with two-dimensional techniques are reduced with three-dimensional measurement techniques. The small measurement errors seen with two-dimensional measurement techniques in this study suggest that the chosen anatomic points and reference wires had acceptably small deviations from the plane of the panoramic reconstruction.

Unlike two-dimensional measurements within a reconstructed image layer, three-dimensional measurements are made between points within a volume and thus are not subject to projective distortion. The challenge arises in defining and selecting the points to be measured. When CBCT images were measured with the three-dimensional tool, it was not possible to locate gonion in the axial slice without referencing the panoramic image layer where the gonial angle was calculated and bisected. This problem is an illustration of the difficulty in using three-dimensional tools to measure anatomic points that have traditionally been defined using two-dimensional image techniques and tools. The three-dimensional measurement tool in the NewTom software was more accurate than the two-dimensional tool for measuring distances where landmarks were defined by visually unambiguous points such as the ends of orthodontic wires. However, the absence of an angle measurement tool that could be used in a three-dimensional volume restricted the operator’s ability to find an analogous point for gonion, which had been readily defined using lines and angles on the two-dimensional plane of a panoramic image. New measuring tools must be developed if clinicians are to take full advantage of the accuracy promised by three-dimensional measurements of CBCT volumes. At the same time, orthodontists need to reassess the definition of cephalometric landmarks that have been described in terms of planar projections of sagittal and coronal anatomy. These definitions may need to be modified for measurement in three-dimensional volumes. New anatomic landmarks and reference planes may need to be adopted to take full advantage of the measurement accuracy and diagnostic potential afforded by CBCT imaging.

The standard deviations for differences in repeated skull measurements of 0.85 mm for posterior mandibular height and 0.6 mm gonion-mental foramen indicate less precision in measurement of skeletal dimensions than was seen with measurement of wire dimensions with three-dimensional measurement techniques. This variability is largely due to the difficulty in determining gonion. The modified angle-bisecting tool used in this study was subject to parallax errors in positioning a pencil within the bisector groove of the tool to mark gonion (Fig. 1). It should be noted that systematic errors in locating skull gonion related to the use of the angle-bisecting tool would have a detrimental impact on image measurements. The possibility of such an error is suggested by the interobserver differences in skull measurement where posterior-mandibular height was overestimated and gonion-mental foramen was underestimated by an average of 0.9 mm by observer B. Experience in making measurements may also play a role in interobserver and intraobserver variability. It might be anticipated that the less-experienced observer B would have greater variability in measurements.

Wire measurement accuracy using the three-dimensional measuring tool is comparable to the accuracy reported by Marmulla and coauthors,¹⁵ who used an acrylic phantom. The mean absolute error of 0.13 mm and standard deviation of 0.09 mm in that study compares with mean absolute errors of 0.29 mm and standard deviation of 0.20 mm in this study. The use of a computer algorithm to localize measurement points with pixel fractionalization in the former study versus observer selection of measurement points by using mouse manipulation of a cursor in this study may be the principle reason for the approximately twofold difference in measurement accuracy.

Variations in skull positioning were incorporated into the design of this study because skull position has been demonstrated to be a factor in measurement accuracy for conventional radiographic imaging and has been cited as an important factor in false-positive and false-negative diagnosis of mandibular asymmetry in panoramic imaging.¹ Farman¹⁶ has argued that the best of modern panoramic units may permit a posteriori adjustments to compensate both for patient position and for differences in arch shape and tooth contact angulations in the maxilla and mandible. But this argument ignores the difficulty in distinguishing distortion resulting from nonideal patient positioning from distortion resulting from skeletal asymmetry. It also overlooks the difficulty in incorporating fiducial landmarks on the patient so that images and measurements can be adjusted after the fact when asymmetry is present. The results of the current study indicate that difficulties associated with patient positioning and uncertainties of measurement accompanying patient asymmetry in panoramic images are not present in CBCT images.

CONCLUSIONS

A number of conclusions are suggested by the results of this study. In contrast to current plane projection (cephalometric) and image layer (panoramic) techniques, measurements of anatomy in CBCT volumes examined in this study were relatively uninfluenced by skull orientation. As is commonly reported for advanced imaging and complex measurement tasks, operator experience has a positive effect on measurement accuracy and reproducibility. For well-defined points, measurement accuracy was expressed by average errors less than 1.2% for two-dimensional measurement techniques and less than 0.6% for three-dimensional measurement techniques. While the measured features and measurement techniques differed from previous studies, average measurement errors from 0.2 mm to 2.1 mm are in line with errors reported for both conventional and cone beam CT.^14,17 With the appropriate choice and definition of landmarks, and the availability of three-dimensional measuring tools, this accuracy has the potential of providing unambiguous information for diagnosis of skeletal asymmetry, longitudinal monitoring of growth, and postsurgical assessment.