Murrayy′s Law in Elastin Haploinsufficient (Eln+/−) and Wild-Type (WT) Mice

Abstract

Using either the principle of minimum energy or constant shear stress, a relation can be derived that predicts the diameters of branching vessels at a bifurcation. This relation, known as Murray′s Law, has been shown to predict vessel diameters in a variety of cardiovascular systems from adult humans to developing chicks. The goal of this study is to investigate Murray′s Law in vessels from mice that are haploinsufficient for the elastin protein (Eln+/−). Elastin is one of the major proteins in the blood vessel wall and is organized in concentric rings, known as lamellae, with smooth muscle cells (SMCs) around the vessel lumen. Eln+/− mice have an increased number of lamellae, as well as smaller, thinner vessels. It is possible that due to decreased amounts of elastin available for vessel wall remodeling during development and in adulthood, Eln+/− vessels would not follow Murray′s Law. We examined vessel bifurcations in six different physiologic regions, including the brain, heart, epidermis, ceocum (or cecum), testes, and intestines, in Eln+/− mice and wild-type (WT) littermates. All vessels were between 40 and 300 μm in diameter. We found that the diameters of both Eln+/− and WT vessels have an average of 13% error from the diameters predicted by Murray′s Law, with no significant differences between genotypes or physiologic regions. The data suggest that vessels are optimized to follow Murray′s Law, despite limitations on the proteins available for growth and remodeling of the vessel wall.

Introduction

Using the principle of minimum energy, Murray [1] derived an equation predicting the diameters of branching vessels in the cardiovascular system. His law was based on minimization of the energy required to synthesize, maintain, and pump blood. Zamir [2] later showed that Murray′s Law predicts constant mean shear stress on the endothelial cells (ECs) within the lumen of branching vessels. Murray′s Law holds relatively well in small to medium sized vessels, excluding the aorta, pulmonary artery, and smallest capillaries [3]. The predictions from Murray′s Law match experimental measurements in human coronary arteries [4,5], extraembryonic vessels in the developing chick [6], and even the larger airways of the lung [7]. Murray′s Law also applies to other fluid transport systems in zoology [8] and botany [9] and can be used as a design criteria in nonphysiologic flow systems, such as a network of pipes [3].

Blood vessels are composed of extracellular matrix (ECM) proteins, such as elastin, collagen, and proteoglycans, and cells, such as ECs, smooth muscle cells (SMCs), and fibroblasts. During vessel development, ECs organize into a tube to form the vessel lumen. For arteries and veins, presumptive SMCs are recruited to the outer wall, forming layers (called lamellae) of SMCs, elastin, and other associated ECM proteins around the ECs. The number of lamellae depends on the size of the animal and location in the vascular tree, but the tension/lamellae is constant [10]. Humans and mice with elastin insufficiency have additional lamellae compared to controls, as well as smaller, thinner vessels [11]. It has been hypothesized that the structural and geometric changes in the vessels of elastin heterozygous mice (Eln+/−) are an adaptation to altered hemodynamic forces caused by reduced elastin levels during development [12,13]. This study investigates Murray′s Law in Eln+/− mice that have altered vessel wall structure and geometry, and cannot produce normal amounts of elastin, a key ECM protein in the vessel wall.

Materials and Methods

Equations.

Murray′s Law relates the diameter of the parent vessel (D₀) to the diameters of the two daughter vessels at a bifurcation (D₁, D₂):

$$D_0^3=D_1^3+D_2^3$$ (1)

Equation (1) can be rearranged to determine how close measurements come to matching Murray′s Law:

$$\mathit{\alpha }=\frac{D_0^3}{D_1^3+D_2^3}$$ (2)

where the theoretical value of α is 1.

Equation (1) can also be rearranged to examine the effects of relative vessel diameter [6]:

$$\frac{D_1}{D_0}={\left({[1+\frac{D_2}{D_1}]}^b\right)}^{-\frac{1}{b}}$$ (3)

$$\frac{D_2}{D_0}=\frac{D_2}{D_1}{\left({[1+\frac{D_2}{D_1}]}^b\right)}^{-\frac{1}{b}}$$ (4)

where b = 3 if Murray′s Law holds true.

Animals and Vessel Diameter Measurements.

Twelve male C57/BLJ6 mice, six Eln+/−, and six wild-type (WT) littermates were used between 3 and 4 months of age. The mice were euthanized by CO₂ inhalation and dissected immediately. All protocols were approved by the Institutional Animal Care and Use Committee. Six physiologic regions, including the brain, heart, epidermis, ceocum (or cecum), testes, and intestines, were chosen to investigate Murray′s Law. The regions were chosen for ease of access to surface vessels and no attempt was made to discriminate between arteries and veins. In the mouse, small surface vessels on the heart are usually veins, and small surface vessels on the brain are usually arteries [14], so both arteries and veins are included in the analyses. The physiologic region was exposed and pictures were taken of vessels and their first generation branches with a Canon Powershot G9 digital camera attached to Zeiss Stemi-2000 C dissecting microscope. The vessels were in the 40–300 μm diameter range and microscope magnifications of 4–5× were used for all images. Two to three pictures were taken for each region in each mouse and analyzed with Image J software (NIH). It was not possible to get clear pictures of each region in every mouse, so the total number of images analyzed for each genotype is presented in the results. Three measurements were taken of each parent vessel immediately before the branch and of the daughter vessels immediately after the branch and averaged (Fig. 1). The ratio α (Eq. (2)) was calculated in Excel (Microsoft) for each set of parent and daughter branches and averaged for each region and mouse genotype. The parameter b (Eqs. (3) and (4)) was fit for all data combined in Matlab (Mathworks, 2011).

Fig. 1.

Representative image of the vessels in the testes of an Eln+/− mouse showing the lines drawn for the average diameter measurements

Statistics.

All data are presented as mean ± SD. Genotypes were compared by unpaired, two-tailed t tests with unequal distributions. Physiologic regions for each genotype were compared by ANOVA followed by Tukey′s post hoc test. P < 0.05 was considered significant.

Results

The average ratios α for each region and genotype are shown in Fig. 2. The averages range from 1.14 to 1.01, which is close to the theoretical value of 1. There are no significant differences between genotypes or regions. The range of all α values is shown in Fig. 3. The range is from 0.50 to 1.90, with an average for all the data of 1.13 ± 0.30. Equations (3) and (4) were used to plot and fit the parameter b to all of the data combined. Equations (3) and (4) fit the data with predicted b values of 2.72 (R²= 0.99) and 2.76 (R²= 0.99), respectively (Fig. 4).

Fig. 2.

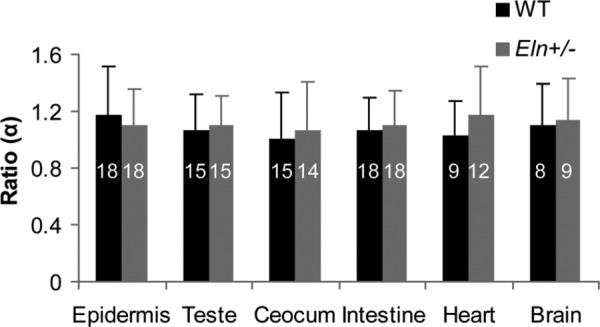
Average ratio α for WT and Eln+/− vessels in different physiologic regions. The ratio is near the predicted value of 1 from Murray′s Law, with no significant differences between genotypes or regions. The number of vessel images used for the ratio calculation for each region and genotype is listed on the columns.

Fig. 3.

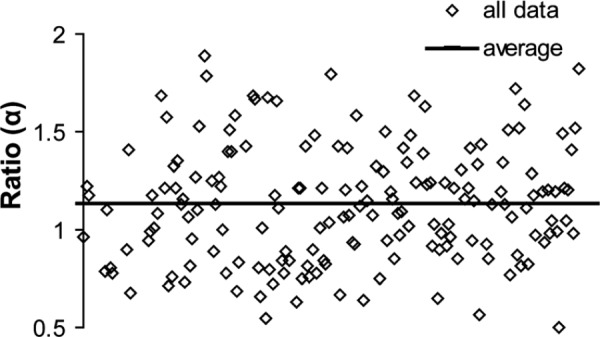
Composite graph of all ratio α measurements and the average for all of the data combined. The average for all the data is α = 1.13 ± 0.30.

Fig. 4.

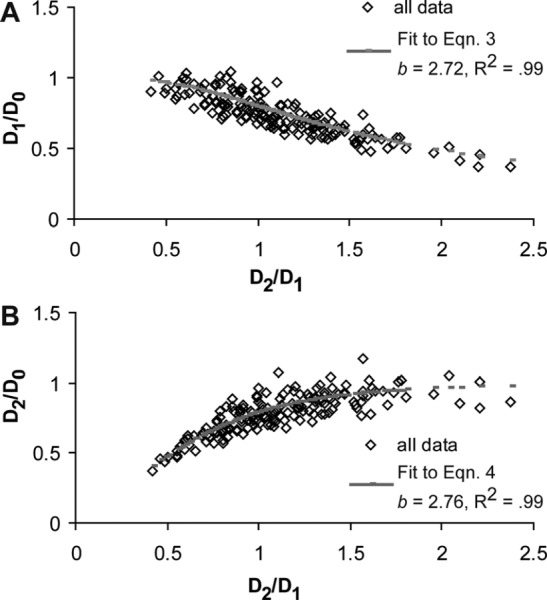
Relative vessel diameters and the fit to (a) Eq. (3) and (b) Eq. (4) for all of the data combined. Fitted values are b = 2.72 (R²= 0.99) and 2.76 (R²= 0.99), respectively, which is near the predicted value of 3 from Murray′s Law.

Discussion

The data presented in this study suggest that both WT and Eln+/− mouse vessels of 40–300 μm in size in multiple physiologic regions follow Murray′s Law. Eln+/− mice have about 60% of the normal elastin levels [12], and have altered vessel wall structure and geometry [11]. It has been suggested that Eln+/− vessels are smaller and thinner because there is a limitation on available elastin to build the wall, but mechanical properties of the vessel must be maintained for proper cardiovascular function [13]. The mechanical properties critically depend on the ratio of elastin to collagen in the wall [15]. To build a wall with the same volume, but less elastin, would require increased collagen amounts and alter the mechanical properties. Reducing the wall volume is one strategy to maintain near normal mechanical properties with less total elastin content. However, the wall volume must be large enough to withstand the circumferential stresses from blood pressure, maintain the shear stresses from blood flow, and provide the volumetric flow required to distribute cardiac output to distal tissues. Despite limitations on the available “building materials” for the vessel wall, Eln+/− vessel diameters are consistent with WT vessels and with the optimal branching diameters predicted by Murray′s Law.

The average ratio α for all of the data is 13% higher than the theoretical value of 1. The fitted parameter b is 2.7–2.8 for all of the data combined. Although this is 10% below the theoretical value of 3, this is close to the values of 2.8–2.9 found by Taber [6] in the developing chick and 2.7 suggested by Kamiya et al. [16]. Discrepancies between the measured and theoretical values may arise from human error in the diameter measurements, as it is difficult to determine the exact inner diameter of the vessel (Fig. 1). The data were very repeatable though, being collected by two different individuals over the course of 2 years with similar results. Discrepancies between the measured and theoretical values may also arise due to the simplifying assumptions of Murray′s Law, namely constant blood flow, constant diameter, straight vessels, and rigid vessel walls [17]. Murray′s Law is based on a cost function that includes minimizing the frictional power losses in circulating blood and the metabolic cost of synthesizing and maintaining the blood volume. Kassab and Fung [18] showed that a cost function including the frictional losses and the metabolic cost of synthesizing and maintaining the vessel wall volume (instead of the blood volume as in Murray′s Law), with an experimentally derived relationship between vessel wall thickness and diameter, provides an exponent b of 2.73 instead of 3, which is much closer to our experimental measurements. Hence the most appropriate cost function remains an open area of investigation.

Instead of using a cost function, the predicted diameters in Murray′s Law can be derived by assuming the mean shear stress on the wall is constant [2]. Like Murray′s Law, the derivation generally assumes constant blood flow, constant diameter, straight vessels, and rigid vessel walls. Painter et al. [17] derived the exact solution for shear stress with pulsatile flow in an elastic tube and showed that Murray′s Law is valid for all but the largest arteries. However, it was still assumed that the vessels are constant diameter, straight tubes filled with an incompressible, viscous fluid that follows the Navier-Stokes equation, which may lead to errors between the measured and experimental values. It has been argued that constant shear stress is the most likely regulatory factor in determining the diameter of branching vessels, as this is a local, cellular-level response, rather than a global optimization [16]. Cells actively regulate the vessel diameter to maintain shear stress after perturbations to the volumetric flow rate. Prolonged alterations to flow, such as the changes that occur during normal vessel development, lead to growth and remodeling of the vessel wall, which requires a net change in the amount and organization of cells and ECM constituents [19]. The current data show that Eln+/− vessels maintain the required diameters to provide a constant shear stress in branching vessels, while being limited on the amount of elastin available for wall remodeling during development and in adulthood. This study highlights the remarkable ability of the developing cardiovascular system to adapt to reductions in the amounts of critical ECM proteins and the resulting hemodynamic changes, while maintaining the required geometry necessary to provide constant shear stress throughout the vascular tree.