Assessing the stability of human locomotion: a review of current measures

Abstract

Falling poses a major threat to the steadily growing population of the elderly in modern-day society. A major challenge in the prevention of falls is the identification of individuals who are at risk of falling owing to an unstable gait. At present, several methods are available for estimating gait stability, each with its own advantages and disadvantages. In this paper, we review the currently available measures: the maximum Lyapunov exponent (λ_S and λ_L), the maximum Floquet multiplier, variability measures, long-range correlations, extrapolated centre of mass, stabilizing and destabilizing forces, foot placement estimator, gait sensitivity norm and maximum allowable perturbation. We explain what these measures represent and how they are calculated, and we assess their validity, divided up into construct validity, predictive validity in simple models, convergent validity in experimental studies, and predictive validity in observational studies. We conclude that (i) the validity of variability measures and λ_S is best supported across all levels, (ii) the maximum Floquet multiplier and λ_L have good construct validity, but negative predictive validity in models, negative convergent validity and (for λ_L) negative predictive validity in observational studies, (iii) long-range correlations lack construct validity and predictive validity in models and have negative convergent validity, and (iv) measures derived from perturbation experiments have good construct validity, but data are lacking on convergent validity in experimental studies and predictive validity in observational studies. In closing, directions for future research on dynamic gait stability are discussed.

1. Introduction

1.1. Rationale

It is generally accepted that ageing is accompanied by an increased risk of falling [1–6], and the same holds for several chronic disorders [7–11]. Owing to demographic developments, the incidence of falls and related costs constitute a growing problem in the industrialized world [12]. A host of interventions to prevent falling and falling-induced injuries have been proposed [13], e.g. strength training [14], Tai Chi [15], the use of hip protectors [16–18] or even air bags [19,20]. However, the effectiveness of such interventions is not as high as desired. Although multidisciplinary approaches, which address several potential risk factors simultaneously, appear more effective than singular approaches [13], their overall effectiveness remains unclear. To prescribe targeted interventions, one first needs to identify those at risk of falling within the general population [21], before one is able to establish the main determinants of fall risk in the individuals in question. In this review, we purport to assess methods that may allow discrimination of individuals at risk of falling. We focus on falls during gait because a significant proportion of falls occur during gait [6], one of the most common human motor activities.

During gait, perturbations arise from internal sources (e.g. neuromuscular) and external sources (e.g. wind, surface friction and/or uneven surfaces). Thus, the probability of falling is dependent not only on the individual's neuro-musculoskeletal capacity, but also on external factors such as the type and magnitude of perturbations encountered in daily life. Obviously, the latter cannot be assessed in a clinical or laboratory setting. It may, however, be possible to assess the ‘stability’ of an individual's gait pattern as a reflection of his or her capacity to walk without falling under given external conditions. But what is gait stability, how can it be measured and are pertinent measures indeed predictive of the probability of falling?

1.2. Stability or the ability to recover from perturbations

For the purpose of this review, we will define pragmatically ‘stable’ gait as gait that does not lead to falls in spite of perturbations.¹ It is useful to first illustrate and develop this notion by applying it to a simple model, the so-called passive dynamic walker (i.e. an in silico simulation or real physical model of a walking human that exploits its passive mechanical properties, rather than uses motors for its control). Passive dynamic walkers can recover from small perturbations, and keep walking after such perturbations without any imposed control [22]. Their stability arises from the intrinsic properties of the model (i.e. masses, inertias, etc.) and the specific movement pattern. Thus, a legged system, even without any form of control, may exhibit some level of stability, simply because of its mechanical properties and movement pattern. Passive dynamic walkers can handle only very small perturbations (for a step down, they can handle perturbations of the order of a few per cent of their leg length at maximum [23]). This ability may seem trivial at first, since such small perturbations affect the gait pattern very little at the time of their occurrence. However, when these small perturbations are not attenuated, their effects may accumulate in subsequent steps to a much larger deviation from the planned state (a state is a set of variables that fully describe a system, and usually consist of both positions (or angles) and derivatives). Many studies have focused on ways to enable dynamic walkers to handle larger perturbations. One solution is to add a controller [24,25]. This controller would be inactive most of the time (since the gait is within its passively stable region), but would be active when a larger perturbation occurs, or when effects of smaller perturbations have accumulated over time [24]. The contribution of such a controller to gait stability depends on several factors. Firstly, the state of the system needs to be correctly monitored (requiring good sensor quality) in order for the controller to perform correctly. Secondly, the controller needs to initiate the correct action given the detected deviation. Finally, the actuators need to be strong, fast and precise enough to successfully perform the chosen corrective action.

Three requirements for achieving stable gait become apparent from the passive dynamic walker example: (i) the system has to be able to recover from or limit the small perturbations that occur during every stride (e.g. owing to small differences in floor height and noise), (ii) the system has to be able to recover from large perturbations, which require a change in behaviour, and (iii) the largest recoverable perturbation specified by the limits of the system needs to be larger than the perturbations encountered. Although these requirements may seem an oversimplification that cannot be applied to human walking, we feel that they may serve to gain a better understanding of human gait stability. We will therefore follow these three requirements of gait stability to structure the problem addressed in this review.

The three requirements for stable walking may be (partially) independent, in which case a perfect measure of either one of them may not predict the probability of falling with certainty. For instance, there may be individuals who invest much effort in attenuating the effects of small perturbations (which could, if not attenuated, add up to cause larger state deviations), because they are unable to handle these (e.g. owing to a lack of muscle strength). These subjects may appear very stable when considering stability measures derived only from unperturbed gait. By contrast, there may also be individuals who do not attenuate the effects of small perturbations, because they can handle larger state deviations rather well (see [26]). Finally, there may be individuals who can handle both small and large perturbations well, but can handle larger perturbations only up to a certain magnitude, for instance, because they have a limited range of joint motion, restricting responses to larger perturbations. Thus, it could be that all three criteria need to be assessed in order to fully evaluate an individual's gait stability. Even then, as stated previously, the ability to recover from perturbations is only part of the equation that governs the probability of falling, the other one being the perturbations a person encounters. Still, this is as close as we may get in the laboratory or the clinical setting at assessing the probability that someone will fall.

1.3. Levels of validity

‘Despite the extensive effort in the area, there is no accepted quantitative way to judge or score the dynamic stability of human locomotion’ [27, p. 31]. While this statement dates back to 1994, it still holds true today [28]. Since 1994, several new measures have been proposed, rendering it difficult to keep track of this rapidly developing field. In order to clarify this situation, the current review aims at providing an overview of measures of gait stability. In doing so, we will explain how these measures are calculated, and summarize what evidence there is that they predict the probability of falling. In relation to the latter objective, we will distinguish four levels of validity.

• (1) Construct validity. Is the relation between the measure and the probability of falling plausible given its definition?

• (2) Predictive validity in the simplest case possible. Is the measure predictive of the probability of falling of a simple model of human gait? Showing that a certain measure works for a very simple model makes it more likely that it will also work for the complex case of actual human gait. Moreover, these studies have the advantage that the probability of falling can be quantified directly.²

• (3) Convergent validity in experimental studies. Does the measure adequately reflect an experimentally induced change in stability? Showing that a certain measure adequately reflects an experimental impairment of stability makes it more likely that the measure actually captures stability in the complex case of human gait.³

• (4) Predictive validity in observational studies. Is the measure related to the probability of falling or incidence of falling in prospective or retrospective observational studies? A correlation of a certain measure to actual fall incidence, preferably determined in a prospective study, can be considered the definitive test of the validity of using the measure as a clinical tool. In principle, such a positive result in observational studies can be the result of spurious correlations. Nevertheless, this is far less likely if the measure has also been shown to be valid according to the criteria listed earlier.⁴

1.4. Outline

This review is organized in the following three parts, each of which is concerned with a different class of measures:

• (1) Measures that reflect (or are associated with) the ability to recover from small perturbations (the maximum Lyapunov exponent, the maximum Floquet multiplier, variability measures, long-range correlations, extrapolated centre of mass concept, concept of stabilizing and destabilizing forces and foot placement estimator (FPE)).

• (2) Measures that reflect the ability to recover from larger perturbations (gait sensitivity norm (GSN), extrapolated centre of mass concept and FPE).

• (3) Measures that reflect the maximum perturbation that can be handled. For each type of measure, we start with a general introduction of that particular class of measures. Then, for each measure, a general description of the measure in question is given, after which its formal calculation is explained, including possible concerns that may be (and have been) raised with regard to these calculations. Finally, an overview of the literature concerning the validity of the measure is presented.

While some of the measures discussed in this review have been used frequently in the study of human gait, others have only rarely been used and some not at all. We nevertheless included these measures, as we believe that they may capture some important properties of gait stability. We chose not to include entropy-based measures, because we are unaware of any studies that address the validity of these measures as predictors of the probability of falls at any of the levels defined above. Moreover, to the best of our knowledge, no clear theoretical link between gait stability and entropy-based measures has been established, and another recent systematic review on gait stability measures [28] did not yield any papers on entropy-based measures.

In §5, we will draw conclusions concerning the best possible choice of dynamic gait stability measures for the moment, and highlight directions for future research. It should be noted that the present review is not a systematic review in a strict sense, but a narrative overview of, as well as a tutorial on, a wide range of stability measures (for systematic reviews on gait stability, see [28,29]). The overview does, however, provide a state of the art of the research on human gait stability (table 1).

Table 1.

Acronyms and symbols used in this study.

symbol	representation
	gait sensitivity norm
b	spatial stability margin vector
bmin	minimum value of b
bτ	temporal stability margin vector
co	size of the perturbation used in calculation of the gait sensitivity norm
θ	total body angular velocity
λL	long-term Lyapunov exponent
λS	short-term Lyapunov exponent
ωo	inverted pendulum eigenfrequency
*	indicates steady-state behaviour
∞	infinity
BoS	base of support
CoMz	vertical component of CoM
CoM	the centre of mass position vector
CoP	centre of pressure vector
d	dimensionality of a system
DCoP	vector between CoP and BoS, in the direction of the velocity of the CoP
DFA	detrended fluctuation analysis
dist	distance between a set of points in state space
f	a function
Fd	destabilizing force vector
FPE	foot placement estimator method
FPE	vector of the foot placement estimator
Fst	stabilizing force vector
Fz	vertical component of the ground reaction force
g	gravitational constant
Htot	total body angular momentum vector
i	gait indicator index
ICoM	total body inertia tensor
J	the Jacobian matrix
j	nearest neighbour pair number
k	stride index
l	equivalent pendulum length of the subject
m	mass of the subject
Md	destabilizing moment vector
n	window size (as used in DFA calculations)
N	time-series length
q	state variable
S	state-space description of the system
t	time
u	number of gait indicators (y) used in the calculation of the gait sensitivity norm
VCoM	velocity vector of the centre of mass
VCoMx	horizontal component of VCoM
VCoMz	vertical component of VCoM
W	vector of work needed to bring the subject to standstill
XCoM	the extrapolated centre of mass position vector
XCoM	the extrapolated centre of mass concept
y	gait indicator used in calculation of the gait sensitivity norm
α	scaling exponent, indicating long range correlations
ϕ	leg angle

2. Measures that reflect the ability to recover from small perturbations

As outlined in the general introduction, we assume that there is some kind of steady-state gait pattern that requires minimal control. The measures described in this section index the impact of continuously present, small perturbations on this steady-state gait pattern. The measures stem from two strands of research, namely dynamical systems theory and biomechanics.

2.1. Measures derived from dynamical systems theory

2.1.1. Background

Formally speaking, in mathematical physics, a dynamical system is any fixed ‘rule’ that describes the time dependence of a point's position in its ambient space. Examples include mathematical models of an inverted pendulum and simple models of human gait. Often, the system will be nonlinear and complex, and several tools have been developed to test whether, and under which conditions, such systems show stable behaviour. Since around 1995, some of these methods have also been used to estimate gait stability [27,30]. However, the equations of human locomotion are not known, and thus numerical rather than analytical methods have to be used, which may introduce problems (e.g. §2.1.3). In this section, four measures derived from dynamical systems theory are described, namely the maximum Lyapunov exponent (§2.1.2), the maximum Floquet multiplier (§2.1.3), variability measures (§2.1.4) and long-range correlations (§2.1.5). These measures reflect the ability to overcome smaller perturbations (for which a change in behaviour (e.g. trip and slip) is not needed) and are calculated from a steady-state walking pattern without any external perturbations other than those present in the test environment or in the system itself.

2.1.2. The maximum Lyapunov exponent

2.1.2.1. General description

Dingwell et al. [31] were the first to use the maximum Lyapunov exponent to estimate gait stability. Since then, the maximum Lyapunov exponent has gained in popularity [2,31–80]. The maximum Lyapunov exponent (λ) quantifies the average logarithmic rate of divergence of a system after a small perturbation [64,81]. The general idea when using the numerical calculation is that, if a system is (or was) at nearly the same state as the current state (i.e. same position, velocity, acceleration, jerk, etc.), either state may be regarded as a perturbation of the other.

The great advantage of this measure is that it may be calculated from any source of kinematic data, regardless of the reference frame in which the data are recorded [59,69]. This allows for using small and cheap (wireless) inertial sensors [34,39,76].

2.1.2.2. Calculation

The calculation of the maximum Lyapunov exponent of human gait data is rather straightforward. The first step is the construction of a proper state space (see appendix A) from kinematic data obtained during a steady-state walking trial. Since stationarity of the time series is a requirement for valid calculation of the maximum Lyapunov exponent, most studies use either acceleration data or differentiated position data.

In principle, any kinematic time series may be chosen as input for state space reconstruction [59,69,82]. Recent literature, however, suggests that trunk kinematic data (as opposed to foot, shank, thigh and pelvis kinematic data) may be most sensitive to differences between, for example, elderly and young subjects [83]. Theoretically, this is understandable, since maintaining stability of the upper body is a critical aspect of human locomotion [84,85]. However, it has never been studied whether joint angles would be even better input variables than trunk kinematics. Indeed, some studies investigating stability in patients with knee osteoarthritis and anterior cruciate ligament ruptures have used knee angle time series [37,40,42,49,50,59,72,86–89]. The idea behind the studies in these patients was either that the main mode of instability arises from buckling or giving way of the knee joint [87] or that joint movements reflect coordination of the segments between which the joint is situated [37,40,42,49,50,59,72,86,88,89].

It is of paramount importance to make sure that the selected state space contains the same number of strides for every condition and subject [60,68], as the estimated maximum Lyapunov exponent of gait data has been shown to increase with increasing time-series length [68]. Bruijn et al. [68] suggested that this may be either due to non-stationarities in the data (i.e. wandering around on the treadmill) or due to nearest neighbours in state space becoming closer together as the state space becomes more densely populated with data. The fact that Bruijn et al. [71] also found similar effects of time-series length in data obtained from a passive dynamic walker with noise suggests that the latter (i.e. initial nearest neighbours moving closer in state space) is a more likely reason, as a passive dynamic walker does not ‘wander around’.

Moreover, in most recent studies, the number of data points per stride was adjusted by time normalizing the state space of n strides length to n × 100 data points, thus ensuring that state spaces contain the same number of both strides and data points for each subject and condition [59,60,68]. An alternative to this procedure is to rescale time on the x-axis of the divergence curve (see below). This overcomes the difficulties associated with interpolation of the time series.

It should be mentioned that relatively large datasets are needed for a statistically precise estimate. Bruijn et al. [68] showed that limited increases in statistical precision were achieved only when the length of the time series was increased beyond 150 strides. Recent research, however, suggests that multiple episodes of shorter data can also be used. Sloot et al. [39], for example, successfully demonstrated the destabilizing effects of galvanic vestibular stimulation at the group level using multiple time series of only seven strides.

The actual calculation of the maximum Lyapunov exponent is performed by either (i) identifying the nearest neighbour in state space for each data point [81] or (ii) identifying the nearest neighbour for data points along a single reference trajectory [90]. It is important to note that, for a continuous series such as a marker position or joint angle time series, the entire data series serves as the reference trajectory. In both of these calculations, the log of the expansion/contraction of the Euclidean distance between these points is calculated.

In the Rosenstein et al. [81] algorithm, the expansion/contraction of points is followed until the end of the time series. A time versus the log of the Euclidean distance curve is calculated for all neighbouring points as they move through their respective trajectories. A mean divergence curve is then calculated for all of these curves (figure 1). The divergence exponents appearing in gait data are calculated as the slope of this mean divergence curve. In most gait studies, this slope is estimated over two regions, from 0 to 1 strides (sometimes also 0–0.5 strides), usually labelled as λ_S, and over 4–10 strides, usually labelled λ_L.

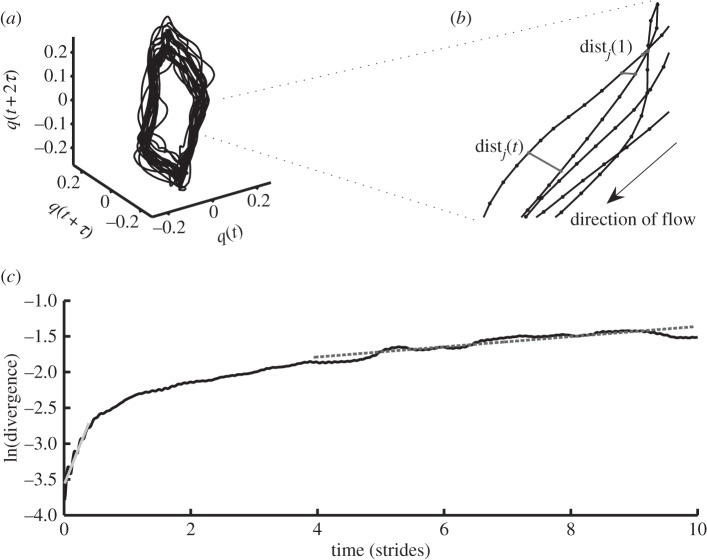
Figure 1.

Calculation of the maximum Lyapunov exponent. (a) A three-dimensional attractor (state space reconstruction of q). (b) Close-up view of part of the attractor; for each point on the attractor, the nearest neighbour was calculated, and divergence of these points was calculated as dist_j(t) (expanded view of part of (a)). (c) Average logarithmic rate of divergence, from which maximum Lyapunov exponents, λ_S and λ_L, can be calculated as the slope of the curve at 0–0.5 strides and at 4–10 strides, respectively (black line: divergence curve; grey line, λ_S: 2.2156; dotted line, λ_L: 0.0712).

In the Wolf et al. [90] algorithm, the neighbouring points are followed for a specified period that is a fraction of the time for one complete orbit of the attractor. The average of the log of the expansion/contraction of distances between points divided by the specified period the points were followed is the maximum Lyapunov exponent. It is important to note that, in the original paper in which the Rosenstein et al. [81] algorithm was first presented, only the slope of the initial region of rapid expansion was defined as the maximum Lyapunov exponent.

Thus, it becomes evident that the Rosenstein et al. [81] algorithm and the Wolf et al. [90] algorithm are calculating a maximum Lyapunov exponent (labelled λ_S or simply maximum Lyapunov exponent, respectively) in a similar manner: the initial rapid exponential separation of two neighbouring points in state space. This is consistent with the definition of a maximum Lyapunov exponent from dynamical systems theory and chaos theory.

In the original methods by Wolf et al. [90] and Rosenstein et al. [81], this exponential rate of divergence is calculated as the rate of divergence per second. However, it has been suggested that, for gait data, the exponential rate of divergence should be expressed per gait cycle [64,68] rather than per second [60]. The assumption underlying this suggestion is that every foot placement in walking represents a possibility to recover from a perturbation, which implies that the rate of divergence per stride (or step) is the factor of importance, and not the rate of divergence per time unit. Besides this logic, there are data from the modelling study of Bruijn et al. [71] to substantiate this idea. In this study, the maximum Lyapunov exponent was calculated as divergence per stride, rather than per second. The results showed that λ_S correlated fairly well with the maximum perturbation the model can handle. When looking at the stride times the model had for the different model configurations (see fig. 3b in [91]), it may be clear that this would not have been the case if the maximum Lyapunov exponent had been calculated as divergence per second, thus emphasizing the notion that the maximum Lyapunov exponent should be calculated as divergence per stride instead of divergence per second. Still, since evidence for this idea of calculating divergence per stride instead of divergence per second is scarce, it is advisable that, in future studies, both divergence per stride and divergence per second are mentioned.

2.1.2.3. Validity of the maximum Lyapunov exponent

Construct validity. There is little doubt that the maximum Lyapunov exponent has a valid theoretical basis [62,64,81]. While any attractor existing in an n-dimensional state space will have n Lyapunov exponents, by definition there can be only one maximum Lyapunov exponent. The maximum Lyapunov exponent describes the greatest rate of expansion of any dimension. Calculation of any Lyapunov exponent beyond the maximum Lyapunov exponent cannot be performed by means of the Rosenstein et al. [81] algorithm and can only be done through careful Gram–Schmidt orthonormalization procedures as with the Wolf et al. [90] algorithm. For this reason, the gait literature reporting λ_S and λ_L now refers to these as divergence exponents, thus recognizing that only λ_S is the exponent first described by Rosenstein et al. [81] as the estimated maximum Lyapunov exponent. The reasoning behind calculating λ_L beyond a visual identification of a region of different slope in a mean divergence curve is somewhat unclear. The region through which λ_L is calculated represents a time when the neighbouring points have almost reached their maximum separation, and the distance between them cannot grow any further because of the bounds of the attractor. This could be calculated in a similar manner with the Wolf et al. [90] algorithm by increasing the specified time period through which the expansion/contraction is calculated (e.g. several orbits of the attractor), but it is unclear what this represents.

Predictive validity in models. Su & Dingwell [92] tested whether the maximum Lyapunov exponent quantifies the ability to recover from small perturbations in a simple model of walking. They used a simple passive dynamic walking model with added noise and found that increasing noise levels led to increases in λ_S, but not in λ_L. Since the model had the same basin of attraction in all noise conditions, increasing noise immediately implied an increased probability of falling for the model. The authors concluded that λ_L quantifies the ‘inherent stability of the model’ [92, p. 806], while λ_S quantifies the ‘risk of falling exhibited by the model’ [92, p. 802], a finding which was replicated by Kurz et al. [93]. Roos & Dingwell [74] extended these findings to a three-dimensional model in a subsequent study, showing that in such a model λ_S was an early indicator of the probability of falling (measured as the percentage of trials in which the model fell over). However, in neither of these studies was the inherent stability of the model actually changed by changing, for instance, the slope angle or some other property of the model (see [94]). In one of our own recent studies, we therefore focused on whether λ_S and/or λ_L were related to the probability of falling (this time quantified as the maximum perturbation the model could handle), when this was altered by changing the properties of the model [71]. Like previous authors, we found that λ_S was correlated with the probability of falling and λ_L was not. Thus, studies investigating simple models consistently suggest that λ_S, but not λ_L, may be a valid predictor of the probability of falling.

Convergent validity in experimental studies. Recent experimental studies in humans seem to confirm the findings obtained in the studies of simple walking models. In an early study, subjects’ feet were desensitized by means of ice water, which led to a less stable gait pattern and higher values of λ_S and λ_L [86]. In a more recent study, Chang et al. [95] reported that walking over an unstable support surface increases values of λ_S, but not of λ_L. Similarly, Sloot et al. [39] and Van Schooten et al. [34] reported that destabilizing subjects by means of galvanic vestibular stimulation led to increased values of λ_S, but not of λ_L. Finally, McAndrew et al. [75] reported that gait destabilization by means of support surface perturbations or visual scene perturbations was reflected in λ_S, but probably not in λ_L. This finding has recently been confirmed by Hak et al. [77], who even showed a dose–response relationship between the amplitude of the perturbations applied and the increase in λ_S. All in all, the findings obtained in experimental studies suggest that, in actual human gait, λ_S, but not λ_L, may be a valid measure to estimate the probability of falling.

Predictive validity in observational studies. Although there are a host of studies that employ the maximum Lyapunov exponent to quantify gait stability in patient and elderly populations, there are only very few studies that directly link them, be it retrospectively or prospectively, to the probability of falling. Lockhart & Liu [2] reported a greater maximum Lyapunov exponent (λ_S) in fall-prone elderly subjects than in normal elderly subjects. Being prone to falling was defined as being unable to avoid slip-induced falls, as assessed in a previous study [96]. It is interesting to mention that fall-prone and non-fall-prone subjects did not walk at the same walking speed, which may in and of itself also influence λ_S. This could be seen as a confounder. However, slip outcomes as measures of fall risk were also assessed at preferred walking speed; and, similarly, it can be assumed that fall risk in daily life is also determined by the quality of gait at the actual chosen speed, for which preferred speed is likely to be representative. In one of our own studies on a cohort of 14 patients with knee osteoarthritis, we did not find a relationship between the number of falls experienced in the year before the measurements and the maximum Lyapunov exponent of knee angle time series [87]. However, in a more recent retrospective study which involved 134 elderly participants, we found that a high λ_S of trunk movement (in combination with higher variability measures) differentiated individuals who had fallen in the previous year from non-fallers [76]. In conclusion, there is growing evidence that λ_S, but not λ_L, may be used to estimate the probability of falling.

2.1.3. The maximum Floquet multiplier

2.1.3.1. General description

The maximum Floquet multiplier quantifies the rate of convergence/divergence of continuous gait variables (e.g. segmental motions and joint angles) towards a limit cycle (e.g. the nominal gait cycle), following a transient perturbation, from one gait cycle to the next. Thus, they rest on the assumption that gait is a periodic motion (i.e. a motion that repeats itself after a certain period of time), and that the gait variable analysed also reflects such limit cycle behaviour (e.g. segment or joint motion, but not stride times or stride lengths).

The maximum Floquet multiplier was first applied in robotic gait to assess the stability of passive dynamic walkers [97]. Typically, in this type of analysis, a periodic solution (i.e. a solution that repeats itself after a certain period of time) is found for the walker, representing a fixed point in a Poincaré section (i.e. the lower dimensional subspace orthogonal to the flow direction of the system that corresponds to a given point in the stride cycle; figure 2). Subsequently, state variables are perturbed repeatedly at this fixed point, so that the maximum Floquet multiplier can be calculated to examine whether the fixed point is stable or unstable (for a more extensive description of this procedure for robotic gait, see [98]). Obviously, this kind of analysis is only possible when the equations of motion are known.

Figure 2.

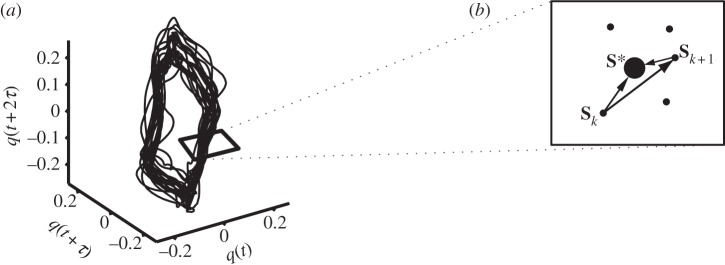
Calculation of the maximum Floquet multiplier. (a) A three-dimensional attractor, with a schematic of the Poincaré section, which is perpendicular to the direction of flow (state space reconstruction of q). (b) Close-up of the Poincaré section (expanded view of part of (a)). The larger point in the middle (S*) represents the limit cycle, that is, the average of all data points in the Poincaré section. The Jacobian maps the relative position (with respect to S*) of all points S_k to the relative position (with respect to S*) of all points S_k+1. The largest Floquet multiplier (the largest eigenvalue of the Jacobian) thus indicates whether the distance from S* grows or shrinks from one cycle to the next.

When using this measure to estimate gait stability in human walking, as was done by Hurmulzu & Bazdogan [27], one of the challenges is to find a substitute for the fixed point, which cannot be calculated from the equations of motion since these are unknown. Another problem is how to perturb the state variables piece by piece. The first problem is usually solved by taking the mean of the trajectory crossings at a Poincaré section of a steady-state walking trial as an approximation of the fixed point [27,30,34,42,43,56,62,68,69,72,74,75,83,92,99,100], which is a reasonable assumption given that steady-state human walking has some degree of stability (i.e. humans can walk without falling every other step). The piecewise perturbation of state variables is then bypassed by regarding the natural variability of human walking to be the result of perturbations (which in this case are no longer piecewise per state variable). Following this procedure, the maximum Floquet multiplier can be calculated without applying actual perturbations.

2.1.3.2. Calculation

Like the maximum Lyapunov exponent, calculating the maximum Floquet multiplier from human gait data requires the construction of a state space from kinematic data (see appendix A). The number of strides covered by this state space should be equal for all subjects and conditions [68], and a considerable number of strides is required to achieve sufficient statistical precision [68].

Floquet theory assumes that a system is strictly periodic, and that the state of a system after one cycle (S_k+1) is a function (f) of its current state (S_k) (as outlined in the general description, this dictates the necessity of using continuous variables displaying limit cycle behaviour to calculate the maximum Floquet multiplier)

2.1

It follows from equation (2.1) that limit cycle trajectories correspond to fixed points (S*) in the Poincaré section (figure 2), i.e.

2.2

To evaluate the effects of small perturbations on S*, a linearization of equation (2.1) is used

2.3

From equation (2.3), it can be seen that the rate at which small perturbations grow or decay is equal to the magnitudes of the eigenvalues of J(S*), which are the Floquet multipliers. Thus, for a limit cycle to be stable, all Floquet multipliers should have a magnitude less than 1. The magnitude of the Floquet multipliers indicates the rate of divergence/convergence over cycles, and the maximum Floquet multiplier is the maximum absolute Floquet multiplier.

In some studies, Poincaré sections are sampled at heelstrike, or some other distinctive point in the gait cycle [27,30,72,101], based on the untested assumption that such points (e.g. heelstrike) represent biologically meaningful events within the gait cycle. In other studies, 101 Poincaré sections were made by time normalizing the state spaces into stride cycles of 101 samples (from 0% to 100%) [62,68,99]. Note that in theory the choice of Poincaré sections is arbitrary as Floquet multipliers should be constant throughout the gait cycle [27], and indeed show low within-stride variability [99].

After the Poincaré sections have been selected, the fixed points (S*) in these Poincaré sections are defined as the average state over all strides in the Poincaré section in question. J(S*) can then be calculated by solving equation (2.4) using a least-squares algorithm, and Floquet multipliers can be obtained by calculating the eigenvalues of J(S*). It must be noted that in some cases not the largest but the mean Floquet multiplier is calculated [27,101]. In these cases, this is believed to give a more ‘overall stability measure’ [27, p. 33] as it quantifies the average divergence/convergence from/to the limit cycle.

2.1.3.3. Validity of the maximum Floquet multiplier

Construct validity. The construct validity of the maximum Floquet multiplier for periodic dynamical systems is outside the scope of this review [27,30]. However, when applied to human walking, some problems arise. To start with, Floquet theory can only be applied to strictly periodic systems, and it is questionable whether human gait is such a system; stride cycles vary in length, and this variability has a non-random structure (see §2.1.5). Moreover, the methods used for numerical calculation of Floquet multipliers from measured data are far from perfect; using the average of all states as a fixed point leads to underestimation of the maximum Floquet multiplier [102]. In conclusion, whereas the construct validity of the maximum Floquet multiplier is good for theoretical systems, it remains questionable for biological systems.

Predictive validity in models. Several studies, using either two- or three-dimensional limit cycle walking models as a basis, reported that the maximum Floquet multiplier did not correlate with the model's probability of falling [23,74,91,92,103]. According to Hobbelen & Wisse [23], this is because the maximum Floquet multiplier assumes equal perturbations of all states, and observes the eigenmode (i.e. the direction of convergence to the limit cycle) with the slowest convergence, which is not necessarily the eigenmode that will bring the walker nearest to a fall. There may be other eigenmodes that show a faster return, but are more important for the actual behaviour. Following this logic, some authors have used the mean instead of the maximum Floquet multiplier to estimate gait stability. However, doing so did not lead to better results for a two-dimensional model [91] and was, as far as we know, never done for a three-dimensional model. Thus, studies on simple models appear to suggest that the maximum Floquet multiplier correlates poorly with the probability of falling.

Convergent validity in experimental studies. Results from studies employing experimental manipulations of stability are to some extent in agreement with the disappointing findings reported using simple models. While gait destabilization by means of visual perturbations or perturbations of the support surface [75] showed the expected effect on the maximum Floquet multiplier, destabilization by means of galvanic vestibular stimulation [34] was shown to have converse effects on the maximum Floquet multiplier from those expected. In summary, experimental studies of human gait show mixed support for the use of the maximum Floquet multiplier as a measure of the probability of falling.

Predictive validity in observational studies. Granata & Lockhart [101] reported that the maximum, not the mean, Floquet multiplier was larger in a group of four fall-prone elderly (i.e. elderly who had a self-reported history of falling) than in four elderly controls. However, apart from the critically small sample size, it should be mentioned that walking speed differed between groups. The authors stated that ‘Stability was not influenced by walking velocity, indicating that group differences in walking speed could not fully explain the differences in stability’ [101, p. 172]. However, walking speed differences between groups, which were not reported in detail, may have been larger than within groups, thus rendering this conclusion questionable.

In sum, it seems that the validity of the maximum Floquet multiplier in modelling, experimental and observational studies is not yet established, which casts doubt on their use as a valid predictor of the probability of falling. A recent review [104] attributed this lack of correlation between the maximum Floquet multiplier and measures of the probability of falling to methodological issues. However, Bruijn et al. [91] showed good correlations between semi-analytically and numerically calculated maximum Floquet multipliers, which renders this conclusion less likely. Moreover, as discussed under predictive validity in model studies, even in those studies it is the case that, when the maximum Floquet multiplier is calculated in a semi-analytical manner, it does not correlate with the probability of falling.

2.1.4. Variability measures

2.1.4.1. General description

When using the term ‘variability’ in this section, we refer to the amount of variability of a certain parameter over strides during walking. Examples of variability measures are stride time and stride width variability, and the variability of trunk movements. It should be noted that these measures are essentially statistical in nature, and, thus, some explanation is needed as to why we discuss them under §2.1. The rationale is that, in certain simple dynamical systems involving stable fixed points with constant white noise, such as the stochastic version of the Haken–Kelso–Bunz model for bimanual coordination [105], an increase in variability in the coordination pattern is indicative of a loss of stability of the coordination pattern in question.⁵ Similarly, increased variability of gait may be indicative of a loss of stability and hence of increased probability of falling. However, it should be kept in mind that measured variability in a complex dynamical system may also arise from the deterministic dynamics of the system itself (e.g. when a chaotic attractor is present, which appears to be the case for human gait [51]). If so, the measured variability is merely a reflection of the multiple degrees of freedom available to the system and does not necessarily imply destabilization of the system.

In practice, variability measured in a biological system is likely to stem from both sources (i.e. noise and deterministic components), and it may be impossible to separate these two sources of measured variability. Still, on a more pragmatic level, if, in an unperturbed environment, we measure the variability of a variable that is critical to the stability of walking, and find that this variability is increased, we may conclude that the probability that a larger state deviation will occur is increased as well, and thus the probability of falling (note that this is independent of the question of whether the variability has a stochastic or deterministic origin, as long as the variability is critical to gait).

It should be kept in mind, however, that variability may be a natural consequence of the multiple degrees of freedom available within the system [106]. Hence, this theoretical argument only holds if we know both the constraints and the control strategy of the system. For instance, consider two subjects with identical anthropometrics, walking with identical trunk motions and equal step width variability, but different step widths. The subject with the smaller step width is more likely to tip over, and, thus, variability alone is not sufficient to describe stability in this case. Both subjects have the same constraints (i.e. keeping the centre of mass (or, rather, the extrapolated centre of mass, see §2.2.2) within the base of support), but have a different control strategy (i.e. one of them walks with a larger step width), and, thus, variability does not in this case index gait stability. Therefore, while variability may be related to stability, this relationship is hardly ever straightforward, since we do not know the control strategies of the nervous system, or the prevailing constraints. Nonetheless, variability measures have unrivalled popularity in the gait community [8,35,46,78,80,86,87,89,107–125]. This may in part be explained by the simplicity of the calculations involved, in combination with easily understandable metrics. Moreover, variability is one of the few measures with proven success in predicting the probability of falling [113,117].

2.1.4.2. Calculation

Although many measures exist to quantify variability, most variability measures are based on the standard deviation of a signal or a variable.

For discrete gait variables (e.g. step times and step width), the variability is usually calculated over the entire data series of values. For continuous gait variables (e.g. joint angle time series and acceleration time series), the time series of the variable is usually ‘cut’ into strides, and these strides are time-normalized (usually to a 0–100% time basis) and aligned. For each of the aligned time intervals, the variability is then calculated, and the mean or sum over these 101 variability values is usually analysed further. When calculating variability in this manner, it is of importance that the data are stationary; non-stationarities in the data would lead to overestimations of variability. To reduce the impact of non-stationarities, variability calculations are usually performed on velocity (or acceleration) time series, rather than on position time series.

Recently, the median absolute deviation was proposed as a measure for gait variability [126]. In general, the median absolute deviation is more robust than the standard deviation, and may thus be a good choice to use as an indicator of variability [126].

In some cases, it may be necessary to normalize the variance to the mean of the variable. This is particularly the case for variables that have certain natural ‘bounds’. For instance, stride times cannot be smaller than 0. Thus, if average stride times are closer to zero, it is to be expected that variability in stride times is lower (since there can be no values of stride times less than 0). Using a model, we recently showed that such normalization procedures indeed lead to better results ([91]; see also below).

It should be noted that, as in the calculation of the maximum Lyapunov exponent and the maximum Floquet multiplier, a considerable number of strides is required to obtain precise and reliable estimates of gait variability. Owings & Grabiner [109] estimated that the precision of estimates of variability measures did not further increase when using more than 200 strides.

2.1.4.3. Validity of variability measures

Construct validity. As mentioned earlier, the validity of variability measures is equivocal and depends on the theoretical framework of choice and the appropriateness of certain assumptions. Increased variability is often regarded as disadvantageous, but sometimes also as a sign of adaptability in that it may be a consequence of the exploitation of the multiple degrees of freedom available within the system. Clearly, much work is needed to reconcile those two views into one coherent framework that is able to predict with certainty when and what variability is ‘good’, and when and what variability is ‘bad’. Without such a coherent framework, it seems we cannot conclude that there is good construct validity for variability measures as predictors of the probability of falling. As outlined in the introduction on variability measures, we believe that an important step in achieving such a coherent framework would be to think in terms of ‘critical’ (or ‘goal equivalent’ [127]) variability, ‘control strategies’ and ‘control constraints’.

Predictive validity in models. Su & Dingwell [92] showed that the probability of falling, as induced by irregularities in a slope a passive dynamic walker was walking on, was reflected by variability in the kinematics (i.e. state variables of the walker), indicating that variability is correlated with the probability of falling. Hobbelen & Wisse [23] went one step further by showing that a variability-based measure (the GSN) can be used as an accurate predictor of a model's capability to overcome perturbations (expressed as the maximum perturbation the model could handle), also when the probability of falling is altered by changing properties of the model (rather than just the irregularities of the slope). Interestingly, in this study, only the GSN when calculated using stride times gave a good indication of the probability of falling, while other variables did not, suggesting that it is important to study variability measures of variables that are critical. Moreover, Hobbelen & Wisse [23] correlated 1/GSN with the maximum perturbation the model could handle, suggesting a nonlinear relationship between variability measures and the probability of falling. In agreement with this, Roos & Dingwell [128] reported that the relationship between variability measures and the probability of falling (expressed as the percentage of trials in which the model did not fall) was far from linear in a three-dimensional passive dynamic walker. They found this to be the case for both variability measures of the kinematic states and step lengths, step widths and step times. Still, it must again be noted that, in this model, the probability of falling was only affected by changing the amplitude of the irregularities in the slope. Bruijn et al. [102] performed similar simulations to those of Hobbelen & Wisse [23] and also examined the kinematic state variability. In doing so, we found that kinematic state variability did not correlate with the probability of falling (expressed as the maximum perturbation the model could handle), whereas the inverse of step time variability correlated fairly well, but we noted that this relationship was dependent on the mean step time. First log-transforming step times and then calculating the inverse of step time variability led to better results, with relationships being more similar across different manipulations of the model. All in all, these findings in model studies suggest that variability measures may indeed be related to the probability of falling. However, this relationship may only exist for the variability of certain critical gait variables and is not necessarily linear.

Convergent validity in experimental studies. Most experimental studies cited in the validity sections of the maximum Lyapunov exponent and the maximum Floquet multiplier also employed variability measures [34,39,75,77,86,95]. Interestingly, no matter which measures were used in these studies, they always reflected increased variability when stability was impaired experimentally. Moreover, besides those studies in which subjects were destabilized experimentally, Dean et al. [129] attached an elastic cord to their subjects (thereby stabilizing them), and showed that this manipulation decreased step width variability. All in all, there appears to be growing evidence from experimental studies that measures of gait variability may be correlated with the probability of falling.

Predictive validity in observational studies. Several observational studies have reported that measures of variability are related to the probability of falling in the elderly [76,113,117,121,122] (for an overview, see [28,119]). Most of these report higher values of gait variability in those elderly with a history of falling (or those elderly who will fall after the assessment, in the case of a prospective study).

It is interesting to note that Maki [113] reported a decreased step width variability in fall-prone subjects. Similarly, Moe-Nilssen & Helbostad [110] reported a lower variability of trunk accelerations in the medio-lateral direction in frail elderly subjects than in healthy elderly subjects, whereas Brach et al. [122] found that both an increase and a decrease in step width variability (expressed as the coefficient of variation) were related to a history of falling. Interestingly, from both modelling [130] and experimental work [112,129,131], it has been suggested that lateral stability (i.e. step width variability) is critical for human walking. Thus, the aforementioned findings of lower variability levels in (supposedly) more unstable populations clearly show that variability measures are predictive of the probability of falling only when the control strategy is invariant between the groups or measurements being compared.

Although gait variability seems to be correlated to the probability of falling in modelling, experimental and observational studies alike, more research into the how and why of this relationship is needed. Moreover, as it stands, it is still an open question which parameters of variability best predict falls since research has shown that some measures of variability may be better predictors than others. In conclusion, studying the variability of the most relevant variable seems of paramount importance.

2.1.5. Long-range correlations

2.1.5.1. General description

Over the past years, it has become evident that gait variations, as discussed in §2.1.4, are not random [132], but exhibit dependencies such that future variations are dependent on past variations. These dependencies manifest themselves as long-range correlations, which can be revealed by detrended fluctuation analysis (DFA; [133]).

It is not immediately obvious why and how long-range correlations relate to dynamic gait stability. However, Hausdorff et al. [132] noted that ‘processes with long-range correlations are generally more error tolerant and resistant to both internal and environmental perturbations’ [132, p. 356], based upon which these authors posed the question of whether the long-range correlations in locomotor control are also a sign of adaptability. This implies that they seem to regard systems with values of the scaling exponent (α) further away from 0.5 as being more stable (because systems with values of α = 0.5 are uncorrelated). Indeed, in several pathologies, patient groups have been shown to have values of α closer to 0.5 than control groups. Nonetheless, while studying the effects of walking speed on α, Jordan et al. [134] found values of α closer to 0.5 at preferred walking speed. Based on the assumption that preferred walking speed is the most stable walking speed (which was confirmed by the effects of speed on λ_S in this study), these authors reasoned that weaker long-range correlations (α closer to 0.5) during walking and running at preferred speed ‘are suggestive of an increased degree of flexibility or adaptability at this speed’ [134, p. 98]. Still, they also mention the fact that patient groups often have values of α closer to 0.5.

The strength of long-range correlations can be calculated for a number of gait parameters, including step length, step time, impulse, duration of contact and peak active force [134–136]. We chose to include this measure in the current review because of its prominence in the gait literature [3,9,35,79,119,132,134–155].

2.1.5.2. Calculation

The calculation of scaling exponents using DFA in this section follows the description of Peng et al. [133].

Because of the nature of the calculation, rather long data series are necessary for the calculation of this measure (i.e. most studies used data series longer than 5 min, although Herman et al. [3] used data series of 2 min). Damouras et al. [137] studied the number of strides required, and recommended a minimum of 600 strides. After a data series has been created from a quantity, the data series in question is integrated first.

The integrated data series is divided into windows of equal length n. In each window, a line is fitted to the data (figure 3). Subsequently, the average fluctuation of the data around the line (i.e. the residual variance) is calculated. This procedure was suggested to work best for n ranging from 16 to N/9 (with N being the length of the data series), to obtain the relationship between n and f(n) (where f(n) is the average residual variance for window size n; [137]). Typically, f(n) will increase with increasing n, and a linear relationship between f(n) and n on a log–log plot indicates the presence of power-law scaling.

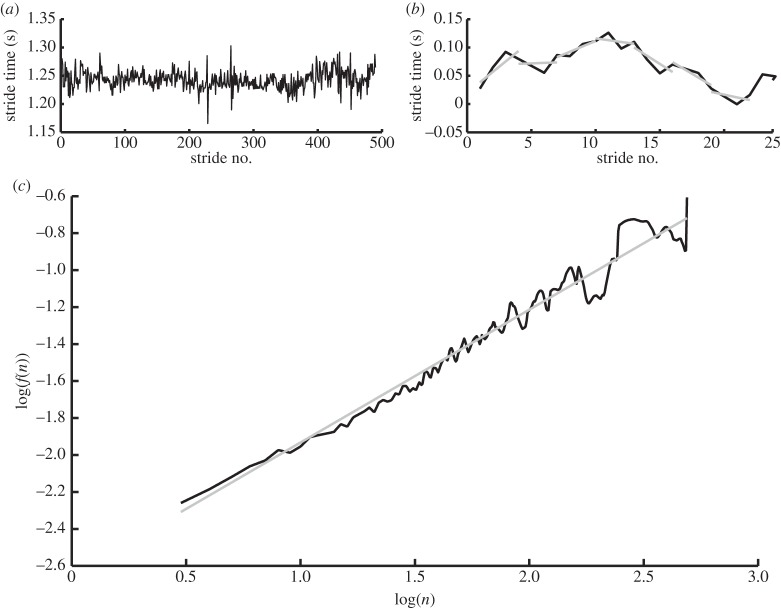
Figure 3.

Calculation of the scaling exponent α. (a) Data series of stride times, sampled at 300 samples per second. (b) Part of the data series of (a) integrated, with linear fits for n = 4. (c) The average residual around fits as shown in (b) (f(n)) is then plotted against n, and the slope of this line is the scaling exponent α (logf(n) versus log(n); black line, data; grey line, fit: α = 0.71871).

The slope of the line relating f(n) to n (on a log–log plot) is the scaling exponent (α). When subsequent strides are completely unrelated, α = 0.5, values of α < 0.5 indicate anti-persistence of the fluctuations, where a large value is more likely to be followed by a smaller value of the variable in question and vice versa, whereas α > 0.5 indicates positive long-range correlations, where a large (small) value is more likely to be followed by another larger (smaller) one. Typically, in human gait, values of 0.5 < α < 1.0 are found.

2.1.5.3. Validity of long-range correlations

Construct validity. As mentioned in §2.1.5.1, the theoretical relationship between long-range correlations and dynamic gait stability is under debate. In our opinion, the argument put forward by Jordan et al. [134] that less correlated gait allows more flexibility, and thus greater stability, is not generally valid; measured variations reflect not only planned variations but also reactions to perturbations [156]. For example, during walking, humans experience perturbations (impacts, sensory and motor noise), and it would be unusual if they did not react to those perturbations in subsequent strides. Reacting properly would automatically lead to some relationship between the previous and current stride, and thus a stronger correlation (either positive or negative, i.e. 0 < |α − 0.5|). In view of this debate, it is interesting to mention that, in general, both patients and elderly subjects are found to have values of α closer to 0.5 than healthy young adults [119], in accordance with the suggestion made by Hausdorff et al. [132] that processes with long-range correlations ‘are generally more error tolerant and resistant to both internal and environmental perturbations’ [132, p. 356]. Nevertheless, this was based on only empirical observations, and not on a clearly articulated theoretical rationale. All in all, it seems that the construct validity of long-range correlations as measures of the probability of falling is weak, and that long-range correlations are in need of a stronger theoretical foundation.

Given the debate about whether values of α closer to 0.5, or higher than 0.5, would predict the probability of falling, the results of modelling, experimental and observational studies are difficult to interpret.

Predictive validity in models. To the best of our knowledge, there are no model studies relating long-range correlations to the probability of falling. However, one study [154] showed that long-range correlations are present in a fairly simple model, indicating that no complex central nervous system is needed for them to arise.

Convergent validity in experimental studies. Long-range correlations were assessed in one study [95] in which stability was impaired experimentally by having subjects walk over a compliant surface, laid out on a circular track. In this study, no differences in long-range correlations between stable and unstable conditions were found.

Predictive validity in observational studies. As far as we know, only one (retrospective) observational study, by Herman et al. [3], has been published to date, which succeeded in discriminating fallers ([25] elderly with a higher level gait disorder) from non-fallers using long-range correlations. In this study, long-range correlations were less strong (i.e. α closer to 0.5) for the fallers than for the non-fallers, even though gait speed, stride time variability and several other parameters were equal between groups.

In sum, the theoretical relationship between long-range correlations and the probability of falling is unclear at present. Moreover, there seems to be only limited modelling, experimental and observational evidence from the literature to support this measure being related to the probability of falling. Still, long-range correlations may help to quantify other relevant aspects of motor control, such as the control strategy used [127,138]. In order for long-range correlations to become a useful measure in predicting the probability of falling, a clear theoretical account is needed as to which values of α (i.e. closer to or higher than 0.5 or perhaps values in between) are to be considered as more stable, and why this is so.

2.2. Measures derived from biomechanics

2.2.1. Background

In simple mechanical systems, stability can be defined in a straightforward manner. A canonical example of such a system is the inverted pendulum, which is often used as a model for human standing (figure 4). In this model, the centre of mass (CoM) needs to be controlled such that it stays over the base of support (BoS). Because walking is not static, this simple model cannot hold and needs to be extended taking into account the velocity of the CoM and BoS. In the current literature, there are several methods available that provide such extensions for the analysis of dynamic gait stability. All of these require at least the measurement (or calculation) of the CoM and BoS positions. Here, we discuss three such measures: the extrapolated centre of mass (XCoM) (§2.2.2), stabilizing and destabilizing forces (§2.2.3) and the FPE (§2.2.4). We refrain from discussing similar concepts that do not include velocities of the CoM as these may be too simplistic for quantifying stability in a dynamic situation [157].

Figure 4.

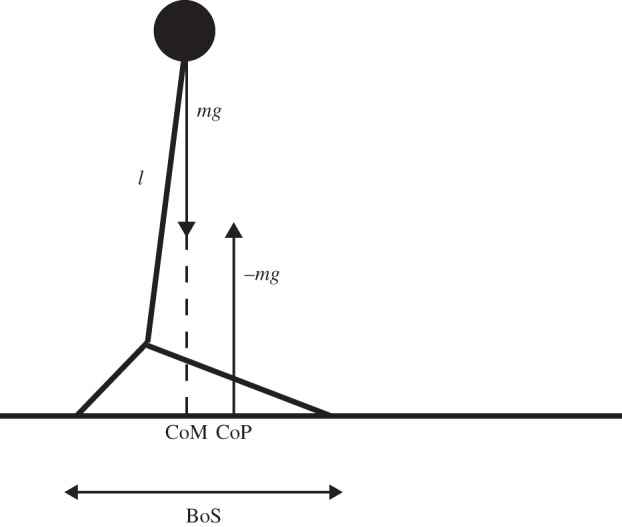
An inverted pendulum model. m, mass; g, gravitational constant (−9.81); l, pendulum length; CoM, centre of mass; BoS, base of support; CoP, centre of pressure.

Since these methods are based on such general principles, they may also be used to assess the ability to overcome large external perturbations of the gait pattern. In this section, we will describe their use in the unperturbed gait pattern. In §3, we will describe their use in perturbed gait.

2.2.2. Extrapolated centre of mass (margin of stability)

2.2.2.1. General description

The extrapolated centre of mass (XCoM) concept extends the classical condition for static equilibrium of an inverted pendulum, in which the CoM must be positioned over the BoS by adding a linear function of the velocity of the CoM to the CoM position [157–159]. The XCoM can be used to calculate both the spatial margin of stability (b) and a temporal stability margin (b_τ). The margin of stability describes the distance between the XCoM and the border of the BoS, whereas the temporal stability margin indicates the time in which the stability boundary of the BoS would be reached without intervention.

In theory, this method describes how close an inverted pendulum is to falling, given the position and velocity of its CoM, and the positions of the margins of its BoS. Although human walking may be described using inverted pendulum models [22], it may be clear that adaptive actions such as moving the arms and trunk are not captured by such a model. In some cases, it may even be unwanted to behave like an inverted pendulum (e.g. when the XCoM is moving past the BoS, and adaptive actions are required [160]). Then, using the theoretical assumption of an inverted pendulum model may be useful to indicate when adaptive actions are needed.

Furthermore, the margin of stability may be seen as a reflection of a control strategy. Hof [158] showed that, for stable walking, the feet should be placed lateral and posterior to the XCoM, and that a deviation of the state of the CoM due to a perturbation can be compensated for by a change in foot position, which can be expressed in terms of the XCoM times a constant. By calculating this constant, insight can be gained into how fast perturbations are accommodated. While this constant can in principle be calculated from unperturbed walking, it should be noted that information on a feedback system can in principle only be obtained by opening the control loop in some way, e.g. by means of perturbations [156].

The XCoM concept has gained considerable popularity over the past decade or so [77,157–159,161–171], although mostly in an experimental context. One of the potential reasons why it has not been used in observational studies could be that both the position of the feet and the CoM need to be measured for the extrapolated centre of mass and margin of safety to be calculated. This requires considerably more (expensive) measurement equipment and time to achieve than many other measures.

2.2.2.2. Calculation

For the full derivation of the formulae from the inverted pendulum model, we refer to Hof et al. [157]. Here, we confine ourselves to a description of how the method may be applied to unperturbed walking.

For the calculation of the margin of stability and the temporal stability margin, first the position of the whole body CoM and BoS need to be known. These can in principle be obtained from kinematic data alone (using a sufficient number of (virtual) markers on the feet), force plate data alone (using a filtering procedure to obtain CoM position from centre of pressure (CoP) data, and assuming that the BoS coincides with the CoP position) [159,172], or a combination of both force plate and kinematic data [157].

Next, the XCoM is calculated as

2.4

with V_CoM being the CoM velocity and ω₀ being the inverted pendulum's eigenfrequency

2.5

where g represents the acceleration of gravity (9.81 m s⁻²) and l is equivalent to the pendulum length of the subject. The margin of stability is defined as

2.6

The most unstable point can be found by identifying the minimum of b (b_min) within a step [159]. Furthermore, to quantify the time available before the XCoM crosses the BoS, b_τ can be estimated using

2.7

this is the time that corrections to the CoM position and/or velocity can be made without the need to move the arms, trunk or the use of a stepping strategy [160]. In theory, if b < 0 or b_τ < 0, stability cannot be recovered without such actions.

In principle, the XCoM concept could be applied to both antero-posterior stability and medio-lateral stability. This works out fine in the analysis of medio-lateral stability, but in the analysis of antero-posterior stability this method will result in negative values for b and b_τ, indicating that gait cannot be stopped within that step. Perhaps this information could be used as an indicator of how easy it is to stop within a step. However, this will also depend on other factors, such as maximum attainable swing speed, ground clearance, etc., which reduces the value of the concept for the antero-posterior direction.

2.2.2.3. Validity of the extrapolated centre of mass

Construct validity. Given its sound mechanical basis, there is little doubt about the construct validity of the extrapolated centre of mass for assessing stability in the frontal plane. For assessing stability in the sagittal plane, however, there is uncertainty about what this measure has to offer, as it quantifies gait as unstable in this plane. It may give an indication as to how far the foot is placed behind the extrapolated centre of mass, which in turn could indicate how many steps need to be taken to recover stability. Also, the variability of the antero-posterior foot placement with respect to the extrapolated centre of mass when walking on level ground may be seen as resulting from movement errors, and thus as a source of instability [173].

Predictive validity in models. Hof [158] showed that a simple model could use the rules imposed by the XCoM to walk, take corners and stop walking. However, this is different from showing that this measure actually predicts the probability of falling for a simple model, and such studies have yet to be undertaken.

Convergent validity in experimental studies. Hoehne et al. [161] used the extrapolated centre of mass in a setting where gait stability was impaired experimentally (by intradermal injections of an anaesthetic solution in the sole of the foot). Results showed that subjects with desensitized feet showed no significant differences in antero-posterior foot placement during normal walking. In another study by Curtze et al. [171], amputees and healthy subjects were asked to walk over a smooth and a rough surface. No differences between surfaces or groups (nor in interaction) were found for the frontal plane margin of stability. However, the amputees walked with significantly wider steps than the controls in both conditions (with no difference between conditions), while the controls increased their step width when walking on the rough surface. These results may suggest that people tend to use a constant margin of stability, and that patients may use an increased step width to compensate for increased trunk sway [171]. However, it must be noted that walking speeds were different between conditions and groups, which renders these results difficult to interpret. In another study by McAndrew Young et al. [173], subjects were destabilized using platform and visual perturbations. In this study, walking speed was kept equal between conditions, but, nevertheless, it was found that during destabilized conditions subjects walked with a higher b, indicating that subjects were actually more stable when walking in a destabilizing environment.

Predictive validity in observational studies. As far as we know, there are no studies that used the extrapolated centre of mass to predict the probability of falling. Future studies should focus on the question of whether subjects at risk of falling can indeed be discriminated from healthy subjects using the extrapolated centre of mass.

2.2.3. Stabilizing and destabilizing forces

2.2.3.1. General description

Duclos et al. [174] introduced the concept of stabilizing and destabilizing forces. It may be viewed as an extension of the method adopted by Delisle et al. [175] to assess stability during lifting. In short, it aims at quantifying the forces needed to stop the CoP motion in the direction of the border of BoS (stabilizing force), and the force needed to bring the CoP outside the BoS, ignoring current velocity (destabilizing force). From these two forces, a ratio of destabilizing over stabilizing force can be calculated. A lower ratio indicates that it is easy to make the body fall over from its current position, and conversely that it requires a large effort to prevent a fall.

2.2.3.2. Calculation

As stated in §2.2.3.1, this method involves the calculation of the ratio of destabilizing over stabilizing force. For the calculation of this measure, positions of CoM, CoP and BoS are necessary, implying measurement of ground reaction forces as well as kinematics of at least the feet and a trunk marker (although full body kinematics may be preferable). In describing the calculations, we follow the description of Duclos et al. [174].

The stabilizing force (F_st) is calculated for each sample by first calculating the work (W) needed to bring the CoM to a standstill (i.e. kinetic energy = 0),

2.8

where m is the mass of the subject and V_CoM is the velocity of the CoM. Realizing that this work can be conceptualized as that delivered by the ground reaction force over the minimum distance between the CoP and the edge of the BoS (D_CoP), we can calculate the theoretical average force (F_st) necessary to bring the CoM to a standstill since

2.9

The destabilizing force, indicating the force needed to tip the subject over, can be calculated from the (minimum) torque (M_d) that would be needed to tip the subject over (assuming that the subject is not moving)

2.10

where F_z is the vertical component of the ground reaction force. If we assume that this destabilizing force (F_d) will be applied at the height of the CoM (CoM_z), we can calculate the required force as

2.11

This destabilizing force is hence the force that needs to be exerted at the CoM to bring the CoP outside the BoS, ignoring instantaneous CoM velocity. An index of stability may then be calculated by dividing the destabilizing force by the stabilizing force. As stated before, this ratio provides an indicator of how easy it is to make the body fall from its current position, or conversely the effort required to prevent a fall.

Since all the above calculations are performed per recorded sample, statistical analysis of the index of stability (or stabilizing and destabilizing forces) requires some averaging procedure. Duclos et al. [174] chose to average over the single stance phase, but, in principle, any phase may be used.

2.2.3.3. Validity of the concept of stabilizing and destabilizing forces

Construct validity. From the description above, it is evident that, in the calculation of the destabilizing force, movement speeds and accelerations are not taken into account. This part of this concept is based on static assumptions, and thus, in accordance with our reasoning in §2.2.1, we regard this measure as too simplistic.

The stabilizing force, in contrast, may be more interesting. It indicates how much effort is required to come to a standstill with the CoM within the BoS. If combined with a theoretical maximum force that can be produced, it can be seen as a predictor of the instants that an extension of the BoS is needed (i.e. when the stabilizing force exceeds the maximum force that can be produced), similar to the model of Pai & Patton [176] for the control of standing still. In this sense, the stabilizing force is also a measure of a margin of stability, just like the extrapolated centre of mass concept (see §2.2.2). However, for walking, it may only be applicable to medio-lateral motions, as walking requires by definition that the CoM moves out of the BoS in the antero-posterior direction during each step.

Given the different nature of the destabilizing and stabilizing forces (i.e. based on static versus dynamic assumptions), it seems inappropriate to use a ratio of these forces. The stabilizing force alone would seem a more appropriate measure.

We are not aware of modelling, experimental or observational studies directly testing the validity of the concept of stabilizing and destabilizing forces.

In conclusion, much work is needed to further develop this measure and to assess its validity. This work should start by developing a more valid equivalent to the destabilizing force, which takes into account the velocity (and acceleration) of the CoM.

2.2.4. Foot placement estimator

2.2.4.1. General description

The FPE is a recently developed measure that estimates where the feet should be placed for stable gait [162,177,178]. The measure is based on the assumption of conservation of angular momentum during the transition from one leg to the other. In short, the FPE estimates where the foot should be placed so that, after the transition from one leg to the other, the system energy is equal to its peak potential energy. In a pendulum gait, involving a perfect exchange between potential and kinetic energy, this would imply that the system would come to a standstill when potential energy reaches its peak (i.e. at its apex, at mid-stance).

2.2.4.2. Calculation

The calculation of the FPE first requires the calculation of total body angular momentum (H_tot), using conventional rigid body mechanics [179]. From the total body angular momentum, total body angular velocity can then be calculated as

2.12

in which I_CoM is the total body inertia, calculated from segment inertias using the parallel axes theorem.

Next, the value of the leg angle (ϕ) for which the post-contact system energy would be equal to the peak potential energy has to be found. This can be achieved by finding a solution to

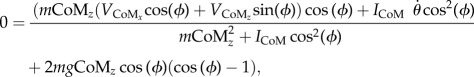2.13

where m is the subject's mass, CoM_z is the height of the CoM, 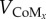and 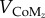are the horizontal and vertical velocity of the CoM and g is the gravitational constant. From here on, simple trigonometry can be used to find the actual position where the foot has to be placed

2.14

If the swing leg is placed in front of this point, coming to a standstill is possible within one stride, without actively braking in the stance phase. If it is placed behind this point, multiple strides are needed to come to a standstill. The distance between foot placement and FPE(ϕ) will thus give an indication of the stability of the gait pattern.

It is important to note that the validity of the FPE depends on four assumptions, namely (i) angular momentum is conserved during foot contact and (ii) leg length, (iii) moment of inertia, and (iv) system energy (potential and kinetic energy) are constant. The validity of these assumptions when calculating the FPE can be tested by using a sensitivity analysis, as has been carried out by Millard et al. [162].

The above equations pertain to planar movements only; three-dimensional movements are not taken into account. Recent work [178] on the FPE has focused on using the FPE in three dimensions. To this aim, three-dimensional walking is actually represented as two-dimensional walking, by creating a ‘plane of progression’ for each moment in time, and projecting all quantities on this plane. In doing so, calculations again become two-dimensional (within the plane of progression). After these two-dimensional calculations, the FPE can be projected back onto the three-dimensional world, so that an estimate of both medio-lateral and antero-posterior foot placement can be obtained.

2.2.4.3. Validity of the foot placement estimator concept

Construct validity. Like the other measures derived from biomechanical models, the FPE has a good construct validity, that is to say, if its assumptions are fulfilled, its laws fully apply. However, there are some differences between the simple models in which these assumptions hold and actual human walking. Millard et al. [162] assessed the FPE as calculated from human walking's sensitivity to deviations from the underlying assumptions. They concluded that assumption violations of human gait could not account for the observed effects of walking speed, as the effects of violations of assumptions were an order of magnitude smaller than the effects of walking speed.

Predictive validity in modelling studies. When introducing the FPE concept, Wight et al. [177] showed that it works well as a control algorithm for a seven-link biped. They succeeded in using the FPE to control the biped's gait, make it start and stop walking, and to overcome perturbations during gait. All in all, it seems that, as long as the assumptions of the measure hold, the FPE works well to control models of human gait. However, it remains to be established if, and how well, the post hoc-calculated FPE from a model that is not controlled by the FPE concept can also be used to predict its probability of falling.

Convergent validity in experimental studies. As of yet, there are no truly experimental studies using the FPE, although there are two studies showing that the underlying assumptions of the concept hold for human gait [162,178]. Studies using experimental manipulations of stability are needed to assess whether the FPE can adequately predict the probability of falling in humans.

Predictive validity in observational studies. To date, there are also no observational studies using the FPE concept, presumably because it is rather novel. Also the fact that full body kinematics and kinetics are needed, which renders the method laborious, may play a role in this regard. Yet, given its strong theoretical validity, it would be interesting to see how well it is able to discriminate fallers from non-fallers.

3. Measures that reflect the ability to recover from larger perturbations

As stated in §1, the ability to overcome larger perturbations may be partially independent from the ability to overcome smaller perturbations. Therefore, this ability should be probed alongside the ability to overcome smaller perturbations. Methods to do so will most probably involve mechanical perturbations of walking subjects. Applying such a mechanical perturbation will require more instrumentation than the measures discussed so far, which may be why they have been used less often. Still, there is a vast body of literature on gait responses following trips, slips and surface perturbations [4]. However, most of this research has focused on the biomechanical nature of the recovery response, quantifying joint torques, muscle activity and so forth, without trying to develop a more global, quantitative measure of dynamic gait stability.

There are, however, some studies that did attempt the latter, and the measures used in those studies will be discussed in the next section; the GSN (§3.1), the extrapolated centre of mass (§3.2) and the FPE (§3.3).

Before addressing these measures, it is useful to discuss some principles that pertain to all perturbation studies and measures derived thereof. Theoretically, to consistently assess dynamic gait stability, a perturbation applied to a subject during walking should (i) have equal magnitude for all conditions and subjects and (ii) be applied at the same instant of the stride cycle for every condition and subject. In real life, however, both of these requirements may be hard to achieve. For instance, it may be possible to generate perturbations with the same force; however, it is difficult to predict whether these perturbations will have the same effect for persons of different body size/mass. Moreover, one may be able to time these perturbations at exactly the same moment within a gait cycle (by using kinematic information to trigger the perturbation), but, nevertheless, since the length of the perturbations is finite, the end of the perturbation may occur at different phases in the gait cycle, depending on stride times.

Apart from these technical difficulties in applying perturbations, there is also the problem of anticipation and adaptation (of both the steady-state gait and the reaction to the perturbations). The problem of anticipation may be hard to overcome because it seems unethical not to inform subjects that at some point of a walking trial they will be perturbed in some way. Still, some studies perturbed subjects without telling them [180], but these have not investigated differences between completely unexpected and more or less expected perturbations. However, anticipation of being perturbed affected the steady-state gait only a little [181,182]. Apart from anticipation, perturbations may cause altered responses to subsequent perturbations. Van der Linden et al. [183] found that, in a set of perturbations, only the reaction to the first perturbation was different from the others. Thus, using multiple perturbations will probably avoid the problem that reactions to perturbations are altered in the course of time. Moreover, anticipation can be reduced by interspersing enough unperturbed periods of gait in between perturbations [182]. However, by repeated perturbations, one will most probably always overestimate the ability to overcome perturbations in real life.

3.1. Gait sensitivity norm

3.2.1. General description

The GSN [23] is a stability measure that was constructed to predict the dynamic stability of limit cycle walkers. It is based on the reaction of a specific gait indicator (e.g. step time and step width) to a specific perturbation (i.e. push, pull and step down). This specific perturbation should be chosen to ‘instigate the important failure modes (ways to fall)’ [23, p. 1214] and the specific gait indicator should be chosen to ‘quantify the characteristics of the walking gait that are directly related to the failure modes’ [23, p. 1214].

While the GSN seems to be a successful construct in robotics [23,184], we are unaware of any literature on the use of the GSN in human walking, apart from some pilot data that we have presented at a conference ([185]; see also §2.2.3).

3.2.2. Calculation

The calculation of the GSN in robotic walking starts with the choice of a perturbation (denoted e₀), and gait indicator(s) (denoted y_i with i the number of the gait indicator).

Next, the value of the gait indicators during steady-state gait is calculated (denoted by 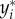). Then, the response to a perturbation can be estimated by assuming a linear relationship between the size of a perturbation (e₀) and the response of the gait indicators to that perturbation

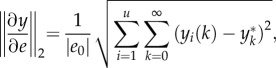3.1

in which y_k(i) is the value of gait indicator i at step k after the perturbation and ||∂y/∂e||₂ is the response to perturbation e₀. From equation (3.1), it can be seen that higher values of ||∂y/∂e||₂ indicate a less stable walker.

While the GSN is rather easy to calculate for robotic walking, this is not the case for human walking for two reasons: (i) the gait indicator(s) cannot be measured for an infinite number of strides after a perturbation and (ii) the natural variability of the chosen gait indicator may vary between conditions (thereby greatly influencing the GSN). The former problem may be resolved by analysing a fixed number of strides after a perturbation. To address the latter problem, Bruijn et al. [185] proposed first normalizing the variance present in the gait indicator to the variance levels found in unperturbed walking, thus accounting for differences in natural variability.

Besides these two obvious problems, the choice of a perturbation type and a gait indicator are much more complex in human walking, in which failure modes may not be as straightforward as in models or robots.

3.2.3. Validity of the gait sensitivity norm

Construct validity. The GSN is a theoretically sound concept, which has as its greatest issue the choice of perturbation type and gait indicators. Still, it has thus far not been applied (except for one pilot study) to human gait, and thus clearly requires further research.

Predictive validity in models. Since it was designed for passive dynamic walkers, it is not surprising that it works well in these types of models in predicting the probability of falling [23].

Convergent validity in experimental studies. In a pilot study, we tested whether the basic assumption of the GSN, namely that the reaction to a perturbation scales linearly with the perturbation size, is valid for human walking [185]. We used a sideways pull as perturbation (with force e₀), and examined two gait indicators (step time and CoM position at heel-contact). We found that, for these gait indicators, this assumption did hold. The GSN as calculated using the CoM position as a gait indictor was lower during faster walking than during slow walking, indicating a more stable walking pattern. Thus, the GSN seems sensitive enough to detect changes in stability caused by differences in walking speed.

As far as we know, there are no other experimental studies, nor observational studies, using the GSN.

3.2. Extrapolated centre of mass (margin of stability)

3.2.1. General description

The use of the extrapolated centre of mass to quantify the ability to recover from small perturbations has been described in §2.2.2. Owing to the general nature of this measure, it can also be used to assess recovery of the gait pattern after a perturbation. To date, however, the extrapolated centre of mass has only been used in this manner in a few studies [161,165,166].

3.2.2. Calculation

For the calculation of the spatial and the temporal margins of stability after a perturbation of gait, we refer to the calculations of these measures from steady-state gait (see §2.2.2.2).

3.2.3. Validity of the extrapolated centre of mass

Construct validity. Given its sound mechanical basis, there is little doubt about the construct validity of the extrapolated centre of mass for assessing stability in the frontal plane after a perturbation. Interestingly, with perturbations, it can also provide insight into how quickly subjects are able to recover stability in the antero-posterior direction after a perturbation (i.e. how quickly the foot placement relative to the extrapolated centre of mass returns to normal).

Predictive validity in models. As stated in §2.2.2.3, Hof [158] showed that a simple model could use the rules imposed by the extrapolated centre of mass to walk straight ahead, take corners and stop walking without falling. All of these actions can be regarded as perturbations of gait, and, thus, it seems that the extrapolated centre of mass as a control strategy for perturbed walking works well for models. Still, it remains to be seen whether it can also be used as a predictor of the probability of falling in such models.

Convergent validity in experimental studies. We are aware only of one study in which the extrapolated centre of mass after a perturbation was used, and gait stability was manipulated, namely that of Hoehne et al. [161]. In this study, gait stability was reduced experimentally by altering cutaneous sensation of the feet by means of an intradermal injection of an anaesthetic solution. This was found to lead to an increase in the antero-posterior distance between the extrapolated centre of mass and the border of the BoS at touchdown after a perturbation, suggesting an increased stability. While this may seem odd at first sight, it could be a strategy to deal with altered system constraints.

Predictive validity in observational studies. As of yet, there are no studies available that test the ability of the extrapolated centre of mass calculated after a perturbation to discriminate fallers from non-fallers.

3.3. Foot placement estimator

3.3.1. General description

The FPE as used to quantify the ability to recover from small perturbations has been described in §2.2.3. Given the general nature of this measure, it can also be used to assess recovery of stability after a perturbation. Basically, all calculations are similar, only this time they are applied to perturbed gait.

3.3.2. Calculation

For the calculation of the FPE after a perturbation of gait, we refer to the calculations of these measures as described for steady-state gait (see §2.2.3.2).

3.3.3. Validity of the foot placement estimator

Construct validity. Given its sound theoretical basis, the FPE has good construct validity, even when applied to perturbed gait. Moreover, while investigating sensitivity to the assumptions of the FPE for gait termination, and landing from a jump, Millard et al. [178] concluded that violations of the assumptions affected results only a little, making the method also valid for these kinds of movements. This makes it likely that these assumptions also hold for gait after a perturbation, although this has not been tested to date.

Predictive validity in models. Given the fact that it was derived from a model, it is not surprising that the FPE concept can be used to control such models, even after perturbations. However, this has only been shown in one study, for a simulation model of a seven-link biped [177]. Still, this study only showed that a biped could be controlled with this concept, not that the probability of falling could be predicted from this concept. Moreover, no data are available on the convergent validity in experimental studies, or on the predictive validity in observational studies for the FPE.

4. Measures that reflect the maximum perturbation that can be handled

As stated in §1, we foresee that the ability to overcome larger perturbations may be different from the ability to overcome the largest perturbation that can be handled under optimal conditions (such as full attention to the gait pattern, etc.). However, since the largest perturbation that can be handled may be hard to assess, and probably only has limited meaning in daily life (where the smaller and larger perturbations will occur more often), we will dedicate only a short paragraph to it. Moreover, because we are not aware of anyone who has used a measure similar to the one we have in mind, we will abandon the structure of the previous two sections, in which we distinguished between ‘general description’, ‘calculation’ and ‘validity’, and discuss these together in the present section.

The maximum allowable perturbation is the maximum perturbation of the gait pattern that a subject can handle, before falling. It is very likely that this will be different for perturbations in different directions, perturbations occurring in different phases of the gait cycle, and so on. Thus, it might not be a very practical measure to use. Of course, it is highly unlikely that for any perturbation there will be a clear-cut boundary between falling and being able to recover. More likely, for any magnitude of perturbation, there is a finite probability that somebody will fall. Assessing the maximum allowable perturbation would thus result in a very long experiment.

Another approach may be to perturb subjects with an equal perturbation magnitude, and see how many times they fall. In fact, the latter method has been used by some and proved to be successful to pinpoint risk factors associated with falling after a trip [4].

5. Discussion

We set out to review existing measures of gait stability, and the different levels of validity that these measures exhibit. In this final concluding paragraph, we will summarize our findings, give directions for best-choice stability measures and indicate directions for future research. We will do so using table 2, which contains for each measure and each validity level we considered one cell, colour coded so that light grey denotes support for a certain measure for a certain level of validity, black denotes falsification of support for a certain measure for a certain level of validity and dark grey denotes conflicting or no data available.

Table 2.

Support at different validity levels for the different stability measures. Each measure and each validity level are represented by one shaded cell, coded such that light grey denotes support for a certain measure for a certain level of validity; black, falsification of support for a certain measure for a certain level of validity; and dark grey, conflicting or no data available. Numbers with an asterisk: *1, the light grey colour here only holds for the stabilizing force; *2, unless the assumption is made that subjects perform a stabilizing strategy when destabilized.

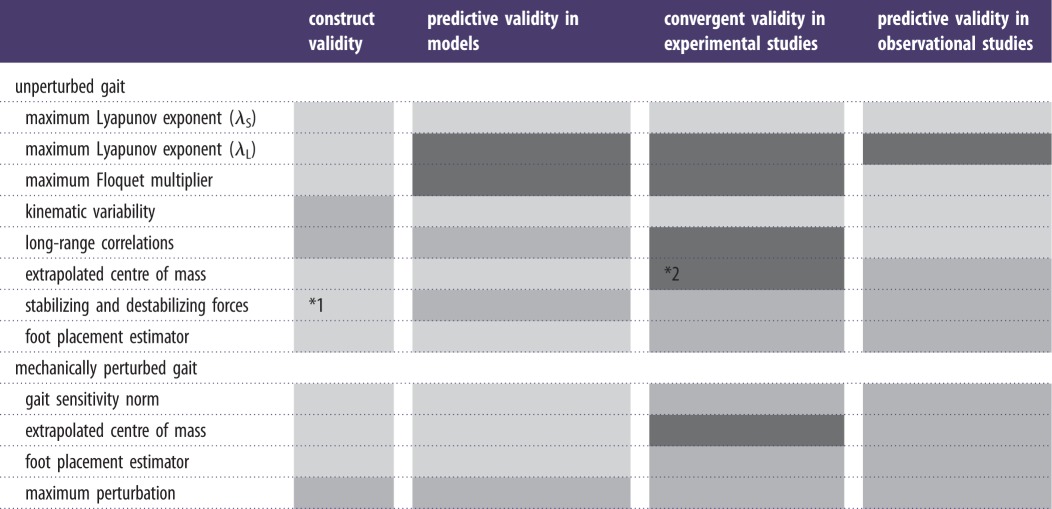5.1. Best measures to assess dynamic gait stability

Given table 2, the choice for a stability measure would, on first pass, amount to looking up the measure with most light grey cells. In doing so, one may conclude that (i) the validity of variability measures and the maximum Lyapunov exponent (λ_S) across all levels is supported best by evidence, (ii) the maximum Floquet multiplier and the maximum Lyapunov exponent (λ_L), while having good construct validity, have negative predictive validity in models, negative convergent validity and (for λ_L) negative predictive validity in observational studies, (iii) long-range correlations lack construct validity and predictive validity, in models and have negative convergent validity, and, lastly, (iv) for measures derived from perturbation experiments there is good construct validity, but data are lacking on convergent validity in experimental studies and predictive validity in observational studies.

Nevertheless, it should be remembered that there are probably three different requirements for gait stability—i.e. (i) the system has to be able to limit or recover from the small perturbations that occur during every stride (e.g. owing to small differences in floor height and noise), (ii) the system has to be able to recover from large perturbations, which require a change in behaviour, and (iii) the largest recoverable perturbation specified by the limits of the system needs to be larger than the perturbations encountered—which may be more or less independent, and that not all measures may be feasible in the practical sense (some for instance require full body kinematics, others just a single accelerometer). Thus, the choice of stability measure will most probably depend on several factors, such as sample size, available time per subject and available equipment, and most probably, in most studies, only one aspect of gait stability will be assessed. As discussed below, it remains to be investigated which aspect of gait stability is related most to the probability of falling, and should thus be assessed, if possible.

5.2. Directions for future research

An obvious first step for future research would be to further validate measures for which evidence for a certain level of validity is lacking. As discussed in §1, we are of the opinion that it is preferable to do so in the more or less logical order in which we presented the three levels of validity. This also implies that we think that attempting to further validate measures that have been proved to be invalid for a previous level of validity may be a useless undertaking. However, it would be good to collect further evidence at lower levels of validity, for measures where this does not yet exist.

A second important direction for future research was already briefly touched upon in the paragraph above on the best choice of stability measures, as well as in §1. It is the relationship between the three requirements for gait stability (ability to overcome small perturbations, ability to overcome larger perturbations and the largest recoverable perturbation) and their relationship to the probability of falling. As of yet, it is not known how each of these three requirements relates to the other two, and how all three of them relate to the probability of falling. Future research should thus focus on how these three requirements are related, and how each of the three requirements contributes to the real-life probability of falling. If the sensitivity and specificity of a measure from one aspect of gait stability are already high, and measures related to the second and third aspect do not add anything, then there is no need to add those to an assessment of stability. However, if including two requirements leads to a marked increase in sensitivity and specificity, then it would make sense to include multiple measures. This kind of research requires large cohort studies, in which all requirements for gait stability are assessed, and the actual incidence of falls is tracked. While in practice it may be difficult to perform such a study, it would most probably lead to very interesting results.

As mentioned in §1, the probability of falling is dependent not only on a person's gait stability, but also on the amount and size of perturbations a person encounters during daily life. This factor has received little attention so far. While it is outside the scope of the current review, factors such as reduced vision or proprioception may lead to more perturbations than expected, e.g. in an environment that contains objects that could cause perturbations (see [186]). Thus, the interplay between environment and person may determine to a large degree how perturbing a certain environment is for a given person. This is important information to adequately predict the probability of falling and should be a focus of future research.

The last direction for future research that we would like to highlight is the development of new stability measures, and the improvement of algorithms to estimate existing parameters to enhance their validity and reliability. In doing so, we believe that it is important to validate them according to the four-step scheme (construct validity, predictive validity in models, convergent validity, predictive validity in observational studies) proposed here.

Appendix A. State spaces

State spaces are spaces in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the state space. For mechanical systems, these spaces mostly contain positions and velocities of all elements of the system. Thus, by describing gait in state space, we have an unambiguous description of the gait pattern. Typically, these experimental data exhibit the structure of an attractor, i.e. a subspace of the d-dimensional state space to which neighbouring trajectories converge [62,187].

To obtain a state estimate of walking, one could measure the positions and velocities of all segments in space, which would yield the exact state of the system. However, if we realize that all segments are coupled and their motions will thus influence each other [188], analysis may focus on trunk movements, or a certain joint angle only. Indeed, the latter approach has been used in several studies [31,63,64].

According to Taken's theorem [82], since the states of walking may be seen as being on an attractor, we do not need to measure all states of the walking system. From one state variable of a system, an attractor can be reconstructed that has similar features tp the original attractor formed from all state variables [82,189]. This can be accomplished by using any state variable of a system and time-delayed copies (figure 5). The number of time-delayed copies can be estimated using a global false nearest neighbour analysis [190], and the time delay can be calculated by using the first minimum in the average mutual information function [191], among other methods. Apart from all the details involved in choosing a delay and embedding dimension [59,192], it should be noted that, mostly, data used to construct state spaces are not filtered, because of the problems associated with filtering nonlinear signals [193].

Figure 5.

Reconstructing a state space using embedding delays. (a) The original recorded velocity signal, with point q(t) and points q(t+τ) and q(t+2τ) (time-normalized first derivative of the time series q). In (b), the original time series (q) from t onwards is plotted on the x-axis, with corresponding values of q(t+τ) on the y-axis, and values of q(t+2τ) on the z-axis (state space reconstruction of q). In matrix form, this state space is

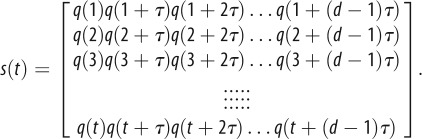
In analysing human gait data, both state spaces formed from a full description of trunk motions and state spaces based on embedding delay are being used. An overview of state space definitions used for analysis of human gait data may be found in Gates & Dingwell [59].