Abstract
Diagnostic test orders to an animal laboratory were explored as a data source for monitoring trends in the incidence of clinical syndromes in cattle. Four years of real data and over 200 simulated outbreak signals were used to compare pre-processing methods that could remove temporal effects in the data, as well as temporal aberration detection algorithms that provided high sensitivity and specificity. Weekly differencing demonstrated solid performance in removing day-of-week effects, even in series with low daily counts. For aberration detection, the results indicated that no single algorithm showed performance superior to all others across the range of outbreak scenarios simulated. Exponentially weighted moving average charts and Holt–Winters exponential smoothing demonstrated complementary performance, with the latter offering an automated method to adjust to changes in the time series that will likely occur in the future. Shewhart charts provided lower sensitivity but earlier detection in some scenarios. Cumulative sum charts did not appear to add value to the system; however, the poor performance of this algorithm was attributed to characteristics of the data monitored. These findings indicate that automated monitoring aimed at early detection of temporal aberrations will likely be most effective when a range of algorithms are implemented in parallel.
Keywords: laboratory, syndromic surveillance, temporal aberration detection, outbreak detection, control charts
1. Introduction
During the past decade, increased awareness of the need to recognize the introduction of pathogens in a monitored population as early as possible has caused a shift in disease surveillance towards systems that can provide timely detection [1,2]. Some monitoring has shifted to pre-diagnostic data, which are available early, but lack specificity for the detection of particular diseases. These data can, however, be aggregated into syndromes, a practice that has led to an increase in the use of the terms ‘syndromic data’ and ‘syndromic surveillance’ [2,3].
Disease outbreak detection is a process similar to that of statistical quality control used in manufacturing, where one or more streams of data are inspected prospectively for abnormalities [2]. For this reason, classical quality control methods have been used extensively in public health monitoring [4,5]. However, these types of control charts are based on the assumption that observations are independently drawn from pre-specified parametric distributions, and therefore their performance is not optimal when applied to raw, unprocessed health data [6], which are typically subjected to the effect of factors other than disease burden. Some of these factors are predictable, such as day-of-week (DOW) effects, seasonal patterns or global trends in the data [2]. These predictable effects can be modelled and removed from the data [7,8]. An alternative is to make use of data-driven statistical methods, such as the Holt–Winters exponential smoothing, which can efficiently account for temporal effects [9].
The use of real data is an essential step in the selection of algorithms and detection parameters, because the characteristics of the baseline (such as temporal effects and noise) are likely to have a significant impact on the performance of the algorithms [10]. However, the limited amount of real data and lack of certainty concerning the consistent labelling of outbreaks in the data prevent a quantitative assessment of algorithm performance using standard measures such as sensitivity and specificity. These issues can be partially overcome using simulated data that can include the controlled injection of outbreaks. Furthermore, this approach has the advantage of allowing for the evaluation of algorithm performance over a wide range of outbreak scenarios [11].
A recent review [12] indicated that few systems have been developed for real- or near-real-time monitoring of animal health data. Previous work [13] has addressed the possibility of using laboratory test requests as a data source for syndromic surveillance in aiming to monitor patterns of disease occurrence in cattle. In this study, these same data streams were used to evaluate different temporal aberration detection algorithms, with the aim of constructing a monitoring system that can operate in near-real-time (i.e. on a daily and weekly basis).
The earlier-outlined points were addressed in an exploratory analysis designed to
— identify pre-processing methods that are effective in removing or dealing with temporal effects in the data;
— explore methods that combine these pre-processing steps with detection algorithms, with the data streams available and being aware of the importance of having a detection process interpretable by the analysts; and
— identify the temporal aberration detection algorithms that can provide high sensitivity and specificity for this specific monitoring system.
A variety of algorithms and pre-processing methods were combined and their performance for near-real-time outbreak detection assessed. Real data were used to select algorithms, whereas sensitivity and specificity were calculated based on simulated data that included the controlled injection of outbreaks.
2. Methods
All methods were implemented using the R environment (http://www.r-project.org/) [14].
2.1. Data source
Four years of historical data from the Animal Health Laboratory (AHL) at the University of Guelph in the province of Ontario, Canada were available from January 2008 to December 2011. The AHL is the primary laboratory of choice for veterinary practitioners submitting samples for diagnosis in food animals in the province of Ontario, Canada. The number of unique veterinary clients currently in the laboratory's database (2008–2012) is 326. The laboratory receives around 65 000 case submissions per year, summing up to over 800 000 individual laboratory tests performed, of which around 10 per cent refer to cattle submissions, the species chosen as the pilot for syndromic surveillance implementation.
A common standard for the classification of syndromes has not been developed in veterinary medicine. Classification was therefore established firstly upon manual review of 3 years of available data, and then creating rules of classification reviewed by a group of experts (a pathologist, a microbiologist and a field veterinarian) until consensus was reached by the group. These rules were implemented in an automated system classification as documented in Dórea et al. [15].
An effort was made to classify every laboratory submission record into at least one syndromic group. Therefore, the final syndromic classification was not only based on a direct relation to clinical syndromes. A ‘syndromic group’ is defined in this system as laboratory submissions: (i) related to diseases from the same organ system; (ii) comprising diagnostic tests for the same specific disease, in the cases of tests requested so frequently that their inclusion in another group would result in their being, alone, responsible for the majority of submissions; or (iii) that have little clinical relevance and should be separated from the previous cases. Sixteen syndromic groups were created. Nine referring to clinical syndromes: gastro-intestinal; mastitis; respiratory; circulatory, hepatic and haematopoietic; nervous; reproductive and abortion; systemic; urinary; and ‘others’. Diagnostics for specific agents assigned to an individual group owing to higher volume (ii above) were bovine leukaemia virus (BLV); bovine viral diarrhoea virus (BVD); Mycobacterium paratuberculosis (Johne's disease) and Neospora caninum. Lastly, the groups created to classify general tests (iii above) were: biochemical profile; other clinical pathology tests; toxicology tests; and non-specific tests (those which could not be classified into any of the previous groups). All 16 syndromic groups were subjected to monitoring using the methods described below.
Individual health events were defined as one syndromic occurrence per herd, that is, multiple test requests associated with a veterinarian visit to the same herd on a given day, when classified into the same syndromic group, are counted as ‘one case’. In comparison with human medicine, this would mean that the herd is the individual patient (not each animal within a herd). Classification is first performed for each requested test. Once each test request is classified into a syndromic group, the data are collapsed by the unique herd identification for each day. Any cases in the database assigned to weekends were summed to the following Monday, and weekends were removed from the data. Only syndromic groups with a median greater than one case per day were monitored daily [13]. It was proposed that the remaining syndromes (seven of 17 in total) would be monitored on a weekly basis; these series are not discussed further in this paper. All the methods described in this paper were carried out for all the syndromic groups monitored daily. As documented in Dórea et al. [13], the time series of daily cases for each of these groups showed very similar statistical properties: daily medians between 2 and 4, except for tests for diagnostic of mastitis and respiratory syndromes, which daily medians were 9 and 1, respectively; strong DOW effect; no global monotonic trends; and weak seasonal effects, especially for the syndromes with lower daily medians.
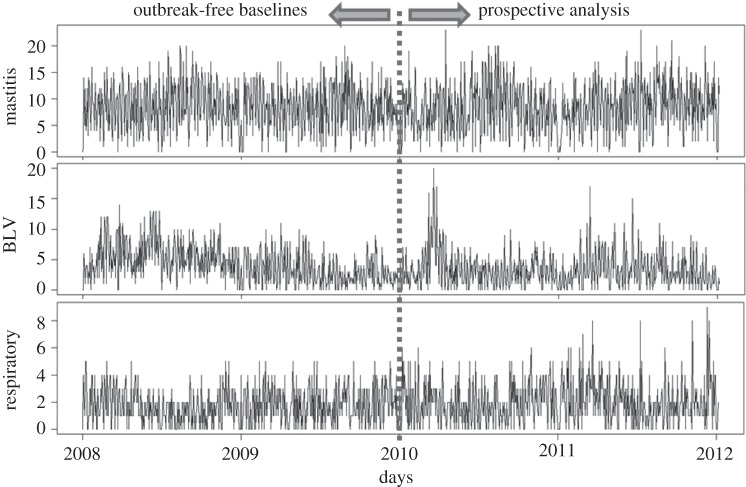
Methods and results will be illustrated using the daily counts of laboratory test requests for identification of BLV. Animals affected by bovine leucosis present a reduction in condition, diarrhoea and tumours in several organs, which can sometimes be palpated through the skin, though more often only the unspecific signs are noted. Tests for BLV are often requested in animals showing a general reduction in condition. This series was chosen due to the statistical similarities to the time series of other syndromic groups, while being the only times series showing evident presence of temporal aberrations (outbreak signals) documented in the historical data. Additionally, the counts of test requests for diagnostic of mastitis (inflammation of the udder in lactating cows) are used to illustrate the particular effect of working with time series with stronger seasonal effects, whereas the daily counts of laboratory submissions for diagnostic of respiratory syndromes are used to illustrate the particular challenges of working with time series with lower daily median. The three time series are shown in figure 1.
Figure 1.
Syndromic groups used to exemplify the times series used in this study. Data from 2008 and 2009 have been analysed in order to remove temporal aberrations, constructing an outbreak-free baseline.
Data from 2008 and 2009 were used as training data. These data had been previously analysed to remove temporal aberrations, creating outbreak-free baselines for each syndromic group [13]. Data from 2010 and 2011 were used to evaluate the performance of detection algorithms trained using those baselines.
2.1.1. Simulated data
In order to simulate the baseline (background behaviour) for each syndromic group the 4 years of data were fitted to a Poisson regression model with variables to account for DOW and month, as previously documented [13]. The predicted value for each day of the year was set to be the mean of a Poisson distribution, and this distribution was sampled randomly to determine the value for that day of a given year, for each of 100 simulated years.
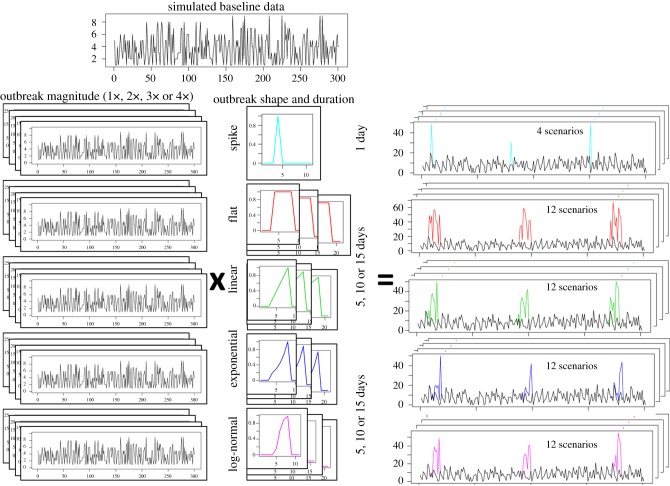
To simulate outbreak signals (temporal aberrations that are hypothesized to be documented in the data stream monitored in the case of an outbreak in the population of interest) that also preserved the temporal effects from the original data, different outbreak signal magnitudes were simulated by multiplying the mean of the Poisson distributions that characterized each day of the baseline data by selected values. Magnitudes of 1, 2, 3 and 4 were used.
Outbreak signal shape (temporal progression), duration and spacing were then determined by overlaying a filter to these outbreak series, representing the fraction of the original magnified count that should be kept. For instance, a filter increasing linearly from 0 to 1 in 5 days (explicitly: 0.2, 0.4, 0.6, 0.8 and 1), when superimposed to an outbreak signal series, would result in 20 per cent of the counts in that series being input (added to the baseline) on the first day, 40 per cent in the second, and so on, until the maximum outbreak signal magnitude would be reached in the last outbreak day. The process and resulting series are summarized in figure 2. As can be seen in figure 2, while the filters had monotonic shapes, the final outbreak signals included the random variability generated by the Poisson distribution. The temporal progression of an outbreak is difficult to predict in veterinary medicine, where the epidemiological unit is the herd rather than individual animals, because a large proportion of transmission is due to indirect contact between farms locally and also over large distances [16]. The same pathogen introduction can result in different temporal progressions in different areas as a result of spatial heterogeneity, as seen in the foot-and-mouth disease outbreak in the UK in 2001 [17] and the bluetongue outbreak in Europe in 2006 [18]. For this reason, several outbreak signal shapes previously proposed in the literature [19,20] were simulated. These shapes were combined to generate the following filters.
— Single spike outbreaks: a value of 1 is assigned to outbreak days, whereas all other days are assigned a value of zero.
— Moving average (flat) outbreaks: each outbreak signal is represented by a sequence of 5, 10 or 15 days (one to three weeks) with a filter value of 1 (outbreak days), separated by days of non-outbreak in which the filter value is zero.
— Linear increase: the filter value increases linearly from 0 in the first day, to 1 in the last day. This linear increase was simulated over 5, 10 and 15 days.
— Exponential increase: the filter value increases exponentially from 0 in the first day, to 1 in the last day. For the duration of 5 days, this was achieved by assigning 1 to the last day, and dividing each day by 1.5 to obtain the value for the preceding day. For the durations of 10 and 15 days, a value of 1.3 was used.
— Lognormal (or sigmoidal) increase: the filter value increases following a lognormal curve from 0 in the first day, to 1 in the last day. The same values for the distribution are used for any outbreak signal length (lognormal(4, 0.3)), but the values corresponding to 5, 10 and 15 equally distributed percentiles from this distribution are used to assign the filter value for outbreaks with these respective durations.
Figure 2.
Synthetic outbreak simulation process. Data with no outbreaks were simulated reproducing the temporal effects in the baseline data. The same process was used to construct series that were for outbreak simulation, but counts were amplified up to four times. Filters of different shape and duration were then multiplied to these outbreak series. The resulting outbreaks were added to the baseline data. (Online version in colour.)
Each filter was composed using one setting of outbreak signal shape and duration, repeated at least 200 times over the 100 simulated years, with a fixed number of non-outbreak days between them. The space between outbreak signals was determined after real data were used to choose the initial settings for the aberration detection algorithms, in order to ensure that outbreak signals were spaced far enough apart to prevent one outbreak from being included in the training data of the next. Each of these filters was then superimposed on the four different outbreak signal magnitude series, generating a total of 52 outbreak signal scenarios to be evaluated independently by each detection algorithm.
2.2. Detection based on removal of temporal effects and use of control charts
2.2.1. Exploratory analysis of pre-processing methods
The retrospective analysis [13] showed that DOW effects were the most important explainable effects in the data streams, and could be modelled using Poisson regression. Weekly cyclical effects can also be removed by differencing [6]. Both of the following alternatives were evaluated to pre-process data in order to remove the DOW effect.
— Poisson regression modelling with DOW and month as predictors. The residuals of the model were saved into a new time series. This time series evolves daily by refitting the model to the baseline plus the current day, and calculating today's residual.
— Five-day differencing. The differenced residuals (the residual at each time point t being the difference between the observed value at t and t−5) were saved as a new time series.
Autocorrelation and normality in the series of residuals were assessed in order to evaluate whether pre-processing was able to transform the weekly- and daily-autocorrelated series into independent and identically distributed observations.
2.2.2. Control charts
The three most commonly used control charts in biosurveillance were compared in this paper: (i) Shewhart charts, appropriate for detecting single spikes in the data; (ii) cumulative sums (CUSUM), appropriate for use in detecting shifts in the process mean; and (iii) the exponentially weighted moving average (EWMA), appropriate for use in detecting gradual increases in the mean [5,6].
The Shewhart chart evaluates a single observation. It is based on a simple calculation of the standardized difference between the current observation and the mean (z-statistic); the mean and standard deviation being calculated based on a temporal window provided by the analyst (baseline).
The CUSUM chart is obtained by
| 2.1 |
where t is the current time point, Dt is the standardized difference between the current observed value and the expected value. The differences are accumulated daily (because at each time point t, the statistic incorporates the value at t−1) over the baseline, but reset to zero when the standardized value of the current difference, summed to the previous cumulative value, is negative. The EWMA calculation includes all previous time points, with each observation's weight reduced exponentially according to its age:
| 2.2 |
where λ is the smoothing parameter (>0) that determines the relative weight of current data to past data, It is the individual observation at time t and E0 is the starting value [5,21].
The mean from values from the baseline are used as the expected value at each time point. Baseline windows of 10–260 days were evaluated for all control charts.
In order to avoid contamination of the baseline with gradually increasing outbreaks it is advised to leave a buffer, or guard-band gap, between the baseline and the current values being evaluated [22–24]. Guard-band lengths of one and two weeks were considered for all algorithms investigated.
One-sided standardized detection limits (magnitude above the expected value) between 1.5 and 3.5 s.d. were evaluated. Based on the standard deviations reported in the literature for detection limits [20,25–27], an arbitrary wide range of values was selected for the initial evaluation of this parameter.
For the EWMA chart, smoothing coefficients from 0.1 to 0.4 were evaluated based on values reported in the literature [27–29].
The three algorithms were applied to the residuals of the pre-processing steps.
2.3. Detection using Holt–Winters exponential smoothing
As an alternative to the removal of DOW effects and sequential application of control charts for detection, a detection model that can handle temporal effects directly was explored [13,30]. While regression models are based on the global behaviour of the time series, the Holt–Winters generalized exponential smoothing is a recursive forecasting method, capable of modifying forecasts in response to recent behaviour of the time series [9,31]. The method is a generalization of the exponentially weighted moving averages calculation. Besides a smoothing constant to attribute weight to mean calculated values over time (level), additional smoothing constants are introduced to account for trends and cyclic features in the data [9]. The time-series cycles are usually set to 1 year, so that the cyclical component reflects seasonal behaviour. However, retrospective analysis of the time series presented in this paper [13] showed that Holt–Winters smoothing [9,31] was able to reproduce DOW effects when the cycles were set to one week. The method suggested by Elbert & Burkom [9] was reproduced using 3- and 5-day-ahead predictions (n = 3 or n = 5), and establishing alarms based on confidence intervals for these predictions. Confidence intervals from 85 to 99% (which correspond to 1–2.6 s.d. above the mean) were evaluated. Retrospective analysis showed that a long baseline yielded stabilization of the smoothing parameters in all time series tested when 2 years of data were used as training. Various baseline lengths were compared relatively with detection performance. All time points in the chosen baseline length, up to n days before the current point, were used to fit the model daily. Then, the observed count of the current time point was compared with the confidence interval upper limit (detection limit) in order to decide whether a temporal aberration should be flagged [13].
2.4. Performance assessment
Two years of data (2010 and 2011) were used to qualitatively assess the performance of the detection algorithms (control charts and Holt–Winters). Detected alarms were plotted against the data in order to compare the results. This preliminary assessment aimed at reducing the range of settings to be evaluated quantitatively for each algorithm using simulated data.
The choice of values for baseline, guard-band and smoothing coefficient (EWMA) was adjusted based on these visual assessments of real data, to ensure that the choices were based on the actual characteristics of the observed data, rather than impacted by artefacts generated by the simulated data. These visual assessments were performed using historical data where aberrations were clearly present—as in the BLV time series—in order to determine how different parameter values impacted: the first day of detection, subsequent detection after the first day, and any change in the behaviour of the algorithm at time points after the aberration. In particular, an evaluation of how the threshold of aberration detection was impacted during and after the aberration days was carried out. Additionally, all data previously treated in order to remove excessive noise and temporal aberrations [13] were also used in these visual assessments, in order to evaluate the effect of parameter choices on the generation of false alarms. The effect of specific data characteristics, such as small seasonal effects or low counts, could be more directly assessed using these visual assessments rather than the quantitative assessments described later.
To optimize the detection thresholds, quantitative measures of sensitivity and specificity were calculated using simulated data. Sensitivity of outbreak detection was calculated as the percentage of outbreaks detected from all outbreaks injected into the data. An outbreak was considered detected when at least one outbreak day generated an alarm. The number of days, during the same outbreak signal, for which each algorithm continued to generate an alarm was also recorded for each algorithm. Algorithms were also applied to the simulated baselines directly, without the injection of any outbreaks, and all the days in which an alarm was generated in those time series were counted as false-positive alarms. Time to detection was recorded as the first outbreak day in which an alarm was generated, and therefore can be evaluated only when comparing the performance of algorithms in scenarios of the same outbreak duration. Sensitivities of outbreak detection were plotted against false-positives in order to calculate the area under the curve (AUC) for the resulting receiver operating characteristic (ROC) curves.
3. Results
3.1. Pre-processing to remove the day-of-week effect
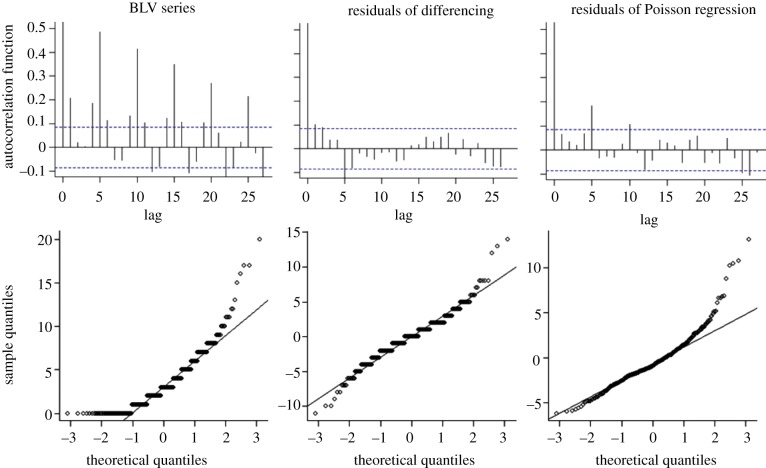
Autocorrelation function plots and normality Q–Q plots are shown in figure 3 for the BLV series, for 2010 and 2011, to allow the two pre-processing methods to be evaluated. Neither method was able to remove the autocorrelations completely, but differencing resulted in smaller autocorrelations and smaller deviation from normality in all time series evaluated. Moreover, differencing retains the count data as discrete values. The Poisson regression had very limited applicability to series with low daily counts, cases in which model fitting was not satisfactory.
Figure 3.
Comparative analysis of the autocorrelation function and normality plots for the BLV series (years 2010 and 2011) before and after pre-processing. (Online version in colour.)
Owing to its ready applicability to time series with low as well as high daily medians, and the fact that it retains the discrete characteristic of the data, differencing was chosen as the pre-processing method to be implemented in the system and evaluated using simulated data.
3.2. Qualitative evaluation of detection algorithms
Based on graphical analysis of the aberration detection results using real data, a baseline of 50 days (10 weeks) seemed to provide the best balance between capturing the behaviour of the data from the training time points and not allowing excessive influence of recent values. Longer baselines tended to reduce the influence of local temporal effects, resulting in excessive number of false alarms generated, for instance, at the beginning of seasonal increases for certain syndromes. Shorter baselines gave local effects too much weight, allowing aberrations to contaminate the baseline, thereby increasing the mean and standard deviation of the baseline, resulting in a reduction of sensitivity.
For the guard-band, the use of one week did not prevent contamination of the baseline with aberrations when these were clearly present. For instance, in outbreak signals simulated to last 15 days, the algorithms became insensitive to the aberrations during the last week of outbreak signal. The guard-band was therefore set to 10 days.
For the EWMA control charts, the number of alarms generated was higher when the smoothing parameter was greater, within the range tested. When evaluating graphically whether these alarms seemed to correspond to true aberrations, a smoothing parameter of 0.2 produced more consistent results across the different series evaluated, and so this parameter value was adopted for the simulated data.
EWMA was more efficient than CUSUM in generating alarms when the series median was shifted from the mean for consecutive days, but no strong peak was observed. EWMA and Shewhart control charts appeared to exhibit complementary performance—aberration shapes missed by one algorithm were generally picked up by the other. CUSUM charts seldom improved overall system performance if the other two types of control chart had been implemented.
The performance of the Holt–Winters method was very similar with 3- and 5-days-ahead predictions. Five-days-ahead prediction was chosen because it provides a longer guard-band between the baseline and the observed data. Because this method is data-driven, using long baselines (2 years) did not cause the model to ignore local effects, but it did allow convergence of the smoothing parameters, eliminating the need to set an initial value. The method was set to read 2 years of data prior to the current time point. The use of longer baselines (up to 3 years) did not improve performance, but it would require longer computational time. The method did not appear to perform well in series characterized by low daily medians. In the case of the respiratory series, for instance, the Holt–Winters method generated 19 alarms over a period of 2 years, most of which seemed to be false alarms based on visual assessment (the control charts generated only five to eight alarms for the same period).
Based on qualitative assessment alone, the range of detection limits to be evaluated using the simulated data could not be narrowed by more than half a unit for the control charts. It was therefore decided to evaluate detection limits (in increments of 0.25) when carrying out the quantitative investigation: 2–3.75 for the Shewhart charts, 1.75–3.5 for CUSUM charts and for EWMA. For the Holt–Winters method, confidence intervals greater or equal to 95% were investigated using simulated data.
3.3. Evaluation using simulated data
Based on the results of the qualitative analysis (baselines of 50 days and a range or guard-band of 10 days), outbreaks were separated by a window of 70 non-outbreak days. In the case of single-day spikes, the separation was 71 days, to ensure that spikes always fell on a different weekday.
As expected, the effect of increased outbreak magnitude was to increase sensitivity (and also to increase the number of days with an alarm, per outbreak signal) and reduce time to detection. Longer outbreak lengths increased the sensitivity per outbreak, but reduced the number of days with alarms per outbreak in shapes with longer initial tails, as linear, exponential and log normal. For these shapes, a longer outbreak length also resulted in longer time to detection.
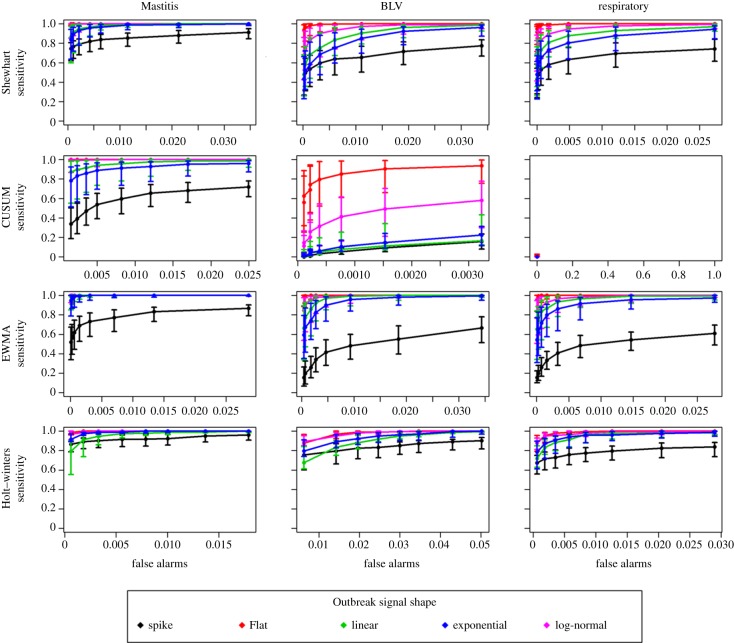
ROC curves for system sensitivities plotted against the number of false alarms are shown in figure 4 for each of the four algorithms evaluated and the three syndromes. Lines in each panel show the median sensitivity for the five different outbreak shapes, along the eight detection limits tested. Error bars represent the 25–75% percentile of 12 scenarios, combining the four scenarios of outbreak magnitude (one to four times the baseline) and the three scenarios of outbreak duration (one to three weeks) simulated. AUC for the plots are shown in table 1, as well as median time to detection for the specific scenario of an outbreak of 10 days. A limited number of detection limits are shown in table 1.
Figure 4.
ROC curves representing median sensitivity of outbreak detection, plotted against number of daily false alarms, for four different algorithms evaluated (rows), applied to data simulating three different syndromes (columns), and using five different outbreak shapes. Detection limits for each plotted point are shown in table 1. Error bars show the 25% to 75% percentile of the point value over four different scenarios of outbreak magnitude (one to four times the baseline) and three different scenarios of outbreak duration (one to three weeks). (Online version in colour.)
Table 1.
Performance evaluation of different detection algorithms. Area under the curve (for sensitivity of outbreak detection) was calculated using the median sensitivity for all scenarios of each outbreak shape (four outbreak magnitudes and three durations), plotted against false-positive alarms, for the different detection limits shown. These curves are shown in figure 4. The median detection days for the four outbreak magnitudes simulated for each outbreak shape, in the scenario of a 10 days outbreak length, are also shown. AUC-sens.day denotes area under the curve for a ROC curve plotting sensitivity per day (median of all scenarios for each outbreak shape) against false-positives. AUC-sens.outb. denotes area under the curve for a ROC curve plotting sensitivity of outbreak detection (median of all scenarios for each outbreak shape) against false-positives.
| detection limits | mastitis |
BLV |
respiratory |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| spike | flat | linear | exponential | log-normal | spike | flat | linear | exponential | log-normal | spike | flat | linear | exponential | log-normal | |||
| Shewhart | AUC-sens.outb. | 0.843 | 0.965 | 0.899 | 0.884 | 0.953 | 0.694 | 0.934 | 0.709 | 0.686 | 0.806 | 0.676 | 0.930 | 0.715 | 0.673 | 0.791 | |
| mean detect. daya | 3.75 | — | 1.11 | 3.39 | 4.93 | 5.07 | — | 1.33 | 4.48 | 5.69 | 5.64 | — | 1.37 | 4.61 | 5.92 | 5.90 | |
| 3.00 | — | 1.20 | 4.47 | 6.63 | 5.83 | — | 1.61 | 5.84 | 7.47 | 6.74 | — | 1.71 | 5.90 | 7.74 | 6.86 | ||
| 2.75 | — | 1.22 | 4.85 | 6.97 | 5.97 | — | 1.72 | 6.27 | 7.94 | 6.91 | — | 1.83 | 6.44 | 8.40 | 7.09 | ||
| 2.00 | — | 1.30 | 5.87 | 8.11 | 6.52 | — | 2.12 | 6.99 | 8.83 | 7.49 | — | 2.23 | 7.27 | 8.88 | 7.52 | ||
| CUSUM | AUC-sens.outb. | 0.654 | 0.975 | 0.912 | 0.868 | 0.972 | 0.501 | 0.777 | 0.504 | 0.505 | 0.554 | — | — | — | — | — | |
| mean detect. daya | 3.50 | — | 1.35 | 5.31 | 8.05 | 6.43 | — | 2.90 | 8.27 | 9.76 | 8.26 | — | — | — | — | — | |
| 2.75 | — | 1.56 | 6.15 | 8.79 | 6.80 | — | 3.57 | 9.03 | 10.00 | 8.60 | — | — | — | — | — | ||
| 2.50 | — | 1.68 | 6.39 | 8.97 | 6.91 | — | 3.72 | 9.10 | 9.83 | 8.73 | — | — | — | — | — | ||
| 1.75 | — | 2.01 | 7.05 | 9.40 | 7.28 | — | 4.07 | 9.00 | 5.00 | 9.02 | — | — | — | — | — | ||
| EWMA | AUC-sens.outb. | 0.737 | 0.971 | 0.965 | 0.946 | 0.971 | 0.559 | 0.961 | 0.797 | 0.764 | 0.889 | 0.563 | 0.952 | 0.800 | 0.747 | 0.859 | |
| mean detect. daya | 3.50 | — | 1.09 | 2.85 | 3.96 | 4.70 | — | 1.27 | 3.81 | 5.10 | 5.15 | — | 1.44 | 3.93 | 5.60 | 5.50 | |
| 2.75 | — | 1.27 | 4.00 | 6.22 | 5.91 | — | 1.76 | 5.56 | 7.38 | 6.67 | — | 1.94 | 5.53 | 7.32 | 6.80 | ||
| 2.50 | — | 1.37 | 4.38 | 6.79 | 6.14 | — | 1.98 | 5.96 | 7.86 | 6.93 | — | 2.14 | 5.98 | 7.76 | 7.10 | ||
| 1.75 | — | 1.66 | 5.34 | 7.94 | 6.68 | — | 2.56 | 7.05 | 8.75 | 7.51 | — | 2.68 | 7.03 | 9.07 | 7.64 | ||
| Holt–Winters | AUC-sens.outb. | 0.916 | 0.976 | 0.879 | 0.940 | 0.966 | 0.835 | 0.890 | 0.793 | 0.851 | 0.897 | 0.814 | 0.912 | 0.832 | 0.865 | 0.910 | |
| mean detect. daya | 0.995 | — | 1.23 | 4.27 | 5.44 | 5.37 | — | 1.45 | 4.81 | 5.74 | 5.71 | — | 1.48 | 4.65 | 5.90 | 5.93 | |
| 0.980 | — | 1.35 | 5.37 | 6.56 | 5.85 | — | 1.74 | 5.74 | 6.69 | 6.24 | — | 1.83 | 5.60 | 6.88 | 6.42 | ||
| 0.975 | — | 1.42 | 5.72 | 6.94 | 6.00 | — | 1.81 | 6.07 | 6.86 | 6.41 | — | 1.96 | 5.79 | 7.14 | 6.55 | ||
| 0.960 | — | 2.11 | 7.32 | 8.39 | 7.03 | — | 2.36 | 7.14 | 8.22 | 7.37 | — | 2.42 | 7.11 | 8.31 | 7.29 | ||
aFor outbreak length of 10 days to peak.
Starting at the first column of figure 4 and table 1, the results for the mastitis simulated series, the sensitivity of detection of spikes and flat outbreaks was highest for the Holt–Winters method. EWMA charts showed low sensitivity for those, but the highest performance for all slow raising outbreak shapes (linear, exponential and log normal). The lowest sensitivity within each algorithm was for the detection of spikes, which is an artefact of the short duration of these outbreaks, compared with all other shapes. Similarly, the relatively high sensitivity for flat outbreaks can be interpreted as a result of the higher number of days with high counts in this scenario. Similarly, the performance for detection in log-normal shapes closely related to the flat outbreaks, being superior to linear and exponential increases. The CUSUM algorithm showed good performance in the mastitis series, but its performance very quickly deteriorated for other series with smaller daily medians, as discussed below.
Median day of first signal for each outbreak, in the scenario of a 10 days to peak outbreak, is shown in table 1 for a few key detection limits. Looking at the median day of detection for the flat and exponential outbreaks in the mastitis series, it is possible to see, for instance, that even though the AUC is higher for the Holt–Winters (more outbreaks detected) when compared with the Shewhart chart, in the case of detection the latter algorithm detects outbreaks earlier than the first.
Moving to syndromes with lower daily counts, figure 4 shows that the performance of all algorithms decreases as daily counts decrease. The problem is critical with the CUSUM algorithm. Because this algorithm resets to zero if the difference in observed counts is lower than the expected counts, its application to a series with a large number of zero counts (respiratory) resulted in no alarm being detected, true or false.
The results show that algorithm performance is not only a function of the syndrome median counts, but also impacted by the baseline behaviour of the syndromic series. EWMA charts, which performed better than Holt–Winter for slow raising outbreaks in the mastitis series, also performed better for flat shapes in the BLV series, but Holt–Winters performed better for exponentially increasing outbreaks. Moving to even lower daily counts, as in the respiratory series, the Holt–Winters method outperformed EWMA charts in all outbreak shapes but flat, the case for which both the EWMA charts and the Shewhart charts showed better performance than Holt–Winters.
The impact of the underlying baseline in the absence of outbreaks is also seen in the range of false-positive values. The same detection limits generated a greater number of false alarms in the BLV series for all algorithms. Except for the BLV series, the number of false alarms generated in every scenario was smaller than 3 per cent (one false alarm in each 30 days of system operation). For the Holt–Winters method, a detection limit of 97.5 per cent would always result in specificity greater than 97 per cent, without loss of sensitivity compared with the lowest detection limits evaluated. For the EWMA charts, a detection limit of 2 s.d. represents the maximum attained specificity without starting to rapidly decrease sensitivity, but the behaviour should be evaluated individually for different syndromes. For the Shewhart chart, such a cut-off seemed to rest on a detection limit of 2.25 s.d. for the lower count series, but for the mastitis series a limit of 2.5 would reduce false alarms with very little reduction in sensitivity.
4. Discussion
A recent review of veterinary syndromic surveillance initiatives [12] concluded that, owing to the current lack of computerized clinical records, laboratory test requests represent the opportunistic data with the greatest potential for implementation of syndromic surveillance systems in livestock medicine. In this study, we have evaluated 2 years of laboratory test request data, using the two preceding years as training data, and illustrated the potential of different combinations of pre-processing methods and detection algorithms for the prospective analysis of these data where the primary aim is aberration detection.
A large number of studies have documented the use of public health data sources in syndromic surveillance, such as data from hospital emergency departments, physician office visits, over-the-counter medicine sales, etc. [32]. In veterinary health, however, the epidemiological unit for clinical data is usually the herd, rather than individual animals [12]. The number of epidemiological units in a catchment area for individual data sources is therefore generally smaller than in public health monitoring, resulting in challenges around handling data with low daily counts, such as those described in this study. It is hoped that the description of the steps taken to prepare these data and to select appropriate detection algorithms together with the results of this evaluation can guide the work of other analysts investigating the potential of syndromic data sources in animal health.
The data used for algorithm training had been previously evaluated retrospectively [13] and were found to have a strong DOW effect. This effect prevented the direct use of control charts without data pre-processing. Regression (using a Poisson model) was not an efficient method to remove daily autocorrelation; in line with a finding previously reported by Lotze et al. [6]. Differencing has been recommended not only to remove DOW effects, but any cyclical patterns in addition to linear trends [6]. Five-day (weekly) differencing demonstrated solid performance in removing the DOW effect, even in series with low daily counts, and preserved the data as count data (integers). Preserving the data as integers is important when using control charts based on count data, and also in order to facilitate the analyst's comprehension of both the observed and the pre-processed data series.
When pre-processed data were subjected to temporal aberration detection using control charts, EWMA performed better than CUSUM. EWMA's superiority in detecting slow shifts in the process mean is expected from its documented use [6]. In the particular time series explored in this paper, the general poor performance of the CUSUM was attributed to the low median values, when compared with traditional data streams used in public health. The injected outbreak signals were simulated to capture the random behaviour of the data, as opposed to being simulated as monotonic increases in a specific shape. Therefore, as seen in figure 2, often the daily counts were close to zero even during outbreak days, as is common for these time series. As a result, the CUSUM algorithm was often reset to zero, decreasing its performance. Shewhart charts showed complementary performance to EWMA charts, detecting single spikes that were missed by the first algorithm.
The use of control charts in pre-processed data was compared with the direct application of the Holt–Winters exponential smoothing. Lotze et al. [6] have pointed out the effectiveness of the Holt–Winters method in capturing seasonality and weekly patterns, but highlighted the potential difficulties in setting the smoothing parameters as well as the problems of 1-day-ahead predictions. In this study, the temporal cycles were set to weeks, and the availability of 2 years of training data allowed convergence of the smoothing parameters without the need to estimate initialization values. Moreover, the method worked well with predictions of up to 5 days ahead, which allows a guard-band to be kept between the training data and the actual observations, avoiding contamination of the training data with undetected outbreaks [22–24]. Our findings confirm the conclusions of Burkom et al. [31] who found, working in the context of human medicine, that the method outperformed ordinary regression, while remaining straightforward to automate.
Analyses using real data were important in tuning algorithm settings to specific characteristics of the background data, such as baselines, smoothing constants and guard-bands. However, analysis on real data can be qualitative only due to the limited amount of data available [33]. The scarcity of data, especially those for which outbreaks days are clearly identified, has been noted as a limitation in the evaluation of biosurveillance systems [34]. Data simulation has been commonly employed to solve the data scarcity problem, the main challenge being that of capturing and reproducing the complexity of both baseline and outbreak data [33,35]. The temporal effects from the background data were captured in this study using a Poisson regression model, and random effects were added by sampling from a Poisson distribution daily, rather than using model estimated values directly. Amplifying background data using multiplicative factors allowed the creation of outbreaks that also preserved the temporal effects observed in the background data.
Murphy & Burkom [24] pointed out the complexity of finding the best performance settings, when developing syndromic surveillance systems, if the shapes of outbreak signals to be detected are unknown. In this study, the use of simulated data allowed evaluation of the algorithms under several outbreak scenarios. Special care was given to outbreak spacing, in order to ensure that the baseline used by each algorithm to estimate detection limits was not contaminated with previous outbreaks.
As the epidemiological unit in animal health is a herd, transmission by direct contact is not usually the main source of disease spread. Indirect contact between farms through the movement of people and vehicles is often a large component of disease spread [36]. The shape of the outbreak signal that will be registered in different health sources is hard to predict, and depends on whether the contacts, which often cover a large geographical area [16], will also be included in the catchment area of the data provider. The temporal progression of outbreaks of fast spreading diseases is often modelled as an exponential progression [37,38], but data from documented outbreaks [18] and the result of models that explicitly take into account the changes in spread patterns owing to spatial heterogeneity [39] more closely resemble linear increases. Linear increases may also be observed when an increase in the incidence of endemic diseases is registered, as opposed to the introduction of new diseases. Owing to these uncertainties, all the outbreak signal shapes previously documented in simulation studies for development of syndromic monitoring were reproduced in this study [11,19,40,41].
Evaluation of outbreak detection performance was based on sensitivity and specificity, metrics traditionally used in epidemiology, combined with using the AUC for a traditional ROC curve [42]. The training data used in this study to simulate background behaviour were previously analysed in order to remove aberrations and excess noise [13]. The number of false alarms when algorithms are implemented using real data are expected to be higher than that observed for simulated data. However, all the detection limits explored generated less than 3 per cent false-alarm days (97% specificity) in the simulated data, which is the general fixed false-alarm rate suggested for biosurveillance system implementations [40]. Because the right tail of the ROC curves was flat in most graphs, it was possible to choose detection limits that provide even low rates of false alarms, with little loss of sensitivity.
Metrics used in the industrial literature to evaluate control charts, such as average run length, are specifically designed for detection of a sustained shift in a parameter [43], which corresponds to the flat outbreak shape simulated in this study, but would be misleading when used to interpret the algorithms' performance for other outbreak scenarios. Therefore, although at times recommended for the evaluation of prospective statistical surveillance [44], performance measures from the industrial literature were not used [43].
The results showed that no single algorithm should be expected to perform optimally across all scenarios. EWMA charts and Holt–Winters exponential smoothing complemented each other's performance, the latter serving as a highly automated method to adjust to changes in the time series that can happen in the future, particularly in the context of an increase in the number of daily counts or seasonal effects. However, Shewhart charts showed earlier detection of signals in some scenarios, and therefore its role in the system cannot be overlooked. The CUSUM charts, however, would not add sensitivity value to the system.
Besides the difference in performance when encountering different outbreak signal shapes, the ‘no method fits all’ problem also applied to the different time series evaluated. The performance of the same algorithm was different between two series with similar daily medians (results not shown). This was likely due to non-explainable effects in the background time series, such as noise and random temporal effects. Therefore, the choice of a detection limit that can provide a desired balance between sensitivity and false alarms would have to be made individually for each syndrome.
The use of these three methods in parallel—differencing + EWMA; differencing + Shewhart; and Holt–Winters exponential smoothing—ensures that algorithms with efficient performance in different outbreak scenarios are used. Methods to implement automated monitoring aimed at early detection of temporal aberration occurrence using multiple algorithms in parallel will be evaluated in future steps of this work.
Acknowledgements
This project was supported financially and in-kind by the Ontario Ministry of Agriculture, Food and Rural Affairs (OMAFA) and the University of Guelph through the Animal Health Strategic Investment (AHSI), managed by the Animal Health Laboratory of the University of Guelph. Thanks are also due to two anonymous reviewers whose detailed input strengthened the way outbreak signals and certain algorithmic details are presented in this paper.
References
- 1.Bravata DM, McDonald KM, Smith WM, Rydzak C, Szeto H, Buckeridge DL, Haberland C, Owens DK. 2004. Systematic review: surveillance systems for early detection of bioterrorism-related diseases. Ann. Intern. Med. 140, 910–922 [DOI] [PubMed] [Google Scholar]
- 2.Shmueli G, Burkom H. 2010. Statistical challenges facing early outbreak detection in biosurveillance. Technometrics 52, 39–51 10.1198/TECH.2010.06134 (doi:10.1198/TECH.2010.06134) [DOI] [Google Scholar]
- 3.Centers for Disease Control and Prevention (CDC) 2006. Annotated bibliography for syndromic surveillance. See http://www.cdc.gov/ncphi/disss/nndss/syndromic.htm .
- 4.Benneyan JC. 1998. Statistical quality control methods in infection control and hospital epidemiology. I. Introduction and basic theory. Infect. Control Hospital Epidemiol. 19, 194–214 10.1086/647795 (doi:10.1086/647795) [DOI] [PubMed] [Google Scholar]
- 5.Woodall WH. 2006. Use of control charts in health-care and public-health surveillance. J. Quality Technol. 38, 89–104 [Google Scholar]
- 6.Lotze T, Murphy S, Shmueli G. 2008. Implementation and comparison of preprocessing methods for biosurveillance data. Adv. Dis. Surveill. 6, 1–20 [Google Scholar]
- 7.Lotze T, Murphy SP, Shmueli G. 2007. Preparing biosurveillance data for classic monitoring. Adv. Dis. Surveill. 2, 55 [Google Scholar]
- 8.Yahav I, Shmueli G. 2007. Algorithm combination for improved performance in biosurveillance systems. In Proc. 2nd NSF Conf. on Intelligence and Security Informatics: Biosurveillance. BioSurveillance'07, pp. 91–102 Berlin, Germany: Springer; See http://dl.acm.org/citation.cfm?id=1768376.1768388. [Google Scholar]
- 9.Elbert Y, Burkom HS. 2009. Development and evaluation of a data-adaptive alerting algorithm for univariate temporal biosurveillance data. Stat. Med. 28, 3226–3248 10.1002/sim.3708 (doi:10.1002/sim.3708) [DOI] [PubMed] [Google Scholar]
- 10.Buckeridge DL, Okhmatovskaia A, Tu S, O'Connor M, Nyulas C, Musen MA. 2008. Predicting outbreak detection in public health surveillance: quantitative analysis to enable evidence-based method selection. AMIA Annu. Symp. Proc. 1, 76–80 [PMC free article] [PubMed] [Google Scholar]
- 11.Jackson ML, Baer A, Painter I, Duchin J. 2007. A simulation study comparing aberration detection algorithms for syndromic surveillance. BMC Med. Inform. Decis. Making 7, 6. 10.1186/1472-6947-7-6 (doi:10.1186/1472-6947-7-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dórea FC, Sanchez J, Revie CW. 2011. Veterinary syndromic surveillance: current initiatives and potential for development. Prev. Vet. Med. 101, 1–17 10.1016/j.prevetmed.2011.05.004 (doi:10.1016/j.prevetmed.2011.05.004) [DOI] [PubMed] [Google Scholar]
- 13.Dórea FC, Revie CW, McEwen BJ, McNab WB, Kelton D, Sanchez J. 2013. Retrospective time series analysis of veterinary laboratory data: preparing a historical baseline for cluster detection in syndromic surveillance. Prev. Vet. Med. 109, 219–227 10.1016/j.prevetmed.2012.10.010 (doi:10.1016/j.prevetmed.2012.10.010) [DOI] [PubMed] [Google Scholar]
- 14.R Core Team 2012. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing: See http://www.R-project.org. [Google Scholar]
- 15.Dórea FC, et al. 2013. Exploratory analysis of methods for automated classification of laboratory test orders into syndromic groups in veterinary medicine. PLoS ONE 8, e57334. 10.1371/journal.pone.0057334 (doi:10.1371/journal.pone.0057334) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gibbens JC, Wilesmith JW, Sharpe CE, Mansley LM, Michalopoulou E, Ryan JBM, Hudson M. 2001. Descriptive epidemiology of the 2001 foot-and-mouth disease epidemic in Great Britain: the first five months. Vet. Rec. 149, 729–743 10.1136/vr.149.24.729 (doi:10.1136/vr.149.24.729) [DOI] [PubMed] [Google Scholar]
- 17.Picado A, Guitian F, Pfeiffer D. 2007. Space–time interaction as an indicator of local spread during the 2001 FMD outbreak in the UK. Prev. Vet. Med. 79, 3–19 10.1016/j.prevetmed.2006.11.009 (doi:10.1016/j.prevetmed.2006.11.009) [DOI] [PubMed] [Google Scholar]
- 18.Santman-Berends IMGA, Stegeman JA, Vellema P, van Schaik G. 2013. Estimation of the reproduction ratio (R0) of bluetongue based on serological field data and comparison with other BTV transmission models. Prev. Vet. Med. 108, 276–284 10.1016/j.prevetmed.2012.11.004 (doi:10.1016/j.prevetmed.2012.11.004) [DOI] [PubMed] [Google Scholar]
- 19.Mandl KD, Reis B, Cassa C. 2004. Measuring outbreak-detection performance by using controlled feature set simulations. Morb. Mortal. Wkly. Rep. 53, 130–136 [PubMed] [Google Scholar]
- 20.Hutwagner LC, Thompson WW, Seeman GM, Treadwell T. 2005. A simulation model for assessing aberration detection methods used in public health surveillance for systems with limited baselines. Stat. Med. 24, 543–550 10.1002/sim.2034 (doi:10.1002/sim.2034) [DOI] [PubMed] [Google Scholar]
- 21.Stoumbos ZG, Reynolds MR, Ryan TP, Woodall WH. 2000. The state of statistical process control as we proceed into the 21st century. J. Am. Stat. Assoc. 95, 992–998 10.1080/01621459.2000.10474292 (doi:10.1080/01621459.2000.10474292) [DOI] [Google Scholar]
- 22.Burkom HS. 2003. Development, adaptation, and assessment of alerting algorithms for biosurveillance. Johns Hopkins APL Tech. Digest. 24, 335–342 [Google Scholar]
- 23.Buckeridge DL, Burkom H, Campbell M, Hogan WR, Moore AW. 2005. Algorithms for rapid outbreak detection: a research synthesis. J. Biomed. Inf. 38, 99–113 10.1016/j.jbi.2004.11.007 (doi:10.1016/j.jbi.2004.11.007) [DOI] [PubMed] [Google Scholar]
- 24.Murphy SP, Burkom H. 2008. Recombinant temporal aberration detection algorithms for enhanced biosurveillance. J. Am. Med. Inf. Assoc. 15, 77–86 10.1197/jamia.M2587 (doi:10.1197/jamia.M2587) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hutwagner LC, Maloney EK, Bean NH, Slutsker L, Martin SM. 1997. Using laboratory-based surveillance data for prevention: an algorithm for detecting Salmonella outbreaks. Emerg. Infect. Dis. 3, 395–400 10.3201/eid0303.970322 (doi:10.3201/eid0303.970322) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Carpenter TE. 2002. Evaluation and extension of the CUSUM technique with an application to Salmonella surveillance. J. Vet. Diagn. Invest. 14, 211–218 10.1177/104063870201400304 (doi:10.1177/104063870201400304) [DOI] [PubMed] [Google Scholar]
- 27.Szarka JL, 3rd, Gan L, Woodall WH. 2011. Comparison of the early aberration reporting system (EARS) W2 methods to an adaptive threshold method. Stat. Med. 30, 489–504 10.1002/sim.3913 (doi:10.1002/sim.3913) [DOI] [PubMed] [Google Scholar]
- 28.Nobre FF, Stroup DF. 1994. A monitoring system to detect changes in public health surveillance data. Int. J. Epidemiol. 23, 408–418 10.1093/ije/23.2.408 (doi:10.1093/ije/23.2.408) [DOI] [PubMed] [Google Scholar]
- 29.Ngo L, Tager IB, Hadley D. 1996. Application of exponential smoothing for nosocomial infection surveillance. Am. J. Epidemiol. 143, 637–647 10.1093/oxfordjournals.aje.a008794 (doi:10.1093/oxfordjournals.aje.a008794) [DOI] [PubMed] [Google Scholar]
- 30.Chatfield C. 1978. The Holt–Winters forecasting procedure. Appl. Stat. 27, 264–279 10.2307/2347162 (doi:10.2307/2347162) [DOI] [Google Scholar]
- 31.Burkom H, Murphy S, Shmueli G. 2007. Automated time series forecasting for biosurveillance. Stat. Med. 26, 4202–4218 10.1002/sim.2835 (doi:10.1002/sim.2835) [DOI] [PubMed] [Google Scholar]
- 32.Hurt-Mullen KJ, Coberly J. 2005. Syndromic surveillance on the epidemiologist's desktop: making sense of much data. Morb. Mortal. Wkly. Rep. 54, 141–146 [PubMed] [Google Scholar]
- 33.Buckeridge DL. 2007. Outbreak detection through automated surveillance: a review of the determinants of detection. J. Biomed. Inf. 40, 370–379 10.1016/j.jbi.2006.09.003 (doi:10.1016/j.jbi.2006.09.003) [DOI] [PubMed] [Google Scholar]
- 34.Lotze TH, Shmueli G, Yahav I, Kass-Hout T, Zhang X. 2011. Simulating and evaluating biosurveillance datasets. In Biosurveillance: methods and case studies (eds T Kass-Hout, X Zhang), pp. 23–51 New York, NY: CRC Press [Google Scholar]
- 35.Buckeridge DL, Switzer P, Owens D, Siegrist D, Pavlin J, Musen M. 2005. An evaluation model for syndromic surveillance: assessing the performance of a temporal algorithm. Morb. Mortal. Wkly. Rep. 54, 109–115 [PubMed] [Google Scholar]
- 36.Dórea FC, Vieira AR, Hofacre C, Waldrip D, Cole DJ. 2010. Stochastic model of the potential spread of highly pathogenic avian influenza from an infected commercial broiler operation in Georgia. Avian Dis. 54(Suppl. 1), 713–719 10.1637/8706-031609-ResNote.1 (doi:10.1637/8706-031609-ResNote.1) [DOI] [PubMed] [Google Scholar]
- 37.Ferguson NM, Donnelly CA, Anderson RM. 2001. The foot-and-mouth epidemic in Great Britain: pattern of spread and impact of interventions. Science 292, 1155–1160 10.1126/science.1061020 (doi:10.1126/science.1061020) [DOI] [PubMed] [Google Scholar]
- 38.Keeling M, et al. 2001. Dynamics of the 2001 UK foot and mouth epidemic: stochastic dispersal in a heterogeneous landscape. Science 294, 813–817 10.1126/science.1065973 (doi:10.1126/science.1065973) [DOI] [PubMed] [Google Scholar]
- 39.Kao RR. 2001. Landscape fragmentation and foot-and-mouth disease transmission. Vet. Rec. 148, 746–747 10.1136/vr.148.24.746 (doi:10.1136/vr.148.24.746) [DOI] [PubMed] [Google Scholar]
- 40.Reis BY, Pagano M, Mandl KD. 2003. Using temporal context to improve biosurveillance. Proc. Natl Acad. Sci. USA 100, 1961–1965 10.1073/pnas.0335026100 (doi:10.1073/pnas.0335026100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hutwagner L, Browne T, Seeman GM, Fleischauer AT. 2005. Comparing aberration detection methods with simulated data. Emerg. Infect. Dis. 11, 314–316 10.3201/eid1102.040587 (doi:10.3201/eid1102.040587) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wagner MM, Wallstrom G. 2006. Methods for algorithm evaluation. In Handbook of biosurveillance (eds Wagner MM, Moore AW, Aryel RM.), pp. 301–310 London, UK: Academic Press [Google Scholar]
- 43.Fraker SE, Woodall WH, Mousavi S. 2008. Performance metrics for surveillance schemes. Quality Eng. 20, 451–464 10.1080/08982110701810444 (doi:10.1080/08982110701810444) [DOI] [Google Scholar]
- 44.Sonesson C, Bock D. 2003. A review and discussion of prospective statistical surveillance in public health. J. R. Stat. Soc. A 166, 5–21 10.1111/1467-985x.00256 (doi:10.1111/1467-985x.00256) [DOI] [Google Scholar]