Abstract
Surfactant molecules can self-assemble into various morphologies under proper combinations of ionic strength, temperature, and flow conditions. At equilibrium, wormlike micelles can transition from entangled to branched and multiconnected structures with increasing salt concentration. Under certain flow conditions, micellar structural transitions follow different trajectories. In this work, we consider the flow of two semidilute wormlike micellar solutions through microposts, focusing on their microstructural and rheological evolutions. Both solutions contain cetyltrimethylammonium bromide and sodium salicylate. One is weakly viscoelastic and shear thickening, whereas the other is strongly viscoelastic and shear thinning. When subjected to strain rates of ∼103 s−1 and strains of ∼103, we observe the formation of a stable flow-induced structured phase (FISP), with entangled, branched, and multiconnected micellar bundles, as evidenced by electron microscopy. The high stretching and flow alignment in the microposts enhance the flexibility and lower the bending modulus of the wormlike micelles. As flexible micelles flow through the microposts, it becomes energetically favorable to minimize the number of end caps while concurrently promoting the formation of cross-links. The presence of spatial confinement and extensional flow also enhances entropic fluctuations, lowering the energy barrier between states, thus increasing transition frequencies between states and enabling FISP formation. Whereas the rheological properties (zero-shear viscosity, plateau modulus, and stress relaxation time) of the shear-thickening precursor are smaller than those of the FISP, those of the shear-thinning precursor are several times larger than those of the FISP. This rheological property variation stems from differences in the structural evolution from the precursor to the FISP.
Keywords: microfluidics, microrheology, mesh size
Surfactant molecules in aqueous solutions can self-assemble into different structures, such as spherical micelles, cylindrical micelles, lamellar phases, and vesicles (1). The morphology of these self-assembled structures is influenced by surfactant concentration, temperature, external additives (e.g., cosurfactants or salts), and flow conditions. Cylindrical micelles in the presence of inorganic or organic salts can self-assemble into large, flexible, and elongated wormlike micelles that exhibit viscoelastic properties (2–4). The ionic strength of the salt screens the electrostatic repulsions between the charged surfactant head groups, promoting cylindrical micellar growth (1–3). At higher salt concentrations, the entangled linear micelles can transition to branched and multiconnected micellar networks, as evidenced by rheological measurements, light scattering techniques, and electron microcopy (EM) imaging (5–18). Additionally, wormlike micellar solutions are known to exhibit a variety of interesting phenomena, some of which are shear banding (19–21), shear thickening (22, 23), shear-induced transitions and instabilities (refs. 4, 24 and references therein), and flow-induced structure formation (3, 12–14, 25–32). Wormlike micelles have also found applications in oil recovery, drag reduction, nanotemplating, and many biomedical and health care products (33–35). Despite widespread use in different fields, the microscopic structures and mechanisms by which wormlike micelles form under flow are not fully understood, and thus remain an active area of research.
We present systematic microstructural and rheological characterizations of stable flow-induced structured phases (FISPs) created by flowing shear-thickening and shear-thinning wormlike micellar solutions through a microfluidic device containing micropost arrays. Using a combination of scanning electron microcopy (SEM), transmission electron microscopy (TEM), and cryogenic-transmission-electron microscopy (Cryo-TEM) with a negative staining procedure for sample contrast enhancement, we demonstrate that the FISP consists of highly entangled, branched, and multiconnected wormlike micellar bundles. Bulk rheometry and microrheometry were conducted to extract the zero-shear viscosity 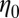 , stress relaxation time
, stress relaxation time 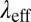 , and elastic modulus
, and elastic modulus 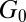 of the FISP. The mesh sizes of the precursors and their FISPs were obtained by TEM images and also estimated by rheological parameters for comparisons. The results are summarized below.
of the FISP. The mesh sizes of the precursors and their FISPs were obtained by TEM images and also estimated by rheological parameters for comparisons. The results are summarized below.
Flow-Induced Structures
Flow-induced structure formation has been reported in solutions of wormlike micelles; however, until now, these structures were all temporary and would disintegrate on cessation of the flow (22, 23, 25, 26, 36). These transient structures were first reported by Rehage and Hoffmann (36), who found that a wormlike micellar solution, an aqueous solution of the cationic surfactant cetylpyridinium chloride ([CPyCl] = 15–100 mM) and the organic salt sodium salicylate ([NaSal] = 11–60 mM), form a gel-like structure under shear flow above a critical shear rate. They referred to this gel-like structure as a shear-induced structure (SIS), because on cessation of the flow, the SIS would disintegrate. Pine and colleagues (25, 26) also observed the appearance of SISs, which form gel-like fingers in wormlike micellar solutions [(0.1–7)/(0.1–7)] mM cetyltrimethylammonium bromide (CTAB)/NaSal and 7.5/7.5 mM of tris(2-hydroxyethyl)-tallowalkyl ammonium acetate (TTAA)/NaSal sheared in a Couette cell. The increase in the shear viscosity of the micellar solution was found to coincide with the onset of SIS formation. In addition, they predicted the existence of wormlike micellar bundles with a diameter of ∼200 nm based on small-angle light scattering (SALS) patterns (25). The relaxation time of the SIS was found to range from several seconds to a couple of hours (26). Similarly, others observed birefringent SIS formation in a solution of surfactant and salt under shear and subsequent disappearance of the birefringent structures after the flow was stopped (24, 37). Based on time-dependent SALS studies under a simple shear flow, Kadoma and van Egmond (12) suggested that CTAB/NaSal-based (0.03/0.24 M) SISs consist of highly elongated and locally concentrated micellar strings. The SIS has since been widely studied using birefringence, light scattering, neutron scattering, X-ray scattering, and NMR (21, 24).
Stable flow-induced structures from wormlike micelles were first reported by Vasudevan et al. (31). A semidilute ([CTAB] = 50 mM/[NaSal] = 16 mM) shear-thickening solution formed a stable gel-like FISP after traversing a microfluidic tapered channel packed with glass beads (20–100 μm in diameter). This stable gel-like FISP occurred from a combination of high strain rates (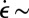 5,000 s−1) and extensional features of the flow. The FISP remained stable for more than a year at room temperature, even after the cessation of flow. Using the same wormlike micellar solution, Dubash et al. (32) formed the FISP using micropost arrays with a 7-μm gap size and found the rheological properties of the FISP to be at least one order of magnitude larger than those of the precursor. Cheung et al. (38) extended this work by adding Nile red dye (a fluorescent dye whose intensity is related to the CTAB concentration) to the precursor and tracked the local micellar concentrations during flow. The micropost configuration allows for variations of the local micellar concentration of up to 25%, which were found to be correlated with FISP formation (10% higher than the average micellar concentration). Whereas the majority of direct observations of transient flow-induced structures have involved purely shear flows, flows that result in stable structure formation, such as the FISP, include both shear and extensional flows, and the rates of strain are generally several orders of magnitude larger than those in the pure shear flows.
5,000 s−1) and extensional features of the flow. The FISP remained stable for more than a year at room temperature, even after the cessation of flow. Using the same wormlike micellar solution, Dubash et al. (32) formed the FISP using micropost arrays with a 7-μm gap size and found the rheological properties of the FISP to be at least one order of magnitude larger than those of the precursor. Cheung et al. (38) extended this work by adding Nile red dye (a fluorescent dye whose intensity is related to the CTAB concentration) to the precursor and tracked the local micellar concentrations during flow. The micropost configuration allows for variations of the local micellar concentration of up to 25%, which were found to be correlated with FISP formation (10% higher than the average micellar concentration). Whereas the majority of direct observations of transient flow-induced structures have involved purely shear flows, flows that result in stable structure formation, such as the FISP, include both shear and extensional flows, and the rates of strain are generally several orders of magnitude larger than those in the pure shear flows.
Effect of Salt on Branched Wormlike Micelles
For semidilute wormlike micellar solutions made with ionic surfactants, the addition of salt can lead to significant structural and rheological transitions (5–17). Multiconnected and branched micellar networks have been observed at equilibrium. Porte et al. (5) reported the formation of branched and multiconnected wormlike micellar networks in ionic micellar solutions with high salt concentrations (CPyCl/hexanol with [NaCl] = 0.2 M). They proposed that multiconnections in the network can slide against each other, yielding high fluidity. Candau et al. (8) performed rheological measurements of wormlike micellar solutions of [CTAB] = 0.35 M and found the zero-shear viscosity and stress relaxation time to reach a maximum, followed by a reduction with increasing salt concentrations ([KBr] = 0.1–2 M). This behavior is related to the transition from entangled linear micelles to multiconnected structures with salt addition (8). Similar trends in the zero-shear viscosity and stress relaxation time with changes to salt concentration were observed in a semidilute wormlike micellar solution with [CTAB] = 0.3 M and [NaNO3] = 0.0–4.0 M by Cappelaere and Cressely (10). The plateau modulus 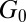 was not found to vary much until after the salt concentration reached the level at which the zero-shear viscosity and stress relaxation time peak. They proposed that the branching of the micelles (with sliding connections) or the shortening of the micelles might lead to the reduction of the zero-shear viscosity. Cappelaere and Cressely (11) subsequently studied the salt (NaNO3) effect on surfactant CPyCl and showed that plateau modulus decreases with increasing salt content. One possible mechanism is that the micellar network junctions might break at a higher salt concentration, leading to shorter micellar length, and hence a drop in the plateau modulus. Schubert et al. (15) used rheology, flow birefringence, and small-angle neutron scattering to quantify important micellar length scales of a wormlike micellar solution of CTAT/Sodium Dodecylbenzenesulfonate (SDBS) with the addition of salt. Both the zero-shear viscosity and stress relaxation time were found to decrease with addition of the hydrotropic salt NaTosylate, which is potentially related to the presence of branched micelles.
was not found to vary much until after the salt concentration reached the level at which the zero-shear viscosity and stress relaxation time peak. They proposed that the branching of the micelles (with sliding connections) or the shortening of the micelles might lead to the reduction of the zero-shear viscosity. Cappelaere and Cressely (11) subsequently studied the salt (NaNO3) effect on surfactant CPyCl and showed that plateau modulus decreases with increasing salt content. One possible mechanism is that the micellar network junctions might break at a higher salt concentration, leading to shorter micellar length, and hence a drop in the plateau modulus. Schubert et al. (15) used rheology, flow birefringence, and small-angle neutron scattering to quantify important micellar length scales of a wormlike micellar solution of CTAT/Sodium Dodecylbenzenesulfonate (SDBS) with the addition of salt. Both the zero-shear viscosity and stress relaxation time were found to decrease with addition of the hydrotropic salt NaTosylate, which is potentially related to the presence of branched micelles.
The organic salt containing salicylate or alkylbenzoate counter-ions can alter the structural and rheological responses in a micellar system differently compared with those of inorganic salts. For example, the Sal ions can penetrate in the interface of the cetyltrimethylammonium-micellar cores, making the micelles more flexible, as observed in NMR studies and molecular simulations (39–41). Double peaks of the zero-shear viscosity have also been observed with increasing organic salt concentrations. The first peak has usually been attributed to the emergence of a multiconnected wormlike micellar structure in which the cross-link points have the ability to slide and promote higher fluidity in the network. With further addition of salt, the micelles can become negatively charged. The effect of Coulomb interactions might reduce the micellar length, increasing the branching density, and hence lower viscosity. Kadoma and van Egmond (13) and Kadoma et al. (14) investigated [CTAB] 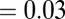 M and [NaSal]
M and [NaSal] 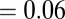 –0.24 M systems with rheological measurements and SALS patterns under shear. They observed double peaks in both the zero-shear viscosity and the stress relaxation time. Furthermore, the evolution of the scattering patterns was found to be correlated to the multiconnected micellar networks of cross-linked micelles. Oelschlaeger et al. (18) studied the wormlike micellar system of [CPyCl] = 0.1 M and [NaSal] = 0.07–0.5 M by using mechanical rheology and optical microrheology to probe the structural and dynamic changes with increasing salt concentrations. They also observed double peaks of the zero-shear viscosity with increasing salt concentrations and related the persistence length and cross-link density to the rheological responses of the micellar system.
–0.24 M systems with rheological measurements and SALS patterns under shear. They observed double peaks in both the zero-shear viscosity and the stress relaxation time. Furthermore, the evolution of the scattering patterns was found to be correlated to the multiconnected micellar networks of cross-linked micelles. Oelschlaeger et al. (18) studied the wormlike micellar system of [CPyCl] = 0.1 M and [NaSal] = 0.07–0.5 M by using mechanical rheology and optical microrheology to probe the structural and dynamic changes with increasing salt concentrations. They also observed double peaks of the zero-shear viscosity with increasing salt concentrations and related the persistence length and cross-link density to the rheological responses of the micellar system.
Results and Discussion
Flow Conditions for FISP Formation.
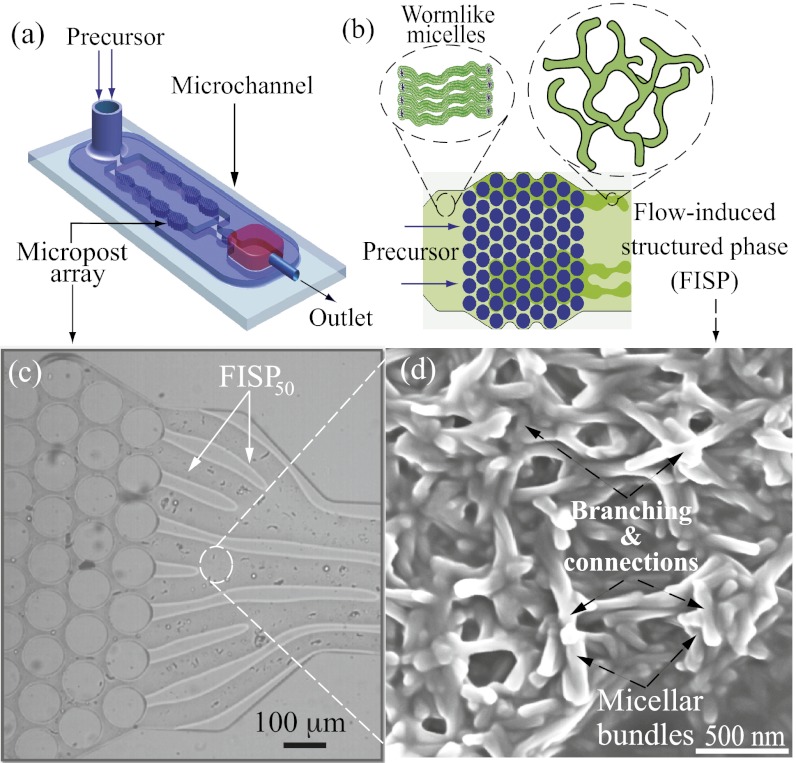
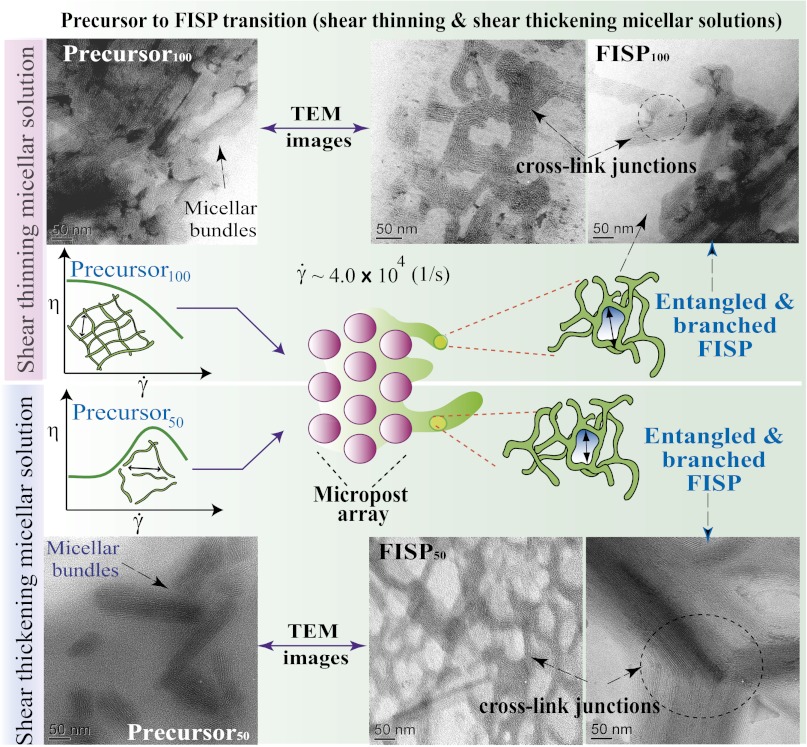
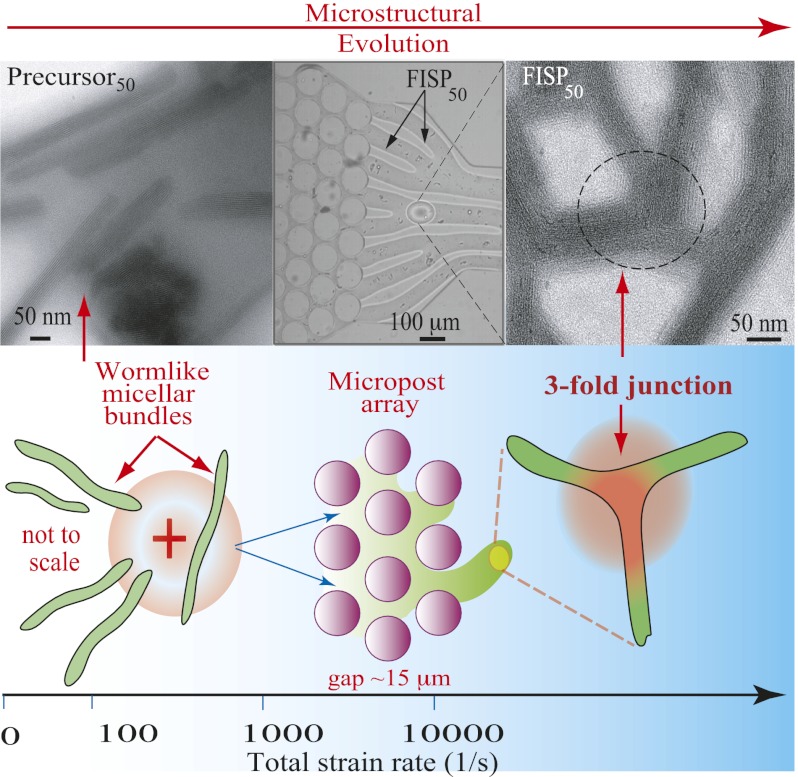
Both precursors used are semidilute and consist of CTAB and NaSal in an aqueous solution. The shear-thickening (aqueous solution with 50 mM CTAB and 16 mM NaSal [precursor50]) and shear-thinning (aqueous solution with 100 mM CTAB and 32 mM NaSal [precursor100]) solutions have the concentration ratio [NaSal]/[CTAB] = 0.32 to maintain proportionality of the electrostatic interaction. The polydimethylsiloxane-glass microfluidic device has a channel height of 75 μm containing a hexagonal array of microposts with a diameter of 100 μm and spacing of 15 μm. The experiments were conducted using an inverted Leica microscope at 23 ± 2 °C. Harvard Apparatus digital pumps were used to pump the precursors through the device at a constant flow rate (15 mL/h). Once the precursors passed through the micropost arrays, the FISP began to emerge. Fig. 1 A and B shows schematics for FISP formation. Fig. 1C shows the actual device with a finger-like FISP. Fig. 1D shows a SEM image of the FISP formed from precursor50 (FISP50), exhibiting entangled, branched, and multiconnected networks.
Fig. 1.
(A and B) Schematics of the microdevice. When the precursor passes through the micropost array, it undergoes high strain rates of 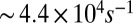 and total strain of
and total strain of 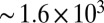 , leading to FISP formation. (C) Snapshot shows the “finger-like” FISP formation. (D) High-resolution SEM image of FISP50 at a magnification of 100,000× under high voltage of 3.00 kV.
, leading to FISP formation. (C) Snapshot shows the “finger-like” FISP formation. (D) High-resolution SEM image of FISP50 at a magnification of 100,000× under high voltage of 3.00 kV.
At a flow rate of 15 mL/h, we estimate a maximum rate of strain of 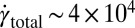 s−1 and a total strain in the arrays of
s−1 and a total strain in the arrays of 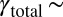 1,600. Also, the onset of the FISP was found to require a minimum strain rate of
1,600. Also, the onset of the FISP was found to require a minimum strain rate of 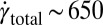 s−1 and a total strain of
s−1 and a total strain of 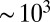 . Even though the stable FISP differs from the reversible SIS, making quantitative comparisons of the critical strain rates required to form these structures should shed insight on the mechanism of FISP formation. To generate the reversible SIS with gel-like shear-thickening behavior from a CTAB/NaSal micellar solution, the critical shear rate has been reported to be around 10–20 s−1, with [CTAB] = 0.08–7.0 mM and a 1:1 salt-to-surfactant molar ratio (25). More recently, Takahashi and Sakata (42) applied a step planar elongation flow to wormlike micellar solutions of [CTAB] = 0.03 M and [NaSal] = 0.03–0.27 M and observed both transient SISs and elongation-induced structures at extension rates of 0.1–1 s−1 and elongation strains of ∼1–10. Moss and Rothstein (43) studied a shear-thinning CTAB/NaSal (both 50 mM) solution passing through a periodic array of cylinders with a diameter of 10 mm and a gap size of 40 mm, a configuration that is three orders of magnitude larger than ours. Elastic instabilities and strain hardening were observed, but no FISP was reported.
. Even though the stable FISP differs from the reversible SIS, making quantitative comparisons of the critical strain rates required to form these structures should shed insight on the mechanism of FISP formation. To generate the reversible SIS with gel-like shear-thickening behavior from a CTAB/NaSal micellar solution, the critical shear rate has been reported to be around 10–20 s−1, with [CTAB] = 0.08–7.0 mM and a 1:1 salt-to-surfactant molar ratio (25). More recently, Takahashi and Sakata (42) applied a step planar elongation flow to wormlike micellar solutions of [CTAB] = 0.03 M and [NaSal] = 0.03–0.27 M and observed both transient SISs and elongation-induced structures at extension rates of 0.1–1 s−1 and elongation strains of ∼1–10. Moss and Rothstein (43) studied a shear-thinning CTAB/NaSal (both 50 mM) solution passing through a periodic array of cylinders with a diameter of 10 mm and a gap size of 40 mm, a configuration that is three orders of magnitude larger than ours. Elastic instabilities and strain hardening were observed, but no FISP was reported.
Modeling wormlike micelles under extensional flow, Turner and Cates (44) predicted a critical extension rate at which the solution undergoes a transition to a “gel” phase consisting of extremely long aligned micellar chains. They assumed a simple reaction scheme in which two micelles fuse only if they are collinear. Again, this gel phase only persists while the flow is active. On the basis of their model, for wormlike micelles with a length of ∼80 nm, a critical strain rate of ∼103 s−1 is required for extensional flow-induced gelation. This strain rate has the same order of magnitude as the one present in our micropost array (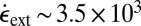 s−1) and is similar to our strain rate threshold for FISP formation.
s−1) and is similar to our strain rate threshold for FISP formation.
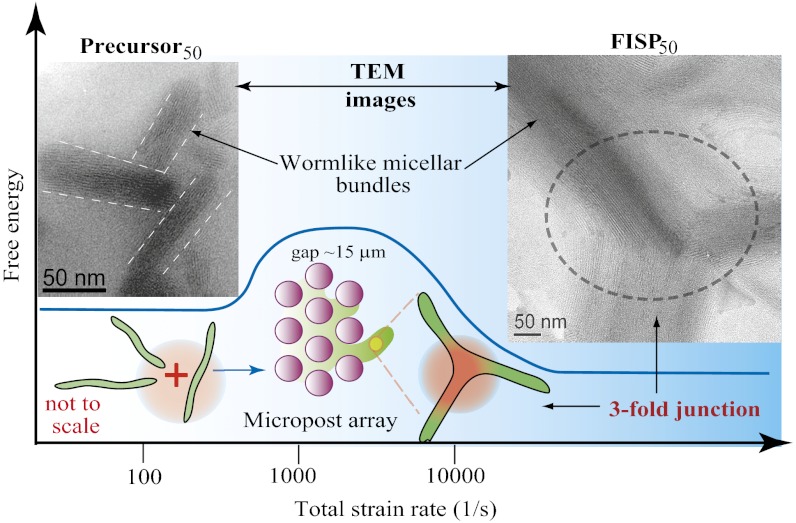
The comparisons described above indicate that high extension rates and spatial confinement are critical for FISP formation. We now propose a potential mechanism for FISP formation (Fig. 2). The high stretching and flow alignment in the micropost array increase the flexibility of the micelles, and hence lower the bending modulus of the micelles (39–41), leading to a decrease in the curvature energy in the cylindrical body of the micelle. The free energy of surfactant molecules in the end cap therefore increases relative to the curvature energy in the cylindrical body of the micelle, lowering the work required to form junctions (1, 6, 7, 15, 16, 45, 46). As flexible adjacent micelles flow through the confined micropost array, it becomes energetically favorable to minimize the number of end caps while promoting the formation of cross-links, yielding highly entangled, branched, and multiconnected wormlike micellar bundles (FISPs) (9, 45, 47). The presence of spatial confinement and high extension in our microdevice also induces entropic fluctuations, making it easier to cross the energy barrier between states, and thus increasing transition frequencies between states, enabling the formation of entangled and branched micellar bundle networks.
Fig. 2.
Micropost configuration enables the high strain rates and strain in the flow, accompanied by the concentration fluctuations in wormlike micelles. The high stretching and flow alignment in the micropost array increase the flexibility of the micelles, and hence lower the bending modulus of the micelles. It becomes energetically favorable for a pair of adjacent micelles to merge when they flow through the confined microposts, promoting the formation of junctions and cross-links and leading to entangled, branched, and multiconnected FISPs.
Microstructural Analysis.
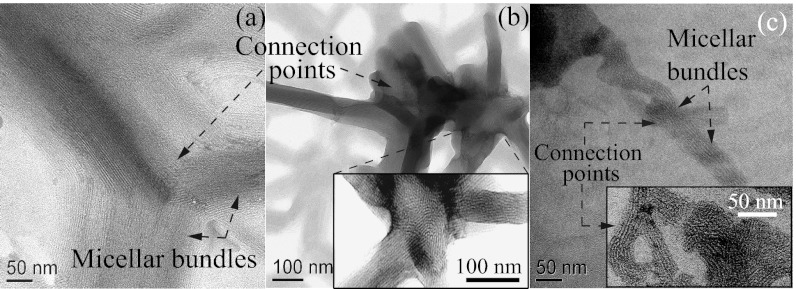
We used a combination of EM techniques (cryo-TEM, TEM, and SEM) to conduct extensive microstructural characterizations of the precursor solutions and their corresponding FISPs. Because the carbon and other light element-based makeup in CTAB/NaSal samples has very low electron density, we used a negative staining procedure with NanoW (Nanoprobes, Inc.) to enhance imaging contrast. Cryo-TEM imaging is desirable because it can capture the true microstructure of a given sample in its native hydrated environment. However, the resolution of cryo-TEM tends to be decreased due to the vitreous ice layer within the sample. Taking these factors into consideration, we performed both cryo-TEM and TEM microscopy of FISP50, as shown in Fig. 3. From the morphological comparison of frozen-hydrated (Fig. 3A) and gradually air-dried (Fig. 3B) samples by cryo-TEM and TEM, we found excellent ultrastructural correlation in both methods. On these grounds, to avoid the decreased resolution caused by imaging through the vitreous ice layer (shown in Fig. 3A as a gray background) with cryo-TEM, we proceeded with room temperature TEM imaging. In Fig. 3, FISP50 consists of branched and entangled electron-dense branches. Because an individual wormlike micelle has a diameter of ∼5 nm and each bundle has a diameter of ∼100 ± 15 nm and a length of ∼350 ± 45 nm, each bundle represents ∼20 parallel wormlike micelles. The electron-dense branches represent wormlike micellar bundles, and the electron-transparent areas are the pores in the microstructure. Both FISP50 and the FISP formed from precursor100 (FISP100) exhibit entangled, branched, and multiconnected bundles with distinct junctions and cross-links, as shown in Fig. 4. The triple junctions shown in Fig. 5 are consistent with those predicted from theoretical and numerical approaches (9, 45, 47).
Fig. 3.
(A) Cryo-TEM image of FISP50. (B and C) TEM images of FISP50. The electron-dense (dark) branches are the wormlike micellar bundles, whereas the bright areas correspond to the pores in the structure. TEM was conducted with a Tecnai T-12 transmission electron microscope. In C, the averaged mesh size 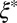 was determined from the geometric mean
was determined from the geometric mean 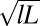 of the smallest (l) and largest (L) distances in the pore.
of the smallest (l) and largest (L) distances in the pore.
Fig. 4.
Each column shows the microstructural transition from the precursor  FISP. (A) TEM image of precursor50. (B) TEM image of entangled and branched micellar bundles of FISP50. (C) TEM image of precursor100. (D) TEM image of entangled and branched network of FISP100. (Insets) Zoomed-in micellar bundles. TEM was conducted with a Tecnai T-12 transmission electron microscope at 120 kV. In all panels, x* represents mesh size ξ*.
FISP. (A) TEM image of precursor50. (B) TEM image of entangled and branched micellar bundles of FISP50. (C) TEM image of precursor100. (D) TEM image of entangled and branched network of FISP100. (Insets) Zoomed-in micellar bundles. TEM was conducted with a Tecnai T-12 transmission electron microscope at 120 kV. In all panels, x* represents mesh size ξ*.
Fig. 5.
(A and B) TEM images of FISP50 show branched, entangled, and multiconnected micellar bundles. (C) TEM image of FISP100 shows entangled, branched, and multiconnected micellar bundles. (Insets) Zoomed-in images where branching points and connection points are presented. TEM was conducted with a Tecnai T-12 transmission electron microscope at 120 kV.
Fig. 4 shows the structural evolution of wormlike micelles from within the precursors to the FISP. Both precursors also exhibit the existence of wormlike micellar bundles with similar diameters (Fig. 4 A and C). The interspacing between bundles in precursor50 is almost sixfold larger than that in precursor100 (Fig. 4 A and C). Also, the linear micellar bundles are densely entangled in precursor100 (Fig. 4C). Similarly, Shikata et al. (9) observed entangled and elongated wormlike micelles from TEM imaging on a shear-thinning solution of [CTAB] = 0.1 M and [NaSal] = 0.3 M. Li et al. (48) performed cryo-TEM microscopy of a shear-thinning solution of [CTAB] = 0.25 M and [NaSal] = 0.15 M, and also showed entangled wormlike micelles. Fig. 4 also exhibits distinct structural transitions from the precursors to their FISPs. Precursor50 shows a less entangled linear bundle structure, whereas FISP50 has highly entangled and branched bundles with open pores. Precursor100 shows dense and entangled linear bundles, whereas FISP100 has a less entangled and branched porous structure. The observed bundle structure in the precursor solutions might be partially caused by the evaporation effect while conducting TEM. Cryo-TEM imaging of the precursor solutions will be performed to verify these structures.
We can estimate the degree of entanglement of the precursor and FISP samples to quantify their structural transitions (49). Assuming all samples have flexible Gaussian chains that are entangled or cross-linked, we can approximate the degree of entanglement in these materials as 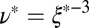 , where
, where 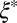 is the mesh size in the sample, which can be determined from the geometric mean
is the mesh size in the sample, which can be determined from the geometric mean 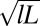 of the smallest (l) and largest (L) distances in the pore, as obtained from TEM images (Fig. 3C). We averaged over 500 pores in 10 different samples for each material to yield the average mesh size
of the smallest (l) and largest (L) distances in the pore, as obtained from TEM images (Fig. 3C). We averaged over 500 pores in 10 different samples for each material to yield the average mesh size 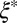 . Table 1 shows the resulting values of
. Table 1 shows the resulting values of 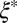 and
and 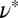 . The mesh size
. The mesh size 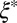 from precursor50 is nearly fourfold larger than that of FISP50, with the degree of entanglement
from precursor50 is nearly fourfold larger than that of FISP50, with the degree of entanglement 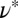 being two orders of magnitude lower than that of FISP50. Although the mesh size
being two orders of magnitude lower than that of FISP50. Although the mesh size 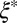 of precursor100 is about half that of FISP100, the degree of entanglement
of precursor100 is about half that of FISP100, the degree of entanglement 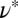 of precursor100 is around sixfold higher than that of FISP100.
of precursor100 is around sixfold higher than that of FISP100.
Table 1.
Mesh size and degree of entanglement of the precursors and FISPs
| Samples |
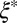 from TEM, nm from TEM, nm |
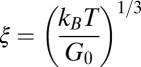 , nm , nm |
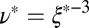 , m−3 , m−3
|
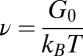 , m−3 , m−3
|
| Precursor50 | 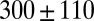 |
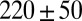 |
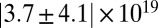 |
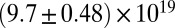 |
| FISP50 | 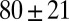 |
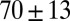 |
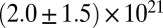 |
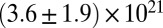 |
| Precursor100 | 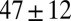 |
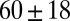 |
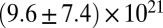 |
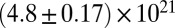 |
| FISP100 | 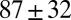 |
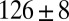 |
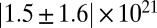 |
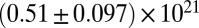 |
Rheological Characterization.
The rheological properties of the precursor solutions and their FISPs were studied with a combination of bulk rheometry and microrheometry.
Bulk Rheometry.
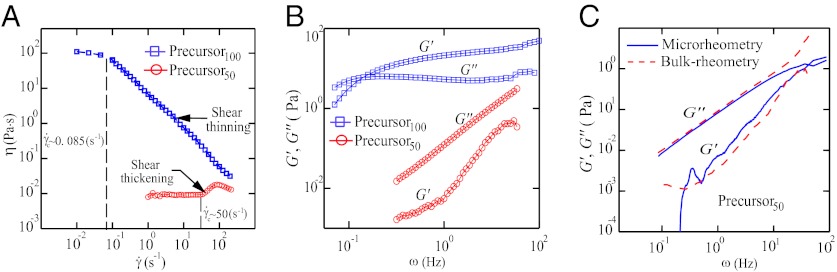
Steady shear rheometry and oscillatory shear rheometry were performed using a stress-controlled rheometer (AR 2000; TA Instruments) on both precursor solutions. The temperature was fixed at 23 °C, and a solvent trap was used to avoid evaporation. Acrylic cone-plate geometry (40 mm in diameter and 2° truncation angle) was used for all measurements. Fig. 6A shows the shear viscosity of the precursors as a function of the shear rate. The zero-shear viscosity 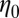 of precursor100 is four orders of magnitude larger than that of precursor50. Precursor50 exhibited a distinct viscosity jump above a critical shear rate (
of precursor100 is four orders of magnitude larger than that of precursor50. Precursor50 exhibited a distinct viscosity jump above a critical shear rate (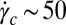 s−1). This jump in the apparent viscosity has been attributed to the formation of a transient SIS created by entangled wormlike micellar networks under shear flow (3, 22, 23, 25, 26). When the shear rate is increased further (
s−1). This jump in the apparent viscosity has been attributed to the formation of a transient SIS created by entangled wormlike micellar networks under shear flow (3, 22, 23, 25, 26). When the shear rate is increased further (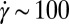 s−1), the wormlike micelles align in the flow direction, leading to a viscosity drop. Precursor100 showed a shear-thinning response above a critical certain shear rate (
s−1), the wormlike micelles align in the flow direction, leading to a viscosity drop. Precursor100 showed a shear-thinning response above a critical certain shear rate (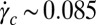 s−1). Shear banding was also observed for precursor100 (SI Shear Rheometry of the Aqueous Solution with 100 mM Cetyltrimethylammonium Bromide and 32 mM Sodium Salicylate).
s−1). Shear banding was also observed for precursor100 (SI Shear Rheometry of the Aqueous Solution with 100 mM Cetyltrimethylammonium Bromide and 32 mM Sodium Salicylate).
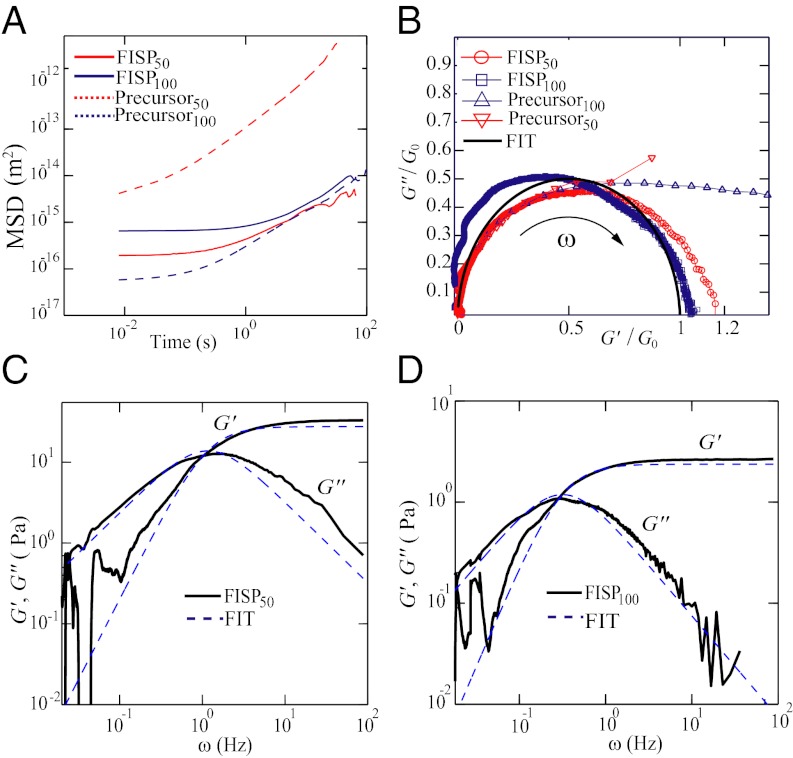
Fig. 6.
(A) Shear viscosity vs. shear rate for both precursors. (B) G′ and G′′ are plotted against the angular frequency ω, under 0.5% strain, using a stress-controlled rheometer. (C) G′ and G′′ vs. ω from precursor50’s bulk rheometry and microrheometry data.
Oscillatory shear experiments were conducted at several strains within the linear viscoelastic regime. The viscoelasticity behavior of the precursors was correlated with a Maxwellian relationship using a single-dominant relaxation time. This stress relaxation time 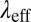 can be extracted from the first crossover between the viscous modulus (
can be extracted from the first crossover between the viscous modulus (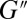 ) and the elastic modulus (
) and the elastic modulus ( ). The plateau modulus
). The plateau modulus 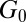 is the value at which
is the value at which 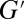 reaches a plateau at high frequencies. The frequency was varied from 0.01 to 100 Hz. Because our stress-controlled rheometer is not sensitive enough to extract the stress relaxation time
reaches a plateau at high frequencies. The frequency was varied from 0.01 to 100 Hz. Because our stress-controlled rheometer is not sensitive enough to extract the stress relaxation time 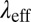 for the weakly viscoelastic precursor50, microrheometry was used to obtain both the stress relaxation time and plateau modulus. Fig. 6C shows good agreement between the bulk rheometry and the microrheometry of precursor50 within the frequency range of the bulk measurements. Several shear oscillatory studies of CTAB-based micellar solutions have shown that at low frequencies (0.01–30 Hz), they closely follow a Maxwellian trend (3, 22, 28, 50, 51). As the frequency increases, the micellar solution starts to deviate from the Maxwell model, presenting a spectrum of relaxation times in the micellar solution where Rouse or Zimm models can be used to describe their dynamical behavior (52, 53).
for the weakly viscoelastic precursor50, microrheometry was used to obtain both the stress relaxation time and plateau modulus. Fig. 6C shows good agreement between the bulk rheometry and the microrheometry of precursor50 within the frequency range of the bulk measurements. Several shear oscillatory studies of CTAB-based micellar solutions have shown that at low frequencies (0.01–30 Hz), they closely follow a Maxwellian trend (3, 22, 28, 50, 51). As the frequency increases, the micellar solution starts to deviate from the Maxwell model, presenting a spectrum of relaxation times in the micellar solution where Rouse or Zimm models can be used to describe their dynamical behavior (52, 53).
Microrheometry.
We performed passive microrheology on precursor50, FISP50, and FISP100 (54, 55). The volumes of the FISP produced in the microdevice were small (∼0.15 μL); thus, rheological properties were measured with microrheology. To facilitate these measurements, the precursor solution was seeded with 1-μm diameter polystyrene microspheres, with 0.01 wt% in the total solution. The seeded solution was then pumped into the microdevice at 15 mL/h. The 2D mean square displacement (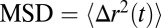 ) of the embedded microbeads in the FISP was calculated and plotted. Some light smoothing using a moving average filter (windows size of 51 frames) was performed on the MSD data before further analysis. The MSD was then related to the complex modulus
) of the embedded microbeads in the FISP was calculated and plotted. Some light smoothing using a moving average filter (windows size of 51 frames) was performed on the MSD data before further analysis. The MSD was then related to the complex modulus 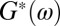 of the FISP, with ω being the frequency. The complex modulus comes from the Stokes–Einstein relation, which shows that the shear-stress relaxation in the locality of the particle is identical to that of the bulk fluid subjected to a shear strain (54). This approach is valid when the length scale of the heterogeneity of the sample is much smaller than the probe particle size, which can be verified by our TEM images (Table 1). Fig. 7A shows the MSD of the precursors and their corresponding FISPs. For precursor50, the mobility of the probe particles decreased for FISP50 (Fig. 7A, solid red curve below the dashed curve). However, the mobility of the probe particles increased for FISP100 (Fig. 7A, solid blue curve) compared with the precursor solution (Fig. 7A, dashed blue curve). This behavior can be explained based on the microstructural evolution by reviewing the TEM images in Fig. 4 C and D and their degrees of entanglement: Precursor100 exhibits more entangled wormlike micelles with a smaller mesh size than those of FISP100. This structural transition, from smaller mesh size and more entangled wormlike micelles to larger mesh size with connected and branched structures, leads to rheological variations between the precursor and FISP.
of the FISP, with ω being the frequency. The complex modulus comes from the Stokes–Einstein relation, which shows that the shear-stress relaxation in the locality of the particle is identical to that of the bulk fluid subjected to a shear strain (54). This approach is valid when the length scale of the heterogeneity of the sample is much smaller than the probe particle size, which can be verified by our TEM images (Table 1). Fig. 7A shows the MSD of the precursors and their corresponding FISPs. For precursor50, the mobility of the probe particles decreased for FISP50 (Fig. 7A, solid red curve below the dashed curve). However, the mobility of the probe particles increased for FISP100 (Fig. 7A, solid blue curve) compared with the precursor solution (Fig. 7A, dashed blue curve). This behavior can be explained based on the microstructural evolution by reviewing the TEM images in Fig. 4 C and D and their degrees of entanglement: Precursor100 exhibits more entangled wormlike micelles with a smaller mesh size than those of FISP100. This structural transition, from smaller mesh size and more entangled wormlike micelles to larger mesh size with connected and branched structures, leads to rheological variations between the precursor and FISP.
Fig. 7.
(A) MSD vs. time for two precursors and their FISPs. The red and blue dashed lines correspond to the precursors, whereas the red and blue solid lines correspond to the FISPs. (B) Cole–Cole plots of the precursors and their FISPs based on the microrheology measurements. The black semicircle corresponds to the single-mode Maxwell fit. (C) G′ and G′′ vs. ω for FISP50 measured from microrheometry. The data are plotted against the dotted curves from the single-mode Maxwell fit. (D) G′ and G′′ vs. ω for FISP100 measured from microrheometry. The data are plotted against the dashed curves from the single-mode Maxwell fit.
The complex modulus is defined as 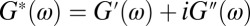 , where
, where 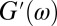 is the elastic modulus and
is the elastic modulus and 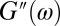 is the viscous modulus. Following Mason (54),
is the viscous modulus. Following Mason (54),
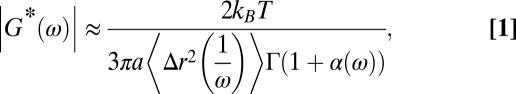 |
where 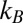 is the Boltzmann constant, T is the absolute temperature, a is the radius of the probe particle,
is the Boltzmann constant, T is the absolute temperature, a is the radius of the probe particle, 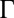 is the γ-function, and
is the γ-function, and
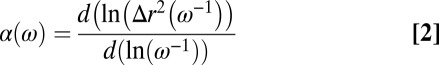 |
is the logarithmic slope of the MSD. For Maxwellian fluids,
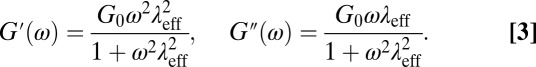 |
The microrheology data were further fitted to a single-mode Maxwellian linear viscoelastic model. Plots of 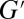 and
and 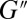 vs. the frequency ω for FISP50 and FISP100 appear in Fig. 7 C and D. Although the blue dashed lines in Fig. 7 C and D follow the Maxwellian fit, the solid black lines correspond to the experimental data. The noise at low frequencies is caused by movement of probe particles in and out of the focus plane during the recording (55). The plateau modulus
vs. the frequency ω for FISP50 and FISP100 appear in Fig. 7 C and D. Although the blue dashed lines in Fig. 7 C and D follow the Maxwellian fit, the solid black lines correspond to the experimental data. The noise at low frequencies is caused by movement of probe particles in and out of the focus plane during the recording (55). The plateau modulus 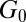 and zero-shear viscosity
and zero-shear viscosity 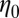 were either measured from the bulk rheometry or calculated based on
were either measured from the bulk rheometry or calculated based on 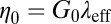 from the microrheology. The rheological data of the precursors and FISPs are also presented in Cole–Cole plots with normalized (
from the microrheology. The rheological data of the precursors and FISPs are also presented in Cole–Cole plots with normalized (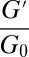 ,
,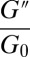 ) (Fig. 7B). By conducting numerical simulation and using a Poisson renewal model, Turner and Cates (56) and Granek and Cates (57) proposed that if a wormlike micellar solution follows a semicircle in a Cole–Cole plot, the solution should follow a single exponential stress relaxation process. However, if the micellar solution exhibits a flattened curve in the Cole–Cole plot (i.e., precursor100), a broad distribution of relaxation times incurs, where the internal micellar dynamics may be dominated by reptation or Rouse breathing. At low frequencies, both precursors and their FISPs fit the semicircle (Fig. 7B, solid black curve) with a mean square error of ∼8–10
) (Fig. 7B). By conducting numerical simulation and using a Poisson renewal model, Turner and Cates (56) and Granek and Cates (57) proposed that if a wormlike micellar solution follows a semicircle in a Cole–Cole plot, the solution should follow a single exponential stress relaxation process. However, if the micellar solution exhibits a flattened curve in the Cole–Cole plot (i.e., precursor100), a broad distribution of relaxation times incurs, where the internal micellar dynamics may be dominated by reptation or Rouse breathing. At low frequencies, both precursors and their FISPs fit the semicircle (Fig. 7B, solid black curve) with a mean square error of ∼8–10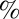 . At larger frequencies (
. At larger frequencies (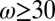 Hz), both precursors start to deviate from the semicircle fit, indicating the existence of a spectrum of relaxation times. With branched and multiconnected micellar bundles, both FISP50 and FISP100 fit the semicircle in the Cole–Cole plot with a mean square error of ∼5–12
Hz), both precursors start to deviate from the semicircle fit, indicating the existence of a spectrum of relaxation times. With branched and multiconnected micellar bundles, both FISP50 and FISP100 fit the semicircle in the Cole–Cole plot with a mean square error of ∼5–12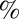 . Higher deviation is observed at higher frequencies. Such behavior had been reported for CTAB-based micellar solutions (14, 22, 28, 51, 58) and other ionic wormlike micellar solutions (59, 60) due to their branching structures.
. Higher deviation is observed at higher frequencies. Such behavior had been reported for CTAB-based micellar solutions (14, 22, 28, 51, 58) and other ionic wormlike micellar solutions (59, 60) due to their branching structures.
Table 2 summarizes the rheological parameters (zero-shear viscosity 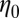 , stress relaxation time
, stress relaxation time 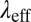 , and plateau modulus
, and plateau modulus 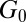 ) of the precursors and the FISPs. Precursor50 is semidilute and weakly viscoelastic. Although the zero shear viscosity for the FISP50 is three orders of magnitude larger than that for precursor50, the values of stress relaxation time and plateau modulus of FISP50 are around 40-fold larger than those of precursor50. These variations are consistent with structural transitions exhibited in the TEM images: Precursor50 is a semidilute wormlike micellar solution, with a mesh size of
) of the precursors and the FISPs. Precursor50 is semidilute and weakly viscoelastic. Although the zero shear viscosity for the FISP50 is three orders of magnitude larger than that for precursor50, the values of stress relaxation time and plateau modulus of FISP50 are around 40-fold larger than those of precursor50. These variations are consistent with structural transitions exhibited in the TEM images: Precursor50 is a semidilute wormlike micellar solution, with a mesh size of 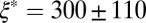 nm and degree of entanglement of
nm and degree of entanglement of 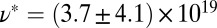 m−3; gel-like FISP50 shows a highly entangled, branched, and multiconnected network with a mesh size of
m−3; gel-like FISP50 shows a highly entangled, branched, and multiconnected network with a mesh size of 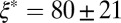 nm and degree of entanglement of
nm and degree of entanglement of 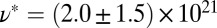 m−3. Similar rheological and structural transitions can be achieved by adding salt in the NaSal/CTAB system at equilibrium: Excess salt ions enable the elongation and flexibility of the micelles, which promote the formation of branched and multiconnected networks (9, 13).
m−3. Similar rheological and structural transitions can be achieved by adding salt in the NaSal/CTAB system at equilibrium: Excess salt ions enable the elongation and flexibility of the micelles, which promote the formation of branched and multiconnected networks (9, 13).
Table 2.
Rheological properties of the precursors and FISPs
| Fluid |
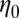 , Pa⋅s , Pa⋅s |
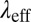 , s , s |
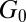 , Pa , Pa |
| Shear-thickening precursor50 | 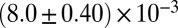 |
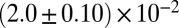 |
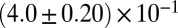 |
| FISP50 | 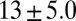 |
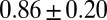 |
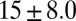 |
| Shear-thinning precursor100 | 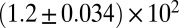 |
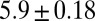 |
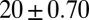 |
| FISP100 | 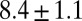 |
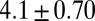 |
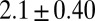 |
Precursor100 exhibits stronger viscoelastic behavior and consists of densely entangled micellar bundles, with  nm and
nm and  m−3. The values of
m−3. The values of 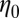 and
and 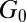 for FISP100 are around 10-fold smaller than those of precursor100, for which
for FISP100 are around 10-fold smaller than those of precursor100, for which 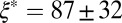 nm and
nm and 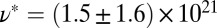 m−3. For FISP100,
m−3. For FISP100, 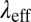 is around 1.4-fold smaller than that of precursor100. Decreases of
is around 1.4-fold smaller than that of precursor100. Decreases of 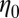 ,
, 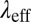 , and
, and 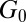 accompanying branched and multiconnected micellar networks have been reported for CTAB-based micellar solutions (7, 8, 51, 58) at equilibrium. The micelles can become negatively charged due to the excess of counter-ions at higher salt concentrations. Coulomb interactions hence become important and induce reductions in the length of micelles (61). Cappelaere and Cressely (11) observed similar trends in the rheological properties of CPCl/NaClO3 solutions with the presence of branched structures. Kadoma and van Egmond (13) and Kadoma et al. (14) also reported a reduction in the rheological properties of the [CTAB] = 0.03 M and [NaSal] = 0.06–0.24 M system with high salt concentrations. In their study,
accompanying branched and multiconnected micellar networks have been reported for CTAB-based micellar solutions (7, 8, 51, 58) at equilibrium. The micelles can become negatively charged due to the excess of counter-ions at higher salt concentrations. Coulomb interactions hence become important and induce reductions in the length of micelles (61). Cappelaere and Cressely (11) observed similar trends in the rheological properties of CPCl/NaClO3 solutions with the presence of branched structures. Kadoma and van Egmond (13) and Kadoma et al. (14) also reported a reduction in the rheological properties of the [CTAB] = 0.03 M and [NaSal] = 0.06–0.24 M system with high salt concentrations. In their study, 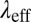 decreased from 5.65 s to 2.18 s on increasing the salt-to-surfactant ratio from 5.5 to 8. Porte et al. (5), Appell et al. (6), and Khatory et al. (7) proposed that the multiconnections formed in the micellar solutions could slide against each other, yielding high fluidity and lower the zero-shear viscosity
decreased from 5.65 s to 2.18 s on increasing the salt-to-surfactant ratio from 5.5 to 8. Porte et al. (5), Appell et al. (6), and Khatory et al. (7) proposed that the multiconnections formed in the micellar solutions could slide against each other, yielding high fluidity and lower the zero-shear viscosity 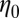 in the micellar structure. Even though this sliding mechanism might be present for both FISP50 and FISP100, variations in the rheological properties from the precursor to the FISP are found to correlate with the degree of entanglement (Table 1).
in the micellar structure. Even though this sliding mechanism might be present for both FISP50 and FISP100, variations in the rheological properties from the precursor to the FISP are found to correlate with the degree of entanglement (Table 1).
Drye and Cates (45) developed a theoretical framework to describe the formation of cross-links and multiconnections in wormlike micellar solutions at equilibrium. They predicted that unsaturated wormlike micelles with no connections or cross-links can evolve into cross-linked or multiconnected wormlike micellar structures under entropic fluctuations. They proposed that micellar cross-links lower the viscosity of wormlike micellar solutions. In equilibrium, entropic fluctuations can be enhanced by adding salt to the micellar system. At salt concentrations threefold lower than those required at equilibrium, entropic fluctuations can be enhanced by spatial confinement and high extension (as present in our setup), making it easier to cross the energy barrier between states, and thus increasing transition frequencies between states, enabling the formation of entangled and branched micellar bundle networks. This flow-induced structural formation is highlighted in Fig. 8.
Fig. 8.
Schematics of the structural transition from the precursor to FISP of both shear-thinning (Upper) and shear-thickening (Lower) wormlike micellar solutions. This phase diagram highlights the transition from semidilute entangled linear micelles to entangled, branched, and multiconnected micellar bundles under flow conditions at low salt concentrations.
Mesh Size.
To determine mesh size, we can either directly measure 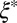 from TEM images or estimate ξ based on polymer molecular theory. Shikata and Pearson (62) proposed that the elasticity of an aqueous wormlike micellar solution of CTAB/NaSal originates from the excess entropy caused by the orientation of some micellar chains between entangled points. Assuming that the wormlike micelles have Gaussian chains, rubber elasticity relates the elastic modulus and the thermal energy to the hydrodynamic correlation length (or the network mesh size ξ) as
from TEM images or estimate ξ based on polymer molecular theory. Shikata and Pearson (62) proposed that the elasticity of an aqueous wormlike micellar solution of CTAB/NaSal originates from the excess entropy caused by the orientation of some micellar chains between entangled points. Assuming that the wormlike micelles have Gaussian chains, rubber elasticity relates the elastic modulus and the thermal energy to the hydrodynamic correlation length (or the network mesh size ξ) as 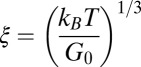 , with
, with 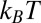 being the thermal energy (63). The plateau modulus
being the thermal energy (63). The plateau modulus 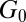 can be obtained from our rheological measurements. For TEM-based predictions of the mesh size, sample preparation and image analysis can cause errors. On the other hand, limitations of the molecular theory and errors in the measurement of plateau modulus
can be obtained from our rheological measurements. For TEM-based predictions of the mesh size, sample preparation and image analysis can cause errors. On the other hand, limitations of the molecular theory and errors in the measurement of plateau modulus 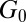 can also introduce difficulties. Despite these factors, Table 1 shows the same general trend for both approaches to determining the mesh size: For precursor50, the mesh size is about fourfold larger than that of FISP50, and for precursor100, the mesh size is about half of that of FISP100. Similar trends also hold for the degree of entanglement:
can also introduce difficulties. Despite these factors, Table 1 shows the same general trend for both approaches to determining the mesh size: For precursor50, the mesh size is about fourfold larger than that of FISP50, and for precursor100, the mesh size is about half of that of FISP100. Similar trends also hold for the degree of entanglement: 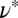 (or the corresponding theoretically determined quantity ν) of precursor50 is two orders of magnitude lower than that of FISP50, and
(or the corresponding theoretically determined quantity ν) of precursor50 is two orders of magnitude lower than that of FISP50, and 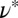 (or ν) of precursor100 is around sixfold higher than that of FISP100. Note that FISP50 and FISP100 have a similar mesh size
(or ν) of precursor100 is around sixfold higher than that of FISP100. Note that FISP50 and FISP100 have a similar mesh size 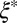 from the TEM images. For FISP100, ξ is larger than
from the TEM images. For FISP100, ξ is larger than 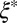 . One possible explanation is that the plateau modulus measured from the microrheology might be lower than the actual value because some precursor can become trapped in the FISP sample, leading to an overestimate of the mesh size.
. One possible explanation is that the plateau modulus measured from the microrheology might be lower than the actual value because some precursor can become trapped in the FISP sample, leading to an overestimate of the mesh size.
In summary, we show that FISPs can be formed from semidilute wormlike micellar solutions. We highlight three key results:
i) FISPs are stable and can form from both shear-thickening and shear-thinning micellar solutions.
ii) FISPs contain highly entangled, branched, and multiconnected micellar bundles formed at low salt concentrations [approximately threefold lower than those formed at equilibrium (5–7)], enabled by the spatial confinement and flow conditions. Micropost arrays allow for high extension and shear rates, which promote flow alignment and high stretching of the wormlike micelles, decreasing their bending rigidity. The free energy of surfactant molecules in end caps therefore increases relative to the curvature energy in the cylindrical micellar body, leading to a decrease in the work required to form junctions. As flexible adjacent micelles flow through the confined microposts, it becomes energetically favorable to minimize the number of end caps while concurrently promoting the formation of cross-links, yielding highly entangled, branched, and multiconnected bundles (FISPs).
iii) Transitions of the rheological properties (zero-shear viscosity, stress relaxation time, and plateau modulus) are associated with structural evolution from the precursor to the FISP, which can be correlated with the mesh size and the degree of entanglement in each system.
Materials and Methods
Precursor Preparation.
Two precursors were used to form the FISP. Both solutions are made with deionized (DI) water, surfactant CTAB (Sigma–Aldrich), and organic salt NaSal (Sigma–Aldrich). The solutions were prepared by adding the appropriate amounts of CTAB and NaSal to DI water and mixing for 4 h using a magnetic stir bar, and they were then left at rest under room temperature for 2 d to equilibrate. For microrheology, the precursor solutions were also seeded with 1-μm diameter polystyrene probe particles (Thermo Scientific) at a final concentration of 0.01 wt%.
Microrheometry.
Once a sufficient amount of the FISPs was generated, DI water was pumped through the inlet of the microdevice to remove any leftover precursor. After the microchannel was rinsed, its inlet and outlet were sealed to avoid evaporation. The microchannel was left at rest for 1 h before microrheometry. An area of ≈1,000 μm2 was selected for video microscopy. Videos were recorded at a magnification of 150× using a Leica DMR-IRB inverted microscope (PI Floutar; 100×/1.30 oil objective with a 1.5× tube lens). Videos consisting of 8,192 frames were taken at 125 fps with a high-speed camera (FASTCAM; Photron).
TEM and SEM Sample Preparation.
TEM grids (Cu-100 mesh; Electron Microscopy Sciences) were placed on a freshly opened holder covered with the precursor or FISP. After 30 s, a 5-μL drop of the NanoW negative stain (Nanoprobes, Inc.) was applied on the material side to enhance imaging contrast. After another 30 s, the residual liquid was blotted off with filter paper and left to air-dry. The same sample preparation procedure was adopted for the SEM.
Cryo-TEM Sample Preparation.
The freeze-plunging method was used for sample cryo-immobilization. Approximately 5 μL of the sample was applied on freshly glow-discharged Quanti-foil R-2/2 grids (Electron Microscopy Sciences). The sample was allowed to adhere to the grids for 30 s before being blotted on filter paper to remove excess solution. The sample was then immediately plunge-frozen by immersion into a reservoir with liquid ethane cooled by liquid nitrogen. The grids with the frozen sample were transferred under liquid nitrogen to the Gatan 626 cryo-holder (Gatan, Inc.) using a cryo-transfer station. After inserting the cryo-holder into the transmission electron microscope, the temperature was maintained below approximately −178 °C at all times during the cryo-imaging.
EM.
TEM samples were imaged by the Tecnai T-12 transmission electron microscope (FEI Co.) at 120 kV with a LaB6 filament, equipped with a cryo-stage. SEM samples were imaged with an FEI Helios scanning electron microscope at 3–5 kV.
Supplementary Material
Acknowledgments
We thank Professor Gerry Fuller and Professor Eliot Fried for fruitful discussions. The EM was performed at the Environmental Molecular Sciences Laboratory at the Pacific Northwest National Laboratory (Grant PNNL-EMSL-39946). This study was supported by National Science Foundation Division of Chemical, Bioengineering, Environmental, and Transport Systems Grant 0852471 (to A.Q.S.). J.J.C. was supported by a Consejo Nacional de Ciencia y Tecnologia PhD fellowship.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
See Author Summary on page 7119 (volume 110, number 18).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1215353110/-/DCSupplemental.
References
- 1.Israelachvili J. Intermolecular and Surface Forces. New York: Academic; 1992. [Google Scholar]
- 2.Cates ME, Candau SJ. Statics and dynamics of worm-like surfactant micelles. J Phys Condens Matter. 1990;2(5):6869–6892. [Google Scholar]
- 3.Rehage H, Hoffmann H. Viscoelastic surfactant solutions: model systems for rheological research. Mol Phys. 1991;74:933–973. [Google Scholar]
- 4.Berret JF. Rheology of wormlike micelles: Equilibrium properties and shear banding transitions. In: Weiss RG, Terech P, editors. Molecular Gels. Dordrecht, The Netherlands: Springer; 2006. pp. 667–720. [Google Scholar]
- 5.Porte G, Gomati R, Haitami OE, Appell J, Marignan JJ. Morphological transformations of the primary surfactant structures in brine-rich mixtures of ternary systems (surfactant/alcohol/brine) J Phys Chem. 1986;90(22):5746–5751. [Google Scholar]
- 6.Appell J, Porte G, Khatory A, Kern A, Candau SJ. Static and dynamic properties of a network of wormlike surfactant micelles (cetylpyridinium chlorate in sodium chlorate brine) J Phys II. 1992;2(5):1045–1052. [Google Scholar]
- 7.Khatory A, et al. Entangled versus multiconnected network of wormlike micelles. Langmuir. 1993;9(4):933–939. [Google Scholar]
- 8.Candau SJ, Khatory A, Lequeux F, Kern F. Rheological behavior of wormlike micelles: Effect of salt content. J Phys IV. 1993;3(C1):197–209. [Google Scholar]
- 9.Shikata T, Hirata H, Kotaka T. Micelle formation of detergent molecules in aqueous media. 2. Role of free salicylate ions on viscoelastic properties of aqueous cetyltrimethylammonium bromide-sodium salicylate solutions. Langmuir. 1988;4(2):354–359. [Google Scholar]
- 10.Cappelaere E, Cressely R. Rheological behavior of an elongated micellar solution at low and high salt concentrations. Colloid Polym Sci. 1998;276(11):1050–1056. [Google Scholar]
- 11.Cappelaere E, Cressely R. Influence of NaClO3 on the rheological behaviour of micellar solution of CPCl. Rheologica Acta. 2000;39(4):346–353. [Google Scholar]
- 12.Kadoma IA, van Egmond JW. “Tuliplike” scattering patterns in wormlike micelles under shear flow. Phys Rev Lett. 1996;76(23):4432–4435. doi: 10.1103/PhysRevLett.76.4432. [DOI] [PubMed] [Google Scholar]
- 13.Kadoma IA, Ylitalo C, van Egmond JW. Structural transitions in wormlike micelles. Rheologica Acta. 1997;36(1):1–12. [Google Scholar]
- 14.Kadoma IA, van Egmond JM. Shear-enhanced orientation and concentration fluctuations in wormlike micelles: Effect of salt. Langmuir. 1997;13(17):4551–4561. [Google Scholar]
- 15.Schubert BA, Kaler EW, Wagner NJ. The microstructure and rheology of mixed cationic/anionic wormlike micelles. Langmuir. 2003;19(10):4079–4089. [Google Scholar]
- 16.Oelschlaeger CI, Waton G, Candau SJ. Rheological behavior of locally cylindrical micelles in relation to their overall morphology. Langmuir. 2003;19(25):10495–10500. [Google Scholar]
- 17.Croce V, Cosgrove T, Maitland G, Hughes T, Karlsson G. Rheology, cryogenic transmission electron spectroscopy, and small-angle neutron scattering of highly viscoelastic wormlike micellar solutions. Langmuir. 2003;19(20):8536–8541. [Google Scholar]
- 18.Oelschlaeger C, Schopferer M, Scheffold F, Willenbacher N. Linear-to-branched micelles transition: A rheometry and diffusing wave spectroscopy (DWS) study. Langmuir. 2009;25(2):716–723. doi: 10.1021/la802323x. [DOI] [PubMed] [Google Scholar]
- 19.Fischer E, Callaghan PT. Shear banding and the isotropic-to-nematic transition in wormlike micelles. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;64(1 Pt 1):011501. doi: 10.1103/PhysRevE.64.011501. [DOI] [PubMed] [Google Scholar]
- 20.Olmsted PD. Perspectives on shear banding in complex fluids. Rheologica Acta. 2008;47(3):283–300. [Google Scholar]
- 21.Manneville S. Recent experimental probes of shear banding. Rheologica Acta. 2008;47(3):301–318. [Google Scholar]
- 22.Hartmann V, Cressely R. Simple salts effects on the characteristics of the shear thickening exhibited by an aqueous micellar solution of CTAB/NaSal. Europhys Lett. 1997;40:691–696. [Google Scholar]
- 23.Hartmann V, Cressely R. Occurrence of shear thickening in aqueous micellar solutions of CTAB with some added organic counterions. Colloid Polym Sci. 1998;276:169–175. [Google Scholar]
- 24.Lerouge S, Berret JF. Shear-induced transitions and instabilities in surfactant wormlike micelles. Advances in Polymer Science. 2010;230:1–71. [Google Scholar]
- 25.Liu Ch, Pine DJ. Shear induced gelation and fracture in micellar solutions. Phys Rev Lett. 1996;77(10):2121–2124. doi: 10.1103/PhysRevLett.77.2121. [DOI] [PubMed] [Google Scholar]
- 26.Hu YT, Boltenhagen P, Pine DJ. Shear thickening in low-concentration solutions of wormlike micelles. I. Direct visualization of transient behavior and phase transitions. J Rheol. 1998;42(5):1185–1208. [Google Scholar]
- 27.Kim WJ, Yang SM. Flow-induced silica structure during in situ gelation of wormy micellar solutions. Langmuir. 2000;16(11):4761–4765. [Google Scholar]
- 28.Kim WJ, Yang SM. Effects of sodium salicylate on the microstructure of an aqueous micellar solution and its rheological responses. J Colloid Interface Sci. 2000;232(2):225–234. doi: 10.1006/jcis.2000.7207. [DOI] [PubMed] [Google Scholar]
- 29.Ouchi M, Takahashi T, Shirakashi M. Shear-induced structure change and flow-instability in start-up Couette flow of aqueous wormlike micelle solution. J Rheol. 2006;50(3):341–352. [Google Scholar]
- 30.Vasudevan M, Shen AQ, Khomani B, Sureshkumar R. Self-similar shear thickening behavior in CTAB/NaSal surfactant solutions. J Rheol. 2008;52(2):527–550. [Google Scholar]
- 31.Vasudevan M, et al. Irreversible nanogel formation in surfactant solutions by microporous flow. Nat Mater. 2010;9(5):436–441. doi: 10.1038/nmat2724. [DOI] [PubMed] [Google Scholar]
- 32.Dubash N, Cardiel J, Cheung P, Shen AQ. A stable flow-induced structured phase in wormlike micellar solutions. Soft Matter. 2011;7(3):876–879. doi: 10.1073/pnas.1215353110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ezrahi S, Tuval E, Aserin A. Properties, main applications and perspectives of worm micelles. Adv Colloid Interface Sci. 2006;128–130:77–102. doi: 10.1016/j.cis.2006.11.017. [DOI] [PubMed] [Google Scholar]
- 34.Lu DL, Cardiel J, Cao GZ, Shen AQ. Nanoporous scaffold with immobilized enzymes during flow-induced gelation for sensitive H2O2 biosensing. Adv Mater. 2010;22(25):2809–2813. doi: 10.1002/adma.201000189. [DOI] [PubMed] [Google Scholar]
- 35.Yang J. Viscoelastic wormlike micelles and their applications. Curr Opin Colloid Interface Sci. 2002;7(5–6):276–281. [Google Scholar]
- 36.Rehage H, Hoffmann H. Rheological properties of viscoelastic surfactant systems. J Phys Chem. 1988;92(16):4712–4719. [Google Scholar]
- 37.Frounfelker BD, Kalur GC, Cipriano BH, Danino D, Raghavan SR. Persistence of birefringence in sheared solutions of wormlike micelles. Langmuir. 2009;25(1):167–172. doi: 10.1021/la8029374. [DOI] [PubMed] [Google Scholar]
- 38.Cheung P, Dubash N, Shen AQ. Local micelle concentration fluctuations in microfluidic flows and its relation to a flow-induced structured phase (FISP) Soft Matter. 2012;8(7):2304–2309. [Google Scholar]
- 39.Wang Z, Larson RG. Molecular dynamics simulations of threadlike cetyltrimethylammonium chloride micelles: Effects of sodium chloride and sodium salicylate salts. J Phys Chem B. 2009;113(42):13697–13710. doi: 10.1021/jp901576e. [DOI] [PubMed] [Google Scholar]
- 40.Mohanty S, Davis HT, McCormick AV. Complementary use of simulations and free energy models for CTAB/NaSal systems. Langmuir. 2001;17(22):7160–7171. [Google Scholar]
- 41.Olsson U, Soderman O, Gudringt P. Characterization of micellar aggregates in viscoelastic surfactant solutions: A nuclear magnetic resonance and light scattering study. J Phys Chem. 1986;90(21):5223–5232. [Google Scholar]
- 42.Takahashi T, Sakata D. Flow-Induced structure change of CTAB/NaSal aqueous solutions in step-planar elongation flow. J Rheol. 2011;55(2):225–240. [Google Scholar]
- 43.Moss GR, Rothstein JP. Flow of wormlike micelle solutions through a periodic array of cylinders. J Nonnewton Fluid Mech. 2010;165(1–2):1505–1515. [Google Scholar]
- 44.Turner MS, Cates ME. Flow-induced phase transitions in rod-like micelles. J Phys Condens Matter. 1992;4(14):3719–3741. [Google Scholar]
- 45.Drye TJ, Cates ME. Living networks: The role of cross-links in entangle surfactant solutions. J Chem Phys. 1992;96(2):1367–1375. [Google Scholar]
- 46.Helfand E, Fredrickson GH. Large fluctuations in polymer solutions under shear. Phys Rev Lett. 1989;62(21):2468–2471. doi: 10.1103/PhysRevLett.62.2468. [DOI] [PubMed] [Google Scholar]
- 47.Yamamoto S, Hyodo SJ. Mesoscopic simulation of the crossing dynamics at an entanglement point of surfactant threadlike micelles. J Chem Phys. 2005;122(20):204907(1)–204907(8). doi: 10.1063/1.1914767. [DOI] [PubMed] [Google Scholar]
- 48.Li XB, Lin ZC, Cai J, Scriven LE, Davis HT. Polymer-induced microstructural transitions in surfactant solutions. J Phys Chem. 1995;99(27):10865–10878. [Google Scholar]
- 49.Graessle WW. Molecular theories for entangled linear, branched and network polymer systems. Adv Polym Sci. 1982;47:67–117. [Google Scholar]
- 50.Galvan-Miyoshi J, Delgado J, Castillo R. Diffusing wave spectroscopy in Maxwellian fluids. Eur Phys J E Soft Matter. 2008;26(4):369–377. doi: 10.1140/epje/i2007-10335-8. [DOI] [PubMed] [Google Scholar]
- 51.Shikata T, Hirata H, Kotaka T. Micelle formation of detergent molecules in aqueous media. 3. Viscoelastic properties of aqueous cetyltrimethylammonium bromide-salicylic acid solutions. Langmuir. 1989;5(2):398–405. [Google Scholar]
- 52.Rouse PE. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J Chem Phys. 1953;21(7):1272–1280. [Google Scholar]
- 53.Zimm BH. Dynamics of polymer molecules in dilute solution: Viscoelasticity, flow birefringence and dielectric loss. J Chem Phys. 1956;24(2):269–278. [Google Scholar]
- 54.Mason TG. Estimating the viscoelastic moduli of complex fluids using the generalized Stokes-Einstein equation. Rheologica Acta. 2000;39(4):371–378. [Google Scholar]
- 55.Squires TM, Manson TG. Fluid mechanics of microrheology. Annu Rev Fluid Mech. 2010;42:413–438. [Google Scholar]
- 56.Turner MS, Cates ME. Linear viscoelasticity of living polymers: A quantitative probe of chemical relaxation times. Langmuir. 1991;7(8):1590–1594. [Google Scholar]
- 57.Granek R, Cates ME. Stress relaxation in living polymers: Results from a Poisson renewal model. J Chem Phys. 1992;96(6):4758–4767. [Google Scholar]
- 58.Kern F, Lemarechal P, Candau SJ, Cates ME. Rheological properties of semi-dilute and concentrated aqueous solutions of cetyltrimethylammonium bromide in the presence of potassium bromide. Langmuir. 1992;8(2):437–440. [Google Scholar]
- 59.Berret JF, Appell J, Porte G. Linear rheology of entangled wormlike micelles. Langmuir. 1993;9(11):2851–2854. [Google Scholar]
- 60.Buchanan M, Atakhorrami M, Palierne JF, MacKintosh FC, Schmidt CF. High-frequency microrheology of wormlike micelles. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72:011504(1)–011504(9). doi: 10.1103/PhysRevE.72.011504. [DOI] [PubMed] [Google Scholar]
- 61.Imae T, Kohsaka T. Size and electrophoretic mobility of tetradecyltrimethylammonium salicylate (C14TASal) micelles in aqueous media. J Phys Chem. 1992;96(24):10030–10035. [Google Scholar]
- 62.Shikata T, Pearson DS. Phase transitions in entanglement networks of wormlike micelles. Langmuir. 1994;10(11):4027–4030. [Google Scholar]
- 63.Doi M, Edwards SF. The Theory of Polymer Dynamics. Oxford: Oxford Univ Press; 1986. [Google Scholar]