Disorder guides protein function

Cellular function requires biomolecules to undergo dynamic transitions that include folding, conformational rearrangements, and large-scale assembly. The result is a highly interdependent network of processes that is maintained by a balance of thermodynamic and kinetic factors. In molecular machines, each constituent biopolymer (i.e., a chain of residues) first folds to a low-energy configuration/ensemble. These ordered polymers can then assemble into sophisticated architectures, which undergo conformational transitions during function. In contrast to the dynamics of macroscopic machines, molecular-level processes are stochastic, where the molecular interactions that ensure structural integrity are weak (i.e., on the scale of energetic fluctuations from solvent). In this dynamic environment, biomolecules constantly fluctuate (1), and the extent of disorder is heterogeneous between residues. Inspired by this, in 2003, Miyashita et al. postulated that biomolecules may exploit disorder to accelerate functional kinetics (2). In their theoretical investigation of protein function, the authors found large levels of strain energy accumulate in isolated residues. The predicted level of strain exceeded the stability of most proteins under cellular conditions, suggesting that these highly-strained regions may locally unfold, or “crack.” By cracking, the molecule may gain configurational entropy and thereby reduce the strain-induced barrier (Fig. 1). Subsequently, many theoretical and computational investigations have found evidence of cracking during function. These studies have primarily used simplified models (3), with which millisecond-scale dynamics are computationally accessible. In contrast, simulations with explicit-solvent models are typically limited to nanoseconds, or occasionally microseconds (4, 5). Because cracking and large-scale rearrangements occur on relatively long timescales (microseconds to milliseconds), evidence of cracking with explicit-solvent models has been sparse. In PNAS, Shan et al. (6) report the most definitive evidence of cracking from explicit-solvent simulations, to date. Using a specialized computer, they performed multiple simulations of EGFR kinase in solvent for tens of microseconds and found cracking to spontaneously occur. Although open questions remain about the precise details of cracking properties, Shan et al.’s study highlights how convergent theoretical descriptions of biological dynamics are emerging as explicit-solvent simulations are pushed to longer timescales.

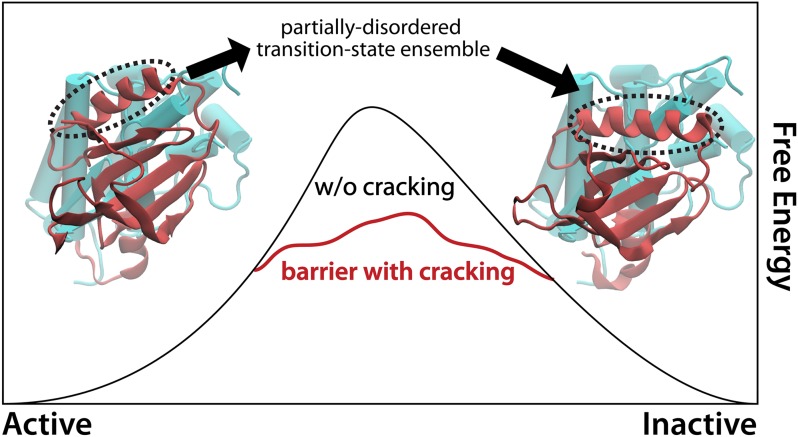
Fig. 1.

Partial unfolding during function, known as cracking (2), was predicted to be a general property that allows proteins to reduce free-energy barriers and accelerate functional kinetics. In EGFR kinase, crystal structures of the active (Left) and inactive (Right) forms might suggest that interconversion can be fully described by simple displacements/rotations. Through the use of many-microsecond molecular dynamics simulations, Shan et al. (6) has directly observed specific residues (circled) partially unfolding and refolding during this transition.

Grounded in the statistical physics of glasses, energy landscape theory (7, 8) provides a framework for understanding the relationship between protein disorder and energetics, at global (folding) and local (cracking) scales. A key finding has been that proteins do not fold along precisely defined pathways, but there is a multitude of routes by which proteins navigate between extended (unfolded) and compact (folded/native) ensembles. The theory further predicts that folding energetics are dominated by the interactions formed in the folded configuration, which has allowed for extensive application of simplified “structure-based” models for folding (3). Although folding of individual domains can often be described as a pseudo first-order phase transition (9), the process is not perfectly cooperative. Many residues cooperatively organize, although some atoms remain free to undergo separate order-disorder events. Simplified models demonstrated this point (10), which was later corroborated by long-timescale simulations from Shaw et al. (11). This intuitive finding is one example of how longer-timescale explicit-solvent simulations are reinforcing predictions from simple models, in this case suggesting a propensity for localized disorder that is separable from full folding transitions.

Simplified models built on energy landscape principles have repeatedly implicated cracking during function. Structure-based models approximate the landscape by a few dominant basins of attraction, each corresponding to an experimentally determined configuration. In doing so, the models use knowledge of these low-energy configurations to provide a first-pass description of the potential energy surface. These models carry the added bonus of being computationally inexpensive, enabling long-timescale simulations to be obtained, even for large assemblies (3, 12, 13). One may then identify statistically significant correlations between cracking and free-energy barriers, as demonstrated for the proteins calmodulin (14), kinesin (15), and adenylate kinase (16), among others. Despite mounting evidence for cracking, it has remained unknown whether cracking would also be predicted by long-timescale explicit-solvent simulations.

Short simulations (nanoseconds) with explicit-solvent models are frequently used to argue that protein functional rearrangements are governed solely by loose “hinge” regions, and not cracking (17). Explicit-solvent simulations may be viewed as the philosophical opposite of energy landscape theory-inspired models. That is, conventional explicit-solvent simulations use a transferable set of parameters, where only the sequence composition of the protein and the initial configuration are provided as input. The global features of the landscape are not assumed a priori, and occasionally the native configuration is not the global energetic minimum (4). The assumption when using these models is that the parameters are accurately calibrated, such that simulation may be considered to be a “computational microscope” (18). In principle, it should be possible to construct a general model that includes all relevant energetic interactions. However, including more detail comes with a price, limiting many simulations to tens of nanoseconds (17), or a few microseconds (4). Although computational capacity continues to increase (19), reversible order-disorder transitions and large-scale conformational rearrangements occur on multimicrosecond (or greater) timescales. Sampling limitations are exacerbated by the fact that functional rearrangements and cracking are stochastic, making their relationship statistical. Thus, the computational demand to quantitatively study cracking is orders of magnitude beyond most available resources.

Unsatisfied with the limited timescales of explicit-solvent simulations, the Shaw group developed a specialized massively parallel machine, called Anton. Now, they can produce over ten microseconds of simulated time, per day (20). This ∼100-fold increase in computing speed was largely enabled by designing a processor tailored to molecular dynamics calculations. Rather than use general-purpose compute cores, the team designed unique hardware that optimizes per-core performance, data management and load balancing of molecular dynamics simulations (20). Standard CPUs are versatile, but they only perform several operations per cycle. The Anton chip forfeits flexibility by hardwiring the arithmetic pipelines, which enables over 1,000 operations per cycle. Shaw et al. demonstrated the incredible power of this approach by performing the first millisecond

The Shan et al. study signifies a turning point in the discussion of cracking and the relationship between explicit-solvent and structure-based models.

explicit-solvent simulation (11), and by folding many small proteins in solvent (21). One remarkable aspect of their simulations has been that the dynamics of small protein folding are qualitatively and quantitatively similar between explicit-solvent models and structure-based approaches. Specifically, the same coordinates capture the underlying barriers and both classes of models yield consistent descriptions of folding thermodynamics.

The Shaw team has now taken aim at protein function, and in the PNAS paper by Shan et al. they report explicit-solvent simulations of EGFR kinase, in which spontaneous large-scale conformational rearrangements occurred (6). With simulations that extend to tens of microseconds, they found that the conformational process is not fully accounted for by a hinge-like description. Rather, the molecule adopts intermediate configurations that appear to be stabilized by disorder in isolated regions (Fig. 1), fully consistent with the cracking paradigm. In the context of nearly a decade of debate, this study stands out as the most clear identification of cracking in explicit-solvent simulations.

The Shan et al. (6) study signifies a turning point in the discussion of cracking and the relationship between explicit-solvent and structure-based models. It is now clear that cracking is predicted by both classes of models, although we must elucidate its extent in different proteins and its precise impact on free-energy barriers. Additionally, the structural character of cracking needs to be further clarified. For example, are there different modes of cracking (e.g., backbone vs. side-chain reorganization)? If so, is there a correlation between a protein’s biological function and the type of cracking used? As we forge forward with these questions, complementary perspectives provided by an array of models will help solidify our understanding of the mechanistic and energetic factors that govern biological dynamics.