3D phenotyping and quantitative trait locus mapping identify core regions of the rice genome controlling root architecture

Significance

Improving the efficiency of root systems should result in crop varieties with better yields, requiring fewer chemical inputs, and that can grow in harsher environments. Little is known about the genetic factors that condition root growth because of roots’ complex shapes, the opacity of soil, and environmental influences. We designed a 3D root imaging and analysis platform and used it to identify regions of the rice genome that control several different aspects of root system growth. The results of this study should inform future efforts to enhance root architecture for agricultural benefit.

Abstract

Identification of genes that control root system architecture in crop plants requires innovations that enable high-throughput and accurate measurements of root system architecture through time. We demonstrate the ability of a semiautomated 3D in vivo imaging and digital phenotyping pipeline to interrogate the quantitative genetic basis of root system growth in a rice biparental mapping population, Bala × Azucena. We phenotyped >1,400 3D root models and >57,000 2D images for a suite of 25 traits that quantified the distribution, shape, extent of exploration, and the intrinsic size of root networks at days 12, 14, and 16 of growth in a gellan gum medium. From these data we identified 89 quantitative trait loci, some of which correspond to those found previously in soil-grown plants, and provide evidence for genetic tradeoffs in root growth allocations, such as between the extent and thoroughness of exploration. We also developed a multivariate method for generating and mapping central root architecture phenotypes and used it to identify five major quantitative trait loci (r² = 24–37%), two of which were not identified by our univariate analysis. Our imaging and analytical platform provides a means to identify genes with high potential for improving root traits and agronomic qualities of crops.

Root systems are high-value targets for crop improvement because of their potential to boost or stabilize yields in saline, dry, and acid soils, improve disease resistance, and reduce the need for unsustainable fertilizers (1–7). Root system architecture (RSA) describes the spatial organization of root systems, which is critical for root function in challenging environments (1–10). Modern genomics could allow us to leverage both natural and engineered variation to breed more efficient crops, but the lack of parallel advances in plant phenomics is widely considered to be a primary hindrance to developing “next-generation” agriculture (3, 11, 12). Root imaging and analysis have been particularly intractable: Decades of phenotyping efforts have failed to identify genes controlling quantitative RSA traits in crop species. Several factors confound RSA gene identification, including polygenic inheritance of root traits, soil opacity, and a complex 3D morphology that can be influenced heavily by the environment. Most phenotyping efforts have relied on small numbers of basic measurements to extrapolate system-wide traits. For example, given the length and mass of a few sample roots and the excavated root system mass, one can estimate the total root length, volume, and average root width of the entire root system (13, 14). Other common measurements involve measuring the root surface exposed on a soil core or pressed against a transparent surface to estimate root coverage at a certain soil horizon. In these cases, the choices of sample roots and phenotyping standards, the size and shape of the container, and the limitations of 2D descriptions of 3D structure are sources of bias. Methods to image the unimpeded growth of entire root systems in 3D could circumvent these problems (15–19). Live 3D imaging can capture complete spatial and developmental aspects of RSA and results in value-added digital data that can be phenotyped repeatedly for any number of traits. To date, such efforts have been limited by a throughput insufficient for quantitative genetic studies.

Here we describe the use of a 3D imaging and phenotyping system to reveal the genetic basis of root architecture. The integrated system leverages prior advances in the areas of hardware, imaging, software, and analysis (17, 20–22). We combined these methods into a semiautomated pipeline to reconstruct and phenotype a well-studied rice mapping population on days 12, 14, and 16 after planting in gellan gum medium. We identified 89 quantitative trait loci (QTLs) at 13 clusters among 25 RSA traits. Several clusters correspond to QTLs previously identified under field and greenhouse conditions; others do not. Apparent tradeoffs at some clusters are consistent with genetic limitations on “ideal” RSA phenotypes. We also used a multivariate-composite QTL approach to extract central RSA phenotypes and identify five large effect QTLs (r² = 24–37%) that control multiple root traits.

Results

Development of a Semiautomated Root Imaging and Analysis Pipeline.

To achieve the throughput necessary to phenotype a mapping population digitally in 3D, we combined three previously published computational advances into a semiautomated pipeline. The three methods we combined are (i) a method to use 2D rotational image series to estimate root traits (20); (ii) GiA Roots, a standalone, graphical user interface-based, freely distributed software with enhanced semiautomated image processing and 2D analysis features (22); and (iii) an implementation of an algorithm that generates 3D reconstructions from rotational image series taken in optical correction tanks (17) as described in Zheng et al. (21). For this study, we constructed a platform with dual imaging setups on a massive table designed to reduce vibrations and maintain the precise calibration necessary for fully automated 3D reconstructions (the basic design is described in ref. 23). We also incorporated a barcoded naming scheme and scanners to enable seamless entry into the computational portion of our pipeline. This part tied together the image processing steps, reconstructions, trait estimations, and quality control steps into a semiautomated series of batch processes, centered on the command line version of GiA Roots.

The pipeline provides physically scaled estimates of 25 RSA traits as output for each sample (Table S1). These traits were designed to describe root network geometries in four ways: (i) the distribution of roots relative to one another and to the soil horizon, (ii) the overall shape of the network, (iii) the extent of that shape, and (iv) the size of the intrinsic network, including approximations of the amount of root–soil interface as well as biomass (Table S1). These traits distinguish features of root systems and complement one another in important ways. For example, a large convex hull value indicates a greater extent of exploration of the soil environment. By also quantifying the relative shape of the convex hull using the width:depth ratio (WDR), we can know if the roots are exploring relatively shallow or deep soil horizons. When we include the size of the intrinsic network (for example the surface area), we get an additional measure of how the root biomass is distributed within the network shape, i.e., are the roots ranging widely and deeply with large gaps between them (low solidity), or are they growing densely together and thoroughly exploring the space (high solidity).

It is important to note that, to describe and differentiate complex morphologies such as root systems, 3D data must be projected into a lower-dimensional “trait space.” Some traits may describe similar aspects of root shape, whereas others may be mathematically interrelated. We do not yet know which traits represent elemental aspects of root growth [known as “phenes” (24)]. Although simpler shapes such as Arabidopsis seeds have been narrowed down to just few phenes (25), our current limited understanding of the genetic, spatial, and functional aspects of root architecture precludes us from knowing the appropriate number of phenes to expect for RSA.

Quantitative Comparisons with a Ground Truth Model Validate Phenotyping Methods.

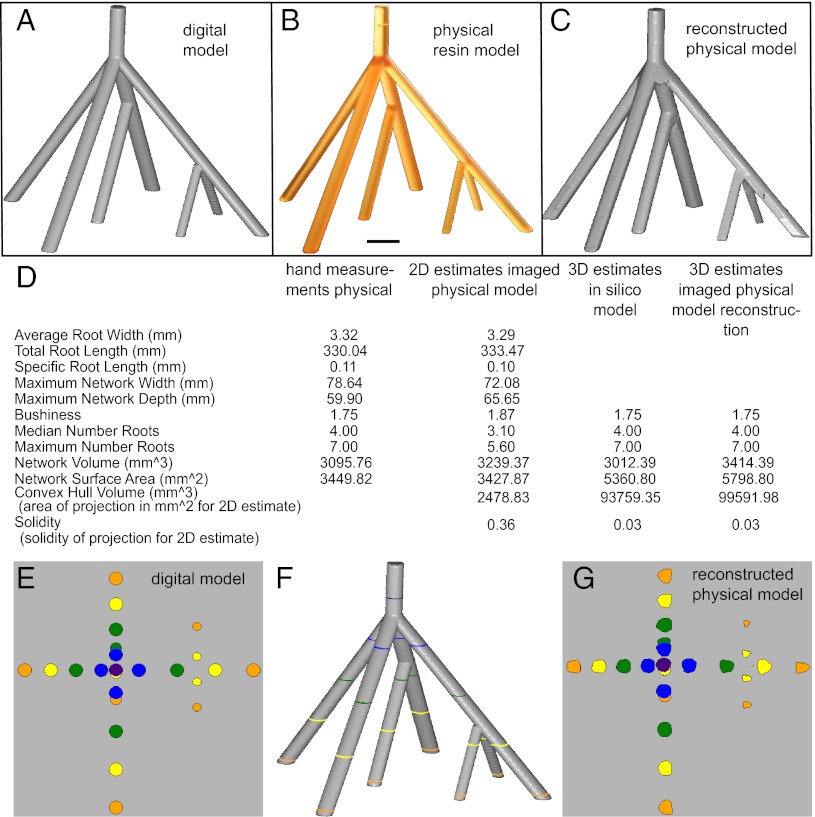
Of the 25 RSA traits, 18 were estimates generated from the average values of the 2D projections in the rotational image series (“2D traits”) using the GiA Roots program, and seven were estimated directly from the 3D reconstructions themselves (“3D traits”) using a set of algorithms developed within the pipeline (Table S1). We previously showed that some 2D RSA estimates could represent a simple 3D root-object accurately using rotational image series (20). However, some 3D shapes, such as the volume of nonconvex shapes, cannot be estimated accurately from 2D projections, particularly from complex root systems. An important piece of the root phenotyping puzzle will be to determine which traits can be measured accurately using estimates derived from 2D data and which require 3D representations (e.g., refs. 17, 26, and 27). To validate the accuracy of our 2D and 3D trait estimations and reconstruction method, we developed a ground truth model. This model was designed in silico to approximate a simple 3D root network for which the precise parameters are known. A physical model then was printed in 3D from resin, imaged, and reconstructed (Fig. 1 A–C; and Methods). The in silico and resin models were highly similar, although the 3D reconstruction of the resin model had a less regular, more flattened, and slightly larger surface area than the in silico model (Fig. 1 E–G). To quantify differences between them, we phenotyped the resin model and compared 2D and 3D trait estimations with those of the in silico model (Fig. 1D). Several important traits, such as total root length, specific root length, and surface area, were modeled with remarkable accuracy using 2D estimates (for our relatively simple model), whereas estimates of root branching frequency were superior in 3D (Fig. 1D). In general, occlusions in 2D images caused by crossing roots will increase with the complexity of the root system and consequently will reduce the accuracy of many 2D estimates, particularly for traits in the network distribution category. We show that 3D estimates can avoid this type of bias but can be biased for other parameters, such as surface area, because the voxelization of image reconstructions imperfectly reflects the smooth surface of a root. Such problems point toward the need for improved algorithms for estimating root traits in 3D (Fig. 1D). Our validations suggest that with our present system, a combination of 2D and 3D traits is the most appropriate approach to identify the genes controlling RSA.

Fig. 1.

(A–C) Ground truth validations of 2D and 3D trait estimations. Images of a digital model (A), a physical resin model (B), and a reconstructed physical model (C). (D) Comparisons of 2D (column 3) and 3D (column 5) trait values from the imaged and reconstructed physical model with hand measurements (column 2) made on the physical model and with estimates of the in silico digital model used to print the physical model (column 4). Note that the 2D convex hull and solidity values are based on 3D projections from rotational image series and thus are under- and overestimated, respectively. (E–G) Horizontal 2D slices of digital (E) or reconstructed (G) models, color-coded by 50-voxel intervals shown in F, illustrate slight irregularities in 3D model reconstruction. (Scale bar in B: 10 mm.)

Comprehensive Digital Phenotyping of a Recombinant Inbred Line Population Reveals Genetic Correlations and Growth Patterns of RSA in Rice.

We applied our integrated phenotyping pipeline to an established rice F6 recombinant inbred line (RIL) population (28). This population, derived from the parental cross Bala × Azucena, has been used to identify a number of root-trait QTLs under conditions ranging from drought stress in the field to various stresses in the greenhouse or under hydroponic conditions and in plants ranging in age from 24 d to maturity (summarized in ref. 29). Thus, RSA traits and QTLs mapped using our 3D system potentially could be correlated with RSA QTLs for established field traits under various stresses.

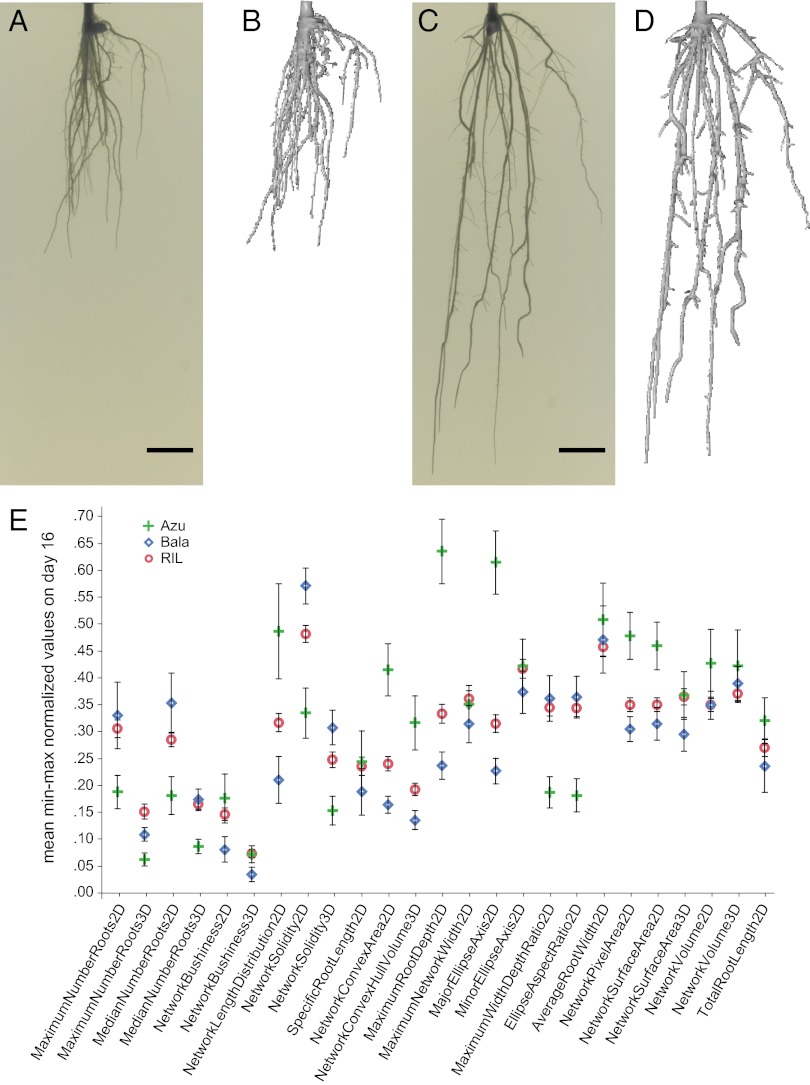
Parental and 171 RILs were imaged at days 12, 14, and 16 postplanting, and ∼1,400 3D models and 2D image sets representing 488 individuals were phenotyped using our semiautomated procedure (Methods, Fig. 2 A–D, and Movies S1 and S2). User involvement was restricted to initial setup; all computations of traits were completely automated. Average RIL values fell between the parents for most traits (Fig. 2E), and root distribution values corresponded to values reported in previous studies of Bala and Azucena in sand and soil (SI Text) (28, 30, 31). In general, Azucena root systems were larger than Bala, both in the extent to which they explored the growth substrate (depth and convex hull) and in their network size parameters (surface area, volume, total root length) (Fig. 2E). In contrast, the Bala architecture is more solid, indicating a more thorough coverage of a limited volume of growth substrate.

Fig. 2.

RSA of rice RILs and parental lines grown in nutrient-enriched gellan gum. Images are from day 16. (A–D) Bala (A) and Azucena (C) raw 2D rotational series images and respective 3D reconstructions (B and D). Movies S1 and S2 convey 3D views. (E) Mean minimum–maximum normalized values of RSA traits in parental and recombinant inbred lines on day 16 are shown. Error bars indicate 95% confidence intervals. (Scale bars in A and C: 10 mm.)

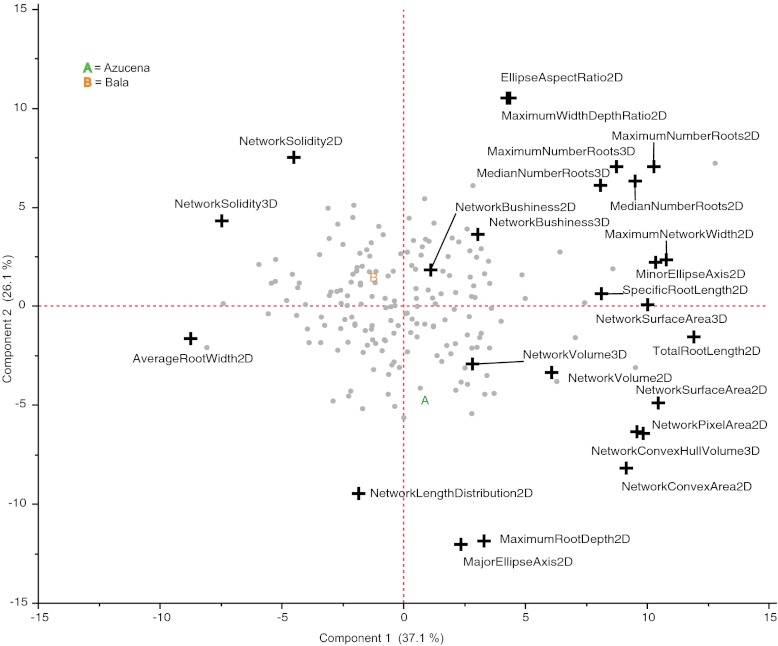
In our Bala × Azucena RIL population, the correlation between two traits can be estimated across all individuals. This phenotypic correlation is the result of correlated influences of environmental factors acting on each plant as well as correlated genetic influences quantified by the correlation of genetic means between traits. In RIL populations, this genetic correlation results from the pleiotropic action of genes on several traits as well as linkage disequilibrium among tightly linked polymorphic loci (32). To provide insight into the genetic structure underlying RSA in the Bala × Azucena mapping population, we generated a correlation matrix from the genetic means of each RIL on day 16 for all 25 traits (Methods and Dataset S1), which we used in a principal component analysis (PCA) (Fig. 3, Fig. S1, and Dataset S1). Two components comprise the majority of genetic trait variation in this population (63%), and no other component comprises more than 13.4%, indicating substantial genetic correlations among these traits. There remains the potential to identify drivers of root growth by comparing the changing correlations among a set of traits for different genotypes, time points, and environmental conditions. In this population, we found that many of the traits with both 2D and 3D analogs had strong correlations, such as network surface area (correlation coefficient = 0.85, P value <. 0001), supporting the fact that these are similar measures. For the solidity 2D ratio (network pixel area 2D/network convex area 2D), the correlation between pixel area (the numerator) and solidity was moderately negative (−0.32, P < 0.0001), indicating, counter intuitively, that increases in root surface area could result in reduced solidities. These data and the strong correlation between pixel area and convex area (0.84, P < 0.0001) suggest that new growth tended to be allocated to expanding the volume of soil exploration rather than filling in the existing volume. The two main components of variation derived by the PCA illustrate many of these complex relationships (Fig. 3). Thus, the genetic structure underlying RSA traits, including whether pleiotropy or tightly linked genes drive various aspects of root growth, cannot be inferred directly from their mathematical relationships but instead will require the identification of the causal genetic elements.

Fig. 3.

PCA on root trait correlations in the RIL and parental lines. Gray dots represent the genetic means of each RIL family; “A” (Azucena) and “B” (Bala) are the parental family means. Crosses indicate the loadings for each trait along the first two components, which comprise 63% of the total genetic variation for all 25 traits. Full PCA statistics are reported in Fig. S1.

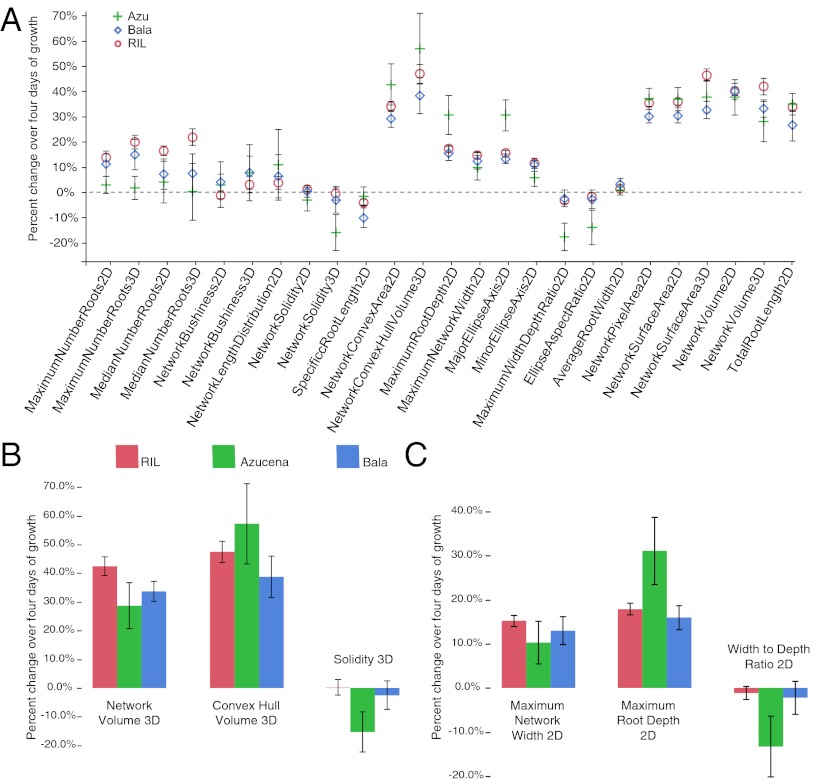
Our noninvasive approach also allowed us to quantify the rates of change for each trait over the 4-d period between days 12 and 16 (Fig. 4 and Table S2). Most plants grew rapidly during this time; for example, the average rate of root elongation for the RIL population was 42.9 mm/d (corresponding to a 8.6%/d increase) (Fig. 4A and Table S2). Remarkably, Bala maintained a consistent 3D solidity (−2.5%), despite a 38.7% increase in convex volume (average daily change = 9.7%), whereas the solidity value for Azucena dropped precipitously (−15.3%) as its convex volume increased by 57.3% (average daily change = 14.3%) (Fig. 4B). The RILs also appeared constrained in their global growth patterns, because 3D solidity changed only 0.2% over 4 d, despite a 47.5% increase in convex hull volume. Similarly, our shape metrics were consistent over time for Bala [−2.2% WDR and −1.8% ellipse aspect ratio (EAR)] and the RILs (−1.2% WDR and −2.7% EAR), whereas Azucena grew predominantly along vertically oriented axes resulting in sharp decreases for WDR (−13.3%) and EAR (−17.0%) (Fig. 4C). These patterns highlight the juxtaposition between an even, compact form of growth versus one that is rangy and deep. Whether these trends are emergent properties of local growth patterns or in part are controlled globally remains an important open question that we can begin to answer by mapping RSA over time and by developing traits that describe specific growth behavior (33, 34).

Fig. 4.

Trait dynamics during 4 d of growth. (A) Percent changes for all 25 traits were calculated by subtracting average day 12 values from day 16 values and dividing by day 12. (B and C) Differences among RILs, Bala, and Azucena in the rates of change for ratios solidity 3D (C) and width:depth 2D and their constituent traits are shown in greater detail. Error bars represent 95% confidence intervals of the mean. All growth rates are reported in Table S2.

Genetic Architecture and Tradeoffs in Root System Growth Control Are Revealed by QTL Analysis of Multiple Univariate Traits.

Using QTL Cartographer (35), we identified 89 univariate QTLs across all days of imaging (Methods, Fig. 5, and Dataset S2). These QTLs covered a range of estimated effect sizes with 95% of QTLs ranging between 6.9% and 14.2% of genetic variation explained and typically colocalized (Fig. 5). We use the term “clusters” to describe QTLs that mapped to the same or proximal markers where there was not a statistically significant reason to separate them [i.e., their 2-logarithm of odds (LOD) intervals overlapped]. At many clusters, traits for days 12, 14, and 16 stacked together, emphasizing the ability of our approach to detect persistent QTLs despite the rapid growth we observed (Fig. 3). Additionally, several 2D and 3D QTLs for analogous traits colocalized, further validating the accuracy of our combined phenotyping approach (Fig. 5 and Dataset S2).

Fig. 5.

Univariate QTLs controlling RSA in a rice Bala × Azucena F6 mapping population. Linkage groups (chromosomes) generated by the Haldane function with QTL hits are shown with centimorgan positions on the left and the marker name on the right. The width of each box represents 1-LOD range, and whiskers are 2-LOD for each QTL. White boxes are day 12 QTL, gray boxes are day 14 QTL, and black boxes are day 16 QTL. Heat maps were generated based on the overlap of 2-LOD ranges with intensities scaled to the entire genome. Full univariate QTL results are reported in Dataset S2.

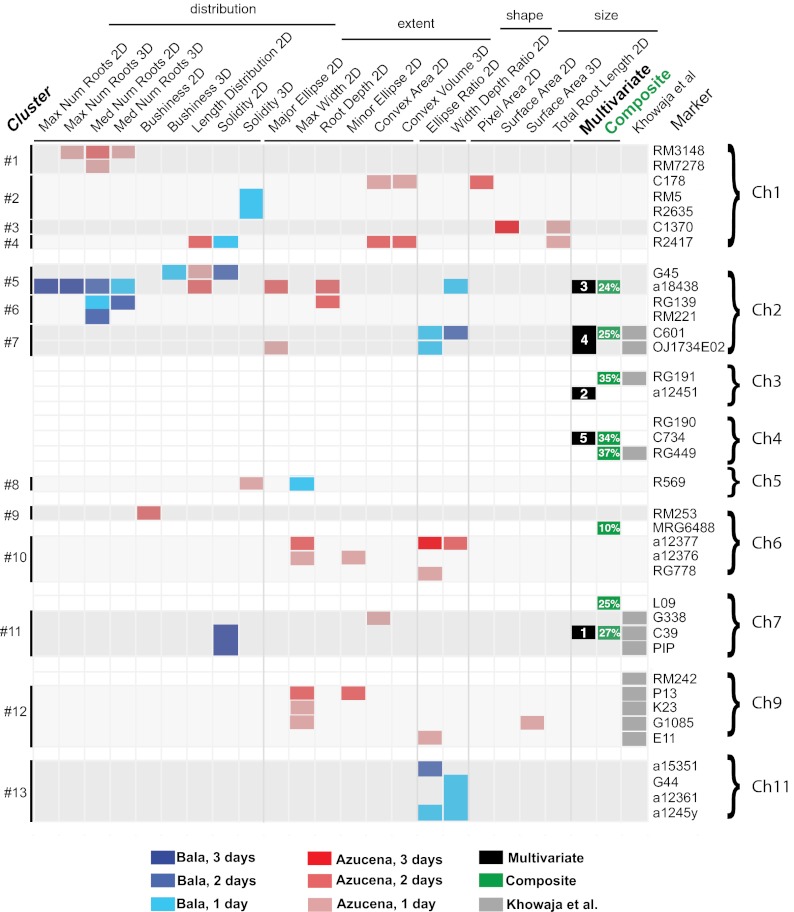
A reanalysis of the large number of QTL results previously generated from this mapping population by Khowaja et al. (29) allowed us to make direct comparisons between our gel-based results and more complex growth environments. Univariate QTL clusters on chromosomes 1, 2, 6, 7, and 9 from our study aligned with hotspots identified by Khowaja et al. for root traits and drought tolerance (Fig. 6), including a QTL at marker C601 that has been used in a breeding program for root improvement (36). These correlations provide strong evidence that RSA QTLs identified in young plants growing in gellan gum can be relevant to agriculture. We also identified a number of clusters (e.g., #1, 2, 5, 10, 13; Fig. 6) containing QTLs for global traits, such as solidity, length distribution, and branching numbers, that by previous phenotyping approaches were either poorly estimated or not possible to measure. Our data demonstrate that a 3D imaging and digital phenotyping approach has the potential to identify genes controlling both known and previously unidentified RSA phenotypes.

Fig. 6.

Genetic landscape of RSA QTL. Blue (Bala) or red (Azucena) color indicates the parent contributing the positive allele. Univariate QTLs on multiple days for the same trait are coded by hue. Columns indicated by darker gray lines separate traits by measurement type. Root trait hotspots identified by Khowaja et al. (29) that colocalize with those identified in this study are shown in gray. Multivariate QTLs are shown in black with significance rank (full results are given in Dataset S3), and the corresponding DFA-derived composite QTLs are shown near them in green, with percentage indicating phenotypic effect size (full results are given in Fig. 8). The composite QTL on chromosome 6 at MRG6488 corresponds to multivariate rank #2 at a18438, and the composite QTL on chromosome 7 at L09 corresponds to multivariate rank #1 at C39. For clarity, only markers associated with QTLs are shown. Clusters are grouped by linearity and proximity on the genetic map.

Examination of QTL clusters revealed the genetic basis of relationships among root traits in unprecedented detail (Fig. 6). For example, length distribution and total root length QTLs were found together in clusters #4 and #5 although their trait values have virtually no correlations and are not intended to describe similar features of RSA (0.10, P < 0.0001). Conversely, WDR and EAR are similar shape descriptors and are almost completely correspondent (0.97, P < 0.0001), but QTLs for these traits colocalize at only three of five loci. These data highlight the fundamental difficulty in identifying the key elements of root architecture a priori.

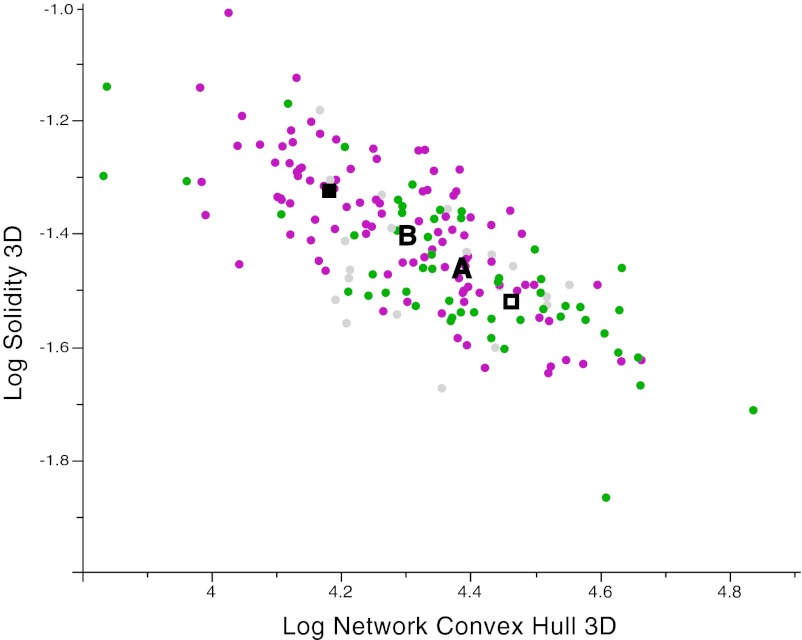
Many of our 25 root traits describe the allocation of biomass in terms of network distribution, extent, and shape, but traits in the intrinsic network size category also can approximate total biomass (e.g., root system volume) (Table S1). For example, a lone cluster (#3) of surface area and root length QTLs suggests that increased biomass could be bred independently of the allocation traits we measured. In contrast, QTLs at cluster #1 controlled biomass allocation as a function of root numbers and distribution but not the overall size of RSA (Fig. 6). Genetic correlations, in this case for biomass allocation traits, may result in genetic tradeoffs when two important phenotypes are negatively correlated because of pleiotropy or tight linkage (37). For example, at cluster #11, six solidity QTLs at which Bala alleles had larger effects colocalized with a convex hull QTL at which the Azucena allele had the larger effect. However, we found no evidence for tightly linked network-size QTLs, suggesting that this locus had no effect on overall root biomass and demonstrating a root allocation tradeoff between thoroughness versus extent of exploration. Comparison of trait covariation in the RIL population confirmed a strong negative genetic correlation (−0.73, P < 0.001) between solidity and convex hull at this locus (Fig. 7). Similar evidence for allocation tradeoffs was observed at clusters #5, 6, 7, and 8 for rooting depth, distribution, and shape (Fig. 6). These observations highlight additional obstacles to breeding functionally advantageous RSAs for different soil and moisture conditions. Nonetheless, the large number of QTLs we identified suggests that in large part, targeted breeding for multiple traits (such as a large and highly branched RSA) can reassemble complex trait variation in desired combinations to serve agronomic goals.

Fig. 7.

Genetic tradeoff for root biomass allocation between thorough and extensive soil exploration at QTL cluster #11. Thoroughness is measured in terms of the solidity (y-axis), and extensiveness is measured in terms of convex hull volume (x-axis). Logarithm-transformed genetic means of each RIL family with either the Azucena (green circles) or Bala allele (magenta circles) at marker C39 (chromosome 7). Gray circles indicate missing marker data. Allele means for Azucena (“A”) or Bala (“B”’) illustrate a genetic tradeoff between these phenotypes. Aggregate maximum allele values at all five multivariate QTL markers for solidity (filled square) or convex hull (open square) are shown.

Multivariate QTL Analysis Identifies Regions Central to RSA Growth Control.

Our PCA (Fig. 3) and examination of QTL clusters (Fig. 6) revealed a complex architecture controlling the root traits identified by our phenotyping algorithms. To identify regions in the genome that have the greatest influence on RSA, we took a multivariate approach, following the multivariate least squares interval mapping (MLSIM) procedure (38). MLSIM can probe the multivariate space of any number of traits and identify pleiotropic or linked QTLs causing correlations among multiple traits. This approach applies multivariate analysis of variance (MANOVA) at many points across the linkage map, with permutation tests to infer genome-wide levels of statistical significance for all traits simultaneously, controlling for multiple tests. This permutation procedure does not assume multivariate normality or other parametric trait distributions. In addition, pairwise graphical analyses among traits in this data set showed little evidence of nonlinearity among RIL genotype means.

MLSIM was focused on a subset of nine 2D traits that were spread across the two major principal components of growth and also represented each of the four biological categories (Table S1): depth, maximum width, convex area, WDR, EAR, length distribution, solidity, maximum number of roots, and average root width. These traits correspond to established field traits with QTLs mapped in previous studies (depth, root width, root numbers) and previously unmapped traits (solidity, convex area, WDR, and EAR).

We ran four separate multivariate analyses, examining multivariate QTLs across the time course of our experiment or respectively for day 12, day 14, or day 16 (Methods and Dataset S3). To examine possible epistatic interactions among QTLs, we used MANOVA to test for pairwise interactions among all multivariate QTLs identified by MLSIM. After correcting for multiple tests, no significant epistatic interactions were detected. We focused on five multivariate QTLs that were significant across all days, because of their consistency during this phase of root development (Fig. 6). The most significant (P < 2.88E-05) multivariate QTL at C39 colocalized with the cluster of solidity QTLs at cluster #11 as well as with previously mapped root trait and drought hotspots for plants grown in soil substrates. The third- (a18438; P < 6.89E-04) and fourth- (C601; P < 2.38E-03) ranked QTLs also hit major clusters common to our univariate study and the meta-analysis (29). Surprisingly the second- (a12451; P < 3.46E-04) and fifth- (C734; P < 3.71E-03) ranked QTLs identified regions on chromosomes 2 and 4, respectively, which had no previous univariate QTL support (even at a relaxed alpha = 0.1). Thus, our multivariate approach can identify highly influential QTLs that are not detected by single-trait analyses. The combined allelic effects of all five multivariate QTLs on solidity and convex volume further strengthened the evidence for a genetic tradeoff between these traits (solid and hollow boxes, Fig. 7). Most importantly, we were able to identify genomic regions that control phenotypes at the intersection of multiple root traits, providing a path to genes central to the control of RSA.

Composite Root Architecture Phenotypes Derived from Multivariate QTLs Can Map Large-Effect QTLs Central to RSA Growth Control.

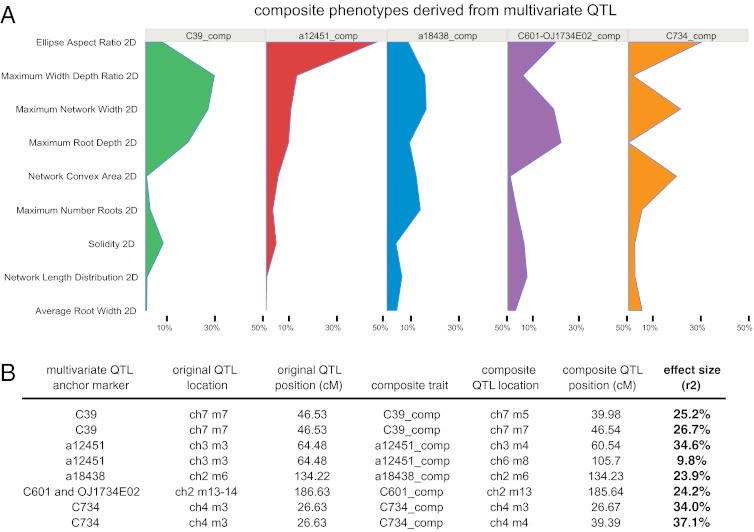
The difficulty in visualizing and interpreting the phenotype and effect size of each multivariate QTL potentially complicates the fine mapping and cloning of genes controlling them. Therefore, we extracted the “composite trait” values from each multivariate QTL using discriminant function analysis (DFA), projected the multivariate phenotypes onto these axes of greatest divergence, and reanalyzed these composite traits by CIM (Methods, Fig. 8, and Table S3). For each multivariate QTL, we used the most significant marker to separate RILs into the two alternative homozygous genotypes. The composite trait represents the axis (combination of phenotypes) where the QTL has strongest effects in the multivariate trait space. Because most traits result from complex combinations of many underlying biological mechanisms (each controlling another trait), the use of DFA composite traits allows us to identify the QTL’s biologically meaningful effects, which we were not able to identify a priori (39, 40). Major effect QTLs (r² = 24–37%, corresponding to differences between homozygotes of 0.68–0.77 genetic SD units) for each composite trait localized to their corresponding multivariate positions as well as to two additional loci (Figs. 6 and 8). Each composite trait was composed of a unique combination of univariate traits that reflect the effects of the underlying gene(s) on RSA. For example, the Bala genotype at the C734 QTL controls an expansive but shallow RSA, whereas the Bala genotype at C601 controls an investment in deep, densely arrayed roots (Fig. 8). Thus, we have developed a general method for extracting composite phenotypes and mapping large-effect QTLs from suites of single traits that alone have small effects. This pattern of large-effect composite traits and small-effect univariate traits is intuitively reasonable, because MANOVA and DFA find the direction with greatest genetic divergence among many correlated traits, whereas a QTL effect on a given trait is an incomplete picture of many pleiotropic aspects of development. This approach appears particularly useful, and may be necessary, to identify the functionally important genes controlling complex morphological traits such as RSA.

Fig. 8.

Multivariate phenotypes and composite QTL analysis. (A) DFA was used to extract the relative contributions of each univariate trait to each multivariate QTL. (B) These data were used to map projected composite phenotypes as univariate QTLs. ch, chromosome; m, marker number on that chromosome.

Discussion

Despite the availability of vast genetic resources, little is known about the genes that contribute to RSA. This knowledge gap exists primarily because of the difficulties in imaging root systems and in identifying relevant quantitative phenotypes from complex topologies (3, 4, 41, 42). Computer simulations supported by empirical field work can suggest ideal root architectures, or ideotypes, that are best suited to a particular environment (10, 43–46). Moreover, root allocation tradeoffs may limit certain RSA combinations, such as between root growth in the topsoil versus deep soil horizons (3, 10, 47, 48), and these tradeoffs may have a genetic basis. Thus, to understand the full architectural possibilities for crop improvement, it is imperative to identify the precise nucleotide polymorphisms that underlie quantitative differences in central RSA traits (49).

We used 3D imaging and digital phenotyping to detect regions of the rice genome that control the growth of RSA. Comparisons of QTL clusters suggest that alleles at several loci influence a tradeoff continuum between extent and thoroughness of root system exploration, which could limit certain architectural combinations. However, they also suggest that quantitative variation in root biomass potentially could be exploited for larger RSA. Our multivariate mapping approach identified five regions of the rice genome that had the most significant impacts on many RSA traits during development. Three of these regions were supported by univariate QTLs, but we also found two other major loci. We showed that all five multivariate QTLs had large effects when mapped as composite traits, making them prime targets for cloning root architecture genes in a crop species. Although it is possible that multiple genes with aggregate effects underlie the multivariate QTLs, they instead may represent single genes controlling central RSA growth processes. We currently are accelerating the gene identification process by combining our imaging and phenotyping system with next-generation sequencing approaches (50, 51).

3D imaging allowed us to interrogate root systems at a global level and thus to expand our analyses beyond what could be traditionally measured by hand or eye. Although 2D systems potentially are cheaper and more accessible to the wider scientific community, mapping genes controlling complex topologies over time may require the precision afforded by 3D imaging. For example, the enormous potential of genomic selection to revolutionize agriculture is grounded in accurate phenotypic predictions tailored to specific environments (52). The current push toward in situ 3D phenotyping (15–19) ultimately will provide a comprehensive view of RSA, because we are able to follow the growth and development of each root through time and space. Furthermore, phenotyping from 3D models will allow direct comparisons of gellan gum and hydroponic data with data from emerging imaging technologies such as X-ray computed tomography and PET-MRI (15, 16, 19, 53), which currently allow analysis of roots in more natural environments at low throughput. Our results also highlight the importance of empirically testing all phenotyping methods to determine their inherent biases (e.g., refs. 17, 27, and 54). The most successful applications of RSA research to agriculture undoubtedly will integrate knowledge gained from a number of complementary approaches (12, 27, 41, 55–57).

Phenotypes and genes identified by any research endeavor eventually will need field-testing. Because of the strong influences of environmental factors on root growth, we see controlled, homogenous conditions as an advantage to identifying genes underlying RSA. Our results support this view, because many univariate and multivariate QTLs that we identified colocalized with previously identified root trait and drought resistance hotspots (29). Incorporating the time domain into future analyses will be another important component of a comprehensive approach to dissecting the genetic basis of RSA. The average RIL root system increased by >42% during 4 d of growth, and many other traits changed at a similar rate (Fig. 4). We found it notable that during this period the solidity and WDRs remained nearly constant in the parental line Bala but dropped dramatically in the parental line Azucena. Genes controlling such architectural trends could be mapped using functions derived from time-course phenotyping data (33, 34). We envision the combination of high-throughput 3D root imaging and multitrait analysis with modern sequencing as a powerful approach to closing the phenotype–genotype gap.

Methods

Growth Conditions.

F6 RIL and parental plants were grown according to Iyer-Pascuzzi et al. (20), except that 0.2% Gelzan (Caisson Laboratory) was used to solidify Yoshida’s nutrient solution. We also pre-germinated surface-sterilized seeds in the dark at 28 °C on plates containing medium identical to that in the cylinders. After 2 d healthy seedlings were transferred to the 2-L sterile glass cylinders. Plants were imaged at days 12, 14, and 16 after transfer. At no point did any root touch the surface of the cylinder and affect 3D structure.

Imaging.

Root systems growing in nutrient-enriched gellan gum were imaged in 360° view by a computer-controlled camera (17, 20). The resulting image sets were uploaded automatically to a server for processing and phenotyping by GiA Roots, a free and extensible software package for the general phenotyping of plant root architecture (www.giaroots.org) (22). An average imaging session lasted 5 min and produced a rotational series of 40 images (9° apart), which were uploaded to a server for processing. Two (43%) or three (39%) replicates were performed for the majority of RILs, although in some cases one (11%), four (5%), or five (1%) replicates were included. Imaging occurred at approximately the same time on each day.

Image Processing.

Images were processed in an automatic phenotyping pipeline centered on GiA Roots (22). Steps consisted of scaling, rotating, and cropping images as a set, creating a greyscale image, and then applying a double adaptive thresholding with preset parameters specific to our imaging conditions to produce binary foreground (root) or background (nonroot) (22). Thresholded image sets were subjected to human quality control using tools built into the pipeline. Rejected images were reprocessed or image sets were removed from the analyses. Because some traits require a skeleton representation of the root network, one further processing step was required to generate medial axis images using an iterative erosion approach. The binary and skeleton images formed the basis for all 2D trait calculations, and pixel values were scaled to millimeters in the appropriate dimension (millimeters, square millimeters, or cubic millimeters; Table S1).

3D Reconstructions.

To reconstruct the 3D shape of RSA from a set of 2D images, we used Rootwork software (21). Rootwork uses harmonic background subtraction to threshold images and preserves the fine detail of root systems using the regularized visual hull (21). We built an adjustable imaging table (23) that allowed us to align the camera and sample to within a few microns, greatly reducing picture-to-picture error in our rotational series and improving the root models.

Trait Calculations.

GiA Roots 2D traits are measurements taken from 2D image series, which are reported as the average values. GiA Roots 3D traits are measurements taken directly from the voxel files of 3D reconstructions via custom algorithms developed as add-ons to the published implementation of GiA Roots via its application programming interface. The technical details of trait computation are presented in Table S1. Our current estimate of the surface area suffers from a jagged, voxelized representation of the smooth shape of the root (Fig. 1D). In the future we plan to improve this estimate by using explicit representations of the root shape, including its surface.

Ground Truth Validation.

The digital model was developed in Python, converted from voxels to a triangular mesh by exporting as “.obj” from Qvox (http://qvox.sourceforge.net), and 3D printed into a physical model made of epoxy resin (FineLine Prototyping). Depth, maximum network width, and the total root length and width of the physical resin model were measured by hand with a set of mechanical calipers. Average root width, specific root length, surface area, and volume were derived from these measurements. 2D and 3D digital estimates of the physical model were obtained by placing the model into the gellan gum, imaging, reconstructing, and running through the GiA Roots phenotyping pipeline. We computed the same 3D estimates for the original digital voxel model to control for artifacts that could be introduced during the imaging and reconstruction process.

Statistical Analyses.

Trait correlations on genetic means and PCA (Fig. S1 and Dataset S1) were performed in JMP Pro-10 (www.jmp.com/software/jmp10/).

Univariate QTL analysis.

QTL analyses was performed in QTL Cartographer [model 6, version 1.16 (35)] with 1,000 permutations for each trait to determine genome-wide significance thresholds at α = 0.05. The initial models were generated by forward and backward stepwise regressions (P = 0.05) with a 2-cM walk speed and a 10-cM window size, including the five default markers as cofactors. We calculated 1.0 and 2.0 LOD confidence limits for each QTL (58).

Multivariate QTL analysis.

Multivariate QTL mapping followed the MLSIM procedure outlined in ref. 38. Briefly, for each point in the genome of each recombinant inbred line, we calculated P_qm, the QTL allele frequency conditional on the flanking marker genotypes. We then used P_qm to predict multivariate phenotypes for each RIL using MANOVA. We determined statistical significance with randomization tests, for which we created 1,000 permuted datasets by randomizing phenotypes relative to genotypes. These genome-wide analyses were repeated sequentially, conditional on the presence of each previously identified QTL, until no further significant QTLs were found.

Identification and confirmation of composite traits defined by multivariate QTLs.

We used DFA to identify traits defined by the observed multivariate QTL. For a specific QTL in the multidimensional trait space, DFA identifies an axis that best separates RIL families by their alleles in that QTL. Each RIL family has a unique projection on the DFA axis, which is defined by a linear combination of all traits used for multivariate QTL mapping. We therefore called this projection a “composite” and treated it as a new univariate trait that maximizes the phenotypic effect of different alleles in this QTL. As a confirmation of the composite trait created by each multivariate QTL, we used QTL Cartographer (as described above) to map the QTL for the composite traits. Colocalization of this new univariate QTL and the previous multivariate QTL supports the validity of our method.