A three-dimensional mathematical and computational model of necrotizing enterocolitis

Abstract

Necrotizing enterocolitis (NEC) is a severe disease that affects the gastrointestinal (GI) tract of premature infants. Different areas of NEC research have often been isolated from one another and progress on the role of the inflammatory response in NEC, on the dynamics of epithelial layer healing, and on the positive effects of breast feeding have not been synthesized to produce a more integrated understanding of the pathogenesis of NEC. We seek to synthesize these areas of research by creating a mathematical model that incorporates the current knowledge on these aspects. Unlike previous models that are based on ordinary differential equations, our mathematical model takes into account not only transient effects but also spatial effects. A system of nonlinear transient partial differential equations is solved numerically using cell-centered finite differences and an explicit Euler method. The model is used to track the evolution of a prescribed initial injured area in the intestinal wall. It is able to produce pathophysiologically realistic results; decreasing the initial severity of the injury in the system and introducing breast feeding to the system both lead to healthier overall simulations, and only a small fraction of epithelial injuries lead to full-blown NEC. In addition, in the model, changing the initial shape of the injured area can significantly alter the overall outcome of a simulation. This finding suggests that taking into account spatial effects may be important in assessing the outcome for a given NEC patient. This model can provide a platform with which to test competing hypotheses regarding pathological mechanisms of inflammation in NEC, suggest experimental approaches by which to clarify pathogenic drivers of NEC, and may be used to derive potential intervention strategies.

1. Introduction

Necrotizing enterocolitis (NEC) is a disease affecting 7-10% of very low birth weight (501-1500g) premature neonates [1, 2] that involves necrosis of the epithelial layer of the gut. NEC is one of the leading causes of surgical emergencies in neonatal intensive care units (NICU) among premature babies [3, 4]. Survivors of NEC often experience sepsis or multisystem organ failure and prolonged NICU stay, leading to increased resource utilization [5]. Long-term consequences include short bowel syndrome, surgical obstructions due to intestinal strictures, and developmental delays due to poor nutritional status. Intestinal immaturity, bacterial invasion of the epithelium, low tissue oxygenation, and an exaggerated inflammatory response are known contributing factors to NEC [6, 7]. Since the relative roles these factors play in the development and course of NEC remain unclear, treatments for NEC are limited to antibiotics and surgery for severe disease and bowel perforation. None of these remedies are specifically targeted at reversing pathogenic drivers except antimicrobials [8]. Yet, there are clear indications that local inflammation, immune vulnerability, and epithelial integrity are all important pathogenic mechanisms in NEC.

Over the past decade, mechanistic computational modeling has been used to gain insights into acute inflammation and associated tissue damage processes in the settings of sepsis and trauma, and has provided initial insights into NEC [9, 10, 11, 12, 13, 14, 15]. We therefore reasoned that a detailed, model-based synthesis of NEC might create an opportunity for improved understanding of the interplay among the mechanisms involved in NEC, suggest an experimental program to test model predictions, and potentially lead to specific, biologically-based interventions in neonates with NEC.

Here we present a model developed for performing such a synthesis. In contrast to another computational model of NEC based on ordinary differential equations [16], this model is a partial differential equation model and takes into account both temporal and spatial effects. Previous agent-based models have also considered spatial and temporal effects [17], but those studies were predominantly focused on the events that initiate NEC, while we have focused on the inflammatory and healing responses that affect the progression of NEC. The three major goals of the paper are to present this original model, show that the model is capable of reproducing physiologically realistic results, and investigate the potential importance of spatial effects such as shape of the injured/inflamed area on the outcome of NEC.

Necrotizing enterocolitis involves a complex interplay between pathogens (e.g. bacteria), the intestinal lining, and the inflammatory response. When the intestinal lining (epithelial layer) is weak, the pathogens in the intestinal lumen can translocate into surrounding regions and instigate an inflammatory response. While the inflammatory response eliminates the pathogens, at the same time it also causes collateral damage to the surrounding tissues. Whether or not full-blown NEC develops depends on multiple factors including the ability of the epithelial layer to heal itself, the speed with which the inflammatory response can eliminate the pathogens, and the severity of the damage caused while the inflammatory response works. Our current model, like most models, is limited in its scope. We consider only the major events that occur during pathogen translocation after an epithelial layer breakdown has occurred and before more severe events such as thrombosis or full thickness necrosis occur. The model can be easily extended to consider factors that may cause the initial epithelial layer breakdown or dynamics that occur after severe NEC has set in (see 3.4).

2. NEC Model

The model we have developed consists of a set of partial differential equations that are solved numerically using finite differences. The equations track concentrations of inflammatory cells, bacteria, and other proteins and molecules involved in the inflammation process. These equations allow us to simulate the dynamics of NEC.

2.1. Intestinal structure and NEC dynamics

The general layered structure of the intestine is shown in Figure 1a. The bacterial density in the lumen of the intestine is typically very high (10³ – 10¹² bacteria/cm³ [18]) and can consist of both commensal and pathogenic bacteria. The epithelial layer that lines the intestine provides a barrier that prevents luminal bacteria from invading the underlying intestinal tissue. If, however, the epithelial layer breaks down and loses integrity, as can occur in NEC, the bacteria can invade the surrounding tissue and instigate an inflammatory response. Our model focuses on the dynamics surrounding bacterial invasion following an epithelial layer breakdown.

Figure 1.

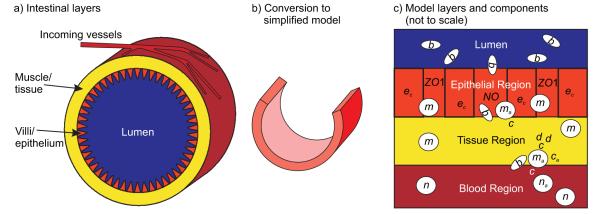
Physical system and model derivation. a) Schematic illustrating the general physiological structure of the intestine. b) To arrive at the simplified computational model, a portion of the intestine is sliced longitudinally and laid out as seen in Figure 3. c) Illustration of the layers used in the simplified model and the model components that typically reside in those layers (see 2.1).

The events occurring during a bacterial invasion are shown in Figure 1c. Bacteria penetrate the epithelial layer through a region of low epithelial integrity and activate resident resting macrophages. Activated macrophages start killing bacteria and produce cytokines and nitric oxide. Pro-inflammatory cytokines activate neutrophils and more macrophages and act on the surrounding tissue to produce tissue damage. Activated neutrophils produce more cytokines and kill bacteria while damaged tissue releases proteins that further activate inflammatory cells. Nitric oxide impairs the appropriate localization of tight junction proteins, thereby inhibiting the ability of the epithelial cells to form a tight barrier. Anti-inflammatory cytokines, produced at a slower rate than the pro-inflammatory cytokines, eventually slow down the inflammatory response. The rate at which the bacteria invade the surrounding tissue, the rate at which the immune system is able to respond, and the effectiveness of the inflammatory response depend on the properties of the inflammatory cells and bacteria, the properties of the layers, and the ability of the epithelial layer to recover in its initial region of low epithelial integrity.

2.2. Motivation for three-dimensional model

While ordinary differential equations have been used to create one-dimensional NEC models [13, 16] that have helped to elucidate certain features of NEC pathogenesis and possible treatment, these studies are limited because they consider only transient effects. The three-dimensional mathematical model for NEC described herein can more closely simulate the actual disease and provides an additional, powerful tool for understanding possible approaches to the problem for the following reasons:

1. The gastrointestinal tract consists of anatomically and functionally distinct compartments, e.g., lumen, epithelium, tissue, and blood (see Figure 1). Relevant model components are present in different locations, e.g., neutrophils normally reside in the blood and move into other compartments only after activation. Therefore, components do not react immediately or at all times. While multi-compartment ordinary differential equation models can serve to simulate such compartmentalization [16], additional dimensions of information may be gained by taking into account delay effects as model components diffuse away from or migrate towards each other.

2. Some of the species involved in the system move in the direction of increasing chemoattractant gradients. For example, the displacement of activated macrophages is related to the spatial gradient of both chemokines/cytokines and bacteria/bacterial products.

3. Different regions of the physical domain have different material properties that affect the component transport, e.g., diffusion in blood can occur faster than diffusion in tissue.

4. Cells interact through extracellular signaling and are connected via tight junctions and gap junctions. The spatial distribution and strength of these junctions affect the permeability of the epithelial layer and the transport of bacteria through this layer [19].

2.3. Model variables, their units, and their interactions

To maintain model simplicity we include only the key players that are directly related to early NEC dynamics while excluding intermediate players in the inflammatory cascade in favor of their downstream products and lumping various players with similar characteristics together. For example, we have grouped all cytokines that promote inflammation (IL-12, IL-18, etc.) into one lumped variable “pro-inflammatory cytokines”.

Because of the use of lumped variables, it is unreasonable to assign specific units to some of the variables. Instead, remaining consistent with [20, 21] (a model upon which the current model is heavily based), the variables are assigned non-specific units such as c_a-units and m_a-units where c_a-units and m_a-units correspond not to a number but to a strength of the corresponding component being represented per cm³ (e.g. strength of c_a per cm³). Only bacteria are given specific units (b-units = 10⁶ bacteria/cm³) in order to maintain consistency with [20, 21].

We list the players and their roles in our model. We have separated the players into those most directly related to the external pathogenic driver, the inflammatory response, and the epithelial barrier.

Pathogenic driver

• b: bacteria - usually initiates the inflammatory cascade in the setting of NEC, which is thought to be strongly associated with lipopolysaccharide (LPS)-producing, Gram-negative bacteria [22, 23].

Inflammatory response

• m: resting macrophage - resting inflammatory cells normally found in the tissue.

• m_a: activated macrophage - activated inflammatory cells. These cells phagocytize bacteria and release pro- and anti-inflammatory cytokines and nitric oxide.

• n: resting neutrophil - resting inflammatory cells normally found in the blood-stream. It is assumed the numbers of these cells in the intestine are constantly replenished by the continual flow of blood through the region. n is therefore set to a constant value, n_b, during simulations and has no affiliated governing equation.

• n_a: activated neutrophil - activated inflammatory cells that move from the blood stream toward the site of infection.

• d: damage/DAMPs - indicates the level of inflammation severity/ tissue damage and corresponds to the levels of damage-associated molecular pattern (DAMP) molecules. These molecules are induced by inflammation in stressed/injured cells and perpetuate inflammation in a feed-forward fashion [15, 24, 25].

• c: pro-inflammatory cytokines - promote the inflammatory response by activating macrophages and neutrophils. This group includes IL-1, IL-6, IL-8, IL-12, IL-18, IFN-γ, TNF-α.

• c_a: exogeneously-derived anti-inflammatory cytokines - inhibit the inflammatory response by slowing down the rates at which immune cells are activated, cytokines and DAMPs are produced, and bacteria are phagocytosed. This group includes TGF-β1, IL-4, and IL-10. For simplicity and clarity of results, we explicitly model only anti-inflammatory cytokine levels that are in excess of normal systemic levels as provided by, for example, maternal breast milk [26] (see 2.6).

Epithelial barrier

• e_c: epithelial cell/layer integrity-indicates the condition/integrity of the epithelial cells that line the intestinal wall and protect the underlying tissue from bacterial invasion.

• NO: nitric oxide - molecule released by activated macrophages and neutrophils; reduces the functional levels of the tight junction protein, ZO1, between epithelial cells [19, 27] and increases corresponding epithelial layer permeability to bacteria.

• ZO1: Zonula occludens-1-tight junction proteins that keep the epithelial cells in the epithelial layer in close apposition and prevent the passage of bacteria into the underlying tissue [19, 27]. ZO1 levels serve as a molecular marker and correlate of overall epithelial layer permeability (see 2.5.3).

We use the list of interactions in Table 1 to model the basic inflammatory cascade. The first eight interactions are slowed down by the anti-inflammatory cytokine c_a by multiplying the reaction rates by a retardation factor R(c_a) defined in equation (2) below. The final interaction is included because production of ZO1 is assumed to be diminished when epithelial cells are dying/losing integrity. Figure 2 illustrates most of these reactions in a diagram that relates the basic inflammatory cascade to the intestinal epithelial barrier.

Table 1.

Interactions for the basic inflammatory cascade.

$m+b\stackrel{k_{mb}}{\to }{m}_a+b$	macrophage activation by bacteria
$m+c\stackrel{k_{mc}}{\to }{m}_a$	macrophage activation by cytokines
$m+d\stackrel{k_{md}}{\to }{m}_a+d$	macrophage activation by DAMPs
$n+c\stackrel{k_{nc}}{\to }{n}_a$	neutrophil activation by cytokines
$n+d\stackrel{k_{nd}}{\to }{n}_a+d$	neutrophil activation by DAMPs
$b+m_a\stackrel{k_{b{m}_a}}{\to }{m}_a$	bacteria destruction by macrophages
$b+n_a\stackrel{k_{b{n}_a}}{\to }{n}_a$	bacteria destruction by neutrophils
$c\stackrel{k_{dc}}{\to }d+c$	cytokine production of damage
$e_c\stackrel{k_p}{\to }2e_c$	proliferation of epithelial cells
$e_c+n_a+b+c\stackrel{k_a}{\to }{n}_a+b+c$	apoptosis of epithelial cells
$e_c\stackrel{k_{Z{e}_c}}{\to }ZO1$	tight junction production
$ZO1+NO\stackrel{k_{ZN}}{\to }NO$	tight junction destruction
$m_a\stackrel{k_{NO{m}_a}}{\to }{m}_a+NO$	macrophage nitric oxide production
$n_a\stackrel{k_{NO{n}_a}}{\to }{n}_a+NO$	neutrophil nitric oxide production
$m_a\stackrel{k_{c{m}_a}}{\to }{m}_a+c$	macrophage production of cytokines
$n_a\stackrel{k_{c{n}_a}}{\to }{n}_a+c$	neutrophil production of cytokines
$\partial e_c∕\partial t\stackrel{k_{Z{e}_{ct}}}{\to }ZO1$	tight junction production/destruction

Figure 2.

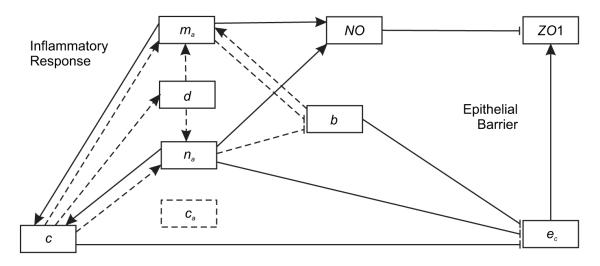
Interactions between the various immune system members and the epithelial layer during an intestinal insult. Members on the left and right side are most directly related to the inflammatory response and epithelial barrier effectiveness, respectively. Dashed lines indicate interactions which are reduced by the presence of anti-inflammatory cytokines. Resting immune cell interactions are not included.

2.4. Partial differential equations

The mathematical model is based on a system of nonlinear transient partial differential equations. In this approach, the concentrations of the components are modeled as continuous functions. Spatial physical processes such as diffusion and chemotaxis (the movement of cells in response to chemical gradients) are modeled by differential operators acting on concentration functions. These operators model physical processes that are not easily modeled by analogous ode models.

The physical domain is three-dimensional consisting of four horizontal regions (Figure 3a). The spatial units in this and other figures are in centimeters. Time is measured in hours. The regions from top to bottom are lumen (blue), epithelial layer (orange), tissue region (two layers in picture, yellow), and circulatory system (red).

Figure 3.

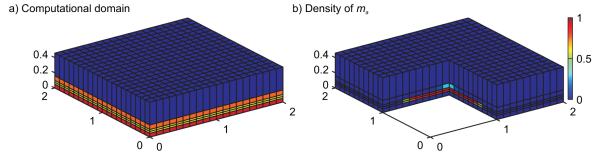
Computational domain and variable representation. a) The computational domain, discretized into a grid of computational cells, is shown. Units are in centimeters. The computational model includes one lumen layer (blue), one epithelial layer (orange), two tissue layers (yellow), and one blood layer (red). b) Simulations track the density of each variable in the computational cells. By cutting away a portion of the computational domain, we can see the macrophage density in the computational cells adjacent to the cut away region.

While the full set of equations, their corresponding parameters, and a description of those parameters can be found in the appendix, we describe here a few of the typical equations used in the model. Many of the terms used in the partial differential equation model were developed in [20, 21].

2.4.1. Bacteria

The partial differential equation for bacteria is given by:

$$\begin{array}{cc}\hfill \frac{\partial b}{\partial t}-\nabla \cdot D_b\nabla b=& k_{\mathit{bg}}b(1-b∕b_{\mathit{max}})-k_{b}b∕(1+b∕∊)\hfill \\ \hfill & -R\left(c_a\right)(k_{{\mathit{bm}}_a}{m}_{a}b+k_{{\mathit{bn}}_a}{n}_{a}b)-k_{\mathit{pp}}b\hfill \end{array}$$ (1)

$$R\left(c_a\right)=\frac{1}{1+k_{{\mathit{Rc}}_a}{(c_a∕{\stackrel{‒}{c}}_a)}^2}$$ (2)

The terms appearing on the right hand side of equation (1) represent, in order, logistic growth of bacteria and elimination of bacteria due to a baseline local immune response (see [21]), activated immune cells, and anti-microbial peptides in breast-milk (see 2.6). A term for bacterial diffusion is included on the left hand side of equation (1). R(c_a) is an anti-inflammatory retardation factor that reduces the severity of the immune response. Here R(c_a) reduces the rate at which activated immune cells eliminate the pathogens.

2.4.2. Macrophages

The partial differential equation for macrophages is given by:

$$\begin{array}{cc}\hfill \frac{\partial m_a}{\partial t}-\nabla & \cdot (D_{m_a}{\nabla }_{m_a}-{\gamma }_{m_{a}c}{m}_a\nabla c-{\gamma }_{m_{a}b}{m}_a\nabla b)\hfill \\ \hfill & =-k_{m_a}{m}_a+R\left(c_a\right)(k_{\mathit{mb}}\mathit{bm}+k_{\mathit{mc}}\mathit{cm}+k_{\mathit{md}}\mathit{dm})\hfill \end{array}$$

Terms on the right hand side include, in order, natural activated macrophage death and macrophage recruitment due to bacteria, pro-inflammatory cytokines, and DAMPs. Recruitment is slowed in the presence of anti-inflammatory cytokines. In addition to allowing activated macrophages to diffuse or wander (▿ (D_ma▿m_a)), macrophages also undergo chemotaxis wherein they travel up gradients of pro-inflammatory cytokines (▿ (m_a▿c)) and bacteria (▿ (m_a▿b)) towards regions of higher pro-inflammatory cytokine and bacterial concentrations.

2.4.3. Pro-inflammatory cytokines

The partial differential equation for pro-inflammatory cytokines is given by:

$$\frac{\partial c}{\partial t}-\nabla \cdot D_c\nabla c=-k_{c}c+R\left(c_a\right)(k_{{\mathit{cm}}_a}{m}_a+k_{{\mathit{cn}}_a}{n}_a)-R\left(c_a\right)(k_{\mathit{nc}}\mathit{cn}+k_{\mathit{mc}}\mathit{cm})$$ (3)

Terms on the right hand side include, in order, pro-inflammatory cytokine decay, production by activated immune cells, and absorption by resting immune cells that become activated. A diffusion term is included on the left hand side. The equations for anti-inflammatory cytokines, nitric oxide, and DAMPs take a similar form.

2.5. Layer modeling

To model the layered structure of the intestine more accurately (Figure 1a), we vary parameter values in the different layers, limit diffusion and chemotaxis between different layers appropriately, and include additional equations for epithelial integrity and ZO1 that are specific to just the epithelial layer.

2.5.1. Layer-dependent parameter values

Some parameters vary depending on which layer is being considered. Resting neutrophils reside only in the blood and thus n is set to n_b there and zero elsewhere. While DAMPs can be produced by both tissue cells and epithelial cells, intestinal epithelial cells tend to be more tolerant to foreign substance; therefore, DAMPs are assumed to be produced only in the tissue and k_dc is set to a constant nonzero value there and zero elsewhere. Resting macrophages reside only in the tissue and epithelial regions, and thus m_max is set to a nonzero constant in those regions and zero elsewhere. Different constant diffusion coefficients are assigned in each layer and are listed in Table 2.

Table 2.

Diffusion parameters

Diffusion Coefficients (cm2/h)	Lumen	Epithelial	Tissue	Blood
Bacteria	6×10−5	5×10−6	3×10−5	4×10−5
Pro-inflammatory Cytokines	2.2×10−5	2.4×10−5	5×10−5	4.8×10−5
Anti-inflammatory Cytokines	2.2×10−5	2.4×10−5	5×10−5	4.8×10−5
Nitric Oxide	2.2×10−5	2.4×10−5	5×10−5	4.8×10−5
Damage/DAMPs	1.2×10−5	5×10−5	5×10−5	2.4×10−5
Activated Macrophages	6×10−6	1×10−5	2.2×10−5	2.4×10−5
Activated Neutrophils	1×10−5	1.5×10−5	6×10−5	8×10−5

2.5.2. Transport into and out of the blood layer

In a healthy state, the blood/tissue barrier has a minimal level of permeability. When the barrier, however, is damaged, its permeability increases. To model this, the vertical diffusion rates for each of the model players at the blood/tissue barrier are chosen to depend on d according to the following formula:

$$D_{\text{effective}}^z=D_{\text{baseline}}^z+(D_{\mathit{max}}^z-D_{\text{baseline}}^z)\frac{d^{1.5}}{d^{1.5}+{(d_{\mathit{max}}-d)}^{1.5}}.$$

When d is at its maximum level of d_max, diffusion between the blood/tissue barrier takes place at the maximal rate of $D_{max}^z$. When there is no damage/DAMPs in the region, diffusion between the blood/tissue barrier takes place at the baseline rate of $D_{baseline}^z$.

$D_{max}^z$ for a particular model player is defined to be equal to the harmonic average of the model player’s isotropic diffusion coefficients in the two layers (listed in Table 2), which is appropriate when the isotropic diffusion coefficients are constant but different in the two layers [28]. $D_{baseline}^z$ is set to zero for the activated immune cells and bacteria. For the molecularly sized model players, cytokines, DAMPs, and nitric oxide, $D_{baseline}^z=D_{max}^z∕10$. As such, when d = 0 no immune cells or bacteria penetrate the blood/tissue barrier whereas cytokines, DAMPS, and nitric oxide are allowed to penetrate the barrier at a low nonzero rate.

The immune cell chemotaxis rates at the blood/tissue barrier are found using the same formula where the maximal vertical chemotaxis rate is found by taking the harmonic average of the isotropic chemotaxis rates in the two layers and the baseline chemotaxis rate is set to zero.

2.5.3. Transport into and out of the epithelial layer

The epithelial layer has a minimal level of permeability unless its barrier function has been compromised (corresponding to low levels of ZO1, see 2.5.3). Therefore, to model the epithelial layer permeability, the vertical diffusion coefficients for diffusion into and out of the epithelial layer are treated in a similar fashion as they were for the blood/tissue barrier with ZO1_max – ZO1 taking the place of d:

$$D_{\text{effective}}^z=D_{\text{baseline}}^z+(D_{\mathit{max}}^z-D_{\text{baseline}}^z)\frac{{(\mathit{ZO}{1}_{\mathit{max}}-\mathit{ZO}1)}^{1.5}}{{(\mathit{ZO}{1}_{\mathit{max}}-\mathit{ZO}1)}^{1.5}+\mathit{ZO}{1}^{1.5}}.$$

Again, $D_{max}^z$ and $D_{baseline}^z$ baseline are the maximum and minimum effective vertical diffusion coefficients that are attainable, respectively. $D_{max}^z$ is the harmonic average of the model player’s isotropic diffusion coefficients from the two layers. $D_{baseline}^z$ is zero for immune cells and bacteria and $D_{max}^z∕10$ for cytokines, DAMPs, and nitric oxide. When ZO1 is at its maximum level, diffusion takes place at the low minimal rate of $D_{baseline}^z$. When ZO1 is zero, diffusion takes place at the maximal rate of $D_{max}^z$.

The vertical chemotaxis coefficients between the epithelial and tissue regions are found similarly, with the maximal vertical chemotaxis rate found using harmonic averaging of the isotropic chemotaxis coefficients in both layers and the baseline chemotaxis rate being zero. While we do allow activated inflammatory cells to diffuse into the lumen when ZO1 levels are low, we do not allow inflammatory cells to actively move up gradients of bacteria and cytokines into the lumen, as activated inflammatory cells are not normally found there.

2.5.4. Using zonula occludens-1 to measure epithelial permeability

To understand why ZO1 was chosen to be the primary determinant of epithelial layer permeability, consider the three routes through which we assume bacteria can translocate: bacterial translocation through the paracellular space (i.e. between epithelial cells), bacterial translocation via transcytosis (i.e. transport) through epithelial cells, and bacterial translocation through regions of dead epithelial cells that offer no barrier to translocation. The levels of ZO1 have been seen to be negatively correlated with rates of translocation through all three of these routes. Translocation rates through the first route are, in fact, directly related to ZO1 since higher levels of tight junction proteins limit translocation through tight junctions. Translocation rates through the second route have been observed to be negatively correlated with ZO1 levels during studies on the effects of NO on epithelial layers and bacterial translocation through those layers [29, 30]. Translocation rates through the third route are also negatively correlated with ZO1 levels as regions of dead cells experience both low levels of ZO1 (dead epithelial cells do not produce ZO1) and higher rates of bacterial translocation through the region that offers no barrier. In all cases, low levels of ZO1 correspond to high translocation rates through each route of translocation and hence, for a simple model, ZO1 serves as a reasonable indicator of translocation rates and the corresponding epithelial layer permeabilities. We should also note that since ZO1 is destroyed by NO and produced by e_c, epithelial layer permeability increases in the presence of NO and decreases as epithelial integrity improves.

2.5.5. Epithelial integrity

The partial differential equation governing epithelial integrity is given by:

$$\frac{\partial e_c}{\partial t}+\nabla \cdot \left(\beta \right(e_c\left)\alpha \right(b)\nabla e_c)=k_p{e}_c(1-e_c∕e_{c,\mathit{max}})-k_a(n_a,c,b)e_c$$ (4)

The first term on the right hand side corresponds to logistic growth of epithelial integrity due to the innate ability of epithelial cells in the epithelial layer to recover from injury when in normal surroundings. The second term on the right hand side corresponds to loss of epithelial integrity due to death of epithelial cells in the epithelial layer because of activated neutrophils, pro-inflammatory cytokines, and bacteria. The nonlinear diffusion term on the left hand side corresponds to the ability of healthy epithelial cells in the epithelial layer to migrate from regions with cells (presumably regions of higher epithelial integrity) into regions without cells (presumably regions of lower epithelial integrity) thereby increasing epithelial integrity in the new region to which the epithelial cells migrated.

The function controlling the rate of epithelial integrity loss is given by:

$$k_a(n_a,c,b)=h(n_a+k_{e_c{n}_{a}c}c)+k_{e_c{n}_{a}b}b,n_{a,\mathit{max}}+k_{e_c{n}_{a}c}{c}_{\mathit{max}}+k_{e_c{n}_{a}b}{b}_{\mathit{max}},q_0)$$

We assume the bacterial population is composed of a mixture of pathogenic and commensal bacteria, with a large fraction of the bacteria being commensal in nature. As such the constants have been chosen so that one neutrophil unit has the most deleterious effect on epithelial cells while one bacterial unit has the least deleterious effect.

As the nonlinear diffusion term arises from epithelial integrity changes due to epithelial cell migration, the nonlinear diffusion term was chosen to closely mimic epithelial cell migration in vitro. The two coefficients on the nonlinear terms are given by:

$$\beta \left(e_c\right)=\frac{e_c^2}{e_c^2+{(e_{c,\mathit{max}}-e_c)}^2};\alpha \left(b\right)=D_{e_c}\frac{{(b_{\mathit{max}}-b)}^{1∕4}}{{(b_{\mathit{max}}-b)}^{1∕4}+b^{1∕4}}.$$

The first coefficient, β(e_c), was chosen from the Buckley-Leverett model of two-phase flow [31]. It is S-shaped and allows no epithelial cell migration when epithelial integrity is low, i.e. for e_c ≈ 0, and maximal epithelial cell migration when epithelial integrity is high, i.e. for e_c ≈ e_c,max.

The second coefficient, α(b), was chosen to inhibit epithelial migration in the presence of the small fraction of pathogenic bacteria that make up the total bacterial population. When the bacterial product LPS comes in contact with the receptor TLR4 on epithelial cells, a signaling process is initiated that eventually causes integrins to adhere tightly to the extracellular matrix, resulting in inhibited epithelial cell migration [32]. When b = 0, α(b) = 1 and migration is uninhibited. When b = b_max, α(b) = 0 and migration is completely inhibited.

2.6. Modeling breastfeeding vs formula feeding

In addition to other substances and cells [33, 34, 35], certain anti-microbial peptides, which affect the destruction of bacteria, as well as anti-inflammatory cytokines are present in breast milk but not in formula [36, 37]. To investigate the possible effects of these latter substances, in our simulations we assume that breast milk contains anti-microbial peptides and anti-inflammatory cytokines, while formula does not.

The last term in equation (1), −k_ppb, is included to model the destruction of bacteria by the anti-microbial peptides in breast milk and is set to zero for formulafed individuals. Larger values of k_pp simulate increased bacteria-killing ability of these anti-microbial peptides.

Premature infants tend to produce lower levels of anti-inflammatory cytokines than mature infants [38]. The effects of these relatively low levels of normal systemic anti-inflammatory cytokines are implicitly included in the cytokine equation (3) while a separate equation is used to describe exogeneously-derived anti-inflammatory cytokines, such as those found in breast milk and produced by the immune cells present in breast milk. In formula-fed individuals, these exogeneously-derived anti-inflammatory cytokine levels, do not exist (i.e. c_a = 0 always) whereas the exogeneously-derived anti-inflammatory cytokine levels are nonzero in breast-fed infants and are governed by the equation found in the appendix. These simplifying model assumptions have been made for simplicity and clarity of results.

2.7. Initial conditions, boundary conditions, parameter values

To assign the initial conditions, we assume that the system initiates in a completely healthy state with the exception of an injury in the epithelial layer where the epithelial integrity is significantly decreased due to some ischemic, traumatic, or other initiating event (see 3.4). The variables corresponding to activated macrophages and neutrophils, pro- and anti-inflammatory cytokines, damage/DAMPs, and nitric oxide are set to zero everywhere. Resting macrophages are set to m_max everywhere except in the lumen and blood where they are set to zero. Bacteria are set to zero everywhere except in the lumen where they take on the value b₀, the largest steady state value found by setting m_a, n_a, ▿ · b, and ∂b/∂t to zero in equation (1). This value depends on k_pp in a way that is consistent with experiment wherein breastfed individuals tend to have lower levels of Gram-negative bacteria in the lumen [39]. Finally, the epithelial integrity and ZO1 concentrations are assumed to be equal to their maximal values everywhere except in the injured region where they are set to some percentage (e.g. 33% or 0%) of their maximal values. ZO1 and e_c are assumed to reside only in the epithelial layer and are not tracked in the other layers.

No flux boundary conditions are maintained on the top and bottom of the computational domain pictured in Figure 3a. Periodic boundary conditions are prescribed on the four sides. Results were not sensitive to the choice of boundary conditions.

Our model contains a large number of parameters. Their values and units are found in Tables 3 and 4 in the appendix. Many of the parameter values are taken directly from the model of Reynolds et al [21]. As with the variable units, we use non-specific units (e.g. c-units) to remain consistent with the Reynolds et al. model. The remaining unknown parameter values were chosen to produce a range of outcomes when varying initial conditions and the feeding regime.

Table 3.

Parameters describing rates of growth and interaction

Parameter	Value	Units	Description
kb	1.5	h−1	Decay rate of bacteria
kbg	0.9	h−1	Growth rate of bacteria (varies for different bacteria)
kbma	1.8	(ma-units)−1h−1	Rate of bacterial destruction by activated macrophages
kbna	1.8	(na-units)−1h−1	Rate of bacterial destruction by activated neutrophils
kc	1	h−1	Cytokine decay rate
kca	0.1	h−1	Anti-inflammatory cytokine decay rate
kcamad	48	ma-units/d-units	Relative effectiveness of d and ma in producing ca
kcamana	0.25	ma-units/na-units	Relative effectiveness of na and ma in producing ca
kcap	0 or 0.04	ca-units/h	Production rate of ca by inflammatory cells
kcaQ	1	ma-units	Constant controlling how quickly production of ca saturates
kcma	0.2	(ma-units)−1h−1	Rate at which macrophages produce cytokines
kcna	0.05	(na-units)−1h−1	Rate at which neutrophils produce cytokines
kd	0.02	h−1	Rate of decay of damage/DAMPs
kdc	0.35	(d-units)/h	Rate of damage/DAMP production by cytokines
kecnab	0.25	na-units/b-units	Relative effectiveness of b and na in killing ec
kecnac	0.5	na-units/c-units	Relative effectiveness of c and na in killing ec
km	0.12	h−1	Resting macrophage decay rate
kma	0.05	h−1	Activated macrophage decay rate
kmb	0.1	(106 bacteria/cm3)−1h−1	Rate of macrophage activation by bacteria
kmc	0.076	(c-units)−1h−1	Rate of macrophage activation by inflammatory cytokines
kmd	0.02	(d-units)−1h−1	Rate of macrophage activation by DAMPs
kna	0.05	h−1	Activated neutrophil decay rate
knc	0.04	(c-units)−1h−1	Rate of neutrophil activation by inflammatory cytokines
knd	0.018	(d-units)−1h−1	Rate of neutrophil activation by DAMPs
kNO	2	h−1	Decay rate of nitric oxide
kNOma	1×105	(NO-units)h−1(ma-units)q1	Rate at which activated macrophages induce NO production
kNOna	1×105	(NO-units)h−1(na-units)q1	Rate at which activated neutrophils induce NO production
kp	0.25	h−1	Rate of proliferation of epithelial cells
kpp	0-0.25	h−1	Destruction rate of bacteria by peptides in breast-milk
kRca	1		Anti-inflammatory cytokine effect on damage/DAMP production
kZec	0.03	(ec-units)−1h−1	Rate of increase of ZO1 by epithelial cells
kZect	2	(ec-units)−1	Rate of change of ZO1 induced by ec growth or decay
kZN	0.75	(NO-units)−1h−1	Rate of destruction of tight junction protein, ZO1, by NO

Table 4.

Other Parameters

Parameter	Units	Value	Description
bmax	20	106 bacteria	Upper bound on maximum amount of b attainable
${\stackrel{‒}{c}}_a$	0.28	ca-units	Special value for anti-inflammatory cytokines
cmax	0.35	c-units	Upper bound on maximum amount of c
dmax	0.92	d-units	Upper bound on maximum amount of d attainable
ec,max	1		Upper bound on maximum amount of ec
∊	0.2	106 bacteria/cm3	Range for bacterial death
Dec	3e-6	cm2/h	Associated with magnitude of diffusion of ec
∊ zec	0.05		Limits ZO1 production when ec concentration is low
γ mac	10−4	cm2/h/b-units	Coefficient for macrophage chemotaxis up cytokine gradients
γ nac	10−4	cm2/h/b-units	Coefficient for neutrophil chemotaxis up cytokine gradients
γ mab	10−4	cm2/h/b-units	Coefficient for macrophage chemotaxis up bacteria gradients
${\stackrel{‒}{m}}_a$	0.01	ma-units	Special value for activated macrophages
mmax	0.67	m-units	Upper bound on maximum amount of m attainable
${\stackrel{‒}{n}}_a$	0.01	na-units	Special value for activated macrophages
na,max	0.62	na-units	Upper bound on maximum amount of na
nb	1	n-units	Neutrophil concentration in blood
q0	0.45		Power in hill function for epithelial apoptosis
q1	3.5		Exponent of nitric oxide production
q2	1.5		Exponent of damage/DAMP production
sca	0 or 0.0125	(ca-units)h−1	Constant source of ca from breast milk
xdc	0.06	c-units	Range for damage/DAMP production
ZO1max	1	ZO1-units	Upper bound on maximum amount of ZO1

2.8. Numerical methods

Simulations were made using the system of PDEs listed in the appendix. The system was discretized using a cell-centered finite difference method. The values of the diffusive terms and the chemotactic gradients were approximated using central differences in space. The values of the chemotactic term contributions were approximated using upwinding with respect to the chemotactic gradient. The variable values in the cells were updated using an explicit forward Euler method. In order to maintain numerical stability, the model time step was chosen to obey the following inequality [40]:

$$\Delta t\le \underset{i}{\overset{\min }{}}\frac{1}{\frac{2D_{x,i}}{\Delta x_i^2}+\frac{2D_{y,i}}{\Delta y_i^2}+\frac{2D_{z,i}}{\Delta z_i^2}+\frac{\mid v_{x,i}\mid }{\Delta x_i}+\frac{\mid v_{y,i}\mid }{\Delta y_i}+\frac{\mid v_{z,i}\mid }{\Delta z_i}}.$$

Here the minimum is taken over all computational cells (indexed by i). D_x,i, D_y,i, and D_z,i correspond to the numerical estimate for the average diffusion coefficient in the x, y, and z directions. v_x,i, v_y,i, v_z,i correspond to the x, y, and z components of the effective velocity vector (proportional to the chemotactic gradient). Δx_i, Δy_i, and Δz_i are the extents of the computational cells in the x, y and z directions.

The numerical method was implemented using MATLAB and is O(Δx,Δt) accurate. The discretized spatial domain used in the simulations consisted of an 80×80×5 grid of computational cells (Figure 3a). Each layer was one cell thick with the exception of the tissue layer which was made to be two cells thick in order to more accurately assess the amount of DAMPs being produced in that layer (DAMPs are assumed to be produced only in the tissue). The simulation time step used to satisfy the above numerical stability condition was 0.1 hrs. The results presented here did not change significantly when the spatial and temporal domains were further refined. Each simulation was run to 2400 hrs of simulation time to guarantee convergence to the simulation’s final steady state. Running each simulation took 1-2 hrs of computational time on a 1.8 GHz processor.

3. Results and discussion

To investigate the validity of the model, simulations were performed for two different epithelial layer injury severities (“total injury” and “partial injury”) and two different feeding conditions (formula-fed and breastfed). To consider the importance of injury area and severity, we also perform a parameter sweep with respect to these two parameters. To consider the effects of space on outcomes, simulations were also performed for three different injured area shapes.

3.1. Simulations considering different injury severity and feeding practices

In the total injury case, the epithelial integrity (e_c) and ZO1 levels inside the injured area are initialized at 0% of their maximal values. In the partial injury case, e_c and ZO1 levels inside the injured area are initialized at 33% of their maximal values. The former situation corresponds to an inflammatory injury in which the epithelial cells have been completely destroyed. The latter situation corresponds to an inflammatory injury in which the epithelial cells have been severely damaged but still retain some of their barrier function.

To model the effects of breast milk (see 2.6) anti-inflammatory cytokines and varying levels of anti-microbial peptides (k_pp = 0.125, 0.1875, and 0.25) are included in simulations with breast milk, but not in simulations with formula.

The shapes used as initial conditions for the injured areas in these simulations are circular and have an area of 0.8 cm² (20% of the total area covered by the epithelial layer). This area was chosen in order to produce runs typical for this model (see 3.2).

As the model is limited in scope, the results tell us about how likely it is that an individual develops NEC, about what dynamics may take place as NEC develops, but not what happens after severe NEC has set in. In addition, while the levels of damage in the tissue at the end of a simulation are meant to serve as the best indicators of the likelihood with which an individual will develop NEC, higher levels of damage, immune cells, cytokines, and nitric oxide and lower levels of epithelial integrity and ZO1 all tend to correspond to more unhealthy outcomes wherein the initial injured area is unable to fully heal.

Particular attention is paid to the epithelial integrity because the epithelial layer is the main barrier to the translocation of bacteria, the initial invoker of the immune response. In addition, in this model the levels of the other variables in a given region are relatively well correlated with the level of epithelial integrity; higher levels of epithelial integrity tend to correspond to healthier levels of the other variables. Nonetheless it is important to note that while levels of epithelial integrity in this model give a reasonable, rough summary of the overall dynamics that take place, in general epithelial integrity may not be a suitable proxy for NEC, especially when events after severe NEC begin to occur.

3.1.1. Case 1 - Total injury, formula-fed

To understand the course of NEC in an unhealthy outcome, as simulated by our model, we first consider a simulation corresponding to the most unhealthy situation on the spectrum of injury that we address here, a formula-fed, total injury case.

Figure 4a shows the average levels of the variables in the stated layers as a function of time. Investigating these levels shows the general dynamics occurring in an unhealthy simulation. An initial bacterial invasion into the epithelial layer and tissue is quickly followed by an inflammatory response through which the immune system quickly controls the invasion. For a period of time, the system appears to be getting healthier. Eventually, however, the tissue continues to slowly produce DAMPs (measured by d) until they reach a critical level at which the rate of macrophage activation by DAMPs exceeds the macrophage death rate. At this point, the number of activated macrophages stops decreasing and starts increasing. A positive feedback loop between DAMPs and activated macrophages, characteristic of inflammation in vivo [41, 42], forms. The eventual outcome is that tissue DAMPs and activated macrophage concentrations reach the maximal values allowed by the system. These elevated levels of damage/DAMPs and activated macrophages contribute to higher levels of cytokines and nitric oxide and lower levels of epithelial integrity and ZO1. In this case, these factors do not allow the injured area to completely heal.

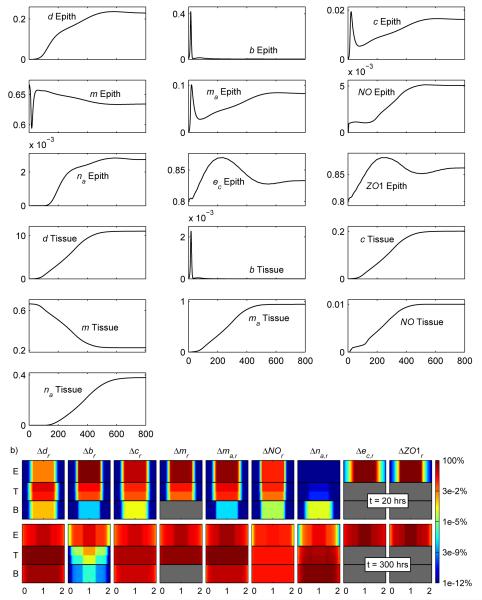
Figure 4.

a) Average levels of each variable in the indicated layer for the simulation corresponding to Case 1-total injury, formula-fed. b) Levels of the variables in the epithelial (E), tissue (T), and blood (B) layers through a cross-section of the computational domain.

In Figure 4b, each graph corresponds to a vertical cross-section through the center of the computational domain and includes only the epithelial (E), tissue (T), and blood (B) layers. To understand the variables being plotted in these cross-sectional plots, consider Δd_r which is defined as:

$$\Delta d_r=\Delta d∕\Delta d_{\mathit{max}};\Delta d=\mid d-d_{\text{healthy}}\mid .$$

Here Δd_max is the maximum of Δd in the epithelial, tissue, and blood layers over all time for a given simulation. d_healthy = 0 and corresponds to the level of damage/DAMPs that should exist when the intestine is completely healthy. The other variables on the graphs are defined similarly. In general, larger values on these graphs correspond to more unhealthy situations.

Figure 4b further illustrates how NEC dynamics consists of an early bacterial invasion followed by excessive damage in the tissue cause by an overactivated immune response. Early on large amounts of bacteria flux in from the lumen, while later on large amounts of DAMPs, activated macrophages, and cytokines are being produced in the tissue. Investigation of the actual terms in the partial differential equations verify that bacteria actively drive the early dynamics in the system, while DAMPs drive dynamics in the system later on. The figure also shows how the model is capable of tracking the spatial details of the system. In this case, the inhomogeneity of the spatial distribution of the injury decreases as time goes on. We discuss the appropriateness of this result later (see 3.4).

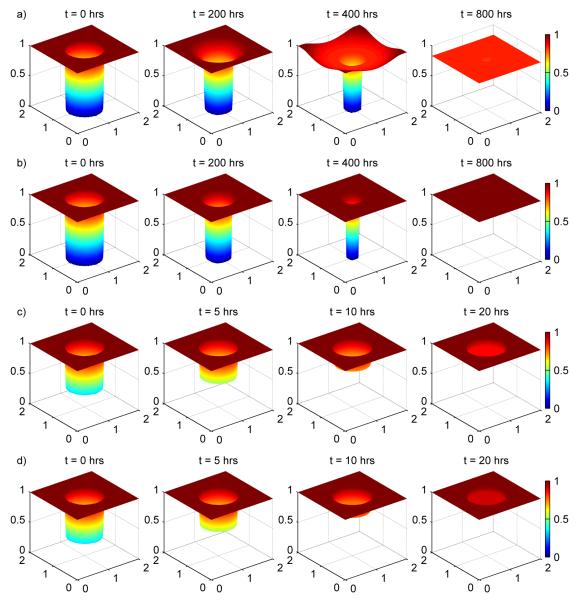
Figure 5a provides a depiction of the injury resolution process, as predicted by the model, by plotting the values of epithelial integrity in the epithelial layer as a function of space at different times. Inside the original injury, the area recovers as the epithelial integrity moves away from zero. Unfortunately, because of the presence of cytokines and bacteria, these areas are never able to fully recover. Outside the original injured area, near the edges, cytokines and bacteria in the interior of the injured area diffuse into those nearby regions and degrade epithelial integrity in those areas. This degradation leads to two different regions where epithelial integrity increases towards some steady state value below 1 (interior of the injured area) and where epithelial integrity decreases towards the same steady state value (near the edge of the injured area). The decay and growth of these two regions, respectively, can be seen in the figure as well as the overall trend towards unhealthy levels of epithelial integrity.

Figure 5.

Injury resolution for a) Case 1-total injury, formula-fed, b) Case 2-total injury, breastfed with k_pp = 0.1875, c) Case 3-partial injury, formula-fed and d) Case 4-partial injury, breastfed with k_pp = 0.1875

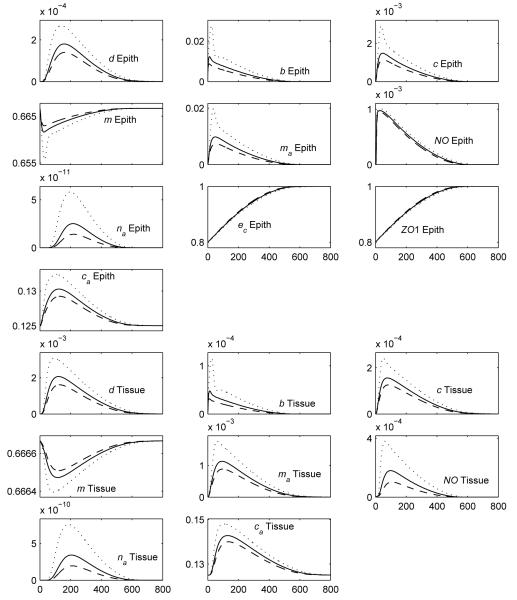
3.1.2. Case 2 - Total injury, breastfed, k_pp = 0.125, k_pp = 0.1875, k_pp = 0.25

Breast-feeding was added, by inclusion of anti-inflammatory cytokines and anti-microbial peptides, to the total injury case. Various levels of anti-microbial peptides were used including k_pp = 0.1875, k_pp = 0.125, and k_pp = 0.25. Results for all three cases are shown in Figure 6, while the results for only k_pp = 0.1875 are shown in Figure 5b. The injury resolution depicted in Figure 5b looks similar for the other two values of k_pp.

Figure 6.

Average levels of each variable in the indicated layer for the simulation corresponding to Case 2-total injury, breastfed. Here, k_pp = 0.1875 corresponds to solid lines, k_pp = 0.125 corresponds to dotted lines, and k_pp = 0.25 corresponds to dashed lines.

In all cases, the injured area heals and a healthy outcome is obtained. In addition, as expected, increasing the anti-microbial peptide strength increases the healthiness of the outcome. The healing process seen in Figure 5b shows that, in contrast to Case 1, the interior of the injured area is able to return fully to health, and members of the inflammatory response are not able to significantly decrease epithelial integrity in the regions adjacent to the injured area.

3.1.3. Case 3 - Partial injury, formula-fed

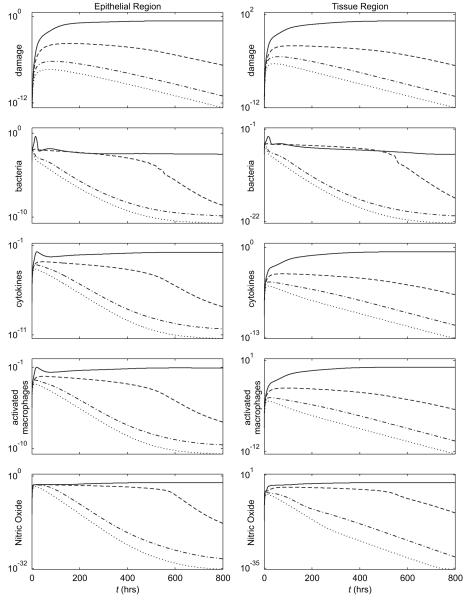
As the graphs of the average levels of the variables in each layer for Case 3 and Case 4 (partial injury, breastfed) look very similar, in shape, to Figure 6, we have plotted multiple cases on the same set of graphs to help more clearly delineate the differences among cases. For the breastfed cases that were plotted, the relative comparisons did not depend on which value of k_pp was chosen so k_pp = 0.1875 was used in these plots. The first set of graphs in Figure 7 plot the average epithelial integrity and ZO1. The second set of graphs in Figure 8 contain the damage/DAMPs, bacteria, cytokine, activated macrophage, and nitric oxide levels. Because these latter levels can differ by orders of magnitude between each case, we have plotted them on a log scale.

Figure 7.

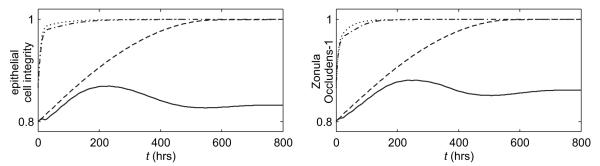
Average levels of the epithelial integrity and ZO1 for Case 1-total injury, formula-fed (solid), Case 2-total injury, breastfed (k_pp = 0.1875) (dashed), Case 3-partial injury, formula-fed (dash-dotted), and Case 4-partial injury, breastfed (k_pp = 0.1875) (dotted).

Figure 8.

Average levels of damage/DAMPs, bacteria, cytokines, activated macrophages, and nitric oxide in the indicated layer for Case 1-total injury, formula-fed (solid), Case 2-total injury, breastfed (k_pp = 0.1875) (dashed), Case 3-partial injury, formula-fed (dash-dotted), and Case 4-partial injury, breastfed (k_pp = 0.1875) (dotted).

Figure 7 shows that the epithelial integrity in the partial injury, formula-fed simulation (dash-dotted line) converges to a healthy level (e_c = 1 = 100%) more quickly than either the total injury, formula-fed Case 1 (solid line) or the total injury, breastfed Case 2 (k_pp = 0.1875, dashed line). Figure 8 shows that Case 3 is also healthier than the total injury cases with respect to bacteria, damage/DAMPs, cytokine, activated macrophage, and nitric oxide levels in the epithelial and tissue regions. Figure 5c shows injury resolution for Case 3. Noting the times for each snapshot shows that the injured area in Case 3 closes much more quickly than either injured area from the total injury cases.

3.1.4. Case 4 - Partial injury, breastfed, k_pp = 0.1875

Adding breastfeeding (k_pp = 0.1875) to Case 3 yields the partial injury, breastfed plots on Figure 7, 8 and 5d. In all figures it is seen that this is the healthiest result yet.

3.1.5. Comparisons

Lowering the severity of the injury can change an unhealthy outcome into a healthy outcome. In addition, adding in breastfeeding by incorporating anti-inflammatory cytokines and anti-microbial peptides into the model can also change an unhealthy outcome into a healthy outcome. Comparing the partial injury, formula-fed outcome to the total injury, breastfed outcome suggests that, in this instance, changing the initial injury severity may be more effective in improving the simulation outcome than is introducing breast feeding. The final simulation shows that decreasing the initial injury severity and introducing breastfeeding simultaneously yields an additive result whereby the outcome is healthier than it would have been if either change had been introduced by itself.

Decreasing injury severity increases the degree of health observed as an outcome of the simulation because the higher epithelial integrity allows in fewer bacteria, which results in a less severe immune response and less overall damage/DAMPs being produced in the tissue.

In the breastfed situation, the anti-microbial peptides kill many of the invading bacteria and lower the number of bacteria available for translocation in the lumen. The reduced bacterial load and presence of anti-inflammatory cytokines lead to a reduced immune response throughout the system. In the partial injury case where breast feeding is introduced, this simply leads to a more healthy outcome. In the total injury case, this leads to an unhealthy situation becoming a healthy situation because the damage/DAMPs being produced by the inflammatory cells remains below the critical level necessary to start the damage-activated macrophage-mediated positive feedback loop that causes unhealthy simulations to occur. Recognizing the importance of anti-microbial peptides, it is interesting to note that administering antibiotics alone has been shown to improve the outcome of NEC patients [43]. This finding demonstrates further consistency of our model with in vivo results.

The simulations also offer insight into the different mechanisms that may dominate the dynamics of injury resolution in NEC. In the total injury cases (e.g. Figure 5b), the e_c values inside the injured area remain at 0% of their maximal values throughout a good portion of the simulation. In the partial injury cases (e.g. Figure 5d), the e_c values inside the injured area quickly grow away from 33% of their maximal values. The total injury case represents an injury in which the epithelial cells have been completely destroyed and epithelial cells outside the injured area must migrate inwards to replace them. The partial injury case represents an injury in which the epithelial cells have been severely damaged but are still able to repair themselves, and thereby the injured area, without needing assistance from outside cells. The slower process of diffusion limits the epithelial healing in the total injury situation while the faster process of epithelial cell proliferation dominates epithelial healing in the partial injury situation. This finding suggests that physiologically there may be times during the course of NEC when it may be more important to try to enhance epithelial migration (akin to diffusion in our model) and other times when it may be more important to try to enhance epithelial proliferation.

3.2. Effects of injury area and severity

While the previous simulations suggest that the outcome of the individual is im proved as initial wound severity is decreased, we investigate this trend more thoroughly by performing a parameter sweep across different initial injury severity levels (initial epithelial integrity and ZO1 levels inside the wound) and initial areas of the injured region. Figure 9 illustrates our main results.

Figure 9.

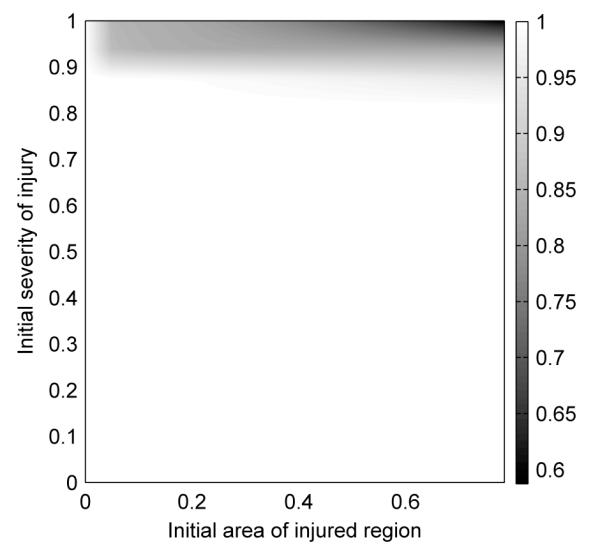
Runs for formula fed individuals were performed using multiple injury severities and fractional areas. The final epithelial integrity level for each run was assigned an appropriate color for its value and plotted here. White corresponds to healthy outcomes while dark corresponds to unhealthy outcomes.

To produce this figure, formula-fed simulations for circular injured areas were run for 600 hrs using multiple sets of parameter values and the final average values of the epithelial integrity levels were plotted. White areas correspond to end average epithelial integrity levels near 1, i.e. completely healthy runs. Dark areas correspond to low end average epithelial integrity levels, i.e. unhealthy runs. The initial injury areas and severities we used in 3.1 were chosen to give typical runs from each of these two regions.

The figure shows that results for the current model depend strongly on the initial severity of the injury and weakly on the initial fractional area of the injured area. Our model also suggests that the majority of neonatal intestinal injuries naturally resolve themselves, which is in agreement with what is seen clinically.

3.3. Simulations considering different injured area shapes

All simulations up to this point have been axisymmetric in nature. Typically, however, the shapes of the injured areas seenin vivo lack such symmetry and a relevant question is: How do the shapes of the injured areas affect the ability of the epithelial layer to recover? Our model is unique because, in contrast with an axisymmetric model, its full three-dimensionality allows us to consider this question in a straightforward fashion.

To investigate this question of how much spatial features of a given epithelial injury can affect the healing process, we considered two additional cases, an irregularly shaped injury and four small circular injuries (Figure 10b and c, respectively). The irregular injured area shape was taken from a picture of an in vitro experiment provided by the lab of David Hackam (personal communication). In each case, the shapes of the injured areas are scaled so that the total resulting area of the injury is equal to the area covered by the large, circular shape used in earlier simulations (0.8 cm²).

Figure 10.

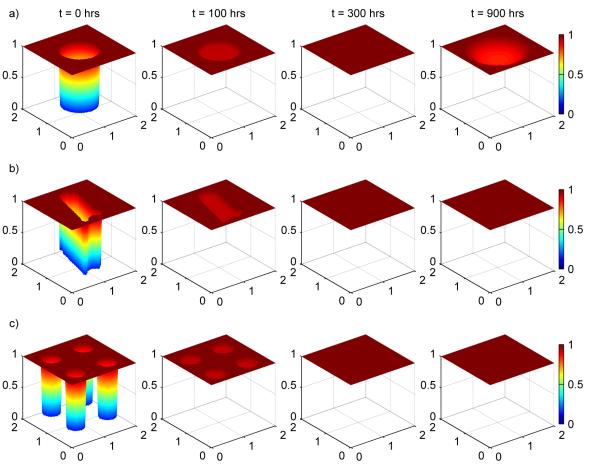
Injury resolution comparison for a large circle (a), an irregular shape (b), and four small circles (c). In all cases, the original injury areas of are equal (0.8 cm²) as are the initial epithelial cell integrity levels inside the injured areas (12.7%). While the latter two time sequences correspond to healthy outcomes, for the large circle the ongoing inflammatory processes below a healed epithelial layer cause the layer to reopen resulting in an unhealthy outcome. The shape of an injured area can, in some cases, drastically change an outcome.

Cases 1-4 were rerun using the irregularly shaped injury and using the four small circular injuries. The resulting simulations do not qualitatively differ from the results already presented for the large, circular injury.

Exploring different initial epithelial integrity levels inside the injured area for formula-fed simulations, however, revealed that there are some situations where changing the initial shape of the injured area can significantly change the outcome of a simulation. Figure 10 shows injury resolution for the three different shapes, each with an initial epithelial integrity level of 12.7% inside the injured areas. For this particular initial epithelial integrity level, a large circular injured area does not heal while the two other injuries do heal.

While significantly different outcomes for different shapes can occur, in our simulations such situations were relatively infrequent (<1% of all possible initial epithelial integrity levels in the injured area yielded such outcomes).

To understand the reason for the differences, we note that in our model, injury resolution, for severe injuries, takes place because epithelial cells near the edge of the injured area migrate towards the center of the injured area. The farther the cells have to migrate to close the injured area, the longer it takes for the injury to heal and the higher the levels of bacteria and activated inflammatory cells become in the tissue below the injured area of the epithelial layer. In the irregular and small circular injury cases, the epithelial cells near the edge of the injured area have to travel less distance in order to resolve the injury. This leads to faster injury healing, fewer bacteria and activated inflammatory cells in the underlying tissue, and overall healthier levels of all variables.

If, as an injured area is healing, the bacteria and activated inflammatory cell levels remain low enough, the immune response will successfully reduce the levels of these cells back to their healthy levels. In particular, the DAMPs produced by the activated macrophages never reach high enough concentrations to instigate the positive damage-activated, macrophage-mediated positive feedback loop. This is the case for the irregular and small circular injury areas seen in the figure. (Simulations were run for 2400 hrs to verify the injuries in these simulations did not reappear.)

If, however, the bacteria and activated inflammatory cell levels become too high, the concentration of produced DAMPs exceeds the critical threshold needed to initiate the damage-activated, macrophage-mediated positive feedback loop to start. In some cases (Case 3 above) the feedback loop initiates an unhealthy outcome before the injured area in the epithelial layer has healed. In other cases, as in Figure 10a, the feedback loop only starts to become important after the injured area appears to be closed. In this latter case, the injured area eventually reappears when DAMPs and activated macrophages in the tissue reach high levels.

3.4. Model limitations and extensions

The study provides insight into the biological processes that can take place during NEC, but there are some limitations to the current model.

While we were able to show that the model can produce some physiologically realistic results, this model has only been validated qualitatively. In order for this model to be used clinically, two primary obstacles must first be overcome in order to more completely validate the model. First, the model has over fifty free parameters, many of whose values are unknown and unavailable in the literature. Second, experimental data for this system are relatively sparse, as spatial experimental data of the same refinement as the current model are hard to obtain. Because of these two issues, we have begun using parameter estimation techniques that can deal with both of these issues in order to obtain parameter values capable of producing results that are in closer agreement with experimental data. We are currently using both temporal and spatial in vitro data obtained from sheets of healing IEC-6 cells to obtain estimates for certain parameters and hope to obtain and utilize data from in vivo experiments as well.

Our model suggests that inhomogeneity of the spatial distribution of the injury, including concentrations of the bacteria, immune cells, proteins, and the molecules in our model, decreases over time. This may be true in some circumstances, particularly for smaller, regularly shaped injured areas over shorter time periods. Clinically, however, this is not seen to be the case in general. More inhomogeneous results can be produced by introducing random/inhomogeneous initial conditions, stochastic terms in our model, and different diffusion and chemotaxis coefficients. Indeed, certain combinations of diffusion and chemotaxis coefficients can induce inhomogeneous patterns in space [44]. We hope to investigate this issue more after we have further refined our other parameter estimates.

The study only investigates the course of NEC after tissue injury has occurred. It is still unclear which factors initiate the pathogenesis of NEC and, for that reason, we have chosen to focus this study on investigating dynamics after NEC has been initiated by imposing an initial injury on the system. As such, we have not yet explicitly included any of the proposed initiating factors in our model. Thus, the current model is not yet capable of producing a simulation that shows the evolution of NEC from a completely healthy system.

Including such possible initiating factors, however, is possible by introducing a variable carrying capacity in the logistic growth term for the epithelial cells corresponding to impaired epithelial growth, an additional sink term to the ZO1 equation corresponding to impaired epithelial function, or an additional source term in the damage/DAMPs equation corresponding to outside sources of DAMPs. Any of these alterations could help us begin to characterize the processes involved in the pathogenesis of NEC. In addition, by carefully choosing a combination of these and other changes we can investigate the consequences of some of the proposed initiating factors on the development of NEC and begin to understand the relative roles of each factor in the pathophysiology of NEC.

In order to model some of the potential initiating factors, as well as a couple of other important factors in NEC, we propose the following model modifications. Intestinal immaturity can be simulated by lowering rates of epithelial cell migration (D_ec), proliferation, and the carrying capacity used in the logistic growth term. Bacterial invasion by different bacterial species can be explored by varying bacterial growth, diffusion, and death rates. Low tissue oxygenation may be considered by adding an additional sink term to the ZO1 equation and a source term to the damage/DAMPs equation. The exaggerated inflammatory response can be investigated by changing the rates at which inflammatory cells interact with bacteria and cytokines. Other potential initiating factors, such as reduced ability of the epithelial cells to clear oxidative stress [17], can be handled in a similar manner.

In addition to considering the effects various factors have on NEC, the model can also be used to consider various treatment strategies.

TLR4 activation on epithelial cells has been shown to lower epithelial cell migration and raise epithelial cell apoptosis [45]. To simulate the proposed treatment of NEC by epithelial cell TLR4 inhibition, the migration rate, proliferation rate, and carrying capacity in the current model could be altered.

It has also been shown that using probiotic bacteria may improve the outcome of NEC by lowering the overall number of pathogenic bacteria available for epithelial barrier penetration [16]. To simulate treatment or prevention of NEC by using probiotic bacteria, we can include an additional equation for probiotic bacteria in our model and grant those bacteria with probiotic qualities such as lower epithelial barrier penetration rates and lower immune activation rates.

Given the importance of breastfeeding in producing positive NEC outcomes (NEC was 6 to 10 times more common in formula-fed, preterm infants in a study by Lucas et al [46]) and the fact that there are multiple competing hypotheses that attempt to explain this result, we can further modify our model to include more aspects of breastfeeding. This includes modeling total systemic, not just exogeneously-derived, anti-inflammatory mediators by finding and using realistic levels of c_a and k_pp for premature infants and including the presence of growth factors and lactoferrin, a compound that promotes the growth of the nonpathogenic Bifidobacterium species [37]. To simulate growth factors, epithelial proliferation and migration rates could be increased. To simulate the effect of lactoferrin, a Bifidobacterium equation, much like the additional equation added for simulating probiotics, could be introduced with breast milk augmenting the growth of the Bifidobacterium. Determining which components of breast milk are of most benefit to a NEC patient could allow for the production of more appropriate infant formula and may aid in the selection of prebiotics to test in the setting of NEC [8].

These suggested modifications to the model illustrate the methods by which our model can be used to begin to investigate the potential effects of contributing factors and treatments during the development and course of NEC. The insights gained from such investigations will become more detailed and useful as the model is further calibrated and refined using parameter estimation.

Providing the model with a more realistic intestinal structure and vasculature will help further investigate the potential importance of spatial effects in NEC. Possible refinements include incorporating the shapes of individual intestinal villi, individual vessels feeding those villi, and a layer of anti-bacterial mucus that can cover the apical side of the epithelial layer in a heterogeneous manner. Implementing a more accurate representation of the vasculature will also allow us to consider the effects of thrombosis as NEC progresses beyond the timeline currently considered by our model. In addition, to understand why NEC favors certain regions of the intestine over others [47] and how it may spread, we are considering employing an interconnected compartment model. Each compartment would consist of a square domain with the same size and shape as used in the model presented here but with different parameter values in each domain to appropriately model the duodenum, jejunum, ileum, proximal large intestine, and distal large intestine.

Though some of the suggested spatial refinements of the model will require minimal readjustment of the computational model, two of the spatial refinements present numerical challenges that should be addressed. While assuming villi are arranged in a periodic fashion can reduce the number of calculations necessary to simulate NEC dynamics with realistically shaped villi, to most efficiently and accurately capture the dynamics in the system, the computational model should no longer use a rectilinear grid for its computations. Setting up an appropriate curvilinear grid for the computations will require some significant adjustments of the current model. In addition, resolving details on the order of blood vessels for either a rectilinear or a curvilinear grid will require more spatial and temporal refinement than that which is currently used. Increasing the refinement only two-fold (i.e. using a 160 × 160 × 10 grid) would increase the computational time necessary for a simulation from 1 – 2 hrs to 32 – 64 hrs. If simulations are to be completed in a reasonable amount of time, any or all of the following computational tools may be necessary: parallel computing, domain decomposition techniques, and adaptive mesh refinement. Making the appropriate computational adjustments, however, would again quickly yield a model appropriate for consideration of NEC dynamics.

4. Conclusions

The PDE model of NEC introduced in this study incorporates key mechanisms of the disease and is able to reproduce expected physiological results. As is expected, decreasing initial injury severity leads to more healthy outcomes. In addition, adding anti-inflammatory cytokines and anti-microbial peptides into the model to simulate breastfed individuals produced simulations that suggested that breastfeeding leads to more healthy outcomes, which is in agreement with clinical data [48]. The model predicts that a relatively small number of injuries lead to full-blown NEC, which is also in agreement with clinical data. The model also shows that, in some cases, spatial inhomogeneities can contribute to significantly different outcomes in NEC. In particular, injuries with greater perimeter per unit area are more likely to heal.

By calibrating parameter values, incorporating further spatial details of the intestine into the model, and adjusting model components to represent different situations, we believe this model can investigate specific issues related to NEC including the relative roles of factors that influence NEC and the potential of various treatment and prevention strategies.

Highlights.

• ● First three-dimensional, PDE model of necrotizing enterocolitis (NEC)

• ● Physiologically realistic simulations of NEC

  • ○ Decreased initial injury severity improves NEC outcome
  • ○ Breast feeding improves NEC outcome
  • ○ Small fraction of intestinal injuries or insults lead to full-blown NEC

• ● Demonstration that spatial inhomogeneities can significantly alter NEC outcome

Appendix.

Partial differential equations used for the model:

$$\begin{array}{cc}\hfill \frac{\partial e_c}{\partial t}+\nabla & \cdot \left(\beta \right(e_c\left)\mathbf{u}\right(e_c,b\left)\right)=k_p{e}_c(1-e_c∕e_{c,\mathit{max}})-k_a(n_a,c,b)e_c\hfill \\ \hfill & k_a(n_a,c,b)=h\left(e_{\mathit{ca}}\right(n_a,c,b),e_{\mathit{ca}}(n_{a,\mathit{max}},c_{\mathit{max}},b_{\mathit{max}}),q_0)\hfill \\ \hfill & e_{\mathit{ca}}(n_a,c,b)=n_a+k_{e_c{n}_{a}c}c+k_{e_c{n}_{a}b}b\hfill \\ \hfill & \beta \left(e_c\right)=h(e_c,e_{c,\mathit{max}},2)\mathbf{u}(e_c,b)=-\alpha \left(b\right)\nabla e_c\hfill \\ \hfill \frac{\partial b}{\partial t}-\nabla & \cdot D_b\nabla b=k_{\mathit{bg}}b(1-b∕b_{\mathit{max}})-k_{b}b(1+b∕∊)\hfill \\ \hfill & -R\left(c_a\right)(k_{{\mathit{bm}}_a}{m}_{a}b+k_{{\mathit{bn}}_a}{n}_{a}b)-k_{\mathit{pp}}b\hfill \\ \hfill \frac{\partial m}{\partial t}=& k_m(m_{\mathit{max}}-m)-R\left(c_a\right)(k_{\mathit{mb}}\mathit{bm}+k_{\mathit{mc}}\mathit{cm}+k_{\mathit{md}}\mathit{dm})\hfill \\ \hfill \frac{\partial m_a}{\partial t}-& \nabla \cdot (D_{m_a}\nabla m_a-{\gamma }_{m_{a}c}{m}_a{\nabla }_c-{\gamma }_{m_{a}b}{m}_a\nabla b)\hfill \\ \hfill & =-k_{m_a}{m}_a+R\left(c_a\right)(k_{\mathit{mb}}\mathit{bm}+k_{\mathit{mc}}\mathit{cm}+k_{\mathit{md}}\mathit{dm})\hfill \\ \hfill \frac{\partial c}{\partial t}-\nabla & \cdot D_c\nabla c=-k_{c}c+R\left(c_a\right)(k_{{\mathit{cm}}_a}{m}_a+k_{{\mathit{cn}}_a}{n}_a)-R\left(c_a\right)(k_{\mathit{nc}}\mathit{cn}+k_{\mathit{mc}}\mathit{cm})\hfill \\ \hfill \frac{\partial c_a}{\partial t}-\nabla & \cdot D_{\mathit{ca}}\nabla c_a=-k_{c_a}{c}_a+s_{c_a}+k_{c_{a}p}\frac{Q}{k_{c_a}Q+Q}\hfill \\ \hfill \frac{\partial \mathit{NO}}{\partial t}-\nabla & \cdot D_{\mathit{NO}}\nabla \mathit{NO}=-k_{\mathit{NO}}\mathit{NO}+k_{\mathit{NO}{m}_a}\frac{m_{q1}^a}{1+{(m_a∕{\stackrel{‒}{m}}_a)}^{q1}}\hfill \\ \hfill & +k_{{\mathit{NOn}}_a}\frac{n_{q1}^a}{1+{(n_a∕{\stackrel{‒}{n}}_a)}^{q1}}\hfill \\ \hfill \frac{\partial \mathit{ZO}1}{\partial t}=& \left(k_{{\mathit{Ze}}_c}{e}_c+k_{{\mathit{Ze}}_{\mathit{ct}}}\frac{\partial e_c}{\partial t}\right){\mathrm{ZO}1}_{\mathit{max}}(1-\mathit{ZO}1∕\mathit{zec})-k_{\mathit{ZN}}\mathit{NO}\cdot \mathit{ZO}1\hfill \\ \hfill & \mathit{zec}=(1-{∊}_{\mathit{zec}})\mathit{ZO}{1}_{\mathit{max}}+{∊}_{\mathit{zec}}(\mathit{ZO}{1}_{\mathit{max}}∕e_{c,\mathit{max}})e_c\hfill \\ \hfill \frac{\partial n_a}{\partial t}-\nabla & \cdot (D_{n_a}\nabla n_a-{\gamma }_{n_{a}c}{n}_a\nabla c)\hfill \\ \hfill & =-k_{n_a}{n}_a+R\left(c_a\right)(k_{\mathit{nc}}\mathit{cn}+k_{\mathit{nd}}\mathit{dn})\hfill \\ \hfill \frac{\partial d}{\partial t}-\nabla & \cdot D_d\nabla d--k_{d}d+k_{\mathit{dc}}\frac{T^{q2}}{x_{\mathit{dc}}^{q_2}+T^{q_2}}\hfill \\ \hfill & T=R\left(c_a\right)c,Q=R\left(c_a\right)(k_{c_a{m}_a{n}_a}{n}_a+m_a+k_{c_a{m}_{a}d}d)\hfill \\ \hfill & R\left(c_a\right)=\frac{1}{1+k_{{\mathit{Rc}}_a}{(c_a∕{\stackrel{‒}{c}}_a)}^2},h(a,b,q)=\frac{a^q}{a^q+{(b-a)}^q}\hfill \end{array}$$