Abstract
Longer target-to-target intervals (TTI) produce greater P300 event-related potential amplitude, which can increase brain–computer interface (BCI) classification accuracy and decrease the number of flashes needed for accurate character classification. However, longer TTIs requires more time for each trial, which will decrease the information transfer rate of BCI. In this paper, a P300 BCI using a 7 × 12 matrix explored new flash patterns (16-, 18- and 21-flash pattern) with different TTIs to assess the effects of TTI on P300 BCI performance. The new flash patterns were designed to minimize TTI, decrease repetition blindness, and examine the temporal relationship between each flash of a given stimulus by placing a minimum of one (16-flash pattern), two (18-flash pattern), or three (21-flash pattern) non-target flashes between each target flashes. Online results showed that the 16-flash pattern yielded the lowest classification accuracy among the three patterns. The results also showed that the 18-flash pattern provides a significantly higher information transfer rate (ITR) than the 21-flash pattern; both patterns provide high ITR and high accuracy for all subjects.
Keywords: Brain–computer interface, Target to target interval, P300, Flash pattern
1 Introduction
Brain–computer interface systems (BCIs) provide a new channel for disabled patients to convey messages and commands. A variety of methods have enabled individuals to control devices and convey messages through BCIs using slow cortical potentials (SCPs) [3], motor imagery [4, 5, 7, 13, 27], steady-state visual evoked potentials (SSVEPs) [13, 35] and P300 potentials [8]. Each type of BCI device has advantages over others for specific functions. P300 BCIs are functionally superior to other BCIs for users attempting to convey verbal information as they offer comparably greater information transfer rate (ITR). The ITR, given in bits per trial, is used as an evaluation measurement in a BCI [26]. Although ITR is an objective measure of performance, when comparing across different paradigms and the value of the information provided at a given ITR, it can be a problematic measure if it is used exclusively [28, 29, 32-34].
The P300 BCI was first described by Farwell and Donchin [8]. P300 BCI paradigms typically present a matrix of characters aligned in rows and columns. Users are required to select characters by focusing their attention to a target character that is either internally derived (e.g., in the case of what is called free-spelling) or ‘copied’ from a set of pre-defined characters. Although P300 BCIs offer excellent ITR relative to other BCI approaches, there remain unexplored opportunities to further improve ITR. Improving classification accuracy for P300 BCI remains a primary focus of many researchers [1]. Applying advanced signal processing and machine learning algorithms to existing P300 BCIs can lead to increased classification accuracy [10, 11, 15, 19, 21, 23, 36]. Modifying the typical P300 BCI paradigm can lead to improvements in the signal-to-noise ratio of P300 s. Indeed, studies have demonstrated higher classification accuracy by increasing the matrix size [2, 16, 17, 30, 33], varying the order of flash sequences [17, 34], varying the stimulus onset asynchrony (SOA) [23, 30], and varying the stimulus rate [25, 33].
While unstudied in the context of BCIs, evidence suggests that longer target-to-target intervals (TTI) produce higher P300 amplitude. TTI is the interval between the start of a target event and the start of another target event. Gonsalvez and Polich [9] reported that P300 amplitude increases with increasing TTI up to about 6–8 s. Martens et al. [24] demonstrated that increasing TTI reduces amplitude attenuation from overlapping P300 potentials, which significantly increases the classification accuracy.
Flashing twice in succession may decrease P300 BCI performance, as the second flash might generate a small P300 or might not even be fully processed due to the “repetition blindness”, repetition blindness is a perceptual phenomenon that can occur when two identical targets are presented in a stream of non-targets at intervals of less than 500 ms [31]. Moreover, short TTIs will lead to epoch “overlaps” which can have a negative impact on the performance of the P300 BCI system [24].
In this paper, TTI was controlled by placing a minimum of one (16-flash pattern), two (18-flash pattern) and three (21-flash pattern) non-target flashes between two target flashes. The goal of this design was to decrease the “repetition blindness” and “overlaps” [18], and search the efficient TTI.
2 Methods
2.1 Experiment set up and stimulus parameters
Experiments were performed according to a protocol approved by the institutional medical ethical committee. All subjects signed an informed consent document before participating in the experiment. Nine healthy subjects (five males and four females; age range 21–27) were recruited from East China University of Science and Technology to participate in the study. All subjects had not previously used a BCI. Electroencephalography (EEG) was recorded using a g.USBamp and a g.EEGcap (Guger Technologies, Graz, Austria) with a sensitivity of 100 μV, band-pass filtered between 0.1 and 30 Hz, and sampled at 256 Hz. EEG electrodes positioned at Fz, Cz, Pz, Oz, C3, C4, P3, P4, P7, P8, O1, and O2 from the extended International 10-20 system. The right mastoid electrode was used as the reference, and the front electrode (FPz) was used as a ground.
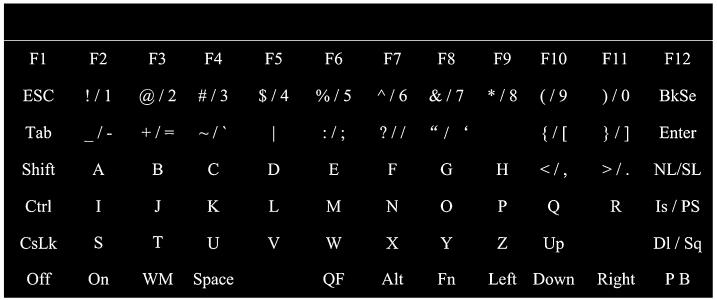
After EEG cap preparation, subjects were seated comfortably in front of an LCD screen and instructed to minimize movement during EEG recordings. Instructions were to focus on a single target character of 7 × 12 matrix of characters (see Fig. 1) and silently count each time that character flashed.
Fig. 1.
The stimulus screen presented to the subject during the experiment
Each subject participated in one experimental session. Sessions were divided into three offline and three online blocks. Each block consisted of one presentation condition (16-, 18-, and 21-flash patterns, described below) randomly ordered for each subject. Offline blocks included 15 character selections and online blocks included 15 selections. Offline data were used to train the signal classifier using Bayesian linear discriminant analysis (BLDA) and obtain the classifier model (see Sect. 2.5) for use in the online blocks.
Each target character was selected from a predefined set of 15 characters. A trial is defined as the number of flashes presented to the subject before a classification decision is made. In offline conditions, feedback was not presented after each trial, because, a subject-specific classifier was not yet created. At the start of each trial, a cue was presented (1 s) to inform the subject which character to focus on. Each flash was presented for 100 ms, followed by a 75 ms delay during which the grey character matrix stayed visible on the LCD. In the online experiment, a copy-spelling task of 15 trials per-block was conducted for each of the three flash patterns. Time for the subjects to select the location of the character was increased to 2 s. The number flashes were adaptively selected by the system, and after the classifier model reached criterion the character selected by the BLDA model was shown to the subject as feedback.
During offline testing, there were 32 flashes of each character in the matrix at each trial. Each block consisted of five trials, each of which involved a different target character. During online testing, the number of flashes per trial was variable, because, the system adjusted this number to optimize performance as described in part 2.5.
Three conditions were tested (“16-flash pattern”, “18-flash pattern” and “21-flash pattern” conditions). For each condition, subjects participated in three offline blocks of 16 trials. Subjects had 5-min rest between each condition in the offline experiment, and the order of conditions was random. After the offline experiment, three online blocks were completed for each condition. Presentation order of the conditions in the online experiment was the same as the offline experiment. In the online experiment, subjects had 2-min rest between each of the three conditions. The online and offline experiment were done within the same day for each subject.
2.2 Laptop keyboard design
Figure 1 shows the display used in this study. We simulated a keyboard using a 7 × 12 matrix. Function keys were arranged on the four sides of the matrix. To decrease interference from adjacent characters, the names of special keys were abbreviated. The goal of this design is to make it easy for users to find target characters and control the laptop. The items contained in the matrix allow for full-keyboard emulation (to be used in future studies). In the current study, only the alphanumeric items were selected.
2.3 The flash pattern design
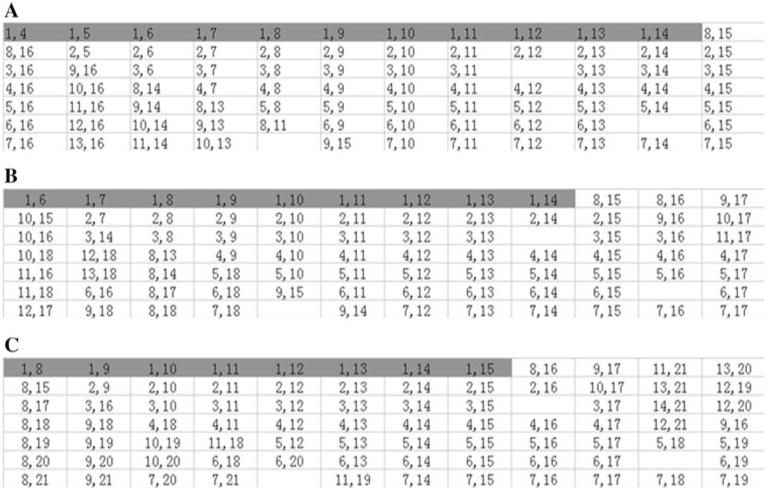
The flash pattern approaches presented here are based on binomial coefficients. The set of k combinations of a set n is denoted by C(n,k) = n!/(k!(n – k)!), 0 ≤ k ≤ n. The number of flashes per trial is n, and k is the number of flashes per trial for each character [17, 18]. In this paper, a 7 × 12 matrix containing 81 characters were used to simulate a laptop keyboard (See Fig. 1). To place a minimum of one (minimum TTI is 350 ms, 16-flash pattern), two (minimum TTI is 525 ms, 18-flash pattern) and three (minimum TTI is 700 ms, 21-flash pattern) non-target flashes between two target flashes and make the flash pattern of each trial random, we used the set of k combinations (k = 2) from set n (n = {16,18,21}, which is the lower limit to achieve these settings when k = 2). C(16, 2), C(18, 2) and C(21, 2) denote the 16-, 18- and 21-flash patterns, respectively. There are n (n = {16, 18, 21}) flash groups which are tagged as “flash1, flash2, …, flashn”. We did not choose k > 2, since k cannot be very high, because, the number of characters that flash at the same time depends on k; increasing k will increase interference from characters neighboring the target when the target is not flashing [18].
Although the order in which flashes are presented is random, the P300 speller system is limited by the settings of minimum TTIs. It is extremely unlikely that a subject would be able to detect the patterns of pseudo-randomized flashing due to the large number of stimulus combinations. To realize the minimum TTIs, when one flash (flash A) occurred, the next flash would not contain any character from flash A for 16-flash pattern, the next two flashes for the 18-flash pattern, and the next three flashes for the 21-flash pattern. Figure 2 shows the configuration of the different flash pattern combinations. In each flash pattern, stimuli are not grouped in rows or columns. For example, the character “F1” would be selected if flash1 and flash4 evoked a P300 in the 16-flash pattern (see Figs. 1, 2a). However, in the 18-flash pattern condition, “F1” would be selected if flash1 and flash6 evoked a P300 (see Figs. 1, 2b).
Fig. 2.
These three panels depict the configuration of different flash patterns: 16-flash pattern (a), 18-flash pattern (b) and 21-flash pattern (c). The numbers indicate which of the n flashes would illuminate the target character. For example, the top left element of panel A would be illuminated during the first and fourth of the 16 flashes. In each panel, flash1 is illuminated (grey part)
We did not use other patterns with less flashes in each trial and longer SOA (SOA = 350, 525, 700 ms) to realize these minimum TTIs. The reason is as follows: based on binomial coefficients, 14-flash pattern also can identify 81 elements in 7 × 12 matrix, since C(14,2) = 91. However, the time to completed all flashes in a trial is 4.9 s (14 × 350 ms, minimum TTI is 350 ms), 7.35 s (14 × 525 ms, minimum TTI is 525 ms), and 9.8 s (14 × 700 ms, minimum TTI is 700 ms). In the present method, the time to complete all flashes in a trial is 2.8 s (16 × 175 ms, minimum TTI is 350 ms), 3.15 s (18 × 175 ms, minimum TTI is 525 ms), and 3.675 s (21 × 175 ms, minimum TTI is 700 ms). Thus, the present method provides a more efficient presentation time and should improve ITR, all things being equal.
2.4 Feature extraction procedure
A third-order Butterworth band-pass filter was used to filter the EEG between 0.1 Hz and 12 Hz. Although the P300 is primarily in the band 0.1–4 Hz [14], it can also be found in higher bands [20]. The EEG was down-sampled from 256 Hz to 36.6 Hz by selecting every seventh sample from the filtered EEG. EEG epochs of 800 ms were extracted from the data. The size of the feature vector was 12 × 29 (12 channels by 29 time points).
2.5 Classification scheme and adaptive settings
Bayesian linear discriminant analysis is an extension of Fisher’s linear discriminant analysis that avoids problems such as overfitting the data [12]. Jin et al. [15] reported that BLDA out-performed LDA when used for classification of signals in a P300 BCI paradigm. Lei et al. [22] reported that BLDA, when they were applied to motor imagery classification, classified more accurately than LDA and SVM. Thus, BDLA was chosen as the classification algorithm for the present study. Depending on the condition, each trial yields 16, 18, or 21 classifier outputs, one output for one flash. The first and second maximum classifier outputs are selected to identify the target character.
The number of trials per average was automatically selected by the system based on the classifier output. To determine if enough evidence is present to select a given character, the classifier was required to select the same character two times in succession. For example, in the beginning, a character [named cha (1)] would be tagged as the likely target based on the first group of classifier outputs. Next, the first and second group of classifier outputs would be averaged and a character [named cha (2)] would be tagged as the likely target based on the averaged outputs. If cha (1) = cha (2), cha (2) trial would be completed and the selected target would be present to the subject as feedback. If it did not meet the criterion, more groups of classifier outputs would be averaged until cha (n) = cha (n – 1). When 16 groups of classifier outputs were used in the average, the output would be the result obtained from 16 average trials [18].
2.6 Practical bit rate
We used two bit rate calculation methods: the practical bit rate and raw bit rate. The analyses of this paper are based on practical bit rate; we only present raw bit rate to facilitate comparisons with other studies. Practical bit rate can estimate the “actual” performance of the BCI system, because, it incorporates the fact that every error results in a penalty of two additional selections. The practical bit rate is calculated by BR × (1 – 2P), where BR is the raw bit rate and P is the online error rate of the system [34]. If P ≥ 50%, the classification accuracy is very low to correct mistakes and the practical bit rate is, therefore, zero.
3 Results
In this paper, TTI was controlled by placing a minimum of one (16-flash pattern), two (18-flash pattern) and three (21-flash pattern) non-target flashes between two target flashes.
3.1 Online results
The online results were used to evaluate the performance of three flash patterns. Table 1 shows the accuracy of online feedback using adaptive strategy. A one-way ANOVA was used to examine the differences in accuracy of feedback among 16-, 18-, and 21-flash patterns (F = 5.58, p < 0.01). The 21-flash and 18-flash patterns yielded significantly higher accuracy than the 16-flash pattern (F = 8.4, p < 0.05; F = 5.3, p < 0.05); however, the difference between 18- and 21-flash pattern did not reach statistical significant (F = 0.3, p = 0.59).
Table 1.
Accuracy of online feedback
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|
| 16-P | ||||||||||
| Acc (%) | 73.2 | 93.3 | 86.7 | 73.3 | 80.0 | 93.3 | 66.7 | 93.3 | 93.3 | 83.7 ± 10.6 |
| ATV | 2.7 | 2.6 | 2.9 | 3.0 | 2.6 | 2.7 | 3.3 | 2.9 | 4.0 | 3.0 ± 0.4 |
| 18-P | ||||||||||
| Acc (%) | 100 | 93.3 | 93.3 | 93.3 | 100 | 86.7 | 80.0 | 100 | 93.3 | 93.3 ± 6.7 |
| ATV | 3.7 | 3.1 | 3.0 | 3.6 | 2.3 | 2.5 | 3.0 | 3.1 | 2.9 | 3.0 ± 0.4 |
| 21-P | ||||||||||
| Acc (%) | 100 | 93.3 | 93.3 | 93.3 | 100 | 93.3 | 86.7 | 100 | 93.3 | 94.8 ± 4.4 |
| ATV | 3.1 | 2.9 | 3.3 | 3.4 | 2.1 | 3.1 | 3.3 | 3.0 | 2.7 | 3.0 ± 0.4 |
“n-p” (n = {16, 18, 21}) corresponds to the 16-, 18- and 21-flash pattern
Acc Classification accuracy, ATV average trials for average of each subject
From Table 1, the 16-flash pattern showed the lowest performance and was most unstable. Statistical significance was not obtained between the 18- and 21-flash patterns in accuracy of online feedback.
Next, the practical and raw bit rates of the 18- and 21-flash patterns were compared. Table 2 shows the online raw bit rate and practical bit rate for 18- and 21-flash pattern using adaptive strategy. The selection time (2 s) of target characters for subjects was included in calculating the Pbr and Br. Raw bit rate calculated with selection time was used to show the online information transfer rate of P300 BCIs which use other error-correction methods [6] except “Backspace”. The average raw bit rate shows the bit rate assuming error correction. In Table 2, the average raw bit rate and average practical bit rate from subjects 1–9 for the 18-flash pattern are higher than those for the 21-flash pattern. Student’s t tests were used to examine differences in raw bit rate and practical bit rate between 18- and 21-flash patterns. The 18-flash pattern yielded significantly higher raw bit rate (p < 0.01) than practical bit rate (p < 0.05). Thus, users are able to finish a task more quickly using the 18-flash pattern than using the 21-flash pattern.
Table 2.
Online raw bit rate and practical bit rate for 18- and 21-flash pattern
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|
| 18-P | ||||||||||
| Br | 28.1 | 31.5 | 29.2 | 25.0 | 40.7 | 29.6 | 22.8 | 32.0 | 30.3 | 29.9 ± 5.0 |
| Pbr | 28.1 | 27.3 | 25.3 | 21.7 | 40.7 | 21.7 | 13.7 | 32.0 | 26.2 | 26.3 ± 7.5 |
| 21-P | ||||||||||
| Br | 28.1 | 26.1 | 23.8 | 23.03 | 39.6 | 24.7 | 21.1 | 29.2 | 28.3 | 27.1 ± 5.4 |
| Pbr | 28.1 | 22.6 | 20.7 | 19.9 | 40.0 | 21.4 | 15.4 | 29.2 | 24.5 | 24.6 ± 7.1 |
“n-p” (n = {18, 21}) corresponds to the 18- and 21-flash pattern. The bit rates are measured in bits/min. The selection time (2 s) of target characters for subjects was included in calculating the Pbr and Br
Pbr practical bit rate, Br raw bit rate
3.2 Offline performance analysis
In the offline analysis, TTI distributions of three patterns and grand waveform for electrode locations (Fz, Cz, Pz, Oz, O1, O2, P7, P8, P3, P4, C3 and C4) are shown in Figs. 3, 4, respectively.
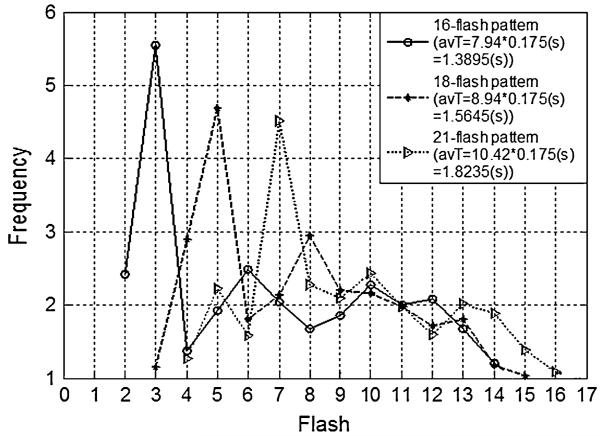
Fig. 3.
Average TTI distribution of 16-, 18- and 21-flash patterns in each run for nine subjects. TTI = flash duration × 0.175 s. The X-axis represents the number of flashes used to calculate TTI. The Y-axis is the frequency of the TTIs in each run. avT is the average TTI of each pattern. avT = (average number of flashes) × 0.175 s. To show the TTI distribution clearly, the frequencies that are ≥1 are shown
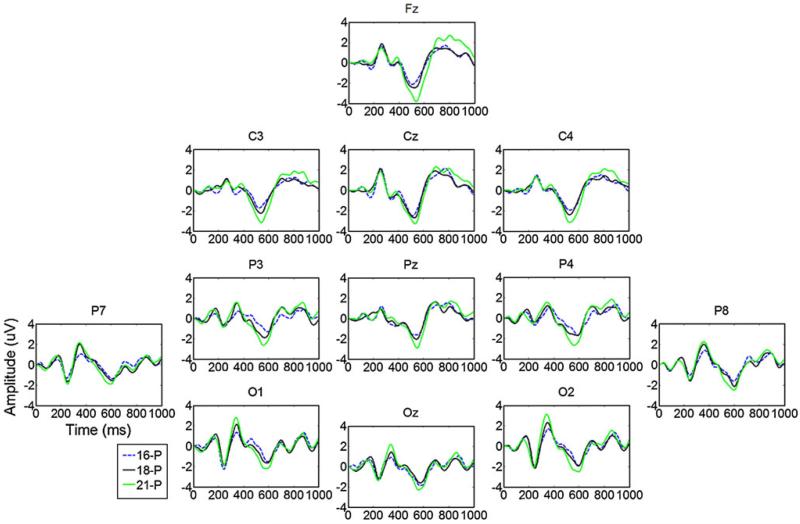
Fig. 4.
Grand averages waveforms for 16-, 18- and 19-flash patterns at electrode sites Fz, Cz, Pz, Oz, O1, O2, P7, P8, P3, P4, C3 and C4. 16-P is 16-flash pattern, 18-P is 18-flash pattern and 21-P is 21-flash pattern
Figure 3 shows average TTI of the 16-flash pattern is shortest (1.3895 s) and average TTI of 21-flash pattern is longest (1.8235 s). Figure 4 shows the grand average P300 amplitude of the 21-flash pattern is the greatest. However, these two patterns (16- and 21-flash pattern) did not obtain the best performance, since an efficient TTI should be selected when considering P300 magnitude and the time necessary to obtain the desired output.
3.3 Offline waveform analysis
A one-way ANOVA was used to examine differences in P300 waveforms ranged from 300–450 ms among 16-, 18-, and 21-flash patterns (p < 0.01 for electrode sites: Pz, Oz, O1, O2, P7 and P8; p < 0.05 for electrode sites: Cz). It shows that the P300 waveforms for the 16-flash pattern is significantly lower than the 18-flash pattern (p < 0.01 for electrode sites: Oz, P7 and P8; p < 0.05 for electrode sites: Cz). The 16-flash pattern is also significantly lower than the 21-flash pattern (p < 0.01 for electrode sites: Cz, Oz, O1, O2, P7 and P8; p < 0.05 for electrode sites: Cz).
4 Discussion
Target-to-target interval was examined by placing a minimum of one (16-flash pattern), two (18-flash pattern) and three (21-flash pattern) non-target flashes between two target flashes. Hill et al. [11] reported that the traditional row/column pattern (RC pattern) has particular spatial properties that lead to better performance than one would expect from its TTIs and Hamming-distances alone. Jin et al. [16, 17] reported that the flash pattern based on binomial coefficients yields better performance than RC pattern. The present method is based on binomial coefficients and to improve the performance of P300 speller by controlling minimum TTIs.
The 16-flash pattern, which has the shortest TTIs, resulted in the lowest classification accuracy of the three patterns. In contrast, the 18- and 21-flash patterns obtained high classification accuracy. These findings illustrate the deleterious effects of TTIs that are very short (see Fig. 3). The minimum TTI of the 16-flash pattern (350 ms) is apparently not long enough to avoid repetition blindness. This study has also demonstrated that the 18-flash pattern with medium TTI rate obtained the highest ITR. These results illustrate the importance of properly selecting TTI (see Fig. 3). Moreover, TTI has a significant effect on the resulting P300 amplitude and signal to noise ratio (see Fig. 4).
Previous studies have demonstrated that the 16-flash pattern is superior to a RC flash pattern [17]. Therefore, a RC comparison condition was not used in the present study. The goal of this paper was to determine the most efficient TTI in terms of BCI speed and accuracy.
Currently, the literature has not agreed upon standard metrics for performance. Many articles present bit rate based only on the amount of time that the system is flashing, what we refer to here as “raw bit rate.” Bit rate calculated in this fashion ignores the time that is necessary between each trial. Although in a real-world setting, these breaks are needed to evaluate feedback, determine what the next selection should be, and then attend to the appropriate location in the display. Therefore, many studies report unrealistically high performance, in terms of bit rate [23, 32, 34]. Here, we have presented practical bit rates and raw bit rates to estimate an ecologically valid representation of P300 BCI performance.
This paper examined and determined an efficient TTI for the P300 BCI. We have shown that an SOA of 525 ms is the most efficient SOA when using the binomial coefficient methods proposed here. User performance is better and more target flashes are detected presumably, because, repetition blindness has been reduced or removed. As the present study relies on manually derived binomial coefficients, future work should examine other possible methods to determine efficient TTI.
Acknowledgements
This work was supported in part by the Grant National Natural Science Foundation of China, under Grant No.61074113 and supported part by Shanghai Leading Academic Discipline Project, Project Number: B504, NIBIB & NINDS, NIH (EB00856), NIDCD, NIH (1 R21 DC010470-01), NIDCD, NIH (1 R15 DC011002-01), and Fundamental Research Funds for the Central Universities, WH1114038, WH0914028.
Contributor Information
Jing Jin, Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education, East China University of Science and Technology, Shanghai 200237, People’s Republic of China.
Eric W. Sellers, Brain–Computer Interface Laboratory, Department of Psychology, East Tennessee State University, 37614 Johnson, TN, USA
Xingyu Wang, Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education, East China University of Science and Technology, Shanghai 200237, People’s Republic of China.
References
- 1.Allison BZ, Neuper C. Could anyone use a BCI? (B + H)CI: the human in brain-computer interfaces and the brain in human–computer interaction. Springer; 2010. pp. 35–54. [Google Scholar]
- 2.Allison BZ, Pineda JA. Effects of SOA and flash pattern manipulations on ERPs, performance, and preference: implications for a BCI system. Int J Psychophysiol. 2006;59(2):127–140. doi: 10.1016/j.ijpsycho.2005.02.007. [DOI] [PubMed] [Google Scholar]
- 3.Birbaumer N, Ghanayim N, Hinterberger T, Iversen I, Kotchoubey B, Kuber A, Perelmouter J, Taub E, Flor H. A spelling device for the paralysed. Nature. 1999;388:297–298. doi: 10.1038/18581. [DOI] [PubMed] [Google Scholar]
- 4.Boord P, Craig A, Tran Y, Nguyen H. Discrimination of left and right leg motor imagery for brain-computer interfaces. Med Biol Eng Comput. 2010;48(4):343–350. doi: 10.1007/s11517-010-0579-0. [DOI] [PubMed] [Google Scholar]
- 5.Brunner C, Billinger M, Vidaurre C, Neuper C. A comparison of univariate, vector, bilinear autoregressive, and band power features for brain-computer interface. Med Biol Eng Comput. 2011;49(11):1337–1346. doi: 10.1007/s11517-011-0828-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dal Seno, Matteucci M, Mainardil L. Online detection of P300 and error potentials in a BCI speller. Comput Intell Neurosci. 2010:307254. doi: 10.1155/2010/307254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dias NS, Kamrunnahar M, Mendes PM, Schiff SJ, Correia JH. Feature selection on movement imagery discrimination and attention detection. Med Biol Eng Comput. 2010;48(4):331–341. doi: 10.1007/s11517-010-0578-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Farwell LA, Donchin E. Talking off the top of your head: toward a mental prosthesis utilizing event-related brain potentials. Electroencephalogr Clin Neurophysiol. 1988;70(6):510–523. doi: 10.1016/0013-4694(88)90149-6. [DOI] [PubMed] [Google Scholar]
- 9.Gonsalvez CL, Polich J. P300 amplitude is determined by target-to-target interval. Psychophysiology. 2002;39(3):388–396. doi: 10.1017/s0048577201393137. [DOI] [PubMed] [Google Scholar]
- 10.Guger C, Daban S, Sellers EW, Holzner C, Krausz G, Carabalona R, Gramatica F, Edlinger G. How many people are able to control a P300-based brain–computer interface (BCI) Neurosci Lett. 2009;462(1):94–98. doi: 10.1016/j.neulet.2009.06.045. [DOI] [PubMed] [Google Scholar]
- 11.Hill J, Farquhar J, Martens S, Bießmann F, Schölkopf B. Effects of stimulus type and of error-correcting code design on bci speller performance: NIPS [on line] 2008 http://books.nips.cc/papers/files/nips21/NIPS2008_0359.pdf.
- 12.Hoffmann U, Vesin JM, Ebrahimi T, Diserens K. An efficient P300-based brain–computer interface for disabled subjects. J Neurosci Meth. 2008;167(1):115–125. doi: 10.1016/j.jneumeth.2007.03.005. [DOI] [PubMed] [Google Scholar]
- 13.Horki P, Solis-Escalante T, Neuper C, Muller-Putz G. Combined motor imagery and SSVEP based BCI control of a DOF artificial upper limb. Med Biol Eng Comput. 2011;49(5):567–577. doi: 10.1007/s11517-011-0750-2. [DOI] [PubMed] [Google Scholar]
- 14.Jansen BH, Allam A, Kota P, Lachance K, Osho A, Sundarean K. An exploratory study of factors affecting single trial P300 detection. IEEE Trans Biomed Eng. 2004;51(6):975–978. doi: 10.1109/TBME.2004.826684. [DOI] [PubMed] [Google Scholar]
- 15.Jin J, Allison BZ, Brunner C, Wang B, Wang XY, Zhang JH, Neuper C, Pfurtscheller G. P300 Chinese imput system based on bayesian LDA. Biomed Tech. 2010;55(1):5–18. doi: 10.1515/BMT.2010.003. [DOI] [PubMed] [Google Scholar]
- 16.Jin J, Horki P, Brunner C, Wang XY, Neuper C, Pfurtscheller G. A new P300 stimulus presentation pattern for EEG-based spelling systems. Biomed Tech. 2010;55(4):203–210. doi: 10.1515/BMT.2010.029. [DOI] [PubMed] [Google Scholar]
- 17.Jin J, Allison BZ, Sellers EW, Brunner C, Horki P, Wang XY, Neuper C. Optimized stimulus presentation patterns for an event-related potential EEG-based brain computer interface. Med Biol Eng Comput. 2011;49(2):181–191. doi: 10.1007/s11517-010-0689-8. [DOI] [PubMed] [Google Scholar]
- 18.Jin J, Allison BZ, Sellers EW, Brunner C, Horki P, Wang XY, Neuper C. Adaptive P300 based control system. J Neural Eng. 2011;8(3):036006. doi: 10.1088/1741-2560/8/3/036006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jung TP, Makeig S, Westerfield M, Townsend J, Courchesne E, Sejnowski TJ. Analysis and visualization of single-trial event-related potentials. Hum Brain Mapp. 2001;14(3):166–185. doi: 10.1002/hbm.1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kolev V, Demiralp T, Yordanova J, Ademoglu A, Isoglu-Alkaç U. Time-frequency analysis reveals multiple functional components during oddball P300. NeuroReport. 1997;8(8):2061–2065. doi: 10.1097/00001756-199705260-00050. [DOI] [PubMed] [Google Scholar]
- 21.Krusienski DJ, Sellers EW, McFarland DJ, Vaughan TM, Wolpaw JR. Toward enhanced P300 speller performance. J Neurosci Meth. 2008;167(1):15–21. doi: 10.1016/j.jneumeth.2007.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lei X, Yang P, Yao DZ. An empirical bayesian framework for brain computer interface. IEEE Trans Neural Syst Rehabil Eng. 2009;17(6):521–529. doi: 10.1109/TNSRE.2009.2027705. [DOI] [PubMed] [Google Scholar]
- 23.Lenhardt A, Kaper M, Ritter HJ. An adaptive P300-based online brain–computer interface. IEEE Trans Neural Syst Rehabil Eng. 2008;16(2):121–130. doi: 10.1109/TNSRE.2007.912816. [DOI] [PubMed] [Google Scholar]
- 24.Martens SMM, Hill NJ, Farquhar J, Scholkopf B. Overlap and refractory effects in a brain–computer interface speller based on the visual P300 event-related potential. J Neural Eng. 2009;6(2):026003. doi: 10.1088/1741-2560/6/2/026003. [DOI] [PubMed] [Google Scholar]
- 25.McFarland DJ, Sarnacki WA, Townsend G, Vaughan T, Wolpaw JR. The P300-based brain–computer interface (BCI): effects of stimulus rate. Clin Neurophysiol. 2011;122(4):731–737. doi: 10.1016/j.clinph.2010.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Obermaier B, Neuper C, Guger C, Pfurtscheller G. Information transfer rate in a five-classes brain–computer interface. IEEE Trans Neural Syst Rehabil Eng. 2001;9(3):283–288. doi: 10.1109/7333.948456. [DOI] [PubMed] [Google Scholar]
- 27.Pfurtscheller G, Neuper C. Motor imagery and direct brain-computer communication. Proc IEEE. 2001;89(7):1123–1134. [Google Scholar]
- 28.Quitadamo LR, Marciani MG, Cardarilli GC, Bianchi L. Describing different brain computer interface systems through a unique model: a UML implementation. Neuroinformatics. 2008;6(2):81–96. doi: 10.1007/s12021-008-9015-0. [DOI] [PubMed] [Google Scholar]
- 29.Quitadamo LR, Abbafati M, Cardarilli GC, Mattia D, Cincotti F, Babiloni F, Marciani MG, Bianchi L. Evaluation of the performance of different P300 based brain-computer interface by means of the efficiency metric. J Neurosci Methods. 2012;203(2):361–368. doi: 10.1016/j.jneumeth.2011.10.010. [DOI] [PubMed] [Google Scholar]
- 30.Salvaris M, Sepulveda F. Visual modifications on the P300 speller BCI paradigm. J Neural Eng. 2009;6(4):046011. doi: 10.1088/1741-2560/6/4/046011. [DOI] [PubMed] [Google Scholar]
- 31.Salvaris M, Sepulveda F. Perceptual Errors in the Farwell and Donchin Matrix Speller; 4th international conference IEEE/EMBS Antalya; 2009.Apr, pp. 275–78. [Google Scholar]
- 32.Sellers EW, Donchin E. A P300-based brain-computer interface: initial tests by ALS patients. Clin Neurophysiol. 2006;117(3):538–548. doi: 10.1016/j.clinph.2005.06.027. [DOI] [PubMed] [Google Scholar]
- 33.Sellers EW, Krusienski DJ, McFarland DJ, Vaughan TM, Wolpaw JR. A P300 event-related potential brain–computer interface (BCI): the effects of matrix size and inter stimulus interval on performance. Biol Psychol. 2006;73(3):242–252. doi: 10.1016/j.biopsycho.2006.04.007. [DOI] [PubMed] [Google Scholar]
- 34.Townsend G, LaPallo BK, Boulay CB, Krusienski DJ, Frye GE, Hauser CK, Schwartz NE, Vaughan TM, Wolpaw JR, Sellers EW. A novel P300-based brain-computer interface stimulus presentation paradigm: moving beyond rows and columns. Clin Neurophysiol. 2010;121(7):1109–1120. doi: 10.1016/j.clinph.2010.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vidal jj. Toward direct brain-computer communication. Annu Rev Biophs Bioeng. 1973;2:157–180. doi: 10.1146/annurev.bb.02.060173.001105. [DOI] [PubMed] [Google Scholar]
- 36.Xu N, Gao XR, Hong B, Miao XB, Gao SK, Yang FH. BCI competition 2003: data Set IIb: Enhancing P300 wave detection using ICA based subspace projections for BCI applications. IEEE Trans Biomed Eng. 2004;51(6):1067–1072. doi: 10.1109/TBME.2004.826699. [DOI] [PubMed] [Google Scholar]